Đề thi HK2 Toán 12 năm học 2016 – 2017 trường THPT Quốc Oai – Hà Nội

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2016 – 2017 .Mời bạn đọc đón xem.

14 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

44 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Trang 1 / mã đề 235
Trường THPT Quốc Oai ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2016 -2017
Môn: Toán ; thời gian 90 phút; mã đề 235
(đề gồm 50 câu trắc nghiệm)
Họ và tên thí sinh:………………………………………………….. số báo danh:…………
C©u 1 :
Đặt
3
1
1
x
dx
I
e
và
1
x
te
. Khẳng định nào trong các khẳng định sau là sai :
A.
3
1
1
11
1
e
e
I dt
tt




B.
x
dt e dx
3
1
11
1
I dt
tt




D.
2
ln 1 2I e e
C©u 2 :
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Biết hình chóp có chiều cao là
3ha
. Thể tích khối chóp là :
A.
3
3Va
B.
3
3
3
a
V
3
3
8
a
V
D.
3
3
a
V
C©u 3 :
Trong không gian với hệ tọa độ
Oxyz
, cho 3 điểm
1;2;3A
,
0;1;1B
,
1;0; 2C
và mặt phẳng
P
có phương trình
20 x y z
. Gọi
M
là điểm thuộc mặt phẳng
P
sao cho giá trị biểu
thức
2 2 2
23 T MA MB MC
nhỏ nhất. Tính khoảng cách từ
M
đến mặt phẳng
: 2 2 3 0 Q x y z
A.
25
3
B.
121
54
24
D.
91
54
C©u 4 :
Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Một mặt phẳng đi qua A’B’
và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Thể tích V của khối A’B’.BAEF là :
A.
3
3
27
a
V
B.
3
23
27
a
V
3
3
18
a
V
D.
3
53
54
a
V
C©u 5 :
Bất phương trình
󰇛

󰇜

có tập nghiệm là :
A.
󰇛

󰇜
B.
󰇛

󰇜
󰇛

󰇜
D.
C©u 6 :
Cho hình chóp đều S.ABCD có AB = a , mặt bên (SAD) tạo với đáy (ABCD) một góc
60
o
. Tính thể
tích V của khối chóp S.ABCD ?
A.
3
2Va
B.
3
3
6
a
V
3
3
2
a
V
D.
3
3
3
a
V
C©u 7 :
Cho hàm số

khẳng định nào sau đây là sai ?
A.
Hàm số đồng biến trên R
B.
Hàm số nghịch biến trên R
C.
Đồ thị hàm số nằm toàn bộ phía trên trục ox
D.
Tập xác định của hàm số là R
C©u 8 :
Cho hàm số
42
25y x x
. Chọn khẳng định đúng?
A.
Hàm số đồng biến trên khoảng
1;0
và
(1; )
B.
Hàm số nghịch biến trên khoảng
;1
và
(1; )
C.
Hàm số nghịch biến trên khoảng
1;0
và
(1; )
D.
Hàm số đồng biến trên khoảng
1;1
C©u 9 :
Trong các số phức thỏa mãn điều kiện
12z z i
là số thực. Hãy tìm
z
có mô đun nhỏ nhất
Trang 2 / mã đề 235
A.
24
55
Zi
B.
24
55
Zi
24
55
Zi
D.
42
55
Zi
C©u 10 :
Trong không gian với hệ tọa độ
Oxyz
, tìm
m
để phương trình
2 2 2
2 2( 2) 2( 3) 8 37 0x y z mx m y m z m
là phương trình của một mặt cầu
A.
24m hay m
B.
42m hay m
C.
42m hay m
D.
24m hay m
C©u 11 :
Điểm biểu diễn của các số phức
7z bi
với
b
, nằm trên đường thẳng có phương trình là:
A.
yx
B.
7yx
7y
D.
7x
C©u 12 :
Cho (P) là đồ thị hàm số
2
45y x x
. Diện tích hình phẳng giới hạn bởi (P) và các tiếp tuyến của
(P) kẻ từ điểm
5
;1
2
A



là :
A.
18
4
B.
9
2
9
4
D.
9
8
C©u 13 :
Tìm hàm số F(x) biết
3
4 6 1F x x x
và đồ thị hàm số
y F x
cắt trục tung tại điểm có tung
độ bằng 2:
A.
42
31F x x x x
B.
3
2F x x x
C.
42
32F x x x x
D.
42
4 6 2F x x x x
C©u 14 :
Cho hàm số
2
1x mx
y
xm

. Tìm m để hàm số đạt cực đại tại
2x
? Một học sinh làm như sau:
Bước 1:
22
2
21
\ , '
x mx m
D R m y
xm
Bước 2: Hàm số đạt cực đại tại
2 '(2) 0 *xy
Bước 3:
2
1
* 4 3 0
3
m
mm
m


Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào?
A.
Sai từ bước 2
B.
Sai từ bước 3
Sai từ bước 1
D.
Đúng
C©u 15 :
Số đường tiệm cận của đồ thị hàm số
1
21
x
y
x
là:
A.
2
B.
1
3
D.
0
C©u 16 :
Cho điểm
2,1,0M
và đường thẳng
11
:
2 1 1
x y z
. Gọi
d
là đường thẳng đi qua
M
, cắt và
vuông góc với
. Khi đó, vectơ chỉ phương của
d
là:
A.
3;0;2u
B.
2; 1;2u
0;3;1u
D.
1; 4; 2u
C©u 17 :
Đường thẳng
6y x m
là tiếp tuyến của đường cong
3
31y x x
khi m bằng
A.
-3 hoặc 1
B.
-5 hoặc 1
-1 hoặc 3
D.
3 hoặc -5
C©u 18 :
Diện tích hình phẳng giới hạn bởi các đường
2
1 ; 0; 0; 2y x y x x
bằng :
A.
35
B.
15
2
3
D.
21
C©u 19 :
Một nhà kho có dạng khối hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB
= a, BC = 2a, chiều cao AA’ = 3a, chắp thêm một khối lăng trụ tam giác đều mà một mặt bên là
A’B’C’D’ và A’B’ là một cạnh đáy của lăng trụ. Tính thể tích của nhà kho ?
Trang 3 / mã đề 235
A.
3
36 3
6
a
B.
3
12 3
2
a
3
3
2
a
D.
3
3 12 3
2
a
C©u 20 :
Cho hàm số
3
3y x x m
(m là thàm số). Để giá trị lớn nhất của hàm số trên đoạn
0; 3


bằng
32
thì m phải bằng:
A.
22
B.
2
2
D.
32
C©u 21 :
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
1
x
y
x
trên đoạn
2;0
lần lượt là:
A.
1
3
và -1
B.
1
3
và -1
3 và -1
D.
0 và -1
C©u 22 :
Đạo hàm của hàm số

là :
A.



B.

󰇛
󰇜



C.

󰇛

󰇜



D.

󰇛
󰇜


C©u 23 :
Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
2
4 ; 0y x y
xung quanh trục Ox là :
A.
2
B.
71
82
512
15
D.
8
3
C©u 24 :
Biết 
, giá trị biểu thức 


là :
A.
󰇛

󰇜
B.
󰇛

󰇜

D.
C©u 25 :
Số phức
3
1zi
có mô đun bằng:
A.
0z
B.
22z 
22z
D.
2z
C©u 26 :
Mệnh đề nào sau đây sai ?
A.
Mặt phẳng
:4 2 3 0P x y
song song với mặt phẳng
: 2 5 0Q x y
.
B.
Mặt phẳng
3 – 2 0xz
có tọa độ vectơ pháp tuyến là
3,0, 1
.
C.
Mặt phẳng
2 3 – 2 0x y z
đi qua gốc tọa độ.
D.
Khoảng cách từ điểm
0 0 0
,,M x y z
đến mặt phẳng
2 2 1 0x y z
là
0 0 0
2 2 1
3
x y z
.
C©u 27 :
Cho số phức
z a bi
. Khi đó số
1
2
zz
là:
A.
2
B.
i
Một số thuần ảo
D.
Một số thực.
C©u 28 :
Hàm số
32
1
32
3
y x x x
đạt cực tiểu tại:
A.
1x
B.
3x 
1
3
x
D.
0x
C©u 29 :
Giá trị của m để phương trình
3
4 3 1x x mx m
có 4 nghiệm phân biệt là :
A.
1;6 3 9m
B.
9 6 3; 1m
C.
6 3 9;6 3 9m
D.
9 6 3;1m
C©u 30 :
Tập nghiệm của bất phương trình  
󰇛
󰇜
là :
Trang 4 / mã đề 235
A.
󰇛

󰇜
B.
󰇛

󰇜
󰇛

󰇜
󰇝

󰇞
D.
󰇛

󰇜
󰇝

󰇞
C©u 31 :
Phương trình 
󰇛

󰇜
 
Có 2 nghiệm x
1,
x
2
thỏa mãn 

 khi :
A.
B.



D.
C©u 32 :
Phương trình tham số của đường thẳng
d
đi qua điểm
1,2,3M
và có vec tơ chỉ phương
(1;3;2)a
là :
A.
1
23
32
xt
yt
zt
B.
1
23
32
xt
yt
zt
1
23
32
xt
yt
zt


D.
1
23
32
xt
yt
zt



C©u 33 :
G
ọi
1
z
là nghiệm phức có phần ảo âm của phương trình
2
2 3 0zz
. Tọa độ điểm
M
biểu diễn
số phức
1
z
là:
A.
( 1; 2 )Mi
B.
( 1; 2)M 
( 1;2)M
D.
( 1; 2)M 
C©u 34 :
Cho
22
11
3; 1f x dx g t dt

. Giá trị của
2
1
23A f x g x dx


là:
A.
9
B.
5
3
D.
2
C©u 35 :
Số nghiêm của phương trình
4
1z
là
A.
2
B.
1
3
D.
4
C©u 36 :
Biết
2
3
1
ln
ln2
x a c
dx
x b d

với a,b,c,d là các số nguyên dương và
;
ac
bd
là các phân số tối giản. Giá
trị của
M ad bc
là :
A.
10
B.
40
8
D.
32
C©u 37 :
Phương trình tiếp tuyến với đồ thị hàm số
32
( ) 3 2y f x x x
tại điểm
0
x
sao cho
0
"( ) 0fx
là:
A.
3 3 0xy
B.
3 3 0xy
3 3 0xy
D.
3 3 0xy
C©u 38 :
Cho hàm số
()y f x
có đồ thị (C) như hình vẽ.
Số nghiệm phân biệt của phương trình
( ) 1fx
là:
A.
2
B.
3
1
D.
0
C©u 39 :
Khẳng định nào sau đây là sai ?
A.
 
B.



D.
 
C©u 40 :
Trong không gian với hệ tọa độ
Oxyz
, cho
2;3;1a 
,
1; 3; 4b 
. Tìm
;ab


A.
171
B.
315
171
D.
315
C©u 41 :
Cho hình trụ có độ dài đường sinh là b và bán kính đường tròn đáy là a. Diện tích toàn phần của
hình trụ là :
Trang 5 / mã đề 235
A.
2
tp
S a b a

B.
2
tp
S a b a

22
tp
S a b a

D.
tp
S a b a

C©u 42 :
Cho hàm số
32
1
( 1) 4
3
y x m x x
(m là thàm số). Giá trị của m để hàm số đã cho nghịch biến
trên R là:
A.
13m
B.
mR
3m
D.
1
3
m
m

C©u 43 :
Nguyên hàm hàm số
sin 2 1f x x
là :
A.
1
cos2
2
f x dx x C
B.
1
cos 2 1
2
f x dx x C
C.
1
cos 2 1
2
f x dx x C
D.
1
cos2
2
f x dx x C
C©u 44 :
Một hình nón có bán kính đáy
3ra
, chiều cao
4ha
. Kí hiệu góc ở đỉnh của hình nón là
2
.
Trong các mệnh đề sau, mệnh đề nào đúng ?
A.
4
sin
5
B.
4
cos
5
C.
D.
4
cot
5
C©u 45 :
Phương trình

có 2 nghiệm phân biệt khi :
A.
B.

D.


C©u 46 :
Tập xác định của hàm số
󰇛

󰇜
là :
A.
󰇛

󰇜
B.
󰇛

󰇜
󰇛

󰇜
󰇛

󰇜
󰇝

󰇞
D.
󰇟

󰇠
C©u 47 :
Một cốc nước có dạng hình trụ đựng nước, chiều cao 16cm, đường kính đáy 6cm, lượng nước trong
cốc cao 10cm. Thả vào cốc nước 4 viên bi có cùng đường kính 4cm. Hỏi nước dâng cao cách mép
cốc bao nhiêu cm ? ( làm tròn sau dấu phẩy hai chữ số thập phân, bỏ qua độ dày cốc ).
A.
1,34cm
B.
1,26cm
1,68cm
D.
1,43cm
C©u 48 :
Trong không gian với hệ tọa độ
Oxyz
, cho
1;2; 1 ,a 
3;4;3b
. Tìm tọa độ của
x
biết
x b a
A.
1;1;2 .x
B.
2; 2;4 .x
2; 2; 4 .x
D.
2;2;4 .x
C©u 49 :
Cho hàm số

khẳng định nào dưới đây là đúng ?
A.
Đồ thị hàm số không có tiệm cận
B.
Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm
cận đứng
C.
Đồ thị hàm số có 1 tiệm cận đứng và không có
tiệm cận ngang
D.
Đồ thị hàm số cắt trục ox
C©u 50 :
Khối đa diện đều loại
3;5
có số mặt là :
A.
20
B.
16
12
D.
8
-----------------------------------------------------Hết------------------------------------------------
Trang 1/ mã đề 239
Trường THPT Quốc Oai ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2016 -2017
Môn: Toán ; thời gian 90 phút; mã đề 239
(đề gồm 50 câu trắc nghiệm)
Họ và tên thí sinh:………………………………………………….. số báo danh:…………
C©u 1 :
Bất phương trình 
󰇛

󰇜


có tập nghiệm là :
A.
󰇛

󰇜
󰇛

󰇜
B.
󰇛

󰇜
D.
C©u 2 :
Đường thẳng
9y x m
là tiếp tuyến của đường cong
32
31y x x
khi m bằng
A.
-6 hoặc 26
B.
-1 hoặc 3
-3 hoặc 1
D.
3 hoặc -5
C©u 3 :
Phương trình tiếp tuyến với đồ thị hàm số
32
( ) 3 2y f x x x
tại điểm
0
x
sao cho
0
"( ) 6fx
là:
A.
20y 
B.
3 3 0xy
20y 
D.
3 3 0xy
C©u 4 :
Cho số phức
54zi
. Số phức
2z
có
A.
Phần thực bằng
3
và phần ảo bằng
4i
.
B.
Phần thực bằng
4
và phần ảo bằng
3
.
C.
Phần thực bằng
5
và phần ảo bằng
4
.
D.
Phần thực bằng
3
và phần ảo bằng
4
.
C©u 5 :
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
x
y
x
trên đoạn
1;3
lần lượt là:
A.
3
4
và
1
2
B.
1
3
và -1
3 và -1
D.
0 và -1
C©u 6 :
Diện tích hình phẳng giới hạn bởi các đường
2
2 ; 0; 1; 3y x y x x
bằng :
A.
21
B.
30
98
3
D.
18
C©u 7 :
Khẳng định nào sau đây là sai ?
A.

B.



D.

C©u 8 :
Phương trình 
󰇛

󰇜
 
Có 2 nghiệm x
1,
x
2
thỏa mãn
khi :
A.

B.
D.
C©u 9 :
Cho hàm số
khẳng định nào dưới đây là đúng ?
A.
Đồ thị hàm số cắt trục ox
B.
Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm
cận đứng
C.
Đồ thị hàm số không có tiệm cận
D.
Đồ thị hàm số có 1 tiệm cận đứng và không có
tiệm cận ngang
C©u 10 :
Một cốc nước có dạng hình trụ đựng nước, chiều cao 12cm, đường kính đáy 4cm, lượng nước trong
cốc cao 8cm. Thả vào cốc nước 4 viên bi có cùng đường kính 2cm. Hỏi nước dâng cao cách mép cốc
bao nhiêu cm ? ( làm tròn sau dấu phẩy hai chữ số thập phân, bỏ qua độ dày cốc ).
A.
2,75cm
B.
2,67cm
2,33cm
D.
2,25cm
C©u 11 :
Cho hai số phức
1
23zi
,
2
12zi
. Tính môđun của số phức
12
2z z z
.
A.
65z
B.
15z
137z
D.
55z
C©u 12 :
Cho hàm số
32
1
( 1) 4
3
y x m x x
(m là thàm số). Giá trị của m để hàm số đã cho đồng biến trên
R là:
A.
Không có giá trị
nào của m thỏa
B.
mR
13m
D.
3m
Trang 2/ mã đề 239
mãn
C©u 13 :
Trong không gian với hệ trục tọa độ
Oxyz
, cho hình hộp
.ABCD A B C D
. Biết
3;2;1A
,
4;2;0C
,
2;1;1B
,
3;5;4D
.Tìm tọa độ
A
của hình hộp
.ABCD A B C D
.
A.
3; 3; 3 .A

B.
3; 3;3 .A

3;3;1 .A
D.
3;3;3 .A
C©u 14 :
Tìm hàm số F(x) biết
2
3 2 1F x x x
và đồ thị hàm số
y F x
cắt trục tung tại điểm có tung
độ bằng e:
A.
32
1F x x x x
B.
2
1F x x x e
C.
32
F x x x x e
D.
2
2F x x x
C©u 15 :
Cho hai số phức
12
, zz
thỏa mãn
12
1zz
,
12
3zz
. Tính
12
zz
:
A.
3
B.
2
4
D.
1
C©u 16 :
Trong các số phức
z
tìm điều kiện :
23z i z i
. Hãy tìm z có mô đun nhỏ nhất
A.
27 6
55
zi
B.
6 27
55
zi
6 27
55
zi
D.
36
55
zi
C©u 17 :
Tập xác định của hàm số
󰇛

󰇜
là :
A.
󰇛

󰇜
B.
󰇛

󰇜
󰇛

󰇜
󰇛

󰇜
󰇝

󰇞
D.
󰇟

󰇠
C©u 18 :
Cho hàm số


khẳng định nào sau đây là sai ?
A.
Đồ thị hàm số nằm toàn bộ phía trên trục ox
B.
Hàm số đồng biến trên R
C.
Hàm số nghịch biến trên R
D.
Tập xác định của hàm số là R
C©u 19 :
Phương trình

có 2 nghiệm phân biệt khi :
A.


B.

D.
C©u 20 :
Trong không gian với hệ tọa độ
Oxyz
, cho điểm
(2;1;0)M
và đường thẳng : .
Viết phương trình của đường thẳng d đi qua điểm M, cắt và vuông góc với .
A.
d:
21
.
1 4 1
x y z

B.
d:
21
.
2 4 1
x y z

C.
d:
21
.
1 4 1
x y z

D.
d:
21
.
1 4 2
x y z


C©u 21 :
Trong không gian với hệ tọa độ
Oxyz
. Hãy viết phương trình mặt cầu (S) có tâm
(2;0;1)I
và tiếp
xúc với đường thẳng d:
12
1 2 1
x y z

.
A.
2 2 2
( 2) ( 1) 4.x y z
B.
2 2 2
( 2) ( 1) 9.x y z
C.
2 2 2
( 1) ( 2) ( 1) 24.x y z
D.
2 2 2
( 2) ( 1) 2.x y z
C©u 22 :
Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
(2;4;1)A
,
( 1;1;3)B
và mặt phẳng
( :)P
3 2 5 0x y z
. Viết phương trình mặt phẳng
Q
đi qua hai điểm A, B và vuông góc với mặt
phẳng
P
.
A.
:2 3 1 0Q y z
B.
:2 3 12 0Q y z
C.
:2 3 11 0Q x z
D.
:2 3 11 0Q y z
C©u 23 :
Đặt
2
2
2
3
1
dx
I
xx
và
2
1tx
. Khẳng định nào trong các khẳng định sau là sai :
x y z11
2 1 1


Trang 3/ mã đề 239
A.
tdt xdx
B.
1
2
1
3
1
dt
I
t
2
2
2
3
1
dt
I
t
D.
22
1xt
C©u 24 :
Cho hàm số
3
3y x x m
(m là thàm số). Để giá trị lớn nhất của hàm số trên đoạn
0; 3


bằng
52
thì m phải bằng:
A.
42
B.
2
22
D.
32
C©u 25 :
Cho hình chóp đều S.ABCD có AC = 2a , mặt bên (SBC) tạo với đáy (ABCD) một góc
45
o
. Tính
thể tích V của khối chóp S.ABCD ?
A.
3
23
3
a
V
B.
3
2
3
a
V
3
2Va
D.
3
2
a
V
C©u 26 :
Cho hàm số
2
1x mx
y
xm

. Tìm m để hàm số đạt cực đại tại
2x
? Một học sinh làm như sau:
Bước 1:
22
2
21
\ , '
x mx m
D R m y
xm
Bước 2: Hàm số đạt cực đại tại
2 '(2) 0 *xy
Bước 3:
2
1
* 4 3 0
3
m
mm
m


Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào?
A.
Sai từ bước 1
B.
Đúng
Sai từ bước 2
D.
Sai từ bước 3
C©u 27 :
Biết
3
2
1
3 ln 1
ln
( 1)
x a c
dx
x b b d

với a,b,c,d là các số nguyên dương và
;
ac
bd
là các phân số tối giản.
Giá trị của
M ac bd
là :
A.
145
B.
20
17
D.
11
C©u 28 :
Nguyên hàm hàm số
cos 3 2f x x
là :
A.
1
sin3
3
f x dx x C
B.
1
sin 3 2
3
f x dx x C
C.
1
sin 3 2
3
f x dx x C
D.
1
sin3
3
f x dx x C
C©u 29 :
Đạo hàm của hàm số

là :
A.

󰇛
󰇜



B.

󰇛

󰇜



C.



D.
󰇛 󰇜

C©u 30 :
Trong không gian với hệ tọa độ
Oxyz
, cho 3 điểm
2;2;3A
,
1; 1;3B
,
3;1; 1C
và mặt phẳng
P
có phương trình
2 8 0xz
. Gọi
M
là điểm thuộc mặt phẳng
P
sao cho giá trị biểu hức
2 2 2
23T MA MB MC
nhỏ nhất. Tính khoảng cách từ
M
đến mặt phẳng
: 2 2 6 0Q x y z
A.
3
2
d
B.
2
3
3
d
D.
4
C©u 31 :
Cho phương trình
2
2 3 0zz
trên tập số phức,có hai nghiệm là
12
,zz
.Khi đó
22
12
zz
có giá trị
là:
Trang 4/ mã đề 239
A.
3
B.
22
2
D.
6
C©u 32 :
Cho
1;0; 3 ; 2;1;2ab
.Khi đó
;ab


có giá trị là
A.
4
B.
8
3
D.
74
C©u 33 :
Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a. Biết hình chóp có chiều cao là
3ha
.
Thể tích khối chóp là :
A.
3
3
4
a
V
B.
3
4
a
V
3
3
a
V
D.
3
3
8
a
V
C©u 34 :
Một nhà kho có dạng khối hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB
= 3m, BC = 6m, chiều cao AA’ = 3m, chắp thêm một khối lăng trụ tam giác đều mà một mặt bên là
A’B’C’D’ và A’B’ là một cạnh đáy của lăng trụ. Tính thể tích của nhà kho ?
A.
3
27 3
2
m
B.
3
27 4 3
2
m
3
54m
D.
3
9 12 3
2
m
C©u 35 :
Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Một mặt phẳng đi qua A’B’
và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Thể tích V của khối C.A’B’FE là :
A.
3
3
27
a
V
B.
3
53
54
a
V
3
53
18
a
V
D.
3
53
27
a
V
C©u 36 :
Tập nghiệm của bất phương trình  
󰇛
󰇜
là :
A.
󰇛

󰇜
B.
󰇛

󰇜
󰇛

󰇜
󰇝
󰇞
D.
󰇛

󰇜
󰇝
󰇞
C©u 37 :
Khối đa diện đều loại
5;3
có số mặt là :
A.
12
B.
14
8
D.
10
C©u 38 :
Giá trị của m để phương trình
3
4 3 1x x mx m
có 4 nghiệm phân biệt là :
A.
9 6 3; 1m
B.
9 6 3;1m
C.
1;6 3 9m
D.
6 3 9;6 3 9m
C©u 39 :
Biết 
, giá trị biểu thức






là :
A.
B.
󰇛
󰇜
D.
󰇛
󰇜
C©u 40 :
Số đường tiệm cận của đồ thị hàm số
1
y
x
là:
A.
2
B.
3
1
D.
0
C©u 41 :
Cho hình trụ có độ dài đường sinh là l và bán kính đường tròn đáy là r. Diện tích toàn phần của hình
trụ là :
A.
2
tp
S r l r

B.
tp
S r l r

2
tp
S r l r

D.
22
tp
S r l r

C©u 42 :
Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
2
9 ; 0y x y
xung quanh trục Ox là :
A.
71
82
B.
3
1296
5
D.
8
3
C©u 43 :
Cho hàm số
32
33y x x
. Chọn khẳng định sai?
Trang 5/ mã đề 239
A.
Hàm số không có cực trị
B.
Hàm số nghịch biến trên khoảng
0;2
C.
Hàm số đồng biến trên khoảng
;0
và
(2; )
D.
Hàm số có hai điểm cực trị
C©u 44 :
Cho số phức
32zi
. Tìm số phức
2
1w z i z
A.
35wi
B.
35wi
78wi
D.
78wi
C©u 45 :
Hàm số
42
2y x x
có điểm cực tiểu là:
A.
0x
B.
1x
2y
D.
1x 
C©u 46 :
Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
có
1;3;4A
,
2;3;0B
,
1; 3;2C 
.
Tìm tọa độ trọng tâm
G
của tam giác
ABC
.
A.
2
;1;1 .
3
G



B.
2;1;2 .G
2
;1;2 .
3
G



D.
2
;2;2 .
3
G



C©u 47 :
Một hình nón có bán kính đáy
1r
, chiều cao
4
3
h
. Kí hiệu góc ở đỉnh của hình nón là
2
.
Trong các mệnh đề sau, mệnh đề nào đúng ?
A.
3
cot
5
B.
3
sin
5
3
tan
5
D.
3
cos
5
C©u 48 :
Cho hàm số
()y f x
có đồ thị (C) như hình vẽ.
Số nghiệm phân biệt của phương trình
1
()
2
fx
là:
A.
3
B.
2
1
D.
0
C©u 49 :
Cho (P) là đồ thị hàm số
2
43y x x
. Diện tích hình phẳng giới hạn bởi (P) và các tiếp tuyến của
(P) kẻ từ điểm
2; 5A
là :
A.
32
3
B.
8
3
16
3
D.
10
3
C©u 50 :
Cho
33
22
2; 3f x dx g t dt

. Giá trị của
3
2
32A f x g x dx


là:
A.
0
B.
-1
12
D.
5
--------------------------------------------------------------Hết----------------------------------------------------------
Trang 1/ mã đề 236
Trường THPT Quốc Oai ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2016 -2017
Môn: Toán ; thời gian 90 phút; mã đề 236
(đề gồm 50 câu trắc nghiệm)
Họ và tên thí sinh:………………………………………………….. số báo danh:…………
C©u 1 :
Trong không gian với hệ tọa độ
Oxyz
, cho
1;2; 1 ,a 
3;4;3b
. Tìm tọa độ của
x
biết
x b a
A.
1;1;2 .x
B.
2; 2; 4 .x
2; 2;4 .x
D.
2;2;4 .x
C©u 2 :
Trong không gian với hệ tọa độ
Oxyz
, cho
2; 3;1a 
,
1; 3; 4b 
. Tìm
;ab


A.
171
B.
315
171
D.
315
C©u 3 :
Đường thẳng
6y x m
là tiếp tuyến của đường cong
3
31y x x
khi m bằng
A.
3 hoặc -5
B.
-3 hoặc 1
-5 hoặc 1
D.
-1 hoặc 3
C©u 4 :
Cho hàm số

khẳng định nào sau đây là sai ?
A.
Hàm số nghịch biến trên R
B.
Tập xác định của hàm số là R
C.
Hàm số đồng biến trên R
D.
Đồ thị hàm số nằm toàn bộ phía trên trục ox
C©u 5 :
Cho hàm số
32
1
( 1) 4
3
y x m x x
(m là thàm số). Giá trị của m để hàm số đã cho nghịch biến
trên R là:
A.
mR
B.
3m
1
3
m
m

D.
13m
C©u 6 :
G
ọi
1
z
là nghiệm phức có phần ảo âm của phương trình
2
2 3 0zz
. Tọa độ điểm
M
biểu diễn
số phức
1
z
là:
A.
( 1; 2)M 
B.
( 1; 2 )Mi
( 1; 2)M 
D.
( 1;2)M
C©u 7 :
Cho hàm số
3
3y x x m
(m là thàm số). Để giá trị lớn nhất của hàm số trên đoạn
0; 3


bằng
32
thì m phải bằng:
A.
32
B.
22
2
D.
2
C©u 8 :
Một cốc nước có dạng hình trụ đựng nước, chiều cao 16cm, đường kính đáy 6cm, lượng nước trong
cốc cao 10cm. Thả vào cốc nước 4 viên bi có cùng đường kính 4cm. Hỏi nước dâng cao cách mép
cốc bao nhiêu cm ? ( làm tròn sau dấu phẩy hai chữ số thập phân, bỏ qua độ dày cốc ).
A.
1,34cm
B.
1,68cm
1,43cm
D.
1,26cm
C©u 9 :
Tập nghiệm của bất phương trình  
󰇛
󰇜
là :
A.
󰇛

󰇜
B.
󰇛

󰇜
󰇛

󰇜
󰇝

󰇞
D.
󰇛

󰇜
󰇝

󰇞
C©u 10 :
Phương trình

có 2 nghiệm phân biệt khi :
A.
B.


D.

C©u 11 :
Cho hình trụ có độ dài đường sinh là b và bán kính đường tròn đáy là a. Diện tích toàn phần của
hình trụ là :
A.
22
tp
S a b a

B.
2
tp
S a b a

tp
S a b a

D.
2
tp
S a b a

C©u 12 :
Cho (P) là đồ thị hàm số
2
45y x x
. Diện tích hình phẳng giới hạn bởi (P) và các tiếp tuyến của
Trang 2/ mã đề 236
(P) kẻ từ điểm
5
;1
2
A



là :
A.
9
4
B.
18
4
9
2
D.
9
8
C©u 13 :
Khẳng định nào sau đây là sai ?
A.
 
B.
 

D.


C©u 14 :
Đạo hàm của hàm số

là :
A.



B.

󰇛
󰇜



C.

󰇛

󰇜



D.

󰇛
󰇜


C©u 15 :
Mệnh đề nào sau đây sai ?
A.
Mặt phẳng
3 – 2 0xz
có tọa độ vectơ pháp tuyến là
3,0, 1
.
B.
Khoảng cách từ điểm
0 0 0
,,M x y z
đến mặt phẳng
2 2 1 0x y z
là
0 0 0
2 2 1
3
x y z
.
C.
Mặt phẳng
2 3 – 2 0x y z
đi qua gốc tọa độ.
D.
Mặt phẳng
:4 2 3 0P x y
song song với mặt phẳng
: 2 5 0Q x y
.
C©u 16 :
Cho hình chóp đều S.ABCD có AB = a , mặt bên (SAD) tạo với đáy (ABCD) một góc
60
o
. Tính thể
tích V của khối chóp S.ABCD ?
A.
3
3
6
a
V
B.
3
2Va
3
3
2
a
V
D.
3
3
3
a
V
C©u 17 :
Cho số phức
z a bi
. Khi đó số
1
2
zz
là:
A.
2
B.
i
Một số thực.
D.
Một số thuần ảo
C©u 18 :
Biết
2
3
1
ln
ln2
x a c
dx
x b d

với a,b,c,d là các số nguyên dương và
;
ac
bd
là các phân số tối giản. Giá
trị của
M ad bc
là :
A.
10
B.
40
8
D.
32
C©u 19 :
Trong không gian với hệ tọa độ
Oxyz
, cho 3 điểm
1;2;3A
,
0;1;1B
,
1;0; 2C
và mặt phẳng
P
có phương trình
20 x y z
. Gọi
M
là điểm thuộc mặt phẳng
P
sao cho giá trị biểu
thức
2 2 2
23 T MA MB MC
nhỏ nhất. Tính khoảng cách từ
M
đến mặt phẳng
: 2 2 3 0 Q x y z
A.
91
54
B.
121
54
24
D.
25
3
C©u 20 :
Cho hàm số
2
1x mx
y
xm

. Tìm m để hàm số đạt cực đại tại
2x
? Một học sinh làm như sau:
Bước 1:
22
2
21
\ , '
x mx m
D R m y
xm
Bước 2: Hàm số đạt cực đại tại
2 '(2) 0 *xy
Bước 3:
2
1
* 4 3 0
3
m
mm
m


Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào?
A.
Sai từ bước 3
B.
Sai từ bước 2
Sai từ bước 1
D.
Đúng
Trang 3/ mã đề 236
C©u 21 :
Cho điểm
2,1,0M
và đường thẳng
11
:
2 1 1
x y z
. Gọi
d
là đường thẳng đi qua
M
, cắt và
vuông góc với
. Khi đó, vectơ chỉ phương của
d
là:
A.
0;3;1u
B.
1; 4; 2u
2; 1;2u
D.
3;0;2u
C©u 22 :
Hàm số
32
1
32
3
y x x x
đạt cực tiểu tại:
A.
3x 
B.
0x
1x
D.
1
3
x
C©u 23 :
Tìm hàm số F(x) biết
3
4 6 1F x x x
và đồ thị hàm số
y F x
cắt trục tung tại điểm có tung
độ bằng 2:
A.
42
32F x x x x
B.
3
2F x x x
C.
42
4 6 2F x x x x
D.
42
31F x x x x
C©u 24 :
Trong các số phức thỏa mãn điều kiện
12z z i
là số thực. Hãy tìm
z
có mô đun nhỏ nhất
A.
42
55
Zi
B.
24
55
Zi
24
55
Zi
D.
24
55
Zi
C©u 25 :
Trong không gian với hệ tọa độ
Oxyz
, tìm
m
để phương trình
2 2 2
2 2( 2) 2( 3) 8 37 0x y z mx m y m z m
là phương trình của một mặt cầu
A.
24m hay m
B.
42m hay m
C.
24m hay m
D.
42m hay m
C©u 26 :
Một nhà kho có dạng khối hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB
= a, BC = 2a, chiều cao AA’ = 3a, chắp thêm một khối lăng trụ tam giác đều mà một mặt bên là
A’B’C’D’ và A’B’ là một cạnh đáy của lăng trụ. Tính thể tích của nhà kho ?
A.
3
36 3
6
a
B.
3
12 3
2
a
3
3
2
a
D.
3
3 12 3
2
a
C©u 27 :
Nguyên hàm hàm số
sin 2 1f x x
là :
A.
1
cos 2 1
2
f x dx x C
B.
1
cos2
2
f x dx x C
C.
1
cos2
2
f x dx x C
D.
1
cos 2 1
2
f x dx x C
C©u 28 :
Một hình nón có bán kính đáy
3ra
, chiều cao
4ha
. Kí hiệu góc ở đỉnh của hình nón là
2
.
Trong các mệnh đề sau, mệnh đề nào đúng ?
A.
4
sin
5
B.
4
cot
5
4
tan
5
D.
4
cos
5
C©u 29 :
Diện tích hình phẳng giới hạn bởi các đường
2
1 ; 0; 0; 2y x y x x
bằng :
A.
35
B.
2
3
15
D.
21
C©u 30 :
Biết 
, giá trị biểu thức 


là :
A.

B.
󰇛

󰇜
󰇛

󰇜
D.
Trang 4/ mã đề 236
C©u 31 :
Khối đa diện đều loại
3;5
có số mặt là :
A.
12
B.
16
8
D.
20
C©u 32 :
Cho hàm số

khẳng định nào dưới đây là đúng ?
A.
Đồ thị hàm số không có tiệm cận
B.
Đồ thị hàm số có 1 tiệm cận đứng và không có
tiệm cận ngang
C.
Đồ thị hàm số cắt trục ox
D.
Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm
cận đứng
C©u 33 :
Cho
22
11
3; 1f x dx g t dt

. Giá trị của
2
1
23A f x g x dx


là:
A.
5
B.
9
3
D.
2
C©u 34 :
Phương trình tham số của đường thẳng
d
đi qua điểm
1,2,3M
và có vec tơ chỉ phương
(1;3;2)a
là :
A.
1
23
32
xt
yt
zt
B.
1
23
32
xt
yt
zt
1
23
32
xt
yt
zt



D.
1
23
32
xt
yt
zt


C©u 35 :
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
1
x
y
x
trên đoạn
2;0
lần lượt là:
A.
3 và -1
B.
1
3
và -1
1
3
và -1
D.
0 và -1
C©u 36 :
Bất phương trình
󰇛

󰇜

có tập nghiệm là :
A.
󰇛

󰇜
󰇛

󰇜
B.
󰇛

󰇜
D.
C©u 37 :
Điểm biểu diễn của các số phức
7z bi
với
b
, nằm trên đường thẳng có phương trình là:
A.
7x
B.
7yx
yx
D.
7y
C©u 38 :
Phương trình 
󰇛

󰇜
 
Có 2 nghiệm x
1,
x
2
thỏa mãn 

 khi :
A.
B.
D.



C©u 39 :
Số nghiêm của phương trình
4
1z
là
A.
2
B.
3
4
D.
1
C©u 40 :
Đặt
3
1
1
x
dx
I
e
và
1
x
te
. Khẳng định nào trong các khẳng định sau là sai :
A.
3
1
11
1
I dt
tt




B.
x
dt e dx
2
ln 1 2I e e
D.
3
1
1
11
1
e
e
I dt
tt




C©u 41 :
Phương trình tiếp tuyến với đồ thị hàm số
32
( ) 3 2y f x x x
tại điểm
0
x
sao cho
0
"( ) 0fx
là:
A.
3 3 0xy
B.
3 3 0xy
3 3 0xy
D.
3 3 0xy
C©u 42 :
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Biết hình chóp có chiều cao là
3ha
. Thể tích khối chóp là :
A.
3
3
3
a
V
B.
3
3Va
3
3
8
a
V
D.
3
3
a
V
C©u 43 :
Số đường tiệm cận của đồ thị hàm số
1
21
x
y
x
là:
Trang 5/ mã đề 236
A.
3
B.
2
1
D.
0
C©u 44 :
Tập xác định của hàm số
󰇛

󰇜
là :
A.
󰇛

󰇜
B.
󰇟

󰇠
󰇛

󰇜
󰇝

󰇞
D.
󰇛

󰇜
󰇛

󰇜
C©u 45 :
Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Một mặt phẳng đi qua A’B’
và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Thể tích V của khối A’B’.BAEF là :
A.
3
23
27
a
V
B.
3
53
54
a
V
3
3
27
a
V
D.
3
3
18
a
V
C©u 46 :
Số phức
3
1zi
có mô đun bằng:
A.
2z
B.
22z
22z 
D.
0z
C©u 47 :
Cho hàm số
()y f x
có đồ thị (C) như hình vẽ.
Số nghiệm phân biệt của phương trình
( ) 1fx
là:
A.
1
B.
3
2
D.
0
C©u 48 :
Giá trị của m để phương trình
3
4 3 1x x mx m
có 4 nghiệm phân biệt là :
A.
9 6 3;1m
B.
9 6 3; 1m
C.
1;6 3 9m
D.
6 3 9;6 3 9m
C©u 49 :
Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
2
4 ; 0y x y
xung quanh trục Ox là :
A.
71
82
B.
512
15
2
D.
8
3
C©u 50 :
Cho hàm số
42
25y x x
. Chọn khẳng định đúng?
A.
Hàm số đồng biến trên khoảng
1;0
và
(1; )
B.
Hàm số đồng biến trên khoảng
1;1
C.
Hàm số nghịch biến trên khoảng
;1
và
(1; )
D.
Hàm số nghịch biến trên khoảng
1;0
và
(1; )
-----------------------------------------------------------Hết------------------------------------------------------
Trang 1 / mã đề 240
Trường THPT Quốc Oai ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2016 -2017
Môn: Toán ; thời gian 90 phút; mã đề 240
(đề gồm 50 câu trắc nghiệm)
Họ và tên thí sinh:………………………………………………….. số báo danh:…………
C©u 1 :
Trong không gian với hệ tọa độ
Oxyz
. Hãy viết phương trình mặt cầu (S) có tâm
(2;0;1)I
và tiếp
xúc với đường thẳng d:
12
1 2 1
x y z

.
A.
2 2 2
( 2) ( 1) 4.x y z
B.
2 2 2
( 2) ( 1) 2.x y z
C.
2 2 2
( 2) ( 1) 9.x y z
D.
2 2 2
( 1) ( 2) ( 1) 24.x y z
C©u 2 :
Biết
3
2
1
3 ln 1
ln
( 1)
x a c
dx
x b b d

với a,b,c,d là các số nguyên dương và
;
ac
bd
là các phân số tối giản.
Giá trị của
M ac bd
là :
A.
145
20
C.
17
D.
11
C©u 3 :
Trong không gian với hệ tọa độ
Oxyz
, cho điểm
(2;1;0)M
và đường thẳng : .
Viết phương trình của đường thẳng d đi qua điểm M, cắt và vuông góc với .
A.
d:
21
.
1 4 1
x y z

B.
d:
21
.
1 4 2
x y z


C.
d:
21
.
2 4 1
x y z

D.
d:
21
.
1 4 1
x y z

C©u 4 :
Cho
33
22
2; 3f x dx g t dt

. Giá trị của
3
2
32A f x g x dx


là:
A.
-1
5
C.
0
D.
12
C©u 5 :
Cho số phức
32zi
. Tìm số phức
2
1w z i z
A.
35wi
35wi
C.
78wi
D.
78wi
C©u 6 :
Bất phương trình 
󰇛

󰇜


có tập nghiệm là :
A.
󰇛

󰇜
C.
D.
󰇛

󰇜
󰇛

󰇜
C©u 7 :
Nguyên hàm hàm số
cos 3 2f x x
là :
A.
1
sin3
3
f x dx x C
B.
1
sin 3 2
3
f x dx x C
C.
1
sin 3 2
3
f x dx x C
D.
1
sin3
3
f x dx x C
C©u 8 :
Một cốc nước có dạng hình trụ đựng nước, chiều cao 12cm, đường kính đáy 4cm, lượng nước trong
cốc cao 8cm. Thả vào cốc nước 4 viên bi có cùng đường kính 2cm. Hỏi nước dâng cao cách mép cốc
bao nhiêu cm ? ( làm tròn sau dấu phẩy hai chữ số thập phân, bỏ qua độ dày cốc ).
A.
2,67cm
2,25cm
C.
2,33cm
D.
2,75cm
C©u 9 :
Khẳng định nào sau đây là sai ?
A.



C.

D.

C©u 10 :
Cho phương trình
2
2 3 0zz
trên tập số phức,có hai nghiệm là
12
,zz
.Khi đó
22
12
zz
có giá trị
là:
x y z11
2 1 1


Trang 2 / mã đề 240
A.
3
22
C.
6
D.
2
C©u 11 :
Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
có
1;3;4A
,
2;3;0B
,
1; 3;2C 
.
Tìm tọa độ trọng tâm
G
của tam giác
ABC
.
A.
2
;1;1 .
3
G



2
;2;2 .
3
G



C.
2;1;2 .G
D.
2
;1;2 .
3
G



C©u 12 :
Cho hàm số
32
1
( 1) 4
3
y x m x x
(m là thàm số). Giá trị của m để hàm số đã cho đồng biến trên
R là:
A.
Không có giá trị
nào của m thỏa
mãn
3m
C.
13m
D.
mR
C©u 13 :
Cho (P) là đồ thị hàm số
2
43y x x
. Diện tích hình phẳng giới hạn bởi (P) và các tiếp tuyến của
(P) kẻ từ điểm
2; 5A
là :
A.
32
3
10
3
C.
8
3
D.
16
3
C©u 14 :
Giá trị của m để phương trình
3
4 3 1x x mx m
có 4 nghiệm phân biệt là :
A.
9 6 3;1m
B.
6 3 9;6 3 9m
C.
9 6 3; 1m
D.
1;6 3 9m
C©u 15 :
Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
(2;4;1)A
,
( 1;1;3)B
và mặt phẳng
( :)P
3 2 5 0x y z
. Viết phương trình mặt phẳng
Q
đi qua hai điểm A, B và vuông góc với mặt
phẳng
P
.
A.
:2 3 12 0Q y z
B.
:2 3 11 0Q y z
C.
:2 3 11 0Q x z
D.
:2 3 1 0Q y z
C©u 16 :
Cho hàm số
2
1x mx
y
xm

. Tìm m để hàm số đạt cực đại tại
2x
? Một học sinh làm như sau:
Bước 1:
22
2
21
\ , '
x mx m
D R m y
xm
Bước 2: Hàm số đạt cực đại tại
2 '(2) 0 *xy
Bước 3:
2
1
* 4 3 0
3
m
mm
m


Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào?
A.
Sai từ bước 2
Sai từ bước 1
C.
Đúng
D.
Sai từ bước 3
C©u 17 :
Phương trình 
󰇛

󰇜
 
Có 2 nghiệm x
1,
x
2
thỏa mãn
khi :
A.

C.
D.
C©u 18 :
Một hình nón có bán kính đáy
1r
, chiều cao
4
3
h
. Kí hiệu góc ở đỉnh của hình nón là
2
.
Trong các mệnh đề sau, mệnh đề nào đúng ?
Trang 3 / mã đề 240
A.
3
cos
5
3
cot
5
C.
3
tan
5
D.
3
sin
5
C©u 19 :
Một nhà kho có dạng khối hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB
= 3m, BC = 6m, chiều cao AA’ = 3m, chắp thêm một khối lăng trụ tam giác đều mà một mặt bên là
A’B’C’D’ và A’B’ là một cạnh đáy của lăng trụ. Tính thể tích của nhà kho ?
A.
3
27 3
2
m
3
54m
C.
3
27 4 3
2
m
D.
3
9 12 3
2
m
C©u 20 :
Phương trình tiếp tuyến với đồ thị hàm số
32
( ) 3 2y f x x x
tại điểm
0
x
sao cho
0
"( ) 6fx
là:
A.
20y 
3 3 0xy
C.
20y 
D.
3 3 0xy
C©u 21 :
Tập xác định của hàm số
󰇛

󰇜
là :
A.
󰇛

󰇜
󰇛

󰇜
󰇛

󰇜
C.
󰇛

󰇜
󰇝

󰇞
D.
󰇟

󰇠
C©u 22 :
Cho hình chóp đều S.ABCD có AC = 2a , mặt bên (SBC) tạo với đáy (ABCD) một góc
45
o
. Tính
thể tích V của khối chóp S.ABCD ?
A.
3
23
3
a
V
3
2
3
a
V
C.
3
2Va
D.
3
2
a
V
C©u 23 :
Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Một mặt phẳng đi qua A’B’
và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Thể tích V của khối C.A’B’FE là :
A.
3
3
27
a
V
3
53
18
a
V
C.
3
53
54
a
V
D.
3
53
27
a
V
C©u 24 :
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
x
y
x
trên đoạn
1;3
lần lượt là:
A.
3
4
và
1
2
1
3
và -1
C.
3 và -1
D.
0 và -1
C©u 25 :
Trong các số phức
z
tìm điều kiện :
23z i z i
. Hãy tìm z có mô đun nhỏ nhất
A.
27 6
55
zi
36
55
zi
C.
6 27
55
zi
D.
6 27
55
zi
C©u 26 :
Diện tích hình phẳng giới hạn bởi các đường
2
2 ; 0; 1; 3y x y x x
bằng :
A.
98
3
30
C.
18
D.
21
C©u 27 :
Trong không gian với hệ tọa độ
Oxyz
, cho 3 điểm
2;2;3A
,
1; 1;3B
,
3;1; 1C
và mặt phẳng
P
có phương trình
2 8 0xz
. Gọi
M
là điểm thuộc mặt phẳng
P
sao cho giá trị biểu hức
2 2 2
23T MA MB MC
nhỏ nhất. Tính khoảng cách từ
M
đến mặt phẳng
: 2 2 6 0Q x y z
A.
2
3
3
d
C.
4
D.
3
2
d
C©u 28 :
Cho số phức
54zi
. Số phức
2z
có
A.
Phần thực bằng
3
và phần ảo bằng
4
.
B.
Phần thực bằng
3
và phần ảo bằng
4i
.
C.
Phần thực bằng
5
và phần ảo bằng
4
.
D.
Phần thực bằng
4
và phần ảo bằng
3
.
C©u 29 :
Cho hàm số
3
3y x x m
(m là thàm số). Để giá trị lớn nhất của hàm số trên đoạn
0; 3


bằng
52
thì m phải bằng:
Trang 4 / mã đề 240
A.
2
42
C.
22
D.
32
C©u 30 :
Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a. Biết hình chóp có chiều cao là
3ha
.
Thể tích khối chóp là :
A.
3
3
4
a
V
3
3
8
a
V
C.
3
4
a
V
D.
3
3
a
V
C©u 31 :
Cho hàm số
()y f x
có đồ thị (C) như hình vẽ.
Số nghiệm phân biệt của phương trình
1
()
2
fx
là:
A.
2
1
C.
0
D.
3
C©u 32 :
Cho hai số phức
12
, zz
thỏa mãn
12
1zz
,
12
3zz
. Tính
12
zz
:
A.
4
1
C.
2
D.
3
C©u 33 :
Cho
1;0; 3 ; 2;1;2ab
.Khi đó
;ab


có giá trị là
A.
8
3
C.
74
D.
4
C©u 34 :
Số đường tiệm cận của đồ thị hàm số
1
y
x
là:
A.
1
3
C.
0
D.
2
C©u 35 :
Cho hai số phức
1
23zi
,
2
12zi
. Tính môđun của số phức
12
2z z z
.
A.
55z
137z
C.
15z
D.
65z
C©u 36 :
Tập nghiệm của bất phương trình  
󰇛
󰇜
là :
A.
󰇛

󰇜
󰇝
󰇞
󰇛

󰇜
C.
󰇛

󰇜
󰇝
󰇞
D.
󰇛

󰇜
C©u 37 :
Cho hình trụ có độ dài đường sinh là l và bán kính đường tròn đáy là r. Diện tích toàn phần của hình
trụ là :
A.
tp
S r l r

22
tp
S r l r

C.
2
tp
S r l r

D.
2
tp
S r l r

C©u 38 :
Trong không gian với hệ trục tọa độ
Oxyz
, cho hình hộp
.ABCD A B C D
. Biết
3;2;1A
,
4;2;0C
,
2;1;1B
,
3;5;4D
.Tìm tọa độ
A
của hình hộp
.ABCD A B C D
.
A.
3;3;3 .A
3; 3; 3 .A

C.
3;3;1 .A
D.
3; 3;3 .A

C©u 39 :
Khối đa diện đều loại
5;3
có số mặt là :
A.
14
10
C.
12
D.
8
C©u 40 :
Biết 
, giá trị biểu thức






là :
Trang 5 / mã đề 240
A.
C.
󰇛
󰇜
D.
󰇛
󰇜
C©u 41 :
Tìm hàm số F(x) biết
2
3 2 1F x x x
và đồ thị hàm số
y F x
cắt trục tung tại điểm có tung
độ bằng e:
A.
2
2F x x x
B.
32
F x x x x e
C.
2
1F x x x e
D.
32
1F x x x x
C©u 42 :
Đường thẳng
9y x m
là tiếp tuyến của đường cong
32
31y x x
khi m bằng
A.
-6 hoặc 26
-3 hoặc 1
C.
-1 hoặc 3
D.
3 hoặc -5
C©u 43 :
Phương trình

có 2 nghiệm phân biệt khi :
A.

C.


D.
C©u 44 :
Đặt
2
2
2
3
1
dx
I
xx
và
2
1tx
. Khẳng định nào trong các khẳng định sau là sai :
A.
tdt xdx
2
2
2
3
1
dt
I
t
C.
1
2
1
3
1
dt
I
t
D.
22
1xt
C©u 45 :
Cho hàm số
khẳng định nào dưới đây là đúng ?
A.
Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm
cận đứng
B.
Đồ thị hàm số không có tiệm cận
C.
Đồ thị hàm số cắt trục ox
D.
Đồ thị hàm số có 1 tiệm cận đứng và không có
tiệm cận ngang
C©u 46 :
Cho hàm số


khẳng định nào sau đây là sai ?
A.
Đồ thị hàm số nằm toàn bộ phía trên trục ox
B.
Hàm số đồng biến trên R
C.
Hàm số nghịch biến trên R
D.
Tập xác định của hàm số là R
C©u 47 :
Cho hàm số
32
33y x x
. Chọn khẳng định sai?
A.
Hàm số nghịch biến trên khoảng
0;2
B.
Hàm số đồng biến trên khoảng
;0
và
(2; )
C.
Hàm số có hai điểm cực trị
D.
Hàm số không có cực trị
C©u 48 :
Hàm số
42
2y x x
có điểm cực tiểu là:
A.
2y
1x 
C.
1x
D.
0x
C©u 49 :
Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
2
9 ; 0y x y
xung quanh trục Ox là :
A.
71
82
8
3
C.
3
D.
1296
5
C©u 50 :
Đạo hàm của hàm số

là :
A.



B.

󰇛
󰇜



C.

󰇛

󰇜



D.
󰇛 󰇜

--------------------------------------------------------Hết--------------------------------------------------
Trang 1/ mã đề 237
Trường THPT Quốc Oai ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2016 -2017
Môn: Toán ; thời gian 90 phút; mã đề 237
(đề gồm 50 câu trắc nghiệm)
Họ và tên thí sinh:………………………………………………….. số báo danh:…………
C©u 1 :
Phương trình 
󰇛

󰇜
 
Có 2 nghiệm x
1,
x
2
thỏa mãn 

 khi :
A.
B.
D.



C©u 2 :
Cho số phức
z a bi
. Khi đó số
1
2
zz
là:
A.
2
B.
Một số thực.
i
D.
Một số thuần ảo
C©u 3 :
Cho hàm số
()y f x
có đồ thị (C) như hình vẽ.
Số nghiệm phân biệt của phương trình
( ) 1fx
là:
A.
0
B.
3
1
D.
2
C©u 4 :
Phương trình tham số của đường thẳng
d
đi qua điểm
1,2,3M
và có vec tơ chỉ phương
(1;3;2)a
là :
A.
1
23
32
xt
yt
zt
B.
1
23
32
xt
yt
zt


1
23
32
xt
yt
zt



D.
1
23
32
xt
yt
zt
C©u 5 :
Đạo hàm của hàm số

là :
A.



B.

󰇛
󰇜



C.

󰇛

󰇜



D.

󰇛
󰇜


C©u 6 :
Mệnh đề nào sau đây sai ?
A.
Mặt phẳng
3 – 2 0xz
có tọa độ vectơ pháp tuyến là
3,0, 1
.
B.
Khoảng cách từ điểm
0 0 0
,,M x y z
đến mặt phẳng
2 2 1 0x y z
là
0 0 0
2 2 1
3
x y z
.
C.
Mặt phẳng
2 3 – 2 0x y z
đi qua gốc tọa độ.
D.
Mặt phẳng
:4 2 3 0P x y
song song với mặt phẳng
: 2 5 0Q x y
.
C©u 7 :
Một hình nón có bán kính đáy
3ra
, chiều cao
4ha
. Kí hiệu góc ở đỉnh của hình nón là
2
.
Trong các mệnh đề sau, mệnh đề nào đúng ?
A.
4
sin
5
B.
4
tan
5
4
cos
5
D.
4
cot
5
Trang 2/ mã đề 237
C©u 8 :
G
ọi
1
z
là nghiệm phức có phần ảo âm của phương trình
2
2 3 0zz
. Tọa độ điểm
M
biểu diễn
số phức
1
z
là:
A.
( 1; 2)M 
B.
( 1; 2)M 
( 1; 2 )Mi
D.
( 1;2)M
C©u 9 :
Biết
2
3
1
ln
ln2
x a c
dx
x b d

với a,b,c,d là các số nguyên dương và
;
ac
bd
là các phân số tối giản. Giá
trị của
M ad bc
là :
A.
10
B.
8
40
D.
32
C©u 10 :
Một nhà kho có dạng khối hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB
= a, BC = 2a, chiều cao AA’ = 3a, chắp thêm một khối lăng trụ tam giác đều mà một mặt bên là
A’B’C’D’ và A’B’ là một cạnh đáy của lăng trụ. Tính thể tích của nhà kho ?
A.
3
36 3
6
a
B.
3
12 3
2
a
3
3 12 3
2
a
D.
3
3
2
a
C©u 11 :
Cho hình trụ có độ dài đường sinh là b và bán kính đường tròn đáy là a. Diện tích toàn phần của
hình trụ là :
A.
2
tp
S a b a

B.
22
tp
S a b a

tp
S a b a

D.
2
tp
S a b a

C©u 12 :
Nguyên hàm hàm số
sin 2 1f x x
là :
A.
1
cos 2 1
2
f x dx x C
B.
1
cos2
2
f x dx x C
C.
1
cos 2 1
2
f x dx x C
D.
1
cos2
2
f x dx x C
C©u 13 :
Cho (P) là đồ thị hàm số
2
45y x x
. Diện tích hình phẳng giới hạn bởi (P) và các tiếp tuyến của
(P) kẻ từ điểm
5
;1
2
A



là :
A.
9
4
B.
18
4
9
8
D.
9
2
C©u 14 :
Tập nghiệm của bất phương trình  
󰇛
󰇜
là :
A.
󰇛

󰇜
󰇝

󰇞
B.
󰇛

󰇜
󰇛

󰇜
󰇝

󰇞
D.
󰇛

󰇜
C©u 15 :
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Biết hình chóp có chiều cao là
3ha
. Thể tích khối chóp là :
A.
3
3Va
B.
3
3
8
a
V
3
3
a
V
D.
3
3
3
a
V
C©u 16 :
Đặt
3
1
1
x
dx
I
e
và
1
x
te
. Khẳng định nào trong các khẳng định sau là sai :
A.
3
1
1
11
1
e
e
I dt
tt




B.
2
ln 1 2I e e
x
dt e dx
D.
3
1
11
1
I dt
tt




C©u 17 :
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
1
x
y
x
trên đoạn
2;0
lần lượt là:
A.
3 và -1
B.
1
3
và -1
1
3
và -1
D.
0 và -1
Trang 3/ mã đề 237
C©u 18 :
Điểm biểu diễn của các số phức
7z bi
với
b
, nằm trên đường thẳng có phương trình là:
A.
7y
B.
7yx
7x
D.
yx
C©u 19 :
Cho hình chóp đều S.ABCD có AB = a , mặt bên (SAD) tạo với đáy (ABCD) một góc
60
o
. Tính thể
tích V của khối chóp S.ABCD ?
A.
3
2Va
B.
3
3
6
a
V
3
3
2
a
V
D.
3
3
3
a
V
C©u 20 :
Số nghiêm của phương trình
4
1z
là
A.
2
B.
1
3
D.
4
C©u 21 :
Một cốc nước có dạng hình trụ đựng nước, chiều cao 16cm, đường kính đáy 6cm, lượng nước trong
cốc cao 10cm. Thả vào cốc nước 4 viên bi có cùng đường kính 4cm. Hỏi nước dâng cao cách mép
cốc bao nhiêu cm ? ( làm tròn sau dấu phẩy hai chữ số thập phân, bỏ qua độ dày cốc ).
A.
1,26cm
B.
1,68cm
1,34cm
D.
1,43cm
C©u 22 :
Trong không gian với hệ tọa độ
Oxyz
, cho
1;2; 1 ,a 
3;4;3b
. Tìm tọa độ của
x
biết
x b a
A.
2;2;4 .x
B.
1;1;2 .x
2; 2; 4 .x
D.
2; 2;4 .x
C©u 23 :
Trong các số phức thỏa mãn điều kiện
12z z i
là số thực. Hãy tìm
z
có mô đun nhỏ nhất
A.
24
55
Zi
B.
42
55
Zi
24
55
Zi
D.
24
55
Zi
C©u 24 :
Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Một mặt phẳng đi qua A’B’
và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Thể tích V của khối A’B’.BAEF là :
A.
3
3
18
a
V
B.
3
53
54
a
V
3
3
27
a
V
D.
3
23
27
a
V
C©u 25 :
Phương trình tiếp tuyến với đồ thị hàm số
32
( ) 3 2y f x x x
tại điểm
0
x
sao cho
0
"( ) 0fx
là:
A.
3 3 0xy
B.
3 3 0xy
3 3 0xy
D.
3 3 0xy
C©u 26 :
Cho
22
11
3; 1f x dx g t dt

. Giá trị của
2
1
23A f x g x dx


là:
A.
5
B.
9
3
D.
2
C©u 27 :
Biết 
, giá trị biểu thức 


là :
A.

B.
󰇛

󰇜
󰇛

󰇜
D.
C©u 28 :
Cho hàm số

khẳng định nào sau đây là sai ?
A.
Hàm số nghịch biến trên R
B.
Đồ thị hàm số nằm toàn bộ phía trên trục ox
C.
Tập xác định của hàm số là R
D.
Hàm số đồng biến trên R
C©u 29 :
Khối đa diện đều loại
3;5
có số mặt là :
A.
16
B.
8
20
D.
12
C©u 30 :
Cho hàm số
3
3y x x m
(m là thàm số). Để giá trị lớn nhất của hàm số trên đoạn
0; 3


bằng
32
thì m phải bằng:
A.
22
B.
2
2
D.
32
C©u 31 :
Trong không gian với hệ tọa độ
Oxyz
, cho
2; 3;1a 
,
1; 3; 4b 
. Tìm
;ab


Trang 4/ mã đề 237
A.
315
B.
171
171
D.
315
C©u 32 :
Diện tích hình phẳng giới hạn bởi các đường
2
1 ; 0; 0; 2y x y x x
bằng :
A.
15
B.
35
2
3
D.
21
C©u 33 :
Cho hàm số
2
1x mx
y
xm

. Tìm m để hàm số đạt cực đại tại
2x
? Một học sinh làm như sau:
Bước 1:
22
2
21
\ , '
x mx m
D R m y
xm
Bước 2: Hàm số đạt cực đại tại
2 '(2) 0 *xy
Bước 3:
2
1
* 4 3 0
3
m
mm
m


Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào?
A.
Sai từ bước 3
B.
Sai từ bước 2
Sai từ bước 1
D.
Đúng
C©u 34 :
Cho hàm số
32
1
( 1) 4
3
y x m x x
(m là thàm số). Giá trị của m để hàm số đã cho nghịch biến
trên R là:
A.
13m
B.
3m
1
3
m
m

D.
mR
C©u 35 :
Cho hàm số

khẳng định nào dưới đây là đúng ?
A.
Đồ thị hàm số không có tiệm cận
B.
Đồ thị hàm số có 1 tiệm cận đứng và không có
tiệm cận ngang
C.
Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm
cận đứng
D.
Đồ thị hàm số cắt trục ox
C©u 36 :
Đường thẳng
6y x m
là tiếp tuyến của đường cong
3
31y x x
khi m bằng
A.
-3 hoặc 1
B.
-1 hoặc 3
-5 hoặc 1
D.
3 hoặc -5
C©u 37 :
Cho điểm
2,1,0M
và đường thẳng
11
:
2 1 1
x y z
. Gọi
d
là đường thẳng đi qua
M
, cắt và
vuông góc với
. Khi đó, vectơ chỉ phương của
d
là:
A.
0;3;1u
B.
1; 4; 2u
2; 1;2u
D.
3;0;2u
C©u 38 :
Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
2
4 ; 0y x y
xung quanh trục Ox là :
A.
2
B.
71
82
8
3
D.
512
15
C©u 39 :
Trong không gian với hệ tọa độ
Oxyz
, tìm
m
để phương trình
2 2 2
2 2( 2) 2( 3) 8 37 0x y z mx m y m z m
là phương trình của một mặt cầu
A.
42m hay m
B.
24m hay m
C.
42m hay m
D.
24m hay m
C©u 40 :
Tìm hàm số F(x) biết
3
4 6 1F x x x
và đồ thị hàm số
y F x
cắt trục tung tại điểm có tung
độ bằng 2:
A.
42
31F x x x x
B.
42
32F x x x x
C.
3
2F x x x
D.
42
4 6 2F x x x x
Trang 5/ mã đề 237
C©u 41 :
Số phức
3
1zi
có mô đun bằng:
A.
2z
B.
22z 
0z
D.
22z
C©u 42 :
Cho hàm số
42
25y x x
. Chọn khẳng định đúng?
A.
Hàm số nghịch biến trên khoảng
;1
và
(1; )
B.
Hàm số đồng biến trên khoảng
1;1
C.
Hàm số nghịch biến trên khoảng
1;0
và
(1; )
D.
Hàm số đồng biến trên khoảng
1;0
và
(1; )
C©u 43 :
Khẳng định nào sau đây là sai ?
A.


B.
 

D.
 
C©u 44 :
Giá trị của m để phương trình
3
4 3 1x x mx m
có 4 nghiệm phân biệt là :
A.
9 6 3;1m
B.
6 3 9;6 3 9m
C.
9 6 3; 1m
D.
1;6 3 9m
C©u 45 :
Số đường tiệm cận của đồ thị hàm số
1
21
x
y
x
là:
A.
0
B.
3
1
D.
2
C©u 46 :
Phương trình

có 2 nghiệm phân biệt khi :
A.

B.
D.


C©u 47 :
Tập xác định của hàm số
󰇛

󰇜
là :
A.
󰇛

󰇜
B.
󰇛

󰇜
󰇝

󰇞
󰇟

󰇠
D.
󰇛

󰇜
󰇛

󰇜
C©u 48 :
Bất phương trình
󰇛

󰇜

có tập nghiệm là :
A.
󰇛

󰇜
B.
󰇛

󰇜
󰇛

󰇜
D.
C©u 49 :
Hàm số
32
1
32
3
y x x x
đạt cực tiểu tại:
A.
1
3
x
B.
1x
3x 
D.
0x
C©u 50 :
Trong không gian với hệ tọa độ
Oxyz
, cho 3 điểm
1;2;3A
,
0;1;1B
,
1;0; 2C
và mặt phẳng
P
có phương trình
20 x y z
. Gọi
M
là điểm thuộc mặt phẳng
P
sao cho giá trị biểu
thức
2 2 2
23 T MA MB MC
nhỏ nhất. Tính khoảng cách từ
M
đến mặt phẳng
: 2 2 3 0 Q x y z
A.
24
B.
91
54
121
54
D.
25
3
-------------------------------------------------------Hết--------------------------------------------------
Trang 1/ mã đề 241
Trường THPT Quốc Oai ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2016 -2017
Môn: Toán ; thời gian 90 phút; mã đề 241
(đề gồm 50 câu trắc nghiệm)
Họ và tên thí sinh:………………………………………………….. số báo danh:…………
C©u 1 :
Đường thẳng
9y x m
là tiếp tuyến của đường cong
32
31y x x
khi m bằng
A.
-1 hoặc 3
3 hoặc -5
C.
-3 hoặc 1
D.
-6 hoặc 26
C©u 2 :
Khẳng định nào sau đây là sai ?
A.



C.

D.

C©u 3 :
Một hình nón có bán kính đáy
1r
, chiều cao
4
3
h
. Kí hiệu góc ở đỉnh của hình nón là
2
.
Trong các mệnh đề sau, mệnh đề nào đúng ?
A.
3
cot
5
3
sin
5
C.
3
tan
5
D.
3
cos
5
C©u 4 :
Tập xác định của hàm số
󰇛

󰇜
là :
A.
󰇛

󰇜
󰇛

󰇜
󰇛

󰇜
C.
󰇛

󰇜
󰇝

󰇞
D.
󰇟

󰇠
C©u 5 :
Cho hàm số
32
33y x x
. Chọn khẳng định sai?
A.
Hàm số nghịch biến trên khoảng
0;2
B.
Hàm số có hai điểm cực trị
C.
Hàm số đồng biến trên khoảng
;0
và
(2; )
D.
Hàm số không có cực trị
C©u 6 :
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
x
y
x
trên đoạn
1;3
lần lượt là:
A.
3 và -1
3
4
và
1
2
C.
1
3
và -1
D.
0 và -1
C©u 7 :
Cho hàm số


khẳng định nào sau đây là sai ?
A.
Hàm số nghịch biến trên R
B.
Tập xác định của hàm số là R
C.
Đồ thị hàm số nằm toàn bộ phía trên trục ox
D.
Hàm số đồng biến trên R
C©u 8 :
Biết
3
2
1
3 ln 1
ln
( 1)
x a c
dx
x b b d

với a,b,c,d là các số nguyên dương và
;
ac
bd
là các phân số tối giản.
Giá trị của
M ac bd
là :
A.
17
20
C.
145
D.
11
C©u 9 :
Nguyên hàm hàm số
cos 3 2f x x
là :
A.
1
sin 3 2
3
f x dx x C
B.
1
sin3
3
f x dx x C
C.
1
sin 3 2
3
f x dx x C
D.
1
sin3
3
f x dx x C
C©u 10 :
Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Một mặt phẳng đi qua A’B’
và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Thể tích V của khối C.A’B’FE là :
A.
3
3
27
a
V
3
53
54
a
V
C.
3
53
18
a
V
D.
3
53
27
a
V
C©u 11 :
Tập nghiệm của bất phương trình  
󰇛
󰇜
là :
Trang 2/ mã đề 241
A.
󰇛

󰇜
󰇛

󰇜
C.
󰇛

󰇜
󰇝
󰇞
D.
󰇛

󰇜
󰇝
󰇞
C©u 12 :
Cho
33
22
2; 3f x dx g t dt

. Giá trị của
3
2
32A f x g x dx


là:
A.
12
0
C.
5
D.
-1
C©u 13 :
Trong không gian với hệ trục tọa độ
Oxyz
, cho hình hộp
.ABCD A B C D
. Biết
3;2;1A
,
4;2;0C
,
2;1;1B
,
3;5;4D
.Tìm tọa độ
A
của hình hộp
.ABCD A B C D
.
A.
3; 3; 3 .A

3;3;1 .A
C.
3;3;3 .A
D.
3; 3;3 .A

C©u 14 :
Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
có
1;3;4A
,
2;3;0B
,
1; 3;2C 
.
Tìm tọa độ trọng tâm
G
của tam giác
ABC
.
A.
2
;1;2 .
3
G



2
;2;2 .
3
G



C.
2
;1;1 .
3
G



D.
2;1;2 .G
C©u 15 :
Phương trình 
󰇛

󰇜
 
Có 2 nghiệm x
1,
x
2
thỏa mãn
khi :
A.
C.
D.

C©u 16 :
Cho hai số phức
12
, zz
thỏa mãn
12
1zz
,
12
3zz
. Tính
12
zz
:
A.
4
2
C.
1
D.
3
C©u 17 :
Cho phương trình
2
2 3 0zz
trên tập số phức,có hai nghiệm là
12
,zz
.Khi đó
22
12
zz
có giá trị
là:
A.
6
22
C.
3
D.
2
C©u 18 :
Cho hình trụ có độ dài đường sinh là l và bán kính đường tròn đáy là r. Diện tích toàn phần của hình
trụ là :
A.
2
tp
S r l r

22
tp
S r l r

C.
2
tp
S r l r

D.
tp
S r l r

C©u 19 :
Phương trình

có 2 nghiệm phân biệt khi :
A.


C.
D.

C©u 20 :
Cho (P) là đồ thị hàm số
2
43y x x
. Diện tích hình phẳng giới hạn bởi (P) và các tiếp tuyến của
(P) kẻ từ điểm
2; 5A
là :
A.
16
3
10
3
C.
32
3
D.
8
3
C©u 21 :
Số đường tiệm cận của đồ thị hàm số
1
y
x
là:
A.
1
3
C.
2
D.
0
C©u 22 :
Cho số phức
32zi
. Tìm số phức
2
1w z i z
A.
78wi
35wi
C.
35wi
D.
78wi
C©u 23 :
Cho hàm số
3
3y x x m
(m là thàm số). Để giá trị lớn nhất của hàm số trên đoạn
0; 3


bằng
52
thì m phải bằng:
A.
2
32
C.
42
D.
22
C©u 24 :
Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
(2;4;1)A
,
( 1;1;3)B
và mặt phẳng
( :)P
3 2 5 0x y z
. Viết phương trình mặt phẳng
Q
đi qua hai điểm A, B và vuông góc với mặt
Trang 3/ mã đề 241
phẳng
P
.
A.
:2 3 12 0Q y z
B.
:2 3 11 0Q y z
C.
:2 3 1 0Q y z
D.
:2 3 11 0Q x z
C©u 25 :
Bất phương trình 
󰇛

󰇜


có tập nghiệm là :
A.
󰇛

󰇜
󰇛

󰇜
󰇛

󰇜
C.
D.
C©u 26 :
Trong không gian với hệ tọa độ
Oxyz
, cho 3 điểm
2;2;3A
,
1; 1;3B
,
3;1; 1C
và mặt phẳng
P
có phương trình
2 8 0xz
. Gọi
M
là điểm thuộc mặt phẳng
P
sao cho giá trị biểu hức
2 2 2
23T MA MB MC
nhỏ nhất. Tính khoảng cách từ
M
đến mặt phẳng
: 2 2 6 0Q x y z
A.
2
3
3
d
C.
4
D.
3
2
d
C©u 27 :
Diện tích hình phẳng giới hạn bởi các đường
2
2 ; 0; 1; 3y x y x x
bằng :
A.
30
98
3
C.
18
D.
21
C©u 28 :
Giá trị của m để phương trình
3
4 3 1x x mx m
có 4 nghiệm phân biệt là :
A.
1;6 3 9m
B.
9 6 3; 1m
C.
6 3 9;6 3 9m
D.
9 6 3;1m
C©u 29 :
Trong không gian với hệ tọa độ
Oxyz
, cho điểm
(2;1;0)M
và đường thẳng : .
Viết phương trình của đường thẳng d đi qua điểm M, cắt và vuông góc với .
A.
d:
21
.
1 4 2
x y z


B.
d:
21
.
2 4 1
x y z

C.
d:
21
.
1 4 1
x y z

D.
d:
21
.
1 4 1
x y z

C©u 30 :
Phương trình tiếp tuyến với đồ thị hàm số
32
( ) 3 2y f x x x
tại điểm
0
x
sao cho
0
"( ) 6fx
là:
A.
3 3 0xy
20y 
C.
20y 
D.
3 3 0xy
C©u 31 :
Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
2
9 ; 0y x y
xung quanh trục Ox là :
A.
8
3
71
82
C.
3
D.
1296
5
C©u 32 :
Hàm số
42
2y x x
có điểm cực tiểu là:
A.
2y
1x 
C.
1x
D.
0x
C©u 33 :
Cho hàm số
2
1x mx
y
xm

. Tìm m để hàm số đạt cực đại tại
2x
? Một học sinh làm như sau:
Bước 1:
22
2
21
\ , '
x mx m
D R m y
xm
Bước 2: Hàm số đạt cực đại tại
2 '(2) 0 *xy
x y z11
2 1 1


Trang 4/ mã đề 241
Bước 3:
2
1
* 4 3 0
3
m
mm
m


Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào?
A.
Đúng
Sai từ bước 1
C.
Sai từ bước 2
D.
Sai từ bước 3
C©u 34 :
Khối đa diện đều loại
5;3
có số mặt là :
A.
8
14
C.
10
D.
12
C©u 35 :
Cho hình chóp đều S.ABCD có AC = 2a , mặt bên (SBC) tạo với đáy (ABCD) một góc
45
o
. Tính
thể tích V của khối chóp S.ABCD ?
A.
3
23
3
a
V
3
2
3
a
V
C.
3
2Va
D.
3
2
a
V
C©u 36 :
Cho
1;0; 3 ; 2;1;2ab
.Khi đó
;ab


có giá trị là
A.
3
8
C.
74
D.
4
C©u 37 :
Tìm hàm số F(x) biết
2
3 2 1F x x x
và đồ thị hàm số
y F x
cắt trục tung tại điểm có tung
độ bằng e:
A.
2
2F x x x
B.
2
1F x x x e
C.
32
1F x x x x
D.
32
F x x x x e
C©u 38 :
Đặt
2
2
2
3
1
dx
I
xx
và
2
1tx
. Khẳng định nào trong các khẳng định sau là sai :
A.
tdt xdx
1
2
1
3
1
dt
I
t
C.
22
1xt
D.
2
2
2
3
1
dt
I
t
C©u 39 :
Cho hàm số
32
1
( 1) 4
3
y x m x x
(m là thàm số). Giá trị của m để hàm số đã cho đồng biến trên
R là:
A.
Không có giá trị
nào của m thỏa
mãn
3m
C.
13m
D.
mR
C©u 40 :
Trong không gian với hệ tọa độ
Oxyz
. Hãy viết phương trình mặt cầu (S) có tâm
(2;0;1)I
và tiếp
xúc với đường thẳng d:
12
1 2 1
x y z

.
A.
2 2 2
( 2) ( 1) 2.x y z
B.
2 2 2
( 2) ( 1) 4.x y z
C.
2 2 2
( 2) ( 1) 9.x y z
D.
2 2 2
( 1) ( 2) ( 1) 24.x y z
C©u 41 :
Đạo hàm của hàm số

là :
A.



B.
󰇛 󰇜

C.

󰇛
󰇜



D.

󰇛

󰇜



C©u 42 :
Một nhà kho có dạng khối hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB
= 3m, BC = 6m, chiều cao AA’ = 3m, chắp thêm một khối lăng trụ tam giác đều mà một mặt bên là
A’B’C’D’ và A’B’ là một cạnh đáy của lăng trụ. Tính thể tích của nhà kho ?
A.
3
27 3
2
m
3
27 4 3
2
m
C.
3
54m
D.
3
9 12 3
2
m
Trang 5/ mã đề 241
C©u 43 :
Biết 
, giá trị biểu thức






là :
A.
󰇛
󰇜
C.
D.
󰇛
󰇜
C©u 44 :
Cho hàm số
khẳng định nào dưới đây là đúng ?
A.
Đồ thị hàm số cắt trục ox
B.
Đồ thị hàm số không có tiệm cận
C.
Đồ thị hàm số có 1 tiệm cận đứng và không có
tiệm cận ngang
D.
Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm
cận đứng
C©u 45 :
Một cốc nước có dạng hình trụ đựng nước, chiều cao 12cm, đường kính đáy 4cm, lượng nước trong
cốc cao 8cm. Thả vào cốc nước 4 viên bi có cùng đường kính 2cm. Hỏi nước dâng cao cách mép cốc
bao nhiêu cm ? ( làm tròn sau dấu phẩy hai chữ số thập phân, bỏ qua độ dày cốc ).
A.
2,67cm
2,25cm
C.
2,33cm
D.
2,75cm
C©u 46 :
Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a. Biết hình chóp có chiều cao là
3ha
.
Thể tích khối chóp là :
A.
3
3
4
a
V
3
3
8
a
V
C.
3
4
a
V
D.
3
3
a
V
C©u 47 :
Cho hai số phức
1
23zi
,
2
12zi
. Tính môđun của số phức
12
2z z z
.
A.
137z
15z
C.
55z
D.
65z
C©u 48 :
Cho số phức
54zi
. Số phức
2z
có
A.
Phần thực bằng
5
và phần ảo bằng
4
.
B.
Phần thực bằng
4
và phần ảo bằng
3
.
C.
Phần thực bằng
3
và phần ảo bằng
4
.
D.
Phần thực bằng
3
và phần ảo bằng
4i
.
C©u 49 :
Trong các số phức
z
tìm điều kiện :
23z i z i
. Hãy tìm z có mô đun nhỏ nhất
A.
27 6
55
zi
36
55
zi
C.
6 27
55
zi
D.
6 27
55
zi
C©u 50 :
Cho hàm số
()y f x
có đồ thị (C) như hình vẽ.
Số nghiệm phân biệt của phương trình
1
()
2
fx
là:
A.
2
0
C.
3
D.
1
------------------------------------------------------Hết--------------------------------------------------
Trang 1/ mã đề 238
Trường THPT Quốc Oai ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2016 -2017
Môn: Toán ; thời gian 90 phút; mã đề 238
(đề gồm 50 câu trắc nghiệm)
Họ và tên thí sinh:………………………………………………….. số báo danh:…………
C©u 1 :
Trong các số phức thỏa mãn điều kiện
12z z i
là số thực. Hãy tìm
z
có mô đun nhỏ nhất
A.
24
55
Zi
B.
42
55
Zi
24
55
Zi
D.
24
55
Zi
C©u 2 :
Giá trị của m để phương trình
3
4 3 1x x mx m
có 4 nghiệm phân biệt là :
A.
6 3 9;6 3 9m
B.
9 6 3; 1m
C.
9 6 3;1m
D.
1;6 3 9m
C©u 3 :
Cho điểm
2,1,0M
và đường thẳng
11
:
2 1 1
x y z
. Gọi
d
là đường thẳng đi qua
M
, cắt và
vuông góc với
. Khi đó, vectơ chỉ phương của
d
là:
A.
2; 1;2u
B.
0;3;1u
1; 4; 2u
D.
3;0;2u
C©u 4 :
Phương trình

có 2 nghiệm phân biệt khi :
A.
B.


D.

C©u 5 :
Mệnh đề nào sau đây sai ?
A.
Khoảng cách từ điểm
0 0 0
,,M x y z
đến mặt phẳng
2 2 1 0x y z
là
0 0 0
2 2 1
3
x y z
.
B.
Mặt phẳng
:4 2 3 0P x y
song song với mặt phẳng
: 2 5 0Q x y
.
C.
Mặt phẳng
2 3 – 2 0x y z
đi qua gốc tọa độ.
D.
Mặt phẳng
3 – 2 0xz
có tọa độ vectơ pháp tuyến là
3,0, 1
.
C©u 6 :
Cho hàm số
3
3y x x m
(m là thàm số). Để giá trị lớn nhất của hàm số trên đoạn
0; 3


bằng
32
thì m phải bằng:
A.
32
B.
2
22
D.
2
C©u 7 :
G
ọi
1
z
là nghiệm phức có phần ảo âm của phương trình
2
2 3 0zz
. Tọa độ điểm
M
biểu diễn
số phức
1
z
là:
A.
( 1; 2)M 
B.
( 1; 2 )Mi
( 1;2)M
D.
( 1; 2)M 
C©u 8 :
Cho hàm số

khẳng định nào sau đây là sai ?
A.
Hàm số đồng biến trên R
B.
Đồ thị hàm số nằm toàn bộ phía trên trục ox
C.
Hàm số nghịch biến trên R
D.
Tập xác định của hàm số là R
C©u 9 :
Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
2
4 ; 0y x y
xung quanh trục Ox là :
A.
2
B.
8
3
512
15
D.
71
82
C©u 10 :
Cho hàm số

khẳng định nào dưới đây là đúng ?
A.
Đồ thị hàm số cắt trục ox
B.
Đồ thị hàm số không có tiệm cận
C.
Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm
D.
Đồ thị hàm số có 1 tiệm cận đứng và không có
Trang 2/ mã đề 238
cận đứng
tiệm cận ngang
C©u 11 :
Đạo hàm của hàm số

là :
A.

󰇛
󰇜



B.

󰇛

󰇜



C.



D.

󰇛
󰇜


C©u 12 :
Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Một mặt phẳng đi qua A’B’
và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Thể tích V của khối A’B’.BAEF là :
A.
3
3
27
a
V
B.
3
23
27
a
V
3
53
54
a
V
D.
3
3
18
a
V
C©u 13 :
Tập xác định của hàm số
󰇛

󰇜
là :
A.
󰇛

󰇜
B.
󰇛

󰇜
󰇝

󰇞
󰇟

󰇠
D.
󰇛

󰇜
󰇛

󰇜
C©u 14 :
Cho
22
11
3; 1f x dx g t dt

. Giá trị của
2
1
23A f x g x dx


là:
A.
5
B.
3
2
D.
9
C©u 15 :
Số nghiêm của phương trình
4
1z
là
A.
1
B.
4
2
D.
3
C©u 16 :
Khẳng định nào sau đây là sai ?
A.
 
B.

 
D.


C©u 17 :
Diện tích hình phẳng giới hạn bởi các đường
2
1 ; 0; 0; 2y x y x x
bằng :
A.
15
B.
35
2
3
D.
21
C©u 18 :
Trong không gian với hệ tọa độ
Oxyz
, cho
1;2; 1 ,a 
3;4;3b
. Tìm tọa độ của
x
biết
x b a
A.
2; 2; 4 .x
B.
2;2;4 .x
1;1;2 .x
D.
2; 2;4 .x
C©u 19 :
Biết
2
3
1
ln
ln2
x a c
dx
x b d

với a,b,c,d là các số nguyên dương và
;
ac
bd
là các phân số tối giản. Giá
trị của
M ad bc
là :
A.
8
B.
10
32
D.
40
C©u 20 :
Cho hàm số
2
1x mx
y
xm

. Tìm m để hàm số đạt cực đại tại
2x
? Một học sinh làm như sau:
Bước 1:
22
2
21
\ , '
x mx m
D R m y
xm
Bước 2: Hàm số đạt cực đại tại
2 '(2) 0 *xy
Bước 3:
2
1
* 4 3 0
3
m
mm
m


Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào?
A.
Sai từ bước 3
B.
Đúng
Sai từ bước 2
D.
Sai từ bước 1
C©u 21 :
Tìm hàm số F(x) biết
3
4 6 1F x x x
và đồ thị hàm số
y F x
cắt trục tung tại điểm có tung
độ bằng 2:
A.
42
4 6 2F x x x x
B.
42
31F x x x x
C.
3
2F x x x
D.
42
32F x x x x
Trang 3/ mã đề 238
C©u 22 :
Phương trình tiếp tuyến với đồ thị hàm số
32
( ) 3 2y f x x x
tại điểm
0
x
sao cho
0
"( ) 0fx
là:
A.
3 3 0xy
B.
3 3 0xy
3 3 0xy
D.
3 3 0xy
C©u 23 :
Cho (P) là đồ thị hàm số
2
45y x x
. Diện tích hình phẳng giới hạn bởi (P) và các tiếp tuyến của
(P) kẻ từ điểm
5
;1
2
A



là :
A.
9
4
B.
18
4
9
2
D.
9
8
C©u 24 :
Đường thẳng
6y x m
là tiếp tuyến của đường cong
3
31y x x
khi m bằng
A.
-5 hoặc 1
B.
3 hoặc -5
-3 hoặc 1
D.
-1 hoặc 3
C©u 25 :
Trong không gian với hệ tọa độ
Oxyz
, cho 3 điểm
1;2;3A
,
0;1;1B
,
1;0; 2C
và mặt phẳng
P
có phương trình
20 x y z
. Gọi
M
là điểm thuộc mặt phẳng
P
sao cho giá trị biểu
thức
2 2 2
23 T MA MB MC
nhỏ nhất. Tính khoảng cách từ
M
đến mặt phẳng
: 2 2 3 0 Q x y z
A.
24
B.
121
54
25
3
D.
91
54
C©u 26 :
Hàm số
32
1
32
3
y x x x
đạt cực tiểu tại:
A.
0x
B.
1
3
x
3x 
D.
1x
C©u 27 :
Cho số phức
z a bi
. Khi đó số
1
2
zz
là:
A.
Một số thực.
B.
2
i
D.
Một số thuần ảo
C©u 28 :
Cho hàm số
32
1
( 1) 4
3
y x m x x
(m là thàm số). Giá trị của m để hàm số đã cho nghịch biến
trên R là:
A.
3m
B.
1
3
m
m

13m
D.
mR
C©u 29 :
Điểm biểu diễn của các số phức
7z bi
với
b
, nằm trên đường thẳng có phương trình là:
A.
7y
B.
7x
7yx
D.
yx
C©u 30 :
Nguyên hàm hàm số
sin 2 1f x x
là :
A.
1
cos 2 1
2
f x dx x C
B.
1
cos2
2
f x dx x C
C.
1
cos 2 1
2
f x dx x C
D.
1
cos2
2
f x dx x C
C©u 31 :
Cho hình trụ có độ dài đường sinh là b và bán kính đường tròn đáy là a. Diện tích toàn phần của
hình trụ là :
A.
2
tp
S a b a

B.
22
tp
S a b a

2
tp
S a b a

D.
tp
S a b a

C©u 32 :
Phương trình 
󰇛

󰇜
 
Có 2 nghiệm x
1,
x
2
thỏa mãn 

 khi :
A.
B.
D.



Trang 4/ mã đề 238
C©u 33 :
Cho hàm số
()y f x
có đồ thị (C) như hình vẽ.
Số nghiệm phân biệt của phương trình
( ) 1fx
là:
A.
2
B.
0
1
D.
3
C©u 34 :
Trong không gian với hệ tọa độ
Oxyz
, tìm
m
để phương trình
2 2 2
2 2( 2) 2( 3) 8 37 0x y z mx m y m z m
là phương trình của một mặt cầu
A.
42m hay m
B.
42m hay m
C.
24m hay m
D.
24m hay m
C©u 35 :
Số phức
3
1zi
có mô đun bằng:
A.
22z 
B.
2z
0z
D.
22z
C©u 36 :
Đặt
3
1
1
x
dx
I
e
và
1
x
te
. Khẳng định nào trong các khẳng định sau là sai :
A.
2
ln 1 2I e e
B.
3
1
11
1
I dt
tt




x
dt e dx
D.
3
1
1
11
1
e
e
I dt
tt




C©u 37 :
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
1
x
y
x
trên đoạn
2;0
lần lượt là:
A.
3 và -1
B.
1
3
và -1
0 và -1
D.
1
3
và -1
C©u 38 :
Khối đa diện đều loại
3;5
có số mặt là :
A.
16
B.
12
20
D.
8
C©u 39 :
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Biết hình chóp có chiều cao là
3ha
. Thể tích khối chóp là :
A.
3
3
a
V
B.
3
3
3
a
V
3
3Va
D.
3
3
8
a
V
C©u 40 :
Biết 
, giá trị biểu thức 


là :
A.
󰇛

󰇜
B.

󰇛

󰇜
D.
C©u 41 :
Một hình nón có bán kính đáy
3ra
, chiều cao
4ha
. Kí hiệu góc ở đỉnh của hình nón là
2
.
Trong các mệnh đề sau, mệnh đề nào đúng ?
A.
4
cos
5
B.
4
tan
5
4
sin
5
D.
4
cot
5
C©u 42 :
Bất phương trình
󰇛

󰇜

có tập nghiệm là :
A.
B.
󰇛

󰇜
D.
󰇛

󰇜
󰇛

󰇜
Trang 5/ mã đề 238
C©u 43 :
Một nhà kho có dạng khối hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB
= a, BC = 2a, chiều cao AA’ = 3a, chắp thêm một khối lăng trụ tam giác đều mà một mặt bên là
A’B’C’D’ và A’B’ là một cạnh đáy của lăng trụ. Tính thể tích của nhà kho ?
A.
3
12 3
2
a
B.
3
3 12 3
2
a
3
36 3
6
a
D.
3
3
2
a
C©u 44 :
Một cốc nước có dạng hình trụ đựng nước, chiều cao 16cm, đường kính đáy 6cm, lượng nước trong
cốc cao 10cm. Thả vào cốc nước 4 viên bi có cùng đường kính 4cm. Hỏi nước dâng cao cách mép
cốc bao nhiêu cm ? ( làm tròn sau dấu phẩy hai chữ số thập phân, bỏ qua độ dày cốc ).
A.
1,43cm
B.
1,26cm
1,34cm
D.
1,68cm
C©u 45 :
Tập nghiệm của bất phương trình  
󰇛
󰇜
là :
A.
󰇛

󰇜
B.
󰇛

󰇜
󰇝

󰇞
󰇛

󰇜
󰇝

󰇞
D.
󰇛

󰇜
C©u 46 :
Trong không gian với hệ tọa độ
Oxyz
, cho
2; 3;1a 
,
1; 3; 4b 
. Tìm
;ab


A.
171
B.
171
315
D.
315
C©u 47 :
Cho hàm số
42
25y x x
. Chọn khẳng định đúng?
A.
Hàm số nghịch biến trên khoảng
;1
và
(1; )
B.
Hàm số đồng biến trên khoảng
1;1
C.
Hàm số nghịch biến trên khoảng
1;0
và
(1; )
D.
Hàm số đồng biến trên khoảng
1;0
và
(1; )
C©u 48 :
Số đường tiệm cận của đồ thị hàm số
1
21
x
y
x
là:
A.
0
B.
1
3
D.
2
C©u 49 :
Cho hình chóp đều S.ABCD có AB = a , mặt bên (SAD) tạo với đáy (ABCD) một góc
60
o
. Tính thể
tích V của khối chóp S.ABCD ?
A.
3
2Va
B.
3
3
6
a
V
3
3
2
a
V
D.
3
3
3
a
V
C©u 50 :
Phương trình tham số của đường thẳng
d
đi qua điểm
1,2,3M
và có vec tơ chỉ phương
(1;3;2)a
là :
A.
1
23
32
xt
yt
zt



B.
1
23
32
xt
yt
zt
1
23
32
xt
yt
zt


D.
1
23
32
xt
yt
zt
-------------------------------------------------------------Hết----------------------------------------------------------
Trang 1/ mã đề 242
Trường THPT Quốc Oai ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2016 -2017
Môn: Toán ; thời gian 90 phút; mã đề 242
(đề gồm 50 câu trắc nghiệm)
Họ và tên thí sinh:………………………………………………….. số báo danh:…………
C©u 1 :
Cho hàm số
khẳng định nào dưới đây là đúng ?
A.
Đồ thị hàm số cắt trục ox
B.
Đồ thị hàm số không có tiệm cận
C.
Đồ thị hàm số có 1 tiệm cận đứng và không có
tiệm cận ngang
D.
Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm
cận đứng
C©u 2 :
Cho hàm số
32
33y x x
. Chọn khẳng định sai?
A.
Hàm số không có cực trị
B.
Hàm số có hai điểm cực trị
C.
Hàm số nghịch biến trên khoảng
0;2
D.
Hàm số đồng biến trên khoảng
;0
và
(2; )
C©u 3 :
Tập nghiệm của bất phương trình  
󰇛
󰇜
là :
A.
󰇛

󰇜
󰇝
󰇞
󰇛

󰇜
C.
󰇛

󰇜
D.
󰇛

󰇜
󰇝
󰇞
C©u 4 :
Cho hình chóp đều S.ABCD có AC = 2a , mặt bên (SBC) tạo với đáy (ABCD) một góc
45
o
. Tính
thể tích V của khối chóp S.ABCD ?
A.
3
23
3
a
V
3
2
a
V
C.
3
2
3
a
V
D.
3
2Va
C©u 5 :
Cho hàm số
2
1x mx
y
xm

. Tìm m để hàm số đạt cực đại tại
2x
? Một học sinh làm như sau:
Bước 1:
22
2
21
\ , '
x mx m
D R m y
xm
Bước 2: Hàm số đạt cực đại tại
2 '(2) 0 *xy
Bước 3:
2
1
* 4 3 0
3
m
mm
m


Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào?
A.
Sai từ bước 2
Đúng
C.
Sai từ bước 1
D.
Sai từ bước 3
C©u 6 :
Tìm hàm số F(x) biết
2
3 2 1F x x x
và đồ thị hàm số
y F x
cắt trục tung tại điểm có tung
độ bằng e:
A.
2
2F x x x
B.
2
1F x x x e
C.
32
F x x x x e
D.
32
1F x x x x
C©u 7 :
Đặt
2
2
2
3
1
dx
I
xx
và
2
1tx
. Khẳng định nào trong các khẳng định sau là sai :
A.
tdt xdx
1
2
1
3
1
dt
I
t
C.
2
2
2
3
1
dt
I
t
D.
22
1xt
C©u 8 :
Trong không gian với hệ trục tọa độ
Oxyz
, cho hình hộp
.ABCD A B C D
. Biết
3;2;1A
,
4;2;0C
,
2;1;1B
,
3;5;4D
.Tìm tọa độ
A
của hình hộp
.ABCD A B C D
.
Trang 2/ mã đề 242
A.
3;3;3 .A
3; 3; 3 .A

C.
3;3;1 .A
D.
3; 3;3 .A

C©u 9 :
Trong không gian với hệ tọa độ
Oxyz
, cho 3 điểm
2;2;3A
,
1; 1;3B
,
3;1; 1C
và mặt phẳng
P
có phương trình
2 8 0xz
. Gọi
M
là điểm thuộc mặt phẳng
P
sao cho giá trị biểu hức
2 2 2
23T MA MB MC
nhỏ nhất. Tính khoảng cách từ
M
đến mặt phẳng
: 2 2 6 0Q x y z
A.
2
4
C.
3
2
d
D.
3
3
d
C©u 10 :
Khẳng định nào sau đây là sai ?
A.



C.

D.

C©u 11 :
Khối đa diện đều loại
5;3
có số mặt là :
A.
14
8
C.
12
D.
10
C©u 12 :
Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Một mặt phẳng đi qua A’B’
và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Thể tích V của khối C.A’B’FE là :
A.
3
53
54
a
V
3
53
18
a
V
C.
3
3
27
a
V
D.
3
53
27
a
V
C©u 13 :
Trong không gian với hệ tọa độ
Oxyz
. Hãy viết phương trình mặt cầu (S) có tâm
(2;0;1)I
và tiếp
xúc với đường thẳng d:
12
1 2 1
x y z

.
A.
2 2 2
( 2) ( 1) 9.x y z
B.
2 2 2
( 2) ( 1) 4.x y z
C.
2 2 2
( 1) ( 2) ( 1) 24.x y z
D.
2 2 2
( 2) ( 1) 2.x y z
C©u 14 :
Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a. Biết hình chóp có chiều cao là
3ha
.
Thể tích khối chóp là :
A.
3
3
4
a
V
3
3
8
a
V
C.
3
3
a
V
D.
3
4
a
V
C©u 15 :
Cho phương trình
2
2 3 0zz
trên tập số phức,có hai nghiệm là
12
,zz
.Khi đó
22
12
zz
có giá trị
là:
A.
22
6
C.
3
D.
2
C©u 16 :
Cho hàm số


khẳng định nào sau đây là sai ?
A.
Hàm số đồng biến trên R
B.
Tập xác định của hàm số là R
C.
Hàm số nghịch biến trên R
D.
Đồ thị hàm số nằm toàn bộ phía trên trục ox
C©u 17 :
Tập xác định của hàm số
󰇛

󰇜
là :
A.
󰇛

󰇜
󰇛

󰇜
󰇛

󰇜
󰇝

󰇞
C.
󰇛

󰇜
D.
󰇟

󰇠
C©u 18 :
Cho hàm số
32
1
( 1) 4
3
y x m x x
(m là thàm số). Giá trị của m để hàm số đã cho đồng biến trên
R là:
A.
3m
13m
C.
mR
D.
Không có giá trị
nào của m thỏa
mãn
C©u 19 :
Biết 
, giá trị biểu thức 





Trang 3/ mã đề 242
là :
A.
C.
󰇛
󰇜
D.
󰇛
󰇜
C©u 20 :
Nguyên hàm hàm số
cos 3 2f x x
là :
A.
1
sin 3 2
3
f x dx x C
B.
1
sin3
3
f x dx x C
C.
1
sin 3 2
3
f x dx x C
D.
1
sin3
3
f x dx x C
C©u 21 :
Biết
3
2
1
3 ln 1
ln
( 1)
x a c
dx
x b b d

với a,b,c,d là các số nguyên dương và
;
ac
bd
là các phân số tối giản.
Giá trị của
M ac bd
là :
A.
17
20
C.
145
D.
11
C©u 22 :
Diện tích hình phẳng giới hạn bởi các đường
2
2 ; 0; 1; 3y x y x x
bằng :
A.
30
18
C.
98
3
D.
21
C©u 23 :
Phương trình tiếp tuyến với đồ thị hàm số
32
( ) 3 2y f x x x
tại điểm
0
x
sao cho
0
"( ) 6fx
là:
A.
3 3 0xy
20y 
C.
20y 
D.
3 3 0xy
C©u 24 :
Cho số phức
32zi
. Tìm số phức
2
1w z i z
A.
78wi
78wi
C.
35wi
D.
35wi
C©u 25 :
Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
2
9 ; 0y x y
xung quanh trục Ox là :
A.
8
3
71
82
C.
1296
5
D.
3
C©u 26 :
Cho hàm số
()y f x
có đồ thị (C) như hình vẽ.
Số nghiệm phân biệt của phương trình
1
()
2
fx
là:
A.
2
0
C.
1
D.
3
C©u 27 :
Giá trị của m để phương trình
3
4 3 1x x mx m
có 4 nghiệm phân biệt là :
A.
1;6 3 9m
B.
6 3 9;6 3 9m
C.
9 6 3; 1m
D.
9 6 3;1m
C©u 28 :
Đạo hàm của hàm số

là :
A.



B.
󰇛 󰇜

Trang 4/ mã đề 242
C.

󰇛
󰇜



D.

󰇛

󰇜



C©u 29 :
Cho hai số phức
12
, zz
thỏa mãn
12
1zz
,
12
3zz
. Tính
12
zz
:
A.
4
1
C.
2
D.
3
C©u 30 :
Cho (P) là đồ thị hàm số
2
43y x x
. Diện tích hình phẳng giới hạn bởi (P) và các tiếp tuyến của
(P) kẻ từ điểm
2; 5A
là :
A.
10
3
16
3
C.
32
3
D.
8
3
C©u 31 :
Cho
33
22
2; 3f x dx g t dt

. Giá trị của
3
2
32A f x g x dx


là:
A.
12
0
C.
5
D.
-1
C©u 32 :
Phương trình 
󰇛

󰇜
 
Có 2 nghiệm x
1,
x
2
thỏa mãn
khi :
A.

C.
D.
C©u 33 :
Cho số phức
54zi
. Số phức
2z
có
A.
Phần thực bằng
5
và phần ảo bằng
4
.
B.
Phần thực bằng
4
và phần ảo bằng
3
.
C.
Phần thực bằng
3
và phần ảo bằng
4i
.
D.
Phần thực bằng
3
và phần ảo bằng
4
.
C©u 34 :
Một nhà kho có dạng khối hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB
= 3m, BC = 6m, chiều cao AA’ = 3m, chắp thêm một khối lăng trụ tam giác đều mà một mặt bên là
A’B’C’D’ và A’B’ là một cạnh đáy của lăng trụ. Tính thể tích của nhà kho ?
A.
3
9 12 3
2
m
3
27 3
2
m
C.
3
54m
D.
3
27 4 3
2
m
C©u 35 :
Trong các số phức
z
tìm điều kiện :
23z i z i
. Hãy tìm z có mô đun nhỏ nhất
A.
27 6
55
zi
6 27
55
zi
C.
6 27
55
zi
D.
36
55
zi
C©u 36 :
Hàm số
42
2y x x
có điểm cực tiểu là:
A.
2y
1x 
C.
0x
D.
1x
C©u 37 :
Cho hàm số
3
3y x x m
(m là thàm số). Để giá trị lớn nhất của hàm số trên đoạn
0; 3


bằng
52
thì m phải bằng:
A.
32
42
C.
2
D.
22
C©u 38 :
Bất phương trình 
󰇛

󰇜


có tập nghiệm là :
A.
󰇛

󰇜
󰇛

󰇜
󰇛

󰇜
C.
D.
C©u 39 :
Trong không gian với hệ tọa độ
Oxyz
, cho điểm
(2;1;0)M
và đường thẳng : .
Viết phương trình của đường thẳng d đi qua điểm M, cắt và vuông góc với .
A.
d:
21
.
1 4 1
x y z

B.
d:
21
.
2 4 1
x y z

C.
d:
21
.
1 4 2
x y z


D.
d:
21
.
1 4 1
x y z

C©u 40 :
Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
(2;4;1)A
,
( 1;1;3)B
và mặt phẳng
( :)P
x y z11
2 1 1


Trang 5/ mã đề 242
3 2 5 0x y z
. Viết phương trình mặt phẳng
Q
đi qua hai điểm A, B và vuông góc với mặt
phẳng
P
.
A.
:2 3 12 0Q y z
B.
:2 3 11 0Q y z
C.
:2 3 1 0Q y z
D.
:2 3 11 0Q x z
C©u 41 :
Đường thẳng
9y x m
là tiếp tuyến của đường cong
32
31y x x
khi m bằng
A.
-6 hoặc 26
-1 hoặc 3
C.
-3 hoặc 1
D.
3 hoặc -5
C©u 42 :
Một hình nón có bán kính đáy
1r
, chiều cao
4
3
h
. Kí hiệu góc ở đỉnh của hình nón là
2
.
Trong các mệnh đề sau, mệnh đề nào đúng ?
A.
3
sin
5
3
cot
5
C.
3
tan
5
D.
3
cos
5
C©u 43 :
Số đường tiệm cận của đồ thị hàm số
1
y
x
là:
A.
1
2
C.
3
D.
0
C©u 44 :
Cho hai số phức
1
23zi
,
2
12zi
. Tính môđun của số phức
12
2z z z
.
A.
137z
15z
C.
65z
D.
55z
C©u 45 :
Một cốc nước có dạng hình trụ đựng nước, chiều cao 12cm, đường kính đáy 4cm, lượng nước trong
cốc cao 8cm. Thả vào cốc nước 4 viên bi có cùng đường kính 2cm. Hỏi nước dâng cao cách mép cốc
bao nhiêu cm ? ( làm tròn sau dấu phẩy hai chữ số thập phân, bỏ qua độ dày cốc ).
A.
2,33cm
2,25cm
C.
2,75cm
D.
2,67cm
C©u 46 :
Phương trình

có 2 nghiệm phân biệt khi :
A.

C.


D.
C©u 47 :
Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
có
1;3;4A
,
2;3;0B
,
1; 3;2C 
.
Tìm tọa độ trọng tâm
G
của tam giác
ABC
.
A.
2
;2;2 .
3
G



2
;1;2 .
3
G



C.
2
;1;1 .
3
G



D.
2;1;2 .G
C©u 48 :
Cho hình trụ có độ dài đường sinh là l và bán kính đường tròn đáy là r. Diện tích toàn phần của hình
trụ là :
A.
2
tp
S r l r

2
tp
S r l r

C.
22
tp
S r l r

D.
tp
S r l r

C©u 49 :
Cho
1;0; 3 ; 2;1;2ab
.Khi đó
;ab


có giá trị là
A.
8
3
C.
74
D.
4
C©u 50 :
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
x
y
x
trên đoạn
1;3
lần lượt là:
A.
3
4
và
1
2
0 và -1
C.
3 và -1
D.
1
3
và -1
------------------------------------------------------Hết-----------------------------------------------------
BẢNG ĐÁP ÁN 1
Cau
235
236
237
238
1
C
D
C
B
2
B
D
B
D
3
D
B
D
C
4
B
A
C
D
5
B
D
B
A
6
B
C
B
C
7
B
B
C
A
8
A
D
A
C
9
D
C
B
C
10
D
D
B
C
11
D
D
A
A
12
C
A
C
B
13
C
D
A
D
14
A
B
A
B
15
A
B
D
B
16
D
A
D
D
17
A
C
C
C
18
C
C
C
B
19
B
A
B
A
20
A
B
D
C
21
A
B
A
D
22
B
C
A
B
23
C
A
B
A
24
B
A
D
C
25
C
A
D
D
26
D
B
C
D
27
D
D
C
A
28
A
D
A
C
29
A
B
C
B
30
C
B
A
A
31
C
D
A
A
32
D
D
C
A
33
D
C
B
A
34
C
C
A
D
35
D
B
C
D
36
C
A
A
B
37
A
A
B
B
38
A
C
D
C
39
B
C
B
B
40
D
A
B
C
41
A
C
D
A
42
A
A
D
D
43
C
B
A
A
44
B
D
D
B
45
C
A
D
B
46
B
B
A
C
47
B
C
D
D
48
D
C
C
D
49
B
B
B
B
50
A
A
B
A
BẢNG ĐÁP ÁN 2
Cau
239
240
241
242
1
B
B
D
D
2
A
C
A
A
3
A
B
B
A
4
D
D
B
C
5
A
D
D
C
6
C
A
B
C
7
B
C
D
C
8
C
A
A
A
9
B
A
A
B
10
B
C
B
A
11
D
D
C
C
12
A
A
A
A
13
D
D
C
D
14
C
C
A
D
15
D
B
B
B
16
D
B
C
A
17
B
A
A
A
18
B
D
C
D
19
C
C
D
D
20
D
A
A
A
21
D
B
C
A
22
D
B
A
C
23
C
C
C
C
24
A
A
B
B
25
B
B
A
C
26
A
A
C
D
27
C
C
B
C
28
C
A
B
D
29
B
B
A
B
30
D
C
B
B
31
D
D
D
A
32
D
B
D
B
33
B
C
B
D
34
B
D
D
D
35
B
A
B
D
36
C
C
C
C
37
A
D
D
B
38
A
A
D
B
39
B
C
A
C
40
A
D
A
B
41
A
B
D
A
42
C
A
B
A
43
A
B
D
B
44
D
B
D
D
45
A
A
A
D
46
C
B
C
B
47
B
D
C
B
48
A
D
C
B
49
C
D
B
C
50
C
C
C
A
| 1/44
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Trường THPT Quốc Oai
ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2016 -2017
Môn: Toán ; thời gian 90 phút; mã đề 235
(đề gồm 50 câu trắc nghiệm)
Họ và tên thí sinh:………………………………………………….. số báo danh:………… C©u 1 : 3 Đặ dx t I   và x
t e 1. Khẳng định nào trong các khẳng định sau là sai : x e 1 1 3 e 1  1 1  3 I   dt    1 1  I   2
ln e e   1  2 A. t t 1 B. x dt e dx C. I   dt   D. e 1   t t 1 1
C©u 2 : Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Biết hình chóp có chiều cao là
h a 3 . Thể tích khối chóp là : 3 a 3 3 a 3 3 a A. 3 V a 3 B. V C. V D. V  3 8 3
C©u 3 : Trong không gian với hệ tọa độ Oxyz , cho 3 điểm A1;2;3 , B0;1;  1 , C 1;0; 2   và mặt phẳng
P có phương trình x y z  2  0 . Gọi M là điểm thuộc mặt phẳng P sao cho giá trị biểu thức 2 2 2
T MA  2MB  3MC nhỏ nhất. Tính khoảng cách từ M đến mặt phẳng
Q : 2x y  2z 3  0 2 5 121 91 A. B. C. 24 D. 3 54 54
C©u 4 : Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Một mặt phẳng đi qua A’B’
và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Thể tích V của khối A’B’.BAEF là : 3 a 3 3 2a 3 3 a 3 3 5a 3 A. V B. V C. V D. V  27 27 18 54
C©u 5 : Bất phương trình có tập nghiệm là : A. B. C. D.
C©u 6 : Cho hình chóp đều S.ABCD có AB = a , mặt bên (SAD) tạo với đáy (ABCD) một góc 60o . Tính thể
tích V của khối chóp S.ABCD ? 3 a 3 3 3a 3 a 3 A. 3 V a 2 B. V C. V D. V  6 2 3 C©u 7 :
Cho hàm số khẳng định nào sau đây là sai ?
A. Hàm số đồng biến trên R
B. Hàm số nghịch biến trên R
C. Đồ thị hàm số nằm toàn bộ phía trên trục ox
D. Tập xác định của hàm số là R C©u 8 : Cho hàm số 4 2
y x  2x  5 . Chọn khẳng định đúng?
A. Hàm số đồng biến trên khoảng  1  ;0 và (1;)
B. Hàm số nghịch biến trên khoảng  ;    1 và (1; )
C. Hàm số nghịch biến trên khoảng  1  ;0 và (1;)
D. Hàm số đồng biến trên khoảng  1   ;1
C©u 9 : Trong các số phức thỏa mãn điều kiện z  
1 z  2i là số thực. Hãy tìm z có mô đun nhỏ nhất Trang 1 / mã đề 235 2 4 2 4 2 4 4 2 A. Z   i B. Z   i C. Z    i D. Z   i 5 5 5 5 5 5 5 5
C©u 10 : Trong không gian với hệ tọa độ Oxyz , tìm m để phương trình 2 2 2
x y z  2mx  2(m  2) y  2(m  3)z  8m  37  0 là phương trình của một mặt cầu A. m  2  hay m  4 B. m  4  hay m  2 C. m  4  hay m  2  D. m  2  hay m  4
C©u 11 : Điểm biểu diễn của các số phức z  7  bi với b
, nằm trên đường thẳng có phương trình là: A. y x
B. y x  7 C. y  7 D. x  7
C©u 12 : Cho (P) là đồ thị hàm số 2
y x  4x  5 . Diện tích hình phẳng giới hạn bởi (P) và các tiếp tuyến của  5  (P) kẻ từ điểm A ; 1    là :  2  18 9 9 9 A. B. C. D. 4 2 4 8
C©u 13 : Tìm hàm số F(x) biết Fx 3
 4x  6x 1 và đồ thị hàm số y F x cắt trục tung tại điểm có tung độ bằng 2:
A. F x 4 2
x  3x x 1
B. F x 3
x x  2
C. F x 4 2
x  3x x  2
D. F x 4 2
 4x  6x x  2 C©u 14 : 2 x mx 1 Cho hàm số y
. Tìm m để hàm số đạt cực đại tại x  2 ? Một học sinh làm như sau: x m 2 2
x  2mx m 1
Bước 1: D R \  m , y '   x m2
Bước 2: Hàm số đạt cực đại tại x  2  y '(2)  0  * m  1  Bước 3:   2
*  m  4m  3  0   m  3 
Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào? A. Sai từ bước 2 B. Sai từ bước 3 C. Sai từ bước 1 D. Đúng C©u 15 : 1 x
Số đường tiệm cận của đồ thị hàm số y  2x  là: 1 A. 2 B. 1 C. 3 D. 0 C©u 16 :   Cho điể x 1 y 1 z
m M 2,1,0 và đường thẳng  :  
. Gọi d là đường thẳng đi qua M , cắt và 2 1 1 
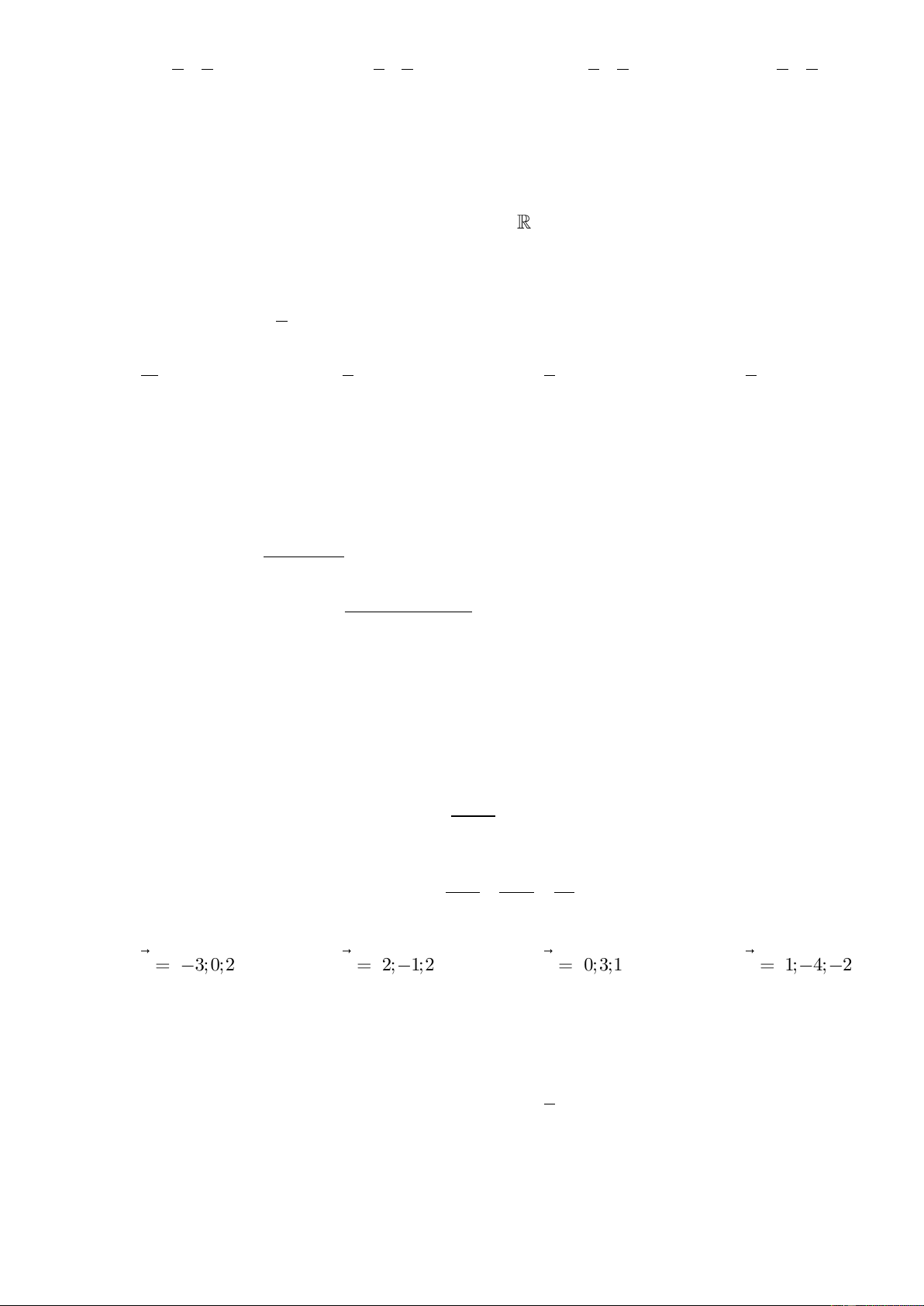
vuông góc với  . Khi đó, vectơ chỉ phương của d là: A. u 3;0;2 B. u 2; 1;2 C. u 0;3;1 D. u 1; 4; 2
C©u 17 : Đường thẳng y  6x m là tiếp tuyến của đường cong 3
y x  3x 1 khi m bằng A. -3 hoặc 1 B. -5 hoặc 1 C. -1 hoặc 3 D. 3 hoặc -5
C©u 18 : Diện tích hình phẳng giới hạn bởi các đường y  x  2
1 ; y  0; x  0; x  2 bằng : 2 A. 35 B. 15 C. D. 21 3
C©u 19 : Một nhà kho có dạng khối hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB
= a, BC = 2a, chiều cao AA’ = 3a, chắp thêm một khối lăng trụ tam giác đều mà một mặt bên là
A’B’C’D’ và A’B’ là một cạnh đáy của lăng trụ. Tính thể tích của nhà kho ? Trang 2 / mã đề 235 36  3 12  3 3 a 3 312  3 A. 3 a B. 3 a C. D. 3 a 6 2 2 2
C©u 20 : Cho hàm số 3
y  3x x m (m là thàm số). Để giá trị lớn nhất của hàm số trên đoạn 0; 3   bằng
3 2 thì m phải bằng: A. 2 2 B. 2 C.  2 D. 3 2 C©u 21 : x 1
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2  ;0 lần lượt là: x  trên đoạn   1 1 1 A. và -1 B.  và -1 C. 3 và -1 D. 0 và -1 3 3
C©u 22 : Đạo hàm của hàm số là : A. B. C. D.
C©u 23 : Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 2
y  4  x ; y  0 xung quanh trục Ox là : 71 512 8 A. 2 B. C. D.  82 15 3 C©u 24 :
Biết , giá trị biểu thức là : A. B. C. D.
C©u 25 : Số phức z    i3 1 có mô đun bằng: A. z  0 B. z  2  2 C. z  2 2 D. z  2
C©u 26 : Mệnh đề nào sau đây sai ?
A. Mặt phẳng  P : 4x  2y  3  0 song song với mặt phẳng Q : 2xy  5  0 .
B. Mặt phẳng 3x – z  2  0 có tọa độ vectơ pháp tuyến là 3, 0,  1  .
C. Mặt phẳng 2x  3y – 2z  0 đi qua gốc tọa độ.
2x  2y z 1
D. Khoảng cách từ điểm M x , y , z đến mặt phẳng 2x  2y z 1  0 là 0 0 0 . 0 0 0  3 C©u 27 : 1
Cho số phức z a bi . Khi đó số  z z  là: 2 A. 2 B. i
C. Một số thuần ảo D. Một số thực. C©u 28 : 1 Hàm số 3 2 y
x x  3x  2 đạt cực tiểu tại: 3 1 A. x  1 B. x  3  C. x D. x  0 3
C©u 29 : Giá trị của m để phương trình 3
4 x  3 x 1  mx m có 4 nghiệm phân biệt là :
A. m 1;6 3  9
B. m 9  6 3;  1
C. m 6 3  9;6 3  9
D. m 9  6 3;  1
C©u 30 : Tập nghiệm của bất phương trình là : Trang 3 / mã đề 235 A. B. C. D.
C©u 31 : Phương trình
Có 2 nghiệm x1, x2 thỏa mãn khi : A. B. C. D.
C©u 32 : Phương trình tham số của đường thẳng d đi qua điểm M 1,2,3 và có vec tơ chỉ phương a (1;3;2) là : x  1   tx  1   tx  1 tx  1 t     A. y  2   3t B. y  2   3t C. y  2   3t
D. y  2  3t     z  3   2tz  3   2tz  3  2tz  3  2t
C©u 33 : Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z  2z  3  0 . Tọa độ điểm M biểu diễn 1 số phức z là: 1 A. M ( 1  ; 2i) B. M ( 1  ; 2  ) C. M ( 1  ;2) D. M ( 1  ; 2) C©u 34 : 2 2 2 Cho
f xdx  3; g t dt  1   
. Giá trị của A  2 f
 x3gxdx  là: 1 1 1 A. 9 B. 5 C. 3 D. 2
C©u 35 : Số nghiêm của phương trình 4 z  1 là A. 2 B. 1 C. 3 D. 4 C©u 36 : 2 ln x a c a c Biết dx   ln 2 
với a,b,c,d là các số nguyên dương và ;
là các phân số tối giản. Giá 3 x b d b d 1
trị của M ad bc là : A. 10 B. 40 C. 8 D. 32
C©u 37 : Phương trình tiếp tuyến với đồ thị hàm số 3 2
y f (x)  x  3x  2 tại điểm x sao cho f "(x )  0 là: 0 0
A. 3x y  3  0
B. 3x y  3  0 C. 3
x y 3  0
D. 3x y  3  0 C©u 38 :
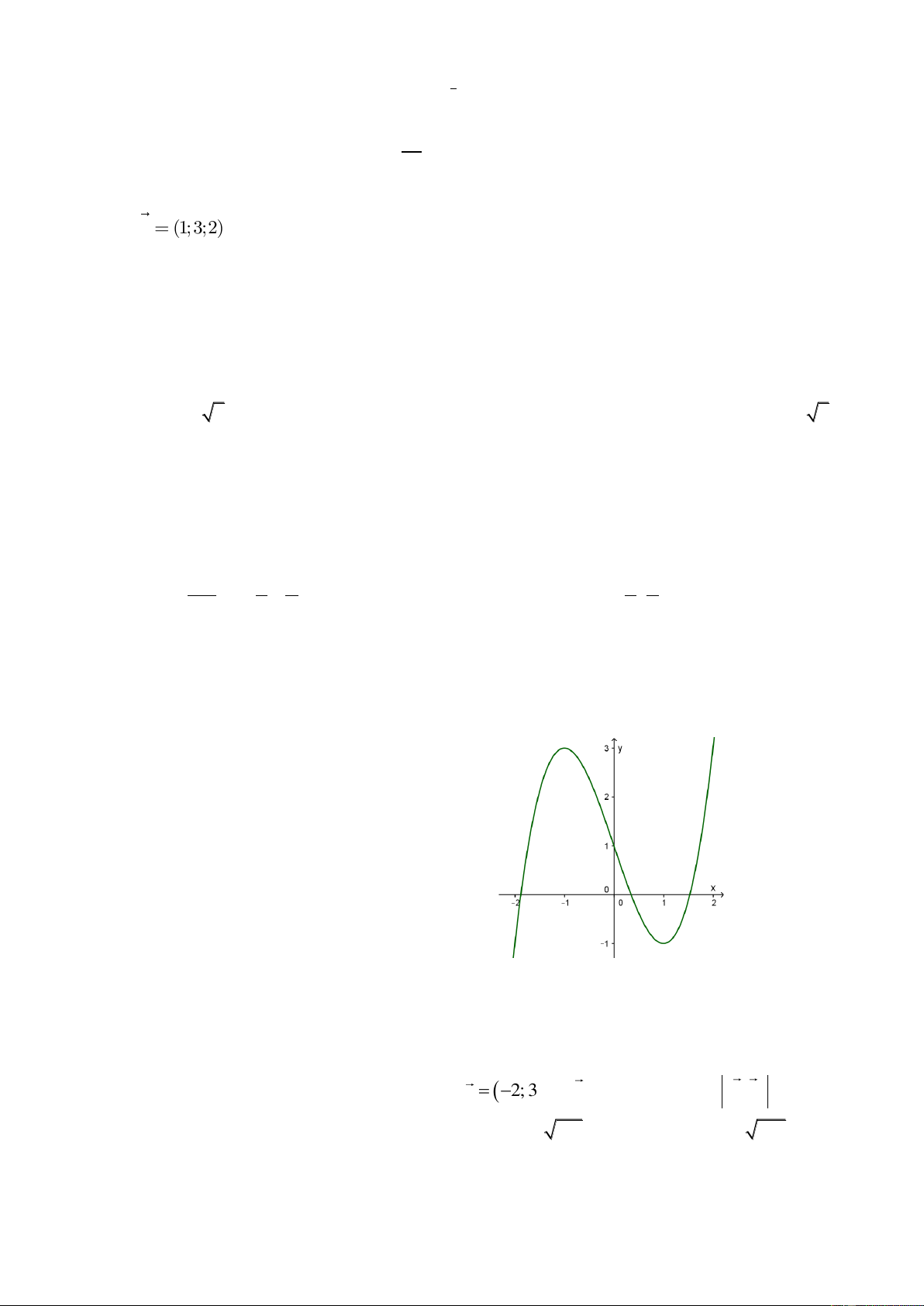
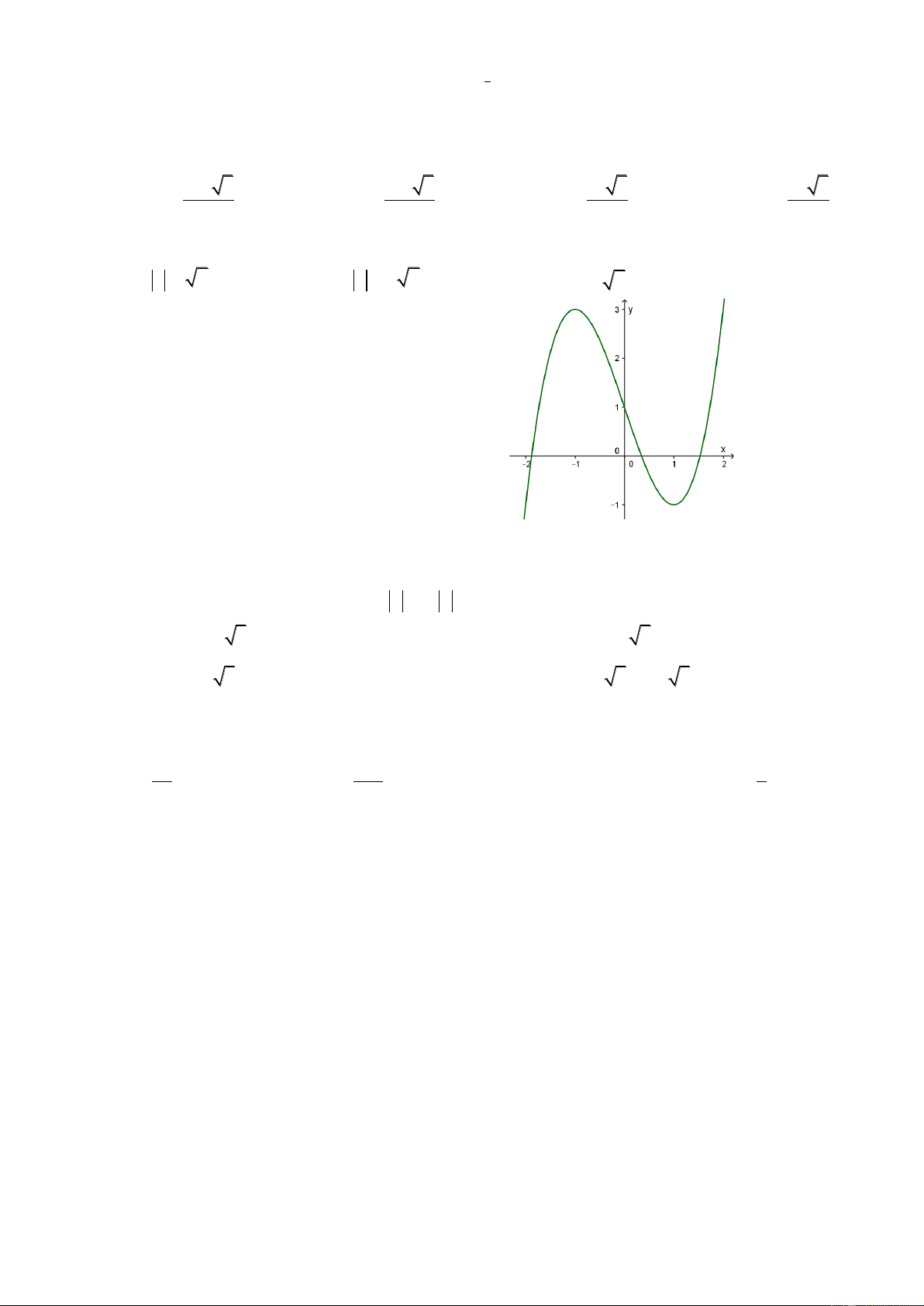
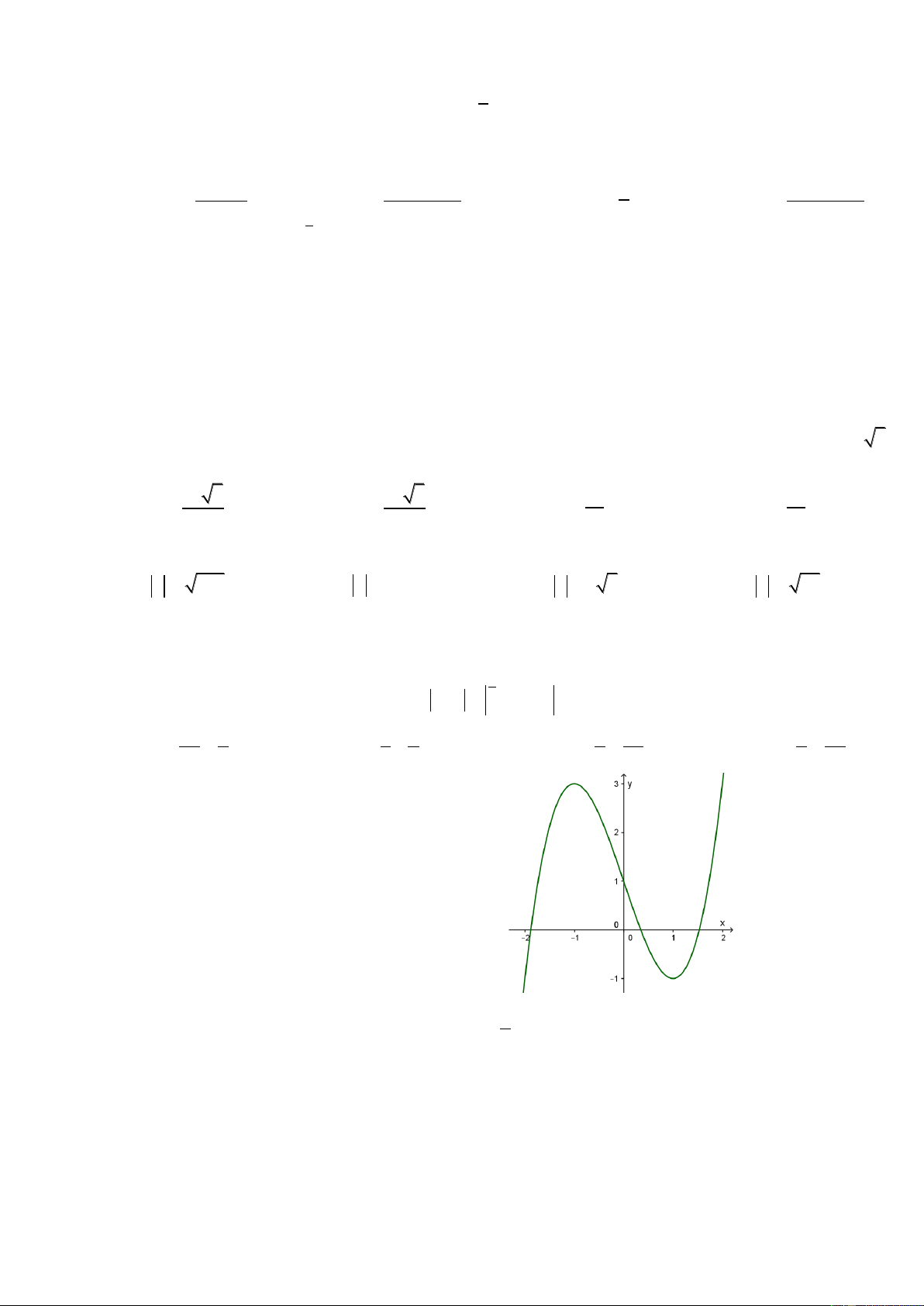
Cho hàm số y f (x) có đồ thị (C) như hình vẽ.
Số nghiệm phân biệt của phương trình f (x)  1  là: A. 2 B. 3 C. 1 D. 0
C©u 39 : Khẳng định nào sau đây là sai ? A. B. C. D.
C©u 40 : Trong không gian với hệ tọa độ Oxyz , cho a   2  ; 3; 
1 , b  1;  3; 4 . Tìm  ; a b   A. 171 B. 315 C. 171 D. 315
C©u 41 : Cho hình trụ có độ dài đường sinh là b và bán kính đường tròn đáy là a. Diện tích toàn phần của hình trụ là : Trang 4 / mã đề 235
A. S  2 a b a
S   a 2b a
S  2 a b  2a
S   a b a tp   B. tp   C. tp   D. tp   C©u 42 : 1 Cho hàm số 3 2
y   x  (m 1)x  4x (m là thàm số). Giá trị của m để hàm số đã cho nghịch biến 3 trên R là: m  1  A. 1   m  3 B. m   R C. m  3 D.  m  3 C©u 43 :
Nguyên hàm hàm số f x  sin 2x   1 là : 1 A. f  x 1 dx  cos 2x C B. f
 xdx  cos2x 1C 2 2 1 C. f
 xdx   cos2x 1C D. f  x 1 dx   cos 2x C 2 2
C©u 44 : Một hình nón có bán kính đáy r  3a , chiều cao h  4a . Kí hiệu góc ở đỉnh của hình nón là 2 .
Trong các mệnh đề sau, mệnh đề nào đúng ? 4 4 4 A. sin   B. cos  C. C. D. cot   5 5 5
C©u 45 : Phương trình có 2 nghiệm phân biệt khi : A. B. C. D. C©u 46 :
Tập xác định của hàm số là : A. B. C. D.
C©u 47 : Một cốc nước có dạng hình trụ đựng nước, chiều cao 16cm, đường kính đáy 6cm, lượng nước trong
cốc cao 10cm. Thả vào cốc nước 4 viên bi có cùng đường kính 4cm. Hỏi nước dâng cao cách mép
cốc bao nhiêu cm ? ( làm tròn sau dấu phẩy hai chữ số thập phân, bỏ qua độ dày cốc ). A. 1,34cm B. 1,26cm C. 1,68cm D. 1,43cm
C©u 48 : Trong không gian với hệ tọa độ Oxyz , cho a  1;2; 
1 , b  3; 4;3 . Tìm tọa độ của x biết
x b a
A. x  1;1; 2. B. x   2  ; 2  ;4. C. x   2  ; 2  ; 4  .
D. x  2; 2; 4.
C©u 49 : Cho hàm số khẳng định nào dưới đây là đúng ?
A. Đồ thị hàm số không có tiệm cận
B. Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm cận đứng
C. Đồ thị hàm số có 1 tiệm cận đứng và không có
D. Đồ thị hàm số cắt trục ox tiệm cận ngang
C©u 50 : Khối đa diện đều loại 3;  5 có số mặt là : A. 20 B. 16 C. 12 D. 8
-----------------------------------------------------Hết------------------------------------------------ Trang 5 / mã đề 235
Trường THPT Quốc Oai
ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2016 -2017
Môn: Toán ; thời gian 90 phút; mã đề 239
(đề gồm 50 câu trắc nghiệm)
Họ và tên thí sinh:………………………………………………….. số báo danh:…………
C©u 1 : Bất phương trình có tập nghiệm là : A. B. C. D.
C©u 2 : Đường thẳng y  9x m là tiếp tuyến của đường cong 3 2
y x  3x 1 khi m bằng A. -6 hoặc 26 B. -1 hoặc 3 C. -3 hoặc 1 D. 3 hoặc -5
C©u 3 : Phương trình tiếp tuyến với đồ thị hàm số 3 2
y f (x)  x  3x  2 tại điểm x sao cho f "(x )  6 là: 0 0
A. y  2  0
B. 3x y  3  0 C. y  2  0
D. 3x y  3  0
C©u 4 : Cho số phức z  5  4i . Số phức z  2 có
A. Phần thực bằng 3 và phần ảo bằng 4  i .
B. Phần thực bằng 4
 và phần ảo bằng 3 .
C. Phần thực bằng 5 và phần ảo bằng 4  .
D. Phần thực bằng 3 và phần ảo bằng 4  . C©u 5 : x
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  1;3 lần lượt là: x  trên đoạn   1 3 1 1 A. và B.  và -1 C. 3 và -1 D. 0 và -1 4 2 3
C©u 6 : Diện tích hình phẳng giới hạn bởi các đường y  x  2
2 ; y  0; x  1; x  3 bằng : 98 A. 21 B. 30 C. D. 18 3
C©u 7 : Khẳng định nào sau đây là sai ? A. B. C. D.
C©u 8 : Phương trình
Có 2 nghiệm x1, x2 thỏa mãn khi : A. B. C. D.
C©u 9 : Cho hàm số khẳng định nào dưới đây là đúng ?
A. Đồ thị hàm số cắt trục ox
B. Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm cận đứng
C. Đồ thị hàm số không có tiệm cận
D. Đồ thị hàm số có 1 tiệm cận đứng và không có tiệm cận ngang
C©u 10 : Một cốc nước có dạng hình trụ đựng nước, chiều cao 12cm, đường kính đáy 4cm, lượng nước trong
cốc cao 8cm. Thả vào cốc nước 4 viên bi có cùng đường kính 2cm. Hỏi nước dâng cao cách mép cốc
bao nhiêu cm ? ( làm tròn sau dấu phẩy hai chữ số thập phân, bỏ qua độ dày cốc ). A. 2,75cm B. 2,67cm C. 2,33cm D. 2,25cm
C©u 11 : Cho hai số phức z  2  3i , z 1 2i . Tính môđun của số phức z  z  2 z . 1  1 2 2 A. z  65 B. z  15 C. z  137 D. z  5 5 C©u 12 : 1 Cho hàm số 3 2 y
x  (m 1)x  4x (m là thàm số). Giá trị của m để hàm số đã cho đồng biến trên 3 R là: Không có giá trị A. B. m   R C. 1   m  3 D. m  3 nào của m thỏa Trang 1/ mã đề 239 mãn
C©u 13 : Trong không gian với hệ trục tọa độ Oxyz , cho hình hộp ABC . D A BCD   . Biết A 3  ;2;  1 ,
C 4;2;0 , B 2  ;1; 
1 , D3;5;4 .Tìm tọa độ A của hình hộp ABC . D A BCD   . A. A 3  ; 3  ; 3  . B. A 3  ; 3  ;3. C. A 3  ;3;  1 . D. A 3  ;3;3.
C©u 14 : Tìm hàm số F(x) biết Fx 2
 3x  2x 1 và đồ thị hàm số y F x cắt trục tung tại điểm có tung độ bằng e:
A. F x 3 2
x x x 1
B. F x 2
x x e 1 C.   3 2
F x x x x e
D. F x 2
x x  2
C©u 15 : Cho hai số phức z , z thỏa mãn z z 1, z z  3 . Tính z z : 1 2 1 2 1 2 1 2 A. 3 B. 2 C. 4 D. 1
C©u 16 : Trong các số phức z tìm điều kiện : z i z  2 3i . Hãy tìm z có mô đun nhỏ nhất 27 6 6 27 6 27 3 6 A. z   i B. z    i C. z    i D. z   i 5 5 5 5 5 5 5 5 C©u 17 :
Tập xác định của hàm số là : A. B. C. D. C©u 18 : Cho hàm số
khẳng định nào sau đây là sai ?
A. Đồ thị hàm số nằm toàn bộ phía trên trục ox
B. Hàm số đồng biến trên R
C. Hàm số nghịch biến trên R
D. Tập xác định của hàm số là R
C©u 19 : Phương trình có 2 nghiệm phân biệt khi : A. B. C. D. C©u 20 : x 1 y 1 z
Trong không gian với hệ tọa độ Oxyz , cho điểm M (2;1;0) và đường thẳng :   . 2 1 1 
Viết phương trình của đường thẳng d đi qua điểm M, cắt và vuông góc với . x  2 y 1 z x  2 y 1 z A. d:   . B. d:   . 1 4 1 2 4  1 x  2 y 1 z x  2 y 1 z C. d:   . D. d:   . 1 4  1 1 4  2 
C©u 21 : Trong không gian với hệ tọa độ Oxyz . Hãy viết phương trình mặt cầu (S) có tâm I (2;0;1) và tiếp x 1 y z  2
xúc với đường thẳng d:   . 1 2 1 A. 2 2 2
(x  2)  y  (z 1)  4. B. 2 2 2
(x  2)  y  (z 1)  9. C. 2 2 2
(x 1)  ( y  2)  (z 1)  24. D. 2 2 2
(x  2)  y  (z 1)  2.
C©u 22 : Trong không gian với hệ tọa độ Oxyz , cho hai điểm ( A 2; 4;1) , B( 1
 ;1;3) và mặt phẳng (P) :
x  3y  2z  5  0 . Viết phương trình mặt phẳng Q đi qua hai điểm A, B và vuông góc với mặt
phẳng  P.
A. Q : 2y  3z 1  0
B. Q : 2y  3z 12  0
C. Q : 2x  3z 11  0
D. Q : 2y  3z 11  0 C©u 23 : 2 Đặ dx t I   và 2 t
x 1 . Khẳng định nào trong các khẳng định sau là sai : 2  2 x x 1 3 Trang 2/ mã đề 239 1 dt 2 dt I   
A. tdt xdx B. I  2 t 1 C. 2  D. 2 2 x t 1 1 t 1 2 3 3
C©u 24 : Cho hàm số 3
y  3x x m (m là thàm số). Để giá trị lớn nhất của hàm số trên đoạn 0; 3   bằng
5 2 thì m phải bằng: A. 4 2 B. 2 C. 2 2 D. 3 2
C©u 25 : Cho hình chóp đều S.ABCD có AC = 2a , mặt bên (SBC) tạo với đáy (ABCD) một góc 45o . Tính
thể tích V của khối chóp S.ABCD ? 3 2 3a 3 a 2 3 a A. V B. V C. 3 V a 2 D. V  3 3 2 C©u 26 : 2 x mx 1 Cho hàm số y
. Tìm m để hàm số đạt cực đại tại x  2 ? Một học sinh làm như sau: x m 2 2    Bướ x 2mx m 1
c 1: D R \   m , y '   x m2
Bước 2: Hàm số đạt cực đại tại x  2  y '(2)  0  * m  1  Bước 3:   2
*  m  4m  3  0   m  3 
Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào? A. Sai từ bước 1 B. Đúng C. Sai từ bước 2 D. Sai từ bước 3 C©u 27 : 3 3  ln x a 1 c a c Biết dx   ln 
với a,b,c,d là các số nguyên dương và ;
là các phân số tối giản. 2 (x 1) b b d b d 1
Giá trị của M ac bd là : A. 145 B. 20 C. 17 D. 11 C©u 28 :
Nguyên hàm hàm số f x  cos3x  2 là : 1 A. f  x 1
dx   sin 3x C B. f
 xdx   sin3x2C 3 3 1 C. f
 xdx  sin3x2C D. f  x 1 dx  sin 3x C 3 3
C©u 29 : Đạo hàm của hàm số là : A. B. C. D.
C©u 30 : Trong không gian với hệ tọa độ Oxyz , cho 3 điểm A 2  ;2;3 , B1; 1
 ;3 ,C 3;1;  1 và mặt phẳng
Pcó phương trình x2z 8  0. Gọi M là điểm thuộc mặt phẳng P sao cho giá trị biểu hức 2 2 2
T  2MA MB  3MC nhỏ nhất. Tính khoảng cách từ M đến mặt phẳng
Q:x  2y 2z 6  0 3 3 A. d B. 2 C. d D. 4 2 3
C©u 31 : Cho phương trình 2
z  2z  3  0 trên tập số phức,có hai nghiệm là z , z .Khi đó 2 2 zz có giá trị 1 2 1 2 là: Trang 3/ mã đề 239 A. 3 B. 2 2 C. 2 D. 6
C©u 32 : Cho a  1;0; 3
 ;b  2;1;2 .Khi đó  ; a b   có giá trị là A. 4 B. 8 C. 3 D. 74
C©u 33 : Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a. Biết hình chóp có chiều cao là h a 3 .
Thể tích khối chóp là : 3 a 3 3 a 3 a 3 a 3 A. V B. V C. V D. V  4 4 3 8
C©u 34 : Một nhà kho có dạng khối hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB
= 3m, BC = 6m, chiều cao AA’ = 3m, chắp thêm một khối lăng trụ tam giác đều mà một mặt bên là
A’B’C’D’ và A’B’ là một cạnh đáy của lăng trụ. Tính thể tích của nhà kho ? 27 3 27 4  3 912  3 A. 3 m B. 3 m C. 3 54m D. 3 m 2 2 2
C©u 35 : Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Một mặt phẳng đi qua A’B’
và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Thể tích V của khối C.A’B’FE là : 3 a 3 3 5a 3 3 5a 3 3 5a 3 A. V B. V C. V D. V  27 54 18 27
C©u 36 : Tập nghiệm của bất phương trình là : A. B. C. D.
C©u 37 : Khối đa diện đều loại 5;  3 có số mặt là : A. 12 B. 14 C. 8 D. 10
C©u 38 : Giá trị của m để phương trình 3
4 x  3 x 1  mx m có 4 nghiệm phân biệt là :
A. m 9  6 3;  1
B. m 9  6 3;  1
C. m 1;6 3  9
D. m 6 3  9;6 3  9
C©u 39 : Biết , giá trị biểu thức là : A. B. C. D. C©u 40 : 1
Số đường tiệm cận của đồ thị hàm số y  là: x A. 2 B. 3 C. 1 D. 0
C©u 41 : Cho hình trụ có độ dài đường sinh là l và bán kính đường tròn đáy là r. Diện tích toàn phần của hình trụ là :
A. S  2 r l r
S   r l r
S   r 2l r
S  2 r l  2r tp   B. tp   C. tp   D. tp  
C©u 42 : Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 2
y  9  x ; y  0 xung quanh trục Ox là : 71 1296 8 A. B. 3 C. D.  82 5 3
C©u 43 : Cho hàm số 3 2
y x  3x  3
 . Chọn khẳng định sai? Trang 4/ mã đề 239
A. Hàm số không có cực trị
B. Hàm số nghịch biến trên khoảng 0; 2
Hàm số đồng biến trên khoảng  ;  0và
D. Hàm số có hai điểm cực trị C. (2; )  C©u 44 : 2 Cho số phức z 3
2i . Tìm số phức w z 1 i z A. w 3 5i B. w 3 5i C. w 7 8i D. w 7 8i C©u 45 : Hàm số 4 2
y x x  2 có điểm cực tiểu là: A. x  0 B. x  1 C. y  2 D. x  1 
C©u 46 : Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A1;3;4, B 2  ;3;0 , C  1  ;3;2.
Tìm tọa độ trọng tâm G của tam giác ABC .  2   2   2  A. G  ;1;1 .   B. G  2  ;1;2. C. G  ;1; 2 .  
D. G  ; 2; 2 .    3   3   3  C©u 47 : 4
Một hình nón có bán kính đáy r  1 , chiều cao h
. Kí hiệu góc ở đỉnh của hình nón là 2 . 3
Trong các mệnh đề sau, mệnh đề nào đúng ? 3 3 3 3 A. cot   B. sin   C. tan  D. cos  5 5 5 5 C©u 48 :
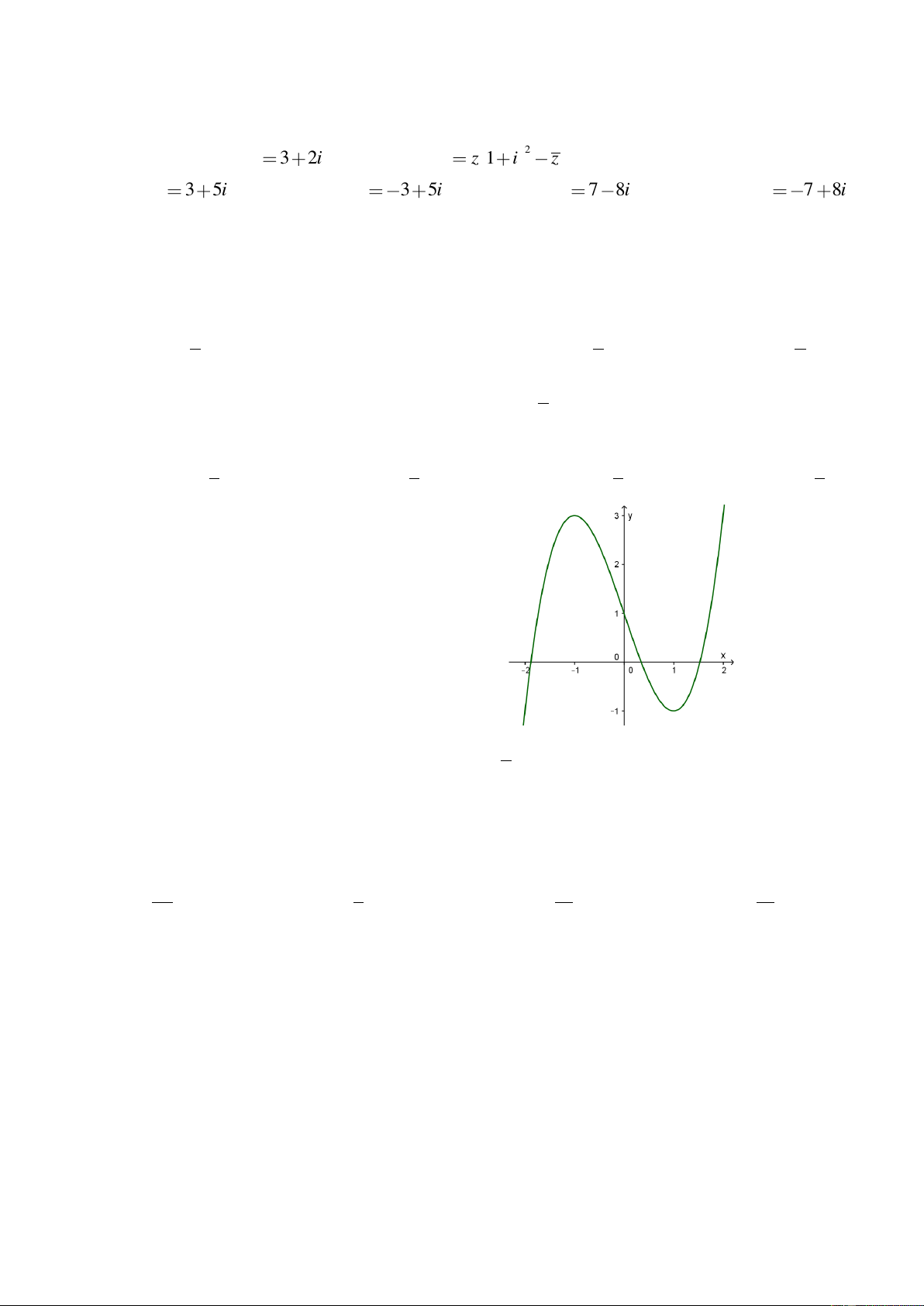
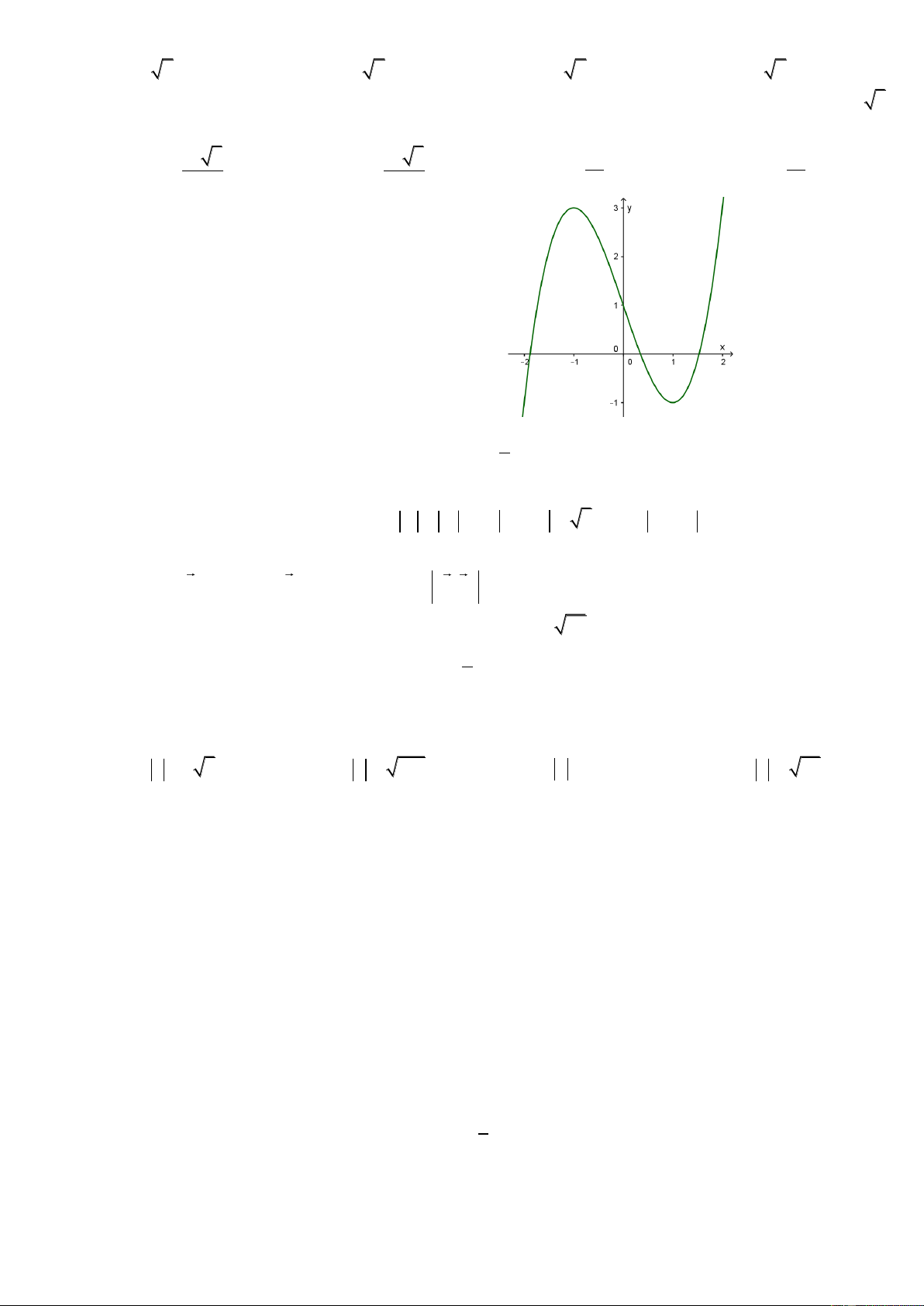
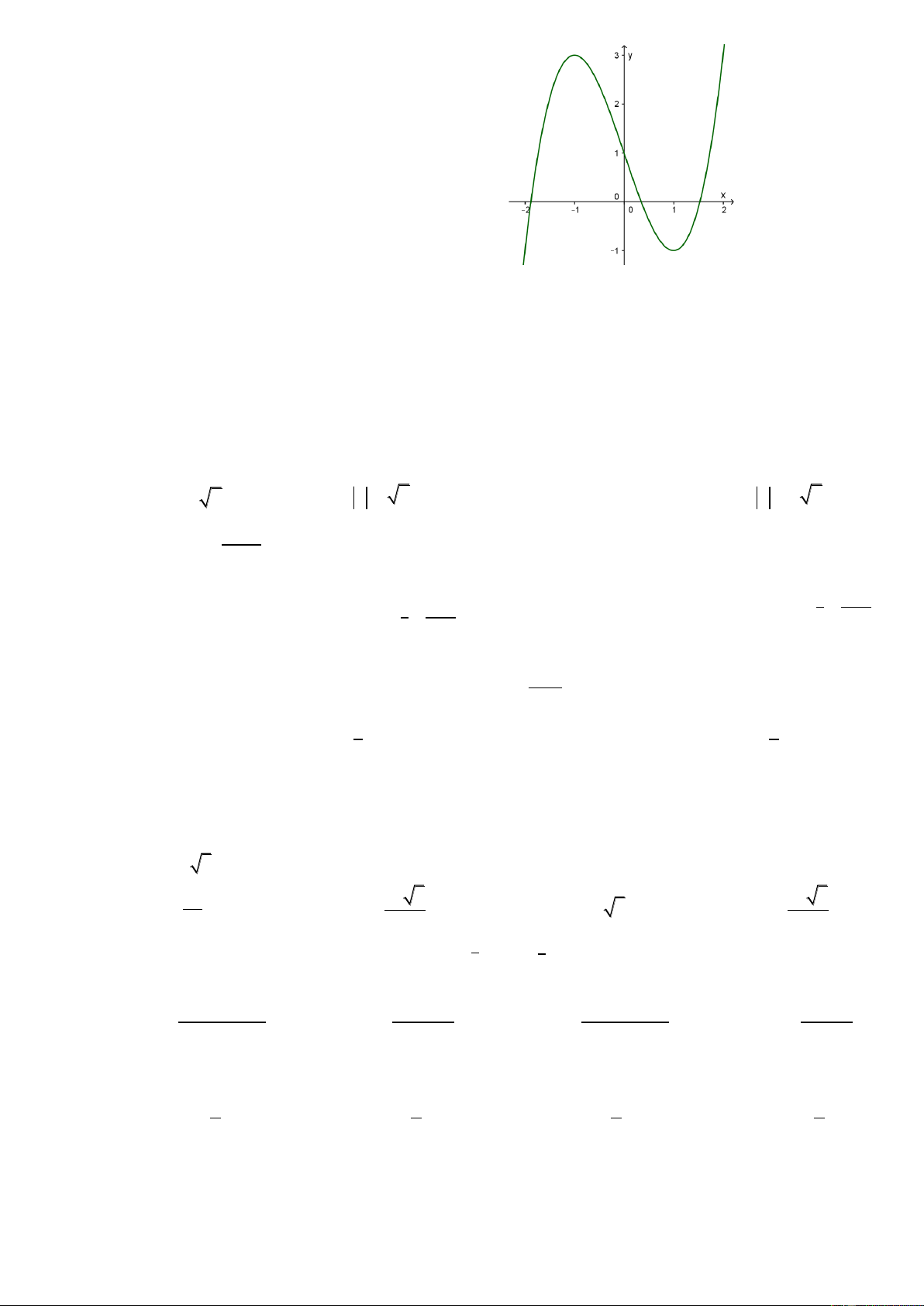
Cho hàm số y f (x) có đồ thị (C) như hình vẽ.
Số nghiệm phân biệt của phương trình 1 f (x)  là: 2 A. 3 B. 2 C. 1 D. 0
C©u 49 : Cho (P) là đồ thị hàm số 2
y x  4x  3 . Diện tích hình phẳng giới hạn bởi (P) và các tiếp tuyến của
(P) kẻ từ điểm A2; 5   là : 32 8 16 10 A. B. C. D. 3 3 3 3 C©u 50 : 3 3 3 Cho
f xdx  2; g t dt  3   
. Giá trị của A  3 f
 x2gxdx  là: 2 2 2 A. 0 B. -1 C. 12 D. 5
--------------------------------------------------------------Hết---------------------------------------------------------- Trang 5/ mã đề 239
Trường THPT Quốc Oai
ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2016 -2017
Môn: Toán ; thời gian 90 phút; mã đề 236
(đề gồm 50 câu trắc nghiệm)
Họ và tên thí sinh:………………………………………………….. số báo danh:…………
C©u 1 : Trong không gian với hệ tọa độ Oxyz , cho a  1;2; 
1 , b  3; 4;3 . Tìm tọa độ của x biết
x b a
A. x  1;1; 2. B. x   2  ; 2  ; 4  . C. x   2  ; 2  ;4.
D. x  2; 2; 4.
C©u 2 : Trong không gian với hệ tọa độ Oxyz , cho a   2  ; 3; 
1 , b  1;  3; 4 . Tìm  ; a b   A. 171 B. 315 C. 171 D. 315
C©u 3 : Đường thẳng y  6x m là tiếp tuyến của đường cong 3
y x  3x 1 khi m bằng A. 3 hoặc -5 B. -3 hoặc 1 C. -5 hoặc 1 D. -1 hoặc 3 C©u 4 :
Cho hàm số khẳng định nào sau đây là sai ?
A. Hàm số nghịch biến trên R
B. Tập xác định của hàm số là R
C. Hàm số đồng biến trên R
D. Đồ thị hàm số nằm toàn bộ phía trên trục ox C©u 5 : 1 Cho hàm số 3 2
y   x  (m 1)x  4x (m là thàm số). Giá trị của m để hàm số đã cho nghịch biến 3 trên R là: m  1  A. m   R B. m  3 C. D. 1   m  3 m  3
C©u 6 : Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z  2z  3  0 . Tọa độ điểm M biểu diễn 1 số phức z là: 1 A. M ( 1  ; 2  ) B. M ( 1  ; 2i) C. M ( 1  ; 2) D. M ( 1  ;2) C©u 7 : Cho hàm số 3
y  3x x m (m là thàm số). Để giá trị lớn nhất của hàm số trên đoạn 0; 3   bằng
3 2 thì m phải bằng: A. 3 2 B. 2 2 C. 2 D.  2
C©u 8 : Một cốc nước có dạng hình trụ đựng nước, chiều cao 16cm, đường kính đáy 6cm, lượng nước trong
cốc cao 10cm. Thả vào cốc nước 4 viên bi có cùng đường kính 4cm. Hỏi nước dâng cao cách mép
cốc bao nhiêu cm ? ( làm tròn sau dấu phẩy hai chữ số thập phân, bỏ qua độ dày cốc ). A. 1,34cm B. 1,68cm C. 1,43cm D. 1,26cm
C©u 9 : Tập nghiệm của bất phương trình là : A. B. C. D.
C©u 10 : Phương trình có 2 nghiệm phân biệt khi : A. B. C. D.
C©u 11 : Cho hình trụ có độ dài đường sinh là b và bán kính đường tròn đáy là a. Diện tích toàn phần của hình trụ là :
A. S  2 a b  2a
S   a 2b a
S   a b a
S  2 a b a tpB. tp   C. tp   D. tp  
C©u 12 : Cho (P) là đồ thị hàm số 2
y x  4x  5 . Diện tích hình phẳng giới hạn bởi (P) và các tiếp tuyến của Trang 1/ mã đề 236  5  (P) kẻ từ điểm A ; 1    là :  2  9 18 9 9 A. B. C. D. 4 4 2 8
C©u 13 : Khẳng định nào sau đây là sai ? A. B. C. D.
C©u 14 : Đạo hàm của hàm số là : A. B. C. D.
C©u 15 : Mệnh đề nào sau đây sai ?
A. Mặt phẳng 3x – z  2  0 có tọa độ vectơ pháp tuyến là 3, 0,  1  .
2x  2y z 1
B. Khoảng cách từ điểm M x , y , z đến mặt phẳng 2x  2y z 1  0 là 0 0 0 . 0 0 0  3
C. Mặt phẳng 2x  3y – 2z  0 đi qua gốc tọa độ.
D. Mặt phẳng  P : 4x  2y  3  0 song song với mặt phẳng Q : 2xy  5  0 .
C©u 16 : Cho hình chóp đều S.ABCD có AB = a , mặt bên (SAD) tạo với đáy (ABCD) một góc 60o . Tính thể
tích V của khối chóp S.ABCD ? 3 a 3 3 3a 3 a 3 A. V B. 3 V a 2 C. V D. V  6 2 3 C©u 17 : 1
Cho số phức z a bi . Khi đó số  z z  là: 2 A. 2 B. i C. Một số thực.
D. Một số thuần ảo C©u 18 : 2 ln x a c a c Biết dx   ln 2 
với a,b,c,d là các số nguyên dương và ;
là các phân số tối giản. Giá 3 x b d b d 1
trị của M ad bc là : A. 10 B. 40 C. 8 D. 32
C©u 19 : Trong không gian với hệ tọa độ Oxyz , cho 3 điểm A1;2;3 , B0;1;  1 , C 1;0; 2   và mặt phẳng
P có phương trình x y z  2  0 . Gọi M là điểm thuộc mặt phẳng P sao cho giá trị biểu thức 2 2 2
T MA  2MB  3MC nhỏ nhất. Tính khoảng cách từ M đến mặt phẳng
Q : 2x y  2z 3  0 91 121 2 5 A. B. C. 24 D. 54 54 3 C©u 20 : 2 x mx 1 Cho hàm số y
. Tìm m để hàm số đạt cực đại tại x  2 ? Một học sinh làm như sau: x m 2 2    Bướ x 2mx m 1
c 1: D R \   m , y '   x m2
Bước 2: Hàm số đạt cực đại tại x  2  y '(2)  0  * m  1  Bước 3:   2
*  m  4m  3  0   m  3 
Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào? A. Sai từ bước 3 B. Sai từ bước 2 C. Sai từ bước 1 D. Đúng Trang 2/ mã đề 236 C©u 21 :   Cho điể x 1 y 1 z
m M 2,1,0 và đường thẳng  :  
. Gọi d là đường thẳng đi qua M , cắt và 2 1 1 
vuông góc với  . Khi đó, vectơ chỉ phương của d là: A. u 0;3;1 B. u 1; 4; 2 C. u 2; 1;2 D. u 3;0;2 C©u 22 : 1 Hàm số 3 2 y
x x  3x  2 đạt cực tiểu tại: 3 1 A. x  3  B. x  0 C. x  1 D. x  3
C©u 23 : Tìm hàm số F(x) biết Fx 3
 4x  6x 1 và đồ thị hàm số y F x cắt trục tung tại điểm có tung độ bằng 2:
A. F x 4 2
x  3x x  2
B. F x 3
x x  2
C. F x 4 2
 4x  6x x  2
D. F x 4 2
x  3x x 1
C©u 24 : Trong các số phức thỏa mãn điều kiện z  
1 z  2i là số thực. Hãy tìm z có mô đun nhỏ nhất 4 2 2 4 2 4 2 4 A. Z   i B. Z    i C. Z   i D. Z   i 5 5 5 5 5 5 5 5
C©u 25 : Trong không gian với hệ tọa độ Oxyz , tìm m để phương trình 2 2 2
x y z  2mx  2(m  2) y  2(m  3)z  8m  37  0 là phương trình của một mặt cầu A. m  2  hay m  4 B. m  4  hay m  2 C. m  2  hay m  4 D. m  4  hay m  2 
C©u 26 : Một nhà kho có dạng khối hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB
= a, BC = 2a, chiều cao AA’ = 3a, chắp thêm một khối lăng trụ tam giác đều mà một mặt bên là
A’B’C’D’ và A’B’ là một cạnh đáy của lăng trụ. Tính thể tích của nhà kho ? 36  3 12  3 3 a 3 312  3 A. 3 a B. 3 a C. D. 3 a 6 2 2 2 C©u 27 :
Nguyên hàm hàm số f x  sin 2x   1 là : 1 A. f
 xdx  cos2x 1C B. f  x 1 dx   cos 2x C 2 2 1 C. f  x 1 dx  cos 2x C D. f
 xdx   cos2x 1C 2 2
C©u 28 : Một hình nón có bán kính đáy r  3a , chiều cao h  4a . Kí hiệu góc ở đỉnh của hình nón là 2 .
Trong các mệnh đề sau, mệnh đề nào đúng ? 4 4 4 4 A. sin   B. cot   C. tan  D. cos  5 5 5 5
C©u 29 : Diện tích hình phẳng giới hạn bởi các đường y  x  2
1 ; y  0; x  0; x  2 bằng : 2 A. 35 B. C. 15 D. 21 3 C©u 30 :
Biết , giá trị biểu thức là : A. B. C. D. Trang 3/ mã đề 236
C©u 31 : Khối đa diện đều loại 3;  5 có số mặt là : A. 12 B. 16 C. 8 D. 20
C©u 32 : Cho hàm số khẳng định nào dưới đây là đúng ?
A. Đồ thị hàm số không có tiệm cận
B. Đồ thị hàm số có 1 tiệm cận đứng và không có tiệm cận ngang
C. Đồ thị hàm số cắt trục ox
D. Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm cận đứng C©u 33 : 2 2 2 Cho
f xdx  3; g t dt  1   
. Giá trị của A  2 f
 x3gxdx  là: 1 1 1 A. 5 B. 9 C. 3 D. 2
C©u 34 : Phương trình tham số của đường thẳng d đi qua điểm M 1,2,3 và có vec tơ chỉ phương a (1;3;2) là : x  1   tx  1   tx  1 tx  1 t     A. y  2   3t B. y  2   3t
C. y  2  3t D. y  2   3t     z  3   2tz  3   2tz  3  2tz  3  2tC©u 35 : x 1
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2  ;0 lần lượt là: x  trên đoạn   1 1 1 A. 3 và -1 B. và -1 C.  và -1 D. 0 và -1 3 3
C©u 36 : Bất phương trình có tập nghiệm là : A. B. C. D.
C©u 37 : Điểm biểu diễn của các số phức z  7  bi với b
, nằm trên đường thẳng có phương trình là: A. x  7
B. y x  7 C. y x D. y  7
C©u 38 : Phương trình
Có 2 nghiệm x1, x2 thỏa mãn khi : A. B. C. D.
C©u 39 : Số nghiêm của phương trình 4 z  1 là A. 2 B. 3 C. 4 D. 1 C©u 40 : 3 Đặ dx t I   và x
t e 1. Khẳng định nào trong các khẳng định sau là sai : x e 1 1 3 e 1  3  1 1  1 1  I   2
ln e e   1  2 I   dt    A. I   dt   B. xD.    dt e dx C. t t 1  t t 1 e 1  1
C©u 41 : Phương trình tiếp tuyến với đồ thị hàm số 3 2
y f (x)  x  3x  2 tại điểm x sao cho f "(x )  0 là: 0 0
A. 3x y  3  0 B. 3
x y 3  0
C. 3x y  3  0
D. 3x y  3  0
C©u 42 : Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Biết hình chóp có chiều cao là
h a 3 . Thể tích khối chóp là : 3 a 3 3 a 3 3 a A. V B. 3 V a 3 C. V D. V  3 8 3 C©u 43 : 1 x
Số đường tiệm cận của đồ thị hàm số y  2x  là: 1 Trang 4/ mã đề 236 A. 3 B. 2 C. 1 D. 0 C©u 44 :
Tập xác định của hàm số là : A. B. C. D.
C©u 45 : Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Một mặt phẳng đi qua A’B’
và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Thể tích V của khối A’B’.BAEF là : 3 2a 3 3 5a 3 3 a 3 3 a 3 A. V B. V C. V D. V  27 54 27 18
C©u 46 : Số phức z   i3 1 có mô đun bằng: A. z  2 B. z  2 2 C. z  2  2 D. z  0 C©u 47 :
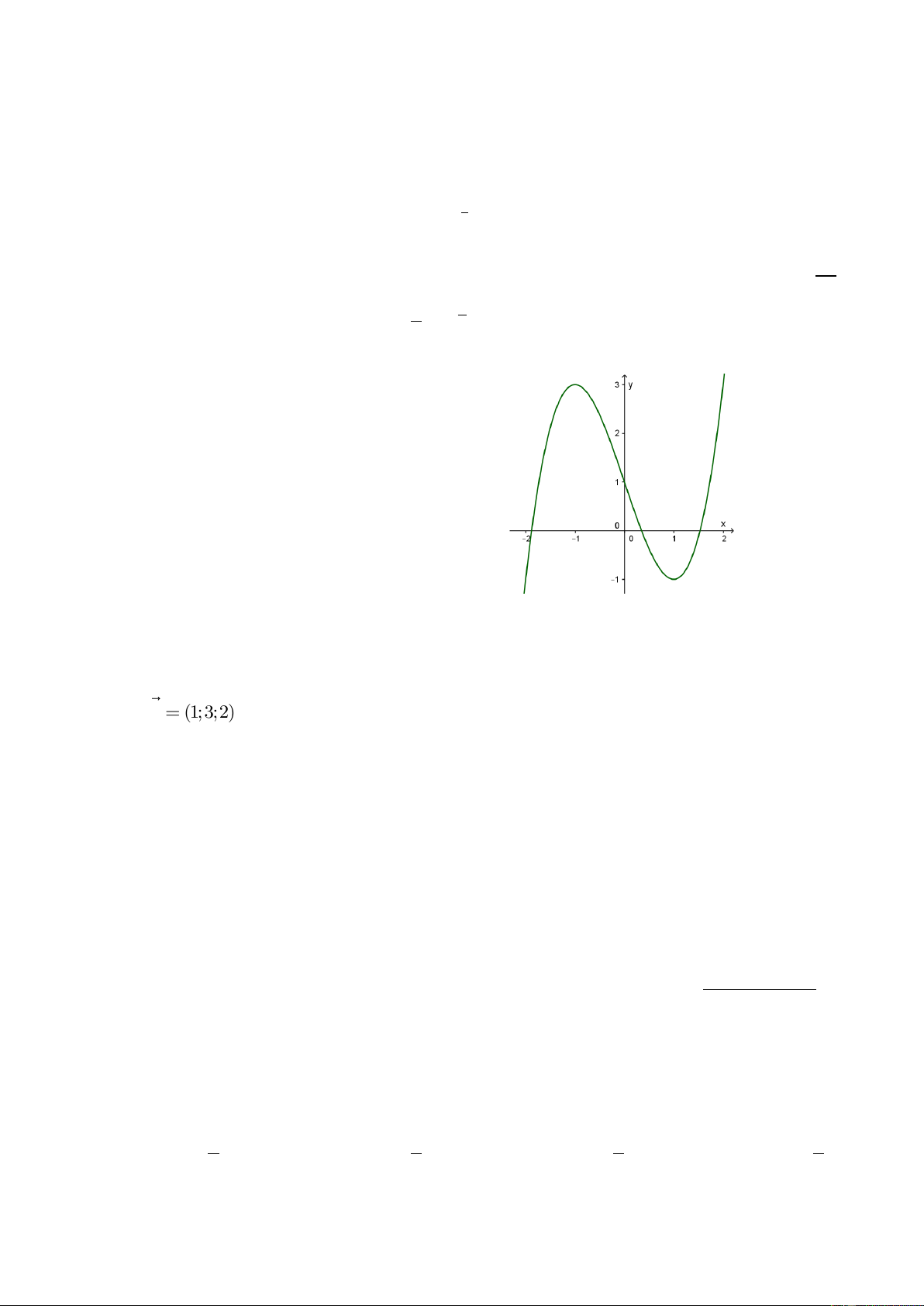
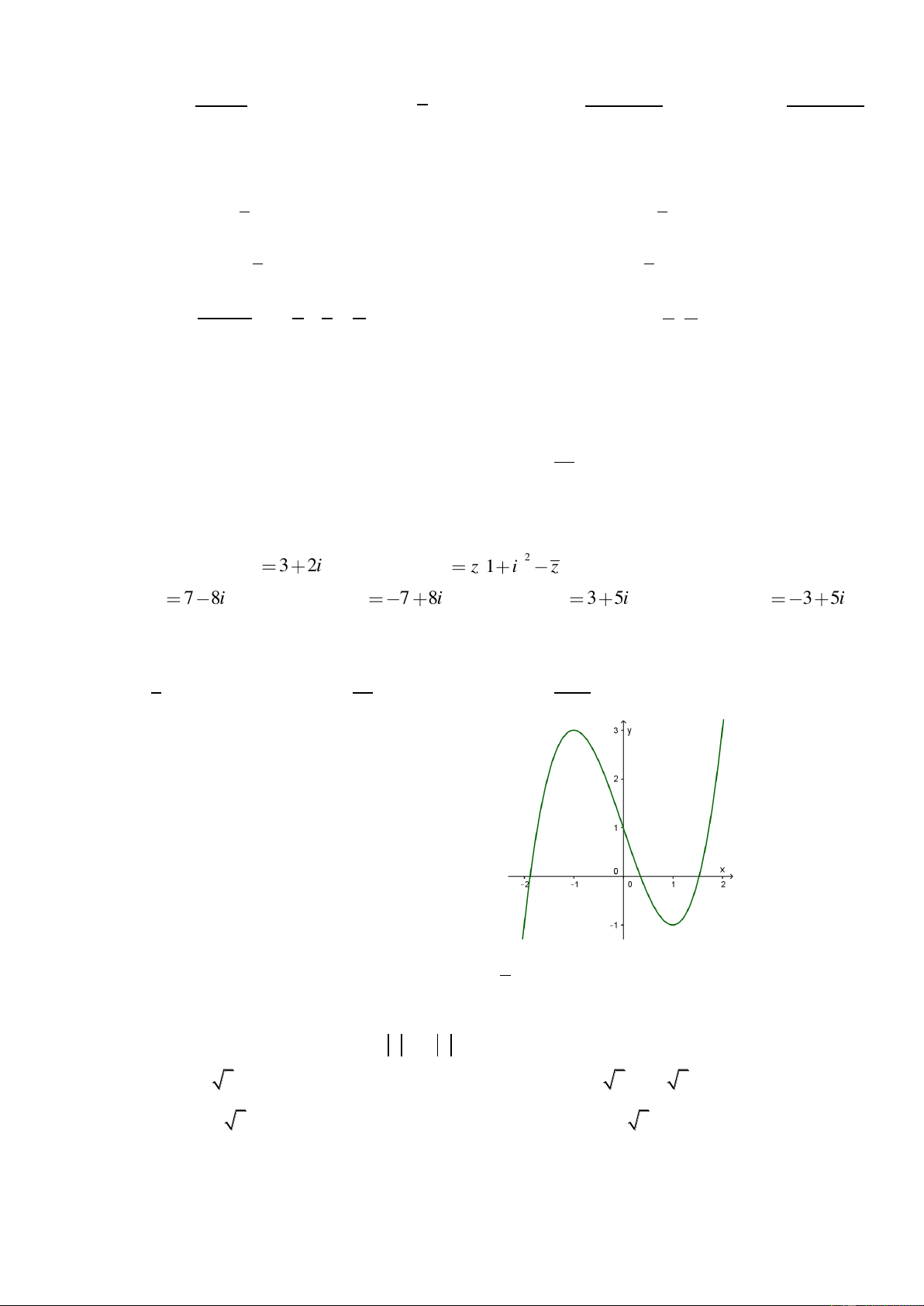
Cho hàm số y f (x) có đồ thị (C) như hình vẽ.
Số nghiệm phân biệt của phương trình f (x)  1  là: A. 1 B. 3 C. 2 D. 0
C©u 48 : Giá trị của m để phương trình 3
4 x  3 x 1  mx m có 4 nghiệm phân biệt là :
A. m 9  6 3;  1
B. m 9  6 3;  1
C. m 1;6 3  9
D. m 6 3  9;6 3  9
C©u 49 : Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 2
y  4  x ; y  0 xung quanh trục Ox là : 71 512 8 A. B. C. 2 D.  82 15 3
C©u 50 : Cho hàm số 4 2
y x  2x  5 . Chọn khẳng định đúng?
A. Hàm số đồng biến trên khoảng  1  ;0 và (1;)
B. Hàm số đồng biến trên khoảng  1   ;1
C. Hàm số nghịch biến trên khoảng  ;    1 và (1; )
D. Hàm số nghịch biến trên khoảng  1  ;0 và (1;)
-----------------------------------------------------------Hết------------------------------------------------------ Trang 5/ mã đề 236
Trường THPT Quốc Oai
ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2016 -2017
Môn: Toán ; thời gian 90 phút; mã đề 240
(đề gồm 50 câu trắc nghiệm)
Họ và tên thí sinh:………………………………………………….. số báo danh:…………
C©u 1 : Trong không gian với hệ tọa độ Oxyz . Hãy viết phương trình mặt cầu (S) có tâm I (2;0;1) và tiếp x 1 y z  2
xúc với đường thẳng d:   . 1 2 1 A. 2 2 2
(x  2)  y  (z 1)  4. B. 2 2 2
(x  2)  y  (z 1)  2. C. 2 2 2
(x  2)  y  (z 1)  9. D. 2 2 2
(x 1)  ( y  2)  (z 1)  24. C©u 2 : 3 3  ln x a 1 c a c Biết dx   ln 
với a,b,c,d là các số nguyên dương và ;
là các phân số tối giản. 2 (x 1) b b d b d 1
Giá trị của M ac bd là : A. 145 B. 20 C. 17 D. 11 C©u 3 : x 1 y 1 z
Trong không gian với hệ tọa độ Oxyz , cho điểm M (2;1;0) và đường thẳng :   . 2 1 1 
Viết phương trình của đường thẳng d đi qua điểm M, cắt và vuông góc với . x  2 y 1 z x  2 y 1 z A. d:   . B. d:   . 1 4 1 1 4  2  x  2 y 1 z x  2 y 1 z C. d:   . D. d:   . 2 4  1 1 4  1 C©u 4 : 3 3 3 Cho
f xdx  2; g t dt  3   
. Giá trị của A  3 f
 x2gxdx  là: 2 2 2 A. -1 B. 5 C. 0 D. 12 C©u 5 : 2 Cho số phức z 3
2i . Tìm số phức w z 1 i z A. w 3 5i B. w 3 5i C. w 7 8i D. w 7 8i
C©u 6 : Bất phương trình có tập nghiệm là : A. B. C. D. C©u 7 :
Nguyên hàm hàm số f x  cos3x  2 là : 1 A. f  x 1
dx   sin 3x C B. f
 xdx   sin3x2C 3 3 1 C. f
 xdx  sin3x2C D. f  x 1 dx  sin 3x C 3 3
C©u 8 : Một cốc nước có dạng hình trụ đựng nước, chiều cao 12cm, đường kính đáy 4cm, lượng nước trong
cốc cao 8cm. Thả vào cốc nước 4 viên bi có cùng đường kính 2cm. Hỏi nước dâng cao cách mép cốc
bao nhiêu cm ? ( làm tròn sau dấu phẩy hai chữ số thập phân, bỏ qua độ dày cốc ). A. 2,67cm B. 2,25cm C. 2,33cm D. 2,75cm
C©u 9 : Khẳng định nào sau đây là sai ? A. B. C. D.
C©u 10 : Cho phương trình 2
z  2z  3  0 trên tập số phức,có hai nghiệm là z , z .Khi đó 2 2 zz có giá trị 1 2 1 2 là: Trang 1 / mã đề 240 A. 3 B. 2 2 C. 6 D. 2
C©u 11 : Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A1;3;4, B 2  ;3;0 , C  1  ;3;2.
Tìm tọa độ trọng tâm G của tam giác ABC .  2   2   2  A. G  ;1;1 .  
B. G  ; 2; 2 .   C. G  2  ;1;2. D. G  ;1; 2 .    3   3   3  C©u 12 : 1 Cho hàm số 3 2 y
x  (m 1)x  4x (m là thàm số). Giá trị của m để hàm số đã cho đồng biến trên 3 R là: Không có giá trị
A. nào của m thỏa B. m  3 C. 1   m  3 D. m   R mãn
C©u 13 : Cho (P) là đồ thị hàm số 2
y x  4x  3 . Diện tích hình phẳng giới hạn bởi (P) và các tiếp tuyến của
(P) kẻ từ điểm A2; 5   là : 32 10 8 16 A. B. C. D. 3 3 3 3
C©u 14 : Giá trị của m để phương trình 3
4 x  3 x 1  mx m có 4 nghiệm phân biệt là :
A. m 9  6 3;  1
B. m 6 3  9;6 3  9
C. m 9  6 3;  1
D. m 1;6 3  9
C©u 15 : Trong không gian với hệ tọa độ Oxyz , cho hai điểm ( A 2; 4;1) , B( 1
 ;1;3) và mặt phẳng (P) :
x  3y  2z  5  0 . Viết phương trình mặt phẳng Q đi qua hai điểm A, B và vuông góc với mặt
phẳng  P.
A. Q : 2y  3z 12  0
B. Q : 2y  3z 11  0
C. Q : 2x  3z 11  0
D. Q : 2y  3z 1  0 C©u 16 : 2 x mx 1 Cho hàm số y
. Tìm m để hàm số đạt cực đại tại x  2 ? Một học sinh làm như sau: x m 2 2    Bướ x 2mx m 1
c 1: D R \   m , y '   x m2
Bước 2: Hàm số đạt cực đại tại x  2  y '(2)  0  * m  1  Bước 3:   2
*  m  4m  3  0   m  3 
Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào? A. Sai từ bước 2 B. Sai từ bước 1 C. Đúng D. Sai từ bước 3
C©u 17 : Phương trình
Có 2 nghiệm x1, x2 thỏa mãn khi : A. B. C. D. C©u 18 : 4
Một hình nón có bán kính đáy r  1 , chiều cao h
. Kí hiệu góc ở đỉnh của hình nón là 2 . 3
Trong các mệnh đề sau, mệnh đề nào đúng ? Trang 2 / mã đề 240 3 3 3 3 A. cos  B. cot   C. tan  D. sin   5 5 5 5
C©u 19 : Một nhà kho có dạng khối hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB
= 3m, BC = 6m, chiều cao AA’ = 3m, chắp thêm một khối lăng trụ tam giác đều mà một mặt bên là
A’B’C’D’ và A’B’ là một cạnh đáy của lăng trụ. Tính thể tích của nhà kho ? 27 3 27 4  3 912  3 A. 3 m B. 3 54m C. 3 m D. 3 m 2 2 2
C©u 20 : Phương trình tiếp tuyến với đồ thị hàm số 3 2
y f (x)  x  3x  2 tại điểm x sao cho f "(x )  6 là: 0 0
A. y  2  0
B. 3x y  3  0
C. y  2  0
D. 3x y  3  0 C©u 21 :
Tập xác định của hàm số là : A. B. C. D.
C©u 22 : Cho hình chóp đều S.ABCD có AC = 2a , mặt bên (SBC) tạo với đáy (ABCD) một góc 45o . Tính
thể tích V của khối chóp S.ABCD ? 3 2 3a 3 a 2 3 a A. V B. V C. 3 V a 2 D. V  3 3 2
C©u 23 : Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Một mặt phẳng đi qua A’B’
và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Thể tích V của khối C.A’B’FE là : 3 a 3 3 5a 3 3 5a 3 3 5a 3 A. V B. V C. V D. V  27 18 54 27 C©u 24 : x
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  trên đoạn 1;  3 lần lượt là: x 1 3 1 1 A. và B.  và -1 C. 3 và -1 D. 0 và -1 4 2 3
C©u 25 : Trong các số phức z tìm điều kiện : z i z  2 3i . Hãy tìm z có mô đun nhỏ nhất 27 6 3 6 6 27 6 27 A. z   i B. z   i C. z    i D. z    i 5 5 5 5 5 5 5 5
C©u 26 : Diện tích hình phẳng giới hạn bởi các đường y  x  2
2 ; y  0; x  1; x  3 bằng : 98 A. B. 30 C. 18 D. 21 3
C©u 27 : Trong không gian với hệ tọa độ Oxyz , cho 3 điểm A 2  ;2;3 , B1; 1
 ;3 ,C 3;1;  1 và mặt phẳng
Pcó phương trình x2z 8  0. Gọi M là điểm thuộc mặt phẳng P sao cho giá trị biểu hức 2 2 2
T  2MA MB  3MC nhỏ nhất. Tính khoảng cách từ M đến mặt phẳng
Q:x  2y 2z 6  0 3 3 A. 2 B. d C. 4 D. d  3 2
C©u 28 : Cho số phức z  5  4i . Số phức z  2 có
A. Phần thực bằng 3 và phần ảo bằng 4  .
B. Phần thực bằng 3 và phần ảo bằng 4  i .
C. Phần thực bằng 5 và phần ảo bằng 4  .
D. Phần thực bằng 4
 và phần ảo bằng 3 .
C©u 29 : Cho hàm số 3
y  3x x m (m là thàm số). Để giá trị lớn nhất của hàm số trên đoạn 0; 3   bằng
5 2 thì m phải bằng: Trang 3 / mã đề 240 A. 2 B. 4 2 C. 2 2 D. 3 2
C©u 30 : Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a. Biết hình chóp có chiều cao là h a 3 .
Thể tích khối chóp là : 3 a 3 3 a 3 3 a 3 a A. V B. V C. V D. V  4 8 4 3 C©u 31 :
Cho hàm số y f (x) có đồ thị (C) như hình vẽ.
Số nghiệm phân biệt của phương trình 1 f (x)  là: 2 A. 2 B. 1 C. 0 D. 3
C©u 32 : Cho hai số phức z , z thỏa mãn z z 1, z z  3 . Tính z z : 1 2 1 2 1 2 1 2 A. 4 B. 1 C. 2 D. 3
C©u 33 : Cho a  1;0; 3
 ;b  2;1;2 .Khi đó  ; a b   có giá trị là A. 8 B. 3 C. 74 D. 4 C©u 34 : 1
Số đường tiệm cận của đồ thị hàm số y  là: x A. 1 B. 3 C. 0 D. 2
C©u 35 : Cho hai số phức z  2  3i , z 1 2i . Tính môđun của số phức z  z  2 z . 1  1 2 2 A. z  5 5 B. z  137 C. z  15 D. z  65
C©u 36 : Tập nghiệm của bất phương trình là : A. B. C. D.
C©u 37 : Cho hình trụ có độ dài đường sinh là l và bán kính đường tròn đáy là r. Diện tích toàn phần của hình trụ là :
A. S   r l r
S  2 r l  2r
S   r 2l r
S  2 r l r tp   B. tp   C. tp   D. tp  
C©u 38 : Trong không gian với hệ trục tọa độ Oxyz , cho hình hộp ABC . D A BCD   . Biết A 3  ;2;  1 ,
C 4;2;0 , B 2  ;1; 
1 , D3;5;4 .Tìm tọa độ A của hình hộp ABC . D A BCD   . A. A 3  ;3;3. B. A 3  ; 3  ; 3  . C. A 3  ;3;  1 . D. A 3  ; 3  ;3.
C©u 39 : Khối đa diện đều loại 5;  3 có số mặt là : A. 14 B. 10 C. 12 D. 8
C©u 40 : Biết , giá trị biểu thức là : Trang 4 / mã đề 240 A. B. C. D.
C©u 41 : Tìm hàm số F(x) biết Fx 2
 3x  2x 1 và đồ thị hàm số y F x cắt trục tung tại điểm có tung độ bằng e:
A. F x 2
x x  2 B.   3 2
F x x x x e
C. F x 2
x x e 1
D. F x 3 2
x x x 1
C©u 42 : Đường thẳng y  9x m là tiếp tuyến của đường cong 3 2
y x  3x 1 khi m bằng A. -6 hoặc 26 B. -3 hoặc 1 C. -1 hoặc 3 D. 3 hoặc -5
C©u 43 : Phương trình có 2 nghiệm phân biệt khi : A. B. C. D. C©u 44 : 2 Đặ dx t I   và 2 t
x 1 . Khẳng định nào trong các khẳng định sau là sai : 2  2 x x 1 3 2 1 dtdt I  
A. tdt xdx B. I  2 t 1 C. 2 t 1 D. 2 2 x t 1 2 1 3 3
C©u 45 : Cho hàm số khẳng định nào dưới đây là đúng ?
A. Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm
B. Đồ thị hàm số không có tiệm cận cận đứng
C. Đồ thị hàm số cắt trục ox
D. Đồ thị hàm số có 1 tiệm cận đứng và không có tiệm cận ngang C©u 46 : Cho hàm số
khẳng định nào sau đây là sai ?
A. Đồ thị hàm số nằm toàn bộ phía trên trục ox
B. Hàm số đồng biến trên R
C. Hàm số nghịch biến trên R
D. Tập xác định của hàm số là R
C©u 47 : Cho hàm số 3 2
y x  3x  3
 . Chọn khẳng định sai?
Hàm số đồng biến trên khoảng  ;  0và
A. Hàm số nghịch biến trên khoảng 0; 2 B. (2; ) 
C. Hàm số có hai điểm cực trị
D. Hàm số không có cực trị C©u 48 : Hàm số 4 2
y x x  2 có điểm cực tiểu là: A. y  2 B. x  1  C. x  1 D. x  0
C©u 49 : Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 2
y  9  x ; y  0 xung quanh trục Ox là : 71 8 1296 A. B. C. 3 D.  82 3 5
C©u 50 : Đạo hàm của hàm số là : A. B. C. D.
--------------------------------------------------------Hết-------------------------------------------------- Trang 5 / mã đề 240
Trường THPT Quốc Oai
ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2016 -2017
Môn: Toán ; thời gian 90 phút; mã đề 237
(đề gồm 50 câu trắc nghiệm)
Họ và tên thí sinh:………………………………………………….. số báo danh:…………
C©u 1 : Phương trình
Có 2 nghiệm x1, x2 thỏa mãn khi : A. B. C. D. C©u 2 : 1
Cho số phức z a bi . Khi đó số  z z  là: 2 A. 2 B. Một số thực. C. i
D. Một số thuần ảo C©u 3 :
Cho hàm số y f (x) có đồ thị (C) như hình vẽ.
Số nghiệm phân biệt của phương trình f (x)  1  là: A. 0 B. 3 C. 1 D. 2
C©u 4 : Phương trình tham số của đường thẳng d đi qua điểm M 1,2,3 và có vec tơ chỉ phương a (1;3;2) là : x  1   tx  1 tx  1 tx  1   t     A. y  2   3t B. y  2   3t
C. y  2  3t D. y  2   3t     z  3   2tz  3  2tz  3  2tz  3   2t
C©u 5 : Đạo hàm của hàm số là : A. B. C. D.
C©u 6 : Mệnh đề nào sau đây sai ?
A. Mặt phẳng 3x – z  2  0 có tọa độ vectơ pháp tuyến là 3, 0,  1  .
2x  2y z 1
B. Khoảng cách từ điểm M x , y , z đến mặt phẳng 2x  2y z 1  0 là 0 0 0 . 0 0 0  3
C. Mặt phẳng 2x  3y – 2z  0 đi qua gốc tọa độ.
D. Mặt phẳng  P : 4x  2y  3  0 song song với mặt phẳng Q : 2xy  5  0 .
C©u 7 : Một hình nón có bán kính đáy r  3a , chiều cao h  4a . Kí hiệu góc ở đỉnh của hình nón là 2 .
Trong các mệnh đề sau, mệnh đề nào đúng ? 4 4 4 4 A. sin   B. tan  C. cos  D. cot   5 5 5 5 Trang 1/ mã đề 237
C©u 8 : Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z  2z  3  0 . Tọa độ điểm M biểu diễn 1 số phức z là: 1 A. M ( 1  ; 2) B. M ( 1  ; 2  ) C. M ( 1  ; 2i) D. M ( 1  ;2) C©u 9 : 2 ln x a c a c Biết dx   ln 2 
với a,b,c,d là các số nguyên dương và ;
là các phân số tối giản. Giá 3 x b d b d 1
trị của M ad bc là : A. 10 B. 8 C. 40 D. 32
C©u 10 : Một nhà kho có dạng khối hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB
= a, BC = 2a, chiều cao AA’ = 3a, chắp thêm một khối lăng trụ tam giác đều mà một mặt bên là
A’B’C’D’ và A’B’ là một cạnh đáy của lăng trụ. Tính thể tích của nhà kho ? 36  3 12  3 312  3 3 a 3 A. 3 a B. 3 a C. 3 a D. 6 2 2 2
C©u 11 : Cho hình trụ có độ dài đường sinh là b và bán kính đường tròn đáy là a. Diện tích toàn phần của hình trụ là :
A. S  2 a b a
S  2 a b  2a
S   a b a
S   a 2b a tp   B. tp   C. tp   D. tp   C©u 12 :
Nguyên hàm hàm số f x  sin 2x   1 là : 1 A. f
 xdx  cos2x 1C B. f  x 1 dx   cos 2x C 2 2 1 C. f
 xdx   cos2x 1C D. f  x 1 dx  cos 2x C 2 2
C©u 13 : Cho (P) là đồ thị hàm số 2
y x  4x  5 . Diện tích hình phẳng giới hạn bởi (P) và các tiếp tuyến của  5  (P) kẻ từ điểm A ; 1    là :  2  9 18 9 9 A. B. C. D. 4 4 8 2
C©u 14 : Tập nghiệm của bất phương trình là : A. B. C. D.
C©u 15 : Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Biết hình chóp có chiều cao là
h a 3 . Thể tích khối chóp là : 3 a 3 3 a 3 a 3 A. 3 V a 3 B. V C. V D. V  8 3 3 C©u 16 : 3 Đặ dx t I   và x
t e 1. Khẳng định nào trong các khẳng định sau là sai : x e 1 1 3 e 1  1 1  3 I   dt    I   2
ln e e   1  2 1 1  A. t t 1 B. C. x dt e dx D. I   dt   e 1   t t 1 1 C©u 17 : x 1
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2  ;0 lần lượt là: x  trên đoạn   1 1 1 A. 3 và -1 B.  và -1 C. và -1 D. 0 và -1 3 3 Trang 2/ mã đề 237
C©u 18 : Điểm biểu diễn của các số phức z  7  bi với b
, nằm trên đường thẳng có phương trình là: A. y  7
B. y x  7 C. x  7
D. y x
C©u 19 : Cho hình chóp đều S.ABCD có AB = a , mặt bên (SAD) tạo với đáy (ABCD) một góc 60o . Tính thể
tích V của khối chóp S.ABCD ? 3 a 3 3 3a 3 a 3 A. 3 V a 2 B. V C. V D. V  6 2 3
C©u 20 : Số nghiêm của phương trình 4 z  1 là A. 2 B. 1 C. 3 D. 4
C©u 21 : Một cốc nước có dạng hình trụ đựng nước, chiều cao 16cm, đường kính đáy 6cm, lượng nước trong
cốc cao 10cm. Thả vào cốc nước 4 viên bi có cùng đường kính 4cm. Hỏi nước dâng cao cách mép
cốc bao nhiêu cm ? ( làm tròn sau dấu phẩy hai chữ số thập phân, bỏ qua độ dày cốc ). A. 1,26cm B. 1,68cm C. 1,34cm D. 1,43cm
C©u 22 : Trong không gian với hệ tọa độ Oxyz , cho a  1;2; 
1 , b  3; 4;3 . Tìm tọa độ của x biết
x b a
A. x  2; 2; 4.
B. x  1;1; 2. C. x   2  ; 2  ; 4  . D. x   2  ; 2  ;4.
C©u 23 : Trong các số phức thỏa mãn điều kiện z  
1 z  2i là số thực. Hãy tìm z có mô đun nhỏ nhất 2 4 4 2 2 4 2 4 A. Z   i B. Z   i C. Z    i D. Z   i 5 5 5 5 5 5 5 5
C©u 24 : Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Một mặt phẳng đi qua A’B’
và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Thể tích V của khối A’B’.BAEF là : 3 a 3 3 5a 3 3 a 3 3 2a 3 A. V B. V C. V D. V  18 54 27 27
C©u 25 : Phương trình tiếp tuyến với đồ thị hàm số 3 2
y f (x)  x  3x  2 tại điểm x sao cho f "(x )  0 là: 0 0
A. 3x y  3  0
B. 3x y  3  0 C. 3
x y 3  0
D. 3x y  3  0 C©u 26 : 2 2 2 Cho
f xdx  3; g t dt  1   
. Giá trị của A  2 f
 x3gxdx  là: 1 1 1 A. 5 B. 9 C. 3 D. 2 C©u 27 :
Biết , giá trị biểu thức là : A. B. C. D. C©u 28 :
Cho hàm số khẳng định nào sau đây là sai ?
A. Hàm số nghịch biến trên R
B. Đồ thị hàm số nằm toàn bộ phía trên trục ox
C. Tập xác định của hàm số là R
D. Hàm số đồng biến trên R
C©u 29 : Khối đa diện đều loại 3;  5 có số mặt là : A. 16 B. 8 C. 20 D. 12
C©u 30 : Cho hàm số 3
y  3x x m (m là thàm số). Để giá trị lớn nhất của hàm số trên đoạn 0; 3   bằng
3 2 thì m phải bằng: A. 2 2 B.  2 C. 2 D. 3 2
C©u 31 : Trong không gian với hệ tọa độ Oxyz , cho a   2  ; 3; 
1 , b  1;  3; 4 . Tìm  ; a b   Trang 3/ mã đề 237 A. 315 B. 171 C. 171 D. 315
C©u 32 : Diện tích hình phẳng giới hạn bởi các đường y  x  2
1 ; y  0; x  0; x  2 bằng : 2 A. 15 B. 35 C. D. 21 3 C©u 33 : 2 x mx 1 Cho hàm số y
. Tìm m để hàm số đạt cực đại tại x  2 ? Một học sinh làm như sau: x m 2 2    Bướ x 2mx m 1
c 1: D R \   m , y '   x m2
Bước 2: Hàm số đạt cực đại tại x  2  y '(2)  0  * m  1  Bước 3:   2
*  m  4m  3  0   m  3 
Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào? A. Sai từ bước 3 B. Sai từ bước 2 C. Sai từ bước 1 D. Đúng C©u 34 : 1 Cho hàm số 3 2
y   x  (m 1)x  4x (m là thàm số). Giá trị của m để hàm số đã cho nghịch biến 3 trên R là: m  1  A. 1   m  3 B. m  3 C. D. m   R m  3
C©u 35 : Cho hàm số khẳng định nào dưới đây là đúng ?
A. Đồ thị hàm số không có tiệm cận
B. Đồ thị hàm số có 1 tiệm cận đứng và không có tiệm cận ngang
C. Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm
D. Đồ thị hàm số cắt trục ox cận đứng
C©u 36 : Đường thẳng y  6x m là tiếp tuyến của đường cong 3
y x  3x 1 khi m bằng A. -3 hoặc 1 B. -1 hoặc 3 C. -5 hoặc 1 D. 3 hoặc -5 C©u 37 :   Cho điể x 1 y 1 z
m M 2,1,0 và đường thẳng  :  
. Gọi d là đường thẳng đi qua M , cắt và 2 1 1 
vuông góc với  . Khi đó, vectơ chỉ phương của d là: A. u 0;3;1 B. u 1; 4; 2 C. u 2; 1;2 D. u 3;0;2
C©u 38 : Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 2
y  4  x ; y  0 xung quanh trục Ox là : 71 8 512 A. 2 B. C. D.  82 3 15
C©u 39 : Trong không gian với hệ tọa độ Oxyz , tìm m để phương trình 2 2 2
x y z  2mx  2(m  2) y  2(m  3)z  8m  37  0 là phương trình của một mặt cầu A. m  4  hay m  2 B. m  2  hay m  4 C. m  4  hay m  2  D. m  2  hay m  4
C©u 40 : Tìm hàm số F(x) biết Fx 3
 4x  6x 1 và đồ thị hàm số y F x cắt trục tung tại điểm có tung độ bằng 2:
A. F x 4 2
x  3x x 1
B. F x 4 2
x  3x x  2
C. F x 3
x x  2
D. F x 4 2
 4x  6x x  2 Trang 4/ mã đề 237
C©u 41 : Số phức z   i3 1 có mô đun bằng: A. z  2 B. z  2  2 C. z  0 D. z  2 2
C©u 42 : Cho hàm số 4 2
y x  2x  5 . Chọn khẳng định đúng?
A. Hàm số nghịch biến trên khoảng  ;    1 và (1; )
B. Hàm số đồng biến trên khoảng  1   ;1
C. Hàm số nghịch biến trên khoảng  1  ;0 và (1;)
D. Hàm số đồng biến trên khoảng  1  ;0 và (1;)
C©u 43 : Khẳng định nào sau đây là sai ? A. B. C. D.
C©u 44 : Giá trị của m để phương trình 3
4 x  3 x 1  mx m có 4 nghiệm phân biệt là :
A. m 9  6 3;  1
B. m 6 3  9;6 3  9
C. m 9  6 3;  1
D. m 1;6 3  9 C©u 45 : 1 x
Số đường tiệm cận của đồ thị hàm số y  2x  là: 1 A. 0 B. 3 C. 1 D. 2
C©u 46 : Phương trình có 2 nghiệm phân biệt khi : A. B. C. D. C©u 47 :
Tập xác định của hàm số là : A. B. C. D.
C©u 48 : Bất phương trình có tập nghiệm là : A. B. C. D. C©u 49 : 1 Hàm số 3 2 y
x x  3x  2 đạt cực tiểu tại: 3 1 A. x B. x  1 C. x  3  D. x  0 3
C©u 50 : Trong không gian với hệ tọa độ Oxyz , cho 3 điểm A1;2;3 , B0;1;  1 , C 1;0; 2   và mặt phẳng
P có phương trình x y z  2  0 . Gọi M là điểm thuộc mặt phẳng P sao cho giá trị biểu thức 2 2 2
T MA  2MB  3MC nhỏ nhất. Tính khoảng cách từ M đến mặt phẳng
Q : 2x y  2z 3  0 91 121 2 5 A. 24 B. C. D. 54 54 3
-------------------------------------------------------Hết-------------------------------------------------- Trang 5/ mã đề 237
Trường THPT Quốc Oai
ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2016 -2017
Môn: Toán ; thời gian 90 phút; mã đề 241
(đề gồm 50 câu trắc nghiệm)
Họ và tên thí sinh:………………………………………………….. số báo danh:…………
C©u 1 : Đường thẳng y  9x m là tiếp tuyến của đường cong 3 2
y x  3x 1 khi m bằng A. -1 hoặc 3 B. 3 hoặc -5 C. -3 hoặc 1 D. -6 hoặc 26
C©u 2 : Khẳng định nào sau đây là sai ? A. B. C. D. C©u 3 : 4
Một hình nón có bán kính đáy r  1 , chiều cao h
. Kí hiệu góc ở đỉnh của hình nón là 2 . 3
Trong các mệnh đề sau, mệnh đề nào đúng ? 3 3 3 3 A. cot   B. sin   C. tan  D. cos  5 5 5 5 C©u 4 :
Tập xác định của hàm số là : A. B. C. D. C©u 5 : Cho hàm số 3 2
y x  3x  3
 . Chọn khẳng định sai?
A. Hàm số nghịch biến trên khoảng 0; 2
B. Hàm số có hai điểm cực trị
Hàm số đồng biến trên khoảng  ;  0và
D. Hàm số không có cực trị C. (2; )  C©u 6 : x
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  1;3 lần lượt là: x  trên đoạn   1 3 1 1 A. 3 và -1 B. và C.  và -1 D. 0 và -1 4 2 3 C©u 7 : Cho hàm số
khẳng định nào sau đây là sai ?
A. Hàm số nghịch biến trên R
B. Tập xác định của hàm số là R
C. Đồ thị hàm số nằm toàn bộ phía trên trục ox
D. Hàm số đồng biến trên R C©u 8 : 3 3  ln x a 1 c a c Biết dx   ln 
với a,b,c,d là các số nguyên dương và ;
là các phân số tối giản. 2 (x 1) b b d b d 1
Giá trị của M ac bd là : A. 17 B. 20 C. 145 D. 11 C©u 9 :
Nguyên hàm hàm số f x  cos3x  2 là : 1 A. f
 xdx  sin3x2C B. f  x 1
dx   sin 3x C 3 3 1 C. f
 xdx   sin3x2C D. f  x 1 dx  sin 3x C 3 3
C©u 10 : Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Một mặt phẳng đi qua A’B’
và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Thể tích V của khối C.A’B’FE là : 3 a 3 3 5a 3 3 5a 3 3 5a 3 A. V B. V C. V D. V  27 54 18 27
C©u 11 : Tập nghiệm của bất phương trình là : Trang 1/ mã đề 241 A. B. C. D. C©u 12 : 3 3 3 Cho
f xdx  2; g t dt  3   
. Giá trị của A  3 f
 x2gxdx  là: 2 2 2 A. 12 B. 0 C. 5 D. -1
C©u 13 : Trong không gian với hệ trục tọa độ Oxyz , cho hình hộp ABC . D A BCD   . Biết A 3  ;2;  1 ,
C 4;2;0 , B 2  ;1; 
1 , D3;5;4 .Tìm tọa độ A của hình hộp ABC . D A BCD   . A. A 3  ; 3  ; 3  . B. A 3  ;3;  1 . C. A 3  ;3;3. D. A 3  ; 3  ;3.
C©u 14 : Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A1;3;4, B 2  ;3;0 , C  1  ;3;2.
Tìm tọa độ trọng tâm G của tam giác ABC .  2   2   2  A. G  ;1; 2 .  
B. G  ; 2; 2 .   C. G  ;1;1 .   D. G  2  ;1;2.  3   3   3 
C©u 15 : Phương trình
Có 2 nghiệm x1, x2 thỏa mãn khi : A. B. C. D.
C©u 16 : Cho hai số phức z , z thỏa mãn z z 1, z z  3 . Tính z z : 1 2 1 2 1 2 1 2 A. 4 B. 2 C. 1 D. 3
C©u 17 : Cho phương trình 2
z  2z  3  0 trên tập số phức,có hai nghiệm là z , z .Khi đó 2 2 zz có giá trị 1 2 1 2 là: A. 6 B. 2 2 C. 3 D. 2
C©u 18 : Cho hình trụ có độ dài đường sinh là l và bán kính đường tròn đáy là r. Diện tích toàn phần của hình trụ là :
A. S   r 2l r
S  2 r l  2r
S  2 r l r
S   r l r tpB. tp   C. tp   D. tp  
C©u 19 : Phương trình có 2 nghiệm phân biệt khi : A. B. C. D.
C©u 20 : Cho (P) là đồ thị hàm số 2
y x  4x  3 . Diện tích hình phẳng giới hạn bởi (P) và các tiếp tuyến của
(P) kẻ từ điểm A2; 5   là : 16 10 32 8 A. B. C. D. 3 3 3 3 C©u 21 : 1
Số đường tiệm cận của đồ thị hàm số y  là: x A. 1 B. 3 C. 2 D. 0 C©u 22 : 2 Cho số phức z 3
2i . Tìm số phức w z 1 i z A. w 7 8i B. w 3 5i C. w 3 5i D. w 7 8i
C©u 23 : Cho hàm số 3
y  3x x m (m là thàm số). Để giá trị lớn nhất của hàm số trên đoạn 0; 3   bằng
5 2 thì m phải bằng: A. 2 B. 3 2 C. 4 2 D. 2 2
C©u 24 : Trong không gian với hệ tọa độ Oxyz , cho hai điểm ( A 2; 4;1) , B( 1
 ;1;3) và mặt phẳng (P) :
x  3y  2z  5  0 . Viết phương trình mặt phẳng Q đi qua hai điểm A, B và vuông góc với mặt Trang 2/ mã đề 241
phẳng  P.
A. Q : 2y  3z 12  0
B. Q : 2y  3z 11  0
C. Q : 2y  3z 1  0
D. Q : 2x  3z 11  0
C©u 25 : Bất phương trình có tập nghiệm là : A. B. C. D.
C©u 26 : Trong không gian với hệ tọa độ Oxyz , cho 3 điểm A 2  ;2;3 , B1; 1
 ;3 ,C 3;1;  1 và mặt phẳng
Pcó phương trình x2z 8  0. Gọi M là điểm thuộc mặt phẳng P sao cho giá trị biểu hức 2 2 2
T  2MA MB  3MC nhỏ nhất. Tính khoảng cách từ M đến mặt phẳng
Q:x  2y 2z 6  0 3 3 A. 2 B. d C. 4 D. d  3 2
C©u 27 : Diện tích hình phẳng giới hạn bởi các đường y  x  2
2 ; y  0; x  1; x  3 bằng : 98 A. 30 B. C. 18 D. 21 3
C©u 28 : Giá trị của m để phương trình 3
4 x  3 x 1  mx m có 4 nghiệm phân biệt là :
A. m 1;6 3  9
B. m 9  6 3;  1
C. m 6 3  9;6 3  9
D. m 9  6 3;  1 C©u 29 : x 1 y 1 z
Trong không gian với hệ tọa độ Oxyz , cho điểm M (2;1;0) và đường thẳng :   . 2 1 1 
Viết phương trình của đường thẳng d đi qua điểm M, cắt và vuông góc với . x  2 y 1 z x  2 y 1 z A. d:   . B. d:   . 1 4  2  2 4  1 x  2 y 1 z x  2 y 1 z C. d:   . D. d:   . 1 4 1 1 4  1
C©u 30 : Phương trình tiếp tuyến với đồ thị hàm số 3 2
y f (x)  x  3x  2 tại điểm x sao cho f "(x )  6 là: 0 0
A. 3x y  3  0 B. y  2  0
C. y  2  0
D. 3x y  3  0
C©u 31 : Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 2
y  9  x ; y  0 xung quanh trục Ox là : 8 71 1296 A. B. C. 3 D.  3 82 5 C©u 32 : Hàm số 4 2
y x x  2 có điểm cực tiểu là: A. y  2 B. x  1  C. x  1 D. x  0 C©u 33 : 2 x mx 1 Cho hàm số y
. Tìm m để hàm số đạt cực đại tại x  2 ? Một học sinh làm như sau: x m 2 2    Bướ x 2mx m 1
c 1: D R \   m , y '   x m2
Bước 2: Hàm số đạt cực đại tại x  2  y '(2)  0  * Trang 3/ mã đề 241 m  1  Bước 3:   2
*  m  4m  3  0   m  3 
Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào? A. Đúng B. Sai từ bước 1 C. Sai từ bước 2 D. Sai từ bước 3
C©u 34 : Khối đa diện đều loại 5;  3 có số mặt là : A. 8 B. 14 C. 10 D. 12
C©u 35 : Cho hình chóp đều S.ABCD có AC = 2a , mặt bên (SBC) tạo với đáy (ABCD) một góc 45o . Tính
thể tích V của khối chóp S.ABCD ? 3 2 3a 3 a 2 3 a A. V B. V C. 3 V a 2 D. V  3 3 2
C©u 36 : Cho a  1;0; 3
 ;b  2;1;2 .Khi đó  ; a b   có giá trị là A. 3 B. 8 C. 74 D. 4
C©u 37 : Tìm hàm số F(x) biết Fx 2
 3x  2x 1 và đồ thị hàm số y F x cắt trục tung tại điểm có tung độ bằng e:
A. F x 2
x x  2
B. F x 2
x x e 1
C. F x 3 2
x x x 1 D.   3 2
F x x x x e C©u 38 : 2 Đặ dx t I   và 2 t
x 1 . Khẳng định nào trong các khẳng định sau là sai : 2  2 x x 1 3 1 dt 2 dt I   
A. tdt xdx B. I  2 t 1 C. 2 2 x t 1 D. 2  1 t 1 2 3 3 C©u 39 : 1 Cho hàm số 3 2 y
x  (m 1)x  4x (m là thàm số). Giá trị của m để hàm số đã cho đồng biến trên 3 R là: Không có giá trị
A. nào của m thỏa B. m  3 C. 1   m  3 D. m   R mãn
C©u 40 : Trong không gian với hệ tọa độ Oxyz . Hãy viết phương trình mặt cầu (S) có tâm I (2;0;1) và tiếp x 1 y z  2
xúc với đường thẳng d:   . 1 2 1 A. 2 2 2
(x  2)  y  (z 1)  2. B. 2 2 2
(x  2)  y  (z 1)  4. C. 2 2 2
(x  2)  y  (z 1)  9. D. 2 2 2
(x 1)  ( y  2)  (z 1)  24.
C©u 41 : Đạo hàm của hàm số là : A. B. C. D.
C©u 42 : Một nhà kho có dạng khối hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB
= 3m, BC = 6m, chiều cao AA’ = 3m, chắp thêm một khối lăng trụ tam giác đều mà một mặt bên là
A’B’C’D’ và A’B’ là một cạnh đáy của lăng trụ. Tính thể tích của nhà kho ? 27 3 27 4  3 912  3 A. 3 m B. 3 m C. 3 54m D. 3 m 2 2 2 Trang 4/ mã đề 241
C©u 43 : Biết , giá trị biểu thức là : A. B. C. D.
C©u 44 : Cho hàm số khẳng định nào dưới đây là đúng ?
A. Đồ thị hàm số cắt trục ox
B. Đồ thị hàm số không có tiệm cận
C. Đồ thị hàm số có 1 tiệm cận đứng và không có
D. Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm tiệm cận ngang cận đứng
C©u 45 : Một cốc nước có dạng hình trụ đựng nước, chiều cao 12cm, đường kính đáy 4cm, lượng nước trong
cốc cao 8cm. Thả vào cốc nước 4 viên bi có cùng đường kính 2cm. Hỏi nước dâng cao cách mép cốc
bao nhiêu cm ? ( làm tròn sau dấu phẩy hai chữ số thập phân, bỏ qua độ dày cốc ). A. 2,67cm B. 2,25cm C. 2,33cm D. 2,75cm
C©u 46 : Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a. Biết hình chóp có chiều cao là h a 3 .
Thể tích khối chóp là : 3 a 3 3 a 3 3 a 3 a A. V B. V C. V D. V  4 8 4 3
C©u 47 : Cho hai số phức z  2  3i , z 1 2i . Tính môđun của số phức z  z  2 z . 1  1 2 2 A. z  137 B. z  15 C. z  5 5 D. z  65
C©u 48 : Cho số phức z  5  4i . Số phức z  2 có
A. Phần thực bằng 5 và phần ảo bằng 4  .
B. Phần thực bằng 4
 và phần ảo bằng 3 .
C. Phần thực bằng 3 và phần ảo bằng 4  .
D. Phần thực bằng 3 và phần ảo bằng 4  i .
C©u 49 : Trong các số phức z tìm điều kiện : z i z  2 3i . Hãy tìm z có mô đun nhỏ nhất 27 6 3 6 6 27 6 27 A. z   i B. z   i C. z    i D. z    i 5 5 5 5 5 5 5 5 C©u 50 :
Cho hàm số y f (x) có đồ thị (C) như hình vẽ. 1
Số nghiệm phân biệt của phương trình f (x)  là: 2 A. 2 B. 0 C. 3 D. 1
------------------------------------------------------Hết-------------------------------------------------- Trang 5/ mã đề 241
Trường THPT Quốc Oai
ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2016 -2017
Môn: Toán ; thời gian 90 phút; mã đề 238
(đề gồm 50 câu trắc nghiệm)
Họ và tên thí sinh:………………………………………………….. số báo danh:…………
C©u 1 : Trong các số phức thỏa mãn điều kiện z  
1 z  2i là số thực. Hãy tìm z có mô đun nhỏ nhất 2 4 4 2 2 4 2 4 A. Z   i B. Z   i C. Z    i D. Z   i 5 5 5 5 5 5 5 5
C©u 2 : Giá trị của m để phương trình 3
4 x  3 x 1  mx m có 4 nghiệm phân biệt là :
A. m 6 3  9;6 3  9
B. m 9  6 3;  1
C. m 9  6 3;  1
D. m 1;6 3  9 C©u 3 :   Cho điể x 1 y 1 z
m M 2,1,0 và đường thẳng  :  
. Gọi d là đường thẳng đi qua M , cắt và 2 1 1 
vuông góc với  . Khi đó, vectơ chỉ phương của d là: A. u 2; 1;2 B. u 0;3;1 C. u 1; 4; 2 D. u 3;0;2
C©u 4 : Phương trình có 2 nghiệm phân biệt khi : A. B. C. D.
C©u 5 : Mệnh đề nào sau đây sai ?
2x  2y z 1
A. Khoảng cách từ điểm M x , y , z đến mặt phẳng 2x  2y z 1  0 là 0 0 0 . 0 0 0  3
B. Mặt phẳng  P : 4x  2y  3  0 song song với mặt phẳng Q : 2xy  5  0 .
C. Mặt phẳng 2x  3y – 2z  0 đi qua gốc tọa độ.
D. Mặt phẳng 3x – z  2  0 có tọa độ vectơ pháp tuyến là 3, 0,  1  . C©u 6 : Cho hàm số 3
y  3x x m (m là thàm số). Để giá trị lớn nhất của hàm số trên đoạn 0; 3   bằng
3 2 thì m phải bằng: A. 3 2 B.  2 C. 2 2 D. 2
C©u 7 : Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z  2z  3  0 . Tọa độ điểm M biểu diễn 1 số phức z là: 1 A. M ( 1  ; 2) B. M ( 1  ; 2i) C. M ( 1  ;2) D. M ( 1  ; 2  ) C©u 8 :
Cho hàm số khẳng định nào sau đây là sai ?
A. Hàm số đồng biến trên R
B. Đồ thị hàm số nằm toàn bộ phía trên trục ox
C. Hàm số nghịch biến trên R
D. Tập xác định của hàm số là R
C©u 9 : Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 2
y  4  x ; y  0 xung quanh trục Ox là : 8 512 71 A. 2 B. C. D.  3 15 82
C©u 10 : Cho hàm số khẳng định nào dưới đây là đúng ?
A. Đồ thị hàm số cắt trục ox
B. Đồ thị hàm số không có tiệm cận
C. Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm
D. Đồ thị hàm số có 1 tiệm cận đứng và không có Trang 1/ mã đề 238 cận đứng tiệm cận ngang
C©u 11 : Đạo hàm của hàm số là : A. B. C. D.
C©u 12 : Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Một mặt phẳng đi qua A’B’
và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Thể tích V của khối A’B’.BAEF là : 3 a 3 3 2a 3 3 5a 3 3 a 3 A. V B. V C. V D. V  27 27 54 18 C©u 13 :
Tập xác định của hàm số là : A. B. C. D. C©u 14 : 2 2 2 Cho
f xdx  3; g t dt  1   
. Giá trị của A  2 f
 x3gxdx  là: 1 1 1 A. 5 B. 3 C. 2 D. 9
C©u 15 : Số nghiêm của phương trình 4 z  1 là A. 1 B. 4 C. 2 D. 3
C©u 16 : Khẳng định nào sau đây là sai ? A. B. C. D.
C©u 17 : Diện tích hình phẳng giới hạn bởi các đường y  x  2
1 ; y  0; x  0; x  2 bằng : 2 A. 15 B. 35 C. D. 21 3
C©u 18 : Trong không gian với hệ tọa độ Oxyz , cho a  1;2; 
1 , b  3;4;3 . Tìm tọa độ của x biết
x b a A. x   2  ; 2  ; 4  .
B. x  2; 2; 4.
C. x  1;1; 2. D. x   2  ; 2  ;4. C©u 19 : 2 ln x a c a c Biết dx   ln 2 
với a,b,c,d là các số nguyên dương và ;
là các phân số tối giản. Giá 3 x b d b d 1
trị của M ad bc là : A. 8 B. 10 C. 32 D. 40 C©u 20 : 2 x mx 1 Cho hàm số y
. Tìm m để hàm số đạt cực đại tại x  2 ? Một học sinh làm như sau: x m 2 2    Bướ x 2mx m 1
c 1: D R \   m , y '   x m2
Bước 2: Hàm số đạt cực đại tại x  2  y '(2)  0  * m  1  Bước 3:   2
*  m  4m  3  0   m  3 
Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào? A. Sai từ bước 3 B. Đúng C. Sai từ bước 2 D. Sai từ bước 1
C©u 21 : Tìm hàm số F(x) biết Fx 3
 4x  6x 1 và đồ thị hàm số y F x cắt trục tung tại điểm có tung độ bằng 2:
A. F x 4 2
 4x  6x x  2
B. F x 4 2
x  3x x 1
C. F x 3
x x  2
D. F x 4 2
x  3x x  2 Trang 2/ mã đề 238
C©u 22 : Phương trình tiếp tuyến với đồ thị hàm số 3 2
y f (x)  x  3x  2 tại điểm x sao cho f "(x )  0 là: 0 0
A. 3x y  3  0
B. 3x y  3  0 C. 3
x y 3  0
D. 3x y  3  0
C©u 23 : Cho (P) là đồ thị hàm số 2
y x  4x  5 . Diện tích hình phẳng giới hạn bởi (P) và các tiếp tuyến của  5  (P) kẻ từ điểm A ; 1    là :  2  9 18 9 9 A. B. C. D. 4 4 2 8
C©u 24 : Đường thẳng y  6x m là tiếp tuyến của đường cong 3
y x  3x 1 khi m bằng A. -5 hoặc 1 B. 3 hoặc -5 C. -3 hoặc 1 D. -1 hoặc 3
C©u 25 : Trong không gian với hệ tọa độ Oxyz , cho 3 điểm A1;2;3 , B0;1;  1 , C 1;0; 2   và mặt phẳng
P có phương trình x y z  2  0 . Gọi M là điểm thuộc mặt phẳng P sao cho giá trị biểu thức 2 2 2
T MA  2MB  3MC nhỏ nhất. Tính khoảng cách từ M đến mặt phẳng
Q : 2x y  2z  3  0 121 2 5 91 A. 24 B. C. D. 54 3 54 C©u 26 : 1 Hàm số 3 2 y
x x  3x  2 đạt cực tiểu tại: 3 1 A. x  0 B. x C. x  3  D. x  1 3 C©u 27 : 1
Cho số phức z a bi . Khi đó số  z z  là: 2 A. Một số thực. B. 2 C. i
D. Một số thuần ảo C©u 28 : 1 Cho hàm số 3 2
y   x  (m 1)x  4x (m là thàm số). Giá trị của m để hàm số đã cho nghịch biến 3 trên R là: m  1  A. m  3 B. C. 1   m  3 D. m   R m  3
C©u 29 : Điểm biểu diễn của các số phức z  7  bi với b
, nằm trên đường thẳng có phương trình là: A. y  7 B. x  7 C. y x  7
D. y x C©u 30 :
Nguyên hàm hàm số f x  sin 2x   1 là : 1 A. f
 xdx   cos2x 1C B. f  x 1 dx   cos 2x C 2 2 1 C. f
 xdx  cos2x 1C D. f  x 1 dx  cos 2x C 2 2
C©u 31 : Cho hình trụ có độ dài đường sinh là b và bán kính đường tròn đáy là a. Diện tích toàn phần của hình trụ là :
A. S  2 a b a
S  2 a b  2a
S   a 2b a
S   a b a tp   B. tp   C. tp   D. tp  
C©u 32 : Phương trình
Có 2 nghiệm x1, x2 thỏa mãn khi : A. B. C. D. Trang 3/ mã đề 238 C©u 33 :
Cho hàm số y f (x) có đồ thị (C) như hình vẽ.
Số nghiệm phân biệt của phương trình f (x)  1  là: A. 2 B. 0 C. 1 D. 3
C©u 34 : Trong không gian với hệ tọa độ Oxyz , tìm m để phương trình 2 2 2
x y z  2mx  2(m  2) y  2(m  3)z  8m  37  0 là phương trình của một mặt cầu A. m  4  hay m  2 B. m  4  hay m  2  C. m  2  hay m  4 D. m  2  hay m  4
C©u 35 : Số phức z    i3 1 có mô đun bằng: A. z  2  2 B. z  2 C. z  0 D. z  2 2 C©u 36 : 3 Đặ dx t I   và x
t e 1. Khẳng định nào trong các khẳng định sau là sai : x e 1 1 3 e 1  1 1  I   2
ln e e   1  2 3 1 1  I   dt    A. B. I   dt   C. x dt e dx D. t t 1    t t 1 e 1 1 C©u 37 : x 1
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2  ;0 lần lượt là: x  trên đoạn   1 1 1 A. 3 và -1 B. và -1 C. 0 và -1 D.  và -1 3 3
C©u 38 : Khối đa diện đều loại 3;  5 có số mặt là : A. 16 B. 12 C. 20 D. 8
C©u 39 : Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Biết hình chóp có chiều cao là
h a 3 . Thể tích khối chóp là : 3 a 3 a 3 3 a 3 A. V B. V C. 3 V a 3 D. V  3 3 8 C©u 40 :
Biết , giá trị biểu thức là : A. B. C. D.
C©u 41 : Một hình nón có bán kính đáy r  3a , chiều cao h  4a . Kí hiệu góc ở đỉnh của hình nón là 2 .
Trong các mệnh đề sau, mệnh đề nào đúng ? 4 4 4 4 A. cos  B. tan  C. sin   D. cot   5 5 5 5
C©u 42 : Bất phương trình có tập nghiệm là : A. B. C. D. Trang 4/ mã đề 238
C©u 43 : Một nhà kho có dạng khối hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB
= a, BC = 2a, chiều cao AA’ = 3a, chắp thêm một khối lăng trụ tam giác đều mà một mặt bên là
A’B’C’D’ và A’B’ là một cạnh đáy của lăng trụ. Tính thể tích của nhà kho ? 12  3 312  3 36  3 3 a 3 A. 3 a B. 3 a C. 3 a D. 2 2 6 2
C©u 44 : Một cốc nước có dạng hình trụ đựng nước, chiều cao 16cm, đường kính đáy 6cm, lượng nước trong
cốc cao 10cm. Thả vào cốc nước 4 viên bi có cùng đường kính 4cm. Hỏi nước dâng cao cách mép
cốc bao nhiêu cm ? ( làm tròn sau dấu phẩy hai chữ số thập phân, bỏ qua độ dày cốc ). A. 1,43cm B. 1,26cm C. 1,34cm D. 1,68cm
C©u 45 : Tập nghiệm của bất phương trình là : A. B. C. D.
C©u 46 : Trong không gian với hệ tọa độ Oxyz , cho a   2  ; 3; 
1 , b  1;  3; 4 . Tìm  ; a b   A. 171 B. 171 C. 315 D. 315
C©u 47 : Cho hàm số 4 2
y x  2x  5 . Chọn khẳng định đúng?
A. Hàm số nghịch biến trên khoảng  ;    1 và (1; )
B. Hàm số đồng biến trên khoảng  1   ;1
C. Hàm số nghịch biến trên khoảng  1  ;0 và (1;)
D. Hàm số đồng biến trên khoảng  1  ;0 và (1;) C©u 48 : 1 x
Số đường tiệm cận của đồ thị hàm số y  2x  là: 1 A. 0 B. 1 C. 3 D. 2
C©u 49 : Cho hình chóp đều S.ABCD có AB = a , mặt bên (SAD) tạo với đáy (ABCD) một góc 60o . Tính thể
tích V của khối chóp S.ABCD ? 3 a 3 3 3a 3 a 3 A. 3 V a 2 B. V C. V D. V  6 2 3
C©u 50 : Phương trình tham số của đường thẳng d đi qua điểm M 1,2,3 và có vec tơ chỉ phương a (1;3;2) là : x  1 tx  1   tx  1 tx  1   t    
A. y  2  3t B. y  2   3t C. y  2   3t D. y  2   3t     z  3  2tz  3   2tz  3  2tz  3   2t
-------------------------------------------------------------Hết---------------------------------------------------------- Trang 5/ mã đề 238
Trường THPT Quốc Oai
ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2016 -2017
Môn: Toán ; thời gian 90 phút; mã đề 242
(đề gồm 50 câu trắc nghiệm)
Họ và tên thí sinh:………………………………………………….. số báo danh:…………
C©u 1 : Cho hàm số khẳng định nào dưới đây là đúng ?
A. Đồ thị hàm số cắt trục ox
B. Đồ thị hàm số không có tiệm cận
C. Đồ thị hàm số có 1 tiệm cận đứng và không có
D. Đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm tiệm cận ngang cận đứng C©u 2 : Cho hàm số 3 2
y x  3x  3
 . Chọn khẳng định sai?
A. Hàm số không có cực trị
B. Hàm số có hai điểm cực trị
Hàm số đồng biến trên khoảng  ;  0và
C. Hàm số nghịch biến trên khoảng 0; 2 D. (2; ) 
C©u 3 : Tập nghiệm của bất phương trình là : A. B. C. D.
C©u 4 : Cho hình chóp đều S.ABCD có AC = 2a , mặt bên (SBC) tạo với đáy (ABCD) một góc 45o . Tính
thể tích V của khối chóp S.ABCD ? 3 2 3a 3 a 3 a 2 A. V B. V C. V D. 3 V a 2 3 2 3 C©u 5 : 2 x mx 1 Cho hàm số y
. Tìm m để hàm số đạt cực đại tại x  2 ? Một học sinh làm như sau: x m 2 2    Bướ x 2mx m 1
c 1: D R \   m , y '   x m2
Bước 2: Hàm số đạt cực đại tại x  2  y '(2)  0  * m  1  Bước 3:   2
*  m  4m  3  0   m  3 
Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào? A. Sai từ bước 2 B. Đúng C. Sai từ bước 1 D. Sai từ bước 3
C©u 6 : Tìm hàm số F(x) biết Fx 2
 3x  2x 1 và đồ thị hàm số y F x cắt trục tung tại điểm có tung độ bằng e:
A. F x 2
x x  2
B. F x 2
x x e 1 C.   3 2
F x x x x e
D. F x 3 2
x x x 1 C©u 7 : 2 Đặ dx t I   và 2 t
x 1 . Khẳng định nào trong các khẳng định sau là sai : 2  2 x x 1 3 1 dt 2 dt I   
A. tdt xdx B. I  2 t 1 C. 2  D. 2 2 x t 1 1 t 1 2 3 3
C©u 8 : Trong không gian với hệ trục tọa độ Oxyz , cho hình hộp ABC . D A BCD   . Biết A 3  ;2;  1 ,
C 4;2;0 , B 2  ;1; 
1 , D3;5;4 .Tìm tọa độ A của hình hộp ABC . D A BCD   . Trang 1/ mã đề 242 A. A 3  ;3;3. B. A 3  ; 3  ; 3  . C. A 3  ;3;  1 . D. A 3  ; 3  ;3.
C©u 9 : Trong không gian với hệ tọa độ Oxyz , cho 3 điểm A 2  ;2;3 , B1; 1
 ;3 ,C 3;1;  1 và mặt phẳng
Pcó phương trình x2z 8  0. Gọi M là điểm thuộc mặt phẳng P sao cho giá trị biểu hức 2 2 2
T  2MA MB  3MC nhỏ nhất. Tính khoảng cách từ M đến mặt phẳng
Q:x2y 2z 6  0 3 3 A. 2 B. 4 C. d D. d  2 3
C©u 10 : Khẳng định nào sau đây là sai ? A. B. C. D.
C©u 11 : Khối đa diện đều loại 5;  3 có số mặt là : A. 14 B. 8 C. 12 D. 10
C©u 12 : Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Một mặt phẳng đi qua A’B’
và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Thể tích V của khối C.A’B’FE là : 3 5a 3 3 5a 3 3 a 3 3 5a 3 A. V B. V C. V D. V  54 18 27 27
C©u 13 : Trong không gian với hệ tọa độ Oxyz . Hãy viết phương trình mặt cầu (S) có tâm I (2;0;1) và tiếp x 1 y z  2
xúc với đường thẳng d:   . 1 2 1 A. 2 2 2
(x  2)  y  (z 1)  9. B. 2 2 2
(x  2)  y  (z 1)  4. C. 2 2 2
(x 1)  ( y  2)  (z 1)  24. D. 2 2 2
(x  2)  y  (z 1)  2.
C©u 14 : Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a. Biết hình chóp có chiều cao là h a 3 .
Thể tích khối chóp là : 3 a 3 3 a 3 3 a 3 a A. V B. V C. V D. V  4 8 3 4
C©u 15 : Cho phương trình 2
z  2z  3  0 trên tập số phức,có hai nghiệm là z , z .Khi đó 2 2 zz có giá trị 1 2 1 2 là: A. 2 2 B. 6 C. 3 D. 2 C©u 16 : Cho hàm số
khẳng định nào sau đây là sai ?
A. Hàm số đồng biến trên R
B. Tập xác định của hàm số là R
C. Hàm số nghịch biến trên R
D. Đồ thị hàm số nằm toàn bộ phía trên trục ox C©u 17 :
Tập xác định của hàm số là : A. B. C. D. C©u 18 : 1 Cho hàm số 3 2 y
x  (m 1)x  4x (m là thàm số). Giá trị của m để hàm số đã cho đồng biến trên 3 R là: Không có giá trị A. m  3 B. 1   m  3 C. m   R D. nào của m thỏa mãn C©u 19 :
Biết , giá trị biểu thức Trang 2/ mã đề 242 là : A. B. C. D. C©u 20 :
Nguyên hàm hàm số f x  cos3x  2 là : 1 A. f
 xdx  sin3x2C B. f  x 1
dx   sin 3x C 3 3 1 C. f
 xdx   sin3x2C D. f  x 1 dx  sin 3x C 3 3 C©u 21 : 3 3  ln x a 1 c a c Biết dx   ln 
với a,b,c,d là các số nguyên dương và ;
là các phân số tối giản. 2 (x 1) b b d b d 1
Giá trị của M ac bd là : A. 17 B. 20 C. 145 D. 11
C©u 22 : Diện tích hình phẳng giới hạn bởi các đường y  x  2
2 ; y  0; x  1; x  3 bằng : 98 A. 30 B. 18 C. D. 21 3
C©u 23 : Phương trình tiếp tuyến với đồ thị hàm số 3 2
y f (x)  x  3x  2 tại điểm x sao cho f "(x )  6 là: 0 0
A. 3x y  3  0 B. y  2  0
C. y  2  0
D. 3x y  3  0 C©u 24 : 2 Cho số phức z 3
2i . Tìm số phức w z 1 i z A. w 7 8i B. w 7 8i C. w 3 5i D. w 3 5i
C©u 25 : Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 2
y  9  x ; y  0 xung quanh trục Ox là : 8 71 1296 A. B. C. D. 3 3 82 5 C©u 26 :
Cho hàm số y f (x) có đồ thị (C) như hình vẽ. 1
Số nghiệm phân biệt của phương trình f (x)  là: 2 A. 2 B. 0 C. 1 D. 3
C©u 27 : Giá trị của m để phương trình 3
4 x  3 x 1  mx m có 4 nghiệm phân biệt là :
A. m 1;6 3  9
B. m 6 3  9;6 3  9
C. m 9  6 3;  1
D. m 9  6 3;  1
C©u 28 : Đạo hàm của hàm số là : A. B. Trang 3/ mã đề 242 C. D.
C©u 29 : Cho hai số phức z , z thỏa mãn z z 1, z z  3 . Tính z z : 1 2 1 2 1 2 1 2 A. 4 B. 1 C. 2 D. 3
C©u 30 : Cho (P) là đồ thị hàm số 2
y x  4x  3 . Diện tích hình phẳng giới hạn bởi (P) và các tiếp tuyến của
(P) kẻ từ điểm A2; 5   là : 10 16 32 8 A. B. C. D. 3 3 3 3 C©u 31 : 3 3 3 Cho
f xdx  2; g t dt  3   
. Giá trị của A  3 f
 x2gxdx  là: 2 2 2 A. 12 B. 0 C. 5 D. -1
C©u 32 : Phương trình
Có 2 nghiệm x1, x2 thỏa mãn khi : A. B. C. D.
C©u 33 : Cho số phức z  5  4i . Số phức z  2 có
A. Phần thực bằng 5 và phần ảo bằng 4  .
B. Phần thực bằng 4
 và phần ảo bằng 3 .
C. Phần thực bằng 3 và phần ảo bằng 4  i .
D. Phần thực bằng 3 và phần ảo bằng 4  .
C©u 34 : Một nhà kho có dạng khối hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB
= 3m, BC = 6m, chiều cao AA’ = 3m, chắp thêm một khối lăng trụ tam giác đều mà một mặt bên là
A’B’C’D’ và A’B’ là một cạnh đáy của lăng trụ. Tính thể tích của nhà kho ? 912  3 27 3 27 4  3 A. 3 m B. 3 m C. 3 54m D. 3 m 2 2 2
C©u 35 : Trong các số phức z tìm điều kiện : z i z  2 3i . Hãy tìm z có mô đun nhỏ nhất 27 6 6 27 6 27 3 6 A. z   i B. z    i C. z    i D. z   i 5 5 5 5 5 5 5 5 C©u 36 : Hàm số 4 2
y x x  2 có điểm cực tiểu là: A. y  2 B. x  1  C. x  0 D. x  1
C©u 37 : Cho hàm số 3
y  3x x m (m là thàm số). Để giá trị lớn nhất của hàm số trên đoạn 0; 3   bằng
5 2 thì m phải bằng: A. 3 2 B. 4 2 C. 2 D. 2 2
C©u 38 : Bất phương trình có tập nghiệm là : A. B. C. D. C©u 39 : x 1 y 1 z
Trong không gian với hệ tọa độ Oxyz , cho điểm M (2;1;0) và đường thẳng :   . 2 1 1 
Viết phương trình của đường thẳng d đi qua điểm M, cắt và vuông góc với . x  2 y 1 z x  2 y 1 z A. d:   . B. d:   . 1 4 1 2 4  1 x  2 y 1 z x  2 y 1 z C. d:   . D. d:   . 1 4  2  1 4  1
C©u 40 : Trong không gian với hệ tọa độ Oxyz , cho hai điểm ( A 2; 4;1) , B( 1
 ;1;3) và mặt phẳng (P) : Trang 4/ mã đề 242
x  3y  2z  5  0 . Viết phương trình mặt phẳng Q đi qua hai điểm A, B và vuông góc với mặt
phẳng  P.
A. Q : 2y  3z 12  0
B. Q : 2y  3z 11  0
C. Q : 2y  3z 1  0
D. Q : 2x  3z 11  0
C©u 41 : Đường thẳng y  9x m là tiếp tuyến của đường cong 3 2
y x  3x 1 khi m bằng A. -6 hoặc 26 B. -1 hoặc 3 C. -3 hoặc 1 D. 3 hoặc -5 C©u 42 : 4
Một hình nón có bán kính đáy r  1 , chiều cao h
. Kí hiệu góc ở đỉnh của hình nón là 2 . 3
Trong các mệnh đề sau, mệnh đề nào đúng ? 3 3 3 3 A. sin   B. cot   C. tan  D. cos  5 5 5 5 C©u 43 : 1
Số đường tiệm cận của đồ thị hàm số y  là: x A. 1 B. 2 C. 3 D. 0
C©u 44 : Cho hai số phức z  2  3i , z 1 2i . Tính môđun của số phức z  z  2 z . 1  1 2 2 A. z  137 B. z  15 C. z  65 D. z  5 5
C©u 45 : Một cốc nước có dạng hình trụ đựng nước, chiều cao 12cm, đường kính đáy 4cm, lượng nước trong
cốc cao 8cm. Thả vào cốc nước 4 viên bi có cùng đường kính 2cm. Hỏi nước dâng cao cách mép cốc
bao nhiêu cm ? ( làm tròn sau dấu phẩy hai chữ số thập phân, bỏ qua độ dày cốc ). A. 2,33cm B. 2,25cm C. 2,75cm D. 2,67cm
C©u 46 : Phương trình có 2 nghiệm phân biệt khi : A. B. C. D.
C©u 47 : Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A1;3;4, B 2  ;3;0 , C 1  ;3;2.
Tìm tọa độ trọng tâm G của tam giác ABC .  2   2   2 
A. G  ; 2; 2 .   B. G  ;1; 2 .   C. G  ;1;1 .   D. G  2  ;1;2.  3   3   3 
C©u 48 : Cho hình trụ có độ dài đường sinh là l và bán kính đường tròn đáy là r. Diện tích toàn phần của hình trụ là :
A. S   r 2l r
S  2 r l r
S  2 r l  2r
S   r l r tpB. tp   C. tp   D. tp  
C©u 49 : Cho a  1;0; 3
 ;b  2;1;2 .Khi đó  ; a b   có giá trị là A. 8 B. 3 C. 74 D. 4 C©u 50 : x
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  1;3 lần lượt là: x  trên đoạn   1 3 1 1 A. và B. 0 và -1 C. 3 và -1 D.  và -1 4 2 3
------------------------------------------------------Hết----------------------------------------------------- Trang 5/ mã đề 242 BẢNG ĐÁP ÁN 1 Cau 235 236 237 238 1 C D C B 2 B D B D 3 D B D C 4 B A C D 5 B D B A 6 B C B C 7 B B C A 8 A D A C 9 D C B C 10 D D B C 11 D D A A 12 C A C B 13 C D A D 14 A B A B 15 A B D B 16 D A D D 17 A C C C 18 C C C B 19 B A B A 20 A B D C 21 A B A D 22 B C A B 23 C A B A 24 B A D C 25 C A D D 26 D B C D 27 D D C A 28 A D A C 29 A B C B 30 C B A A 31 C D A A 32 D D C A 33 D C B A 34 C C A D 35 D B C D 36 C A A B 37 A A B B 38 A C D C 39 B C B B 40 D A B C 41 A C D A 42 A A D D 43 C B A A 44 B D D B 45 C A D B 46 B B A C 47 B C D D 48 D C C D 49 B B B B 50 A A B A BẢNG ĐÁP ÁN 2 Cau 239 240 241 242 1 B B D D 2 A C A A 3 A B B A 4 D D B C 5 A D D C 6 C A B C 7 B C D C 8 C A A A 9 B A A B 10 B C B A 11 D D C C 12 A A A A 13 D D C D 14 C C A D 15 D B B B 16 D B C A 17 B A A A 18 B D C D 19 C C D D 20 D A A A 21 D B C A 22 D B A C 23 C C C C 24 A A B B 25 B B A C 26 A A C D 27 C C B C 28 C A B D 29 B B A B 30 D C B B 31 D D D A 32 D B D B 33 B C B D 34 B D D D 35 B A B D 36 C C C C 37 A D D B 38 A A D B 39 B C A C 40 A D A B 41 A B D A 42 C A B A 43 A B D B 44 D B D D 45 A A A D 46 C B C B 47 B D C B 48 A D C B 49 C D B C 50 C C C A
Document Outline

  • Quoc-Oai.pdf
    • đề 1
    • đề 2
    • đề 3
    • đề 4
    • đề 5
    • đề 6
    • đề 7
    • đề 8
  • đáp an mã 1.pdf
  • đáp an mã 2.pdf