Thông tin
Quiz

Đề thi HK2 Toán 12 năm học 2016 – 2017 trường THPT Trần Hưng Đạo – Hà Nội

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2016 – 2017 .Mời bạn đọc đón xem.

Chủ đề:

Đề HK2 Toán 12 491 tài liệu

Môn:

Toán 12 3.9 K tài liệu

Thông tin:

21 trang 1 năm trước

Tác giả:

Lan Tường

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Đề thi HK2 Toán 12 năm học 2016 – 2017 trường THPT Trần Hưng Đạo – Hà Nội

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2016 – 2017 .Mời bạn đọc đón xem.

39 20 lượt tải Tải xuống

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/21 Mã đề 254

TRƯỜNG THPT TRẦN HƯNG ĐẠO ĐỀ KIỂM TRA HỌC KỲ II, NĂM HỌC 2016 – 2017

THANH XUÂN MÔN: Toán, khối 12

Đề gồm có 05 trang Thời gian làm bài: 90 phút, không kể thời gian phát đề

Họ tên thí sinh:............................................ Số báo danh:.............................................. Mã đề 254

Câu 1. Giải phương trình

9 12 20 0

x x

  

trên tập số phức, được tập nghiệm là

2 4 4 2

;

3 3 3 3

i i

 

 

 

 

. B.

2 4 2 4

;

3 3 3 3

i i

 

 

 

 

1 2 2 1

;

3 3 3 3

i i

 

 

 

 

. D.

4 2 4 2

;

3 3 3 3

i i

 

 

 

 

Câu 2. Cho

I xe x







. Biết rằng

ae b



 trong đó

và

là các số nguyên dương. Khi đó,

a b



bằng

. B.

. C.

. D.

Câu 3. Hàm số

3 2

3 10

y x x x

   

đạt

A. cực đại tại

 

. B. cực đại tại



C. cực tiểu tại

 

. D. cực tiểu tại



Câu 4. Tính

 

1 ln

I x







được kết quả là

. B.

. C.

. D.

Câu 5. Diện tích hình phẳng giới hạn bởi đồ thị hàm số

y e



và hai đường thẳng



là



. B.



. C.

. D.



Câu 6. Đường thẳng

y x

 

và đồ thị hàm số







có số điểm chung là

. B.

. C.

. D.

Câu 7. Cho hàm số

3 2

y x x

  

có đồ thị





và



là tiếp tuyến của





song song với đường

thẳng

3 3,

y x

  



tiếp xúc với





tại điểm có hoành độ

 

. B.

 

. C.

 









. D.



Câu 8. Khi tính

4 d ,

I x x

 



bằng phép đặt

2sin ,

x t



thì được

 

2 1 cos2 d

t t







. B.

 

2 1 cos2 d

t t







. C.

4cos d

t t



. D.

2cos d

t t



Câu 9. Tiếp tuyến của đồ thị hàm số





tại điểm có hoành độ



có phương trình là

y x

 

. B.

y x

  

. C.

y x

  

. D.

y x

 

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/21 Mã đề 254

Câu 10. Cho hai số phức

1 2

2 3 , 3

z i z i

    

. Khi đó,

1 2

z z

 

. B.

. C.

. D.

Câu 11. Tất cả các giá trị của tham số

để hàm số

3 2

y x mx mx

    

nghịch biến trên



là

 









. B.

1 0

  

. C.

1 0

  

. D.

 









Câu 12. Cho số phức

thỏa mãn :









1 3 2 3 4

z i z i i

    

. Khi đó tính được

14 7

5 5

z i

 

. B.

14 7

5 5

z i

 

. C.

13 6

5 5

z i

 

. D.

13 6

5 5

z i

 

Câu 13. Tính

cos d

x x x



bằng phương pháp nguyên hàm từng phần thì đặt

cos

d d

u x

v x x











. B.

d cos d

u x

v x x











. C.

d cos

u x x

v x











. D.

cos d

u x x

v x











Câu 14. Thể tích khối tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường

y x x

 



quay

xung quanh

là



. B.

. C.



. D.

Câu 15. Cho









3 2 3 2 4

z i z i i

    

là phương trình với ẩn

. Nghiệm của phương trình là

3 1

2 2

z i

 

. B.

3 1

2 2

z i

 

. C.

3 1

2 2

z i

  

. D.

3 1

2 2

z i

  

Câu 16. Gọi

là nghiệm phức của phương trình

4 13 0

x x

  

. Giá trị của biểu thức

3 3

1 2

x x



. B.

100

. C.

. D.

Câu 17. Diện tích hình phẳng giới hạn bởi các đồ thị hàm số

y x



và trục tung là

 

1 d

x x





. B.

1 d

x x





. C.

x x



. D.

1 d

x x





Câu 18. Hàm số

 

3 2

2 3

y x mx m x

    có hai điểm cực trị cùng dấu khi và chỉ khi



. B.







 



. C.



   







. D.

 

Câu 19. Tính

 

1 sin d

x x x







được kết quả là



. B.

. C. 2





. D. 1





Câu 20. Tính

cos

sin d

e x x



được kết quả là

sin x

e C

 

. B.

cosx

e C



. C.

sin x

e C



. D.

cosx

e C

 

Câu 21. Cho

x y

là các số thực và hai số phức

2 5

z i

  





3 1 2

z x y i

   

bằng nhau thì:

 









. B.











 



. C.

 





 



. D.















TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/21 Mã đề 254

Câu 22. Hàm số nào sau đây có giá trị lớn nhất trên









. B.

4 2

2 3

y x x

   

. C.

3 1

y x x

  

. D.

y x

 

Câu 23. Cho hai số phức

1 2

z i

  

z i

 

. Khi đó số phức

1 2 1 2

. .

z z z z z

  có phần ảo là



. B.

. C.



. D.

Câu 24. Tính

cos4 d

x x



được kết quả là

sin 4

x C



. B.

sin4

x C

 

. C.

sin 4

x C

 

. D.

sin 4

x C



Câu 25. Đồ thị hàm số

3 2

y x x x

  

cắt đường thẳng





y k x

 

tại ba điểm phân biệt khi và chỉ

khi

thuộc

;

 

 

 

 

. B.

;

 

 

 

 

. C.

 

; \ 1

 

  

 

 

. D.

 

; \ 0

 

 

 

 

Câu 26. Cho hàm số





y f x

 liên tục và có đạo hàm đến cấp hai trên









; ; ;

a b x a b

 . Khẳng định

nào sau đây là sai?

A. Nếu

















0 0

0 ; , 0 ;

f x x a x f x x x b

 

      thì

x x



là một điểm cực tiểu của hàm số.

B. Nếu





f x





thì

x x



là một điểm cực trị của hàm số.

C. Nếu





f x



đổi dấu từ dương sang âm khi

đi qua

thì

x x



là một điểm cực đại của hàm số.

D. Nếu





 

f x



















thì

x x



là một điểm cực trị của hàm số.

Câu 27. Hình tròn tâm





1;2

I  , bán kính



là tập hợp điểm biểu diễn hình học của các số phức

thỏa mãn









1 2

z x y i



   











. B.









1 2

z x y i



   



















1 2

z x y i



   











. D.









1 2

z x y i



   











Câu 28. Thể tích khối tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường

y x

 



quay quanh trục

là



. B.



. C.

. D.

Câu 29. Ha m sô

y x

 

A. Nghi  ch biên trên



. B. Đông biên trên







C. Nghi  ch biên trên







. D. Đông biên trên



Câu 30. Cho hı nh phăng

giơ i ha  n bơ i đô thi 

cos

y x



, tru  c hoa nh, tru  c tung va đươ ng thăng





Thê tı ch khô i tro n xoay sinh bơ i

khi quay quanh tru  c

la

cos d

V x x







. B.

cos d

V x x







. C.

cos d

V x x







. D.

cos d

V x x







TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/21 Mã đề 254

Câu 31. Hàm số

2cos

y x x

 

có giá trị lớn nhất trên



 

 

 

là



 . B.



 . C.



. D.

Câu 32. Cho số phức

3 4

z i

 

, biểu thức

3 10

A z z

  

bằng

. B.

. C.

. D.



Câu 33. Diện tích hình phẳng giới hạn bởi đồ thị hàm số

y x x

 

, trục hoành và hai đường thẳng

3, 4

x x

  

bằng

119

. B.

. C.

201

. D.

Câu 34. Cho hai mặt phẳng









:2 0, : 2 2 3 0

P y z Q x y z

     

và

là giao tuyến của chúng.

Phương trình đường thẳng

là

5 2

2 2

x t

y t

z t

  





 





 



. B.

5 2

2 2

x t

y t

z t

  





 





 



. C.

5 2

2 2

x t

y t

z t

  





 





 



. D.

5 2

2 2

x t

y t

z t

  





 





 



Câu 35. Phương trình đường thẳng đi qua điểm





2;1; 1

 





0; 1; 3

 

là

1 2

3 2

x t

y t

z t







  





  



. B.

2 2

1 2

x t

y t

z t

  





 





  



. C.

x t

y t

z t







  





  



. D.

x t

y t

z t

  





 





  



Câu 36. Cho mặt cầu





2 2 2

: 4 2 2 10 0

S x y z x y z

      

, mặt phẳng





: 2 2 10 0

P x y z

   

Khẳng định nào sau đây là đúng?





và





không có điểm chung.





cắt





theo giao tuyến là đường tròn lớn.





tiếp xúc với









cắt





theo giao tuyến là khác đường tròn lớn.

Câu 37. Trong không gian với hệ tọa độ

Oxyz

, với













2;1; 2 , 1; 3; 1 , 0;2; 1

A B C

   

. Nếu tứ giác

ABCD

là hình bình hành thì tọa độ của

là





1;6; 2



. B.





1;6;2

. C.





1; 6; 2

 

. D.





1;6; 2

 

Câu 38. Mặt phẳng





chứa đường thẳng

1 1 1

1 2 1

x y z

  

 



và điểm





0;2;2

A có phương trình là

5 2 2 0

x y z

   

. B.

5 2 2 0

x y z

   

. C.

5 5 2 0

x z

  

. D.

2 0

x z

  

Câu 39. Cho





1; 3; 1

A 





1; 1; 2

B 





2; 1; 3





0; 1; 1



. Phương trình mặt phẳng chứa

và

song song với

là

2 4 0

x z

  

. B.

2 4 2 0

x z z

   

8 3 4 3 0

x y z

   

. D.

8 3 4 3 0

x y z

   

Câu 40. Cho hai đường thẳng

2 1 2

1 1 1

x y z

  

 

5 2

2 4 1

x y z

 

 

 

, khoảng cách giữa hai

đường thẳng này là

. B.

2 6

. C.

4 6

. D.

3 6

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/21 Mã đề 254

Câu 41. Phương trình mặt cầu đi qua bốn điểm





2; 2; 2

A 





4; 2; 2

 





1; 1; 2



và





1; 2; 1



là

     

2 2 2

1 2 2 25

x y z

     

. B.

     

2 2 2

1 2 2 16

x y z

     

     

2 2 2

1 2 2 16

x y z

     

. D.

     

2 2 2

1 2 2 25

x y z

     

Câu 42. Cho đường thẳng

1 2

1 2 1

x y z

 

 



, và mặt phẳng





: 3 0

P x y z

   

. Gọi



là hình

chiếu của

trên





, khi đó



có một vectơ chỉ phương là





1;2; 1

 



. B.





1; 2; 1

  



. C.





1;2; 1

  



. D.





1;2;1

u 



Câu 43. Cho

2 3

a j k

 

  

. Khi đó tọa độ của



là





2;0; 3



. B.





2; 3;0

 . C.





0;2; 3



. D.





0;2;3

Câu 44. Cho

ABC



với





1;0;0

A ;





0;2;0

B ;





3;0;4

C và

thuộc





Oyz

. Nếu





MC ABC

 thì

tọa độ của

là

3 11

0; ;

2 2

 

 

 

3 11

0; ;

2 2

 



 

 

3 11

0; ;

2 2

 



 

 

3 11

0; ;

2 2

 

 

 

 

Câu 45. Cho mặt phẳng





: 2 3 1 0

P x z

  

. Khi đó





có một vectơ pháp tuyến là





2; 3;0

n  



. B.





2; 3;1

n  



. C.





2; 3; 1

  



. D.





2;0; 3

 



Câu 46. Cho hai đường thẳng

3 1

1 2 1

x y z

 

 



1 2

: 1

x t

y t

z t

 





   





 



, vị trí tương đối hai đường thẳng này là

A. trùng nhau. B. song song với nhau.

C. cắt nhau. D. chéo nhau.

Câu 47. Cho









1;2;2 , 3;0;2

A B . Mặt phẳng trung trực đoạn thẳng

có phương trình là

3 0

x y

  

. B.

1 0

x y

  

. C.

2 2 3 0

x y

  

. D.

1 0

x y

  

Câu 48. Phương trình đường thẳng đi qua





2;1; 1



và có vectơ chỉ phương





1; 2;2

u  



là

2 1 1

1 2 2

x y z

  

 



. B.

1 2

x t

y t

z t

 





  





 



2 1 1

1 2 2

x y z

  

 



. D.

1 2 2

2 1 1

x y z

  

 



Câu 49. Mặt cầu





2 2 2

2 2 2 6 8 4 2 0

x y z x y z

      

có tọa độ tâm

và bán kính

lần lượt là

3 5

;2; 1 ,

2 2

I R

 

  

 

 

. B.

; 2;1 , 5

I R

 

 

 

 

3 25

; 2;1 ,

2 4

I R

 

 

 

 

. D.

;2; 1 , 25

I R

 

  

 

 

Câu 50. Mặt phẳng đi qua





1;2;1

A và song song với mặt phẳng





2 2 0

x y z

   

có phương

trình là

2 1 0

x y z

    

. B.

2 1 0

x y z

   

. C.

2 2 0

x y z

   

. D.

2 1 0

x y z

   

----------HẾT----------

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/21 Mã đề 254

ĐÁP ÁN

1 2 3 4 5 6 7 8 9 10

C A

B D

C B C C A

C D

B A

C B D

B D

B A

C C D

C A

B D

C B D

C D

C A

HƯỚNG DẪN GIẢI

Câu 1. Giải phương trình

9 12 20 0

x x

  

trên tập số phức, được tập nghiệm là:

2 4 4 2

;

3 3 3 3

i i

 

 

 

 

. B.

2 4 2 4

;

3 3 3 3

i i

 

 

 

 

. C.

1 2 2 1

;

3 3 3 3

i i

 

 

 

 

. D.

4 2 4 2

;

3 3 3 3

i i

 

 

 

 

Hướng dẫn giải

Chọn A.

Ta có

9 12 20 0

x x

  



2 4

3 3

2 4

3 3

x i



 



 





Câu 2. Cho

I xe x







. Biết rằng

ae b



 , trong đó

và

là các số nguyên dương. Khi đó,

a b



bằng

. B.

. C.

. D.

Hướng dẫn giải

Chọn C.

Ta có

 

2 2 2

1 1

1 1 2 1

0 0

1 1 1

d d 1

2 2 2

x x x

I xe x e x e

  



      

 

Vì

ae b









. Vậy

a b

 

Câu 3. Hàm số

3 2

3 10

y x x x

   

đạt

A. cực đại tại

 

. B. cực đại tại



C. cực tiểu tại

 

. D. cực tiểu tại



Hướng dẫn giải

Chọn A.

2 3

y x x



  

;

 





 







Ta có bảng biến thiên như sau

Vậy hàm số đạt cực đại tại

 



















TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/21 Mã đề 254

Câu 4. Tính

 

1 ln

I x







được kết quả là

. B.

. C.

. D.

Hướng dẫn giải

Chọn B.

Đặt

ln d d

t x t x

   . Với

x e t

  

;

x e t

  

 

1 ln

I x







   

2 3

1 1 1

1 d 1 0

3 3 3

t t t

       



Câu 5. Diện tích hình phẳng giới hạn bởi đồ thị hàm số

y e



và hai đường thẳng



là



. B.



. C.

. D.



Hướng dẫn giải

Chọn D.

Phương trình hoành độ giao điểm của đồ thị hàm số

y e



và đường thẳng



là

1 0

e x

  

Diện tích hình phẳng cần tìm là

 

1 d ( ) 2

x x

S e x e x e

     



Câu 6. Đường thẳng

y x

 

và đồ thị hàm số







có số điểm chung là

. B.

. C.

. D.

Hướng dẫn giải

Chọn C.

Số điểm chung của hai đồ thị là số nghiệm khác

của phương trình

 

1 1

2 2 2 1 2 3 1 0 1,

2 2

x x x x x x x x



              



Câu 7. Cho hàm số

3 2

y x x

  

có đồ thị





và



là tiếp tuyến của





song song với đường

thẳng

3 3,

y x

  



tiếp xúc với





tại điểm có hoành độ

 

. B.

 

. C.

 









. D.



Hướng dẫn giải

Chọn B.

TXĐ





. Ta có

3 2 2

3 2 3 6

y x x y x x



     

Gọi





0 0

;

M x y

là tiếp điểm của





và



. Tiếp tuyến



song song với đường thẳng

3 3

y x

  

khi và chỉ khi

 

0 0 0 0

3 6 3 1 0 1.

x x x x

        

Câu 8. Khi tính

4 d ,

I x x

 



bằng phép đặt

2sin ,

x t



thì được

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/21 Mã đề 254

 

2 1 cos2 d

t t







. B.

 

2 1 cos2 d

t t







. C.

4cos d

t t



. D.

2cos d

t t



Hướng dẫn giải

Chọn C.

Đặt

2sin d 2cos d

x t x t t

  

Đổi cận

0 0

x t



  

Khi đó

2 2

0 0

4 4sin .2cos d 4cos d .

I t t t t t

 

  

 

Câu 9. Tiếp tuyến của đồ thị hàm số





tại điểm có hoành độ



có phương trình là

y x

 

. B.

y x

  

. C.

y x

  

. D.

y x

 

Hướng dẫn giải

Chọn C.

Gọi

( 1;y )

M  là tiếp điểm của tiếp tuyến với đồ thị





. Vì

 

M C y

 



nên

4 4

1 1 1

   

  

hay

( 1; 2)

 

. Hơn nữa

 









nên

 

( 1) 1

1 1





   

 

Khi đó phương trình tiếp tuyến của





tại tiếp điểm

( 1; 2)

 

là





( 2) 1 ( 1)

y x

     

, hay

y x

  

Câu 10. Cho hai số phức

1 2

2 3 , 3

z i z i

    

. Khi đó,

1 2

z z

 

. B.

. C.

. D.

Hướng dẫn giải

Chọn A.

Ta có

   

1 2

2 2 3 2( 3 ) 8 8 1 65

z z i i i            .

Câu 11. Tất cả các giá trị của tham số

để hàm số

3 2

y x mx mx

    

nghịch biến trên



là

 









. B.

1 0

  

. C.

1 0

  

. D.

 









Hướng dẫn giải

Chọn C.

TXĐ





. Ta có

y x mx m



   

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/21 Mã đề 254

Vì



là hàm bậc hai có hệ số của

khác

nên hàm số đã cho nghịch biến trên



khi

0,y x



  



1 0

0 1 0

m m m



 



       





 



Câu 12. Cho số phức

thỏa mãn









1 3 2 3 4

z i z i i

    

. Khi đó tính được

14 7

5 5

z i

 

. B.

14 7

5 5

z i

 

. C.

13 6

5 5

z i

 

. D.

13 6

5 5

z i

 

Hướng dẫn giải

Chọn D.

Đặt

z a bi

 

với ,a b





, suy ra

z a bi

 









1 3 2 3 4

z i z i i

    

















1 3 2 3 4

a bi i a bi i i

       









3 4 2 3 4

a b a b i i

     

3 4 3

13 6

2 4 6

5 5

a b

z i

a b







 





    

 

  











Chú ý : có thể dùng máy tính để giải bằng cách thử từng kết quả.

Câu 13: Tính

cos d

x x x



bằng phương pháp nguyên hàm từng phần thì đặt

cos

d d

u x

v x x











. B.

d cos d

u x

v x x











. C.

d cos

u x x

v x











. D.

cos d

u x x

v x











Hướng dẫn giải

Chọn B.

Đặt

d cos d

u x

v x x













d d

sin

u x

v x











. Khi đó

cos d

x x x



sin sin d

x x x x





= sin cos

x x x C

 

Câu 14: Thể tích khối tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường

y x x

 



quay

xung quanh

là



. B.

. C.



. D.

Hướng dẫn giải

Chọn C.

Phương trình hoành độ giao điểm của hai đường các đường

y x x

 



là

2 0

x x

 













Thể tích khối tròn xoay

 

2 d

V x x x



 



 

đvtt



Câu 15: Cho









3 2 3 2 4

z i z i i

    

là phương trình với ẩn

. Nghiệm của phương trình là

3 1

2 2

z i

 

. B.

3 1

2 2

z i

 

. C.

3 1

2 2

z i

  

. D.

3 1

2 2

z i

  

Hướng dẫn giải

Chọn B.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/21 Mã đề 254

Ta có:

















3 2 3 2 4 3 2 3 2 4 3 4 3

z i z i i z i zi i i i z i

              

4 3 3 1

3 2 2

z z i



    



Câu 16: Gọi

là nghiệm phức của phương trình

4 13 0

x x

  

. Giá trị của biểu thức

3 3

1 2

x x



. B.

100

. C.

. D.

Hướng dẫn giải

Chọn A.

Ta có:

2 3

4 13 0

2 3

x i

x x

x i

 



   



 



. Khi đó

   

3 3

1 2

2 3 2 3 92 92

x x i i

       

Câu 17: Diện tích hình phẳng giới hạn bởi các đồ thị hàm số

y x



và trục tung là

 

1 d

x x





. B.

1 d

x x





. C.

x x



. D.

1 d

x x





Hướng dẫn giải

Chọn D.

Phương trình hoành độ giao điểm đồ thị hàm số

y x



và trục tung là:

0 0.

x x

  

Phương trình hoành độ giao điểm đồ thị hàm số

y x



và đường thẳng



là:

1 1.

x x

  

Vậy diện tích hình phẳng giới hạn bởi các đồ thị hàm số

y x



và trục tung là

1 d

x x





Câu 18: Hàm số

 

3 2

2 3

y x mx m x

    có hai điểm cực trị cùng dấu khi và chỉ khi



. B.







 



. C.



   







. D.

 

Hướng dẫn giải

Chọn C.

TXĐ:





Ta có





4 3

y x mx m



   

. Vậy





0 4 3 0

y x mx m



     

Hàm số đã cho có hai điểm cực trị cùng dấu khi và chỉ khi phương trình





có hai nghiệm

phân biệt

cùng dấu

   

0 3

2 3 0

m m





  



 

   





   

  



   

  













  















 

Câu 19: Tính

 

1 sin d

x x x







được kết quả là

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/21 Mã đề 254



. B.

. C. 2





. D. 1





Hướng dẫn giải

Chọn B.

Đặt

1 d d

d sin d cos

u x u x

v x x v x

  

 



 

  

 

 

1 cos cos d

I x x x x



   



1 sin 1 1 2



    

Câu 20: Tính

cos

sin d

e x x



được kết quả là

sin x

e C

 

. B.

cosx

e C



. C.

sin x

e C



. D.

cosx

e C

 

Hướng dẫn giải

Chọn D.

Ta có





cos cos cos

sin d d cos

x x x

e x x e x e C

    

 

Câu 21: Cho

x y

là các số thực và hai số phức

2 5

z i

  





3 1 2

z x y i

   

bằng nhau thì

 









. B.











 



. C.

 





 



. D.















Hướng dẫn giải

Chọn A.

Ta có

 

1 2

2 3 1

2 5 3 1 2

5 2

z z i x y i

  



 





         

 

   







Câu 22: Hàm số nào sau đây có giá trị lớn nhất trên









. B.

4 2

2 3

y x x

   

. C.

3 1

y x x

  

. D.

y x

 

Hướng dẫn giải

Chọn B.

Ta có

4 4

y x x



  

0 0

y x



  





0 3



, lim



 

Nên hàm số

4 2

2 3

y x x

   

có giá trị lớn nhất trên



và

max 3





Câu 23: Cho hai số phức

1 2

z i

  

z i

 

. Khi đó số phức

1 2 1 2

. .

z z z z z

  có phần ảo là



. B.

. C.



. D.

Hướng dẫn giải

Cho  n D.

Ta có

1 1

1 2 1 2

z i z i

      

;

2 2

z i z i

    

















1 2 1 2

. . 1 2 2 1 2 2 8

z z z z z i i i i

           

Vậy số phức

1 2 1 2

. .

z z z z z

  có phần ảo là

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/21 Mã đề 254

Câu 24: Tính

cos4 d

x x



được kết quả là

sin 4

x C



. B.

sin4

x C

 

. C.

sin 4

x C

 

. D.

sin 4

x C



Hướng dẫn giải

Cho  n A.

Áp dụng công thức

   

cos d sin

ax b x ax b C

   



nên

cos4 d sin4

x x x C

 



Câu 25: Đồ thị hàm số

3 2

y x x x

  

cắt đường thẳng





y k x

 

tại ba điểm phân biệt khi và chỉ

khi

thuộc

;

 

 

 

 

. B.

;

 

 

 

 

. C.

 

; \ 1

 

  

 

 

. D.

 

; \ 0

 

 

 

 

Hướng dẫn giải

Chọn D.

Phương trình hoành độ giao điểm của đồ thị hàm số

3 2

y x x x

  

và đường thẳng





y k x

 

   

 

3 2 2

2 1 (1) 1 0

0 (2)

x x x k x x x x k

x x k





         



  



Yêu cầu bài toán tương đương

(1)

có ba nghiệm phân biệt, tức

(2)

có hai nghiệm phân biệt

khác

 

1 4 0

; \ 0

1 1 0



 

 



 





 

      

  

 



  

 









Câu 26: Cho hàm số





y f x

 liên tục và có đạo hàm đến cấp hai trên









; ; ;

a b x a b

 . Khẳng định

nào sau đây là sai?

A. Nếu

















0 0

0 ; , 0 ;

f x x a x f x x x b

 

      thì

x x



là một điểm cực tiểu của hàm số.

B. Nếu





f x





thì

x x



là một điểm cực trị của hàm số.

C. Nếu





f x



đổi dấu từ dương sang âm khi

đi qua

thì

x x



là một điểm cực đại của hàm số.

D. Nếu





 

f x



















thì

x x



là một điểm cực trị của hàm số.

Hướng dẫn giải

Chọn B.

Ta biết rằng nếu





f x





và





f x



đổi dấu khi

đi qua

thì

x x



là một điểm cực trị

của hàm số. Vì vậy kết luận ở câu B là chưa đầy đủ.

Thật vậy, ví dụ hàm số





f x x



có









3 ; 0 0

f x x f x x

 

   

Trong khi hàm này không có cực trị.

Câu 27: Hình tròn tâm





1;2

I  , bán kính



là tập hợp điểm biểu diễn hình học của các số phức

thỏa mãn

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/21 Mã đề 254









1 2

z x y i



   











. B.









1 2

z x y i



   



















1 2

z x y i



   











. D.









1 2

z x y i



   











Hướng dẫn giải

Chọn D.

Ta có:









       

2 2 2 2

1 2

1 2 5 1 2 25

z x y i

z x y x y



   



          









Suy ra: tập hợp điểm biểu diễn hình học của các số phức

thỏa mãn









1 2

z x y i



   











là

hình tròn tâm





1;2

I  , bán kính



Câu 28: Thể tích khối tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường

y x

 



quay quanh trục

là



. B.



. C.

. D.

Hướng dẫn giải

Chọn A.

Thể tích khối tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường

y x

 



quay quanh trục

là

   

 

1 1

2 4 2 3

0 0

2 28

1 d 2 1 d

đv

5 3 15

V x x x x x x x

 

            

 

 

 

Câu 29: Ha m sô

y x

 

A. Nghi  ch biên trên



. B. Đông biên trên







C. Nghi  ch biên trên







. D. Đông biên trên



Hướng dẫn giải

Cho  n B.

Ta co







Vì

0 0

y x



  

nên ta có bảng biến thiên













Do đo ha m sô đông biên trên







TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/21 Mã đề 254

Câu 30: Cho hı nh phăng

giơ i ha  n bơ i đô thi 

cos

y x



, tru  c hoa nh, tru  c tung va đươ ng thăng





Thê tı ch khô i tro n xoay sinh bơ i

khi quay quanh tru  c

la

cos d

V x x







. B.

cos d

V x x







. C.

cos d

V x x







. D.

cos d

V x x







Hướng dẫn giải

Cho  n A.

A p du ng công thư c

 

V f x x







Câu 31: Hàm số

2cos

y x x

 

có giá trị lớn nhất trên



 

 

 

là



 . B.



 . C.



. D.

Hướng dẫn giải

Chọn B.

Hàm số liên tục trên đoạn



 

 

 

Ta có

1 2sin

y x



 

. Vậy

 

0 sin

x k

y x k

x k





 





    



 







Vì



 



 

 

nên









0 2



2 2

 

 



 

 

6 6

 

 

 

 

 

nên

max 3



 

 

 

  .

Câu 32: Cho số phức

3 4

z i

 

, biểu thức

3 10

A z z

  

bằng

. B.

. C.

. D.



Hướng dẫn giải

Chọn A.

Ta có

2 2

3 4 5

  

.5 3.5 10 0

    

Câu 33: Diện tích hình phẳng giới hạn bởi đồ thị hàm số

y x x

 

, trục hoành và hai đường thẳng

3, 4

x x

  

bằng

119

. B.

. C.

201

. D.

Hướng dẫn giải

Chọn C.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/21 Mã đề 254

Phương trình hoành độ giao điểm của đồ thị hàm số

y x x

 

với trục hoành là





 

3;4

2 4

;

x x





  

 

  





Vậy diện tích hình phẳng cần tìm là

       

2 0 2 4

3 3 3 3

3 2 0 2

2 0 2 4

3 3

3 2 0

4 d

4 d 4 d 4 d 4 d

4 4 36

201

S x x x

x x x x x x x x x x x x



 



 

 

       

   





   

Câu 34: Cho hai mặt phẳng









:2 0, : 2 2 3 0

P y z Q x y z

     

và

là giao tuyến của chúng.

Phương trình đường thẳng

là

5 2

2 2

x t

y t

z t

  





 





 



. B.

5 2

2 2

x t

y t

z t

  





 





 



. C.

5 2

2 2

x t

y t

z t

  





 





 



. D.

5 2

2 2

x t

y t

z t

  





 





 



Hướng dẫn giải

Chọn C.

Phân tích: Do các đáp đều có điểm đi qua là





5; 1; 2

M  . Ta chỉ cần tính VTCP của

Ta có

 





 

   

 

0; 2; 1

, 2; 1; 2

1; 2; 2

d P Q

u n n



 



 

    



 

 







  



. Chọn đáp án C.

Câu 35: Phương trình đường thẳng đi qua điểm





2;1; 1

 





0; 1; 3

 

là

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/21 Mã đề 254

1 2

3 2

x t

y t

z t







  





  



. B.

2 2

1 2

x t

y t

z t

  





 





  



. C.

x t

y t

z t







  





  



. D.

x t

y t

z t

  





 





  



Hướng dẫn giải

Chọn D.

Ta có





2; 2; 2

  



nên đường thẳng

có một véc tơ chỉ phương là





1; 1; 1

  



Phương trình tham số đường thẳng đi qua





2;1; 1

 

và có vectơ chỉ phương





1; 1; 1

  



là:

x t

y t

z t

  





 





  



Câu 36: Cho mặt cầu





2 2 2

: 4 2 2 10 0

S x y z x y z

      

, mặt phẳng





: 2 2 10 0

P x y z

   

Khẳng định nào sau đây là đúng?





và





không có điểm chung.





cắt





theo giao tuyến là đường tròn lớn.





tiếp xúc với









cắt





theo giao tuyến là khác đường tròn lớn.

Hướng dẫn giải

Chọn C.

Mặt cầu





có tâm





2; 1; 1

 

và bán kính



, đồng thời

 









   

2 2

2 2. 1 2. 1 10

1 2 2

d I P R

    

  

  

Suy ra





tiếp xúc với





Câu 37: Trong không gian với hệ tọa độ

Oxyz

, với













2;1; 2 , 1; 3; 1 , 0;2; 1

A B C

   

. Nếu tứ giác

ABCD

là hình bình hành thì tọa độ của

là





1;6; 2



. B.





1;6;2

. C.





1; 6; 2

 

. D.





1;6; 2

 

Hướng dẫn giải

Chọn A.

Gọi





; ;

D x y z









1; 4;1 , ;2 ; 1

AB DC x y z

       

 

Tứ giác

ABCD

là hình bình hành

1 1

4 2 6

1 1 2

x x

AB DC y y

z z

   

 

 

       

 

 

    

 

 

Vậy





1;6; 2



Câu 38: Mặt phẳng





chứa đường thẳng

1 1 1

1 2 1

x y z

  

 



và điểm





0;2;2

A có phương trình là

5 2 2 0

x y z

   

. B.

5 2 2 0

x y z

   

. C.

5 5 2 0

x z

  

. D.

2 0

x z

  

Hướng dẫn giải

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/21 Mã đề 254

Chọn D.

Đường thẳng

đi qua





1; 1;1

B  và có một vectơ chỉ phương là





1;2; 1

 



Gọi



là một vectơ pháp tuyến của mặt phẳng





, ta có

 

1;2; 1

1; 3; 1

n u

n AB



  





   





 

 

Chọn

 

, 5;0; 5

n u AB

 

   

 

  

Phương trình mặt phẳng





là









5 0 5 2 0 2 0

x z x z

        

Câu 39: Cho





1; 3; 1

A 





1; 1; 2

B 





2; 1; 3





0; 1; 1



. Phương trình mặt phẳng chứa

và

song song với

là

2 4 0

x z

  

. B.

2 4 2 0

x z z

   

8 3 4 3 0

x y z

   

. D.

8 3 4 3 0

x y z

   

Hướng dẫn giải

Chọn C.

Vectơ chỉ phương

là





2; 4;1

u  



Vectơ chỉ phương

là





2;0; 4

  











, 16;6; 8

AB CD

n u u

  

  

Phương trình mặt phẳng chứa

và song song với





 

1; 3; 1

16;6; 8

VTPT

đi q









 







là

















:16 1 6 3 8 1 0

P x y z

     

8 3 4 3 0

x y z

    

Câu 40: Cho hai đường thẳng

2 1 2

1 1 1

x y z

  

 

5 2

2 4 1

x y z

 

 

 

, khoảng cách giữa hai

đường thẳng này là

. B.

2 6

. C.

4 6

. D.

3 6

Hướng dẫn giải

Chọn B.

Cách 1:

Gọi

là đoạn vuông góc chung của hai đường thẳng chéo nhau

và





1 2

M d N d

  .

Vì





2 ; 1 ;2

M d M t t t

     

và





2 ;5 4 ;2

N d N t t t

  

   

Suy ra





2 2; 4 6;

MN t t t t t t

  

       



Đường thẳng

và

lần lượt có VTCP là





1;1;1

u 



và





2; 4; 1

  



Ta có:

     

. 0

1 2 2 1 4 6 1 0

2 2 2 4 4 6 1 0

. 0

MN u

t t t t t t

MN d

t t t t t t

MN u





   

         





  

  

   



  



         







 



 

Từ đó suy ra

2 2 4

; ;

3 3 3

 

 

 

 



và

2 6

MN MN 



Vậy khoảng cách giữa hai đường thẳng

và

bằng

2 6

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/21 Mã đề 254

Cách 2 :

Áp dụng công thức tính khoảng cách giữa 2 đường thẳng chéo nhau

và

là:

1 2

, .

d d

u u MN

u u

 

 



 

 

  

 





1 2

M d N d

  .

Câu 41: Phương trình mặt cầu đi qua bốn điểm





2; 2; 2

A 





4; 2; 2

 





1; 1; 2



và





1; 2; 1



là

     

2 2 2

1 2 2 25

x y z

     

. B.

     

2 2 2

1 2 2 16

x y z

     

     

2 2 2

1 2 2 16

x y z

     

. D.

     

2 2 2

1 2 2 25

x y z

     

Hướng dẫn giải

Chọn D.

Phương trình mặt cầu dưới dạng khai triển:

2 2 2

2 2 2 0

x y z ax by cz d

      

Mặt cầu qua

, , ,

A B C D

4 4 4 12 1

8 4 4 24 2

2 2 4 6 2

2 4 2 6 16

a b c d a

a b c d b

a b c d c

a b c d d

     

 

 

       

 

 

      

 

       

 

Suy ra mặt cầu có tâm





1; 2;2

I  và bán kính

     

2 2 2

1 2 2 16 5

     

Câu 42: Cho đường thẳng

1 2

1 2 1

x y z

 

 



, và mặt phẳng





: 3 0

P x y z

   

. Gọi



là hình

chiếu của

trên





, khi đó



có một vectơ chỉ phương là





1;2; 1

 



. B.





1; 2; 1

  



. C.





1;2; 1

  



. D.





1;2;1

u 



Hướng dẫn giải

Chọn A.

Phương pháp tự luận

Đường thẳng

1 2

1 2 1

x y z

 

 



đi qua điểm





1;2;0

M 

Ta thấy điểm





1;2;0

M 

thuộc mặt phẳng





: 3 0

P x y z

   

Lấy điểm





2;4;1

N d

 

Phương trình đường thẳng



đi qua





2;4;1

N 

và vuông góc với





: 3 0

P x y z

   

là:

: 4

x t

y t

z t

  





  





 



Gọi



là giao điểm của



và





, suy ra tọa độ



thỏa mãn:

   

2 4 1 3 0

t t t t

          

2 8 1

; ;

3 3 3

 



  

 

 

Khi đó hình chiếu



đi qua hai điểm

và



nên có vectơ chỉ phương là :

1 2 1

; ;

3 3 3



 

 

 

 



hay





3 1;2; 1

u u



  

 

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/21 Mã đề 254

Phương pháp trắc nghiệm:

Hình chiếu của đường thẳng

xuống mặt phẳng





là đường thẳng có một véc tơ chỉ

phương

   

, ,

P P

u u n n

 



 

   

. Áp dụng trong bài này với

 





1; 1; 1

  



và





1;2;1

u  



, ta

suy ra





1; 2;1

u   



. Vậy chọn





1;2; 1

u u

   

 

Câu 43: Cho

2 3

a j k

 

  

. Khi đó tọa độ của



là





2;0; 3



. B.





2; 3;0

 . C.





0;2; 3



. D.





0;2;3

Hướng dẫn giải

Chọn C.

Ta có:













2 3 2. 0;1;0 3 0;0;1 0;2; 3

a j k

     

  

Câu 44: Cho

ABC



với





1;0;0

A ;





0;2;0

B ;





3;0;4

C và

thuộc





Oyz

. Nếu





MC ABC

 thì

tọa độ của

là

3 11

0; ;

2 2

 

 

 

3 11

0; ;

2 2

 



 

 

3 11

0; ;

2 2

 



 

 

3 11

0; ;

2 2

 

 

 

 

Hướng dẫn giải

Chọn B.

Ta có

thuộc





Oyz

nên tọa độ





0; ;

M a b

Lại có





3; ;4

MC a b

  



;





1;2;0

AB  



;





2;0;4

AC 



Vì

 

3 2 0

. 0

6 4 4 0

. 0

MC AB MC AB

MC ABC

MC AC



 





  

 



 

    

   

  







 











 

Vậy tọa độ

3 11

0; ;

2 2

 



 

 

Câu 45: Cho mặt phẳng





: 2 3 1 0

P x z

  

. Khi đó





có một vectơ pháp tuyến là





2; 3;0

n  



. B.





2; 3;1

n  



. C.





2; 3; 1

  



. D.





2;0; 3

 



Hướng dẫn giải

Chọn D.

Phương trình mặt phẳng có dạng





: 0

P Ax By Cz D

   

có vectơ pháp tuyến là





; ;

n A B C





. Vậy





: 2 3 1 0

P x z

  

có vectơ pháp tuyến là





2;0; 3

 



Câu 46: Cho hai đường thẳng

3 1

1 2 1

x y z

 

 



1 2

: 1

x t

y t

z t

 





   





 



, vị trí tương đối hai đường thẳng này là

A. trùng nhau. B. song song với nhau.

C. cắt nhau. D. chéo nhau.

Hướng dẫn giải

Chọn C.

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/21 Mã đề 254

Phương trình đường thẳng

3 1

1 2 1

x y z

 

 



có vectơ chỉ phương là





1;2;1

n  



Phương trình đường thẳng

1 2

: 1

x t

y t

z t

 





   





 



có vectơ chỉ phương là





2;1; 1



 



Ta thấy

n k n





 

Viết lại phương trình đường

thẳng về dạng tham số như sau:

: 0 2

x t

d y t

z t



 







 







  



Xét hệ phương trình

1 2 3

1 0 2

t t



  







   







   



1 2

t t





 





  







 





Hệ có nghiệm





và



, suy ra hai đường thẳng cắt nhau.

Câu 47: Cho





1;2;2

A ,





3;0;2

B . Mặt phẳng trung trực đoạn thẳng

có phương trình là

3 0

x y

  

. B.

1 0

x y

  

. C.

2 2 3 0

x y

  

. D.

1 0

x y

  

Hướng dẫn giải

Chọn D.

Mặt phẳng cần tìm đi qua





2;1;2

I là trung điểm của đoạn thẳng

và nhận





2; 2;0

AB  



làm véc tơ pháp tuyến.

Suy ra phương trình mặt phẳng cần tìm là









2 2 2 1 0

x y

   

hay

1 0

x y

  

Câu 48: Phương trình đường thẳng đi qua





2;1; 1



và có vectơ chỉ phương





1; 2;2

u  



là

2 1 1

1 2 2

x y z

  

 



. B.

1 2

x t

y t

z t

 





  





 



2 1 1

1 2 2

x y z

  

 



. D.

1 2 2

2 1 1

x y z

  

 



Hướng dẫn giải

Chọn C.

Câu 49: Mặt cầu





2 2 2

2 2 2 6 8 4 2 0

x y z x y z

      

có tọa độ tâm

và bán kính

lần lượt là

3 5

;2; 1 ,

2 2

I R

 

  

 

 

. B.

; 2;1 , 5

I R

 

 

 

 

3 25

; 2;1 ,

2 4

I R

 

 

 

 

. D.

;2; 1 , 25

I R

 

  

 

 

Hướng dẫn giải

Chọn A.





2 2 2

2 2 2 6 8 4 2 0

x y z x y z

      

2 2 2

3 4 2 1 0

x y z x y z

       

Gọi





; ;

I a b c

là tâm của mặt cầu





. Ta có

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/21 Mã đề 254

2 3

a a



    ;

2 4 2

b b

    

;

2 2 1

c c

    

;2; 1



 

 

 

 

Bán kính

 

3 5

2 1 1

2 2

 

      

 

 

Câu 50: Mặt phẳng đi qua





1;2;1

A và song song với mặt phẳng





2 2 0

x y z

   

có phương

trình là

2 1 0

x y z

    

. B.

2 1 0

x y z

   

. C.

2 2 0

x y z

   

. D.

2 1 0

x y z

   

Hướng dẫn giải

Chọn D.

Gọi







là mặt phẳng cần tìm.

Vì











nên có dạng :





2 0 2

x y z d d

     









1;2;1A



 nên ta có:

2.1 2 1 0 1

d d

      

Vậy phương trình mặt phẳng







là:

2 1 0

x y z

   

Bấm Tải xuống để xem toàn bộ.

| 1/21

| | Tải xuống

Preview text:

TRƯỜNG THPT TRẦN HƯNG ĐẠO
ĐỀ KIỂM TRA HỌC KỲ II, NĂM HỌC 2016 – 2017 THANH XUÂN MÔN: Toán, khối 12
Đề gồm có 05 trang
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Họ tên thí sinh:............................................ Số báo danh:.............................................. Mã đề 254 Câu 1. Giải phương trình 2
9x 12x  20  0 trên tập số phức, được tập nghiệm là  2 4 4 2   2 4 2 4 
A.   i;  i .
B.   i;  i .  3 3 3 3   3 3 3 3  1 2 2 1   4 2 4 2 
C.   i;  i .
D.   i;  i . 3 3 3 3   3 3 3 3  1 2 ae  b Câu 2. Cho 1x I  xe dx  . Biết rằng I 
trong đó a và b là các số nguyên dương. Khi đó, 2 0 a  b bằng A. 1. B. 0 . C. 2 . D. 4 . 1 Câu 3. Hàm số 3 2 y 
x  x  3x 10 đạt 3
A. cực đại tại x  1  .
B. cực đại tại x  3 .
C. cực tiểu tại x  1  .
D. cực tiểu tại x  1 . 2 e   x2 1 ln Câu 4. Tính I  dx  được kết quả là x e 13 1 5 4 A. . B. . C. . D. . 3 3 3 3 Câu 5.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số x
y  e và hai đường thẳng y  1, x  1 là A. e  1. B. e  1. C. e . D. e  2 . x  1 Câu 6.
Đường thẳng y  2x và đồ thị hàm số y  có số điểm chung là x  2 A. 1. B. 0 . C. 2 . D. 4 . Câu 7. Cho hàm số 3 2
y  x  3x  2 có đồ thị C  và  là tiếp tuyến của C  song song với đường
thẳng y  3x  3,  tiếp xúc với C  tại điểm có hoành độ  x  1  A. x  3  . B. x  1  . C.  . D. x  1 . x  1  2 Câu 8. Khi tính 2 I  4  x dx, 
bằng phép đặt x  2 sin t, thì được 0   2 2 2 2 A.
2 1 cos 2t dt  . B.
2 1 cos 2t dt  . C. 2 4 cos tdt  . D. 2 2 cos tdt  . 0 0 0 0 4 Câu 9.
Tiếp tuyến của đồ thị hàm số y  tại điểm có hoành độ 1  có phương trình là x 1
A. y  x  2 .
B. y  x  1.
C. y  x  3 .
D. y  x 1.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/21 Mã đề 254
Câu 10. Cho hai số phức z  2  3i, z  3  i . Khi đó, z  2z  1 2 1 2 A. 65 . B. 63 . C. 89 . D. 41 . 1
Câu 11. Tất cả các giá trị của tham số m để hàm số 3 2 y  
x  mx  mx  2 nghịch biến trên  là 3 m  1  m  1  A.  . B. 1   m  0 . C. 1   m  0 . D.  . m  0  m  0 
Câu 12. Cho số phức z thỏa mãn : z 1 3i  z 2  i  3  4i . Khi đó tính được 14 7 14 7 13 6 13 6 A. z   i . B. z   i . C. z   i . D. z   i . 5 5 5 5 5 5 5 5
Câu 13. Tính x cos d x x 
bằng phương pháp nguyên hàm từng phần thì đặt u   cos x u   x u   d x x u   cos d x x A.  . B.  . C.  . D.  . dv  d x x  dv  cos d x x  dv  cos x  dv  x 
Câu 14. Thể tích khối tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường 2
y  2x  x , y  0 quay xung quanh Ox là 4 4 16 16 A. . B. . C. . D. . 3 3 15 15
Câu 15. Cho z 3  2i  3z  2i  4  i là phương trình với ẩn z . Nghiệm của phương trình là 3 1 3 1 3 1 3 1 A. z   i . B. z   i . C. z    i . D. z    i . 2 2 2 2 2 2 2 2
Câu 16. Gọi x , x là nghiệm phức của phương trình 2
x  4x 13  0 . Giá trị của biểu thức 3 3 x  x 1 2 1 2 A. 92 . B. 100 . C. 36 . D. 18 .
Câu 17. Diện tích hình phẳng giới hạn bởi các đồ thị hàm số 3
y  x , y  1 và trục tung là 1 1 1 1 A.  3 x    1 dx . B. 3 1 x dx  . C. 3 x dx  . D. 3 1 x dx  . 0 0 0 0 1 Câu 18. Hàm số 3 2 y 
x  2mx  m  3 x có hai điểm cực trị cùng dấu khi và chỉ khi 3 m  1  3 3   m   A. m  1. B.   3 . C. 4 . D. m  3 . m     4 m  1   2
Câu 19. Tính  x   1 sin d x x  được kết quả là 0    A. . B. 2 . C. 2  . D. 1 . 2 2 2 Câu 20. Tính cos x e sin d x x  được kết quả là A. sin x e  C . B. cos x e  C . C. sin x e  C . D. cos x e  C .
Câu 21. Cho x, y là các số thực và hai số phức z  2
  5i , z  3x 1  y  2 i bằng nhau thì: 2   1  1  1 x  1  x  x  1 x  A.  . B.  3 . C.  . D.  3 . y  7   y  3  y  3     y  7 
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/21 Mã đề 254
Câu 22. Hàm số nào sau đây có giá trị lớn nhất trên  ? x 1 A. y  . B. 4 2
y  x  2x  3 . C. 3
y  x  3x  1. D. 2 y  4  x . x  2
Câu 23. Cho hai số phức z  1
  2i , z  2  i . Khi đó số phức z  z .z  z .z có phần ảo là 1 2 1 2 1 2 A. 9  . B. 10 . C. 8  . D. 0 . Câu 24. Tính cos 4 d x x  được kết quả là 1 1
A. sin 4x  C .
B.  sin 4x  C .
C.  sin 4x  C .
D. sin 4x  C . 4 4
Câu 25. Đồ thị hàm số 3 2
y  x  2x  x cắt đường thẳng y  k  x  
1 tại ba điểm phân biệt khi và chỉ khi k thuộc  1   1   1   1  A.  ;    . B.  ;     . C.  ;   \     1 . D.  ;  \     0 .  4   4   4   4 
Câu 26. Cho hàm số y  f  x liên tục và có đạo hàm đến cấp hai trên a;b; x  a;b . Khẳng định 0   nào sau đây là sai?
A. Nếu f  x  0 x
  a; x , f  x  0 x
  x ;b thì x  x là một điểm cực tiểu của hàm số. 0     0  0
B. Nếu f  x  0 thì x  x là một điểm cực trị của hàm số. 0  0
C. Nếu f  x đổi dấu từ dương sang âm khi x đi qua x thì x  x là một điểm cực đại của hàm số. 0 0  f   x  0 D. Nếu 
thì x  x là một điểm cực trị của hàm số. 0 f    x  0 
Câu 27. Hình tròn tâm I  1
 ; 2 , bán kính r  5 là tập hợp điểm biểu diễn hình học của các số phức z thỏa mãn
z   x  
1   y  2i  z    x  
1   y  2i A.  . B.  . z  5   z  5  
z   x  
1   y  2i  z    x  
1   y  2i C.  . D.  . z  5   z  5  
Câu 28. Thể tích khối tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường 2
y  x 1, y  0 , x  0 ,
x  1 quay quanh trục Ox là 28 4 28 4 A. . B. . C. . D. . 15 3 15 3 Câu 29. Hà m số 2 y  x 1
A. Nghi ̣ ch biến trên  .
B. Đồng biến trên 0;  .
C. Nghi ̣ ch biến trên 0;  .
D. Đồng biến trên  . 
Câu 30. Cho hı̀ nh phẳng D giớ i ha ̣ n bởi đồ thi ̣y  cos x , tru ̣ c hoà nh, tru ̣ c tung và đườ ng thẳng x  . 2
Thể tı́ ch khối trò n xoay sinh bởi D khi quay quanh tru ̣ c Ox là     2 2 2 2 A. 2 V   cos d x x  . B. 2
V   cos x dx  . C. 2 V  cos d x x  .
D. V   cos d x x  . 0 0 0 0
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/21 Mã đề 254   
Câu 31. Hàm số y  x  2 cos x có giá trị lớn nhất trên 0;  là 2      A.  2 . B.  3 . C.  . D. 2 . 6 6 1 2
Câu 32. Cho số phức z  3  4i , biểu thức A 
z  3 z 10 bằng 5 A. 0 . B. 5 . C. 10 . D. 5  .
Câu 33. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y  x  4x , trục hoành và hai đường thẳng
x  3, x  4 bằng 119 201 A. . B. 44 . C. . D. 36 . 4 4
Câu 34. Cho hai mặt phẳng  P : 2y  z  0, Q : x  2y  2z  3  0 và d là giao tuyến của chúng.
Phương trình đường thẳng d là x  5   2t x  5   2t x  5   2t x  5   2t    
A.  y  1 t .
B.  y  1 t .
C.  y  1 t .
D.  y  1 t .
z  2  2t     z  2  2t  z  2  2t  z  2  2t 
Câu 35. Phương trình đường thẳng đi qua điểm A 2  ;1;   1 , B 0; 1  ; 3   là x  2t x  2   2t x  t x  2   t     A. y  1   2t .
B. y  1 2t . C. y  1   t .
D. y  1 t .
z  3 2t     z  1 2t  z  3  t  z  1 t 
Câu 36. Cho mặt cầu S  2 2 2
: x  y  z  4x  2 y  2z 10  0 , mặt phẳng  P : x  2y  2z 10  0 .
Khẳng định nào sau đây là đúng?
A.  P và  S  không có điểm chung.
B.  P cắt  S  theo giao tuyến là đường tròn lớn.
C.  P tiếp xúc với  S  .
D.  P cắt  S  theo giao tuyến là khác đường tròn lớn.
Câu 37. Trong không gian với hệ tọa độ Oxyz , với A 2;1; 2  , B 1; 3  ;   1 , C 0; 2;   1 . Nếu tứ giác
ABCD là hình bình hành thì tọa độ của D là A. 1;6;2 . B. 1;6;2 . C. 1;6;2 . D.  1  ;6; 2   . x 1 y  1 z 1
Câu 38. Mặt phẳng  P chứa đường thẳng d :  
và điểm A 0; 2; 2 có phương trình là 1 2 1 
A. 5x  2 y  z  2  0 . B. 5x  2 y  z  2  0 . C. 5x  5z  2  0 .
D. x  z  2  0 .
Câu 39. Cho A 1; 3; 
1 , B 1; 1; 2 , C 2; 1; 3 , D 0; 1;  
1 . Phương trình mặt phẳng chứa AB và
song song với CD là
A. x  2z  4  0 .
B. 2x  4z  z  2  0 .
C. 8x  3y  4z  3  0 .
D. 8x  3y  4z  3  0 . x  2 y  1 z  2 x y  5 z  2
Câu 40. Cho hai đường thẳng d :   , d :   , khoảng cách giữa hai 1 1 1 1 2 2 4 1 đường thẳng này là 5 2 6 4 6 3 6 A. . B. . C. . D. . 6 3 3 2
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/21 Mã đề 254
Câu 41. Phương trình mặt cầu đi qua bốn điểm A2; 2; 2 , B 4;  2;  2 , C 1; 1;  2 và D 1; 2;   1 là 2 2 2 2 2 2 A.  x  
1   y  2   z  2  25 . B.  x  
1   y  2   z  2  16 . 2 2 2 2 2 2 C.  x  
1   y  2   z  2  16 . D.  x  
1   y  2   z  2  25 . x  1 y  2 z
Câu 42. Cho đường thẳng d :  
, và mặt phẳng  P  : x  y  z  3  0 . Gọi d là hình 1 2 1
chiếu của d trên  P , khi đó d có một vectơ chỉ phương là    
A. u  1; 2;  1 .
B. u  1;  2;   1 . C. u   1  ; 2;   1 .
D. u  1; 2;  1 .    
Câu 43. Cho a  2 j  3k . Khi đó tọa độ của a là A. 2;0; 3   . B. 2; 3  ; 0 . C. 0; 2; 3   . D. 0;2;3 . Câu 44. Cho A
 BC với A1;0;0 ; B 0; 2;0 ; C 3;0;4 và M thuộc Oyz . Nếu MC   ABC  thì
tọa độ của M là  3 11   3 11   3 11   3 11 A. 0; ;   B. 0;  ;   C. 0; ;    D. 0;  ;     2 2   2 2   2 2   2 2 
Câu 45. Cho mặt phẳng  P  : 2x  3z 1  0 . Khi đó  P có một vectơ pháp tuyến là    
A. n  2;  3;0 .
B. n  2;  3;  1 .
C. n  2;  3;   1 .
D. n  2;0;  3 .
x  1  2t x  3 y z  1 
Câu 46. Cho hai đường thẳng d :  
,  : y  1 t , vị trí tương đối hai đường thẳng này là 1 2 1 z  t  A. trùng nhau.
B. song song với nhau. C. cắt nhau. D. chéo nhau.
Câu 47. Cho A 1; 2; 2, B 3;0;2 . Mặt phẳng trung trực đoạn thẳng AB có phương trình là
A. x  y  3  0 .
B. x  y 1  0 .
C. 2x  2 y  3  0 .
D. x  y 1  0 . 
Câu 48. Phương trình đường thẳng đi qua A2;1; 
1 và có vectơ chỉ phương u  1;2; 2 là x  1 2t x  2 y 1 z 1  A.   .
B. y  2  t . 1 2  2 z  2  t  x  2 y 1 z 1 x 1 y  2 z  2 C.   . D.   . 1 2 2 2 1 1 
Câu 49. Mặt cầu  S  : 2 2 2
2x  2 y  2z  6x  8y  4z  2  0 có tọa độ tâm I và bán kính R lần lượt là  3  5  3  A. I  ; 2; 1  , R    . B. I ; 2  ;1 , R  5   .  2  2  2   3  25  3  C. I ; 2  ;1 , R    .
D. I  ; 2; 1 , R  25   .  2  4  2 
Câu 50. Mặt phẳng đi qua A1;2 
;1 và song song với mặt phẳng  P : 2x  y  z  2  0 có phương trình là A. 2
 x  y  z 1  0 .
B. x  2 y  z 1  0 .
C. 2x  y  z  2  0 .
D. 2x  y  z 1  0 .
----------HẾT----------
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/21 Mã đề 254 ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A C A B D C B C C A C D B C B A D C B D A B D A D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B D A B A B A C C D C A D C B D A C B D C D C A D HƯỚNG DẪN GIẢI Câu 1. Giải phương trình 2
9x 12x  20  0 trên tập số phức, được tập nghiệm là:  2 4 4 2   2 4 2 4  1 2 2 1   4 2 4 2 
A.   i;  i .
B.   i;  i . C.   i;  i . D.   i;  i .  3 3 3 3   3 3 3 3  3 3 3 3   3 3 3 3  Hướng dẫn giải Chọn A.  2 4 x   i  3 3 Ta có 2
9x 12x  20  0   2 4  x   i  3 3 1 2 ae  b Câu 2. Cho 1x I  xe dx  . Biết rằng I 
, trong đó a và b là các số nguyên dương. Khi đó, 2 0 a  b bằng A. 1. B. 0 . C. 2 . D. 4 . Hướng dẫn giải Chọn C. 1 1 2 2 2     e x 1 x 1 1 x 1 Ta có 1 1 I  xe dx   e d  2 1 x  1   e    2 2 0 2 0 0 ae  b Vì I 
 a  1 , b  1. Vậy a  b  2 . 2 1 Câu 3. Hàm số 3 2 y 
x  x  3x 10 đạt 3
A. cực đại tại x  1  .
B. cực đại tại x  3 .
C. cực tiểu tại x  1  .
D. cực tiểu tại x  1 . Hướng dẫn giải Chọn A.  x  1 2
y  x  2x  3 ; y  0  x  3 
Ta có bảng biến thiên như sau x  1  3  y  0  0   y 
Vậy hàm số đạt cực đại tại x  1 
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/21 Mã đề 254 2 e   x2 1 ln Câu 4. Tính I  dx  được kết quả là x e 13 1 5 4 A. . B. . C. . D. . 3 3 3 3 Hướng dẫn giải Chọn B. 1
Đặt t  ln x  dt 
dx . Với x  e  t  1 ; 2
x  e  t  2 x 2 e   x2 1 ln 2 2 2 1 3 1 1 I  dx 
 1 t  dt   1 t   0   x 1 3 3 3 e 1 Câu 5.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số x
y  e và hai đường thẳng y  1, x  1 là A. e  1. B. e  1. C. e . D. e  2 . Hướng dẫn giải Chọn D.
Phương trình hoành độ giao điểm của đồ thị hàm số x
y  e và đường thẳng y  1 là x
e  1  x  0 . 1 1
Diện tích hình phẳng cần tìm là   x   1 d  ( x S e x
e  x)  e  2 . 0 0 x  1 Câu 6.
Đường thẳng y  2x và đồ thị hàm số y  có số điểm chung là x  2 A. 1. B. 0 . C. 2 . D. 4 . Hướng dẫn giải Chọn C.
Số điểm chung của hai đồ thị là số nghiệm khác 2 của phương trình x  1 1 2  x   2
 x  x  2 2  x  1  2
 x  3x  1  0  x  1, x  . x  2 2 Câu 7. Cho hàm số 3 2
y  x  3x  2 có đồ thị C  và  là tiếp tuyến của C  song song với đường
thẳng y  3x  3,  tiếp xúc với C  tại điểm có hoành độ  x  1  A. x  3  . B. x  1  . C.  . D. x  1 . x  1  Hướng dẫn giải Chọn B.
TXĐ D   . Ta có 3 2 2
y  x  3x  2  y  3x  6x
Gọi M  x ; y là tiếp điểm của C  và  . Tiếp tuyến  song song với đường thẳng 0 0  y  3
 x  3 khi và chỉ khi 3x  6x  3    x  2 2 1  0  x  1. 0 0 0 0 2 Câu 8. Khi tính 2 I  4  x dx, 
bằng phép đặt x  2 sin t, thì được 0
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/21 Mã đề 254   2 2 2 2 A.
2 1 cos 2t  dt  .
B. 2 1 cos 2t  dt  . C. 2 4 cos tdt  . D. 2 2 cos tdt  . 0 0 0 0 Hướng dẫn giải Chọn C.
Đặt x  2 sin t  dx  2 cos d t t Đổi cận
x  0  t  0 
x  2  t  2   2 2 Khi đó 2 2 I 
4  4 sin t.2costdt  4 cos d t t.   0 0 4 Câu 9.
Tiếp tuyến của đồ thị hàm số y  tại điểm có hoành độ 1  có phương trình là x 1
A. y  x  2 .
B. y  x  1.
C. y  x  3 .
D. y  x 1. Hướng dẫn giải Chọn C. 4 Gọi M ( 1
 ; y ) là tiếp điểm của tiếp tuyến với đồ thị C  . Vì M C : y  nên M x 1 4 4 4  4  y    2  , hay M ( 1  ; 2
 ) . Hơn nữa y  nên y (  1)   1  . M x 1 1  1 M  x  2 1 1 2 1
Khi đó phương trình tiếp tuyến của C  tại tiếp điểm M ( 1  ; 2  ) là y  (2)  1   x  ( 1
 ) , hay y  x  3 .
Câu 10. Cho hai số phức z  2  3i, z  3  i . Khi đó, z  2z  1 2 1 2 A. 65 . B. 63 . C. 89 . D. 41 . Hướng dẫn giải Chọn A.
Ta có z  2z  2  3i  2(3  i)  8  i  8   2 2 1  65 . 1 2 1
Câu 11. Tất cả các giá trị của tham số m để hàm số 3 2 y  
x  mx  mx  2 nghịch biến trên  là 3 m  1  m  1  A.  . B. 1   m  0 . C. 1   m  0 . D.  . m  0  m  0  Hướng dẫn giải Chọn C.
TXĐ D   . Ta có 2
y  x  2mx  m .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/21 Mã đề 254
Vì y là hàm bậc hai có hệ số của 2
x khác 0 nên hàm số đã cho nghịch biến trên  khi  1   0
y  0,x   2  
 m  m  0  1   m  0 .   0 y 
Câu 12. Cho số phức z thỏa mãn z 1 3i  z 2  i  3  4i . Khi đó tính được 14 7 14 7 13 6 13 6 A. z   i . B. z   i . C. z   i . D. z   i . 5 5 5 5 5 5 5 5 Hướng dẫn giải Chọn D.
Đặt z  a  bi với ,
a b   , suy ra z  a  bi .
z 1 3i  z 2  i  3  4i  a  bi 1 3i  a  bi2  i  3  4i .  13 a 
3a  4b  3   5 13 6
 3a  4b  2a  b i  3  4i      z   i . 2a  b  4 6  5 5  b     5
Chú ý : có thể dùng máy tính để giải bằng cách thử từng kết quả.
Câu 13: Tính x cos d x x 
bằng phương pháp nguyên hàm từng phần thì đặt u   cos x u   x u   d x x u   cos d x x A.  . B.  . C.  . D.  . dv  d x x  dv  cos d x x  dv  cos x  dv  x  Hướng dẫn giải Chọn B. u   x du  dx Đặt    . Khi đó x cos d x x 
= x sin x  sin d x x 
= x sin x  cos x  C dv  cos d x x  v  sin x 
Câu 14: Thể tích khối tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường 2
y  2x  x , y  0 quay xung quanh Ox là 4 4 16 16 A. . B. . C. . D. . 3 3 15 15 Hướng dẫn giải Chọn C.
Phương trình hoành độ giao điểm của hai đường các đường 2
y  2x  x , y  0 là  x  2 2
2x  x  0  x  0  2 2 16
Thể tích khối tròn xoay V    2
2x  x  dx  = . đvtt  15 0
Câu 15: Cho z 3  2i  3z  2i  4  i là phương trình với ẩn z . Nghiệm của phương trình là 3 1 3 1 3 1 3 1 A. z   i . B. z   i . C. z    i . D. z    i . 2 2 2 2 2 2 2 2 Hướng dẫn giải Chọn B.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/21 Mã đề 254
Ta có: z 3  2i  3z  2i  4  i  z 3  2i  3zi  2i  4  i  3  i  z  4  3i 4  3i 3 1  z   z   i . 3  i 2 2
Câu 16: Gọi x , x là nghiệm phức của phương trình 2
x  4x 13  0 . Giá trị của biểu thức 3 3 x  x 1 2 1 2 A. 92 . B. 100 . C. 36 . D. 18 . Hướng dẫn giải Chọn A.
 x  2  3i 3 3 Ta có: 2 1
x  4x 13  0  3 3 
. Khi đó x  x  2  3i  2  3i  9  2  92 1 2     x  2  3i  2
Câu 17: Diện tích hình phẳng giới hạn bởi các đồ thị hàm số 3
y  x , y  1 và trục tung là 1 1 1 1 A.  3 x    1 dx . B. 3 1 x dx  . C. 3 x dx  . D. 3 1 x dx  . 0 0 0 0 Hướng dẫn giải Chọn D.
Phương trình hoành độ giao điểm đồ thị hàm số 3
y  x và trục tung là: 3
x  0  x  0.
Phương trình hoành độ giao điểm đồ thị hàm số 3
y  x và đường thẳng y  1 là: 3
x  1  x  1.
Vậy diện tích hình phẳng giới hạn bởi các đồ thị hàm số 3
y  x , y  1 và trục tung là 1 3 1 x dx  . 0 1 Câu 18: Hàm số 3 2 y 
x  2mx  m  3 x có hai điểm cực trị cùng dấu khi và chỉ khi 3 m  1  3 3   m   A. m  1. B.   3 . C. 4 . D. m  3 . m     4 m  1  Hướng dẫn giải Chọn C. TXĐ: D  .  Ta có 2
y  x  4mx  m  3 . Vậy 2
y  0  x  4mx  m  3  0 .
Hàm số đã cho có hai điểm cực trị cùng dấu khi và chỉ khi phương trình y  0 có hai nghiệm
phân biệt x , x cùng dấu 1 2  3   0   2  2    3  0 m m m     3     4 3  m      m  3       4 m  3 . m  1  0    0    m  1  1 1   m  3   2
Câu 19: Tính  x   1 sin d x x  được kết quả là 0
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/21 Mã đề 254    A. . B. 2 . C. 2  . D. 1 . 2 2 2 Hướng dẫn giải Chọn B. u   x 1 du  dx Đặt    . dv  sin d x x v   cos x     2 
I    x   2 1 cos x  cos d x x  2  1 sin x  11  2 . 0 0 0 Câu 20: Tính cos x e sin d x x  được kết quả là A. sin x e  C . B. cos x e  C . C. sin x e  C . D. cos x e  C . Hướng dẫn giải Chọn D. Ta có cos x cos x     cos sin d d cos x e x x e x  e  C   .
Câu 21: Cho x, y là các số thực và hai số phức z  2
  5i , z  3x 1  y  2 i bằng nhau thì 2   1  1  1 x  1  x  x  1 x  A.  . B.  3 . C.  . D.  3 . y  7   y  3  y  3     y  7  Hướng dẫn giải Chọn A. 2  3x 1  x  1
Ta có z  z  2
  5i  3x  1 y  2 i    . 1 2    5     y  2 y  7  
Câu 22: Hàm số nào sau đây có giá trị lớn nhất trên  ? x 1 A. y  . B. 4 2
y  x  2x  3 . C. 3
y  x  3x  1. D. 2 y  4  x . x  2 Hướng dẫn giải Chọn B. Ta có 3
y  4x  4x y  0  x  0 , y 0  3 , lim y   . x Nên hàm số 4 2
y  x  2x  3 có giá trị lớn nhất trên  và max y  3. 
Câu 23: Cho hai số phức z  1
  2i , z  2  i . Khi đó số phức z  z .z  z .z có phần ảo là 1 2 1 2 1 2 A. 9  . B. 10 . C. 8  . D. 0 . Hướng dẫn giải Cho ̣ n D.
Ta có z  1 2i  z  1 2i ; z  2  i  z  2  i . 1 1 2 2
z  z .z  z .z  1   2i
2  i  1 2i 2  i  8  . 1 2 1 2      
Vậy số phức z  z .z  z .z có phần ảo là 0 . 1 2 1 2
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/21 Mã đề 254 Câu 24: Tính cos 4 d x x  được kết quả là 1 1
A. sin 4x  C .
B.  sin 4x  C .
C.  sin 4x  C .
D. sin 4x  C . 4 4 Hướng dẫn giải Cho ̣ n A. 1 1
Áp dụng công thức cos ax  b dx  sin ax  b  C  nên cos 4 d x x  s in4x  C  a 4
Câu 25: Đồ thị hàm số 3 2
y  x  2x  x cắt đường thẳng y  k  x  
1 tại ba điểm phân biệt khi và chỉ khi k thuộc  1   1   1   1  A.  ;    . B.  ;     . C.  ;   \     1 . D.  ;  \     0 .  4   4   4   4  Hướng dẫn giải Chọn D.
Phương trình hoành độ giao điểm của đồ thị hàm số 3 2
y  x  2x  x và đường thẳng
y  k  x   1 :  x  1 3 2
x  2x  x  k  x   1 (1)   x   1  2
x  x  k   0   2
x  x  k  0 (2) 
Yêu cầu bài toán tương đương (1) có ba nghiệm phân biệt, tức (2) có hai nghiệm phân biệt  1   0 1   4k  0 k    1  khác 1      
4  k   ;  \     0 . 2 1 1 k  0 k  0    4  k  0 
Câu 26: Cho hàm số y  f  x liên tục và có đạo hàm đến cấp hai trên a;b; x  a;b . Khẳng định 0  
nào sau đây là sai?
A. Nếu f  x  0 x
  a; x , f  x  0 x
  x ;b thì x  x là một điểm cực tiểu của hàm số. 0     0  0
B. Nếu f  x  0 thì x  x là một điểm cực trị của hàm số. 0  0
C. Nếu f  x đổi dấu từ dương sang âm khi x đi qua x thì x  x là một điểm cực đại của hàm số. 0 0  f   x  0 D. Nếu 
thì x  x là một điểm cực trị của hàm số. 0 f    x  0  Hướng dẫn giải Chọn B.
Ta biết rằng nếu f  x  0 và f  x đổi dấu khi x đi qua x thì x  x là một điểm cực trị 0  0  0 0
của hàm số. Vì vậy kết luận ở câu B là chưa đầy đủ.
Thật vậy, ví dụ hàm số   3
f x  x có f  x 2
 3x ; f  x  0  x  0 .
Trong khi hàm này không có cực trị.
Câu 27: Hình tròn tâm I  1
 ; 2 , bán kính r  5 là tập hợp điểm biểu diễn hình học của các số phức z thỏa mãn
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/21 Mã đề 254
z   x  
1   y  2i  z    x  
1   y  2i A.  . B.  . z  5   z  5  
z   x  
1   y  2i  z    x  
1   y  2i C.  . D.  . z  5   z  5   Hướng dẫn giải Chọn D. z    x  
1   y  2i 2 2 2 2 Ta có: 
 z   x  
1   y  2  5   x  
1   y  2  25 . z  5   z    x  
1   y  2i
Suy ra: tập hợp điểm biểu diễn hình học của các số phức z thỏa mãn  là z  5  
hình tròn tâm I  1
 ; 2 , bán kính r  5 .
Câu 28: Thể tích khối tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường 2
y  x 1, y  0 , x  0 ,
x  1 quay quanh trục Ox là 28 4 28 4 A. . B. . C. . D. . 15 3 15 3 Hướng dẫn giải Chọn A.
Thể tích khối tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường 2
y  x 1, y  0 , x  0 ,
x  1 quay quanh trục Ox là 1 1 1 5 2  x 2  28 V   2 x   1 dx   4 2 x  2x   3 1 dx    x  x     đvtt . 5 3 15 0 0   0 Câu 29: Hà m số 2 y  x 1
A. Nghi ̣ ch biến trên  .
B. Đồng biến trên 0;  .
C. Nghi ̣ ch biến trên 0;  .
D. Đồng biến trên  . Hướng dẫn giải Cho ̣ n B. x Ta có y  . 2 x 1
Vì y  0  x  0 nên ta có bảng biến thiên x  0  y  0    y
Do đó hà m số đồng biến trên 0;  .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/21 Mã đề 254 
Câu 30: Cho hı̀ nh phẳng D giớ i ha ̣ n bởi đồ thi ̣y  cos x , tru ̣ c hoà nh, tru ̣ c tung và đườ ng thẳng x  . 2
Thể tı́ ch khối trò n xoay sinh bởi D khi quay quanh tru ̣ c Ox là     2 2 2 2 A. 2 V   cos d x x  . B. 2
V   cos x dx  . C. 2 V  cos d x x  .
D. V   cos d x x  . 0 0 0 0 Hướng dẫn giải Cho ̣ n A. b Áp du ̣ ng công thứ c 2 V  
f  x dx  . a   
Câu 31: Hàm số y  x  2 cos x có giá trị lớn nhất trên 0;  là 2      A.  2 . B.  3 . C.  . D. 2 . 6 6 Hướng dẫn giải Chọn B.   
Hàm số liên tục trên đoạn 0;  . 2      x   k 2 1  6
Ta có y  1 2 sin x . Vậy y  0  sin x    k  2 5  x   k 2  6     Vì x  0;  nên x  . 2    6         
Do y 0  2 , y    , y   3   nên max y   3 .  2  2  6  6    6 0;  2    1 2
Câu 32: Cho số phức z  3  4i , biểu thức A 
z  3 z 10 bằng 5 A. 0 . B. 5 . C. 10 . D. 5  . Hướng dẫn giải Chọn A. 1 Ta có 2 2 z  3  4  5 2
 A  .5  3.5 10  0 . 5
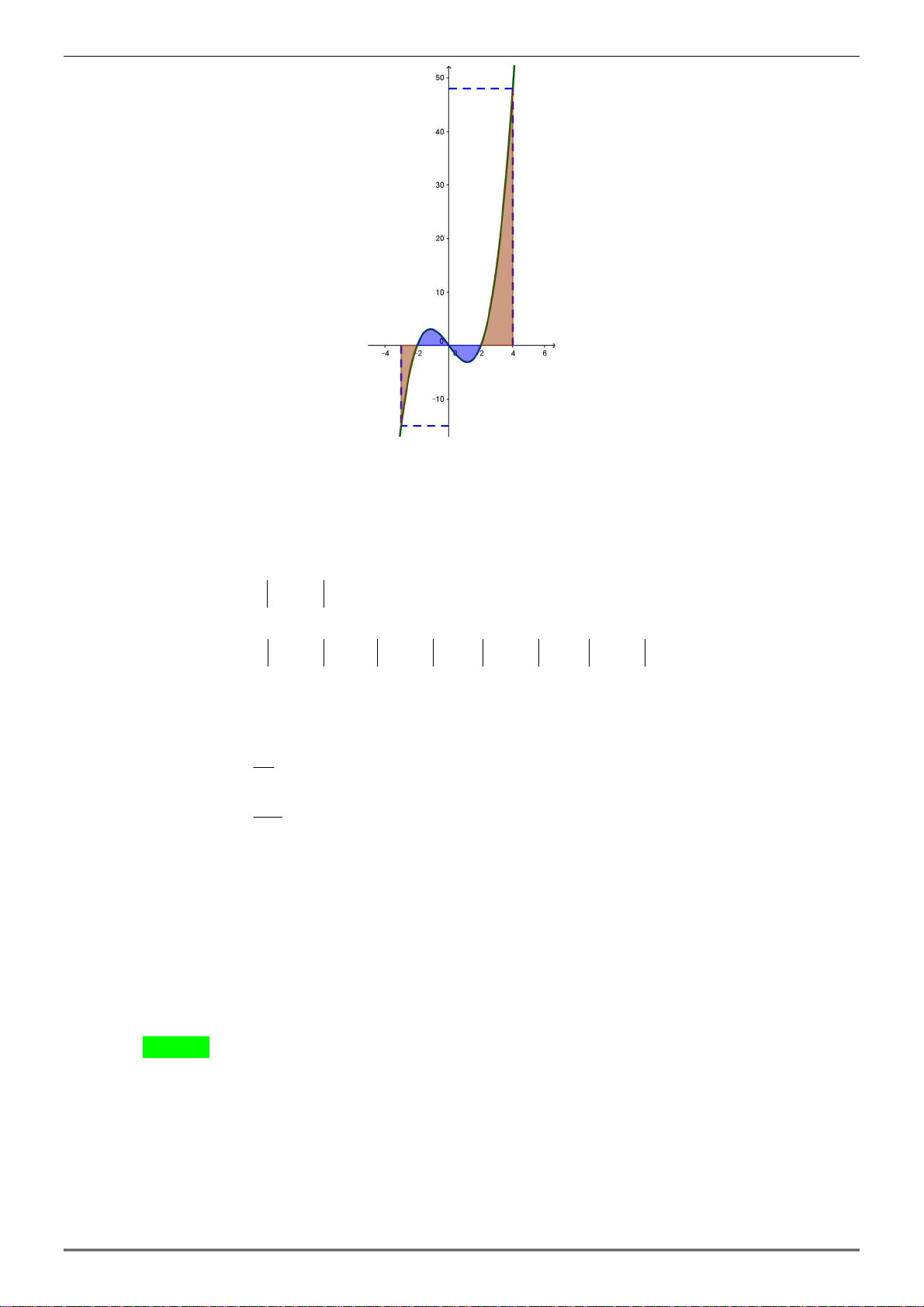
Câu 33: Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y  x  4x , trục hoành và hai đường thẳng
x  3, x  4 bằng 119 201 A. . B. 44 . C. . D. 36 . 4 4 Hướng dẫn giải Chọn C.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/21 Mã đề 254
Phương trình hoành độ giao điểm của đồ thị hàm số 3
y  x  4x với trục hoành là
 x  0 3; 4 3
x  4x  0   .  x  2   ; 3 4 
Vậy diện tích hình phẳng cần tìm là 4 3 S 
x  4x dx 3 2 0 2 4 3 3 3 3 
x  4x dx 
x  4x dx 
x  4x dx 
x  4x dx     3 2 0 2 2 0 2 4    3
4x  x dx    3
x  4xdx   3
4x  x dx   3
x  4xdx 3 2 0 2 25   4  4  36 4 201  4
Câu 34: Cho hai mặt phẳng  P : 2y  z  0, Q : x  2y  2z  3  0 và d là giao tuyến của chúng.
Phương trình đường thẳng d là x  5   2t x  5   2t x  5   2t x  5   2t    
A.  y  1 t .
B.  y  1 t .
C.  y  1 t .
D.  y  1 t .
z  2  2t     z  2  2t  z  2  2t  z  2  2t  Hướng dẫn giải Chọn C.
Phân tích: Do các đáp đều có điểm đi qua là M  5
 ; 1; 2 . Ta chỉ cần tính VTCP của d .  n    P   0; 2;    1 Ta có   u    d
nP, nQ  2; 1;  2 . Chọn đáp án C.  
nQ  1;  2; 2 
Câu 35: Phương trình đường thẳng đi qua điểm A 2  ;1;   1 , B 0; 1  ; 3   là
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/21 Mã đề 254 x  2t x  2   2t x  t x  2   t     A. y  1   2t .
B. y  1 2t . C. y  1   t .
D. y  1 t .
z  3 2t     z  1 2t  z  3  t  z  1 t  Hướng dẫn giải Chọn D.   Ta có AB  2; 2  ; 2
  nên đường thẳng AB có một véc tơ chỉ phương là u  1; 1  ;   1 . 
Phương trình tham số đường thẳng đi qua A 2  ;1;  
1 và có vectơ chỉ phương u  1; 1  ;   1 x  2   t 
là: y  1 t .
z  1 t 
Câu 36: Cho mặt cầu S  2 2 2
: x  y  z  4x  2 y  2z 10  0 , mặt phẳng  P : x  2y  2z 10  0 .
Khẳng định nào sau đây là đúng?
A.  P và  S  không có điểm chung.
B.  P cắt  S  theo giao tuyến là đường tròn lớn.
C.  P tiếp xúc với  S  .
D.  P cắt  S  theo giao tuyến là khác đường tròn lớn. Hướng dẫn giải Chọn C.
Mặt cầu  S  có tâm I 2; 1  ;  
1 và bán kính R  4 , đồng thời 2  2.  1  2.  1 10 d  12
I , P    R .   2   2 3 1 2 2
Suy ra  P tiếp xúc với  S  .
Câu 37: Trong không gian với hệ tọa độ Oxyz , với A 2;1; 2  , B 1; 3  ;   1 , C 0; 2;   1 . Nếu tứ giác
ABCD là hình bình hành thì tọa độ của D là A. 1;6;2 . B. 1;6;2 . C. 1;6;2 . D.  1  ;6; 2   . Hướng dẫn giải Chọn A.   Gọi D  ; x ;
y z  , AB  1; 4   ;1 , DC   ;
x 2  y; 1 z .  1    x x  1    
Tứ giác ABCD là hình bình hành  AB  DC   4
  2  y  y  6 . 1  1 z     z  2    Vậy D 1;6; 2   . x 1 y  1 z 1
Câu 38: Mặt phẳng  P chứa đường thẳng d :  
và điểm A 0; 2; 2 có phương trình là 1 2 1 
A. 5x  2 y  z  2  0 . B. 5x  2 y  z  2  0 . C. 5x  5z  2  0 .
D. x  z  2  0 . Hướng dẫn giải
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/21 Mã đề 254 Chọn D. 
Đường thẳng d đi qua B 1; 1  ; 
1 và có một vectơ chỉ phương là u  1; 2;   1 .   
n  u  1;2;   1
Gọi n là một vectơ pháp tuyến của mặt phẳng  P , ta có   .
n  AB  1; 3  ;   1    
Chọn n  u, AB   5  ;0; 5 .  
Phương trình mặt phẳng  P là 5
  x  0  5 z  2  0  x  z  2  0 .
Câu 39: Cho A 1; 3; 
1 , B 1; 1; 2 , C 2; 1; 3 , D 0; 1;  
1 . Phương trình mặt phẳng chứa AB và
song song với CD là
A. x  2z  4  0 .
B. 2x  4z  z  2  0 .
C. 8x  3y  4z  3  0 .
D. 8x  3y  4z  3  0 . Hướng dẫn giải Chọn C. 
Vectơ chỉ phương AB là u  2;  4;  1 . AB 
Vectơ chỉ phương CD là u  2;0;  4 . CD    
n  u ,u   16;6; 8 AB CD  đi qua A  1; 3;  1
Phương trình mặt phẳng chứa AB và song song với CD :   VTPT n   16;6; 8 
là  P  : 16 x  
1  6  y  3  8 z  
1  0  8x  3 y  4z  3  0 . x  2 y  1 z  2 x y  5 z  2
Câu 40: Cho hai đường thẳng d :   , d :   , khoảng cách giữa hai 1 1 1 1 2 2 4 1 đường thẳng này là 5 2 6 4 6 3 6 A. . B. . C. . D. . 6 3 3 2 Hướng dẫn giải Chọn B. Cách 1:
Gọi MN là đoạn vuông góc chung của hai đường thẳng chéo nhau d và d M  d , N  d . 1 2  1 2
Vì M  d  M 2  t; 1  t; 2  t và N  d  N 2t ;
 5  4t ; 2  t . 2   1   
Suy ra MN  2t  t  2; 4
 t  t  6; t
   t  .  
Đường thẳng d và d lần lượt có VTCP là u  và u  2; 4; 1 . d  d 1;1;  1 1 2 1 2   t   0 MN  d MN.u  0  t  t  
 t  t   t    t   d 1 2 2 1 4 6 1 0 1   1       Ta có: 
       4 MN  d  MN.u  0
2 2t  t  2  4 4
 t  t  6 1 t  t  0 t '  2        d    2  3   2 2 4   2 6 Từ đó suy ra MN  ; ;  
 và MN  MN  .  3 3 3  3 2 6
Vậy khoảng cách giữa hai đường thẳng d và d bằng . 1 2 3
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/21 Mã đề 254 Cách 2 :
Áp dụng công thức tính khoảng cách giữa 2 đường thẳng chéo nhau d và d là: 1 2
  
u ,u .MN d d 1 2   h   
, M  d , N  d . 1 2  u  , u  d d 1 2  
Câu 41: Phương trình mặt cầu đi qua bốn điểm A2; 2; 2 , B 4;  2;  2 , C 1; 1;  2 và D 1; 2;   1 là 2 2 2 2 2 2 A.  x  
1   y  2   z  2  25 . B.  x  
1   y  2   z  2  16 . 2 2 2 2 2 2 C.  x  
1   y  2   z  2  16 . D.  x  
1   y  2   z  2  25 . Hướng dẫn giải Chọn D.
Phương trình mặt cầu dưới dạng khai triển: 2 2 2
x  y  z  2ax  2by  2cz  d  0
4a  4b  4c  d  1  2 a  1  8
 a  4b  4c  d  2  4 b   2  Mặt cầu qua ,
A B,C, D    2a 2b 4c d 6        c  2
 2a 4b 2c d 6        d  1  6   2 2 2
Suy ra mặt cầu có tâm I 1; 2
 ; 2 và bán kính R   
1  2  2 16  5 x  1 y  2 z
Câu 42: Cho đường thẳng d :  
, và mặt phẳng  P  : x  y  z  3  0 . Gọi d là hình 1 2 1
chiếu của d trên  P , khi đó d có một vectơ chỉ phương là    
A. u  1; 2;  1 .
B. u  1;  2;   1 . C. u   1  ; 2;   1 .
D. u  1; 2;  1 . Hướng dẫn giải Chọn A.
Phương pháp tự luận x  1 y  2 z Đường thẳng d :  
đi qua điểm M 1; 2;0 . 1 2 1
Ta thấy điểm M 1; 2;0 thuộc mặt phẳng  P  : x  y  z  3  0
Lấy điểm N 2; 4;  1  d
Phương trình đường thẳng  đi qua N 2; 4; 
1 và vuông góc với  P  : x  y  z  3  0 là:
 x  2  t 
 :  y  4  t  z  1 t 
Gọi M  là giao điểm của  và  P , suy ra tọa độ M  thỏa mãn: 4  2 8 1 
 2  t  4  t   1 t   3  0  t   M   ; ;    3  3 3 3 
Khi đó hình chiếu d  đi qua hai điểm M và M  nên có vectơ chỉ phương là :   1 2 1    u  ; ; hay u  3u   MM  1;2;  1 MM     3 3 3 
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/21 Mã đề 254
Phương pháp trắc nghiệm:
Hình chiếu của đường thẳng d xuống mặt phẳng  P là đường thẳng có một véc tơ chỉ 
     phương u   u , n
 , n  . Áp dụng trong bài này với n    và u   , ta d  1;2  ;1 P 1; 1;  1 1 d  P  P         suy ra u  1  ; 2
 ;1 . Vậy chọn u  u  1; 2; 1  . 1   1      
Câu 43: Cho a  2 j  3k . Khi đó tọa độ của a là A. 2;0; 3   . B. 2; 3  ; 0 . C. 0; 2; 3   . D. 0;2;3 . Hướng dẫn giải Chọn C.   
Ta có: a  2 j  3k  2.0;1;0  30;0  ;1  0; 2; 3   Câu 44: Cho A
 BC với A1;0;0 ; B 0; 2;0 ; C 3;0;4 và M thuộc Oyz . Nếu MC   ABC  thì
tọa độ của M là  3 11   3 11   3 11   3 11 A. 0; ;   B. 0;  ;   C. 0; ;    D. 0;  ;     2 2   2 2   2 2   2 2  Hướng dẫn giải Chọn B.
Ta có M thuộc Oyz nên tọa độ M 0; a;b .   
Lại có MC  3;  ;
a 4  b ; AB   1
 ; 2; 0 ; AC  2;0; 4    3 a   MC  AB  MC.AB  0  3   2a  0   2
Vì MC   ABC   
       MC  AC 6  4  MC AC  4  b  0 11 . 0    b    2  3 11 
Vậy tọa độ M 0;  ;   .  2 2 
Câu 45: Cho mặt phẳng  P  : 2x  3z 1  0 . Khi đó  P có một vectơ pháp tuyến là    
A. n  2;  3;0 .
B. n  2;  3;  1 .
C. n  2;  3;   1 .
D. n  2;0;  3 . Hướng dẫn giải Chọn D.
Phương trình mặt phẳng có dạng  P  : Ax  By  Cz  D  0 có vectơ pháp tuyến là   n   ; A ;
B C  . Vậy  P : 2x  3z 1  0 có vectơ pháp tuyến là n  2;0;  3 .
x  1  2t x  3 y z  1 
Câu 46: Cho hai đường thẳng d :  
,  : y  1 t , vị trí tương đối hai đường thẳng này là 1 2 1 z  t  A. trùng nhau.
B. song song với nhau. C. cắt nhau. D. chéo nhau. Hướng dẫn giải Chọn C.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/21 Mã đề 254 x  3 y z  1 
Phương trình đường thẳng d :  
có vectơ chỉ phương là n  1; 2;  1 . d 1 2 1
x  1  2t  
Phương trình đường thẳng  : y  1 t có vectơ chỉ phương là n   .  2;1;  1 z  t   
Ta thấy n  k.n . d 
x  3  t 
Viết lại phương trình đường d thẳng về dạng tham số như sau: d : y  0  2t
z  1 t   1 t  1  t 1
  2t  3  t  2  
Xét hệ phương trình 1 t  0  2t  t  1 2t  .
t  1 t   t  1  t  
Hệ có nghiệm t  0 và t  1, suy ra hai đường thẳng cắt nhau.
Câu 47: Cho A 1;2;2 , B 3;0; 2 . Mặt phẳng trung trực đoạn thẳng AB có phương trình là
A. x  y  3  0 .
B. x  y 1  0 .
C. 2x  2 y  3  0 .
D. x  y 1  0 . Hướng dẫn giải Chọn D. 
Mặt phẳng cần tìm đi qua I 2;1; 2 là trung điểm của đoạn thẳng AB và nhận AB  2; 2  ; 0 làm véc tơ pháp tuyến.
Suy ra phương trình mặt phẳng cần tìm là 2 x  2  2 y  
1  0 hay x  y 1  0 . 
Câu 48: Phương trình đường thẳng đi qua A2;1; 
1 và có vectơ chỉ phương u  1;2; 2 là x  1 2t x  2 y 1 z 1  A.   .
B. y  2  t . 1 2  2 z  2  t  x  2 y 1 z 1 x 1 y  2 z  2 C.   . D.   . 1 2 2 2 1 1  Hướng dẫn giải Chọn C.
Câu 49: Mặt cầu  S  : 2 2 2
2x  2 y  2z  6x  8y  4z  2  0 có tọa độ tâm I và bán kính R lần lượt là  3  5  3  A. I  ; 2; 1  , R    . B. I ; 2  ;1 , R  5   .  2  2  2   3  25  3  C. I ; 2  ;1 , R    .
D. I  ; 2; 1 , R  25   .  2  4  2  Hướng dẫn giải Chọn A. S  : 2 2 2
2x  2 y  2z  6x  8y  4z  2  0 2 2 2
 x  y  z  3x  4 y  2z  1  0 Gọi I  ; a ;
b c là tâm của mặt cầu  S  . Ta có
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/21 Mã đề 254 3   3  2
 a  3  a  ; 2  b  4   b  2 ; 2
 c  2  c  1   I ; 2; 1    2  2  2  3  2 5 Bán kính 2 R    2    1 1     2  2
Câu 50: Mặt phẳng đi qua A1;2 
;1 và song song với mặt phẳng  P : 2x  y  z  2  0 có phương trình là A. 2
 x  y  z 1  0 .
B. x  2 y  z 1  0 .
C. 2x  y  z  2  0 .
D. 2x  y  z 1  0 . Hướng dẫn giải Chọn D.
Gọi   là mặt phẳng cần tìm.
Vì   //  P nên có dạng : 2x  y  z  d  0d  2   . A1; 2 
;1   nên ta có: 2.1 2 1 d  0  d  1  .
Vậy phương trình mặt phẳng   là: 2x  y  z 1  0 .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/21 Mã đề 254