Đề thi HK2 Toán 12 năm học 2016 – 2017 trường THPT Việt Đức – Hà Nội

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2016 – 2017 .Mời bạn đọc đón xem.

38 19 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

22 trang 8 tháng trước

Tác giả:

Profile Lan Tường
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 1/22 Mã đề 570
SỞ GD-ĐT HÀ NỘI ĐỀ KIỂM TRA HỌC KÌ II
TRƯỜNG THPT VIỆT ĐỨC MÔN TOÁN – LỚP 12
Năm học: 2016 – 2017
(Đề thi gồm có 06 trang) Thời gian làm bài: 90 phút, không kể thời gian phát đề
Mã đề 570
Câu 1: Giải bài toán tính diện tích hình phẳng giới hạn bởi các đường
2
y
,
x
ye
,
1
x
. Bốn bạn
An, Bảo, Cần và Dũng cho 4 công thức khác nhau. Hãy chọn công thức đúng
A. Cần

1
ln 2
x
Sex

. B. Bảo

ln 2
1
2d
x
Se x

.
C. Dũng
ln 2
1
2d
x
Se x

. D. An

1
ln 2
2d
x
Se x

.
Câu 2: Tìm nguyên hàm
Fx
của hàm số
2sin3 .sin5
fx x x
thỏa
3
42
F



A.
 
1
2sin2 sin8 3
4
Fx x x

. B.
 
1
2sin 2 sin8 1
4
Fx x x

.
C.
 
1
4sin 2 sin8 2
8
Fx x x

. D.
 
1
4sin 2 sin8 1
8
Fx x x

.
Câu 3: Nguyên hàm
3
cot d
Fx xx
là
A.

2
1
cot ln sin
2
Fx x x C

. B.

2
1
cot ln sin
2
Fx x x C

.
C.

2
1
cot ln sin
2
Fx x x C

. D.

2
1
cot ln cos
2
Fx x x C

.
Câu 4: Cho hai đường thẳng gồm
d
có phương trình
xyz

,
d
có phương trình
11
xy z

.
Ta có khoảng cách giữa
d
và
d
bằng
A.
1
. B.
2
. C.
2
. D.
3
.
Câu 5: Thể tích
V
khi quay
22
: 4 4 0
Ex y

quanh trục
Ox
bằng
A.
8
.
3
B.
4.
C.
4
.
3
D.
16
.
3
Câu 6: Viết phương trình mặt cầu
S
đi qua hai điểm
3; 1; 2
A

,
1; 1; 2
B và có tâm thuộc trục
Oz
.
A.

2
22
1 10.
xy z
B.
222
2100.
xyz z

C.

2
22
1 12.
xy z
D.
222
2100.
xyz z

Câu 7: Giả sử
4
0
sin3 sin 2 d 2
a
Ixxx
b

, với
a
b
là phân số tối giản. Ta có giá trị của
ab
là
A.
8
. B.
15
. C.
10
. D.
13
.
Câu 8: Tập hợp các điểm trong mặt phẳng phức biểu diễn số phức
z
thỏa mãn điều kiện
1
zi

là
A. Một đường tròn. B. Hai đường thẳng.
C. Hai đường tròn. D. Một đường thẳng.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 2/22 Mã đề 570
Câu 9: Trong không gian với hệ trục tọa độ
,
Oxyz
cho hình chóp tứ giác đều
.,
SABCD
đáy
ABCD
là
hình vuông nằm trong mặt phẳng
,
Oxy
AC DB O

(
O
là gốc tọa độ),
2
;0;0 ,
2
A




đỉnh
0;0;9 .
S
Ta có thể tích khối chóp
.
SABCD
bằng
A. 3 (đvtt). B.
32
(đvtt). C. 4 (đvtt). D. 9 (đvtt).
Câu 10: Biết rằng
fx
là một hàm số liên tục trên
và

9
0
d9.
fx x
Khi đó giá trị của

3
0
3d
fxx
là
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 11: Cho số phức
,zabiab
. Ta có phần ảo của số phức
2
24
zzi

bằng
A.
2
ab b

. B.
224
ab b

. C.
224
ab b

. D.
224
ab b

.
Câu 12: Trên mặt phẳng phức,
M
và
N
là các điểm biểu diễn của
12
,
zz
, trong đó
12
,
zz
là hai nghiệm
của phương trình
2
4130
zz

. Độ dài
MN
là
A.
12
. B.
4
. C.
6
. D.
8
.
Câu 13: Trong không gian
Oxyz
, cho tam giác
ABC
có
5; 0; 0
A
,
1; 1;1
B
,
3;3; 4
C
. Mặt phẳng
P
đi qua
A
,
B
và cách
C
một khoảng bằng
2
có phương trình là
A.
2250
xyz

. B.
2250
xyz

.
C.
2250
xyz

. D.
2250
xyz

.
Câu 14: Tìm số phức liên hợp của số phức
223
zi i

.
A.
64

. B.
64

. C.
64
zi

. D.
64
zi

.
Câu 15: Trong không gian
Oxyz
cho các điểm
1; 1; 1 , 2; 0 ; 1 , 1; 2; 1
ABC

,
D
là điểm sao cho
ABCD
là hình bình hành. Ta có tọa độ
D
là
A.
2; 3;3 .
D 
B.
2; 3; 3 .
D

C.
2;3; 3 .
D
D.
2;3; 3 .
D

Câu 16: Nếu
112
f
,
fx
liên tục và

4
1
d17
fxx
. Giá trị của
4
f
bằng
A.
9.
B.
5.
C.
29.
D.
19.
Câu 17: Cho số phức
z
thoả
zi

. Tìm số phức
z
có môđun nhỏ nhất?
A.
86
55
zi

. B.
86
55
zi

. C.
86
55
zi

. D.
86
55
zi

.
Câu 18: Gọi
H
là hình phẳng giới hạn bởi các đường
tan
0,
4
yx
Ox
xx

. Quay
H
xung quanh trục
Ox
ta được khối tròn xoay có thể tích bằng
A.

1
4
đvtt
. B.

2
4
đvtt
. C.

2
4
đvtt
. D.
2
đvtt
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 3/22 Mã đề 570
Câu 19: Nguyên hàm
22
3d
x
Fx x
là
A.

22
3
2ln3
x
Fx C

. B.
22
3ln3
x
Fx C

.
C.
22
3
x
Fx C

. D.

2
3
9
x
Fx C
.
Câu 20: Trong không gian với hệ trục
Oxyz
cho hai điểm
1; 2; 3 , 0;1; 5
AB

, gọi
I
là điểm trên
đoạn thẳng
AB
sao cho
2
IA IB
. Giả sử tọa độ của điểm
;;
I abc
thì
abc

bằng
A.
4
. B.
5
. C.
8
3
. D.
17
3
.
Câu 21: Tính tích phân
1
0
1
d
23
x
x
bằng
A.
15
ln
23
. B.
13
ln
25
. C.
3
20
. D.
1
ln 2
2
.
Câu 22: Nguyên hàm


5
d
32
x
Fx
x
là
A.


4
1
83 2
Fx C
x

. B.


4
1
23 2
Fx C
x

.
C.


4
1
43 2
Fx C
x

. D.


4
1
83 2
Fx C
x

.
Câu 23: Nguyên hàm
31d
Fx x x

là
A.
 
3
2
31 .
9
Fx x C

B.
 
3
1
31 .
3
Fx x C

C.
 
3
2
31 .
3
Fx x C

D.

2
31 .
9
Fx x C

Câu 24: Trong mặt phẳng phức
, gọi
A
,
B
,
C
lần lượt là ba điểm biểu diễn các số phức
1
34
zi

;
2
52
zi

;
3
13

. Số phức biểu diễn bởi điểm
D
để
ABCD
là hình bình hành là
A.
7
i

. B.
19
i
. C.
19
i
. D.
79
i

.
Câu 25: Biết

0
24d0
b
xx

. Khi đó
b
nhận giá trị bằng
A.
1
2
b
b
. B.
0
4
b
b
. C.
0
2
b
b
. D.
1
4
b
b
.
Câu 26: Diện tích hình phẳng giới hạn bởi hai Parabol
2
4
x
y và
2
3
2
x
yx

là
A. 12
ñvtt
. B. 8
ñvtt
. C. 4
ñvtt
. D. 16
ñvtt
.
Câu 27: Trong không gian
Oxyz
cho đường thẳng :
dx y z

, gọi
d
là hình chiếu vuông góc của
d
lên mặt phẳng tọa độ
Oyz
. Ta có phương trình
d
là:
A.
0
.
2
x
yt
zt
B.
.
xt
yt
zt
C.
0
2.
1
x
yt
zt


D.
0
.
x
yt
zt
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 4/22 Mã đề 570
Câu 28: Tích phân
1
0
d
x
b
Ixexa
e

. Khi đó
2
ab
bằng
A.
5.
B.
6.
C.
7.
D.
3.
Câu 29: Phần ảo của số phức
2017
1
1
i
z
i



là
A.
1.
B.
1.
C.
.
i
D.
.
i
Câu 30: Cho
9
3
0
1 d
Ix xx

. Đặt
3
1
tx

. Ta có
A.

1
32
2
31 2d.
Ittt

B.

2
33
1
31 d.
Ittt

C.

1
33
2
31 d.
Ittt

D.

1
33
2
1d.
Ittt

Câu 31: Trong không gian với hệ tọa hệ trục
Oxyz
, cho hai đường thẳng
312
:
124
xyz
d


và
:3 1 5
xyz

. Trong bốn đường thẳng
Ox
,
Oy
,
Oz
và
, đường thẳng
d
tạo với
đường thẳng nào một góc lớn nhất?
A.
Oy
. B.
. C.
Ox
. D.
Oz
.
Câu 32: Tìm tập hợp các điểm biểu diễn số phức
z
, biết số phức
2
z
có điểm biểu diễn nằm trên trục
hoành
A. Đường thẳng
yx
. B. Trục tung và trục hoành.
C. Trục tung. D. Trục hoành.
Câu 33: Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
:3 4 5 10 0
Pxyz

và đường
thẳng
d
đi qua 2 điểm
1; 0; 2
M
,
3; 2; 0
N
. Gọi
là góc giữa đường thẳng
d
và mặt
phẳng
P
. Ta có
A.
90

. B.
45

. C.
60

. D.
30

.
Câu 34: Nguyên hàm
3
.d
x
Fx xe x
là
A.
3
1.
x
Fx x e C

. B.
32
.
x
Fx xe x C

.
C.

33
11
.
39
xx
Fx xe e C

. D.

33
11
.
39
xx
Fx xe e C

.
Câu 35: Phương trình
2
118130
ziz i

có hai nghiệm là
A.
4;52
ii

. B.
4;52
ii

. C.
4;52
ii

. D.
4;52
ii

.
Câu 36: Trong không gian với hệ trục tọa độ
Oxyz
, cho hai mặt phẳng
:30
Pxz

và
:2 2 3 0
Qyz

. Ta có góc giữa hai mặt phẳng
P
và
Q
bằng
A.
2
. B.
4
. C.
3
. D.
6
.
Câu 37: Trong không gian với hệ trục
Oxyz
, cho hai điểm
1; 2; 5
A
,
1; 5; 5
B
.
Tìm điểm
COz
sao cho tam giác
ABC
có diện tích nhỏ nhất?
A.
0;0;6
C
. B.
0; 0;5
C
. C.
0;0;4
C
. D.
0;0;2
C
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 5/22 Mã đề 570
Câu 38: Nguyên hàm của hàm số

4
3
d
x
Fx xe x
là
A.

4
4
4
x
xe
Fx C

. B.

4
4
x
xe
Fx C

.
C.

4
1
4
x
Fx e C

. D.

4
4
x
e
Fx C

.
Câu 39: Trong không gian với hệ trục
Oxyz
cho hai điểm
3;1;1
A
,
2; 1; 4
B

. Hãy viết phương
trình mặt phẳng
P
đi qua
A
,
B
và vuông góc với mặt phẳng
:2 3 4 0
Qxyz
 
.
A.
513 290
xyz

. B.
13 5 5 0
xyz

.
C.
13 5 3 0
xyz

. D.
312 220
xyz

.
Câu 40: Cho
ln 2
0
1d
x
Iexa
b

. Khi đó
A.
ab
. B.
ab
. C.
1
ab
. D.
ab
.
Câu 41: Cho mặt phẳng
:30
Pxyz

và điểm
1; 2; 3
A
, hình chiếu vuông góc của
A
lên
P
có tọa độ là
A.
1;1; 2
. B.
0;1; 2
. C.
1; 2; 0
. D.
2;1; 0
.
Câu 42: Cho
z
,
12 74
zi i

. Khi đó
21
z
là
A.
65
. B.
61
. C.
8
. D.
5
.
Câu 43: Cho
0
a
và
1,
aC
là hằng số. Phát biểu nào sau đây đúng?
A.
22
dln.
xx
axa aC

B.
22
d.
xx
axa C

C.
dln.
xx
axa aC

D.
2
2
d.
2ln
x
x
a
ax C
a

Câu 44: Cho
fx
là một hàm số liên tục trên
thỏa mãn

1
0
d3
ft t
và

1
1
d2.
fu u

Khi đó

0
1
d
fx x
bằng ?
A.
5.
B. 5. C. 1. D.
1.
Câu 45: Cho mặt cầu
222
: 4240
Sx yz x y z

. Viết phương trình mặt phẳng tiếp xúc với mặt
cầu tại điểm
1; 1; 0
M
.
A.
2230
xyz

. B.
2210
xyz

.
C.
0
xy

. D.
210
xy

.
Câu 46: Nguyên hàm

2
21
d
2
xx
Fx x
x

là
A.

2
47ln 2
2
x
Fx x x C

. B.
2
4ln 2
Fx x x x C

.
C.
2
2ln 2
Fx x x x C

. D.
2
47ln 2
Fx x x x C

.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 6/22 Mã đề 570
Câu 47: Trong không gian
Oxyz
cho điểm
1; 1; 1 , 3; 5; 7
AB
. Gọi
S
là tập hợp điểm
;;
Mxyz
thoả mãn
222
MA MB AB

. Chọn kết luận đúng
A.
S
là mặt cầu có phương trình

222
13456
xyz

.
B.
S
là mặt phẳng trung trực của đoạn
AB
.
C.
S
là mặt cầu có phương trình

222
23414
xyz

.
D.
S
là đường tròn có phương trình

222
13414
xyz

.
Câu 48: Nguyên hàm

sin
d
32cos
x
Fx x
x
là
A.

1
ln 3 2cos
3
Fx x C

. B.

1
ln 3 2cos
2
Fx x C

.
C.

1
ln 3 2cos
3
Fx x C

. D.

1
ln 3 2cos
2
Fx x C

.
Câu 49: Cho
4
2
1
11
d
a
xx
xb
x




với
a
b
là phân số tối giản. Khi đó
ab
bằng
A.
140
. B.
39
. C.
9
. D.
31
.
Câu 50: Diện tích của hình phẳng
H
giới hạn bởi
2
20
0
yyx
xy


bằng
A.
27
2
đvdt. B.
27
4
đvdt. C.
9
2
đvdt. D.
9
4
đvdt.
----------HẾT----------
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 7/22 Mã đề 570
BẢNG ĐÁP ÁN - HKII – LỚP 12 - TRƯỜNG THPT VIỆT ĐỨC – HÀ NỘI
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
D
B C
A
D
D
A
A
A
B C
B B C
C
A
A
A
C
A
D
A
D
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
B D
A
C
C
C
B C
C
B C
B C
B B B A
D
A
B A
C
B D
C
HƯỚNG DẪN GIẢI
Câu 1: Giải bài toán tính diện tích hình phẳng giới hạn bởi các đường
2
y
,
x
ye
,
1
x
. Bốn bạn
An, Bảo, Cần và Dũng cho 4 công thức khác nhau. Hãy chọn công thức đúng
A. Cần
1
ln2
(2 )d
x
Sex

. B. Bảo
ln2
1
(2)d
x
Se x

.
C. Dũng
ln 2
1
2d
x
Se x

. D. An
1
ln2
(2)d
x
Se x

.
Hươ ng dân gia i
Chọn D.
Ta có:
2ln2
x
ex . Do đó diện tích cần tìm là
1
ln2
(2)d
x
Se x

(vì
2ln2
x
ekhix).
Câu 2: Tìm nguyên hàm
()
Fx
của hàm số
() 2sin3.sin5
fx x x
thỏa
3
42
F



A.

1
( ) 2sin 2 sin 8 3
4
Fx x x

. B.

1
( ) 2sin 2 sin8 1
4
Fx x x

.
C.

1
() 4sin2 sin8 2
8
Fx x x

. D.

1
( ) 4sin 2 sin8 1
8
Fx x x

.
Hươ ng dân gia i
Chọn D.
Ta có

1
'( ) 4sin 2 sin8 1 cos2 cos8 2sin5 .sin3
8
Fx x x x x x x




.
Và
3
42
F



.
Câu 3: Nguyên hàm
3
cot d
Fx xx
là
A.

2
1
cot ln sin
2
Fx x x C

. B.

2
1
cot ln sin
2
Fx x x C

.
C.

2
1
cot ln sin
2
Fx x x C

. D.

2
1
cot ln os
2
Fx x c x C

.
Hướng dẫn giải
Chọn B.

3
2
1
cot d 1 cot d
sin
F x xx xx
x





2
1
cot d cot d
sin
xx xx
x


2
1cos
cot d d
sin sin
x
xx x
xx



1
cot dcot d sin
sin
xx x
x


2
1
cot ln sin
2
xxC

.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 8/22 Mã đề 570
Câu 4: Cho hai đường thẳng gồm
d
có phương trình
xyz

,
d
có phương trình
11
xy z

.
Ta có khoảng cách giữa
d
và
d
bằng
A.
1
. B.
2
. C.
2
. D.
3
.
Hướng dẫn giải
Chọn C.
:
dx y z

qua
0; 0;0
O
và có VTCP
1;1;1
a
.
:11
dx y z

qua
0;1; 1
A
có VTCP
1;1;1
a
.
0;1; 1
OA


;

; 2;1;1
OA a




.
//
Od dd



 
22
2
222
;
21 1
;; 2
111
OA a
ddd dOd
a







.
Câu 5: Thể tích
V
khi quay
22
: 4 4 0
Ex y

quanh trục
Ox
bằng
A.
8
.
3
B.
4.
C.
4
.
3
D.
16
.
3
Hướng dẫn giải
Chọn A.

2
22 2
: 4 4 0 1
4
x
Ex y y

.
Thể tích
22
2
2
22
d 1 d.
4
x
Vyx x







Bấm máy tính tích phân này, ta được
8
.
3
V
Câu 6: Viết phương trình mặt cầu
S
đi qua hai điểm
3; 1; 2
A

,
1; 1; 2
B
và có tâm thuộc trục
Oz
A.

2
22
1 10.
xy z B.
222
2100.
xyz z

C.

2
22
1 12.
xy z D.
222
2100.
xyz z

Hướng dẫn giải
Chọn D.
Gọi
0; 0;
IcOz
là tâm của mặt cầu
S
.
S
qua
22
,
A B IA IB IA IB


22 2
222
31 2 112 1.
ccc

Vậy, tâm
0;0; 1
I
; bán kính

22
3
31 21 11
RIA  
.
Phương trình mặt cầu

2
22 222
: 1 11 2 10 0.
Sxy z x yz z
 
Câu 7: Giả sử
4
0
sin3 sin 2 d 2
a
Ixxx
b

, với
a
b
là phân số tối giản. Ta có giá trị của
ab
là
A.
8
. B.
15
. C.
10
. D.
13
.
Hươ ng dân gia i
Cho n D.
x
y
2
1
2
1
O
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 9/22 Mã đề 570
Ta có:

44
00
1
sin 3 sin 2 d cos cos5 d
2


Ixxx xxx

4
0
11 1 1532
sin sin5 sin sin
25 245410




xx

.
Vậy ta có:
3
a
,
10
b
nên
13

ab
.
Câu 8: Tập hợp các điểm trong mặt phẳng phức biểu diễn số phức
z
thỏa mãn điều kiện
1
zi

là
A. Một đường tròn. B. Hai đường thẳng. C. Hai đường tròn. D. Một đường thẳng.
Hươ ng dân gia i
Cho n A.
Đặt

với
,
xy
.
Ta có:
 
22
22
111111
 
zi x yii x y x y
.
Vậy tập hợp điểm biểu diễn số phức
z
là đường tròn tâm
0;1
I
, bán kính là
1
R
.
Câu 9: Trong không gian với hệ trục tọa độ
,
Oxyz
cho hình chóp tứ giác đều
.,
SABCD
đáy
ABCD
là
hình vuông nằm trong mặt phẳng
,
Oxy
AC DB O

(
O
là gốc tọa độ),
2
;0;0 ,
2
A




đỉnh
0;0;9 .
S
Ta có thể tích khối chóp
.
SABCD
bằng
A. 3 (đvtt). B.
32
(đvtt). C. 4 (đvtt). D. 9 (đvtt).
Hươ ng dân gia i
Chọn A.
Ta có:
SO
là đường cao của khối chóp.
9
SO
.
2
2
AO

2
2.21.
2
AB AO

Vậy
.
11
.. .9.13
33
S ABCD ABCD
VSOS

(đvtt).
Câu 10: Biết rằng
fx
là một hàm số liên tục trên
và

9
0
d9.
fx x
Khi đó giá trị của

3
0
3d
fxx
là
A.
3
. B.
2
. C.
4
. D.
1
.
Hươ ng dân gia i
Chọn A.

3
0
3d
Ifxx
.
Đặt
33dd
xt x t

.
Đổi cận:
00
xt

.
39
xt

.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 10/22 Mã đề 570
 
99
00
d1
.d3.
33
t
ft ft t


Câu 11: Cho số phức
,zabiab
. Ta có phần ảo của số phức
2
24
zzi

bằng
A.
2
ab b

. B.
224
ab b

. C.
224
ab b

. D.
224
ab b

.
Hướng dẫn giải.
Chọn B.
Ta có:

2
222
24 2 4 2 22 4
z z i a bi a bi i a b abi a bi i
 
22
2224
ab a abb i
 . Vậy phần ảo là
224
ab b

.
Câu 12: Trên mặt phẳng phức,
M
và
N
là các điểm biểu diễn của
12
,
zz
, trong đó
12
,
zz
là hai nghiệm
của phương trình
2
4130
zz

. Độ dài
MN
là
A.
12
. B.
4
. C.
6
. D.
8
.
Hướng dẫn giải.
Chọn C.
2
23
4130
23
zi
zz
zi



. Giả sử
M
và
N
có toạ độ là
2; 3 , 2; 3
MN


0; 6 6
MN MN

 
.
Câu 13: Trong không gian
Oxyz
, cho tam giác
ABC
có
5; 0; 0
A
,
1; 1;1
B
,
3;3; 4
C
. Mặt phẳng
P
đi qua
A
,
B
và cách
C
một khoảng bằng
2
có phương trình là
A.
2250
xyz

. B.
2250
xyz

. C.
2250
xyz

. D.
2250
xyz

.
Hướng dẫn giải:
Chọn B.
Gọi
:0
PAxByCzD

với
222
0
ABC

.
Ta có:
,
AB P
nên
50 5
04
AD D A
ABCD B C A






Mà



2
22
222
334
,2 27202 4
ABCD
dC P C A A C C A
ABC

 

2
2
332 248 41 0
166 41 0
CA
AA
AC


+ Với
2
CA
, chọn
1, 2
AC

nên
2, 5
BD
 
:2250
Pxyz

+ Với
166 41 0
AC

, chọn
166, 41
CA

nên
2, 205
BD

: 41 2 166 205
Pxy z
Câu 14: Tìm số phức liên hợp của số phức
223
zi i

.
A.
64

. B.
64

. C.
64
zi

. D.
64
zi

.
Hướng dẫn giải:
Chọn B.
223 64
zi i i

64
zi

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 11/22 Mã đề 570
Câu 15: Trong không gian
Oxyz
cho các điểm
1; 1; 1 , 2; 0 ; 1 , 1; 2; 1
ABC

,
D
là điểm sao cho
ABCD
là hình bình hành. Ta có tọa độ
D
là
A.
2; 3;3 .
D 
B.
2; 3; 3 .
D

C.
2;3; 3 .
D
D.
2;3; 3 .
D

Hướng dẫn giải
Chọn C.
Ta có
ABCD
là hình bình hành nên


21 1 2
01 2 3 2;3;3.
3
111
BACD D D
BACD D D
DBACD
D
xx xx x x
AB DC y y y y y y D
zzzzz
z








 
Câu 16: Nếu
112
f
,
fx
liên tục và

4
1
d17
fxx
. Giá trị của
4
f
bằng
A.
9.
B.
5.
C.
29.
D.
19.
Hướng dẫn giải
Chọn C
Ta có
   
4
4
/
1
1
17 d 4 1 4 14 1 17 12 29
fxxfx f f f f

.
Câu 17: Cho số phức
z
thoả
zi

. Tìm số phức
z
có môđun nhỏ nhất?
A.
86
55
zi

. B.
86
55
zi

. C.
86
55
zi

. D.
86
55
zi

.
Hướng dẫn giải
Chọn A.
Gọi
xyi

có điểm biểu diễn là
;
Mxy
, gt
433
xyi



22
439
xy

do đó tập hợp điểm
M
là đường tròn
C
tâm
4; 3
I
bán kính
3
R
.
Môđun
zOM
nhỏ nhất khi
M
là giao điểm của
C
và đoạn
OI
(gần gốc
O
nhất)
Mà PT đt
:3 4 0
OI x y

(đt qua 2 điểm
0;0
O và
4; 3
I
)
Giải hệ


22
439
34 0
xy
xy


ta được
32
5
24
5
x
y

hay
8
5
6
5
x
y

Tính độ dài
OM
ta chọn
8
5
6
5
x
y

. Vậy
86
55
zi

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 12/22 Mã đề 570
Câu 18: Gọi
H
là hình phẳng giới hạn bởi các đường
tan
0,
4
yx
Ox
xx

. Quay
H
xung quanh trục
Ox
ta được khối tròn xoay có thể tích bằng
A.

1
4
đvtt
. B.

2
4
đvtt
. C.

2
4
đvtt
. D.
2
đvtt
.
Hướng dẫn giải
Chọn A.
Thể tích
4
2
0
tan d
Vxx
=

44
2
00
1tan d d
xx x



=
44
00
tan
xx

=

1
4
đvtt
Câu 19: Nguyên hàm
22
3d
x
Fx x
là
A.

22
3
2ln3
x
Fx C

. B.
22
3ln3
x
Fx C

.
C.
22
3
x
Fx C

. D.

2
3
9
x
Fx C
.
Hướng dẫn giải
Chọn A
Theo công thức tinh nguyên hàm của hàm hợp d
ln
x
x
a
ax
a


Suy ra đáp án
A
đúng.
2
4
6
5
x
y
d
M
I
O
π
2
2
2
x
y
π
4
O
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 13/22 Mã đề 570
Câu 20: Trong không gian với hệ trục
Oxyz
cho hai điểm
1; 2; 3 , 0;1; 5
AB

, gọi
I
là điểm trên
đoạn thẳng
AB
sao cho
2
IA IB
. Giả sử tọa độ của điểm
;;
I abc
thì
abc

bằng
A.
4
. B.
5
. C.
8
3
. D.
17
3
.
Hướng dẫn giải
Chọn C
Vì
I
thuộc đoạn thẳng
AB
và
22
IA IB IA IB


1;2;3
IA a b c


,
;1 ; 5
IB a b c


Vì
2
IA IB


nên ta có hệ:



1
3
12.
4
221
3
325
13
3
a
aa
bbb
cc
c






8
3
abc

.
Câu 21: Tính tích phân
1
0
1
d
23
x
x
bằng
A.
15
ln
23
. B.
13
ln
25
. C.
3
20
. D.
1
ln 2
2
.
Hướng dẫn giải
Chọn A.
Ta có:

1
0
1
11 1 15
dln23 ln5ln3ln
0
232223
xx
x

Câu 22: Nguyên hàm


5
d
32
x
Fx
x
là
A.


4
1
83 2
Fx C
x

. B.


4
1
23 2
Fx C
x

.
C.


4
1
43 2
Fx C
x

. D.


4
1
83 2
Fx C
x

.
Hướng dẫn giải
Chọn D.
Ta có:




 
55 4 4
d3 2
d1 11 1
.
22
32 32 432 832
x
x
Fx C C
xx x x







Câu 23: Nguyên hàm
() 3 1d
Fx x x

là
A.

3
2
() 3 1 .
9
Fx x C

B.

3
1
() 3 1 .
3
Fx x C

C.

3
2
() 3 1 .
3
Fx x C

D.
2
() 3 1 .
9
Fx x C

Hướng dẫn giải
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 14/22 Mã đề 570
Chọn A.
Ta có

3
1
2
3
2
11(31)2
( ) 3 1 (3 1) (3 1) 3 1 .
3
339
2
x
Fx x dx x d x C x C


Câu 24: Trong mặt phẳng phức
, gọi
A
,
B
,
C
lần lượt là ba điểm biểu diễn các số phức
1
34
zi

;
2
52
zi

;
3
13

. Số phức biểu diễn bởi điểm
D
để
ABCD
là hình bình hành là
A.
7
i

. B.
19
i
. C.
19
i
. D.
79
i

.
Hướng dẫn giải
Chọn D.
Ta có
3; 4
A
,
5; 2
B
và
1; 3
C
8; 6 ; 1 ; 3 .
DD
AB DC x y


Tứ giác
ABCD
là hình bình hành khi và chỉ khi:
AB DC
 
18
36
D
D
x
y


7
9
D
D
x
y

. Do đó
7;9
D
.
Vậy số phức biểu diễn bởi điểm
D
để
ABCD
là hình bình hành là:
79
i

Câu 25: Biết

0
24d0
b
xx

. Khi đó
b
nhận giá trị bằng
A.
1
2
b
b
. B.
0
4
b
b
. C.
0
2
b
b
. D.
1
4
b
b
.
Hướng dẫn giải
Chọn B.


22
0
0
0
24d0 4 0 40
4
b
b
b
xx xx bb
b

.
Câu 26: Diện tích hình phẳng giới hạn bởi hai Parabol
2
4
x
y và
2
3
2
x
yx

là
A. 12
ñvtt
. B. 8
ñvtt
. C. 4
ñvtt
. D. 16
ñvtt
.
Hướng dẫn giải
Chọn B.
Phương trình hoành độ giao điểm:
22
0
3
4
42
x
xx
x
x

.
Diện tích hình phẳng giới hạn là
4
22
0
3d
42
xx
Sxx




4
4
223
0
0
33
3 d 8 dvdt
424
xxx
Sx x

 


.
Câu 27: Trong không gian
Ox
yz
cho đường thẳng :
dx y z

, gọi
d
là hình chiếu vuông góc của
d
lên mặt phẳng tọa độ
()
Oyz
. Ta có phương trình
d
là:
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 15/22 Mã đề 570
A.
0
.
2
x
yt
zt
B.
.
xt
yt
zt
C.
0
2.
1
x
yt
zt


D.
0
.
x
yt
zt
Hướng dẫn giải:
Chọn D.
Ta có: phương trình mặt phẳng
(Oyz)
là
0
x
. Gọi
A
là giao của
d
với mặt phẳng
(Oyz)
thì
(0;0;0)
A
Lấy
(1;1;1) (d)
M
. Gọi
H
là hình chiếu vuông góc của
M
lên
(Oyz)
Phương trình
MH
đi qua
(1;1;1)
M và nhận vectơ
(1;0;0)
i
làm pvt.
PT MH
1
1
1
xt
y
z

tọa độ điểm
H
là giao của
()
Oyz
và đường thẳng
MH
nên
(0;1;1)
H
Phương trình
(')
dAH
đi qua
(0;0;0)
A và nhận
(0;1;1)
AH

làm vpt
0
(d') :
x
yt
zt
Câu 28: Tích phân
1
0
d
x
b
Ixexa
e

. Khi đó
2
ab
bằng
A.
5.
B.
6.
C.
7.
D.
3.
Hướng dẫn giải:
Chọn A.
Đặt
xx
u x du dx
dv e dx v e






khi đó:
1
11
00
0
12
|d | 1
xx x
Ixe ex e
ee



Từ đó suy ra:
1; 2
ab

nên
25
ab

.
Câu 29: Phần ảo của số phức
2017
1
1
i
z
i



là
A.
1.
B.
1.
C.
.
i
D.
.
i
Hướng dẫn giải
Chọn C.
Ta có
2017
2017 504.4 1 504.4
1
.1. .
1
i
ziiiiii
i




Câu 30: Cho
9
3
0
1 d
Ix xx

. Đặt
3
1
tx

. Ta có
A.

1
32
2
31 2d.
Ittt

B.

2
33
1
31 d.
Ittt

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 16/22 Mã đề 570
C.

1
33
2
31 d.
Ittt

D.

1
33
2
1d.
Ittt

Hướng dẫn giải
Chọn C.
Đặt
32
3
113dd.
txtxttx

Đổi cận: Với
01, 9 2.
xtxt
 
 
92 1
32 33
3
01 2
1 d 1 ..3d31 d.
Ix xx tttt ttt


Câu 31: Trong không gian với hệ tọa hệ trục
Oxyz
, cho hai đường thẳng
312
:
124
xyz
d


và
:3 1 5
xyz

. Trong bốn đường thẳng
Ox
,
Oy
,
Oz
và
, đường thẳng
d
tạo với
đường thẳng nào một góc lớn nhất?
A.
Oy
. B.
. C.
Ox
. D.
Oz
.
Hướng dẫn giải
Chọn C.
d
có vectơ chỉ phương là
1; 2; 4
d
u

.
Ox
có vectơ chỉ phương là
1; 0; 0
i
và có

.
1
cos ,
21
.
d
d
iu
Ox d
iu



Oy
có vectơ chỉ phương là
0;1;0
j
và có

.
2
cos ,
21
.
d
d
ju
Oy d
ju



Oz
có vectơ chỉ phương là
0; 0;1
k
và có

.
4
cos ,
21
.
d
d
ku
Oz d
ku



có vectơ chỉ phương là
1;1;1
u

và có

.
7
cos ,
3. 21
.
d
d
uu
d
uu



Do đó, đường thẳng
Ox
tạo với
d
một góc lớn nhất.
Câu 32: Tìm tập hợp các điểm biểu diễn số phức
z
, biết số phức
2
z
có điểm biểu diễn nằm trên trục
hoành
A. Đường thẳng
yx
. B. Trục tung và trục hoành.
C. Trục tung. D. Trục hoành.
Hướng dẫn giải
Chọn B.
Đặt
,,zxyixy
. Ta có:
222
2
zxy xy
 có điểm biểu diễn nằm trên trục hoành nên
2
z
là một số thực.
Vậy
0
0
0
x
xy
y

hay tập hợp điểm biểu diễn số phức
z
là trục hoành và trục tung.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 17/22 Mã đề 570
Câu 33: Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
:3 4 5 10 0
Pxyz

và đường
thẳng
d
đi qua 2 điểm
1; 0; 2
M
,
3; 2; 0
N
. Gọi
là góc giữa đường thẳng
d
và mặt
phẳng
P
. Ta có
A.
90

. B.
45

. C.
60

. D.
30

.
Hướng dẫn giải.
Chọn C.
Mặt phẳng
P
có vectơ pháp tuyến là
3; 4; 5
n

.
Đường thẳng đi qua 2 điểm
,
MN
có vec tơ chỉ phương là
4;2; 2
uMN


.
Ta có:

222222
.
3.4 4.2 5 2
3
Sin
2
.
345.422
nu
nu


 


60

Câu 34: Nguyên hàm
3
.d
x
Fx xe x
là
A.
3
1.
x
Fx x e C

. B.
32
.
x
Fx xe x C

.
C.

33
11
.
39
xx
Fx xe e C

. D.

33
11
.
39
xx
Fx xe e C

.
Hướng dẫn giải.
Chọn C.
Đặt
3
3
dd
1
dd
3
x
x
ux
ux
ve
ue x

Khi đó:
3
.d
x
Fx xe x
33 33
1111
.. ..
3339
xx xx
xe e dx xe e C
 
Câu 35: Phương trình
2
(1 ) 18 13 0
ziz i

có hai nghiệm là
A.
4;52
ii

. B.
4;52
ii

. C.
4;52
ii

. D.
4;52
ii

.
Hướng dẫn giải
Chọn B

2
2
(1 ) 4 18 13 9 3
iii

Phương trình đã cho có hai nghiệm phức là

193
4
2
193
52
2
ii
xi
ii
xi




.
Câu 36: Trong không gian với hệ trục tọa độ
Oxyz
, cho hai mặt phẳng
:30
Pxz

và
:2 2 3 0
Qyz

. Ta có góc giữa hai mặt phẳng
P
và
Q
bằng
A.
2
. B.
4
. C.
3
. D.
6
.
Hướng dẫn giải
ChọnC
Mặt phẳng
P
có một vectơ pháp tuyến là
1; 0; 1
P
n

.
Mặt phẳng
Q
có một vectơ pháp tuyến là
0; 2; 2
Q
n

.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 18/22 Mã đề 570


.
1.0 0.2 1.2
1
cos ,
2
114 4
PQ
PQ
nn
PQ
nn





Vậy góc giữa hai mặt phẳng
P
và
Q
bằng
3
Câu 37: Trong không gian với hệ trục
Oxyz
, cho hai điểm
1; 2; 5
A
,
1; 5; 5
B
.
Tìm điểm
COz
sao
cho tam giác
ABC
có diện tích nhỏ nhất?
A.
0;0;6
C
. B.
0; 0;5
C
. C.
0;0;4
C
. D.
0;0;2
C
.
Hướng dẫn giải
Chọn B.
Do điểm


1; 2; 5
0;0;
1; 5; 5
CA t
COz C t
CB t




Ta có

,35;25;7
CA CB t t



 

2
11 7
,13549
22 2
ABC
SCACB t




.
Vậy tam giác
ABC
có diện tích nhỏ nhất bằng
7
2
, đạt khi
5 0;0;5
tC
Câu 38: Nguyên hàm của hàm số

4
3
d
x
Fx xe x
là
A.

4
4
4
x
xe
Fx C

. B.

4
4
x
xe
Fx C

.
C.

4
1
4
x
Fx e C

. D.

4
4
x
e
Fx C

.
Hướng dẫn giải
Chọn C.
Ta đặt
433
1
d4d d d
4
tx t xxxx t
  

4 4
3
11 1
dd
44 4
xtt x
Fx xe x et e C e C



Câu 39: Trong không gian với hệ trục
Oxyz
cho hai điểm
3;1;1
A
,
2; 1; 4
B

. Hãy viết phương
trình mặt phẳng
P
đi qua
A
,
B
và vuông góc với mặt phẳng
:2 3 4 0
Qxyz
 
.
A.
513 290
xyz

. B.
13 5 5 0
xyz

.
C.
13 5 3 0
xyz

. D.
312 220
xyz

.
Hướng dẫn giải
Chọn B.
Ta có
1; 2; 5
AB


, VTPT của
Q
là

2; 1; 3
Q
n


.
VTPT của
P
là


,1;13;5
Q
nABn




.
Phương trình mp
:1 3 13 1 5 1 0 13 5 5 0
Px y z xyz

.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 19/22 Mã đề 570
Câu 40: Cho
ln 2
0
1d
x
Iexa
b

. Khi đó
A.
ab
. B.
ab
. C.
1
ab
. D.
ab
.
Hướng dẫn giải
Chọn B.
Đặt
22
2
2d 2d
111d2dd
1
xxxx
x
tt tt
te te et extt x
et

.
Đổi cận:
00
xt

,
ln 2 1
xt

.
Khi đó
11 1
2
22 2
00 0
11
2d21 d22d22
11 1
t
It t tJ
tt t






.
Tính
1
2
0
1
d
1
Jt
t
.
Đặt
2
tan d 1 tan d
tut uu
 .
Đổi cận:
00
tu

,
1
4
tu

.
Khi đó

2
44
2
00
1tan d
d
1tan 4
uu
Ju
u



.
Vậy
22 2 2
42
Iab

 
.
Câu 41: Cho mặt phẳng
:30
Pxyz

và điểm
1; 2; 3
A
, hình chiếu vuông góc của
A
lên
P
có tọa độ là
A.
1;1; 2
. B.
0;1; 2
. C.
1; 2; 0
. D.
2;1; 0
.
Hướng dẫn giải
Chọn B.
Phương trình đường thẳng
d
đi qua
A
và
P
là:

1
2,
3
xt
ytt
zt



Gọi
H
là hình chiếu vuông góc của
A
lên
P

1;2;3
0;1; 2
30
1
HHH
Htt t H
Hd P
xyz
t







Câu 42: Cho
z
,
12 74
zi i

. Khi đó
21
z
là
A.
65
. B.
61
. C.
8
. D.
5
.
Hướng dẫn giải
Chọn A.
Ta có:

74
12 74 32
12
i
zi iz i
i

. Vậy
32
zi

Khi đó

22
21232 174 74 65
zii 
Câu 43: Cho
0
a
và
1,
aC
là hằng số. Phát biểu nào sau đây đúng?
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 20/22 Mã đề 570
A.
22
dln.
xx
axa aC

B.
22
d.
xx
axa C

C.
dln.
xx
axa aC

D.
2
2
d.
2ln
x
x
a
ax C
a

Hướng dẫn giải
Chọn D
Ta có

2
22
11
2.
22ln
x
xx
a
adx ad x C
a


và
.
ln
x
x
a
adx C
a

Câu 44: Cho
fx
là một hàm số liên tục trên
thỏa mãn

1
0
d3
ft t
và

1
1
d2.
fu u

Khi đó

0
1
d
fx x
bằng ?
A.
5.
B. 5. C. 1. D.
1.
Hướng dẫn giải
Chọn A
Ta có
 
11 0
00 1
d3 d3 d 3.
ft t fx x fx x
 

Lại có
 
11
11
d2 d2
fu u fx x

 

  
10 0
11 1
dd235 d5.
fx x fx x fx x

  

Câu 45: Cho mặt cầu
222
: 4240
Sx yz x y z

. Viết phương trình mặt phẳng tiếp xúc với mặt
cầu tại điểm
1; 1; 0
M
.
A.
2230
xyz

. B.
2210
xyz

. C.
0
xy

. D.
210
xy

.
Hướng dẫn giải
Chọn B.
Ta có: Mặt cầu
S
có tâm
2;1; 2
I
. Mặt phẳng
tiếp xúc với mặt cầu
S
tại
1; 1; 0
M
qua
1; 1; 0
M
và nhận
1; 2; 2
MI


làm vectơ pháp tuyến.
Phương trình mặt phẳng
:2210
xyz

.
Câu 46: Nguyên hàm

2
21
d
2
xx
Fx x
x

là
A.

2
47ln 2
2
x
Fx x x C

. B.
2
4ln 2
Fx x x x C

.
C.
2
2ln 2
Fx x x x C

. D.
2
47ln 2
Fx x x x C

.
Hướng dẫn giải
Chọn A.
Ta có:

22
21 7
d4d47ln2
222
xx x
Fx x x x x x C
xx







.
Câu 47: Trong không gian
Oxyz
cho điểm
1; 1; 1 , 3; 5; 7
AB
. Gọi
S
là tập hợp điểm
;;
Mxyz
thoả mãn
222
MA MB AB

. Chọn kết luận đúng
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 21/22 Mã đề 570
A.
S
là mặt cầu có phương trình

222
13456
xyz

.
B.
S
là mặt phẳng trung trực của đoạn
AB
.
C.
S
là mặt cầu có phương trình

222
23414
xyz

.
D.
S
là đường tròn có phương trình

222
13414
xyz

.
Hướng dẫn giải
Chọn C.
Ta có
222
MA MB AB MAB
 vuông tại
M
(định lí đảo Pitago).
Suy ra tập hợp điểm
M
là mặt cầu tâm
I
đường kính
AB
(với
I
là trung điểm
AB
).

2; 4; 6 2 14 14
AB AB R

và
2; 3; 4
I
.
Vậy mặt cầu là

222
:2 3 414
Sx y z

.
Câu 48: Nguyên hàm

sin
d
32cos
x
Fx x
x
là
A.

1
ln 3 2cos
3
Fx x C

. B.

1
ln 3 2cos
2
Fx x C

.
C.

1
ln 3 2cos
3
Fx x C

. D.

1
ln 3 2cos
2
Fx x C

.
Hướng dẫn giải
Chọn B.

d3 2cos
sin 1 1
dln32cos
32cos 2 32cos 2
x
x
Fx x x C
xx



.
Câu 49: Cho
4
2
1
11
d
a
xx
xb
x




với
a
b
là phân số tối giản. Khi đó
ab
bằng
A.
140
. B.
39
. C.
9
. D.
31
.
Hướng dẫn giải
Cho n D
Ta có:
4
4
2
2
1
1
11 1 35
d2
24
x
xxx
xx
x







Suy ra:
35
31
4
a
ab
b

Câu 50: Diện tích của hình phẳng
H
giới hạn bởi
2
20
0
yyx
xy


bằng
A.
27
2
đvdt. B.
27
4
đvdt. C.
9
2
đvdt. D.
9
4
đvdt.
Hướng dẫn giải
Chọn C
Ta có:
22
20 2
0
yyx xyy
xy x y





Phương trình tung độ giao điểm:
22
0
230
3
y
yyyyy
y

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Trang 22/22 Mã đề 570
Diện tích hình phẳng cần tìm là:
 
3
333
3
22 22
000
0
39
2d 3d 3 d
232
y
Syyyyyyyyyyy





.
| 1/22
| | Tải xuống

Có thể bạn quan tâm:

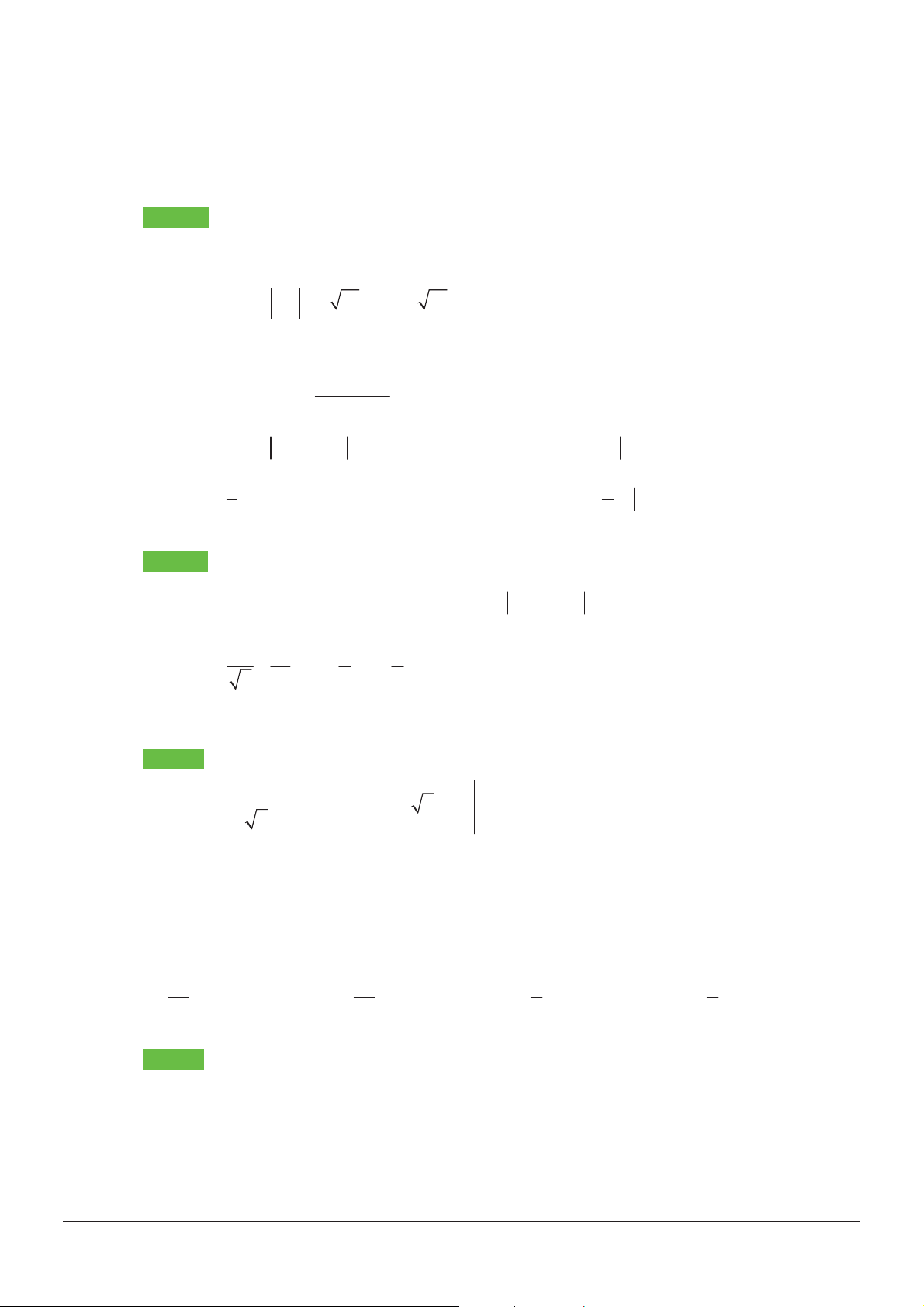
Preview text:

SỞ GD-ĐT HÀ NỘI
ĐỀ KIỂM TRA HỌC KÌ II
TRƯỜNG THPT VIỆT ĐỨC
MÔN TOÁN – LỚP 12
Năm học: 2016 – 2017
(Đề thi gồm có 06 trang)
Thời gian làm bài: 90 phút, không kể thời gian phát đề Mã đề 570
Câu 1: Giải bài toán tính diện tích hình phẳng giới hạn bởi các đường y  2 , x
y e , x  1 . Bốn bạn
An, Bảo, Cần và Dũng cho 4 công thức khác nhau. Hãy chọn công thức đúng 1 ln 2
A. Cần   2 x Se dx . B. Bảo    x S e  2dx . ln 2 1 ln 2 1 C. Dũng x S e  2 dx  . D. An    x S e  2dx . 1 ln 2    3
Câu 2: Tìm nguyên hàm F x của hàm số f x  2sin 3 .
x sin 5x thỏa F     4  2 1 1
A. F x  2sin 2x  sin8x  3 .
B. F x  2sin 2x  sin8x 1. 4 4 1 1
C. F x  4sin 2x  sin8x  2 .
D. F x  4sin 2x  sin8x 1. 8 8
Câu 3: Nguyên hàm F x 3  cot x dx  là 1 1
A. F x 2
  cot x  ln sin x C .
B. F x 2
  cot x  ln sin x C . 2 2 1 1
C. F x 2
 cot x  ln sin x C .
D. F x 2
  cot x  ln cos x C . 2 2
Câu 4: Cho hai đường thẳng gồm d có phương trình x y z , d có phương trình x y 1  z 1.
Ta có khoảng cách giữa d và d bằng A. 1. B. 2 . C. 2 . D. 3 .
Câu 5: Thể tích V khi quay E 2 2
: x  4y  4  0 quanh trục Ox bằng 8 4 16 A. . B. 4 . C. . D. . 3 3 3 Câu 6:
Viết phương trình mặt cầu S  đi qua hai điểm A3;1; 2
 , B1;1;2 và có tâm thuộc trục Oz .
A. x y   z  2 2 2 1  10. B. 2 2 2
x y z  2z 10  0.
C. x y   z  2 2 2 1  12. D. 2 2 2
x y z  2z 10  0.  4 a a
Câu 7: Giả sử I  sin 3x sin 2x dx  2 
, với là phân số tối giản. Ta có giá trị của a b là b b 0 A. 8 . B. 15 . C. 10 . D. 13 .
Câu 8: Tập hợp các điểm trong mặt phẳng phức biểu diễn số phức z thỏa mãn điều kiện z i  1 là
A. Một đường tròn.
B. Hai đường thẳng. C. Hai đường tròn.
D. Một đường thẳng.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 1/22 Mã đề 570
Câu 9: Trong không gian với hệ trục tọa độ Oxyz, cho hình chóp tứ giác đều S.ABCD, đáy ABCD là  2 
hình vuông nằm trong mặt phẳng Oxy, AC DB O (O là gốc tọa độ), A  ;0;0,  đỉnh 2   
S 0;0;9. Ta có thể tích khối chóp S.ABCD bằng A. 3 (đvtt). B. 3 2 (đvtt). C. 4 (đvtt). D. 9 (đvtt). 9 3
Câu 10: Biết rằng f x là một hàm số liên tục trên  và f
 xdx  9. Khi đó giá trị của f 3xdx  là 0 0 A. 3 . B. 2 . C. 4 . D. 1.
Câu 11: Cho số phức z a bi a, b  . Ta có phần ảo của số phức 2
z  2z  4i bằng
A. ab b  2 .
B. 2ab  2b  4 .
C. 2ab  2b  4 .
D. 2ab  2b  4 .
Câu 12: Trên mặt phẳng phức, M và N là các điểm biểu diễn của z , z , trong đó z , z là hai nghiệm 1 2 1 2 của phương trình 2
z  4z 13  0 . Độ dài MN là A. 12. B. 4 . C. 6 . D. 8 .
Câu 13: Trong không gian Oxyz , cho tam giác ABC có A5;0;0 , B1;1;  1 , C  3;  3;4 . Mặt phẳng
P đi qua A, B và cách C một khoảng bằng 2 có phương trình là
A. x  2y  2z  5  0 .
B. x  2y  2z  5  0 .
C. x  2y  2z  5  0 .
D. x  2y  2z  5  0 .
Câu 14: Tìm số phức liên hợp của số phức z  2i 2  3i .
A. z  6  4i .
B. z  6  4i .
C. z  6  4i .
D. z  6  4i .
Câu 15: Trong không gian Oxyz cho các điểm A1;1;  1 , B2;0;  1 , C 1;2; 
1 , D là điểm sao cho
ABCD là hình bình hành. Ta có tọa độ D là A. D 2; 3  ;3.
B. D 2;3;3. C. D 2;3; 3  .
D. D 2;3; 3  . 4
Câu 16: Nếu f  
1  12 , f x liên tục và f
 xdx 17. Giá trị của f 4 bằng 1 A. 9. B. 5. C. 29. D. 19.
Câu 17: Cho số phức z   thoả z  4  3i  3 . Tìm số phức z có môđun nhỏ nhất? 8 6 8 6 8 6 8 6
A. z   i .
B. z    i .
C. z   i .
D. z    i . 5 5 5 5 5 5 5 5 y  tan x
Câu 18: Gọi  H  là hình phẳng giới hạn bởi các đường Ox 
. Quay  H  xung quanh trục Ox    x  0, x   4
ta được khối tròn xoay có thể tích bằng  2  2 
A. 1 đvtt  . B.  đvtt  . C.   đvtt . D. 2  đvtt  . 4 4 4
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 2/22 Mã đề 570
Câu 19: Nguyên hàm F x 2 x2  3 dx  là 2 x2 3
A. F x   C .
B. F x 2x2  3 ln 3  C . 2ln 3 2 3 x C.   2 2  3 x F xC .
D. F x   C . 9
Câu 20: Trong không gian với hệ trục Oxyz cho hai điểm A1;2;3, B 0;1; 5
  , gọi I là điểm trên
đoạn thẳng AB sao cho IA  2IB . Giả sử tọa độ của điểm I  ; a ;
b c thì a b c bằng 8 17 A. 4  . B. 5 . C.  . D.  . 3 3 1 1
Câu 21: Tính tích phân dx  bằng 2x  3 0 1 5 1 3 3 1 A. ln . B. ln . C. . D. ln 2 . 2 3 2 5 20 2 dx
Câu 22: Nguyên hàm F x   là 3 2x5 1 1
A. F x    C .
B. F x   C . 83 2x4 23 2x4 1 1
C. F x    C .
D. F x   C . 43  2x4 83 2x4
Câu 23: Nguyên hàm F x  3x 1dx  là 2 1
A. F x  3x  3 1  C.
B. F x  3x  3 1  C. 9 3 2
C. F x  3x  3 1  C.
D. F x 2  3x 1  C. 3 9
Câu 24: Trong mặt phẳng phức  , gọi A , B , C lần lượt là ba điểm biểu diễn các số phức z  3  4i ; 1
z  5  2i ; z  1 3i . Số phức biểu diễn bởi điểm D 2 3
để ABCD là hình bình hành là A. 7  i . B. 1 9i . C. 1 9i .
D. 7  9i . b
Câu 25: Biết 2x  4dx  0 . Khi đó b nhận giá trị bằng 0 b 1 b  0 b  0 b 1 A.  . B.  . C.  . D.  . b  2 b  4 b  2 b  4 2 x 2 x
Câu 26: Diện tích hình phẳng giới hạn bởi hai Parabol y  và y    3x là 4 2 A. 12 ñvtt . B. 8ñvtt . C. 4 ñvtt . D. 16 ñvtt .
Câu 27: Trong không gian Oxyz cho đường thẳng d : x y z , gọi d là hình chiếu vuông góc của d
lên mặt phẳng tọa độ Oyz . Ta có phương trình d là: x  0 x tx  0 x  0    
A. y t .
B. y t.
C. y  2  t.
D. y t . z  2t     z tz  1 tz t
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 3/22 Mã đề 570 1  b Câu 28: Tích phân x
I xe dx a  
. Khi đó a  2b bằng e 0 A. 5. B. 6. C. 7. D. 3. 2017 1 i
Câu 29: Phần ảo của số phức z    là 1 i A. 1. B. 1. C. .i D. .i  9 Câu 30: Cho 3
I x 1 x dx  . Đặt 3
t  1 x . Ta có 0 1 2
A. I  3  3 1 t  2 2t dt. B. I  3 3
1 t  3tdt. 2 1 1 1
C. I  3  3
1 t  3tdt.
D. I    3
1 t  3tdt. 2 2 x  3 y 1 z  2
Câu 31: Trong không gian với hệ tọa hệ trục Oxyz , cho hai đường thẳng d :   và 1 2 4
 : x  3  y 1  z  5. Trong bốn đường thẳng Ox , Oy , Oz và  , đường thẳng d tạo với
đường thẳng nào một góc lớn nhất? A. Oy . B.  . C. Ox . D. Oz .
Câu 32: Tìm tập hợp các điểm biểu diễn số phức z , biết số phức 2
z có điểm biểu diễn nằm trên trục hoành
A. Đường thẳng y x .
B. Trục tung và trục hoành. C. Trục tung. D. Trục hoành.
Câu 33: Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng P :3x  4y  5z 10  0 và đường
thẳng d đi qua 2 điểm M 1;0;2 , N 3;2;0 . Gọi  là góc giữa đường thẳng d và mặt
phẳng P . Ta có A.   90 . B.   45. C.   60 . D.   30 .
Câu 34: Nguyên hàm   3  . x F x x e dx  là
A.       3 1 . x F x x e C . B.   3 2  . x F x
x e x C . 1 1 x 1 x 1 C.   3 3  . x F x
x e e C . D.   3 3  . x F x
x e e C . 3 9 3 9
Câu 35: Phương trình 2
z  1 iz 18 13i  0 có hai nghiệm là
A. 4  i;  5  2i .
B. 4  i;  5  2i .
C. 4  i; 5  2i .
D. 4  i; 5  2i .
Câu 36: Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt phẳng P : x z  3  0 và
Q: 2y  2z  3  0. Ta có góc giữa hai mặt phẳng P và Q bằng     A. . B. . C. . D. . 2 4 3 6
Câu 37: Trong không gian với hệ trục Oxyz , cho hai điểm A1;2;5 , B 1;  5;5 . Tìm điểm  C Oz
sao cho tam giác ABC có diện tích nhỏ nhất? A. C 0;0;6 .
B. C 0;0;5.
C. C 0;0;4 .
D. C 0;0;2 .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 4/22 Mã đề 570
Câu 38: Nguyên hàm của hàm số   4 3 x
F x x e dx  là 4 4  x x e 4 x xe
A. F x    C .
B. F x    C . 4 4 1 4 x e C.   4  x F x   eC .
D. F x   C . 4 4
Câu 39: Trong không gian với hệ trục Oxyz cho hai điểm A3;1;  1 , B 2;1; 4  . Hãy viết phương
trình mặt phẳng P đi qua A , B và vuông góc với mặt phẳng Q : 2x y  3z  4  0.
A. 5x 13y z  29  0 .
B. x 13y  5z  5  0 .
C. x 13y  5z  3  0 .
D. 3x 12y  2z  2  0 . ln 2  Câu 40: Cho x I
e 1 dx a   . Khi đó b 0
A. a b .
B. a b . C. ab  1.
D. a b .
Câu 41: Cho mặt phẳng P : x y z  3  0 và điểm A1;2; 3
  , hình chiếu vuông góc của A lên
P có tọa độ là A. 1;1;2 . B. 0;1; 2   . C. 1;2;0 . D. 2;1;0 .
Câu 42: Cho z   , z 1 2i  7  4i . Khi đó 2z 1 là A. 65 . B. 61 . C. 8 . D. 5 .
Câu 43: Cho a  0 và a  1, C là hằng số. Phát biểu nào sau đây đúng? A. 2x 2 d x a
x a ln a C.  B. 2x 2 d x a
x a C.  2 x a C. x d x
a x a ln a C.  D. 2x a dx   C.  2ln a 1 1
Câu 44: Cho f x là một hàm số liên tục trên  thỏa mãn f
 tdt  3 và f
 udu  2. Khi đó 0 1 0 f
 xdx bằng ? 1 A. 5. B. 5. C. 1. D. 1.
Câu 45: Cho mặt cầu S  2 2 2
: x y z  4x  2y  4z  0 . Viết phương trình mặt phẳng tiếp xúc với mặt
cầu tại điểm M 1; 1;  0.
A. x  2y  2z  3  0 .
B. x  2y  2z 1  0 .
C. x y  0 .
D. 2x y 1  0 . 2 x  2x 1
Câu 46: Nguyên hàm F x  dx  là x  2 2 x
A. F x 
 4x  7ln x  2  C .
B. F x   2
x  4xln x  2  C . 2
C. F x 2
x  2x  ln x  2  C .
D. F x 2
x  4x  7ln x  2  C .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 5/22 Mã đề 570
Câu 47: Trong không gian Oxyz cho điểm A1; 1; 
1 , B 3; 5; 7 . Gọi S  là tập hợp điểm M  ;
x y; z thoả mãn 2 2 2
MA MB AB . Chọn kết luận đúng
A. S  là mặt cầu có phương trình  x  2   y  2  z  2 1 3 4  56 .
B. S  là mặt phẳng trung trực của đoạn AB .
C. S  là mặt cầu có phương trình  x  2   y  2  z  2 2 3 4  14 .
D. S  là đường tròn có phương trình  x  2   y  2   z  2 1 3 4  14 . x
Câu 48: Nguyên hàm F x sin  dx  là 3  2cos x
A. F x 1
  ln 3  2cos x C .
B. F x 1
 ln 3 2cos x C . 3 2
C. F x 1
 ln 3 2cos x C .
D. F x 1
  ln 3 2cos x C . 3 2 4  1 1  a a Câu 49: Cho x   dx  
với là phân số tối giản. Khi đó a b bằng 2   x x b b 1 A. 140 . B. 39 . C. 9 . D. 31. 2
y  2y x  0
Câu 50: Diện tích của hình phẳng H  giới hạn bởi  bằng x y  0 27 27 9 9 A. đvdt. B. đvdt. C. đvdt. D. đvdt. 2 4 2 4
----------HẾT----------
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 6/22 Mã đề 570
BẢNG ĐÁP ÁN - HKII – LỚP 12 - TRƯỜNG THPT VIỆT ĐỨC – HÀ NỘI
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D D B C A D D A A A B C B B C C A A A C A D A D B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B D A C C C B C C B C B C B B B A D A B A C B D C HƯỚNG DẪN GIẢI
Câu 1: Giải bài toán tính diện tích hình phẳng giới hạn bởi các đường y  2 , x
y e , x  1 . Bốn bạn
An, Bảo, Cần và Dũng cho 4 công thức khác nhau. Hãy chọn công thức đúng 1 ln 2 A. Cần  (2 x Se )dx  . B. Bảo  ( x S e  2)dx  . ln 2 1 ln 2 1 C. Dũng x S e  2 dx  . D. An  ( x S e  2)dx  . 1 ln 2
Hướng dẫn giải Chọn D. 1 Ta có: x
e  2  x  ln 2 . Do đó diện tích cần tìm là  ( x S e  2)dx  (vì x
e  2 khi x  ln 2 ). ln 2    3
Câu 2: Tìm nguyên hàm F(x) của hàm số f (x)  2sin 3 .
x sin 5x thỏa F     4  2 1 1
A. F(x)  2sin 2x  sin 8x  3.
B. F(x)  2sin 2x  sin8x 1. 4 4 1 1
C. F(x)  4sin 2x  sin 8x  2.
D. F(x)  4sin 2x  sin 8x 1. 8 8
Hướng dẫn giải Chọn D. 1   
Ta có F '(x)   4sin 2x sin8x 1  cos 2x  cos8x  2sin 5 .xsin 3x  .  8     3 Và F    .  4  2
Câu 3: Nguyên hàm F x 3  cot x dx  là 1 1
A. F x 2
  cot x  ln sin x C .
B. F x 2
  cot x  ln sin x C . 2 2 1 1
C. F x 2
 cot x  ln sin x C .
D. F x 2   cot x  ln o
c sx C . 2 2 Hướng dẫn giải Chọn B.   1 F x 1 3  cot d x x  1 cot d x x    cot d x x  cot d x x   2   sin x  2 sin x 1 cos x  1 1 cot d x x  dx     cot d x cotx  d   sin x 2
  cot x  ln sin x C . 2 sin x sin x sin x 2
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 7/22 Mã đề 570
Câu 4: Cho hai đường thẳng gồm d có phương trình x y z , d có phương trình x y 1  z 1.
Ta có khoảng cách giữa d và d bằng A. 1. B. 2 . C. 2 . D. 3 . Hướng dẫn giải Chọn C.
d : x y z qua O 0;0;0 và có VTCP a  1;1;  1 . 
d : x y 1  z 1 qua A0;1; 
1 có VTCP a  1;1;  1 .    OA  0;1;  1 ;  ;
OA a  2;1;  1   .    ; OA a 2   2 1     2 2 1
O d   d //d  d d; d  d O; d     2 . 2 2 2 a 1 1 1
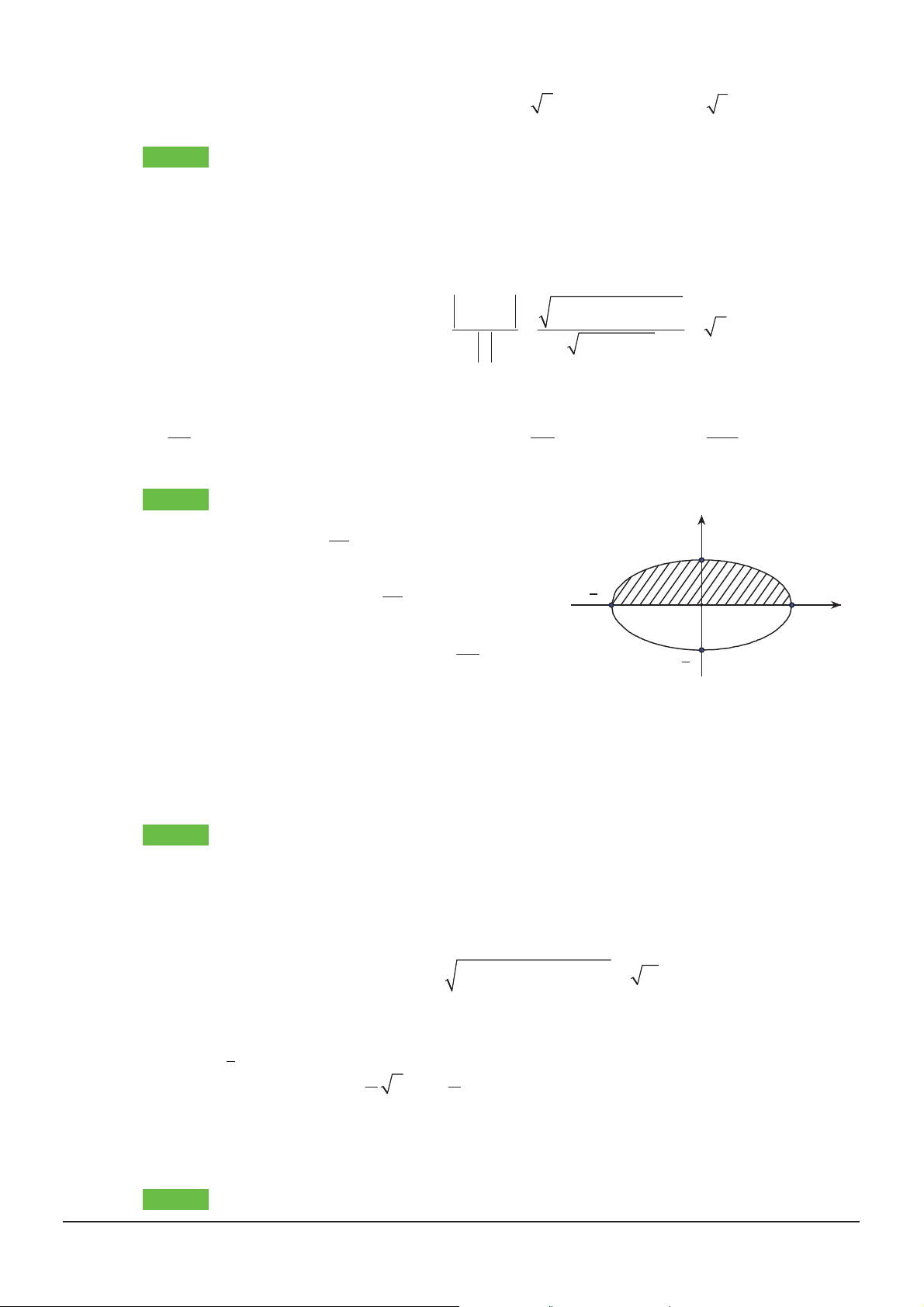
Câu 5: Thể tích V khi quay E 2 2
: x  4y  4  0 quanh trục Ox bằng 8 4 16 A. . B. 4 . C. . D. . 3 3 3 Hướng dẫn giải Chọn A. 2 yEx 2 2 2
: x  4 y  4  0   y  1. 4 1 2 2 2  x  Thể tích 2
V   y dx     1 d .x 2 4 2 2   O 2 x 8
Bấm máy tính tích phân này, ta được V  . 3 1 Câu 6:
Viết phương trình mặt cầu S  đi qua hai điểm A3;1; 2
 , B1;1;2 và có tâm thuộc trục Oz
A. x y   z  2 2 2 1  10. B. 2 2 2
x y z  2z 10  0.
C. x y   z  2 2 2 1  12. D. 2 2 2
x y z  2z 10  0. Hướng dẫn giải Chọn D.
Gọi I 0;0;cOz là tâm của mặt cầu S  . S qua 2 2 ,
A B IA IB IA IB
  2    c2      c2 2 2 2 3 1 2 1 1 2  c  1  .
Vậy, tâm I 0;0; 
1 ; bán kính R IA
  2    2 3 3 1 2 1  11 .
Phương trình mặt cầu S x y   z  2 2 2 2 2 2 :
1  11  x y z  2z 10  0.  4 a a
Câu 7: Giả sử I  sin 3x sin 2x dx  2 
, với là phân số tối giản. Ta có giá trị của a b là b b 0 A. 8 . B. 15 . C. 10 . D. 13 .
Hướng dẫn giải Cho ̣ n D.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 8/22 Mã đề 570   4 4 1
Ta có: I  sin 3x sin 2 d x x  
cos xcos5xdx 2 0 0  4 1  1  1   1 5  3 2  sin x  sin 5x  sin  sin      . 2  5  2  4 5 4  10 0
Vậy ta có: a  3, b  10 nên a b 13 .
Câu 8: Tập hợp các điểm trong mặt phẳng phức biểu diễn số phức z thỏa mãn điều kiện z i  1 là
A. Một đường tròn.
B. Hai đường thẳng. C. Hai đường tròn.
D. Một đường thẳng.
Hướng dẫn giải Cho ̣ n A.
Đặt z x yi với x, y   .
Ta có: z i   x yi i   x   y  2   x   y  2 2 2 1 1 1 1 1  1 .
Vậy tập hợp điểm biểu diễn số phức z là đường tròn tâm I 0; 
1 , bán kính là R  1 .
Câu 9: Trong không gian với hệ trục tọa độ Oxyz, cho hình chóp tứ giác đều S.ABCD, đáy ABCD là  2 
hình vuông nằm trong mặt phẳng Oxy, AC DB O (O là gốc tọa độ), A  ;0;0,  đỉnh 2   
S 0;0;9. Ta có thể tích khối chóp S.ABCD bằng A. 3 (đvtt). B. 3 2 (đvtt). C. 4 (đvtt). D. 9 (đvtt).
Hướng dẫn giải Chọn A.
Ta có: SO là đường cao của khối chóp. SO  9 . 2 AO   2 AB AO 2  . 2  1. 2 2 1 1 Vậy V  .S . O S  .9.1  3 (đvtt). S .ABCD 3 ABCD 3 9 3
Câu 10: Biết rằng f x là một hàm số liên tục trên  và f
 xdx  9. Khi đó giá trị của f 3xdx  là 0 0 A. 3 . B. 2 . C. 4 . D. 1.
Hướng dẫn giải Chọn A. 3 I f  3xdx. 0
Đặt 3x t  3dx  dt .
Đổi cận: x  0  t  0 .
x  3  t  9 .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 9/22 Mã đề 570 9 9  f  t dt 1 .  f
 tdt  3. 3 3 0 0
Câu 11: Cho số phức z a bi a, b  . Ta có phần ảo của số phức 2
z  2z  4i bằng
A. ab b  2 .
B. 2ab  2b  4 .
C. 2ab  2b  4 .
D. 2ab  2b  4 . Hướng dẫn giải. Chọn B.
Ta có: z z i  a bi2 2
 a bi 2 2 2 4 2
 4i a b  2abi  2a  2bi  4i   2 2
a b  2a  2ab  2b  4i . Vậy phần ảo là 2ab  2b  4.
Câu 12: Trên mặt phẳng phức, M và N là các điểm biểu diễn của z , z , trong đó z , z là hai nghiệm 1 2 1 2 của phương trình 2
z  4z 13  0 . Độ dài MN là A. 12. B. 4 . C. 6 . D. 8 . Hướng dẫn giải. Chọn C. z  2   3i 2
z  4z 13  0  
. Giả sử M và N có toạ độ là M  2;  3, N  2  ;  3 z  2  3i  
MN 0;  6  MN  6 .
Câu 13: Trong không gian Oxyz , cho tam giác ABC có A5;0;0 , B1;1;  1 , C  3;  3;4 . Mặt phẳng
P đi qua A, B và cách C một khoảng bằng 2 có phương trình là
A. x  2y  2z  5  0 . B. x  2y  2z  5  0 . C. x  2y  2z  5  0 . D. x  2y  2z  5  0 . Hướng dẫn giải: Chọn B.
Gọi P : Ax By Cz D  0 với 2 2 2
A B C  0 . 5
A D  0 D  5A Ta có: ,
A B P nên    
A B C D  0
B C  4A 3
A  3B  4C D
Mà d C,P  2 
 2  7C  20A  2 A C  C  4A2 2 2 2 2 2
A B CC  2A 2
 332A  248A  41  0  166   A  41C  0
+ Với C  2A , chọn A  1, C  2 nên B  2, D  5
  P : x  2y  2z 5  0
+ Với 166 A  41C  0 , chọn C 166, A  41 nên B  2, D  205 
 P : 41x  2y 166z  205
Câu 14: Tìm số phức liên hợp của số phức z  2i 2  3i .
A. z  6  4i .
B. z  6  4i .
C. z  6  4i .
D. z  6  4i . Hướng dẫn giải: Chọn B.
z  2i 2  3i  6  4i z  6  4i
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 10/22 Mã đề 570
Câu 15: Trong không gian Oxyz cho các điểm A1;1;  1 , B2;0;  1 , C 1;2; 
1 , D là điểm sao cho
ABCD là hình bình hành. Ta có tọa độ D là A. D 2; 3  ;3.
B. D 2;3;3. C. D 2;3; 3  .
D. D 2;3; 3  . Hướng dẫn giải Chọn C.
Ta có ABCD là hình bình hành nên
x x x x 2 1  1 xx  2 B A C D D D     
AB DC  y y y y  0 1  2  y
 y  3  DB A C D D D 2;3; 3.
z z z z        zz   B A C D 1    1 1 3 DD 4
Câu 16: Nếu f  
1  12 , f x liên tục và f
 xdx 17. Giá trị của f 4 bằng 1 A. 9. B. 5. C. 29. D. 19. Hướng dẫn giải Chọn C 4 4 Ta có / 17  f
 xdx f x  f 4 f  1 f 4 14 f  1 1712  29. 1 1
Câu 17: Cho số phức z   thoả z  4  3i  3 . Tìm số phức z có môđun nhỏ nhất? 8 6 8 6 8 6 8 6
A. z   i .
B. z    i .
C. z   i .
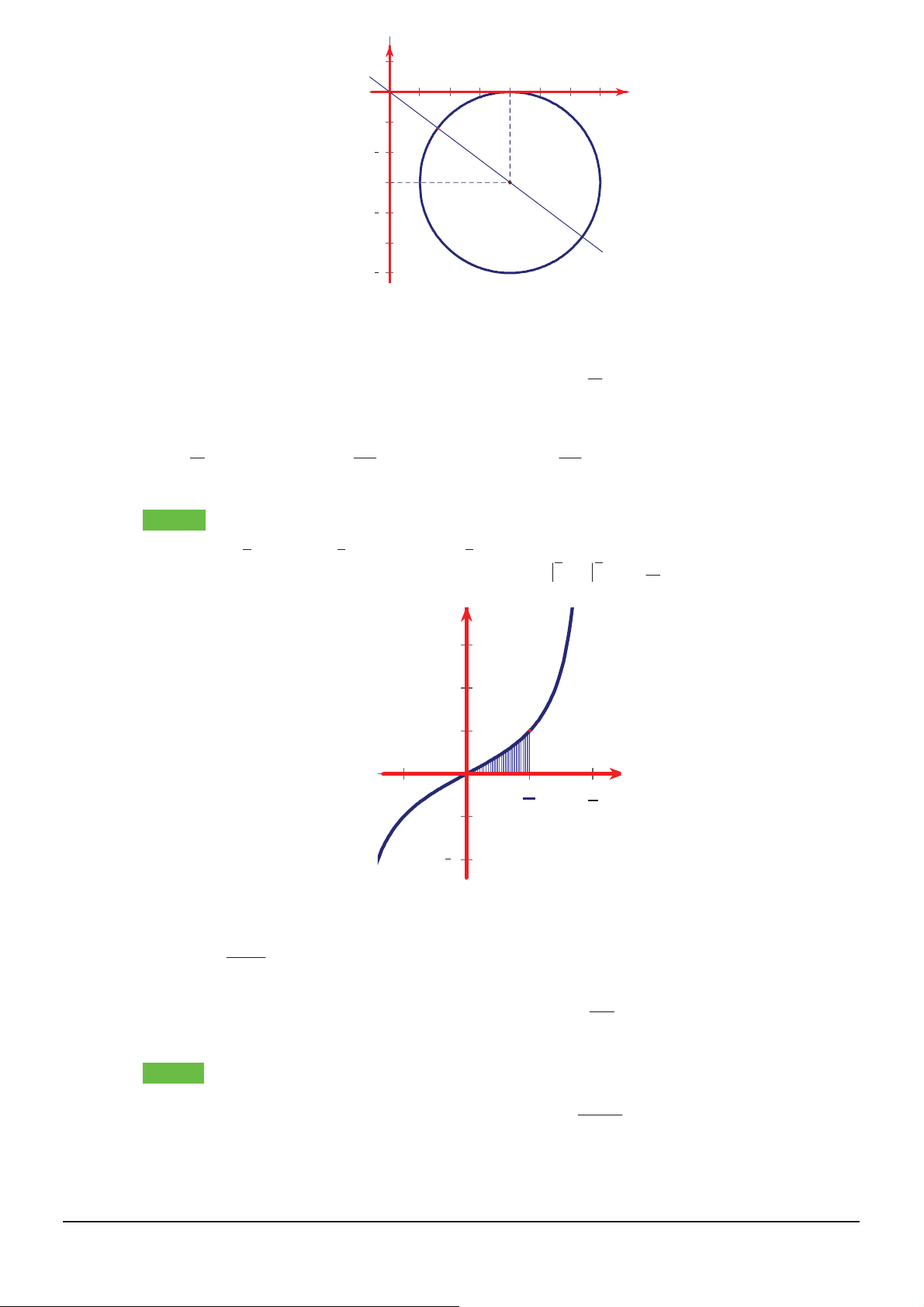
D. z    i . 5 5 5 5 5 5 5 5 Hướng dẫn giải Chọn A.
Gọi  x yi có điểm biểu diễn là M  ;
x y , gt  x  4   y  3i  3  x  2
4   y  32  9
do đó tập hợp điểm M là đường tròn C tâm I 4; 3 bán kính R  3 .
Môđun z OM nhỏ nhất khi M là giao điểm của C và đoạn OI (gần gốc O nhất)
Mà PT đt OI : 3x  4y  0 (đt qua 2 điểm O 0;0 và I 4; 3 )  32  8   x x   x  2
4   y  32  9   Giải hệ 5 5  ta được  hay  3
 x  4y  0 24  6 y       y  5  5  8 x   8 6 Tính độ dài 5 OM ta chọn 
. Vậy z   i 6  5 5 y    5
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 11/22 Mã đề 570 y O 5 x M 2 I 4 d 6 y  tan x
Câu 18: Gọi  H  là hình phẳng giới hạn bởi các đường Ox 
. Quay  H  xung quanh trục Ox    x  0, x   4
ta được khối tròn xoay có thể tích bằng  2  2 
A. 1 đvtt  . B.  đvtt  . C.   đvtt . D. 2  đvtt  . 4 4 4 Hướng dẫn giải Chọn A.    4 4 4    Thể tích 2 V  tan d x x  =  2
1 tan x dx  dx   = 4 4
tan x x =1 đvtt  0 0 4 0 0 0 y 2 O π π x 4 2 2
Câu 19: Nguyên hàm F x 2 x2  3 dx  là 2 x2 3
A. F x   C .
B. F x 2x2  3 ln 3  C . 2ln 3 2 3 x C.   2 2  3 x F xC .
D. F x   C . 9 Hướng dẫn giải Chọn A x   a
Theo công thức tinh nguyên hàm của hàm hợp x a dx    ln a
Suy ra đáp án A đúng.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 12/22 Mã đề 570
Câu 20: Trong không gian với hệ trục Oxyz cho hai điểm A1;2;3, B 0;1; 5
  , gọi I là điểm trên
đoạn thẳng AB sao cho IA  2IB . Giả sử tọa độ của điểm I  ; a ;
b c thì a b c bằng 8 17 A. 4  . B. 5 . C.  . D.  . 3 3 Hướng dẫn giải Chọn C  
Vì I thuộc đoạn thẳng AB và IA  2IB IA  2  IB  
IA  1 a; 2  ;
b 3  c , IB  a;1 ; b 5   c   Vì IA  2
IB nên ta có hệ:  1 a   1   a  2  .a 3    8
  b     b 4 2 2 1  b  
a b c   . 3   3 3   c  2    5   c  13 c    3 1 1
Câu 21: Tính tích phân dx  bằng 2x  3 0 1 5 1 3 3 1 A. ln . B. ln . C. . D. ln 2 . 2 3 2 5 20 2 Hướng dẫn giải Chọn A. 1 1 1 1 1 1 5 Ta có:
dx  ln 2x  3   ln5ln3  ln 2x  3 2 0 2 2 3 0 dx
Câu 22: Nguyên hàm F x   là 3 2x5 1 1
A. F x    C .
B. F x   C . 83 2x4 23 2x4 1 1
C. F x    C .
D. F x   C . 43  2x4 83 2x4 Hướng dẫn giải Chọn D. dx 1 d 3  2x 1  1   1
Ta có: F x      .   C   C    3 2x5 2 3 2x5 2  4  3 2x4     8  3 2x4
Câu 23: Nguyên hàm F (x)  3x 1 dx  là 2 1
A. F(x)  3x  3 1  C.
B. F(x)  3x  3 1  C. 9 3 2 2
C. F(x)  3x  3 1  C.
D. F(x) 
3x 1  C. 3 9 Hướng dẫn giải
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 13/22 Mã đề 570 Chọn A. 3 1 2 1 1 (3x 1) 2 Ta có F(x)  3x 1dx
(3x 1) d (3x 1)   C    3x  3 2 1  C. 3 3 3 9 2
Câu 24: Trong mặt phẳng phức  , gọi A , B ,C lần lượt là ba điểm biểu diễn các số phức z  3  4i ; 1
z  5  2i ; z  1 3i . Số phức biểu diễn bởi điểm D 2 3
để ABCD là hình bình hành là A. 7  i . B. 1 9i . C. 1 9i .
D. 7  9i . Hướng dẫn giải Chọn D.
Ta có A3;4 , B5; 2
  và C 1;3  
AB  8;6; DC  1 x ;3 y . D D
Tứ giác ABCD là hình bình hành khi và chỉ khi:   1   x  8 x  7 AB DC D   D   . Do đó D  7;  9. 3  y  6  y  9 DD
Vậy số phức biểu diễn bởi điểm D để ABCD là hình bình hành là: 7  9i b
Câu 25: Biết 2x  4dx  0 . Khi đó b nhận giá trị bằng 0 b 1 b  0 b  0 b 1 A.  . B.  . C.  . D.  . b  2 b  4 b  2 b  4 Hướng dẫn giải Chọn B. b  bb
2x  4dx  0   0 2 x  4x 2
 0  b  4b  0   . 0 b  4 0 2 x 2 x
Câu 26: Diện tích hình phẳng giới hạn bởi hai Parabol y  và y    3x là 4 2 A. 12 ñvtt . B. 8ñvtt . C. 4 ñvtt . D. 16 ñvtt . Hướng dẫn giải Chọn B. 2 2 x xx  0
Phương trình hoành độ giao điểm:    3x  . 4 2  x  4 4 2 2 xx
Diện tích hình phẳng giới hạn là S      3x  dx 4  2 0  4 4 2 2 3  3x   3x x
S  3x  dx      8 dvdt .  4   2 4 0  0
Câu 27: Trong không gian Oxyz cho đường thẳng d : x y z , gọi d là hình chiếu vuông góc của d
lên mặt phẳng tọa độ (Oyz) . Ta có phương trình d là:
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 14/22 Mã đề 570x  0 x tx  0 x  0    
A. y t .
B. y t.
C. y  2  t.
D. y t . z  2t     z tz  1 tz tHướng dẫn giải: Chọn D.
Ta có: phương trình mặt phẳng (Oyz) là x  0 . Gọi A là giao của d với mặt phẳng (Oyz) thì ( A 0;0;0)
Lấy M (1;1;1) (d) . Gọi H là hình chiếu vuông góc của M lên (Oyz) 
Phương trình MH đi qua M (1;1;1) và nhận vectơ i(1;0;0) làm pvt. x  1 t
PT MH y 1 tọa độ điểm H là giao của (Oyz) và đường thẳng MH nên H (0;1;1) z 1  
Phương trình (d ')  AH đi qua (
A 0;0;0) và nhận AH  (0;1;1) làm vpt x  0 
(d ') : y t z t  1  b Câu 28: Tích phân x
I xe dx a  
. Khi đó a  2b bằng e 0 A. 5. B. 6. C. 7. D. 3. Hướng dẫn giải: Chọn A. u   xdu dx 1    xx 1 x 2 Đặt    khi đó: 1 1
I  xe |  e dx   e |  1   xx 0 0 dv e dxv  e e e 0
Từ đó suy ra: a  1;b  2 nên a  2b  5 . 2017 1 i
Câu 29: Phần ảo của số phức z    là 1 i A. 1. B. 1. C. .i D. .i Hướng dẫn giải Chọn C. 2017 1 i  Ta có 2017 504.4 1  504.4 z   iii
.i  1.i i.   1 i  9 Câu 30: Cho 3
I x 1 x dx  . Đặt 3
t  1 x . Ta có 0 1 2
A. I  3  3 1 t  2 2t dt. B. I  3 3
1 t  3tdt. 2 1
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 15/22 Mã đề 570 1 1
C. I  3  3
1 t  3tdt.
D. I    3
1 t  3tdt. 2 2 Hướng dẫn giải Chọn C. Đặt 3 3 2
t  1 x t  1 x  3t dt  d . x
Đổi cận: Với x  0  t  1, x  9  t  2. 9 2 3
I x 1 x dx     1t  1 3 2
.t.3t dt  3  3 1 t  3 t dt. 0 1 2 x  3 y 1 z  2
Câu 31: Trong không gian với hệ tọa hệ trục Oxyz , cho hai đường thẳng d :   và 1 2 4
 : x  3  y 1  z  5. Trong bốn đường thẳng Ox , Oy , Oz và  , đường thẳng d tạo với
đường thẳng nào một góc lớn nhất? A. Oy . B.  . C. Ox . D. Oz . Hướng dẫn giải Chọn C. 
d có vectơ chỉ phương là u  1;2;4 . d     i.ud 1
Ox có vectơ chỉ phương là i  1;0;0 và có cosOx, d      i . u 21 d    j.ud 2
Oy có vectơ chỉ phương là j  0;1;0 và có cosOy, d      j . u 21 d    k.ud 4
Oz có vectơ chỉ phương là k  0;0; 
1 và có cosOz, d      k . u 21 d    u .u   d 7
có vectơ chỉ phương là u
và có cos, d       1;1;  1 u . u 3. 21  d
Do đó, đường thẳng Ox tạo với d  một góc lớn nhất.
Câu 32: Tìm tập hợp các điểm biểu diễn số phức z , biết số phức 2
z có điểm biểu diễn nằm trên trục hoành
A. Đường thẳng y x .
B. Trục tung và trục hoành. C. Trục tung. D. Trục hoành. Hướng dẫn giải Chọn B.
Đặt z x yi, x, y   . Ta có: 2 2 2
z x y  2xy có điểm biểu diễn nằm trên trục hoành nên 2
z là một số thực. x  0 Vậy xy  0  
hay tập hợp điểm biểu diễn số phức z là trục hoành và trục tung.  y  0
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 16/22 Mã đề 570
Câu 33: Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng P :3x  4y  5z 10  0 và đường
thẳng d đi qua 2 điểm M 1;0;2 , N 3;2;0 . Gọi  là góc giữa đường thẳng d và mặt
phẳng P . Ta có A.   90 . B.   45. C.   60 . D.   30 . Hướng dẫn giải. Chọn C.
Mặt phẳng P có vectơ pháp tuyến là n  3; 4;5 .  
Đường thẳng đi qua 2 điểm M , N có vec tơ chỉ phương là u MN  4;2;2 .   . n u 3.4  4.2   5   2   3 Ta có: Sin         60 2 2 2 2 2 2 n . u 3  4  5 . 4  2  2 2
Câu 34: Nguyên hàm   3  . x F x x e dx  là
A.       3 1 . x F x x e C . B.   3 2  . x F x
x e x C . 1 1 x 1 x 1 C.   3 3  . x F x
x e e C . D.   3 3  . x F x
x e e C . 3 9 3 9 Hướng dẫn giải. Chọn C. du  dx u   x  Đặt    x 1 3 3 du e d x x v e  3 1 x 1 x 1 x 1 Khi đó:   3  . x F x x e dx  3 3 3 3  .  .  .  . x x e e dx x e e C  3 3 3 9
Câu 35: Phương trình 2
z  (1 i)z 18 13i  0 có hai nghiệm là
A. 4  i;  5  2i .
B. 4  i;  5  2i .
C. 4  i; 5  2i .
D. 4  i; 5  2i . Hướng dẫn giải Chọn B
   i    i    i2 2 (1 ) 4 18 13 9 3 
1 i  9  3ix   4  i
Phương trình đã cho có hai nghiệm phức là 2  . 
1 i  9  3ix   5   2i  2
Câu 36: Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt phẳng P : x z  3  0 và
Q: 2y  2z  3  0. Ta có góc giữa hai mặt phẳng P và Q bằng     A. . B. . C. . D. . 2 4 3 6 Hướng dẫn giải ChọnC 
Mặt phẳng P có một vectơ pháp tuyến là n  1;0;  1 . P 
Mặt phẳng Qcó một vectơ pháp tuyến là n  0; 2; 2 . Q
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 17/22 Mã đề 570    n n    P Q . P Q 1.0 0.2 1.2 1 cos ,      n n 11 4  4 2 P Q
Vậy góc giữa hai mặt phẳng P và Qbằng 3
Câu 37: Trong không gian với hệ trục Oxyz , cho hai điểm A1;2;5 , B 1;  5;5 . Tìm điểm  sao C Oz
cho tam giác ABC có diện tích nhỏ nhất? A. C 0;0;6 .
B. C 0;0;5.
C. C 0;0;4 .
D. C 0;0;2 . Hướng dẫn giải Chọn B.  CA  1;2;5t
Do điểm C Oz C 0;0;t    CB  1;5;5t   1   1 7 Ta có  , CA CB         3
 5t;25t;7 S C , A CB  13  t   . ABC 5 2 49 2   2 2 7
Vậy tam giác ABC có diện tích nhỏ nhất bằng , đạt khi t  5  C 0;0;5 2
Câu 38: Nguyên hàm của hàm số   4 3 x
F x x e dx  là 4 4  x x e 4 x xe
A. F x    C .
B. F x    C . 4 4 1 4 x e C.   4  x F x   eC .
D. F x   C . 4 4 Hướng dẫn giải Chọn C. 1 Ta đặt 4 3 3
t  x  dt  4
x dx x dx   dt 4   4  x 1 t 1 t 1 4 3  d   d  x F x x e x
e t   e C   eC   4 4 4
Câu 39: Trong không gian với hệ trục Oxyz cho hai điểm A3;1;  1 , B 2;1; 4  . Hãy viết phương
trình mặt phẳng P đi qua A , B và vuông góc với mặt phẳng Q : 2x y  3z  4  0.
A. 5x 13y z  29  0 .
B. x 13y  5z  5  0 .
C. x 13y  5z  3  0 .
D. 3x 12y  2z  2  0 . Hướng dẫn giải Chọn B.  
 Ta có AB  1; 2; 5 , VTPT của Q là n  2;1; 3  . Q      
 VTPT của P là n  AB,n   1; 1  3;5 . Q     
 Phương trình mp P 
:1 x  3 13 y   1  5 z  
1  0  x 13y  5z  5  0 .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 18/22 Mã đề 570 ln 2  Câu 40: Cho x I
e 1 dx a   . Khi đó b 0
A. a b .
B. a b . C. ab  1.
D. a b . Hướng dẫn giải Chọn B. t t t t x x x x 2 d 2 d  Đặt 2 2
t e 1  t e 1  e t 1  e dx  2tdt  dx   . x 2 e t 1
 Đổi cận: x  0  t  0 , x  ln 2  t  1. 1 2 1 1 t  1  1  Khi đó I  2 dt  2 1 dt  2  2 dt  2  2J    . 2  2  2 t 1  t 1 t 1 0 0 0 1 1  Tính J  dt  . 2 t 1 0  Đặt t u t   2 tan d
1 tan udu . 
 Đổi cận: t  0  u  0 , t  1 u  . 4    2 4 1 tan u  4 du   Khi đó J   du    . 2 1 tan u 4 0 0    Vậy I  2  2
 2   a b  2. 4 2
Câu 41: Cho mặt phẳng P : x y z  3  0 và điểm A1;2; 3
  , hình chiếu vuông góc của A lên
P có tọa độ là A. 1;1;2 . B. 0;1; 2   . C. 1;2;0 . D. 2;1;0 . Hướng dẫn giải Chọn B. x  1 t
Phương trình đường thẳng d đi qua A và  P là: y  2  t ,t 
z  3t
Gọi H là hình chiếu vuông góc của A lên P       
H d  P
H 1 t;2 t; 3 t H 0;1; 2    
x y z  3  0  t   1  H H H
Câu 42: Cho z   , z 1 2i  7  4i . Khi đó 2z 1 là A. 65 . B. 61 . C. 8 . D. 5 . Hướng dẫn giải Chọn A. i
Ta có: z   i 7 4
1 2  7  4i z
 3 2i . Vậy z  3  2i 1 2i
Khi đó z     i 2 2 2 1
2 3 2 1  7  4i  7  4  65
Câu 43: Cho a  0 và a  1, C là hằng số. Phát biểu nào sau đây đúng?
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 19/22 Mã đề 570 A. 2x 2 d x a
x a ln a C.  B. 2x 2 d x a
x a C.  2 x a C. x d x
a x a ln a C.  D. 2x a dx   C.  2ln a Hướng dẫn giải Chọn D 2 a x a x 1 x 1 x Ta có 2 2 a dx a d   2x  .  C và x a dx   C.  2 2 ln a ln a 1 1
Câu 44: Cho f x là một hàm số liên tục trên  thỏa mãn f
 tdt  3 và f
 udu  2. Khi đó 0 1 0 f
 xdx bằng ? 1 A. 5. B. 5. C. 1. D. 1. Hướng dẫn giải Chọn A 1 1 0 Ta có f
 tdt  3 f
 xdx  3 f
 xdx  3. 0 0 1 1 1
Lại có f udu  2  f xdx  2    1 1  1 0 0  f
 xdx f
 xdx  2    3    5  f
 xdx  5  . 1 1 1 
Câu 45: Cho mặt cầu S  2 2 2
: x y z  4x  2y  4z  0 . Viết phương trình mặt phẳng tiếp xúc với mặt
cầu tại điểm M 1; 1;  0.
A. x  2y  2z  3  0 . B. x  2y  2z 1  0 . C. x y  0 .
D. 2x y 1  0 . Hướng dẫn giải Chọn B.
Ta có: Mặt cầu S  có tâm I 2;1; 2
  . Mặt phẳng   tiếp xúc với mặt cầu S tại  M 1; 1;  0 qua M 1; 1;
 0 và nhận MI  1;2;2 làm vectơ pháp tuyến.
Phương trình mặt phẳng   : x  2y  2z 1  0 . 2 x  2x 1
Câu 46: Nguyên hàm F x  dx  là x  2 2 x
A. F x 
 4x  7ln x  2  C .
B. F x   2
x  4xln x  2  C . 2
C. F x 2
x  2x  ln x  2  C .
D. F x 2
x  4x  7ln x  2  C . Hướng dẫn giải Chọn A. 2 2 x  2x 1  7  x
Ta có: F x  dx x  4  dx
 4x  7 ln x  2  C    . x  2  x  2  2
Câu 47: Trong không gian Oxyz cho điểm A1; 1; 
1 , B 3; 5; 7 . Gọi S  là tập hợp điểm M  ;
x y; z thoả mãn 2 2 2
MA MB AB . Chọn kết luận đúng
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 20/22 Mã đề 570
A. S  là mặt cầu có phương trình  x  2   y  2  z  2 1 3 4  56 .
B. S  là mặt phẳng trung trực của đoạn AB .
C. S  là mặt cầu có phương trình  x  2   y  2  z  2 2 3 4  14 .
D. S  là đường tròn có phương trình  x  2   y  2   z  2 1 3 4  14 . Hướng dẫn giải Chọn C. Ta có 2 2 2
MA MB AB MA
B vuông tại M (định lí đảo Pitago).
Suy ra tập hợp điểm M là mặt cầu tâm I đường kính AB (với I là trung điểm AB ).   AB  2
 ; 4; 6  AB  2 14  R  14 và I  2;  3; 4.
Vậy mặt cầu là S   x  2   y  2  z  2 : 2 3 4  14 . x
Câu 48: Nguyên hàm F x sin  dx  là 3  2cos x
A. F x 1
  ln 3  2cos x C .
B. F x 1
 ln 3 2cos x C . 3 2
C. F x 1
 ln 3 2cos x C .
D. F x 1
  ln 3 2cos x C . 3 2 Hướng dẫn giải Chọn B. F x sin x 1 d 3 2cos x 1  dx
 ln 3 2cos x C   . 3  2 cos x 2 3  2cos x 2 4  1 1  a a Câu 49: Cho x   dx  
với là phân số tối giản. Khi đó a b bằng 2   x x b b 1 A. 140 . B. 39 . C. 9 . D. 31. Hướng dẫn giải Cho ̣ n D 4 4 2  1 1   x 1  35 Ta có: x   dx      2 x    2  x x   2 x  4 1 1 a  35 Suy ra: 
a b  31 b   4 2
y  2y x  0
Câu 50: Diện tích của hình phẳng H  giới hạn bởi  bằng x y  0 27 27 9 9 A. đvdt. B. đvdt. C. đvdt. D. đvdt. 2 4 2 4 Hướng dẫn giải Chọn C 2 2
y  2y x  0
x   y  2y Ta có:    x y  0 x   yy  0
Phương trình tung độ giao điểm: 2 2
y  2y  y y  3y  0    y  3
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 21/22 Mã đề 570
Diện tích hình phẳng cần tìm là: 3 3       y S yy  2y 3 3
dy y  3y dy  
3y y  3 3 9 2 2 2 2 dy   y    .  2 3  2 0 0 0 0
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Trang 22/22 Mã đề 570