Đề thi HK2 Toán 12 năm học 2019 – 2020 trường THPT Tân Phú – Đồng Nai

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2019 – 2020 .Mời bạn đọc đón xem.

20 10 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 1

SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2019– 2020

ĐỒNG NAI Môn thi: TOÁN – KHỐI 12

TRƯỜNG THPT TÂN PHÚ Thời gian : 90 phút – Trắc Nghiệm, không kể thời gian phát đề

Câu 1: Cho

 

d3I f x x





 

4 3 dJ f x x







bng:

. B.

. C.

. D.

Câu 2: Tính tích phân

2020





2020.ln2 1I 

. B.

2020

2I 

. C.

2020.ln2I 

. C.

2020I 

Câu 3: Có bao nhiêu giá tr thc ca

 có

 

2 5 d 4

x x a  



. B.

. C.

. D. Vô s.

Câu 4: Cho hàm s

 

liên tn

 

1;e

, bit

 





 

e1f 



 

.ln dI f x x x







bng

4I 

. B.

3I 

. C.

1I 

. D.

0I 

Câu 5: Tính

I x x



eI 

. B.

eI 

. C.

3e 2eI 

. D.

eI 

Câu 6: Tính tích phân

 

2 1 d

I x e x



bt

21ux

v e x

. M 

 

2 1 2 d

I x e e x  



. B.

 

2 1 d

I x e e x  



 

2 1 d

I x e e x  



. D.

 

2 1 2 d

I x e e x  



Câu 7: Tính tích phân

cos sin dI x x x







bt

costx

, m 

dI t t



. B.

dI t t



. C.

dI t t







. D.

dI t t







Đề thi HK II – THPT Tân Phú – Đồng Nai Page 2

Câu 8: Cho hàm s

 

y f x

liên tc trên . Bit

 

. d 2x f x x 



, hãy tính

 

dI f x x



2I 

. B.

1I 

. C.

I 

. D.

4I 

Câu 9: Din tích

hình phng gii hn bng

21y x x  

, trc hoành,

1x 

và

2x 

là

S 

. B.

S 

. C.

S 

. D.

S 

Câu 10: 

 

2dx x x



. B.

   

2 d 2x x x x x dx  



   

2 d 2x x x x x dx  



. D.

   

2 d 2x x x x x dx   



Câu 11: Cho hình phng

 

c gii hn bng

0x 





0y 

và

sinyx

. Th tích

ca khi tròn xoay to thành khi quay

 

xung quanh trc

c tính theo công thc

sin dV x x







. B.

sin dV x x







. C.

 

sin dV x x







. D.

sin dV x x







Câu 12: Mt chic máy bay chuyi vn tc

   

10 m/sv t t t

vi

là thi gian

 giây k t khi máy bay bu chuyng. Bit vn tc

 

200 m/s

thì nó r

 

500 m

. B.

 

2000 m

. C.

 

4000

. D.

 

2500

Câu 13: Cho hình phng

gii hn bng cong

2 cosyx

, trng thng

0x 





. Khi tròn xoay to thành khi quay

quanh trc hoành có th tích

bng bao nhiêu?





. B.





. C.

 





. D.

 





Đề thi HK II – THPT Tân Phú – Đồng Nai Page 3

Câu 14: Phn thc và phn o ca s phc

12zi

lt là:

và

. C.

và

. D.

và

Câu 15: S phc liên hp ca s phc

12zi

là

12i

. B.

12i

. C.

2 i

. D.

12i

Câu 16: Cho  

3 4 .zi  



là:

. B.

. C.

. D.

Câu 17: Tp hp tt c m biu din các s phc

tha mãn:

24zi  

ng tròn có tâm

và

bán kính

lt là:

 

2; 1I 

;

4R 

. B.

 

2; 1I 

;

2R 

. C.

 

2; 1I 

;

4R 

. D.

 

2; 1I 

;

 

2; 1I 

Câu 18: Trong mt phng t

Oxy

, Gi

lm biu din s phc

12i

44i

3i

. S phc biu din trng tâm tam giác

ABC

là

13i

. B.

13i

. C.

39i

. D.

39i

Câu 19: Cho s phc

23zi

a s phc

 

1w i z

26w 

. B.

37w 

. C.

5w 

. D.

4w 

Câu 20: Tìm t m biu din ca s phc

  

2 3 4







 

1; 4

. B.

 

1;4

. C.

 

1; 4

. D.

 

1;4

Câu 21: Cho hai s phc

23zi

45zi  

. Tính

z z z

22zi  

. B.

22zi  

. C.

22zi

. D.

22zi

Câu 22: Cho s phc

z a bi

 

,ab

tha mãn

1 3 0z i z i   

. Tính

3S a b

S 

. B.

3S 

. C.

3S 

. D.

S 

Câu 23: Tng phn thc và phn o ca s phc

tho mãn

 

12iz i z i   

bng

. B.

2

. C.

. D.

6

Câu 24: Cho s phc

z a bi

 

, , 0a b a

tha mãn

1 2 5zi  

và

. 10zz

. Tính

P a b

4P 

. B.

4P 

. C.

2P 

. D.

2P 

Câu 25: Gi

là các nghim c

8 25 0zz  

. Giá tr

zz

bng

. B.

. C.

. D.

Câu 26: Trong không gian vi h t

,Oxyz

m

 

2; 3; 4A

 

6; 2; 2B

. Tìm t 

.AB

 

4;3;4AB 

. B.

 

4; 1; 2AB   

. C.

 

2;3;4AB 

. D.

 

4; 1;4AB 

Câu 27: Trong không gian vi h t 

Oxyz

  m

 

3;2;1A

 

1;3;2B 

;

 

2;4; 3C 

. Tích vô

ng

.AB AC

là

. B.

2

. C.

. D.

6

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 4

Câu 28: Trong không gian vi h t

Oxyz

m

 

3;2;8M

 

0;1;3N

và

 

2; ;4Pm

. Tìm



tam giác

MNP

vuông ti

25m 

. B.

4m 

. C.

1m 

. D.

10m 

Câu 29: Trong không gian vi h t

Oxyz

, cho hình hp

.ABCD A B C D

   

, bit t

 

3;2;1A 

 

4;2;0C

 

2;1;1B





 

3;5;4D



. Tìm t



 

3;3;1A





. B.

 

3;3;3A





. C.

 

3; 3; 3A





. D.

 

3; 3;3A





Câu 30: Trong không gian vi h t

Oxyz

, cho mt c

   

1 3 9x y z    

. Tìm

t tâm

và bán kính

ca mt c

 

1;3;0I 

;

3R 

. B.

 

1; 3;0I 

;

9R 

. C.

 

1; 3;0I 

;

3R 

. D.

 

1;3;0I 

;

9R 

Câu 31: Trong không gian

Oxyz

   m

 

1;2;3M

và

 

1;2; 1N 

. Mt c ng kính

có



   

2 1 20x y z    

. B.

   

2 1 5x y z    

   

2 1 5x y z    

. D.

   

2 1 20x y z    

Câu 32: Trong không gian

Oxyz

, mt phng

 

: 2 3 3 0P x y z   

có mn là

 

1; 2;3

. B.

 

1;2; 3

. C.

 

1;2; 3

. D.

 

1;2;3

Câu 33: Trong không gian

Oxyz



 

:2 2 0P x y z   

 

1; 2;2Q 

. B.

 

1; 1; 1N 

. C.

 

2; 1; 1P 

. D.

 

1;1; 1M 

Câu 34: Trong không gian

Oxyz

m

 

1;2;1A 

và

 

2;1;0B

. Mt ph

và vuông góc

vi



3 6 0x y z   

. B.

3 6 0x y z   

. C.

3 5 0x y z   

. D.

3 6 0x y z   

Câu 35: Trong không gian vi h t

Oxyz

, mt phng chm

 

1; 0;1A

 

1; 2; 2B 

và song song

vi trc



2 2 0yz  

. B.

2 3 0xz  

. C.

2 1 0yz  

. D.

0x y z  

Câu 36: Trong h trc t 

Oxyz

 u kin ca

 hai mt phng

 

:2 2 0P x y z  

và

 

: 1 0Q x y mz   

ct nhau là

m 

. B.

m 

. C.

1m 

. D.

m 

Câu 37: Trong không gian

Oxyz

ng thng

1 2 1

x y z







ng thng

có m



Đề thi HK II – THPT Tân Phú – Đồng Nai Page 5

 

1;2;1u 

. B.

 

2;1;0u 

. C.

 

2;1;1u 

. D.

 

1;2;0u 

Câu 38: Trong không gian

Oxyz

ng thng

1 2 3

2 1 2

x y z

  







 

2; 1; 2Q 

. B.

 

1; 2; 3M   

. C.

 

1; 2; 3P

. D.

 

2;1; 2N 

Câu 39: Trong không gian

Oxyz

 ng th   m

 

1;4; 7A 

và vuông góc vi mt phng

2 2 3 0x y z   



1 4 7

1 2 2

x y z  





. B.

1 4 7

x y z  





1 4 7

1 2 2

x y z  





. D.

1 4 7

1 2 2

x y z  





Câu 40: Trong không gian

Oxyz

ng thng cha trc

 là

















. B.

















. C.

















. D.

















Câu 41: Trong không gian

,Oxyz

ng thng

3 2 4

1 1 2

x y z

  





ct mt phng

 

Oxy

tm có ta

 là

 

3; 2; 0 .

 

3; 2; 0 .

 

1; 0; 0 .

 

1; 0; 0 .

Câu 42: Trong không gian

Oxyz

, cho mt phng

 

:2 3 0P x y z   

ng thng

2 1 5

x y z







Tính khong cách t d n mt phng

 

( ;( ))

d d P 

. B.

( ;( )) 6d d P 

. C.

( ;( )) 1d d P 

. D.

( ;( ))

d d P 

Câu 43: Trong không gian

Oxyz

tính khong cách t m

 

1;2; 3M 

n mt phng

 

: 2 2 2 0   P x y z

. B.

. C.

. D.

Câu 44: Trong không gian

Oxyz

a mt cu có tâm

 

1;2; 1I 

và tip xúc mt phng

 

: 2 2 8 0P x y z   

     

2 2 2

1 2 1 3x y z     

     

2 2 2

1 2 1 9x y z     

     

2 2 2

1 2 1 3x y z     

     

2 2 2

1 2 1 9x y z     

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 6

Câu 45: Trong không gian vi h trc t

Oxyz



 

:2 2 0P x y z m   



 

2 2 2

: 2 4 6 2 0S x y z x y z      





 





 



 





. B.

. C.

. D.

Câu 46: Trong không gian

Oxyz

m

 

1;2;3M

. Hình chiu ca

lên trc

m

 

1;0;3P

. B.

 

0;2;0Q

. C.

 

1;0;0R

. D.

 

0;0;3S

Câu 47: Trong không gian vi h t

Oxyz

m

 

3; 1;2M 

. m

i xng vi

qua mt

phng

 

Oyz

là

 

0; 1;2N 

. B.

 

3;1; 2N 

. C.

 

3; 1;2N 

. D.

 

0;1; 2N 

Câu 48: Trong không gian

Oxyz

m

 

5;7; 13M 

. Gi

là hình chiu vuông góc ca

trên mt

phng

 

Oyz

. T m

là?

 

5;0; 13H 

. B.

 

0;7; 13H 

. C.

 

5;7;0H

. D.

 

0; 7;13H 

Câu 49: Cho hình vuông

ABCD

cnh

. Trên hai tia

,Bx

vuông góc vi mt phng

 

ABCD

và cùng

chiu lt l m

sao cho

;

BM 

2DN a

. Tính góc



gia hai mt phng

 

AMN

và

 

CMN





. B.





. C.





. D.





Câu 50: [4]Cho hàm s

 

y f x

 th ca hàm s

 

y f x







t

( ) 2 ( ) ( 1)g x f x x  

. M 



     

1 3 5g g g  

     

5 1 3g g g  

     

1 5 3g g g  

     

3 5 1g g g  

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 7

HƯỚNG DẪN GIẢI

Câu 1: [2D3-2.1-1] Cho

 

d3I f x x





 

4 3 dJ f x x







bng:

. B.

. C.

. D.

Lời giải

Chọn B.

Ta có

   

2 2 2

0 0 0

4 3 d 4 d 3 d 4.3 3 6J f x x f x x x x      





  

Câu 2: [2D3-2.1-2] Tính tích phân

2020





2020.ln2 1I 

. B.

2020

2I 

. C.

2020.ln2I 

. C.

2020I 

Lời giải

Chọn C.

Ta có:

2020

lnIx

 

2020

ln 2 ln1

2020.ln2

Câu 3: [2D3-2.1-2] Có bao nhiêu giá tr thc ca

 có

 

2 5 d 4

x x a  



. B.

. C.

. D. Vô s.

Lời giải

Chọn A.

Ta có

 

2 5 d 4

x x a  



 

x x a   

4 4 0aa   

2a  

Câu 4: [2D3-2.3-2] Cho hàm s

 

liên t  n

 

1;e

, bit

 





 

e1f 

  

 

.ln dI f x x x







bng

4I 

. B.

3I 

. C.

1I 

. D.

0I 

Lời giải

Chọn D.

Cách 1: Ta có

       

.ln d .ln . d e 1 1 1 0I f x x x f x x f x x f



       



Đề thi HK II – THPT Tân Phú – Đồng Nai Page 8

t

 

v f x x

v f x



























Suy ra

   

 

.ln d ln d e 1 1 1 0

I f x x x f x x x f



       



Câu 5: [2D3-2.3-2] Tính

I x x



eI 

. B.

eI 

. C.

3e 2eI 

. D.

eI 

Lời giải

Chọn A.

t

d e d

























e e d

I x x



2e e e

  

2 2 2

2e e e e e    

Câu 6: [2D3-2.2-1] Tính tích phân

 

2 1 d

I x e x



bt

21ux

v e x

. M nào sau



 

2 1 2 d

I x e e x  



. B.

 

2 1 d

I x e e x  



 

2 1 d

I x e e x  



. D.

 

2 1 2 d

I x e e x  



Lời giải

Chọn A.

 

2 1 d

I x e x



t

21ux

v e x

d 2dux

ve

 

2 1 2 d

I x e e x   



Câu 7: [2D3-2.2-2] Tính tích phân

cos sin dI x x x







bt

costx

, m 

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 9

dI t t



. B.

dI t t



. C.

dI t t







. D.

dI t t







Lời giải

Chọn A.

t

costx

d sin dt x x  

sin d dx x t  

i cn:

01xt  

;



  



 

dI t t



dtt



Câu 8: [2D3-2.2-2] Cho hàm s

 

y f x

liên tc trên . Bit

 

. d 2x f x x 



, hãy tính

 

dI f x x



2I 

. B.

1I 

. C.

I 

. D.

4I 

Lời giải

Chọn D.

Xét tích phân

 

. d 2x f x x 



, ta có

t

xt

xx

i cn: Khi

0x 

thì

0t 

; Khi

2x 

thì

4t 



 

. d 2x f x x 



 

dt 2

ft



 

dt 4ft



 

d4f x x



hay

4I 

Câu 9: [2D3-3.1-1] Din tích

hình phng gii hn bng

21y x x  

, trc hoành,

1x 

và

2x 

là

S 

. B.

S 

. C.

S 

. D.

S 

Lời giải

Chọn A.

Din tích hình phng cn tìm là

2 1 d

S x x x   



Đề thi HK II – THPT Tân Phú – Đồng Nai Page 10

 

2dx x x



. B.

   

2 d 2x x x x x dx  



   

2 d 2x x x x x dx  



. D.

   

2 d 2x x x x x dx   



Lời giải

Chọn D



   

2 d 2S x x x x x dx    



Câu 11: [2D3-3.3-1] Cho hình phng

 

c gii hn bng

0x 





0y 

và

sinyx

Th tích

ca khi tròn xoay to thành khi quay

 

xung quanh trc

c tính theo công

thc

sin dV x x







. B.

sin dV x x







. C.

 

sin dV x x







. D.

sin dV x x







Lời giải

Chọn B.

Ta có th tích ca khi tròn xoay cn tính là

sin dV x x







Câu 12: [2D3-3.5-2] Mt chic máy bay chuyi vn tc

   

10 m/sv t t t

vi

là th giây k t khi máy bay bu chuyng. Bit

vn tc

 

200 m/s

 

500 m

. B.

 

2000 m

. C.

 

4000

. D.

 

2500

Lời giải

Chọn D.

- Tht vn tc

 

200 m/s

là nghim c

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 11

10 200tt

10 200 0tt   













 

10 st

- ng máy bay di chuy

 

10 ds t t t











 

2500



Câu 13: [2D3-3.3-2] Cho hình phng

gii hn bng cong

2 cosyx

, trng

thng

0x 





. Khi tròn xoay to thành khi quay

quanh trc hoành có th tích

bng bao

nhiêu?





. B.





. C.

 





. D.

 





Lời giải

Chọn D.

Th tích khi tròn xoay khi quay

quanh trc hoành có th tích là:

dV y x







 

2 cos dxx







 

2 sinxx





 





Câu 14: [2D4-1.1-1] Phn thc và phn o ca s phc

12zi

lt là:

và

. C.

và

. D.

và

Lời giải

Chọn C.

S phc

12zi

có phn thc và phn o lt là

và

Câu 15: [2D4-1.1-1] S phc liên hp ca s phc

12zi

là

12i

. B.

12i

. C.

2 i

. D.

12i

Lời giải

S phc liên hp ca s phc

12zi

là

12zi

Câu 16: [2D4-1.1-1] Cho  

3 4 .zi  

 

là:

. B.

. C.

. D.

Lời giải

Chọn B.

Ta có

 

3 4 5.z    

Câu 17: [2D4-1.2-2] . Tp hp tt c m biu din các s phc

tha mãn:

24zi  

ng tròn

có tâm

và bán kính

lt là:

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 12

 

2; 1I 

;

4R 

. B.

 

2; 1I 

;

2R 

. C.

 

2; 1I 

;

4R 

. D.

 

2; 1I 

;

 

2; 1I 

Lời giải

Chọn A.

Gi s phc

 

,z x iy x y  

Ta có:

   

2 4 2 1 4z i x y i        

   

2 1 16xy    

Vy tp hp tt c m biu din các s phc

tha mãn:

24zi  

ng tròn có tâm

 

2; 1I 

và có bán kính

4R 

Câu 18: [2D4-1.2-2] Trong mt phng t 

Oxy

, Gi

l    m biu din s phc

12i

44i

3i

. S phc biu din trng tâm tam giác

ABC

là

13i

. B.

13i

. C.

39i

. D.

39i

Lời giải

Chọn B.

Ta có

 

1; 2A 

 

4; 4B 

 

0; 3C 

nên trng tâm

ca tam giác ABC có t là

 

1; 3G 

. Do

 phc biu dim

là

13i

Câu 19: [2D4-2.2-1] Cho s phc

23zi

a s phc

 

1w i z

26w 

. B.

37w 

. C.

5w 

. D.

4w 

Lời giải

Chọn A.

Ta có

 

1w i z

  

1 2 3ii  

5 i

 

5 1 26w    

Câu 20: [2D4-2.2-1] Tìm t m biu din ca s phc

  

2 3 4







 

1; 4

. B.

 

1;4

. C.

 

1; 4

. D.

 

1;4

Lời giải

Chọn A.

Ta có

  

2 3 4







5 14







  

5 14 3 2

ii



13 52

i



14i  

m biu din cho s phc

có t

 

1; 4

Câu 21: [2D4-2.1-1] Cho hai s phc

23zi

45zi  

. Tính

z z z

22zi  

. B.

22zi  

. C.

22zi

. D.

22zi

Lời giải

Chọn A.

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 13

z z z

 

2 3 4 5ii    

22i  

Câu 22: [2D4-2.3-2] Cho s phc

z a bi

 

,ab

tha mãn

1 3 0z i z i   

. Tính

3S a b

S 

. B.

3S 

. C.

3S 

. D.

S 

Lời giải

Chọn B.

Gi s phc

z a bi

 

,ab



 

1 3 0a bi i a b i     

 





1 3 0a b a b i      

b a b









   





















Suy ra

1 3. 3

S    

Câu 23: [2D4-2.3-2] Tng phn thc và phn o ca s phc

tho mãn

 

12iz i z i   

bng

. B.

2

. C.

. D.

6

Lời giải

Chọn C.

t

z x yi

 

,xy



      

1 2 1 2iz i z i i x yi i x yi i          

 

2 0 4

x y x

x y yi i

  



      







, suy ra

6xy

Câu 24: [2D4-2.2-3] Cho s phc

z a bi

 

, , 0a b a

tha mãn

1 2 5zi  

và

. 10zz

. Tính

P a b

4P 

. B.

4P 

. C.

2P 

. D.

2P 

Lời giải

Chọn A.

T gi thit

1 2 5zi  

và

. 10zz

ta có h 

   

1 2 25



   











  











 

2 5 10











  

















hay











. Vy

2P 

Câu 25: [2D4-4.1-2] Gi

là các nghim c

8 25 0zz  

. Giá tr

zz

bng

. B.

. C.

. D.

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 14

Lời giải

Chọn C.



8 25 0zz  













   

4 3 4 3z z i i     

6i

6

Câu 26: [2H3-1.1-1] Trong không gian vi h t

,Oxyz

m

 

2; 3; 4A

 

6; 2; 2B

. Tìm ta

 

.AB

 

4;3;4AB 

. B.

 

4; 1; 2AB   

. C.

 

2;3;4AB 

. D.

 

4; 1;4AB 

ng dn gii

Chn B.

Ta có:

 

4; 1; 2AB   

Câu 27: [2H3-1.2-1] Trong không gian vi h t

Oxyz

m

 

3;2;1A

 

1;3;2B 

;

 

2;4; 3C 

ng

.AB AC

là

. B.

2

. C.

. D.

6

Hướng dẫn giải

Chọn A.

Ta có:

 

4;1;1AB 

và

 

1;2; 4AC   

. Vy

. 4 2 4 2A B AC    

Câu 28: [2H3-1.2-1] Trong không gian vi h t

Oxyz

m

 

3;2;8M

 

0;1;3N

và

 

2; ;4Pm

. Tìm

 tam giác

MNP

vuông ti

25m 

. B.

4m 

. C.

1m 

. D.

10m 

Lời giải

Chọn D.

Ta có

 

3; ;1 5NM 

 

2; 1 ;1NP m

Do tam giác

MNP

vuông ti

nên

. 0 6 1 5 0 10NM NP m m        

Câu 29: [2H3-1.2-2] Trong không gian vi h t

Oxyz

, cho hình hp

.ABCD A B C D

   

, bit t

 

3;2;1A 

 

4;2;0C

 

2;1;1B





 

3;5;4D



. Tìm t



 

3;3;1A





. B.

 

3;3;3A





. C.

 

3; 3; 3A





. D.

 

3; 3;3A





Lời giải

Chọn B.

Gi

;2;







m ca

và

;3;









m ca



.ABCD A B C D

   

là hình hp nên

AII A



là hình bình hành nên

 

3;3;3AI A I A

  

  

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 15

Câu 30: [2H3-1.3-1] Trong không gian vi h t 

Oxyz

, cho mt c   

   

1 3 9x y z    

. Tìm t tâm

và bán kính

ca mt c

 

1;3;0I 

;

3R 

. B.

 

1; 3;0I 

;

9R 

. C.

 

1; 3;0I 

;

3R 

. D.

 

1;3;0I 

;

9R 

Hướng dẫn giải

Chọn C.

Mt c

 

1; 3;0I 

và bán kính

3R 

Câu 31: [2H3-1.3-1] Trong không gian

Oxyz

m

 

1;2;3M

và

 

1;2; 1N 

. Mt cng kính



   

2 1 20x y z    

. B.

   

2 1 5x y z    

   

2 1 5x y z    

. D.

   

2 1 20x y z    

Hướng dẫn giải

Chọn C.

Mt cng kính

có tâm

 

0;2;1I

m

và bán kính

5R IM

t c

   

2 1 5x y z    

Câu 32: [2H3-2.2-1] Trong không gian

Oxyz

, mt phng

 

: 2 3 3 0P x y z   

có mn là

 

1; 2;3

. B.

 

1;2; 3

. C.

 

1;2; 3

. D.

 

1;2;3

Lời giải

Chọn B.

Mn ca mt phng

 

là

 

1;2; 3n 

Câu 33: [2H3-2.4-1] Trong không gian

Oxyz



 

:2 2 0P x y z   

 

1; 2;2Q 

. B.

 

1; 1; 1N 

. C.

 

2; 1; 1P 

. D.

 

1;1; 1M 

Lời giải

Chọn B.

Thay t m



 

:2 2 0P x y z   



 

2.1 2 2 2 0 4 0      

nên

 

QP

 

2.1 1 1 2 0 0 0      

nên

 

NP

 

2.2 1 1 2 0 2 0      

nên

 

PP

2.1 1 1 2 0 2 0      

nên

 

MP

Câu 34: [2H3-2.3-2] Trong không gian

Oxyz

m

 

1;2;1A 

và

 

2;1;0B

. Mt phng qua 

và

vuông góc vi



Đề thi HK II – THPT Tân Phú – Đồng Nai Page 16

3 6 0x y z   

. B.

3 6 0x y z   

. C.

3 5 0x y z   

. D.

3 6 0x y z   

Lời giải

Chọn B.

Ta có

 

3; 1; 1AB   

Mt phng cn tìm vuông góc vi

nên nhn

 

3; 1; 1AB   

n.

a mt phng cn tìm là

     

3 1 2 1 0x y z     

3 6 0x y z    

Câu 35: [2H3-2.3-2] Trong không gian vi h t

Oxyz

, mt phng chm

 

1; 0;1A

 

1; 2; 2B 

và song song vi trc



2 2 0yz  

. B.

2 3 0xz  

. C.

2 1 0yz  

. D.

0x y z  

Lời giải

Chọn A.

Gi

 

là mt phng cn tìm.

 

//P Ox

nên

 

:0P by cz d  

 

chm

 

1; 0;1A

 

1; 2; 2B 

nên

2 2 0

b c d





  



  



Ta chn

12bc   



2d 

V

 

: 2 2 0P y z  

Câu 36: [2H3-2.7-1] Trong h trc t

Oxyz

u kin ca

 hai mt phng

 

:2 2 0P x y z  

và

 

: 1 0Q x y mz   

ct nhau là

m 

. B.

m 

. C.

1m 

. D.

m 

Lời giải

Chọn A.

Mt phng

 

   n

 

2;2; 1

n 

, Mt phng

 

   n

 

1;1;

nm

. Hai mt phng

 

và

 

ct nhau khi và ch n không cùng







Câu 37: [2H3-3.1-1] Trong không gian

Oxyz

ng thng

1 2 1

x y z







ng thng

có mt

 

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 17

 

1;2;1u 

. B.

 

2;1;0u 

. C.

 

2;1;1u 

. D.

 

1;2;0u 

Lời giải

Chọn A.

Câu 38: Trong không gian

Oxyz

ng thng

1 2 3

2 1 2

x y z

  







 

2; 1; 2Q 

. B.

 

1; 2; 3M   

. C.

 

1; 2; 3P

. D.

 

2;1; 2N 

Lời giải

Chọn C

Câu 39: Ta có:

 

1 2 1

2 2 1;2;3

3 2 3

x t x

y t y P d

z t z



  





     





  



.[2H3-3.2-1] Trong không gian

Oxyz

ng thng

m

 

1;4; 7A 

và vuông góc vi mt phng

2 2 3 0x y z   



1 4 7

1 2 2

x y z  





. B.

1 4 7

x y z  





1 4 7

1 2 2

x y z  





. D.

1 4 7

1 2 2

x y z  





Lời giải

Chọn D.

ng thng m

 

1;4; 7A 

và vuông góc vi mt phng

2 2 3 0x y z   

nên có mt

 

 

1;2; 2u 



1 4 7

1 2 2

x y z  





Câu 40: [2H3-3.2-1] Trong không gian

Oxyz

ng thng cha trc

 là

















. B.

















. C.

















. D.

















Lời giải

Chọn B.

Trc

qua

 

0;0;0O

 

 

0;1;0j 



















Câu 41: [2H3-3.3-2] Trong không gian

,Oxyz

ng thng

3 2 4

1 1 2

x y z

  





ct mt phng

 

Oxy

ti

m có t là

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 18

 

3; 2; 0 .

 

3; 2; 0 .

 

1; 0; 0 .

 

1; 0; 0 .

Lời giải

Chọn D.

 cng thng

là:

 

d y t







  









 

:0Oxy z 

T m ca

và

 

Oxy

ng vi

tha mãn

4 2 0 2tt    

















T m ca

và

 

Oxy

là

 

1;0;0 .

Câu 42: Trong không gian

Oxyz

, cho mt phng

 

:2 3 0P x y z   

ng thng

2 1 5

x y z







Tính khong cách t d n mt phng

 

( ;( ))

d d P 

. B.

( ;( )) 6d d P 

. C.

( ;( )) 1d d P 

. D.

( ;( ))

d d P 

Lời giải

Chọn D

Ta có

. 0 ( )

n u d P

Ly

(0;0; 2)Md

222

2.0 1.0 1.( 2) 3

( ;( )) ( ;( ))

2 1 1

d d P d M P

   

  



Câu 43: [2H3-2.6-1] Trong không gian

Oxyz

tính khong cách t m

 

1;2; 3M 

n mt phng

 

: 2 2 2 0   P x y z

. B.

. C.

. D.

Lời giải

Chọn C.

Ta có

 

, d M P

 

1 2.2 2. 3 2

1 2 2

   



  

Câu 44: [2H3-2.6-2] Trong không gian

Oxyz

a mt cu có tâm

 

1;2; 1I 

và tip xúc mt phng

 

: 2 2 8 0P x y z   

     

2 2 2

1 2 1 3x y z     

     

2 2 2

1 2 1 9x y z     

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 19

     

2 2 2

1 2 1 3x y z     

     

2 2 2

1 2 1 9x y z     

Lời Giải

Chọn B

Ta có:

 

   

1 4 2 8

1 2 2

d I P

  

  

   

Do mt cu có tâm

 

1;2; 1I 

và tip xúc mt phng

 

: 2 2 8 0P x y z   

có bán kính

 

;3R d I P



     

2 2 2

1 2 1 9x y z     

Câu 45: [2H3-2.7-3] Trong không gian vi h trc t

Oxyz



 

:2 2 0P x y z m   

và



 

2 2 2

: 2 4 6 2 0S x y z x y z      





 



 



 





. B.

. C.

. D.

Lời giải

Chọn C.

 

có tâm

 

1; 2;3I 

và bán kính

4R 





lên

 



 

2.1 2 2.3 6

2 1 2

IH d I P

   

  

  



 

có chu vi là



nên có bán kính là





 



 



 





IH R r  

16 12

m

  

66m  









  





















Câu 46: [2H3-1.1-1] Trong không gian

Oxyz

m

 

1;2;3M

. Hình chiu ca

lên trc

m

 

1;0;3P

. B.

 

0;2;0Q

. C.

 

1;0;0R

. D.

 

0;0;3S

Lời giải

Chọn B.

Hình chiu ca

 

1;2;3M

lên trc

m

 

0;2;0Q

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 20

Câu 47: [2H3-1.1-1] Trong không gian vi h t

Oxyz

m

 

3; 1;2M 

. m

i xng vi

qua mt phng

 

Oyz

là

 

0; 1;2N 

. B.

 

3;1; 2N 

. C.

 

3; 1;2N 

. D.

 

0;1; 2N 

Hướng dẫn giải

Chọn C.

Vì

i xng vi

qua mt phng

 

Oyz

nên

 

3; 1;2N 

Câu 48: [2H3-1.1-1] Trong không gian

Oxyz

m

 

5;7; 13M 

. Gi

là hình chiu vuông góc ca

trên mt phng

 

Oyz

. T m

là?

 

5;0; 13H 

. B.

 

0;7; 13H 

. C.

 

5;7;0H

. D.

 

0; 7;13H 

Lời giải

Chọn B.

là hình chiu vuông góc ca

trên mt phng t

 

Oyz

nên

 

0;7; 13H 

Câu 49: P[2H3-4.1-4] Cho hình vuông

ABCD

cnh

. Trên hai tia

,Bx

vuông góc vi mt phng

 

ABCD

và cùng chiu lt lm

sao cho

;

BM 

2DN a

. Tính góc



gia

hai mt phng

 

AMN

và

 

CMN





. B.





. C.





. D.





Hướng dẫn giải

Chọn D.

Cách 1: Gn h trc t :

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 21

Ta có:

 

0;0;0B

 

0; ;0Aa

 

;0;0Ca

0;0;







 

; ;2N a a a

0; ;

AM a









 

0;0;2AN a

, 2 ; ;

AM AN a a













n ca mp

 

AMN

; 0;

CM a









 

0; ; 2CN a a

, ;2 ;

CM CN a a















n ca mp

 

CMN



4 4 4 4

cos 0

4 . 4

16 16

a a a a







   



  

Cách 2:

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 22

Tacó:

 

c.c.cAMN CMN  

nên k

CH MN

ti

thì

AH MN

Mà

   

AMN CMN MN

nên góc



gia hai mt phng

 

AMN

và

 

CMN

là góc gia hai

ng thng

, HA HC

Ta có:

MC BC MB  

5NC CD ND a  

2 2 2

49 9

16 4

MN ME EN a    

2 2 2

cos

MC NC MN

MCN

MC NC





sin

MCN

. .sin

MCN

S MC NC MCN  

T 

MCN

CH a AH

  

. Do

2 2 2

AH CH AC

nên tam giác

AHC

vuông ti

Vy góc ging thng

, HA HC

bng

90

Câu 50: [4]Cho hàm s

 

y f x

 th ca hàm s

 

y f x





t

( ) 2 ( ) ( 1)g x f x x  

M 

     

1 3 5g g g  

. B.

     

5 1 3g g g  

     

1 5 3g g g  

. D.

     

3 5 1g g g  

Lời giải

Đề thi HK II – THPT Tân Phú – Đồng Nai Page 23

Chọn C.

Gi

,SS

là din tích hai phn hình phng gii hn b th

 



ng thng

yx



hình v.

             

2 2 [ ' 1 ] ' 3 1 0 3 1S f x x dx g x dx g g g g



          



         

2 2 [ ' 1 ] ' 3 5 0S f x x dx g x dx g g        



   

35gg

Mt khác t  th ta có

SS

22SS

(3) ( 1) (3) (5) ( 1) (5)g g g g g g       

Vy

( 1) (5) (3)g g g  

Bấm Tải xuống để xem toàn bộ.

| 1/23

| | Tải xuống

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2019– 2020 ĐỒNG NAI
Môn thi: TOÁN – KHỐI 12
TRƯỜNG THPT TÂN PHÚ Thời gian : 90 phút – Trắc Nghiệm, không kể thời gian phát đề 2 2 Câu 1: Cho I  f
 xdx  3. Khi đó J  4 f
 x3dx  bằng: 0 0 A. 2 . B. 6 . C. 8 . D. 4 . 2020 2 dx Câu 2:
Tính tích phân I   . x 1
A. I  2020.ln 2 1. B. 2020 I  2 .
C. I  2020.ln 2 . C. I  2020 . a Câu 3:
Có bao nhiêu giá trị thực của a để có 2x  5dx  a  4 0 A. 1. B. 0 . C. 2 . D. Vô số. e f  x e Câu 4:
Cho hàm số f  x liên tục trong đoạn 1;e , biết dx  1 
, f e  1. Khi đó I  f   x.ln d x x x 1 1 bằng A. I  4 . B. I  3 . C. I  1. D. I  0 . 2 Câu 5: Tính  ex I x dx  . 1 A. 2 I  e . B. 2 I   e . C. 2 I  3e  2e . D. I  e . 1 Câu 6: Tính tích phân  2   1 x I x
e dx bằng cách đặt u  2x 1, d x
v  e dx . Mệnh đề nào sau đây đúng? 0 1 1 1 1 A.  2   1 x  2 x I x e e dx  .
B.  2   x 2 1 x I x e  e dx  . 0 0 0 0 1 1 1 1
C.  2   x 2 1 x I x e  e dx  . D.  2   1 x  2 x I x e e dx  . 0 0 0 0  2 Câu 7: Tính tích phân 4
I  cos x sin x dx 
bằng cách đặt t  cos x , mệnh đề nào dưới đây đúng ? 0   1 1 2 2 A. 4
I  t dt  . B. 4
I   t dt  . C. 4
I  t dt  . D. 4
I   t dt  . 0 0 0 0
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 1 2 4 Câu 8:
Cho hàm số y  f  x liên tục trên . Biết . x f
  2xdx  2, hãy tính I  f  xdx 0 0 1 A. I  2 . B. I  1. C. I  . D. I  4 . 2 Câu 9:
Diện tích S hình phẳng giới hạn bởi các đường 3
y  x  2x 1, trục hoành, x  1 và x  2 là 31 49 21 39 A. S  . B. S  . C. S  . D. S  . 4 4 4 4
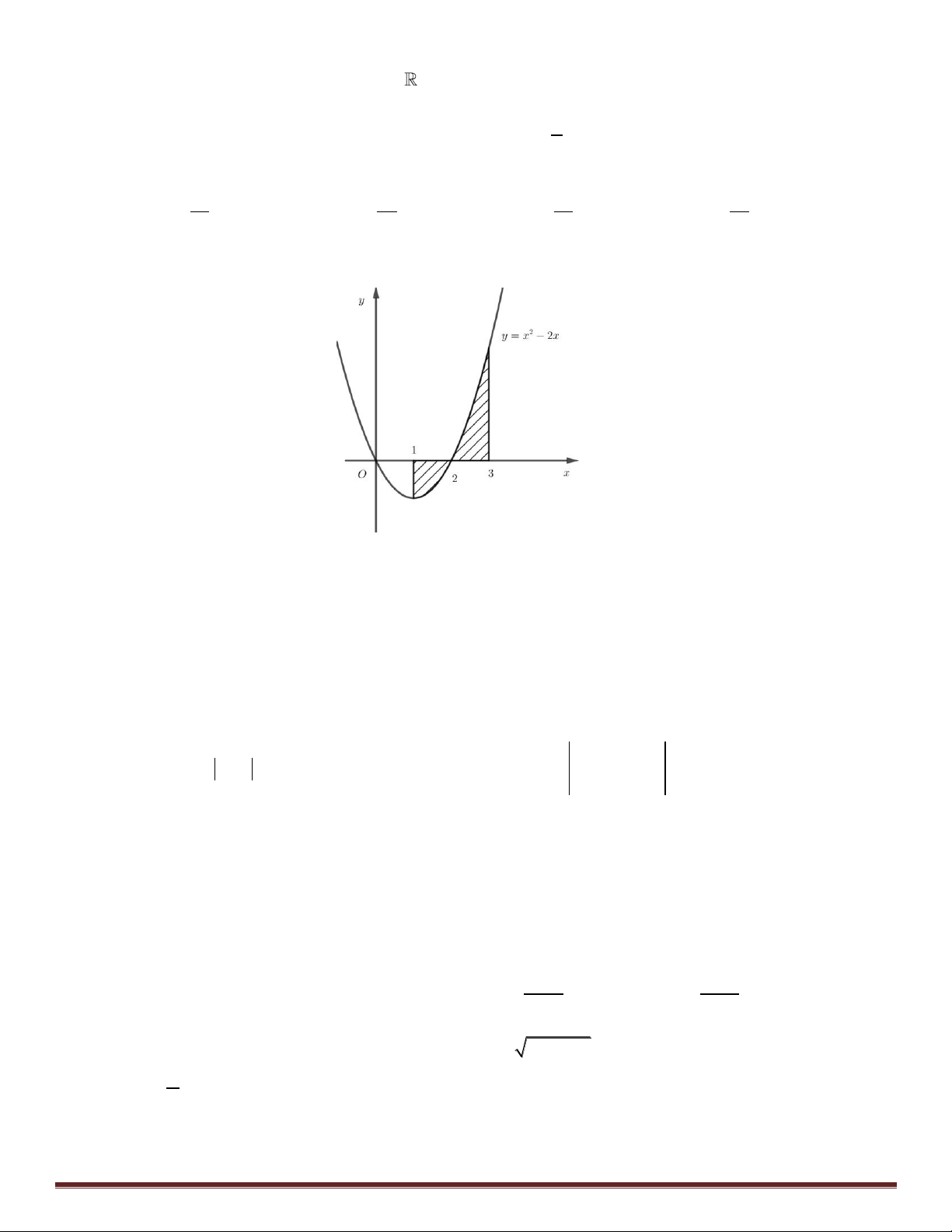
Câu 10: iện t ch ph n h nh phẳng gạch ch o trong h nh v n đư c t nh theo c ng th c nào dưới đây? 3 2 3 A.  2
x  2xdx . B.  2
x  2xdx   2
x  2xdx . 1 1 2 2 3 2 3 C.  2
x  2xdx   2
x  2xdx . D.  2
x  2xdx   2
x  2x dx . 1 2 1 2
Câu 11: Cho hình phẳng  D đư c giới hạn bởi các đường x  0 , x   , y  0 và y  sin x . Thể tích V
của khối tròn xoay tạo thành khi quay  D xung quanh trục Ox đư c tính theo công th c   
A. V   sin x dx  . B. 2 V   sin d x x  .
C. V   sin xdx . D. 0 0 0  2 V  sin d x x  . 0
Câu 12: Một chiếc máy bay chuyển động tr n đường ăng với vận tốc v t 2
 t 10t m/s với t là thời gian
đư c t nh theo đơn vị giây kể từ khi máy bay bắt đ u chuyển động. Biết khi máy ay đạt vận tốc
200m/s thì nó rời đường ăng. Quãng đường máy ay đã di chuyển tr n đường ăng là 4000 2500 A. 500m . B. 2000m . C. m . D. m . 3 3
Câu 13: Cho hình phẳng D giới hạn bởi đường cong y  2  cos x , trục hoành và các đường thẳng x  0 ,  x 
. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 2
A. V   1.
B. V   1.
C. V      1 .
D. V      1 .
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 2
Câu 14: Ph n thực và ph n ảo của số ph c z  1 2i l n lư t là: A. 2 và 1 B. 1 và 2i . C. 1 và 2 . D. 1 và i .
Câu 15: Số ph c liên h p của số ph c z  1 2i là A. 1 2i . B. 1   2i . C. 2  i . D. 1   2i .
Câu 16: Cho số ph c z  3
  4 .i M đun của số ph c z là: A. 3 . B. 5 . C. 4 . D. 7 .
Câu 17: Tập h p tất cả các điểm biểu diễn các số ph c z thỏa mãn: z  2  i  4 là đường tròn có tâm I và
bán kính R l n lư t là: A. I  2  ;  1 ; R  4 . B. I  2  ; 
1 ; R  2 . C. I 2;   1 ; R  4 .
D. I 2;   1 ; I 2;   1 .
Câu 18: Trong mặt phẳng tọa độ Oxy , Gọi A , B , C l n lư t là các điểm biểu diễn số ph c 1
  2i , 4  4i , 3
 i . Số ph c biểu diễn trọng tâm tam giác ABC là A. 1  3i . B. 1 3i . C. 3   9i . D. 3  9i .
Câu 19: Cho số ph c z  2  3i . M đun của số ph c w  1 i z
A. w  26 .
B. w  37 .
C. w  5 . D. w  4 .
23i4i
Câu 20: Tìm tọa độ điểm biểu diễn của số ph c z  . 3  2i A.  1  ; 4  . B. 1; 4 . C. 1; 4   . D.  1  ;4
Câu 21: Cho hai số ph c z  2  3i , z  4
  5i . Tính z  z  z . 1 2 1 2 A. z  2   2i . B. z  2   2i .
C. z  2  2i .
D. z  2  2i .
Câu 22: Cho số ph c z  a  bi a,b   thỏa mãn z 1 3i  z i  0 . Tính S  a  3b . 7 7 A. S   . B. S  3. C. S  3  . D. S  . 3 3
Câu 23: Tổng ph n thực và ph n ảo của số ph c z thoả mãn iz  1 i z  2  i bằng A. 2 . B. 2  . C. 6 . D. 6  .
Câu 24: Cho số ph c z  a  bi  ,
a b  , a  0 thỏa mãn z 1 2i  5 và .
z z  10 . Tính P  a  b .
A. P  4 . B. P  4  . C. P  2  .
D. P  2 .
Câu 25: Gọi z , z là các nghiệm của phương tr nh 2
z  8z  25  0 . Giá trị z  z bằng 1 2 1 2 A. 8 . B. 5 . C. 6 . D. 3 .
Câu 26: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A2; 3; 4 , B6; 2; 2 . Tìm tọa độ v ctơ . AB
A. AB  4;3;4 . B. AB  4; 1  ; 2
  . C. AB   2  ;3;4. D. AB  4; 1  ;4 .
Câu 27: Trong không gian với hệ tọa độ Oxyz , cho a điểm A3;2;  1 , B  1
 ;3;2 ; C 2;4;  3 . Tích vô hướng A . B AC là A. 2 . B. 2  . C. 10 . D. 6  .
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 3
Câu 28: Trong không gian với hệ tọa độ Oxyz , cho a điểm M 3; 2;8 , N 0;1;3 và P 2; ;
m 4 . Tìm m để
tam giác MNP vuông tại N . A. m  25. B. m  4 . C. m  1  . D. m  10  .
Câu 29: Trong không gian với hệ tọa độ Oxyz , cho hình hộp ABC . D A B  C  D
  , biết tọa độ A 3  ;2;  1 ,
C 4;2;0 , B 2  ;1; 
1 , D3;5; 4 . Tìm tọa độ A . A. A 3  ;3;  1 . B. A 3  ;3;3. C. A 3  ; 3  ; 3  . D. A 3  ; 3  ;3. 2 2
Câu 30: Trong không gian với hệ tọa độ Oxyz , cho mặt c u có phương tr nh  x     y   2 1 3  z  9 . Tìm
tọa độ tâm I và bán kính R của mặt c u đó. A. I  1
 ;3;0 ; R  3. B. I 1; 3
 ;0 ; R  9. C. I 1; 3
 ;0 ; R  3. D. I  1  ;3;0 ; R  9.
Câu 31: Trong không gian Oxyz , cho hai điểm M 1; 2;  3 và N  1  ;2; 
1 . Mặt c u đường kính MN có phương tr nh là 2 2 2 2 A. 2
x   y  2   z   1  20 . B. 2
x   y  2   z   1  5 . 2 2 2 2 C. 2
x   y  2   z   1  5 . D. 2
x   y  2   z   1  20 .
Câu 32: Trong không gian Oxyz , mặt phẳng  P : x  2y  3z  3  0 có một vectơ pháp tuyến là A. 1; 2  ;3. B. 1;2; 3  . C.  1  ;2; 3  . D. 1; 2;3 .
Câu 33: Trong không gian Oxyz , điểm nào dưới đây nằm tr n mặt phẳng  P : 2x  y  z  2  0 . A. Q 1; 2  ;2 . B. N 1; 1  ;  1 . C. P 2; 1  ;  1 .
D. M 1;1;   1 .
Câu 34: Trong không gian Oxyz , cho hai điểm A 1  ;2; 
1 và B 2;1;0 . Mặt phẳng qua đi A và vuông góc
với AB có phương tr nh là
A. 3x  y  z  6  0 .
B. 3x  y  z  6  0 . C. x  3y  z  5  0 . D. x  3y  z  6  0 .
Câu 35: Trong không gian với hệ tọa độ Oxyz , mặt phẳng ch a hai điểm A1; 0;  1 , B  1  ; 2; 2 và song song
với trục Ox có phương tr nh là
A. y  2z  2  0 .
B. x  2z  3  0 .
C. 2y  z 1  0 .
D. x  y  z  0 .
Câu 36: Trong hệ trục tọa độ Oxyz , điều kiện của m để hai mặt phẳng  P : 2x  2y  z  0 và
Q: x  y  mz 1 0 cắt nhau là 1 1 1 A. m   . B. m  . C. m  1  . D. m   . 2 2 2 x  2 y 1 z
Câu 37: Trong không gian Oxyz , cho đường thẳng d : 
 . Đường thẳng d có một vec tơ chỉ 1  2 1 phương là
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 4 A. u  1  ;2;1 .
B. u  2;1;0 .
C. u  2;1;1 . D. u  1  ;2;0 . 4   3   2   1   x 1 y  2 z  3
Câu 38: Trong không gian Oxyz , đường thẳng d :  
đi qua điểm nào dưới đây? 2 1  2
A. Q 2; 1; 2 . B. M  1
 ;  2; 3. C. P1; 2; 3 . D. N  2  ;1;  2 .
Câu 39: Trong không gian Oxyz , đường thẳng đi qua điểm A1; 4;7 và vuông góc với mặt phẳng
x  2y  2z  3  0 có phương tr nh là x 1 y  4 z  7 x 1 y  4 z  7 A.   . B.   . 1 2 2  1 4 7  x 1 y  4 z  7 x 1 y  4 z  7 C.   . D.   . 1 2  2  1 2 2 
Câu 40: Trong không gian Oxyz , đường thẳng ch a trục Oy có phương tr nh tham số là x  0 x  0 x  t x  0    
A.  y  1 .
B.  y  t .
C.  y  0 .
D.  y  0 .     z  t  z  0  z  0  z  t  x  3 y  2 z  4
Câu 41: Trong không gian Oxyz, đường thẳng d :  
cắt mặt phẳng Oxy tại điểm có tọa 1 1  2 độ là A.  3  ; 2; 0. B. 3;  2; 0. C.  1  ; 0; 0. D. 1; 0; 0. x y z  2
Câu 42: Trong không gian Oxyz , cho mặt phẳng  P : 2x  y  z  3  0 và đường thẳng d :   . 2 1 5 
Tính khoảng cách từ d đến mặt phẳng  P . 1 6
A. d (d;(P))  .
B. d(d;(P))  6 .
C. d(d;(P))  1.
D. d (d; (P))  . 6 6
Câu 43: Trong không gian Oxyz tính khoảng cách từ điểm M 1; 2;  3 đến mặt phẳng
P: x  2y 2z 2  0. 11 1 A. . B. . C. 3 . D. 1 3 3
Câu 44: Trong không gian Oxyz , phương tr nh nào dưới đây là phương tr nh của mặt c u có tâm I 1; 2;   1
và tiếp xúc mặt phẳng  P : x  2y  2z 8  0 ? 2 2 2 2 2 2 A.  x  
1   y  2   z   1  3 B.  x  
1   y  2   z   1  9 2 2 2 2 2 2 C.  x  
1   y  2   z   1  3 D.  x  
1   y  2   z   1  9
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 5
Câu 45: Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng  P : 2x  y  2z  m  0 và mặt c u S 2 2 2
: x  y  z  2x  4y  6z  2  0 . Có ao nhi u giá trị nguy n của m để mặt phẳng  P cắt
mặt c u S  theo giao tuyến là đường tròn T  có chu vi ằng 4 3 . A. 3 . B. 4 . C. 2 . D. 1.
Câu 46: Trong không gian Oxyz , cho điểm M 1; 2; 
3 . Hình chiếu của M lên trục Oy là điểm
A. P 1;0;3 .
B. Q 0;2;0 .
C. R 1;0;0 .
D. S 0;0;3 .
Câu 47: Trong không gian với hệ tọa độ Oxyz , cho điểm M 3;1; 2 . Điểm N đối x ng với M qua mặt phẳng Oyz là
A. N 0;1;2 .
B. N 3;1; 2 . C. N  3  ;1;2 .
D. N 0;1; 2 .
Câu 48: Trong không gian Oxyz , cho điểm M 5;7; 1  
3 . Gọi H là hình chiếu vuông góc của M trên mặt
phẳng Oyz . Tọa độ điểm H là? A. H 5;0; 1  3. B. H 0;7; 1  3 .
C. H 5;7;0 . D. H 0; 7  ;13 .
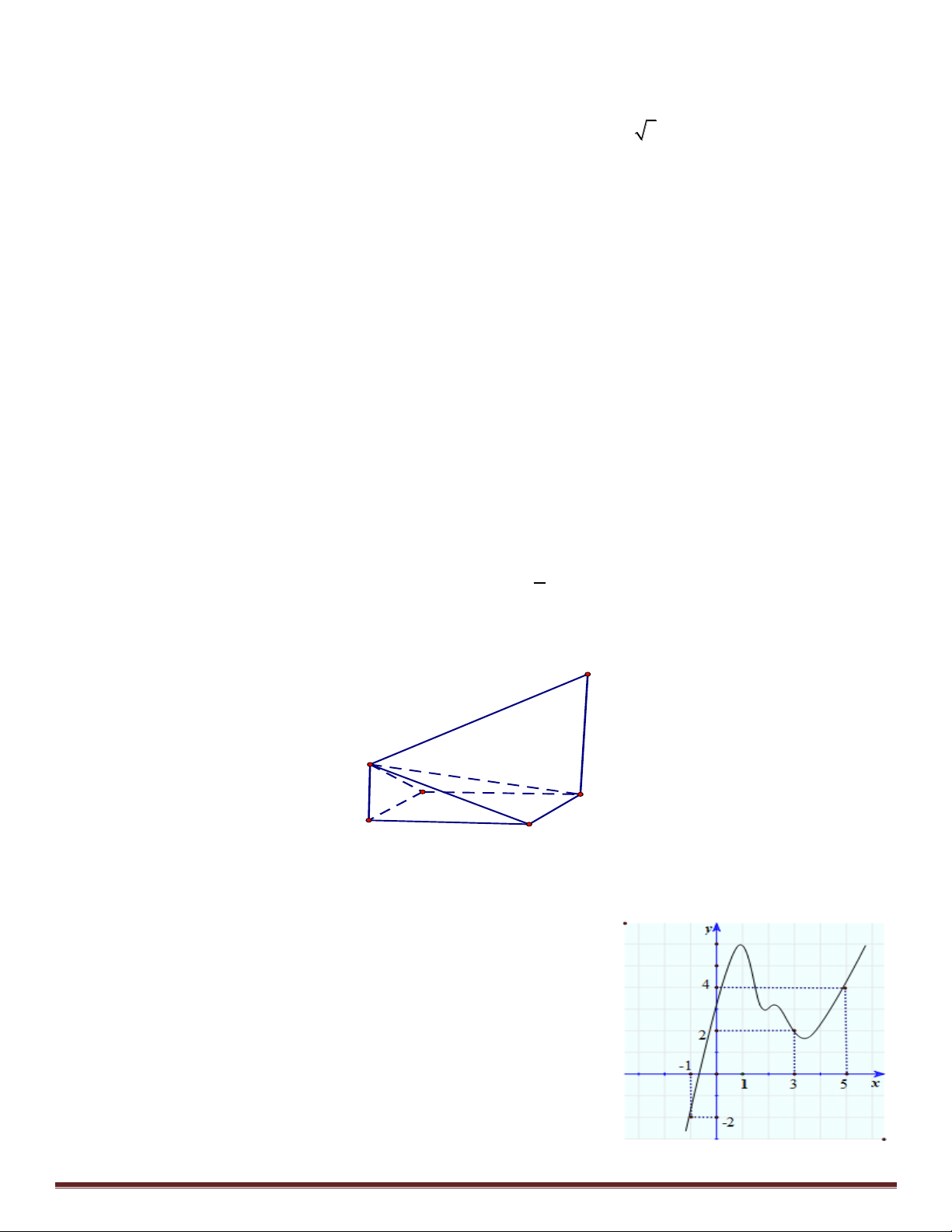
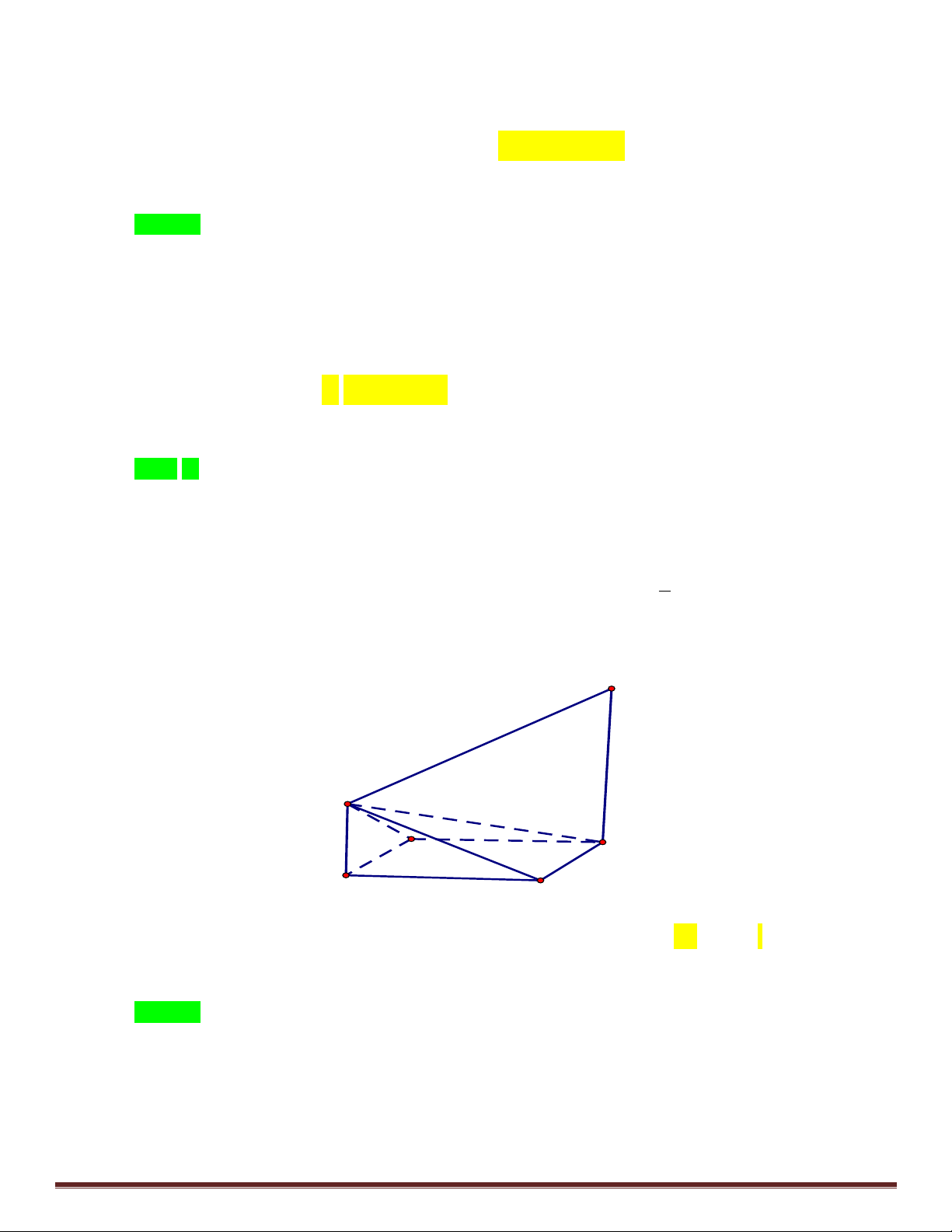
Câu 49: Cho hình vuông ABCD cạnh a . Trên hai tia Bx, Dy vuông góc với mặt phẳng  ABCD và cùng a
chiều l n lư t lấy hai điểm M , N sao cho BM 
; DN  2a . Tính góc  giữa hai mặt phẳng 4
 AMN và CMN. N M A D B C A.   30 . B.   60 . C.   45 . D.   90 .
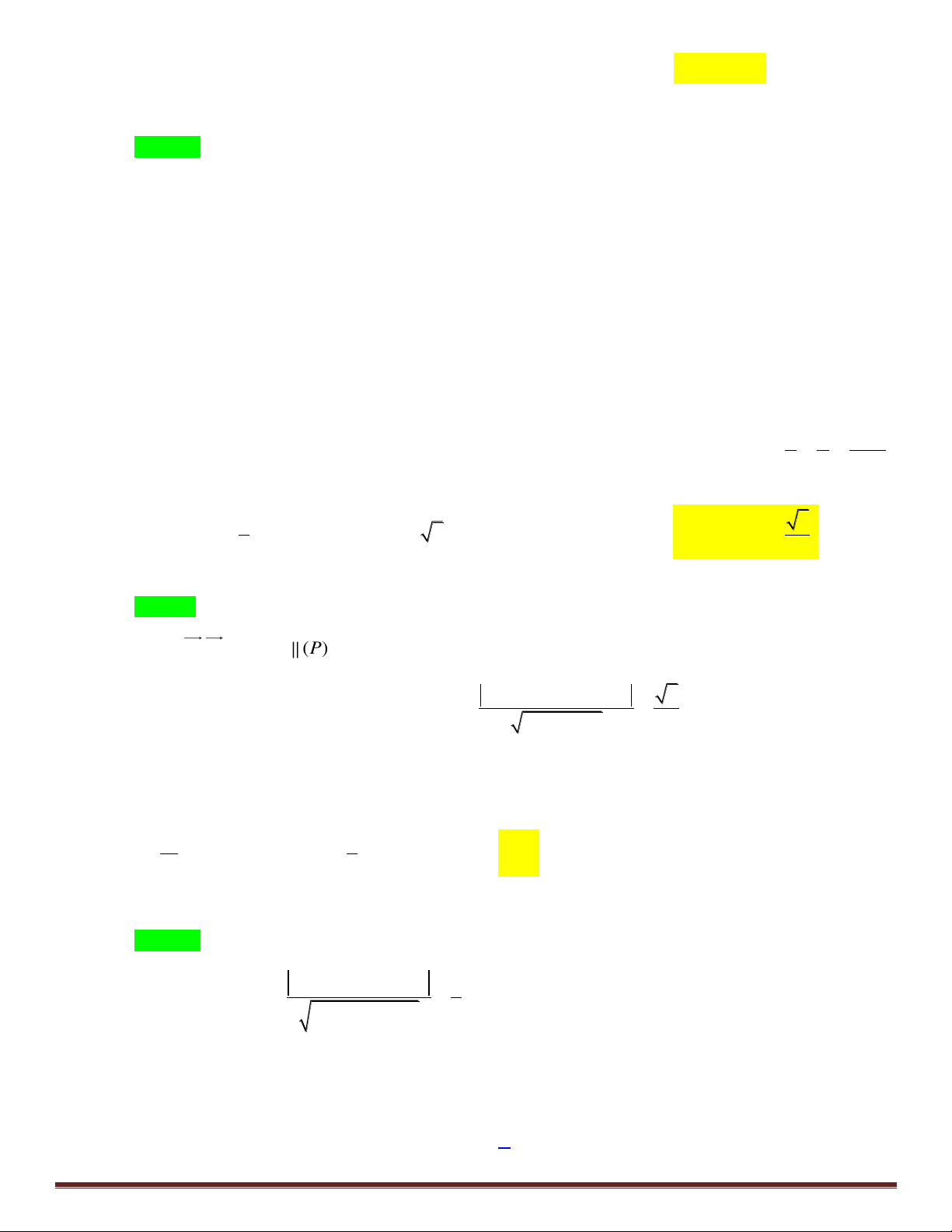
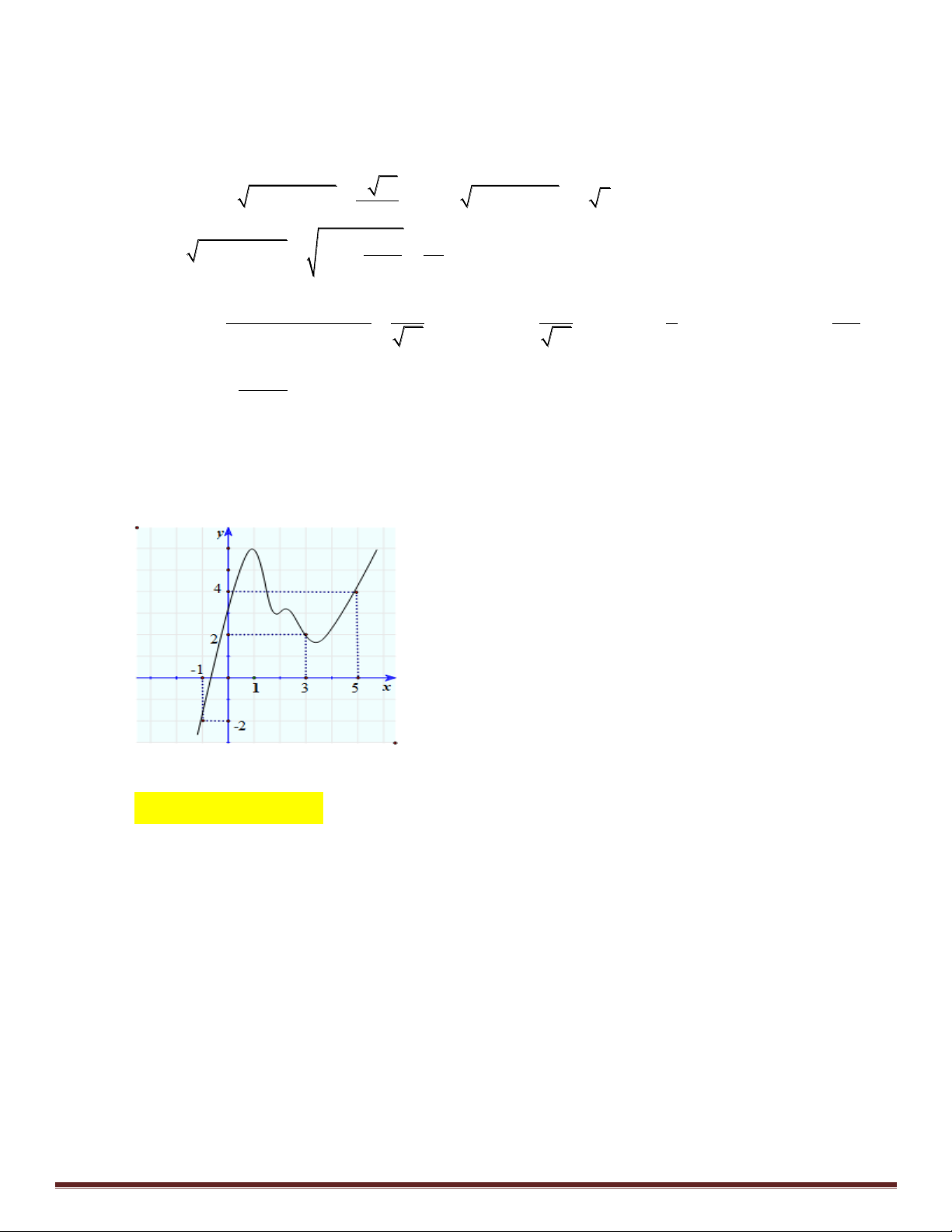
Câu 50: [4]Cho hàm số y  f  x . Đồ thị của hàm số y  f  x như h nh n. Đặt 2
g(x)  2 f (x)  (x 1) . Mệnh đề nào dưới đây đúng ? A. g  
1  g 3  g 5 .
B. g 5  g   1  g 3 . C. g  
1  g 5  g 3 .
D. g 3  g 5  g   1 .
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 6 HƯỚNG DẪN GIẢI 2 2 Câu 1:
[2D3-2.1-1] Cho I  f
 xdx  3. Khi đó J  4 f
 x3dx  bằng: 0 0 A. 2 . B. 6 . C. 8 . D. 4 . Lời giải Chọn B. 2 2 2 2
Ta có J  4 f
 x3dx  4 f 
 xdx3 dx  4.33x  6  . 0 0 0 0 2020 2 dx Câu 2:
[2D3-2.1-2] Tính tích phân I   . x 1
A. I  2020.ln 2 1. B. 2020 I  2 .
C. I  2020.ln 2 . C. I  2020 . Lời giải Chọn C. 2020 2
Ta có: I  ln x   2020 ln 2 ln1  2020.ln2. 1 a Câu 3:
[2D3-2.1-2] Có bao nhiêu giá trị thực của a để có 2x  5dx  a  4 0 A. 1. B. 0 . C. 2 . D. Vô số. Lời giải Chọn A. a a
Ta có 2x  5dx  a  4   2
x  5x  a  4 2
 a  4a  4  0  a  2  0 0 e f  x Câu 4:
[2D3-2.3-2] Cho hàm số f  x liên tục trong đoạn 1;e , biết dx  1 
, f e  1. Khi đó x 1 e I  f   x.ln d x x bằng 1 A. I  4 . B. I  3 . C. I  1. D. I  0 . Lời giải Chọn D. e e e 1 Cách 1: Ta có I  f   x.ln d
x x  f  x.ln x  f
 x. dx  f e111 0 . 1 x 1 1
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 7  dx u   ln x  du  Cách 2: Đặt    x . dv  f  
xdx v  f  x e e e f x Suy ra I  f   x.ln d
x x  f  x   ln x  dx  f  e111 0. 1 x 1 1 2 Câu 5: [2D3-2.3-2] Tính  ex I x dx  . 1 A. 2 I  e . B. 2 I   e . C. 2 I  3e  2e . D. I  e . Lời giải Chọn A. u   x du dx Đặt    .
 dv  ex dx v  ex 2 Khi đó 2  ex  ex I x dx  2 2 2 e e ex    2 2 2
 2e  e e  e  e . 1 1 1 1 Câu 6:
[2D3-2.2-1] Tính tích phân  2   1 x I x
e dx bằng cách đặt u  2x 1, d x
v  e dx . Mệnh đề nào sau 0 đây đúng? 1 1 1 1 A.  2   1 x  2 x I x e e dx  .
B.  2   x 2 1 x I x e  e dx  . 0 0 0 0 1 1 1 1
C.  2   x 2 1 x I x e  e dx  . D.  2   1 x  2 x I x e e dx  . 0 0 0 0 Lời giải Chọn A. 1  2   1 x I x
e dx , đặt u  2x 1, d x
v  e dx  du  2dx , x v  e . 0 1   2   1 1 x  2 x I x e e dx  . 0 0  2 Câu 7:
[2D3-2.2-2] Tính tích phân 4
I  cos x sin x dx 
bằng cách đặt t  cos x , mệnh đề nào dưới đây đúng 0 ?
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 8   1 1 2 2 A. 4
I  t dt  . B. 4
I   t dt  . C. 4
I  t dt  . D. 4
I   t dt  . 0 0 0 0 Lời giải Chọn A.
Đặt t  cos x  dt  sin x dx  sin x dx  d  t . 
Đổi cận: x  0  t 1; x   t  0 . 2 0 1 Khi đó 4 I  t  dt 4  t dt  . 1 0 2 4 Câu 8:
[2D3-2.2-2] Cho hàm số y  f  x liên tục trên . Biết . x f
  2xdx  2, hãy tính I  f  xdx 0 0 1 A. I  2 . B. I  1. C. I  . D. I  4 . 2 Lời giải Chọn D. 2 Xét tích phân . x f
  2xdx  2, ta có 0 Đặ t t 2 x  d t  d x x 
. Đổi cận: Khi x  0 thì t  0 ; Khi x  2 thì t  4. 2 2 4 4 4 o đó 1 . x f
  2xdx  2  f
 tdt  2  f
 tdt  4  f
 xdx  4 hay I  4. 2 0 2 2 0 Câu 9:
[2D3-3.1-1] Diện tích S hình phẳng giới hạn bởi các đường 3
y  x  2x 1, trục hoành, x  1 và x  2 là 31 49 21 39 A. S  . B. S  . C. S  . D. S  . 4 4 4 4 Lời giải Chọn A. 2 31
Diện tích hình phẳng c n tìm là 3 S 
x  2x 1 dx   . 4 1
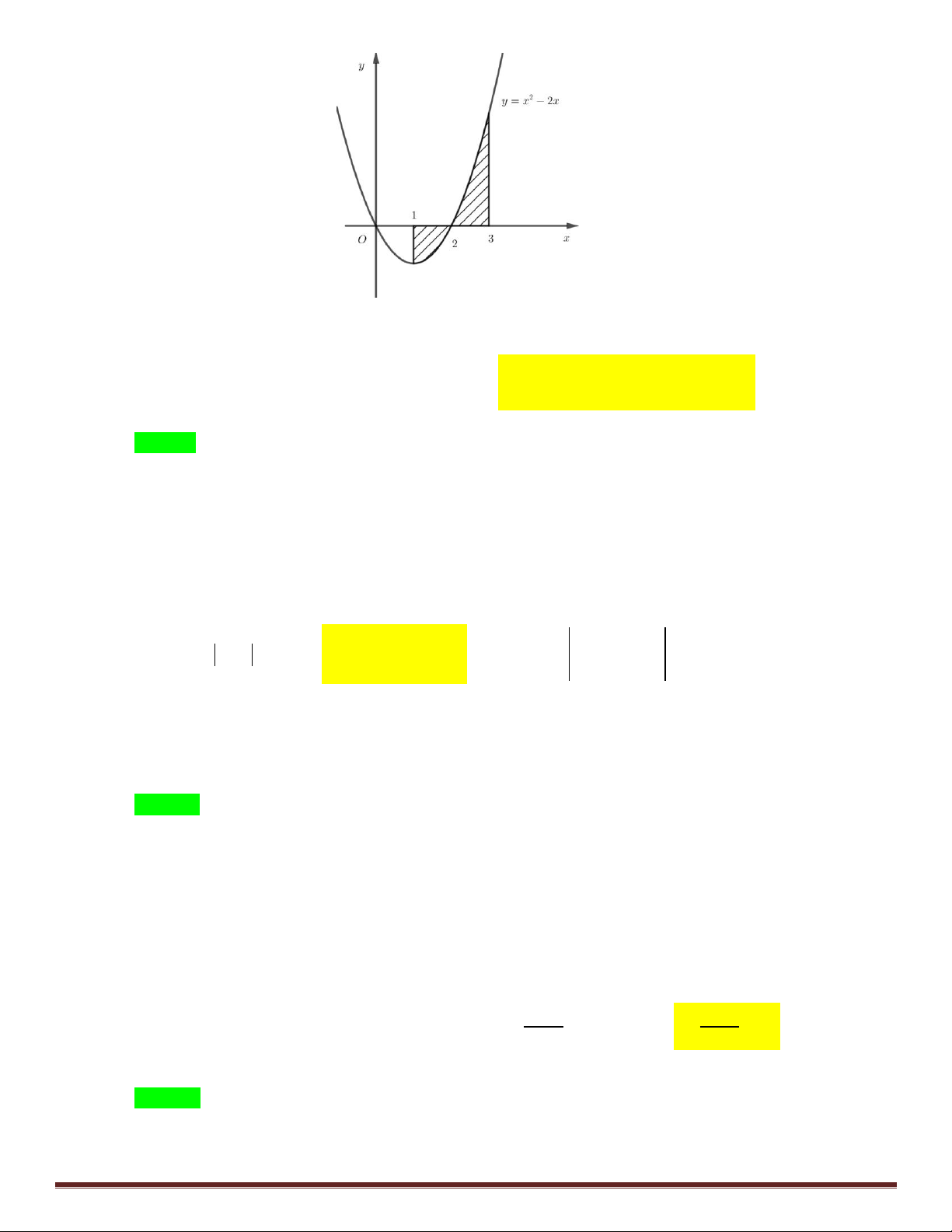
Câu 10: iện t ch ph n h nh phẳng gạch ch o trong h nh v n đư c t nh theo c ng th c nào dưới đây?
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 9 3 2 3 A.  2
x  2xdx . B.  2
x  2xdx   2
x  2xdx . 1 1 2 2 3 2 3 C.  2
x  2xdx   2
x  2xdx . D.  2
x  2xdx   2
x  2x dx . 1 2 1 2 Lời giải Chọn D 2 3
iện t ch ph n gạch ch o là: S   2x  2xdx   2x  2xdx. 1 2
Câu 11: [2D3-3.3-1] Cho hình phẳng  D đư c giới hạn bởi các đường x  0 , x   , y  0 và y  sin x .
Thể tích V của khối tròn xoay tạo thành khi quay  D xung quanh trục Ox đư c tính theo công th c   
A. V   sin x dx  . B. 2 V   sin d x x  .
C. V   sin xdx . D. 0 0 0  2 V  sin d x x  . 0 Lời giải Chọn B. 
Ta có thể tích của khối tròn xoay c n tính là 2 V   sin d x x  . 0
Câu 12: [2D3-3.5-2] Một chiếc máy bay chuyển động tr n đường ăng với vận tốc v t 2
 t 10t m/s với t
là thời gian đư c t nh theo đơn vị giây kể từ khi máy bay bắt đ u chuyển động. Biết khi máy ay đạt
vận tốc 200m/s thì nó rời đường ăng. Quãng đường máy ay đã di chuyển tr n đường ăng là 4000 2500 A. 500m . B. 2000m . C. m . D. m . 3 3 Lời giải Chọn D.
- Thời điểm máy ay đạt vận tốc 200m/s là nghiệm của phương tr nh:
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 10 t  2 t 10t  200 2
 t 10t  200  10 0    t 10s . t  20 
- Quãng đường máy bay di chuyển tr n đường ăng là: 10 10 3  t  2500
s    2t 10tdt 2    5t   m.  3  3 0 0
Câu 13: [2D3-3.3-2] Cho hình phẳng D giới hạn bởi đường cong y  2  cos x , trục hoành và các đường 
thẳng x  0 , x 
. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao 2 nhiêu?
A. V   1.
B. V   1.
C. V      1 .
D. V      1 . Lời giải Chọn D.
Thể tích khối tròn xoay khi quay D quanh trục hoành có thể tích là:   2 2  2
V   y dx 
  2cos xdx  2xsin x 2    1 . 0 0 0
Câu 14: [2D4-1.1-1] Ph n thực và ph n ảo của số ph c z  1 2i l n lư t là: A. 2 và 1 B. 1 và 2i . C. 1 và 2 . D. 1 và i . Lời giải Chọn C.
Số ph c z  1 2i có ph n thực và ph n ảo l n lư t là 1 và 2 .
Câu 15: [2D4-1.1-1] Số ph c liên h p của số ph c z  1 2i là A. 1 2i . B. 1   2i . C. 2  i . D. 1   2i . Lời giải
Số ph c liên h p của số ph c z  1 2i là z  1 2i .
Câu 16: [2D4-1.1-1] Cho số ph c z  3
  4 .i M đun của số ph c z là: A. 3 . B. 5 . C. 4 . D. 7 . Lời giải Chọn B.
Ta có z   2 2 3  4  5.
Câu 17: [2D4-1.2-2] . Tập h p tất cả các điểm biểu diễn các số ph c z thỏa mãn: z  2  i  4 là đường tròn
có tâm I và bán kính R l n lư t là:
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 11 A. I  2  ;  1 ; R  4 . B. I  2  ; 
1 ; R  2 . C. I 2;   1 ; R  4 .
D. I 2;   1 ; I 2;   1 . Lời giải Chọn A.
Gọi số ph c z  x  iy  , x y   Ta có: 2 2
z  2  i  4   x  2   y  
1 i  4   x  2   y   1  16
Vậy tập h p tất cả các điểm biểu diễn các số ph c z thỏa mãn: z  2  i  4 là đường tròn có tâm I  2  ; 
1 và có bán kính R  4 .
Câu 18: [2D4-1.2-2] Trong mặt phẳng tọa độ Oxy , Gọi A , B , C l n lư t là các điểm biểu diễn số ph c 1
  2i , 4  4i , 3
 i . Số ph c biểu diễn trọng tâm tam giác ABC là A. 1  3i . B. 1 3i . C. 3   9i . D. 3  9i . Lời giải Chọn B. Ta có A 1  ; 2   , B4; 4  ,C 0; 3
  nên trọng tâm G của tam giác ABC có tọa độ là G1;  3 . Do
đó, số ph c biểu diễn điểm G là 1 3i .
Câu 19: [2D4-2.2-1] Cho số ph c z  2  3i . M đun của số ph c w  1 i z
A. w  26 .
B. w  37 .
C. w  5 . D. w  4 . Lời giải Chọn A.
Ta có w  1 i z  1 i2  3i  5  i , w    2 2 5 1  26 .
23i4i
Câu 20: [2D4-2.2-1] Tìm tọa độ điểm biểu diễn của số ph c z  . 3  2i A.  1  ; 4  . B. 1; 4 . C. 1; 4   . D.  1  ;4 Lời giải Chọn A.
23i4i 514i 514i32i   i Ta có z    13 52   1   4i . 3  2i 3  2i 13 13
o đó điểm biểu diễn cho số ph c z có tọa độ  1  ; 4  .
Câu 21: [2D4-2.1-1] Cho hai số ph c z  2  3i , z  4
  5i . Tính z  z  z . 1 2 1 2 A. z  2   2i . B. z  2   2i .
C. z  2  2i .
D. z  2  2i . Lời giải Chọn A.
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 12
z  z  z  2  3i   4  5i  2   2i . 1 2
Câu 22: [2D4-2.3-2] Cho số ph c z  a  bi a,b   thỏa mãn z 1 3i  z i  0 . Tính S  a  3b . 7 7 A. S   . B. S  3. C. S  3  . D. S  . 3 3 Lời giải
Chọn B.
Gọi số ph c z  a  bi , a,b  
Ta có phương tr nh: a  bi 2 2
1 3i  a  b i  0  a     2 2 1
b  3  a  b i  0     a 1  0  a 1     4 2 2 b
  3 a  b  0 b    3 4 Suy ra S  1   3.  3. 3
Câu 23: [2D4-2.3-2] Tổng ph n thực và ph n ảo của số ph c z thoả mãn iz  1 i z  2  i bằng A. 2 . B. 2  . C. 6 . D. 6  . Lời giải Chọn C.
Đặt z  x  yi  , x y 
 . Khi đó iz 1i z  2
 i  ix  yi 1ix  yi  2  i        x  y x 2 y 0 x 4 2  yi  2  i    
, suy ra x  y  6 . y  2 y  2
Câu 24: [2D4-2.2-3] Cho số ph c z  a  bi  ,
a b  , a  0 thỏa mãn z 1 2i  5 và . z z  10 . Tính
P  a  b .
A. P  4 . B. P  4  . C. P  2  .
D. P  2 . Lời giải Chọn A.   a  2
1  b  22  25
Từ giả thiết z 1 2i  5 và .
z z  10 ta có hệ phương tr nh  2 2
a  b 10
a  2b  5
a  2b  5        a 1 a 3      hay  . Vậy P  2  . 2 2 a  b 10   2b  5  2 2  b 10 b   3  b  1
Câu 25: [2D4-4.1-2] Gọi z , z là các nghiệm của phương tr nh 2
z  8z  25  0 . Giá trị z  z bằng 1 2 1 2 A. 8 . B. 5 . C. 6 . D. 3 .
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 13 Lời giải Chọn C.
z  4  3i X t phương tr nh 2
z  8z  25  0 1  
 z  z  4  3i  4 3i  6i  6 . 1 2     z  4  3i  1
Câu 26: [2H3-1.1-1] Trong không gian với hệ tọa độ Oxyz, cho hai điểm A2; 3; 4 , B6; 2; 2 . Tìm tọa độ v ctơ . AB
A. AB  4;3;4 . B. AB  4; 1  ; 2
  . C. AB   2  ;3;4. D. AB  4; 1  ;4 . Hướng dẫn giải Chọn B. Ta có: AB  4; 1  ; 2   .
Câu 27: [2H3-1.2-1] Trong không gian với hệ tọa độ Oxyz , cho a điểm A3;2;1 , B  1
 ;3;2 ; C 2;4;  3 . T ch v hướng A . B AC là A. 2 . B. 2  . C. 10 . D. 6  . Hướng dẫn giải Chọn A. Ta có: AB   4  ;1;  1 và AC   1
 ;2; 4. Vậy A .
B AC  4  2  4  2 .
Câu 28: [2H3-1.2-1] Trong không gian với hệ tọa độ Oxyz , cho a điểm M 3; 2;8 , N 0;1;3 và P 2; ; m 4
. Tìm m để tam giác MNP vuông tại N . A. m  25. B. m  4 . C. m  1  . D. m  10  . Lời giải Chọn D. Ta có NM  3; ; 1
5 , NP  2;m   1 ; 1 .
Do tam giác MNP vuông tại N nên NM.NP  0  6  m 1 5  0  m  1  0 .
Câu 29: [2H3-1.2-2] Trong không gian với hệ tọa độ Oxyz , cho hình hộp ABC . D A B  C  D   , biết tọa độ A 3  ;2;  1
C 4;2;0 B 2  ;1;  1 D3;5; 4 , , ,
. Tìm tọa độ A . A. A 3  ;3;  1 . B. A 3  ;3;3. C. A 3  ; 3  ; 3  . D. A 3  ; 3  ;3. Lời giải Chọn B.  1 1   1 5  Gọi I ; 2; 
 là trung điểm của AC và I ;3; 
 là trung điểm của B D    2 2   2 2  Do ABC . D A B  C  D
  là hình hộp nên AII A
  là hình bình hành nên AI  A I  A 3  ;3;3.
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 14
Câu 30: [2H3-1.3-1] Trong không gian với hệ tọa độ Oxyz , cho mặt c u có phương tr nh
x 2  y  2 2 1
3  z  9 . Tìm tọa độ tâm I và bán kính R của mặt c u đó. A. I  1
 ;3;0 ; R  3. B. I 1; 3
 ;0 ; R  9. C. I 1; 3
 ;0 ; R  3. D. I  1  ;3;0 ; R  9. Hướng dẫn giải Chọn C.
Mặt c u đã cho có tâm I 1; 3
 ;0 và bán kính R  3.
Câu 31: [2H3-1.3-1] Trong không gian Oxyz , cho hai điểm M 1; 2;  3 và N  1  ;2;  1 . Mặt c u đường kính
MN có phương tr nh là 2 2 2 2 A. 2
x   y  2   z   1  20 . B. 2
x   y  2   z   1  5 . 2 2 2 2 C. 2
x   y  2   z   1  5 . D. 2
x   y  2   z   1  20 . Hướng dẫn giải Chọn C.
Mặt c u đường kính MN có tâm I 0; 2; 
1 là trung điểm MN và bán kính R  IM  5 o đó mặ 2 2
t c u này có phương tr nh 2
x   y  2   z   1  5 .
Câu 32: [2H3-2.2-1] Trong không gian Oxyz , mặt phẳng  P : x  2y 3z  3  0 có một vectơ pháp tuyến là A. 1; 2  ;3. B. 1;2; 3  . C.  1  ;2; 3  . D. 1; 2;3 . Lời giải Chọn B.
Một vectơ pháp tuyến của mặt phẳng  P là n  1; 2;  3 .
Câu 33: [2H3-2.4-1] Trong không gian Oxyz , điểm nào dưới đây nằm tr n mặt phẳng  P : 2x  y  z  2  0 . A. Q 1; 2  ;2 . B. N 1; 1  ;  1 . C. P 2; 1  ;  1 .
D. M 1;1;   1 . Lời giải Chọn B.
Thay tọa độ các điểm Q , N , P , M l n lư t vào phương tr nh  P : 2x  y  z  2  0 ta đư c: 2.1  2
   2 2  0  4  0 nên QP . 2.1  
1 1 2  0  0  0 nên N  P . 2.2   
1 1 2  0  2  0 nên P  P . 2.111 2  0  2
  0 nên M P .
Câu 34: [2H3-2.3-2] Trong không gian Oxyz , cho hai điểm A 1  ;2; 
1 và B 2;1;0 . Mặt phẳng qua đi A và
vuông góc với AB có phương tr nh là
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 15
A. 3x  y  z  6  0 .
B. 3x  y  z  6  0 . C. x  3y  z  5  0 . D. x  3y  z  6  0 . Lời giải Chọn B.
Ta có AB  3;1;  1 .
Mặt phẳng c n tìm vuông góc với AB nên nhận AB  3;1;  1 làm vectơ pháp tuyến.
o đó phương tr nh của mặt phẳng c n tìm là 3 x  
1   y  2   z  
1  0  3x  y  z  6  0 .
Câu 35: [2H3-2.3-2] Trong không gian với hệ tọa độ Oxyz , mặt phẳng ch a hai điểm A1; 0;1 , B 1  ; 2; 2
và song song với trục Ox có phương tr nh là
A. y  2z  2  0 .
B. x  2z  3  0 .
C. 2y  z 1  0 .
D. x  y  z  0 . Lời giải Chọn A.
Gọi  P là mặt phẳng c n tìm.
Do  P // Ox nên P : by  cz  d  0 . c  d  0
Do  P ch a các điểm A1; 0;  1 , B  1  ; 2; 2 nên 
 2b  c  0 .
2b  2c  d  0
Ta chọn b  1 c  2
 . Khi đó d  2 .
Vậy phương tr nh P : y  2z  2  0 .
Câu 36: [2H3-2.7-1] Trong hệ trục tọa độ Oxyz , điều kiện của m để hai mặt phẳng  P : 2x  2y  z  0 và
Q: x  y  mz 1 0 cắt nhau là 1 1 1 A. m   . B. m  . C. m  1  . D. m   . 2 2 2 Lời giải Chọn A.
Mặt phẳng  P có vectơ pháp tuyến n  2;2; 
1 , Mặt phẳng Q có vectơ pháp tuyến P
n  1;1; m . Hai mặt phẳng  P và Q cắt nhau khi và chỉ khi hai vectơ pháp tuyến không cùng Q   phương 1  m  . 2 x  2 y 1 z
Câu 37: [2H3-3.1-1] Trong không gian Oxyz , cho đường thẳng d : 
 . Đường thẳng d có một 1  2 1 vec tơ chỉ phương là
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 16 A. u  1  ;2;1 .
B. u  2;1;0 .
C. u  2;1;1 . D. u  1  ;2;0 . 4   3   2   1   Lời giải Chọn A. x 1 y  2 z  3
Câu 38: Trong không gian Oxyz , đường thẳng d :  
đi qua điểm nào dưới đây? 2 1  2
A. Q 2; 1; 2 . B. M  1
 ;  2; 3. C. P1; 2; 3 . D. N  2  ;1;  2 . Lời giải Chọn C x 1 2t x 1   Câu 39: Ta có: t 0
y  2  t y  2  P1;2;3 d .[2H3-3.2-1] Trong không gian Oxyz , đường thẳng   z  3  2t z  3  
đi qua điểm A1;4;7 và vuông góc với mặt phẳng x  2y  2z 3  0 có phương tr nh là x 1 y  4 z  7 x 1 y  4 z  7 A.   . B.   . 1 2 2  1 4 7  x 1 y  4 z  7 x 1 y  4 z  7 C.   . D.   . 1 2  2  1 2 2  Lời giải Chọn D.
Đường thẳng đi qua điểm A1;4;7 và vuông góc với mặt phẳng x  2y  2z 3  0 nên có một    vectơ chỉ x y z
phương u  1;2; 2
  có phương tr nh là: 1 4 7   . 1 2 2 
Câu 40: [2H3-3.2-1] Trong không gian Oxyz , đường thẳng ch a trục Oy có phương tr nh tham số là x  0 x  0 x  t x  0    
A.  y  1 .
B.  y  t .
C.  y  0 .
D.  y  0 .     z  t  z  0  z  0  z  t  Lời giải Chọn B. x  0 
Trục Oy qua O 0;0;0 và có vectơ chỉ phương j  0;1;0 n n có phương tr nh  y  t . z  0  x  3 y  2 z  4
Câu 41: [2H3-3.3-2] Trong không gian Oxyz, đường thẳng d :   Oxy tại 1 1  cắt mặt phẳng   2 điểm có tọa độ là
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 17 A.  3  ; 2; 0. B. 3;  2; 0. C.  1  ; 0; 0. D. 1; 0; 0. Lời giải Chọn D. x  3 t 
Phương tr nh tham số của đường thẳng d là: d  : y  2
  t , Oxy: z  0 . z  4 2t  x  1 
Tọa độ giao điểm của d và Oxy ng với t thỏa mãn 4  2t  0  t  2   y  0 z  0 
Tọa độ giao điểm của d và Oxy là 1;0;0. x y z  2
Câu 42: Trong không gian Oxyz , cho mặt phẳng  P : 2x  y  z  3  0 và đường thẳng d :   . 2 1 5 
Tính khoảng cách từ d đến mặt phẳng  P . 1 6
A. d (d;(P))  .
B. d(d;(P))  6 .
C. d(d;(P))  1.
D. d (d; (P))  . 6 6 Lời giải Chọn D
Ta có n .u  0  d (P) P d 2.0 1.0 1.( 2  )  3 6 Lấy M (0;0; 2
 ) d , d(d;(P))  d(M;(P))   2 2 2   6 2 1 1
Câu 43: [2H3-2.6-1] Trong không gian Oxyz tính khoảng cách từ điểm M 1; 2;  3 đến mặt phẳng
P: x  2y 2z 2  0. 11 1 A. . B. . C. 3 . D. 1 3 3 Lời giải Chọn C. 1 2.2  2. 3    2 9
Ta có d M ,P    3.    2 2 2 3 1 2 2
Câu 44: [2H3-2.6-2] Trong không gian Oxyz , phương tr nh nào dưới đây là phương tr nh của mặt c u có tâm I 1; 2;  
1 và tiếp xúc mặt phẳng  P : x  2y  2z 8  0 ? 2 2 2 2 2 2 A.  x  
1   y  2   z   1  3 B.  x  
1   y  2   z   1  9
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 18 2 2 2 2 2 2 C.  x  
1   y  2   z   1  3 D.  x  
1   y  2   z   1  9 Lời Giải Chọn B 1 4  2  8 9
Ta có: d I;P    3 .
  2   2 2 3 1 2 2
Do mặt c u có tâm I 1;2;  
1 và tiếp xúc mặt phẳng  P : x  2y  2z 8  0 có bán kính 2 2 2
R  d I;P  3 n n có phương tr nh là:  x  
1   y  2   z   1  9 .
Câu 45: [2H3-2.7-3] Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng  P : 2x  y  2z  m  0 và mặt c u S 2 2 2
: x  y  z  2x  4y  6z  2  0 . Có ao nhi u giá trị nguy n của m để mặt phẳng
P cắt mặt c u S theo giao tuyến là đường tròn T  có chu vi ằng 4 3 . A. 3 . B. 4 . C. 2 . D. 1. Lời giải Chọn C.
S có tâm I 1; 2
 ;3 và bán kính R  4 .
Gọi H là h nh chiếu của I lên P . 2.1 2  2.3  m m  6
Khi đó IH  d I,P   .    2 2 2 3 2 1 2  Đường tròn  4 3
T  có chu vi là 4 3 nên có bán kính là r   2 3 . 2
P cắt mặt c u S theo giao tuyến là đường tròn T  có chu vi ằng 4 3 m  m   m 12 2 2  IH  R  6 r 
 16 12  m  6  6 6 6     . 3 m  6  6  m  0
Vậy có 2 giá trị nguy n của m thỏa mãn.
Câu 46: [2H3-1.1-1] Trong không gian Oxyz , cho điểm M 1; 2; 
3 . Hình chiếu của M lên trục Oy là điểm
A. P 1;0;3 .
B. Q 0;2;0 .
C. R 1;0;0 .
D. S 0;0;3 . Lời giải Chọn B.
Hình chiếu của M 1; 2; 
3 lên trục Oy là điểm Q 0; 2;0 .
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 19
Câu 47: [2H3-1.1-1] Trong không gian với hệ tọa độ Oxyz , cho điểm M 3;1; 2 . Điểm N đối x ng với
M qua mặt phẳng Oyz là
A. N 0;1;2 .
B. N 3;1; 2 . C. N  3  ;1;2 .
D. N 0;1; 2 . Hướng dẫn giải Chọn C.
Vì N đối x ng với M qua mặt phẳng Oyz nên N  3  ;1;2 .
Câu 48: [2H3-1.1-1] Trong không gian Oxyz , cho điểm M 5;7; 1  
3 . Gọi H là hình chiếu vuông góc của
M trên mặt phẳng Oyz . Tọa độ điểm H là? A. H 5;0; 1  3. B. H 0;7; 1  3 .
C. H 5;7;0 . D. H 0; 7  ;13 . Lời giải Chọn B.
Do H là hình chiếu vuông góc của M trên mặt phẳng tọa độ Oyz nên H 0;7; 1  3 .
Câu 49: P[2H3-4.1-4] Cho hình vuông ABCD cạnh a . Trên hai tia Bx, Dy vuông góc với mặt phẳng  a
ABCD và cùng chiều l n lư t lấy hai điểm M , N sao cho BM  ; DN  2a . Tính góc  giữa 4
hai mặt phẳng  AMN  và CMN  . N M A D B C A.   30 . B.   60 . C.   45 . D.   90 . Hướng dẫn giải Chọn D.
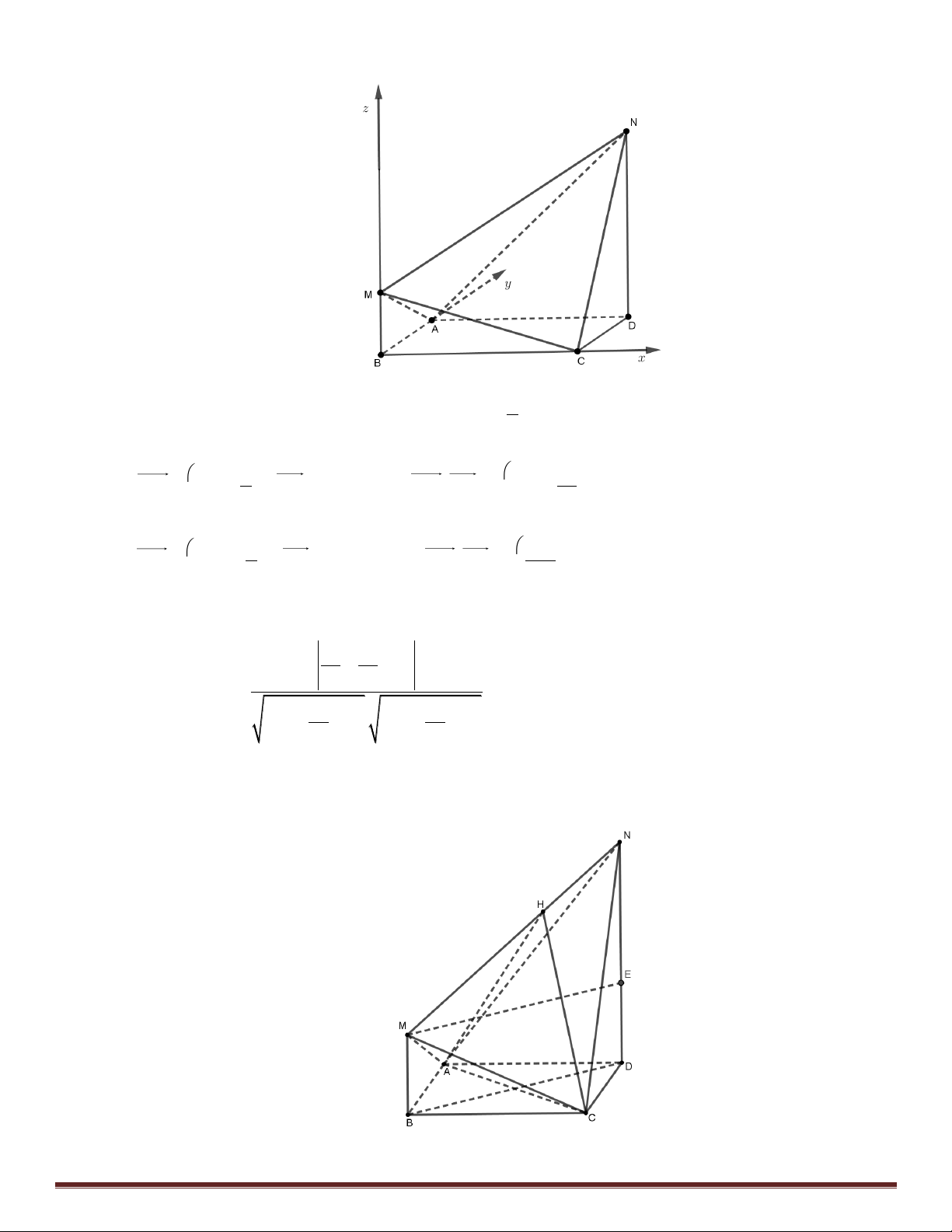
Cách 1: Gắn hệ trục tọa độ như h nh v :
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 20  a 
Ta có: B 0;0;0 , A0; ; a 0 , C  ;
a 0;0 , M 0;0;   , N  ; a ; a 2a .  4   a  2  a  AM  0;  ; a 
 , AN  0;0;2a, 2 2
AM , AN      2  a ;
; a  là vectơ pháp tuyến của mp  AMN  .  4   4   a  2  a  CM   ; a 0;   , CN  0; ; a 2a , 2 2 CM,CN     
; 2a ; a  là vectơ pháp tuyến của mp  4   4  CMN. 4 4 a a 4   a 2 2 o đó: cos   0   90 . 4 4 a a 4 4 4 4 4a   a . 4a   a 16 16 Cách 2:
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 21 Tacó: A  MN  C
 MN c.c.c nên kẻ CH  MN tại H thì AH  MN .
Mà  AMN  CMN   MN nên góc  giữa hai mặt phẳng  AMN  và CMN  là góc giữa hai đường thẳng H , A HC . a 17 Ta có: 2 2 MC  BC  MB  , 2 2
NC  CD  ND  a 5 , 4 2 49a 9a 2 2 2 MN 
ME  EN  2a   . 16 4 2 2 2
MC  NC  MN 2 2 1 9a cos MCN   9  sin MCN  .  S
 MC.NC.sin MCN  . MC.NC MCN 85 85 2 8 S Từ đó: 2 MCN CH 
 a  AH . Do 2 2 2
AH  CH  AC nên tam giác AHC vuông tại H . MN
Vậy góc giữa hai đường thẳng H ,
A HC bằng 90 .
Câu 50: [4]Cho hàm số y  f  x . Đồ thị của hàm số y  f  x như h nh n. Đặt 2
g(x)  2 f (x)  (x 1) .
Mệnh đề nào dưới đây đúng ? A. g  
1  g 3  g 5 .
B. g 5  g   1  g 3 . C. g  
1  g 5  g 3 .
D. g 3  g 5  g   1 . Lời giải
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 22 Chọn C.
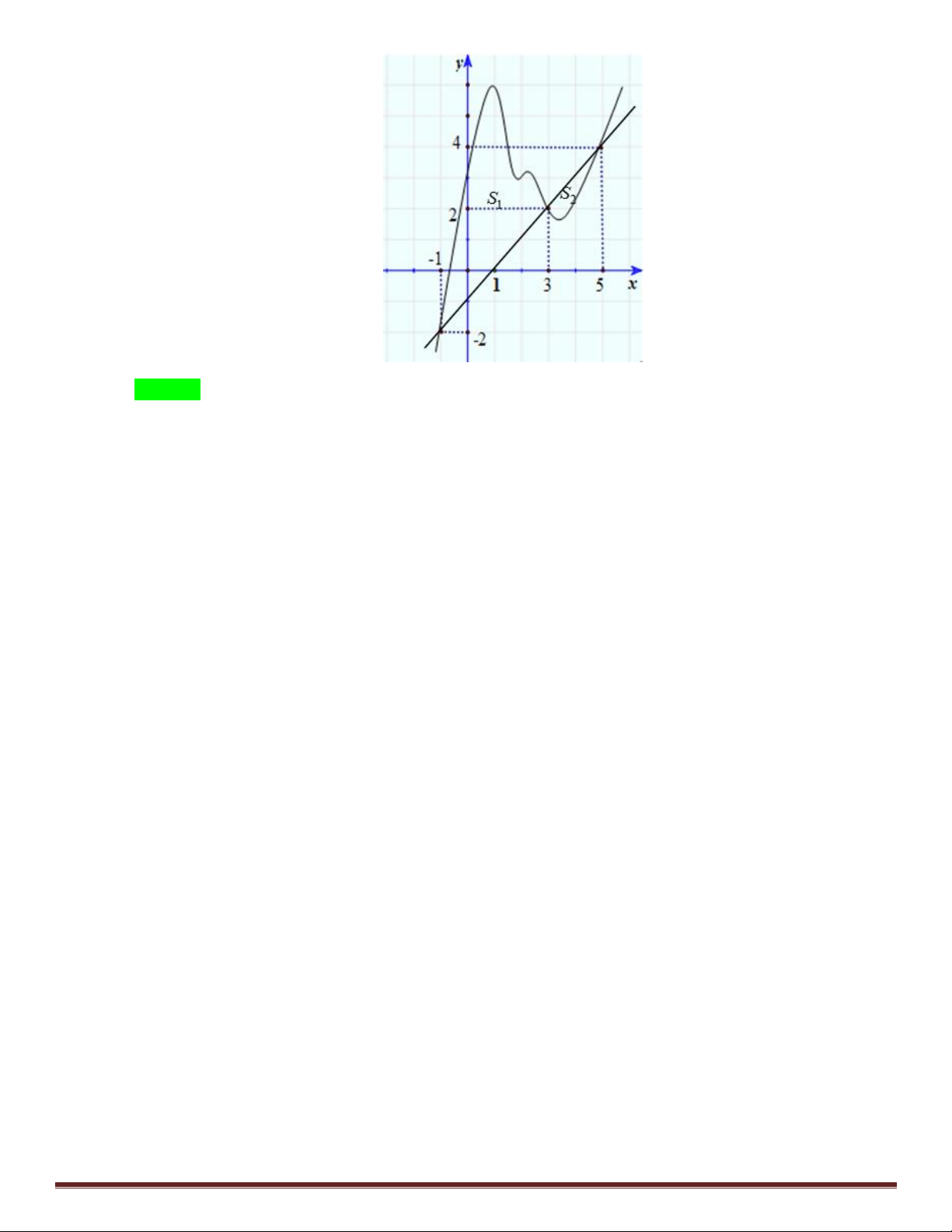
Gọi S , S là diện tích hai ph n hình phẳng giới hạn bởi đồ thị f  x và đường thẳng y  x –1 như 1 2 hình v . 3 3
2S  2 [f ' x  x 1 ]dx 
g ' x dx  g 3  g 1
  0  g 3  g 1    1               1  1  5 5 2S  2
 [f ' x  x 1 ]dx   g ' x dx  g 3  g 5  0   2           3 3
 g 3  g 5 .
Mặt khác từ đồ thị ta có S  S  2S  2S  g(3)  g( 1
 )  g(3)  g(5)  g( 1  )  g(5) 1 2 1 2 Vậy g( 1  )  ( g 5)  ( g 3) .
Đề thi HK II – THPT Tân Phú – Đồng Nai Page 23

Đề thi HK2 Toán 12 năm học 2019 – 2020 trường THPT Tân Phú – Đồng Nai

Thông tin :

Tài liệu liên quan:

Đề kiểm tra cuối kì 2 Toán 12 năm 2023 – 2024 sở GD&ĐT Vĩnh Long

Đề kiểm tra học kỳ 2 Toán 12 năm 2023 – 2024 sở GD&ĐT Bình Dương

Đề cuối học kì 2 Toán 12 năm 2023 – 2024 trường THPT Lê Hồng Phong – Quảng Nam

Đề cuối kì 2 Toán 12 năm 2023 – 2024 trường THPT Lê Hồng Phong – Đắk Lắk

Đề cuối học kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Thị xã Quảng Trị