Đề thi học kì 2 môn Toán lớp 12 năm 2023 - Đề 2

Đây là tài liệu tham khảo giúp các bạn có thêm nhiều tài liệu để ôn tập thật tốt cho kì thi học kì 2 sắp tới. Mời các bạn cùng tham khảo chi tiết và tải về bài viết dưới đây nhé.

20 10 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

ĐỀ KIỂM TRA CUỐI HỌC KỲ II – NĂM 2022-2023-ĐỀ 2

Môn: TOÁN 12

Thời gian làm bài: 90phút

Câu 1: Cho biết

 

là một nguyên hàm của hàm số

 

. Biểu thức

 

df x x



bằng

 

. B.

 

F x C





. C.

 

F x C

. D.

 

xF x C

Câu 2: Cho hàm số

 

y f x

liên tục trên

 

;ab

. Gọi

là hình phẳng giới hạn bởi đồ thị của hàm

số

 

y f x

, trục hoành và hai đường thẳng

, ( )x a x b a b  

. Thể tích của khối tròn xoay

tạo thành khi quay

quanh trục hoành được tính theo công thức?

 

V f x x



. B.

 

V f x x







. C.

 

V f x x







. D.

 

V f x x







Câu 3: Nếu

   

2, 1f x dx f x dx  



thì

 

f x dx



bằng

2

. B.

. C.

3

. D.

Câu 4: Cho hai số phức

2 3 , 4z i z i    

. Số phức

z z z

có môđun là

. B.

. C.

2 13

. D.

2 17

Câu 5: Cho các số thực

 

,a b a b

và hàm số

 

y f x

có đạo hàm là hàm liên tục trên . Mệnh đề

nào sau đây là đúng?

     

f x x f a f b







. B.

     

f x x f b f a







     

f x x f b f a







. D.

     

f x x f a f b







Câu 6: Trong không gian với hệ trục tọa độ

Oxyz

, cho

2 4 6a i j k   

. Tọa độ của

là

 

2; 4;6

. B.

 

2;4; 6

. C.

 

1; 2;3

. D.

 

1;2; 3

Câu 7: Cho hàm số

 

y f x

có đồ thị như hình vẽ bên dưới. Diện tích

của miền được tô đậm như

hình vẽ được tính theo công thức nào sau đây?

 

dS f x x



. B.

 

dS f x x



. C.

 

dS f x x



. D.

 

dS f x x



Câu 8: Trong không gian

Oxyz

, cho đường thẳng

có phương trình

 

y t t







  





  



. Hỏi đường

thẳng

đi qua điểm nào sau đây

 

2;3; 2B 

. B.

 

2; 3;2C 

. C.

 

1; 1;1A 

. D.

 

2;3;2D

Câu 9: Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức







-2

-1

A. Điểm

B. Điểm

C. Điểm

D. Điểm

Câu 10: Cho hàm số

 

cos



. Trong các khẳng định sau, khẳng định nào đúng?

 

d cot .f x x x C



 

d tan .f x x x C



 

d tan .f x x x C  



 

d cot .f x x x C  



Câu 11: Tất cả các nghiệm phức của phương trình

2 17 0zz  

là

1 4 ; 1 4 .ii

4.i

2 4 ; 2 4 .ii

16 .i

Câu 12: Trong không gian

Oxyz

, phương trình mặt cầu

 

có tâm

 

1;1; 2I 

và bán kính

3r 

là

       

2 2 2

: 1 1 2 9.S x y z     

       

2 2 2

: 1 1 2 9.S x y z     

       

2 2 2

: 1 1 2 3.S x y z     

       

2 2 2

: 1 1 2 3.S x y z     

Câu 13: Trong không gian với hệ trục tọa độ

Oxyz

, cho hai mặt phẳng

 

và

 

lần lượt có vectơ

pháp tuyến

và



. Gọi



là góc giữa mặt phẳng

 

và

 

. công thức nào sau đây đúng?

sin









. B.

cos









. C.

sin









. D.

cos









Câu 14: Cho số phức

15zi  

. Phần ảo của số phức

bằng

. B.

5

. D.

1

Câu 15: Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 4 6 1 0S x y z x y z      

. Tâm của mặt cầu

 

có tọa độ là

 

1;2; 3

. B.

 

2;4; 6

. C.

 

1; 2;3

. D.

 

2; 4;6

Câu 16: Trong không gian

Oxyz

, cho phương trình mặt phẳng

 

: 2 2 0P x z  

. Một vectơ pháp

tuyến của

 

là

 

2;0; 1

. B.

 

2; 1;0

 

0; 1;2

. D.

 

2; 1;2

Câu 17: Trong không gian

,Oxyz

cho phương trình của hai đường thẳng:

2 1 1

x y z







và

1 1 2

x y z







. Vị trí tương đối của hai đường thẳng

và

là

,dd

cắt nhau. B.

,dd

chéo nhau. C.

,dd

song song. D.

,dd

trùng nhau.

Câu 18: Tính

25x

e dx





ta được kết quả nào sau đây

















Câu 19: Trong không gian

,Oxyz

cho mặt phẳng

 

:2 3 3 0.x y z



   

Mặt phẳng nào sau đây song

song với mặt phẳng

 



 

:2 3 3 0.Q x y z   

 

: 3 3 0.x y z



   

 

:2 3 2 0.x y z



   

 

:2 3 3 0.P x y z   

Câu 20: Gọi

là diện tích hình phẳng giới hạn bởi hai đường



và

4yx

. Tính

3ln3





4 3ln3.

Câu 21: Tính tích phân

I dx









5ln3.

I 

4ln3 1.I 

1 4ln2.I 

2 5ln2.I 

Câu 22: Trong không gian với hệ tọa độ

,Oxyz

cho hai điểm

( )

2;0; 2I -

và

( )

2;3;2A

. Mặt cầu

( )

có

tâm

và đi qua điểm

có phương trình là

   

2 2 25.x y z    

   

2 2 5.x y z    

   

2 2 5.x y z    

   

2 2 25.x y z    

Câu 23: Giá trị các số thực

,ab

thỏa mãn

( )

2 1 1 2a b i i i+ + + = +

(với

là đơn vị ảo ) là

0; 1.ab

; 0.

ab

1; 1.ab

; 1.

ab

Câu 24: Trong không gian với hệ tọa độ

,Oxyz

đường thẳng đi qua hai điểm

( )

3;1; 6A -

và

( )

5;3; 2B -

có phương trình tham số là













  















  















  















  



Câu 25: Trong không gian

Oxyz

, gọi

 

;;M a b c

là giao điểm của đường thẳng

1 3 2

2 1 1

x y z

  





và mặt phẳng

 

:2 3 4 4 0P x y z   

. Tính

T a b c  

T 

. B.

6T 

. C.

4T 

. D.

T 

Câu 26: Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức

thỏa mãn điều kiện

22zi  

là

A. Đường tròn tâm

 

1; 2I 

, bán kính

2R 

B. Đường tròn tâm

 

2;1I 

, bán kính

2R 

C. Đường tròn tâm

 

2; 1I 

, bán kính

2R 

D. Đường tròn tâm

 

1;2I 

, bán kính

2R 

Câu 27: Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

   

2;1;1 , 1;2;1AB

. Tọa độ trung điểm

của đoạn thẳng

là?

;1;







. B.

 

3;1;0I 

. C.

; ;0









. D.

; ;1







Câu 28: Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

2;1;8M 

. Gọi

là hình chiếu vuông góc

của

trên mặt phẳng

 

Oxy

. Tọa độ của điểm

là

 

0;1;8H

. B.

 

2;1;0H 

. C.

 

0;0;8H

. D.

 

2;0;8H 

Câu 29: Tính tích phân

sinI xdx







I 

I 

I 

I   

Câu 30: Trong không gian với hệ trục tọa độ

,Oxyz

cho ba điểm

     

2;0;0 , 0;3;0 , 0;0;5 .A B C

Mặt

phẳng

 

ABC

có phương trình là

3 2 5

x y z

  

. B.

5 3 2

x y z

  

. C.

2 3 5

x y z

  

. D.

2 3 5

x y z

  

Câu 31: Gọi

,zz

là hai nghiệm phân biệt của phương trình

3 4 0zz  

trên tập số phức. Tính giá

trị của biểu thức

P z z

. B.

. C.

. D.

Câu 32: Cho số phức z thỏa mãn

 

2 3 2 0i z i   

. Phần thực của số phức

là

. B.

. C.



. D.



Câu 33: Trong không gian

Oxyz

, mặt phẳng

 

:2 2 6 0P x y z   

. Khoảng cách từ gốc tọa độ đến

mặt phẳng

 

bằng:

. B.

. C.

. D.

Câu 34: Cho số phức

 

,z a bi a b  R

. Khẳng định nào sau đây đúng?

z a b

. B.

z a b

. C.

z a b

. D.

z a b

Câu 35: Trong không gian, cắt vật thể bởi hai mặt phẳng

 

:1Px

và

 

:2Qx

. Biết một mặt

phẳng tùy ý vuông góc với trục

tại điểm có hoành độ

 

12xx  

cắt theo thiết diện là

một hình vuông có cạnh bằng

6 x

. Thể tích của vật thể giới hạn bởi hai mặt phẳng

   

,PQ

bằng:



. B.

. C.

. D.



Câu 36: Tính nguyên hàm

 

ln 2





bằng cách đặt

lntx

ta được nguyên hàm nào sau đây?











. B.

2



. C.

 





. D.

 

2d



Câu 37: Cho

cos4 cos d







x x x

với

,,abc

là các số nguyên,

0c

và

tối giản. Tổng

abc

bằng

77

. B. 103. C.

17

. D. 43.

Câu 38: Trong không gian với hệ tọa độ

Oxyz

, cho

 

2 2 2

: 4 2 10 14 0S x y z x y z      

. Mặt

phẳng

 

: 4 5 0P x z   

cắt mặt cầu

 

theo một đường tròn

 

. Toạ độ tâm

của

 

là

 

3;1; 2H

. B.

 

7;1; 3H

. C.

 

9;1;1H

. D.

 

1;1; 1H

Câu 39: Giá trị của

xe dx



bằng

300

300 900e

. B.

300

300 900e

. C.

 

300

299 1

900

e 

. D.

 

300

299 1

900

e 

Câu 40: Trong không gian hệ trục

Oxyz

, cho

 

:2 2 6 0x y z



   

. Gọi mặt phẳng

 

:0x y cz d



   

không qua

, song song với mặt phẳng

 



và

   

 

,2d





. Tính

.cd

.3cd

. B.

. 12cd

. C.

.6cd

. D.

.0cd

Câu 41: Tính diện tích hình phẳng (phần tô đậm) giới hạn bởi hai đường

4yx

;

2yx

như hình

vẽ bên dưới là





. B.

. C.

. D.



Câu 42: Cho số phức

z x yi

( với

,xy

) thoả mãn

2 5 14 7z iz i   

. Tính

xy

. B.

1

. C.

. D.

Câu 43: Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

với

     

2;2;2 , 0;1;1 , 1; 2; 3A B C   

. Tính diện tích

của tam giác

ABC

53S 

. B.

S 

. C.

S 

. D.

52S 

Câu 44: Trong không gian

Oxyz

, mặt phẳng

 



đi qua hai điểm

   

1;0;0 , 2;2;0AB

và vuông góc

với mặt phẳng

 

: 2 0P x y z   

có phương trình là

2 4 0x y z   

. B.

10x y z   

. C.

2 3 2 0x y z   

. D.

2 2 0x y z   

Câu 45: Biết phương trình

 

z 0 ,z m n m n   

có một nghiệm là

13i

. Tính

3nm

4

6

3V 

16

Câu 46: Cho hàm số

   

36 0;a, ,f x ax bx x c a b c     

có hai điểm cực trị là

6

và

Gọi

 

y g x

là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

 

y f x

. Diện tích

hình phẳng giới hạn bởi hai đường

 

y f x

và

 

y g x

bằng

160

128.

64

672

Câu 47: Cho hàm số

 

y f x

là hàm liên tục có tích phân trên

 

0;2

thỏa điều kiện

 

6df x x xf x x



. Tính

 

dI f x x



32I 

. B.

8I 

. C.

6I 

. D.

24I 

Câu 48: Trong không gian

Oxyz

, cho hai điểm

   

2; 2;1 , 1;2; 3MA  

và đường thẳng

2 2 1

x y z







. Gọi

 

1; ;u a b

là một vectơ chỉ phương của đường thẳng



đi qua



vuông góc với đường thẳng

đồng thời cách điểm

một khoảng nhỏ nhất. Giá trị

2ab

là

. B.

. C.

. D.

Câu 49: Trong không gian với hệ tọa độ

Oxyz

, gọi mặt phẳng

 

:7 0P x by cz d   

(với

, , , 0b c d c

) đi qua điểm

 

1;3;5A

. Biết mặt phẳng

 

song song với trục

và khoảng

cách từ gốc tọa độ đến mặt phẳng

 

bằng

. Tính

T b c d  

4T 

. B.

78T 

. C.

61T 

. D.

7T 

Câu 50: Gọi

là tập hợp tất cả các số phức

để số phức





có phần ảo bằng

. Biết rằng

3zz

với

,z z S

, giá trị nhỏ nhất của

2zz

bằng

3 5 3 2

3 5 3

. C.

53

. D.

2 5 2 3

BẢNG ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT

1.C

2.C

3.C

4.C

5.B

6.B

7.A

8.A

9.D

10.B

11.A

12.A

13.D

14.C

15.C

16.A

17.A

18.C

19.C

20.D

21.C

22.A

23.C

24.C

25.B

26.B

27.D

28.B

29.A

30.C

31.D

32.C

33.D

34.B

35.C

36.A

37.C

38.D

39.D

40.A

41.C

42.A

43.A

44.D

45.A

46.B

47.A

48.D

49.C

50.A

Câu 1: Cho biết

 

là một nguyên hàm của hàm số

 

. Biểu thức

 

df x x



bằng

 

. B.

 

F x C





. C.

 

F x C

. D.

 

xF x C

Lời giải

Chọn C

   

d.f x x F x C



Câu 2: Cho hàm số

 

y f x

liên tục trên

 

;ab

. Gọi

là hình phẳng giới hạn bởi đồ thị của hàm

số

 

y f x

, trục hoành và hai đường thẳng

, ( )x a x b a b  

. Thể tích của khối tròn xoay

tạo thành khi quay

quanh trục hoành được tính theo công thức?

 

V f x x



. B.

 

V f x x







. C.

 

V f x x







. D.

 

V f x x







Lời giải

Chọn C

Thể tích của khối tròn xoay tạo thành khi quay

quanh trục hoành được tính theo công thức

 

V f x x







Câu 3: Nếu

   

2, 1f x dx f x dx  



thì

 

f x dx



bằng

2

. B.

. C.

3

. D.

Lời giải

Chọn C

Ta có

     

4 4 2

2 1 1

d d d 3.f x x f x x f x x   

  

Câu 4: Cho hai số phức

2 3 , 4z i z i    

. Số phức

z z z

có môđun là

. B.

. C.

2 13

. D.

2 17

Lời giải

Chọn C

Ta có

6 4 6 4 2 13.z z z i z       

Câu 5: Cho các số thực

 

,a b a b

và hàm số

 

y f x

có đạo hàm là hàm liên tục trên . Mệnh đề

nào sau đây là đúng?

     

f x x f a f b







. B.

     

f x x f b f a







     

f x x f b f a







. D.

     

f x x f a f b







Lời giải

Chọn B

Ta có

       

f x x f x f b f a



  



Câu 6: Trong không gian với hệ trục tọa độ

Oxyz

, cho

2 4 6a i j k   

. Tọa độ của

là

 

2; 4;6

. B.

 

2;4; 6

. C.

 

1; 2;3

. D.

 

1;2; 3

Lời giải

Chọn B

Ta có

 

2 4 6 2;4; 6a i j k      

nên

 

2;4; 6a   

Câu 7: Cho hàm số

 

y f x

có đồ thị như hình vẽ bên dưới. Diện tích

của miền được tô đậm như

hình vẽ được tính theo công thức nào sau đây?

 

dS f x x



. B.

 

dS f x x



. C.

 

dS f x x



. D.

 

dS f x x



Lời giải

Chọn A

Ta có

   

ddS f x x f x x  



Câu 8: Trong không gian

Oxyz

, cho đường thẳng

có phương trình

 

y t t







  





  



. Hỏi đường

thẳng

đi qua điểm nào sau đây

 

2;3; 2B 

. B.

 

2; 3;2C 

. C.

 

1; 1;1A 

. D.

 

2;3;2D

Lời giải

Chọn A

Với

0t 

thì đường thẳng

đi qua điểm

 

2;3; 2B 

Câu 9: Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức







-2

-1

A. Điểm

B. Điểm

C. Điểm

D. Điểm

Lời giải

Chọn D

  

1 1 1

z i z

i i i





     

  

có điểm biểu diễn là điểm

Câu 10: Cho hàm số

 

cos



. Trong các khẳng định sau, khẳng định nào đúng?

 

d cot .f x x x C



 

d tan .f x x x C



 

d tan .f x x x C  



 

d cot .f x x x C  



Lời giải

Chọn B

Lý thuyết.

Câu 11: Tất cả các nghiệm phức của phương trình

2 17 0zz  

là

1 4 ; 1 4 .ii

4.i

2 4 ; 2 4 .ii

16 .i

Lời giải

Chọn A

2 17 0





   







Câu 12: Trong không gian

Oxyz

, phương trình mặt cầu

 

có tâm

 

1;1; 2I 

và bán kính

3r 

là

       

2 2 2

: 1 1 2 9.S x y z     

       

2 2 2

: 1 1 2 9.S x y z     

       

2 2 2

: 1 1 2 3.S x y z     

       

2 2 2

: 1 1 2 3.S x y z     

Lời giải

Chọn A

Phương trình mặt cầu

 

có tâm

 

1;1; 2I 

và bán kính

3r 

là

     

2 2 2

1 1 2 9x y z     

Câu 13: Trong không gian với hệ trục tọa độ

Oxyz

, cho hai mặt phẳng

 

và

 

lần lượt có vectơ

pháp tuyến

và



. Gọi



là góc giữa mặt phẳng

 

và

 

. công thức nào sau đây đúng?

sin









. B.

cos









. C.

sin









. D.

cos









Lời giải

Chọn D

Ta có:

cos









Câu 14: Cho số phức

15zi  

. Phần ảo của số phức

bằng

. B.

5

. D.

1

Lời giải

Chọn C

Ta có:

15zi  

suy ra phần ảo bằng

5

Câu 15: Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 4 6 1 0S x y z x y z      

. Tâm của mặt cầu

 

có tọa độ là

 

1;2; 3

. B.

 

2;4; 6

. C.

 

1; 2;3

. D.

 

2; 4;6

Lời giải

Chọn C

Tâm của mặt cầu

 

có tọa độ là

 

1; 2;3

Câu 16: Trong không gian

Oxyz

, cho phương trình mặt phẳng

 

: 2 2 0P x z  

. Một vectơ pháp

tuyến của

 

là

 

2;0; 1

. B.

 

2; 1;0

 

0; 1;2

. D.

 

2; 1;2

Lời giải

Chọn A

Một vectơ pháp tuyến của

 

là

 

2;0; 1

Câu 17: Trong không gian

,Oxyz

cho phương trình của hai đường thẳng:

2 1 1

x y z







và

1 1 2

x y z







. Vị trí tương đối của hai đường thẳng

và

là

,dd

cắt nhau. B.

,dd

chéo nhau. C.

,dd

song song. D.

,dd

trùng nhau.

Lời giải

Chọn A

Vec tơ chỉ phương của

là

 

2; 1;1u 

, vec tơ chỉ phương của

là

 

1;1; 2u





Vì hai vec tơ

,uu



không cùng phương nên

,dd

cắt nhau hoặc

,dd

chéo nhau.

Xét hệ gồm hai phương trình của

,:dd

  





  









  



Hệ này có nghiệm duy nhất:

   

; ; 2; 1;2x y z 

Vậy

,dd

cắt nhau.

Câu 18: Tính

25x

e dx





ta được kết quả nào sau đây

















Lời giải

Chọn C

Áp dụng

ax b ax b

e dx e C







Câu 19: Trong không gian

,Oxyz

cho mặt phẳng

 

:2 3 3 0.x y z



   

Mặt phẳng nào sau đây song

song với mặt phẳng

 



 

:2 3 3 0.Q x y z   

 

: 3 3 0.x y z



   

 

:2 3 2 0.x y z



   

 

:2 3 3 0.P x y z   

Lời giải

Chọn C

   



vì

2 3 1 3

2 3 1 2



  



Câu 20: Gọi

là diện tích hình phẳng giới hạn bởi hai đường



và

4yx

. Tính

3ln3





4 3ln3.

Lời giải

Chọn D

Xét phương trình:





  







Vậy

4 0,7.S x dx

   



Câu 21: Tính tích phân

I dx









5ln3.

I 

4ln3 1.I 

1 4ln2.I 

2 5ln2.I 

Lời giải

Chọn C

( )

1 4ln 1 1 4ln2.

I dx dx x x

æö

= = - = - + = -

èø

òò

Câu 22: Trong không gian với hệ tọa độ

,Oxyz

cho hai điểm

( )

2;0; 2I -

và

( )

2;3;2A

. Mặt cầu

( )

có

tâm

và đi qua điểm

có phương trình là

   

2 2 25.x y z    

   

2 2 5.x y z    

   

2 2 5.x y z    

   

2 2 25.x y z    

Lời giải

Chọn A

Bán kính mặt cầu

25 5.R IA= = =

Vậy phương trình mặt cầu là:

   

2 2 25.x y z    

Câu 23: Giá trị các số thực

,ab

thỏa mãn

( )

2 1 1 2a b i i i+ + + = +

(với

là đơn vị ảo ) là

0; 1.ab

; 0.

ab

1; 1.ab

; 1.

ab

Lời giải

Chọn C

( )

2 1 1 2a b i i i+ + + = +

( ) ( )

2 1 1 . 1 2a b i iÛ - + + = +

2 1 1 1

1 2 1

ìì

- = =

ïï

ÛÛ

íí

ïï

+ = =

ïï

îî

Câu 24: Trong không gian với hệ tọa độ

,Oxyz

đường thẳng đi qua hai điểm

( )

3;1; 6A -

và

( )

5;3; 2B -

có phương trình tham số là













  















  















  















  



Lời giải

Chọn C

( )

2;2;4AB =

uuur

đường thẳng

có một vectơ chỉ phương

( )

1;1;2u =

phương trình tham số của đường thẳng

là













  



Câu 25: Trong không gian

Oxyz

, gọi

 

;;M a b c

là giao điểm của đường thẳng

1 3 2

2 1 1

x y z

  





và mặt phẳng

 

:2 3 4 4 0P x y z   

. Tính

T a b c  

T 

. B.

6T 

. C.

4T 

. D.

T 

Lời giải

Chọn B

Vì

Md

nên

 

1 2 ;3 ;2M t t t   

Mặt khác

 

MP

     

2 1 2 3 3 4 2 4 0t t t        

1t

 

1;2;3M

Vậy

6T 

Câu 26: Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức

thỏa mãn điều kiện

22zi  

là

A. Đường tròn tâm

 

1; 2I 

, bán kính

2R 

B. Đường tròn tâm

 

2;1I 

, bán kính

2R 

C. Đường tròn tâm

 

2; 1I 

, bán kính

2R 

D. Đường tròn tâm

 

1;2I 

, bán kính

2R 

Lời giải

Chọn B

Gọi

z x yi

         

2 2 2 2

2 2 2 1 2 2 1 2 2 1 4z i x y i x y x y                 

Vậy tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức

là đường tròn tâm

 

2;1I 

bán kính

2R 

Câu 27: Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

   

2;1;1 , 1;2;1AB

. Tọa độ trung điểm

của đoạn thẳng

là?

;1;







. B.

 

3;1;0I 

. C.

; ;0









. D.

; ;1







Lời giải

Chọn D

Ta có:

2 1 1 2 1 1

;;

2 2 2

  







; ;1









Câu 28: Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

2;1;8M 

. Gọi

là hình chiếu vuông góc

của

trên mặt phẳng

 

Oxy

. Tọa độ của điểm

là

 

0;1;8H

. B.

 

2;1;0H 

. C.

 

0;0;8H

. D.

 

2;0;8H 

Lời giải

Chọn B

Hình chiếu vuông góc của

trên mặt phẳng

 

Oxy

là

 

2;1;0H 

Câu 29: Tính tích phân

sinI xdx







I 

I 

I 

I   

Lời giải

Chọn A

sin cos 1 .

I x dx x



    



Câu 30: Trong không gian với hệ trục tọa độ

,Oxyz

cho ba điểm

     

2;0;0 , 0;3;0 , 0;0;5 .A B C

Mặt

phẳng

 

ABC

có phương trình là

3 2 5

x y z

  

. B.

5 3 2

x y z

  

. C.

2 3 5

x y z

  

. D.

2 3 5

x y z

  

Lời giải

Chọn C

Câu 31: Gọi

,zz

là hai nghiệm phân biệt của phương trình

3 4 0zz  

trên tập số phức. Tính giá

trị của biểu thức

P z z

. B.

. C.

. D.

Lời giải

Chọn D

3 4 0zz  

có

9 16 7     

phương trình đã cho có hai nghiệm phân biệt:

1 2 1 2

3 7 3 7

; 4.

z z P z z

   

     

Câu 32: Cho số phức z thỏa mãn

 

2 3 2 0i z i   

. Phần thực của số phức

là

. B.

. C.



. D.



Lời giải

Chọn C

 

2 3 1 8

2 3 2 0

2 5 5

i z i z z i



         



Vậy phần thực của số phức

là



Câu 33: Trong không gian

Oxyz

, mặt phẳng

 

:2 2 6 0P x y z   

. Khoảng cách từ gốc tọa độ đến

mặt phẳng

 

bằng:

. B.

. C.

. D.

Chọn D

Lời giải

Ta có:

 

, 2.

2 2 1

d O P 

  

Câu 34: Cho số phức

 

,z a bi a b  R

. Khẳng định nào sau đây đúng?

z a b

. B.

z a b

. C.

z a b

. D.

z a b

Chọn B

Lời giải

Câu 35: Trong không gian, cắt vật thể bởi hai mặt phẳng

 

:1Px

và

 

:2Qx

. Biết một mặt

phẳng tùy ý vuông góc với trục

tại điểm có hoành độ

 

12xx  

cắt theo thiết diện là

một hình vuông có cạnh bằng

6 x

. Thể tích của vật thể giới hạn bởi hai mặt phẳng

   

,PQ

bằng:



. B.

. C.

. D.



Chọn C

Lời giải

Thể tích của vật thể giới hạn bởi hai mặt phẳng:

   

d 6 d 93V S x x x x



   



(đvtt).

Câu 36: Tính nguyên hàm

 

ln 2





bằng cách đặt

lntx

ta được nguyên hàm nào sau đây?











. B.

2



. C.

 





. D.

 

2d



Lời giải

Chọn A

Đặt

ln d d   xt x t

. Khi đó

   

ln 2 2

d d 1 d





  





  

x t t

x x t t

Câu 37: Cho

cos4 cos d







x x x

với

,,abc

là các số nguyên,

0c

và

tối giản. Tổng

abc

bằng

77

. B. 103. C.

17

. D. 43.

Lời giải

Chọn C

 

1 1 1 2 13

cos4 cos d cos5 cos3 d sin5

sin3

32 2 5 30 60









   













x x xx x x x x

Suy ra

13 30 13 60 17







        









b a b c

Câu 38: Trong không gian với hệ tọa độ

Oxyz

, cho

 

2 2 2

: 4 2 10 14 0S x y z x y z      

. Mặt

phẳng

 

: 4 5 0P x z   

cắt mặt cầu

 

theo một đường tròn

 

. Toạ độ tâm

của

 

là

 

3;1; 2H

. B.

 

7;1; 3H

. C.

 

9;1;1H

. D.

 

1;1; 1H

Lời giải

Chọn C

Mặt cầu

 

có tâm

 

2;1; 5I

và mặt phẳng

 

có VTPT

 

1;0;4n

Vì mặt phẳng

 

cắt mặt cầu

 

theo một đường tròn

 

nên tâm

của

 

là hình

chiếu của

lên mặt phẳng

 

Đường thẳng

qua

 

2;1; 5I

và nhận

 

1;0;4n

là VTCP có phương trình là

 













  



. Khi đó

   

2 ;1; 5 4    IH P H t t

Ta có

   

12 5 44 5 0       ttt

. Suy ra

 

1;1; 1H

Câu 39: Giá trị của

xe dx



bằng

300

300 900e

. B.

300

300 900e

. C.

 

300

299 1

900

e 

. D.

 

300

299 1

900

e 

Lời giải

Chọn D

Đặt

du dx

dv e x























30 10 30

30 30

I xe e x  



 

300 30 10 300 300 300

1 1 1 1 1 1

299 1

3 900 3 900 900 900

e e e e e      

Câu 40: Trong không gian hệ trục

Oxyz

, cho

 

:2 2 6 0x y z



   

. Gọi mặt phẳng

 

:0x y cz d



   

không qua

, song song với mặt phẳng

 



và

   

 

,2d





. Tính

.cd

.3cd

. B.

. 12cd

. C.

.6cd

. D.

.0cd

Lời giải

Chọn A

Ta có

 



song song với

 



nên

c 

 

x y z d



    

Chọn

   

0;0; 6A





khi đó

   

 

3 2 3

d d A

  



  

Mặt khác

   

 

;2d





d



 













  









.3cd

Câu 41: Tính diện tích hình phẳng (phần tô đậm) giới hạn bởi hai đường

4yx

;

2yx

như hình

vẽ bên dưới là





. B.

. C.

. D.



Lời giải

Chọn C

Ta có phương trình hoành độ giao điểm

4 2 2 0x x x x      

1; 2xx   

Dựa vào hình vẽ

 

2 4 2

S x x dx x x dx



        



Câu 42: Cho số phức

z x yi

( với

,xy

) thoả mãn

2 5 14 7z iz i   

. Tính

xy

. B.

1

. C.

. D.

Lời giải

Chọn A

Ta có

     

2 5 14 7 2 5 14 7 2 5 5 2 14 7z iz i x yi i x yi i x y x y i i                  

2 5 14 3

5 2 7 4

x y x

x y y

   



    



    



Câu 43: Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

với

     

2;2;2 , 0;1;1 , 1; 2; 3A B C   

. Tính diện tích

của tam giác

ABC

53S 

. B.

S 

. C.

S 

. D.

52S 

Lời giải

Chọn A

Ta có

     

2 2 2

1 2 1 3 1 26BC         

Ta có:

: 1 3 ,

BC y t t







  









. Gọi

là hình chiếu vuông góc của

lên

Khi đó

   

;1 3 ;1 4 2; 1 3 ; 1 4H BC H t t t AH t t t            

Ta có

9 5 78

26 9 0

26 26

AH BC t t AH        

Suy ra diện tích tam giác

ABC

bằng:

1 5 3

ABC

S AH BC





Cách 2.

Ta có:

ABC

S AB AC





Với

     

2; 1; 1 , 3; 4; 5 1; 7;5 5 3AB AC AB AC AB AC              

Suy ra

1 5 3

ABC

S AB AC



  

Câu 44: Trong không gian

Oxyz

, mặt phẳng

 



đi qua hai điểm

   

1;0;0 , 2;2;0AB

và vuông góc

với mặt phẳng

 

: 2 0P x y z   

có phương trình là

2 4 0x y z   

. B.

10x y z   

. C.

2 3 2 0x y z   

. D.

2 2 0x y z   

Lời giải

Chọn D

Ta có

 

1;2;0AB 

 

1;1;1

n 

 

   

 

, 2; 1; 1

n AB

n AB n











    











Phương trình mặt phẳng

 



là:

 

2 1 0 2 2 0x y z x y z        

Câu 45: Biết phương trình

 

z 0 ,z m n m n   

có một nghiệm là

13i

. Tính

3nm

4

6

3V 

16

Lời giải

Chọn A

Vì phương trình

 

z 0 ,z m n m n   

có một nghiệm là

13i

nên

   

1 3 1 3 0 1 6 9 3 0i m i n i m mi n           

   

8 3 2 0m n m i      

8 0 2

2 0 10

m n m

     



    



  



Câu 46: Cho hàm số

   

36 0;a, ,f x ax bx x c a b c     

có hai điểm cực trị là

6

và

Gọi

 

y g x

là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

 

y f x

. Diện tích

hình phẳng giới hạn bởi hai đường

 

y f x

và

 

y g x

bằng

160

128.

64

672

Lời giải

Chọn B

   

3 2 2

36 3 2 36f x ax bx x c f x ax bx



       

Theo bài ta được

 

   

6 0 3 6 2 . 6 36 0

3 2 2 . 2 36 0

f a b





      















  





9 3 1

3 9 6

a b a

a b b

   







  



   

3 2 2

6 36 ; 3 12 36f x x x x c f x x x



       

;

Đường thẳng đi qua hai điểm cực trị của hàm số

 

3 12 36 . 32x 24

y f x x x x c



       





là

 

32 24y g x x c    

Xét phương trình hoành độ giao điểm hai đồ thị

6 36 32 24 2

x x x c x c x







         







Vậy diện tích hình phẳng giới hạn bởi hai đường

 

y f x

và

 

y g x

bằng

 

     

2 2 2

3 2 3 2 3 2

6 6 2

6 36 32 24 6 4 24 6 4 24S x x x c x c dx x x x dx x x x dx



  

               

  

128

Câu 47: Cho hàm số

 

y f x

là hàm liên tục có tích phân trên

 

0;2

thỏa điều kiện

 

6df x x xf x x



. Tính

 

dI f x x



32I 

. B.

8I 

. C.

6I 

. D.

24I 

Lời giải

Chọn A

Ta có

 

6df x x xf x x



. Đặt

 

dxf x x a



Khi đó

 

2 4 2

66f x x a f x x a    

Do đó

 

d 6 da xf x x x x a x  



24 2 24

a x a a a



        





Nên

 

6 24f x x

Vậy

 

   

d 6 24 d 2 24 32I f x x x x x x      



Câu 48: Trong không gian

Oxyz

, cho hai điểm

   

2; 2;1 , 1;2; 3MA  

và đường thẳng

2 2 1

x y z







. Gọi

 

1; ;u a b

là một vectơ chỉ phương của đường thẳng



đi qua



vuông góc với đường thẳng

đồng thời cách điểm

một khoảng nhỏ nhất. Giá trị

2ab

là

. B.

. C.

. D.

Lời giải

Chọn D

Đường thẳng

có vectơ chỉ phương

 

2;2; 1

u 

;

 

1; ;u a b

là một vectơ chỉ phương của

đường thẳng



Theo đề,

2 2 0 2 2d a b b a        

Mặt khác,

     

3;4; 4 , 4 4 ; 4 3 ;3 4 12 8; 6 10;3 4MA MA u a b b a a a a



            



Nên

 

     

2 2 2

12 8 6 10 3 4

MA u

a a a



    



  



189 288 180

5 8 5







Xét

   

 

189 288 180 72 90

5 8 5

a a a a

f a f a

  



  



 

72 90

0 0 72 90 0

5 8 5

f a a a











      









Bảng biến thiên

Vậy khoảng cách từ

đến



nhỏ nhất khi

0 2 2 4a b a b     

Câu 49: Trong không gian với hệ tọa độ

Oxyz

, gọi mặt phẳng

 

:7 0P x by cz d   

(với

, , , 0b c d c

) đi qua điểm

 

1;3;5A

. Biết mặt phẳng

 

song song với trục

và khoảng

cách từ gốc tọa độ đến mặt phẳng

 

bằng

. Tính

T b c d  

4T 

. B.

78T 

. C.

61T 

. D.

7T 

Lời giải

Chọn C

có véc tơ chỉ phương

 

0;1;0j 

( ):7 0P x by cz d   

có véc tơ pháp tuyến

 

7; ;n b c

 

( )/ / . 0 0 :7 0P oy n j b P x cx d       

   

1;3;5 , 7 5 0 5 7A A P c d d c        

. Do đó

 

:7 5 7 0P x cx c   

khoảng cách từ gốc tọa độ đến mặt phẳng

()P

bằng

nên ta có

 

, 3 2 3 2 25 70 49 18 49

d O P c c c



       



 

7 70 833 0 17 0 78 61

c c c c d b c d





             







Câu 50: Gọi

là tập hợp tất cả các số phức

để số phức





có phần ảo bằng

. Biết rằng

3zz

với

,z z S

, giá trị nhỏ nhất của

2zz

bằng

3 5 3 2

3 5 3

. C.

53

. D.

2 5 2 3

Lời giải

Chọn A

Giả sử

 

,.z x yi x y  

   

w z x y i

x y x y



     



   

có phần ảo bằng

 

   

1 2 4

      



Vậy điểm biểu diễn số phức

,zz

thuộc đường tròn tâm

 

1,2I

, bán kính

2R 

Đặt

1 1 2 2

1 2 ; 1 2x z i x z i     

 

1 2 1

; : 4x x C x y  

Ta xét

1 2 1 2 1 2 1 2 1 2

2 2 3 6 2 3 6 2 2 3 6z z x x i x x i z z x x i              

   

2 2 2

1 2 1 2 1 2 1 2 2 1 1 2 2 1

3 9 . . 9 . . 1x x x x x xxx x x x x x x          

 

2 2 2

1 2 1 2 1 2 2 1 1 2

2 4 2 . . 4 16 2 18 2 18x x x x x xx x x x           

Do đó

2 3 5 3 2zz  

Bấm Tải xuống để xem toàn bộ.

| 1/20

| | Tải xuống

Preview text:

ĐỀ KIỂM TRA CUỐI HỌC KỲ II – NĂM 2022-2023-ĐỀ 2 Môn: TOÁN 12
Thời gian làm bài: 90phút Câu 1:
Cho biết F x là một nguyên hàm của hàm số f x . Biểu thức f  xdx  bằng
A. F  x .
B. F x  C .
C. F  x  C .
D. xF  x  C . Câu 2:
Cho hàm số y  f x liên tục trên  ;
a b . Gọi D là hình phẳng giới hạn bởi đồ thị của hàm
số y  f x , trục hoành và hai đường thẳng x  ,
a x  b (a  b) . Thể tích của khối tròn xoay
tạo thành khi quay D quanh trục hoành được tính theo công thức? b b b b A. V  f  xdx . B. 2 V   f
 xdx. C. 2 V   f
 xdx. D. 2 2 V   f  xdx . a a a a 2 4 4
f  x dx  2, f  x dx  1   
f  x dx  Câu 3: Nếu 1 1 thì 2 bằng A. 2  . B. 3 . C. 3  . D. 1. Câu 4:
Cho hai số phức z  2  3i, z  4
  i . Số phức z  z  z có môđun là 1 2 1 2 A. 13 . B. 2 2 . C. 2 13 . D. 2 17 . Câu 5: Cho các số thực ,
a ba  b và hàm số y  f  x có đạo hàm là hàm liên tục trên . Mệnh đề
nào sau đây là đúng? b b A. f 
 xdx  f a f b . B. f 
 xdx  f b f a . a a b b C. f
 xdx  f b f a. D. f
 xdx  f a f b. a a Câu 6:
Trong không gian với hệ trục tọa độ Oxyz , cho a  2
 i  4 j  6k . Tọa độ của a là A. 2; 4  ;6 . B.  2  ;4; 6   . C. 1; 2  ;  3 . D.  1  ;2; 3  . Câu 7:
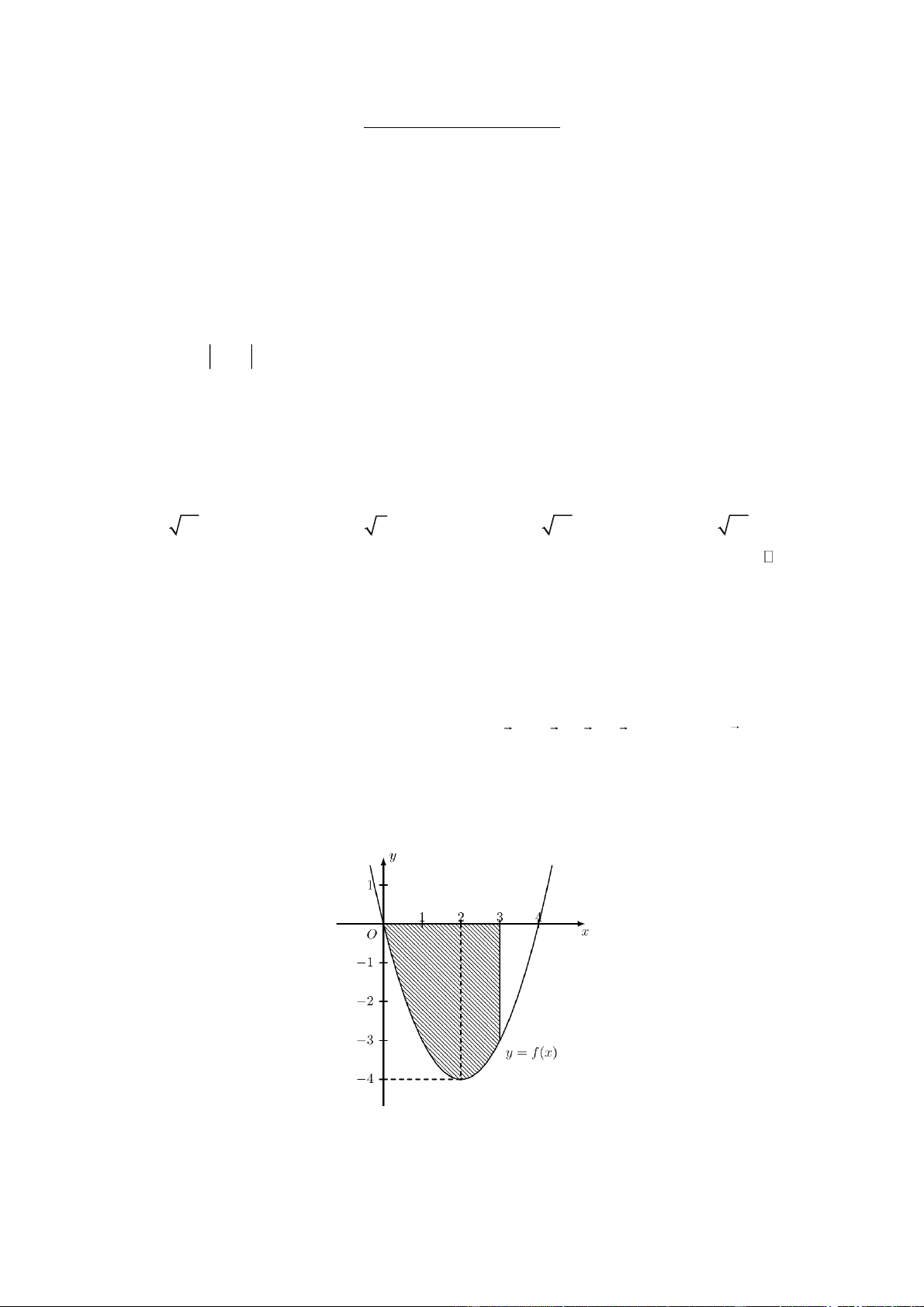
Cho hàm số y  f  x có đồ thị như hình vẽ bên dưới. Diện tích S của miền được tô đậm như
hình vẽ được tính theo công thức nào sau đây? 3 4 3 4
A. S   f  xdx.
B. S   f
 xdx. C. S  f  xdx . D. S  f  xdx . 0 0 0 0 x  2  t  Câu 8:
Trong không gian Oxyz , cho đường thẳng d có phương trình  y  3  t t   . Hỏi đường z  2   t 
thẳng d đi qua điểm nào sau đây A. B2;3; 2   . B. C  2  ; 3  ;2 . C. A1; 1  ;  1 .
D. D 2;3;2 . i  3 Câu 9:
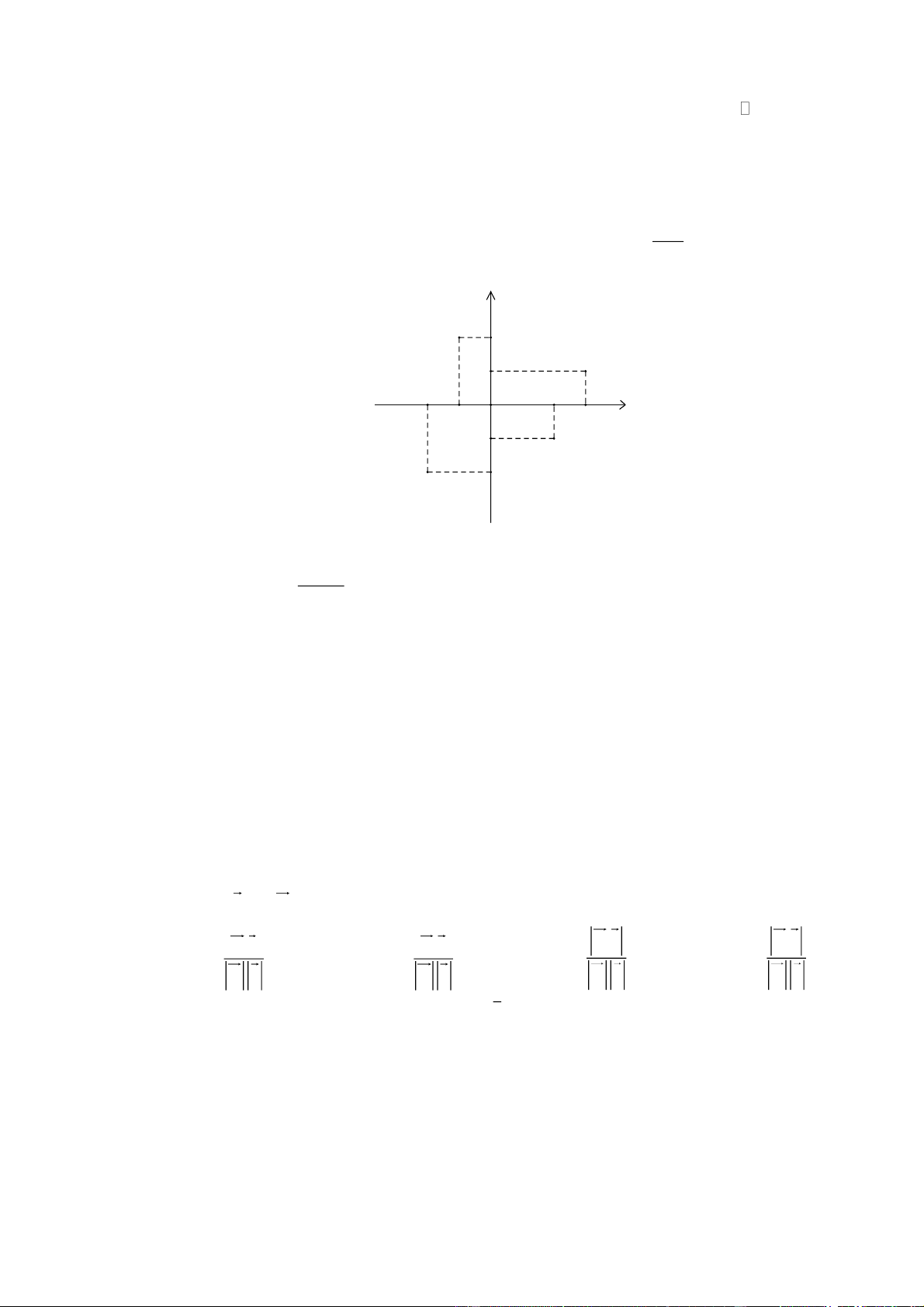
Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức z  ? 1 i y A 2 C 1 O x -2 -1 2 3 -1 D -2 B A. Điểm . B B. Điểm . D
C. Điểm C. D. Điểm . A 1
Câu 10: Cho hàm số f  x 
. Trong các khẳng định sau, khẳng định nào đúng? 2 cos x A. f
 xdx  cot x C. B. f
 xdx  tan x C. C. f
 xdx  tan xC. D. f
 xdx  cot xC.
Câu 11: Tất cả các nghiệm phức của phương trình 2
z  2z 17  0 là A. 1 4 ; i 1 4 . i B. 4 . i
C. 2  4i; 2  4 . i D. 1  6 .i
Câu 12: Trong không gian Oxyz , phương trình mặt cầu  S  có tâm I  1  ;1; 2
  và bán kính r  3 là 2 2 2 2 2 2
A. S  :  x   1   y  
1   z  2  9.
B. S  :  x   1   y  
1   z  2  9. 2 2 2 2 2 2
C. S  :  x   1   y  
1   z  2  3.
D. S  :  x   1   y  
1   z  2  3.
Câu 13: Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt phẳng  P và Q lần lượt có vectơ
pháp tuyến n và n . Gọi  là góc giữa mặt phẳng P và Q . công thức nào sau đây đúng?   n .n n .n n .n n .n A. sin   . B. co s  . C. sin   . D. co s  . n n n n n n n n
Câu 14: Cho số phức z  1
 5i . Phần ảo của số phức z bằng A. 1. B. 5 C. 5  . D. 1.
Câu 15: Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2x  4y  6z 1  0 . Tâm của mặt cầu
S có tọa độ là A. 1;2; 3  . B. 2;4; 6  . C.  1  ; 2  ;3. D.  2  ; 4  ;6.
Câu 16: Trong không gian Oxyz , cho phương trình mặt phẳng P : 2x  z  2  0 . Một vectơ pháp
tuyến của P là A. 2;0;  1  . B. 2; 1  ;0 C. 0; 1  ;2. D. 2; 1  ;2. x y z 1
Câu 17: Trong không gian Oxyz, cho phương trình của hai đường thẳng: d :   1 2 1  và 1 x  3 y z d :   d và d là 2 1 1 2
 . Vị trí tương đối của hai đường thẳng 1 2
A. d , d cắt nhau.
B. d , d chéo nhau.
C. d , d song song.
D. d , d trùng nhau. 1 2 1 2 1 2 1 2 Câu 18: Tính 2 x5 e dx 
ta được kết quả nào sau đây 2 x5 e 2 x5 e A. 2 x5 2e  C. B.   C. C.  C. D. 2 x 5 5  e  C. 5  2
Câu 19: Trong không gian Oxyz, cho mặt phẳng   : 2x 3y  z 3  0. Mặt phẳng nào sau đây song
song với mặt phẳng  ?
A. Q : 2x  3y  z  3  0.
B.   : x 3y  z 3  0.
C.   : 2x  3y  z  2  0.
D. P : 2x 3y  z 3  0. 3
Câu 20: Gọi S là diện tích hình phẳng giới hạn bởi hai đường y 
và y  4  x . Tính S. x 4 10 4 A. B. 3ln 3  C.  . D. 4 3ln 3. 3. 3 3 1 x  3
Câu 21: Tính tích phân I  dx  x 1 0 7 A. I   5ln 3.
B. I  4ln 31.
C. I 1 4ln 2.
D. I  2 5ln 2. 2
Câu 22: Trong không gian với hệ tọa độ Oxyz, cho hai điểm I (2;0;- ) 2 và A(2;3; )
2 . Mặt cầu (S) có
tâm I và đi qua điểm A có phương trình là 2 2 2 2 A.  x   2 2
 y  z  2  25. B.  x   2 2
 y  z  2  5. 2 2 2 2 C.  x   2 2
 y  z  2  5. D.  x   2 2
 y  z  2  25.
Câu 23: Giá trị các số thực a, b thỏa mãn 2a + (b + 1+ i)i = 1+ 2i (với i là đơn vị ảo ) là 1 1
A. a  0;b  1. B. a  ;b  0.
C. a  1;b  1. D. a  ;b  1. 2 2
Câu 24: Trong không gian với hệ tọa độ Oxyz, đường thẳng đi qua hai điểm A(3;1;- ) 6 và B(5;3;- ) 2
có phương trình tham số là
x  5  2t
x  6  2t x  5  t x  3 t    
A.  y  3  2t
B.  y  4  2t
C.  y  3  t
D.  y  1 t     z  2   4t  z  1   4t  z  2   2t  z  6   2t  x 1 y  3 z  2
Câu 25: Trong không gian Oxyz , gọi M a;b;c là giao điểm của đường thẳng d :   2 1  1
và mặt phẳng P : 2x  3y  4z  4  0. Tính T  a b  c . 5 3 A. T   . B. T  6 . C. T  4 . D. T  . 2 2
Câu 26: Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z thỏa mãn điều kiện z  i  2  2 là
A. Đường tròn tâm I 1;  2 , bán kính R  2 .
B. Đường tròn tâm I  2  ; 
1 , bán kính R  2 .
C. Đường tròn tâm I 2;  
1 , bán kính R  2 .
D. Đường tròn tâm I  1
 ;2, bán kính R  2 .
Câu 27: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A2;1;  1 , B 1  ;2;  1 . Tọa độ trung điểm
của đoạn thẳng AB là?  1 2   3 1   1 3  A. I ;1;   . B. I  3  ;1;0 . C. I  ;  ; 0   . D. I ; ;1    3 3   2 2   2 2 
Câu 28: Trong không gian với hệ tọa độ Oxyz , cho điểm M  2
 ;1;8. Gọi H là hình chiếu vuông góc
của M trên mặt phẳng Oxy . Tọa độ của điểm H là
A. H 0;1;8 . B. H  2  ;1;0.
C. H 0;0;8 . D. H  2  ;0;8 .  4
Câu 29: Tính tích phân I  sin xdx  . 0 2 2 2 2 A. I  1 . B. I  . C. I   . D. I  1   . 2 2 2 2
Câu 30: Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A2;0;0, B0;3;0,C 0;0;5. Mặt
phẳng  ABC có phương trình là x y z x y z x y z x y z A.    1. B.    1. C.    1. D.    0 . 3 2 5 5 3 2 2 3 5 2 3 5
Câu 31: Gọi z , z là hai nghiệm phân biệt của phương trình 2
z  3z  4  0 trên tập số phức. Tính giá 1 2
trị của biểu thức P  z  z . 1 2 A. 4 2 . B. 2 . C. 2 2 . D. 4 .
Câu 32: Cho số phức z thỏa mãn 2 i z  3i  2  0 . Phần thực của số phức z là 8 1 1 8 A. . B. . C.  . D.  . 5 5 5 5
Câu 33: Trong không gian Oxyz , mặt phẳng P : 2x  2y  z  6  0 . Khoảng cách từ gốc tọa độ đến
mặt phẳng  P bằng: A. 0 . B. 6 . C. 3 . D. 2 .
Câu 34: Cho số phức z  a  bi  ,
a b R . Khẳng định nào sau đây đúng? A. 2 2
z  a  b . B. 2 2
z  a  b . C. 3 3
z  a  b . D. 2 2
z  a  b .
Câu 35: Trong không gian, cắt vật thể bởi hai mặt phẳng P : x  1
 và Q: x  2 . Biết một mặt
phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x 1
  x  2 cắt theo thiết diện là
một hình vuông có cạnh bằng 6  x . Thể tích của vật thể giới hạn bởi hai mặt phẳng  P,Q bằng: 33 33 A. 93 . B. . C. 93 . D.  . 2 2 ln  2
Câu 36: Tính nguyên hàm d  x
x bằng cách đặt t  ln x ta được nguyên hàm nào sau đây? x ln x  2    2 A. 1 d   t . B. d  t t. C. d  t t .
D. t  2dt .  t  t  2 2 t  4 2 b Câu 37: Cho cos 4 cos d    b x x x
với a, b, c là các số nguyên, c  0 và tối giản. Tổng  a c c 6
a  b  c bằng A. 77  . B. 103. C. 17  . D. 43.
Câu 38: Trong không gian với hệ tọa độ Oxyz , cho S  2 2 2
: x  y  z  4x  2y 10z 14  0 . Mặt
phẳng P : x  4z  5  0 cắt mặt cầu S  theo một đường tròn C . Toạ độ tâm H của C là A. H  3  ;1; 2   . B. H  7  ;1;  3 . C. H 9;1;  1 . D. H 1;1;  1  . 10
Câu 39: Giá trị của 30 x xe dx  bằng 0 1 1 A. 300 3  00  900e . B. 300 300  900e . C.  300 299e   1 . D.  300 299e   1 . 900 900
Câu 40: Trong không gian hệ trục Oxyz , cho   : 2x  2y  z  6  0 . Gọi mặt phẳng
: x y cz d  0 không qua O, song song với mặt phẳng  và d ,  2. Tính . c d ? A. . c d  3 . B. . c d 12. C. . c d  6. D. . c d  0 .
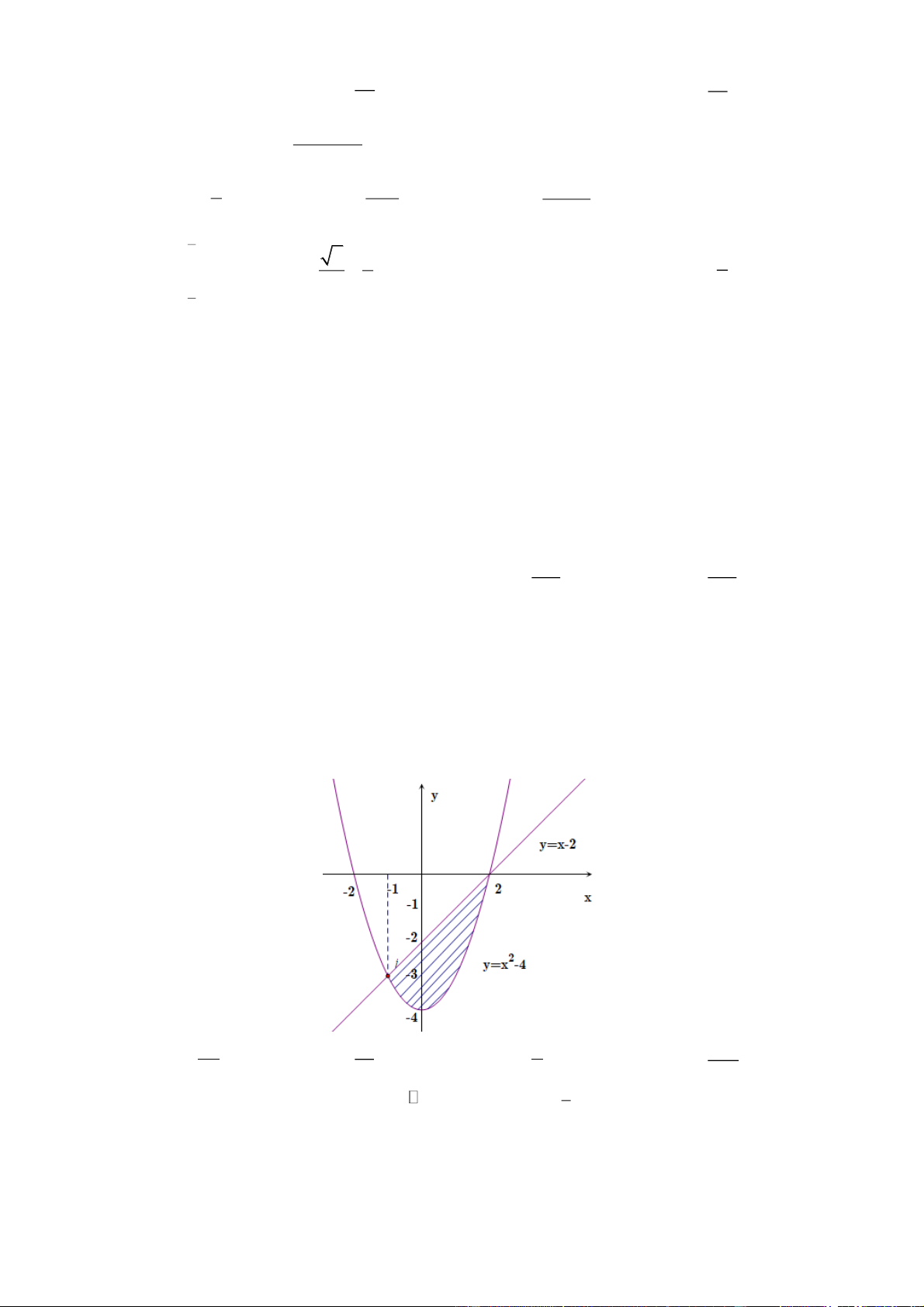
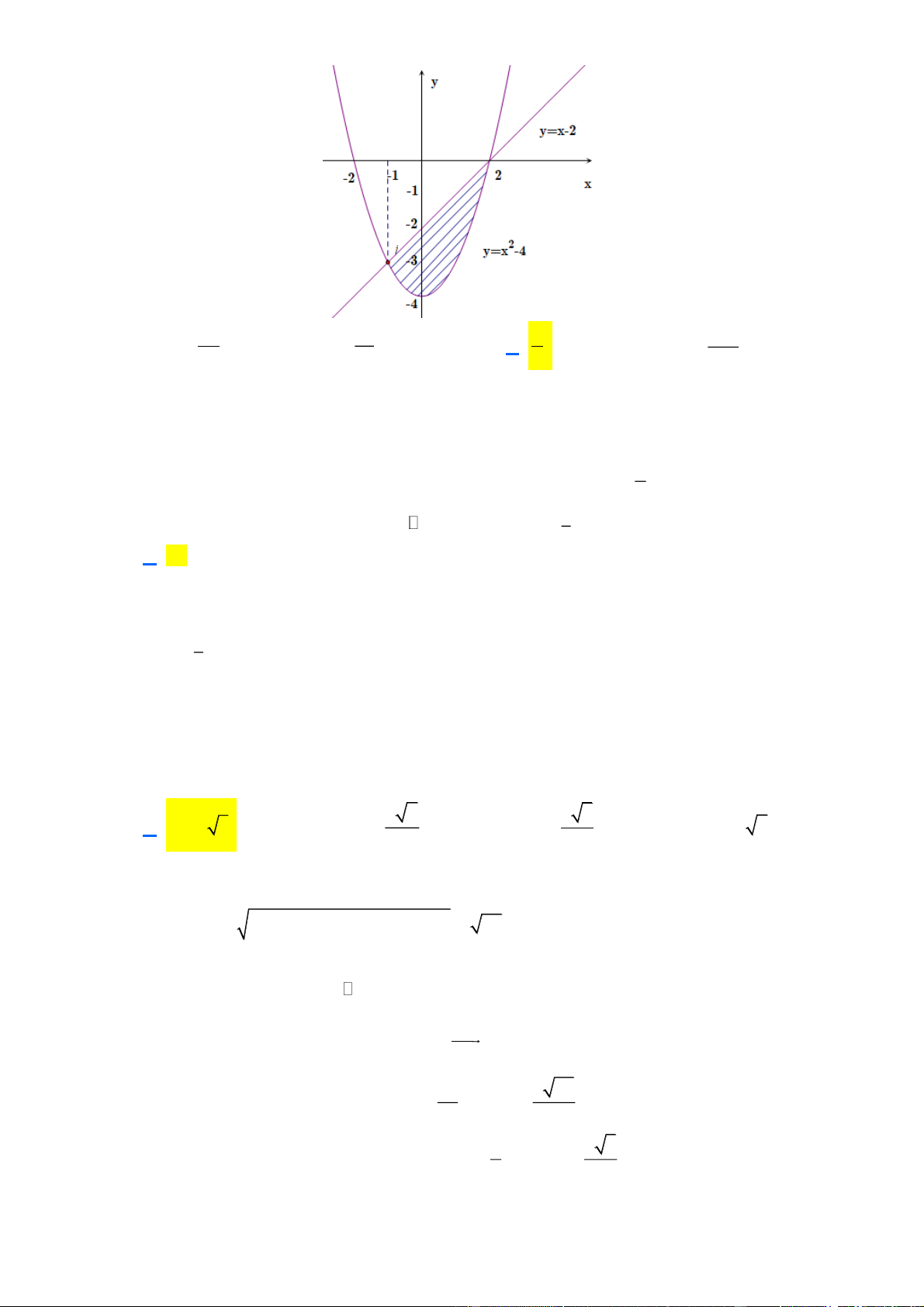
Câu 41: Tính diện tích hình phẳng (phần tô đậm) giới hạn bởi hai đường 2
y  x  4 ; y  x  2 như hình vẽ bên dưới là 9 33 9 33 A. S  . B. . C. . D. . 2 2 2 2   
Câu 42: Cho số phức z x
yi ( với x, y  ) thoả mãn 2z 5iz  1
 47i . Tính x y A. 7 . B. 1. C. 1. D. 5 . Câu 43: Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC với
A2;2;2, B0;1;  1 ,C  1  ; 2  ; 3
 . Tính diện tích S của tam giác ABC . 5 2 5 3
A. S  5 3 . B. S  . C. S  . D. S  5 2 . 2 2
Câu 44: Trong không gian Oxyz , mặt phẳng   đi qua hai điểm A1;0;0, B2;2;0 và vuông góc
với mặt phẳng P : x  y  z  2  0 có phương trình là
A. x  y  2z  4  0 .
B. x  y  z 1  0 .
C. 2x  y  3z  2  0 . D. 2x  y  z  2  0 .
Câu 45: Biết phương trình 2 z  z
m  n  0 ,
m n   có một nghiệm là 13i . Tính n  3m A. 4  B. 6
C. V  3 D. 16
Câu 46: Cho hàm số f  x 3 2
 ax bx 36x  c a  0;a, ,
b c   có hai điểm cực trị là 6  và 2 .
Gọi y  g  x là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y  f  x . Diện tích
hình phẳng giới hạn bởi hai đường y  f  x và y  g  x bằng A. 160 B. 128. C. 64 D. 672
Câu 47: Cho hàm số y  f  x là hàm liên tục có tích phân trên 0;  2 thỏa điều kiện 2 f  x  2 2 4  6x  xf
 xdx. Tính I  f  xdx . 0 0 A. I  32  . B. I  8  . C. I  6  . D. I  24  .
Câu 48: Trong không gian Oxyz , cho hai điểm M  2  ; 2;  1 , A1;2;  3 và đường thẳng x 1 y  5 z d :   u  1; ;
a b là một vectơ chỉ phương của đường thẳng  đi qua M , 2 2 1  . Gọi  
 vuông góc với đường thẳng d đồng thời cách điểm A một khoảng nhỏ nhất. Giá trị a  2b là A. 2 . B. 3 . C. 1. D. 4 .
Câu 49: Trong không gian với hệ tọa độ Oxyz , gọi mặt phẳng P : 7x  by  cz  d  0 (với ,
b c, d  , c  0 ) đi qua điểm A1;3;5 . Biết mặt phẳng  P song song với trục Oy và khoảng
cách từ gốc tọa độ đến mặt phẳng  P bằng 3 2 . Tính T  b  c  d . A. T  4  .
B. T  78 .
C. T  61.
D. T  7 . 1 1
Câu 50: Gọi S là tập hợp tất cả các số phức z để số phức w |  z |  có phần ảo bằng . Biết rằng z 1 4
z  z  3 với z , z  S , giá trị nhỏ nhất của z  2z bằng 1 2 1 2 1 2 A. 3 5  3 2 B. 3 5  3. C. 5  3 .
D. 2 5  2 3 .
BẢNG ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT 1.C 2.C 3.C 4.C 5.B 6.B 7.A 8.A 9.D 10.B 11.A 12.A 13.D 14.C 15.C 16.A 17.A 18.C 19.C 20.D 21.C 22.A 23.C 24.C 25.B 26.B 27.D 28.B 29.A 30.C 31.D 32.C 33.D 34.B 35.C 36.A 37.C 38.D 39.D 40.A 41.C 42.A 43.A 44.D 45.A 46.B 47.A 48.D 49.C 50.A Câu 1:
Cho biết F x là một nguyên hàm của hàm số f x . Biểu thức f  xdx  bằng
A. F  x .
B. F x  C .
C. F  x  C .
D. xF  x  C . Lời giải Chọn C f
 xdx  FxC. Câu 2:
Cho hàm số y  f x liên tục trên  ;
a b . Gọi D là hình phẳng giới hạn bởi đồ thị của hàm
số y  f x , trục hoành và hai đường thẳng x  ,
a x  b (a  b) . Thể tích của khối tròn xoay
tạo thành khi quay D quanh trục hoành được tính theo công thức? b b b b A. V  f  xdx . B. 2 V   f
 xdx. C. 2 V   f
 xdx. D. 2 2 V   f  xdx . a a a a Lời giải Chọn C
Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức b 2 V   f  xdx. a 2 4 4
f  x dx  2, f  x dx  1   
f  x dx  Câu 3: Nếu 1 1 thì 2 bằng A. 2  . B. 3 . C. 3  . D. 1. Lời giải Chọn C 4 4 2 Ta có f
 xdx  f
 xdx  f
 xdx  3  . 2 1 1 Câu 4:
Cho hai số phức z  2  3i, z  4
  i . Số phức z  z  z có môđun là 1 2 1 2 A. 13 . B. 2 2 . C. 2 13 . D. 2 17 . Lời giải Chọn C Ta có 2 2
z  z  z  6  4i  z  6  4  2 13. 1 2 Câu 5: Cho các số thực ,
a ba  b và hàm số y  f  x có đạo hàm là hàm liên tục trên . Mệnh đề
nào sau đây là đúng? b b A. f 
 xdx  f a f b . B. f 
 xdx  f b f a . a a b b C. f
 xdx  f b f a. D. f
 xdx  f a f b. a a Lời giải Chọn B b b Ta có f 
 xdx  f x  f b f a. a a Câu 6:
Trong không gian với hệ trục tọa độ Oxyz , cho a  2
 i  4 j  6k . Tọa độ của a là A. 2; 4  ;6 . B.  2  ;4; 6   . C. 1; 2  ;  3 . D.  1  ;2; 3  . Lời giải Chọn B Ta có a  2
 i  4 j  6k   2  ;4; 6
  nên a   2  ;4; 6   . Câu 7:
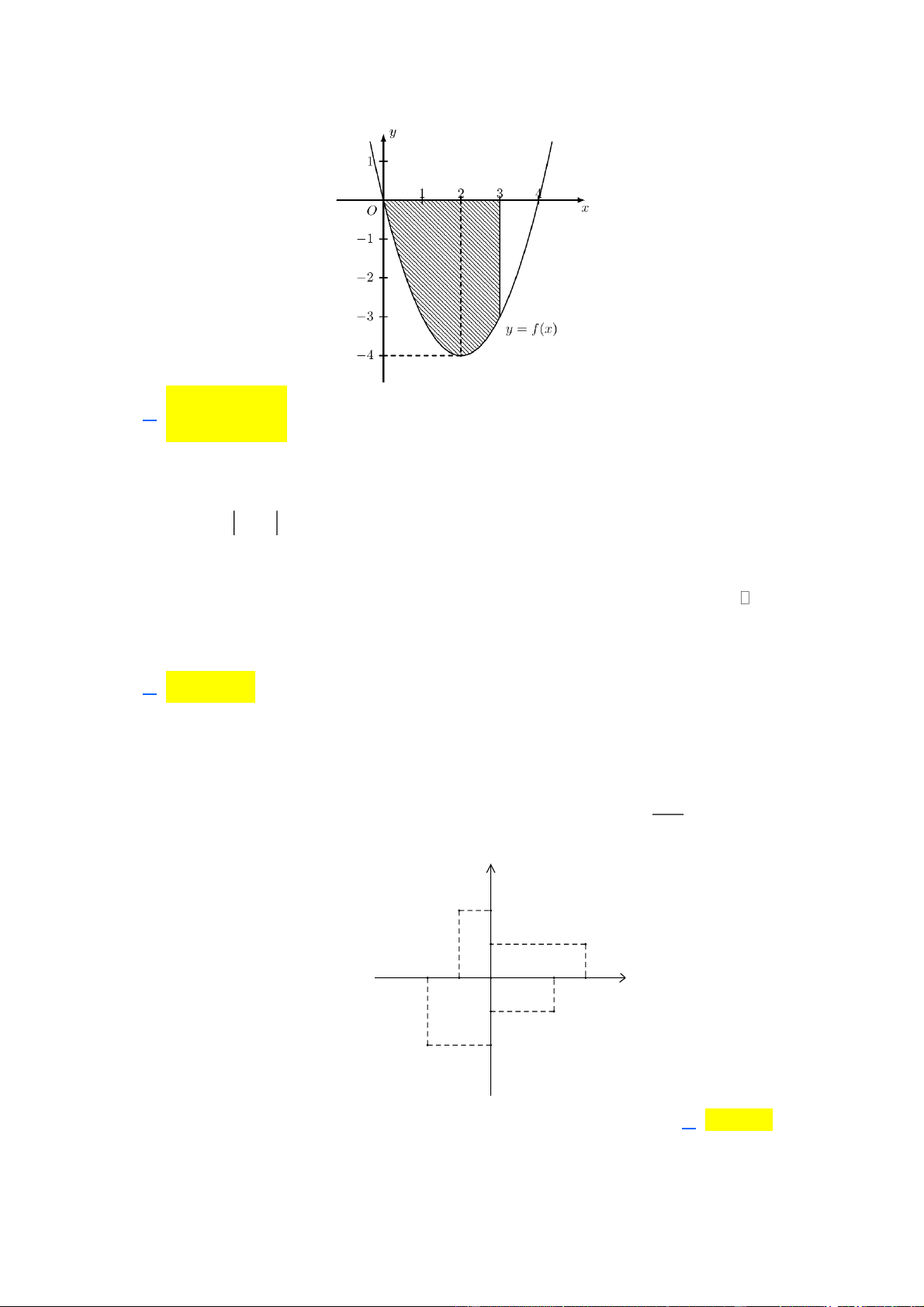
Cho hàm số y  f  x có đồ thị như hình vẽ bên dưới. Diện tích S của miền được tô đậm như
hình vẽ được tính theo công thức nào sau đây? 3 4 3 4
A. S   f  xdx.
B. S   f
 xdx. C. S  f  xdx . D. S  f  xdx . 0 0 0 0 Lời giải Chọn A 3 3 Ta có S  f
 x dx   f  xdx. 0 0 x  2  t  Câu 8:
Trong không gian Oxyz , cho đường thẳng d có phương trình  y  3  t t   . Hỏi đường z  2   t 
thẳng d đi qua điểm nào sau đây A. B2;3; 2   . B. C  2  ; 3  ;2 . C. A1; 1  ;  1 .
D. D 2;3;2 . Lời giải Chọn A
Với t  0 thì đường thẳng d đi qua điểm B2;3; 2   . i  3 Câu 9:
Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức z  ? 1 i y A 2 C 1 O x -2 -1 2 3 -1 D -2 B A. Điểm . B B. Điểm . D
C. Điểm C. D. Điểm . A Lời giải Chọn D i  3
i 31i z        i  i 
có điểm biểu diễn là điểm . A i 1 2i z 1 1 1 1
Câu 10: Cho hàm số f  x 
. Trong các khẳng định sau, khẳng định nào đúng? 2 cos x A. f
 xdx  cot x C. B. f
 xdx  tan x C. C. f
 xdx  tan xC. D. f
 xdx  cot xC. Lời giải Chọn B Lý thuyết.
Câu 11: Tất cả các nghiệm phức của phương trình 2
z  2z 17  0 là A. 1 4 ; i 1 4 . i B. 4 . i
C. 2  4i; 2  4 . i D. 1  6 .i Lời giải Chọn A z 1 4i 2
z  2z 17  0   . z 1 4i
Câu 12: Trong không gian Oxyz , phương trình mặt cầu  S  có tâm I  1  ;1; 2
  và bán kính r  3 là 2 2 2 2 2 2
A. S  :  x   1   y  
1   z  2  9.
B. S  :  x   1   y  
1   z  2  9. 2 2 2 2 2 2
C. S  :  x   1   y  
1   z  2  3.
D. S  :  x   1   y  
1   z  2  3. Lời giải Chọn A
Phương trình mặt cầu S  có tâm I  1  ;1; 2
  và bán kính r  3 là
x  2  y  2 z  2 1 1 2  9 .
Câu 13: Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt phẳng  P và Q lần lượt có vectơ
pháp tuyến n và n . Gọi  là góc giữa mặt phẳng P và Q . công thức nào sau đây đúng?   n .n n .n n .n n .n A. sin   . B. co s  . C. sin   . D. co s  . n n n n n n n n Lời giải Chọn D n .n Ta có: co s  . n n
Câu 14: Cho số phức z  1
 5i . Phần ảo của số phức z bằng A. 1. B. 5 C. 5  . D. 1. Lời giải Chọn C Ta có: z  1
 5i suy ra phần ảo bằng 5  .
Câu 15: Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2x  4y  6z 1  0 . Tâm của mặt cầu
S có tọa độ là A. 1;2; 3  . B. 2;4; 6  . C.  1  ; 2  ;3. D.  2  ; 4  ;6. Lời giải Chọn C
Tâm của mặt cầu S  có tọa độ là  1  ; 2  ;3.
Câu 16: Trong không gian Oxyz , cho phương trình mặt phẳng P : 2x  z  2  0 . Một vectơ pháp
tuyến của P là A. 2;0;  1  . B. 2; 1  ;0 C. 0; 1  ;2. D. 2; 1  ;2. Lời giải Chọn A
Một vectơ pháp tuyến của P là 2;0;  1  . x y z 1
Câu 17: Trong không gian Oxyz, cho phương trình của hai đường thẳng: d :   1 2 1  và 1 x  3 y z d :   d và d là 2 1 1 2
 . Vị trí tương đối của hai đường thẳng 1 2
A. d , d cắt nhau.
B. d , d chéo nhau.
C. d , d song song.
D. d , d trùng nhau. 1 2 1 2 1 2 1 2 Lời giải Chọn A
Vec tơ chỉ phương của d là u  2; 1  ; 
1 , vec tơ chỉ phương của d là u  1;1; 2   . 1 2
Vì hai vec tơ u,u không cùng phương nên d , d cắt nhau hoặc d , d chéo nhau. 1 2 1 2
x  2y  0 
x  2z  2
Xét hệ gồm hai phương trình của d , d :  1 2 x  y  3 
2y  z  0
Hệ này có nghiệm duy nhất:
 ;x ;yz  2; 1  ;2
Vậy d , d cắt nhau. 1 2 Câu 18: Tính 2 x5 e dx 
ta được kết quả nào sau đây 2 x5 e 2 x5 e A. 2 x5 2e  C. B.   C. C.  C. D. 2 x 5 5  e  C. 5  2 Lời giải Chọn C axb 1  Áp dụng ax b e dx  e  C  . a
Câu 19: Trong không gian Oxyz, cho mặt phẳng   : 2x 3y  z 3  0. Mặt phẳng nào sau đây song
song với mặt phẳng  ?
A. Q : 2x  3y  z  3  0.
B.   : x 3y  z 3  0.
C.   : 2x  3y  z  2  0.
D. P : 2x 3y  z 3  0. Lời giải Chọn C  2 3  1 3  / /   vì    2 3  . 1 2 3
Câu 20: Gọi S là diện tích hình phẳng giới hạn bởi hai đường y 
và y  4  x . Tính S. x 4 10 4 A. B. 3ln 3  C.  . D. 4 3ln 3. 3. 3 3 Lời giải Chọn D 3 x 1 3 Xét phương trình:  3 4  x  .  Vậy S   4  x dx 0,7.  x x  3 x 1 1 x  3
Câu 21: Tính tích phân I  dx  x 1 0 7 A. I   5ln 3.
B. I  4ln 31.
C. I 1 4ln 2.
D. I  2 5ln 2. 2 Lời giải Chọn C 1 1 - æ ö 1 x 3 4 I dx 1 ç = = - d ÷ ò òç
÷ x = (x- 4ln x + 1) = 1- 4ln 2. ç ÷ 0 x + 1 è x + 1ø 0 0
Câu 22: Trong không gian với hệ tọa độ Oxyz, cho hai điểm I (2;0;- ) 2 và A(2;3; )
2 . Mặt cầu (S) có
tâm I và đi qua điểm A có phương trình là 2 2 2 2 A.  x   2 2
 y  z  2  25. B.  x   2 2
 y  z  2  5. 2 2 2 2 C.  x   2 2
 y  z  2  5. D.  x   2 2
 y  z  2  25. Lời giải Chọn A
Bán kính mặt cầu R = IA = 25 = 5. 2 2
Vậy phương trình mặt cầu là:  x   2 2
 y  z  2  25.
Câu 23: Giá trị các số thực a, b thỏa mãn 2a + (b + 1+ i)i = 1+ 2i (với i là đơn vị ảo ) là 1 1
A. a  0;b  1. B. a  ;b  0.
C. a  1;b  1. D. a  ;b  1. 2 2 Lời giải Chọn C
2a + (b + 1+ i)i = 1+ 2i Û (2a- ) 1 + (b + ) 1 .i = 1+ 2i ìï 2a- 1= 1 ìï a = 1 ï ï Û í Û í . ï b + 1= 2 ï b = 1 ïî ïî
Câu 24: Trong không gian với hệ tọa độ Oxyz, đường thẳng đi qua hai điểm A(3;1;- ) 6 và B(5;3;- ) 2
có phương trình tham số là
x  5  2t
x  6  2t x  5  t x  3 t    
A.  y  3  2t
B.  y  4  2t
C.  y  3  t
D.  y  1 t     z  2   4t  z  1   4t  z  2   2t  z  6   2t  Lời giải Chọn C uuur AB = (2; 2; ) 4 r
Þ đường thẳng AB có một vectơ chỉ phương u = (1;1;2). x  5  t 
Þ phương trình tham số của đường thẳng AB là y  3 t . z  2   2t  x 1 y  3 z  2
Câu 25: Trong không gian Oxyz , gọi M a;b;c là giao điểm của đường thẳng d :   2 1  1
và mặt phẳng P : 2x  3y  4z  4  0. Tính T  a b  c . 5 3 A. T   . B. T  6 . C. T  4 . D. T  . 2 2 Lời giải Chọn B
Vì M  d nên M  1
  2t ;3t ;2 t
Mặt khác M P  2 1
  2t33t 42t 4  0 t 1  M 1;2;  3 Vậy T  6 .
Câu 26: Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z thỏa mãn điều kiện z  i  2  2 là
A. Đường tròn tâm I 1;  2 , bán kính R  2 .
B. Đường tròn tâm I  2  ; 
1 , bán kính R  2 .
C. Đường tròn tâm I 2;  
1 , bán kính R  2 .
D. Đường tròn tâm I  1
 ;2, bán kính R  2 . Lời giải Chọn B
Gọi z  x  yi z  i 
  x    y  i   x  2  y  2   x  2   y  2 2 2 2 1 2 2 1 2 2 1  4
Vậy tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z là đường tròn tâm I  2  ;  1 , bán kính R  2 .
Câu 27: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A2;1;  1 , B 1  ;2;  1 . Tọa độ trung điểm
của đoạn thẳng AB là?  1 2   3 1   1 3  A. I ;1;   . B. I  3  ;1;0 . C. I  ;  ; 0   . D. I ; ;1    3 3   2 2   2 2  Lời giải Chọn D  2 1 1 2 11  1 3  Ta có: I ; ;    I ; ;1   .  2 2 2   2 2 
Câu 28: Trong không gian với hệ tọa độ Oxyz , cho điểm M  2
 ;1;8. Gọi H là hình chiếu vuông góc
của M trên mặt phẳng Oxy . Tọa độ của điểm H là
A. H 0;1;8 . B. H  2  ;1;0.
C. H 0;0;8 . D. H  2  ;0;8 . Lời giải Chọn B
Hình chiếu vuông góc của M trên mặt phẳng Oxy là H  2  ;1;0.  4
Câu 29: Tính tích phân I  sin xdx  . 0 2 2 2 2 A. I  1 . B. I  . C. I   . D. I  1   . 2 2 2 2 Lời giải Chọn A  4  2 4
I  sin x dx   cos x 1 .  | 0 2 0
Câu 30: Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A2;0;0, B0;3;0,C 0;0;5. Mặt
phẳng  ABC có phương trình là x y z x y z x y z x y z A.    1. B.    1. C.    1. D.    0 . 3 2 5 5 3 2 2 3 5 2 3 5 Lời giải Chọn C
Câu 31: Gọi z , z là hai nghiệm phân biệt của phương trình 2
z  3z  4  0 trên tập số phức. Tính giá 1 2
trị của biểu thức P  z  z . 1 2 A. 4 2 . B. 2 . C. 2 2 . D. 4 . Lời giải Chọn D 2
z  3z  4  0 có   9 16  7
 phương trình đã cho có hai nghiệm phân biệt: 3   i 7 3   i 7 z  ; z 
 P  z  z  4. 1 2 1 2 2 2
Câu 32: Cho số phức z thỏa mãn 2 i z  3i  2  0 . Phần thực của số phức z là 8 1 1 8 A. . B. . C.  . D.  . 5 5 5 5 Lời giải Chọn C     i 2 3i 1 8 2
z  3i  2  0  z 
 z    i . 2  i 5 5 1
Vậy phần thực của số phức z là  . 5
Câu 33: Trong không gian Oxyz , mặt phẳng P : 2x  2y  z  6  0 . Khoảng cách từ gốc tọa độ đến
mặt phẳng  P bằng: A. 0 . B. 6 . C. 3 . D. 2 . Chọn D Lời giải 6
Ta có: d O,P   2. 2   2  2 2 2 1
Câu 34: Cho số phức z  a  bi  ,
a b R . Khẳng định nào sau đây đúng? A. 2 2
z  a  b . B. 2 2
z  a  b . C. 3 3
z  a  b . D. 2 2
z  a  b . Chọn B Lời giải
Câu 35: Trong không gian, cắt vật thể bởi hai mặt phẳng P : x  1
 và Q: x  2 . Biết một mặt
phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x 1
  x  2 cắt theo thiết diện là
một hình vuông có cạnh bằng 6  x . Thể tích của vật thể giới hạn bởi hai mặt phẳng  P,Q bằng: 33 33 A. 93 . B. . C. 93 . D.  . 2 2 Chọn C Lời giải 2 2
Thể tích của vật thể giới hạn bởi hai mặt phẳng: V  S
 xdx   6 x2dx  93(đvtt). 1  1  ln  2
Câu 36: Tính nguyên hàm d  x
x bằng cách đặt t  ln x ta được nguyên hàm nào sau đây? x ln x  2    2 A. 1 d   t . B. d  t t. C. d  t t .
D. t  2dt .  t  t  2 2 t Lời giải Chọn A 1 ln x  2 t  2   Đặ 2
t t  ln x  dt  dx . Khi đó dx  dt  1 d     t . x x ln x t  t   4 2 b Câu 37: Cho cos 4 cos d    b x x x
với a, b, c là các số nguyên, c  0 và tối giản. Tổng  a c c 6
a  b  c bằng A. 77  . B. 103. C. 17  . D. 43. Lời giải Chọn C    4 4 1 x x x      x x 4 1  1 1  2 13 cos 4 cos d cos 5 cos 3 dx 
sin 5x  sin 3x     . 2 2  5 3     30 60 6 6 6 a  30 
Suy ra b  13  a  b  c  30 13  60  1  7 . c  60  
Câu 38: Trong không gian với hệ tọa độ Oxyz , cho S  2 2 2
: x  y  z  4x  2y 10z 14  0 . Mặt
phẳng P : x  4z  5  0 cắt mặt cầu  S  theo một đường tròn C . Toạ độ tâm H của C là A. H  3  ;1; 2   . B. H  7  ;1;  3 . C. H 9;1;  1 . D. H 1;1;  1  . Lời giải Chọn C
Mặt cầu S  có tâm I 2;1; 5
  và mặt phẳng P có VTPT n   1  ;0;4 .
Vì mặt phẳng  P cắt mặt cầu S  theo một đường tròn C nên tâm H của C là hình
chiếu của I lên mặt phẳng  P .
Đường thẳng IH qua I 2;1; 5
  và nhận n   1
 ;0;4 là VTCP có phương trình là x  2  t  y 1
t   . Khi đó IH P  H 2t;1; 5   4t. z  5   4  t
Ta có 2 t  4 5
  4t5  0  t 1. Suy ra H 1;1;  1  . 10
Câu 39: Giá trị của 30 x xe dx  bằng 0 1 1 A. 300 3  00  900e . B. 300 300  900e . C.  300 299e   1 . D.  300 299e   1 . 900 900 Lời giải Chọn D du  dx u   x  10 Đặ 1 x 1 t    30 10 30 x 1  I  xe  e dx  30 x 30  0 dv  e d x x v  e  30 30  30 1 1 1 x 1 1 1 1 300 30 10 300 300  e  e  e  e    300 299e 1 . 0  3 900 3 900 900 900
Câu 40: Trong không gian hệ trục Oxyz , cho   : 2x  2y  z  6  0 . Gọi mặt phẳng
: x y cz d  0 không qua O, song song với mặt phẳng  và d ,  2. Tính . c d ? A. . c d  3 . B. . c d 12. C. . c d  6. D. . c d  0 . Lời giải Chọn A 1
Ta có   song song với   nên c      1 : x  y  z  d  0 . 2 2  d  d
Chọn A0;0; 6  khi đó d      d  A   3 2 3 ; ,   . 3 3 2  d 3 d  3
d  0L
Mặt khác d  ;   2 3 2   2      . c d  3 3 3 d  3  d    6N
Câu 41: Tính diện tích hình phẳng (phần tô đậm) giới hạn bởi hai đường 2
y  x  4 ; y  x  2 như hình vẽ bên dưới là 9 33 9 33 A. S  . B. . C. . D. . 2 2 2 2 Lời giải Chọn C
Ta có phương trình hoành độ giao điểm 2 2
x  4  x  2  x  x  2  0  x  1  ; x  2 . 2 2 9
Dựa vào hình vẽ S   x  2   2
x  4 dx   2
x  x  2dx    . 2 1  1    
Câu 42: Cho số phức z x
yi ( với x, y  ) thoả mãn 2z 5iz  1
 47i . Tính x y A. 7 . B. 1. C. 1. D. 5 . Lời giải Chọn A Ta có 2z  5iz  1
 4 7i  2x  yi5ix  yi  1
 4 7i  2x 5y   5
 x  2yi  1  4 7i
2x  5y  1  4 x  3    
 x  y  7 .  5
 x  2y  7  y  4 Câu 43: Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC với
A2;2;2, B0;1;  1 ,C  1  ; 2  ; 3
 . Tính diện tích S của tam giác ABC . 5 2 5 3
A. S  5 3 . B. S  . C. S  . D. S  5 2 . 2 2 Lời giải Chọn A 2 2 2
Ta có BC    1   2    1   3    1  26 . x  t  
Ta có: BC :  y  1 3t ,t  . Gọi H là hình chiếu vuông góc của A lên BC . y 1 4t 
Khi đó H  BC  H  t
 ;13t;1 4t  AH   t   2; 1  3t; 1   4t . 9 5 78
Ta có AH  BC  26t  9  0  t    AH  . 26 26 1 5 3
Suy ra diện tích tam giác ABC bằng: S  .AH.BC  . ABC  2 2 Cách 2. 1 Ta có: S  AB  AC . ABC  2 Với AB   2  ; 1  ;  1 , AC   3  ; 4  ; 5
   AB  AC  1; 7
 ;5  AB  AC  5 3 . 1 5 3 Suy ra S  AB  AC  . ABC  2 2
Câu 44: Trong không gian Oxyz , mặt phẳng   đi qua hai điểm A1;0;0, B2;2;0 và vuông góc
với mặt phẳng P : x  y  z  2  0 có phương trình là
A. x  y  2z  4  0 .
B. x  y  z 1  0 .
C. 2x  y  3z  2  0 . D. 2x  y  z  2  0 . Lời giải Chọn D
Ta có AB  1;2;0 , n  1;1;    1 P  n    AB 
 n  AB,n      2; 1;       1 P   n     n P
Phương trình mặt phẳng   là: 2x  
1  y  z  0  2x  y  z  2  0
Câu 45: Biết phương trình 2 z  z
m  n  0 ,
m n   có một nghiệm là 13i . Tính n  3m A. 4  B. 6
C. V  3 D. 16 Lời giải Chọn A Vì phương trình 2 z  z
m  n  0 ,
m n   có một nghiệm là 13i 2
nên 1 3i  m1 3i  n  0  1 6i  9  m  3mi  n  0   8
  m n3m 2i  0  8
  m  n  0 m  2     
 n  3m  4 . m  2  0 n 10
Câu 46: Cho hàm số f  x 3 2
 ax bx 36x  c a  0;a, ,
b c   có hai điểm cực trị là 6  và 2 .
Gọi y  g  x là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y  f  x . Diện tích
hình phẳng giới hạn bởi hai đường y  f  x và y  g  x bằng A. 160 B. 128. C. 64 D. 672 Lời giải Chọn B f  x 3 2
 ax bx  x  c f x 2 36
 3ax  2bx 36 .  f    6    0 3  a   6  2  2 . b  6   36  0 9
 a  b  3 a 1 Theo bài ta được         f   2  0 3  a  22  2 . b 2  36  0 3
 a  b  9 b   6  f x 3 2
 x  x  x  c f x 2 6 36 ;
 3x 12x 36 ;
Đường thẳng đi qua hai điểm cực trị của hàm số  
y  f  x   1 2 2
3x 12x  36. x   32x  c  24  
là y  g  x  3
 2x  c  24 .  3 3  x  6  
Xét phương trình hoành độ giao điểm hai đồ thị 3 2
x  6x  36x  c  3
 2x  c  24  x  2   x  2 
Vậy diện tích hình phẳng giới hạn bởi hai đường y  f  x và y  g  x bằng 2  S    2 2 3 2
x  6x  36x  c   3
 2x  c  24 dx    3 2
x  6x  4x  24dx    3 2
x  6x  4x  24dx 6  6  2  128 .
Câu 47: Cho hàm số y  f  x là hàm liên tục có tích phân trên 0;  2 thỏa điều kiện 2 f  x  2 2 4  6x  xf
 xdx. Tính I  f  xdx . 0 0 A. I  32  . B. I  8  . C. I  6  . D. I  24  . Lời giải Chọn A 2 2 Ta có f  2 x  4  6x  xf
 xdx. Đặt xf
 xdx  a . 0 0 Khi đó f  2 x  4
 x  a  f x 2 6  6x  a . 2 2 2 2   Do đó 3 ax a  xf
 xdx  x   2
6x  adx 4
 a   x 
  a  24  2a  a  2  4 .  2 2  0 0 0 Nên f  x 2  6x  24 . 2 2 2 Vậy I  f
 xdx   2
6x  24dx   3
2x  24x  3  2 . 0 0 0
Câu 48: Trong không gian Oxyz , cho hai điểm M  2  ; 2;  1 , A1;2;  3 và đường thẳng x 1 y  5 z d :   u  1; ;
a b là một vectơ chỉ phương của đường thẳng  đi qua M , 2 2 1  . Gọi  
 vuông góc với đường thẳng d đồng thời cách điểm A một khoảng nhỏ nhất. Giá trị a  2b là A. 2 . B. 3 . C. 1. D. 4 . Lời giải Chọn D
Đường thẳng d có vectơ chỉ phương u  2;2;  1 ; u  1; ;
a b là một vectơ chỉ phương của d đường thẳng  .
Theo đề,   d  2 2a b  0  b  2a  2 .
Mặt khác, MA  3;4; 4  M ,
A u  4a  4 ; b  4  3 ;
b 3a  4  12a  8;  6a 10;3a  4   . 2 2 2 M , A u 12a  8
 6a 10  3a  4   2
189a  288a 180 Nên d  , A           . 2 2 u 1 a  b 2 5a  8a  5 2 2
189a  288a 180 72a  90a
Xét f a   f  a  . 2   5a  8a  5  2
5a  8a  52 a  0  f a 2 72a 90a 2  0   
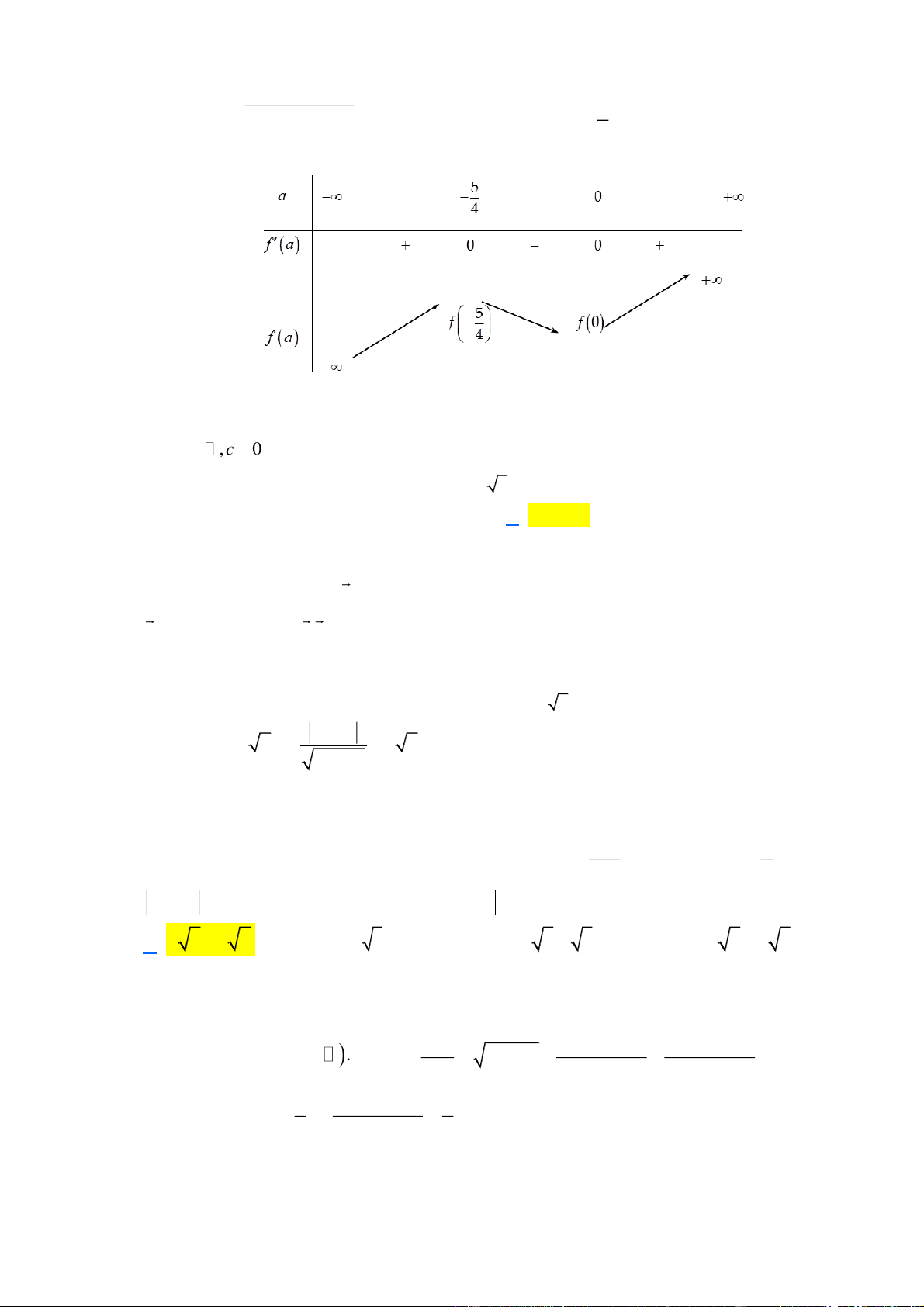
  a  a    . 5  8  5 0 72 90 0 2 5 2 a a a    4 Bảng biến thiên
Vậy khoảng cách từ A đến  nhỏ nhất khi a  0  b  2  a  2b  4 .
Câu 49: Trong không gian với hệ tọa độ Oxyz , gọi mặt phẳng P : 7x  by  cz  d  0 (với ,
b c, d  , c  0 ) đi qua điểm A1;3;5 . Biết mặt phẳng  P song song với trục Oy và khoảng
cách từ gốc tọa độ đến mặt phẳng  P bằng 3 2 . Tính T  b  c  d . A. T  4  .
B. T  78 .
C. T  61.
D. T  7 . Lời giải Chọn C
Oy có véc tơ chỉ phương j  0;1; 0 . (P) : 7x  by  cz  d  0 có véc tơ pháp tuyến n7; ;
b c (P) / /oy  .
n j  0  b  0  P : 7x  cx  d  0 .
Do A1;3;5, AP  7  5c  d  0  d  5
 c 7 . Do đó P:7x cx 5c 7  0.
khoảng cách từ gốc tọa độ đến mặt phẳng (P) bằng 3 2 nên ta có  c  d O,  P 5 7 2  3 2 
 3 2  25c  70c  49 18 2 49  c  . 2 2 7  c c  7 2
7c  70c  833  0   c  1  7 
c  0  d  78  b c  d  61 c  17  1 1
Câu 50: Gọi S là tập hợp tất cả các số phức z để số phức w |  z |  có phần ảo bằng . Biết rằng z 1 4
z  z  3 với z , z  S , giá trị nhỏ nhất của z  2z bằng 1 2 1 2 1 2 A. 3 5  3 2 B. 3 5  3. C. 5  3 .
D. 2 5  2 3 . Lời giải Chọn A 1 x 1 y
Giả sử z  x  yi  , x y  . 2 2 w |  z |   x  y   i . z 1 x  2 1  y x  2 2 2 1  y w 1 y 1 2 2 có phần ảo bằng 
  x 1  y  2  4 . 2     4 x   2 1  y 4
Vậy điểm biểu diễn số phức z , z I 1, 2 R  1
2 thuộc đường tròn tâm  , bán kính 2.
Đặt x  z 1 2 ;
i x  z 1 2i x ; x  C : x  y  4 1 1 2 2 .   2 2 1 2 1 .
Ta xét z  2z  x  2x  3  6i  x  2x  3  6i  z  2z  x  2x  3  6i 1 2 1 2 1 2 1 2 1 2 2 2 2
x  x  3  x  x
 9  x  x  x .x  x .x  9  x .x  x .x  1  1 2 1 2 1 2  1 2 2 1  1 2 2 1 2 2 2 x  2x
 x  4 x  2 x .x  x .x  4 16  2 18  x  2x  18 . 1 2 1 2  1 2 2 1 1 2
Do đó z  2z  3 5  3 2 . 1 2

Đề thi học kì 2 môn Toán lớp 12 năm 2023 - Đề 2

Thông tin :

Tài liệu liên quan:

Đề kiểm tra cuối kì 2 Toán 12 năm 2023 – 2024 sở GD&ĐT Vĩnh Long

Đề kiểm tra học kỳ 2 Toán 12 năm 2023 – 2024 sở GD&ĐT Bình Dương

Đề cuối học kì 2 Toán 12 năm 2023 – 2024 trường THPT Lê Hồng Phong – Quảng Nam

Đề cuối kì 2 Toán 12 năm 2023 – 2024 trường THPT Lê Hồng Phong – Đắk Lắk

Đề cuối học kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Thị xã Quảng Trị