SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HCM
ĐỀ KIỂM TRA HỌC KÌ II
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
Năm học: 2018 – 2019
−−−−−−−−−−−−
Môn TOÁN – Khối: 11 Thời gian: 90 phút
(Không kể thời gian phát đề)
Họ và tên học sinh: ……………………………………………………Số báo danh:………………………… Bài 1: Tính 3 2 x x 5x 6 a) + − − A = lim . (1 điểm) x − → 2 2 2x + 5x + 2 b) B = lim + − (1 điểm) →+∞ ( 2 25x 10x 5x x ). 2 c) x − 4 C = lim . (1 điểm) − 2
x→(−2) x + 2x
Bài 2: Xét tính liên tục của hàm số sau tại x = 3. o  2 x 8 1  − − x 3
y = f (x)  ( > ) =  x − 3 (1 điểm) 3 x 6 x 3  − ( ≤ )
Bài 3: Cho hàm số y = − 2
1 x . Chứng minh rằng: y.y '+ x = 0 ; x ∀ ∈ (−1 ; ) 1 . (1 điểm) 2 2x 3x 1
Bài 4: Tìm phương trình tiếp tuyến ( − +
D) của đồ thị (C): y =
biết (D) vuông góc x + 2
với đường thẳng (d):y = −3x +5. (1 điểm)
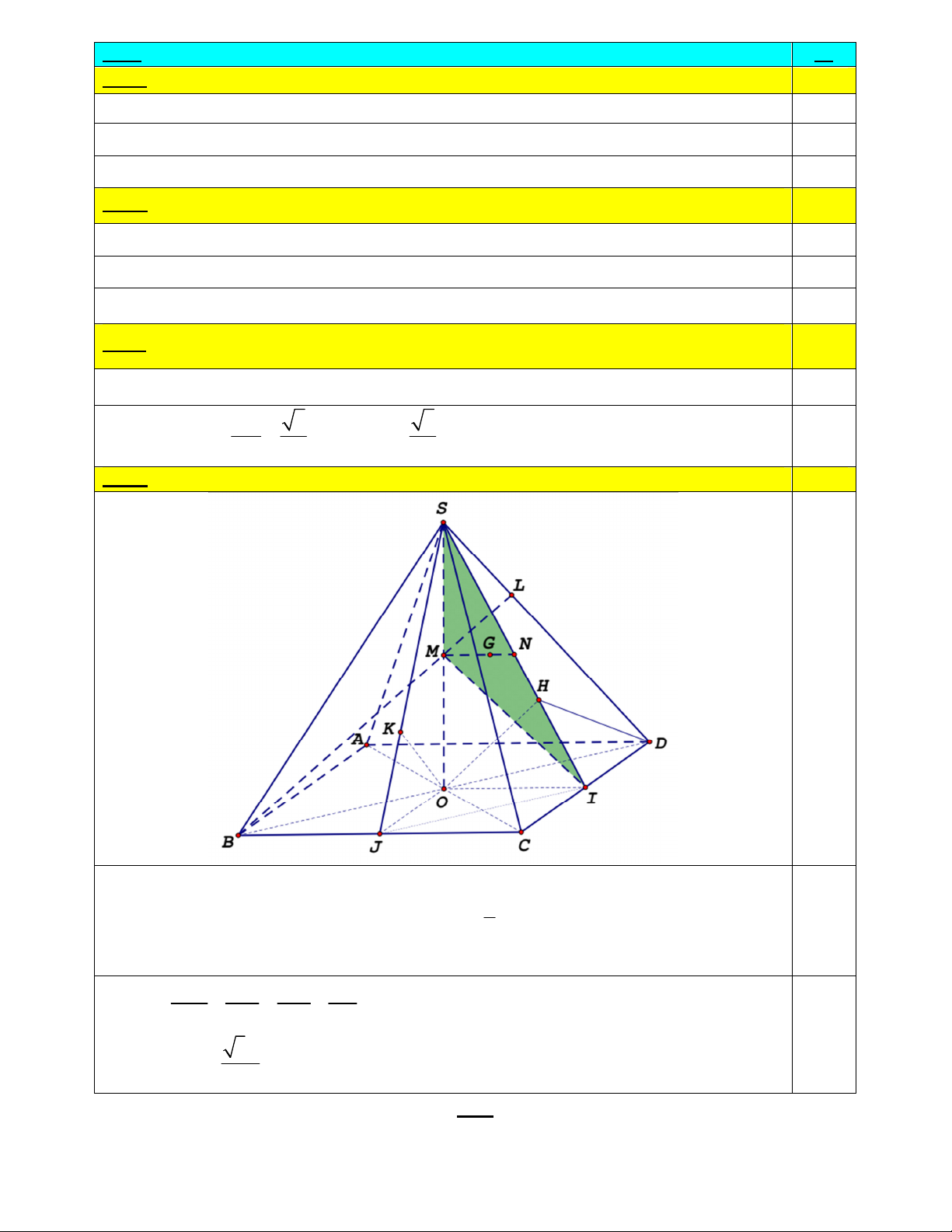
Bài 5: Cho hình chóp S.ABCD có đáy là hình vuông tâm O, cạnh AB = a; SO ⊥ a 3
mp(ABCD); SO = 2 . Gọi I là trung điểm của cạnh CD; H là hình chiếu của O lên
đường thẳng SI.
a) Chứng minh rằng: BD ⊥ mp(SAC). (1 điểm)
b) Chứng minh rằng: mp(HOD) ⊥ mp(SCD). (1 điểm)
c) Tính góc giữa đường thẳng OD và mặt phẳng (SCD). (1 điểm)
d) Trên cạnh SD, lấy điểm L sao cho LD = 2LS. Gọi M là giao điểm của SO và BL; G
là trọng tâm ∆MSI. Tính khoảng cách từ điểm G đến mặt phẳng (SBC). (1 điểm) HẾT
ĐÁP ÁN & BIỂU ĐIỂM (Đề 2) Bài 1: 3đ 3 2 x x 5x 6 Câu a: + − − A = lim 1đ x→− 2 2 2x + 5x + 2 ( x + 2)( 2 x − x − 3) 2 x − x − 3 = lim = lim = −1. 0.25x4
x→−2 ( x + 2)(2x + ) 1 x→ 2 − 2x +1 Câu b: B = lim + − 1đ →+∞ ( 2 25x 10x 5x x ). ( 2 25x +10x) 2 − 25x 10 = lim = lim = 1. x→+∞ 2 25 0.25x4
x +10x + 5x x→+∞ 10 25 + + 5 x 2 x − 4 Câu c: C = lim . 1đ − 2 x→−2 x + 2x 2 − x. −2 2 − x = lim − x = lim
= +∞ (Hs tách thành x + 2. x − 2 : không chấm) 0.25x4 − →(−2)− x −x ( 2 − − x) x→(−2) −x 2 − − x  2 x − 8 −1  x 3
Bài 2: Xét tính liên tục của y = f (x) ( > ) =  x − 3 tại x = 3. o 1đ 3x − 6 (x ≤  3) • f(3) = 3. 0.25
• lim f ( x) = lim (3x − 6) = 3. 0.25 x 3− x 3− → → 2 x − 8 −1 x + 3
• lim f ( x) = lim = lim = 3. 0.25 x 3+ → x 3+ → x − 3 x 3+ 2 → x − 8 +1
• lim f ( x) = lim f ( x) = f (3) nên f liên tục tại x = 3. o 0.25 x 3+ x 3− → → Bài 3: 2
y = 1− x . Chứng minh y.y '+ x = ; 0 x ∀ ∈ ( 1 − ; ) 1 . 1đ ( 2 1− x )' −x   2 −x • y ' = = ⇒ .
y y ' = 1 − x .
 = −x ⇒ y.y '+ x = 0 0.25x4 2 2 2 1 2 − x 1− x  1− x  2 2x − 3x + 1
Bài 4: Pttt ( D) của (C): y = f(x) =
, biết ( D) ⊥ (d): y = −3x + 5. 1đ x + 2 2 2x + 8x − 7 • y ' = 0.25 ( x + 2)2 1 x = 1 o
• Gọi x là hoành độ tiếp điểm. Từ gt: ) = ⇔ . 0.25 o f ’(xo  3 x = −5 o x − 1 • x = 1 : PTTT y = . o 3 0.25x2 x − 61 • x = 5 − : PTTT y = . o 3 Bài 5: 4đ
Câu a: BD⊥(SAC) 1đ
• ABCD là hình vuông nên BD ⊥ AC 0.25x2
• SO ⊥ ( ABCD ) nên BD ⊥ S . O 0.25
• Vậy BD ⊥ ( SAC ). 0.25
Câu b: H là hình chiếu vuông góc của O lên SI. Chứng minh: ( HOD) ⊥ (SCD). 1đ
• OH ⊥ SI ( gt ). 0.25
• CD ⊥ ( SOI ) ⇒ OH ⊥ C . D 0.25
• Vậy OH ⊥ ( SCD ) . Suy ra ( HOD) ⊥ ( SCD). 0.25x2 Câu c: ϕ  = OD ;   
SCD  . 1đ       
• OH ⊥ ( SCD) nên ϕ = ODH . 0.25x2 OH 6 6 ⇒ • ∆OHD : sinϕ = = ϕ = arc sin . 0.25x2 OD 4 4 Câu d: 1đ
• Từ gt suy ra M trung điểm SO. Gọi N là trung điểm SI. 1
• Vì MN // (SBC) nên d(G; (SBC)) = d(M; (SBC)) =
d (O;( SBC )). 0.25x2 2
• Gọi J trung điểm BC. Kẻ OK ⊥ SJ ⇒ d (O;( SBC )) = OK . 1 1 1 16 • S ∆ OJ : = + = . 2 2 2 2 OK OS OJ 3a 0.25x2 3.a
• d(G; (SBC)) = . 8 HẾT