Đề thi học kì 2 Toán 12 năm 2019 – 2020 trường Nguyễn Khuyến – Bình Dương

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2019 – 2020 .Mời bạn đọc đón xem.

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

21 trang 8 tháng trước

Tác giả:

Profile Lan Tường
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
TRƯỜNG THCS - THPT NGUYỄN KHUYẾN
.
ĐỀ KIỂM TRA HỌC KÌ 2
NĂM HỌC 2019 - 2020
Môn thi: TOÁN - Lớp: 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Đề thi gồm 05 trang - 50 câu trắc nghiệm
------------------------------
Họ và tên: ……………………………………………………… SBD: …………………
Câu 1. Tìm số phức
z
thỏa mãn
3 2 1 3z i i
.
A.
25zi
. B.
25zi
. C.
25zi
. D.
25zi
.
Câu 2. Tìm họ nguyên hàm của hàm số
x
f x e
.
A.
. B.
x
f x dx e C
.
C.
x
f x dx e C
. D.
x
f x dx e C

.
Câu 3. Cho hai số phức
1
12zi
và
2
34zi
. Phần thực của số phức
12
zz
bằng
A.
2
. B.
4
. C.
2
. D.
6
.
Câu 4. Gọi
1
z
là nghiệm có phần ảo dương của phương trình
2
2 5 0 zz
. Tính
2
1
A z i
A.
2
. B.
10
. C.
2
. D.
2
.
Câu 5. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
:2 3 4 1 0x y z
. Véc-tơ nào
dưới đây là một véc-tơ pháp tuyến của mặt phẳng
?
A.
1
2; 3;4n 
. B.
3
2; 3;1n 
. C.
4
3;4;1n 
. D.
2
2;3; 4n 
.
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 3
:
1 2 1
x y z

. Véc-tơ nào
dưới đây vuông góc với véc-tơ chỉ phương của đường thẳng
?
A.
3
2; 3;4u 
. B.
4
2;3; 4u 
. C.
1
2;3;4u
. D.
2
2;3;4u 
.
Câu 7. Cho hàm số
fx
thỏa mãn
52
. 3 6f x f x x x

,
x
, biết rằng
01f
. Tính
2
1f
.
A.
2
1 100f
. B.
2
13f
. C.
2
1 81f
. D.
2
16f
.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
P
:
50x y z
. Điểm nào dưới
đây thuộc
P
?
A.
0;0; 5
. B.
0;5;0
. C.
0;0;5
. D.
5;0;0
.
Câu 9. Tìm họ nguyên hàm của hàm số
1
.
21
fx
x
A.
1
.ln 2 1 .
2
f x dx x C
B.
ln 2 1 .f x dx x C
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
C.
2
2
.
21
f x dx C
x

D.
1
ln 2 1 .
2
f x dx x C
Câu 10. Biết
1
0
dx 10fx
và
1
0
dx 30,gx
khi đó
1
0
dxg x f x


bằng
A.
20.
B.
20.
C.
40.
D.
40.
Câu 11. Môđun của số phức
34i
bằng
A.
7
. B.
8
. C.
6
. D.
5
.
Câu 12. Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 3 0zz
. Giá trị
22
12
zz
bằng
A.
2
. B.
10
. C.
2
. D.
4
.
Câu 13. Nếu
3
1
5f x dx
và
2
1
2f x dx
thì
3
2
f x dx
bằng
A.
7
. B.
3
. C.
3
. D.
7
.
Câu 14. Cho hàm số
y f x
có đạo hàm liên tục trên đoạn
1;2
,
11f
và
2 11f
. Tính tích
phân
2
1
f x dx
.
A.
10
. B.
12
. C.
9
. D.
10
.
Câu 15. Diện tích hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây
A.
1
2
0
2 ( 2 ) .S x x dx
B.
1
2
0
2 ( 2 ) .S x x dx
1.T 
C.
1
2
0
2 ( 2 ) .S x x dx
8.T
D.
1
2
0
2 ( 2 ) .S x x dx
Câu 16. Trong không gian với hệ tọa độ
Oxyz
cho hai mặt phẳng
( ):2 3 3 5 0P x y z
và
( ): 1 0Q y z
. Tính góc gữa
()P
và
()Q
.
A.
2
B.
3
C.
4
D.
6
Câu 17. Nếu
1
0
1010f x dx
thì
1
0
2 f x dx
bằng
A.
4040
. B.
3030
. C.
1010
. D.
2020
.
Câu 18. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
5;0;0 , 0; 4;0 , 0;0;6A B C
. Mặt phẳng
qua ba điểm
,,A B C
có phương trình
A.
5 4 6 0x y z
. B.
5 4 6 1x y z
. C.
0
5 4 6
x y z
. D.
1
5 4 6
x y z
.
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
Câu 19. Họ tất cả các nguyên hàm của hàm số
sin 6f x x x
là
A.
2
cos 3 .F x x x C
B.
cos .F x x C
C.
2
cos 6 .F x x x C
D.
2
cos 3 .F x x x C
Câu 20. Trong không gian
Oxyz
, mặt phẳng
chứa trục
Ox
và đi qua điểm
2; 5;7A
có phương
trình là:
A.
7 5 0.yz
B.
7 5 0.yz
C.
5 7 0.yz
D.
5 7 0.yz
Câu 21. Họ tất cả các nguyên hàm của hàm số
2
1
x
fx
x
trên khoảng
1;
là:
A.
3ln 1F x x x C
. B.
2
3
1
F x x C
x
.
C.
3ln 1F x x x C
. D.
2
3
1
F x x C
x
.
Câu 22. Trong không gian với hệ trục tọa độ
Oxyz
, cho hai điểm
2;1;0 , 0;3;4AB
. Mặt phẳng
trung trực của đoạn thẳng
AB
có phương trình là
A.
2 3 4 4 0x y z
. B.
2 3 4 4 0x y z
.
C.
2 3 4 4 0x y z
. D.
2 5 0x y z
.
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
2;0;2 , 0;2;0AB
. Gọi
S
là mặt cầu
nhận
AB
làm đường kính. Diện tích của mặt cầu
S
bằng
A.
36
. B.
8
. C.
16
. D.
12
.
Câu 24. Trên mặt phẳng tọa độ, điểm biểu diễn số phức
2
12zi
là điểm nào dưới đây
A.
3; 4K 
. B.
5; 4I
. C.
4;5E
. D.
3;4N
.
Câu 25. Cho hàm số
y f x
thỏa mãn
3 5sinf x x

và
01f
. Mệnh đề nào dưới đây đúng?
A.
3 5cos 6f x x x
. B.
3 5cos 6f x x x
.
C.
3 5cos 6f x x x
. D.
3 5cos 6f x x x
.
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, cho vectơ
1;0;3a
và
2;2;5b 
. Tích vô hướng
.a a b
bằng
A.
3
. B.
23
. C.
9
. D.
5
.
Câu 27. Trong không gian với hệ toạ độ
Oxyz
, cho đường thẳng
1 2 3
( ):
1 2 3
x y z
d

. Điểm nào
dưới đây thuộc đường thẳng
()d
?
A.
(1; 2;3).P
B.
(1;2;3).N
C.
( 1;2; 3).M 
D.
( 1;2;3).Q
Câu 28. Cho số phức
2zi
. Tính
1
z
.
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
A.
5
. B.
5
. C.
3
. D.
5
5
.
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, mặt phẳng đi qua điểm
1;1;1M
và vuông góc với
đường thẳng
1 2 3
:
3 2 1
x y z
có phương trình là
A.
30x y z
. B.
3 2 0x y z
.
C.
3 2 6 0x y z
. D.
2 3 6 0x y z
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
,cho mặt cầu
S
có tâm
1;0;0I
và đi qua điểm
0;0;1M
. Phương trình của
S
là
A.
2
22
: 1 2S x y z
. B.
2
22
: 1 2S x y z
.
C.
2
22
: 1 2S x y z
. D.
2
22
: 1 2S x y z
.
Câu 31. Cho
9
0
d9f x x
. Tính
3
0
3dI f x x
.
A.
27.
B.
9.
C.
6
. D.
3
.
Câu 32. Số phức liên hợp của số phức
3 2 3z i i
là
A.
67zi
. B.
97zi
. C.
97zi
. D.
67zi
.
Câu 33. Trong không gian với hệ trục tọa độ
Oxyz
, hình chiếu vuông góc của điểm
1;2;3M
trên mặt
phẳng
Oxy
có tọa độ là
A.
1;2;0
. B.
1;0;3
. C.
1;0;0
. D.
0;2;3
.
Câu 34. Tìm họ nguyên hàm của hàm số
cos2f x x
.
A.
2sin2f x dx x C
. B.
1
sin2
2
f x dx x C
.
C.
1
sin2
2
f x dx x C
. D.
2sin2f x dx x C
.
Câu 35. Trong không gian với hệ tọa độ
Oxyz
, hình chiếu vuông góc của điểm
1;2; 3M 
trên trục
Oy
có tọa độ là
A.
1;0;0Q
. B.
0;0; 3N
. C.
0;2;0E
. D.
1;2;0P
.
Câu 36. Số phức đối của số phức
34i
là:
A.
43i
. B.
34i
. C.
34i
. D.
34i
.
Câu 37. Tìm họ nguyên hàm của hàm số
2
2020
x
fx
x
.
A.
2
d ln 2020f x x x C
. B.
2
d ln 2020f x x x C
.
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 5
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
C.
2
1
d 2020
2
f x x x C
. D.
2
d 2020f x x x C
.
Câu 38. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
2 2 2
: 4 2 6 5 0S x y z x y z
.
Bán kính của mặt cầu đã cho bằng
A.
19
. B.
3
. C.
9
. D.
19
.
Câu 39. Trong không gian với hệ toạ độ
Oxyz
, cho mặt cầu
2 2 2
: 1 1 1 9S x y z
. Tâm
của
S
có toạ độ là
A.
1;1;1
. B.
1;1; 1
. C.
1; 1;1
. D.
1;1;1
.
Câu 40. Trong không gian với hệ toạ độ
Oxyz
, phương trình nào dưới đây là phương trình của đường
thẳng đi qua điểm
0;2;3A
và vuông góc với mặt phẳng
: 3 5 0P x y z
.
A.
3 3 0x y z
. B.
23
3
xt
yt
zt


. C.
32
13
xt
yt
zt

. D.
3 3 0x y z
.
Câu 41. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1; 2;3E 
. Gọi
E
là hình chiếu vuông góc
của
E
lên mặt phẳng
Oxz
. Khoảng cách từ
E
đến trục
Oy
bằng
A.
13
. B.
14
. C.
10
. D.
5
.
Câu 42. Trong không gian với hệ tọa độ
Oxyz
, véc tơ nào dưới đây là một véc tơ chỉ phương của
đường thẳng đi qua hai điểm
2;3; 1E 
và
2; 1;3F
?
A.
4
1; 1;1u 
. B.
3
1; 1; 1u
. C.
2
0;1;1u
. D.
1
1;1;1u
.
Câu 43. Biết
Fx
là một nguyên hàm của hàm số
cosf x x x
và
01F
. Tính
F
.
A.
2
F
. B.
1F
. C.
1F

. D.
2
F

Câu 44. Cho hàm số
2
F x x
là một nguyên hàm của hàm số
2x
f x e
. Tìm nguyên hàm của hàm số
2x
f x e
.
A.
22
dx
x
f x e x x C
. B.
22
dx
x
f x e x x C
.
C.
22
dx 2 2
x
f x e x x C
. D.
22
dx 2 2
x
f x e x x C
.
Câu 45. Tìm họ nguyên hàm của hàm số
2020 .
x
fx
A.
1
2020
2020 .
1
x
x
dx C
x

B.
2020 2020 ln .
xx
dx x C
C.
2020
2020 .
ln2020
x
x
dx C
D.
1
2020 2020 .
xx
dx C

Câu 46. Số phức nào dưới đây là số thuần ảo?
A.
2020.
B.
2.i
C.
2020 .i
D.
1 3 .i
Câu 47. Biết phương trình
2
0z az b
nhận số phức
1zi
là nghiệm. Tính tổng
S a b
.
A.
4S
. B.
2S 
. C.
0S
. D.
4S 
.
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Câu 48. Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
2;0;0A
,
0;6;0B
,
0;0;5C
và điểm
N
sao cho
ON OA OB OC
. Một mặt phẳng
P
thay đổi cắt các đoạn thẳng
, , ,OA OB OC ON
lần lượt tại các điểm
1 1 1 1
, , ,A B C N
thỏa mãn
1 1 1
2020
OA OB OC
OA OB OC
và
1 0 0 0
;;N x y z
. Khi đó
A.
0 0 0
7
2020
x y z
. B.
0 0 0
9
2020
x y z
.
C.
0 0 0
11
2020
x y z
. D.
0 0 0
13
2020
x y z
.
Câu 49. Biết
2
2
2
cos
sin
6
cos 1 sin
1
.
m
x
n
x
xx
dx a
be
e

trong đó
, , ,a b m n
là các số nguyên dương,
m
n
là phân số
tối giản. Tính
S a b m n
.
A.
9S
. B.
12S
. C.
10S
. D.
11S
.
Câu 50. Cho
fx
là một nguyên hàm của
gx
trên , thỏa mãn
1
22
f



,
2
0
1
2
xg x dx
và
2
0
f x dx a b

, trong đó
,ab
là các số hữu tỉ. Tính
2P a b
.
A.
1
2
P
. B.
0P
. C.
1P
. D.
1
2
P 
.
-------------------- HẾT --------------------
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
BẢNG ĐÁP ÁN
1.A
2.C
3.B
4.A
5.A
6.C
7.D
8.A
9.D
10.A
11.D
12.A
13.C
14.D
15.A
16.A
17.D
18.D
19.A
20.B
21.A
22.D
23.D
24.A
25.B
26.A
27.C
28.D
29.C
30.D
31.D
32.C
33.A
34.B
35.C
36.C
37.D
38.B
39.B
40.B
41.C
42.A
43.C
44.C
45.C
46.C
47.C
48.D
49.C
50.B
HƯNG DN GIẢI CHI TIT
Câu 1. Tìm số phức
z
thỏa mãn
3 2 1 3z i i
.
A.
25zi
. B.
25zi
. C.
25zi
. D.
25zi
.
Lời giải
Chọn A
Ta có
3 2 1 3 2 5 2 5z i i z i z i
.
Câu 2. Tìm họ nguyên hàm của hàm số
x
f x e
.
A.
. B.
x
f x dx e C
.
C.
x
f x dx e C
. D.
x
f x dx e C

.
Lời giải
Chọn C
Ta có
x x x
f x dx e dx e d x e C
.
Câu 3. Cho hai số phức
1
12zi
và
2
34zi
. Phần thực của số phức
12
zz
bằng
A.
2
. B.
4
. C.
2
. D.
6
.
Lời giải
Chọn B
Ta có :
12
1 2 3 4 1 2 3 4 4 2z z i i i i i
Suy ra : Phần thực của số phức
12
zz
bằng
4
.
Câu 4. Gọi
1
z
là nghiệm có phần ảo dương của phương trình
2
2 5 0 zz
. Tính
2
1
A z i
A.
2
. B.
10
. C.
2
. D.
2
.
Lời giải
Chọn A
Ta có
22
22
1 2 1 2
2 5 0 2 1 4 1 2
1 2 1 2



z i z i
z z z z z i
z i z i
Vì
1
z
là nghiệm có phần ảo dương nên :
1
12zi
.
2 2 2
22
1
1 2 1 2 0 2 2 A z i i i i i
.
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
Câu 5. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
:2 3 4 1 0x y z
. Véc-tơ nào
dưới đây là một véc-tơ pháp tuyến của mặt phẳng
?
A.
1
2; 3;4n 
. B.
3
2; 3;1n 
. C.
4
3;4;1n 
. D.
2
2;3; 4n 
.
Lời giải
Chọn A
có một véc-tơ pháp tuyến là
1
2; 3;4n 
.
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 3
:
1 2 1
x y z

. Véc-tơ nào
dưới đây vuông góc với véc-tơ chỉ phương của đường thẳng
?
A.
3
2; 3;4u 
. B.
4
2;3; 4u 
. C.
1
2;3;4u
. D.
2
2;3;4u 
.
Lời giải
Chọn C
có véc-tơ chỉ phương là
1;2; 1u
.
Ta có
11
. 1 .2 2.3 1 .4 0u u u u
.
Câu 7. Cho hàm số
fx
thỏa mãn
52
. 3 6f x f x x x

,
x
, biết rằng
01f
. Tính
2
1f
.
A.
2
1 100f
. B.
2
13f
. C.
2
1 81f
. D.
2
16f
.
Lời giải
Chọn D
Ta có:
11
52
00
. d 3 6 df x f x x x x x


5
2
.
11
00
5
. d .d
2
f x f x x f x f x

1
2
0
1
2
fx
22
11
10
22
ff
.
22
1 5 1
10
2 2 2
ff
51
22

3
2
16f
.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
P
:
50x y z
. Điểm nào dưới
đây thuộc
P
?
A.
0;0; 5
. B.
0;5;0
. C.
0;0;5
. D.
5;0;0
.
Lời giải
Chọn A
Ta có:
0 0 5 5 0
0;0; 5
thuộc
P
.
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
Câu 9. Tìm họ nguyên hàm của hàm số
1
.
21
fx
x
A.
1
.ln 2 1 .
2
f x dx x C
B.
ln 2 1 .f x dx x C
C.
2
2
.
21
f x dx C
x

D.
1
ln 2 1 .
2
f x dx x C
Lời giải
Chọn D
Ta có
1
ln 2 1 .
2
f x dx x C
Câu 10. Biết
1
0
dx 10fx
và
1
0
dx 30,gx
khi đó
1
0
dxg x f x


bằng
A.
20.
B.
20.
C.
40.
D.
40.
Lời giải
Chọn A
Ta có
1 1 1
0 0 0
dx dx dx 30 10 20.g x f x g x f x


Câu 11. Môđun của số phức
34i
bằng
A.
7
. B.
8
. C.
6
. D.
5
.
Lời giải
Chọn D
Ta có:
22
3 4 3 4 5i
.
Câu 12. Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 3 0zz
. Giá trị
22
12
zz
bằng
A.
2
. B.
10
. C.
2
. D.
4
.
Lời giải
Chọn A
Áp dụng định lý Viét ta có :
12
2zz
và
12
3zz
.
2
22
1 2 1 2 1 2
22z z z z z z
.
Câu 13. Nếu
3
1
5f x dx
và
2
1
2f x dx
thì
3
2
f x dx
bằng
A.
7
. B.
3
. C.
3
. D.
7
.
Lời giải
Chọn C
Ta có:
3 3 2
2 1 1
5 2 3.f x dx f x dx f x dx
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
Câu 14. Cho hàm số
y f x
có đạo hàm liên tục trên đoạn
1;2
,
11f
và
2 11f
. Tính tích
phân
2
1
f x dx
.
A.
10
. B.
12
. C.
9
. D.
10
.
Lời giải
Chọn D
Ta có:
2
2
1
1
2 1 11 1 10.f x dx f x f f
Câu 15. Diện tích hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây
A.
1
2
0
2 ( 2 ) .S x x dx
B.
1
2
0
2 ( 2 ) .S x x dx
1.T 
C.
1
2
0
2 ( 2 ) .S x x dx
8.T
D.
1
2
0
2 ( 2 ) .S x x dx
Lời giải
Chọn A
Ta có
11
22
00
2 [ ( 2)] . 2 ( 2 ) .S x x dx x x dx

Câu 16. Trong không gian với hệ tọa độ
Oxyz
cho hai mặt phẳng
( ):2 3 3 5 0P x y z
và
( ): 1 0Q y z
. Tính góc gữa
()P
và
()Q
.
A.
2
B.
3
C.
4
D.
6
Lời giải
Chọn A
.
(2;3; 3), (0;1;1) cos 0
2
.
PQ
pQ
PP
nn
nn
nn

Câu 17. Nếu
1
0
1010f x dx
thì
1
0
2 f x dx
bằng
A.
4040
. B.
3030
. C.
1010
. D.
2020
.
Lời giải
Chọn D
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
Ta có
11
00
2 2 2.1010 2020f x dx f x dx

Câu 18. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
5;0;0 , 0; 4;0 , 0;0;6A B C
. Mặt phẳng
qua ba điểm
,,A B C
có phương trình
A.
5 4 6 0x y z
. B.
5 4 6 1x y z
. C.
0
5 4 6
x y z
. D.
1
5 4 6
x y z
.
Lời giải
Chọn D
Phương trình mặt phẳng đi qua ba điểm
,,A B C
là:
1
5 4 6
x y z
Câu 19. Họ tất cả các nguyên hàm của hàm số
sin 6f x x x
là
A.
2
cos 3 .F x x x C
B.
cos .F x x C
C.
2
cos 6 .F x x x C
D.
2
cos 3 .F x x x C
Lời giải
Chọn A
Ta có
2
sin 6 cos 3f x dx x x dx x x C

.
Câu 20. Trong không gian
Oxyz
, mặt phẳng
chứa trục
Ox
và đi qua điểm
2; 5;7A
có phương
trình là:
A.
7 5 0.yz
B.
7 5 0.yz
C.
5 7 0.yz
D.
5 7 0.yz
Lời giải
Chọn B
Ta có mặt phẳng
chứa trục
Ox
và đi qua điểm
2; 5;7A
nên suy ra
; 0; 7; 5n i OA


. Khi đó
: 7 5 0 :7 5 0y z y z

Câu 21. Họ tất cả các nguyên hàm của hàm số
2
1
x
fx
x
trên khoảng
1; 
là:
A.
3ln 1F x x x C
. B.
2
3
1
F x x C
x
.
C.
3ln 1F x x x C
. D.
2
3
1
F x x C
x
.
Lời giải
Chọn A
23
d 1 d 3ln 1
11
x
x x x x C
xx





Do
1;x 
nên
3ln 1 3ln 1x x C x x C
.
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
Vây
3ln 1F x x x C
với mọi
1;x 
Câu 22. Trong không gian với hệ trục tọa độ
Oxyz
, cho hai điểm
2;1;0 , 0;3;4AB
. Mặt phẳng
trung trực của đoạn thẳng
AB
có phương trình là
A.
2 3 4 4 0x y z
. B.
2 3 4 4 0x y z
.
C.
2 3 4 4 0x y z
. D.
2 5 0x y z
.
Lời giải
Chọn D
Mặt phẳng trung trực của đoạn thẳng
AB
đi qua trung điểm của
AB
là
1;2;2I
và nhận
véctơ
2;2;4AB
làm véctơ pháp tuyến.
Phương trình mặt phẳng trung trực của đoạn thẳng
AB
là:
2 1 2 2 4 2 0 2 5 0x y z x y z
.
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
2;0;2 , 0;2;0AB
. Gọi
S
là mặt cầu
nhận
AB
làm đường kính. Diện tích của mặt cầu
S
bằng
A.
36
. B.
8
. C.
16
. D.
12
.
Lời giải
Chọn D
Vì mặt cầu có đường kính
AB
nên bán kính
23
3
22
AB
R
.
Diện tích mặt cầu là
2
4 12SR


.
Câu 24. Trên mặt phẳng tọa độ, điểm biểu diễn số phức
2
12zi
là điểm nào dưới đây
A.
3; 4K 
. B.
5; 4I
. C.
4;5E
. D.
3;4N
.
Lời giải
Chọn A
2
12zi
=
34i
.
Vậy điểm biểu diễn số phức
z
là
3; 4K 
.
Câu 25. Cho hàm số
y f x
thỏa mãn
3 5sinf x x

và
01f
. Mệnh đề nào dưới đây đúng?
A.
3 5cos 6f x x x
. B.
3 5cos 6f x x x
.
C.
3 5cos 6f x x x
. D.
3 5cos 6f x x x
.
Lời giải
Chọn B
Ta có:
d 3 5sin d 3 5cosf x f x x x x x x C

.
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
Mặt khác:
0 1 6 3 5cos 6f C f x x x
.
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, cho vectơ
1;0;3a
và
2;2;5b 
. Tích vô hướng
.a a b
bằng
A.
3
. B.
23
. C.
9
. D.
5
.
Lời giải
Chọn A
Ta có:
3; 2; 2 . 3 0 6 3a b a a b
.
Câu 27. Trong không gian với hệ toạ độ
Oxyz
, cho đường thẳng
1 2 3
( ):
1 2 3
x y z
d

. Điểm nào
dưới đây thuộc đường thẳng
()d
?
A.
(1; 2;3).P
B.
(1;2;3).N
C.
( 1;2; 3).M 
D.
( 1;2;3).Q
Lời giải
Chọn C.
Câu 28. Cho số phức
2zi
. Tính
1
z
.
A.
5
. B.
5
. C.
3
. D.
5
5
.
Lời giải
Chọn D.
Ta có :
22
1 1 1 1 5
.
25
21
z z i
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, mặt phẳng đi qua điểm
1;1;1M
và vuông góc với
đường thẳng
1 2 3
:
3 2 1
x y z
có phương trình là
A.
30x y z
. B.
3 2 0x y z
.
C.
3 2 6 0x y z
. D.
2 3 6 0x y z
.
Lời giải
Chọn C
Ta có:
Đường thẳng
có một vecto chỉ phương
3;2;1u
.
Mặt phẳng vuông góc với
có vecto pháp tuyến
3;2;1n
.
Phương trình mặt phẳng đi qua
1;1;1M
có vecto pháp tuyến
3;2;1n
là
3 1 2 1 1 0x y z
3 2 6 0x y z
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
,cho mặt cầu
S
có tâm
1;0;0I
và đi qua điểm
0;0;1M
. Phương trình của
S
là
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 14
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
A.
2
22
: 1 2S x y z
. B.
2
22
: 1 2S x y z
.
C.
2
22
: 1 2S x y z
. D.
2
22
: 1 2S x y z
.
Lời giải
Chọn D
Ta có :
1;0;1IM 
2IM
.
Mặt cầu
S
có tâm
1;0;0I
và đi qua
0;0;1M
suy ra
2R IM
.
Phương trình mặt cầu
2
22
: 1 2S x y z
.
Câu 31. Cho
9
0
d9f x x
. Tính
3
0
3dI f x x
.
A.
27.
B.
9.
C.
6
. D.
3
.
Lời giải
Chọn D
Ta có
3 3 9 9
0 0 0 0
1 1 1
3 d 3 d 3 d d 3.
3 3 3
I f x x f x x f t t f x x
Câu 32. Số phức liên hợp của số phức
3 2 3z i i
là
A.
67zi
. B.
97zi
. C.
97zi
. D.
67zi
.
Lời giải
Chọn C
Ta có
3 2 3 6 9 2 3 9 7z i i i i i
.
Vậy
97zi
.
Câu 33. Trong không gian với hệ trục tọa độ
Oxyz
, hình chiếu vuông góc của điểm
1;2;3M
trên mặt
phẳng
Oxy
có tọa độ là
A.
1;2;0
. B.
1;0;3
. C.
1;0;0
. D.
0;2;3
.
Lời giải
Chọn A
Hình chiếu vuông góc của điểm
1;2;3M
trên mặt phẳng
Oxy
là
1;2;0H
.
Câu 34. Tìm họ nguyên hàm của hàm số
cos2f x x
.
A.
2sin2f x dx x C
. B.
1
sin2
2
f x dx x C
.
C.
1
sin2
2
f x dx x C
. D.
2sin2f x dx x C
.
Lời giải
Chọn B
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 15
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
Ta có
1
sin2
2
f x dx x C
Câu 35. Trong không gian với hệ tọa độ
Oxyz
, hình chiếu vuông góc của điểm
1;2; 3M 
trên trục
Oy
có tọa độ là
A.
1;0;0Q
. B.
0;0; 3N
. C.
0;2;0E
. D.
1;2;0P
.
Lời giải
Chọn C
Ta có: Hình chiếu vuông góc của điểm
1;2; 3M 
trên trục
Oy
có tọa độ là
0;2;0E
.
Câu 36. Số phức đối của số phức
34i
là:
A.
43i
. B.
34i
. C.
34i
. D.
34i
.
Lời giải
Chọn C
Số phức đối của số phức
34i
là
34i
Câu 37. Tìm họ nguyên hàm của hàm số
2
2020
x
fx
x
.
A.
2
d ln 2020f x x x C
. B.
2
d ln 2020f x x x C
.
C.
2
1
d 2020
2
f x x x C
. D.
2
d 2020f x x x C
.
Lời giải
Chọn D
2 2 2
22
1 1 1
d d d 2020 .2 2020 2020
22
2020 2020
x
f x x x x x C x C
xx

Câu 38. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
2 2 2
: 4 2 6 5 0S x y z x y z
.
Bán kính của mặt cầu đã cho bằng
A.
19
. B.
3
. C.
9
. D.
19
.
Lời giải
Chọn B
Gọi phương trình mặt cầu
S
có dạng
2 2 2
2 2 2 0x y z ax by cz d
.
Có
2, 1, 3, 5a b c d
.
Suy ra bán kính của mặt cầu
S
bằng
2 2 2 2 2 2
2 1 3 5 3r a b c d
.
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 16
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
Câu 39. Trong không gian với hệ toạ độ
Oxyz
, cho mặt cầu
2 2 2
: 1 1 1 9S x y z
. Tâm
của
S
có toạ độ là
A.
1;1;1
. B.
1;1; 1
. C.
1; 1;1
. D.
1;1;1
.
Lời giải
Chọn B
Ta có
2 2 2
: 1 1 1 9S x y z
suy ra toạ độ tâm của
S
là
1;1; 1I
bán kính
3R
.
Câu 40. Trong không gian với hệ toạ độ
Oxyz
, phương trình nào dưới đây là phương trình của đường
thẳng đi qua điểm
0;2;3A
và vuông góc với mặt phẳng
: 3 5 0P x y z
.
A.
3 3 0x y z
. B.
23
3
xt
yt
zt


. C.
32
13
xt
yt
zt

. D.
3 3 0x y z
.
Lời giải
Chọn B
Mặt phẳng
: 3 5 0P x y z
có vectơ pháp tuyến là
1; 3;1n 
.
Đường thẳng
d
đi qua điểm
0;2;3A
và vuông góc với mặt phẳng
: 3 5 0P x y z
nhận vectơ
1; 3;1n 
là vectơ chỉ phương có phương trình là
23
3
xt
yt
zt


.
Câu 41. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1; 2;3E 
. Gọi
E
là hình chiếu vuông góc
của
E
lên mặt phẳng
Oxz
. Khoảng cách từ
E
đến trục
Oy
bằng
A.
13
. B.
14
. C.
10
. D.
5
.
Lời giải
Chọn C
Vì
E
là hình chiếu vuông góc của
E
lên mặt phẳng
Oxz
nên
1;0;3E
.
,0 1 9 10d E y
.
Câu 42. Trong không gian với hệ tọa độ
Oxyz
, véc tơ nào dưới đây là một véc tơ chỉ phương của
đường thẳng đi qua hai điểm
2;3; 1E 
và
2; 1;3F
?
A.
4
1; 1;1u 
. B.
3
1; 1; 1u
. C.
2
0;1;1u
. D.
1
1;1;1u
.
Lời giải
Chọn A
Ta có đường thẳng
EF
có véc tơ chỉ phương là
4; 4;4EF 
4
4u
.
Câu 43. Biết
Fx
là một nguyên hàm của hàm số
cosf x x x
và
01F
. Tính
F
.
A.
2
F
. B.
1F
. C.
1F

. D.
2
F

Lời giải
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 17
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
Chọn C
Ta có
00
0 0 0
0 cos dx= d sin sin sin dx cos 2F F x x x x x x x x

.
Mà
01F
, suy ra
2 0 1FF
.
Câu 44. Cho hàm số
2
F x x
là một nguyên hàm của hàm số
2x
f x e
. Tìm nguyên hàm của hàm số
2x
f x e
.
A.
22
dx
x
f x e x x C
. B.
22
dx
x
f x e x x C
.
C.
22
dx 2 2
x
f x e x x C
. D.
22
dx 2 2
x
f x e x x C
.
Lời giải
Chọn C
Vì hàm số
2
F x x
là một nguyên hàm của hàm số
2x
f x e
nên
2
2
x
F x x f x e

suy
ra
2
2
x
x
fx
e
. Có
22
4
24
xx
x
e xe
fx
e
.
Vậy nên
2 2 2 2
2 2 2
42
2 4 2 4
dx= . dx dx 2 4 dx 2 2
x x x x
xx
xx
e xe e xe
f x e e x x x C
ee

.
Cách 2. Dùng nguyên hàm từng phần
Vì hàm số
2
F x x
là một nguyên hàm của hàm số
2x
f x e
nên
2
2
x
F x x f x e

suy
ra
2
2
x
x
fx
e
.
Có
2 2 2 2 2 2 2
2
2
dx= d 2 e dx . 2 2 2 .
x x x x x
x
x
f x e e f x f x e f x e x C x x C
e
Câu 45. Tìm họ nguyên hàm của hàm số
2020 .
x
fx
A.
1
2020
2020 .
1
x
x
dx C
x

B.
2020 2020 ln .
xx
dx x C
C.
2020
2020 .
ln2020
x
x
dx C
D.
1
2020 2020 .
xx
dx C

Lời giải
Chọn C
Câu 46. Số phức nào dưới đây là số thuần ảo?
A.
2020.
B.
2.i
C.
2020 .i
D.
1 3 .i
Lời giải
Chọn C
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 18
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
Câu 47. Biết phương trình
2
0z az b
nhận số phức
1zi
là nghiệm. Tính tổng
S a b
.
A.
4S
. B.
2S 
. C.
0S
. D.
4S 
.
Lời giải
Chọn C.
• Cách 1
Ta có số phức
1zi
là một nghiệm của phương trình
2
0z az b
2
1 1 0i a i b
20a b a i
0
20
ab
a


0S a b
Vậy ta có:
0S a b
.
• Cách 2
Ta có:
1zi
1zi
2
2
1zi
2
2 2 0zz
(1).
Mặt khác
z
là nghiệm của phương trình
2
0z az b
(2).
Từ (1) và (2), ta có:
2
2
a
b

0S a b
.
Câu 48. Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
2;0;0A
,
0;6;0B
,
0;0;5C
và điểm
N
sao cho
ON OA OB OC
. Một mặt phẳng
P
thay đổi cắt các đoạn thẳng
, , ,OA OB OC ON
lần lượt tại các điểm
1 1 1 1
, , ,A B C N
thỏa mãn
1 1 1
2020
OA OB OC
OA OB OC
và
1 0 0 0
;;N x y z
. Khi đó
A.
0 0 0
7
2020
x y z
. B.
0 0 0
9
2020
x y z
.
C.
0 0 0
11
2020
x y z
. D.
0 0 0
13
2020
x y z
.
Lời giải
Chọn D
Ta có:
2;6;5ON OA OB OC
2;6;5N
.
Ta thấy
2; 6; 5OA OB OC
.
Gọi
1
;0;0Aa
,
1
0; ;0Bb
,
1
0;0;Cc
lần lượt là giao điểm của mặt phẳng
P
với các đoạn
thẳng
,,OA OB OC
. Ta có:
02a
;
06b
;
05c
.
Như vậy ta có:
1
OA a
,
1
OB b
,
1
OC c
.
Mặt phẳng
P
đi qua
1 1 1
,,A B C
nên có phương trình
:1
x y z
P
a b c
.
Theo đề ta có:
1 1 1
2020
OA OB OC
OA OB OC
2 6 5
2020
abc
2 6 5
1
2020 2020 2020abc
1 3 5
1010 1010 2020
1
a b c
:1
x y z
P
a b c
đi qua điểm
1 3 5
;;
1010 1010 2020
N



.
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 19
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
Ta thấy
1 3 5 1
;;
1010 1010 2020 2020
ON ON




N
thuộc đoạn
ON
.
Ta có
NP
,
N ON
nên
N
là giao điểm của
P
với đoạn
ON
.
Suy ra
1 0 0 0
;;N N x y z
0 0 0
1 3 5
;;
1010 1010 2020
x y z
.
0 0 0
13
2020
x y z
.
Câu 49. Biết
2
2
2
cos
sin
6
cos 1 sin
1
.
m
x
n
x
xx
dx a
be
e

trong đó
, , ,a b m n
là các số nguyên dương,
m
n
là phân số
tối giản. Tính
S a b m n
.
A.
9S
. B.
12S
. C.
10S
. D.
11S
.
Lời giải
Chọn C
Ta có:
22
222
222
1
cos 1 sin
sin
sin
sin sin
666
cos 1 sin cos 1 sin cos 1 sin
xx
x
x
xx
x x x x x x
I dx dx dx
e
ee





Đặt
sin cost x dt xdx
2
1 1 1 1
1 1 1
2
2
1
1 1 1 1
2 2 2 2
1
1 . 1 . 2 .
t t t
t t t
t
t
t
I dt t e dt t e dt t e dt
e
.
11
11
2
2
11
22
1
1 . 2 .
tt
tt
t e dt t e dt A B
t





.
Xét tích phân:
1
1
2
2
1
2
1
1.
t
t
A t e dt
t




Đặt
2
1
1
2
2
1
1.
t
t
t
t
ut
du tdt
dv e dt
ve
t







.
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 20
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
1
11
2
3
1
2
2
1
1
. 2 . 1
1
4
2
tt
tt
A t e t e dt B
e

.
3
2
1
4
11
1
3
4
.
2
m
n
a
b
I A B a
m
e
be
n
.
Vậy
10S a b m n
.
*Cách khác
Đặt
sin cost x dt xdx
.
Đổi cận:
1
62
xt
;
1
2
xt
.
2
2
2
2
1 1 1 1
1 1 1
ln
2
2
22
1
1 1 1 1
2 2 2 2
1
1 2 1 2
1 1 1 . .
t
tt
t
t t t
t
t
t
I dt t e dt t e dt e e dt
t t t t
e

2
1
1
ln
2
1
2
12
1.
t
t
t
e dt
tt




.
Đặt
2
2
1 1 2
ln 1u t t du dt
t t t



.
Đổi cận:
13
2ln2
22
tu
;
10tu
.
3
0
3
2
2ln2
2
3
3
2
2ln2
2
1
0
4
1
1 1 1
3
3
4
2ln2
4.
2
2
uu
a
b
e
I e du e e
m
e
n



.
Vậy
10S a b m n
.
Câu 50. Cho
fx
là một nguyên hàm của
gx
trên , thỏa mãn
1
22
f



,
2
0
1
2
xg x dx
và
2
0
f x dx a b

, trong đó
,ab
là các số hữu tỉ. Tính
2P a b
.
A.
1
2
P
. B.
0P
. C.
1P
. D.
1
2
P 
.
Lời giải
Chọn B
NHÓM TOÁN VD – VDC NGUYN KHUYN-BNH DƯƠNG-2020
https://www.facebook.com/groups/toanvd.vdc Trang 21
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Do
fx
là một nguyên hàm của
gx
nên
'f x g x
.
Khi đó:
22
00
1
'
2
I xg x dx xf x dx



.
Đặt
'
u x du dx
dv f x dx v f x







.
2 2 2
0 0 0
1
..
2
2 2 4 2
0
I x f x f x dx f f x dx f x dx



.
2
0
1
24
f x dx
.
Ta có:
11
, 2 0
24
a b P a b
.
-------------------- HẾT --------------------
| 1/21
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NHÓM TOÁN VD – VDC
NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020
TRƯỜNG THCS - THPT NGUYỄN KHUYẾN
ĐỀ KIỂM TRA HỌC KÌ 2 NĂM HỌC 2019 - 2020
Môn thi: TOÁN - Lớp: 12 N H
Thời gian làm bài: 90 phút (không kể thời gian phát đề) Ó M T .
Đề thi gồm 05 trang - 50 câu trắc nghiệm
------------------------------ O Á N
Họ và tên: ……………………………………………………… SBD: ………………… V Câu 1. Tìm số phức     . D z thỏa mãn z 3 2i 1 3i – A. z  2  5i .
B. z  2  5i .
C. z  2  5i . D. z  2   5i . VDC Câu 2.
Tìm họ nguyên hàm của hàm số   x f x e  . A.    x
f x dx e C . B.    x f x dx e   C . C.    x f x dx e   C . D.    x f x dx eC . Câu 3.
Cho hai số phức z  1 2i và z  3  4i . Phần thực của số phức z z bằng 1 2 1 2 A. 2  . B. 4 . C. 2 . D. 6  . Câu 4.
Gọi z là nghiệm có phần ảo dương của phương trình 2
z  2z  5  0 . Tính A   z i 1 2 1 A. 2 . B. 10 . C. 2 . D. 2 . Câu 5.
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng   :2x 3y  4z 1 0 . Véc-tơ nào
dưới đây là một véc-tơ pháp tuyến của mặt phẳng   ? N H
A. n  2;  3; 4 .
B. n  2;  3;1 . C. n  3  ;4;1 .
D. n  2;3;  4 . 2   4   3   1   Ó M T x y z Câu 6.
Trong không gian với hệ tọa độ Oxyz , cho đường thẳng 1 2 3  :   . Véc-tơ nào O 1  2 1  Á
dưới đây vuông góc với véc N
-tơ chỉ phương của đường thẳng  ? V
A. u  2;  3; 4 .
B. u  2;3;  4 .
C. u  2;3; 4 . D. u  2  ;3;4 . 2   1   4   3   D – VDC Câu 7.
Cho hàm số f x thỏa mãn f xf  x 5 2 .
 3x  6x , x
  , biết rằng f 0 1. Tính 2 f   1 . A. 2 f   1  100 . B. 2 f   1  3 . C. 2 f   1  81. D. 2 f   1  6 . Câu 8.
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : x y z  5  0. Điểm nào dưới đây thuộc P? A. 0;0; 5   . B. 0;5;0 . C. 0;0;5 . D. 5;0;0 . Câu 9.
Tìm họ nguyên hàm của hàm số f x 1  . 2x 1 1 A. f
 xdx  .ln2x 1C. B. f
 xdx  ln 2x1  . C 2
https://www.facebook.com/groups/toanvd.vdc Trang 1 NHÓM TOÁN VD – VDC
NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020 2  C. f
 xdx       C D. f  x 1 dx ln 2x 1 C. 2x   . 2 1 2 N 1 1 1 H Câu 10. Biết f
 xdx 10 và g
 xdx  30, khi đó g
 x f xdx bằng Ó  M T 0 0 0 A. 20. B. 20.  C. 40.  D. 40. O Á
Câu 11. Môđun của số phức 3  4i bằng N V A. 7 . B. 8 . C. 6 . D. 5 . D
Câu 12. Gọi z , z là hai nghiệm phức của phương trình 2
z  2z  3  0 . Giá trị 2 2 z z bằng 1 2 1 2 – VDC A. 2  . B. 10 . C. 2 . D. 4  . 3 2 3 Câu 13. Nếu f
 xdx  5 và f
 xdx  2 thì f xdx  bằng 1 1 2 A. 7 . B. 3  . C. 3 . D. 7  .
Câu 14. Cho hàm số y f x có đạo hàm liên tục trên đoạn 1;2, f  
1  1 và f 2  11. Tính tích 2 phân f   xdx. 1 A. 10  . B. 12 . C. 9 . D. 10 .
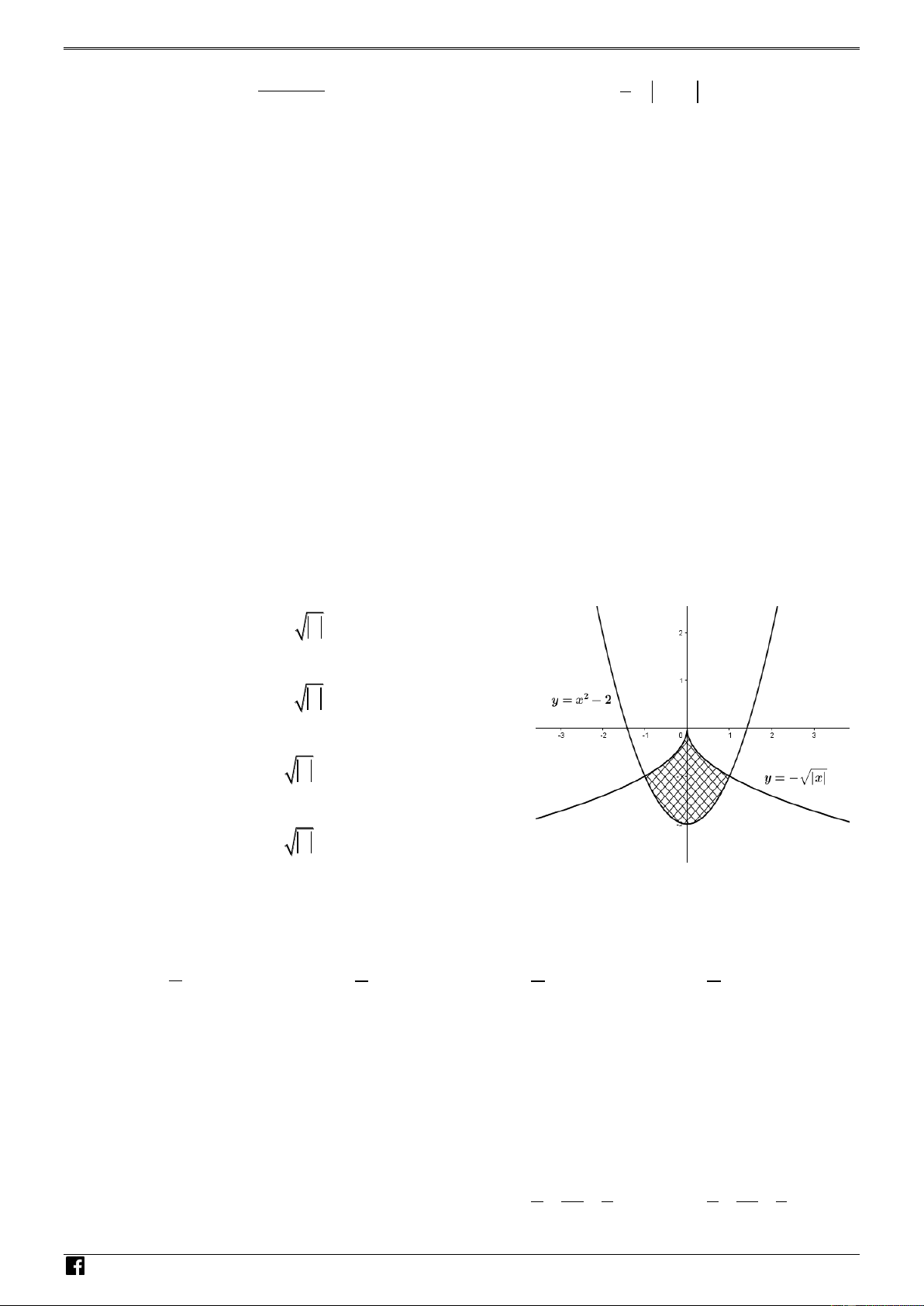
Câu 15. Diện tích hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây 1 A. 2
S  2 (x  2  x )d . x  0 1 B. 2
S  2 (x  2  x )d . xT  1.  N 0 H Ó 1 M T C. 2
S  2 (x  2  x )d . xT  8. O 0 Á 1 N 2 V
D. S  2 (x  2  x )d . x  D 0 – VDC
Câu 16. Trong không gian với hệ tọa độ Oxyz cho hai mặt phẳng ( )
P : 2x  3y  3z  5  0 và ( )
Q : y z 1  0 . Tính góc gữa (P) và (Q) .     A. B. C. D. 2 3 4 6 1 1 Câu 17. Nếu f
 xdx 1010 thì 2 f xdx  bằng 0 0 A. 4040 . B. 3030 . C. 1010 . D. 2020 .
Câu 18. Trong không gian với hệ tọa độ Oxyz , cho ba điểm A5;0;0, B0; 4
 ;0,C0;0;6 . Mặt phẳng qua ba điểm , A ,
B C có phương trình x y z x y z
A. 5x  4y  6z  0.
B. 5x  4y  6z  1. C.    0 . D.   1. 5 4  6 5 4  6
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM TOÁN VD – VDC NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020
Câu 19. Họ tất cả các nguyên hàm của hàm số f x  sin x  6x là
A. F x 2
 cos x 3x  . C
B. F x  cos x  . C N H
C. F x 2
 cos x  6x  . C
D. F x 2
 cos x 3x  . C Ó M T
Câu 20. Trong không gian Oxyz , mặt phẳng   chứa trục Ox và đi qua điểm A2; 5  ;7 có phương O trình là: Á N
A. 7 y  5z  0. B. 7 y  5z  0.
C. 5y  7z  0. D. 5y  7z  0. V D x
Câu 21. Họ tất cả các nguyên hàm của hàm số f x 2  trên khoảng  1  ; là: – x 1 VDC 3
A. F x  x  3ln  x   1  C .
B. F x  x   C . x  2 1 3
C. F x  x  3ln  x   1  C .
D. F x  x    . x   C 2 1
Câu 22. Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm A 2
 ;1;0, B0;3;4. Mặt phẳng
trung trực của đoạn thẳng AB có phương trình là
A. 2x  3y  4z  4  0 .
B. 2x  3y  4z  4  0 .
C. 2x  3y  4z  4  0 .
D. x y  2z  5  0 .
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A2;0;2, B0;2;0 . Gọi  S  là mặt cầu
nhận AB làm đường kính. Diện tích của mặt cầu S  bằng N A. 36 . B. 8 . C. 16 . D. 12 . H Ó
Câu 24. Trên mặt phẳng tọa độ, điểm biểu diễn số phức z    i2 1 2
là điểm nào dưới đây M T A. K  3  ; 4  . B. I 5; 4   . C. E  4  ;5. D. N  3  ;4 . O Á N
Câu 25. Cho hàm số y f x thỏa mãn f  x  3  5sin x và f 0  1. Mệnh đề nào dưới đây đúng? V D
A. f x  3x  5cos x  6 .
B. f x  3x  5cos x  6 . – VDC
C. f x  3x  5cos x  6 .
D. f x  3x  5cos x  6.
Câu 26. Trong không gian với hệ tọa độ Oxyz , cho vectơ a  1;0;3 và b   2
 ;2;5. Tích vô hướng .
a a b bằng A. 3  . B. 23 . C. 9 . D. 5  . x 1 y  2 z  3
Câu 27. Trong không gian với hệ toạ độ Oxyz , cho đường thẳng (d ) :   . Điểm nào 1 2 3
dưới đây thuộc đường thẳng (d) ? A. P(1; 2  ;3). B. N(1; 2;3). C. M ( 1  ;2; 3  ). D. ( Q 1  ;2;3). 1
Câu 28. Cho số phức z  2  i . Tính . z
https://www.facebook.com/groups/toanvd.vdc Trang 3 NHÓM TOÁN VD – VDC
NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020 5 A. 5 . B. 5 . C. 3 . D. . 5 N
Câu 29. Trong không gian với hệ tọa độ Oxyz , mặt phẳng đi qua điểm M 1;1;  1 và vuông góc với H Ó x 1 y  2 z  3 M T đường thẳng  :   có phương trình là 3 2 1 O
A. x y z  3  0 .
B. 3x  2y z  0 . Á N
C. 3x  2y z  6  0 .
D. x  2y  3z  6  0 . V D
Câu 30. Trong không gian với hệ tọa độ Oxyz ,cho mặt cầu S  có tâm I 1;0;0 và đi qua điểm – M 0;0; 
1 . Phương trình của S  là VDC
A. S   x  2 2 2 :
1  y z  2 .
B. S   x  2 2 2 :
1  y z  2 .
C. S   x  2 2 2 :
1  y z  2 .
D. S   x  2 2 2 :
1  y z  2 . 9 3 Câu 31. Cho f
 xdx  9. Tính I f  3xdx. 0 0 A. 27. B. 9. C. 6 . D. 3 .
Câu 32. Số phức liên hợp của số phức z  3 i2  3i là
A. z  6  7i .
B. z  9  7i . C. z  9  7i .
D. z  6  7i .
Câu 33. Trong không gian với hệ trục tọa độ Oxyz , hình chiếu vuông góc của điểm M 1; 2;3 trên mặt
phẳng Oxy có tọa độ là A. 1; 2;0 . B. 1;0;3 . C. 1;0;0 . D. 0; 2;3 . N H
Câu 34. Tìm họ nguyên hàm của hàm số f x  cos 2x . Ó M T A. f
 xdx  2sin2xC . B. f  x 1 dx  sin 2x C . 2 O Á N C.    . D. f
 xdx  2
 sin 2x C . V f  x 1 dx sin 2x C 2 D –
Câu 35. Trong không gian với hệ tọa độ Oxyz , hình chiếu vuông góc của điểm M  1  ;2;  3 trên trục VDC
Oy có tọa độ là A. Q  1  ;0;0 . B. N 0;0; 3   .
C. E 0;2;0 . D. P  1  ;2;0 .
Câu 36. Số phức đối của số phức 3  4i là: A. 4  3i . B. 3  4i . C. 3   4i . D. 3   4i . x
Câu 37. Tìm họ nguyên hàm của hàm số f x  . 2 x  2020 A. f
 xx   2 d
ln x  2020  C . B. f
 xx   2 d ln
x  2020  C .
https://www.facebook.com/groups/toanvd.vdc Trang 4 NHÓM TOÁN VD – VDC
NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020 1 C. f  x 2 dx
x  2020  C . D. f  x 2 dx
x  2020  C . 2 N
Câu 38. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S  2 2 2
: x y z  4x  2y  6z  5  0 . H Ó
Bán kính của mặt cầu đã cho bằng M T A. 19 . B. 3 . C. 9 . D. 19 . O 2 2 2 Á
Câu 39. Trong không gian với hệ toạ độ Oxyz , cho mặt cầu S  :  x   1   y   1   z   1  9. Tâm N V
của  S  có toạ độ là D A. 1;1  ;1 . B. 1;1;  1  . C. 1; 1  ;  1 . D.  1  ;1;  1 . – VDC
Câu 40. Trong không gian với hệ toạ độ Oxyz , phương trình nào dưới đây là phương trình của đường
thẳng đi qua điểm A0;2;3 và vuông góc với mặt phẳng P : x  3y z  5  0 . x tx t  
A. x  3y z  3  0 .
B. y  2  3t . C. y  3   2t .
D. x  3y z  3  0 .   z  3  tz  1 3t
Câu 41. Trong không gian với hệ tọa độ Oxyz , cho điểm E  1  ; 2  ; 
3 . Gọi E là hình chiếu vuông góc
của E lên mặt phẳng Oxz . Khoảng cách từ E đến trục Oy bằng A. 13 . B. 14 . C. 10 . D. 5 .
Câu 42. Trong không gian với hệ tọa độ Oxyz , véc tơ nào dưới đây là một véc tơ chỉ phương của
đường thẳng đi qua hai điểm E  2  ;3;  1 và F 2; 1  ;3 ? A. u  1; 1  ;1 . B. u  1; 1  ; 1  .
C. u  0;1;1 .
D. u  1;1;1 . 1   2   3   4  
Câu 43. Biết F x là một nguyên hàm của hàm số f x  x cos x và F 0  1. Tính F   .   N
A. F    .
B. F    1.
C. F    1  .
D. F     H 2 2 Ó M T Câu 44. Cho hàm số   2
F x x là một nguyên hàm của hàm số   2x
f x e . Tìm nguyên hàm của hàm số O   2x f x e . Á N A. f   x 2x 2
e dx  x x C . B. f   x 2x 2
e dx  x x C . V D x x – C. f   x 2 2
e dx  2x  2x C . D. f   x 2 2
e dx  2x  2x C . VDC
Câu 45. Tìm họ nguyên hàm của hàm số   2020 .x f x x 1  x 2020 A. 2020 dx   C.  B. 2020x  2020x dx ln x  . Cx 1 x 2020xC. 2020 dx   C.  D. x x 1 2020 dx  2020  . C  ln 2020
Câu 46. Số phức nào dưới đây là số thuần ảo? A. 2020. B. 2  . i C. 2020 . i D. 1 3 . i
Câu 47. Biết phương trình 2
z az b  0 nhận số phức z  1 i là nghiệm. Tính tổng S a b . A. S  4 . B. S  2  . C. S  0 . D. S  4  .
https://www.facebook.com/groups/toanvd.vdc Trang 5 NHÓM TOÁN VD – VDC
NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020
Câu 48. Trong không gian với hệ tọa độ Oxyz , cho các điểm A2;0;0 , B 0;6;0 , C 0;0;5 và điểm N
sao cho ON OA OB OC . Một mặt phẳng  P thay đổi cắt các đoạn thẳng N OA OB OC H O , A O ,
B OC,ON lần lượt tại các điểm A , B ,C , N thỏa mãn    2020 và 1 1 1 1 Ó OA OB OC 1 1 1 M T N x ; y ; z . Khi đó 1  0 0 0  O Á 7 9
A. x y z  .
B. x y z  . N 0 0 0 2020 0 0 0 2020 V D 11 13 –
C. x y z  .
D. x y z  . 0 0 0 0 0 0 2020 2020 VDC  2
2 cos x 1 sin x 1 Câu 49. Biết dx a   trong đó , a , b ,
m n là các số nguyên dương, m là phân số 2 cos m xn sin e . n x b e 6
tối giản. Tính S a b m n . A. S  9 . B. S  12 . C. S  10 .
D. S  11.     1 2 1
Câu 50. Cho f x là một nguyên hàm của g x trên , thỏa mãn f    ,
xg xdx   và  2  2 2 0  2 f
 xdx a b , trong đó a,b là các số hữu tỉ. Tính P a2b. 0 1 1 A. P  . B. P  0 . C. P  1 . D. P   . 2 2 N H Ó
-------------------- HẾT -------------------- M T O Á N V D – VDC
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM TOÁN VD – VDC NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020 BẢNG ĐÁP ÁN 1.A 2.C 3.B 4.A 5.A 6.C 7.D 8.A 9.D 10.A N 11.D 12.A 13.C 14.D 15.A 16.A 17.D 18.D 19.A 20.B H 21.A 22.D 23.D 24.A 25.B 26.A 27.C 28.D 29.C 30.D Ó 31.D 32.C 33.A 34.B 35.C 36.C 37.D 38.B 39.B 40.B M T 41.C 42.A 43.C 44.C 45.C 46.C 47.C 48.D 49.C 50.B O Á
HƯỚNG DẪN GIẢI CHI TIẾT N V Câu 1.
Tìm số phức z thỏa mãn z  3  2i  1 3i . D A. z  2  5i .
B. z  2  5i .
C. z  2  5i . D. z  2   5i . – VDC Lời giải Chọn A
Ta có z  3  2i 1 3i z  2
  5i z  2  5i . Câu 2.
Tìm họ nguyên hàm của hàm số   x f x e  . A.    x
f x dx e C . B.    x f x dx e   C .   C.    x f x dx e   C . D.    x f x dx eC . Lời giải Chọn C Ta có    xx        x f x dx e dx e d x e   C . N Câu 3.
Cho hai số phức z  1 2i và z  3  4i . Phần thực của số phức z z bằng H 1 2 1 2 Ó A. 2  . B. 4 . C. 2 . D. 6  . M T Lời giải O Á Chọn B N V
Ta có : z z  1 2i  3  4i  1 2i  3  4i  4  2i 1 2   D – VDC
Suy ra : Phần thực của số phức z z bằng 4 . 1 2 Câu 4.
Gọi z là nghiệm có phần ảo dương của phương trình 2
z  2z  5  0 . Tính A   z i 1 2 1 A. 2 . B. 10 . C. 2 . D. 2 . Lời giải Chọn A z   iz   2 2 1 2 1 2i Ta có 2 2
z  2z  5  0  z  2z 1  4   z   1  2i     z 1  2  iz 1 2i
Vì z là nghiệm có phần ảo dương nên : z  1 2i . 1 1
A  z i2  1 2i i2  1 i2 2 2
 2i  0  2  2 . 1
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM TOÁN VD – VDC NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020 Câu 5.
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng   :2x 3y  4z 1 0 . Véc-tơ nào
dưới đây là một véc-tơ pháp tuyến của mặt phẳng   ? N     H
A. n  2; 3; 4 .
B. n  2; 3;1 . C. n  3; 4;1 .
D. n  2;3; 4 . 2   4   3   1   Ó M T Lời giải O Chọn A Á N V
  có một véc-tơ pháp tuyến là n  2;3;4 . 1   D – x y z  VDC Câu 6.
Trong không gian với hệ tọa độ Oxyz , cho đường thẳng 1 2 3  :   . Véc-tơ nào 1  2 1 
dưới đây vuông góc với véc-tơ chỉ phương của đường thẳng  ?
A. u  2;  3; 4 .
B. u  2;3;  4 .
C. u  2;3; 4 . D. u  2  ;3;4 . 2   1   4   3   Lời giải Chọn C
 có véc-tơ chỉ phương là u   1  ;2;  1 . Ta có . u u  1  .2  2.3 1
 .4  0  u u . 1     1 Câu 7.
Cho hàm số f x thỏa mãn f xf  x 5 2 .
 3x  6x , x
  , biết rằng f 0 1. Tính 2 f   1 . A. 2 f   1  100 . B. 2 f   1  3 . C. 2 f   1  81. D. 2 f   1  6 . N Lời giải H Ó M T Chọn D 1 1 O 5 5 2 Á Ta có: f
 x.f xdx  3x 6x dx  . N 2 0 0 V D 1 1 1 – 5    1 1 1 2 2 2 f
 x.f xdx f
 x.d f x  f x  f  1 f 0. VDC 2 2 2 2 0 0 0 1 5 1 2  f   2 1   5 1 f 0    3 2  f   1  6 . 2 2 2 2 2 Câu 8.
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : x y z  5  0. Điểm nào dưới đây thuộc P? A. 0;0; 5   . B. 0;5;0 . C. 0;0;5 . D. 5;0;0 . Lời giải Chọn A
Ta có: 0  0  5  5  0  0;0; 5
  thuộc P.
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM TOÁN VD – VDC NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020 Câu 9.
Tìm họ nguyên hàm của hàm số f x 1  . 2x 1 1 N A. f
 xdx  .ln2x 1C. B. f
 xdx  ln 2x1  . C H 2 Ó M T 2  C. f
 xdx       C D. f  x 1 dx ln 2x 1 C. 2x   . 2 1 2 O Á N Lời giải V Chọn D D – VDC Ta có f  x 1 dx
ln 2x 1  C. 2 1 1 1 Câu 10. Biết f
 xdx 10 và g
 xdx  30, khi đó g
 x f xdx  bằng 0 0 0 A. 20. B. 20.  C. 40.  D. 40. Lời giải Chọn A 1 1 1 Ta có g
 x f xdx  g
 xdx  f
 xdx  3010  20. 0 0 0
Câu 11. Môđun của số phức 3  4i bằng A. 7 . B. 8 . C. 6 . D. 5 . Lời giải Chọn D N H Ta có: 2 2
3  4i  3  4  5 . Ó M T
Câu 12. Gọi z , z là hai nghiệm phức của phương trình 2
z  2z  3  0 . Giá trị 2 2 z z bằng 1 2 1 2 O A. 2  . B. 10 . C. 2 . D. 4  . Á N Lời giải V D Chọn A – VDC
Áp dụng định lý Viét ta có : z z  2 và z z  3. 1 2 1 2
z z  z z 2 2 2  2z z  2  . 1 2 1 2 1 2 3 2 3 Câu 13. Nếu f
 xdx  5 và f
 xdx  2 thì f xdx  bằng 1 1 2 A. 7 . B. 3  . C. 3 . D. 7  . Lời giải Chọn C 3 3 2 Ta có: f
 xdx f
 xdxf
 xdx  52  3. 2 1 1
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM TOÁN VD – VDC NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020
Câu 14. Cho hàm số y f x có đạo hàm liên tục trên đoạn 1;2, f  
1  1 và f 2  11. Tính tích 2 phân f   xdx. N 1 H Ó A. 10  . B. 12 . C. 9 . D. 10 . M T Lời giải O Á Chọn D N 2 V 2        D Ta có: f
 xdx f xf 2 f  1 11 1 10. 1 1 – VDC
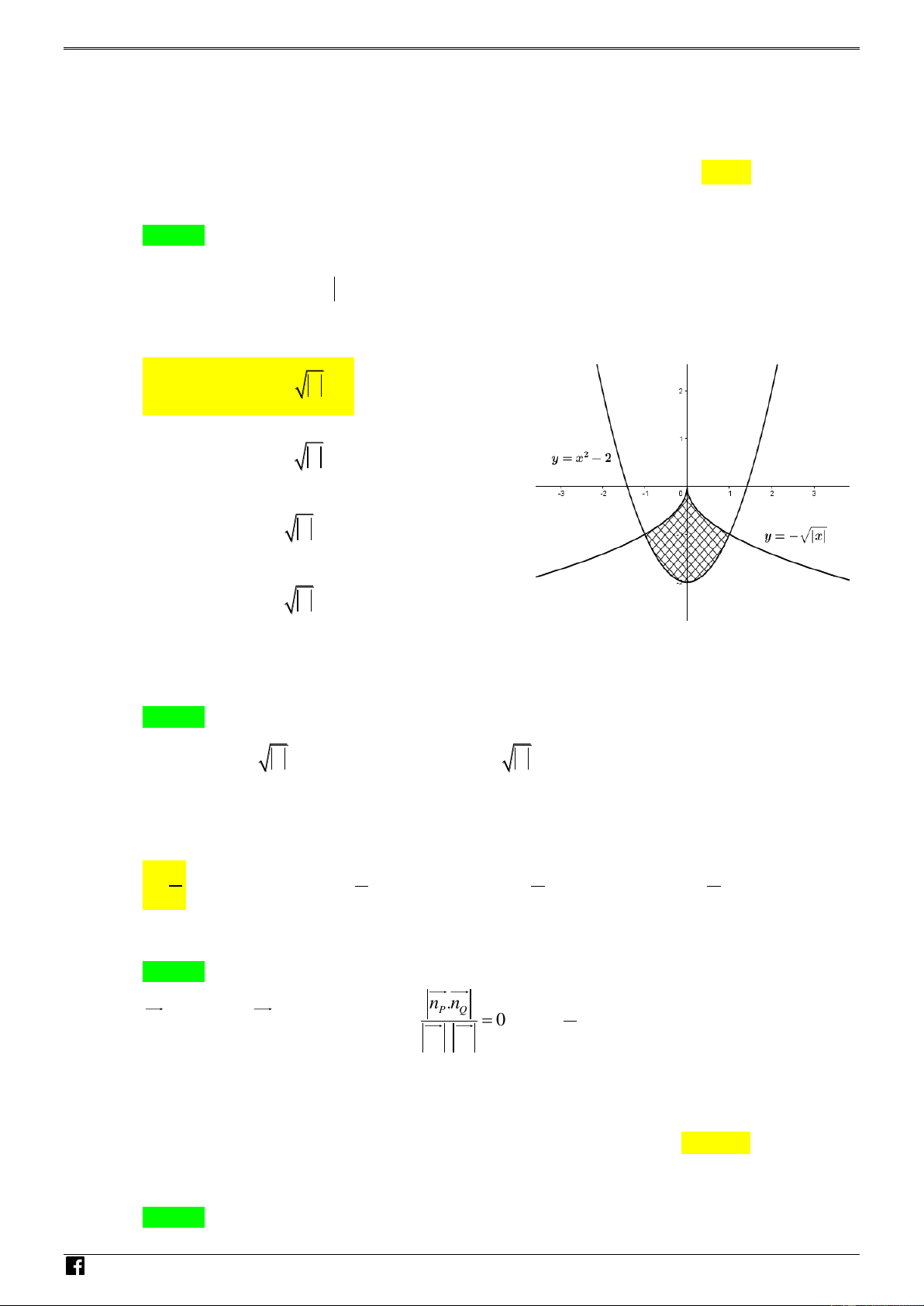
Câu 15. Diện tích hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây 1 A. 2
S  2 (x  2  x )d . x 0 1 B. 2
S  2 (x  2  x )d . xT  1.  0 1 C. 2
S  2 (x  2  x )d . xT  8. 0 1 D. 2
S  2 (x  2  x )d . x 0 Lời giải N Chọn A H Ó 1 1 2 2 M T Ta có S  2 [
x  (x  2)]d .
x  2 (x  2  x )d . x   0 0 O
Câu 16. Trong không gian với hệ tọa độ Oxyz cho hai mặt phẳng ( )
P : 2x  3y  3z  5  0 và Á N ( )
Q : y z 1  0 . Tính góc gữa (P) và (Q) . V D     – A. B. C. D. VDC 2 3 4 6 Lời giải Chọn A n .nP Q n  (2;3; 3
 ), n  (0;1;1)  cos   0    p Q n . n 2 P P 1 1 Câu 17. Nếu f
 xdx 1010 thì 2 f xdx  bằng 0 0 A. 4040 . B. 3030 . C. 1010 . D. 2020 . Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM TOÁN VD – VDC NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020 1 1 Ta có 2 f
 xdx  2 f
 xdx  2.1010  2020 0 0 N H
Câu 18. Trong không gian với hệ tọa độ Oxyz , cho ba điểm A5;0;0, B0; 4
 ;0,C0;0;6 . Mặt phẳng Ó M T qua ba điểm , A ,
B C có phương trình x y z x y z O
A. 5x  4y  6z  0.
B. 5x  4y  6z  1. C.    0 . D.   1.   Á 5 4 6 5 4 6 N V Lời giải D – Chọn D VDC Phương trình mặ x y z t phẳng đi qua ba điểm , A , B C là:   1 5 4  6
Câu 19. Họ tất cả các nguyên hàm của hàm số f x  sin x  6x là
A. F x 2
 cos x 3x  . C
B. F x  cos x  . C
C. F x 2
 cos x  6x  . C
D. F x 2
 cos x 3x  . C Lời giải Chọn A Ta có f
 xdx   xx 2 sin
6 dx   cos x  3x C .
Câu 20. Trong không gian Oxyz , mặt phẳng   chứa trục Ox và đi qua điểm A2; 5  ;7 có phương trình là:
A. 7 y  5z  0. B. 7 y  5z  0.
C. 5y  7z  0. D. 5y  7z  0. N H Lời giải Ó M T Chọn B O
Ta có mặt phẳng   chứa trục Ox và đi qua điểm A2; 5  ;7 nên suy ra Á N n   ;iOA             0; 7; 5   : 7 y 5z 0 : 7 y 5z 0 V   . Khi đó     D x
Câu 21. Họ tất cả các nguyên hàm của hàm số f x 2  trên khoảng  1  ; là: – x 1 VDC 3
A. F x  x  3ln  x   1  C .
B. F x  x   C . x  2 1 3
C. F x  x  3ln  x   1  C .
D. F x  x    . x   C 2 1 Lời giải Chọn A x  2  3  dx  1
dx x  3ln x 1  C    x 1  x 1 Do x  1
 ; nên x 3ln x 1 C x 3lnx   1  C .
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM TOÁN VD – VDC NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020
Vây F x  x  3ln  x  
1  C với mọi x  1  ;
Câu 22. Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm A 2
 ;1;0, B0;3;4. Mặt phẳng N H
trung trực của đoạn thẳng AB có phương trình là Ó         M T
A. 2x 3y 4z 4 0 .
B. 2x 3y 4z 4 0 . O
C. 2x  3y  4z  4  0 .
D. x y  2z  5  0 . Á N Lời giải V D Chọn D – VDC
Mặt phẳng trung trực của đoạn thẳng AB đi qua trung điểm của AB là I  1  ;2;2 và nhận
véctơ AB  2;2;4 làm véctơ pháp tuyến.
Phương trình mặt phẳng trung trực của đoạn thẳng AB là: 2 x  
1  2 y  2  4 z  2  0  x y  2z  5  0 .
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A2;0;2, B0;2;0 . Gọi  S  là mặt cầu
nhận AB làm đường kính. Diện tích của mặt cầu S  bằng A. 36 . B. 8 . C. 16 . D. 12 . Lời giải Chọn D AB 2 3
Vì mặt cầu có đường kính AB nên bán kính R    3 . N 2 2 H Ó Diện tích mặt cầu là 2
S  4 R  12 . M T
Câu 24. Trên mặt phẳng tọa độ, điểm biểu diễn số phức z    i2 1 2
là điểm nào dưới đây O Á N A. K  3  ; 4  . B. I 5; 4   . C. E  4  ;5. D. N  3  ;4 . V D Lời giải – VDC Chọn A
z    i2 1 2 = 3   4i .
Vậy điểm biểu diễn số phức z là K  3  ; 4  .
Câu 25. Cho hàm số y f x thỏa mãn f  x  3  5sin x và f 0  1. Mệnh đề nào dưới đây đúng?
A. f x  3x  5cos x  6 .
B. f x  3x  5cos x  6 .
C. f x  3x  5cos x  6 .
D. f x  3x  5cos x  6. Lời giải Chọn B
Ta có: f x  f
 xdx  35sin xdx 3x5cosxC .
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM TOÁN VD – VDC NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020
Mặt khác: f 0 1 C  6  f x  3x  5cos x  6 .
Câu 26. Trong không gian với hệ tọa độ Oxyz , cho vectơ a  1;0;3 và b   2
 ;2;5. Tích vô hướng N H .
a a b bằng Ó   M T A. 3  . B. 23 . C. 9 . D. 5  . O Á Lời giải N Chọn A V D
Ta có: a b  3; 2  ; 2    .
a a b  3 0  6  3  . – VDC x 1 y  2 z  3
Câu 27. Trong không gian với hệ toạ độ Oxyz , cho đường thẳng (d ) :   . Điểm nào 1 2 3
dưới đây thuộc đường thẳng (d) ? A. P(1; 2  ;3). B. N(1; 2;3). C. M ( 1  ;2; 3  ). D. ( Q 1  ;2;3). Lời giải Chọn C. 1
Câu 28. Cho số phức z  2  i . Tính . z 5 A. 5 . B. 5 . C. 3 . D. . 5 Lời giải Chọn D. N 1 1 1 1 5 H Ta có :     . 2 2 Ó z z 2  i  5 2 1 M T
Câu 29. Trong không gian với hệ tọa độ Oxyz , mặt phẳng đi qua điểm M 1;1;  1 và vuông góc với O Á x 1 y  2 z  3 N đường thẳng  :   có phương trình là V 3 2 1 D
A. x y z  3  0 .
B. 3x  2y z  0 . – VDC
C. 3x  2y z  6  0 .
D. x  2y  3z  6  0 . Lời giải Chọn C Ta có:
Đường thẳng  có một vecto chỉ phương u   3;2;  1 .
Mặt phẳng vuông góc với  có vecto pháp tuyến n  3; 2;  1 .
Phương trình mặt phẳng đi qua M 1;1; 
1 có vecto pháp tuyến n  3; 2;  1 là 3 x   1  2 y  
1  z 1  0  3x  2y z  6  0 .
Câu 30. Trong không gian với hệ tọa độ Oxyz ,cho mặt cầu S  có tâm I 1;0;0 và đi qua điểm M 0;0; 
1 . Phương trình của S  là
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM TOÁN VD – VDC NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020
A. S   x  2 2 2 :
1  y z  2 .
B. S   x  2 2 2 :
1  y z  2 .
C. S   x  2 2 2 :
1  y z  2 .
D. S   x  2 2 2 :
1  y z  2 . N H Ó Lời giải M T Chọn D O Á Ta có : IM   1  ;0;  1  IM  2 . N V D
Mặt cầu S  có tâm I 1;0;0 và đi qua M 0;0; 
1 suy ra R IM  2 . – VDC
Phương trình mặt cầu S  x  2 2 2 :
1  y z  2 . 9 3 Câu 31. Cho f
 xdx  9. Tính I f  3xdx. 0 0 A. 27. B. 9. C. 6 . D. 3 . Lời giải Chọn D 3 3 9 9 1 1 1 Ta có I f
 3xdx f
 3xd3x  f
 tdt f  xdx 3  . 3 3 3 0 0 0 0
Câu 32. Số phức liên hợp của số phức z  3 i2  3i là
A. z  6  7i .
B. z  9  7i . C. z  9  7i .
D. z  6  7i . Lời giải N Chọn C H Ó M T
Ta có z  3 i2  3i  6  9i  2i  3  9  7i . O
Vậy z  9  7i . Á N V
Câu 33. Trong không gian với hệ trục tọa độ Oxyz , hình chiếu vuông góc của điểm M 1; 2;3 trên mặt D
phẳng Oxy có tọa độ là – VDC A. 1; 2;0 . B. 1;0;3 . C. 1;0;0 . D. 0; 2;3 . Lời giải Chọn A
Hình chiếu vuông góc của điểm M 1; 2;3 trên mặt phẳng Oxy là H 1;2;0 .
Câu 34. Tìm họ nguyên hàm của hàm số f x  cos 2x . A. f
 xdx  2sin2xC . B. f  x 1 dx  sin 2x C . 2 C. f  x 1
dx   sin 2x C . D. f
 xdx  2
 sin 2x C . 2 Lời giải Chọn B
https://www.facebook.com/groups/toanvd.vdc Trang 14
NHÓM TOÁN VD – VDC NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020 Ta có f  x 1 dx  sin 2x C 2 N
Câu 35. Trong không gian với hệ tọa độ Oxyz , hình chiếu vuông góc của điểm M  1  ;2;  3 trên trục H Ó M T
Oy có tọa độ là O A. Q  1  ;0;0 . B. N 0;0; 3
  . C. E0;2;0 . D. P 1  ;2;0 . Á N V Lời giải D – Chọn C VDC
Ta có: Hình chiếu vuông góc của điểm M  1  ;2; 
3 trên trục Oy có tọa độ là E 0;2;0 .
Câu 36. Số phức đối của số phức 3  4i là: A. 4  3i . B. 3  4i . C. 3   4i . D. 3   4i . Lời giải Chọn C
Số phức đối của số phức 3  4i là 3   4i x
Câu 37. Tìm họ nguyên hàm của hàm số f x  . 2 x  2020 A. f
 xx   2 d
ln x  2020  C . B. f
 xx   2 d ln
x  2020  C . 1 C. f  x 2 dx
x  2020  C . D. f  x 2 dx
x  2020  C . 2 N H Lời giải Ó M T Chọn D O x 1 1 1 2 2 2 Á f
 xdx  dx  d  
x 2020  .2 x 2020 C x 2020 C N 2 2  2  2 x 2020 x 2020 V D –
Câu 38. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S  2 2 2
: x y z  4x  2y  6z  5  0 . VDC
Bán kính của mặt cầu đã cho bằng A. 19 . B. 3 . C. 9 . D. 19 . Lời giải Chọn B
Gọi phương trình mặt cầu S  có dạng 2 2 2
x y z  2ax  2by  2cz d  0 .
Có a  2, b  1, c  3, d  5 .
Suy ra bán kính của mặt cầu S  bằng 2 2 2 2 2 2 r
a b c d  2 1  3  5  3 .
https://www.facebook.com/groups/toanvd.vdc Trang 15
NHÓM TOÁN VD – VDC NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020 2 2 2
Câu 39. Trong không gian với hệ toạ độ Oxyz , cho mặt cầu S  :  x   1   y   1   z   1  9. Tâm
của  S  có toạ độ là N A. 1;1  ;1 . B. 1;1;  1  . C. 1; 1  ;  1 . D.  1  ;1;  1 . H Ó Lời giải M T Chọn B 2 2 2 O
Ta có S  :  x   1   y   1   z   1
 9 suy ra toạ độ tâm của S  là I 1;1;  1 bán kính Á N R  3 . V D
Câu 40. Trong không gian với hệ toạ độ Oxyz , phương trình nào dưới đây là phương trình của đường –
thẳng đi qua điểm A0; 2;3 và vuông góc với mặt phẳng P : x  3y z  5  0 . VDC x tx t  
A. x  3y z  3  0 .
B. y  2  3t . C. y  3   2t .
D. x  3y z  3  0 .   z  3  tz  1 3tLời giải Chọn B
Mặt phẳng  P : x  3y z  5  0 có vectơ pháp tuyến là n  1; 3  ;  1 .
Đường thẳng d  đi qua điểm A0;2;3 và vuông góc với mặt phẳng P : x 3y z 5  0 x t
nhận vectơ n  1; 3  ; 
1 là vectơ chỉ phương có phương trình là  y  2  3t . z  3t
Câu 41. Trong không gian với hệ tọa độ Oxyz , cho điểm E  1  ; 2  ; 
3 . Gọi E là hình chiếu vuông góc
của E lên mặt phẳng Oxz . Khoảng cách từ E đến trục Oy bằng N H A. 13 . B. 14 . C. 10 . D. 5 . Ó M T Lời giải O Chọn C Á N
Vì E là hình chiếu vuông góc của E lên mặt phẳng Oxz nên E 1  ;0;3 . V   D
d E ,0y  1 9  10 . – VDC
Câu 42. Trong không gian với hệ tọa độ Oxyz , véc tơ nào dưới đây là một véc tơ chỉ phương của
đường thẳng đi qua hai điểm E  2  ;3;  1 và F 2; 1  ;3 ? A. u  1; 1  ;1 . B. u  1; 1  ; 1  .
C. u  0;1;1 .
D. u  1;1;1 . 1   2   3   4   Lời giải Chọn A
Ta có đường thẳng EF có véc tơ chỉ phương là EF  4; 4  ;4  4u . 4
Câu 43. Biết F x là một nguyên hàm của hàm số f x  x cos x và F 0  1. Tính F   .  
A. F    .
B. F    1.
C. F    1  .
D. F     2 2 Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 16
NHÓM TOÁN VD – VDC NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020 Chọn C     
Ta có F    F 0  x cos d x x = d
x sin x  x sin x  sin d x x  cos x  2     . N 0 0 0 0 0 H Ó M T
Mà F 0  1, suy ra F    2   F 0  1  . O Á Câu 44. Cho hàm số   2
F x x là một nguyên hàm của hàm số   2x
f x e . Tìm nguyên hàm của hàm số N V   2x f x e . D x x A. f   x 2 2
e dx  x x C . B. f   x 2 2
e dx  x x C . – VDC C. f   x 2x 2
e dx  2x  2x C . D. f   x 2x 2
e dx  2x  2x C . Lời giải Chọn C Vì hàm số   2
F x x là một nguyên hàm của hàm số   2x
f x e nên       2 2 x F x x f x e suy 2x 2 x e  4 x xe
ra f x 
. Có f  x 2 2  . 2 x e 4 x e 2 x 2 x 2 x 2 e xe e xe x 2 4 x 2 4 x Vậy nên f   x 2 2 e dx = .e dx  dx   x
x x C    . x x 2 4  2 dx 2 2 4 2 e e
Cách 2. Dùng nguyên hàm từng phần Vì hàm số   2
F x x là một nguyên hàm của hàm số   2x
f x e nên       2 2 x F x x f x e suy N 2x H
ra f x  . 2 x Ó e M T x x x x x 2 2 2 2 2 2 x 2 2 O Có f
 xe dx= e d 
f x  f xe 2 f
 xe dx  .e 2x C  2x2x C. 2 x Á e N V
Câu 45. Tìm họ nguyên hàm của hàm số   2020 .x f x  D – x 1  x 2020 x x VDC A. 2020 dx   C. 
B. 2020 dx  2020 ln x  . C x 1 x 2020xC. 2020 dx   C.  D. x x 1 2020 dx  2020  . C ln 2020 Lời giải Chọn C
Câu 46. Số phức nào dưới đây là số thuần ảo? A. 2020. B. 2  . i C. 2020 . i D. 1 3 . i Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc Trang 17
NHÓM TOÁN VD – VDC NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020
Câu 47. Biết phương trình 2
z az b  0 nhận số phức z  1 i là nghiệm. Tính tổng S a b . A. S  4 . B. S  2  . C. S  0 . D. S  4  . Lời giải N H Ó Chọn C. M T • Cách 1 O
Ta có số phức z  1 i là một nghiệm của phương trình 2
z az b  0 Á    2 a b 0 N
 1i  a1i b  0  a b a  2i  0  
S a b  0 V a  2  0 D
Vậy ta có: S a b  0 . – VDC • Cách 2
Ta có: z  1 i z 1  i   z  2 2 1  i 2
z  2z  2  0 (1).
Mặt khác z là nghiệm của phương trình 2
z az b  0 (2). a  2  Từ (1) và (2), ta có: 
S a b  0. b   2
Câu 48. Trong không gian với hệ tọa độ Oxyz , cho các điểm A2;0;0 , B 0;6;0 , C 0;0;5 và điểm
N sao cho ON OA OB OC . Một mặt phẳng  P thay đổi cắt các đoạn thẳng OA OB OC O , A O ,
B OC,ON lần lượt tại các điểm A , B ,C , N thỏa mãn    2020 và 1 1 1 1 OA OB OC 1 1 1 N x ; y ; z . Khi đó 1  0 0 0  7 9
A. x y z  .
B. x y z  . 0 0 0 2020 0 0 0 2020 N 11 13
C. x y z  .
D. x y z  . H 0 0 0 2020 0 0 0 2020 Ó M T Lời giải O Chọn D Á N
Ta có: ON OA OB OC  2;6;5  N 2;6;5 . V D
Ta thấy OA  2;OB  6;OC  5 . – VDC Gọi A ; a 0; 0 , B 0; ;
b 0 , C 0; 0; c lần lượt là giao điểm của mặt phẳng  P với các đoạn 1   1   1   thẳng O , A O ,
B OC . Ta có: 0  a  2 ; 0  b  6 ; 0  c  5 .
Như vậy ta có: OA a , OB b , OC c . 1 1 1 x y z
Mặt phẳng  P đi qua A , B ,C nên có phương trình  P :   1. 1 1 1 a b c Theo đề OA OB OC ta có:    2 6 5 2020     2 6 5 2020    1 OA OB OC a b c 2020a 2020b 2020c 1 1 1 1 3 5 1010 1010 2020     x y z  1 3 5  1   P : 
 1 đi qua điểm N ; ;   . a b c a b c 1010 1010 2020 
https://www.facebook.com/groups/toanvd.vdc Trang 18
NHÓM TOÁN VD – VDC NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020  1 3 5  1 Ta thấy ON  ; ;  ON  
N thuộc đoạn ON . 1010 1010 2020  2020 N
Ta có N P , NON nên N là giao điểm của  P với đoạn ON . H Ó M T 1 3 5
Suy ra N  N x ; y ; zx  ; y  ; z  . 1  0 0 0  0 0 0 1010 1010 2020 O Á N 13
x y z . V 0 0 0 2020 D –  2 VDC
2 cos x 1 sin x 1 Câu 49. Biết dx a   trong đó , a , b ,
m n là các số nguyên dương, m là phân số 2 cos m xn n sin x e . b e 6
tối giản. Tính S a b m n . A. S  9 . B. S  12 . C. S  10 .
D. S  11. Lời giải Chọn C   
cos x 1 sin x2
cos x 1 sin x2
cos x 1 sin x2 2 2 2 Ta có: I dx dx dx    2 2  1 cos x 1 sin x sin x    sin sin sin x x x e e e 6 6 6
Đặt t  sin x dt  cos xdx N H Ó M T O 2 Á 1 1 t 1 1 1 1 1 1 2 t t t  2 N I dt  1 t . t e dt  1 t . t e dt  2t. t e dt     . 1     V t 1 1 1 1 t e D 2 2 2 2 – 1 1 1 1 VDC 1 t t    2  1 . t  2 . t t e dt t e
dt A B     . 2  t  1 1 2 2 1 1 1 t    Xét tích phân: 2  1 . t A t e dt    2  t  1 2 2 u   tdu  2tdt   Đặt 1   t     1 1 .  dv  1 . t t e dt t      2 v e   t
https://www.facebook.com/groups/toanvd.vdc Trang 19
NHÓM TOÁN VD – VDC NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020 1 1 1 1 t t  1 2
  . t 1  2 . t A t e t e dt  1  B  . 3 1 2 2 4e N 2 H Ó a 1 M T  1 1 b   4
I A B 1  a    . O 3 m m  3 Á 2  4e . n b e N n  2 V D
Vậy S a b m n  10 . – VDC *Cách khác
Đặt t  sin x dt  cos xdx .   Đổ 1 i cận: x
t  ; x   t 1. 6 2 2 1 t  2 2 1 t 1  1 1 1 1 1 2  1 2 t    1 2 t   ln 2 tI dt t 1 t e dt t 1 t   e dt  1  . t e .e dt        2    2  2 2 1 tt t   t t  1 1 1 1 t e 2 2 2 2 1 1 1 2 t     ln 2 t   1  . t e dt   . 2  t t  1 2   Đặ 1 1 2
t u t   ln  2
t   du  1  dt   . 2 tt t  N H Đổ 1 3 i cận: t
u    2ln 2 ; t 1 u  0. Ó 2 2 M T a 1 O 3 0  Á  0 3 2  2ln 2 e b   u u 1 4 N 2  I e du e  3 1 e  1  1   . 3 V   2ln 2 4 m  3 3 2   2ln 2 2 4.e D 2 n  2 – VDC
Vậy S a b m n  10 .     1 2 1
Câu 50. Cho f x là một nguyên hàm của g x trên , thỏa mãn f    ,
xg xdx   và  2  2 2 0  2 f
 xdx a b , trong đó a,b là các số hữu tỉ. Tính P a2b. 0 1 1 A. P  . B. P  0 . C. P  1 . D. P   . 2 2 Lời giải Chọn B
https://www.facebook.com/groups/toanvd.vdc Trang 20 NHÓM TOÁN VD – VDC
NGUYỄN KHUYẾN-BÌNH DƯƠNG-2020
Do f x là một nguyên hàm của g x nên f ' x  g x .   2 2 N 1 H
Khi đó: I xg xdx xf 'xdx    . Ó 2 0 0 M T u   x  du dx  O Đặt    . Á dv f ' 
xdx v f  x N V    D  2 2 2      1 –  I  .
x f x 2  f
 xdx  .ff
   xdx   f
 xdx  . VDC 2  2  4 2 0 0 0 0  2   f x 1 dx     . 2 4 0 1 1
Ta có: a   , b
P a  2b  0 . 2 4
-------------------- HẾT -------------------- N H Ó M T O Á N V D – VDC
https://www.facebook.com/groups/toanvd.vdc Trang 21