Đề thi học kì 2 Toán 12 năm 2019 – 2020 trường THPT An Dương Vương – TP HCM

SỞ GIÁO DỤC & ĐÀO TẠO
ĐỀ THI HỌC KỲ 2 NĂM 2019-2020 THPT AN DƯƠNG VƯƠNG Môn Toán lớp 12
Thời gian làm bài: 65 phút; Mã đề thi: 132 (35 câu trắc nghiệm)
Họ, tên thí sinh:..................................................................... Mã số: .............................
Câu 1: Trong không gian Oxyz, đường thẳng đi qua hai điểm A4; 2  ;5 và B3;1;  1 có một vectơ chỉ phương là     A. u  1; 3  ;4 . B. u  1; 1  ;4 . C. u   1  ; 3  ;4 . D. u  1; 3  ; 4   .
Câu 2: Cho hàm số y  f  x liên tục trên đoạn  ;
a b . Thể tích V của vật thể tròn xoay sinh ra khi
quay xung quanh trục Ox hình phẳng được giới hạn bởi các đường: y  f  x , trục hoành, hai
đường thẳng x  a và x  b được tính theo công thức b b b b A. V   f  x dx. B. V  f
 x dx. C. V   f  x 2dx  . D. V   f  x 2dx  . a a a a
Câu 3: Tìm họ nguyên hàm của hàm số f  x 2  3x 1 A. 6x . B. 3 x  x  C . C. 6x  C . D. 3 x  x  C .
Câu 4: Cho số phức  có điểm biểu diễn là M như hình vẽ bên dưới.
Tìm số phức liên hợp  . A.  1 2i . B.   2   i . C.   1   2i . D.   2   i . 1 Câu 5: Tính tích phân 2 1 5 x I   dx  . 0 125 60 A. I  . B. I  25.ln 5 . C. I  37, 28. D. I  . 2ln 5 ln 5
Câu 6: Tính diện tích S của hình phẳng được giới hạn bởi đồ thị hàm số 3 2 y  x  3x và trục hoành. 27 27 A. S   . B. S  4 . C. S  6 . D. S  . 4 4
Câu 7: Tính môđun của số phức z thỏa mãn đẳng thức 1 i z  3  5i . A. z  2 . B. z  1. C. z  17 . D. z  4 .
Câu 8: Tìm phần ảo của số phức z  1 2i3i   1 . A. 7 . B. 1. C. i . D. 2 5 . x  y z 
Câu 9: Trong không gian Oxyz, cho điểm A1; 2  ;  1 và đường thẳng 1 1 d :   . Tính số 2 1 1
đo góc giữa hai đường thẳng OA và d . A. 0 60 . B. 0 30 . C. 0 45 . D. 0 120 .
Câu 10: Trong không gian Oxyz, viết phương trình chính tắc của đường thẳng đi qua điểm A 1
 ;4;3 và vuông góc với mặt phẳng P :3x  y  2z  4  0. x 1 y  4 z  3 x 1 y  4 z  3 A.   . B.   . 3 1 2  3 1 2  x  3 y 1 z  2 x 1 y  4 z  3 C.   . D.   . 1  4 3 3  1  2
Câu 11: Trong không gian Oxyz, hình chiếu của điểm A7;5; 4
  lên mặt phẳng tọa độ Oxz là A. A 0;5; 4  . B. A 7;0; 4 . C. A 0;5;0 . D. A 7;5;0 . 1   3   1   2   1 2 2 Câu 12: Cho f  xdx  3 và f
 xdx  4. Tính I  f  xdx . 0 0 1 A. I  1. B. I  1. C. I  7 . D. I  7 .
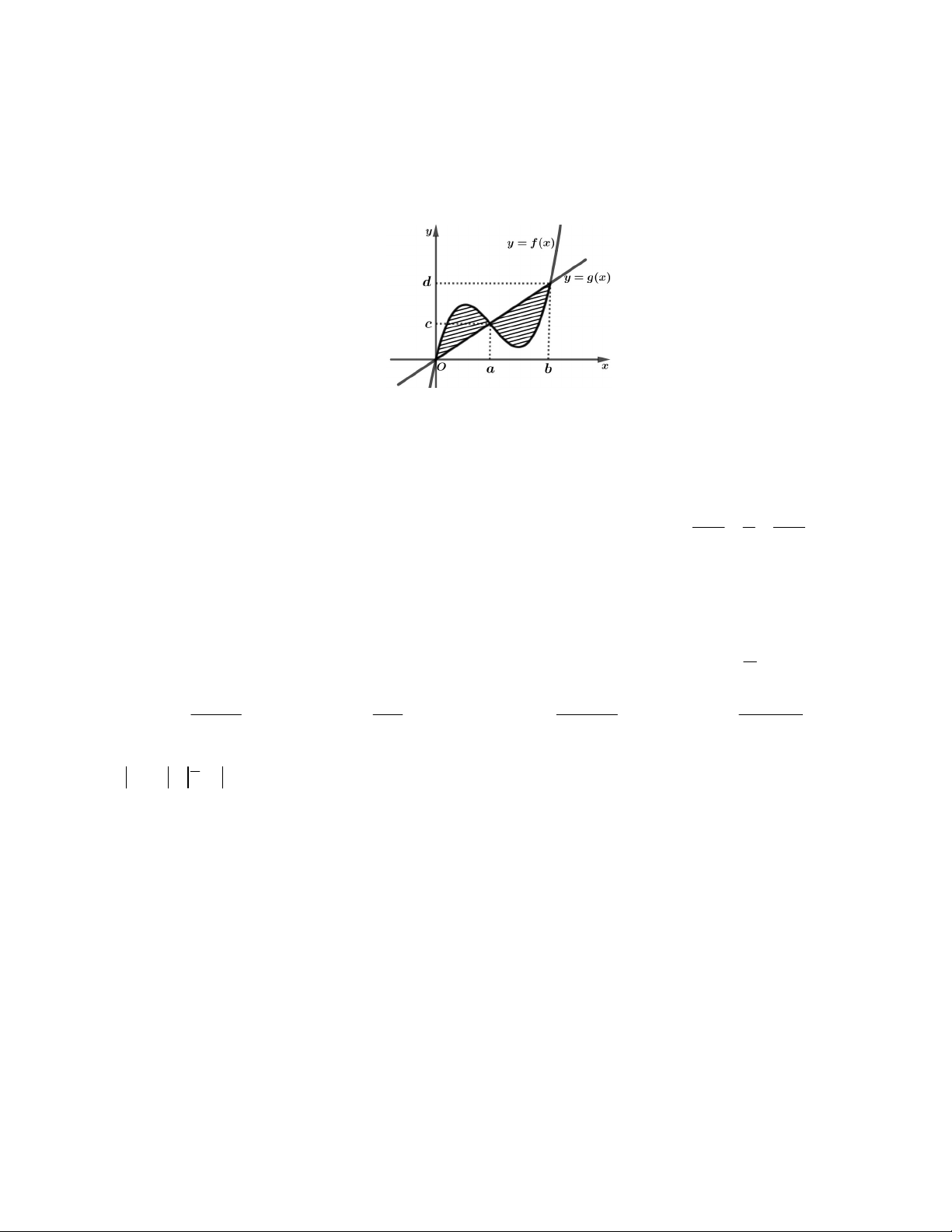
Câu 13: Cho hình phẳng được giới hạn bởi đường cong y  f  x và đường thẳng y  g  x như
hình vẽ bên dưới. Công thức đúng để tính diện tích S của hình phẳng này là c d a b A. S   f
 x gxdx g 
 x f xdx  . B. S   f
 x gxdx g 
 x f xdx  . 0 c 0 a a b a b C. S   f
 x gxdx g 
  x f xdx  . D. S   f
 x gxdx  f 
 x gxdx  . 0 a 0 a x  y z 
Câu 14: Trong không gian Oxyz, xét vị trị tương đối giữa đường thẳng 1 1 d :   và mặt 2 3 1
phẳng P : 2x  y  z  3  0 . A. d // P . B. d  P . C. d  P .
D. d cắt và không vuông góc P .
Câu 15: Thể tích V của vật thể tròn xoay được tạo ra khi quay xung quanh trục Ox hình phẳng 
được giới hạn bởi các đường: y  tan x , trục hoành, trục tung và đường thẳng x  là 4 4  21  1   4   A. V  . B. V  . C. V  . D. V  . 4 100 4 4
Câu 16: Trong mặt phẳng tọa độ Oxy, tập hợp điểm biểu diễn số phức z thỏa mãn đẳng thức z  2i  z 1 là
A. Đường thẳng 2x  4y  3  0 .
B. Đường thẳng 4x  2y  3  0 .
C. Đường tròn  x  2   y  2 2 1  1
D. Đường thẳng 2x  4 y  3  0 . Câu 17: Biết    x
f x dx  xe  C . Tính f   1 . A. f   1  e . B. f   1  0. C. f   2 1  e . D. f   1  2e .
Câu 18: Trong không gian Oxyz, viết phương trình mặt cầu có tâm I 1; 3
 ;2 và tiếp xúc với mặt
phẳng   : x  2y  2z 1  0 .
A.  x  2   y  2   z  2 1 3 2 16 .
B.  x  2   y  2   z  2 1 3 2  4 .
C.  x  2   y  2   z  2 1 3 2  4 .
D.  x  2   y  2   z  2 1 3 2  16.
Câu 19: Một vật chuyển động với hàm vận tốc v tính theo biến thời gian t là   2 v t  t  t ( m / s ).
Tính quãng đường vật đi được từ lúc bắt đầu chuyến động đến thời điểm nó đạt vận tốc 20m / s. 88 8600 175 117 A. m . B. m. C. m . D. m. 3 3 6 2
Câu 20: Trong không gian Oxyz, cho điểm M 1;2; 3   . Gọi ,
A B,C lần lượt là hình chiếu của
điểm M lên ba trục tọa độ Ox, Oy và Oz. Khi đó phương trình mặt phẳng  ABClà
A. 6x  3y  2z  6  0 .
B. 6x  3y  2z  6  0 . C. 6x  3y  2z  0 .
D. x  2y  3z 14  0 .
Câu 21: Gọi z , z là hai nghiệm phức của phương trình 2 z  2z  2  0 . Tính 2 2 T  z  z . 1 2 1 2 A. T  0 . B. T  2 2 . C. T  4 . D. T  2 .
Câu 22: Một vật thể trong không gian được giới hạn bởi hai mặt phẳng x  0 và x  2 , mặt phẳng
vuông góc với trục Ox tại điểm x 0  x  2 cắt vật thể trên tạo ra thiết diện là tam giác vuông
cân có cạnh huyền bằng 2
2 4  x . Thể tích V của vật thể trên là 64 64 16 16 A. V   . B. V  . C. V   . D. V  . 3 3 3 3 4 1
Câu 23: Cho hàm số f  x liên tục trên R và f
 xdx  2020. Tính I  .xf  2 3x   1dx. 1 0 1010 2020 A. I  6060 . B. I 1010 . C. I  . D. I  . 3 3 x  y z
Câu 24: Trong không gian Oxyz, cho điểm A1;2;4 và đường thẳng d  1 :   . Gọi 2 1 3 Aa; ;
b c là điểm đối xứng với A qua đường thẳng d . Tính S  a  b  c . A. S  5. B. S  3. C. S  0 . D. S  7
Câu 25: Cho hàm số trùng phương 4 2
y  5x 15mx  4 có đồ thị C và có 3 điểm cực trị. Biết m 
hình phẳng được giới hạn bởi đồ thị C và tiếp tuyến của C tại điểm cực tiểu có diện tích m  m 
bằng 324. Khi đó giá trị của tham số m thỏa mãn mệnh đề nào dưới đây? 5 5 A. 5  m  7 . B. m  7 . C.  m  5. D. 0  m  . 2 2
Câu 26: Trong không gian Oxyz , viết phương trình đường thẳng  đi qua điểm A2; 1  ;3 chứa  trong mặt phẳng  x y z
P : x  2y  z 3  0 và vuông góc với đường thẳng 1 d :   . 1 3 5 x  2 y 1 z  3 x  7 y  4 z 1 A.  :   . B.  :   . 7 4 1 2 1 3 x  2 y 1 z  3 x  2 y 1 z  3 C.  :   . D.  :   . 1 7 4 7 4 1
Câu 27: Cho số phức z thỏa mãn đẳng thức z  2i  3 . Biết rằng trong mặt phẳng tọa độ Oxy , tập
hợp điểm biểu diễn số phức   1 i z  i là một đường tròn. Tâm I và bán kính r của đường tròn đó là
A. I 2;3; r  3 2 . B. I  2  ;3; r  3 2 .
C. I 2;3; r  3 2 . D. I 0;2; r  3. z 
Câu 28: Tìm môđun của số phức z biết rằng 2 A 
là một số thực và B   z  3i 1 là số 1 i phức thuần ảo. A. z  4 . B. z  3 . C. z  10 . D. z  5 .  4 2   1 Câu 29: Biết 2 2x sin x dx    
, với a,b,c là các số nguyên. Tính T  a  b  c . a b c 0 A. T  28 . B. T  44 . C. T  41. D. T  24 .  
Câu 30: Cho hàm số f  x thỏa mãn f  x 4  và f 0 1. Tính 3 f   . 1 2x  2  A. 1 4ln 2 . B. 1 ln 4 C. 1 ln 4 . D. 1 4ln 2 .
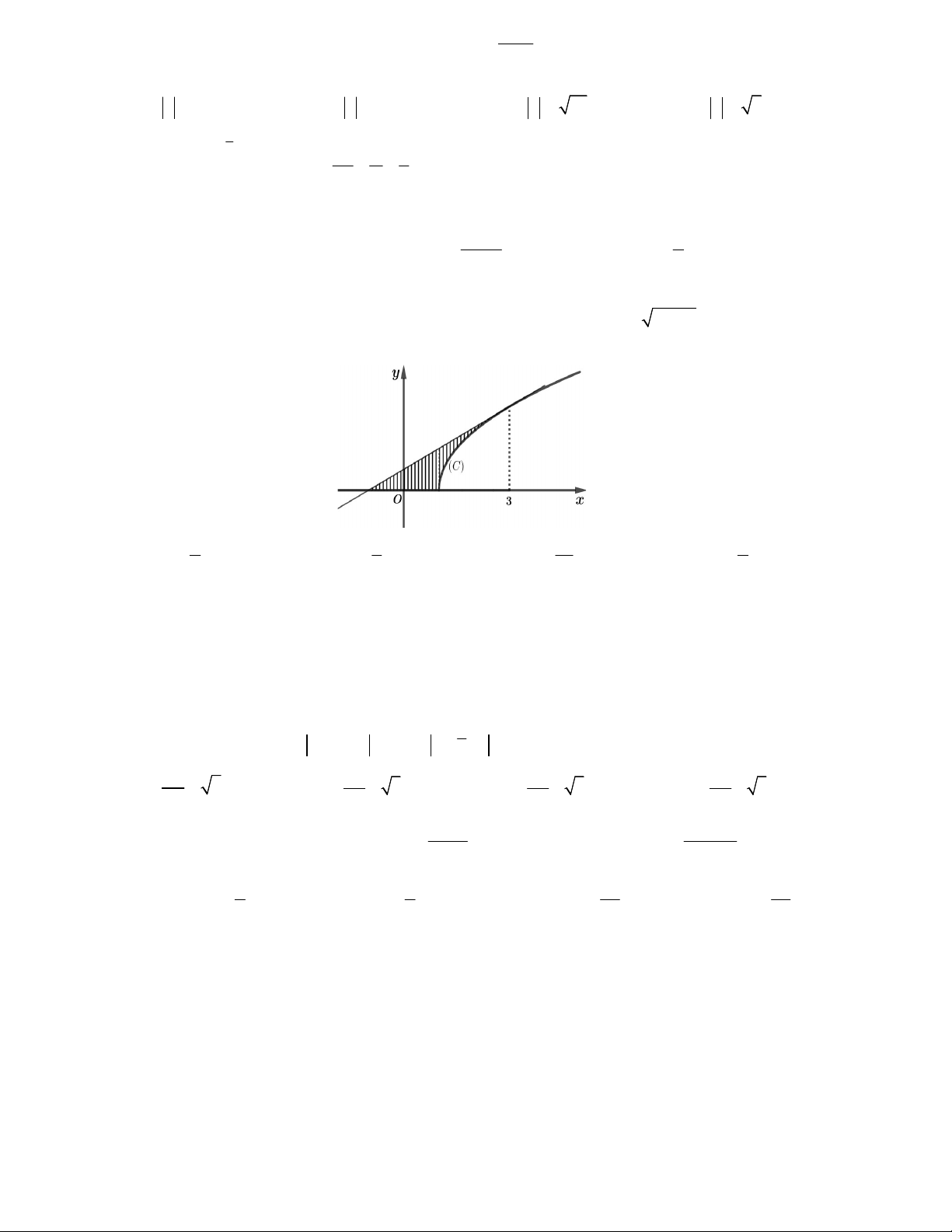
Câu 31: Tính diện tích hình phẳng được giới hạn bởi đồ thị C : y  2x  2 , tiếp tuyến của đồ thị
C tại điểm x  3 và trục hoành. (hình vẽ tham khảo) 4 1 10 7 A. S  . B. S  . C. S  . D. S  . 3 3 3 3
Câu 32: Cho hàm số f  x liên tục trên R thỏa mãn     2 x f x x x e   2 2 1 1 x  f  x, x   R và 1 f 0  1  . Tính I  f  xdx . 0 A. I  2e . B. I  e . C. I  e . D. I  2e .
Câu 33: Trong mặt phẳng tọa độ Oxy, gọi H  là hình phẳng biểu diễn các số phức z thỏa mãn
đồng thời hai điều kiện z 1 2i  2 và z  z  i  7 . Tính diện tích hình phẳng H  . 4 2 2 4 A.  3 . B.  3 . C.  3 . D.  3 . 3 3 3 3 2 2 2 f x
Câu 34: Cho hàm số f  x thỏa f  x  và f  2    ln3. Tính I  dx  . 2 x 1   x  2 3 1 9 9 27 27 A. I  1   ln . B. I 1 ln . C. I  1 ln . D. I 1 ln . 2 2 4 4
Câu 35: Trong không gian Oxyz, cho mặt phẳng   : x  3y  2z  5  0 và điểm A2; 8  ;3 . Trong
số các đường thẳng đi qua gốc tọa độ O và song song với mặt phẳng   , gọi d  là đường thẳng
sao cho khoảng cách từ điểm A đến d  đạt giá trị nhỏ nhất. Khi đó, đường thẳng d  đi qua điểm nào? A. P4;2;5 . B. Q 5;1;3 . C. N 1;1;  1 . D. M  4  ;2;  1 . ----------- HẾT ----------
SỞ GDĐT TP.HCM KỲ THI HỌC KỲ 2 NĂM HỌC 2019-2020
THPT AN DƯƠNG VƯƠNG MÔN TOÁN LỚP 12. Thời gian: 25 phút
PHẦN TỰ LUẬN (3 điểm) Câu 1 (0,5 điểm).
Cho các số thực x, y thỏa mãn đẳng thức x  1 3yi  2  4i . Tính giá trị của P  xy . 1
Câu 2 (0,5 điểm). Tìm hàm số f  x biết f x  và f 0 1. 2 cos 2x 1 2x
Câu 3 (0,5 điểm). Tính tích phân I    dx . 1 x 2 2 0 Câu 4 (0,5 điểm).
Trong không gian Oxyz, viết phương trình mặt phẳng P đi qua điểm A1; 2
 ;0 và chứa đường thẳng x  2 y z 1 d :   . 2 1 3  Câu 5 (0,5 điểm). x 1 y z 1
Trong không gian Oxyz, cho đường thẳng  :  
. Viết phương trình mặt cầu (S) có tâm 2 1 1 I 1;3; 2
  và cắt đường thẳng  tại hai điểm A, B sao cho  0 AIB  120 . Câu 6 (0,5 điểm). z  z i
Cho số phức z thỏa mãn đẳng thức
 2i  z  2  i . Tìm giá trị nhỏ nhất của P  z  2  . 2 2 ---HẾT---
PHIẾU ĐÁP ÁN TRẮC NGHIỆM
THI HỌC KỲ 2 NĂM HỌC 2019-2020 Mã đề: 132 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 A B C D
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 A B C D Mã đề: 209 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 A B C D
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 A B C D Mã đề: 357 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 A B C D
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 A B C D Mã đề: 485 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 A B C D
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 A B C D CÂU NỘI DUNG ĐIỂM   x    y x 2 1 3 i  2  4i   1   3y  4 0,25 1
Với x  2; y  1  T  xy  2 0,25 f  x 1 1  dx  tan 2x  C  0.25 2 cos 2x 2 2
f 0 1  C 1. Vậy f x 1  tan 2x 1 0,25 2 1 2x I    dx 1 x 2 2 0 0,25 3 Đặt 2
t  1 x  dt  2x dx . Đổi cận: x  0  t  1; x  1  t  2 . 2 2 1 1 1 I  dt     0,25 2 t t 2 1 1  Đt d đi qua M 2;0; 
1 và có VTCP là u  2;1; 3  d     0,25 4
Mp (P) có một VTPT là: n  u , MA  5; 1  ;3 p d   
Ptmp P : 5x  y  3z  7  0 0,25
Gọi H là hình chiếu của tâm I lên đường thẳng  .
Tính: AH  d I,  2 3 0,25
Tam giác IAH vuông tại H có: IH R  IA   4 3 5 0 cos 60 0,25
Ptmc S  x  2   y  2   z  2 : 1 3 2  48
Đặt z  x  yi (x, y  R)  Ta có: z z 1 1 2
 2i  z  2  i  y  x  2x  0,25 2 2 2 2 Khi đó: i   P  z  2   x  22 1 2  x  2x   2  2  Xét: 2 6         x  g x x  2 1 1 2 2 2  x  2x  g   x  2x  2 2 x  2x 1 ; g   x  0    2   2  x  2  2 0,25
Kết luận: GTNN của P là 3
THI HỌC KỲ 2: ĐÁP ÁN PHẦN TỰ LUẬN