Thông tin
Quiz

Đề thi học kì 2 Toán 12 năm 2019 – 2020 trường THPT Hoàng Hoa Thám – TP HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2019 – 2020 .Mời bạn đọc đón xem.

Chủ đề:

Đề HK2 Toán 12 488 tài liệu

Môn:

Toán 12 3.9 K tài liệu

Thông tin:

19 trang 1 năm trước

Tác giả:

Lan Tường

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Đề thi học kì 2 Toán 12 năm 2019 – 2020 trường THPT Hoàng Hoa Thám – TP HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2019 – 2020 .Mời bạn đọc đón xem.

27 14 lượt tải Tải xuống

SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM

TRƯỜNG THPT HOÀNG HOA THÁM

ĐỀ CHÍNH THỨC

(Đề gồm 04 trang)

ĐỀ KIỂM TRA HỌC KỲ 2

NĂM HỌC: 2019 – 2020

Môn: TOÁN – Lớp 12

Thời gian làm bài: 90 phút

Mã đề

132

Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.

Họ, tên thí sinh:.......................................................................Số báo danh:...........................................

I. PHẦN TRẮC NGHIỆM (8,0 điểm)

Câu 1: Gọi

là nghiệm phức có phần ảo âm của phương trình

2 5 0

z z

  

. Tìm tọa độ điểm biểu diễn số

phức

7 4



trên mặt phẳng phức ?





3; 2





3; 2







1; 2







1; 2

Câu 2: Trong không gian

Oxyz

cho

(3; 1;2), (4;2; 6).

a b   

 

Tính tọa độ của vectơ

a b



 

a b

 

 

(1;3; 8).



a b

 

 

(7;1; 4).



a b

 

 

( 1; 3; 8).

 

a b

 

 

( 7; 1;4).

 

Câu 3: Tổng phần thực và phần ảo của số phức

thoả mãn





1 2

iz i z i

   

bằng



. B.

. C.

. D.



Câu 4: Trong không gian với hệ toạ độ

Oxyz

cho









2; 0;2 , 2;2; 0

A B

. Mệnh đề nào sau đây đúng ?

OAB



vuông tại

OAB



đều

OAB



vuông cân tại

OAB



chỉ cân tại

Câu 5: Hàm số





y f x



liên tục trên

2; 9

 

 

 





F x

là một nguyên hàm của hàm số





f x

trên

2; 9

 

 

 

và









2 5, 9 4

F F

 

. Mệnh đề nào sau đây đúng ?

 

f x dx 



. B.

 

f x dx





. C.

 

f x dx





. D.

 

f x dx

 



Câu 6: Trong không gian với hệ tọa độ

Oxyz

cho









1;2; 3 , 3; 4; 7 .

M N



Mặt phẳng nào sau đây là mặt phẳng

trung trực của đoạn thẳng





: 5 15 0

P x y z

   





: 2 2 10 15 0

P x y z

   





: 2 2 10 15 0

P x y z

   





: 5 15 0

P x y z

   

Câu 7: Trong không gian

Oxyz

, cho điểm





3;1; 0

. Tìm tọa độ điểm

là hình chiếu vuông góc của điểm

trên trục





3; 0; 0

. B.





1; 0; 0

. C.





0;1; 0

. D.





3; 0;1

Câu 8: Nghiệm của bất phương trình





log 2 8 4

x x

   

là

6 4

2 4



   



 





. B.



 









. C.

6 4

2 4



   



 





. D.



 









Câu 9: Trong không gian với hệ toạ độ

Oxyz

, tính độ dài

biết

là hình chiếu vuông góc của





1;2; 3

lên mặt phẳng





Oyz

Câu 10: Tính:

J dx







Câu 11: Trong không gian

Oxyz

, tìm giá trị của tham số

để mặt phẳng





: 2 3 5 0

P x y mz

   

vuông

góc với mặt phẳng





Oxy

 



. B.



. C.



. D.



Câu 12: Tính thể tích của khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn bởi đồ thị hàm

số





y x x

 

với trục hoành.

512

(đvtt) B.

(đvtt) C.

512



(đvtt) D.



(đvtt)

Câu 13: Cho hàm số





f x

liên tục trên



và

 

f x dx







. Khi đó

 

2 cos sin

f x xdx





bằng



. B.

. C.

. D.

Câu 14: Tìm a sao cho

. . 4

x e dx







Câu 15: Tìm họ nguyên hàm của hàm số

( )

5 2

f x





5 ln 5 2

5 2

x C

  





ln 5 2

5 2

x C

  









5 2



 





ln 5 2

5 2 5

x C

  





Câu 16: Trong không gian

Oxyz

mặt cầu tâm





2; 1; 3



và tiếp xúc với mp





Oxy

có phương trình là













2 2 2

2 1 3 9

x y z

     













2 2 2

2 1 3 9

x y z

     













2 2 2

2 1 3 4

x y z

     













2 2 2

2 1 3 1

x y z

     

Câu 17: Trong không gian

Oxyz

, tìm giá trị của tham số

để đường thẳng

2 1 1

3 1 2

x y z

  

 



vuông

góc với mặt phẳng

( ) : 6 4 5 0

x my z



   

 

. B.



. C.

 

. D.



Câu 18: Tập nghiệm của bất phương trình

2 2

log 6 log 8 0

x x

  

là

(0 ; 4]

(0 ; 16]

2 ; 4

 

 

 

4 ; 16

 

 

 

Câu 19: Trong không gian

Oxyz

cho đường thẳng

 

6 5

: 2

x t

d y t





 



 











và mặt phẳng





: 3 2 1 0.

P x y

  

Góc

giữa đường thẳng





và mặt phẳng





bằng

Câu 20: Cho số phức

3 2

z i

 

. Tìm phần thực và phần ảo của số phức

A. Phần thực bằng



và phần ảo bằng



. B. Phần thực bằng

và phần ảo bằng



C. Phần thực bằng

và phần ảo bằng

. D. Phần thực bằng

và phần ảo bằng

Câu 21: Trong mặt phẳng

Oxy

điểm biểu diễn của số phức

5 4

z i

 

là





5; 4

 

. B.





5; 4

. C.





5;4



. D.





5; 4



Câu 22: Cho số phức

thỏa mãn













3 2 4 1 2

i z i i z

    

. Mô đun của

bằng

Câu 23: Nếu

( ) 17

f x dx 



và

( ) 12

f x dx 



thì

( )

f x dx



bằng



Câu 24: Tập nghiệm của bất phương trình

1 2x 1

5 5

7 7

x x

  

   

 

 

 



 

 

 

 

 

   

có dạng





;

S a b



. Tính

A b a

 



 

Câu 25: Số nghiệm của phương trình

2 2

2 2 15

x x 

 

là

A. 2. B.

. C. 0 D. 3.

Câu 26: Nghiệm của phương trình

2 1

2 0

x 

 

là

 

. B.

 

. C.



. D.



Câu 27: Trong không gian

Oxyz

mặt phẳng

2 1 0

x y z

   

có một véctơ pháp tuyến là





1; 2; 1

  







1;2; 1

  







1;2; 1

 







1; 2; 1

   



Câu 28: Biết

;

S a b

 



 

 

là tập nghiệm của bất phương trình

3.9 10.3 3 0.

x x

  

Tìm

T b a

 

T 

. B.



. C.



. D.



Câu 29: Trong không gian

Oxyz

cho điểm





2; 1; 1

 

và mặt phẳng





: 16 12 15 4 0.

P x y z

   

Gọi

là hình chiếu vuông góc của

lên





. Tính độ dài

A. 55. B.

. C.

. D.

Câu 30: Trong không gian

Oxyz

cho mặt cầu





2 2 2

: 4 2 6z 3 0

S x y z x y

      

. Bán kính của mặt cầu





là:

Câu 31: Tổng tất cả các nghiệm của phương trình









2 2 2

log 1 log 1 log 3 5

x x x

    

bằng

. B.

. C.

. D.

Câu 32: Trong không gian với hệ tọa độ

Oxyz

, mặt phẳng

( ) : 2 2 5 0

P x y z

   

cắt mặt cầu

2 2 2

( ) : ( 2) ( 3) ( 3) 100

S x y z

     

theo giao tuyến là đường tròn

( )

. Tính bán kính

của

( )



. B.



. C.



. D.



Câu 33: Tìm kết quả đúng.

x x

e dx xe C

 

  



x x

e dx e C

 

 



x x

e dx e C

 

  



x x

e dx xe C

 

 



Câu 34: Trong không gian

Oxyz

cho





là đường thẳng đi qua điểm





1;2; 3

và vuông góc với mặt phẳng





: 4 3 7 2 0

P x y z

   

. Phương trình tham số của





là

1 4

2 3

3 7

x t

y t

z t





 



 





 





. B.

1 4

2 3

3 7

x t

y t

z t





  



  





  





. C.

1 3

2 4

3 7

x t

y t

z t





 



 





 





. D.

1 4

2 3

3 7

x t

y t

z t





  



  





  





Câu 35: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số

( ) :

C y x x

 

và

( ) :

P y x x

 

S 



S 



Câu 36: Tổng các nghiệm của phương trình

2 2 3

log log 9. log 3

x x

 

là

. B.

. C.

. D.



Câu 37: Trong không gian

Oxyz

, cho điểm





3;1;0

và mặt phẳng





: 2 2 1 0

P x y z

   

. Tìm tọa độ điểm

là hình chiếu vuông góc của điểm

trên mặt phẳng









1; 3; 2







1; 1;1







1; 3; 2

 





1;1; 1

 

Câu 38: Diện tích hình phẳng phần tô đậm trong hình vẽ bằng:

y = f(x)

0-2

 

f x dx





   

0 0

2 2

f x dx f x dx





 

   

1 2

2 1

f x dx f x dx





 

   

2 2

0 0

f x dx f x dx





 

Câu 39: Hàm số nào sau đây là một nguyên hàm của

cos2

y x



sin 2

y x

 

2 sin 2

y x

 

sin 2

y x



sin 2

y x



Câu 40: Cho tích phân

 

1 sin 2 .

I x xdx



 



Chọn đẳng thức đúng?

 

1 cos 2 cos2

I x x xdx



   



 

1 cos 2 cos 2

I x x xdx



   



 

1 1

1 cos 2 cos 2

2 2

I x x xdx



   



 

1 cos 2 cos 2

I x x xdx



   



----------- HẾT PHẦN TRẮC NGHIỆM----------

SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM

TRƯỜNG THPT HOÀNG HOA THÁM

ĐỀ CHÍNH THỨC

(Đề gồm 04 trang)

ĐỀ KIỂM TRA HỌC KỲ 2

NĂM HỌC: 2019 – 2020

Môn: TOÁN – Lớp 12

Thời gian làm bài: 90 phút

Mã đề

209

Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.

Họ, tên thí sinh:.......................................................................Số báo danh:...........................................

I. PHẦN TRẮC NGHIỆM (8,0 điểm)

Câu 1: Số nghiệm của phương trình

 

 

x 2 2 x

2 2 15

là

A. 2. B. 3. C.

. D. 0

Câu 2: Tìm họ nguyên hàm của hàm số





f(x)

5x 2

 



 





dx 5

5x 2

  





5ln 5x 2 C

5x 2

  





dx 1

ln 5x 2 C

5x 2 5

  





ln 5x 2 C

5x 2

Câu 3: Tổng phần thực và phần ảo của số phức

thoả mãn





   

iz 1 i z 2i

bằng

. B.

. C.



. D.



Câu 4: Tập nghiệm của bất phương trình

  

2 2

log x 6log x 8 0

là

 

 

2 ; 4

(0 ; 4]

 

 

4 ; 16

(0 ; 16]

Câu 5: Cho số phức

 

z 3 2i

. Tìm phần thực và phần ảo của số phức

A. Phần thực bằng

và phần ảo bằng

. B. Phần thực bằng



và phần ảo bằng



C. Phần thực bằng

và phần ảo bằng

. D. Phần thực bằng

và phần ảo bằng



Câu 6: Trong không gian

Oxyz

, cho điểm





A 3;1;0

. Tìm tọa độ điểm

là hình chiếu vuông góc của điểm

trên trục





H 3;0;0





H 1;0;0





H 0;1;0





H 3;0;1

---------------

-----------------

Câu 7: Trong không gian

Oxyz,

cho

   

 

a (3; 1;2),b (4;2; 6).

Tính tọa độ của vectơ



 

a b

 

 

a b



(7;1; 4).

 

 

a b



(1;3; 8).

 

 

a b

 

( 1; 3;8).

 

 

a b

 

( 7; 1;4).

Câu 8: Trong không gian với hệ toạ độ

Oxyz,

, tính độ dài

biết

là hình chiếu vuông góc của





M 1;2;3

lên mặt phẳng





Oyz .

Câu 9: Trong không gian

Oxyz,

cho





là đường thẳng đi qua điểm





M 1;2;3

và vuông góc với mặt phẳng





   

P : 4x 3y 7z 2 0

. Phương trình tham số của





là



  



  





  



x 1 4t

y 2 3t

z 3 7t

. B.



  



  





  



x 1 4t

y 2 3t

z 3 7t

. C.



 



 





 



x 1 4t

y 2 3t

z 3 7t

. D.



 



 





 



x 1 3t

y 2 4t

z 3 7t

Câu 10: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số

 

và

 

(P) : y x x



S 13

C. 

D. 

Câu 11: Trong không gian

Oxyz,

cho mặt cầu





      

2 2 2

S : x y z 4x 2y 6z 3 0

. Bán kính của mặt cầu





là:

Câu 12: Cho hàm số





f x

liên tục trên



và

 







f x dx 12

. Khi đó

 





f 2cosx sin xdx

bằng



. B.

. C.

. D.

Câu 13: Tìm a sao cho





x.e .dx 4



a 0



a 2



a 1



a 4

Câu 14: Trong không gian với hệ tọa độ Oxyz, cho











M 1;2;3 , N 3;4; 7 .

Mặt phẳng nào sau đây là mặt phẳng

trung trực của đoạn thẳng





   

P : x y 5z 15 0





   

P : 2x 2y 10z 15 0





   

P :2x 2y 10z 15 0





   

P : x y 5z 15 0

Câu 15: Trong không gian

Oxyz

, tìm giá trị của tham số

để đường thẳng



 

 



y 1

x 2 z 1

d :

3 1 2

vuông góc

với mặt phẳng

    

( ) :6x my 4z 5 0



m 26

. B.

 

m 2

. C.



m 2

. D.

 

m 26

Câu 16: Trong không gian

Oxyz,

mặt phẳng

   

x 2y z 1 0

có một véctơ pháp tuyến là





  



n 1;2; 1





  



n 1; 2; 1





 



n 1;2; 1





   



n 1; 2; 1

Câu 17: Biết

 



 

S a;b

là tập nghiệm của bất phương trình

  

x x

3.9 10.3 3 0.

Tìm

 

T b a.



. B.



T 1

. C.



T 2

. D.



Câu 18: Trong không gian

Oxyz,

cho đường thẳng

 



 



 









x 6 5t

d : y 2 t

z 1

và mặt phẳng





  

P : 3x 2y 1 0.

Góc

giữa đường thẳng





và mặt phẳng





bằng

Câu 19: Hàm số







y f x

liên tục trên

 

 

2;9





F x

là một nguyên hàm của hàm số





f x

trên

 

 

2;9

và









 

F 2 5, F 9 4

. Mệnh đề nào sau đây đúng ?

 





f x dx 20

. B.

 





f x dx 1

. C.

 





f x dx 9

. D.

 

 



f x dx 1

Câu 20: Diện tích hình phẳng phần tô đậm trong hình bên bằng:

y = f(x)

0-2

 





f x dx

   





 

0 0

2 2

f x dx f x dx

   





 

1 2

2 1

f x dx f x dx

   





 

2 2

0 0

f x dx f x dx

Câu 21: Nếu





f(x)dx 17

và





f(x)dx 12

thì



f(x)dx

bằng



Câu 22: Tính thể tích của khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn bởi đồ thị hàm

số





 

y x 4 x

với trục hoành.



512

(đvtt) B.



(đvtt) C.

(đvtt) D.

512

(đvtt)

Câu 23: Tính:





ln x

J dx



Câu 24: Gọi

là nghiệm phức có phần ảo âm của phương trình

  

z 2z 5 0

. Tìm tọa độ điểm biểu diễn số

phức



7 4i

trên mặt phẳng phức ?





P 3; 2







Q 3; 2







N 1; 2





M 1; 2

Câu 25: Tập nghiệm của bất phương trình

  

   



   

   

x x 1 2x 1

5 5

7 7

có dạng







S a;b

. Tính

 

A b a

 

A 1



A 2



A 1

 

A 2

Câu 26: Cho số phức

thỏa mãn













    

3 2i z 4 1 i 2 i z

. Mô đun của

bằng

Câu 27: Trong không gian với hệ toạ độ

Oxyz,

cho









A 2;0;2 , B 2;2;0

. Mệnh đề nào sau đây đúng ?



OAB

vuông tại



OAB

đều



OAB

chỉ cân tại



OAB

vuông cân tại

Câu 28: Trong không gian

Oxyz,

cho điểm





 

A 2; 1; 1

và mặt phẳng





   

P :16x 12y 15z 4 0.

Gọi

là

hình chiếu vuông góc của

lên





. Tính độ dài

AH.

A. 55. B.

. C.

. D.

Câu 29: Trong không gian

Oxyz

, tìm giá trị của tham số

để mặt phẳng





   

P : 2x 3y mz 5 0

vuông

góc với mặt phẳng





Oxy

 



. B.



m 5

. C.



m 1

. D.



m 0

Câu 30: Tổng tất cả các nghiệm của phương trình









    

2 2 2

log x 1 log x 1 log 3x 5

bằng

. B.

. C.

. D.

Câu 31: Trong không gian với hệ tọa độ

Oxyz

, mặt phẳng

   

(P) : 2x 2y z 5 0

cắt mặt cầu

     

2 2 2

(S) : (x 2) (y 3) (z 3) 100

theo giao tuyến là đường tròn

(C)

. Tính bán kính

của

(C)



r 8

. B.



r 10

. C.



r 64

. D.



r 16

Câu 32: Tìm kết quả đúng.

 

  



x x

e dx xe C

 

 



x x

e dx e C

 

  



x x

e dx e C

 

 



x x

e dx xe C

Câu 33: Trong mặt phẳng

Oxy,

điểm biểu diễn của số phức

 

z 5 4i

là





5;4

. B.





 

5; 4

. C.







5;4

. D.







5; 4

Câu 34: Nghiệm của phương trình



 

2x 1

2 0

là

 

x 2

. B.



x 1

. C.

 

x 1

. D.



x 2

Câu 35: Tổng các nghiệm của phương trình

 

2 2 3

log x log 9.log x 3

là

. B.

. C.

. D.



Câu 36: Trong không gian

Oxyz

, cho điểm





A 3;1;0

và mặt phẳng





   

P : 2x 2y z 1 0

. Tìm tọa độ điểm

là hình chiếu vuông góc của điểm

trên mặt phẳng











H 1;3; 2







H 1; 1;1





 

H 1; 3;2





 

H 1;1; 1

Câu 37: Nghiệm của bất phương trình





   

log x 2x 8 4

là



 







x 6

x 4

. B.



   



 



6 x 4

2 x 4

. C.



 







x 6

x 4

. D.



   



 



6 x 4

2 x 4

Câu 38: Cho tích phân

 



 



I x 1 sin2xdx.

Chọn đẳng thức đúng?

 



   



I x 1 cos2x cos2xdx

 



   



1 1

I x 1 cos2x cos2xdx

2 2

 



   



I x 1 cos2x cos2xdx

 



   



I x 1 cos2x cos2xdx

Câu 39: Trong không gian

Oxyz,

mặt cầu tâm







I 2; 1; 3

và tiếp xúc với mp





Oxy

có phương trình là













     

2 2 2

x 2 y 1 z 3 9













     

2 2 2

x 2 y 1 z 3 4













     

2 2 2

x 2 y 1 z 3 1













     

2 2 2

x 2 y 1 z 3 9

Câu 40: Hàm số nào sau đây là một nguyên hàm của



y cos 2x

 

y 2sin2x



y sin2x

 

y sin 2x



y sin2x

-----------------------------------------------

----------- HẾT PHẦN TRẮC NGHIỆM----------

SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM

TRƯỜNG THPT HOÀNG HOA THÁM

ĐỀ CHÍNH THỨC

(Đề gồm 04 trang)

ĐỀ KIỂM TRA HỌC KỲ 2

NĂM HỌC: 2019 – 2020

Môn: TOÁN – Lớp 12

Thời gian làm bài: 90 phút

Mã đề

357

Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.

Họ, tên thí sinh:.......................................................................Số báo danh:...........................................

I. PHẦN TRẮC NGHIỆM (8,0 điểm)

Câu 1: Gọi

là nghiệm phức có phần ảo âm của phương trình

  

z 2z 5 0

. Tìm tọa độ điểm biểu diễn số

phức



7 4i

trên mặt phẳng phức ?







N 1; 2







Q 3; 2





M 1; 2





P 3; 2

Câu 2: Tập nghiệm của bất phương trình

  

   



   

   

x x 1 2x 1

5 5

7 7

có dạng







S a; b

. Tính

 

A b a



A 2

 

A 2

 

A 1



A 1

Câu 3: Trong không gian

Oxyz

, cho điểm





A 3;1;0

và mặt phẳng





   

P : 2x 2y z 1 0

. Tìm tọa độ điểm

là hình chiếu vuông góc của điểm

trên mặt phẳng











H 1;3; 2







H 1; 1;1





 

H 1; 3;2





 

H 1;1; 1

Câu 4: Trong không gian

Oxyz,

cho





là đường thẳng đi qua điểm





M 1;2;3

và vuông góc với mặt phẳng





   

P : 4x 3y 7z 2 0

. Phương trình tham số của





là



 



 





 



x 1 4t

y 2 3t

z 3 7t

. B.



  



  





  



x 1 4t

y 2 3t

z 3 7t

. C.



  



  





  



x 1 4t

y 2 3t

z 3 7t

. D.



 



 





 



x 1 3t

y 2 4t

z 3 7t

Câu 5: Tính thể tích của khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn bởi đồ thị hàm

số





 

y x 4 x

với trục hoành.



512

(đvtt) B.



(đvtt) C.

(đvtt) D.

512

(đvtt)

Câu 6: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số

 

và

 

(P) : y x x



S 13



Câu 7: Trong không gian với hệ toạ độ

Oxyz,

, tính độ dài

biết

là hình chiếu vuông góc của





M 1;2;3

lên mặt phẳng





Oyz .

Câu 8: Tìm a sao cho





x.e .dx 4



a 0



a 2



a 1



a 4

Câu 9: Tìm kết quả đúng.

 

 



x x

e dx e C

 

  



x x

e dx e C

 

 



x x

e dx xe C

 

  



x x

e dx xe C

Câu 10: Cho hàm số





f x

liên tục trên



và

 







f x dx 12

. Khi đó

 





f 2cosx sinxdx

bằng

. B.



. C.

. D.

Câu 11: Tính:





ln x

J dx



Câu 12: Trong không gian

Oxyz

, tìm giá trị của tham số

để đường thẳng



 

 



y 1

x 2 z 1

d :

3 1 2

vuông góc

với mặt phẳng

    

( ) : 6x my 4z 5 0



m 26

. B.

 

m 2

. C.



m 2

. D.

 

m 26

Câu 13: Trong không gian với hệ tọa độ Oxyz, cho











M 1;2;3 , N 3;4; 7 .

Mặt phẳng nào sau đây là mặt phẳng

trung trực của đoạn thẳng





   

P : x y 5z 15 0





   

P : 2x 2y 10z 15 0





   

P : x y 5z 15 0





   

P :2x 2y 10z 15 0

Câu 14: Hàm số nào sau đây là một nguyên hàm của



y cos 2x



y sin2x

 

y sin 2x

 

y 2sin2x



y sin2x

Câu 15: Trong không gian

Oxyz,

cho

   

 

a (3; 1;2),b (4;2; 6).

Tính tọa độ của vectơ



 

a b

 

 

a b



(7;1; 4).

 

 

a b

 

( 1; 3;8).

 

 

a b



(1;3; 8).

 

 

a b

 

( 7; 1;4).

Câu 16: Trong không gian

Oxyz,

mặt cầu tâm







I 2; 1; 3

và tiếp xúc với mp





Oxy

có phương trình là













     

2 2 2

x 2 y 1 z 3 9













     

2 2 2

x 2 y 1 z 3 4













     

2 2 2

x 2 y 1 z 3 1













     

2 2 2

x 2 y 1 z 3 9

Câu 17: Diện tích hình phẳng phần tô đậm trong hình bên bằng:

y = f(x)

0-2

 





f x dx

   





 

1 2

2 1

f x dx f x dx

   





 

0 0

2 2

f x dx f x dx

   





 

2 2

0 0

f x dx f x dx

Câu 18: Hàm số







y f x

liên tục trên

 

 

2;9





F x

là một nguyên hàm của hàm số





f x

trên

 

 

2;9

và









 

F 2 5, F 9 4

. Mệnh đề nào sau đây đúng ?

 





f x dx 1

. B.

 





f x dx 9

. C.

 

 



f x dx 1

. D.

 





f x dx 20

Câu 19: Nếu





f(x)dx 17

và





f(x)dx 12

thì



f(x)dx

bằng



Câu 20: Cho số phức

thỏa mãn













    

3 2i z 4 1 i 2 i z

. Mô đun của

bằng

Câu 21: Cho số phức

 

z 3 2i

. Tìm phần thực và phần ảo của số phức

A. Phần thực bằng

và phần ảo bằng

. B. Phần thực bằng



và phần ảo bằng



C. Phần thực bằng

và phần ảo bằng

. D. Phần thực bằng

và phần ảo bằng



Câu 22: Nghiệm của phương trình



 

2x 1

2 0

là

 

x 2

. B.



x 2

. C.

 

x 1

. D.



x 1

Câu 23: Trong không gian

Oxyz

, cho điểm





A 3;1;0

. Tìm tọa độ điểm

là hình chiếu vuông góc của điểm

trên trục





H 1;0;0





H 3;0;0





H 3;0;1

-----------------D.





H 0;1;0

Câu 24: Số nghiệm của phương trình

 

 

x 2 2 x

2 2 15

là

A. 3. B. 2. C.

. D. 0

Câu 25: Trong không gian

Oxyz

, tìm giá trị của tham số

để mặt phẳng





   

P : 2x 3y mz 5 0

vuông

góc với mặt phẳng





Oxy



m 0

. B.



m 1

. C.

 



. D.



m 5

Câu 26: Tìm họ nguyên hàm của hàm số





f(x)

5x 2

  





dx 1

ln 5x 2 C

5x 2 5

  





ln 5x 2 C

5x 2

 



 





dx 5

5x 2

  





5ln 5x 2 C

5x 2

Câu 27: Trong không gian

Oxyz,

cho điểm





 

A 2; 1; 1

và mặt phẳng





   

P :16x 12y 15z 4 0.

Gọi

là

hình chiếu vuông góc của

lên





. Tính độ dài

AH.

A. 55. B.

. C.

. D.

Câu 28: Tập nghiệm của bất phương trình

  

2 2

log x 6log x 8 0

là

(0 ; 16]

 

 

2 ; 4

 

 

4 ; 16

(0 ; 4]

Câu 29: Tổng tất cả các nghiệm của phương trình









    

2 2 2

log x 1 log x 1 log 3x 5

bằng

. B.

. C.

. D.

Câu 30: Trong không gian với hệ tọa độ

Oxyz

, mặt phẳng

   

(P) : 2x 2y z 5 0

cắt mặt cầu

     

2 2 2

(S) :(x 2) (y 3) (z 3) 100

theo giao tuyến là đường tròn

(C)

. Tính bán kính

của

(C)



r 8

. B.



r 10

. C.



r 64

. D.



r 16

Câu 31: Biết

 



 

S a;b

là tập nghiệm của bất phương trình

  

x x

3.9 10.3 3 0.

Tìm

 

T b a.



. B.



T 1

. C.



. D.



T 2

Câu 32: Trong không gian

Oxyz,

mặt phẳng

   

x 2y z 1 0

có một véctơ pháp tuyến là





  



n 1; 2; 1





  



n 1;2; 1





 



n 1;2; 1





   



n 1; 2; 1

Câu 33: Trong không gian

Oxyz,

cho đường thẳng

 



 



 









x 6 5t

d : y 2 t

z 1

và mặt phẳng





  

P : 3x 2y 1 0.

Góc

giữa đường thẳng





và mặt phẳng





bằng

Câu 34: Tổng các nghiệm của phương trình

 

2 2 3

log x log 9.log x 3

là

. B.

. C.

. D.



Câu 35: Tổng phần thực và phần ảo của số phức

thoả mãn





   

iz 1 i z 2i

bằng

. B.



. C.

. D.



Câu 36: Trong mặt phẳng

Oxy,

điểm biểu diễn của số phức

 

z 5 4i

là





5;4

. B.







5;4

. C.





 

5; 4

. D.







5; 4

Câu 37: Cho tích phân

 



 



I x 1 sin2xdx.

Chọn đẳng thức đúng?

 



   



I x 1 cos2x cos2xdx

 



   



1 1

I x 1 cos2x cos2xdx

2 2

 



   



I x 1 cos2x cos2xdx

 



   



I x 1 cos2x cos2xdx

Câu 38: Trong không gian

Oxyz,

cho mặt cầu





      

2 2 2

S : x y z 4x 2y 6z 3 0

. Bán kính của mặt cầu





là:

Câu 39: Nghiệm của bất phương trình





   

log x 2x 8 4

là



 







x 6

x 4

. B.



   



 



6 x 4

2 x 4

. C.



 







x 6

x 4

. D.



   



 



6 x 4

2 x 4

Câu 40: Trong không gian với hệ toạ độ

Oxyz,

cho









A 2;0;2 , B 2;2;0

. Mệnh đề nào sau đây đúng ?



OAB

vuông tại



OAB

đều



OAB

chỉ cân tại



OAB

vuông cân tại

-----------------------------------------------

----------- HẾT PHẦN TRẮC NGHIỆM----------

SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM

TRƯỜNG THPT HOÀNG HOA THÁM

ĐỀ CHÍNH THỨC

(Đề gồm 04 trang)

ĐỀ KIỂM TRA HỌC KỲ 2

NĂM HỌC: 2019 – 2020

Môn: TOÁN – Lớp 12

Thời gian làm bài: 90 phút

Mã đề

485

Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.

Họ, tên thí sinh:.......................................................................Số báo danh:...........................................

I. PHẦN TRẮC NGHIỆM (8,0 điểm)

Câu 1: Tính:

J dx







Câu 2: Trong không gian

Oxyz

cho điểm





2; 1; 1

 

và mặt phẳng





: 16 12 15 4 0.

P x y z

   

Gọi

là

hình chiếu vuông góc của

lên





. Tính độ dài

A. 55. B.

. C.

. D.

Câu 3: Tính thể tích của khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn bởi đồ thị hàm

số





y x x

 

với trục hoành.

512



(đvtt) B.



(đvtt) C.

(đvtt) D.

512

(đvtt)

Câu 4: Nghiệm của phương trình

2 1

2 0

x 

 

là

 

. B.

 

. C.



. D.



Câu 5: Tổng phần thực và phần ảo của số phức

thoả mãn





1 2

iz i z i

   

bằng

. B.



. C.



. D.

Câu 6: Cho hàm số





f x

liên tục trên



và

 

f x dx







. Khi đó

 

2 cos sin

f x xdx





bằng

. B.

. C.

. D.



Câu 7: Hàm số





y f x



liên tục trên

2; 9

 

 

 





F x

là một nguyên hàm của hàm số





f x

trên

2; 9

 

 

 

và









2 5, 9 4

F F

 

. Mệnh đề nào sau đây đúng ?

 

f x dx





. B.

 

f x dx 



. C.

 

f x dx





. D.

 

f x dx

 



Câu 8: Nếu

( ) 17

f x dx 



và

( ) 12

f x dx 



thì

( )

f x dx



bằng



Câu 9: Trong không gian với hệ tọa độ

Oxyz

, mặt phẳng

( ) : 2 2 5 0

P x y z

   

cắt mặt cầu

2 2 2

( ) : ( 2) ( 3) ( 3) 100

S x y z

     

theo giao tuyến là đường tròn

( )

. Tính bán kính

của

( )



. B.



. C.



. D.



Câu 10: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số

( ) :

C y x x

 

và

( ) :

P y x x

 



S 

Câu 11: Trong không gian

Oxyz

, tìm giá trị của tham số

để đường thẳng

2 1 1

3 1 2

x y z

  

 



vuông

góc với mặt phẳng

( ) : 6 4 5 0

x my z



   

 

. B.



. C.



. D.

 

Câu 12: Gọi

là nghiệm phức có phần ảo âm của phương trình

2 5 0

z z

  

. Tìm tọa độ điểm biểu diễn số

phức

7 4



trên mặt phẳng phức ?





3; 2







3; 2





1; 2







1; 2

Câu 13: Tìm a sao cho

. . 4

x e dx







Câu 14: Biết

;

S a b

 



 

 

là tập nghiệm của bất phương trình

3.9 10.3 3 0.

x x

  

Tìm

T b a

 



. B.



. C.



. D.

T 

Câu 15: Trong không gian

Oxyz

mặt cầu tâm





2; 1; 3



và tiếp xúc với mp





Oxy

có phương trình là













2 2 2

2 1 3 9

x y z

     













2 2 2

2 1 3 4

x y z

     













2 2 2

2 1 3 1

x y z

     













2 2 2

2 1 3 9

x y z

     

Câu 16: Diện tích hình phẳng phần tô đậm trong hình bên bằng:

y = f(x)

0-2

 

f x dx





   

1 2

2 1

f x dx f x dx





 

   

0 0

2 2

f x dx f x dx





 

   

2 2

0 0

f x dx f x dx





 

Câu 17: Trong không gian

Oxyz

cho đường thẳng

 

6 5

: 2

x t

d y t





 



 











và mặt phẳng





: 3 2 1 0.

P x y

  

Góc

giữa đường thẳng





và mặt phẳng





bằng

Câu 18: Tập nghiệm của bất phương trình

2 2

log 6 log 8 0

x x

  

là

(0 ; 4]

(0 ; 16]

2 ; 4

 

 

 

4 ; 16

 

 

 

Câu 19: Cho số phức

thỏa mãn













3 2 4 1 2

i z i i z

    

. Mô đun của

bằng

Câu 20: Trong không gian

Oxyz

, tìm giá trị của tham số

để mặt phẳng





: 2 3 5 0

P x y mz

   

vuông

góc với mặt phẳng





Oxy



. B.

 



. C.



. D.



Câu 21: Trong không gian

Oxyz

cho

(3; 1;2), (4;2; 6).

a b   

 

Tính tọa độ của vectơ

a b



 

a b

 

 

( 7; 1; 4).

 

a b

 

 

(1; 3; 8).



a b

 

 

( 1; 3; 8).

 

a b

 

 

(7;1; 4).



Câu 22: Trong không gian

Oxyz

, cho điểm





3;1;0

. Tìm tọa độ điểm

là hình chiếu vuông góc của điểm

trên trục





1; 0; 0





3; 0;1

-----------------C.





3;0; 0





0;1; 0

Câu 23: Cho tích phân

 

1 sin 2 .

I x xdx



 



Chọn đẳng thức đúng?

 

1 cos 2 cos 2

I x x xdx



   



 

1 1

1 cos 2 cos 2

2 2

I x x xdx



   



 

1 cos 2 cos 2

I x x xdx



   



 

1 cos 2 cos 2

I x x xdx



   



Câu 24: Trong không gian

Oxyz

mặt phẳng

2 1 0

x y z

   

có một véctơ pháp tuyến là





1;2; 1

  







1; 2; 1

  







1; 2; 1

   







1;2; 1

 



Câu 25: Nghiệm của bất phương trình





log 2 8 4

x x

   

là

6 4

2 4



   



 





. B.



 









. C.

6 4

2 4



   



 





. D.



 









Câu 26: Tập nghiệm của bất phương trình

1 2x 1

5 5

7 7

x x

  

   

 

 

 



 

 

 

 

 

   

có dạng





;

S a b



. Tính

A b a

 



 

Câu 27: Trong không gian với hệ toạ độ

Oxyz

cho









2; 0;2 , 2;2; 0

A B

. Mệnh đề nào sau đây đúng ?

OAB



vuông tại

OAB



đều

OAB



chỉ cân tại

OAB



vuông cân tại

Câu 28: Trong không gian

Oxyz

, cho điểm





3;1;0

và mặt phẳng





: 2 2 1 0

P x y z

   

. Tìm tọa độ điểm

là hình chiếu vuông góc của điểm

trên mặt phẳng









1;1; 1

 





1; 1;1







1; 3; 2







1; 3; 2

 

Câu 29: Số nghiệm của phương trình

2 2

2 2 15

x x 

 

là

. B. 0 C. 2. D. 3.

Câu 30: Tìm họ nguyên hàm của hàm số

( )

5 2

f x





ln 5 2

5 2

x C

  









5 2



 





ln 5 2

5 2 5

x C

  





5 ln 5 2

5 2

x C

  





Câu 31: Tìm kết quả đúng.

x x

e dx xe C

 

 



x x

e dx xe C

 

  



x x

e dx e C

 

 



x x

e dx e C

 

  



Câu 32: Trong không gian với hệ toạ độ

Oxyz

, tính độ dài

biết

là hình chiếu vuông góc của





1;2; 3

lên mặt phẳng





Oyz

Câu 33: Tổng các nghiệm của phương trình

2 2 3

log log 9. log 3

x x

 

là

. B.

. C.

. D.



Câu 34: Trong không gian với hệ tọa độ Oxyz, cho









1;2; 3 , 3; 4; 7 .

M N



Mặt phẳng nào sau đây là mặt

phẳng trung trực của đoạn thẳng





: 5 15 0

P x y z

   





: 2 2 10 15 0

P x y z

   





: 5 15 0

P x y z

   





: 2 2 10 15 0

P x y z

   

Câu 35: Trong mặt phẳng

Oxy

điểm biểu diễn của số phức

5 4

z i

 

là





5; 4

. B.





5;4



. C.





5; 4

 

. D.





5; 4



Câu 36: Tổng tất cả các nghiệm của phương trình









2 2 2

log 1 log 1 log 3 5

x x x

    

bằng

. B.

. C.

. D.

Câu 37: Hàm số nào sau đây là một nguyên hàm của

cos2

y x



sin 2

y x



2 sin 2

y x

 

sin 2

y x

 

sin 2

y x



Câu 38: Cho số phức

3 2

z i

 

. Tìm phần thực và phần ảo của số phức

A. Phần thực bằng

và phần ảo bằng



. B. Phần thực bằng

và phần ảo bằng

C. Phần thực bằng

và phần ảo bằng

. D. Phần thực bằng



và phần ảo bằng



Câu 39: Trong không gian

Oxyz

cho mặt cầu





2 2 2

: 4 2 6z 3 0

S x y z x y

      

. Bán kính của mặt cầu





là:

Câu 40: Trong không gian

Oxyz

cho





là đường thẳng đi qua điểm





1;2; 3

và vuông góc với mặt phẳng





: 4 3 7 2 0

P x y z

   

. Phương trình tham số của





là

1 4

2 3

3 7

x t

y t

z t





  



  





  





. B.

1 4

2 3

3 7

x t

y t

z t





 



 





 





. C.

1 3

2 4

3 7

x t

y t

z t





 



 





 





. D.

1 4

2 3

3 7

x t

y t

z t





  



  





  





----------- HẾT PHẦN TRẮC NGHIỆM------------

KIỂM TRA HỌC KỲ 2

NĂM HỌC: 2019 – 2020

Môn Toán – Lớp 12

II. PHẦN TỰ LUẬN (2,0 điểm – Thời gian làm bài: 18 phút)

Câu 1 (1,0 điểm). Tính tích phân

 







sin

1 2 cos

I dx



Câu 2 (1,0 điểm). Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm





 

2; 3; 1

 

(1; 2; 3)

Viết phương trình mặt phẳng trung trực của đoạn thẳng

----HẾT----

ĐÁP ÁN TOÁN 12 – HK2

MÃ ĐỀ : 132

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

A B C B D D A D D A B C D B D B C D A D

21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

D A A C A A C C B D B C C A A B B B C C

MÃ ĐỀ : 209

A C A C A A A D C D D D B D B C C A D B

21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

MÃ ĐỀ : 357

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

A C B B A A B C D A D C D C C D B D A B

MÃ ĐỀ : 485

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

D C B D B B B B C C D D C A D A D C D B

TỰ LUẬN

Câu Nộ dung Điểm

Tính tích phân

 







sin

1 2 cos

I dx



ặt

    

1 2 cos 2 sin .

t x dt xdx

0.2

Đổi cận:



  







  



0 3

x t



0.2

   



1 1 1 1

2 2 3

0.2x3

Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm





 

2; 3; 1

 

(1; 2; 3)

Viết phương trình mặt phẳng





là mặt trung trực của đoạn thẳng

là trung điểm

 

  

 

 

1 1

; ; 2

2 2

AB M

0.2

 









    





 

3; 5; 2

Qua M

vtpt n AB

0.2





  

: 3 5 2 0.

ptmp P x y z

0.4

Bấm Tải xuống để xem toàn bộ.

| 1/19

| | Tải xuống

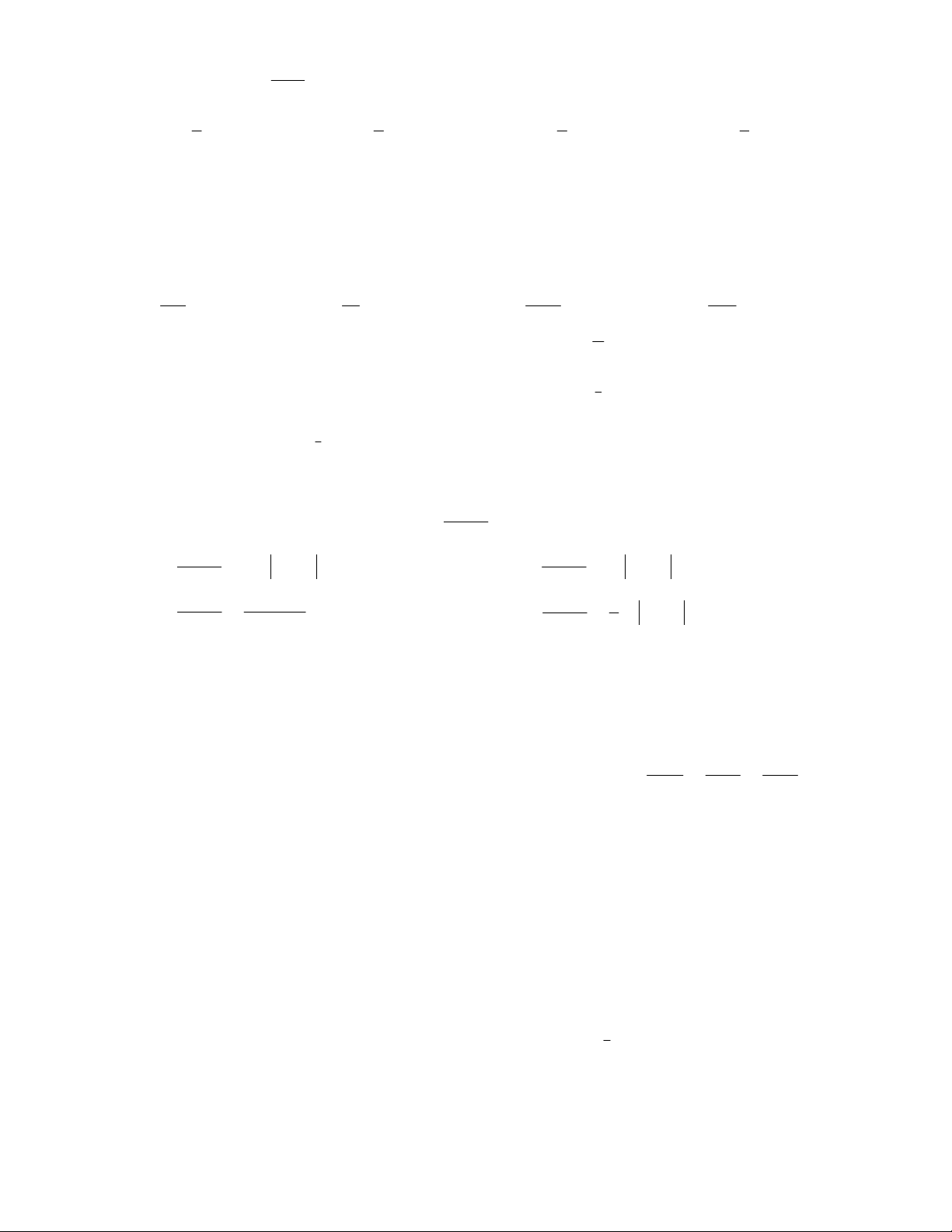
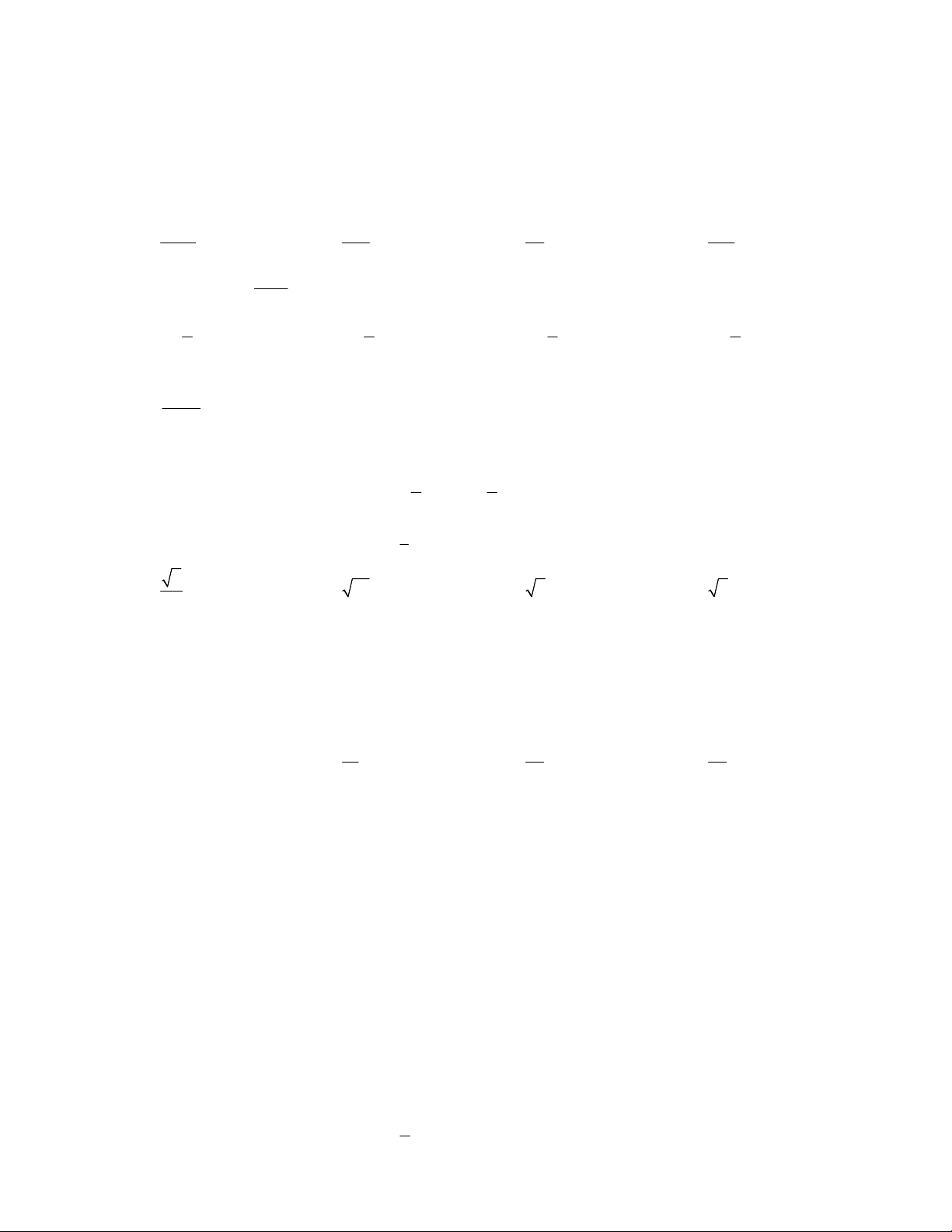
Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM ĐỀ KIỂM TRA HỌC KỲ 2
TRƯỜNG THPT HOÀNG HOA THÁM NĂM HỌC: 2019 – 2020 Môn: TOÁN – Lớp 12 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút (Đề gồm 04 trang) Mã đề 132
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ, tên thí sinh:.......................................................................Số báo danh:...........................................
I. PHẦN TRẮC NGHIỆM (8,0 điểm)
Câu 1: Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z  2z  5  0 . Tìm tọa độ điểm biểu diễn số 1 7  4i phức trên mặt phẳng phức ? z1 A. P 3;  2 B. Q 3;2 C. N 1;   2 D. M 1; 2    
Câu 2: Trong không gian Oxyz, cho a  (3;1;2),b  (4;2;6). Tính tọa độ của vectơ a b     A. a  b  (1;3;8). B. a b  (7;1;4).    
C. a  b  (1;3; 8). D. a  b  (7;1;4).
Câu 3: Tổng phần thực và phần ảo của số phức z thoả mãn iz  1iz  2  i bằng A. 2 . B. 2 . C. 6 . D. 6 .
Câu 4: Trong không gian với hệ toạ độ Oxyz, cho A2;0;2, B 2;2;0. Mệnh đề nào sau đây đúng ? A. OAB vuông tại O B. OAB đều
C. OAB vuông cân tại O D. OAB chỉ cân tại O
Câu 5: Hàm số y  f x liên tục trên 2;9 F x là một nguyên hàm của hàm số f x trên 2;9   .     và
F 2  5, F 9  4. Mệnh đề nào sau đây đúng ? 9 9 9 9 A. f  xdx  20. B. f  xdx  9. C. f  xdx  1. D. f  xdx  1. 2 2 2 2
Câu 6: Trong không gian với hệ tọa độ Oxyz, cho M 1;2;3, N 3;4;7. Mặt phẳng nào sau đây là mặt phẳng
trung trực của đoạn thẳng MN .
A. P : x y  5z 15  0
B. P : 2x  2y 10z 15  0
C. P : 2x  2y 10z 15  0
D. P : x  y  5z 15  0
Câu 7: Trong không gian Oxyz , cho điểm A3;1; 
0 . Tìm tọa độ điểm H là hình chiếu vuông góc của điểm A trên trục Ox . A. H 3;0;0. B. H 1;0;  0 . C. H 0;1;  0 . D. H 3;0;  1 .
Câu 8: Nghiệm của bất phương trình log  2 x  2x  8  4 là 1  2  6   x  4 x  6   6   x  4 x  6  A.  . B.  . C.  . D.  . 2  x  4      x  4  2  x  4  x  4 
Câu 9: Trong không gian với hệ toạ độ Oxyz, , tính độ dài OH biết H là hình chiếu vuông góc của M 1;2;3 lên mặt phẳng Oyz. A. 10 B. 5 C. 14 D. 13 e 2 ln x Câu 10: Tính: J  dx  x 1 1 1 3 1 A. J  B. J  C. J  D. J  3 4 2 2
Câu 11: Trong không gian Oxyz , tìm giá trị của tham số m để mặt phẳng P : 2x  3y  mz  5  0 vuông
góc với mặt phẳng Oxy. A. m   . B. m  0 . C. m  1 . D. m  5 .
Câu 12: Tính thể tích của khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn bởi đồ thị hàm
số y  x 4  x với trục hoành. 512 32 512 32 A. (đvtt) B. (đvtt) C. (đvtt) D. (đvtt) 15 3 15 3 2 1 3
Câu 13: Cho hàm số f x liên tục trên  và f
 xdx  12 . Khi đó f  2cosxsinxdx bằng 1 3 A. 6 . B. 12 . C. 24 . D. 6 . a x Câu 14: Tìm a sao cho 2 x.e .dx  4  . 0 A. a  0 B. a  2 C. a  1 D. a  4 1
Câu 15: Tìm họ nguyên hàm của hàm số f (x)  5x  2 dx dx A.  5 ln 5x  2 C  B.  ln 5x  2 C 5x  2  5x  2 dx 5 dx 1 C.  C  D.  ln 5x  2 C 5x  2   5x  2 2 5x  2 5
Câu 16: Trong không gian Oxyz, mặt cầu tâm I 2;1;3 và tiếp xúc với mpOxy có phương trình là 2 2 2 2 2 2
A. x  2  y   1  z  3  9
B. x 2  y   1  z  3  9 2 2 2 2 2 2
C. x 2  y   1  z  3  4
D. x 2  y   1  z  3  1 x  2 y 1 z  1
Câu 17: Trong không gian Oxyz , tìm giá trị của tham số m để đường thẳng d :   vuông 3 1 2
góc với mặt phẳng () : 6x  my  4z  5  0 . A. m  26 . B. m  2 . C. m  2 . D. m  26 .
Câu 18: Tập nghiệm của bất phương trình 2
log x  6 log x  8  0 là 2 2 A. (0 ; 4] B. (0 ; 16] C. 2  ; 4      D. 4 ; 16   x   65t 
Câu 19: Trong không gian Oxyz, 
cho đường thẳng d : y   2  t 
và mặt phẳng P : 3x 2y 1  0. Góc z   1 
giữa đường thẳng d và mặt phẳng P bằng A. 0 45 B. 0 30 C. 0 60 D. 0 90
Câu 20: Cho số phức z  3  2i . Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng 3 và phần ảo bằng2i .
B. Phần thực bằng 3 và phần ảo bằng 2 .
C. Phần thực bằng 3 và phần ảo bằng 2i .
D. Phần thực bằng 3 và phần ảo bằng 2 .
Câu 21: Trong mặt phẳng Ox ,
y điểm biểu diễn của số phức z  5  4i là A. 5;4. B. 5;4. C. 5;4. D. 5; 4  .
Câu 22: Cho số phức z thỏa mãn 3 2iz  41i  2  iz . Mô đun của z bằng 3 A. 10 B. C. 3 D. 5 4 10 8 10 Câu 23: Nếu f(x)dx  17  và f(x)dx  12  thì f(x)dx  bằng 0 0 8 A. 5 B. 15 C. 29 D. 5 2 x x  1  2x 1 5   5     
Câu 24: Tập nghiệm của bất phương trình          
có dạng S  a;b. Tính A  b a 7   7 A. A  1 B. A  2 C. A  1 D. A  2
Câu 25: Số nghiệm của phương trình x2 2 2 2 x   15 là A. 2. B. 1 . C. 0 D. 3.
Câu 26: Nghiệm của phương trình 2x 1  1 2   0 là 8 A. x  1  . B. x  2 . C. x  2 . D. x  1 .
Câu 27: Trong không gian Oxyz, mặt phẳng x  2y  z  1  0 có một véctơ pháp tuyến là     A. n  1;2;  1 B. n  1;2;  1 C. n  1;2;  1 D. n  1;2;  1 Câu 28: Biết S a;b   x x
  là tập nghiệm của bất phương trình 3.9 10.3  3  0. Tìm T  b a. 10 8 A. T  . B. T  1. C. T  2 . D. T  . 3 3
Câu 29: Trong không gian Oxyz, cho điểm A2;1; 
1 và mặt phẳng P: 16x 12y 15z  4  0. Gọi H
là hình chiếu vuông góc của A lên P. Tính độ dài AH. 11 11 22 A. 55. B. . C. . D. . 5 25 5
Câu 30: Trong không gian Oxyz, cho mặt cầu S 2 2 2
: x  y  z  4x  2y  6z  3  0 . Bán kính của mặt cầu S là: A. 3 B. 14 C. 11 D. 17
Câu 31: Tổng tất cả các nghiệm của phương trình log x 1  log x  1  log 3x  5 bằng 2   2 2   A. 5 . B. 7 . C. 6 . D. 4 .
Câu 32: Trong không gian với hệ tọa độ Oxyz , mặt phẳng (P) : 2x  2y  z  5  0 cắt mặt cầu 2 2 2
(S) : (x  2)  (y  3)  (z  3)  100 theo giao tuyến là đường tròn (C). Tính bán kính r của (C). A. r  10 . B. r  16 . C. r  8 . D. r  64 .
Câu 33: Tìm kết quả đúng. A. x  x e dx xe   C  B. x  x e dx e  C  C. x  x e dx e   C  D. x  x e dx xe  C 
Câu 34: Trong không gian Oxyz, cho d là đường thẳng đi qua điểm M 1;2; 
3 và vuông góc với mặt phẳng
P: 4x  3y 7z 2  0. Phương trình tham số của d là x   1 4t     x   1  4t  x   1  3t  x   1  4t  A. y   2  3t     . B. y   2  3t  . C. y   2  4t  . D. y   2  3t  . z   37t     z   3  7t  z   3  7t  z   3  7t 
Câu 35: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 (C) : y  x  x và 2 (P) : y  x  x 37 9 81 A. S  B. S  C. S  D. S  13 12 4 12
Câu 36: Tổng các nghiệm của phương trình 2
log x  log 9.log x  3 là 2 2 3 17 A. 8 . B. . C. 2 . D. 2 . 2
Câu 37: Trong không gian Oxyz , cho điểm A3;1;0 và mặt phẳng P : 2x  2y  z 1  0 . Tìm tọa độ điểm
H là hình chiếu vuông góc của điểm A trên mặt phẳng P. A. H 1;3;2 B. H 1;1;  1 C. H 1;3;2 D. H 1;1;  1
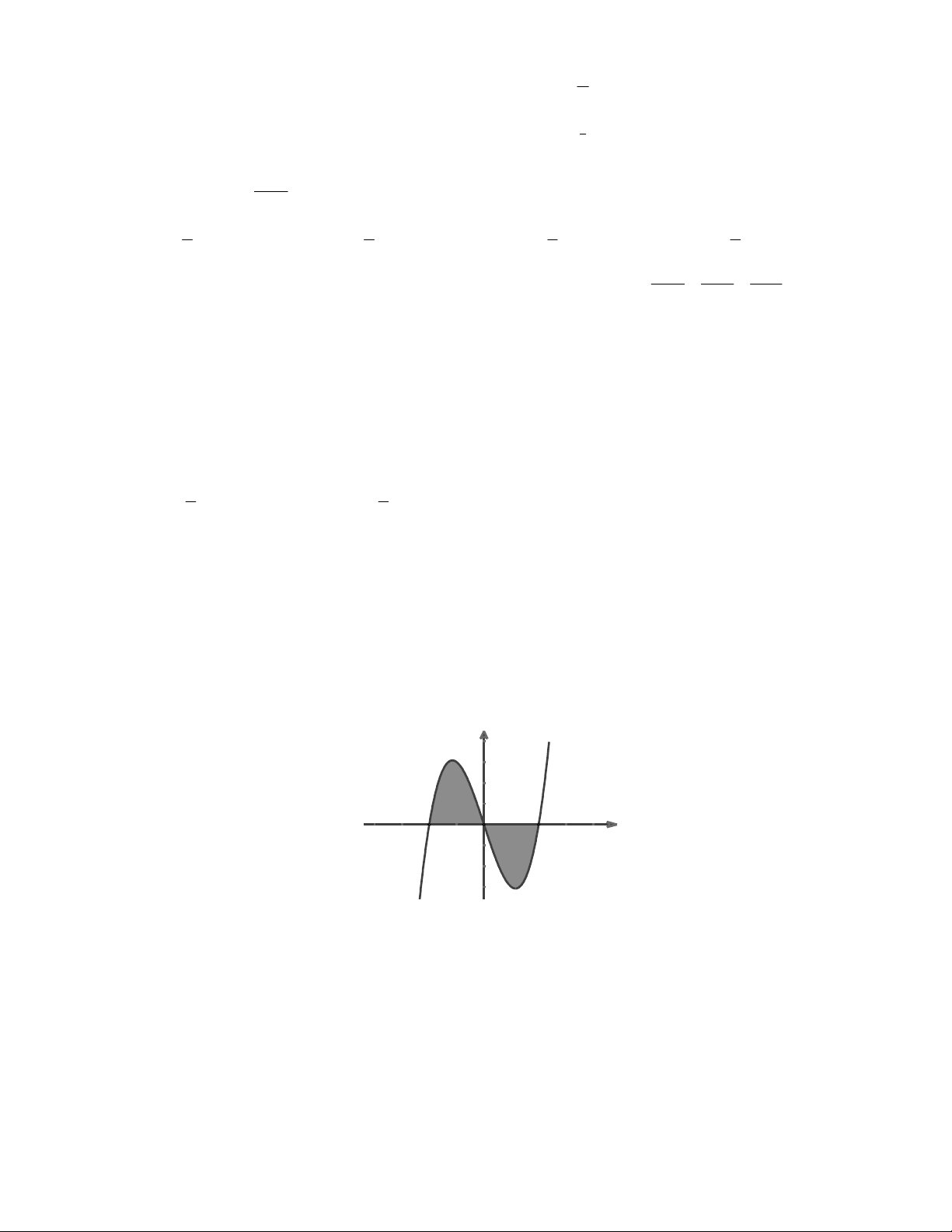
Câu 38: Diện tích hình phẳng phần tô đậm trong hình vẽ bằng: y y = f(x) -2 0 2 x 2 0 0 A. f  xdx B. f  xdx  f  xdx 2 2 2 1 2 2 2 C. f  xdx  f  xdx D. f  xdx  f  xdx 2 1 0 0
Câu 39: Hàm số nào sau đây là một nguyên hàm của y  cos 2x ? 1 1 A. y   sin 2x B. y  2  sin2x C. y  sin 2x D. y  sin 2x 2 2  4
Câu 40: Cho tích phân I  x  
1sin2xdx. Chọn đẳng thức đúng? 0    1 A. I  x   4 1 cos2x  cos2xdx  B. I   x   4 4 1 cos 2x  cos2xdx 2  0 0 0    1 1  C. I   x   4 4 1 cos 2x  cos2xdx
I   x 1 cos2x  cos2xdx 2 2  D.   4 4  0 0 0 0
----------- HẾT PHẦN TRẮC NGHIỆM----------
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM ĐỀ KIỂM TRA HỌC KỲ 2
TRƯỜNG THPT HOÀNG HOA THÁM NĂM HỌC: 2019 – 2020 Môn: TOÁN – Lớp 12 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút (Đề gồm 04 trang) Mã đề 209
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ, tên thí sinh:.......................................................................Số báo danh:...........................................
I. PHẦN TRẮC NGHIỆM (8,0 điểm)
Câu 1: Số nghiệm của phương trình x2 2  x 2 2  15 là A. 2. B. 3. C. 1. D. 0 1
Câu 2: Tìm họ nguyên hàm của hàm số f(x)  5x  2 dx 5 A.    C B.    5x  dx 5ln 5x 2 C  2 5x  22 5x  2 C.     dx 1 ln 5x 2 C D.    5x  dx ln 5x 2 C  2 5 5x  2
Câu 3: Tổng phần thực và phần ảo của số phức z thoả mãn iz  1  iz  2i bằng A. 6 . B. 2 . C. 2 . D. 6 .
Câu 4: Tập nghiệm của bất phương trình 2
log x  6log x  8  0 là 2 2 A. 2 ; 4   B. (0 ; 4] C. 4 ; 16   D. (0 ; 16]
Câu 5: Cho số phức z  3  2i . Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng 3 và phần ảo bằng 2 .
B. Phần thực bằng 3 và phần ảo bằng 2i .
C. Phần thực bằng 3 và phần ảo bằng 2i .
D. Phần thực bằng 3 và phần ảo bằng 2 .
Câu 6: Trong không gian Oxyz , cho điểm A3;1;0 . Tìm tọa độ điểm H là hình chiếu vuông góc của điểm A trên trục Ox . A. H3;0;0 B. H1;0;0 C. H0;1;0
D. H3;0;1 --------------- -----------------    
Câu 7: Trong không gian Oxyz, cho a  (3;1;2),b  (4;2;6). Tính tọa độ của vectơ a  b     A. a  b  (7;1; 4). B. a  b  (1; 3;8).    
C. a  b  (1; 3;8).
D. a  b  (7; 1;4).
Câu 8: Trong không gian với hệ toạ độ Oxyz, , tính độ dài OH biết H là hình chiếu vuông góc của M1;2;3 lên mặt phẳng Oyz. A. 10 B. 5 C. 14 D. 13
Câu 9: Trong không gian Oxyz, cho d là đường thẳng đi qua điểm M1;2;3 và vuông góc với mặt phẳng
P:4x  3y 7z  2  0. Phương trình tham số của d là x  1 4t x  1 4t x  1  4t x  1 3t     A. y  2  3t . B. y  2  3t . C. y  2  3t . D. y  2  4t . z  3      7t z  3   7t z  3   7t z  3   7t
Câu 10: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số  3 (C) : y x  x và   2 (P) : y x x A.  9 S B. S  13 C.  81 S D.  37 S 4 12 12
Câu 11: Trong không gian Oxyz, cho mặt cầu   2  2  2 S : x y
z  4x  2y  6z  3  0 . Bán kính của mặt cầu S là: A. 3 B. 14 C. 11 D. 17 2 1 3
Câu 12: Cho hàm số f x liên tục trên  và f xdx  
12 . Khi đó  f2cosxsinxdx bằng 1  3 A. 6 . B. 12 . C. 24 . D. 6 . a x Câu 13: Tìm a sao cho 2 x.e .dx   4 . 0 A. a  0 B. a  2 C. a  1 D. a  4
Câu 14: Trong không gian với hệ tọa độ Oxyz, cho M1;2;3, N3;4;7. Mặt phẳng nào sau đây là mặt phẳng
trung trực của đoạn thẳng MN .
A. P : x  y  5z  15  0
B. P : 2x  2y 10z  15  0
C. P : 2x  2y  10z 15  0
D. P : x  y  5z  15  0 x  2 y  1 z  1
Câu 15: Trong không gian Oxyz , tìm giá trị của tham số m để đường thẳng d :   vuông góc 3 1 2
với mặt phẳng () : 6x  my  4z  5  0 . A. m  26 . B. m  2 . C. m  2 . D. m  26 .
Câu 16: Trong không gian Oxyz, mặt phẳng x  2y  z  1  0 có một véctơ pháp tuyến là     A. n  1;2;1 B. n  1;2;1 C. n  1;2;1 D. n  1;2;1
Câu 17: Biết S  a; b x x 
 là tập nghiệm của bất phương trình 3.9  10.3  3  0. Tìm T  b  a. 10 8 A. T  . B. T  1 . C. T  2 . D. T  . 3 3 x  6  5t 
Câu 18: Trong không gian Oxyz, cho đường thẳng d : y  2  t và mặt phẳng P : 3x  2y  1  0. Góc z   1
giữa đường thẳng d và mặt phẳng P bằng A. 0 45 B. 0 30 C. 0 60 D. 0 90
Câu 19: Hàm số y  f x liên tục trên 2;9 . Fx là một nguyên hàm của hàm số fx trên 2;9 và    
F2  5, F9  4 . Mệnh đề nào sau đây đúng ? 9 9 9 9 A. f xdx   20 . B. f xdx   1. C. f xdx   9 . D. f xdx    1 . 2 2 2 2
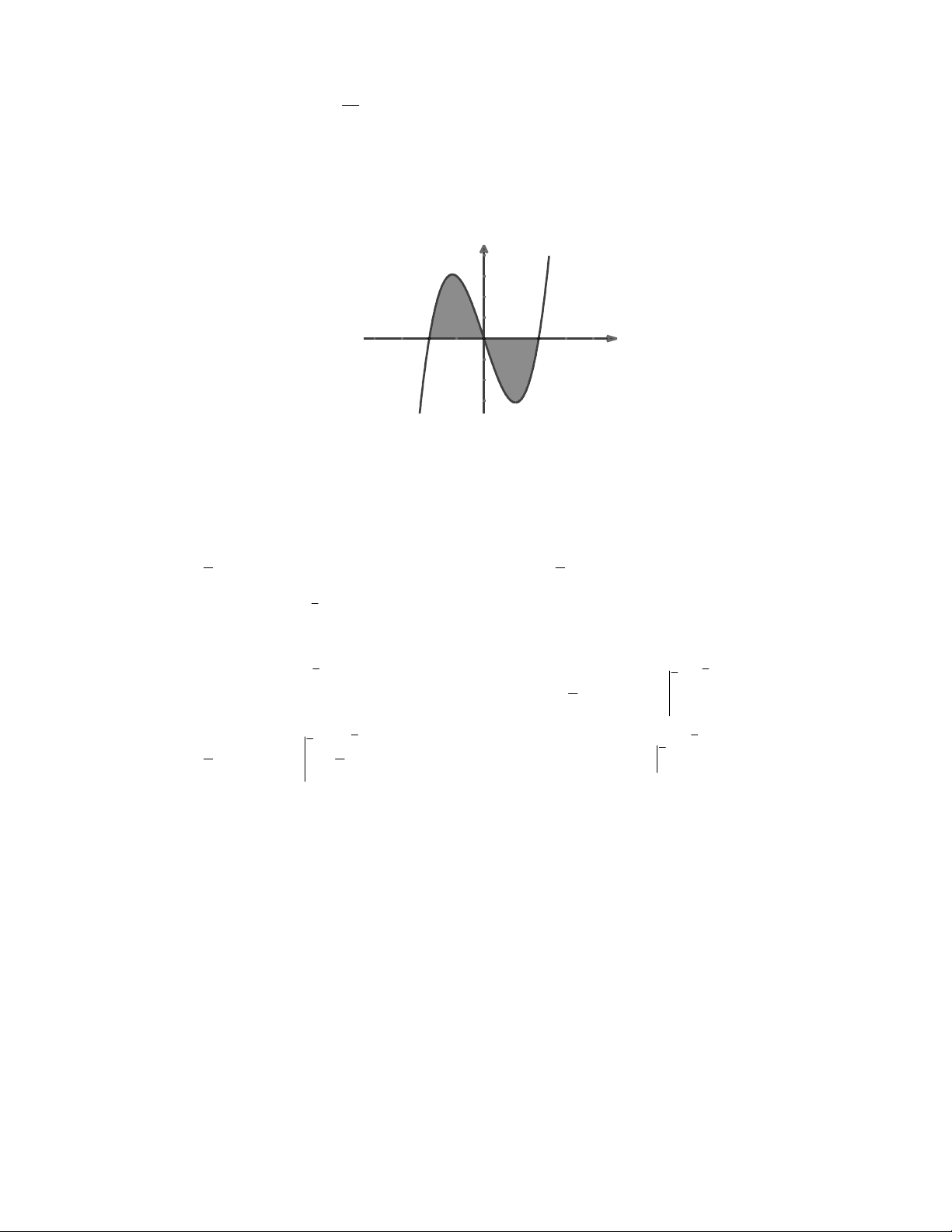
Câu 20: Diện tích hình phẳng phần tô đậm trong hình bên bằng: y y = f(x) -2 0 2 x 2 0 0 A.  fxdx B. f xdx    fxdx 2 2 2 1 2 2 2 C. f xdx   fxdx D. f xdx   fxdx 2 1 0 0 10 8 10 Câu 21: Nếu f(x)dx   17 và f(x)dx   12 thì  f(x)dx bằng 0 0 8 A. 29 B. 5 C. 5 D. 15
Câu 22: Tính thể tích của khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn bởi đồ thị hàm
số y  x4  x với trục hoành. 512 32 32 512 A. (đvtt) B. (đvtt) C. (đvtt) D. (đvtt) 15 3 3 15 e 2 ln x Câu 23: Tính: J   dx x 1 1 3 1 1 A. J  B. J  C. J  D. J  2 2 3 4
Câu 24: Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z  2z  5  0 . Tìm tọa độ điểm biểu diễn số 1 7  4i phức trên mặt phẳng phức ? z1 A. P3; 2 B. Q3;2 C. N1;  2 D. M1; 2 2 x x1 2x     1 5 5
Câu 25: Tập nghiệm của bất phương trình     
có dạng S  a; b . Tính A  b  a  7   7  A. A  1 B. A  2 C. A  1 D. A  2
Câu 26: Cho số phức z thỏa mãn 3  2iz  41  i  2  iz . Mô đun của z bằng 3 A. B. 10 C. 5 D. 3 4
Câu 27: Trong không gian với hệ toạ độ Oxyz, cho A2;0;2, B2;2;0 . Mệnh đề nào sau đây đúng ? A. OAB vuông tại O B. OAB đều C. OAB chỉ cân tại O D. OAB vuông cân tại O
Câu 28: Trong không gian Oxyz, cho điểm A2;1;1 và mặt phẳng P :16x  12y 15z  4  0. Gọi H là
hình chiếu vuông góc của A lên P . Tính độ dài AH. 11 11 22 A. 55. B. . C. . D. . 5 25 5
Câu 29: Trong không gian Oxyz , tìm giá trị của tham số m để mặt phẳng P : 2x  3y  mz  5  0 vuông
góc với mặt phẳng Oxy . A. m   . B. m  5 . C. m  1. D. m  0 .
Câu 30: Tổng tất cả các nghiệm của phương trình log x  1  log x  1 log 3x  5 bằng 2 2 2  A. 5 . B. 4 . C. 6 . D. 7 .
Câu 31: Trong không gian với hệ tọa độ Oxyz , mặt phẳng (P) : 2x  2y  z  5  0 cắt mặt cầu  2   2   2
(S) : (x 2) (y 3) (z 3)  100 theo giao tuyến là đường tròn (C) . Tính bán kính r của (C) . A. r  8 . B. r  10 . C. r  64 . D. r  16 .
Câu 32: Tìm kết quả đúng. A.       x x e dx xe C B.      x x e dx e C C.       x x e dx e C D.      x x e dx xe C
Câu 33: Trong mặt phẳng Oxy, điểm biểu diễn của số phức z  5  4i là A. 5;4. B. 5;4. C. 5;4. D. 5;4.
Câu 34: Nghiệm của phương trình 2x1 1 2   0 là 8 A. x  2 . B. x  1 . C. x  1. D. x  2 .
Câu 35: Tổng các nghiệm của phương trình 2
log x  log 9.log x  3 là 2 2 3 17 A. 8 . B. . C. 2 . D. 2 . 2
Câu 36: Trong không gian Oxyz , cho điểm A3;1;0 và mặt phẳng P : 2x  2y  z  1  0 . Tìm tọa độ điểm
H là hình chiếu vuông góc của điểm A trên mặt phẳng P . A. H1;3;2 B. H1;1;  1 C. H1; 3;2 D. H1;1;1
Câu 37: Nghiệm của bất phương trình log x 2x 8 4 là 1  2      2 x  6 6  x  4 x  6 6  x  4 A.  . B. . C. . D. . x      4 2  x   4 x   4 2  x   4  4
Câu 38: Cho tích phân I  x  
1sin2xdx. Chọn đẳng thức đúng? 0    4 4 4 1 1
A. I  x  1cos2x  cos2xdx
B. I   x  1cos2x  cos2xdx 2 2 0 0 0    4 4 1  4
C. I   x  1cos2x  cos2xdx D. I  x  1 4 cos2x  cos2xdx 2 0  0 0 0
Câu 39: Trong không gian Oxyz, mặt cầu tâm I2;1;3 và tiếp xúc với mpOxy có phương trình là
A.   2    2    2 x 2 y 1 z 3  9
B.   2    2    2 x 2 y 1 z 3  4
C.   2    2    2 x 2 y 1 z 3  1
D.   2    2    2 x 2 y 1 z 3  9
Câu 40: Hàm số nào sau đây là một nguyên hàm của y  cos 2x ? 1 1 A. y  2 sin 2x B. y  sin 2x C. y   sin 2x D. y  sin 2x 2 2
-----------------------------------------------
----------- HẾT PHẦN TRẮC NGHIỆM----------
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM ĐỀ KIỂM TRA HỌC KỲ 2
TRƯỜNG THPT HOÀNG HOA THÁM NĂM HỌC: 2019 – 2020 Môn: TOÁN – Lớp 12 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút (Đề gồm 04 trang) Mã đề 357
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ, tên thí sinh:.......................................................................Số báo danh:...........................................
I. PHẦN TRẮC NGHIỆM (8,0 điểm)
Câu 1: Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z  2z  5  0 . Tìm tọa độ điểm biểu diễn số 1 7  4i phức trên mặt phẳng phức ? z1 A. N1;  2 B. Q3;2 C. M1; 2 D. P3; 2 2 x x1 2x     1 5 5
Câu 2: Tập nghiệm của bất phương trình     
có dạng S  a; b . Tính A  b  a  7   7  A. A  2 B. A  2 C. A  1 D. A  1
Câu 3: Trong không gian Oxyz , cho điểm A3;1;0 và mặt phẳng P : 2x  2y  z  1  0 . Tìm tọa độ điểm
H là hình chiếu vuông góc của điểm A trên mặt phẳng P . A. H1;3;2 B. H1;1;  1 C. H1; 3;2 D. H1;1;1
Câu 4: Trong không gian Oxyz, cho d là đường thẳng đi qua điểm M1;2;3 và vuông góc với mặt phẳng
P:4x  3y 7z  2  0. Phương trình tham số của d là x  1 4t x  1 4t x  1  4t x  1 3t     A. y  2  3t . B. y  2  3t . C. y  2  3t . D. y  2  4t . z  3      7t z  3   7t z  3   7t z  3   7t
Câu 5: Tính thể tích của khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn bởi đồ thị hàm
số y  x4  x với trục hoành. 512 32 32 512 A. (đvtt) B. (đvtt) C. (đvtt) D. (đvtt) 15 3 3 15
Câu 6: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số  3 (C) : y x  x và   2 (P) : y x x 9 81 37 A. S  B. S  13 C. S  D. S  4 12 12
Câu 7: Trong không gian với hệ toạ độ Oxyz, , tính độ dài OH biết H là hình chiếu vuông góc của M1;2;3 lên mặt phẳng Oyz. A. 13 B. 5 C. 10 D. 14 a x Câu 8: Tìm a sao cho 2 x.e .dx   4 . 0 A. a  0 B. a  2 C. a  1 D. a  4
Câu 9: Tìm kết quả đúng. A.      x x e dx e C B.       x x e dx e C C.      x x e dx xe C D.       x x e dx xe C 2 1 3
Câu 10: Cho hàm số f x liên tục trên  và f xdx  
12 . Khi đó  f2cosxsinxdx bằng 1  3 A. 12 . B. 6 . C. 24 . D. 6 . e 2 ln x Câu 11: Tính: J   dx x 1 1 3 1 1 A. J  B. J  C. J  D. J  2 2 3 4 x  2 y  1 z  1
Câu 12: Trong không gian Oxyz , tìm giá trị của tham số m để đường thẳng d :   vuông góc 3 1 2
với mặt phẳng () : 6x  my  4z  5  0 . A. m  26 . B. m  2 . C. m  2 . D. m  26 .
Câu 13: Trong không gian với hệ tọa độ Oxyz, cho M1;2;3, N3;4;7. Mặt phẳng nào sau đây là mặt phẳng
trung trực của đoạn thẳng MN .
A. P : x  y  5z  15  0
B. P : 2x  2y 10z 15  0
C. P : x  y  5z  15  0
D. P : 2x  2y  10z  15  0
Câu 14: Hàm số nào sau đây là một nguyên hàm của y  cos 2x ? 1 1 A. y  sin 2x B. y   sin 2x C. y  2sin 2x D. y  sin 2x 2 2   
Câu 15: Trong không gian Oxyz, cho a  (3;1;2),b  (4;2;6). Tính tọa độ của vectơ a  b     A. a  b  (7;1;4).
B. a  b  (1; 3;8).     C. a  b  (1; 3; 8).
D. a  b  (7; 1;4).
Câu 16: Trong không gian Oxyz, mặt cầu tâm I2;1;3 và tiếp xúc với mpOxy có phương trình là
A.   2    2    2 x 2 y 1 z 3  9
B.   2    2    2 x 2 y 1 z 3  4
C.   2    2    2 x 2 y 1 z 3  1
D.   2    2    2 x 2 y 1 z 3  9
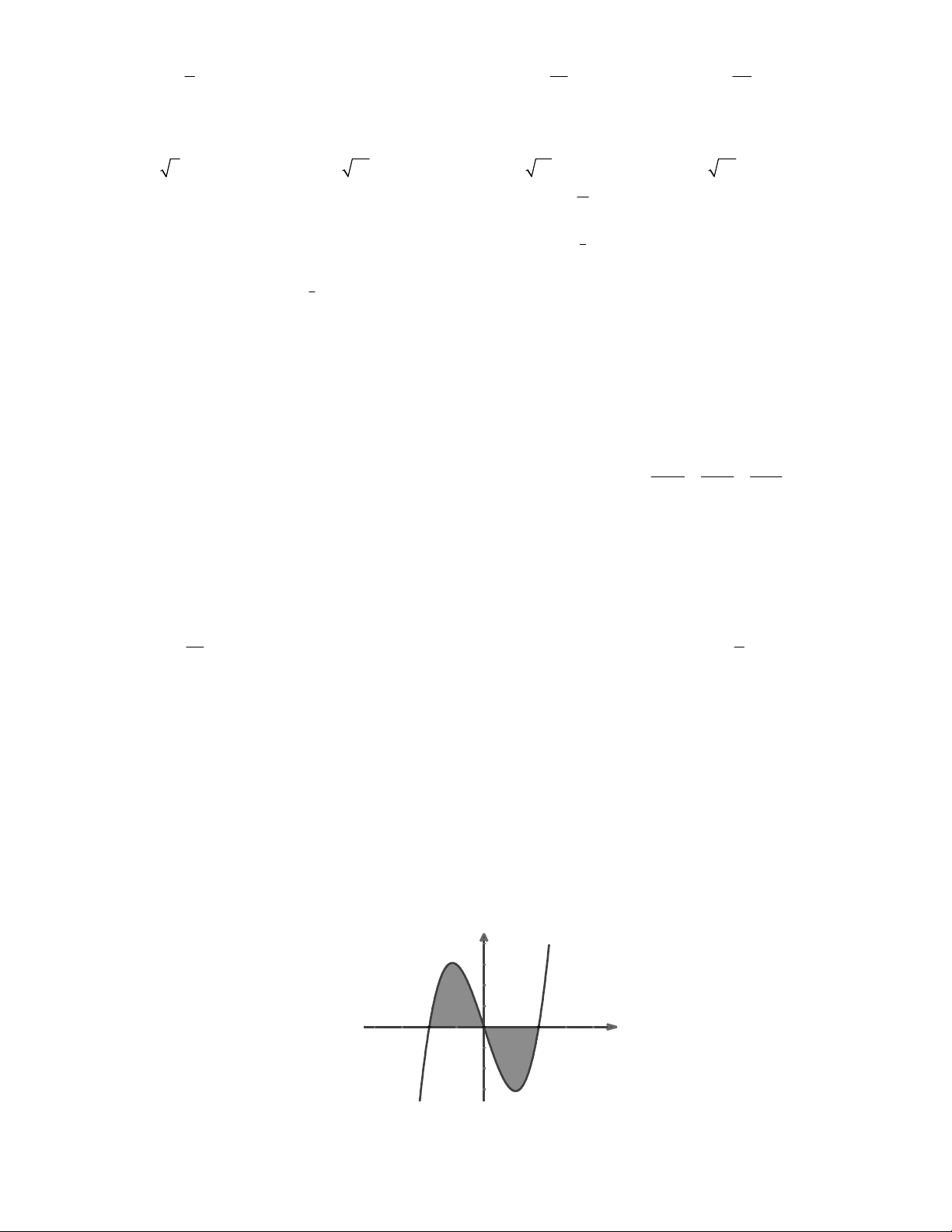
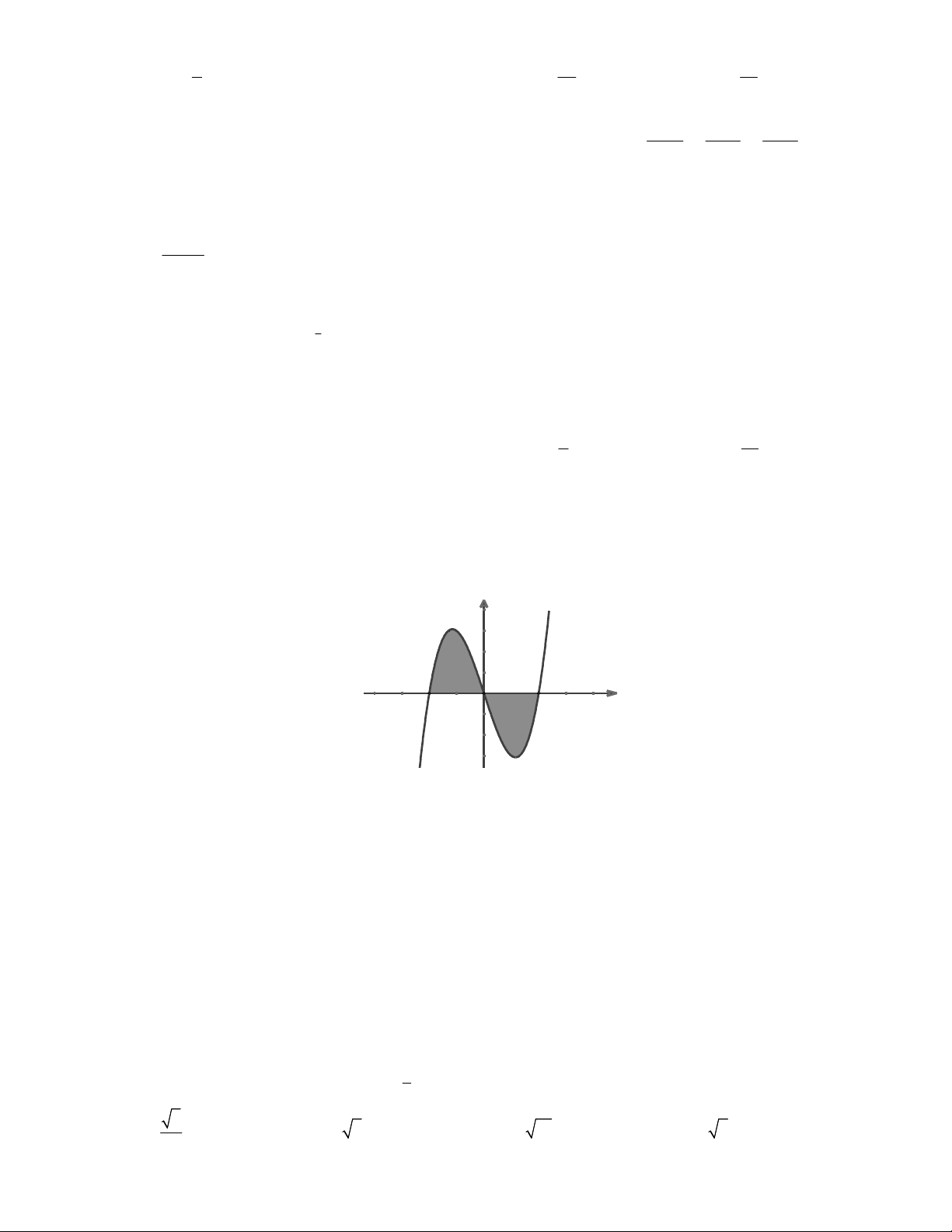
Câu 17: Diện tích hình phẳng phần tô đậm trong hình bên bằng: y y = f(x) -2 0 2 x 2 1 2 A.  fxdx B. f xdx   fxdx 2 2 1 0 0 2 2 C. f xdx    fxdx D. f xdx   fxdx 2 2 0 0
Câu 18: Hàm số y  f x liên tục trên 2;9 . Fx là một nguyên hàm của hàm số fx trên 2;9 và    
F2  5, F9  4 . Mệnh đề nào sau đây đúng ? 9 9 9 9 A. f xdx   1. B. f xdx   9 . C. f xdx    1 . D. f xdx   20 . 2 2 2 2 10 8 10 Câu 19: Nếu f(x)dx   17 và f(x)dx   12 thì  f(x)dx bằng 0 0 8 A. 29 B. 5 C. 5 D. 15
Câu 20: Cho số phức z thỏa mãn 3  2iz  41  i  2  iz . Mô đun của z bằng 3 A. B. 10 C. 5 D. 3 4
Câu 21: Cho số phức z  3  2i . Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng 3 và phần ảo bằng 2 .
B. Phần thực bằng 3 và phần ảo bằng 2i .
C. Phần thực bằng 3 và phần ảo bằng 2i .
D. Phần thực bằng 3 và phần ảo bằng 2 .
Câu 22: Nghiệm của phương trình 2x1 1 2   0 là 8 A. x  2 . B. x  2 . C. x  1. D. x  1 .
Câu 23: Trong không gian Oxyz , cho điểm A3;1;0 . Tìm tọa độ điểm H là hình chiếu vuông góc của điểm A trên trục Ox . A. H1;0;0 B. H3;0;0
C. H3;0;1 -----------------D. H0;1;0
Câu 24: Số nghiệm của phương trình x2 2  x 2 2  15 là A. 3. B. 2. C. 1. D. 0
Câu 25: Trong không gian Oxyz , tìm giá trị của tham số m để mặt phẳng P : 2x  3y  mz  5  0 vuông
góc với mặt phẳng Oxy . A. m  0 . B. m  1. C. m   . D. m  5 . 1
Câu 26: Tìm họ nguyên hàm của hàm số f(x)  5x  2 A.     dx 1 ln 5x 2 C B.    5x  dx ln 5x 2 C  2 5 5x  2 dx 5 C.    C D.    5x  dx 5ln 5x 2 C  2 5x  22 5x  2
Câu 27: Trong không gian Oxyz, cho điểm A2;1;1 và mặt phẳng P :16x  12y 15z  4  0. Gọi H là
hình chiếu vuông góc của A lên P . Tính độ dài AH. 11 11 22 A. 55. B. . C. . D. . 5 25 5
Câu 28: Tập nghiệm của bất phương trình 2
log x  6log x  8  0 là 2 2 A. (0 ; 16] B. 2 ; 4   C. 4 ; 16   D. (0 ; 4]
Câu 29: Tổng tất cả các nghiệm của phương trình log x  1  log x  1  log 3x  5 bằng 2 2 2  A. 5 . B. 4 . C. 6 . D. 7 .
Câu 30: Trong không gian với hệ tọa độ Oxyz , mặt phẳng (P) : 2x  2y  z  5  0 cắt mặt cầu  2   2   2
(S) :(x 2) (y 3) (z 3)  100 theo giao tuyến là đường tròn (C) . Tính bán kính r của (C) . A. r  8 . B. r  10 . C. r  64 . D. r  16 .
Câu 31: Biết S  a; b x x 
 là tập nghiệm của bất phương trình 3.9  10.3  3  0. Tìm T  b  a. 10 8 A. T  . B. T  1 . C. T  . D. T  2 . 3 3
Câu 32: Trong không gian Oxyz, mặt phẳng x  2y  z  1  0 có một véctơ pháp tuyến là     A. n  1;2;1 B. n  1;2;1 C. n  1;2;1 D. n  1;2;1 x  6  5t 
Câu 33: Trong không gian Oxyz, cho đường thẳng d : y  2  t và mặt phẳng P : 3x  2y  1  0. Góc z   1
giữa đường thẳng d và mặt phẳng P bằng A. 0 30 B. 0 60 C. 0 90 D. 0 45
Câu 34: Tổng các nghiệm của phương trình 2
log x  log 9.log x  3 là 2 2 3 17 A. 8 . B. 2 . C. . D. 2 . 2
Câu 35: Tổng phần thực và phần ảo của số phức z thoả mãn iz  1 iz  2i bằng A. 2 . B. 2 . C. 6 . D. 6 .
Câu 36: Trong mặt phẳng Oxy, điểm biểu diễn của số phức z  5  4i là A. 5;4. B. 5;4. C. 5;4. D. 5;4.  4
Câu 37: Cho tích phân I  x  
1sin2xdx. Chọn đẳng thức đúng? 0    4 4 4 1 1
A. I  x  1cos2x  cos2xdx
B. I   x  1cos2x  cos2xdx 2 2 0 0 0    4 4 1  4
C. I   x  1cos2x  cos2xdx D. I  x  1 4 cos2x  cos2xdx 2 0  0 0 0
Câu 38: Trong không gian Oxyz, cho mặt cầu   2  2  2 S : x y
z  4x  2y  6z  3  0 . Bán kính của mặt cầu S là: A. 14 B. 3 C. 11 D. 17
Câu 39: Nghiệm của bất phương trình log x 2x 8 4 là 1  2      2 x  6 6  x  4 x  6 6  x  4 A.  . B. . C. . D. . x      4 2  x   4 x   4 2  x   4
Câu 40: Trong không gian với hệ toạ độ Oxyz, cho A2;0;2, B2;2;0 . Mệnh đề nào sau đây đúng ? A. OAB vuông tại O B. OAB đều C. OAB chỉ cân tại O D. OAB vuông cân tại O
-----------------------------------------------
----------- HẾT PHẦN TRẮC NGHIỆM----------
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM ĐỀ KIỂM TRA HỌC KỲ 2
TRƯỜNG THPT HOÀNG HOA THÁM NĂM HỌC: 2019 – 2020 Môn: TOÁN – Lớp 12 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút (Đề gồm 04 trang) Mã đề 485
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ, tên thí sinh:.......................................................................Số báo danh:...........................................
I. PHẦN TRẮC NGHIỆM (8,0 điểm) e 2 ln x Câu 1: Tính: J  dx  x 1 1 1 1 3 A. J  B. J  C. J  D. J  4 2 3 2
Câu 2: Trong không gian Oxyz, cho điểm A2;1; 
1 và mặt phẳng P: 16x 12y 15z  4  0. Gọi H là
hình chiếu vuông góc của A lên P. Tính độ dài AH. 11 11 22 A. 55. B. . C. . D. . 5 25 5
Câu 3: Tính thể tích của khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn bởi đồ thị hàm
số y  x 4  x với trục hoành. 512 32 32 512 A. (đvtt) B. (đvtt) C. (đvtt) D. (đvtt) 15 3 3 15
Câu 4: Nghiệm của phương trình 2x 1  1 2   0 là 8 A. x  1  . B. x  2 . C. x  1 . D. x  2 .
Câu 5: Tổng phần thực và phần ảo của số phức z thoả mãn iz  1iz  2  i bằng A. 6 . B. 2 . C. 6 . D. 2 . 2 1 3
Câu 6: Cho hàm số f x liên tục trên  và f
 xdx  12 . Khi đó f  2cosxsinxdx bằng 1 3 A. 6 . B. 12 . C. 24 . D. 6 .
Câu 7: Hàm số y  f x liên tục trên 2;9 F x là một nguyên hàm của hàm số f x trên 2;9   .     và F  
2  5, F 9  4. Mệnh đề nào sau đây đúng ? 9 9 9 9 A. f  xdx  9. B. f  xdx  20. C. f  xdx  1. D. f  xdx  1. 2 2 2 2 10 8 10 Câu 8: Nếu f(x)dx  17  và f(x)dx  12  thì f(x)dx  bằng 0 0 8 A. 5 B. 5 C. 29 D. 15
Câu 9: Trong không gian với hệ tọa độ Oxyz , mặt phẳng (P) : 2x  2y  z  5  0 cắt mặt cầu 2 2 2
(S) : (x  2)  (y  3)  (z  3)  100 theo giao tuyến là đường tròn (C). Tính bán kính r của (C). A. r  8 . B. r  10 . C. r  64 . D. r  16 .
Câu 10: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 (C) : y  x  x và 2 (P) : y  x  x 9 37 81 A. S  B. S  13 C. S  D. S  4 12 12 x  2 y 1 z  1
Câu 11: Trong không gian Oxyz , tìm giá trị của tham số m để đường thẳng d :   vuông 3 1 2
góc với mặt phẳng () : 6x  my  4z  5  0 . A. m  2 . B. m  26 . C. m  2 . D. m  26 .
Câu 12: Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z  2z  5  0 . Tìm tọa độ điểm biểu diễn số 1 7  4i phức trên mặt phẳng phức ? z1 A. Q 3;2 B. P 3;  2 C. N 1;   2 D. M 1; 2 a x Câu 13: Tìm a sao cho 2 x.e .dx  4  . 0 A. a  1 B. a  2 C. a  0 D. a  4 Câu 14: Biết S a;b   x x
  là tập nghiệm của bất phương trình 3.9 10.3  3  0. Tìm T  b a. 8 10 A. T  2 . B. T  1. C. T  . D. T  . 3 3
Câu 15: Trong không gian Oxyz, mặt cầu tâm I 2;1;3 và tiếp xúc với mpOxy có phương trình là 2 2 2 2 2 2
A. x  2  y   1  z  3  9
B. x  2  y   1  z  3  4 2 2 2 2 2 2
C. x 2  y   1  z  3  1
D. x 2 y   1  z  3  9
Câu 16: Diện tích hình phẳng phần tô đậm trong hình bên bằng: y y = f(x) -2 0 2 x 2 1 2 A. f  xdx B. f  xdx  f  xdx 2 2 1 0 0 2 2 C. f  xdx  f  xdx D. f  xdx  f  xdx 2 2 0 0 x   65t 
Câu 17: Trong không gian Oxyz, 
cho đường thẳng d : y   2  t 
và mặt phẳng P : 3x 2y 1  0. Góc z   1 
giữa đường thẳng d và mặt phẳng P bằng A. 0 45 B. 0 30 C. 0 90 D. 0 60
Câu 18: Tập nghiệm của bất phương trình 2
log x  6 log x  8  0 là 2 2 A. (0 ; 4] B. (0 ; 16] C. 2  ; 4      D. 4 ; 16  
Câu 19: Cho số phức z thỏa mãn 3 2iz  41i  2 iz . Mô đun của z bằng 3 A. B. 5 C. 10 D. 3 4
Câu 20: Trong không gian Oxyz , tìm giá trị của tham số m để mặt phẳng P : 2x  3y  mz  5  0 vuông
góc với mặt phẳng Oxy. A. m  5 . B. m   . C. m  0 . D. m  1 .    
Câu 21: Trong không gian Oxyz, cho a  (3; 1
 ;2),b  (4;2;6). Tính tọa độ của vectơ a b    
A. a  b  (7;1;4). B. a b  (1; 3;8).    
C. a  b  (1;3; 8). D. a  b  (7;1;4).
Câu 22: Trong không gian Oxyz , cho điểm A3;1;0. Tìm tọa độ điểm H là hình chiếu vuông góc của điểm A trên trục Ox . A. H 1;0;  0 B. H 3;0; 
1 -----------------C. H 3;0;0 D. H 0;1;  0  4
Câu 23: Cho tích phân I  x  
1sin2xdx. Chọn đẳng thức đúng? 0    1 1 A. I  x   4 1 cos2x  cos2xdx  B. I   x   4 4 1 cos 2x  cos2xdx 2 2  0 0 0    1  C. I   x   4 4 1 cos2x  cos 2xdx
I   x 1 cos2x  cos2xdx 2  D.   4 4  0 0 0 0
Câu 24: Trong không gian Oxyz, mặt phẳng x  2y  z  1  0 có một véctơ pháp tuyến là     A. n  1;2;  1 B. n  1;2;  1 C. n  1;2;  1 D. n  1;2;  1
Câu 25: Nghiệm của bất phương trình log  2 x  2x  8  4  là 1  2 6  x  4 x  6 6  x  4 x  6 A.     2  x  4 . B. . C. . D. .      x  4  2  x  4  x  4  2 x x  1  2x 1 5   5     
Câu 26: Tập nghiệm của bất phương trình          
có dạng S  a;b. Tính A  b a 7   7 A. A  1 B. A  1 C. A  2 D. A  2
Câu 27: Trong không gian với hệ toạ độ Oxyz, cho A2;0;2, B 2;2;0. Mệnh đề nào sau đây đúng ? A. OAB vuông tại O B. OAB đều C. OAB chỉ cân tại O D. OAB vuông cân tại O
Câu 28: Trong không gian Oxyz , cho điểm A3;1;0 và mặt phẳng P : 2x  2y  z 1  0 . Tìm tọa độ điểm
H là hình chiếu vuông góc của điểm A trên mặt phẳng P. A. H 1;1;  1 B. H 1;1;  1 C. H 1;3;2 D. H 1;3;2
Câu 29: Số nghiệm của phương trình x2 2 2 2 x   15 là A. 1 . B. 0 C. 2. D. 3. 1
Câu 30: Tìm họ nguyên hàm của hàm số f (x)  5x  2 dx dx 5 A.  ln 5x  2 C  B.  C 5x  2  5x  2 5x 22 dx 1 dx C.  ln 5x  2 C  D.  5 ln 5x  2 C 5x  2 5  5x  2
Câu 31: Tìm kết quả đúng. A. x  x e dx xe  C  B. x  x e dx xe   C  C. x  x e dx e  C  D. x  x e dx e   C 
Câu 32: Trong không gian với hệ toạ độ Oxyz, , tính độ dài OH biết H là hình chiếu vuông góc của M 1;2;  3 lên mặt phẳng Oyz. A. 10 B. 5 C. 14 D. 13
Câu 33: Tổng các nghiệm của phương trình 2
log x  log 9.log x  3 là 2 2 3 17 A. 8 . B. 2 . C. . D. 2 . 2
Câu 34: Trong không gian với hệ tọa độ Oxyz, cho M 1;2;3, N 3;4;7. Mặt phẳng nào sau đây là mặt
phẳng trung trực của đoạn thẳng MN .
A. P : x  y  5z 15  0
B. P : 2x  2y 10z 15  0
C. P : x y  5z 15  0
D. P : 2x  2y 10z 15  0
Câu 35: Trong mặt phẳng Ox ,
y điểm biểu diễn của số phức z  5  4i là A. 5;4. B. 5;4. C. 5;4. D. 5; 4  .
Câu 36: Tổng tất cả các nghiệm của phương trình log x 1  log x  1  log 3x  5 bằng 2   2 2   A. 7 . B. 6 . C. 4 . D. 5 .
Câu 37: Hàm số nào sau đây là một nguyên hàm của y  cos 2x ? 1 1 A. y  sin 2x B. y  2 sin 2x C. y   sin 2x D. y  sin 2x 2 2
Câu 38: Cho số phức z  3  2i . Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng 3 và phần ảo bằng 2 .
B. Phần thực bằng 3 và phần ảo bằng 2i .
C. Phần thực bằng 3 và phần ảo bằng 2 .
D. Phần thực bằng 3 và phần ảo bằng2i .
Câu 39: Trong không gian Oxyz, cho mặt cầu S 2 2 2
: x  y  z  4x  2y  6z  3  0 . Bán kính của mặt cầu S là: A. 14 B. 3 C. 11 D. 17
Câu 40: Trong không gian Oxyz, cho d là đường thẳng đi qua điểm M 1;2; 
3 và vuông góc với mặt phẳng
P: 4x  3y 7z 2  0. Phương trình tham số của d là x   1 4t     x   1  4t  x   1  3t  x   1  4t  A. y   2  3t     . B. y   2  3t  . C. y   2  4t  . D. y   2  3t  . z   3 7t     z   3  7t  z   3  7t  z   3  7t 
----------- HẾT PHẦN TRẮC NGHIỆM------------ KIỂM TRA HỌC KỲ 2 NĂM HỌC: 2019 – 2020 Môn Toán – Lớp 12
II. PHẦN TỰ LUẬN (2,0 điểm – Thời gian làm bài: 18 phút)  2
Câu 1 (1,0 điểm). Tính tích phân   sinx I  dx. 1  2cosx 2 0
Câu 2 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz , cho hai điểm A2;3;1, B(1;2;3).
Viết phương trình mặt phẳng trung trực của đoạn thẳng AB . ----HẾT---- ĐÁP ÁN TOÁN 12 – HK2 MÃ ĐỀ : 132 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20
A B C B D D A D D A B C D B D B C D A D
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
D A A C A A C C B D B C C A A B B B C C MÃ ĐỀ : 209 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20
A C A C A A A D C D D D B D B C C A D B
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
C A C A C B B B D D A C D C B B A B D B MÃ ĐỀ : 357 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20
D D B A A D A B B D C B C A A D C C C B
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
A C B B A A B C D A D C D C C D B D A B MÃ ĐỀ : 485 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20
C B A A A A D B A C A B B A D C A D C C
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
D C B D B B B B C C D D C A D A D C D B TỰ LUẬN Câu Nộ dung Điểm  2 1 Tính tích phân   sin x I dx. 1  2cosx2 0
Đặt t  1  2 cosx  dt  2 sin xdx. 0.2  
Đổi cận: x   t  1  2 0.2 x  0  t   3 1 1   1 dt I  1 1   1 . 0.2x3 2 2 t 2 t 3 3 3
Trong không gian với hệ tọa độ Oxyz , cho hai điểm A2;3;1, B(1;2;3). 2
Viết phương trình mặt phẳng P  là mặt trung trực của đoạn thẳng AB . M là trung điểm  1 1  AB  M  ; ;2 0.2  2 2      Qua M 0.2 P   
: vtpt n  AB  3;5;  2 P     0.2
ptmp P  : 3x  5y  2z  0. 0.4