SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ II TPHCM NĂM HỌC 2019- 2020
TRƯỜNG THPT LÊ TRỌNG TẤN Môn : Toán – Khối : 12
Thời gian làm bài: 90 phút
(Đề bài gồm 35 câu trắc nghiệm và 3 câu tự luận) ĐỀ CHÍNH THỨC Mã đề thi 485
Họ, tên học sinh:..................................................................... Mã số: .............................
PHẦN I - TRẮC NGHIỆM (gồm 35 câu, mỗi câu 0,2 điểm)
Câu 1: Cho hình phẳng D giới hạn bởi đường cong x
y  e , trục hoành và các đường thẳng x  0, x 1.
Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ? 2 e 1 2  (e 1) 2 e 2  (e 1) A. V  . B. V  . C. V  . D. V  2 2 2 2     
Câu 2: Trong không gian với hệ trục tọa độ Oxyz, cho a  i  2 j  3k . Tọa độ của vectơ a là: A. 2; 3  ;  1 . B.  3  ;2;  1 . C. 2; 1  ; 3  . D.  1  ;2;  3 .
Câu 3: Trong không gian với hệ trục toạ độ Oxyz , cho mặt phẳng   : x  3y  2z  6  0 . Vecto nào
không phải là vecto pháp tuyến của   ?     A. n  1  ;3;2 . B. n  2;6; 4 . C. n  1;3; 2 . D. n  1;3;2 . 2   3   1  
Câu 4: Trong không gian Oxyz , cho mặt cầu S  x   y  2  z  2 2 : 4
1  25 . Tọa độ tâm I và bán kính
R của mặt cầu S  là A. I 0;4   1 và R  5 . B. I 0;4;  1 và R  5 . C. I 0;4;  1 và R  25 . D. I 0;4;  1 và R  25 .
Câu 5: Phương trình bậc hai: 2
z  4z  6  0 trên tập số phức có hai nghiệm là: A. z  2  10 i B. z  2  2 i C. z  2  2 i D. z  2  2 1
Câu 6: Họ tất cả các nguyên hàm của hàm số 2 f (x)  x  3x  là x 3 2 x 3x 3 2 x 3x 1 A.   ln x  C . B.    C . 3 2 2 3 2 x 3 2 x 3x 3 2 x 3x C.   ln x  C . D.   ln x  C . 3 2 3 2
Câu 7: Cho z  2  3i, z  2  3 .i Kết quả nào sau đây đúng? 1 2 A. z .z  13. B. z .z  0. C. z .z  5  . D. z .z  4. 1 2 1 2 1 2 1 2
Câu 8: Cho hai số phức z  4  2i , z  2  i . Phần ảo của số phức z  z bằng 1 2 1 2 A. 1  B. 1 C. i D. i  e Câu 9: Tính tích phân 2 I  x ln d x x  . 1 1 2 1 1 A. I   3 2e   1 . B. 3 I  e 1. C. I   3 2e   1 . D. I   3 2e   1 2 9 9 9
Câu 10: Diện tích hình phẳng giới hạn bởi 2
y  x  5x  6, y  0, x  0, x  2 có kết quả là 58 56 55 52 . . . . A. 3 B. 3 C. 3 D. 3
Câu 11: Họ tất cả các nguyên hàm của hàm số f  x 2  sin 2020x  3x là: 1 A. 3 cos 2020x  x  C . B. 2020cos 2020x  6x  C 2020 1 C. 3 cos 2020x  x  C .
D. 2020cos 2020x  6x  C . 2020
Câu 12: Môđun của số phức z  1 3i bằng A. 8 . B. 11 . C. 10 . D. 2 1 2  x 
Câu 13: Tính tích phân I  f (x)dx  
1. Tính tích phân K   f  d .x 2 0 0   1 A.  1 . B. 2. C. . D. 1. 2 2 1
Câu 14: Tìm họ nguyên hàm của hàm số f (x)  1. 2 cos x
A. f (x)dx x  tan x  C  . B. f (x)dx  tan x  C  .
C. f (x)dx  tan x  x  C  .
D. f (x)dx  tan x  x  C  .
Câu 15: Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A2;4;  1 , B 1  ;1;3 và mặt phẳng
P: x 3y  2z 5  0. Một mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có
phương trình dạng ax  by  cz 11  0. Tính a  b  c A. a  b  c  3. B. a  b  c  5. C. a  b  c  10. D. a  b  c  7  . 1 3
Câu 16: Cho số phức z    i . Số phức 2
w  1  z  z , khi đó w bằng? 2 2 A. 1 B. 3 C. 0 D. 2
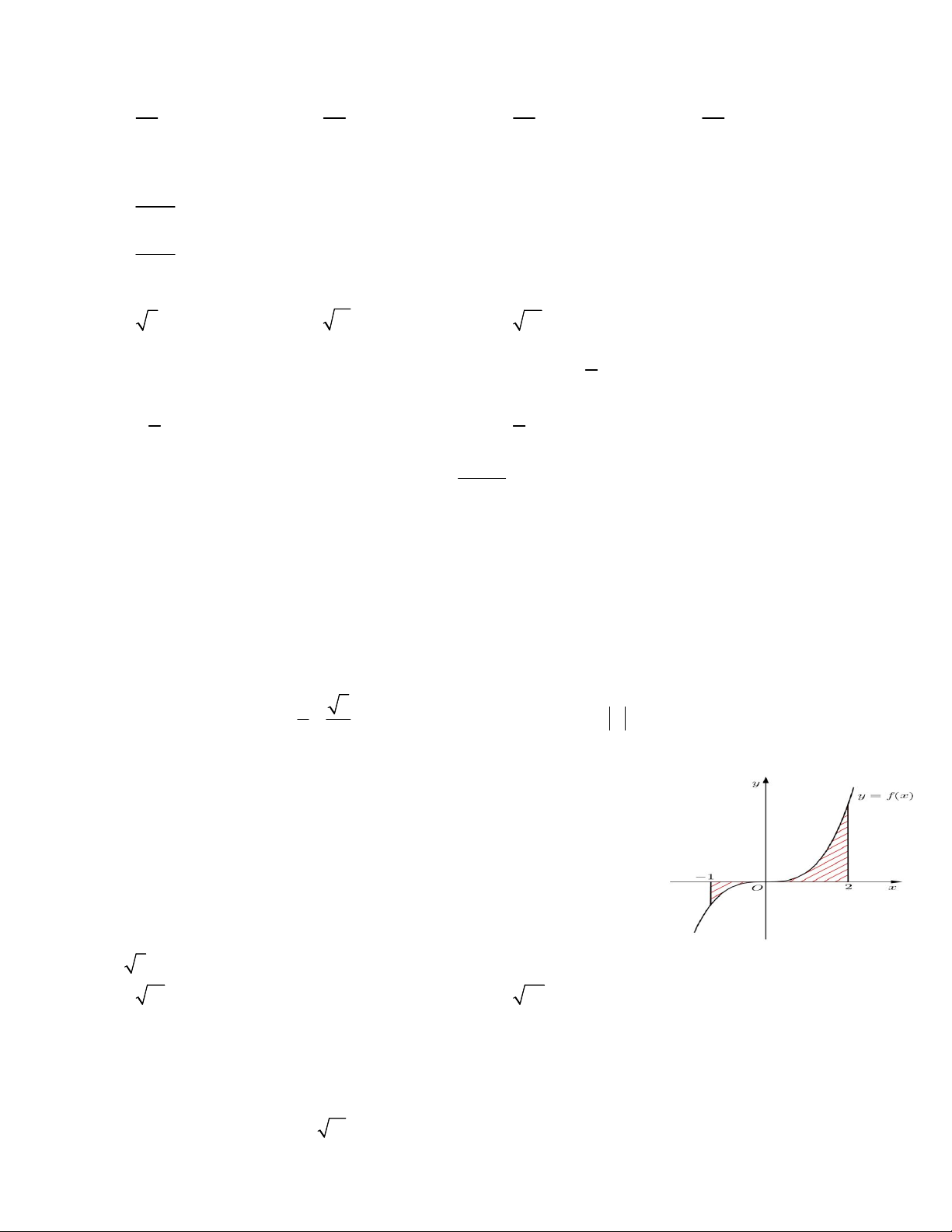
Câu 17: Gọi S là diện tích hình phẳng (H) giới hạn bởi các đường
y  f (x) , trục hoành và hai đường thẳng x  1
 , x  2 (như hình vẽ 0 2 bên). Đặt a  f (x)dx,b  f (x)dx  
, mệnh đề nào dưới đây đúng ? 1  0 A. S  b  a . B. S  b   a . C. S  b  a . D. S  b   a .
Câu 18: Gọi z ; z là các nghiệm phức của phương trình 1 2 2
z  5z  4  0 . Khi đó giá trị của biểu thức 4 4 A  z  z là : 1 2 A. 13 B. 23 C. 23 D. -23
Câu 19: Trong không gian Oxyz cho điểm I 0;2; 
1 . Mặt cầu S có tâm I và S đi qua điểm C 1; 1
 ;2 . Phương trình mặt cầu S là:
A.  x  2   y  2   z  2 1 1 1  5 .
B. x   y  2   z  2 2 2 1  11 .
C. x   y  2   z  2 2 2 1  11 .
D. x   y  2   z  2 2 2 1  11 2 x  2x  3
Câu 20: Một nguyên hàm của hàm số f  x  là x 1 2 x 2 x A.  3x  6ln x 1 B.  3x  6ln x 1 . 2 2 2 x 2 x C.  3x  6ln x 1 . D.  3x  6ln  x   1 2 2
Câu 21: Tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn: z  2  i  4 là đường tròn có tâm I
và bán kính R lần lượt là: A. I  2  ;  1 ; R  4 . B. I 2;  1 ; I 2;  1 . C. I 2;  1 ; R  4 . D. I  2  ;  1 ; R  2    x u e Câu 22: Đặt   x I e sin xdx và 
. Trong các khẳng định sau, khẳng định nào đúng? dv  0  sin xdx   A. x   cos x I e x  e cos xdx  B. x  cos x I e x  e cos xdx  0 0     C.  x cos  x I e x e coxdx D.   x cos  x I e x e cosxdx 0  0  0 0
Câu 23: Cho số phức z  1 2i , giá trị của số phức w  z  iz là? A. 3  3i B. 3  3i C. 2  i D. 1 i
Câu 24: Một nguyên hàm F (x) của hàm số 3 2
f (x)  3x  2x 1 thỏa mãn điều kiện F (2)  3 là 3 2 37 3 2 37 A. 4 3 F (x)  x  x  x  . B. 4 3 F (x)  x  x  x  . 4 3 3 4 3 3 3 2 3 2 C. 4 3 F (x)  x  x  x . D. 4 3
F(x)  x  x  x  C . 4 3 4 3
Câu 25: Trong không gian Oxyz, đường thẳng đi qua điểm M 2;1;4 và vuông góc với mặt phẳng
P: 2x  2y  3z 8  0 có phương trình là x  2 y  2 z  3 x  2 y 1 z  4 A.   . B.   .. 2 1 4  2 2 3  x  2 y 1 z  4 x  2 y  2 z 3 C.   . D.   . 2 2 3  2 1 4 
Câu 26: Cho ba mặt phẳng ( ) : x  y  2z 1  0 ; ( ) : x  y  z  2  0 và ( ) : x  y  5  0 . Trong các
mệnh đề sau, mệnh đề nào sai? A. ( )  ( ) B. ( )  ( ) C. ( )  ( ) D. ( )  ( ) Câu 27: Cho tam giác ABC : ( A 2;2;2), (
B 4;0;3),C(0;1;0). Diện tích của tam giác này bằng bao nhiêu? 75 95 55 65 A. đvdt B. đvdt C. đvdt D. đvdt 2 2 2 2 1 xdx Câu 28: Cho  a  b ln 2  c ln 3  với , a ,
b c là các số hữu tỉ. Giá trị của 3a  b  c bằng x  22 0 A. -1. B. -2. C. 1. D. 2.
Câu 29: Trong không gian Oxyz , cho hai điểm A(1; 2;1), B(2; 1; 2) . Điểm M trên trục Ox và cách đều hai
điểm A, B có tọa độ là  3   1   1 3   1 1 3  A. M ; 0;0   . B. M ; 0;0   . C. M 0; ;   . D. M ; ;   .  2   2   2 2   2 2 2   
Câu 30: Trong không gian với hệ tọa độ Oxyz , cho hai vecơ u  m 1;2;3 và v  1;m  2;  1 . Giá trị của  
m để hai vectơ u và v vuông góc là: A. m  2 . B. m  1. C. m  2  . D. m  1  .
Câu 31: Trong không gian với hệ toạ độ Oxyz, cho điểm A(1;0;2) và đường thẳng (d) có phương x 1 y z 1 trình  
. Viết phương trình đường thẳng (Δ) đi qua A vuông góc và cắt (d) 1 1 2 x 1 y z  2 x 1 y z  2 A.   B.   1 1 1 1 1 1  x 1 y z  2 x 1 y z  2 C.   D.   2 2 1 1 3  1
Câu 32: Cho số phức z thỏa mãn điều kiện 2z iz  2  5i . Số phức z cần tìm là: A. z  3  4i B. z  3  4i C. z  4  3i D. z  4  3i 2 1
Câu 33: Cho hàm số f  x liên tục trên ℝ và f 2  16, f
 xdx  4. Tính tích phân I  .xf   2xdx 0 0 A. 20 B. 12 C. 13 D. 7
Câu 34: Tìm số phức z thỏa mãn z  2  z và  z  
1  z  i là số thực. A. z  1 2 .i B. z  1 2 .i C. z  2  .i D. z  1 2 .i
Câu 35: Trong không gian với hệ tọa độ Oxyz tìm tất cả các giá trị của tham số m để đường thẳng x  2 y 1 z d : 
 song song với mặt phẳng P x    m 2 : 2 1 2 y  m z 1  0. 2 1 1 A. m  1  . B. m 1  ;  3 . C. m  3.
D. Không có giá trị nào của m .
II- PHẦN TỰ LUẬN ( 3,0 điểm) 1 5
Câu 1. (1 điểm) Tính tích phân: I  x  2 x   1 d .x 0
Câu 2. (1 điểm) Cho số phức z thỏa mãn: z 1 2i  zi 15  i . Tìm mô đun của z.
Câu 3. (1 điểm) Cho A1; 3
 ;2 và mặt phẳng P : 2x  y 3z 1 0. Viết phương trình tham số của
đường thẳng d đi qua A và vuông góc với P. ----------- HẾT ----------
ĐÁP ÁN ĐỀ KIỂM TRA HKII MÔN TOÁN 12 Năm học : 2019 – 2020 I . TRẮC NGHIỆM: Câu 132 209 357 485 1 C C A D 2 D A D D 3 C D C D 4 B D B B 5 C B B B 6 D D D C 7 A C B A 8 A B D A 9 B D A C 10 A B D A 11 B D C A 12 D A A C 13 B D C B 14 A C B D 15 D A B B 16 B A B C 17 A C C C 18 D C A D 19 B B B D 20 D B C B 21 C D C D 22 B D A C 23 A A C A 24 C A D A 25 A D D C 26 A B A D 27 D A A D 28 A C D A 29 B B B A 30 C A D C 31 A A C B 32 D D D B 33 C C D D 34 C B B B 35 B B D A II. TỰ LUẬN: 1 5
Câu 1. (1 điểm) Tính tích phân: I  x 2 x   1 d .x 0 1 * Đặt 2
t  x 1 dt  2xdx  xdx  dt (0,25 điểm) 2 * Đổi cận: (0,25 điểm) 2 1 * 5 I  t dt  (0,25 điểm) 2 1 6 1 t 21 *   (0,25 điểm) 2 6 4
Câu 2. (1 điểm) Cho số phức z thỏa mãn: z 1 2i  zi 15  i Tìm mô đun của z.
*  x  yi1 2i   x  yii  15  i (0,25 điểm)
*  x  2xi  yi  2y  xi  y  15  i (0,25 điểm) x  3y 15 x  3 *     (0,25 điểm) x  y 1 y  4 * z  5 (0,25 điểm)
Câu 3. (1 điểm) Cho A1; 3
 ;2 và mặt phẳng P : 2x  y  3z 1 0. Viết phương trình tham số của
đường thẳng d đi qua A và vuông góc với P. 
* P có pháp véc tơ n  2;1;3 (0,25 điểm) 
* Vì d  P nên d nhận n  2;1;3 làm chỉ phương (0,25 điểm) x 1 2t  * d : y  3   t t  (0,5 điểm) z  23t 