Đề thi học kì 2 Toán 12 năm 2019 – 2020 trường THPT Thủ Đức – TP HCM

TRƯỜNG THPT THỦ ĐỨC
ĐỀ KIỂM TRA HỌC KÌ II – KHỐI 12 MÃ ĐỀ NĂM HỌC: 2019 – 2020
Môn: TOÁN - Thời gian: 90 phút. 178
I. PHẦN TRẮC NGHIỆM (7,5 điểm)
Câu 1. Cho số phức z thoả mãn . z 2  i  z  3  11i . Tìm z . A. z  39 . B. z  97 . C. z  101. D. z  85 . x  3 t x  2  3t  
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng d : y  4  t và d: y  5  3t . z  5 2t   z  3  6t 
Mệnh đề nào sau đây đúng?
A. Hai đường thẳng d và d trùng nhau.
B. Hai đường thẳng d và d cắt nhau.
C. Hai đường thẳng d và d chéo nhau.
D. Hai đường thẳng d và d song song với nhau.
Câu 3. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S  : 2 2 2
x  y  z  4x 10y  6z  2  0. Lúc
đó tâm I và bán kính R của mặt cầu S  là
A. Tâm I 2;5;3 , R  2 10 .
B. Tâm I  2;5;3 , R  2 10 .
C. Tâm I 2;5;3 , R  6 .
D. Tâm I  2;5; 3 , R  6 .
Câu 4. Điểm biểu diễn của số phức z    i2 4 3 là A. 7;24 . B. 7; 2  4 . C. 7;24 . D. 7; 2  4 . x
Câu 5. Họ tất cả các nguyên hàm của hàm số f  x  cos là 2 x x A. F x  sin  C .
B. F  x  2sin  C . 2 2 x x
C. F  x  2sin  C . D. F  x 1  sin  C . 2 2 2 2 Câu 6. Cho 2 3 I  x x 1 dx  . Đặt 3
t  x 1 . Khẳng định nào sau đây sai? 1 3 2 3 2 4 2 A. I  tdt.  B. 2 2tdt  3x dx . C. 2 I  t dt  . D. I  6  . 3 3 9 2 2   
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho AO  2i  3k . Tọa độ điểm A là A. A2; 3  ;0 . B. A 2  ;0;3 . C. A 2  ;3;0 . D. A2;0; 3  . 1 1 3 2
Câu 8. Cho hàm số y  f  x liên tục trên đoạn 0;  1 và thỏa mãn f  xdx 1; f  2xdx 13. Giá 0 1 6 1 trị của 2 I  x f   3xdx là 0 A. 6. B. 7. C. 9. D. 8.
Câu 9. Cho hai số phức z  52  43i và z  63 27i . Số phức z  2z có phần ảo bằng 1 2 1 2 A. 16. B. 11. C. 97. D. 11.
Mã đề 178 Đề kiểm tra gồm có 4 trang Trang 1/4 15 15 Câu 10. Cho f
 xdx 10 . Khi đó 123 f   x dx  bằng 11 11 A. 18. B. 18 . C. 48. D. 78.
Câu 11. Trong không gian với hệ tọa độ Oxyz , phương trình của mặt phẳng P đi qua điểm
M 1;0;2 và song song với mặt phẳng Q : 7x  6y  4z  5  0 là
A. 7x  6 y  4z 15  0 .
B. 7x  6 y  4z 1  0 .
C. 7x  6 y  4z 15  0 .
D. 7x  6 y  4z 1  0.
Câu 12. Diện tích S của hình phẳng H  giới hạn bởi các đường cong 3 2 y  x  2x 12x và 2 y  3x là 937 397 343 160 A. S  . B. S  . C. S  . D. S  . 12 4 12 3 1
Câu 13. Cho hàm số f  x thỏa f  x  92x  41 và f 0  4 . Tính f  xdx  . 0 5 7 7 5 A. . B.  . C. . D.  . 6 6 6 6 0 9 9 Câu 14. Nếu f  xdx  23 và f
 xdx  11 thì f xdx  bằng 2 2 0 A. 34. B. 12. C. 34 . D. 12 . x  2  3t 
Câu 15. Trong không gian với hệ tọa độ Oxyz , đường thẳng d : y  5  4t có một vectơ chỉ phương là z  6 7t      A. u  3; 4  ;7 . B. u  2;5;6 . C. u  3; 4;7 . D. u  3; 4  ;7 . 1   3   2   4  
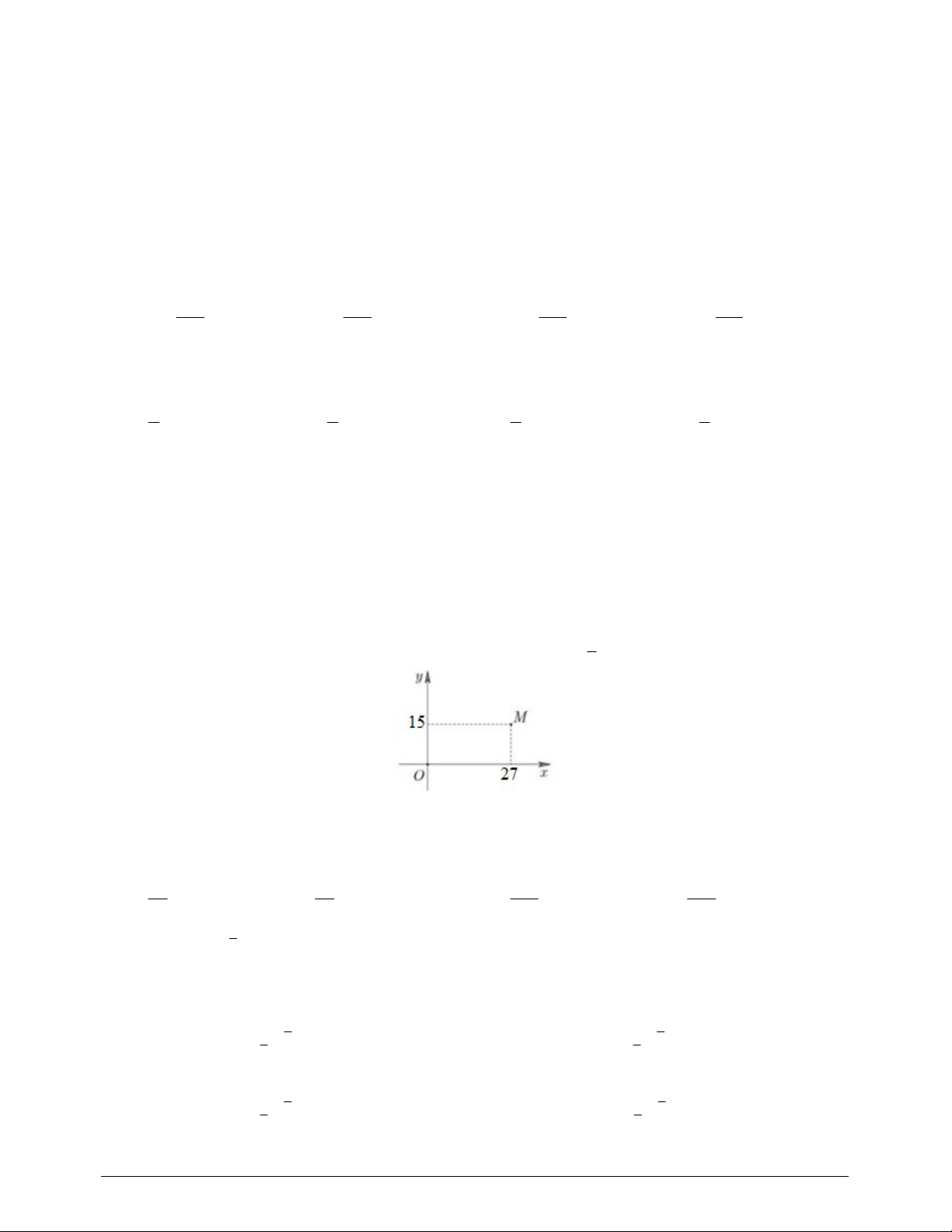
Câu 16. Cho số phức z biểu diễn bởi điểm M trong hình. Số phức z là A. 15  27i . B. 27 15i . C. 15  27i . D. 27 15i .
Câu 17. Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 2 y  x  4x và y  0 quanh trục Ox là 32 32 512 512 A.  . B. . C.  . D. . 3 3 15 15  4
Câu 18. Cho I  8 xsin xdx . Nếu đặt u  8 x và dv  sin xdx thì I được tính bằng công thức nào 0 dưới đây?    4  4 A. I  8  x 4 cos |x  cos xdx  . B. I  8  x 4 cos |x  cos xdx  . 0 0 0 0    4  4 C. I  8  x 4 cos |x  cos xdx  . D. I  8  x 4 cos |x  cos xdx  . 0 0 0 0
Mã đề 178 Đề kiểm tra gồm có 4 trang Trang 2/4 Câu 19. Gọi ,
A B là điểm biểu diễn hai nghiệm phức của phương trình 2
z  5z  9  0 trên mặt phẳng toạ
độ Oxy . Tìm toạ độ trung điểm M của đoạn AB .  5   11  A. M 5;0 . B. M ;0   . C. M 0; 11. D. M 0;  .  2   2   
Câu 20. Môđun của số phức z thỏa mãn 1 2i z  12 11i bằng 110 A. 8 . B. 55 . C. 53 . D. . 2
Câu 21. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A7;1;5 và B9;1;3 . Phương trình nào
sau đây không phải là phương trình đường thẳng AB ? x  4 y  4 z  2 x  9 y 1 z  3 A.   . B.   . 1 1 1  1 1 1 x  9 y 1 z  3
C. x 8  y  4  z . D.   . 2 2 2
Câu 22. Gọi z , z là hai nghiệm phức của phương trình 2 z  4z  5  0 . Tính 2 2 A  z  z . 1 2 1 2 A. 2 10 . B. 20 . C. 10 . D. 10 .
Câu 23. Cho số phức z thỏa mãn z 1112i  2 . Tìm giá trị lớn nhất của z . A. 265 . B. 2  265 . C. 4  265 . D. 265  2 .
Câu 24. Trong không gian với hệ tọa độ Oxyz , mặt phẳng   qua A2;1;5 và chứa trục Ox có  b
vectơ pháp tuyến n  a; ;
b c. Khi đó tỉ số là c b 1 b b b 1 A.  . B.  5 . C.  5 . D.   . c 5 c c c 5 Câu 25. Cho hàm số 3 2
y  x  3x 10x có đồ thị C . Gọi S là diện tích hình phẳng giới hạn bởi C 
và trục hoành. Phát biểu nào sau đây đúng? 0 5 A. S    3 2
x  3x 10xdx   3 2 x  3x 10xdx . 2 0 0 5 B. S    3 2
x  3x 10xdx   3 2 x  3x 10xdx . 2 0 5 5 C. S    3 2 x  3x 10xdx . D. S    3 2 x  3x 10xdx . 2 2 x  1   t 
Câu 26. Trong không gian với hệ tọa độ Oxyz , cho điểm M 4;1; 
1 và đường thẳng  : y  2   3t . z  2  t  Gọi H  ; a ;
b c là hình chiếu của M lên  . Lúc đó a  b  c bằng A. 5. B. 1. C. 1. D. 3  . x  
Câu 27. Họ tất cả các nguyên hàm của hàm số f x 1    là  2  2x 1 2x  1  A.  C . B.  C . C.  C . D.  C . ln 2 2x ln 2 ln 2 2x ln 2
Mã đề 178 Đề kiểm tra gồm có 4 trang Trang 3/4
Câu 28. Trong không gian với hệ tọa độ Oxyz , phương trình của mặt cầu S  có tâm I 1; 2;3 và tiếp
xúc với mặt phẳng P : 2x  9y  9z 123  0 là
A.  x  2   y  2   z  2 1 2 3  166 .
B.  x  2   y  2   z  2 1 2 3  156 .
C.  x  2   y  2   z  2 1 2 3  156 .
D.  x  2   y  2   z  2 1 2 3  166 .
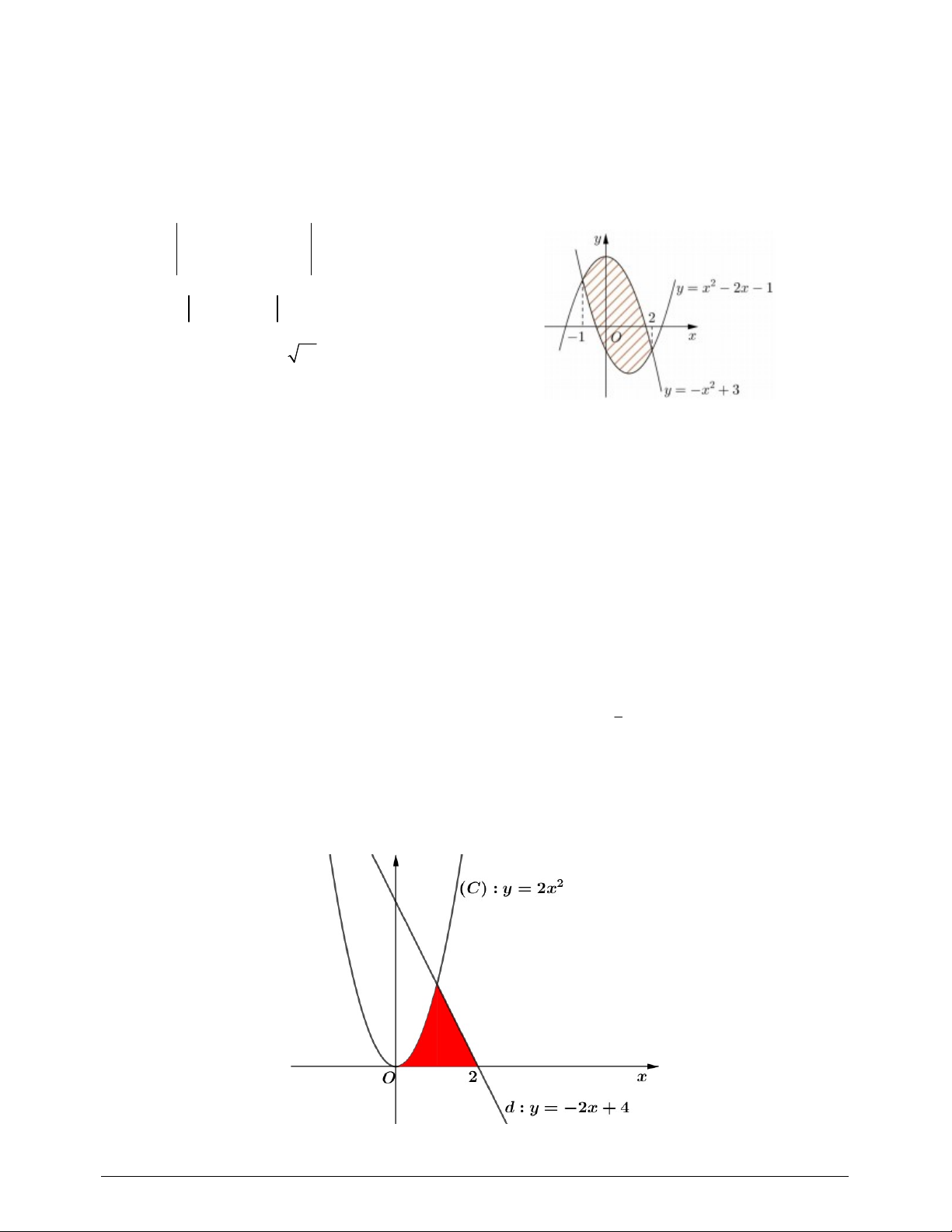
Câu 29. Kết quả nào dưới đây sai khi tính diện tích S phần hình phẳng gạch chéo theo hình sau 2 A. S    2 2x  2x  4dx . 1 2 B. 2 S  2x  2x  4dx  . 1
C. giá trị S thỏa: S  83;. 2 D. S    2 2  x  2x  4dx. 1 
Câu 30. Trong không gian với hệ tọa độ Oxyz , một vectơ pháp tuyến của mặt phẳng
23x  20y  21z 1  0 là     A. n  23; 2  0; 2
 1 . B. n  23;20;21 . C. n  23; 20; 21 . D. n  20; 23; 21 . 2   1   3   4  
II. PHẦN TỰ LUẬN (2,5 điểm)
Câu 1. (0,75 điểm) Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng trung trực của đọan AC biết A1; 3  ; 2  , C 3;1;4. 
Câu 2. (0,75 điểm) Tính tích phân 4 I  cos . x sin xdx  . 0
Câu 3. (0,5 điểm) Cho số phức z  a  bi a,b   thỏa 2  3i z  2z 16  3 .i Tính giá trị biểu thức P  3a  . b
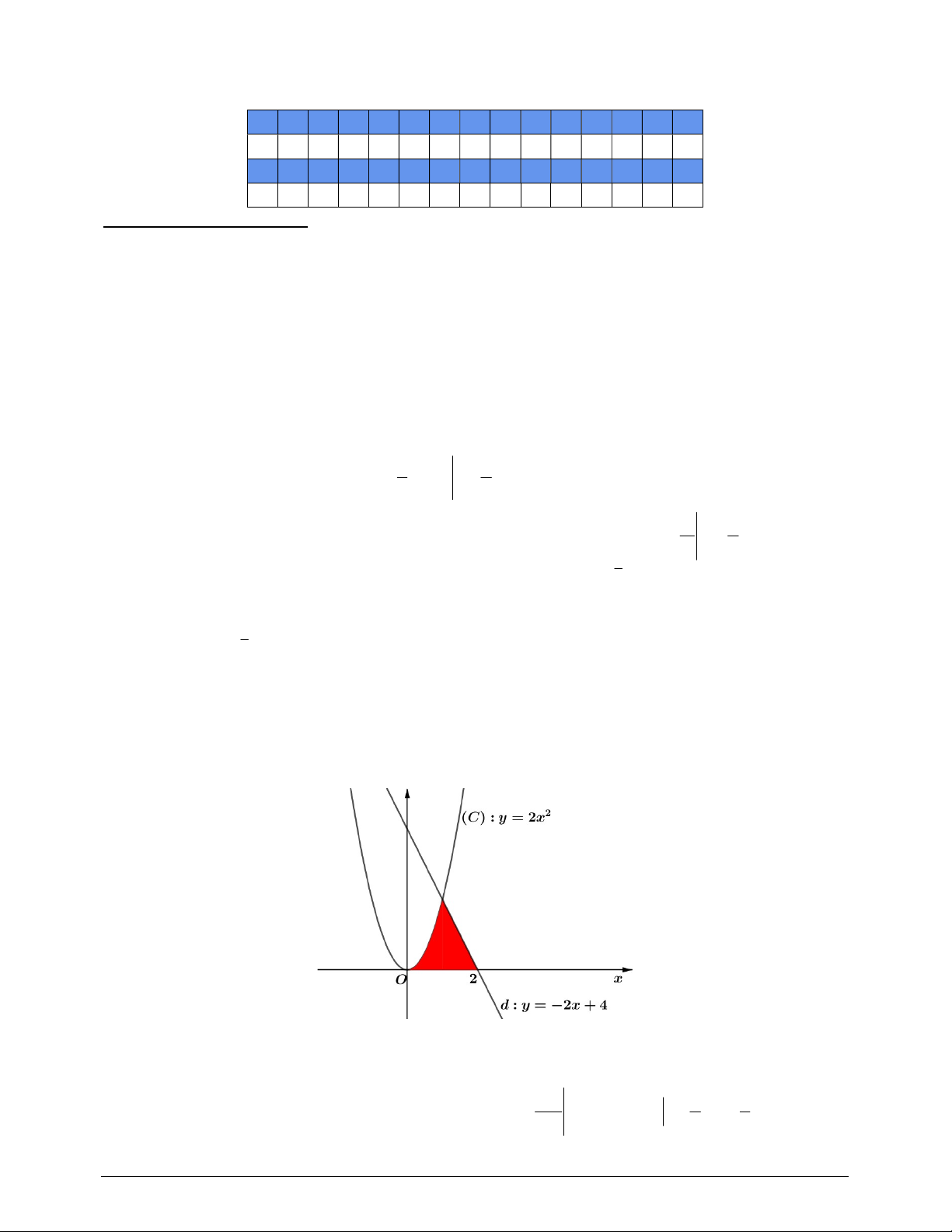
Câu 4. (0,5 điểm) Cho hàm số 2
y  2x có đồ thị C  và đường thẳng d : y  2x  4 được vẽ trên cùng
một hệ trục tọa độ như hình bên dưới. Tính diện tích của phần hình phẳng được tô đậm như trong hình. -----Hết-----
Mã đề 178 Đề kiểm tra gồm có 4 trang Trang 4/4 ĐÁP ÁN
PHẦN TRẮC NGHIỆM: (0.25x30)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 D A A B C A B C D A C A B B D
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 D C B B C A D B C B D D A C B
II. PHẦN TỰ LUẬN (2,5đ)
Câu 1. (0,75 điểm) Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng trung trực
của đọan AC biết A1; 3  ; 2  , C  3  ;1;4. Trung điểm AC : B  1  ; 1  ;  1 (0,25đ) 
Vecto pháp tuyến của mặt phẳng AC   4
 ;4;6  22;2;3 (0,25đ)
 Ptmp : 2(x 1)  2( y 1)  3(z 1)  0  2x  2y  3z  3  0 (0,25đ) 
Câu 2. (0,75 điểm) Tính tích phân 4 I  cos . x sin xdx  . 0   1  2 4 4 5 I  cos . x sin d x x   cos d x (cosx)   cos x    (0,25đx3) 5 5 0 0 0 1 1 1 5 t 2
Cách khác: Đặt t  cos x  dt   sin xdx . (0,25đ) 4 I   t dt  (0,25đ) 4  t dt    . (0,25đ) 5 5 1 1 1
Câu 3. (0,5 điểm) Cho số phức z  a  bi a,b   thỏa 2  3i z  2z 16  3 .i Tính giá trị biểu thức P  3a  . b
Ta có: 2  3i z  2z 16  3i  2  3ia  bi  2a  bi 16  3i (0,25đ)     a  b a 1 4
3  3ai  16  3i  
. (0,25đ) Vậy P  3a  b  1. (0,25đ) b   4 
Câu 4. (0,5 điểm) Cho hàm số 2
y  2x có đồ thị C  và đường thẳng d : y  2x  4 được vẽ trên cùng
một hệ trục tọa độ như hình bên dưới. Tính diện tích của phần hình phẳng được tô đậm như trong hình. x  1 Ta có 2 2 2x  2
 x  4  2x  2x  4  0   x  2 1 2 1 3 2 2x 2 5
Căn cứ vào đồ thị ta có: 2 S  2x dx  
2x 4dx (0,25đ)   2
x  4x  1 (0,25đ) 1 3 3 3 0 1 0
Mã đề 178 Đề kiểm tra gồm có 4 trang Trang 5/4