Đề thi học kì 2 Toán 12 năm 2019 – 2020 trường THPT Trần Phú – Hà Nội

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2019 – 2020 .Mời bạn đọc đón xem.

23 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

13 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Trang 1/12 - Mã đề thi 001
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT TRẦN PHÚ - HOÀN KIẾM
Đề kiểm tra có 6 trang
ĐỀ KIỂM TRA HỌC KÌ II NĂM HỌC 2019-2020
MÔN: TOÁN 12
Thời gian làm bài: 90 phút;
(50 câu trắc nghiệm)
Mã đề 001
Họ, tên thí sinh: ..................................................................... Số báo danh: .............................
Câu 1: Trong không gian Oxyz , phương trình đường thẳng d đi qua điểm
(1; 6;4)
A
và song song với
đường thẳng
2
4
5
x t
d y t
z t
là:
A.
1 6 4
1 1 1
x y z
B.
1 6 4
2 4 5
x y z
C.
1 1 1
1 6 4
x y z
D.
2 4 5
1 1 1
x y z
Câu 2: Trong không gian Oxyz , cho đường thẳng d có phương trình
1 2
3
2
x t
y
z t
, một vecto chỉ phương
của d có toạ độ là:
A.
(1;3;2)
B.
(2;0; 1)
C.
D.
(3;3;1)
Câu 3: Nếu
15
5
( ) 30
f x dx
thì
3
1
(5 )f x dx
bằng
A.
15
B.
6
C.
10
D.
5
Câu 4: Diện tích hình phẳng giới hạn bởi các đồ thị các hàm số y = x
2
, y = 0, x = 1 bằng
A.
1
2
B.
1
3
C.
3
D.
1
Câu 5: Trong không gian Oxyz , cho đường thẳng
3
:
3 1 1
x y z
d
và mặt phẳng
( ): 2 1 0
P x z
.
Gọi
là đường thẳng nằm trên (P), cắt và vuông góc với d, đường thẳng
có phương trình là:
A.
3 2
1 5
2
x t
y t
z t
B.
3 1
1 5
2
x t
y t
z t
C.
3 2
1 5
2
x t
y t
z t
D.
3
1 5
2 2
x t
y t
z t
Câu 6: Cho hàm số
( )f x
liên tục trên R. Biết
(4) 4, (1) 3
f f
. Tính
4
1
'( )f x dx
bằng
A.
12
B. 7 C.
1
D.
1
Câu 7: Cho
( )F x
là một nguyên hàm của hàm số
1
( ) sin
4 1
f x x
x
. Biết
(0) 5
F
, tính
( )
F
A.
5
5 ln(4 1)
4
B.
5
7 ln(4 1)
4
C.
1
5 ln(4 1)
4
D.
1
7 ln(4 1)
4
Trang 2/12 - Mã đề thi 001
Câu 8: Cho số phức
z
thoả mãn
3 4 5z z i
. Phần ảo của z là
A.
1
B.
5
2
C.
1
D.
5
2
Câu 9: Cho số phức
( , )z a bi a b R
thoả mãn
1
z z i
. Nếu
2z i
nhỏ nhất thì
2 3a b
bằng
A. -1 B.
5
C. 1 D.
5
Câu 10: Trong không gian Oxyz , cho
(1;4; 2) ( 5; 2;8)
A B
, phương trình mặt cầu đường kính AB là:
A.
2 2 2
( 3) ( 3) ( 5) 172
x y z
B.
2 2 2
( 2) ( 1) ( 3) 172
x y z
C.
2 2 2
( 2) ( 1) ( 3) 43
x y z
D.
2 2 2
( 2) ( 1) ( 3) 43
x y z
Câu 11: Cho
A(4;1;-1), B(2;1;0), C(5;-1;4)
Toạ độ điểm D thoả mãn ABCD là hình bình hành là
A.
B.
C.
1
(3;1; )
2
D.
9 5
( ;0; )
2 2
Câu 12: Cho số phức
5
3 2
4
z i
i
. Phần thực của z là
A.
29
17
B.
17
4
C.
7
D.
71
17
Câu 13: Cho số phức
z
thoả mãn
5
z
. Môđun của số phức
(4 )z i
bằng
A.
5 17
B.
5 17
C.
20
D.
15
Câu 14: Tìm
( 2 )
x x
e dx
được kết quả là
A.
2
ln 2
x
x
e
B.
2
ln 2
x x
e
C
C.
2
ln 2
x
x
e C
D.
2 ln 2
x x
e C
Câu 15: Cho số phức
z
có phần thực bằng 3, phần ảo là số thực dương,
13
z
. Số phức
z
bằng
A.
3 2i
B.
3 2i
C.
3 2i
D.
3 2i
Câu 16: Trong không gian Oxyz, cho mặt phẳng (P) chứa 2 điểm
(1;4;0), N(2; 1;3)
M
và song song
với đường thẳng d là giá của vectơ
a
. Một vectơ pháp tuyến của mặt phẳng (P) có toạ độ là
A. (4; 1; -5) B.
( 26;23; 11)
C.
(23; 11; 26)
D. (1; -5; 3)
Câu 17: Trong không gian Oxyz , mặt cầu
2 2 2
( ) 4 8 6 3 0
S x y z x y z
có tâm I, toạ độ điểm
I là
A.
( 4;8; 6)
B.
( 2;4; 3)
C.
(2; 4;3)
D.
(4; 8;6)
Câu 18: Trong không gian Oxyz , cho mặt phẳng
( ) 2 4 0
P x y z
và mặt phẳng
( ) 4 2 5 0
Q x y mz
. Giá trị của m để mặt phẳng (P) vuông góc với mặt phẳng (Q) là:
A.
0m
B.
10m
C.
2m
D.
1m
Câu 19: Cho số phức
z
thoả mãn
2 7 8z zi i
. Phần thực của
z
bằng
A.
22
5
B.
9
5
C.
9
5
D.
22
5
Câu 20: Trong không gian Oxyz . mặt phẳng (P) đi qua điểm
(1;4; 5)
A
và vuông góc với đường thẳng
d
1
2 1
x y
z
có phương trình:
A.
2 2 0x y
B.
4 5 1 0x y z
C.
4 5 40 0x y z
D.
2 7 0x y z
Trang 3/12 - Mã đề thi 001
Câu 21: Cho
2020
1
ln
e
e
dx
x x
. Nếu đặt
ln x u
thì
2020
1
ln
e
e
dx
x x
bằng
A.
2020
e
e
udu
B.
2020
1
e
e
du
u
C.
2020
1
udu
D.
2020
1
1
du
u
Câu 22: Cho
2
7
0
sin cos x xdx
. Đặt
sin x t
thì
2
7
0
sin cos x xdx
bằng
A.
2
7
0
t dt
B.
1
7
0
cost xdt
C.
1
7
0
t dt
D.
2
7
0
cos
t xdx
Câu 23: Trên tập số phức, cho phương trình
2
0z z m
với tham số
m R
. Gọi S là tập các giá trị
nguyên của m thuộc
10;10
sao cho phương trình đó có hai nghiệm phân biệt
1 2
;z z
đồng thời thoả
mãn
1 1
z z
và
2 2
z z
Tập S có số phần tử là
A.
4
B.
6
C.
0
D.
11
Câu 24: Trong không gian Oxyz cho
(5; 1;4)
M
. Toạ độ điểm M’ là hình chiếu của M lên mặt phẳng
Oxy là
A.
B.
(5;0;4)
C.
(0; 1;4)
D.
(0;0;4)
Câu 25: Cho số phức z được biểu diễn hình học bởi điểm M(-4; 3) trên mặt phẳng toạ độ Oxy. Số phức z
bằng
A.
4 3z i
B.
4 3z i
C.
4 3i
D.
4 3z i
Câu 26: Cho số phức
z
thoả mãn
1 3
z
. Tập hợp điểm M biểu diễn số phức z trên mặt phẳng toạ độ
Oxy là
A. Đường tròn tâm I(-1; 0), bán kính R = 3 B. Đường tròn tâm I(-1; 0), bán kính R = 9
C. Đường tròn tâm I(1; 0), bán kính R = 9 D. Đường tròn tâm I(1; 0), bán kính R = 3
Câu 27: Cho
(3) (3) 5, (1) (1) 4
f g f g
và
3
1
( ) '( ) 20
f x g x dx
. Tính
3
1
'( )g( )f x x dx
bằng
A.
11
B.
1
C.
0
D.
11
Câu 28: Cho hình phẳng giới hạn bởi đồ thị các hàm số
x
e , y=100lnx, 1, x= 5
y x
. Diện tích miền
hình phẳng trên được tính theo công thức
A.
5
x
1
100ln e
x dx
B.
5
x
1
(e 100ln )x dx
C.
5
x
1
(100ln e )x dx
D.
5
x
1
(100ln e )x dx
Câu 29: Cho hình phẳng giới hạn bởi đồ thị các hàm số
x
e , 0, 0, x= 1
y y x
. Quay miền hình
phẳng trên quanh trục Ox được vật thể tròn xoay có thể tích là
A.
2
( 1)
2
e
B.
2
( 1)
2
e
C.
( 1)
2
e
D.
( 1)
2
e
Trang 4/12 - Mã đề thi 001
Câu 30: Cho
2
0
( ) 5
f x dx
. Tính
2
0
(2 ( ) cos )f x x dx
bằng
A.
11
B.
9
C. 10 D.
10
2
Câu 31: Cho hình phẳng giới hạn bởi đồ thị các hàm số
( ), 0, , x b ( a b)
y f x y x a
. Quay
miền hình phẳng trên quanh trục Ox được vật thể tròn xoay có thể tích được tính theo công thức nào dưới
đây
A.
( )
b
a
f x dx
B.
( )
b
a
f x dx
C.
2
[ ( )]
b
a
f x dx
D.
2
[ ( )]
b
a
f x dx
Câu 32: Trong không gian Oxyz , cho đường thẳng d có phương trình
1
3
1 2
x t
y t
z t
và điểm
(0; 6;0)
A
.
Điểm
( ; ; )
o o o
H x y z
thuộc d sao cho độ dài đoạn AH nhỏ nhất, giá trị
o o o
T x y z
bằng:
A.
7
B.
1
C.
4
D.
0
Câu 33: Trong không gian Oxyz , mặt cầu tâm
(1;4;3)
A
bán kính R=10 cắt trục Ox tại 2 điểm M và N.
Độ dài đoạn MN là
A.
2 99
B.
99
C.
2 75
D.
75
Câu 34: Cho
1 2
;z z
là hai nghiệm của phương trình
2
4 5 0z z
trên tập số phức. Tính
1 2
A z z
bằng
A.
2 5
B.
4
C.
10
D.
5
Câu 35: Cho số phức
2 3z i
. Môđun của số phức z bằng
A.
7
B.
5
C.
2 3
D.
13
Câu 36: Cho hai hàm số
u x và v x
liên tục trên R
(được viết tắt là
u
và
v
). Mệnh đề nào sau đây
đúng?
A.
( )'. ' .uv dx uv u v dx
B.
. ( )' ' .uvdx uv u v dx
C.
' . ' ' '.u v dx u v uv dx
D.
'. ' .uv dx uv u v dx
Câu 37: Trong không gian Oxyz, khoảng cách từ điểm
(1;0;3)
A
tới mặt phẳng
( ) 2 5 0
P x y z
bằng:
A.
1
B.
5
6
C.
4
D.
4
6
Câu 38: Cho hai số phức
1 2
5 2 , 4z i z i
. Số phức
2
1 2
2z z
bằng
A.
18 2i
B.
18 29i
C.
29 18i
D.
29 18i
Câu 39: Cho
3 9
1 3
( ) 7, ( ) 2
f x dx f x dx
. Tính
9
1
( )f x dx
bằng
A.
5
B.
9
C.
14
D.
5
Câu 40: Trong không gian Oxyz , cho mặt phẳng
( ): 4 0
P x y z
và mặt phẳng
( ) : -2 3 0
Q x z
. Gọi
là góc giữa 2 mặt phẳng (P) và (Q),
cos
bằng:
A.
3
15
B.
2
15
C.
3
15
D.
2
42
Trang 5/12 - Mã đề thi 001
Câu 41: Gọi
z
là căn bậc hai của số phức
w 8i
,
z
có phần thực và phần ảo cùng dương, đặt
2 2023
1 .....A z z z
.
Số phức A có phần thực là
A.
2022
1 8
65
B.
1012
8 1
5
C.
1012
1 8
5
D.
2022
1 8
65
Câu 42: Trong không gian Oxyz , cho
1
3 2
1 3
10 2
x t
d y t
z t
và
2
14 14 4
19 14 2
x y z
d
. Phương trình
mặt cầu tiếp xúc với
1
d
và
2
d
và có bán kính nhỏ nhất là:
A.
2 2 2
( 2) ( 1) 25
x y z
B.
2 2 2
( 3) ( 2) ( 3) 25
x y z
C.
2 2 2
( 3) ( 2) ( 3) 33
x y z
D.
2 2 2
( 1) ( 3) ( 2) 33
x y z
Câu 43: Trong không gian với hệ toạ độ Oxyz cho đường thẳng
2 1
: ( )
2 1 1
x m y m z m
d m R
. Biết với mọi m, đường thẳng d luôn nằm trên một mặt phẳng
cố định. Gọi
0
m
là giá trị của m để đường thẳng d cách điểm B(4; -3; 1) một khoảng bé nhất,
0
m
thuộc
khoảng nào dưới đây
A.
1;2
B.
5;7
C.
4; 1
D.
2;5
Câu 44: Trong không gian Oxyz , cho
(1; 7;2), N(5;1;4)
M
. Mặt phẳng (
) đi qua N và cách M một
khoảng lớn nhất có phương trình
0Ax By z D
. Tính A+B+D
A.
11
B.
7
C.
12
D.
14
Câu 45: Cho một xe máy đang chuyển động đều với vận tốc 6m/s thì tăng tốc với gia tốc là
2
2 /a m s
.
Quãng đường xe máy đi được kể từ khi tăng tốc đến lúc vận tốc xe đạt 14m/s bằng
A.
14m
B.
40m
C.
44m
D.
28m
Câu 46: Cho hàm số
( )y f t
liên tục trên R và hàm số
'( )y f t
có đồ thị như sau:
Chọn khẳng định đúng
A.
( 1) (5) (3)f f f
B.
(3) ( 1) (5)f f f
C.
( 1) (3) (5)f f f
D.
(3) (5) ( 1)
f f f
Câu 47: Nếu
9
1
( )
8
f
x
dx
x
thì
3
1
( )f x dx
bằng
A.
8
B.
4
C.
22
D.
16
Trang 6/12 - Mã đề thi 001
Câu 48: Cho hàm số f(x) liên tục và khác 0
0;2
x
. Biết
2
'( ) (2 1) ( ) 0;2
f x x f x x
và
1
(0)
20
f
. Tính
2
1
( )f x dx
được kết quả là
A.
1 7
ln
9 4
B.
97
6
C.
4
D.
1 7
ln
9 4
Câu 49: Cho số phức
z
thoả mãn
4 7 5
z i
. Trên mặt phẳng Oxy, tập hợp điểm M biểu diễn số
phức w thoả mãn
w 2 4z i
là một đường tròn có bán kính bằng
A.
5
2
B. 5 C. 10 D.
5
Câu 50: Trong không gian với hệ toạ độ Oxyz cho mặt cầu (S) tâm I có phương trình:
2 2 2
(x 1) ( 2) 25
y z
và mặt phẳng (P) có phương trình: x + 2y – 3z + D = 0. Đường thẳng
thay đổi luôn nằm trên mặt phẳng (P) sao cho tồn tại hai mặt phẳng qua
, tiếp xúc với mặt cầu (S) và
tạo với nhau góc
0
60
. Gọi J là hình chiếu vuông góc của I lên
. Có bao nhiêu giá trị nguyên của D sao
cho tập hợp các điểm J là hai đường tròn phân biệt?
A.
42
B.
75
C.
37
D.
43
-----------------------------------------------
----------- HẾT -----------
made cautron dapan
001 1 A
001
2 B
001 3 B
001 4 B
001 5 A
001 6
C
001 7 D
001 8 B
001 9
D
001 10 C
001 11 B
001 12
D
001 13 A
001 14 C
001 15
C
001 16 C
001 17 C
001 18
B
001 19 B
001 20 D
001 21 D
001 22 C
001 23 D
001 24 A
001 25 B
001 26 D
001 27 A
001 28 A
001 29 A
001 30 A
001 31 D
001 32 A
001 33 C
001 34 A
001
35 A
001 36 D
001 37 D
001 38 D
001 39 B
001 40 C
001 41 B
001 42 C
001 43 A
001 44 C
001 45 B
001 46 D
001 47 B
001 48 D
001 49 C
001 50 D
Trang 7/12 - Mã đề thi 001
HƯỚNG DẪN GIẢI
Câu 23: Trên tập số phức, cho phương trình
2
0z z m
với tham số
m R
. Gọi S là tập các giá trị
nguyên của m thuộc
10;10
sao cho phương trình đó có hai nghiệm phân biệt
1 2
;z z
đồng thời thoả
mãn
1 1
z z
và
2 2
z z
Tập S có số phần tử là
A.
4
B.
6
C.
0
D.
11
Lời giải
Chọn D
1 1
2 2
z z
z z
1 2
,z z
là số thực
Để phương trình có 2 nghiệm phân biệt:
1
0
4
m
Đề bài yêu cầu
10;10 , 10 0
m m Z m
Vậy có 11 giá trị thỏa mãn yêu cầu đề bài
Câu 41: Gọi
z
là căn bậc hai của số phức
w 8i
,
z
có phần thực và phần ảo cùng dương, đặt
2 2023
1 .....A z z z
.
Số phức A có phần thực là
A.
2022
1 8
65
B.
1012
8 1
5
C.
1012
1 8
5
D.
2022
1 8
65
Lời giải
Chọn B
Có
2 2
2 2 2
8 4 2.2 4 2 2.2 2 2 2z i z i i i i
2 2
2 2
2 2
z i
z i
z i
1012
1012
2
2024
506
1012 2 1012 1012
1012 1012
2 2
1
1 8
1
1 1 1 2 2
1 8 1 8 1 2 2 1 8
1 8 8 1
1 2 1 2 1 2 5 5
z
i
z
A
z z i
i i
i
i i
Câu 42: Trong không gian Oxyz , cho
1
3 2
1 3
10 2
x t
d y t
z t
và
2
14 14 4
19 14 2
x y z
d
. Phương trình
mặt cầu tiếp xúc với
1
d
và
2
d
và có bán kính nhỏ nhất là:
A.
2 2 2
( 2) ( 1) 25
x y z
B.
2 2 2
( 3) ( 2) ( 3) 25
x y z
C.
2 2 2
( 3) ( 2) ( 3) 33
x y z
D.
2 2 2
( 1) ( 3) ( 2) 33
x y z
Lời giải
Chọn C
Gọi MN là đoạn vuông góc chung, suy ra mặt cầu cần tìm là mặt cầu đường kính MN
Cách 1:
Chọn
1
2
1
2
3 2 ;1 3 ; 10 2 t
14 19 ; 14 14 ;4 2
. 0
1;4; 8 , 5;0;2 3;2; 3 , 33
. 0
M t t d
N k k k d
MN u
M N I IM R
MN u
Trang 8/12 - Mã đề thi 001
Cách 2: Dễ thấy
1 2
d d
Gọi
P
là mặt phẳng thỏa mãn
1
2
2
5;0;2
d P
P d N N
d P
Gọi
Q
là mặt phẳng thỏa mãn
2
1
1
1;4; 8
d Q
Q d M M
d Q
Câu 43: Trong không gian với hệ toạ độ Oxyz cho đường thẳng
2 1
: ( )
2 1 1
x m y m z m
d m R
. Biết với mọi m, đường thẳng d luôn nằm trên một mặt phẳng
cố định. Gọi
0
m
là giá trị của m để đường thẳng d cách điểm B(4; -3; 1) một khoảng bé nhất,
0
m
thuộc
khoảng nào dưới đây
A.
1;2
B.
5;7
C.
4; 1
D.
2;5
Lời giải
Chọn A
Cách 1
Từ phương trình đường thẳng
d
có
2 1 3
/ :
2 2 2 1 2 1
4 1 3
2 1
: 1 0
3 3
x m z m x z
t
a c a c
t c
x m y m x y
b d b d
t
x z x y
P x y z
Gọi H là hình chiếu vuông góc của B lên
P
, đường thẳng d đi qua H là đườn thẳng cần tìm
Có phương trình
4
3
1
x t
BH y t
z t
1
BH P H m
Cách 2: đường thẳng d luôn nằm trên 1 mặt phẳng cố định. Chọn 2 giá trị ngẫu nhiên của m
0
1
0 :
2 1 1
1 1 1
1 :
2 2 1
x y z
m d
x y z
m d
Viết phương trình mặt phẳng
P
chứa
0 1
,d d
: 1 0
P x y z
Gọi H là hình chiếu vuông góc của B lên
P
Có phương trình
4
3
1
x t
BH y t
z t
1
BH P H m
Cách 3
Trang 9/12 - Mã đề thi 001
Gọi
2 2 2
0 0 . 0
2 0 2 1
2 0
; 2 1;
. . 2 1 2 . 0 m 3 3 0 m
0 2
3 3 0
0
0 3
1
0, 1 2 0
2
d
P
P Ax By Cz D A B C d P n n
A B C C A B
P Ax By A B z D
M m m m d M P
A m B m A B m D m A B B D
A B
A B
B D
B D
TH
B A B C koTM
TH
B
0
Chọn
1
1 1
1
A
B C
D
: 1 0
P x y z
Cách 4: *Lập ptmp (Q) qua B và vuông góc d: 2x + y - z – 4 = 0
* (Q) cắt d tại A(….), A phụ thuộc m
* Tính đoạn BA (phụ thuộc tham số m - bậc 2), tìm m để BA nhỏ nhất => m = 1
Câu 44: Trong không gian Oxyz , cho
(1; 7;2), N(5;1;4)
M
. Mặt phẳng (
) đi qua N và cách M một
khoảng lớn nhất có phương trình
0Ax By z D
. Tính A+B+D
A.
11
B.
7
C.
12
D.
14
Lời giải
Chọn C
Mặt phẳng
qua N và cách M một khoảng lớn nhất
2 4 18 0
2 4 18 12
MN
mp
N
x y z
A B D
Câu 45: Cho một xe máy đang chuyển động đều với vận tốc 6m/s thì tăng tốc với gia tốc là
2
2 /a m s
.
Quãng đường xe máy đi được kể từ khi tăng tốc đến lúc vận tốc xe đạt 14m/s bằng
A.
14m
B.
40m
C.
44m
D.
28m
Lời giải
Chọn B
Vận tốc xe máy
6 6 2
t
v at t
Thời gian tăng tốc đến khi vận tốc đạt
14 /m s
6 2 14 4
t t s
Vậy quãng đường
4
0
6 2 40
S t dt m
Câu 46: Cho hàm số
( )y f t
liên tục trên R và hàm số
'( )y f t
có đồ thị như sau:
Trang 10/12 - Mã đề thi 001
Chọn khẳng định đúng
A.
( 1) (5) (3)f f f
B.
(3) ( 1) (5)f f f
C.
( 1) (3) (5)f f f
D.
(3) (5) ( 1)
f f f
Lời giải
Chọn D
Ta có bảng biến thiên
Từ BBT suy ra trong ba giá trị
1 , 3 , 5
f f f
thì
3f
lớn nhất
So sánh diện tích 2 phần ta có:
3 5
1 3
3 5
1 3
3 1 3 5
1 5
3 5 1
f t dt f t dt
f t f t
f f f f
f f
f f f
Câu 47: Nếu
9
1
( )
8
f
x
dx
x
thì
3
1
( )f x dx
bằng
A.
8
B.
4
C.
22
D.
16
Lời giải
Chọn B
Có
9
1
1
8 2
f x
I dx x t dx tdt
x x
Đổi cận
x 1 9
t 1 3
Trang 11/12 - Mã đề thi 001
3 3 3
1 1 1
2 8 4 4
I f t dt f t dt f x dx
Câu 48: Cho hàm số f(x) liên tục và khác 0
0;2
x
. Biết
2
'( ) (2 1) ( ) 0;2
f x x f x x
và
1
(0)
20
f
. Tính
2
1
( )f x dx
được kết quả là
A.
1 7
ln
9 4
B.
97
6
C.
4
D.
1 7
ln
9 4
Lời giải
Chọn D
2 2
2
2
2
2
1
2 1 2 1
1 1
1 1 1
0 20
20 20
1 1 7
ln
20 9 4
f x f x
x dx x dx
f x f x
x x C f x
f x x x C
f C
C
f x f x dx
x x
Câu 49: Cho số phức
z
thoả mãn
4 7 5
z i
. Trên mặt phẳng Oxy, tập hợp điểm M biểu diễn số
phức w thoả mãn
w 2 4z i
là một đường tròn có bán kính bằng
A.
5
2
B. 5 C. 10 D.
5
Lời giải
Chọn C
Có
4 7 5 (1)
z i
4
2 4 2
2
4
1 , 2 4 7 5
2
10 7 10
10
w i
w z i z
w i
i
w i
R
Câu 50: Trong không gian với hệ toạ độ Oxyz cho mặt cầu (S) tâm I có phương trình:
2 2 2
(x 1) ( 2) 25
y z
và mặt phẳng (P) có phương trình: x + 2y – 3z + D = 0. Đường thẳng
thay đổi luôn nằm trên mặt phẳng (P) sao cho tồn tại hai mặt phẳng qua
, tiếp xúc với mặt cầu (S) và
tạo với nhau góc
0
60
. Gọi J là hình chiếu vuông góc của I lên
. Có bao nhiêu giá trị nguyên của D sao
cho tập hợp các điểm J là hai đường tròn phân biệt?
A.
42
B.
75
C.
37
D.
43
Lời giải
Chọn D
Trang 12/12 - Mã đề thi 001
Gọi J là hình chiếu vuông góc của I lên đường thẳng
TH1
60 IJ 30 2 10
o o
MJN N IJ JN
Suy ra J thuộc mặt cầu tâm I bán kính 10
Mà
J P
Suy ra để tập hợp điểm J là đường tròn thì
,
10
I P
d
( mp cắt m/cầu theo giao tuyến là một đường tròn)
TH2
5 10
120 60 .2
3 3
o o
MJN IJN IJ
Suy ra J thuộc mặt cầu tâm I bán kính
10
3
Mà
J P
Suy ra để tập hợp điểm J là đường tròn thì
,
10
3
I P
d
1 0 6
10
5 21,602
14 3
D
D
Suy ra có 43 gia trị nguyên của (D-5) có 43 giá trị nguyên của D.
----------- HẾT -----------
| 1/13
| | Tải xuống

Có thể bạn quan tâm:

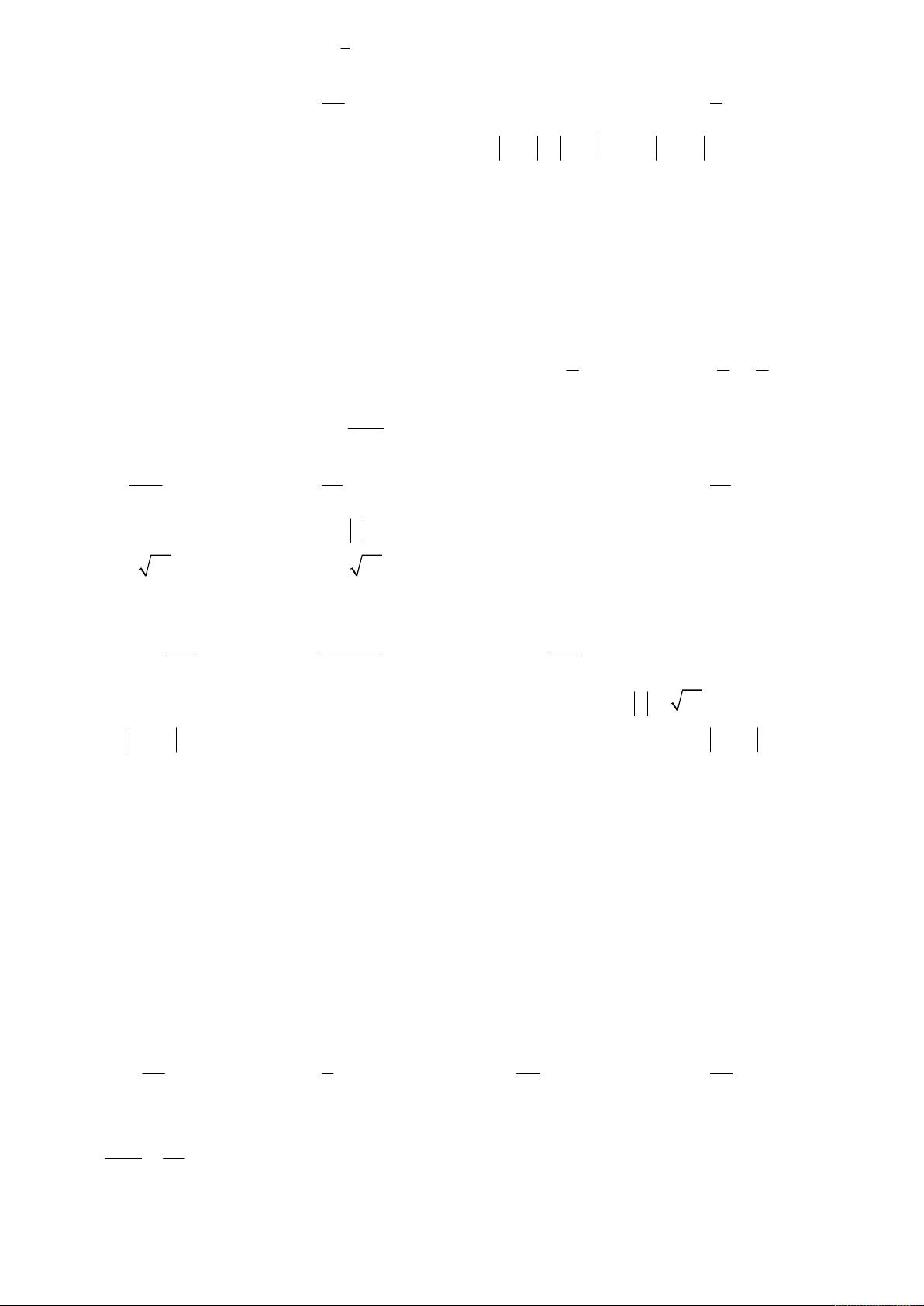
Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ KIỂM TRA HỌC KÌ II NĂM HỌC 2019-2020
TRƯỜNG THPT TRẦN PHÚ - HOÀN KIẾM MÔN: TOÁN 12
Thời gian làm bài: 90 phút;
(50 câu trắc nghiệm)
Đề kiểm tra có 6 trang Mã đề 001
Họ, tên thí sinh: ..................................................................... Số báo danh: .............................
Câu 1: Trong không gian Oxyz , phương trình đường thẳng d đi qua điểm ( A 1; 6  ;4) và song song với
x  2  t
đường thẳng d y  4  t là:
z  5  tx 1 y  6 z  4 x 1 y  6 z  4 A.   B.   1  1 1  2 4 5 x 1 y 1 z 1 x  2 y  4 z  5 C.   D.   1 6  4 1 1  1
x  1  2t
Câu 2: Trong không gian Oxyz , cho đường thẳng d có phương trình  y  3 , một vecto chỉ phương
z  2  t
của d có toạ độ là: A. (1;3; 2) B. (2;0; 1  ) C. (2;3; 1  ) D. (3;3;1) 15 3 Câu 3: Nếu
f (x)dx  30  thì f (5x)dx  bằng 5 1 A. 15 B. 6 C. 10 D. 5
Câu 4: Diện tích hình phẳng giới hạn bởi các đồ thị các hàm số y = x2, y = 0, x = 1 bằng 1 1 A. B. C. 3 D. 1 2 3 x y z  3
Câu 5: Trong không gian Oxyz , cho đường thẳng d :  
và mặt phẳng (P) : x  2z 1  0 . 3 1 1
Gọi  là đường thẳng nằm trên (P), cắt và vuông góc với d, đường thẳng  có phương trình là: x  3   2tx  3  1t
x  3  2tx  3   t     A. y  1   5t B. y  1   5t
C. y  1 5t D. y  1   5t
z  2  t     z  2  tz  2   tz  2  2t  4
Câu 6: Cho hàm số f (x) liên tục trên R. Biết f (4)  4, f (1)  3 . Tính f '(x)dx  bằng 1 A. 12 B. 7 C. 1 D. 1 1
Câu 7: Cho F (x) là một nguyên hàm của hàm số f (x)  sin x
. Biết F (0)  5 , tính F ( ) 4x 1 5 5 1 1 A. 5  ln(4 1) B. 7  ln(4 1) C. 5  ln(4 1) D. 7  ln(4 1) 4 4 4 4
Trang 1/12 - Mã đề thi 001
Câu 8: Cho số phức z thoả mãn z  3z  4  5i . Phần ảo của z là 5  5 A. 1 B. C. 1 D. 2 2
Câu 9: Cho số phức z a bi (a,b R) thoả mãn z 1  z i . Nếu z  2i nhỏ nhất thì 2a  3b bằng A. -1 B. 5 C. 1 D. 5 
Câu 10: Trong không gian Oxyz , cho ( A 1; 4; 2)  B( 5  ; 2
 ;8) , phương trình mặt cầu đường kính AB là: A. 2 2 2
(x  3)  ( y  3)  (z  5)  172 B. 2 2 2
(x  2)  ( y 1)  (z  3)  172 C. 2 2 2
(x  2)  ( y 1)  (z  3)  43 D. 2 2 2
(x  2)  ( y 1)  (z  3)  43
Câu 11: Cho A(4;1;-1), B(2;1;0), C(5;-1;4) Toạ độ điểm D thoả mãn ABCD là hình bình hành là 1 9 5 A. (3; 1  ;3) B. (7; 1  ;3) C. (3;1;  ) D. ( ;0; ) 2 2 2 5
Câu 12: Cho số phức z  3  2i  . Phần thực của z là 4  i 29  17 71 A. B. C. 7  D. 17 4 17
Câu 13: Cho số phức z thoả mãn z  5 . Môđun của số phức z(4  i) bằng A. 5 17 B. 5  17 C. 20 D. 15
Câu 14: Tìm ( x  2x e )dx  được kết quả là x  2x e x 2x x 2x A. e B. C C. e   C
D. x  2x e ln 2  C ln 2 ln 2 ln 2
Câu 15: Cho số phức z có phần thực bằng 3, phần ảo là số thực dương, z  13 . Số phức z bằng A. 3  2i B. 3  2i C. 3  2i D. 3  2i
Câu 16: Trong không gian Oxyz, cho mặt phẳng (P) chứa 2 điểm M (1; 4;0), N(2; 1  ;3) và song song 
với đường thẳng d là giá của vectơ a(5;1; 4) . Một vectơ pháp tuyến của mặt phẳng (P) có toạ độ là A. (4; 1; -5) B. ( 26  ;23; 11  ) C. (23; 11  ; 26  ) D. (1; -5; 3)
Câu 17: Trong không gian Oxyz , mặt cầu 2 2 2
(S ) x y z  4x  8 y  6z  3  0 có tâm I, toạ độ điểm I là A. ( 4  ;8; 6)  B. ( 2  ; 4; 3  ) C. (2; 4  ;3) D. (4; 8  ;6)
Câu 18: Trong không gian Oxyz , cho mặt phẳng (P) 2x y z  4  0 và mặt phẳng
(Q) 4x  2 y mz  5  0 . Giá trị của m để mặt phẳng (P) vuông góc với mặt phẳng (Q) là: A. m  0 B. m  10 C. m  2  D. m  1 
Câu 19: Cho số phức z thoả mãn 2z zi  7i  8 . Phần thực của z bằng 22 9 9  22 A. B. C. D. 5 5 5 5
Câu 20: Trong không gian Oxyz . mặt phẳng (P) đi qua điểm ( A 1;4; 5
 ) và vuông góc với đường thẳng x 1 y d
z có phương trình: 2 1 
A. 2x y  2  0
B. x  4 y  5z 1  0
C. x  4 y  5z  40  0
D. 2x y z  7  0
Trang 2/12 - Mã đề thi 001 2020 e 2020 1 e 1 Câu 21: Cho dx
. Nếu đặt ln x u thì dx  bằng x ln x x ln x e e 2020 e 2020 e 1 2020 2020 1 A. uduB. duC. uduD. duu u e e 1 1   2 2 Câu 22: Cho 7 sin x cos xdx
. Đặt sin x t thì 7 sin x cos xdx  bằng 0 0   2 1 1 2 A. 7 t dtB. 7 t cos xdtC. 7 t dtD. 7 t cos xdx  0 0 0 0
Câu 23: Trên tập số phức, cho phương trình 2
z z m  0 với tham số m R . Gọi S là tập các giá trị nguyên của m thuộc  10 
;10 sao cho phương trình đó có hai nghiệm phân biệt z ; z đồng thời thoả 1 2
mãn z z và z z Tập S có số phần tử là 1 1 2 2 A. 4 B. 6 C. 0 D. 11
Câu 24: Trong không gian Oxyz cho M (5; 1
 ; 4) . Toạ độ điểm M’ là hình chiếu của M lên mặt phẳng Oxy là A. (5; 1  ;0) B. (5;0; 4) C. (0; 1  ;4) D. (0;0; 4)
Câu 25: Cho số phức z được biểu diễn hình học bởi điểm M(-4; 3) trên mặt phẳng toạ độ Oxy. Số phức z bằng A. z  4   3i B. z  4   3i C. 4  3i
D. z  4  3i
Câu 26: Cho số phức z thoả mãn z 1  3 . Tập hợp điểm M biểu diễn số phức z trên mặt phẳng toạ độ Oxy là
A. Đường tròn tâm I(-1; 0), bán kính R = 3
B. Đường tròn tâm I(-1; 0), bán kính R = 9
C. Đường tròn tâm I(1; 0), bán kính R = 9
D. Đường tròn tâm I(1; 0), bán kính R = 3 3 3
Câu 27: Cho f (3)  g(3)  5, f (1)  g(1)  4 và
f (x)g '(x)dx  20  . Tính
f '(x) g(x)dx  bằng 1 1 A. 1  1 B. 1 C. 0 D. 11
Câu 28: Cho hình phẳng giới hạn bởi đồ thị các hàm số x
y  e , y=100lnx, x  1, x= 5 . Diện tích miền
hình phẳng trên được tính theo công thức 5 5 A. x 100ln x  e dxB. x
(e 100 ln x)dx  1 1 5 5 C. x
(100ln x  e )dxD. x
(100 ln x  e )dx  1 1
Câu 29: Cho hình phẳng giới hạn bởi đồ thị các hàm số x
y  e , y  0, x  0, x= 1. Quay miền hình
phẳng trên quanh trục Ox được vật thể tròn xoay có thể tích là 2 (e 1) 2 (e 1) (e 1) (e 1) A. B. C. D. 2 2 2 2
Trang 3/12 - Mã đề thi 001   2 2 Câu 30: Cho
f (x)dx  5 
. Tính (2 f (x)  cos x)dx  bằng 0 0  A. 11 B. 9 C. 10 D. 10  2
Câu 31: Cho hình phẳng giới hạn bởi đồ thị các hàm số y f (x), y  0, x a, x  b ( a  b) . Quay
miền hình phẳng trên quanh trục Ox được vật thể tròn xoay có thể tích được tính theo công thức nào dưới đây b b b b A. f (x) dxB. f (x) dxC. 2
[f (x)] dxD. 2
 [f (x)] dxa a a a
x  1  t
Câu 32: Trong không gian Oxyz , cho đường thẳng d có phương trình  y  3  t và điểm ( A 0; 6  ;0) . z  1 2t
Điểm H (x ; y ; z ) thuộc d sao cho độ dài đoạn AH nhỏ nhất, giá trị T x y z bằng: o o o o o o A. 7 B. 1 C. 4 D. 0
Câu 33: Trong không gian Oxyz , mặt cầu tâm (
A 1;4;3) bán kính R=10 cắt trục Ox tại 2 điểm M và N.
Độ dài đoạn MN là A. 2 99 B. 99 C. 2 75 D. 75
Câu 34: Cho z ; z là hai nghiệm của phương trình 2
z  4z  5  0 trên tập số phức. Tính A z z 1 2 1 2 bằng A. 2 5 B. 4 C. 10 D. 5
Câu 35: Cho số phức z  2 
3i . Môđun của số phức z bằng A. 7 B. 5 C. 2  3 D. 13
Câu 36: Cho hai hàm số u xvà v x liên tục trên R (được viết tắt là u và v ). Mệnh đề nào sau đây đúng?
A. (uv) '.dx uv u ' . v dx   B. .
uv dx  (uv) ' u ' . v dx   C. u ' .
v dx u 'v ' uv '.dx  
D. uv '.dx uv u ' . v dx  
Câu 37: Trong không gian Oxyz, khoảng cách từ điểm (
A 1;0;3) tới mặt phẳng (P) 2x y z  5  0 bằng: 5 4 A. 1 B. C. 4 D. 6 6
Câu 38: Cho hai số phức z  5  2i, z  4  i . Số phức 2
z  2z bằng 1 2 1 2 A. 18  2i B. 18  29i C. 29 18i D. 29  18i 3 9 9 Câu 39: Cho
f (x)dx  7, f (x)dx  2   . Tính f (x)dx  bằng 1 3 1 A. 5  B. 9 C. 14 D. 5
Câu 40: Trong không gian Oxyz , cho mặt phẳng (P) : x y z  4  0 và mặt phẳng
(Q) : -2x z  3  0 . Gọi  là góc giữa 2 mặt phẳng (P) và (Q), cos bằng: 3  2 3 2 A. B. C. D. 15 15 15 42
Trang 4/12 - Mã đề thi 001
Câu 41: Gọi z là căn bậc hai của số phức w  8i , z có phần thực và phần ảo cùng dương, đặt 2 2023
A  1 z z  .....  z
. Số phức A có phần thực là 2022 1  8 1012 8 1 1012 1  8 2022 1  8 A. B. C. D. 65 5 5 65
x  3  2tx 14 y 14 z  4
Câu 42: Trong không gian Oxyz , cho d y  1 3t và d   . Phương trình 1 2  19 14 2  z  10   2t
mặt cầu tiếp xúc với d và d và có bán kính nhỏ nhất là: 1 2 A. 2 2 2
(x  2)  ( y 1)  z  25 B. 2 2 2
(x  3)  ( y  2)  (z  3)  25 C. 2 2 2
(x  3)  ( y  2)  (z  3)  33 D. 2 2 2
(x 1)  ( y  3)  (z  2)  33 Câu 43: Trong không gian với hệ toạ độ Oxyz cho đường thẳng x m y  2m 1 z m d :  
(m R) . Biết với mọi m, đường thẳng d luôn nằm trên một mặt phẳng 2 1 1 
cố định. Gọi m là giá trị của m để đường thẳng d cách điểm B(4; -3; 1) một khoảng bé nhất, m thuộc 0 0 khoảng nào dưới đây A.  1  ; 2 B. 5;7 C.  4  ;   1 D. 2;5
Câu 44: Trong không gian Oxyz , cho M (1; 7
 ; 2), N(5;1;4) . Mặt phẳng ( ) đi qua N và cách M một
khoảng lớn nhất có phương trình Ax By z D  0 . Tính A+B+D A. 1  1 B. 7 C. 12  D. 14
Câu 45: Cho một xe máy đang chuyển động đều với vận tốc 6m/s thì tăng tốc với gia tốc là 2
a  2m / s .
Quãng đường xe máy đi được kể từ khi tăng tốc đến lúc vận tốc xe đạt 14m/s bằng A. 14m B. 40m C. 44m D. 28m
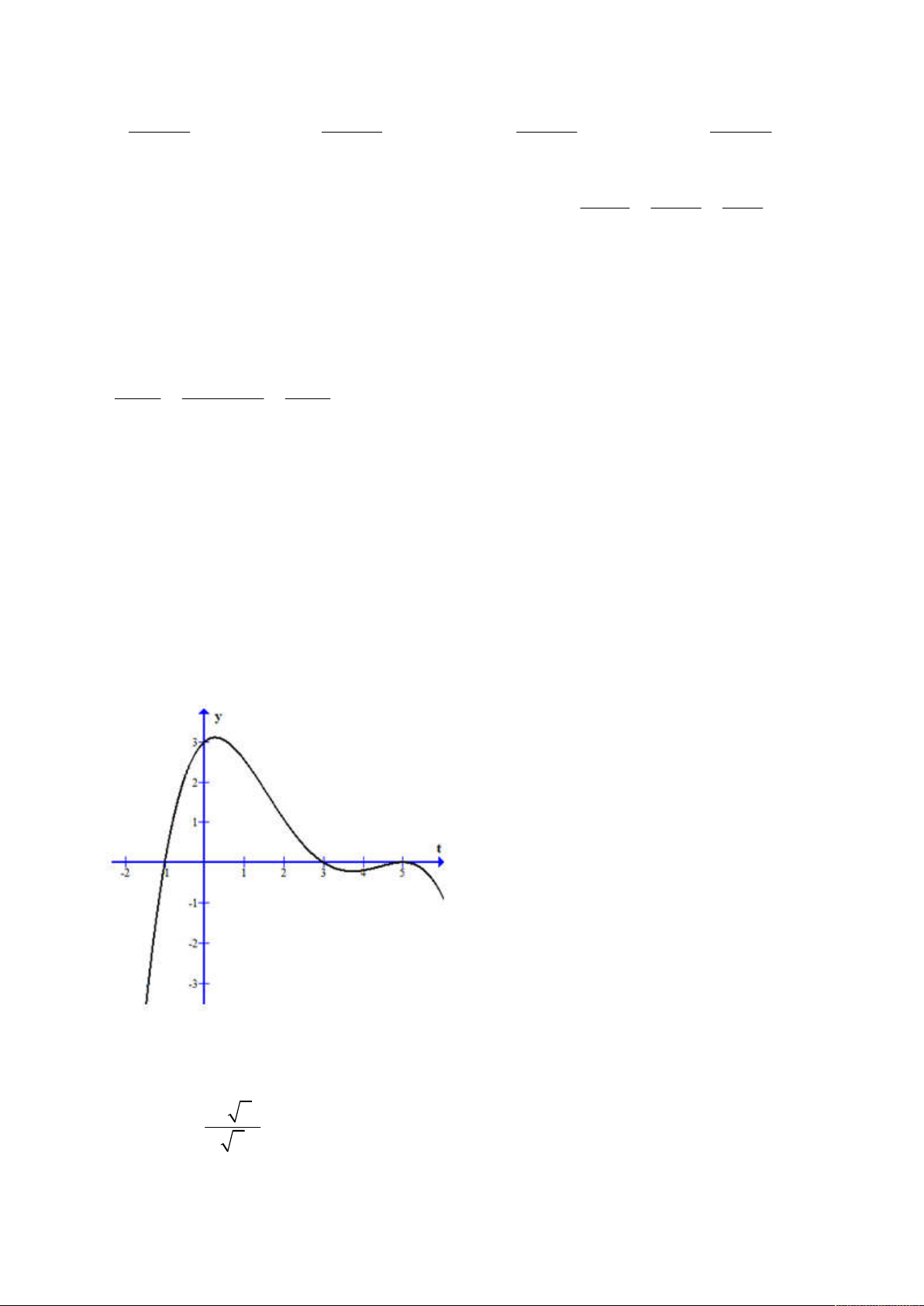
Câu 46: Cho hàm số y f (t) liên tục trên R và hàm số y f '(t) có đồ thị như sau: Chọn khẳng định đúng A. f ( 1
 )  f (5)  f (3)
B. f (3)  f ( 1  )  f (5) C. f ( 1
 )  f (3)  f (5)
D. f (3)  f (5)  f ( 1  ) 9 f ( x) 3 Câu 47: Nếu dx  8  thì f (x)dx  bằng x 1 1 A. 8 B. 4 C. 22 D. 16
Trang 5/12 - Mã đề thi 001
Câu 48: Cho hàm số f(x) liên tục và khác 0 x  0;2 . Biết 2
f '(x)  (2x 1) f (x) x  0;2 và 1 2 f (0)  . Tính f (x)dx  được kết quả là 20 1 1  7 97  1 7 A. ln B. C. 4 D. ln 9 4 6 9 4
Câu 49: Cho số phức z thoả mãn z  4i  7  5 . Trên mặt phẳng Oxy, tập hợp điểm M biểu diễn số
phức w thoả mãn w  2z  4  i là một đường tròn có bán kính bằng 5 A. B. 5 C. 10 D. 5 2
Câu 50: Trong không gian với hệ toạ độ Oxyz cho mặt cầu (S) tâm I có phương trình: 2 2 2
(x1)  y  (z  2)  25 và mặt phẳng (P) có phương trình: x + 2y – 3z + D = 0. Đường thẳng 
thay đổi luôn nằm trên mặt phẳng (P) sao cho tồn tại hai mặt phẳng qua  , tiếp xúc với mặt cầu (S) và tạo với nhau góc 0
60 . Gọi J là hình chiếu vuông góc của I lên  . Có bao nhiêu giá trị nguyên của D sao
cho tập hợp các điểm J là hai đường tròn phân biệt? A. 42 B. 75 C. 37 D. 43
-----------------------------------------------
----------- HẾT -----------
Trang 6/12 - Mã đề thi 001 made cautron dapan 001 1 A 001 2 B 001 3 B 001 4 B 001 5 A 001 6 C 001 7 D 001 8 B 001 9 D 001 10 C 001 11 B 001 12 D 001 13 A 001 14 C 001 15 C 001 16 C 001 17 C 001 18 B 001 19 B 001 20 D 001 21 D 001 22 C 001 23 D 001 24 A 001 25 B 001 26 D 001 27 A 001 28 A 001 29 A 001 30 A 001 31 D 001 32 A 001 33 C 001 34 A 001 35 A 001 36 D 001 37 D 001 38 D 001 39 B 001 40 C 001 41 B 001 42 C 001 43 A 001 44 C 001 45 B 001 46 D 001 47 B 001 48 D 001 49 C 001 50 D HƯỚNG DẪN GIẢI
Câu 23: Trên tập số phức, cho phương trình 2
z z m  0 với tham số m R . Gọi S là tập các giá trị nguyên của m thuộc  10 
;10 sao cho phương trình đó có hai nghiệm phân biệt z ; z đồng thời thoả 1 2
mãn z z và z z Tập S có số phần tử là 1 1 2 2 A. 4 B. 6 C. 0 D. 11 Lời giải Chọn D  z z 1 1 
z , z là số thực 1 2 z z  2 2 1
Để phương trình có 2 nghiệm phân biệt:   0  m  4
Đề bài yêu cầu m  10 
;10, m Z  10   m  0
Vậy có 11 giá trị thỏa mãn yêu cầu đề bài
Câu 41: Gọi z là căn bậc hai của số phức w  8i , z có phần thực và phần ảo cùng dương, đặt 2 2023
A  1 z z  .....  z
. Số phức A có phần thực là 2022 1  8 1012 8 1 1012 1  8 2022 1  8 A. B. C. D. 65 5 5 65 Lời giải Chọn B 2 2 Có 2 2 2
z  8i z  4  2.2i  4  2  2.2i  2i  2  2i
z  2  2i
z  2  2i z  2   2i  1 1 z   2 2024 z 1012 1 8i1012 A    1 z 1 z 1 2  2i 1 8 i 506 1012 2   1012 1 8 1 2i 2   1012 1012 1012 1 8 1 8 8 1       i 2 2 1 2i 1 2i 1  2 5 5
x  3  2tx 14 y 14 z  4
Câu 42: Trong không gian Oxyz , cho d y  1 3t và d   . Phương trình 1 2  19 14 2  z  10   2t
mặt cầu tiếp xúc với d và d và có bán kính nhỏ nhất là: 1 2 A. 2 2 2
(x  2)  ( y 1)  z  25 B. 2 2 2
(x  3)  ( y  2)  (z  3)  25 C. 2 2 2
(x  3)  ( y  2)  (z  3)  33 D. 2 2 2
(x 1)  ( y  3)  (z  2)  33 Lời giải Chọn C
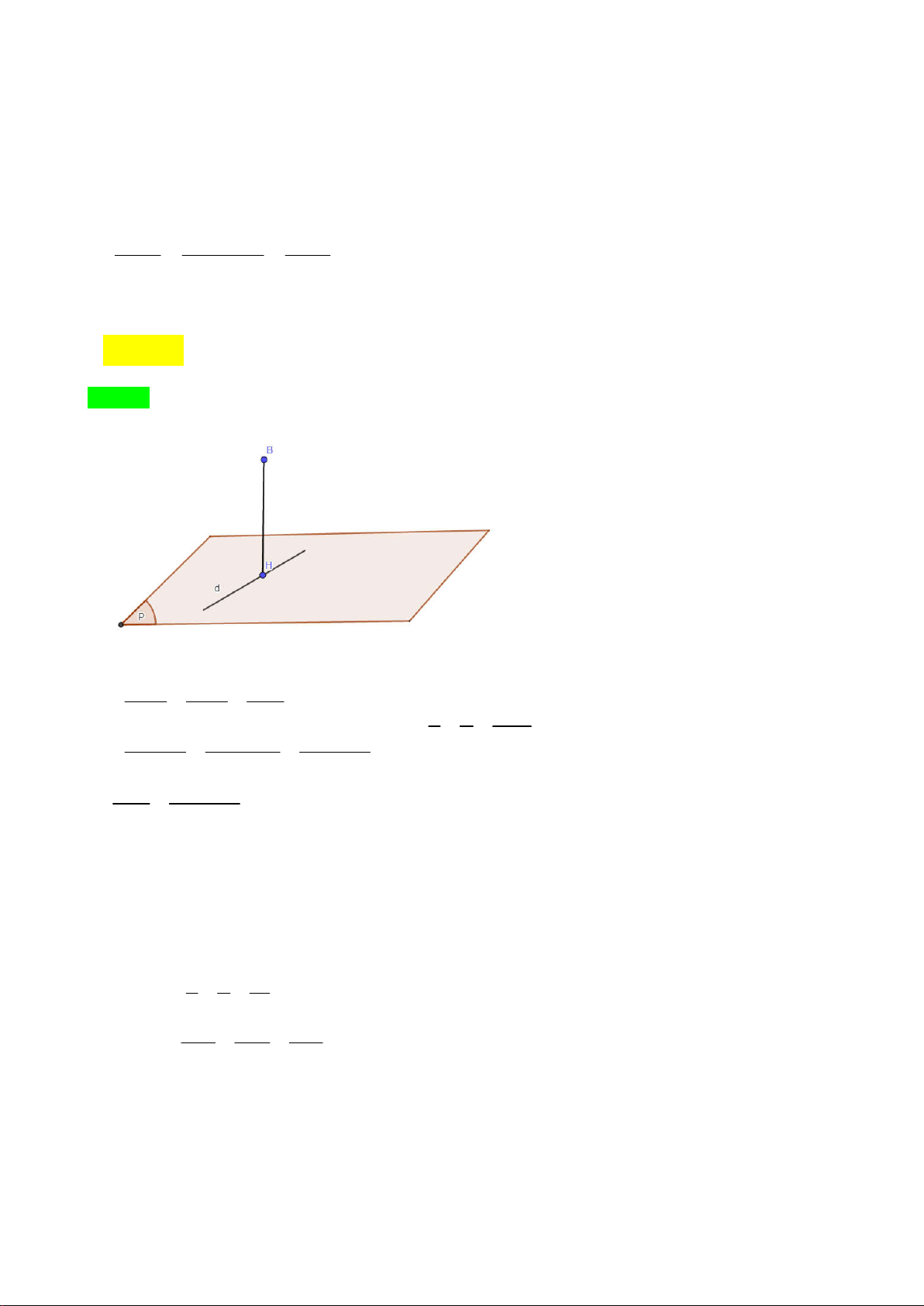
Gọi MN là đoạn vuông góc chung, suy ra mặt cầu cần tìm là mặt cầu đường kính MN Cách 1: Chọn
M 3  2t;1 3t; 10  2 t  d1 N  14 
19k; 14 14k; 4  2k   d 2    MN.u  0 1
  
M 1; 4; 8, N 5;0; 2  I 3; 2; 3
 , IM R  33 MN.u  0  2
Trang 7/12 - Mã đề thi 001
Cách 2: Dễ thấy d d 1 2 d P  1  
Gọi  P là mặt phẳng thỏa mãn 
  P  d N N 5;0; 2 2   d P   2   d Q  2  
Gọi Q là mặt phẳng thỏa mãn 
 Q  d M M 1; 4; 8 1   d Q   1   Câu 43: Trong không gian với hệ toạ độ Oxyz cho đường thẳng x m y  2m 1 z m d :  
(m R) . Biết với mọi m, đường thẳng d luôn nằm trên một mặt phẳng 2 1 1 
cố định. Gọi m là giá trị của m để đường thẳng d cách điểm B(4; -3; 1) một khoảng bé nhất, m thuộc 0 0 khoảng nào dưới đây A.  1  ; 2 B. 5;7 C.  4  ;   1 D. 2;5 Lời giải Chọn A Cách 1
Từ phương trình đường thẳng d có  x m z m x z t      2 1 3  a c a c   t / c :     2x  2m y  2m 1 2x y 1 b d b d t       4 1 3 x z 2x y 1  
  P : x y z 1  0 3 3
Gọi H là hình chiếu vuông góc của B lên  P , đường thẳng d đi qua H là đườn thẳng cần tìm x  4  t
BH   P  H m  1
Có phương trình BH y  3   tz 1 t
Cách 2: đường thẳng d luôn nằm trên 1 mặt phẳng cố định. Chọn 2 giá trị ngẫu nhiên của m x y z m  0  d :   0 2 1 1  x 1 y 1 z 1 m  1  d :   1 2 2 1
Viết phương trình mặt phẳng  P chứa d , d   P : x y z 1  0 0 1
Gọi H là hình chiếu vuông góc của B lên  P x  4  t
BH   P  H m  1
Có phương trình BH y  3   tz 1 tCách 3
Trang 8/12 - Mã đề thi 001 Gọi  
PAx By Cz D   2 2 2
0 A B C  0 d   P  n .n  0 Pd
 2A B C  0  C  2A B   1
  PAx By  2A Bz D  0 M  ; m 2
m 1; m  d M  P   . A m  .
B 2m  
1  2A B.m D  0 m 
m 3A  3B  B D  0 m  3
A  3B  0
A B  0  2     B D  0  B D  0  3  TH1 B  0,  
1 2  A B C  0koTM TH 2 B  0  A  1  Chọn B  1   C   1
  P : x y z 1  0 D 1 
Cách 4: *Lập ptmp (Q) qua B và vuông góc d: 2x + y - z – 4 = 0
* (Q) cắt d tại A(….), A phụ thuộc m
* Tính đoạn BA (phụ thuộc tham số m - bậc 2), tìm m để BA nhỏ nhất => m = 1
Câu 44: Trong không gian Oxyz , cho M (1; 7
 ; 2), N(5;1;4) . Mặt phẳng ( ) đi qua N và cách M một
khoảng lớn nhất có phương trình Ax By z D  0 . Tính A+B+D A. 1  1 B. 7 C. 12  D. 14 Lời giải Chọn C
Mặt phẳng   qua N và cách M một khoảng lớn nhất MN    
mp   N     
   2x  4 y z 18  0
A B D  2  4 18  12 
Câu 45: Cho một xe máy đang chuyển động đều với vận tốc 6m/s thì tăng tốc với gia tốc là 2
a  2m / s .
Quãng đường xe máy đi được kể từ khi tăng tốc đến lúc vận tốc xe đạt 14m/s bằng A. 14m B. 40m C. 44m D. 28m Lời giải Chọn B
Vận tốc xe máy v
 6  at  6  2t t
Thời gian tăng tốc đến khi vận tốc đạt14m / s
 6  2t  14  t  4s 4
Vậy quãng đường S
6  2tdt  40m  0
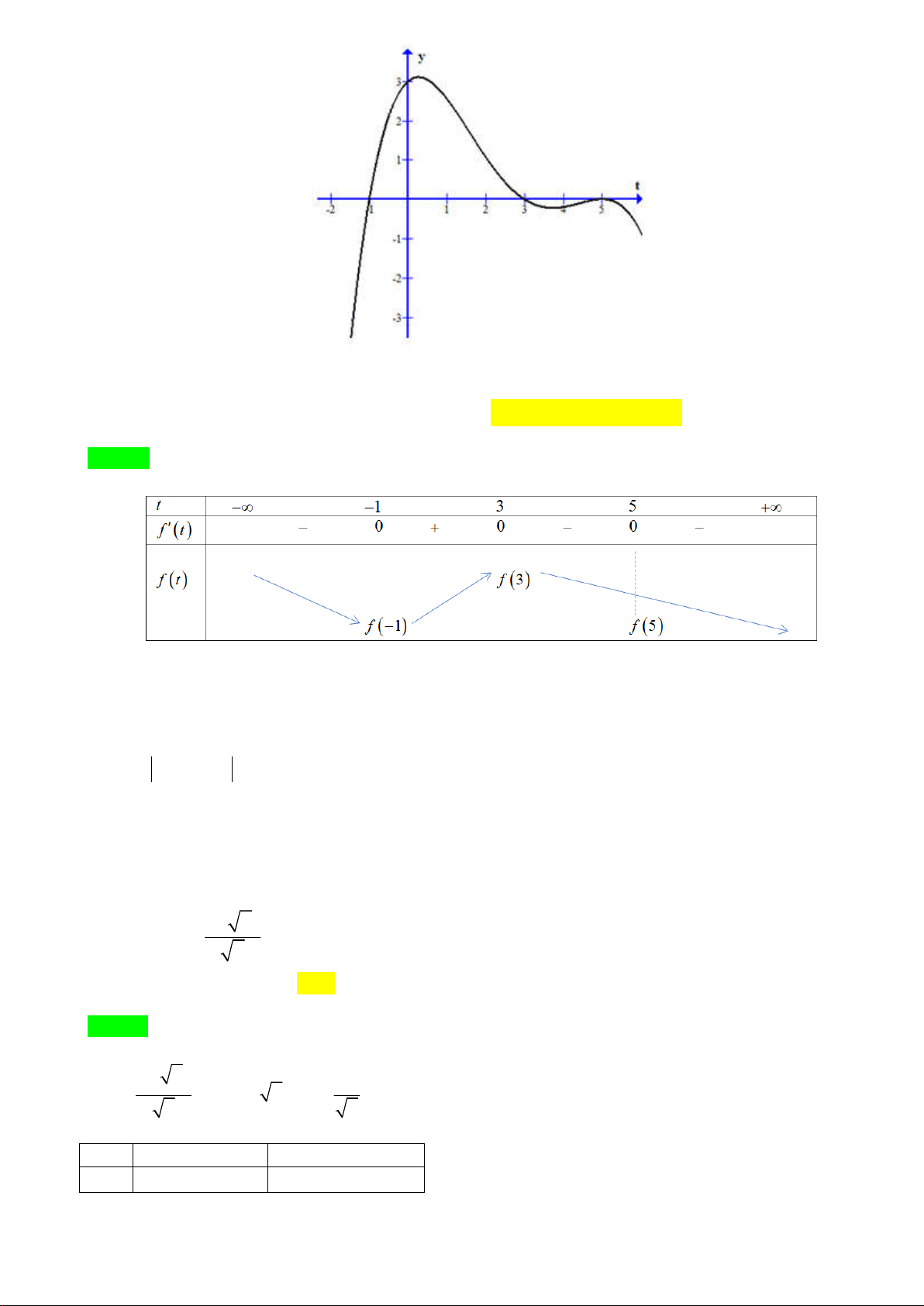
Câu 46: Cho hàm số y f (t) liên tục trên R và hàm số y f '(t) có đồ thị như sau:
Trang 9/12 - Mã đề thi 001 Chọn khẳng định đúng A. f ( 1
 )  f (5)  f (3)
B. f (3)  f ( 1  )  f (5) C. f ( 1
 )  f (3)  f (5)
D. f (3)  f (5)  f ( 1  ) Lời giải Chọn D
Ta có bảng biến thiên
Từ BBT suy ra trong ba giá trị f  
1 , f 3, f 5 thì f 3 lớn nhất
So sánh diện tích 2 phần ta có: 3 5
f t dt  
  f tdt 1 3
f t  3   f t  5 1  3
f 3  f  
1  f 3  f 5  f   1  f 5
f 3  f 5  f   1 9 f ( x) 3 Câu 47: Nếu dx  8  thì f (x)dx  bằng x 1 1 A. 8 B. 4 C. 22 D. 16 Lời giải Chọn B Có f x 9   1 I
dx  8 x t dx  2tdt  1 x x Đổi cận x 1 9 t 1 3
Trang 10/12 - Mã đề thi 001 3 3 3 I  2
f t dt  8 
f t dt  4 
f xdx  4    1 1 1
Câu 48: Cho hàm số f(x) liên tục và khác 0 x  0;2 . Biết 2
f '(x)  (2x 1) f (x) x  0;2 và 1 2 f (0)  . Tính f (x)dx  được kết quả là 20 1 1  7 97  1 7 A. ln B. C. 4 D. ln 9 4 6 9 4 Lời giải Chọn D f  xf  x  2x 1  dx  2x 1 dx 2  2    f xf x 1  1  2 
x x C f x  f x 2
x x C 1 1  1 f 0     C  20  20 C 20 2 1  1 7 f x  
f xdx  ln 2 1 x x  20 9 4
Câu 49: Cho số phức z thoả mãn z  4i  7  5 . Trên mặt phẳng Oxy, tập hợp điểm M biểu diễn số
phức w thoả mãn w  2z  4  i là một đường tròn có bán kính bằng 5 A. B. 5 C. 10 D. 5 2 Lời giải Chọn C
Có z  4i  7  5 (1) w  4  i
w  2z  4  i z  2 2 w  4  i   1 ,2   4i  7  5 2
w 10  7i  10  R  10
Câu 50: Trong không gian với hệ toạ độ Oxyz cho mặt cầu (S) tâm I có phương trình: 2 2 2
(x1)  y  (z  2)  25 và mặt phẳng (P) có phương trình: x + 2y – 3z + D = 0. Đường thẳng 
thay đổi luôn nằm trên mặt phẳng (P) sao cho tồn tại hai mặt phẳng qua  , tiếp xúc với mặt cầu (S) và tạo với nhau góc 0
60 . Gọi J là hình chiếu vuông góc của I lên  . Có bao nhiêu giá trị nguyên của D sao
cho tập hợp các điểm J là hai đường tròn phân biệt? A. 42 B. 75 C. 37 D. 43 Lời giải Chọn D
Trang 11/12 - Mã đề thi 001
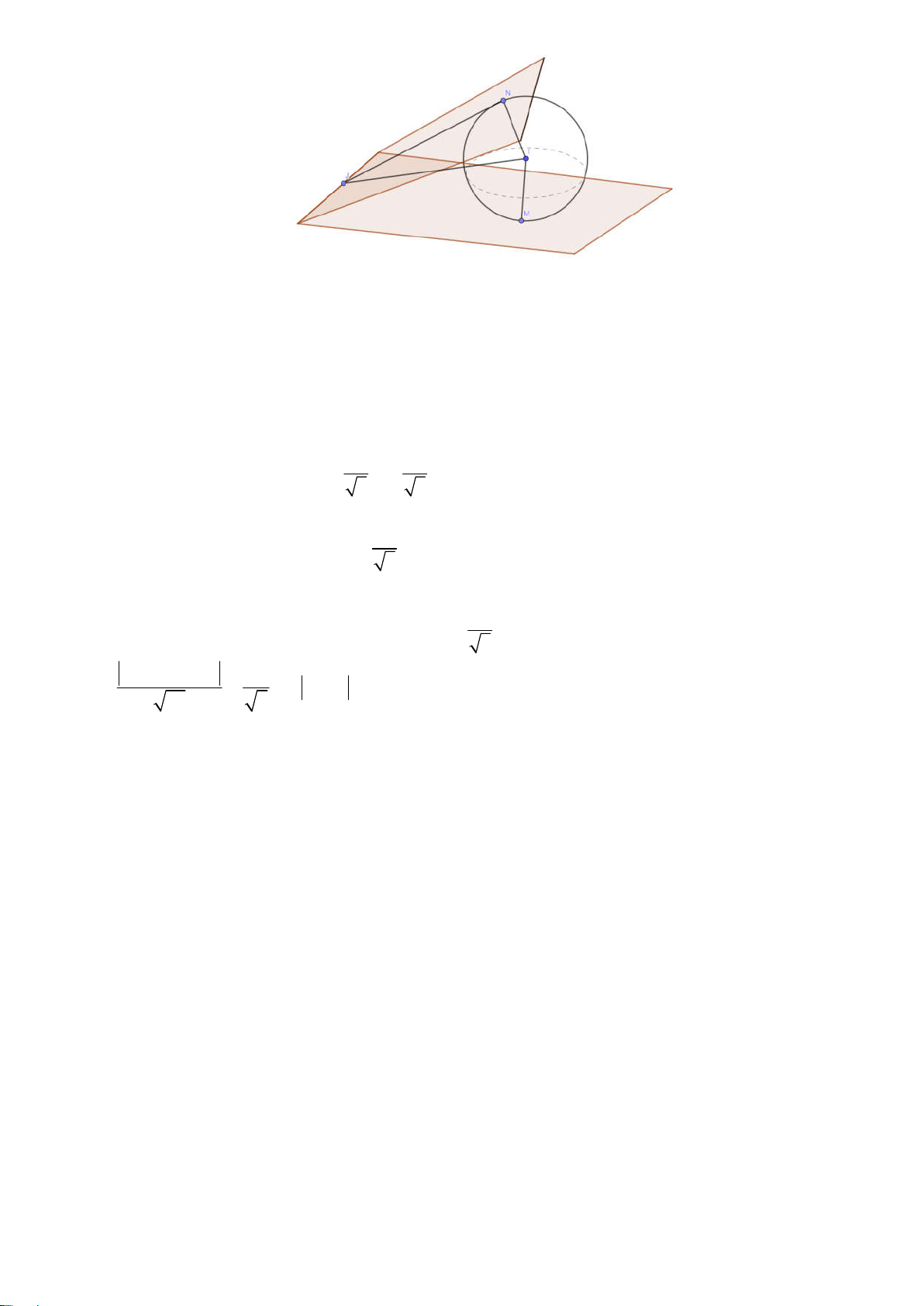
Gọi J là hình chiếu vuông góc của I lên đường thẳng  TH1    60o  IJ  30o MJN N
IJ  2JN  10
Suy ra J thuộc mặt cầu tâm I bán kính 10
Mà J     P
Suy ra để tập hợp điểm J là đường tròn thì d
 10 ( mp cắt m/cầu theo giao tuyến là một đường tròn) I ,P TH2   o o 5 10
MJN  120  IJN  60  IJ  .2  3 3 10
Suy ra J thuộc mặt cầu tâm I bán kính 3
Mà J     P 10
Suy ra để tập hợp điểm J là đường tròn thì d  I ,P 3 1 0  6  D 10    D  5  21, 602 14 3
Suy ra có 43 gia trị nguyên của (D-5)  có 43 giá trị nguyên của D.
----------- HẾT -----------
Trang 12/12 - Mã đề thi 001
Document Outline

  • tranphu
  • b347f9a2
    • Table1