Đề thi học kì 2 Toán 12 năm học 2018 – 2019 sở GD&ĐT Tây Ninh

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2018 – 2019 .Mời bạn đọc đón xem.

38 19 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

16 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Trang 1/16
SỞ GIÁO DỤC VÀ ĐÀO TẠO TÂY NINH
ĐỀ THI HỌC KỲ II
NĂM HỌC 2018 – 2019
Môn: Toán – Lớp 12
Thời gian: 90 phút (Không kể thời gian phát đề)
I – PHẦN TRẮC NGHIỆM
Câu 1: Cho bốn số phức có điểm biểu diễn lần lượt là
,,,MNPQ
như hình vẽ bên. Số phức có mô đun lớn
nhất là số phức có điểm biểu diễn là
A.
N
. B.
P
. C.
Q
. D.
M
.
Câu 2: Diện tích hình phẳng giới hạn bởi các đường
()
2ye x=+
và
()
2
x
yex=+
là
A.
2
4
e-
. B.
2
4
e +
. C.
2
2
e-
. D.
2
2
e +
.
Câu 3. Trong không gian
Oxyz
, cho hai điểm

1; 3; 2 , 3; 2; 4AB
. Vectơ
AB

có tọa độ là:
A.

2;5;6
. B.

2;5;6
. C.

4;1; 2
. D.

2; 5;6
.
Câu 4.
2
1
4
32
dx
x
bằng
A.
411
ln
35
. B.
4
ln55
3
. C.
11
4ln
5
. D.
111
ln
35
.
Câu 5. Thể tích của một khối trụ có bán kính đáy
4r
và chiều cao
42h
bằng
A.
32 2
. B.
128 2
. C.
16 2
. D.
64 2
.
Câu 6. Trong không gian
Oxyz
, cho hai vectơ

2;2; 1a 
và

3; 2;6b 
. Mệnh đề nào dưới đây đúng?
A.

3
cos ,
7
ab

. B.

3
cos ,
7
ab 

. C.

4
cos ,
21
ab 

. D.

4
cos ,
21
ab

.
Câu 7. Diện tích hình phẳng gạch chéo trong hình vẽ bên dưới được tính bởi công thức nào dưới đây?
A.

1
2
2
224dSxxx
 
. B.

1
2
46dSxx

.
C.

1
2
46dSxx

. D.

1
2
2
224dSxxx

.
Câu 8. Nguyên hàm của hàm số

2
1
2fx x
x

là
Trang 2/16
A.
2
1
x
C
x

. B.
2
ln
x
xC
. C.
1
2 C
x

. D.
22ln
x
xC
.
Câu 9. Cho số phức
zabi
,
,ab
thỏa mãn
53ziz
. Giá trị của
5ab
bằng
A.
3
. B.
13
. C.
8
. D.
11
.
Câu 10. Diện tích hình phẳng giới hạn bởi các đường
3
1
x
ye , 0y ,
1
x
và
2x
là
A.
26
3
3
ee
. B.
26
2
3
ee
. C.
62
3
3
ee
. D.
62
2
3
ee
.
Câu 11. Cho số phức
z
thỏa mãn

2
12 1zii
. Môđun của số phức đã cho bằng
A.
13
. B.
13
. C. 1. D.
5
.
Câu 12. Cho số phức
z thỏa mãn
25 1zizi
. Phần ảo của số phức đã cho là
A.
5i
. B.
8
. C.
5
. D.
8i
.
Câu 13: Nguyên hàm của hàm số

32
f
xxx
là
A.
43
11
.
43
xC
B.
43
.
x
xC
C.
2
32 .
x
xC
D.
43
11
.
34
x
xC
Câu 14: Cho hình phẳng
H
giới hạn bởi các đường
2
5, 0, 0, 3.yx y x x Gọi
V
là thể tích khối
tròn xoay được tạo thành khi quay
H
xung quanh trục
.Ox
Mệnh đề nào dưới đây đúng?
A.

3
2
2
0
5d.Vx x
B.

3
2
0
5d.Vxx
C.

3
2
2
0
5d.Vx x
D.

3
2
0
5d.Vx x
Câu 15. Cho khối nón có độ dài đường sinh bằng
23a
, góc giữa đường sinh và mặt đáy bằng
o
30 . Thể
tích của khối nón đã cho bằng
A.
3
3 a
. B.
3
3a
. C.
3
33a
. D.
3
33a
.
Câu 16. Cho tích phân

1
0
dx 3fx
và

1
0
dx 6gx
, khi đó
 
1
0
3dxfx gx


bằng
A.
3
. B.
15
. C. 21. D.
3
.
Câu 17: Trong không gian
Oxyz
cho tam giác ABC với
(1; 3; 2)A
,
(3;4;5)B
,
(1; 2; 3)C
. Độ dài đường
trung tuyến

A
MM BC
của tam giác
A
BC
bằng
A.
25
. B. 44 . C.
6
. D.
211
.
Câu 18: Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
3, 0, 1,
x
yyxxe
. Mệnh đề nào dưới
đây đúng?
A.
1
3d
e
x
Sx
. B.
1
3d
e
x
Sx
. C.
2
1
3d
e
x
Sx
. D.
2
1
3d
e
x
Sx
.
Câu 19. Biết
Fx
là một nguyên hàm của hàm số

1
fx
x
và
21F
. Tính
4F
.
A.
45 2F  . B.

45 2F  . C.

4422F  . D.

4522F  .
Câu 20. Cho số phức
z
thỏa mãn
263zz i
. Tổng phần thực và phần ảo số phức
z
bằng
A.
5
. B.
3
. C. 1 . D. 2 .
Câu 21. Trong không gian
Oxyz
cho hai điểm

5; 3; 2A 
và
1; 1; 4B
. Mặt phẳng đi qua
A
và vuông
góc với đường thẳng
A
B có phương trình là
A.
32 190xyz
. B.
23190xy z
. C.
2370xy z 
. D.
32 230xyz
.
Trang 3/16
Câu 22. Nguyên hàm của hàm số
54e3
xx
fx
là
A.
5
4e 3
ln 5
x
x
x
C
. B.
5
4e 3
log5
x
x
x
C
. C.
5ln5 4e
xx
C
. D.
54e3
xx
C
.
Câu 23. Số phức liên hợp với số phức
78i
là
A.
78i
. B.
87i
. C.
87i
. D.
78i
.
Câu 24. Nguyên hàm của hàm số

2
34sin5cos
f
xx x x
là
A.
3
4cos 5sin
x
xxC. B.
3
4cos 5sin
x
xxC.
C.
3
4cos 5sin
x
xxC. D.
64cos5sin
x
xxC
.
Câu 25. Trong không gian
Oxyz
, khoảng cách giữa hai mặt phẳng
: 2 2 10 0Pxyz
và
: 4 2 4 7 0Qxyz
bằng
A.
9
2
. B.
13
6
. C.
17
3
. D.
13
3
.
Câu 26. Số phức có phần thực bằng
5
và phần ảo bằng
6
là
A.
56i
. B.
56i
. C.
56i
. D.
56i
.
Câu 27. Cho

2
1
21d20fx x
. Tính

5
3
d.I
f
xx
A.
10I
. B.
20I
. C.
30I
. D.
40I
.
Câu 28. Điểm nào trong hình vẽ dưới đây là điểm biểu diễn số phức
13?zi
A.
M
. B.
P
. C.
Q
. D.
N
.
Câu 29. Cho hình trụ có diện tích xung quanh bằng
50
và có thiết diện qua trục hình trụ là một hình
vuông. Đường kính của đường tròn đáy của hình trụ đã cho bằng
A.
52
. B.
52
2
. C.
52
. D.
52
2
.
Câu 30. Cho hình nón có đường sinh bằng
3a
và bán kính đường tròn đáy bằng
2a
. Diện tích xung quanh
của hình nón đã cho bằng
A.
2
3 a
. B.
2
6 a
. C.
2
45
3
a
. D.
2
12 a
.
Câu 31. Nguyên hàm của hàm số

42ln
f
xx x
là
A.
22
2ln 3
x
xxC. B.
22
2ln
x
xx C. C.
22
2ln
x
xx C. D.
22
2ln 3
x
xxC.
Câu 32. Thể tích khối cầu ngoại tiếp lăng trụ tam giác đều có tất cả các cạnh bằng
23a
là
A.
3
28 a
. B.
3
28 7
3
a
. C.
3
28
3
a
. D.
3
28 7
7
a
.
Câu 33. Trong không gian
Oxyz
, cho mặt phẳng

:20Pxyz
và hai điểm
6;4; 7A
,
2;2; 1B
. Điểm
;;
M
abc P
và thỏa
22
3TMA MB
đạt giá trị lớn nhất. Mệnh đề nào sau
đây là đúng?
A.
0ac
. B.
2372019abc
.C.
0abc
. D.
4ab
.
Trang 4/16
Câu34. Cho
4
2
3
23
dln2ln3ln7
3
x
xa b c
xx

với
, , abc
. Giá trị của
237abc
bằng
A.
9
. B.
6
. C.
15
. D.
3
.
Câu 35.
Một khối cầu có thể tích bằng
288
thì diện tích mặt cầu đó bằng
A.
144
3
. B.
128
. C.
72
. D.
144
.
Câu 36. Cho

1
2
0
dln2ln3
3

x
xab c
x
với ,a
,b
c là các số hữu tỉ. Giá trị của
8 abc
bằng
A.
1
. B.
2
. C.
1
. D.
2
.
Câu 37: Cho hàm số
yf
x
có đồ thị là đường cong
'
yf
x
cắt trục
O
x
tại 3 điểm có hoành độ
a
,
b
,
c
như hình vẽ. Mệnh đề nào dưới đây là đúng?
A.
f
c
f
a
f
b
. B.
f
b
f
a
f
c
.
C.
f
c
f
b
f
a
. D.
f
a
f
c
f
b
.
Câu 38:
Cho

2
2
0
1cos
x
xdx a b c


với
a
,
b
,
c
là các số hữu tỉ. Giá trị của
43ab c
bằng
A. 1 . B. 2 . C. 4. D. 0.
Câu 39. Nguyên hàm của hàm số

4sin5 .cos
f
xxx
là .
A.
2
sin 4 sin 6
3
x
xC
. B.
11
cos 4 cos 6
23
x
xC
.
C.
4
cos5 .sin
5
x
xC
. D.
11
cos 4 cos6
23
x
xC
.
Câu 40. Cho hàm số
yf
x
có bảng biến thiên như hình vẽ
Tính diện tích hình phẳng được giới hạn bởi các đường
yf
x
;
0y
;
2x 
và
2x
.
A.
3
. B.
4
. C.
6
. D.
5
.
II – PHẦN TỰ LUẬN
Câu 1:
Tìm nguyên hàm của
Fx
của hàm số
3
3
x
fx x e
biết
0 2019.F
Câu 2: Cho hình chóp
.S ABC
có đáy
A
BC
là tam giác đều cạnh
a
. Mặt bên
SAB
là tam giác cân với
120ASB 
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Xác định tâm và tính thể tích
của khối cầu ngoại tiếp hình chóp.
------------- HẾT -------------
x

2
0
2

y
0
0
0


y
1
2
2
Trang 5/16
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
B C D A D C A A D C B B A C C B D A D C
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
B A A B B D D C A B A B A D D C D C B C
LỜI GIẢI CHI TIẾT
I – PHẦN TRẮC NGHIỆM
Câu 1: Cho bốn số phức có điểm biểu diễn lần lượt là
,,,MNPQ
như hình vẽ bên. Số phức có mô đun lớn
nhất là số phức có điểm biểu diễn là
A.
N
. B.
P
. C.
Q
. D.
M
.
Lời giải
Chọn B
Gọi
1234
,,,zzzz
là các số phức có điểm biểu diễn lần lượt là
,,,MNPQ
.
11
25ziz=+ =
,
22
13 10ziz=- + =
33
32 13ziz=- + =
,
44
22 22ziz=- - =
Vậy số phức có mô đun lớn nhất là số phức có điểm biểu diễn là điểm
P
Câu 2: Diện tích hình phẳng giới hạn bởi các đường
()
2ye x=+
và
()
2
x
yex=+
là
A.
2
4
e-
. B.
2
4
e +
. C.
2
2
e-
. D.
2
2
e +
.
Lời giải
Chọn C
Phương trình hoành độ giao điểm:
()
()
0
22
1
x
x
ex ex
x
é
=
ê
+=+
ê
=
ë
Diện tích hình phẳng
()
111
12
000
ex - ex e x
xx
SexdxdxdxSS==-=-
òòò
1
2
1
0
1
ex
0
22
xe
Sdxe===
ò
1
2
0
x
Sxedx=
ò
Đặt
,
xx
u x du dx
dv e dx v e
ìì
==
ïï
ïï
íí
ïï
==
ïï
îî
()
1
2
0
11
1
00
xx xx
Sxe edxxee=- =-=
ò
Vậy:
2
2
e
S
-
=
Trang 6/16
Câu 3. Trong không gian
Oxyz
, cho hai điểm

1; 3; 2 , 3; 2; 4AB

. Vectơ
AB

có tọa độ là:
A.

2;5;6
. B.

2;5;6
. C.

4;1; 2
. D.

2; 5;6
.
Lời giải
Chọn D

2; 5;6AB 

.
Câu 4.
2
1
4
32
dx
x
bằng
A.
411
ln
35
. B.
4
ln55
3
. C.
11
4ln
5
. D.
111
ln
35
.
Lời giải
Chọn A
33
3
1
11
414 44411
4ln32ln11ln5ln
32 32 3 3 3 35
dx dx x
xx



.
Câu 5. Thể tích của một khối trụ có bán kính đáy
4r
và chiều cao
42h
bằng
A.
32 2
. B.
128 2
. C.
16 2
. D.
64 2
.
Lời giải
Chọn D
Ta có
22
.4 .4 2 64 2Vrh


.
Câu 6. Trong không gian
Oxyz
, cho hai vectơ

2;2; 1a 
và

3; 2;6b 
. Mệnh đề nào dưới đây
đúng?
A.

3
cos ,
7
ab

. B.

3
cos ,
7
ab 

. C.

4
cos ,
21
ab 

. D.

4
cos ,
21
ab

.
Lời giải
Chọn C
Ta có




22
22 2 2
2.3 2. 2 1 .6
.4
cos ,
21
.
22 1.3 2 6
ab
ab
ab






.
Câu 7. Diện tích hình phẳng gạch chéo trong hình vẽ bên dưới được tính bởi công thức nào dưới đây?
A.

1
2
2
224dSxxx

. B.

1
2
46dSxx

.
C.

1
2
46dSxx

. D.

1
2
2
224dSxxx

.
Lời giải
Chọn A
Trang 7/16
Ta có diện tích hình phẳng cần tìm

11
22 2
22
531d224dSxxxxx xxx





.
Câu 8. Nguyên hàm của hàm số

2
1
2fx x
x
 là
A.
2
1
x
C
x

. B.
2
ln
x
xC. C.
1
2 C
x

. D.
22ln
x
xC
.
Lời giải
Chọn A
Ta có

2
2
11
d2 d
f
xx x xx C
xx





.
Câu 9. Cho số phức
zabi
,
,ab
thỏa mãn
53ziz
. Giá trị của
5ab
bằng
A.
3
. B.
13
. C.
8
. D.
11
.
Lời giải
Chọn D
Ta có
53ziz
22
53abi i a b

22
53abiab
.
22
5
30
aab
b


22
5
10 25 9
3
a
aa a
b



8
5
3
a
b


(thỏa điều kiện).
Vậy
511ab
.
Câu 10. Diện tích hình phẳng giới hạn bởi các đường
3
1
x
ye , 0y ,
1
x
và
2x
là
A.
26
3
3
ee
. B.
26
2
3
ee
. C.
62
3
3
ee
. D.
62
2
3
ee
.
Lời giải
Chọn C
Phương trình hoành độ giao điểm
3
10
x
e
0x
1;2
.
Diện tích hình phẳng là

2
3
1
1d
x
Sex
2
3
1
1
3
x
xe




62
11
21
33
ee




=
62
3
3
ee
.
Vậy
62
3
3
ee
S

.
Câu 11. Cho số phức
z
thỏa mãn

2
12 1zii
. Môđun của số phức đã cho bằng
A.
13
. B.
13
. C. 1. D.
5
.
Lời giải
Chọn B
Ta có:

2
12 1zii
23zi
.
Do đó:
23zi

2
2
23 13 .
Câu 12. Cho số phức
z
thỏa mãn

25 1zizi
. Phần ảo của số phức đã cho là
A.
5i
. B.
8
. C.
5
. D.
8i
.
Lời giải
Chọn B
Gọi

,,zxyi xy
.
Trang 8/16
Ta có:
 
25 1 25 1zizixyiixyii

25
xy
ix
y
x
y
i 
2
5
x
xy
yxy


22
5
xy
x


5
8
x
y


Khi đó:
58zi
. Vậy số phức
z
có phần ảo là
8
.
Câu 13: Nguyên hàm của hàm số

32
f
xxx
là
A.
43
11
.
43
xC
B.
43
.
x
xC
C.
2
32 .
x
xC
D.
43
11
.
34
x
xC
Lời giải
Chọn A
Ta có:

32 3 2 4 3
11
ddd
43
x
xx xxxx x xC

Câu 14: Cho hình phẳng
H
giới hạn bởi các đường
2
5, 0, 0, 3.yx y x x
Gọi
V
là thể tích khối
tròn xoay được tạo thành khi quay
H
xung quanh trục
.Ox
Mệnh đề nào dưới đây đúng?
A.

3
2
2
0
5d.Vx x
B.

3
2
0
5d.Vxx
C.

3
2
2
0
5d.Vx x
D.

3
2
0
5d.Vx x
Lời giải
Chọn C
Áp dụng công thức tính thể tích khối tròn xoay khi quay hình phẳng được giới hạn bởi các đường
2
5, 0, 0, 3yx y x x quanh trục
Ox
, ta có

3
2
2
0
5d.Vx x
Câu 15. Cho khối nón có độ dài đường sinh bằng 23a , góc giữa đường sinh và mặt đáy bằng
o
30
. Thể
tích của khối nón đã cho bằng
A.
3
3 a
. B.
3
3a
. C.
3
33a
. D.
3
33a
.
Lời giải
Chọn C
Gọi
I
là đỉnh của khối nón,
O
là tâm đáy,
A
thuộc đường tròn đáy,
l
là đường sinh,
r
là bán
kính đáy,
h
là chiều cao của khối nón.
Theo giả thiết ta có tam giác
IOA
vuông tại
O
,
o
30IAO
,
23la
.
o
3
.cos30 .2 3 3
2
rl a a
,
o
1
.sin30 .2 3 3
2
hl a a
.
Thể tích khối nón là:

2
23
11
3333
33
Vrh aa a

 .
30
h
l
r
O
I
A
Trang 9/16
Câu 16. Cho tích phân

1
0
dx 3fx
và

1
0
dx 6gx
, khi đó
 
1
0
3dxfx gx


bằng
A.
3
. B.
15
. C.21. D.
3
.
Lời giải
Chọn B
Ta có
   
111
000
3 dx dx 3 dx 3 3.6 15fx gx fx gx



Câu 17: Trong không gian
Oxyz
cho tam giác ABC với
(1; 3; 2)A
,
(3;4;5)B
,
(1; 2; 3)C
. Độ dài đường
trung tuyến

A
MM BC
của tam giác
A
BC
bằng
A.
25
. B.
44
. C.
6
. D.
211
.
Lời giải
Chọn D
Ta có đường trung tuyến
A
M nên
M
là trung điểm cạnh
B
C
do đó
1; 3; 4 2; 6; 2MAM


2
22
262211AM
.
Câu 18: Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
3, 0, 1,
x
yy
xxe
. Mệnh đề nào dưới
đây đúng?
A.
1
3d
e
x
Sx
. B.
1
3d
e
x
Sx
. C.
2
1
3d
e
x
Sx
. D.
2
1
3d
e
x
Sx
.
Lời giải
Chọn A
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
yf
x
, trục
(0)Ox y
và các đường
,
x
ax b
được tính theo công thức

d
b
a
S
f
xx
.
Vì
30
x
nên
1
3d
e
x
Sx
.
Câu 19. Biết
Fx
là một nguyên hàm của hàm số

1
fx
x
và
21F
. Tính

4F
.
A.
45 2F 
. B.

45 2F 
. C.

4422F 
. D.

4522F 
.
Lời giải
Chọn D
Giả sử
 
1
dd2Fx f x x x x C
x


.
Vì
2 1 1 22 122 2 122FCCFxx
.
Vậy
44122522F  .
Câu 20. Cho số phức
z
thỏa mãn
263zz i
. Tổng phần thực và phần ảo số phức
z
bằng
A.
5
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn C
Đặt
,,zabiab
.
Ta có:

26 2
263 2 63
23 3
aa a
zz iabi abi i
bb b






.
Trang 10/16
Vậy
1ab
.
Câu 21. Trong không gian
Oxyz
cho hai điểm
5; 3; 2A 
và
1; 1; 4B
. Mặt phẳng đi qua
A
và vuông
góc với đường thẳng
A
B có phương trình là
A.
32 190xyz
. B.
23190xy z
.
C.
2370xy z 
. D.
32 230xyz
.
Lời giải
Chọn B
Mặt phẳng đi qua
A
và vuông góc với đường thẳng
A
B
có vectơ pháp tuyến
4;2;6nAB

nên có phương trình là
45236202 3190xyz xyz
.
Câu 22. Nguyên hàm của hàm số
54e3
xx
fx
là
A.
5
4e 3
ln 5
x
x
x
C
. B.
5
4e 3
log5
x
x
x
C
.
C.
5ln5 4e
xx
C
. D.
54e3
xx
C
.
Lời giải
Chọn A


5
d54e3d5d4ed3d 4e3
ln 5
x
xx x x x
f
xx x x x x xC

.
Câu 23. Số phức liên hợp với số phức
78i
là
A.
78i
. B.
87i
. C.
87i
. D.
78i
.
Lời giải
Chọn A
Số phức
,zabiab suy ra số phức liên hợp của
z
là
zabi
.
Vậy số phức liên hợp với số phức
78i
là
78i
.
Câu 24. Nguyên hàm của hàm số

2
34sin5cos
f
xx x x
là
A.
3
4cos 5sin
x
xxC. B.
3
4cos 5sin
x
xxC.
C.
3
4cos 5sin
x
xxC. D.
64cos5sin
x
xxC
.
Lời giải
Chọn B


23
d 3 4sin 5cos d 4cos 5sin
f
xx x x xxx x xC 

.
Câu 25. Trong không gian
Oxyz
, khoảng cách giữa hai mặt phẳng
: 2 2 10 0Pxyz
và
: 4 2 4 7 0Qxyz
bằng
A.
9
2
. B.
13
6
. C.
17
3
. D.
13
3
.
Lời giải
Chọn B
Ta có
212 10
424 7

nên

P
và

Q
song song với nhau.
Lấy

0;0;5
M
P
thì
,dP Q
,dM Q
222
4.0 2.0 4.5 7
424


13
6
.
Câu 26. Số phức có phần thực bằng
5
và phần ảo bằng
6
là
A.
56i
. B.
56i
. C.
56i
. D.
56i
.
Lời giải
Trang 11/16
Chọn D
Theo định nghĩa, số phức có phần thực bằng
5
và phần ảo bằng
6
là
56i
.
Câu 27. Cho

2
1
21d 20fx x
. Tính

5
3
d.I
f
xx
A.
10I
. B.
20I
. C.
30I
. D.
40I
.
Lời giải
Chọn D
Xét tích phân

2
1
21d
J
fx x
.
Đặt
1
21 d d.
2
x
tx t
Đổi cận:
x
1 2
t
3
5
  
255
133
11
21d dt d.
22
Jf
xx
f
t
f
xx

Theo giả thiết:
 
55
33
1
d 20 d 40.
2
fx x fx x

Câu 28. Điểm nào trong hình vẽ dưới đây là điểm biểu diễn số phức
13?zi
A.
M
. B.
P
. C.
Q
. D.
N
.
Lời giải
Chọn C
Số phức
13zi
được biểu diễn bởi điểm có tọa độ
1; 3
chọn điểm
.Q
Câu 29. Cho hình trụ có diện tích xung quanh bằng
50
và có thiết diện qua trục hình trụ là một hình
vuông. Đường kính của đường tròn đáy của hình trụ đã cho bằng
A.52. B.
52
2
. C.52
. D.
52
2
.
Lời giải
Chọn A
Theo giả thiết: thiết diện qua trục hình trụ là một hình vuông
ld
.
2
xq
SRl
50dl
2
50d
2
50d
52d
.
Câu 30. Cho hình nón có đường sinh bằng
3a
và bán kính đường tròn đáy bằng
2a
. Diện tích xung quanh
của hình nón đã cho bằng
A.
2
3 a
. B.
2
6 a
. C.
2
45
3
a
. D.
2
12 a
.
Lời giải
Chọn B
Ta có
xq
SRl
.2 .3 aa
2
6 a
.
Trang 12/16
Câu 31. Nguyên hàm của hàm số
42ln
f
xx x
là
A.
22
2ln 3
x
xxC
. B.
22
2ln
x
xx C
. C.
22
2ln
x
xx C
. D.
22
2ln 3
x
xxC
.
Lời giải
Chọn A
d42lnd
f
xx x xx

2
2ln d2
x
x

2
22ln 2d
x
xxx

22
22ln
x
xxC
22
2ln 3
x
xxC.
Câu 32.
Thể tích khối cầu ngoại tiếp lăng trụ tam giác đều có tất cả các cạnh bằng
23a
là
A.
3
28 a
. B.
3
28 7
3
a
. C.
3
28
3
a
. D.
3
28 7
7
a
.
Lời giải
Chọn B
Gọi
O
,
O
lần lượt là tâm tam giác
A
BC
,
A
BC

và
I
là trung điểm
OO
. Khi đó
I
là tâm mặt
cầu ngoại tiếp lăng trụ.
23OO a
3OI a
;
23
.2 3.
32
OA a
2a
.
Bán kính mặt cầu
rIA
22
OA OI
22
43aa
7a
.
Thể tích khối cầu:
3
4
7
3
Va
3
28 7
3
a
.
Câu 33. Trong không gian
Oxyz
, cho mặt phẳng
:20Pxyz
và hai điểm
6;4; 7A
,
2;2; 1B
. Điểm
;;
M
abc P
và thỏa
22
3TMA MB
đạt giá trị lớn nhất. Mệnh đề nào sau
đây là đúng?
A.
0ac
. B.
2372019abc
.
C.
0abc
. D.
4ab
.
Lời giải
Chọn A
Gọi I là điểm thỏa mãn:

3
30 0;1;2 0;1;2
13
OA OB
IA IB OI I



.
Khi đó, với mọi điểm
;;
M
xyz P
, ta luôn có:
22
222
22 2
322.3323TMIIA MIIB MI MIIAIBIA IB MIIA IB  
 
.
Vì I ,
A
,
B
cố định nên
22
3IA IB
là hằng số.
Do đó,
T đạt GTLN
2
2
M
I
đạt GTLN
M
I
đạt GTNN
M
IP M
là hình chiếu vuông góc của I trên
P
Trang 13/16













1
2
21;2;1
12
cïng ph−¬ng
1
111
P
x
xyz
MP
yM
xy z
IM n
z
.
1a
,
2b
,
1c
.
Vậy
0ac
.
Câu34. Cho
4
2
3
23
dln2ln3ln7
3
x
xa b c
xx

với
, , abc
. Giá trị của
237abc
bằng
A.
9
. B.
6
. C.
15
. D.
3
.
Lời giải
Chọn D
Ta có:



44 4
4
2
3
33 3
3
23 1 1
d d d ln 3 ln 28 ln18
3.3 3
xx
x
xx xxx
xx xx xx







14
ln ln14 ln 9 ln 2 2ln 3 ln 7
9

.
1a
,
2b 
,
1c
.
Vậy
2373abc
.
Câu 35. Một khối cầu có thể tích bằng
288
thì diện tích mặt cầu đó bằng
A.
144
3
. B.
128
. C.
72
. D.
144
.
Lời giải
Chọn D
Gọi bán kính của khối cầu là
R
.
Thể tích khối cầu là
33
4
288 216 6
3
 VR R R
.
Diện tích mặt cầu là
2
4 4 .36 144  SR
.
Câu 36. Cho

1
2
0
dln2ln3
3

x
xab c
x
với ,a
,b
c là các số hữu tỉ. Giá trị của
8 abc
bằng
A.
1
. B.
2
. C.
1
. D.
2
.
Lời giải
Chọn C
  
11 1
22 2
00 0
33 1 1
dd3.d
3
33 3








xx
x
xx
x
xx x
1
0
331
ln 3 ln 4 ln 3 1 2ln 2 ln 3
34 4




x
x
.
Suy ra
1
4
2
1


a
b
c
.
Vậy
81abc
.
Câu 37: Cho hàm số
yf
x
có đồ thị là đường cong
'
yf
x
cắt trục
O
x
tại 3 điểm có hoành độ
a
,
b
,
c
như hình vẽ. Mệnh đề nào dưới đây là đúng?
Trang 14/16
A.
f
c
f
a
f
b
. B.
f
b
f
a
f
c
.
C.
f
c
f
b
f
a
. D.
f
a
f
c
f
b
.
Lời giải
Chọn D
Gọi
1
S ,
2
S lần lượt là diện tích hình giới hạn bởi đồ thị hàm số
'
f
x
với các đường
Ox
,
x
a
,
x
b
và diện tích hình giới hạn bởi đồ thị
'
f
x
với các đường
Ox
,
x
c
,
x
b
Ta có
 
1
'' 0
bb
aa
Sfxdx fxdxfafb

f
a
f
b
Và
 
2
'' 0
cc
bb
Sfxdxfxfcfb

f
c
f
b
Từ đồ thị
'
f
x
ta thấy
12
SS
f
a
f
b
f
c
f
b
f
a
f
c
Vậy
f
a
f
c
f
b
.
Câu 38: Cho

2
2
0
1cos
x
xdx a b c


với
a
,
b
,
c
là các số hữu tỉ. Giá trị của
43ab c
bằng
A. 1 . B. 2 . C. 4. D. 0.
Lời giải
Chọn C
Với

222
000
1cos cosI x x dx xdx x xdx



.
Ta thấy
2
2
2
1
0
1
2
28
0
Ixdxx

.
Gọi
2
2
0
cosIxxdx
Đặt
cos sin
u x du dx
dv xdx v x





Áp dụng công thức tích phân từng phần ta có
2
2
0
sin sin
2
0
Ixx xdx

sin cos 1
22
2
00
xx x


.
Trang 15/16
Do đó
2
12
1
82
II I

 
. Suy ra
1
8
a
,
1
2
b
,
1c 
.
Vậy

11
434. 3.14
82
ab c
.
Câu 39. Nguyên hàm của hàm số

4sin5 .cos
f
xxx
là .
A.
2
sin 4 sin 6
3
x
xC
. B.
11
cos 4 cos 6
23
x
xC
.
C.
4
cos5 .sin
5
x
xC
. D.
11
cos 4 cos6
23
x
xC
.
Lời giải
Chọn B.

cos6 cos 4 1 1
4sin 5 .cos .d 2 sin 6 sin 4 d 2 cos6 cos 4
64 3 2
xx
x
xx x x x C x x C





.
Câu 40. Cho hàm số
yf
x
có bảng biến thiên như hình vẽ
Tính diện tích hình phẳng được giới hạn bởi các đường
yf
x
;
0y
;
2x 
và
2x
.
A.
3
. B. 4 . C.
6
. D.
5
.
Lời giải
Chọn C.
Gọi
S
là diện tích hình phẳng được giới hạn bởi các đường
yf
x
;
0y
;
2x 
và
2x
  
202
220
ddd0220Sfxxfxxfxxff ff






12 21 6
.
II – PHẦN TỰ LUẬN
Câu 1:
Tìm nguyên hàm của
Fx
của hàm số
3
3
x
fx x e
biết

0 2019.F
Lời giải
 

4
3
33
4
xx
x
Fx
f
xdx x e dx e x C

Mà
0 2019F
4
0
0
3.0 2019
4
eC
2020C

4
3 2020
4
x
x
Fx e x
Câu 2: Cho hình chóp
.S ABC
có đáy
A
BC
là tam giác đều cạnh
a
. Mặt bên
SAB
là tam giác cân với
120ASB  và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Xác định tâm và tính thể tích
của khối cầu ngoại tiếp hình chóp.
Lời giải
x

2
0
2

y
0
0
0


y
1
2
2
Trang 16/16
Gọi
H
là trung điểm của
A
B .
Gọi
I
;
J
lần lượt là tâm của đường tròn ngoại tiếp
A
BC
và
SAB
.
Do
A
BC
đều nên
I
CH
và
CH AB
.
SAB
cân tại
S
nên
JSH
và
SH AB
.
Ta có:





SAB ABC
SAB ABC AB
SH ABC
SH SAB CH SAB
CH ABC




.
Trong mặt phẳng
SCH
dựng
//
//
Ix SH
J
yCH

Ix ABC
Jy SAB
I
x
;
J
y
lần lượt là trục đường tròn ngoại tiếp
A
BC
và
SAB
.
Trong mặt phẳng
SCH
:
OIx OAOBOC
Ix Jy O
OJy OAOBOS






OA OB OC OS
.
O
là tâm mặt cầu ngoại tiếp hình chóp
.S ABC
.
Ta có
13
36
a
OJ IH CH

.
Áp dụng định lí sin trong tam giác
SAB
ta có:
3
22
sin 2sin 2sin120 3
SAB
A
BABaa
RJSJS
SS

.
Bán kính mặt cầu ngoại tiếp hình chóp
.S ABC
là:
22
22
3315
636
aaa
ROJSJ





.
Thể tích mặt cầu là
3
3
3
4415515
336 54
aa
VR






.
------------- HẾT -------------
O
J
I
H
C
B
A
S
J
H
B
A
S
| 1/16
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO TÂY NINH
ĐỀ THI HỌC KỲ II
NĂM HỌC 2018 – 2019
Môn: Toán – Lớp 12
Thời gian: 90 phút (Không kể thời gian phát đề)
I – PHẦN TRẮC NGHIỆM
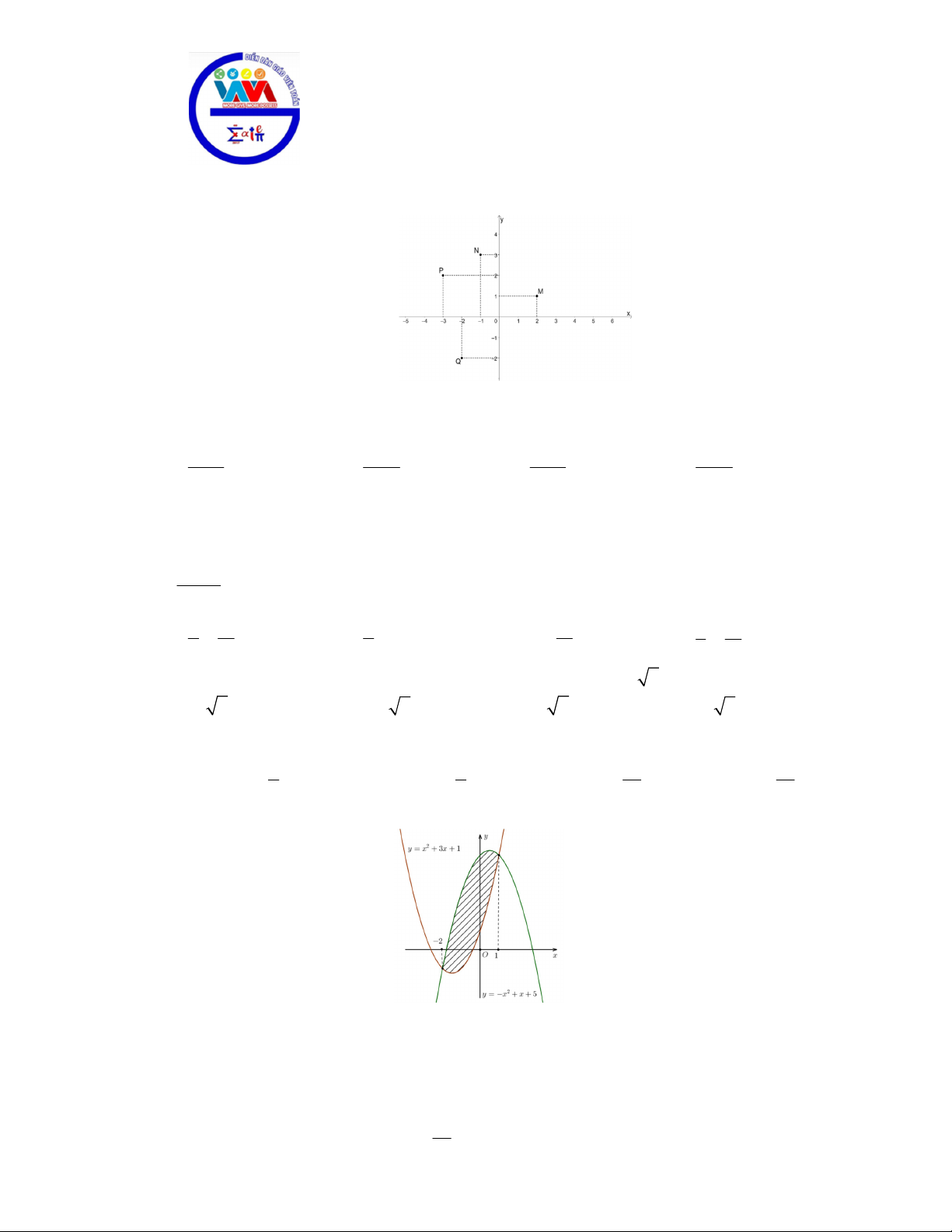
Câu 1: Cho bốn số phức có điểm biểu diễn lần lượt là M , N , P,Q như hình vẽ bên. Số phức có mô đun lớn
nhất là số phức có điểm biểu diễn là A. N . B. P . C. Q . D. M .
Câu 2: Diện tích hình phẳng giới hạn bởi các đường y = (e + ) 2 x và = (2 x y + e )x là e- 2 e + 2 e- 2 e + 2 A. . B. . C. . D. . 4 4 2 2 
Câu 3. Trong không gian Oxyz , cho hai điểm A1;3; 2  , B3; 2
 ;4. Vectơ AB có tọa độ là: A. 2;5;6 . B.  2;  5;6. C. 4;1;2 . D. 2; 5  ;6 . 2 4 Câu 4. dx  bằng 3x  2 1 4 11 4 11 1 11 A. ln . B. ln 55 . C. 4ln . D. ln . 3 5 3 5 3 5
Câu 5. Thể tích của một khối trụ có bán kính đáy r  4 và chiều cao h  4 2 bằng A. 32 2 . B. 128 2 . C. 16 2 . D. 64 2 .  
Câu 6. Trong không gian Oxyz , cho hai vectơ a  2;2; 
1 và b  3;2;6 . Mệnh đề nào dưới đây đúng?         A. a b 3 cos ,  . B. a b 3 cos ,   . C. a b 4 cos ,   . D. a b 4 cos ,  . 7 7 21 21
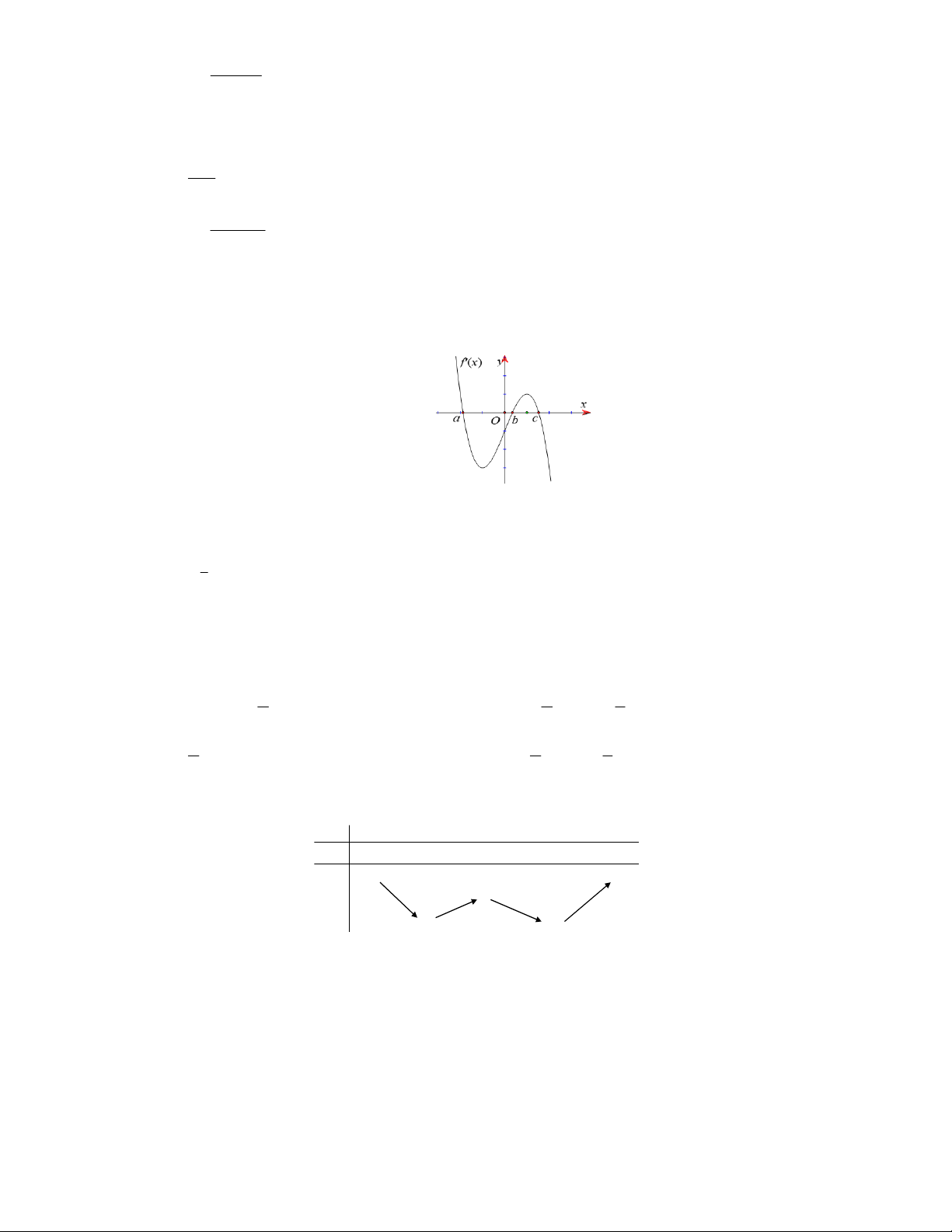
Câu 7. Diện tích hình phẳng gạch chéo trong hình vẽ bên dưới được tính bởi công thức nào dưới đây? 1 1 A. S    2
2x  2x  4dx .
B. S   4x  6dx . 2 2 1 1
C. S   4x  6dx .
D. S    2
2x  2x  4dx . 2 2 1
Câu 8. Nguyên hàm của hàm số f x  2x  là 2 x Trang 1/16 1 1 A. 2 x   C . B. 2
x  ln x C .
C. 2   C .
D. 2x  2ln x C . x x
Câu 9. Cho số phức z a bi , a, b   thỏa mãn z  5  3i z . Giá trị của 5a b bằng A. 3  . B. 13 . C. 8  . D. 11.
Câu 10. Diện tích hình phẳng giới hạn bởi các đường 3 1 x y
e , y  0 , x 1 và x  2 là 2 6 3  e e 2 6 2  e e 6 2 e e  3 6 2 e e  2 A. . B. . C. . D. . 3 3 3 3
Câu 11. Cho số phức z thỏa mãn z    i2 1 2
i 1. Môđun của số phức đã cho bằng A. 13 . B. 13 . C. 1. D. 5 .
Câu 12. Cho số phức z thỏa mãn z  2  5i  z i  
1 . Phần ảo của số phức đã cho là A. 5i . B. 8 . C. 5 . D. 8  i .
Câu 13: Nguyên hàm của hàm số   3 2
f x x x là 1 1 1 1 A. 4 3
x x C. B. 4 3
x x C. C. 2
3x  2x C. D. 4 3
x x C. 4 3 3 4
Câu 14: Cho hình phẳng H  giới hạn bởi các đường 2
y x  5, y  0, x  0, x  3. Gọi V là thể tích khối
tròn xoay được tạo thành khi quay H  xung quanh trục .
Ox Mệnh đề nào dưới đây đúng? 3 3 3 3 2 2
A. V   2
x  5 d .x B. V   2x 5d .x C. V   2x 5 d .x D. V   2x 5d .x 0 0 0 0
Câu 15. Cho khối nón có độ dài đường sinh bằng 2a 3 , góc giữa đường sinh và mặt đáy bằng o 30 . Thể
tích của khối nón đã cho bằng A. 3 3 a . B. 3 3a . C. 3 3 3 a . D. 3 3 3a . 1 1 1
Câu 16. Cho tích phân f
 xdx  3và g
 xdx  6, khi đó  f
 x3gxdx  bằng 0 0 0 A. 3  . B. 15  . C. 21. D. 3.
Câu 17: Trong không gian Oxyz cho tam giác ABC với A(1; 3; 2) , B(3; 4;5) , C(1; 2;3) . Độ dài đường
trung tuyến AM M BC của tam giác ABC bằng A. 2 5 . B. 44 . C. 6 . D. 2 11 .
Câu 18: Gọi S là diện tích hình phẳng giới hạn bởi các đường  3x y
, y  0, x 1, x e . Mệnh đề nào dưới đây đúng? e e e e A.  3x S dx  . B.   3x S dx  . C. 2   3 x S dx  . D. 2  3 x S dx  . 1 1 1 1
Câu 19. Biết F x là một nguyên hàm của hàm số   1 f x
và F 2 1. Tính F 4 . x
A. F 4  5  2 .
B. F 4  5  2 .
C. F 4  4  2 2 . D. F 4  5  2 2 .
Câu 20. Cho số phức z thỏa mãn z  2z  6  3i . Tổng phần thực và phần ảo số phức z bằng A. 5 . B. 3 . C. 1  . D. 2 .
Câu 21. Trong không gian Oxyz cho hai điểm A5; 3; 2 và B1;1;4 . Mặt phẳng đi qua A và vuông
góc với đường thẳng AB có phương trình là
A. 3x  2 y z 19  0 . B. 2x y  3z 19  0 . C. 2x y  3z  7  0 . D. 3x  2 y z  23  0 . Trang 2/16
Câu 22. Nguyên hàm của hàm số   5x 4ex f x    3 là 5x 5x A.
 4ex  3x C . B.
 4ex  3x C . C. 5x ln 5  4ex C . D. 5x  4ex  3  C . ln 5 log 5
Câu 23. Số phức liên hợp với số phức 7 8i là A. 7  8i . B. 8  7i . C. 8  7i . D. 7  8i .
Câu 24. Nguyên hàm của hàm số f x 2
 3x  4sin x  5cos x là A. 3
x  4cos x  5sin x C . B. 3
x  4cos x  5sin x C . C. 3
x  4cos x  5sin x C .
D. 6x  4cos x  5sin x C .
Câu 25. Trong không gian Oxyz , khoảng cách giữa hai mặt phẳng P: 2x y  2z 10  0 và
Q: 4x  2y  4z 7  0 bằng 9 13 17 13 A. . B. . C. . D. . 2 6 3 3
Câu 26. Số phức có phần thực bằng 5 và phần ảo bằng 6 là A. 5  6i .
B. 5  6i .
C. 5  6i . D. 5  6i . 2 5 Câu 27. Cho f
 2x 1dx  20 . Tính I f  xd .x 1 3 A. I 10 . B. I  20 . C. I  30 . D. I  40 .
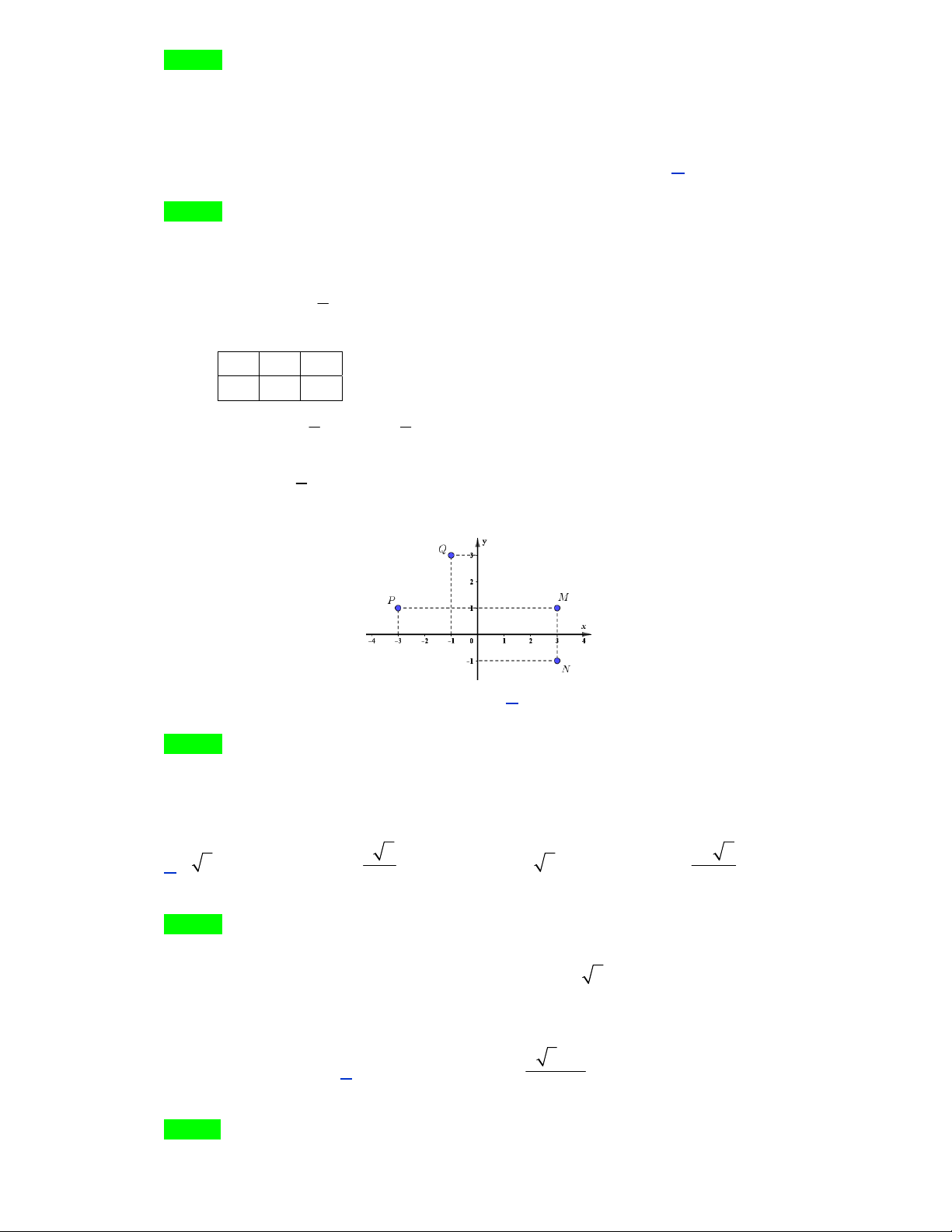
Câu 28. Điểm nào trong hình vẽ dưới đây là điểm biểu diễn số phức z  1   3i? A. M . B. P . C. Q . D. N .
Câu 29. Cho hình trụ có diện tích xung quanh bằng 50 và có thiết diện qua trục hình trụ là một hình
vuông. Đường kính của đường tròn đáy của hình trụ đã cho bằng 5 2 5 2 A. 5 2 . B. . C. 5 2 . D. . 2 2
Câu 30. Cho hình nón có đường sinh bằng 3a và bán kính đường tròn đáy bằng 2a . Diện tích xung quanh
của hình nón đã cho bằng 2 4 5 a A. 2 3 a . B. 2 6 a . C. . D. 2 12 a . 3
Câu 31. Nguyên hàm của hàm số f x  4x2  ln x là A. 2 2
2x ln x  3x C . B. 2 2
2x ln x x C . C. 2 2
2x ln x x C . D. 2 2
2x ln x  3x C .
Câu 32. Thể tích khối cầu ngoại tiếp lăng trụ tam giác đều có tất cả các cạnh bằng 2a 3 là 28 7 28 28 7 A. 3 28a . B. 3 a . C. 3  a . D. 3 a . 3 3 7
Câu 33. Trong không gian Oxyz , cho mặt phẳng P : x y z  2  0 và hai điểm A6;4; 7 , B 2;2; 
1 . Điểm M a;b;cP và thỏa 2 2
T MA  3MB đạt giá trị lớn nhất. Mệnh đề nào sau đây là đúng?
A. a c  0 .
B. 2a  3b  7c  2019 .C. a b c  0 .
D. a b  4 . Trang 3/16 4 2x  3 Câu34. Cho
dx a ln 2  b ln 3  c ln 7 
với a, b, c   . Giá trị của 2a  3b  7c bằng 2 x  3x 3 A. 9  . B. 6 . C. 15 . D. 3.
Câu 35. Một khối cầu có thể tích bằng 288 thì diện tích mặt cầu đó bằng 144 A. . B. 128 . C. 72. D. 144. 3 1 Câu 36. Cho d   ln 2  ln 3  x x a b c
với a, b, c là các số hữu tỉ. Giá trị của 8a b c bằng x 32 0 A. 1. B. 2 . C. 1  . D. 2  .
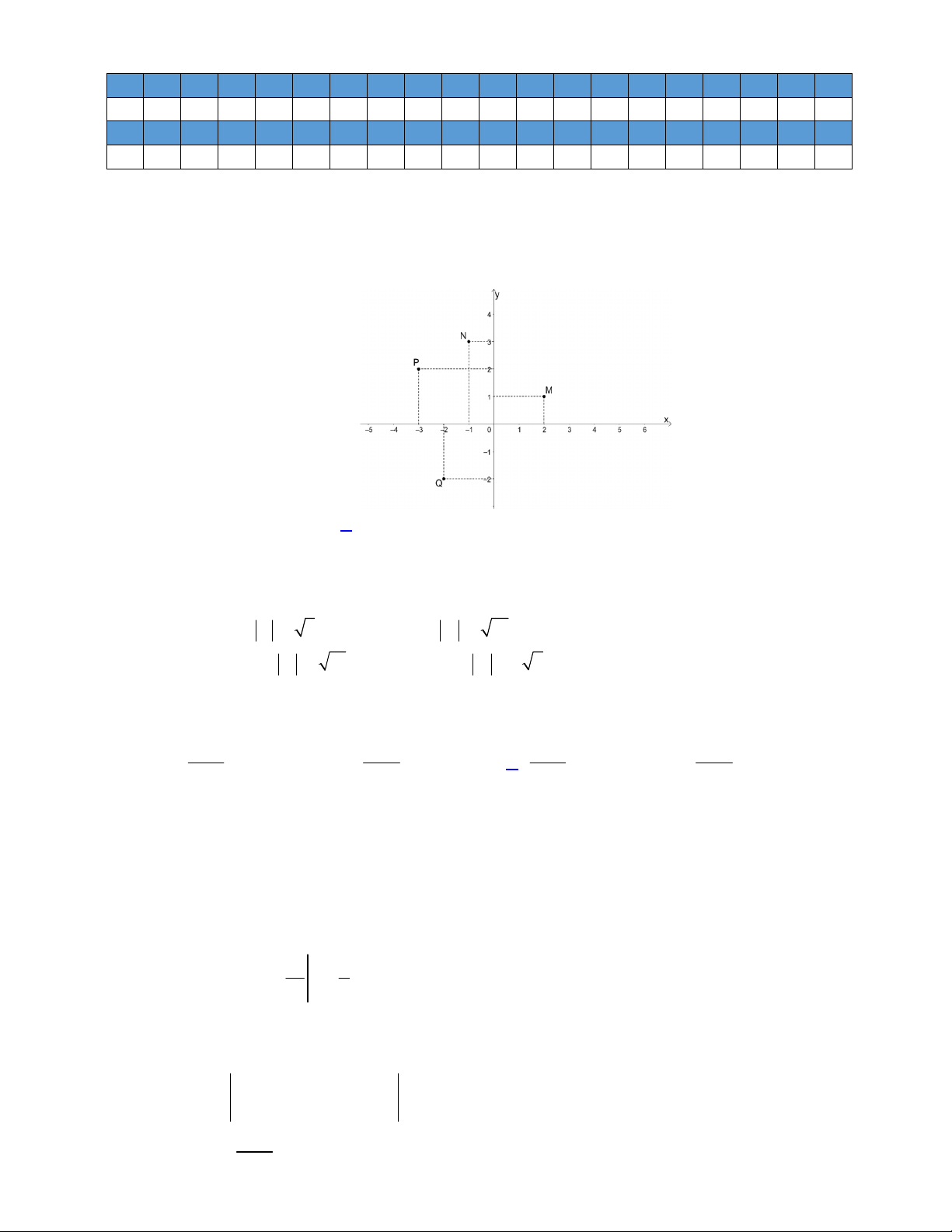
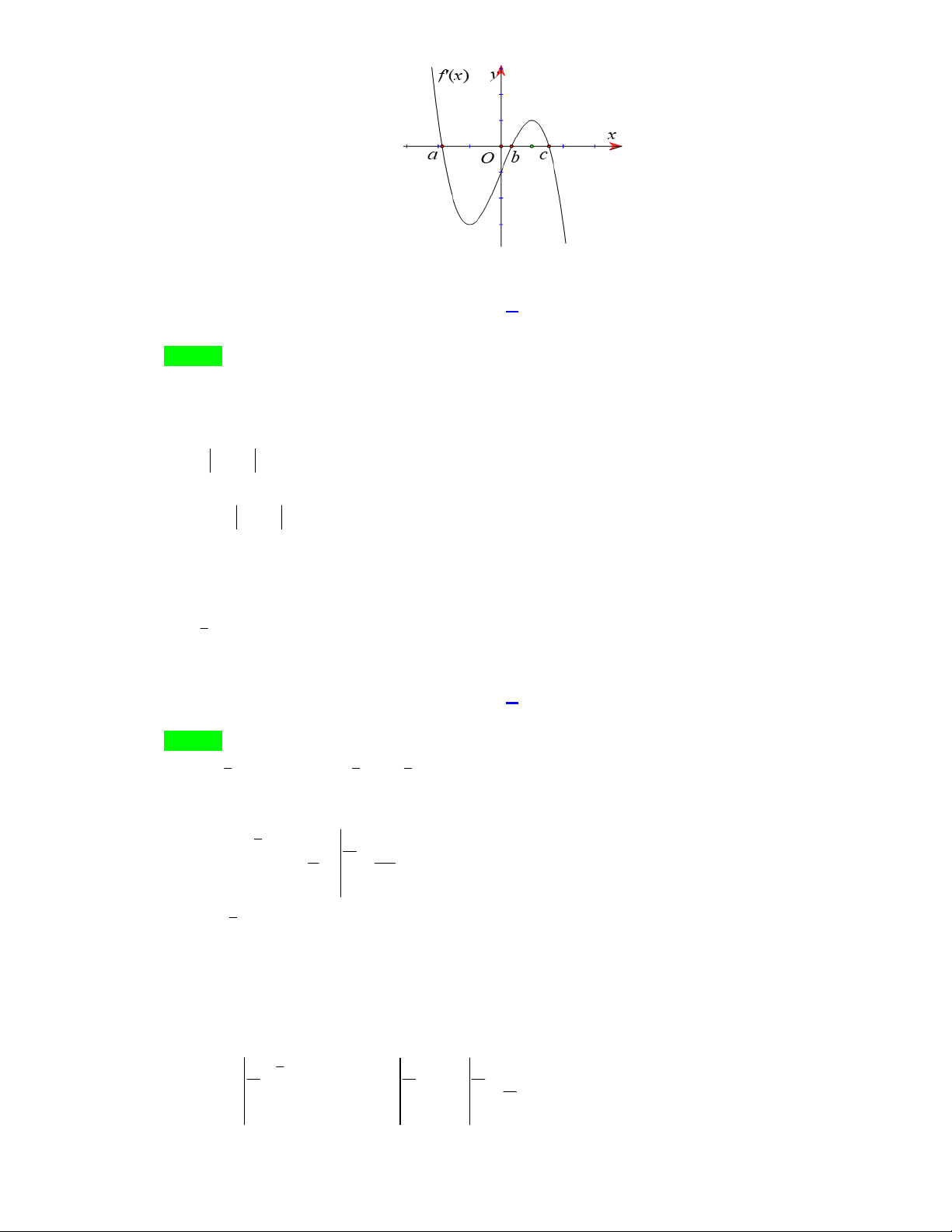
Câu 37: Cho hàm số y f x có đồ thị là đường cong y f ' x cắt trục Ox tại 3 điểm có hoành độ a ,b
, c như hình vẽ. Mệnh đề nào dưới đây là đúng?
A. f c  f a  f b.
B. f b  f a  f c.
C. f c  f b  f a.
D. f a  f c  f b.  2 Câu 38: Cho x  1cos x 2
dx a  b  c với a , b , c là các số hữu tỉ. Giá trị của 4a b  3c bằng 0 A. 1. B. 2  . C. 4. D. 0.
Câu 39. Nguyên hàm của hàm số f x  4sin 5 . x cos x là . 2 1 1
A.  sin 4x  sin 6x C .
B.  cos 4x  cos 6x C . 3 2 3 4 1 1 C. cos5 .
x sin x C .
D. cos 4x  cos 6x C . 5 2 3
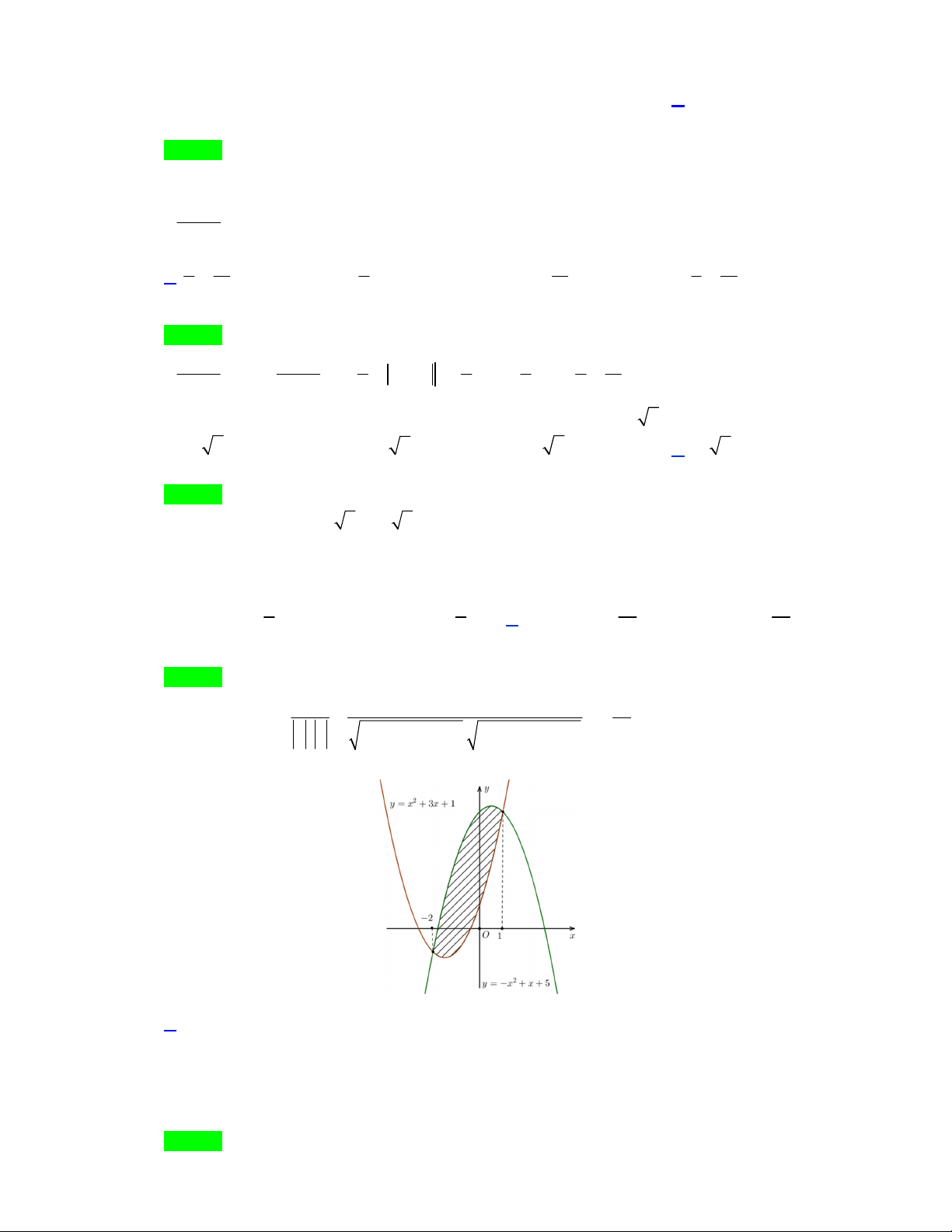
Câu 40. Cho hàm số y f x có bảng biến thiên như hình vẽ x  2  0 2  y 0 0 0   y 1 2  2 
Tính diện tích hình phẳng được giới hạn bởi các đường y f  x ; y  0 ; x  2  và x  2 . A. 3. B. 4 . C. 6 . D. 5. II – PHẦN TỰ LUẬN
Câu 1: Tìm nguyên hàm của F x của hàm số   3 x
f x x e  3 biết F 0  2019.
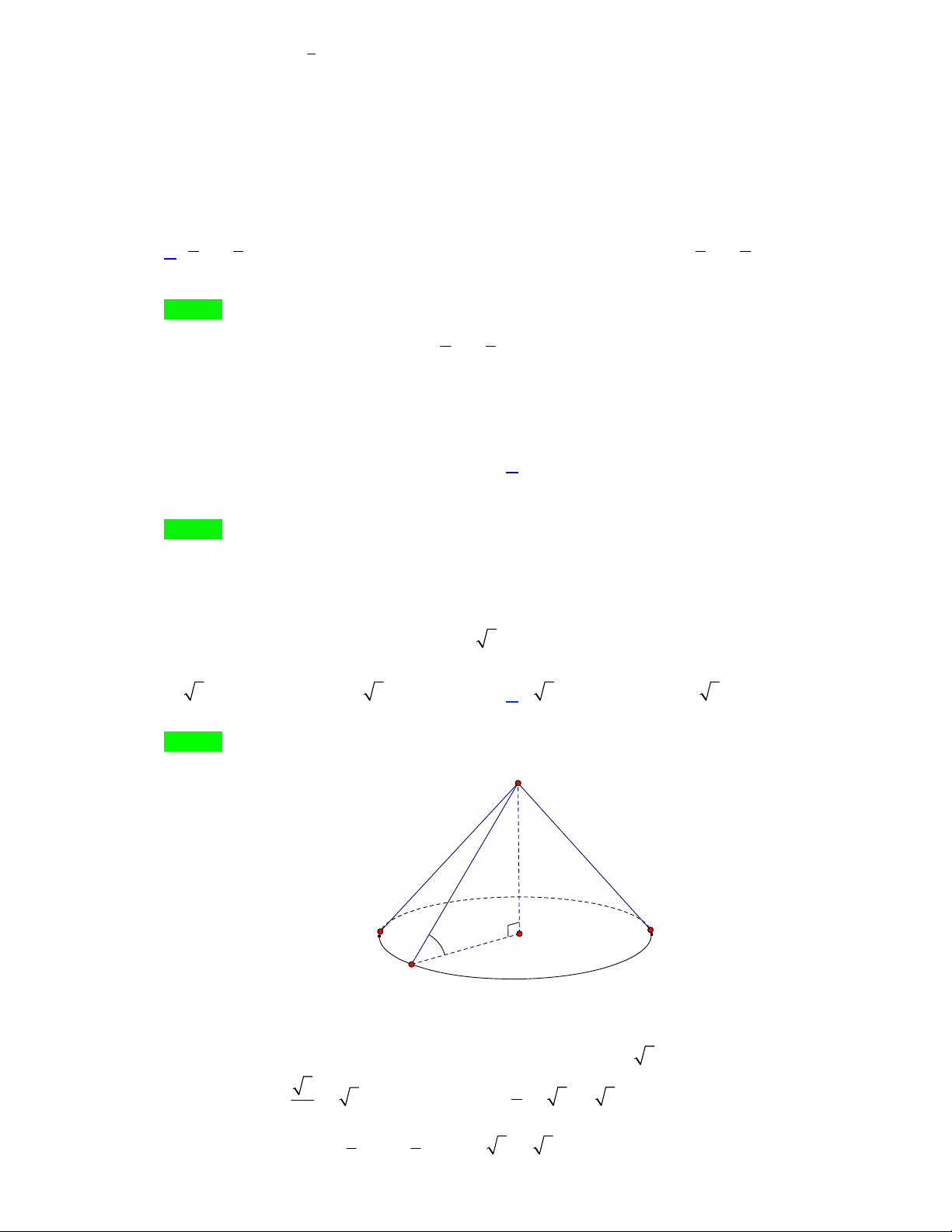
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Mặt bên SAB là tam giác cân với 
ASB 120 và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Xác định tâm và tính thể tích
của khối cầu ngoại tiếp hình chóp.
------------- HẾT ------------- Trang 4/16 BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 B C D A D C A A D C B B A C C B D A D C
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 B A A B B D D C A B A B A D D C D C B C
LỜI GIẢI CHI TIẾT
I – PHẦN TRẮC NGHIỆM
Câu 1: Cho bốn số phức có điểm biểu diễn lần lượt là M , N , P,Q như hình vẽ bên. Số phức có mô đun lớn
nhất là số phức có điểm biểu diễn là A. N . B. P . C. Q . D. M . Lời giải Chọn B
Gọi z , z , z , z là các số phức có điểm biểu diễn lần lượt là M , N, P,Q . 1 2 3 4
z = 2 +i z = 5 , z = -1+ 3i z = 10 1 1 2 2
z = -3+ 2i z = 13 , z = -2- 2i z = 2 2 3 3 4 4
Vậy số phức có mô đun lớn nhất là số phức có điểm biểu diễn là điểm P
Câu 2: Diện tích hình phẳng giới hạn bởi các đường y = (e + ) 2 x và = (2 x y + e )x là e- 2 e + 2 e- 2 e + 2 A. . B. . C. . D. . 4 4 2 2 Lời giải Chọn C éx =
Phương trình hoành độ giao điểm: (e + ) x = ( x + e ) 0 2 2 x  êê x =1 ë 1 1 1
Diện tích hình phẳng = ò (ex- x ) = ex - ex S e x dx dx
x dx = S - S ò ò 1 2 0 0 0 1 2 x 1 e S = ex dx = e = 1 ò 2 0 2 0 1 u ìï = x du ìï = dx x S = xe dx ï ï í í 2 ò Đặt , x x ïdv = e dx v ï = e 0 ïî ïî 1 1 1 x x x x S = xe
- e dx = xe -e =1 2 ò ( ) 0 0 0 e - 2 Vậy: S = 2 Trang 5/16 
Câu 3. Trong không gian Oxyz , cho hai điểm A1;3; 2  , B3; 2
 ;4. Vectơ AB có tọa độ là: A. 2;5;6 . B.  2;  5;6. C. 4;1;2 . D. 2; 5  ;6 . Lời giải Chọn D 
AB  2;5;6 . 2 4 Câu 4. dx  bằng 3x  2 1 4 11 4 11 1 11 A. ln . B. ln 55 . C. 4ln . D. ln . 3 5 3 5 3 5 Lời giải Chọn A 3 3 4 1 4 3 4 4 4 11 dx  4
dx  ln 3x  2  ln11 ln 5  ln   . 1 3x  2 3x  2 3 3 3 3 5 1 1
Câu 5. Thể tích của một khối trụ có bán kính đáy r  4 và chiều cao h  4 2 bằng A. 32 2 . B. 128 2 . C.16 2 . D. 64 2 . Lời giải Chọn D Ta có 2 2
V   r h  .4 .4 2  64 2 .  
Câu 6. Trong không gian Oxyz , cho hai vectơ a  2;2; 
1 và b  3;2;6 . Mệnh đề nào dưới đây đúng?         A.a b 3 cos ,  . B. a b 3 cos ,   . C.a b 4 cos ,   . D.a b 4 cos ,  . 7 7 21 21 Lời giải Chọn C     . a b 2.3  2. 2   1  .6 4
Ta có cosa,b           . a . b 2  2   2 1 . 3   2  2 2 2 2 2 21  6
Câu 7. Diện tích hình phẳng gạch chéo trong hình vẽ bên dưới được tính bởi công thức nào dưới đây? 1 1 A. S    2
2x  2x  4dx .
B. S   4x  6dx . 2 2 1 1
C. S   4x  6dx .
D. S    2
2x  2x  4dx . 2 2 Lời giải Chọn A Trang 6/16 1 1
Ta có diện tích hình phẳng cần tìm 2
S  x x  5   
 2x 3x 1dx     2 2
x  2x  4dx. 2  2 1
Câu 8. Nguyên hàm của hàm số f x  2x  là 2 x 1 1 A. 2 x   C . B. 2
x  ln x C .
C. 2   C .
D. 2x  2ln x C . x x Lời giải Chọn A  1  1 Ta có f  x 2 dx  2x
dx x   C  . 2   x x
Câu 9. Cho số phức z a bi , a, b   thỏa mãn z  5  3i z . Giá trị của 5a b bằng A. 3  . B.13 . C. 8  . D. 11. Lời giải Chọn D
Ta có z  5  3i z 2 2
a bi  5  3i a b a   b   2 2 5
3 i a b . a  5   8 2 2
a  5  a ba      2 2
 a 10a  25  a  9   5 (thỏa điều kiện). b   3  0 b   3    b   3 
Vậy 5a b  1  1.
Câu 10. Diện tích hình phẳng giới hạn bởi các đường 3 1 x y
e , y  0 , x 1 và x  2 là 2 6 3  e e 2 6 2  e e 6 2 e e  3 6 2 e e  2 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn C
Phương trình hoành độ giao điểm 3 1 x
e  0  x  0 1;2 . 2 2  1   1   1  6 2 e e  3
Diện tích hình phẳng là   3 1 x Se dx 3xx e   6 2
 2  e  1 e     = .  3   3   3  3 1 1 6 2 e e  3 Vậy S  . 3
Câu 11. Cho số phức z thỏa mãn z    i2 1 2
i 1. Môđun của số phức đã cho bằng A. 13 . B. 13 . C. 1. D. 5 . Lời giải Chọn B
Ta có: z    i2 1 2
i 1  z  2  3i . Do đó: z  2
  3i   2 2 2  3  13 .
Câu 12. Cho số phức z thỏa mãn z  2  5i  z i  
1 . Phần ảo của số phức đã cho là A. 5i . B. 8 . C. 5 . D. 8  i . Lời giải Chọn B
Gọi z x yi,  ,x y . Trang 7/16
Ta có: z  2  5i  z i  
1  x yi  2  5i   x yii   1
 x  2  y 5i  x y x yi
x  2  x y
2x y  2  x  5       
y  5  x yx  5 y  8 
Khi đó: z  5  8i . Vậy số phức z có phần ảo là 8 .
Câu 13: Nguyên hàm của hàm số   3 2
f x x x là 1 1 1 1 A. 4 3
x x C. B. 4 3
x x C. C. 2
3x  2x C. D. 4 3
x x C. 4 3 3 4 Lời giải Chọn A 1 1 Ta có:  3 2 x x  3 2 4 3
dx x dx x dx x x C   4 3
Câu 14: Cho hình phẳng H  giới hạn bởi các đường 2
y x  5, y  0, x  0, x  3. Gọi V là thể tích khối
tròn xoay được tạo thành khi quay H  xung quanh trục .
Ox Mệnh đề nào dưới đây đúng? 3 3 3 3 2 2
A. V   2
x  5 d .x B. V   2x 5d .x C. V   2x 5 d .x D. V   2x 5d .x 0 0 0 0 Lời giải Chọn C
Áp dụng công thức tính thể tích khối tròn xoay khi quay hình phẳng được giới hạn bởi các đường 3 2 2
y x  5, y  0, x  0, x  3 quanh trục Ox , ta có V   2x 5 d .x 0
Câu 15. Cho khối nón có độ dài đường sinh bằng 2a 3 , góc giữa đường sinh và mặt đáy bằng o 30 . Thể
tích của khối nón đã cho bằng A. 3 3 a . B. 3 3a . C. 3 3 3 a . D. 3 3 3a . Lời giải Chọn C I h l O 30 r A
Gọi I là đỉnh của khối nón, O là tâm đáy, A thuộc đường tròn đáy, l là đường sinh, r là bán
kính đáy, h là chiều cao của khối nón.
Theo giả thiết ta có tam giác IOA vuông tại O ,  o
IAO  30 , l  2a 3 . 3 1 o
r l.cos30  .2a 3  3a , o
h l.sin 30  .2a 3  a 3 . 2 2 1 1
Thể tích khối nón là: V   r h   3a2 2 3
a 3  3 3 a . 3 3 Trang 8/16 1 1 1
Câu 16. Cho tích phân f
 xdx  3và g
 xdx  6, khi đó  f
 x3gxdx  bằng 0 0 0 A. 3  . B. 15  . C. 21. D.3. Lời giải Chọn B 1 1 1 Ta có  f
 x3gxdx  f
 xdx 3 g
 xdx  33.6  15  0 0 0
Câu 17: Trong không gian Oxyz cho tam giác ABC với A(1; 3; 2) , B(3; 4;5) , C(1; 2;3) . Độ dài đường
trung tuyến AM M BC của tam giác ABC bằng A. 2 5 . B. 44 . C. 6 . D. 2 11 . Lời giải Chọn D
Ta có đường trung tuyến AM nên M là trung điểm cạnh BC do đó 
M 1;3;4  AM  2;6;2  AM   2 2 2 2  6  2  2 11 .
Câu 18: Gọi S là diện tích hình phẳng giới hạn bởi các đường  3x y
, y  0, x 1, x e . Mệnh đề nào dưới đây đúng? e e e e A.  3x S dx  . B.   3x S dx  . C. 2   3 x S dx  . D. 2  3 x S dx  . 1 1 1 1 Lời giải Chọn A
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y f x , trục Ox (y  0) và các đường b
x a, x b được tính theo công thức S f  x dx. a e
Vì 3x  0 nên  3x S dx  . 1
Câu 19. Biết F x là một nguyên hàm của hàm số   1 f x
và F 2 1. Tính F 4 . x
A. F 4  5  2 .
B. F 4  5  2 .
C. F 4  4  2 2 . D. F 4  5  2 2 . Lời giải Chọn D
Giả sử F x  f  x 1 dx
dx  2 x C  . x
Vì F 2 11  2 2  C C 1 2 2  F x  2 x 1 2 2 .
Vậy F 4  4 1 2 2  5  2 2 .
Câu 20. Cho số phức z thỏa mãn z  2z  6  3i . Tổng phần thực và phần ảo số phức z bằng A. 5 . B. 3 . C. 1  . D. 2 . Lời giải Chọn C
Đặt z a bi ,a,b . a a  a
Ta có: z z   i a bi  a bi 2 6 2 2 6 3 2  6  3i     . b   2b  3 b   3  Trang 9/16
Vậy a b  1  .
Câu 21. Trong không gian Oxyz cho hai điểm A5; 3; 2 và B1;1;4 . Mặt phẳng đi qua A và vuông
góc với đường thẳng AB có phương trình là
A. 3x  2 y z 19  0 .
B. 2x y  3z 19  0 .
C. 2x y  3z  7  0 .
D. 3x  2 y z  23  0 . Lời giải Chọn B  
Mặt phẳng đi qua A và vuông góc với đường thẳng AB có vectơ pháp tuyến n AB   4;  2;6 nên có phương trình là 4
 x 5  2 y 3  6z  2  0  2x y 3z 19  0 .
Câu 22. Nguyên hàm của hàm số   5x 4ex f x    3 là 5x 5x A.
 4ex  3x C . B.
 4ex  3x C . ln 5 log 5
C. 5x ln 5  4ex C .
D. 5x  4ex  3  C . Lời giải Chọn A x
     x x    x x 5 d 5 4e
3 d  5 d  4 e d  3 d   4ex f x x x x x x  3x C    . ln 5
Câu 23. Số phức liên hợp với số phức 7 8i là A. 7  8i . B. 8  7i . C.8  7i . D. 7  8i . Lời giải Chọn A
Số phức z a bi a,b  suy ra số phức liên hợp của z là z a bi .
Vậy số phức liên hợp với số phức 7 8i là 7  8i .
Câu 24. Nguyên hàm của hàm số f x 2
 3x  4sin x  5cos x là A. 3
x  4cos x  5sin x C . B. 3
x  4cos x  5sin x C . C. 3
x  4cos x  5sin x C .
D. 6x  4cos x  5sin x C . Lời giải Chọn B f
 xx   2x x x 3 d 3 4sin 5cos
dx x  4 cos x  5sin x C .
Câu 25. Trong không gian Oxyz , khoảng cách giữa hai mặt phẳng P: 2x y  2z 10  0 và
Q: 4x  2y  4z 7  0 bằng 9 13 17 13 A. . B. . C. . D. . 2 6 3 3 Lời giải Chọn B 2 1 2 1  0 Ta có   
nên P và Q song song với nhau. 4 2 4 7  4.0  2.0  4.5  7 13
Lấy M 0;0;5P thì d P,Q  d M,Q   . 2 2 2 4  2  4 6
Câu 26. Số phức có phần thực bằng 5 và phần ảo bằng 6 là A. 5  6i .
B. 5  6i .
C. 5  6i . D. 5  6i . Lời giải Trang 10/16 Chọn D
Theo định nghĩa, số phức có phần thực bằng 5 và phần ảo bằng 6 là 5  6i . 2 5 Câu 27. Cho f
 2x 1dx  20 . Tính I f  xd .x 1 3 A. I 10 . B. I  20 . C. I  30 . D. I  40 . Lời giải Chọn D 2
Xét tích phân J f 2x   1dx . 1 1
Đặt 2x 1  t  dx  dt. 2 Đổi cận: x 1 2 t 3 5 2 5 5 J f   x   1 x f  t 1 2 1 d dt  f  xd .x 2 2 1 3 3 5 5 1 Theo giả thiết:  f
 xdx  20  f
 xdx  40. 2 3 3
Câu 28. Điểm nào trong hình vẽ dưới đây là điểm biểu diễn số phức z  1   3i? A. M . B. P . C. Q . D. N . Lời giải Chọn C Số phức z  1
  3i được biểu diễn bởi điểm có tọa độ  1
 ;3  chọn điểm Q.
Câu 29. Cho hình trụ có diện tích xung quanh bằng 50 và có thiết diện qua trục hình trụ là một hình
vuông. Đường kính của đường tròn đáy của hình trụ đã cho bằng 5 2 5 2 A. 5 2 . B. . C. 5 2 . D. . 2 2 Lời giải Chọn A
Theo giả thiết: thiết diện qua trục hình trụ là một hình vuông  l d .
S  2 Rl  50   dl 2  50   d 2
d  50  d  5 2 . xq
Câu 30. Cho hình nón có đường sinh bằng 3a và bán kính đường tròn đáy bằng 2a . Diện tích xung quanh
của hình nón đã cho bằng 2 4 5 a A. 2 3 a . B. 2 6 a . C. . D. 2 12 a . 3 Lời giải Chọn B
Ta có S   Rl   .2 . a 3a 2  6a . xq Trang 11/16
Câu 31. Nguyên hàm của hàm số f x  4x2  ln x là A. 2 2
2x ln x  3x C . B. 2 2
2x ln x x C . C. 2 2
2x ln x x C . D. 2 2
2x ln x  3x C . Lời giải Chọn A f
 xdx  4x
 2ln xdx    x  2 2 ln d 2x  2
 2x 2 ln x  2 d x x  2
x   x 2 2 2 ln  x C 2 2
 2x ln x  3x C .
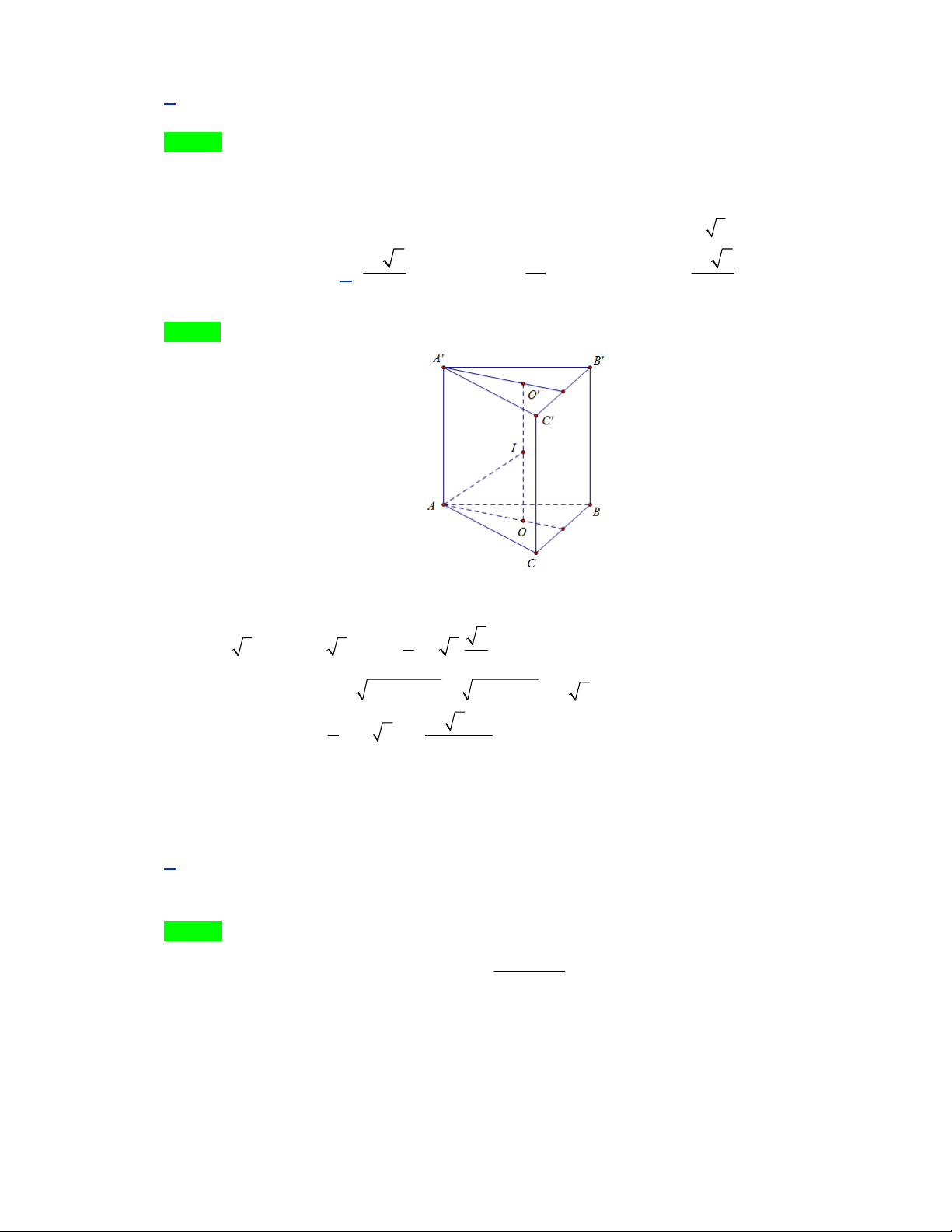
Câu 32. Thể tích khối cầu ngoại tiếp lăng trụ tam giác đều có tất cả các cạnh bằng 2a 3 là 28 7 28 28 7 A. 3 28a . B. 3 a . C. 3  a . D. 3 a . 3 3 7 Lời giải Chọn B
Gọi O , O lần lượt là tâm tam giác ABC , AB C
  và I là trung điểm OO . Khi đó I là tâm mặt
cầu ngoại tiếp lăng trụ. 2 3
OO  2a 3  OI a 3 ; OA  .2a 3.  2a . 3 2
Bán kính mặt cầu r IA 2 2  OA OI 2 2
 4a  3a a 7 . 3 28 7 a
Thể tích khối cầu: V   a 3 4 7  . 3 3
Câu 33. Trong không gian Oxyz , cho mặt phẳng P : x y z  2  0 và hai điểm A6;4; 7 , B2;2; 
1 . Điểm M a;b;cP và thỏa 2 2
T MA  3MB đạt giá trị lớn nhất. Mệnh đề nào sau đây là đúng?
A. a c  0 .
B. 2a  3b  7c  2019 .
C. a b c  0 .
D. a b  4 . Lời giải Chọn A       OA  3OB
Gọi I là điểm thỏa mãn: IA  3IB  0  OI
 0;1;2  I 0;1;2. 1 3
Khi đó, với mọi điểm M x; y; zP, ta luôn có:          
T  MI IA2  MI IB2 2
  MI MI IAIB 2 2 2 2 2 3 2 2 . 3
IA  3IB  2
MI IA  3IB .
Vì I , A , B cố định nên 2 2
IA  3IB là hằng số.
Do đó, T đạt GTLN 2
 2MI đạt GTLN  MI đạt GTNN
MI  P  M là hình chiếu vuông góc của I trên PTrang 12/16 M P
x y z  2 x  1         
  y  2  M x y z 1;2; 1 1 2 .
IM cïng ph−¬ng  n P      1 1 1 z   1  a  1
 , b  2 , c 1.
Vậy a c  0 . 4 2x  3 Câu34. Cho
dx a ln 2  b ln 3  c ln 7 
với a, b, c   . Giá trị của 2a  3b  7c bằng 2 x  3x 3 A. 9  . B. 6 . C. 15 . D. 3. Lời giải Chọn D Ta có: 4 4 2x  3
x   x  3 4  1 1  dx  dx   dx     
ln x x3 4  ln28ln18 2 x  3x . x x  3     3 x x 3  3 3 3 14  ln
 ln14  ln 9  ln 2  2ln 3  ln 7 . 9
a 1, b  2  , c 1.
Vậy 2a  3b  7c  3 .
Câu 35. Một khối cầu có thể tích bằng 288 thì diện tích mặt cầu đó bằng 144 A. . B. 128 . C. 72. D.144. 3 Lời giải Chọn D
Gọi bán kính của khối cầu là R . 4 Thể tích khối cầu là 3 3
V  R  288  R  216  R  6 . 3 Diện tích mặt cầu là 2
S  4R  4 .  36  144 . 1 Câu 36. Cho d   ln 2  ln 3  x x a b c
với a, b, c là các số hữu tỉ. Giá trị của 8a b c bằng x 32 0 A.1. B. 2 . C. 1  . D. 2  . Lời giải Chọn C 1 1 1 x x 3 3  1 1    dx  dx    3. d  x    x  32 x  32  x  3  x 32  0 0 0  1  3  3 1  ln x  3 
 ln 4   ln 3 1    2ln 2  ln 3   .  x  3  4 4 0  1 a    4  Suy ra  b  2 .  c  1   
Vậy 8a b c  1.
Câu 37: Cho hàm số y f x có đồ thị là đường cong y f ' x cắt trục Ox tại 3 điểm có hoành độ a ,b
, c như hình vẽ. Mệnh đề nào dưới đây là đúng? Trang 13/16
A. f c  f a  f b.
B. f b  f a  f c.
C. f c  f b  f a.
D. f a  f c  f b. Lời giải Chọn D
Gọi S , S lần lượt là diện tích hình giới hạn bởi đồ thị hàm số f ' x với các đường Ox , x a , 1 2
x b và diện tích hình giới hạn bởi đồ thị f ' x với các đường Ox , x c , x b Ta có b b S
f ' x dx   f ' x dx f a f b  0  f a  f b 1           a a c c Và S
f ' x dx f ' x f c f b  0  f c  f b 2           b b
Từ đồ thị f ' x ta thấy S S f a  f b  f c  f b  f a  f c 1 2
Vậy f a  f c  f b .  2 Câu 38: Cho x  1cos x 2
dx a  b  c với a , b , c là các số hữu tỉ. Giá trị của 4a b  3c bằng 0 A. 1. B. 2  . C. 4. D. 0. Lời giải Chọn C    2 2 2 Với I x
 1cos xdx xdxxcos xdx   . 0 0 0   2 2 1  Ta thấy 2
I xdx x  1 2  . 2 8 0 0  2
Gọi I x cos xdx 2  0 u   xdu dx Đặt   
dv  cos xdxv  sin x
Áp dụng công thức tích phân từng phần ta có     2 
I x sin x 2  sin xdx x xx   . 2  sin 2 cos 2 1 2 0 0 0 0 Trang 14/16 2   1 1
Do đó I I I
 1. Suy ra a  , b  , c  1. 1 2 8 2 8 2 1 1
Vậy 4a b  3c  4.   3.  1  4 . 8 2
Câu 39. Nguyên hàm của hàm số f x  4sin 5 . x cos x là . 2 1 1
A.  sin 4x  sin 6x C .
B.  cos 4x  cos 6x C . 3 2 3 4 1 1 C. cos5 .
x sin x C .
D. cos 4x  cos 6x C . 5 2 3 Lời giải Chọn B.   x x x     x x cos 6x cos 4x 1 1 4sin 5 .cos .d 2 sin 6 sin 4 dx  2  
C   cos 6x  cos 4x C   .  6 4  3 2
Câu 40. Cho hàm số y f x có bảng biến thiên như hình vẽ x  2  0 2  y 0 0 0   y 1 2  2 
Tính diện tích hình phẳng được giới hạn bởi các đường y f  x ; y  0 ; x  2  và x  2 . A. 3. B. 4 . C. 6 . D.5. Lời giải Chọn C.
Gọi S là diện tích hình phẳng được giới hạn bởi các đường y f  x ; y  0 ; x  2  và x  2 2  S f   x 0 dx f   x 2 dx f
 xdx   f 0 f  2
    f 2  f 0     2  2  0  1 2  2    1  6 . II – PHẦN TỰ LUẬN
Câu 1: Tìm nguyên hàm của F x của hàm số   3 x
f x x e  3 biết F 0  2019. Lời giải
F x  f
 xdx   x x x e   4 3 3 x dx
e  3x C 4 4 0 Mà F 0  2019 0 
e  3.0  C  2019  C  2020 4 4
F xx x
e  3x  2020 4
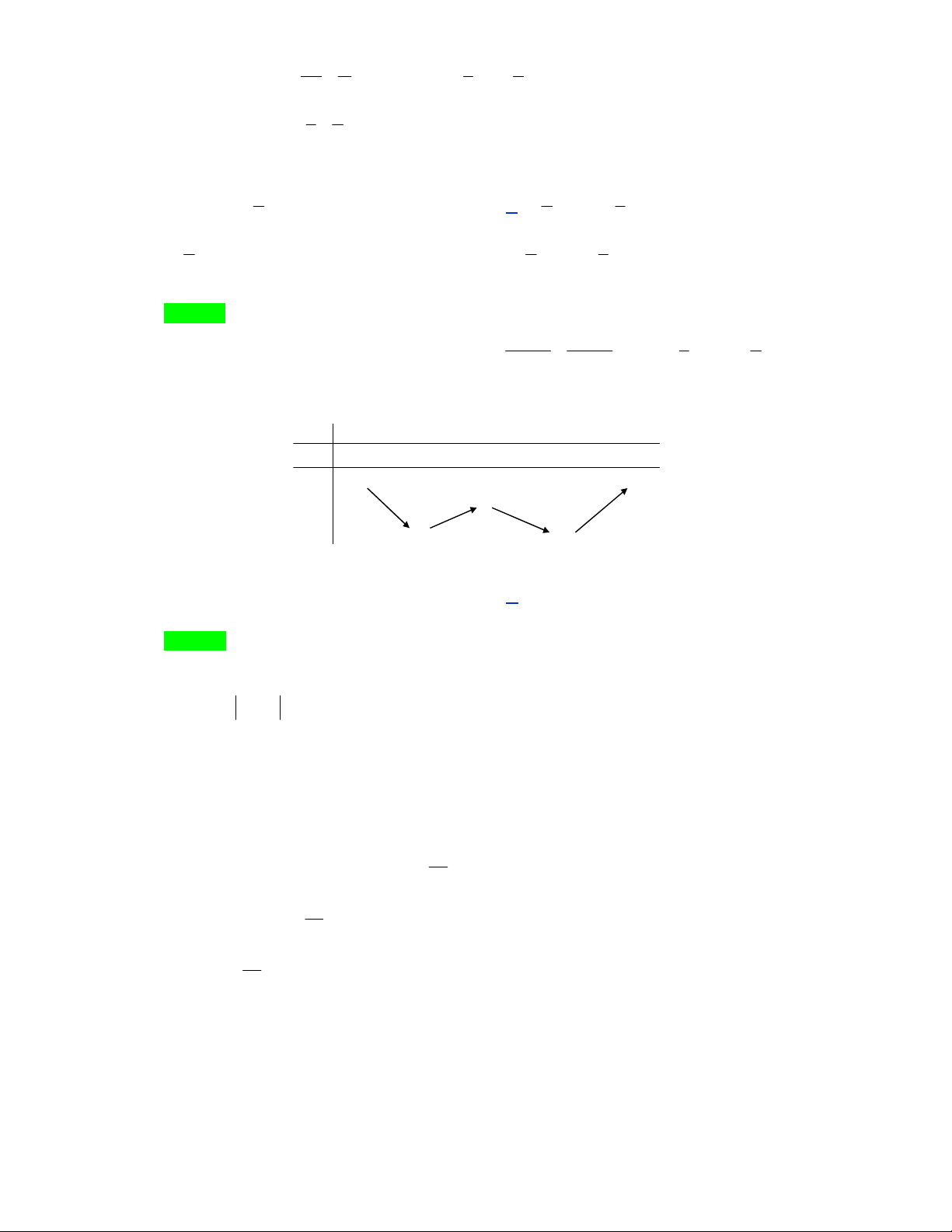
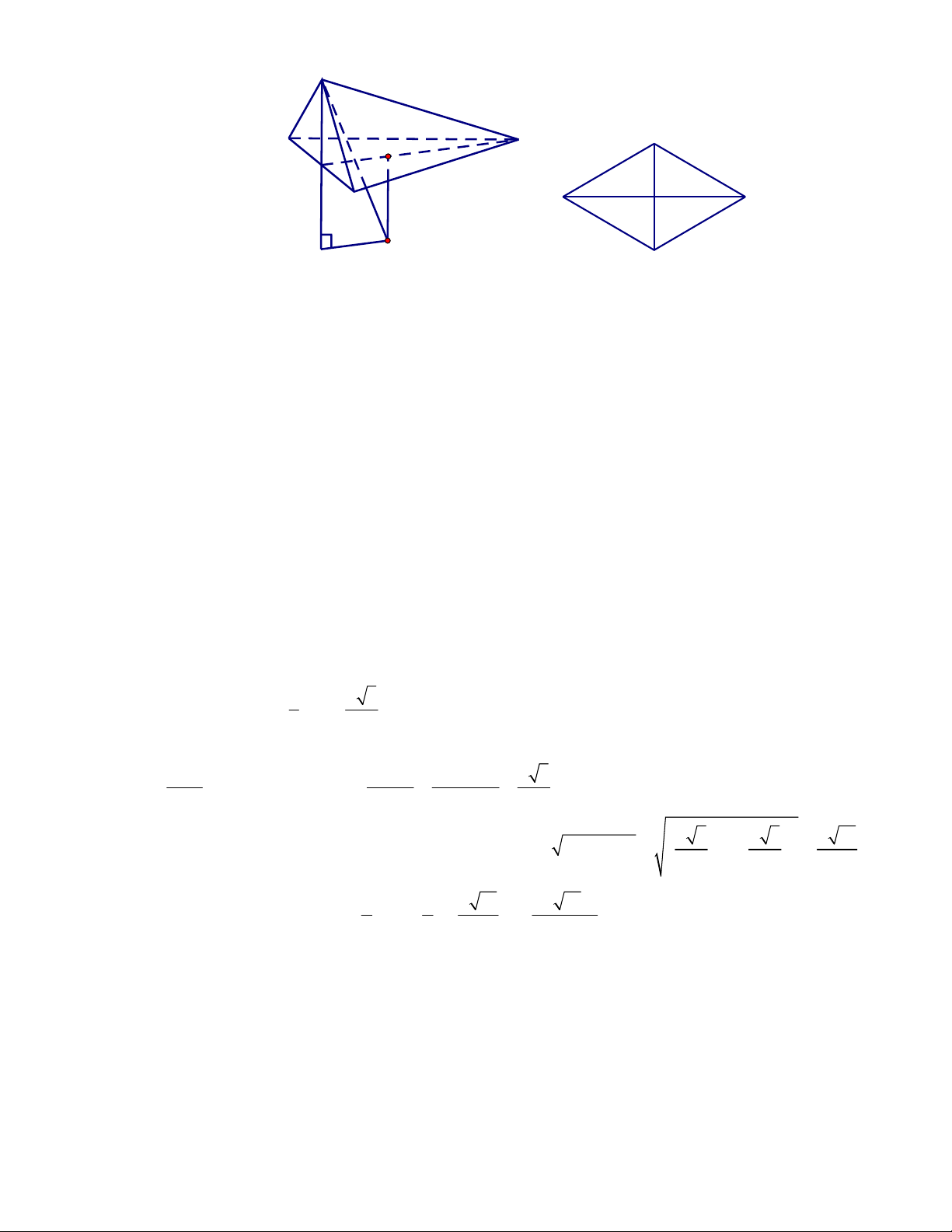
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Mặt bên SAB là tam giác cân với 
ASB 120 và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Xác định tâm và tính thể tích
của khối cầu ngoại tiếp hình chóp. Lời giải Trang 15/16 S S A I C H B A H B O J J
Gọi H là trung điểm của AB .
Gọi I ; J lần lượt là tâm của đường tròn ngoại tiếp ABC và SAB  . Do A
BC đều nên I CH và CH AB . SAB
cân tại S nên J SH và SH AB .
 SAB   ABC 
SAB   ABC   AB
SH   ABC Ta có:    . SH   SAB CH   SAB  CH    ABC  Ix // SH
Ix   ABC
Trong mặt phẳng SCH  dựng    Jy // CHJy   SAB
Ix ; Jy lần lượt là trục đường tròn ngoại tiếp ABC và SAB  . O Ix O
A OB OC
Trong mặt phẳng SCH : Ix Jy O     O   Jy
OA OB OS
OA OB OC OS .
O là tâm mặt cầu ngoại tiếp hình chóp S.ABC . 1 a 3
Ta có OJ IH CH  . 3 6
Áp dụng định lí sin trong tam giác SAB ta có: AB AB a a 3  2R
 2JS JS    . sin SAB S 2sin S 2sin120 3 2 2
a 3   a 3  a 15
Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là: 2 2
R OJ SJ         . 6   3  6     3 3     4 4 a 15 5 15a Thể tích mặt cầu là 3
V   R      . 3 3  6  54  
------------- HẾT ------------- Trang 16/16