Đề thi học kì 2 Toán 8 năm 2019 – 2020 trường THCS Nguyễn Trãi – TP HCM
Nhằm giúp các em học sinh lớp 8 có sự chuẩn bị tốt nhất cho đợt kiểm tra định kỳ cuối học kì 2 môn Toán lớp 8, THCS.TOANMATH.com giới thiệu đến các em PDF đề thi + đáp án + lời giải chi tiết đề thi học kì 2 Toán 8 năm học 2019 – 2020 trường THCS Nguyễn Trãi, quận Bình Tân, thành phố Hồ Chí Minh.
Preview text:
UBND QUẬN BÌNH TÂN
ĐỀ KIỂM TRA HỌC KÌ II TRƯỜNG THCS NGUYỄN TRÃI Năm học: 2019 – 2020 Môn: Toán 8 ĐỀ C HÍNH THỨC Ngày kiểm tra: 22 /6/2020 (Đề có 01 trang)
Thời gian: 90 phút (không kể thời gian phát đề) Câu 1. (3 điểm)
1. Giải các phương trình a) 7x – 10 = 4x + 11 b) 4 3 x 1 2 x 2 x 2 x 4
2. Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số : 6x – 2 ≥ 0
Câu 2.(1 điểm) Cho mảnh vườn hình chữ nhật có chiều dài hơn chiều rộng 4m. Tính diện tích
mảnh vườn hình chữ nhật biết chu vi hình chữ nhật là 20m ? Câu 3. (1điểm)
Một người đi xe máy từ A đến B với vân tốc 40 km/h . Lúc về, người đó đi với vận tốc
30 km/h, nên thời gian về nhiều hơn thời gian đi là 45 phút. Tính quãng đường AB. Câu 4. (1điểm)
Nhân dịp Quốc tế phụ nữ 20 tháng 10, siêu thị đồng loạt giảm giá 10%. Mẹ bạn Lan đã
đến mua 1 Tivi. Khi thanh toán, mẹ bạn Lan là khách hàng VIP nên được giảm thêm 10% sau
khi đã giảm lần 1 thì giá Tivi còn 15 390 000 đồng. Hỏi giá Tivi ban đầu là bao nhiêu
Câu 5. (1 điểm) Để đo chiều rộng của dòng sông người ta dùng thước và giác kế ngang xác
định được các điểm như hình vẽ. Tính chiều rộng dòng sông
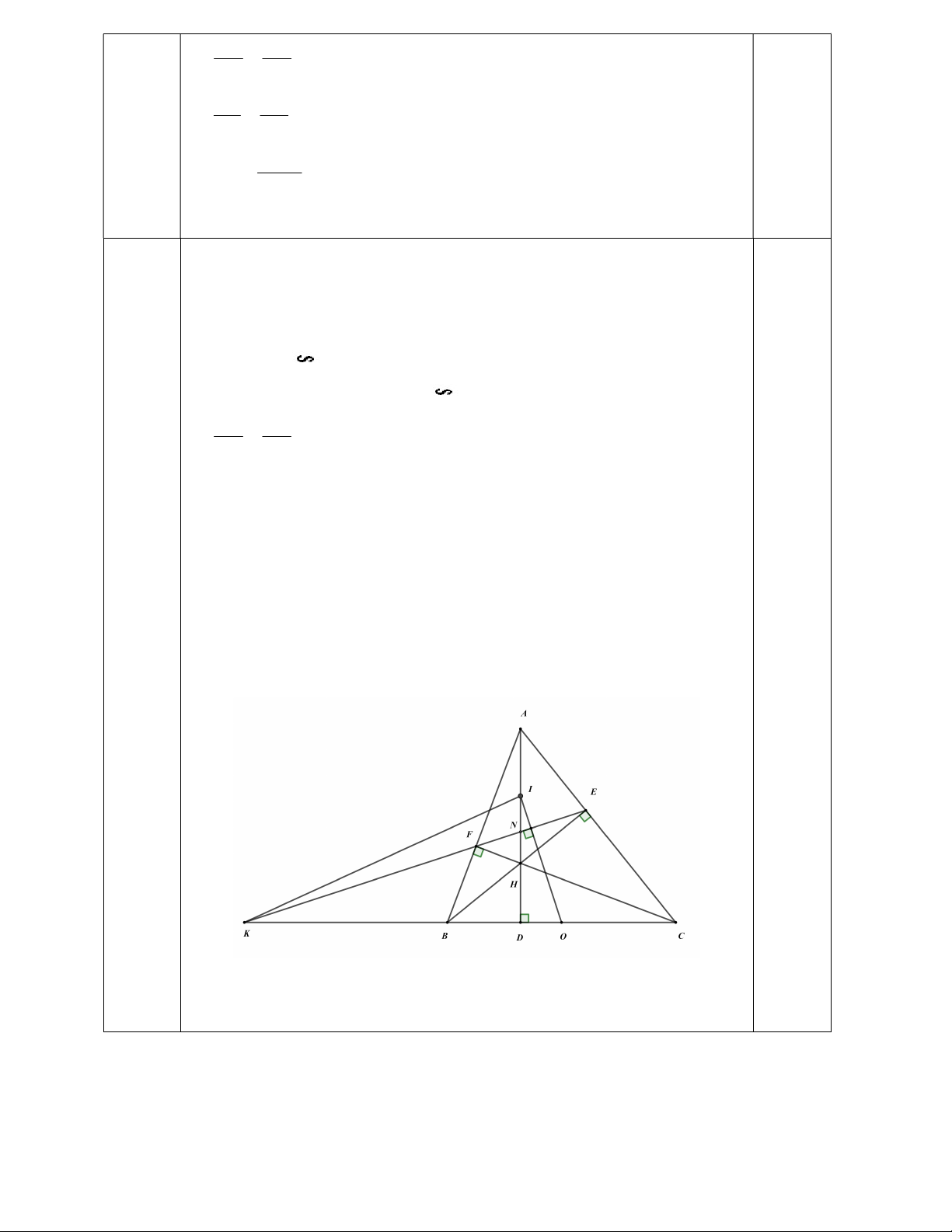
Câu 6. (3 điểm) Cho tam giác ABC có ba góc nhọn (AB < AC). Kẻ đường cao BE, AK và CF cắt nhau tại H. a) Chứng minh: ABK C BF
b) Chứng minh: AF.AB AE.AC
c) Gọi N là giao điểm của AK và EF, D là giao điểm của đường thẳng BC và đường thẳng
EF và O, I lần lượt là trung điểm của BC và AH. Chứng minh ON vuông góc DI. Hết
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA HỌC KÌ II NĂM HỌC 2019 - 2020 MÔN TOÁN LỚP 8 Câu Đáp án Điểm 1a 1.a. 7x-10 = 4x+11 7x-4x = 10 +11 0,25đ 3x = 21 0,25đ x = 7 0,25đ
vậy tập nghiệm của phương trình là: S 7 0,25đ 2a 1.b . 4 3 x 1 (1) 2 x 2 x 2 x 4 MTC (x 2)(x 2) ĐKXĐ: x 2; x 2 0,25đ 4 3 x 1 (1) x 2 x 2 (x 2)(x 2) 4(x 2) 3(x 2) x 1 0,25đ (x 2)(x 2) (x 2)(x 2)
4(x 2) 3(x 2) x 1
4x 8 3x 6 x 1 0 6x 3 0 6x 3 1 x (Nhận) 2 0,25đ
Vậy tập nghiệm của phương trình là: 1 S 2 0,25đ 3a 3x 1 0 3x 1 0,25đ 1 0,25đ x 3 Vậy 1 S x / x 0,25đ 3
Biểu diễn tập nghiệm trên trục số 0,25đ 2
Nửa chu vi hình chữ nhật là: 20:2=10 (m)
Gọi x (m) là chiều dài hình chữ nhật (x 0)
Chiều rộng hình chữ nhật là: x 4 (m) 0,25đ
Theo đề bài ta có phương trình: x x 4 10 0,25đ
2x 14 x 7 (tm) 0,25đ
Chiều dài hình chữ nhật là 7 m
Chiều rộng hình chữ nhật là 3 m
Diện tích hình chữ nhật là: 2 7.3 21 (m ) 0,25đ 3
Gọi x (km) là quãng đường AB.( x > 0) x x Thời gian đi: (giờ) ; thời gian về: (giờ) 0,25đ 40 30 3
Vì thời gian về nhiều hơn thời gian đi là 45 phút = giờ nên ta có 4 x x 3 phương trình: – = 0,25đ 30 40 4
Giải PT ta được: x = 90 (thỏa đ/k) 0,25đ
Vậy quãng đường AB là: 90 km 0,25đ 4
Gọi x ( đồng) là giá Tivi ban đầu. (x > 0)
Giá Tivi sau khi giảm 10% lần đầu là : x.(100% - 10%) = 0,9x 0,25đ (đồng)
Giá Tivi sau khi giảm 10% lần hai là: 0,25đ
0,9x.(100% - 10%) = 0,81x(đồng)
Theo đề bài, ta có phương trình: 0,81x = 15 390 000 0,25đ x = 19 000 000 ( nhận)
Vậy giá Tivi ban đầu là 19 000 000 đồng 0,25đ 5 AB AE Ta có: DE AE AB // DE AB AC
(hệ quả của định lí Talet) 0,25 DE CE AB 120 0,25 2 3 0,25 2.120 AB 80 3
Vậy chiều rộng dòng sông là 80 m 0,25 6 a) Xét ABK và C BF có: ABC là góc chung 0,25đ 0 AKB CFB 90 0,25đ Nên 0,5đ ABK C BF (g-g) b) Chứng minh được: 0,5đ ABE A CF (g-g) AB AE AC AF 0,25đ AF.AB AE.AC 0,25 đ
c) Chứng minh được OI là trung trực của EF 0.5đ
OI EF OI DN DN là đường cao của D OI
Ta có: IK DO IK là đường cao của D OI
Mà DN và IK cắt nhau tại N N là trực tâm của D OI 0,25đ ON DI 0,25đ