Đề thi học kì 2 Toán 8 năm 2023 – 2024 phòng GD&ĐT Ninh Hòa – Khánh Hòa

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KÌ II NĂM HỌC 2023 - 2024 THỊ XÃ NINH HÒA MÔN TOÁN - LỚP 8
Thời gian làm bài: 90 phút (Không tính thời gian phát đề)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,00 điểm)
Chọn một đáp án đúng trong các phương án A, B, C, D ở mỗi câu sau và ghi vào bài làm:
Câu 1: Đường thẳng nào sau đây song song với đường thẳng y = 3x 1? A. y = 3  x 1. B. y = 1  3x . C. y = 3x  3. D. y = 3  x  3 .
Câu 2: Trong hộp có 11 viên bi gồm 2 viên bi màu xanh, 4 viên bi màu đỏ, 5 viên bi màu
vàng. Các viên bi có hình dạng và kích thước giống hệt nhau. Chọn ngẫu nhiên một viên bi.
Xác suất của biến cố “Viên bi được chọn có màu đỏ” là 2 4 5 6 A. . B. . C. . D. . 11 11 11 11
Câu 3: Trong các phương trình sau phương trình nào không phải là phương trình bậc nhất một ẩn?
A. 1  x  0.
B. 1  2 y  0. C. 3  x  5  0. D. 2 2x  x  0.
Câu 4: Phương trình nào sau đây nhận x  2 là nghiệm?
A. 4x 8  0.
B. 3x  6  0.
C. 2x  3  1  . x
D. x  2  4  . x
Câu 5: Tuổi của Bố hiện nay là 45 tuổi, 5 năm trước tuổi của Bố là A. 50 tuổi. B. 44 tuổi. C. 35 tuổi. D. 40 tuổi.
Câu 6: Gọi x (km/h) là vận tốc của canô thứ nhất. Canô thứ hai có vận tốc lớn hơn vận tốc canô
thứ nhất là 4 (km/h) . Khi đó vận tốc của canô thứ hai được biểu thị là x
A. x  4 km/h.
B. 4.x km/h. C. x   4 k / m h. D. km/h. 4
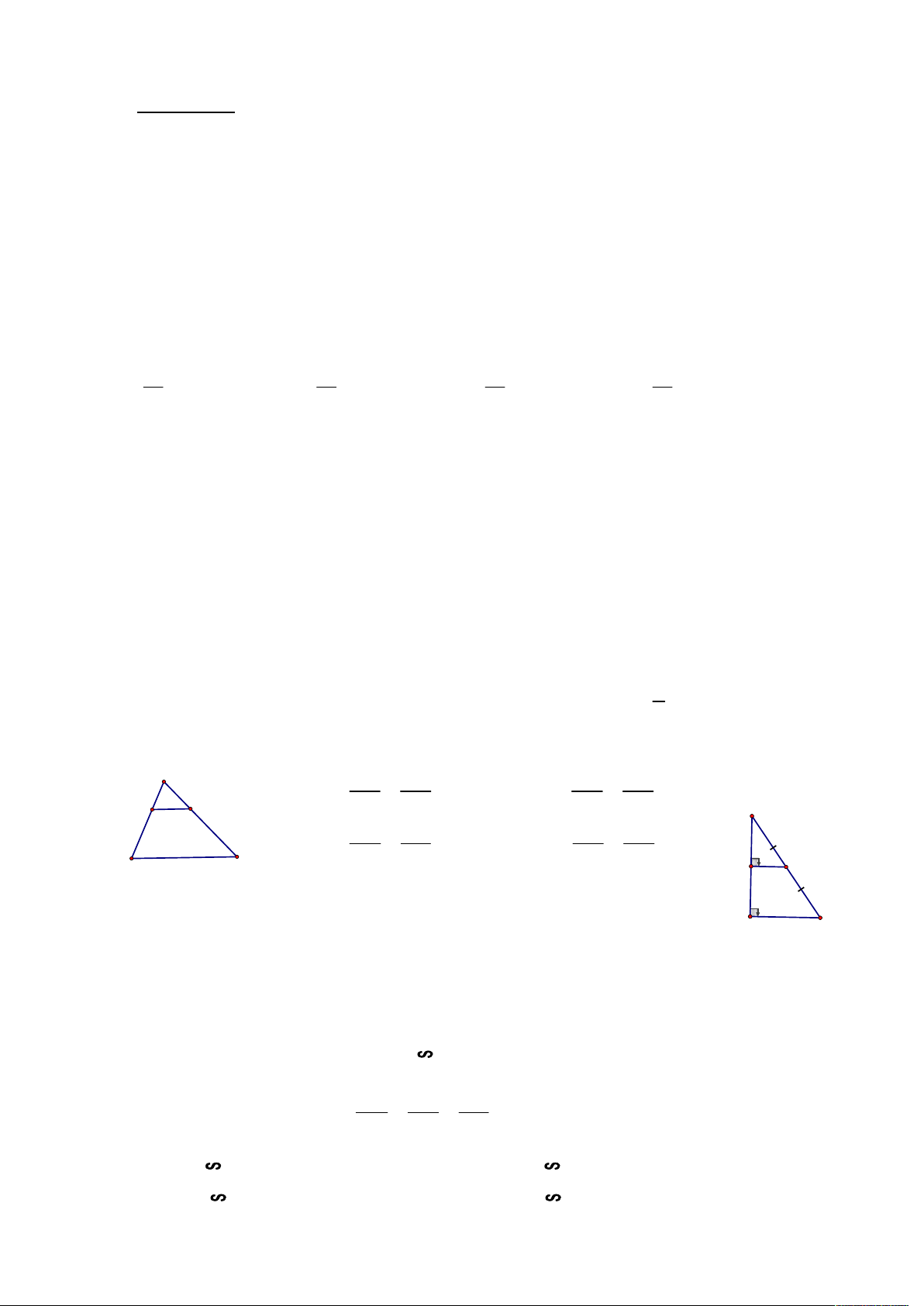
Câu 7: Cho hình vẽ (Hình 1a), biết DE //BC . Khẳng định nào sau đây đúng? A AE DE AD DE A.  . B.  . E D AC BC DB BC N AD AE AE AB C.  . D.  . AB EC AC AC B C F Hình 1a E
Câu 8: : Cho hình vẽ (Hình 1b), khi đó đoạn thẳng EF được gọi là
A. Đường trung bình của MNP .
B. Đường cao của MNP . M Hình 1b P
C. Đường phân giác của MNP .
D. Đường trung tuyến của MNP  .
Câu 9: Trong các khẳng định sau, khẳng định nào sai?
A. Hai tam giác bằng nhau thì đồng dạng với nhau.
B. Hai tam giác đồng dạng với nhau thì bằng nhau.
C. Nếu ABC  MNP thì ABC MNP 
với tỉ số đồng dạng là 1 .
D. Hai tam giác cùng đồng dạng với tam giác thứ 3 thì chúng đồng dạng. AB AC BC
Câu 10: Nếu ABC và DEF có   thì DF DE EF A. ABC DEF .
B. ABC EDF .
C. ABC FDE .
D. ABC DFE .
Đề kiểm tra HKII năm học 2023-2024 – Môn Toán lớp 8 - Trang 1/2 -
Câu 11: Cho hình vẽ (Hình 1c), biết AD là phân giác của 
ABC , BD  3cm , CD  4cm . A
Khẳng định nào sau đây đúng? AB 3 AB 4 A.  . B.  . AD 4 AC 3 AB 3 AD 3 3 4 C.  . D.  . AC 4 AC 4 B C D Hình 1c
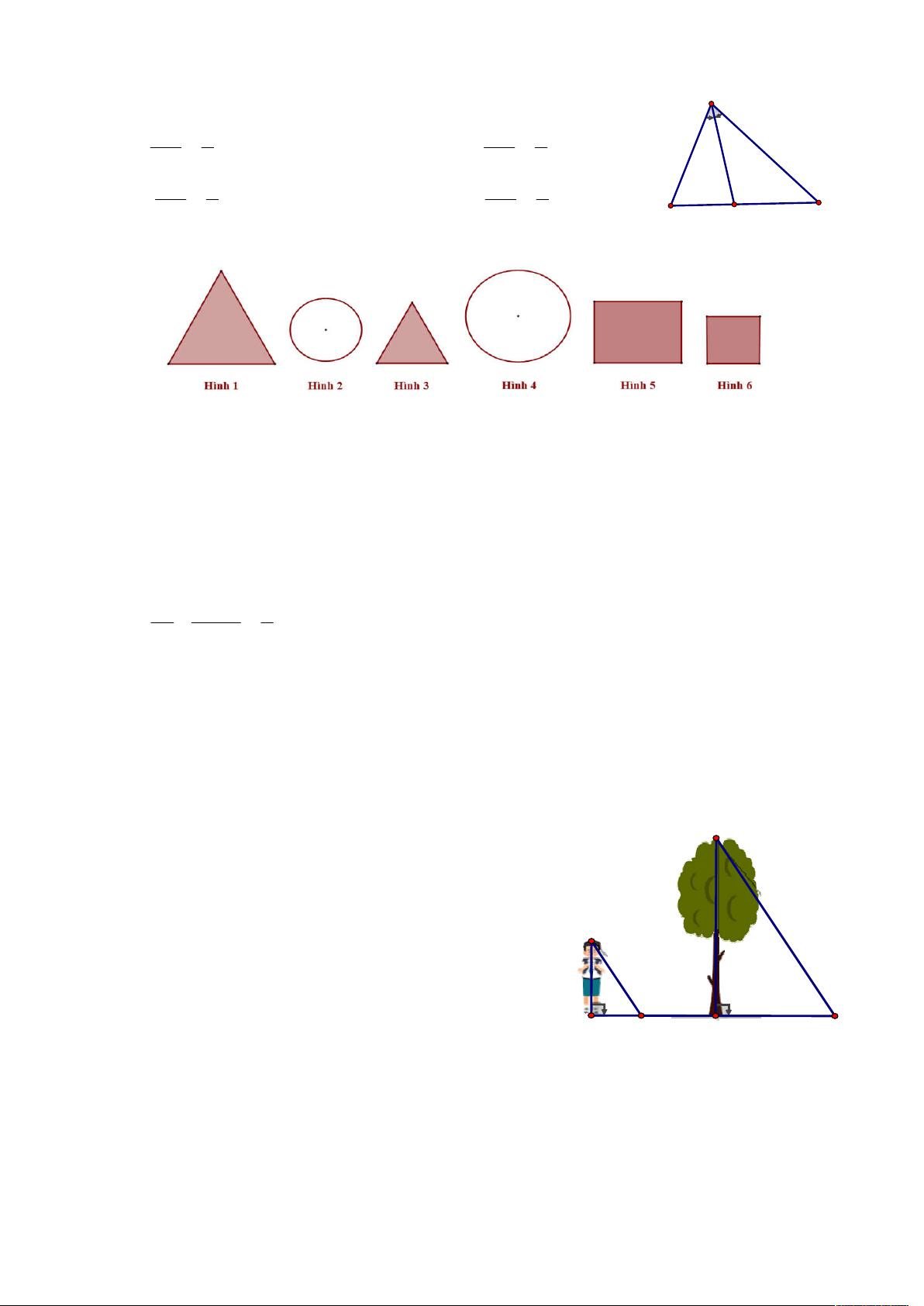
Câu 12: Hình 2 đồng dạng với hình nào trong các hình bên dưới? A. Hình 1. B. Hình 3. C. Hình 4. D. Hình 6.
PHẦN II. TỰ LUẬN (7,00 điểm)
Câu 13 (1,50 điểm): Giải các phương trình sau
a) 7 x  21  0.
b) 5 x  3  4x  6  3. x   1 . 2x 2x  5 1 c)   . 3 6 2
Câu 14 (1,50 điểm): Một ô tô đi từ A đến B với vận tốc 50 km/h , rồi đi từ B về A với vận tốc
lớn hơn vận tốc lúc đi là 10 km/h . Tính quãng đường AB, biết thời gian về ít hơn thời gian đi là 24 phút.
Câu 15 (1,00 điểm): Trong hộp chứa 8 tấm thẻ cùng loại được đánh số lần lượt là 2; 4; 5; 7;
10; 13; 15; 17. Lấy ra ngẫu nhiên 1 thẻ từ hộp. Tính xác suất của các biến cố:
a) A: “Số ghi trên thẻ là số chẵn”. B
b) B: “Số ghi trên thẻ là số nguyên tố” .
Câu 16 (0,50 điểm): Một người cao 1,5 mét có bóng
trên mặt đất dài 0,5 mét. Cùng lúc ấy, một cây cao gần
đó có bóng trên mặt đất dài 3 mét (hình bên minh họa). E Tính chiều cao của cây.
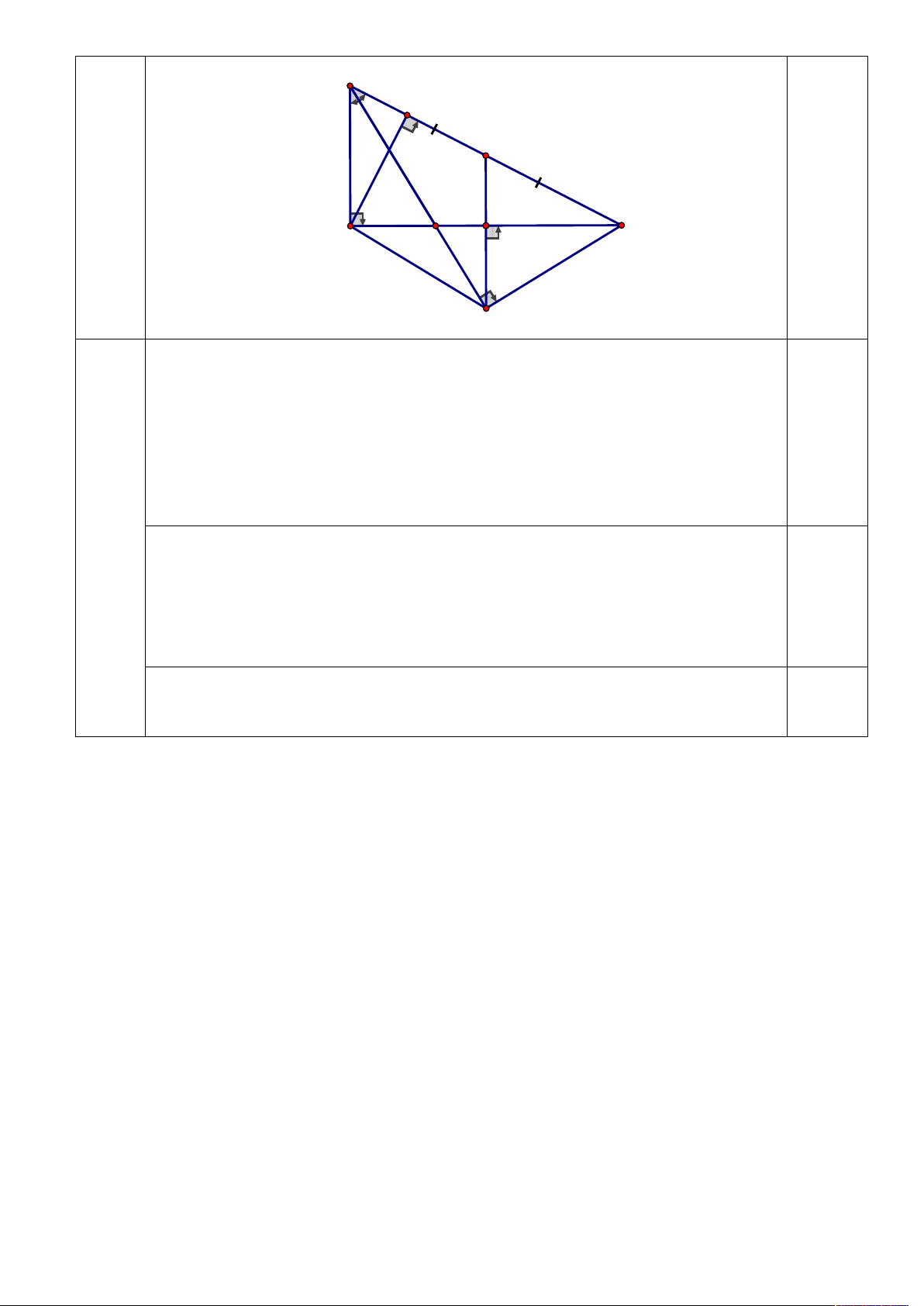
Câu 17 (2,50 điểm): Cho ABC vuông tại A 1,5m
 AB  AC , đường cao AD D BC . 0,5m 3m D F A C a) Chứng minh AB  C ∽ DB  . A b) Tia phân giác của 
ABC cắt AC tại E . Từ C vẽ đường thẳng vuông góc với đường
thẳng BE tại F . Chứng minh . EA EC  .
EB EF , từ đó suy ra   EAF  FBA .
c) Kẻ FH vuông góc với AC tại H và I là trung điểm của BC . Chứng minh H là
trung điểm của AC và ba điểm I , H , F thẳng hàng. -------- HẾT ------
(Đề có 02 trang, giáo viên coi kiểm tra không giải thích gì thêm)
Đề kiểm tra HKII năm học 2023-2024 – Môn Toán lớp 8 - Trang 2/2 -
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ II THỊ XÃ NINH HÒA NĂM HỌC 2023 - 2024 MÔN TOÁN 8 B ẢN CHÍNH
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,00 điểm)
Mỗi câu đúng được 0,25 điểm Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án C B D B D C A A B D C C
PHẦN II. TỰ LUẬN : (7,00 điểm) Câu
Hướng dẫn chấm - Đáp án Điểm
a) 7 x  21  0 0,50 13.a 7 x  21 0,25 x  3 0,25
Vậy phương trình có nghiệm là x = 3.
b) 5 x  3  4x  6  3. x   1 0,50
5 x  3  4x  6  3x 3 0,25 13.b 6x  6 x 1 0,25
Vậy phương trình có nghiệm là x = 1. 2x 2x  5 1 c)   0,50 3 6 2 2 .2 x 2x  5 1.3   0,25 13.c 3.2 6 2.3
4 x  2x  5 3 2x 8 x  4 0,25
Vậy phương trình có nghiệm là x = 4.
Một ô tô đi từ A đến B với vận tốc 50km/h, rồi đi từ B về A với vận tốc lớn
hơn vận tốc lúc đi là 10km/h. Tính quãng đường AB, biết thời gian về ít 1,50
hơn thời gian đi là 24 phút. 2 +) Đổi 24 phút = h. 5 0,25
+) Gọi quãng đường AB là x (km) (x > 0). x 14.a
+) Thời gian đi (từ A đến B) là (h). 50 0,25 x x
+) Thời gian về (từ B về A ) là = (h). 50 + 10 60 0,25
+) Vì thời gian về ít hơn thời gian đi là 24 phút nên ta có phương trình x x 2 0,25 − = 50 60 5
 6x − 5x = 120  x = 120 (thỏa ĐK) . 0,25
Vậy quãng đường AB dài 120 km. 0,25
Trong hộp chứa 8 tấm thẻ cùng loại được đánh số lần lượt là 2; 4; 5; 7; 10;
13; 15; 17. Lấy ra ngẫu nhiên 1 thẻ từ hộp. Tính xác suất của các biến cố: 1,00
a) A: “Số ghi trên thẻ là số chẵn”.
b) B: “Số ghi trên thẻ là số nguyên tố” .
a) +) Có 3 kết quả thuận lợi cho biến cố “Số ghi trên thẻ là số chẵn” là: thẻ 0,25
số 2; thẻ số 4; thẻ số 10. 15 3
+) Xác suất để biến cố A xảy ra là . 0,25 8
b) +) Có 5 kết quả thuận lợi cho biến cố “Số ghi trên thẻ là số nguyên tố” là: 0,25
thẻ số 2; thẻ số 5; thẻ số 7; thẻ số 13; thẻ số 17 5
+) Xác suất để biến cố A xảy ra là . 8 0,25
(Nếu hs không xác định các kết quả thuận lợi ở cả 2 ý thì trừ 0,25 điểm cho toàn câu)
Một người cao 1,5 mét có bóng trên mặt đất dài 0,5 mét. Cùng lúc ấy, một
cây cao gần đó có bóng trên mặt đất dài 3 mét (hình bên minh họa). Tính 0,50 chiều cao của cây.  
Ta có: EF //BC suy ra C  F (hai góc đồng vị).
Xét ABC và DEF  , ta có:   0
A  D  90 và   C  F (cmt) Suy ra: A  BC ∽ D  EF (g – g) 0,25 16 AC AB   DF DE AC.DE 3.1,5  AB    9 (m) . DF 0,5
Vậy chiều cao của cây là 9 m 0,25 .
(học sinh không cần vẽ lại hình)
Cho ABC vuông tại A  AB  AC  , đường cao AD  D BC  1,00 Chứng minh AB  C ∽ DB  . A B D 17.a A C
Xét ABC và DBA  , ta có: 0,50   0
ADB  CAB  90 (gt)  ABC là góc chung 0,25 Suy ra AB  C ∽ DB  . A (g-g) 0,25 Tia phân giác của 
ABC cắt AC tại E . Từ C vẽ đường thẳng vuông góc với
đường thẳng BE tại F . Chứng minh . EA EC  .
EB EF , từ đó suy ra 0,75   EAF  FBA . B D A C E F +) Xét EAB  và EFC  , ta có:   0
EAB  EFC  90 (gt). 0,25 17.b  
AEB  FEC (đối đỉnh). Suy ra EA  B ∽ EF  C (g – g). EA EB   . EF EC 0,25  . EA EC  . EB EF (đccm). +) Xét EAF  và EBC , ta có:  
AEF  BEC (đối đỉnh); EA EF  (vì . EA EC  . EB EF ). EB EC 0,25 Suy ra EA  F ∽ EB  C (c – g – c)  
 EAF  EBC , mà  
FBA  EBC (vì BE là tia phân giác của  ABC ). Suy ra   EAF  FBA
c) Kẻ FH vuông góc với AC tại H và I là trung điểm của BC . 0,75
Chứng minh H là trung điểm của AC và ba điểm I , H , F thẳng hàng. B D I A C E H F +) Ta có:  
EAF  FBA (cmt)  
FCE  FBA (vì EA  B ∽ EF  C ) 0,25 Suy ra  
EAF  FCE  A
 FC cân tại F .
mà FH  AC (gt)
Suy ra H là trung điểm của AC . 17.c +) Xét A  BC , ta có :
H là trung điểm của AC (cmt). 0,25
I là trung điểm của BC (gt).
Suy ra HI là đường trung bình của A  BC .
 HI //AB , mà FH //AB (vì cùng vuông góc với AC ) 0,25
Suy ra ba điểm I , H , F thẳng hàng.
Ghi chú: Mọi cách giải khác nếu đúng vẫn ghi điểm tối đa theo từng phần tương ứng.
Document Outline

• Đề kiểm tra HKII năm học 2023-2024 - Môn Toán lớp 8
• Đáp án kiểm tra HKII năm học 2023-2024 - Môn Toán lớp 8