Đề thi học kì 2 Toán 8 năm 2023 – 2024 phòng GD&ĐT thành phố Ninh Bình

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KÌ II
THÀNH PHỐ NINH BÌNH
Năm học 2023 - 2024. MÔN TOÁN 8
Thời gian: 90 phút (không kể thời gian giao đề)
(Đề gồm 13 câu, 02 trang)
Phần I. Trắc nghiệm (2,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng trong mỗi câu sau vào bài làm.
Câu 1. Trong hộp có 11 viên bi gồm 2 viên bi màu xanh, 4 viên bi màu đỏ, 5 viên bi màu vàng.
Các viên bi có hình dạng và kích thước giống hệt nhau. Chọn ngẫu nhiên một viên bi. Xác suất
của biến cố “Viên bi được chọn có màu vàng” bằng:
A. 2 B. 4 C. 5 D. 6 11 11 11 11
Câu 2. Tỉ lệ học sinh bị cận thị ở một trường trung học cơ sở là 26%. Gặp ngẫu nhiên một học
sinh của trường thì xác suất học sinh đó không bị cận thị là:
A. 0,74 B. 0,84 C. 0,26 D. 0,5
Câu 3. Phương trình bậc nhất một ẩn là: A. 3x + 2y - 6 = 0 B. 2 x = 4 C. 3x + 6 = 0 D. 2 y - x + 1 = 0
Câu 4. Nghiệm của phương trình: 5x + 3 = 18 là:
A. x = - 3 B. x = - 5 C. x = 5 D. x = 3
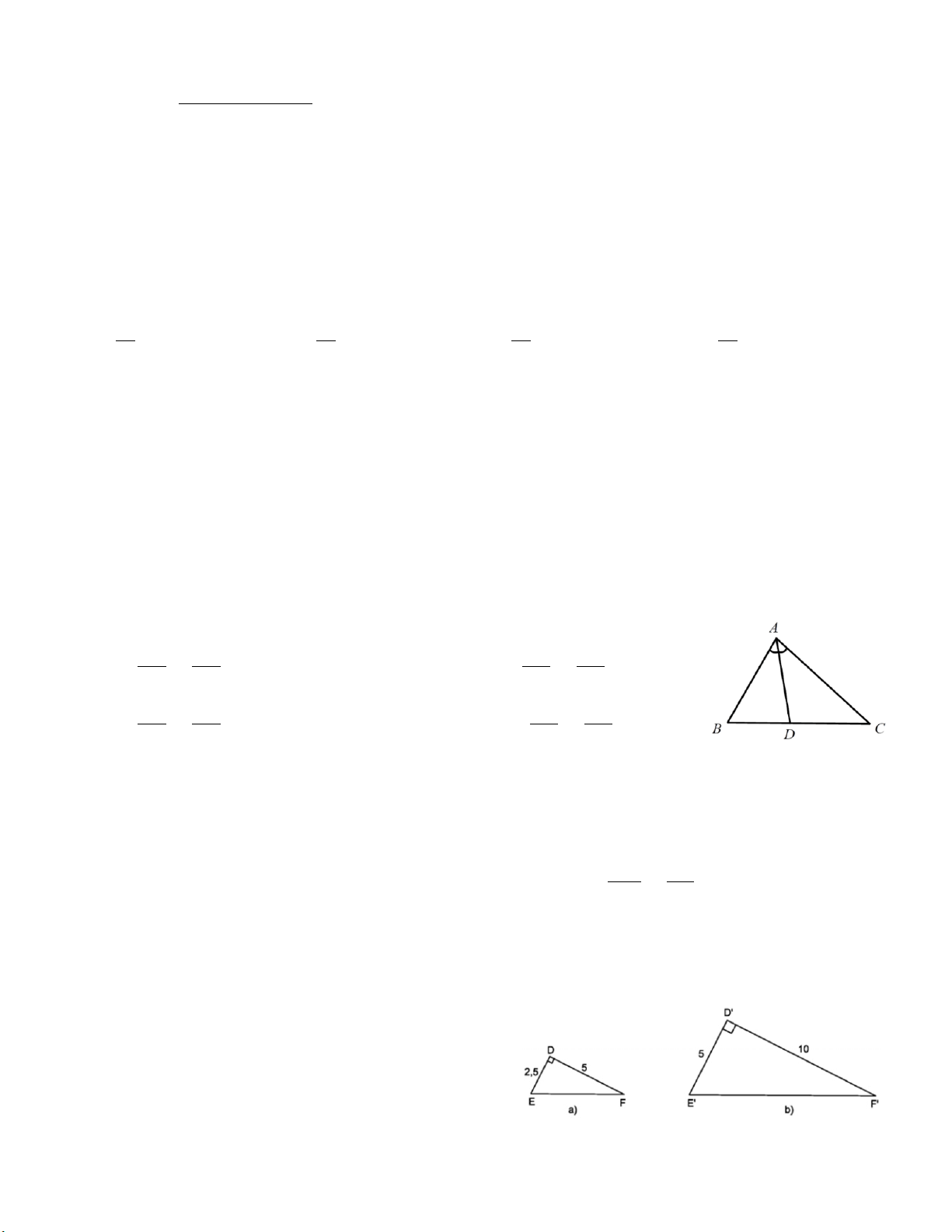
Câu 5. Cho ΔABC có AD là phân giác trong của góc A thì khẳng định đúng là: A. DC AB = B. AB AC = DB AC DB DC C. AB DC = D. ` AB DC = DB AC DB AC Câu 6. Cho O ∆ AB∽ I
∆ MN có OA = 4cm,IM = 6cm, MN = 15cm thì AB bằng: A. 2 cm B. 3 cm C. 4 cm D. 10 cm
Câu 7. Cho tam giác ABC và tam giác MNP có   o AB BC A = M = 90 , = thì : MN NP A. AB ∆ C∽ M ∆ NP B. AB ∆ C∽ P ∆ MN C. AB ∆ C∽ N ∆ MP D. AB ∆ C∽ M ∆ PN
Câu 8. Cho hình vẽ, biết  0
E = 70 thì số đo góc E' là : A. 0 90 B. 0 20 C. 0 110 D. 0 70
Phần II. Tự luận (8,0 điểm)
Câu 9 (3,0 điểm) Giải các phương trình sau: 1) 3x – 4 = 5 2) 5x – 8 = 7x + 24
3) 9 −( 2x −8) = 5(3 – 2x) 4) 5x −1 3 − 4x x + 7 + = 2 − 6 2 3
Câu 10. (1,5 điểm)
Bác Tô đi siêu thị mua 15 kg trái cây gồm 2 loại cam và xoài. Biết cam có giá 20 000
đồng/1 kg và xoài có giá 35 000 đồng/1 kg. Hỏi bác Tô đã mua bao nhiêu kg cam, bao nhiêu kg
xoài? Biết tổng số tiền bác Tô phải trả là 420 000 đồng.
Câu 11 (2,0 điểm)
Cho tam giác ABC vuông tại A có AB > AC. D là một điểm tùy ý trên cạnh BC. Qua D kẻ
tia Dx vuông góc với BC, cắt AB tại M, cắt CA tại N.
1) Chứng minh rằng các tam giác ABC và tam giác DNC đồng dạng.
2) Tính CN và DN nếu AB = 8cm, AC = 6cm và 2 CD = CB . 5
Câu 12 (1,0 điểm)
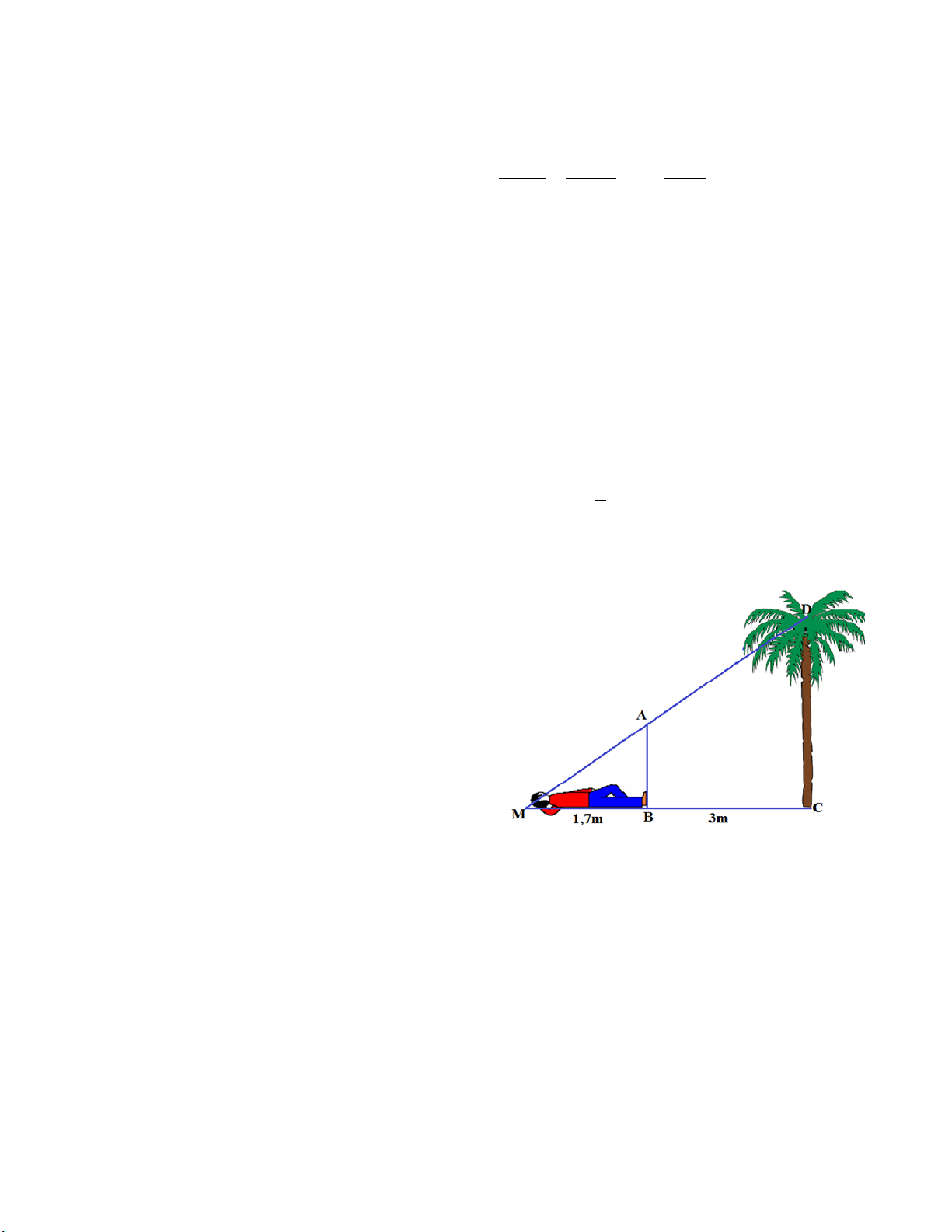
Bạn Hoàng muốn đo chiều cao của một
cây dừa mọc thẳng đứng trong sân, bạn dùng
một cây cọc AB dài 1,5m và chiều dài thân mình
để đo. Bạn nằm cách gốc cây 3m (tính từ chân
của bạn) và bạn cắm cọc thẳng đứng dưới chân
mình thì bạn thấy đỉnh thân cọc và đỉnh cây
thẳng hàng với nhau. Em hãy giúp bạn tính chiều
cao của cây dừa, biết bạn Hoàng cao 1,7m (làm
tròn kết quả đến hàng phần mười).
Câu 13 (0,5 điểm). Giải phương trình: x + 24 x + 25 x + 26 x + 27 x + 2036 + + + + = 0 1996 1995 1994 1993 4 Hết./.
Thí sinh không sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên thí sinh: ................................................... Số báo danh.................... ...........................
Giám thị số 1:.......................................................... ... Giám thị số 2: ................ ..............................
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM
THÀNH PHỐ NINH BÌNH
ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KÌ II
NĂM HỌC 2023 -2024. MÔN TOÁN 8
(Hướng dẫn chấm gồm 03 trang)
I. Hướng dẫn chung:
- Dưới đây chỉ là hướng dẫn tóm tắt của một cách giải.
- Bài làm của học sinh phải chi tiết, lập luận chặt chẽ, tính toán chính xác mới cho điểm tối đa.
- Bài làm của học sinh đúng đến đâu cho điểm tới đó.
- Nếu học sinh có cách giải khác hoặc có vấn đề phát sinh thì tổ chấm trao đổi và thống nhất cho
điểm nhưng không vượt quá số điểm dành cho câu đó hoặc phần đó.
II. Hướng dẫn chấm và biểu điểm:
Phần I. Trắc nghiệm (2,0 điểm): Mỗi câu trả lời đúng được 0,25 điểm. Câu 1 2 3 4 5 6 7 8 Đáp án C A C D B D A D
Phần II. Tự luận (8,0 điểm) Câu Nội dung Điểm 1) 3x – 4 = 5 3x = 9 0,75 x = 3
Vậy phương trình có nghiệm x = 3 9 2) 5x – 8 = 7x + 24 (3,0 5x - 7x = 24 + 8 điểm) - 2x = 32 0,75 x = -16
Vậy phương trình có nghiệm x = - 16
3) 9 −( 2x −8) = 5(3 – 2x) 9 - 2x + 8 = 15 - 10x 0,75 - 2x + 10x = 15 - 9 - 8 8x = - 2 - 1 x = 4 - 1
Vậy phương trình có nghiệm x = 4 5x −1 3 − 4x x + 7 4) + = 2 − 6 2 3 5x - 1 3(3 - 4x) 6.2 2(x + 7) + = - 6 6 6 6
5x - 1 + 9 - 12x = 12 - 2x -14 0,75
5x - 12x + 2x = 12 - 14 + 1 - 9 - 5x = - 10 x = 2
Vậy phương trình có nghiệm x = 2
Gọi số kilogam cam bác Tô mua là x ( kg, x>0, x < 15)
Thì số kilogam xoài bác Tô mua là 15 – x (kg) 0,5
Số tiền bác Tô mua cam là 20000x ( đồng)
Số tiền bác Tô mua xoài là 35000(15 – x) ( đồng) 0,25 10
Vì tổng số tiền bác Tô phải trả là 420 000 đồng, nên ta có phương trình: 0,25
(1,5 20000x + 35000(15 - x) = 420000 điểm)
20000x + 35000(15 - x) = 420000
20000x + 525000 - 35000x = 420000 0,25 - 15000x = - 105000 x = 7 (tm)
Vậy bác Tô đã mua 7 kg cam, 8 kg xoài. 0,25 Vẽ đúng hình, 0,25 ghi đúng GT - KL 11 2,5 điểm
1) Xét ∆ABC và ∆DNC có   o A = D = 90 (gt) ,  C chung 0,5 ⇒ AB ∆ C∽ D ∆ NC (g - g) 0,25 2) Ta có A ∆ BC∽ DNC ∆ ( cm ở ý 1) 0,25 AB BC AC ⇒ = =
(cặp cạnh tương ứng tỉ lệ) (*) DN NC DC Xét AB ∆ C vuông tại A 2 2 2
⇒ BC = AB + AC ( Định lí Pythagore) 0,25 2 2 2
⇒ BC = 8 + 6 = 100 ⇒ BC = 10 cm 2 2 Mà CD = CB ⇒ CD = .10 = 4 (cm) 5 5 0,25
Thay AB = 8cm, AC = 6 cm, BBC = 10 cm, CD = 4 cm vào (*), ta được: 8 10 6 8 . 4 16 10 . 4 20 = = ⇒ DN = = (cm); NC = = (cm) 0,25 DN NC 4 6 3 6 3 Chứng minh A ∆ MB∽ D ∆ MC (g - g) 0,25 MB AB ⇒ = 12 MC DC (1,0 1,7 1,5 ⇒ = 0,25 điểm) 1,7 + 3 DC ⇒ DC ≈ 4,1
Vậy cây dừa cao khoảng 0,25 4,1 m. Hình vẽ (0,25) x + 24 x + 25 x + 26 x + 27 x + 2036 + + + + = 0 1996 1995 1994 1993 4 13 x + 24 x + 25 x + 26 x + 27 x + 2036 + 1 + + 1 + + 1 + + 1 + - 4 = 0 (0,5 1996 1995 1994 1993 4 0,25 điểm) x + 2020 x + 2020 x + 2020 x + 2 + + + 020 x + 2020 + = 0 1996 1995 1994 1993 4  1 1 1 1 1 (x + 2020) + + + +  =   0 1996 1995 1994 1993 4  1 1 1 1 1 x + 2020 = 0 ( vì + + + + ≠ 0) 0,25 1996 1995 1994 1993 4 x = - 2020
Vậy phương trình có nghiệm x = - 2020
Document Outline

• Câu 2. Tỉ lệ học sinh bị cận thị ở một trường trung học cơ sở là 26%. Gặp ngẫu nhiên một học sinh của trường thì xác suất học sinh đó không bị cận thị là:
• Phần II. Tự luận (8,0 điểm)