SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HÓA
ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2017-2018
TRƯỜNG THPT DƯƠNG ĐÌNH NGHỆ Môn: Toán-Lớp 11
(Đề thi gồm có 02 trang)
Thời gian làm bài: 90 phút ĐỀ 111
A. PHẦN TRẮC NGHIỆM (3 điểm):
Câu 1. lim2n  3 bằng A. . B. 3. C. 5. D. .  1 3n a a Câu 2. Biết lim
 ( a, b là hai số tự nhiên và tối giản). Giá trị của a  b n 1 3  b bằng b 1 A. 3. B. . C. 0. D. 4. 3 Câu 3. 2
lim(x  2x  3) bằng x 1  A. 5. B. 0. C. 4. D. 4.  x  2 a a Câu 4. Biết lim
  ( a, b là hai số tự nhiên và tối giản). Giá trị của a  b bằng
x 1 2x b b A. 3. B. 1. C. 3.  D. 1. 2n  3 Câu 5: lim bằng 2 n  2n  4 A. 2. B. 1. C. 0. D. . 
Câu 6. Biết rằng phương trình 5 3
x  x  3x 1  0 có duy nhất 1 nghiệm x , mệnh đề nào dưới đây đúng ? 0
A. x  0;1 . B. x  1;0 . C. x  1; 2 . D. x  2; 1 . 0   0   0   0   Câu 7. Cho hàm số 3 2
y  x  2x  3x  2. Giá trị của y  1 bằng A. 7. B. 4. C. 2. D. 0.
Câu 8. Đạo hàm của hàm số y  sin 2x bằng A. y  cos 2 .
x B. y  2 cos 2 .
x C. y  2 cos 2 .
x D. y   cos 2 . x x 1
Câu 9. Đạo hàm của hàm số y  bằng x 1 2 2 2 A. y  . y  . y  .  B. y  1. C. D. x  2 1 x  2 1 x 1
Câu 10. Đạo hàm của hàm số 2
y  x 1 bằng x 1 x
A. y  2x. B. y  . C. y  . D. y  . 2 2 x 1 2 2 x 1 2 x 1
Câu 11. Biết AB cắt mặt phẳng   tại điểm I IA  IB thỏa mãn
3 , mệnh đề nào dưới đây đúng ? A. 4d  ,
A    3d B, . B. 3d  ,
A    d B, . C. 3d  ,
A    4d B, . D. d  ,
A    3d B, .
Câu 12. Mệnh đề nào dưới đây sai ?
A. Đường thẳng vuông góc với mặt phẳng khi và chỉ khi góc giữa chúng bằng o 90 .
B. Góc giữa hai đường thẳng bằng góc giữa 2 vectơ chỉ phương của 2 đường thẳng đó.
C. Hai mặt phẳng vuông góc với nhau khi và chỉ khi góc giữa chúng bằng o 90 .
D. Góc giữa hai mặt phẳng là góc giữa 2 đường thẳng lần lượt vuông góc với 2 mặt phẳng đó.
B. PHẦN TỰ LUẬN (7 điểm):
Câu 1 (1 điểm). Tính các giới hạn sau: x 1  2 a.  3 2
lim x  2x  x   1 ; b. lim . x x3 x  3
Câu 2 (1 điểm). Tính đạo hàm cấp 1 của mỗi hàm số sau: x 
a. y  x  x  2 2 x  4; b. 2 2 1 y  cot  tan . x 2
 x2  4x   5
Câu 3 (1 điểm). Tìm giá trị của tham số a để hàm số khi x  f x   1 ( ) x 1
liên tục tại x  1. 0 2x  a khi x  1
Câu 4 (1 điểm). Cho hàm số f  x  cos 2 . x 50
Gọi C là đồ thị của hàm số   y  f
x. Viết phương trình 
tiếp tuyến của C tại điểm có hoành độ x  . 6
Câu 5 (3 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA   ABCD và góc giữa
SD với mặt đáy bằng o
45 . Gọi M , N, P lần lượt là các điểm trên cạnh ,
SA SC, SD sao cho SM  M , A
SN  2NC và SP  2 . PD
a. Chứng minh rằng SAC  B ;
D SAB  SBC.
b. Chứng minh rằng AP  N . P
c. Tính côsin của góc giữa 2 mặt phẳng MCD và BNP.
…………………………Hết………………………..
SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HÓA
ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2017-2018
TRƯỜNG THPT DƯƠNG ĐÌNH NGHỆ Môn: Toán-Lớp 11
(Đề thi gồm có 02 trang)
Thời gian làm bài: 90 phút ĐỀ 112
A. PHẦN TRẮC NGHIỆM (3 điểm): Câu 1. lim  2  n  3 bằng A. . B. 3. C. 5. D. .  1 4n a a Câu 2. Biết lim
 ( a, b là hai số tự nhiên và tối giản). Giá trị của a  b n 1 4  b b bằng 1 A. 4. B. . C. 5. D. 0. 4 Câu 3. 2
lim(x  2x  3) bằng x 1  A.1. B. 2. C. 3. D. 6. x  3 a a Câu 4. Biết lim
  ( a, b là hai số tự nhiên và tối giản). Giá trị của a  b bằng
x 1 4x b b 1 A. 5. B. 3.  C. 5.  D.  . 4 2 2n  3 Câu 5. lim bằng 2 n  2n  4 A. 2. B. 1. C. 0. D. . 
Câu 6. Biết rằng phương trình 7 4
x  3x  6x  6  0 có duy nhất một nghiệm x , mệnh đề nào dưới đây đúng ? 0
A. x  0;1 . B. x  1;0 . C. x  1; 2 . D. x  2; 1 . 0   0   0   0   Câu 7. Cho hàm số 3 2
y  x  2x  3x  2. Giá trị của y  1 bằng A. 7. B. 4. C. 2. D. 0.
Câu 8. Đạo hàm của hàm số y   sin 2x bằng
A. y  cos 2x. B. y  2 cos 2x. C. y  2 cos 2 .
x D. y   cos 2x. 2x 1
Câu 9. Đạo hàm của hàm số y  bằng x 1 2 1 3 A. y  . y  . y  .  B. y  1. C. D. x  2 1 x  2 1 2 (x 1)
Câu 10. Đạo hàm của hàm số 2
y  x  5 bằng x 1 x
A. y  5x. B. y  . C. y  . D. y  . 2 2 x  5 2 2 x  5 2 x  5
Câu 11. Biết AB cắt mặt phẳng   tại điểm I IA  IB thỏa mãn
4 , mệnh đề nào dưới đây đúng ? A. d  ,
A    4d B, . B. 4d  ,
A    d B, . C. 3d  ,
A    4d B, . D. 4d  ,
A    3d B, .
Câu 12. Mệnh đề nào dưới đây sai ?
A. Hai mặt phẳng vuông góc với nhau khi và chỉ khi góc giữa chúng bằng o 90 .
B. Đường thẳng vuông góc với mặt phẳng khi và chỉ khi góc giữa chúng bằng o 90 .
C. Góc giữa hai đường thẳng bằng góc giữa 2 vectơ chỉ phương của 2 đường thẳng đó.
D. Góc của hai mặt phẳng là góc giữa 2 đường thẳng lần lượt vuông góc với 2 mặt phẳng đó.
B. PHẦN TỰ LUẬN (7 điểm):
Câu 1 (1 điểm). Tính các giới hạn sau: x  7  3 a.  4 3
lim 5x  9x  2; b. lim . x x2 x  2
Câu 2 (1 điểm). Tính đạo hàm cấp 1 của mỗi hàm số sau: 3 x 1
a. y  x  x  2 2 x  2; b. 2 y  cot  tan . x 3
 x2  5x   6
Câu 3 (1 điểm). Tìm giá trị của tham số a để hàm số khi x  3 f (x)   x  3
liên tục tại x  3. 0 xa 1 khi x 3
Câu 4 (1 điểm). Cho hàm số f  x  cos 2 . x 58
Gọi C là đồ thị của hàm số   y  f
x. Viết phương trình 
tiếp tuyến của C tại điểm có hoành độ x  . 6
Câu 5 (3 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA   ABCD, góc giữa SD với mặt đáy bằng o
45 . Gọi M , N, P lần lượt là các điểm trên cạnh ,
SA SC, SD sao cho SM  , MA SN  3NC và SP  3 . PD
a. Chứng minh rằng SAC  B ;
D SAB  SBC.
b. Chứng minh rằng AP  N . P
c. Tính côsin của góc giữa 2 mặt phẳng MCD và BNP.
…………………………Hết………………………..
SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HÓA
ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2017-2018
TRƯỜNG THPT DƯƠNG ĐÌNH NGHỆ Môn: Toán-Lớp 11
(Đề thi gồm có 02 trang)
Thời gian làm bài: 90 phút ĐỀ 113
A. PHẦN TRẮC NGHIỆM (3 điểm):
Câu 1. lim5n  2 bằng A. 2. B. 3. C. .  D. .  1 3.4n a a Câu 2. Biết lim
 ( a, b là hai số tự nhiên và tối giản). Giá trị của a  b 5.4n b b bằng 1 3 A. 6. B. 8. C. . D. . 5 5 Câu 3. 2
lim(x  2x  5) bằng x 1  A. 2. B. 5. C. 4. D. .  x  2 a a Câu 4. Biết lim
  ( a, b là hai số tự nhiên và tối giản). Giá trị của a  b bằng:
x 4  3x b b 1 A. 2. B. 4.  C. 4. D. . 4 2 2n  3 Câu 5. lim bằng 4 2 n  2n  4 A. 2. B. 1. C. 0. D. . 
Câu 6. Biết rằng phương trình 5 3
x  x  2x  3  0 có duy nhất 1 nghiệm x , mệnh đề nào dưới đây đúng ? 0
A. x  0;1 . B. x  1;0 . C. x  2; 1 . D. x  1; 2 . 0   0   0   0   Câu 7. Cho hàm số 3 2
y  x  2x  2. Giá trị của y  1 bằng A. 7. B. 4. C. 2. D. 0.
Câu 8. Đạo hàm của hàm số y  cos 2x bằng
A. y  2 sin 2 .
x B. y  2 sin 2x. C. y  sin 2 .
x D. y   sin 2x. x  2
Câu 9. Đạo hàm của hàm số y  bằng 2x  3 1 1 7 7 A. y  . y  . y  . y  .  B. C. D. 2x  32 2 2x  32 2x  3
Câu 10. Đạo hàm của hàm số 3
y  x 1 bằng 2 3x 3x 1 2 x A. y  . B. y  . C. y  . D. y  . 3 2 x 1 3 2 x 1 3 2 x 1 3 x 1
Câu 11. Biết AB cắt mặt phẳng   tại điểm I IA  IB thỏa mãn
5 , mệnh đề nào dưới đây đúng ? A. 5d  ,
A    d B, . B. d  ,
A    5d B, . C. 5d  ,
A    4d B, . D. 4d  ,
A    5d B, .
Câu 12. Mệnh đề nào dưới đây sai ?
A. Hai mặt phẳng phân biệt cùng vuông góc với 1 đường thẳng thì song song.
B. Đường thẳng vuông góc với mặt phẳng khi và chỉ khi góc giữa chúng bằng o 90 .
C. Hai mặt phẳng vuông góc với nhau khi và chỉ khi góc giữa chúng bằng o 90 .
D. Hai mặt phẳng phân biệt cùng vuông góc với 1 mặt phẳng thì song song.
B. PHẦN TỰ LUẬN (7 điểm):
Câu 1 (1 điểm). Tính các giới hạn sau: x  3  2 a.  3 2
lim 2x  2x  x   1 ; b. lim . x x1 x 1
Câu 2 (1 điểm). Tính đạo hàm của mỗi hàm số sau: 4 x 1
a. y  x  x  2 2 x  3; b. 2 y  cot  tan . x 4  x2  x   2 khi x  2
Câu 3 (1 điểm). Tìm giá trị của tham số a để hàm số f (x)   x  2
liên tục tại x  2. 0   a  x k hi x  2
Câu 4 (1 điểm). Cho hàm số f  x  cos 2 . x 62
Gọi C là đồ thị của hàm số   y  f
x. Viết phương trình 
tiếp tuyến của C tại điểm có hoành độ x  . 6
Câu 5 (3 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA   ABCD và góc giữa
SD với mặt đáy bằng o
45 . Gọi M , N, P lần lượt là các điểm trên cạnh ,
SA SC, SD sao cho SM  , MA
SN  4NC và SP  4 . PD
a. Chứng minh rằng SAC  B ;
D SAB  SBC.
b. Chứng minh rằng AP  N . P
c. Tính côsin của góc giữa 2 mặt phẳng MCD và BNP.
…………………………Hết………………………..
SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HÓA
ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2017-2018
TRƯỜNG THPT DƯƠNG ĐÌNH NGHỆ Môn: Toán-Lớp 11
(Đề thi gồm có 02 trang)
Thời gian làm bài: 90 phút ĐỀ 114
A. PHẦN TRẮC NGHIỆM (3 điểm): Câu 1. lim  3  n  2 bằng
A. . B. . C. 2. D. 1.  1 5n a a Câu 2. Biết lim
 ( a, b là hai số tự nhiên và tối giản). Giá trị của a  b n 1 5  b b bằng 1 A. 6. B. . C. 4.  D. 1. 5 Câu 3. 2
lim(x  2x  3) bằng x 1  A. 3. B. 0. C. 2.  D. .  2x  2 a a Câu 4. Biết lim
  ( a, b là hai số tự nhiên và tối giản). Giá trị của a  b bằng
x 1 3x b b 2 A. 1. B.  . C. 2. D. 5.  3 4 2n  3 Câu 5. lim bằng 4 n  2n  4 A. .  B. 1. C. 0. D. 2.
Câu 6. Biết rằng phương trình 5 3
x  x  2x 1  0 có duy nhất 1 nghiệm x , mệnh đề nào dưới đây đúng ? 0
A. x  0;1 . B. x  1; 2 . C. x  1;0 . D. x  2; 1 . 0   0   0   0   Câu 7. cho hàm số 3 2
y  x  3x  2x  2. Giá trị của y  1 bằng A. 7. B. 4. C. 2. D. 1. 
Câu 8. Đạo hàm của hàm số y  sin 3x bằng A. y  cos 3 .
x B. y   cos 3 .
x C. y  3cos 3 .
x D. y  3cos 3 . x x  2
Câu 9. Đạo hàm của hàm số y  bằng x 1 2 3 2 3 A. y  . B.   C. y  . D. y  .  y . x  2 1 x  2 1 x  2 1 x 1
Câu 10: Đạo hàm của hàm số 2
y  2x 1 bằng x 2x x
A. y  4x. B. y  . C. y  . D. y  . 2 2 2x 1 2 2x 1 2 2x 1
Câu 11. Biết AB cắt mặt phẳng   tại điểm I IA  IB thỏa mãn
6 , mệnh đề nào dưới đây đúng ? A. 6d  ,
A    d B, . B. 6d  ,
A    5d B, . C. d  ,
A    6d B, . D. 5d  ,
A    6d B, .
Câu 12. Mệnh đề nào dưới đây sai ?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
B. Đường thẳng vuông góc với mặt phẳng khi và chỉ khi góc giữa chúng bằng o 90 .
C. Hai mặt phẳng vuông góc với nhau khi và chỉ khi góc giữa chúng bằng o 90 .
D. Góc giữa hai mặt phẳng là góc giữa 2 đường thẳng lần lượt vuông góc với 2 mặt phẳng đó.
B. PHẦN TỰ LUẬN (7 điểm):
Câu 1 (1 điểm). Tính các giới hạn sau: x  5  3 a.  3 2
lim 2x  2x  x   1 ; b. lim . x x4 x  4
Câu 2 (1 điểm). Tính đạo hàm của mỗi hàm số sau: 5 x 1
a. y  x  x  2 2 x  5; b. 2 y  cot  tan . x 5
 x2  4x   5 kh i x  1
Câu 3 (1 điểm). Tìm giá trị của tham số a để hàm số f (x)   x 1
liên tục tại x  1. 0   x  a k hi x  1
Câu 4 (1 điểm). Cho hàm số f  x  cos 2 . x 66
Gọi C là đồ thị của hàm số   y  f
x. Viết phương trình 
tiếp tuyến của C tại điểm có hoành độ x  . 6
Câu 5(3 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA   ABCD và góc giữa
SD với mặt đáy bằng o
45 . Gọi M , N, P lần lượt là các điểm trên cạnh ,
SA SC, SD sao cho SM  , MA
SN  5NC và SP  5 . PD
a. Chứng minh rằng SAC  B ;
D SAB  SBC.
b. Chứng minh rằng AP  N . P
c. Tính côsin của góc giữa 2 mặt phẳng MCD và BNP.
…………………………Hết………………………..
SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HÓA
KỲ THI HỌC KỲ II NĂM HỌC 2017-2018
TRƯỜNG THPT DƯƠNG ĐÌNH NGHỆ Môn: Toán-Lớp 11
(Đáp án gồm có 02 trang)
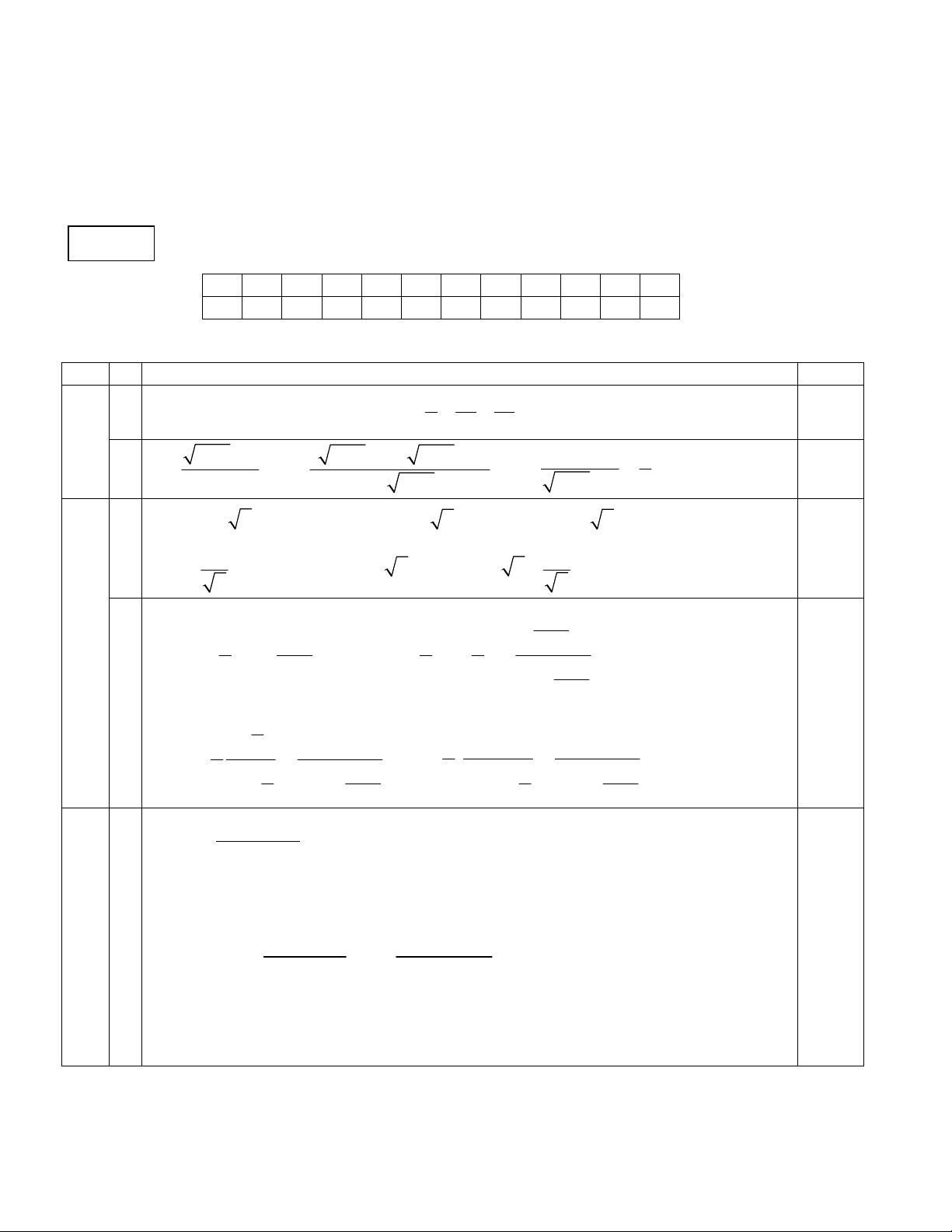
Thời gian làm bài: 90 phút A. Phần trắc ng ĐỀ 111 hiệm: 1 2 3 4 5 6 7 8 9 10 11 12 A D D B C A C B A D D B B. Phần tự luận: Câu Ý Nội dung Điểm 1 a  0.5 3 2  2 1 1 
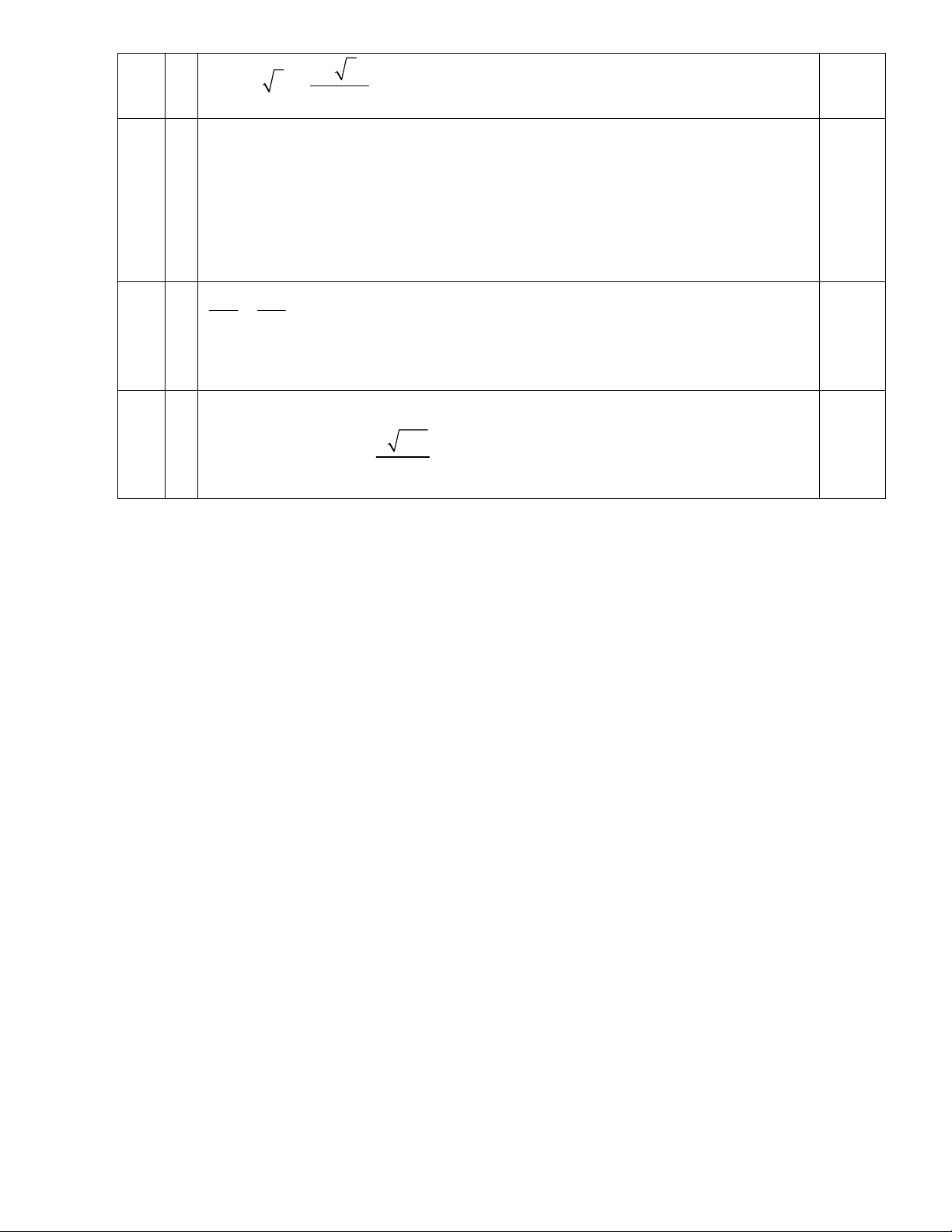
lim x  2x  x   1  3 lim x 1       x 2 3 x  x x x  b x 1  2
( x 1  2)( x 1  2) 1 1 0.5 lim  lim  lim  x3 x  3 x3
(x  3)( x 1  2) x3 x 1  2 4 2 a ' '
y  x  x  2 2
x  4  'y  x  x   2
x    x  x  2 2 4 2 x  4 0.25  1   4 1
 2x  4 2xx 2 x    2 3x  5x x   4.  x  x 0.25 b '  x 1 2 x 1 ' 2  2   2   2 y  cot  tan  'y 2.cot cot       0.25 x 2 x x    2 x 1 cos 2 '  2   2    x  1 ' 2 1 1  2.cot   4cot .  . 0.25 x  x 2 x  1 2 2 2 x 1 sin 2cos 2 2 2 x sin 2 os c x 2 x 2 3
 x2  4x   5 khi x  f x   1 ( ) x 1  2x  a khi x  1 Ta có: 2 x  4x  5 lim f (x)
(x 1)(x  5)  lim  lim
 limx  5  6 0.5 x1 x1 x 1 x1 x 1 x1
f (1)  2  a 0.25
Để hàm số liên tục tại x  1 thì lim f (x)  f  
1  2  a  6  a  4. 0 x1 0.25 4 4k f  4 2 k cos2x  4k  1 4k f   1 2 sin2x Ta có 4k2 4k f   2 2 cos2x . 4k3 4k f  3 2 sin 2x 50 0.5
Do đó (C) là đồ thị hàm số y  f x   50 2 o c s2x. '   Ta có: y  51 f x  51 2 sin2x.  x  Tiếp tuyến tại điểm 6 có phương trình: '          51   y  y x   y   50        y  2 sin x     2 cos  6  6   6  3  6  3 50    51 3    1 y  2 x   50 2 .    y  x   49 2 3 2 2    6  2  6  50 50 2  3 y  2 . 3x   49 2 6 0.5 5 a BD  AC   BD  (SAC) 0.5 BD  SA BC  AB 
 BC  (SAB)  SBC  SAB. BC  SA 0.5 b SN SP 0.5 
 2  NP / /CD  1 NC PD CD
 SAD  CD  AP2
Từ (1) và (2) suy ra AP  NP. 0.5
c Chỉ ra được mpSAD vuông góc với giao tuyến của 2 mp MCD và BNP 0.5 3
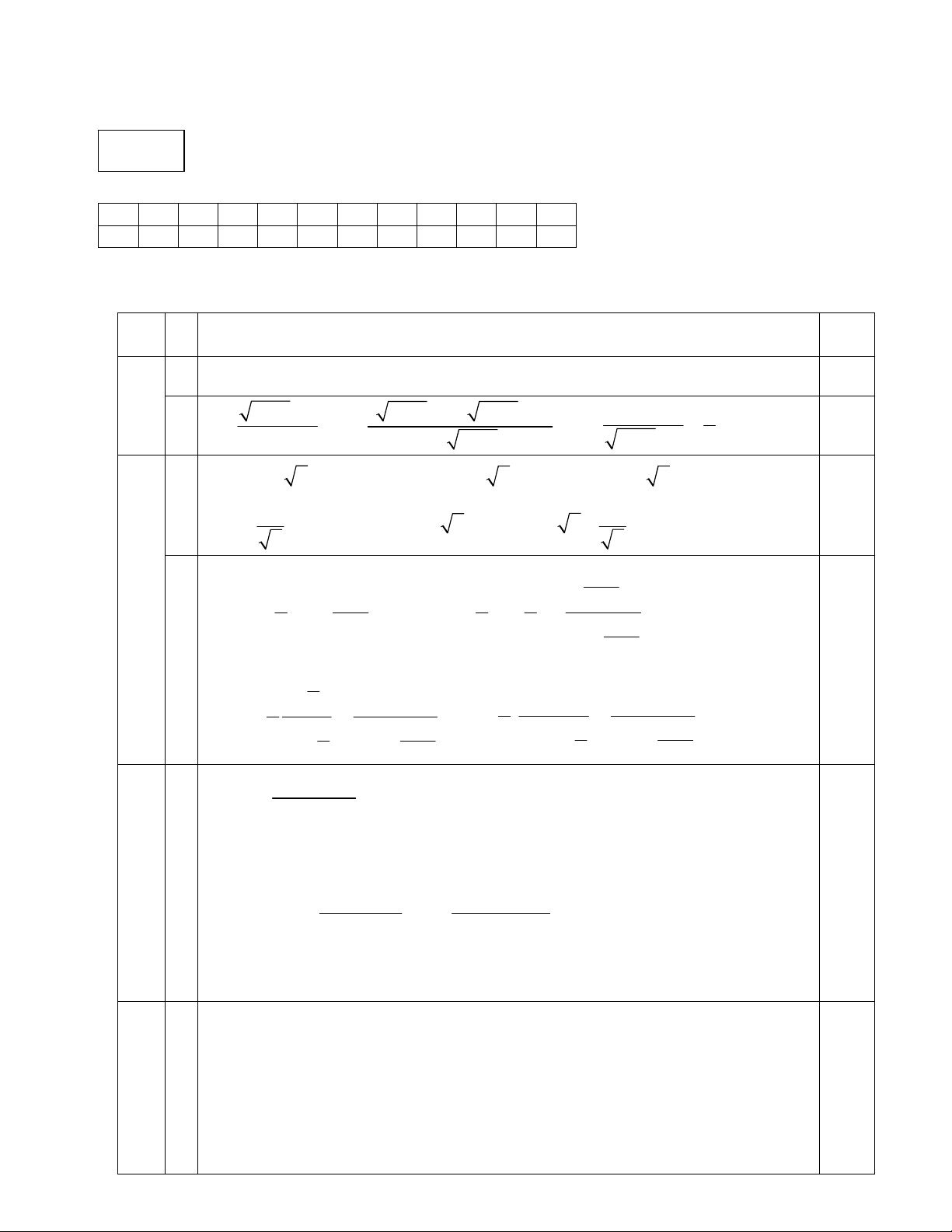
Tính được côsin bằng . 0.5 5 ĐỀ 112 C. Phần trắc nghiệm: 1 2 3 4 5 6 7 8 9 10 11 12 D C B B A A B C D D A C D. Phần tự luận: Câu Ý Nội dung Điể m 1 a  4 3
lim 5x  9x  2   0.5 x b x  7  3
( x  7  3)( x  7  3) 1 1 0.5 lim  lim  lim  x2 x  2 x2
(x  2)( x  7  3) x2 x  7  3 6 2 a ' ' 0.25
y  x  x  2 2
x  2  'y  x  x   2
x    x  x  2 2 2 2 x  2  1   2 1
 2x  2 2xx 2 x    2 3x  5x x   2.  x  x 0.25 b '  x 1 0.25    2 3 x 1 3 3  3 y  cot  tan  ' ' y 2.cot (cot )     x 3 x x  2 x 1 cos 3 '  3   3    x  1 ' 3 1 1  2.cot   6cot .  . x  x 3 x  1 2 3 2 x 1 sin 3cos 2 2 2 x sin 3 os c 0.25 x 3 x 3 3
 x2  5x   6 khi x  f x   3 ( ) x  3  2a 1 khi x  3 Ta có: 2 x  5x  6 lim f (x)
(x  2)(x  3)  lim  lim
 limx 2 1 0.5 x3 x3 x  3 x3 x  3 x3
f (3)  3a  1 0.25
Để hàm số liên tục tại x  3 thì lim f (x)  f 3  a
3 1  1  a  0. 0 x3 0.25 4 4k f  4 2 k cos2x  4k  1 4k f   1 2 sin2x Ta có 4k2 4k f   2 2 cos2x . 4k3 4k f  3 2 sin 2x 58 0.5
Do đó (C) là đồ thị hàm số y  f x   58 2 o c s2 . x ' 59 Ta có: y  f x  59 2 sin2x.  x  Tiếp tuyến tại điểm 6 có phương trình: '          59   y  y x   y   58        y  2 sin x     2 cos  6  6   6  3  6  3 58    59 3    1 y  2 x   58 2 .    y  x   57 2 3 2 2    6  2  6  58 58 2  3 y  2 . 3x   57 2 6 0.5 5 a BD  AC 0.5   BD  (SAC) BD  SA BC  AB 0.5 
 BC  (SAB)  SBC  SAB. BC  SA b SN SP 0.5 
 3  NP / /CD  1 NC PD CD
 SAD  CD  AP2
Từ (1) và(2) suy ra AP  NP. 0.5
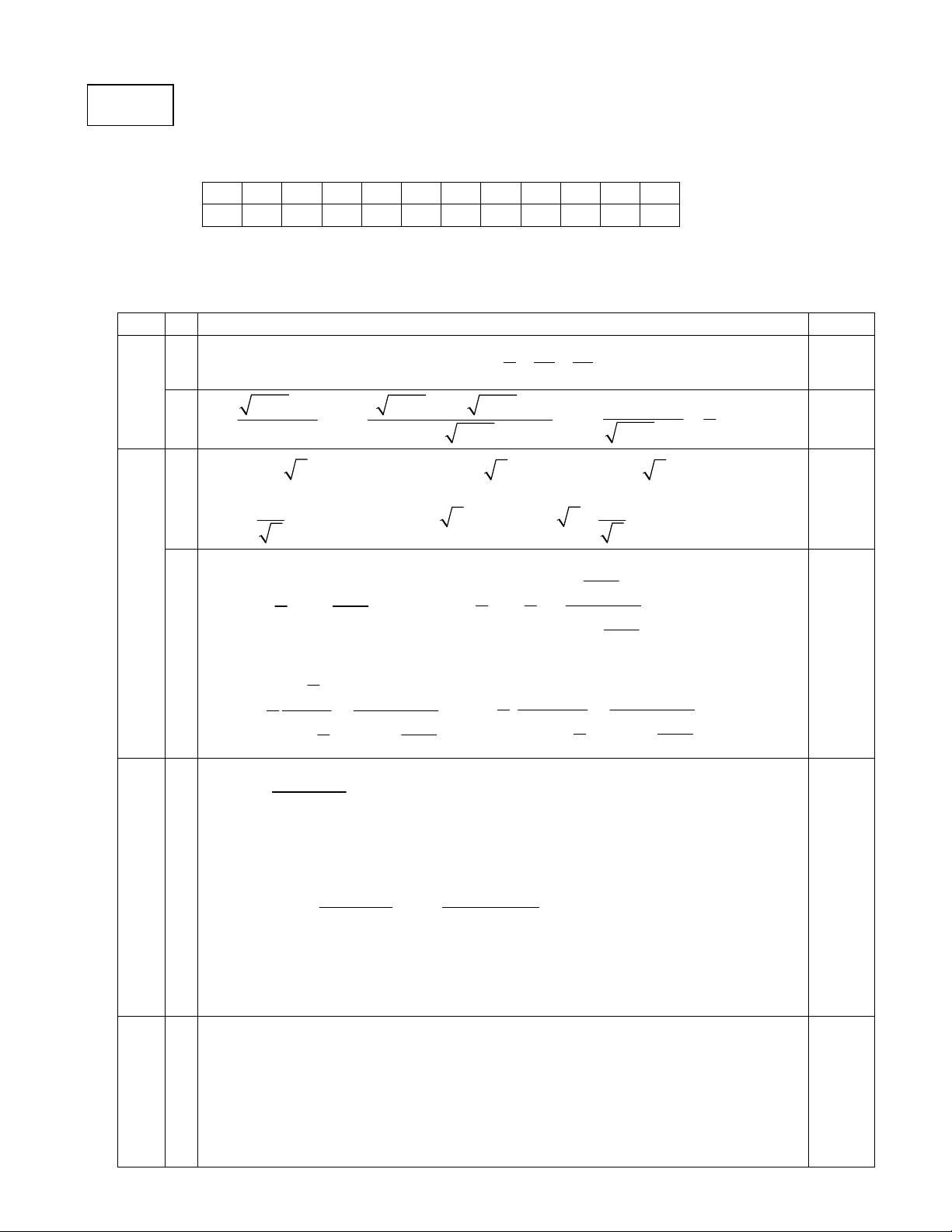
c Chỉ ra được mpSAD vuông góc với giao tuyến của 2 mp MCD và BNP 0.5 2 Tính được côsin bằng . 0.5 2 ĐỀ 113 E. Phần trắc nghiệm: 1 2 3 4 5 6 7 8 9 10 11 12 C B A A C A A A C A B D F. Phần tự luận: Câu Ý Nội dung Điểm 1 a  0.5 3 2  2 1 1 
lim 2x  2x  x   1  3 lim x 2        x 2 3 x  x x x  b x  3  2
( x  3  2)( x  3  2) 1 1 0.5 lim  lim  lim  x 1  x 1 x 1 
(x 1)( x  3  2) x 1  x  3  2 4 2 a ' ' 0.25
y  x  x  2 2
x  3  'y  x  x   2
x    x  x  2 2 3 2 x  3  1   3 1
 2x 3 2xx 2 x    2 3x  5x x   3.  x  x 0.25 b '  x 1    2 4 x 1 4 4  4 y  cot  tan  ' ' y 2.cot (cot )     0.25 x 4 x x  2 x 1 cos 4 '  4   4    x  1 ' 4 1 1  2.cot   8cot .  . x  x 4 x  1 2 4 2 x 1 sin 4cos 2 2 2 x sin 4 os c 0.25 x 4 x 4 3  x2  x   2 khi x  f x   2 ( ) x  2  a  x khi x  2 Ta có: 2 x  x  2 lim f (x)
(x 1)(x  2)  lim  lim  limx   1  3 0.5 x2 x2 x  2 x2 x  2 x2
f (2)  a  2 0.25
Để hàm số liên tục tại x  2 thì lim f (x)  f 2  a  2  3  a  5. x 1  0.25 4 4k f  4 2 k cos2x  4k  1 4k f   1 2 sin2x Ta có 4k2 4k f   2 2 cos2x . 4k3 4k f  3 2 sin 2x 0.5 62
Do đó (C) là đồ thị hàm số y  f x   62 2 o c s2x. ' 63 Ta có: y  f x  63 2 sin2x. 
Tiếp tuyến tại điểm x  có phương trình: 6 '          63   y  y x   y   62        y  2 sin x     2 cos  6  6   6  3  6  3 62    63 3    1 y  2 x   62 2 .    y  x   61 2 3 2 2    6  2  6  62 62 2  3 y  2 . 3x   61 2 0.5 6 5 a BD  AC 0.5   BD  (SAC) BD  SA BC  AB 0.5 
 BC  (SAB)  SBC  SAB. BC  SA b SN SP 
 4  NP / /CD  1 NC PD 0.5 CD
 SAD  CD  AP2 0.5
Từ (1) và(2) suy ra AP  NP.
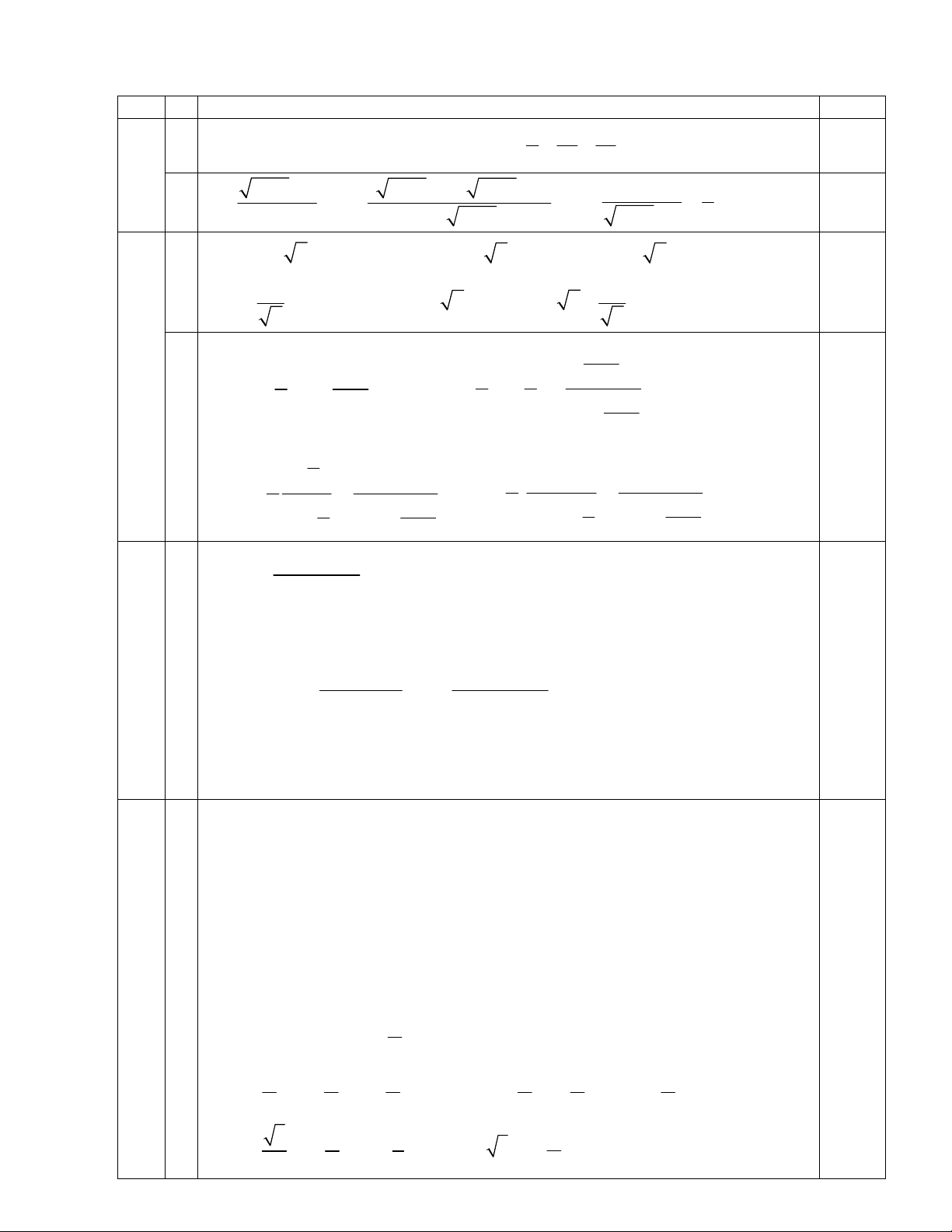
c Chỉ ra được mpSAD vuông góc với giao tuyến của 2 mp MCD và BNP 0.5 7 85 Tính được côsin bằng . 0.5 85 ĐỀ 114 G. Phần trắc nghiệm: 1 2 3 4 5 6 7 8 9 10 11 12 B A C A D C D D B C C A H. Phần tự luận: Câu Ý Nội dung Điểm 1 a  0.5 3 2  2 1 1 
lim 2x  2x  x   1  3 lim x 2        x 2 3 x  x x x  b x  5  3
( x  5  3)( x  5  3) 1 1 0.5 lim  lim  lim  x4 x  4 x4
(x  4)( x  5  3) x4 x  5  3 6 2 a ' ' 0.25
y  x  x  2 2
x  5  'y  x  x   2
x    x  x  2 2 5 2 x  5  1   5 1
 2x 5 2xx  2 x    2 3x  5x x   5.  x  x 0.25 b '  x 1    0.25 2 5 x 1 5 5  5 y  cot  tan  ' ' y 2.cot (cot )     x 5 x x  2 x 1 cos 5 '  5   5    x  1 ' 5 1 1  2.cot   10cot .  . x  x 5 x 1 2 5 2 x 1 sin 5cos 2 2 2 x sin 5 os c x 5 x 5 3
 x2  4x   5 khi x  f x   1 ( ) x 1  x  a khi x  1 Ta có: 2 x  4x  5 lim f (x)
(x 1)(x  5)  lim  lim
 limx  5  6 x1 x1 x 1 x1 x 1 x1 0.5
f (1)  1  a
Để hàm số liên tục trên R thì lim f (x)  f  
1  1 a  6  a  5. 0.25 x1 0.25 4 4k f  4 2 k cos2x  4k  1 4k f   1 2 sin2x Ta có 4k2 4k f   2 2 cos2x . 4k3 4k f  3 2 sin 2x 66 0.5
Do đó (C) là đồ thị hàm số y  f x   66 2 o c s2x. ' 67 Ta có: y  f x  67 2 sin2x.  x  Tiếp tuyến tại điểm 6 có phương trình: '          67   y  y x   y   66        y  2 sin x     2 cos  6  6   6  3  6  3 66    67 3    1 y  2 x   66 2 .    y  x   65 2 3 2 2    6  2  6  66 66 2  3 y  2 . 3x   65 2 6 0.5 5 a BD  AC 0.5   BD  (SAC) BD  SA BC  AB 0.5 
 BC  (SAB)  SBC  SAB. BC  SA b SN SP 0.5 
 5  NP / /CD  1 NC PD CD
 SAD  CD  AP2
Từ (1) và(2) suy ra AP  NP. 0.5
c Chỉ ra được mpSAD vuông góc với giao tuyến của 2 mp MCD và BNP 0.5 9 130 Tính được côsin bằng . 130 0.5