SỞ GD&ĐT VĨNH PHÚC
ĐỀ THI HỌC KÌ 2 NĂM HỌC 2017 - 2018
TRƯỜNG THPT YÊN LẠC 2 MÔN : TOÁN KHỐI 11 -----------
Thời gian làm bài: 90 phút, không kể thời gian giao đề. Đề gồm 02 trang. ———————
Họ và tên thí sinh:........................................................Số báo danh................................
I. PHẦN TRẮC NGHIỆM (2,0 điểm) 1 Câu 1: lim bằng ? x 2  x  3 1 A. 0 B.  C.  D.  2
Câu 2: Giới hạn nào sau đây có kết quả bằng 2. 2n 1 2n 1 2 4n 1 2 4n 1 A. lim B. lim C. lim D. lim n  2 n n  2 n  2 n  2
Câu 3: Cho cấp số cộng u biết u  3
 và u  27. Công sai của cấp số cộng đó là? n  1 6 A. 5 B. 6 C. 7 D. 8
Câu 4: Tiếp tuyến của đồ thị hàm số 3
y  x 3x tại điểm A 1
 ;2 có hệ số góc k bằng ?
A. k  0
B. k  6 C. k  3  D. k  6 
Câu 5: Đạo hàm của hàm số f x  2
cos 2x bằng : A. sin 4x
B.  sin 4x C. 2 sin 2x
D. 2sin 4x
Câu 6: Vi phân của hàm số y  x  2 1 bằng :
A. dy  2x   1 dx
B. dy  2x   1
C. dy  x  2 1 dx
D. dy  2x   1 dx
Câu 7: Cho hình chóp S. D
ABC , đáy ABCD là hình thoi, SA  (ABC )
D . Khẳng định nào sau đây sai ? A. SA  BD
B. AD  SC
C. SC  BD
D. SO  BD
Câu 8: Chóp tứ giác đều S.AB D
C có độ dài cạnh bên và cạnh đáy đều bằng a. Khoảng cách từ S đến
mặt phẳng (ABCD) bằng. a a a A. B. C. a D. 2 3 2
II. PHẦN TỰ LUẬN (8,0 điểm)
Câu 9:(2 điểm). Tìm giới hạn sau: x 1  2 a)  3 2
lim x  3x  2x   1 b) lim . x 2 x3 9  x 2x 1
Câu 10: (1 điểm). Cho hàm số y 
có đồ thị (C). x  2
Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến song song với đường thẳng
 :3x  y  2  0 2
 x  x 12  (x  4  )
Câu 11:(1điểm). Cho hàm số y  f  x   x  4
. Xác định m để hàm số đã cho liên
 mx1(x  4  ) tục tại x  4  .
Câu 12:(3 điểm). Cho hình chóp S.AB D
C , đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt
phẳng (ABCD) và SA  a 2 . Gọi E, F lần lượt là hình chiếu vuông góc của A trên , SB SD .
a) Chứng minh AE  SBC và AF  SDC .
b) Tính góc giữa mặt phẳng SBC và mặt phẳng đáy.
c) Xác định thiết diện của hình chóp cắt bởi mặt phẳng  AEF  .
Tính diện tích của thiết diện theo a.
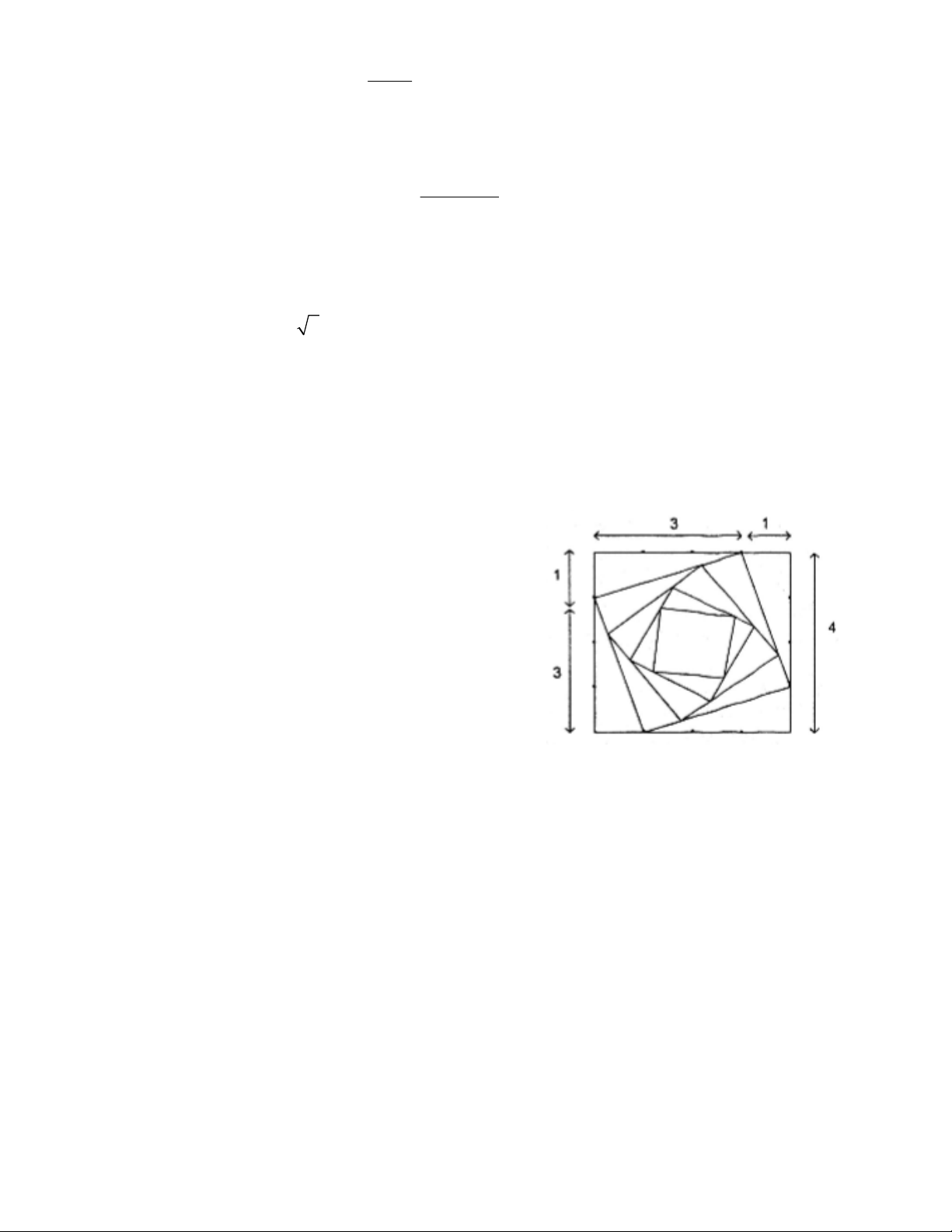
Câu 13:(1điểm). Cho hình vuông C có độ dài cạnh 1
bằng 4. Người ta chia mỗi cạnh của hình vuông thành
bốn phần bằng nhau và nối các điểm chia một cách thích
hợp để được hình vuông C ( tham khảo hình vẽ). Từ 2
hình vuông C tiếp tục làm như vậy để được hình vuông 2
C ,... . Tiếp tục quá trình trên ta được dãy các hình 3
vuông C ,C ,C ,...,C ... . Gọi S , S , S ,..., S ... tương 1 2 3 n 1 2 3 n
ứng là diện tích các hình vuông C ,C ,C ,...,C ... . 1 2 3 n
Tính tổng S  S  S  ...  S  ... 1 2 3 n
----------------------Hết-----------------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KÌ 2 TOÁN 11 NĂM HỌC 2017-2018
I. Trắc nghiệm: Mỗi câu trả lời đúng 0.25 điểm 1A 2C 3B 4A 5D 6D 7B 8D
II. Tự luận:(8 điểm) Câu Nội dung trình bày Điểm Câu 9 x 1  2 a)  3 2
lim x  3x  2x   1 b) lim . (2điểm) x 2 x3 9  x a(1 điểm)  0. 25 đ 3 2  3 2 1 
lim x  3x  2x   1  3 lim x 1     x 2 3 x  x x x  3
lim x   , 0.25 đ x  3 2 1  0.25 đ lim 1    1   0  2 3  x  x x x  Vậy  3 2
lim x  3x  2x   1   0. 25 đ x b(1 điểm) x 1  2
( x 1  2)( x 1  2) 0.25 đ lim  lim 2 x 3  9  x 2 x3
(9  x )( x 1  2) x  3  0.25 đ lim 2 x 3
 (9  x )( x 1  2) 1   0.25 đ lim x 3
 (3  x)( x 1  2) 1  1    0.25 đ (3  3)( 3 1  2) 24 Câu 10: 2x 1 Cho hàm số y 
có đồ thị (C).
(1 điểm). x  2
Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến song song
với đường thẳng  :3x  y  2  0 3 0.25 đ Ta có y '  x  22
Vì tiếp tuyến song song với  :3x  y  2  0 nên ta có hệ số góc của tiếp 3 tuyến k   3 x  22 3 x  1  0.25 đ
 3  x  2 1  2  2   x  2 x  3  Với x  1   y  1
 ta có tiếp điểm A 1  ;  1 0.25 đ
Phương trình tiếp tuyến là: y  3 x  
1 1  3x  y  2  0 ( loại vì trùng  ) Với x  3
  y  5 ta có tiếp điểm B 3;  5 0.25 đ
Phương trình tiếp tuyến là: y  3 x  3  5  3x  y 14  0(thỏa mãn)
Vậy có một tiếp tuyến là: 3x  y 14  0 Câu 11: 2
 x  x 12  (x  4  )
(1điểm).
Cho hàm số y  f  x   x  4
. Xác định m để hàm số đã cho
 mx1(x  4  )
liên tục tại x  4  . TXĐ: D=R 0.25 đ 2 x  x 12
x  4x 3 0.25 đ lim  lim
 lim x 3  7  x 4  x  4 x 4  x  4 x 4  f  4    4  m 1 0.25 đ
Để hàm số liên tục tại x=-4 thì lim f  x  f  4    4  m 1  7
  m  2 . 0.25 đ x 4  KL: Câu 12:
Cho hình chóp S.AB D
C , đáy ABCD là hình vuông cạnh a, SA vuông góc
( 3điểm).
với mặt phẳng (ABCD) và SA  a 2 . Gọi E, F lần lượt là hình chiếu
vuông góc của A trên , SB SD .
a) Chứng minh AE  SBC và AF  SDC .
b) Tính góc giữa mặt phẳng SBC và mặt phẳng đáy.
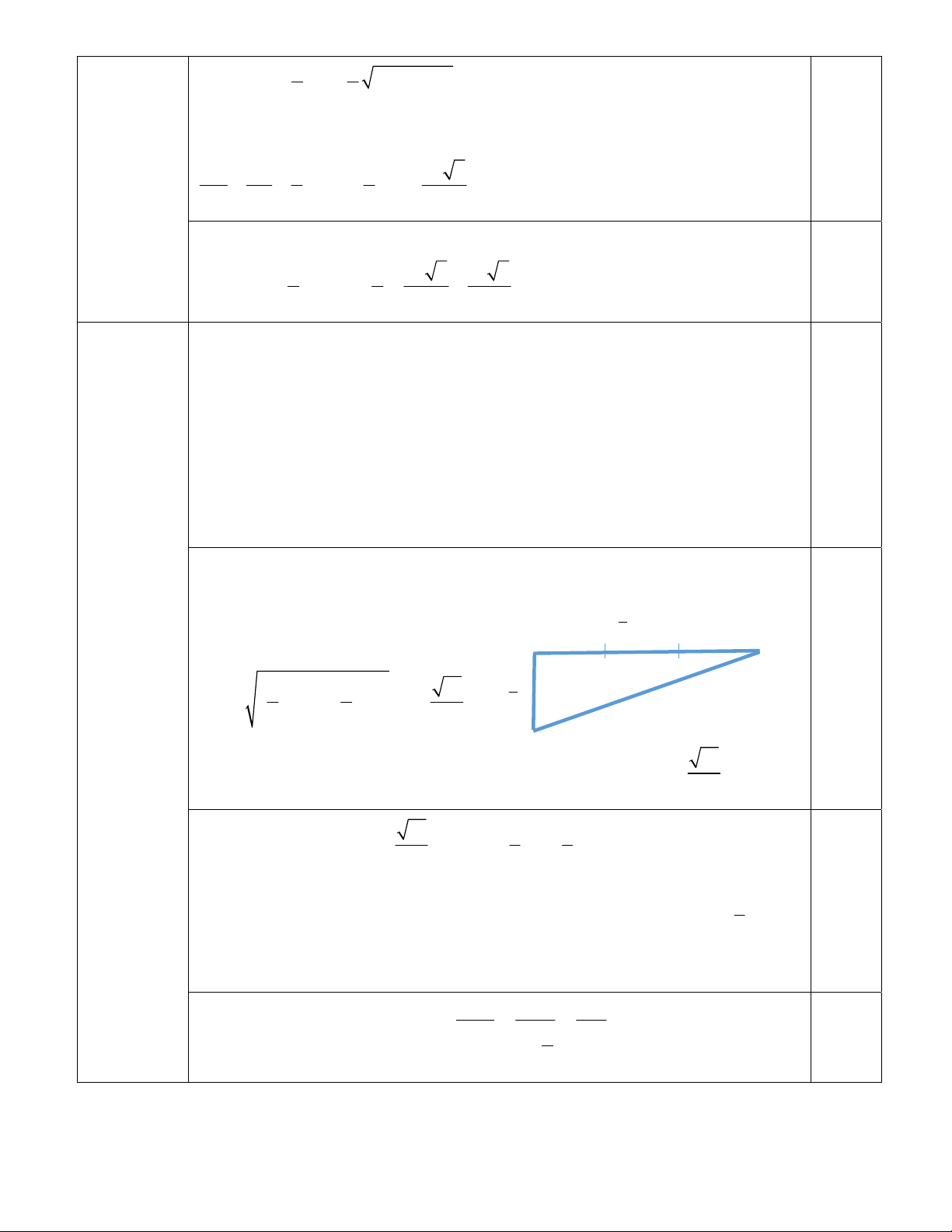
c) Xác định thiết diện của hình chóp cắt bởi mặt phẳng  AEF  . Tính
diện tích của thiết diện theo a. S K F I E D A O B C
a( 1 điểm) Ta có BC  AB, BC  SA  BC  SAB nên BC  AE 0.25 đ
Từ AE  BC, AE  SB  AE  SBC 0.25 đ
Ta có CD  AD,CD  SA  CD  SAD nên CD  AF 0.25 đ
Từ AF  CD, AF  SD  AF  SCD 0.25 đ b( 1 điểm) Ta có 0. 5 đ
SBC ABCD  BC
AB   ABCD, AB  BC
SB  SBC, SB  BC
Nên giữa mặt phẳng SBC, ABCD  S , B AB  S  BA   SA a 2 0. 5 đ Ta có tan    2 0   54 44' AB a
c( 1 điểm) Gọi O  AC  B ,
D I  SO  EF,K=AI SC 0.25 đ
Ta được thiết diện là tứ giác AEKF
Vì AE  SBC , AF  SCD nên 0.25 đ
AE  SC, AF  SC  SC   AEF   AK  SC Từ GT suy ra EF  ,
BD BD  SAC  F
E  SAC  EF  AK Tam giác SA
 C vuông cân tại A mà AK  SC nên K là trung điểm của 0.25 đ 1 1 SC 2 2
 AK  SC 
SA  AC  a 2 2
Ta có I là trọng tâm SA
 C mà EF  BD nên EF SI 2 2 2a 2    EF= BD  BD SO 3 3 3
Tứ giác AEKF có hai đường chéo vuông góc với nhau nên diện tích 0.25 đ 2 1 1 2a 2 a 2
của nó S  AK.EF  . . a  2 2 3 3 Câu 13:
Cho hình vuông C có độ dài cạnh bằng 4. Người ta chia mỗi cạnh của hình 1
( 1điểm).
vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp
để được hình vuông C ( tham khảo hình vẽ). Từ hình vuông C tiếp tục làm 2 2
như vậy để được hình vuông C ,... . Tiếp tục quá trình trên ta được dãy các 3
hình vuông C ,C ,C ,...,C ... . Gọi S , S , S ,..., S ... tương ứng là diện tích 1 2 3 n 1 2 3 n
các hình vuông C ,C ,C ,...,C ... . 1 2 3 n
Tính tổng S  S  S  ...  S  ... 1 2 3 n
Xét dãy a là độ dài cạnh của của dãy hình vuông 0.5 đ n 
C ,C ,C ,...,C ... với a  4 1 2 3 n 1 3a Ta có 4 n 2 2  1   3  10 1 a  a  a  a . a n 1      4 n
 4 n   4 n n  4 an 1 10
Vậy dãy a lập thành cấp số nhân lùi vô hạn với công bội n  4 2  10  5 5 0.25 đ Ta có S  a  a   a  S n  n 2 . n  n2. . 1 1  4  8 n 8   5
Suy ra dãy S lập thành cấp số nhân lùi vô hạn với công bội q  và n  8 S 16 1 S 16 128 0.25 đ Vậy 1
S  S  S  ...  S  ...    1 2 3 n 1 q 5 3 1 8