SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI HỌC KỲ II TP.HỒ CHÍ MINH
NĂM HỌC 2018 – 2019
TRƯỜNG THPT NGUYỄN DU MÔN: TOÁN 11 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút ( Đề có 1 trang )
Họ và tên thí sinh :..................................................................... Số báo danh :................
Bài 1: (1.5 điểm). Tính các giới hạn của các hàm số sau: 2 x  x  6 A  lim . B     .   2 lim x 4x 5 x x  2
x2 x  3x  2
 2x  5  3 khi x  2  2 
Bài 2: (1.0 điểm). Cho hàm số x  4 f (x)  
. Tìm a để hàm số liên tục tại x  2 . 47  2 . a x  khi x  2   12
Bài 3: (1.5 điểm). Tính đạo hàm của các hàm số sau: a) y   2 x    2 3 2 . 3x  2 . b) y  .
x cos x  sin x .
Bài 4: (2.0 điểm). a) Cho đồ thị 3 2
(C) : y  f (x)  x  3x  x 1 . Viết phương trình tiếp tuyến của đồ thị (C) tại điểm A
thuộc đồ thị (C) có hoành độ bằng x  1 0 2x  3
b) Viết phương trình tiếp tuyến của đồ thị (C) : y  f (x) 
, biết tiếp tuyến vuông góc với đường x 1 1
thẳng d : y   x  2019 . 5
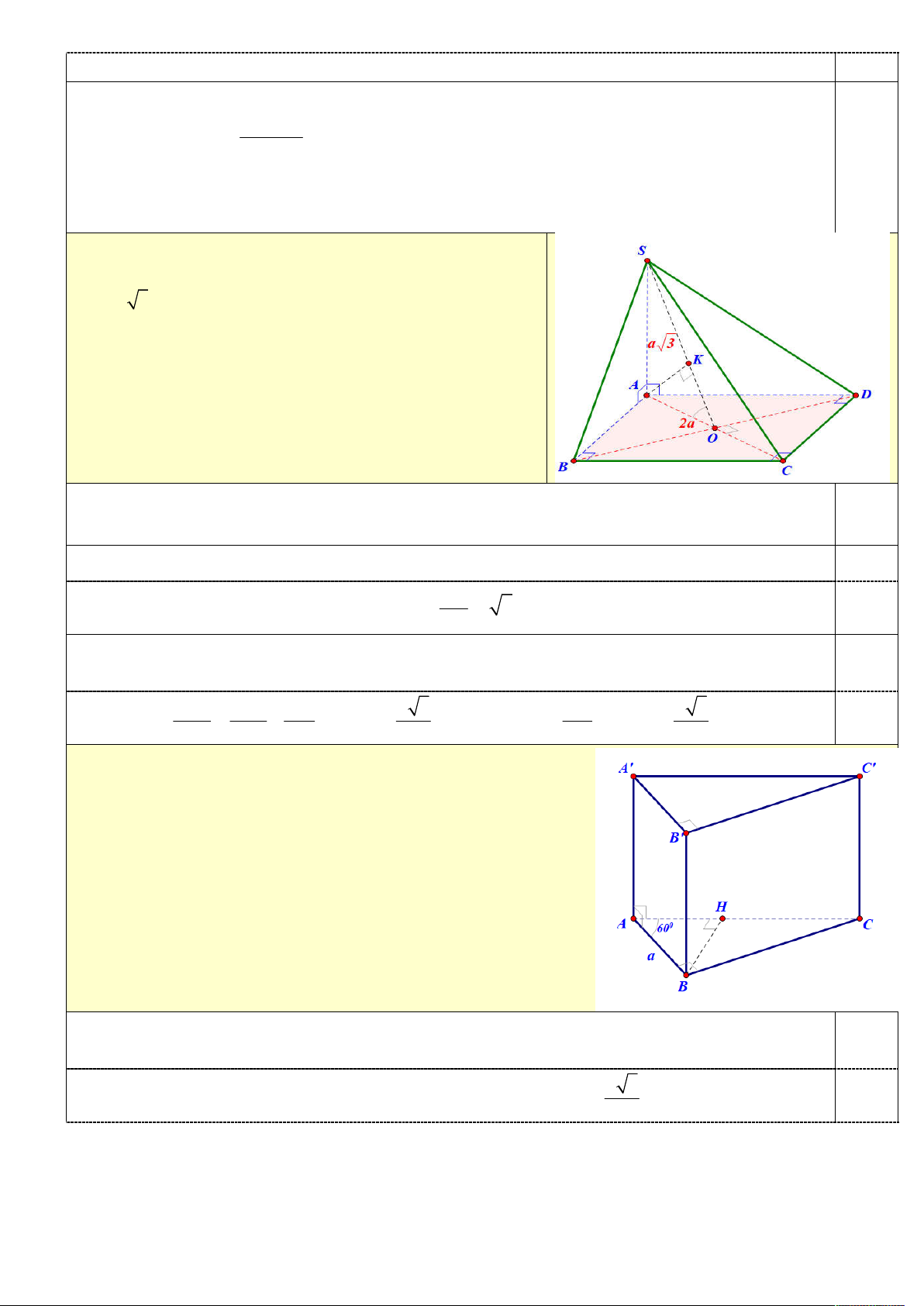
Bài 5: (3.0 điểm). Cho hình chóp tứ giác S.ABCD có mặt đáy  ABCD là hình vuông tâm O , biết cạnh
AC  2a , SA  a 3 và SA   ABCD
a) Chứng minh: BD  (SAC ) và (SAC )  (SBD).
b) Xác định và tính góc giữa đường thẳng SO và ( ABCD) .
c) Tính khoảng cách từ điểm A đến mặt phẳng (SBD).
Bài 6: (1.0 điểm). Cho lăng trụ đứng ABC.A ' B 'C ' có đáy ( ABC ) là tam giác vuông tại B , AB  a ,  0 BAC  60 .
a) Chứng minh: ( A ' AB)  (B ' BC).
b) Tính khoảng cách giữa đường thẳng chéo nhau BB ' và AC. -----Hết-----
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ II LỚP 11 MÔN TOÁN – NH 2018 – 2019 Nội dung Điểm
Bài 1:(1.5 điểm). Tính các giới hạn của các hàm số sau: 2 x  x  6 A  lim . B       2 lim x 4x 5 x x  2
x2 x  3x  2 2 x  x  6
 x  2 x  3 x  3 A  lim  lim /  lim /  5 / 2 x2 x2 x  3x  2  x   1  x  2 x2 x 1 0.75
Nếu còn dạng vô định mà ra đáp số thì giáo viên trừ 0.25 và chỉ trừ 1lần  5  2 2  4 
x  x   x     lim x B
x  x   x        0.75 x  4 5 2 4 5  lim / lim / 2 / x 2  x  4x  5 x  x   4 5   1  1  2   x x   2x  5  3  khi x  2 2 
Bài 2: (1.0 điểm). Cho hàm số x  4 f (x)  
. Tìm a để hàm số liên tục tại x  2 . 47  2 . a x  khi x  2   12 47
 f 2  4a  / 0.25 12 2x  5  3 2 1  lim  lim /  / 0.5 2 x2 x2 x  4
(x  2)( 2x  5  3) 12
+ Hàm số liên tục tại x  2  a  1/ 0.25
Bài 3: (1.5 điểm). Tính đạo hàm của các hàm số sau: a) y   2 x    2 3 2 . 3x  2 . b) y  .
x cos x  sin x . Cách 1: Cách 2: a) Ta có: 4
y  9x  4 / y   2 x    2 x     2 x    2 ' 3 2 '. 3 2 3 2 '. 3x  2 / 0.25 3 y '  36x / / y  x  2
x    x  2 x   3 ' 6 . 3 2 6 . 3 2 /  36x / 0.5
b) y '  (x) 'cos x  (cos x) ' x / sin x '  cos x  .
x sin x /  cos x   . x sin x / 0.75
Bài 4: (2.0 điểm). a) Cho đồ thị 3 2
(C) : y  f (x)  x  3x  x 1 . Viết phương trình tiếp tuyến của đồ thị (C) tại điểm A
thuộc đồ thị (C) có hoành độ bằng x  1 0 2x  3
b) Viết phương trình tiếp tuyến của đồ thị (C) : y  f (x) 
, biết tiếp tuyến vuông góc với đường x 1 1
thẳng d : y   x  2019 . 5 a) Ta có: 2 y '  f (
 x)  3x  6x 1 / và x  1  y  2  / 0.5 0 0 f (
 1)  2 / .Phương trình tiếp tuyến: y  2x / 0.5 5
b) Ta có: y '  f  x   0.25 x  2 1
Vì tiếp tuyến vuông góc với đường thẳng d  k  5 / tt 0.25
Gọi x0 là hoành độ tiếp điểm 5 x  0 Ta có: 0 f (
 x )  k   5  / . 0 tt   x  2 1 x  2   0 0 0.5
x  0  y  3
  PTTT : y  5x  3  0 0  / x  2
  y  7  PTTT : y  5x 17 0 0 
Bài 5: (3.0 điểm). Cho hình chóp tứ giác S.ABCD có mặt đáy
 ABCD là hình vuông tâm O , biết cạnh AC  2a ,
SA  a 3 và SA   ABCD
a) Chứng minh: BD  (SAC ) và (SAC )  (SBD).
b) Xác định và tính góc giữa đường thẳng SO và ( ABCD) .
c) Tính theo a khoảng cách từ điểm A đến mặt phẳng (SBD).
AC  BD(do ABCD hv)/  a) Vì
  BD  (SAC)/  (SAC)  (SBD) / 1.0
AS  BD(do SA  ( ABCD)) /
b) Ta có AO là hình chiếu vuông góc của SO lên  ABCD /  SO ABCD   ;( )  SOA / 0.5  SA  0.5 Tính 0
AC  2a  OA  a/  tan SOA   3  SOA  60 / OA
c) Kẻ AK vuông góc với SO tại K . 0.5
Ta chứng minh được AK  (SBD)/  d  ,
A SBD  AK /   1 1 1 a 3  AK a 3 0.5 Ta có:   /  AK  / hoặc sin SOA  /  AK  / 2 2 2 AK AO SA 2 AO 2
Bài 6: (1.0 điểm). Cho lăng trụ đứng ABC.A ' B 'C ' có đáy ( ABC )
là tam giác vuông tại B , AB  a ,  0
BAC  60 , AA '  2a .
a) Chứng minh: ( A ' AB)  (B ' BC).
b) Tính khoảng cách giữa đường thẳng chéo nhau BB ' và AC. BC  AB  a) Ta có:
  BC  ( A' AB)/  (B ' BC)  ( A' AB) / 0.5 BC  AA' a 3
b) Kẻ BH  AC tại H. Ta chứng minh được d (BB '; AC)  BH /  / 0.5 2