Đề thi học kỳ 2 Toán 12 năm học 2018 – 2019 sở GD&ĐT Bến Tre

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2018 – 2019 .Mời bạn đọc đón xem.

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

19 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Trang 1/6 – Mã đề 210
Câu 1. Cho các số phức
12
13; 53ziz i
. Tìm điểm

;
M
xy biểu diễn số phức
3
z
, biết rằng trong
mặt phẳng phức điểm
M
nằm trên đường thẳng 210xy và môđun của số phức
32 1
32wzz z
đạt giá trị nhỏ nhất.
A.
31
;
55
M



.
B.
31
;
55
M



.
C.
31
;
55
M



.
D.
31
;
55
M




.
Câu 2. Trong không gian Oxyz cho
1; 1; 2 , 2;1;1AB và mặt phẳng
:10Pxyz. Mặt phẳng
Q
chứa ,
A
B và vuông góc với mặt phẳng

P
. Mặt phẳng

Q
có phương trình là:
A.
20xyz
. B.
32 30xyz
. C.
32 30xyz
. D.
0xy
.
Câu 3. Trong không gian Oxyz cho mặt cầu

S có phương trình:
222
24690xyz xyz.
Mặt cầu

S có tâm
I
và bán kính
R
là:
A.

1; 2; 3I  và 5R . B.
1; 2; 3I và 5R .
C.

1; 2; 3I
và
5R
. D.

1; 2; 3I 
và
5R
.
Câu 4. Gọi
1
z ,
2
z là các nghiệm của phương trình
2
490zz
. Giả sử ,
M
N là các điểm biểu diễn
hình học của
1
z ,
2
z trên mặt phẳng phức. Khi đó độ dài của
M
N
là
A. 5 . B. 4 . C. 25. D. 5.
Câu 5. Trong không gian Oxyz , cho mặt cầu
222
:2460Sx y z x y z. Đường tròn giao tuyến
của

S với mặt phẳng

Oxy có bán kính là
A. 6r . B. 14r . C. 3r . D. 5r .
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho điểm
1; 2; 3M . Hình chiếu của
M
trên trục Oy là:
A.
0; 2; 0Q . B.

0;0;3S . C.
1; 0; 0R . D.
1; 0; 3P .
Câu 7. Tìm số phức z
biết:
1150.iz i
A. 32zi
.
B. 32zi . C. 32zi . D. 32zi .
Câu 8. Trong mặt phẳng phức, cho ba điểm , ,
A
BC lần lượt biểu diễn ba số phức
1
1zi,

2
2
1zi
và
3
zai. Để tam giác
BC vuông tại B thì a bằng:
A. 3 . B.
2
. C. 3 . D.
4
.
Câu 9. Tính môđun của số phức
2019
2zii
.
A. 5z . B. 2z . C. 22z . D. 10z .
Câu 10. Gọi
12
,zz là hai nghiệm phức của phương trình
2
90z . Tính
12
zz .
A.
12
3zz. B.
12
4zz i. C.
12
9zz i. D.
12
0zz.
Câu 11. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm

2;0;0 , 0;3;1 , 1;4;2ABC . Độ dài
đường cao từ đỉnh
A
của tam giác
A
BC .
SỞ GIÁO DỤC VÀ ĐÀO TẠO
BẾN TRE
MÃ ĐỀ 210
ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2018 - 2019
MÔN: TOÁN HỌC - LỚP: 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Trang 2/6 – Mã đề 210
A. 3. B.
3
2
.
C.
2
. D. 6.
Câu 12. Trong không gian
Oxyz
, cho các véc tơ
1; 2; 3a
,

2; 4;1b 
,
1; 3; 4c 
. Véc tơ
235vabc

có toạ độ là:
A.

3; 7; 23v
. B.

23;7;3v
. C.

7;3;23v
. D.

7;23;3v
.
Câu 13.
Tìm họ nguyên hàm của hàm số

4
2
23x
fx
x
.
A.
3
3
2
x
C
x
. B.
3
23
3
x
C
x
.
C.
3
23
32
x
C
x
.
D.
3
23
3
x
C
x
.
Câu 14. Trong không gian Oxyz , cho điểm
4;0;0M
và đường thẳng
1
:23
2
x
t
yt
zt



. Gọi
;;Habc
là chân hình chiếu từ
M
lên
. Tính abc.
A.
5
.
B.
7
.
C.
3
. D.
1
.
Câu 15.
Trong không gian Oxyz , đường thẳng nào sau đây nhận
2;3; 4u 
làm véc tơ chỉ phương?
(với
t )
A.
12
23
24
x
t
yt
zt



. B.
2
33
4
x
t
yt
zt



. C.
2
35
43
x
t
yt
zt



. D.
12
33
24
x
t
yt
zt



.
Câu 16.
Trong không gian Oxyz , cho các điểm
1; 0; 1 , 2; 2; 3IA. Mặt cầu

S tâm I và đi qua điểm
A
có phương trình là
A.

22
2
113xyz
.
B.
 
22
2
119xyz
.
C.

22
2
119xyz. D.
 
22
2
113xyz.
Câu 17. Trong không gian Oxyz , cho mặt phẳng
:2 1 0Pxyz. Điểm nào dưới đây thuộc mặt
phẳng

P
?
A.
1; 3; 4Q  . B.

1; 2; 0P . C.
0;1; 2N . D.
2; 1;1M .
Câu 18. Họ nguyên hàm của hàm số
sin
x
f
xe x là
A.
cos
x
F
xe xC
. B.
sin
x
F
xe xC
.
C.
cos
x
Fx e x C . D.

sin
x
Fx e x C .
Câu 19. Cho số phức
,zabiab
theo điều kiện

23 7 2220iz iz i. Tính Sab.
A. 3S . B. 4S  . C. 6S  . D. 2S .
Câu 20. Chọn khẳng định đúng?
A.
2
2
3
3
ln 9
x
x
dx C
.
B.
2
2
3
3
ln 3
x
x
dx C
.
Trang 3/6 – Mã đề 210
C.
21
2
3
3
21
x
x
dx C
x

.
D.
2
9
3
ln 3
x
x
dx C
.
Câu 21. Tìm hàm số
Fx
biết
Fx
là một nguyên hàm của hàm số
f
xx
và
11F
A.

11
2
2
Fx
x

.
B.

2
3
Fx xx .
C.

25
33
Fx xx
.
D.

21
33
Fx xx
.
Câu 22. Tìm số phức liên hợp của số phức
132zi i
A.
1zi
. B.
5zi
. C.
5zi
. D.
1zi
.
Câu 23. Cho số phức
12
23, 45ziz i . Tính
12
zz z.
A. 22zi . B. 22zi . C. 22zi . D. 22zi .
Câu 24. Véc tơ pháp tuyến của mặt phẳng 1
123
x
yz
là
A.

1
6;3;2n

. B.
2
6; 2;3n

. C.
2
3; 6; 2n

. D.
2
2;3;6n

.
Câu 25. Mệnh đề nào dưới đây sai?
A.
ddkfxxkfxx

với 0k . B.



d
f
xx fx
.
C.
ddd
f
xgx x fxx gxx



. D.
   
.d d.d
f
xgx x fx xgx x



.
Câu 26. Trong mặt phẳng
Oxy , điểm
3; 1M biểu diễn số phức
A. 13zi . B. 3zi . C. 13zi . D. 3zi.
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho 3OA k i

. Tọa độ của điểm
A
là:
A.

3;0; 1A . B.

1;0;3A . C.

1;3;0A . D.

3; 1;0A .
Câu 28. Trong không gian
Oxyz
phương trình nào được cho dưới đây là phương trình mặt phẳng

Oyz ?
A.
0
x
.
B. 0yz. C. zyz. D. 0yz.
Câu 29. Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị hàm số
53
yx x và trục hoành.
A.
13
6
S . B.
7
6
S . C.
1
6
S . D.
17
6
S .
Câu 30. Trong không gian
Oxyz
cho đường thẳng
313
:
211
xyz
d

 và mặt phẳng
(): 2 5 0Px yz .Tìm tọa độ giao điểm
M
của đường thẳng d và mặt phẳng ()
P
.
A.
1; 0; 4M
. B.
0;0;5M
. C.
5; 2; 2M 
. D.
3; 1; 3M 
.
Câu 31. Tập hợp các điểm biểu diễn các số phức z thảo mãn 22zizi là đường thẳng .
A. 4210xy. B. 4210xy. C. 4210xy. D. 4610xy.
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho điểm

2;1;1A và mặt phẳng
:2 2 1 0Pxyz .
Phương trình của mặt cầu tâm
A
và tiếp xúc với mặt phẳng
P
là
Trang 4/6 – Mã đề 210
A.

222
2119xyz. B.

222
2112xyz.
C.

222
2114xyz
.
D.

222
21136xyz
.
Câu 33. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
:2 10xyz

và
:2 4 2 0xymz

. Tìm m để hai mặt phẳng
và
song song với nhau.
A.
1m
. B. Không tồn tại
m
. C.
2m 
. D.
2m
.
Câu 34. Biết
1
2
0
21
dln2
1
x
xn
xm


, (với ,mn ). Tính Smn.
A.
1S
. B.
4S
. C.
1S 
. D.
5S 
.
Câu 35. Cho

3
1
d2fx x
và

3
1
d1
g
xx
. Tính
 
3
1
4 2019 dIfx gxx

A.
2025
.
B.
2019
.
C.
2021
.
D.
2027
.
Câu 36. Tính tích phân

1
0
2
x
Ie dx
.
A. 1Ie. B. 2Ie. C. 3Ie. D. 1Ie.
Câu 37.
Phần ảo của số phức
23zi
là :
A. 2. B. 3 . C. 3 . D. 3i .
Câu 38. Trong mặt phẳng tọa độ Oxy cho các điểm ,
A
B như hình vẽ bên.
Trung điểm của đoạn thẳng
A
B biểu diễn số phức
A. 12i . B.
1
2
2
i
.
C. 2 i . D.
1
2
2
i
.
Câu 39. Trong không gian Oxyz , cho đường thẳng
1
:24,
35
xt
dy tt
zt



. Hỏi d đi qua điểm nào dưới
đây?
A.

3; 6;8 . B.

1; 4; 5. C.

1; 2; 3 . D.

0;6;8 .
Câu 40. Trong không gian với hệ tọa độ Oxyz , cho hai mặt phẳng
:2 2 9 0Pxyz
và
:4 2 4 6 0Qxyz. Khoảng cách giữa hai mặt phẳng
P
và
Q bằng
A.
0 . B. 2. C. 1. D. 3.
Câu 41. Cho tích phân

9
2
d6fx x
. Tính tích phân

2
23
1
.1dIxfx x
.
A.
3I . B. 2I . C. 8I . D. 4I .
Trang 5/6 – Mã đề 210
Câu 42. Trong không gian với hệ tọa độ Oxyz , tìm trên trục
Oz
điểm
M
cách đều điểm
2;3;4A và
mặt phẳng
:2 3 17 0Pxyz.
A.
0;0; 3M
.
B.
0;0;3M
.
C.
0;0; 4M
.
D.
0;0;4M
.
Câu 43. Cho tích phân
2
0
.cos dIx xx
và đặt
2
ux , d cos dvxx . Mệnh đề nào sau đây là mệnh đề
đúng?
A.
2
0
0
.sin .sin dIx x x xx

. B.
2
0
0
.sin 2 .sin dIx x x xx

.
C.
2
0
0
.sin 2 .sin dIx x x xx

. D.
2
0
0
.sin .sin dIx x x xx

.
Câu 44. Trong không gian
Oxyz
, cho hai điểm
2; 1;3A 
và
0;3;1B
. Tọa độ trung điểm của đoạn
thẳng
A
B
là:
A.
2; 4; 2 . B.
2; 2; 4 . C.

1;1; 2 . D.

2; 4; 2 .
Câu 45. Cho số phức
12zi
. Tính z .
A.
5z
. B. 5z . C.
3z
. D.
2z
.
Câu 46. Cho hình phẳng

D được giới hạn bởi các đường 0x , 1
x
, 0y và 21yx. Thể tích
V
của khối tròn xoay tạo thành khi quay
D xung quanh trục
Ox
được tính theo công thức:
A.

1
0
21dVxx
. B.
1
0
21dVxx

. C.

1
0
21dVxx

. D.
1
0
21dVxx
.
Câu 47. Một chiếc máy bay chuyển động trên đường băng với vận tốc
2
10 /vt t tm s với t là thời
gian được tính bằng đơn vị giây kể từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận
tốc
200 /ms thì nó rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là:
A.

4000
3
m .
B.

500 m . C.

2500
3
m .
D.

2000 m .
Câu 48. Cho hàm số

f
x thỏa mãn

 
2
4
.'' 15 12,fx fxf x x xx
 và
001ff
.
Giá trị của

2
1f
bằng
A. 8 . B.
5
2
.
C. 10. D. 4.
Câu 49. Cho hai đường thẳng chéo nhau

1
42
:
3
xt
dyt t
z



1
1
:''
'
x
dytt
zt


. Phương trình mặt cầu
có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng
12
,ddlà:
A.

2
2
2
39
2
24
xyz




.
B.

2
2
2
33
2
22
xyz




.
C.

2
2
2
33
2
22
xyz




.
D.

2
2
2
39
2
24
xyz




.
Trang 6/6 – Mã đề 210
Câu 50. Trong mặt phẳng tọa độ

Oxy cho hình phẳng D giới hạn bởi các đường
2
2yx ,
2
8
x
y ,
6yx . Tính diện tích hình phẳng D nằm bên phải của trục tung.
A.
1075
192
S
. B.
135
64
S
. C.
185
24
S
. D.
335
96
S
.
----- HẾT -----
Trang 13/1 – Mã đề 210
SỞ GIÁO DỤC VÀ ĐÀO TẠO
BẾN TRE
MÃ ĐỀ 210
ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2018 - 2019
MÔN: TOÁN HỌC - LỚP: 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Câu 1. Cho các số phức
12
13; 53ziz i
. Tìm điểm

;
M
xy biểu diễn số phức
3
z
, biết rằng trong
mặt phẳng phức điểm
M
nằm trên đường thẳng 210xy và môđun của số phức
32 1
32wzz z
đạt giá trị nhỏ nhất.
A.
31
;
55
M



.
B.
31
;
55
M



.
C.
31
;
55
M



.
D.
31
;
55
M




.
Lời giải
Chọn A
Do
M
nằm trên đường thẳng 210xy nên
21;
M
yy .
Điểm

;
M
xy biểu diễn số phức
3
z
3
21zxyi y yi .
Ta có:
32 1
32321 53213631wzz z y yi i i y y i  

.

2
2
2
1465
63135.
5255
wy y y

 



.
Dấu
"" xảy ra
1
5
y
3
5
x.
Vậy
31
;
55
M



.
Câu 2. Trong không gian Oxyz cho
1; 1; 2 , 2;1; 1AB và mặt phẳng
:10Pxyz. Mặt phẳng
Q chứa ,
A
B và vuông góc với mặt phẳng

P
. Mặt phẳng

Q có phương trình là:
A. 20xyz. B. 3 2 3 0xyz. C. 3 2 3 0xyz. D. 0xy .
Lời giải
Chọn B
Ta có:
1; 2; 1AB 

và
1;1;1
P
n

là một véctơ pháp tuyến của mặt phẳng

P
.
Gọi
0
Q
n

là một véctơ pháp tuyến của mặt phẳng
Q
.
Do mặt phẳng
Q
chứa ,
A
B và vuông góc với mặt phẳng
P
nên:

// , 3; 2; 1
Q
QP
QP
nAB
nABn
nn



 
 
 
.
Chọn
3; 2; 1
Q
n 

.
Phương trình mặt phẳng
Q
đi qua
1; 1; 2A
, có một véctơ pháp tuyến
3; 2; 1
Q
n 

là:
:312 1120Qx y z
30:3 2xyzQ  .
Câu 3. Trong không gian
Oxyz
cho mặt cầu

S có phương trình:
222
24690xyz xyz.
Mặt cầu

S
có tâm I và bán kính
R
là:
A.

1; 2; 3I  và 5R . B.
1; 2; 3I và 5R .
Trang 13/2 – Mã đề 210
C.

1; 2; 3I và 5R . D.

1; 2; 3I  và 5R .
Lời giải
Chọn B
Viết lại phương trình mặt cầu

222
:1 2 35Sx y z .
Mặt cầu

S
có tâm

1; 2; 3I
và
5R .
Câu 4. Gọi
1
z
,
2
z
là các nghiệm của phương trình
2
490zz
. Giả sử
,
M
N là các điểm biểu diễn
hình học của
1
z ,
2
z trên mặt phẳng phức. Khi đó độ dài của
M
N là
A. 5 . B. 4 . C. 25. D. 5.
Lời giải
Chọn
C
Ta có
2
490zz
1
2
25
25
zi
zi


nên
2; 5M
và
2; 5N
.
Suy ra
25MN .
Câu 5. Trong không gian Oxyz , cho mặt cầu
222
:2460Sx y z x y z. Đường tròn giao tuyến
của

S
với mặt phẳng

Oxy
có bán kính là
A. 6r . B.
14r
. C.
3r
. D. 5r .
Lời giải
Chọn
D
Mặt cầu

S
có tâm
1; 2; 3I
và bán kính 14R .
Hình chiếu của I lên mặt phẳng

Oxy là
1; 2; 0H .
Do đó, khoảng cách từ tâm
I đến mặt phẳng
Oxy
là
;3dI Oxy IH
.
Đường tròn giao tuyến có bán kính là
22
5rRd.
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho điểm
1; 2; 3M . Hình chiếu của
M
trên trục Oy là:
A.
0; 2; 0Q . B.

0;0;3S . C.
1; 0; 0R . D.
1; 0; 3P .
Lời giải
Chọn A.
Áp dụng lý thuyết: Điểm
000
;;
M
xyz có hình chiếu vuông góc lên các trục , , Ox Oy Oz lần
lượt là
0
;0;0 ,
Ox
Mx
00
0; ;0 , 0;0;
Oy Oz
M
yM z
. Do đó hình chiếu vuông góc của
1; 2; 3M
trên trục
Oy là
0; 2; 0 .
Câu 7. Tìm số phức z
biết:
1150.iz i
A.
32zi
.
B.
32zi
. C.
32zi
. D.
32zi
.
Lời giải
Chọn B.
Ta có:

15
1150
1
i
iz i z
i

2
22
15 1
155
32.
12
ii
iii
i
i



Câu 8. Trong mặt phẳng phức, cho ba điểm , ,
A
BC lần lượt biểu diễn ba số phức
1
1zi,

2
2
1zi
và
3
zai. Để tam giác
BC vuông tại
B
thì a bằng:
Trang 13/3 – Mã đề 210
A. 3 . B.
2
. C. 3 . D.
4
.
Lời giải
Chọn A.
Ta có
1
11;1ziA

2
2
12 0;2ziiB
3
;1zaiCa . Nên
1; 1AB 

,
;3BC a

.
Để tam giác
A
BC
vuông tại
B
thì
.0AB BC
 
1. 1. 3 0a
3a
.
Câu 9. Tính môđun của số phức
2019
2zii .
A. 5z . B. 2z . C. 22z . D. 10z .
Lời giải
Chọn B.
Ta có
2019
22zii
Nên
2z
.
Câu 10. Gọi
12
,zz
là hai nghiệm phức của phương trình
2
90z 
. Tính
12
zz .
A.
12
3zz. B.
12
4zz i. C.
12
9zz i. D.
12
0zz.
Lời giải
Chọn D.
Theo định lý Vi-ét ta có
12
0zz
Nên
12 12
00zz zz.
Câu 11. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm

2;0;0 , 0;3;1 , 1;4;2ABC
. Độ dài
đường cao từ đỉnh
A
của tam giác
A
BC .
A. 3. B.
3
2
.
C. 2 . D. 6.
Lời giải
Chọn C.
Ta có :
2;3;1 ; 3;4;2AB AC 

,
1;1;1BC 


, 2;1;1AB AC



 
và 3BC .
1
,
2
ABC
SABAC




6
2
.
Gọi
A
H là đường cao của tam giác
A
BC
Khi đó:
2
2
ABC
S
AH
CB

.
Câu 12. Trong không gian Oxyz , cho các véc tơ
1; 2; 3a
,

2; 4;1b 
,
1; 3; 4c 
. Véc tơ
235vabc

có toạ độ là:
A.
3; 7; 23v
. B.
23;7;3v
. C.
7;3;23v
. D.
7;23;3v
.
Lời giải
Chọn A.
Có
22;4;6a
,
36;12;3b
,

55;15;20c 
, nên
235 3;7;23vabc

.
Câu 13. Tìm họ nguyên hàm của hàm số

4
2
23x
fx
x
.
Trang 13/4 – Mã đề 210
A.
3
3
2
x
C
x
. B.
3
23
3
x
C
x
.
C.
3
23
32
x
C
x
.
D.
3
23
3
x
C
x
.
Lời giải
Chọn D.
Có

4
22
2
23
23.
x
f
xxx
x

,


3
22
23
d23.d
3
x
f
xx x x x C
x


.
Câu 14. Trong không gian Oxyz , cho điểm
4;0;0M và đường thẳng
1
:23
2
x
t
yt
zt



. Gọi
;;Habc
là chân hình chiếu từ
M
lên . Tính abc.
A. 5 . B. 7 . C. 3 . D. 1 .
Lời giải
Chọn D.
Ta gọi
1;23;2Ht tt
5;23;2
M
Httt

Do
H
là chân hình chiếu từ
M
lên nên ta có
11
.0 5 6940
14
d
MH u t t t t 

Vậy
35 22
;;
14 14 14
H



1abc
.
Câu 15.
Trong không gian Oxyz , đường thẳng nào sau đây nhận
2;3; 4u 
làm véc tơ chỉ phương?
(với
t )
A.
12
23
24
x
t
yt
zt



.
B.
2
33
4
x
t
yt
zt



.
C.
2
35
43
x
t
yt
zt



.
D.
12
33
24
x
t
yt
zt



.
Lời giải
Chọn D.
Câu 16.
Trong không gian Oxyz , cho các điểm
1; 0; 1 , 2; 2; 3IA. Mặt cầu

S tâm I và đi qua điểm
A
có phương trình là
A.

22
2
113xyz
.
B.
 
22
2
119xyz
.
C.

22
2
119xyz. D.
 
22
2
113xyz.
Lời giải
Chọn B
Bán kính mặt cầu: 3RIA.
Phương trình mặt cầu:
 
22
2
119xyz
.
Câu 17. Trong không gian Oxyz , cho mặt phẳng
:2 1 0Pxyz
. Điểm nào dưới đây thuộc mặt
phẳng
P
?
A.
1; 3; 4Q  . B.

1; 2; 0P . C.
0;1; 2N . D.
2; 1;1M .
Lời giải
Chọn A
Trang 13/5 – Mã đề 210
Thay tọa độ các điểm Q ,
P
,
N
,
M
lần lượt vào phương trình
:2 1 0Pxyz ta được:
2.1 3 4 1 0 (đúng) nên

QP .
2.1 2 1 0
(sai) nên
P
P
.
1210
(sai) nên

NP
.

2.1 1 1 1 0 (sai) nên
M
P .
Câu 18. Họ nguyên hàm của hàm số
sin
x
f
xe x là
A.
cos
x
Fx e x C
. B.
sin
x
Fx e x C
.
C.
cos
x
Fx e x C
. D.

sin
x
Fx e x C
.
Lời giải
Chọn C
Ta có:
sin sin cos
xx x
F x e x dx e dx xdx e x C

.
Câu 19. Cho số phức
,zabiab theo điều kiện

23 7 2220iz iz i. Tính Sab.
A. 3S . B. 4S  . C. 6S  . D. 2S .
Lời giải
Chọn B
Ta có:
23 7 2220iz iz i
23 7 2220i a bi i a bi i
2 2 3 3 7 7 22 20abiaibaib i
24 210 2220ab b ai i
2422 1
210 20 5
ab a
ba b






Vậy
4Sab.
Câu 20. Chọn khẳng định đúng?
A.
2
2
3
3
ln 9
x
x
dx C
.
B.
2
2
3
3
ln 3
x
x
dx C
.
C.
21
2
3
3
21
x
x
dx C
x

.
D.
2
9
3
ln 3
x
x
dx C
.
Lời giải
Chọn A
2
2
3
39
ln 9
x
xx
dx dx C

.
Câu 21. Tìm hàm số
Fx biết
Fx là một nguyên hàm của hàm số
f
xx và
11F
A.

11
2
2
Fx
x

.
B.

2
3
Fx xx .
C.

25
33
Fx xx
.
D.

21
33
Fx xx
.
Lời giải
Chọn D
Trang 13/6 – Mã đề 210
Ta có

2
3
Fx xdx x x C
.
Ta có

21
11 1
33
FCC 
, suy ra

21
33
Fx xx
.
Câu 22.
Tìm số phức liên hợp của số phức
132zi i
A. 1zi. B. 5zi. C. 5zi. D. 1zi.
Lời giải
Chọn B
Ta có
1325 5zi i izi
.
Câu 23.
Cho số phức
12
23, 45ziz i . Tính
12
zz z.
A.
22zi
. B.
22zi
. C.
22zi
. D.
22zi
.
Lời giải
Chọn D
Ta có 23 45 22zii i .
Câu 24. Véc tơ pháp tuyến của mặt phẳng 1
123
x
yz
là
A.

1
6;3;2n

. B.
2
6; 2;3n

. C.
2
3; 6; 2n

. D.
2
2;3;6n

.
Lời giải
Chọn
D
Ta có
163260
123
xyz
xyz

nên véc tơ pháp tuyến của mặt phẳng
1
123
x
yz

là
1
6;3;2n

.
Câu 25. Mệnh đề nào dưới đây sai?
A.
ddkfxxkfxx

với 0k . B.



d
f
xx fx
.
C.
ddd
f
xgx x fxx gxx



. D.
   
.d d.d
f
xgx x fx xgx x



.
Lời giải
Chọn
D
Mệnh đề
.d d.d
f
xgx x fx xgx x



sai.
Câu 26. Trong mặt phẳng
Oxy , điểm
3; 1M biểu diễn số phức
A. 13zi . B. 3zi . C. 13zi . D. 3zi.
Lời giải
Chọn
D
Trong mặt phẳng
Oxy
, điểm
3; 1M
biểu diễn số phức 3zi.
Câu 27.
Trong không gian với hệ tọa độ Oxyz , cho 3OA k i

. Tọa độ của điểm
A
là:
A.

3;0; 1A . B.

1;0;3A . C.

1;3;0A . D.
3; 1;0A .
Lời giải
Chọn
B
Tọa độ của điểm
A
là

1;0;3A .
Trang 13/7 – Mã đề 210
Câu 28. Trong không gian
Oxyz
phương trình nào được cho dưới đây là phương trình mặt phẳng
Oyz ?
A. 0x . B. 0yz. C. zyz. D. 0yz.
Lời giải
Chọn A
Phương trình mặt phẳng

Oyz
qua O có véc tơ pháp tuyến là
1; 0; 0i
Nên phương trình mặt phẳng

Oyz :
0x
.
Câu 29. Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị hàm số
53
yx x và trục hoành.
A.
13
6
S . B.
7
6
S . C.
1
6
S . D.
17
6
S .
Lời giải
Chọn C
Phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành là:
53
0
0
1
x
xx
x


Diện tích
1
53
1
1
6
Sxxdx

Câu 30. Trong không gian Oxyz cho đường thẳng
313
:
211
xyz
d


và mặt phẳng
(): 2 5 0Px yz .Tìm tọa độ giao điểm
M
của đường thẳng d và mặt phẳng ()
P
.
A.

1; 0; 4M
. B.

0;0;5M
. C.

5; 2; 2M 
. D.

3; 1; 3M 
.
Lời giải
Chọn A
Tọa độ điểm
M
là nghiệm của hệ phương trình

21 1
29 0 1;0;4
250 4
xy x
xz y M
xyz z








.
Câu 31. Tập hợp các điểm biểu diễn các số phức z thảo mãn 22zizi là đường thẳng .
A. 4210xy. B. 4210xy. C. 4210xy. D. 4610xy.
Lời giải
Chọn C
Gọi
2
|, , 1zxyixy i .Ta có
222 2
22(2)(1)(2)(2)(1) (2)zizix yixyi x y xy    
4210xy
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho điểm

2;1;1A và mặt phẳng
:2 2 1 0Pxyz .
Phương trình của mặt cầu tâm
A
và tiếp xúc với mặt phẳng
P
là
A.

222
2119xyz. B.

222
2112xyz.
C.

222
2114xyz. D.

222
21136xyz.
Lời giải
Trang 13/8 – Mã đề 210
Chọn C
Mặt cầu tâm

2;1;1A
và tiếp xúc với mặt phẳng

P
có



2
22
2.2 1 2.1 1
,2
212
RdAP



.
Vậy mặt cầu cần tìm có phương trình

222
:2 1 14Sx y z.
Câu 33. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
:2 10xyz
 và
:2 4 2 0xymz

. Tìm
m
để hai mặt phẳng
và
song song với nhau.
A.
1m
. B. Không tồn tại
m
. C.
2m 
. D.
2m
.
Lời giải
Chọn B
Mặt phẳng
và
song song với nhau khi
24 2
12 1 1
m


2
2
m
m
hệ vô nghiệm.
Vậy không tồn tại
m thỏa mãn yêu cầu bài toán.
Câu 34. Biết
1
2
0
21
dln2
1
x
xn
xm


, (với ,mn ). Tính Smn.
A. 1S . B. 4S . C. 1S  . D. 5S  .
Lời giải
Chọn A
Ta có
1
2
11 1
2 2
00 0
0
11
211
dd1dln1ln2
11 12 2
x
xx
xxxxxx
xx x











.
Suy ra
2
1
m
n

. Vậy
1Smn.
Câu 35. Cho

3
1
d2fx x
và

3
1
d1
g
xx
. Tính
 
3
1
4 2019 dIfx gxx


A. 2025 . B. 2019 . C. 2021. D. 2027 .
Lời giải
Chọn D
   
333
111
4 2019 d 4 d 2019 d 4.2 2019.1 2027Ifx gxxfxx gxx



.
Câu 36. Tính tích phân

1
0
2
x
Ie dx
.
A. 1Ie. B. 2Ie. C. 3Ie. D. 1Ie.
Lời giải
Chọn A
Ta có:

1
1
0
0
221
xx
Ie dxexe
.
Trang 13/9 – Mã đề 210
Câu 37. Phần ảo của số phức 23zi là :
A.
2
. B.
3
. C.
3
. D.
3i
.
Lời giải
Chọn C
Câu 38.
Trong mặt phẳng tọa độ Oxy cho các điểm ,
A
B như hình vẽ bên.
Trung điểm của đoạn thẳng
A
B biểu diễn số phức
A.
12i
. B.
1
2
2
i .
C.
2 i
. D.
1
2
2
i .
Lời giải
Chọn B
Ta có:
2;1 , 1;3AB
trung điểm của đoạn thẳng
A
B là
1
;2
2
I



biểu diễn số phức
1
2
2
i .
Câu 39. Trong không gian Oxyz , cho đường thẳng
1
:24,
35
xt
dy tt
zt



. Hỏi d đi qua điểm nào dưới
đây?
A.

3; 6;8 . B.

1; 4; 5. C.

1; 2; 3 . D.

0;6;8 .
Lời giải
Chọn D
Chọn 1t  ta có d đi qua điểm

0;6;8
.
Câu 40. Trong không gian với hệ tọa độ Oxyz , cho hai mặt phẳng
:2 2 9 0Pxyz và

:4 2 4 6 0Qxyz. Khoảng cách giữa hai mặt phẳng

P
và
Q bằng
A.
0 . B. 2 . C. 1. D. 3.
Lời giải
Chọn B
Lấy
0; 3;0 :4 2 4 6 0AQxyz .
Dễ thấy
//
P
Q suy ra
,,2dP Q dAP.
Câu 41.
Cho tích phân

9
2
d6fx x
. Tính tích phân

2
23
1
.1dIxfx x
.
A.
3I . B. 2I . C. 8I . D. 4I .
Lời giải
Chọn B
Đặt
32
1d3dtx t xx .
Trang 13/10 – Mã đề 210
Đổi cận: 12
x
t và 29
x
t.
Vậy

2
23
1
.1dIxfx x

9
2
1
d
3
f
tt
2 .
Câu 42. Trong không gian với hệ tọa độ
Oxyz
, tìm trên trục
Oz
điểm
M
cách đều điểm
2;3;4A
và
mặt phẳng
:2 3 17 0Pxyz
.
A.
0;0; 3M
. B.
0;0;3M
. C.
0;0; 4M
. D.
0;0;4M
.
Lời giải
Chọn B
Gọi
0;0;
M
mOz .
Theo đề:
;
A
MdMP

2
17
13 4
14
m
m

22
14 8 29 34 289mm m m
2
13 78 117 0mm 3m.
Câu 43. Cho tích phân
2
0
.cos dIx xx
và đặt
2
ux
, dcosdvxx . Mệnh đề nào sau đây là mệnh đề
đúng?
A.
2
0
0
.sin .sin dIx x x xx

. B.
2
0
0
.sin 2 .sin dIx x x xx

.
C.
2
0
0
.sin 2 .sin dIx x x xx

. D.
2
0
0
.sin .sin dIx x x xx

.
Lời giải
Chọn C
Đặt
2
d2d
sin
dcosd
uxx
ux
vx
vxx

.
Vậy
2
0
0
.sin 2 .sin dIx x x xx

.
Câu 44. Trong không gian Oxyz , cho hai điểm
2; 1;3A  và
0;3;1B . Tọa độ trung điểm của đoạn
thẳng
A
B là:
A.
2; 4; 2
.
B.
2; 2; 4
.
C.

1; 1; 2
.
D.

2; 4; 2
.
Lời giải
Chọn C
Gọi I là trung điểm của
A
B . Khi đó tọa độ điểm I là:

1
2; 1; 3 , 1; 1; 1 1; 2; 2 .
'1
t
AB AB
t



1;1; 2I .
Vậy chọn
C.
Câu 45. Cho số phức
12zi
. Tính z .
A. 5z . B. 5z . C. 3z . D. 2z .
Lời giải
Chọn B
Trang 13/11 – Mã đề 210
Ta có

2
2
12 5z .
Câu 46. Cho hình phẳng
D
được giới hạn bởi các đường
0x
,
1
x
, 0y và 21yx. Thể tích
V
của khối tròn xoay tạo thành khi quay
D
xung quanh trục
Ox
được tính theo công thức:
A.

1
0
21dVxx
. B.
1
0
21dVxx

. C.

1
0
21dVxx

. D.
1
0
21dVxx
.
Lời giải
Chọn C
Thể tích
V
của khối tròn xoay tạo thành khi quay
D xung quanh trục
Ox
là:


11
2
00
21d 21dVxxxx



.
Câu 47.
Một chiếc máy bay chuyển động trên đường băng với vận tốc
2
10 /vt t tm s với t là thời
gian được tính bằng đơn vị giây kể từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận
tốc
200 /ms thì nó rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là:
A.

4000
3
m .
B.

500 m . C.

2500
3
m .
D.

2000 m .
Lời giải
Chọn C
Khi 200v ta suy ra
2
10 200tt
10t
s
.
Máy bay di chuyển trên đường băng từ thời điểm
0ts tới thời điểm
10ts
Nên suy ra quãng đường di chuyển trên đường băng là:


10
2
0
2500
10 d
3
St tt m
.
Câu 48.
Cho hàm số

f
x thỏa mãn

 
2
4
.'' 15 12,fx fxf x x xx
 và
001ff
.
Giá trị của
2
1f
bằng
A.
8
. B.
5
2
.
C.
10
. D. 4.
Lời giải
Chọn D.
Ta có:

 
2
4
.'' 15 12
f
xfxfxxx

 
4
.1512
f
xfx x x


52
.36,fxfx x x Cx

Mà
001ff
 nên
100 1CC
52
.361fxfx x x
 hay

252
1
361
2
fx x x




263
11
2
22
f
xxxxM
Mà

1
01
2
f
M
 
22
111
121 14
222
ff
.
Trang 13/12 – Mã đề 210
Câu 49. Cho hai đường thẳng chéo nhau

1
42
:
3
xt
dyt t
z



1
1
:''
'
x
dytt
zt


. Phương trình mặt cầu
có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng
12
,dd
là:
A.

2
2
2
39
2
24
xyz




.
B.

2
2
2
33
2
22
xyz




.
C.

2
2
2
33
2
22
xyz




.
D.

2
2
2
39
2
24
xyz




.
Lời giải
Chọn D

11
42
:
3
xt
dyt t d
z


có vectơ chỉ phương
1
2;1; 0u 

22
1
:''
'
x
dytt d
zt


vecctơ chỉ phương
2
0;1; 1u 
Gọi
A
B là đoạn vuông góc chung của
12
,dd với
12
; .
A
dBd
12
(4 2 ; ; 3); (1; '; ')
A
dA tt BdBtt
32 ; ' ; '3AB t t t t

A
B
là đoạn vuông góc chung của
12
,dd

1
2
.0
23.2 ' 0
2' 3
.0
AB u
ttt
tt
AB u








1
2; 1; 3 , 1; 1;1 1; 2; 2 .
'1
t
AB AB
t



Mặt cầu

S
có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng
12
,dd
và chỉ khi
A
B là đường kính của mặt cầu
S

S có tâm là trung điểm I của
A
B ,
3
;0;2
2
I



và bán kính
22
2213
.
222
AB
R


Vậy phương trình mặt cầu

S
:

2
2
2
39
2
24
xyz




.
Câu 50. Trong mặt phẳng tọa độ
Oxy
cho hình phẳng D giới hạn bởi các đường
2
2yx ,
2
8
x
y ,
6yx
. Tính diện tích hình phẳng
D
nằm bên phải của trục tung.
A.
1075
192
S .
B.
135
64
S .
C.
185
24
S .
D.
335
96
S .
Lời giải
Chọn C.
Trang 13/13 – Mã đề 210
x
y
4
2
3
O
Phương trình hoành độ giao điểm giữa các đường cong
2
2
20
8
x
xx.
02
3
26
2
x
xx x

.
2
0
64
8
x
x
xx
 .
Khi đó ta xác định được hình phẳng trên mặt phẳng
Oxy .
3
4
22
2
2
3
0
2
185
2d 6d
8824
xx
Sx xx x





.
| 1/19
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2018 - 2019 BẾN TRE
MÔN: TOÁN HỌC - LỚP: 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề) MÃ ĐỀ 210
Câu 1. Cho các số phức z  1 3i; z  5
  3i . Tìm điểm M  ;
x y biểu diễn số phức z , biết rằng trong 1 2 3
mặt phẳng phức điểm M nằm trên đường thẳng x  2y 1  0 và môđun của số phức
w  3z z  2z đạt giá trị nhỏ nhất. 3 2 1  3 1   3 1   3 1   3 1  A. M  ;   . B. M ;   . C. M ;   . D. M  ;   .  5 5   5 5   5 5   5 5 
Câu 2. Trong không gian Oxyz cho A1;1;2, B2;1; 
1 và mặt phẳng P : x y z 1  0. Mặt phẳng Q chứa ,
A B và vuông góc với mặt phẳng P . Mặt phẳng Q có phương trình là:
A. x y z  2  0 .
B. 3x  2y z  3  0 . C. 3x  2y z  3  0 . D.x y  0 .
Câu 3. Trong không gian Oxyz cho mặt cầu S  có phương trình: 2 2 2
x y z  2x  4 y  6z  9  0 .
Mặt cầu S  có tâm I và bán kính R là:
A. I 1;2;3 và R  5. B. I 1; 2  ;3 và R  5 .
C. I 1;2;3 và R  5. D. I  1
 ;2;3 và R  5 .
Câu 4. Gọi z , z là các nghiệm của phương trình 2
z  4z  9  0 . Giả sử M , N là các điểm biểu diễn 1 2
hình học của z , z trên mặt phẳng phức. Khi đó độ dài của MN là 1 2 A. 5 . B. 4 . C. 2 5 . D. 5 .
Câu 5. Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x y z  2x  4 y  6z  0 . Đường tròn giao tuyến
của S  với mặt phẳng Oxy có bán kính là A. r  6 . B. r  14 . C. r  3. D. r  5 .
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;2;3 . Hình chiếu của M trên trục Oy là:
A. Q 0;2;0 .
B. S 0;0;3 .
C. R 1;0;0.
D. P 1;0;3 .
Câu 7. Tìm số phức z biết: 1 iz 1 5i  0.
A. z  3  2i .
B. z  3  2i .
C. z  3  2i .
D. z  3  2i .
Câu 8. Trong mặt phẳng phức, cho ba điểm ,
A B, C lần lượt biểu diễn ba số phức z  1 i , z  1 i 2  2 1
và z a i . Để tam giác ABC vuông tại B thì a bằng: 3 A. 3 . B. 2  . C. 3 . D. 4  .
Câu 9. Tính môđun của số phức 2019
z  2  i i . A. z  5 . B. z  2 . C. z  2 2 . D. z  10 .
Câu 10. Gọi z , z là hai nghiệm phức của phương trình 2
z  9  0 . Tính z z . 1 2 1 2
A. z z  3 .
B. z z  4i .
C. z z  9i .
D. z z  0 . 1 2 1 2 1 2 1 2
Câu 11. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A2;0;0, B0;3; 
1 ,C 1;4;2 . Độ dài
đường cao từ đỉnh A của tam giác ABC .
Trang 1/6 – Mã đề 210 3 A. 3 . B. . C. 2 . D. 6 . 2   
Câu 12. Trong không gian Oxyz , cho các véc tơ a  1;2;3 , b   2;  4;  1 , c   1;  3;4 . Véc tơ    
v  2a  3b  5c có toạ độ là:    
A. v  3;7;23 .
B. v  23;7;3 .
C. v  7;3;23 .
D. v  7;23;3 . 4 2x  3
Câu 13. Tìm họ nguyên hàm của hàm số f x  . 2 x 3 3 2x 3 3 2x 3 3 2x 3 A. 3 2x   C . B.   C . C.   C . D.   C . x 3 x 3 2x 3 xx  1 t
Câu 14. Trong không gian Oxyz , cho điểm M  4;
 0;0 và đường thẳng  : y  2
  3t . Gọi H a; ; b c z  2  t
là chân hình chiếu từ M lên  . Tính a b c . A. 5 . B. 7 . C. 3  . D. 1  .
Câu 15. Trong không gian Oxyz , đường thẳng nào sau đây nhận u  2;3; 4
  làm véc tơ chỉ phương? (với t   ) x 1 2tx  2  tx  2  tx 1 2t    
A. y  2  3t .
B. y  3 3t .
C. y  3 5t .
D. y  3 3t .
z  2  4t     z  4   tz  4   3tz  2  4t
Câu 16. Trong không gian Oxyz , cho các điểm I 1;0;  1 , A2;2; 3
 . Mặt cầu S  tâm I và đi qua điểm
A có phương trình là
A. x  2  y   z  2 2 1 1  3 .
B. x  2  y   z  2 2 1 1  9 .
C. x  2  y   z  2 2 1 1  9 .
D. x  2  y   z  2 2 1 1  3 .
Câu 17. Trong không gian Oxyz , cho mặt phẳng P : 2x y z 1  0 . Điểm nào dưới đây thuộc mặt phẳng P ? A. Q 1; 3  ; 4   . B. P 1; 2  ;0 . C. N 0;1; 2   . D. M 2; 1  ;  1 .
Câu 18. Họ nguyên hàm của hàm số   x
f x e  sin x là A.   x
F x e  cos x C . B.   x
F x e  sin x C . C.   x
F x e  cos x C . D.   x
F x e  sin x C .
Câu 19. Cho số phức z a bi a,b   theo điều kiện 2  3iz  7iz  22  20i . Tính S a b . A. S  3. B. S  4  . C. S  6  . D. S  2 .
Câu 20. Chọn khẳng định đúng? 2 2 x 3 x x 3 x A. 2 3 dx   C  . B. 2 3 dx   C  . ln 9 ln 3
Trang 2/6 – Mã đề 210 2 x 1  x 9x x 3 C. 2 3 dx   C  . D. 2 3 dx   C  . 2x 1 ln 3
Câu 21. Tìm hàm số F x biết F x là một nguyên hàm của hàm số f x  x và F   1  1
A. F x 1 1   .
B. F x 2  x x . 2 x 2 3
C. F x 2 5  x x  .
D. F x 2 1  x x  . 3 3 3 3
Câu 22. Tìm số phức liên hợp của số phức z  1 i3  2i
A. z  1 i .
B. z  5  i .
C. z  5  i .
D. z  1 i .
Câu 23. Cho số phức z  2  3i, z  4
  5i . Tính z z z . 1 2 1 2
A. z  2  2i . B. z  2   2i .
C. z  2  2i . D. z  2   2i . x y z
Câu 24. Véc tơ pháp tuyến của mặt phẳng    1là 1 2 3    
A. n  6;3; 2 .
B. n  6;2;3 .
C. n  3;6;2 .
D. n  2;3;6 . 2   2   2   1  
Câu 25. Mệnh đề nào dưới đây sai?  A. kf
 xdx k f
 xdx với k  0 . B.f
 xdx  f x. C.f
 x gxdx f
 xdxg
 xdx. D.f
 x.gxdx f
 xd .x g  xdx.
Câu 26. Trong mặt phẳng Oxy , điểm M 3;  1 biểu diễn số phức A. z  1   3i . B. z  3   i .
C. z  1 3i .
D. z  3  i .   
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho OA  3k i . Tọa độ của điểm A là:
A. A3;0;  1 . B. A 1;  0;3. C. A 1;  3;0.
D. A3;1;0 .
Câu 28. Trong không gian Oxyz phương trình nào được cho dưới đây là phương trình mặt phẳng Oyz ? A. x  0 .
B. y z  0 .
C. z y z .
D. y z  0 .
Câu 29. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 5 3
y x x và trục hoành. 13 7 1 17 A. S  . B. S  . C. S  . D. S  . 6 6 6 6 x  3 y 1 z  3
Câu 30. Trong không gian Oxyz cho đường thẳng d :   và mặt phẳng 2 1 1
(P) : x  2y z  5  0 .Tìm tọa độ giao điểm M của đường thẳng d và mặt phẳng (P) . A. M  1;  0;4 .
B. M 0;0;5 . C. M  5;  2  ;2 . D. M  3;  1  ;3 .
Câu 31. Tập hợp các điểm biểu diễn các số phức z thảo mãn z  2  i z  2i là đường thẳng .
A. 4x  2y 1  0 .
B. 4x  2y 1  0 .
C. 4x  2y 1  0 .
D. 4x  6y 1  0 .
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho điểm A2;1; 
1 và mặt phẳng P : 2x y  2z 1  0 .
Phương trình của mặt cầu tâm A và tiếp xúc với mặt phẳng P là
Trang 3/6 – Mã đề 210
A. x  2   y  2   z  2 2 1 1  9 .
B. x  2   y  2   z  2 2 1 1  2 .
C. x  2   y  2   z  2 2 1 1  4 .
D. x  2   y  2   z  2 2 1 1  36 .
Câu 33. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng   : x  2y z 1  0 và
 : 2x  4y mz  2  0. Tìm m để hai mặt phẳng   và   song song với nhau. A. m  1.
B. Không tồn tại m . C. m  2  . D. m  2 . 1 2 x  2 1  Câu 34. Biết dx   n ln 2 
, (với m, n   ). Tính S m n . x 1 m 0 A. S  1. B. S  4 . C. S  1. D. S  5. 3 3 3 Câu 35. Cho f
 xdx  2 và g
 xdx 1. Tính I  4 f
 x 2019gxdx  1 1 1 A. 2025 . B. 2019 . C. 2021. D. 2027 . 1
Câu 36. Tính tích phân   x I e  2dx . 0
A. I e 1.
B. I e  2 .
C. I e  3 .
D. I e 1.
Câu 37. Phần ảo của số phức z  2  3i là : A. 2 . B. 3 . C. 3  . D. 3  i .
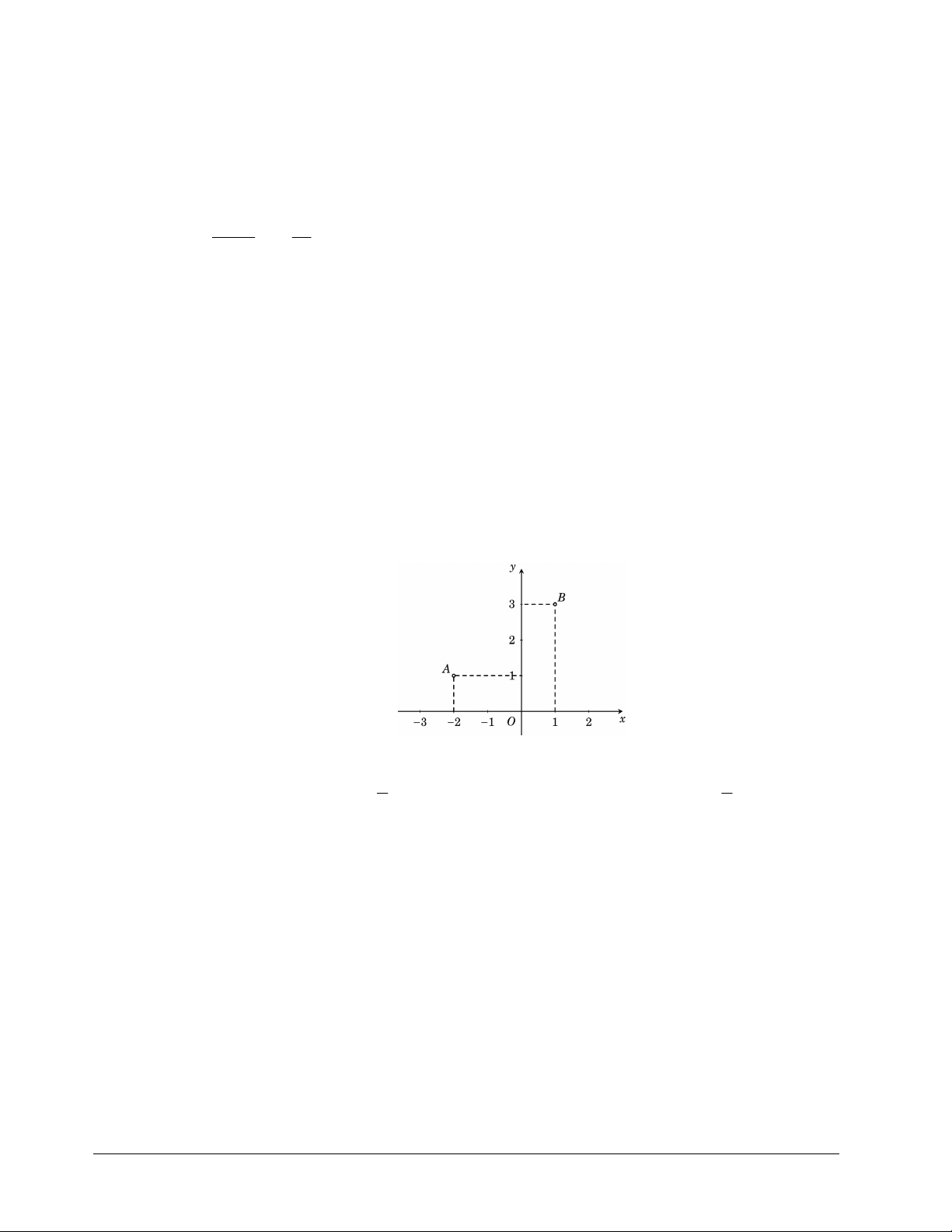
Câu 38. Trong mặt phẳng tọa độ Oxy cho các điểm ,
A B như hình vẽ bên.
Trung điểm của đoạn thẳng AB biểu diễn số phức 1 1 A. 1   2i . B.   2i .
C. 2  i . D. 2  i . 2 2 x 1 t
Câu 39. Trong không gian Oxyz , cho đường thẳng d : y  2  4t ,t  . Hỏi d đi qua điểm nào dưới z  35t  đây? A. 3;6;8 . B. 1; 4  ; 5   . C.  1  ;2;3. D. 0;6;8.
Câu 40. Trong không gian với hệ tọa độ Oxyz , cho hai mặt phẳng P :2x y  2z  9  0 và
Q:4x  2y  4z 6  0. Khoảng cách giữa hai mặt phẳng P và Q bằng A. 0 . B. 2 . C. 1. D. 3 . 9 2
Câu 41. Cho tích phân f
 xdx  6. Tính tích phân 2
I x . f  3 x   1dx . 2 1 A. I  3 . B. I  2 . C. I  8 . D. I  4 .
Trang 4/6 – Mã đề 210
Câu 42. Trong không gian với hệ tọa độ Oxyz , tìm trên trục Oz điểm M cách đều điểm A2;3;4 và
mặt phẳng P:2x  3y z 17  0 .
A. M 0;0; 3 .
B. M 0;0;3 .
C. M 0;0; 4 .
D. M 0;0;4. 
Câu 43. Cho tích phân 2
I x .cosx dx  và đặt 2
u x , dv  cos x dx . Mệnh đề nào sau đây là mệnh đề 0 đúng?     A. 2
I x .sin x x.sin x dx  . B. 2
I x .sin x  2 x.sin x dx  . 0 0 0 0     C. 2
I x .sin x  2 x.sin x dx  . D. 2
I x .sin x x.sin x dx  . 0 0 0 0
Câu 44. Trong không gian Oxyz , cho hai điểm A 2;  1
 ;3 và B0;3; 
1 . Tọa độ trung điểm của đoạn thẳng AB là: A. 2;4; 2   . B.  2;  2;4 . C.  1  ;1;2 . D.  2;  4  ;2 .
Câu 45. Cho số phức z  1 2i . Tính z . A. z  5 . B. z  5 . C. z  3 . D. z  2 .
Câu 46. Cho hình phẳng D được giới hạn bởi các đường x  0 , x  1, y  0 và y  2x 1 . Thể tích
V của khối tròn xoay tạo thành khi quay D xung quanh trục Ox được tính theo công thức: 1 1 1 1
A. V  2x   1dx . B. V   2x 1dx
. C. V   2x  
1dx . D. V  2x 1dx  . 0 0 0 0
Câu 47. Một chiếc máy bay chuyển động trên đường băng với vận tốc v t 2
t 10t m / s với t là thời
gian được tính bằng đơn vị giây kể từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận
tốc 200m / s thì nó rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là: 4000 2500 A. m. B. 500m . C. m.
D. 2000m . 3 3
Câu 48. Cho hàm số f x thỏa mãn  f  x2  f xf x 4 . '
 15x 12x, x
   và f 0  f 0 1. Giá trị của 2 f   1 bằng 5 A. 8 . B. . C. 10 . D. 4 . 2
x  4  2tx  1  
Câu 49. Cho hai đường thẳng chéo nhau d : y t
t   d : y t ' t '  . Phương trình mặt cầu 1   1   z  3   z t  ' 
có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng d , d là: 1   2  2  3  9 2  3  3 A. x
y  z  22 2  2   . B. 2 x
y  z  2    .  2  4  2  2 2  3  3 2  3  9 C. x
y  z  22 2  2   . D. 2 x
y  z  2    .  2  2  2  4
Trang 5/6 – Mã đề 210 2 x
Câu 50. Trong mặt phẳng tọa độ Oxy cho hình phẳng D giới hạn bởi các đường 2
y  2x , y  , 8
y  x  6 . Tính diện tích hình phẳng D nằm bên phải của trục tung. 1075 135 185 335 A. S  . B. S  . C. S  . D. S  . 192 64 24 96 ----- HẾT -----
Trang 6/6 – Mã đề 210
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2018 - 2019 BẾN TRE
MÔN: TOÁN HỌC - LỚP: 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề) MÃ ĐỀ 210
Câu 1. Cho các số phức z  1 3i; z  5
  3i . Tìm điểm M  ;
x y biểu diễn số phức z , biết rằng trong 1 2 3
mặt phẳng phức điểm M nằm trên đường thẳng x  2y 1  0 và môđun của số phức
w  3z z  2z đạt giá trị nhỏ nhất. 3 2 1  3 1   3 1   3 1   3 1  A. M  ;   . B. M ;   . C. M ;   . D. M  ;   .  5 5   5 5   5 5   5 5  Lời giải Chọn A
Do M nằm trên đường thẳng x  2 y 1  0 nên M 2y 1; y . Điểm M  ;
x y biểu diễn số phức z z x yi  2y 1 yi . 3 3
Ta có: w  3z z  2z  3 2y 1  yi  5
  3i  2 1 3i  6y  3 y 1 i . 3 2 1          2  
w   y2    y   2 1 4 6 5 6 3 1   3 5. y       .  5  25 5 3 Dấu "  " xảy ra  1
y   x   . 5 5  3 1  Vậy M  ;   .  5 5 
Câu 2. Trong không gian Oxyz cho A1; 1;  2, B2;1; 
1 và mặt phẳng P : x y z 1  0. Mặt phẳng Q chứa ,
A B và vuông góc với mặt phẳng P . Mặt phẳng Q có phương trình là:
A. x y z  2  0 .
B. 3x  2y z  3  0 . C. 3x  2y z  3  0 . D.x y  0 . Lời giải Chọn B  
Ta có: AB  1;2;  1 và n  1;1; 
1 là một véctơ pháp tuyến của mặt phẳng P . P  
Gọi n  0 là một véctơ pháp tuyến của mặt phẳng Q . Q
Do mặt phẳng Q chứa ,
A B và vuông góc với mặt phẳng P nên:   n AB     Q
   n // AB,n     . Q P 3; 2;  1   n nQ P  Chọn n  3; 2  ;  1 . Q 
Phương trình mặt phẳng Q đi qua A1; 1;
 2, có một véctơ pháp tuyến n  3; 2  ;  1 là: Q
Q:3x   1   2   y   1   
1  z  2  0  Q : 3x  2y z  3  0 .
Câu 3. Trong không gian Oxyz cho mặt cầu S  có phương trình: 2 2 2
x y z  2x  4y  6z  9  0 .
Mặt cầu S  có tâm I và bán kính R là: A. I  1  ;2; 3   và R  5. B. I 1; 2  ;3 và R  5 .
Trang 13/1 – Mã đề 210 C. I 1; 2  ;3 và R  5. D. I  1  ;2; 3   và R  5 . Lời giải Chọn B
Viết lại phương trình mặt cầu S   x  2   y  2   z  2 : 1 2 3  5.
 Mặt cầu S  có tâm I 1; 2
 ;3 và R  5 .
Câu 4. Gọi z , z là các nghiệm của phương trình 2
z  4z  9  0 . Giả sử M , N là các điểm biểu diễn 1 2
hình học của z , z trên mặt phẳng phức. Khi đó độ dài của MN là 1 2 A. 5 . B. 4 . C. 2 5 . D. 5 . Lời giải Chọn C
z  2  5i Ta có 2
z  4z  9  0 1  
nên M 2; 5 và N 2; 5 .
z  2  5i  2 Suy ra MN  2 5 .
Câu 5. Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x y z  2x  4 y  6z  0 . Đường tròn giao tuyến
của S  với mặt phẳng Oxy có bán kính là A. r  6 . B. r  14 . C. r  3. D. r  5 . Lời giải Chọn D
Mặt cầu S  có tâm I 1;2;3 và bán kính R  14 .
Hình chiếu của I lên mặt phẳng Oxy là H 1;2;0 .
Do đó, khoảng cách từ tâm I đến mặt phẳng Oxy là d I;Oxy  IH  3.
Đường tròn giao tuyến có bán kính là 2 2
r R d  5 .
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;2;3 . Hình chiếu của M trên trục Oy là:
A. Q 0;2;0 .
B. S 0;0;3 .
C. R 1;0;0.
D. P 1;0;3 . Lời giải Chọn A.
Áp dụng lý thuyết: Điểm M x ; y ; z có hình chiếu vuông góc lên các trục Ox, Oy, Oz lần 0 0 0 
lượt là M x ;0;0 , M 0; y ;0 , M
0;0; z . Do đó hình chiếu vuông góc của M 1;2;3 Oy 0  Oz  0  Ox 0 
trên trục Oy là 0;2;0 .
Câu 7. Tìm số phức z biết: 1 iz 1 5i  0.
A. z  3  2i .
B. z  3  2i .
C. z  3  2i .
D. z  3  2i . Lời giải Chọn B. i
15i1i 2
1 i  5i  5i Ta có:   i 1 5 1
z 1 5i  0  z     3  2 .i 1 i 2 2 1  i 2
Câu 8. Trong mặt phẳng phức, cho ba điểm ,
A B, C lần lượt biểu diễn ba số phức z  1 i , z  1 i 2  2 1
và z a i . Để tam giác ABC vuông tại B thì a bằng: 3
Trang 13/2 – Mã đề 210 A. 3 . B. 2  . C. 3 . D. 4  . Lời giải Chọn A.
Ta có z  1 i A 1; 1 1  
z  1 i2  2i B 0;2 2    
z a i C a; 1  . Nên AB   1  ;  1 , BC   ; a 3  . 3   
Để tam giác ABC vuông tại B thì . AB BC  0  1.  a 1. 3
   0  a  3  .
Câu 9. Tính môđun của số phức 2019
z  2  i i . A. z  5 . B. z  2 . C. z  2 2 . D. z  10 . Lời giải Chọn B. Ta có 2019
z  2  i i  2 Nên z  2 .
Câu 10. Gọi z , z là hai nghiệm phức của phương trình 2
z  9  0 . Tính z z . 1 2 1 2
A. z z  3 .
B. z z  4i .
C. z z  9i .
D. z z  0 . 1 2 1 2 1 2 1 2 Lời giải Chọn D.
Theo định lý Vi-ét ta có z z  0 1 2
Nên z z  0  z z  0 . 1 2 1 2
Câu 11. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A2;0;0, B0;3; 
1 ,C 1;4;2 . Độ dài
đường cao từ đỉnh A của tam giác ABC . 3 A. 3 . B. . C. 2 . D. 6 . 2 Lời giải Chọn C.      Ta có : AB   2  ;3;  1 ; AC   3;
 4;2 , BC   
1;1;1   AB, AC  2  ;1;1   và BC  3 . 1    6 S
 AB, AC  . ABC 2   2
Gọi AH là đường cao của tam giác ABC 2S Khi đó: ABC AH   2 . CB   
Câu 12. Trong không gian Oxyz , cho các véc tơ a  1;2;3 , b   2;  4;  1 , c   1;  3;4 . Véc tơ    
v  2a  3b  5c có toạ độ là:    
A. v  3;7;23 .
B. v  23;7;3 .
C. v  7;3;23 .
D. v  7;23;3 . Lời giải Chọn A.       
Có 2a  2;4;6 , 3  b  6; 1  2; 3   , 5c   5
 ;15;20, nên v  2a 3b  5c  3;7;23 . 4 2x  3
Câu 13. Tìm họ nguyên hàm của hàm số f x  . 2 x
Trang 13/3 – Mã đề 210 3 3 2x 3 3 2x 3 3 2x 3 A. 3 2x   C . B.   C . C.   C . D.   C . x 3 x 3 2x 3 x Lời giải Chọn D. 4 2x  3  2x 3 Có f x 2 2 
 2x  3.x ,  f
 xdx  2x 3.x  3 2 2 dx    C . 2 x 3 xx  1 t
Câu 14. Trong không gian Oxyz , cho điểm M  4;
 0;0 và đường thẳng  : y  2
  3t . Gọi H a; ; b c z  2  t
là chân hình chiếu từ M lên  . Tính a b c . A. 5 . B. 7 . C. 3  . D. 1  . Lời giải Chọn D. 
Ta gọi H 1 t; 2   3t; 2
t  MH  5 t; 2   3t; 2  t   11
Do H là chân hình chiếu từ M lên  nên ta có MH.u  0  5
  t  6  9t  4t  0  t d 14  3 5 2  2  Vậy H ; ; 
  a b c  1. 14 14 14  
Câu 15. Trong không gian Oxyz , đường thẳng nào sau đây nhận u  2;3; 4
  làm véc tơ chỉ phương? (với t   ) x 1 2tx  2  tx  2  tx 1 2t    
A. y  2  3t .
B. y  3 3t .
C. y  3 5t .
D. y  3 3t .
z  2  4t     z  4   tz  4   3tz  2  4tLời giải Chọn D.
Câu 16. Trong không gian Oxyz , cho các điểm I 1;0;  1 , A2;2; 3
 . Mặt cầu S  tâm I và đi qua điểm
A có phương trình là
A. x  2  y   z  2 2 1 1  3 .
B. x  2  y   z  2 2 1 1  9 .
C. x  2  y   z  2 2 1 1  9 .
D. x  2  y   z  2 2 1 1  3 . Lời giải Chọn B
Bán kính mặt cầu: R IA  3.
 Phương trình mặt cầu: x  2  y  z  2 2 1 1  9 .
Câu 17. Trong không gian Oxyz , cho mặt phẳng P : 2x y z 1  0 . Điểm nào dưới đây thuộc mặt phẳng P ? A. Q 1; 3  ; 4   . B. P 1; 2  ;0 . C. N 0;1; 2   . D. M 2; 1  ;  1 . Lời giải Chọn A
Trang 13/4 – Mã đề 210
Thay tọa độ các điểm Q , P , N , M lần lượt vào phương trình P : 2x y z 1  0 ta được: 2.1  3
   4 1  0 (đúng) nên QP . 2.1  2
  1 0 (sai) nên P P.
1 2 1  0 (sai) nên N P. 2.1  
1 11  0 (sai) nên M P .
Câu 18. Họ nguyên hàm của hàm số   x
f x e  sin x là A.   x
F x e  cos x C . B.   x
F x e  sin x C . C.   x
F x e  cos x C . D.   x
F x e  sin x C . Lời giải Chọn C
Ta có:     x sin  x   sin x F x e x dx e dx
xdx e  cosx C   .
Câu 19. Cho số phức z a bi a,b   theo điều kiện 2  3iz  7iz  22  20i . Tính S a b . A. S  3. B. S  4  . C. S  6  . D. S  2 . Lời giải Chọn B
Ta có: 2  3iz  7iz  22  20i
 2  3ia bi  7ia bi  22  20i
 2a  2bi  3ai  3b  7ai  7b  22  20i
 2a  4b  2b 10ai  22  20i
2a  4b  22 a  1    
2b 10a  2  0 b   5 
Vậy S a b  4 .
Câu 20. Chọn khẳng định đúng? 2 2 x 3 x x 3 x A. 2 3 dx   C  . B. 2 3 dx   C  . ln 9 ln 3 2 x 1  x 9x x 3 C. 2 3 dx   C  . D. 2 3 dx   C  . 2x 1 ln 3 Lời giải Chọn A 2 x x 3 x 2
3 dx  9 dx   C   . ln 9
Câu 21. Tìm hàm số F x biết F x là một nguyên hàm của hàm số f x  x và F   1  1
A. F x 1 1   .
B. F x 2  x x . 2 x 2 3
C. F x 2 5  x x  .
D. F x 2 1  x x  . 3 3 3 3 Lời giải Chọn D
Trang 13/5 – Mã đề 210
Ta có F x 2 
xdx x x C  . 3 Ta có F   2 1
1  1   C  1 C  , suy ra F x 2 1  x x  . 3 3 3 3
Câu 22. Tìm số phức liên hợp của số phức z  1 i3  2i
A. z  1 i .
B. z  5  i .
C. z  5  i .
D. z  1 i . Lời giải Chọn B
Ta có z  1 i3  2i  5  i z  5  i .
Câu 23. Cho số phức z  2  3i, z  4
  5i . Tính z z z . 1 2 1 2
A. z  2  2i .
B. z  2  2i .
C. z  2  2i .
D. z  2  2i . Lời giải Chọn D
Ta có z  2  3i  4  5i  2   2i . x y z
Câu 24. Véc tơ pháp tuyến của mặt phẳng    1là 1 2 3    
A. n  6;3; 2 .
B. n  6;2;3 .
C. n  3;6;2 .
D. n  2;3;6 . 2   2   2   1   Lời giải Chọn D x y z x y z
Ta có    1  6x  3y  2z  6  0 nên véc tơ pháp tuyến của mặt phẳng    1là 1 2 3 1 2 3  n  6;3; 2 . 1  
Câu 25. Mệnh đề nào dưới đây sai?  A. kf
 xdx k f
 xdx với k  0 . B.f
 xdx  f x. C.f
 x gxdx f
 xdxg
 xdx. D.f
 x.gxdx f
 xd .x g  xdx. Lời giải Chọn D Mệnh đề  f
 x.gxdx f
 xd .x g
 xdx sai.
Câu 26. Trong mặt phẳng Oxy , điểm M 3;  1 biểu diễn số phức A. z  1   3i . B. z  3   i .
C. z  1 3i .
D. z  3  i . Lời giải Chọn D
Trong mặt phẳng Oxy , điểm M 3; 
1 biểu diễn số phức z  3  i .   
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho OA  3k i . Tọa độ của điểm A là:
A. A3;0;  1 . B. A 1;  0;3. C. A 1;  3;0.
D. A3;1;0 . Lời giải Chọn B
Tọa độ của điểm A là A 1;  0;3.
Trang 13/6 – Mã đề 210
Câu 28. Trong không gian Oxyz phương trình nào được cho dưới đây là phương trình mặt phẳng Oyz ? A. x  0 .
B. y z  0 .
C. z y z .
D. y z  0 . Lời giải Chọn A
Phương trình mặt phẳng Oyz qua O có véc tơ pháp tuyến là i  1;0;0
Nên phương trình mặt phẳng Oyz : x  0 .
Câu 29. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 5 3
y x x và trục hoành. 13 7 1 17 A. S  . B. S  . C. S  . D. S  . 6 6 6 6 Lời giải Chọn C
Phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành là: x  0 5 3
x x  0   x  1  1 1 Diện tích 5 3 S x x dx   6 1  x  3 y 1 z  3
Câu 30. Trong không gian Oxyz cho đường thẳng d :   và mặt phẳng 2 1 1
(P) : x  2y z  5  0 .Tìm tọa độ giao điểm M của đường thẳng d và mặt phẳng (P) . A. M  1;  0;4 .
B. M 0;0;5 . C. M  5;  2  ;2 . D. M  3;  1  ;3 . Lời giải Chọn A
x  2y  1  x  1   
Tọa độ điểm M là nghiệm của hệ phương trình x  2z  9 
 y  0  M  1  ;0;4 .
x 2y z 5 0      z  4  
Câu 31. Tập hợp các điểm biểu diễn các số phức z thảo mãn z  2  i z  2i là đường thẳng .
A. 4x  2y 1  0 .
B. 4x  2y 1  0 .
C. 4x  2y 1  0 .
D. 4x  6y 1  0 . Lời giải Chọn C Gọi 2
z x yi | x, y  ,i  1  .Ta có 2 2 2 2
z  2  i z  2i  (x  2)  ( y 1)i x  ( y  2)i  (x  2)  ( y 1)  x  ( y  2)
 4x  2y 1  0
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho điểm A2;1; 
1 và mặt phẳng P : 2x y  2z 1  0 .
Phương trình của mặt cầu tâm A và tiếp xúc với mặt phẳng P là
A. x  2   y  2   z  2 2 1 1  9 .
B. x  2   y  2   z  2 2 1 1  2 .
C. x  2   y  2   z  2 2 1 1  4 .
D. x  2   y  2   z  2 2 1 1  36 . Lời giải
Trang 13/7 – Mã đề 210 Chọn C
Mặt cầu tâm A2;1; 
1 và tiếp xúc với mặt phẳng P có   
R d A P 2.2 1 2.1 1 ,   2 . 2   2 2 2 1  2
Vậy mặt cầu cần tìm có phương trình S   x  2   y  2   z  2 : 2 1 1  4 .
Câu 33. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng   : x  2y z 1  0 và
 : 2x  4y mz  2  0. Tìm m để hai mặt phẳng   và   song song với nhau. A. m  1.
B. Không tồn tại m . C. m  2  . D. m  2 . Lời giải Chọn B
Mặt phẳng   và   song song với nhau khi 2 4 m 2  m  2       hệ vô nghiệm. 1 2 1  1  m  2
Vậy không tồn tại m thỏa mãn yêu cầu bài toán. 1 2 x  2 1  Câu 34. Biết dx   n ln 2 
, (với m, n   ). Tính S m n . x 1 m 0 A. S  1. B. S  4 . C. S  1. D. S  5. Lời giải Chọn A Ta có 2 x  2 x   1 2 1 1 1 2 1 1  1   x  1  dx  dx x 1 dx      
x  ln x 1    ln 2 . x 1 x 1  x 1  2  2 0 0 0 0 m  2 Suy ra 
. Vậy S m n  1. n  1  3 3 3 Câu 35. Cho f
 xdx  2 và g
 xdx 1. Tính I  4 f
 x 2019gxdx  1 1 1 A. 2025 . B. 2019 . C. 2021. D. 2027 . Lời giải Chọn D 3 3 3 I  4 f
 x2019gxdx  4 f
 xdx2019 g
 xdx  4.22019.1 2027 . 1 1 1 1
Câu 36. Tính tích phân   x I e  2dx . 0
A. I e 1.
B. I e  2 .
C. I e  3 .
D. I e 1. Lời giải Chọn A 1 1
Ta có:   x  2   x I e dx
e  2x  e 1. 0 0
Trang 13/8 – Mã đề 210
Câu 37. Phần ảo của số phức z  2  3i là : A. 2 . B. 3 . C. 3  . D. 3  i . Lời giải Chọn C
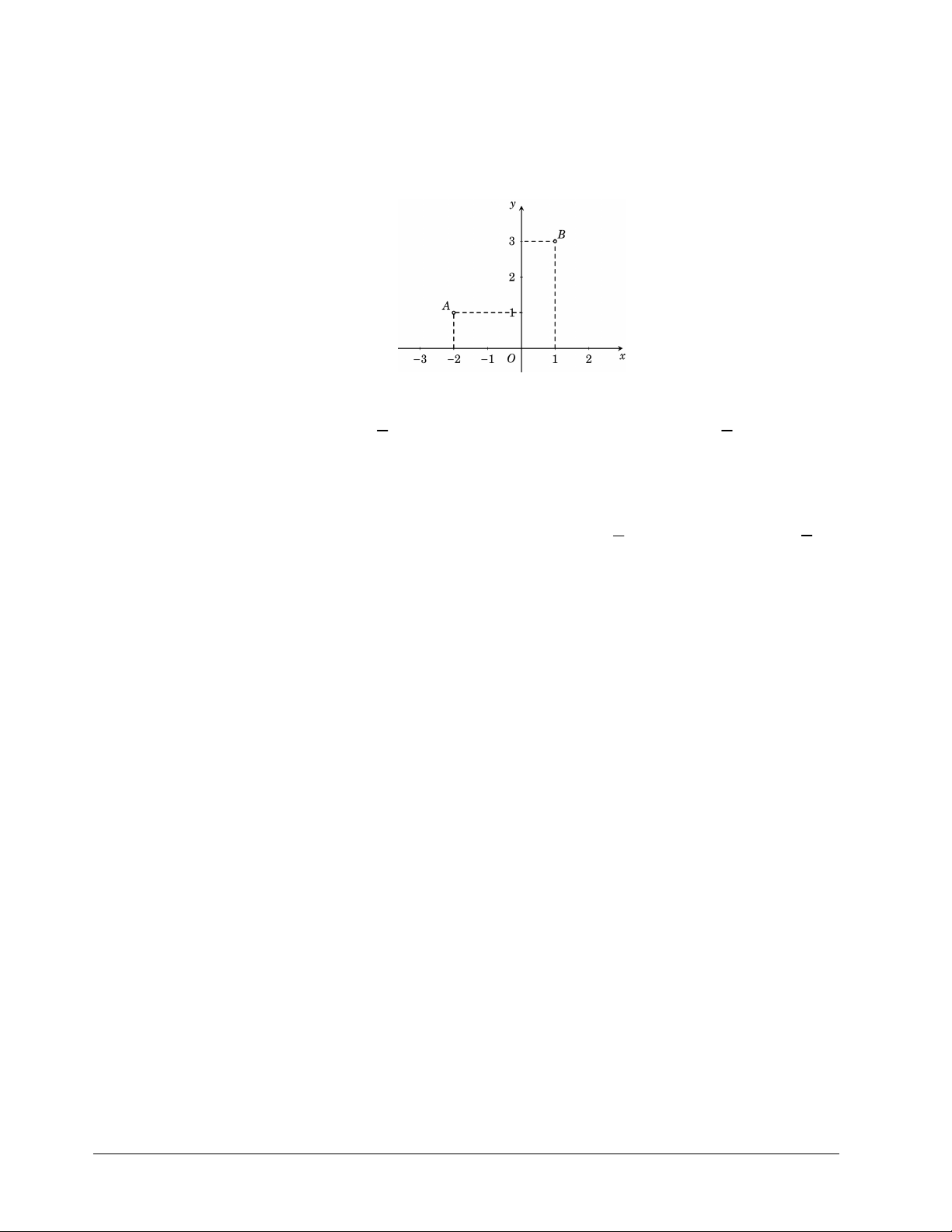
Câu 38. Trong mặt phẳng tọa độ Oxy cho các điểm ,
A B như hình vẽ bên.
Trung điểm của đoạn thẳng AB biểu diễn số phức 1 1 A. 1 2i . B.   2i .
C. 2  i . D. 2  i . 2 2 Lời giải Chọn B  1  1 Ta có: A 2;  
1 , B 1;3 trung điểm của đoạn thẳng AB là I  ;2 
 biểu diễn số phức   2i .  2  2 x 1 t
Câu 39. Trong không gian Oxyz , cho đường thẳng d : y  2  4t ,t  . Hỏi d đi qua điểm nào dưới z  35t  đây? A. 3;6;8 . B. 1; 4  ; 5   . C.  1  ;2;3. D. 0;6;8. Lời giải Chọn D Chọn t  1
ta có d đi qua điểm 0;6;8.
Câu 40. Trong không gian với hệ tọa độ Oxyz , cho hai mặt phẳng P :2x y  2z  9  0 và
Q:4x  2y  4z 6  0. Khoảng cách giữa hai mặt phẳng P và Q bằng A. 0 . B. 2 . C. 1. D. 3 . Lời giải Chọn B
Lấy A0; 3;0Q :4x  2y  4z  6  0 .
Dễ thấy P // Q suy ra d P,Q  d  ,
A P  2 . 9 2
Câu 41. Cho tích phân f
 xdx  6. Tính tích phân 2
I x . f  3 x   1dx . 2 1 A. I  3 . B. I  2 . C. I  8 . D. I  4 . Lời giải Chọn B Đặt 3 2
t x 1 dt  3x dx .
Trang 13/9 – Mã đề 210
Đổi cận: x  1 t  2 và x  2  t  9 . 2 9 1 Vậy 2
I x . f  3 x   1dx f
 tdt  2. 3 1 2
Câu 42. Trong không gian với hệ tọa độ Oxyz , tìm trên trục Oz điểm M cách đều điểm A2;3;4 và
mặt phẳng P:2x  3y z 17  0 .
A. M 0;0; 3 .
B. M 0;0;3 .
C. M 0;0; 4 .
D. M 0;0;4. Lời giải Chọn B
Gọi M 0;0;mOz . m
Theo đề: AM d M ;P   m  2 17 13 4    2 m m   2 14 8
29  m  34m  289 14 2
 13m  78m 117  0  m  3. 
Câu 43. Cho tích phân 2
I x .cosx dx  và đặt 2
u x , dv  cos x dx . Mệnh đề nào sau đây là mệnh đề 0 đúng?     A. 2
I x .sin x x.sin x dx  . B. 2
I x .sin x  2 x.sin x dx  . 0 0 0 0     C. 2
I x .sin x  2 x.sin x dx  . D. 2
I x .sin x x.sin x dx  . 0 0 0 0 Lời giải Chọn C 2 u x
du  2x dx Đặt    .
dv  cos x dxv  sin x   Vậy 2
I x .sin x  2 x.sin x dx  . 0 0
Câu 44. Trong không gian Oxyz , cho hai điểm A2;1;3 và B 0;3; 
1 . Tọa độ trung điểm của đoạn thẳng AB là: A. 2;4; 2   . B.  2;  2;4 . C.  1  ;1;2 . D.  2;  4  ;2 . Lời giải Chọn C
Gọi I là trung điểm của AB . Khi đó tọa độ điểm I là: t   1   
A2;1;3, B1; 1  ;  1  AB   1  ; 2  ; 2  .  I  1  ;1;2. t  '  1  Vậy chọn C.
Câu 45. Cho số phức z  1 2i . Tính z . A. z  5 . B. z  5 . C. z  3 . D. z  2 . Lời giải Chọn B
Trang 13/10 – Mã đề 210 Ta có z    2 2 1 2  5 .
Câu 46. Cho hình phẳng D được giới hạn bởi các đường x  0 , x  1, y  0 và y  2x 1 . Thể tích
V của khối tròn xoay tạo thành khi quay D xung quanh trục Ox được tính theo công thức: 1 1 1 1
A. V  2x   1dx . B. V   2x 1dx
. C. V   2x  
1dx . D. V  2x 1dx  . 0 0 0 0 Lời giải Chọn C
Thể tích V của khối tròn xoay tạo thành khi quay D xung quanh trục Ox là: 1 1 2
V    2x 1 dx   2x    1dx . 0 0
Câu 47. Một chiếc máy bay chuyển động trên đường băng với vận tốc v t 2
t 10t m / s với t là thời
gian được tính bằng đơn vị giây kể từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận
tốc 200m / s thì nó rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là: 4000 2500 A. m. B. 500m . C. m.
D. 2000m . 3 3 Lời giải Chọn C
Khi v  200 ta suy ra 2
t 10t  200  t  10 s .
Máy bay di chuyển trên đường băng từ thời điểm t  0s tới thời điểm t 10s 10 2500
Nên suy ra quãng đường di chuyển trên đường băng là: S   2t 10tdt   m. 3 0
Câu 48. Cho hàm số f x thỏa mãn  f  x2  f xf x 4 . '
 15x 12x, x
   và f 0  f 0 1. Giá trị của 2 f   1 bằng 5 A. 8 . B. . C. 10 . D. 4 . 2 Lời giải Chọn D. Ta có:
f x2  f xf x 4 . '
 15x 12x   f
  xf x  4 .
  15x 12x
f  xf x 5 2 .
 3x  6x C, x   
Mà f 0  f 0 1 nên 1  0  0  C C 1 1
f  xf x 5 2 .
 3x  6x 1 hay 2
f x  5 2
  3x  6x 1 2   1 1 2 f x 6 3
x  2x x M 2 2 Mà f   1 0  1   M 2 1 1 1 2 f   2
1   2 1  f   1  4 . 2 2 2
Trang 13/11 – Mã đề 210
x  4  2tx  1  
Câu 49. Cho hai đường thẳng chéo nhau d : y t
t   d : y t ' t '  . Phương trình mặt cầu 1   1   z  3   z t  ' 
có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng d , d là: 1   2  2  3  9 2  3  3 A. x
y  z  22 2  2   . B. 2 x
y  z  2    .  2  4  2  2 2  3  3 2  3  9 C. x
y  z  22 2  2   . D. 2 x
y  z  2    .  2  2  2  4 Lời giải Chọn D
x  4  2t  
d : y t
t    d có vectơ chỉ phương u  2;  1;0 1   1   1 z  3  x  1  
d : y t ' t '   d vecctơ chỉ phương u2  0;1;  1 2   2 z t  ' 
Gọi AB là đoạn vuông góc chung của d , d với Ad ; B d . 1   2  1 2  Ad  (4
A  2t; t; 3); B d B(1; t ';  t ')  AB   3
  2t ; t ' t;  t ' 3 1 2    . AB u  0   2t  3 . 2
  t ' t  0 1    
AB là đoạn vuông góc chung của d , d     1   2    . AB u  0
2t 't  3   2 t  1   
A2;1;3, B1; 1  ;  1  AB   1  ; 2  ; 2  . t '  1 
Mặt cầu S  có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng d , d và chỉ khi 1   2 
AB là đường kính của mặt cầu S  2 2   3  AB 2  2 1 3
S  có tâm là trung điểm I của AB , I ;0;2 
 và bán kính R    .  2  2 2 2 2  3  9
Vậy phương trình mặt cầu S  : x
y  z  22 2    .  2  4 2 x
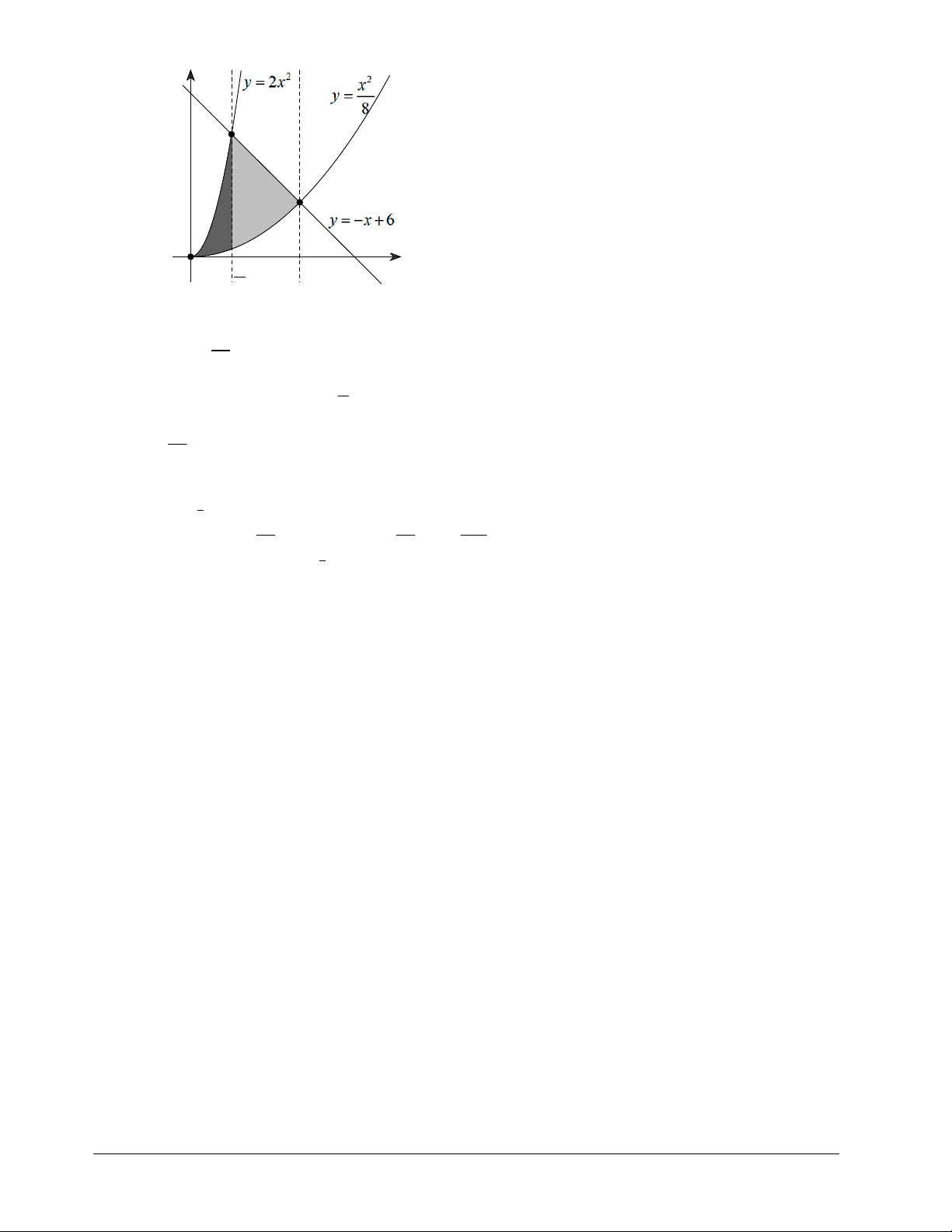
Câu 50. Trong mặt phẳng tọa độ Oxy cho hình phẳng D giới hạn bởi các đường 2
y  2x , y  , 8
y  x  6 . Tính diện tích hình phẳng D nằm bên phải của trục tung. 1075 135 185 335 A. S  . B. S  . C. S  . D. S  . 192 64 24 96 Lời giải Chọn C.
Trang 13/12 – Mã đề 210 y x O 3 4 2
Phương trình hoành độ giao điểm giữa các đường cong 2 x 2 2x   x  0 . 8 x 3 2 0
2x  x  6  x  . 2 2 x x0
 x  6  x  4 . 8
Khi đó ta xác định được hình phẳng trên mặt phẳng Oxy . 3 2 2 4 2  x   x  185 2
S  2x  dx  x  6 dx  .  8   8  24 0 3 2
Trang 13/13 – Mã đề 210
Document Outline

  • đê DEHDG-HK2-LOP-12-SGD-BEN-TRE-2019 (1).pdf
  • DEHDG-HK2-LOP-12-SGD-BEN-TRE-2019 (1).pdf