Đề thi học sinh giỏi cấp tỉnh Toán 12 năm 2021 – 2022 sở GD&ĐT Lạng Sơn

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LẠNG SƠN
LỚP 12 NĂM HỌC 2021 - 2022
Môn thi: TOÁN lớp 12 THPT
Thời gian: 180 phút (không kể thời gian giao đề)
ĐỀ THI CHÍNH THỨC
(Đề thi gồm 01 trang, 05 câu) Câu 1 (5,0 điểm).
a) Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y  x  (m 1)x  (m 1)x 1 có hai 4 3
điểm cực trị x , x thỏa mãn x  x  . 1 2 1 2 3 2x  2 b) Cho hàm số y 
có đồ thị C  . Cho d là tiếp tuyến của C  tại điểm M  x ; y , 0 0  x 1
d cắt hai đường tiệm cận của C  lần lượt tại A và B . Tính độ dài ,
IA IB theo x ( I là giao 0
điểm của hai đường tiệm cận) và tìm bán kính lớn nhất của đường tròn nội tiếp tam giác IAB . Câu 2 (5,0 điểm). 1 3 2 a) Giải phương trình: 4
4 sin x  2 cos 2x  sin 4x   sin x . 2 2 2 3 3 2
x  y  9 y  x  28y  30 
b) Giải hệ phương trình sau  .
 2  y  5  x  2x  6 
Câu 3 (2,0 điểm). Cho 2021 tấm thẻ được đánh số theo thứ tự từ 1 đến 2021 (mỗi tấm thẻ được
đánh duy nhất một số và không có hai thẻ nào có số giống nhau). Các tấm thẻ được úp xuống mặt
bàn và không nhìn thấy số trên thẻ. Bốc ngẫu nhiên 1 tấm thẻ, tính xác xuất để số ghi trên tấm thẻ
a) Chia hết cho cả 6 và 15 .
b) Chia hết cho 2, hoặc chia hết cho 3 hoặc chia hết cho 5.
Câu 4 (2,0 điểm). Một cửa hàng bán quýt loại I với giá là 50.000 đồng/kg. Với giá bán này thì cửa
hàng chỉ bán được khoảng 40kg mỗi ngày. Cửa hàng dự định giảm giá bán, ước tính nếu cửa hàng
cứ giảm 5000 đồng/kg thì số quýt bán được tăng thêm là 50kg. Xác định giá bán để cửa hàng đó
thu được lợi nhuận lớn nhất, biết rằng giá nhập mỗi kg quýt ban đầu là 30.000 đồng?
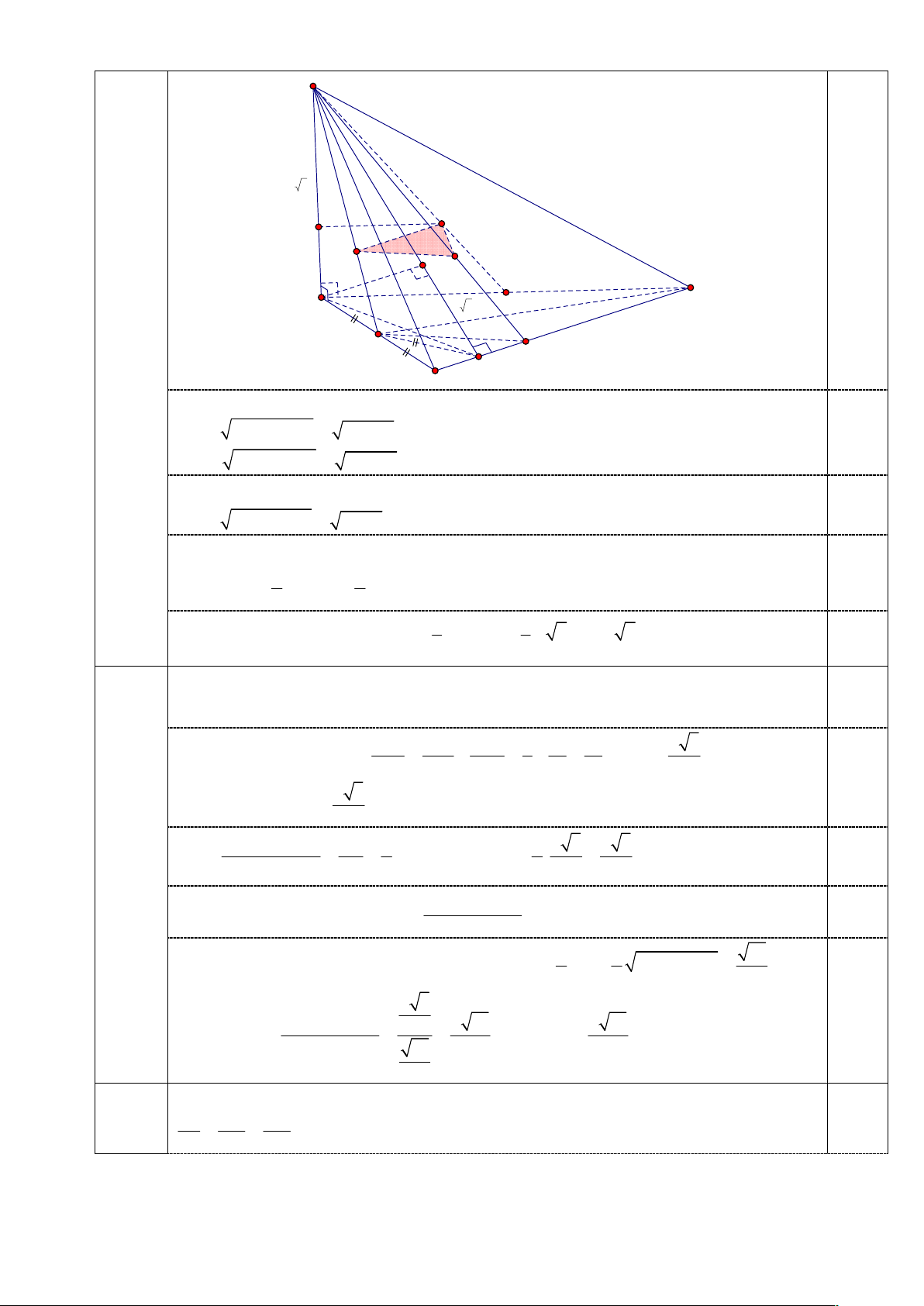
Câu 5. (6,0 điểm). Cho tứ diện ABCD với AB   BCD và AB  2 2 . Tam giác ACD có ba góc
nhọn, đường cao AK  2 6 và AC  5, AD  7 .
a) Tính thể tích khối tứ diện ABCD .
b) Gọi L là trung điểm của BC . Tính góc tạo bởi đường thẳng KL và mặt phẳng  ACD .
c) Gọi M , N lần lượt là trọng tâm các tam giác ABC, ABD và I là tâm đường tròn nội tiếp
tam giác ACD . Tính khoảng cách từ điểm D đến mặt phẳng  MNI  .
---------------------Hết---------------------
Họ và tên thí sinh: ………………………………….......... Số báo danh…………...........
Chữ kí giám thị số 1: …...............………Chữ kí giám thị số 2:…......................………....
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LẠNG SƠN
LỚP 12 NĂM HỌC 2021 - 2022
HƯỚNG DẪN CHẤM THI MÔN TOÁN LỚP 12 THPT
(Hướng dẫn chấm gồm 05 trang)
Chú ý: Những cách giải khác HDC mà đúng thì cho điểm theo thang điểm đã định. Câu Nội dung Điểm 1a 2
y  3x  2m  
1 x  m   1 (2,5 đ)
Để hàm số có hai điểm cực trị x , x thì phương trình y  0 phải có 2 nghiệm phân biệt tức 1 2 0,5 2
là  '  m   1  3m   1  0  5  33 m  2 2
 m  5m  2  0   0,5  5  33 m   2 4 3  4 3
Theo đề bài x  x    1 2 3 a 3 0,5 4 2
m  5m  2 4 3 2  
 m  5m 14  0 3 3 m  2    0,5 m  7 
Kết hợp với điều kiện, có m  2, m  7 là các giá trị cần tìm 0,5 1b
Đồ thị C  có tiệm cận đứng x  1, tiệm cận ngang y  2  I 1; 2 (2,5 đ) 4 0,5 y  , x   1.  x  2 1
Phương trình tiếp tuyến d của C  tại điểm có hoành độ x là 0 2 4 2x  4x  2 0 0 y   x  , x  1.  0 x  2 1 x 1 0 0,5 0  2x  6  Tọa độ điểm 0 A 1; 
 , B 2x 1; 2 . 0  x 1  0  8 Khi đó IA 
, IB  2 x 1 . 0 0,5 x 1 0
Tam giác IAB vuông tại I có I .
A IB  16 . Gọi p, S , r lần lượt nửa chu vi, diện tích và bán
kính đường tròn nội tiếp tam giác IAB . Ta có S . IA IB . IA IB 16 0,5 r      4  2 2 . p 2 2
IA  IB  IA  IB 2 . IA IB  2 . IA IB 2 16  32 x  3
Vậy Max r   4  2 2 khi IA  IB  4 0   . 0,5 x  1   0 2a 1 3 2 4 (2,5 đ)
4 sin x  2 cos 2x  sin 4x   sin x 0,5 2 2 2 1 3 2 4  4 sin x  2  2
1 2sin x  sin 4x   sin x 2 2 2
 2sin x  2 1 1 2 2 1  sin 4x   sin x 2 2 2 0,5 1 1 2 2  cos 2x  sin 4x   sin x 2 2 2 1  cos4x 1 1 2   sin 4x   sin x 2 2 2 2 1 1 2  cos 4x  sin 4x  sin x 0,5 2 2 2     sin 4x   sin x   0,5  4      2 4x   x  k 2 x    k  4  12 3     k  0,5  3 2
4x     x  k2  x   k  4  20 5 2b 3 3 2
x  y  9 y  x  28y  30    1 (2,5 đ)
 2 y  5 x  2x 6  2  x  5 0,5 ĐK:  . y  2  3 PT   3
1  x  x   y  3   y  3 Xét hàm số   3
f t  t  t có f t  2 '
 3t 1  0, t    0,5
Suy ra f t  là hàm số đồng biến, liên tục trên  .
Phương trình f  x  f  y  3  x  y  3  y  x  3 0,5
Thay y  x  3 vào phương trình 2 ta được 5  x  x  3 0,5 x  3 x  3   
 x  1  x  4  y  1 2
x  5x  4  0   0,5 x  4 
Vậy hệ phương trình có nghiệm duy nhất 4;  1 . 3a
Số cách chọn ra 1 tấm thẻ từ 2021 tấm thẻ là n   2021. (1,0 đ)
Gọi X là biến cố "Số trên thẻ bốc ra chia hết cho cả 6 và 15", vậy X là biến cố "Số trên 0,5
thẻ bốc ra chia hết cho 30”  2021
Số các số thỏa mãn là n  X    67  . 30    0,5 n  X  67
Do đó, xác suất cầm tìm bằng P  X    . n  2021 3b
Gọi A là biến cố "Số trên thẻ bốc ra chia hết cho 2". (1,0 đ)
Gọi B là biến cố "Số trên thẻ bốc ra chia hết cho 3".
Gọi C là biến cố "Số trên thẻ bốc ra chia hết cho 5". 0,25 Khi đó:
A  B là biến cố "Số trên thẻ bốc ra chia hết cho 6".
B  C là biến cố "Số trên thẻ bốc ra chia hết cho 15".
A  C là biến cố "Số trên thẻ bốc ra chia hết cho 10".
A  B  C là biến cố "Số trên thẻ bốc ra chia hết cho 30", đây chính là biến cố X ở ý a.
A  B  C là biến cố "Số trên thẻ bốc ra hoặc chia hết cho 2, hoặc chia hết cho 3 hoặc chia
hết cho 5" và đây là biến cố cần tính xác suất.  2021  2021  2021 n  A 
 1010; n  B 
 673; n  A   404  0,25 2   3   5         2021  2021  2021
n  A  B 
 336; n  A  C  
 202; n  B  C    134  6   10   15        0,25
n  A  B  C   n  X   67
Vậy xác suất cần tìm là
P  A  B  C   P  A  P  B  P C 
P  A  B  P  A  C   P  B  C   P  A  B  C  0,25
1010  673  404  336  202 134  67 1482   . 2021 2021 4
Gọi x là giá bán thực tế của mỗi kg quýt, ( x : đồng; 30000  x  50000 đồng). (2,0 đ)
Khi đó số kg bán thêm được là: 0,5 50 1 50000  x.  50000  x . 5000 100
Do đó số kg quýt bán được tương ứng với giá bán x : 1 1 40 
50000  x   x  540 100 100
Gọi f (x) là hàm lợi nhuận thu được ( f (x) : đồng). 0,5  1  1
Ta có: f (x)   x  540 .    x  30000 2  
x  840x 16200000  100  100
Bài toán trở thành tìm GTLN của 1 2 f (x)  
x  840x 16200000 với 30000  x  50000 . 100 1 0,5
f ' x   x  840 50 1
f ' x  0  
x  840  0  x  42000 50
Vì hàm f  x liên tục trên 30000  x  50000 nên ta có: f 30000  0
f 42000  1440000 0,5
f 50000  800000
Vậy với x  42000 thì f  x đạt GTLN.
Vậy để cửa hàng đó thu được lợi nhuận lớn nhất thì giá bán thực tế của mỗi kg quýt là 42.000 đồng. 5a A (2,5 đ) 2 2 7 5 N Z M T I G D B 2 6 4 5 L E K C 1
Áp dụng định lí Pitago cho các tam giác vuông ACK, ADK thì ta có 2 2 CK 
AC  AK  25  24  1; 1,0 2 2 DK 
AD  AK  49  25  5 , suy ra CD  6 .
AB   BCD  AB  BK , áp dụng định lí Pitago cho tam giác vuông ABK ta có 0,5 2 2 BK 
AK  AB  24  8  4 .
Vì CD  AK, CD  AB  CD   ABK   CD  BK . 1 1 0,5 Ta có S  BK.CD  4 6  12 . BCD 2 2 1 1
Thể tích khối chóp đã cho bằng V  A . B S  .2 2.12  8 2 (đvtt). 0,5 3 BCD 3 5b
Kẻ BT  AK (1), vì CD   ABK   CD  BT 2 . (2,5 đ) 0,5
Từ (1) và (2) suy ra BT   ACD , vậy thì d B; ACD  BT   . 1 1 1 1 1 3 4 3
Tam giác ABK vuông nên       BT  , vậy thì 2 2 2 BT BA BK 8 16 16 3 0,5 4 3
d B; ACD  BT  .   3 d  ; L  ACD CL 1 1 4 3 2 3 Ta có    
 d L; ACD  .  .   0,5 d  ; B  ACD CB 2   2 3 3 d  ; L  ACD Ta gọi  ;
KL  ACD  sin      . 0,5 KL 1 1 17
KL là trung tuyến tam giác vuông BKC suy ra 2 2 KL  BC  BK  KC  . 2 2 2 2 3 0,5 d  ; L  ACD   4 51 4 51 Do đó, 3 sin        arcsin . KL 17 51 51 2 5c
Gọi AI  CD  E, AN  BD  G . Vì CI , DI là phân giác của các tam giác ACE, DCE nên (1,0 đ) AI AC AD 0,5   . IE CE DE AI AC  AD AC  AD 5  7
Theo tính chất tỉ lệ thức thì     2 . IE CE  DE CD 6 AM AN AM AN AI
Theo tính chất trọng tâm thì ta có   2 , do đó   vậy thì ML NG ML NG IE
MI || LE, MN || LG (theo Ta-lét đảo) suy ra MNI  || (BCD) . AZ AN 2 2 0,5
Ta gọi Z  MNI   AB  Z    2  BZ  . ZB NG 3
Do đó, d  D MNI   d B MNI  2 2 ; ;  BZ  . 3
---------------------Hết---------------------