Đề thi học sinh giỏi cấp tỉnh Toán THCS năm 2023 – 2024 sở GD&ĐT Quảng Nam

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THCS TỈNH QUẢNG NAM NĂM HỌC 2023 – 2024 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề) Khóa thi ngày: 12/4/2024 Câu 1. (4,5 điểm) 2x  8 x  3 x  2 x 1 2 x a) Cho biểu thức A    , với x  4. x  x  6 x  2 x  3 x  x
Rút gọn biểu thức A và tìm tất cả các số nguyên x thỏa mãn A  . 12 2 x
b) Tìm tất cả các cặp số nguyên  ; x y thỏa mãn 3 x 
 2xy  2x  y  4  0. 2 Câu 2. (4,5 điểm) 3x a) Giải phương trình  x  4 . 3x 1 1 2   x   1 2y   1  x  2  0
b) Giải hệ phương trình  . 2 2
4xy  4y  4xy  x  2y  6  0 Câu 3. (3,0 điểm)
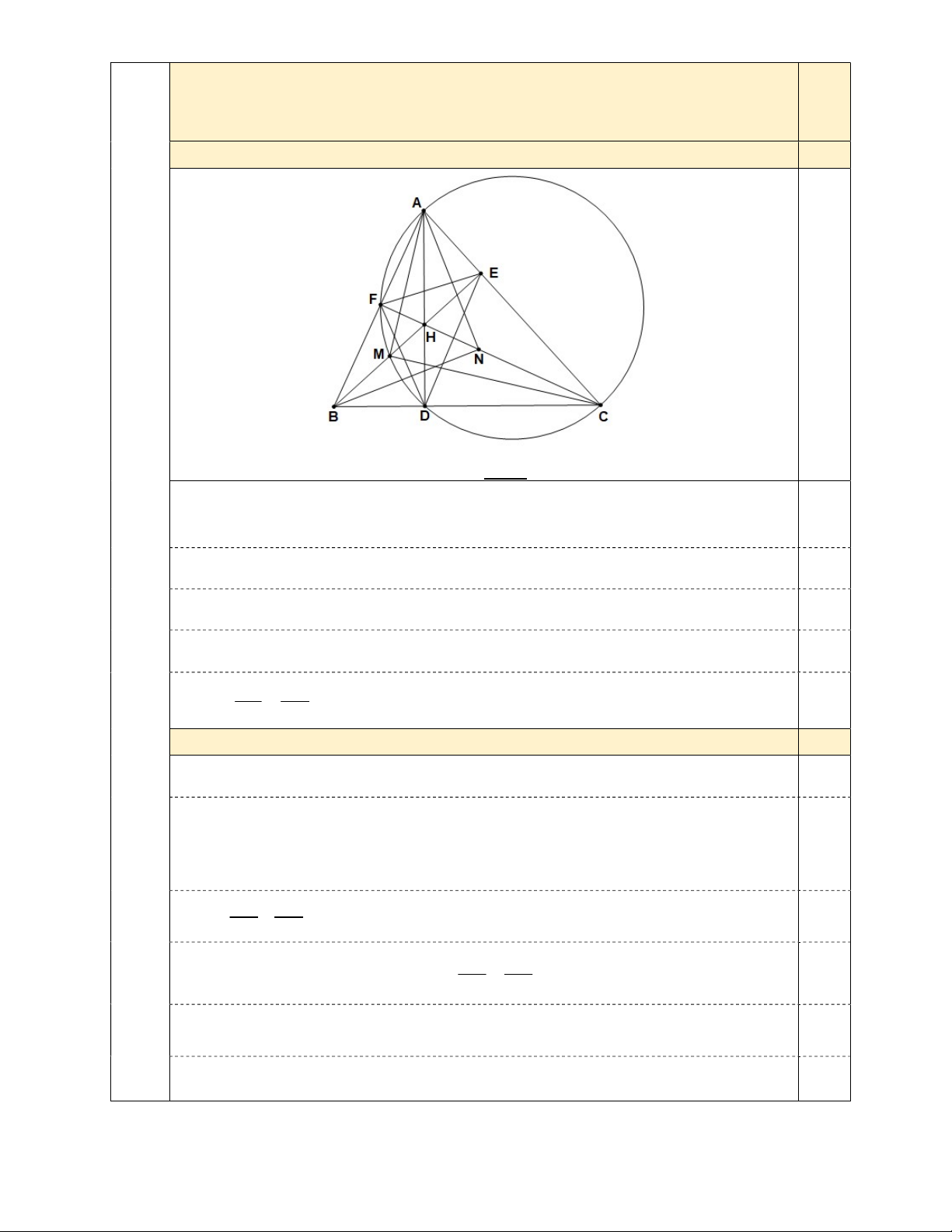
Cho tam giác nhọn ABC (AB  AC) có ba đường cao AD, BE, CF đồng quy tại H. Đường
tròn đường kính AC cắt đoạn thẳng BH tại M. Trên đoạn thẳng HC lấy điểm N sao cho AM  AN.
a) Chứng minh EB.EH  ED.EF .
b) Chứng minh N thuộc đường tròn ngoại tiếp tam giác ABD. Câu 4. (4,0 điểm)
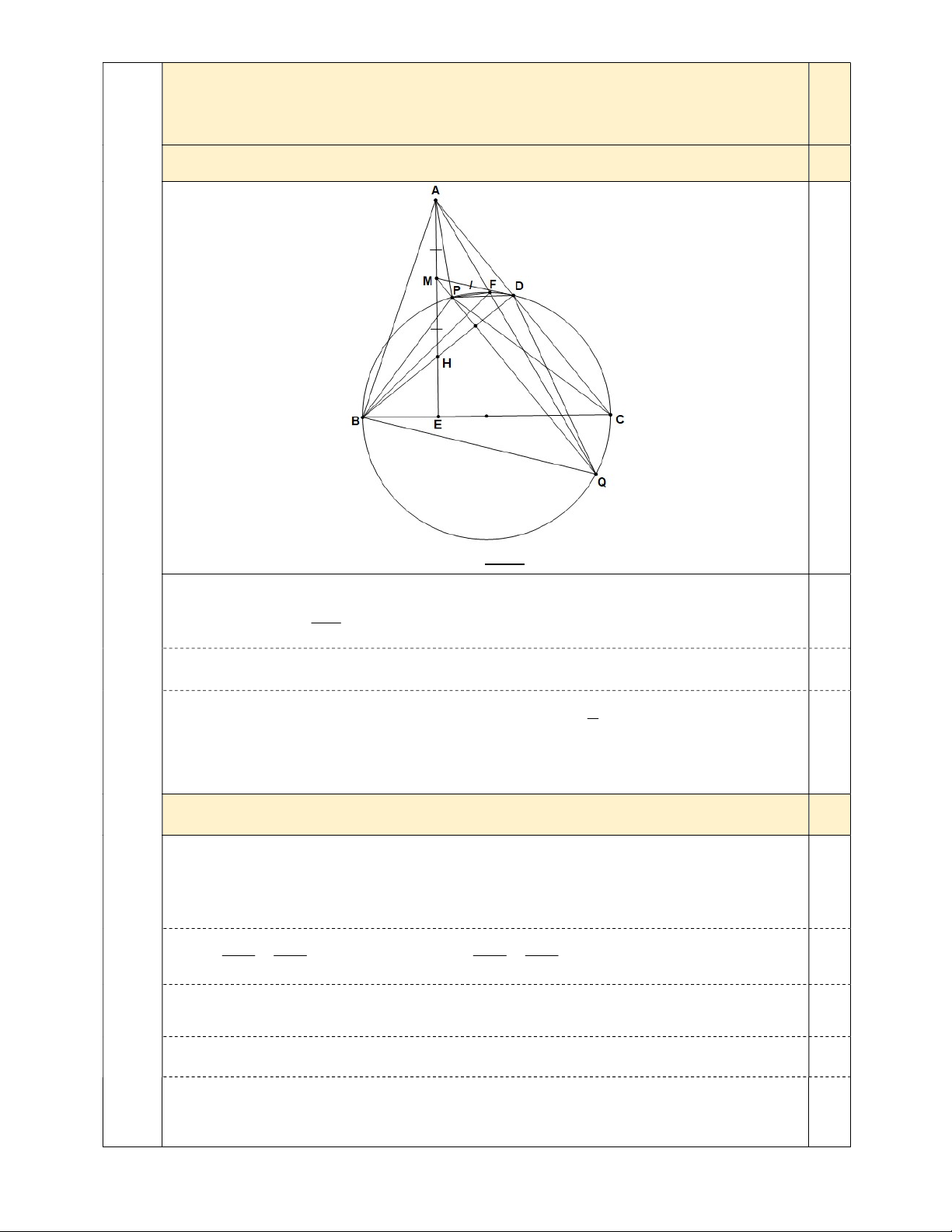
Cho tam giác nhọn ABC (AB  AC) có hai đường cao AE, BD cắt nhau tại H. Đường trung
trực của đoạn thẳng DH cắt AE tại M, cắt đường tròn ngoại tiếp tam giác BCD tại P và Q (P nằm giữa M và Q).
a) Chứng minh MD là tiếp tuyến của đường tròn ngoại tiếp tam giác BCD. b) Chứng minh  APM   AQM   CBD.
c) Đường thẳng AQ cắt đường tròn ngoại tiếp tam giác BCD tại F (F khác Q). Chứng minh  APB   FPB. Câu 5. (4,0 điểm)
a) Cho p là số nguyên tố. Tìm tất cả các số nguyên dương b sao cho nghiệm của phương trình bậc hai 2
x  bx  bp  0 là số nguyên.
b) Cho ba số thực dương , x y, z thỏa mãn 2 2 2
x  y  z  3. Tìm giá trị lớn nhất của biểu  1   1   1  thức 2 2 2 2 2 2 P  xy x  y   yz y  z   zx z  x        .  z   x   y  ---------- HẾT ----------
- Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
- Thí sinh không được sử dụng máy tính cầm tay.
- Họ và tên thí sinh:......................................................; Số báo danh...........................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THCS TỈNH QUẢNG NAM NĂM HỌC 2023 - 2024 HDC CHÍNH THỨC
HƯỚNG DẪN CHẤM MÔN TOÁN
(Hướng dẫn chấm có 08 trang) Câu Đáp án Điểm 2x  8 x  3 x  2 x 1 2 x a) Cho biểu thức A    , với x  4. Rút gọn x  x  6 x  2 x  3 2,5 x  x
biểu thức A và tìm tất cả các số nguyên x thỏa mãn A  . 12 2 1  x x x    2 1  Ta có: 2x  8 x  3 2x  8 x  3 x 1  và   x  x  6  x 2 x 3 x  2 x  2 x  2 0,5    2x 8 x 3 x 1 2 x A     x  2 x  3 x  2 x  3
2x  8 x  3   x  
1  x  3 2 x  x  2   0,25 x  2 x  3
2x 8 x  3  x  3 x  x  3  2x  4 x Câu 1   0,25 x  2 x  3 (4,5 đ)  x  x  2 x x 2 x     0,5
x  2 x  3  x  2 x 3 x  3 x  x x x  x 1 x 1 A      0,25 12 x  3 12 x  3 12  12   x   1  x  3 0,25  x  2 x 15  0
  x 3 x  5  0  x  3  0 0,5  x  9
Kết hợp với x  4 suy ra các số nguyên x thỏa mãn yêu cầu bài toán là: 5;6;7;8;9. Trang 1/8 2 x
b) Tìm tất cả các cặp số nguyên  ; x y thỏa mãn 3 x 
 2xy  2x  y  4  0 . 2,0 2 2 x
Giả sử tồn tại cặp số nguyên  ; x y thỏa mãn 3 x 
 2xy  2x  y  4  0  1 2   3 2
1  2x  x  4xy  4x  2y  8  0 0,25 2  x 2x   1  2y2x   1  22x   1  6   x   2 2 1 x  2 y  2  6 0,25
Suy ra số nguyên 2x 1 là ước của 6. Do 2x 1 không chia hết cho 2 nên 2x 13;3;1;  1 . 0,25 x  1 2x 1  3 x  1  Trường hợp 1:      3 (loại). 0,25 2 x  2y  2  2 2y  3 y      2 2x 1  3 x  2  x  2  Trường hợp 2:      (thỏa mãn (1)). 0,25 2 x  2y  2  2  2y  4  y  2  2x 1  1 x  0 x  0 Trường hợp 3:      (thỏa mãn (1)). 0,25 2 x  2y  2  6 2y  8 y  4 x  1 2x 1  1  x  1  Trường hợp 4:      5 (loại). 0,25 2 x  2y  2  6 2y  5 y      2
Vậy có hai cặp số nguyên thỏa mãn yêu cầu bài toán:  ; x y   2  ; 2  ,  0,25 ; x y  0;4 . Trang 2/8 3x a) Giải phương trình  x  4  1 2,0 3x 1 1 3x 1  0 Điều kiện: 1   x   . 0,25 x  4  0 3   x 2 2 3 1 1
Phương trình (1) tương đương với  x  4 3x 1 1  0,25 3x 1   1  3x 1  1   x  4 3x 1 1  3x 1 1  x  4 0,25 2 2
 3x 1  x  4 1   3x 1   x  4   1  x  4  x  2 0,5 x  2 x  2  0  x  2     
 x  0  x  5 (nhận) 0,5 x  4 2   x  2 2 x  5x  0  x  5 
Vậy phương trình đã cho có một nghiệm: x  5. 0,25 2   x   1 2y   1  x  2  0
b) Giải hệ phương trình    1 2,5 2 2
4xy  4y  4xy  x  2y  6  0 2 x   1 2y   1   x   1 1 0 
Câu 2 Hệ PT (1) tương đương với  2 2 4xy  4y 
4xy4yx     (4,5 đ) 1 2x 6y 7 0 0,5 2   x   1 2y   1   x   1 1  0   2 4y  x   1  4y  x   1  x   1  2x   1  32y   1  2  0 2   x   1 2y   1  x   1 1 0  0,25    x    y  2 1 2 1  2 x   1  32y   1  2  0 2ab  a 1 0  2ab   a   1  0
Đặt a  x 1, b  2y 1, ta có hệ:   2  0,25
ab  2a  3b  2  0  2 ab  2a   1  3b  0  2ab  a 1  0 2ab  a 1  0      b  0 2 0,25 ab  4ab  3b  0  ab  4a 3  0  2ab  a 1  0 a  1  x  2      (thỏa mãn (1)) b  0 b  0  1 0,5   y     2 2ab  a 1  0 a 1 x     0   (thỏa mãn (1)) 0,5 ab  4a  3  0 b   1  y  1 x  2  x  0
Vậy hệ phương trình đã cho có hai nghiệm:  1 ,  . 0,25 y    y  1   2 Trang 3/8
Cho tam giác nhọn ABCAB  AC có ba đường cao AD, BE,CF đồng quy tại
H. Đường tròn đường kính AC cắt đoạn thẳng BH tại M. Trên đoạn thẳng HC 3,0
lấy điểm N sao cho AM  AN.
a) Chứng minh EB.EH  ED.EF 1,5 0,25
(Hình vẽ phục vụ câu a: 0,25 điểm) Ta có:  BED  
BAD (vì tứ giác ABDE nội tiếp) 0,25  FEH  
BAD (vì tứ giác AEHF nội tiếp) Câu 3 Suy ra  BED   FEH (1) 0,25 (3,0 đ) Ta có:  EBD  
EFH (2) (vì tứ giác BCEF nội tiếp). 0,25
Từ (1) và (2) suy ra EBD và E  FH đồng dạng. 0,25 EB ED Do đó:   EB.EH  ED.EF. 0,25 EF EH
b) Chứng minh N thuộc đường tròn ngoại tiếp tam giác ABD. 1,5 Ta có: 2 2 AN =AM =AE.AC (3) (vì A
 MC vuông tại M có đường cao ME) 0,25 Ta có:  EAF   BAC ,  AEF  
ABC (vì tứ giác BCEF nội tiếp) 0,25 Suy ra AEF và A  BC đồng dạng. AE AF Do đó =  AE.AC  AF.AB (4) 0,25 AB AC AN AF Từ (3) và (4) suy ra 2 AN  AF.AB   . 0,25 AB AN Lại có  NAB   FAN nên ABN và A
 NF đồng dạng, suy ra  ANB   AFN  90. 0,25
Do đó N thuộc đường tròn đường kính AB, hay N thuộc đường tròn ngoại tiếp 0,25 A  BD . Trang 4/8
Cho tam giác nhọn ABCAB  AC có hai đường cao AE,BD cắt nhau tại H.
Đường trung trực của đoạn thẳng DH cắt AE tại M, cắt đường tròn ngoại tiếp tam 4,0
giác BCD tại P và Q ( P nằm giữa M và Q ).
a) Chứng minh MD là tiếp tuyến của đường tròn ngoại tiếp tam giác BCD. 1,5 0,25
(Hình vẽ phục vụ câu a: 0,25 điểm)
Vì M thuộc đường trung trực của đoạn thẳng DH và ADH vuông tại D nên Câu 4 AH (4,0 đ) MD = MH = MA= . Suy ra  MDH   MHD (1) 0,5 2
Vì tứ giác CDHE nội tiếp nên  BCD   MHD (2) 0,25 Từ (1) và (2) suy ra  MDH   BCD hay  MDB   1 BCD  sđ  DPB . 2 0,5
Hơn nữa, cung bị chắn bởi dây DB là  DPB nằm bên trong góc  MDB.
Vậy MD là tiếp tuyến của đường tròn ngoại tiếp tam giác BCD. b) Chứng minh  APM   AQM   CBD. 1,5 Ta có:  MDP  
MQD (vì MD là tiếp tuyến của đường tròn ngoại tiếp B  CD )  DMP   QMD 0,5
Suy ra MPD và MDQ đồng dạng. MP MD MP MA Do đó  , mà MD  MA nên  . 0,25 MD MQ MA MQ Ta lại có  PMA  
AMQ nên PMA và AMQ đồng dạng, suy ra  PAM   AQM . 0,25 Do đó  APM   AQM   APM   PAM   HMQ 0,25  90   MHD  90   EHB 0,25   CBD Trang 5/8
c) Đường thẳng AQ cắt đường tròn ngoại tiếp tam giác BCD tại F ( F khác Q ). 1,0 Chứng minh  APB   FPB.
(Hình vẽ phục vụ câu c: 0,25 điểm) 0,25  APB   AQB   APM   MPB   AQM   MQB   APM    AQM   MPB   MQB 0,25   CBD  180   QPB  
PQB (theo kết quả câu b))   CBD  180   QDB   PCB  
CBD 180  90    QDC  BCD    DCP  
CBD 180  90    DQP  BCD    DQP 0,25   CBD  90   BCD  180 (3)
Vì tứ giác BPFQ nội tiếp nên  FPB   AQB  180 (4) 0,25 Từ (3) và (4) suy ra  APB   FPB .
Một cách khác chứng minh  APB   AQB 180 như sau: Ta có:  DBP   DCP   DQP   CDQ   CBQ   CPQ (vì PQ // CD )  MPB  PBQ   PQB (vì 
MPB là góc ngoài của tam giác BPQ)  APM   AQM  
CBD (theo kết quả câu b))  APB  AQB   APM   MPB   AQM   MQB   APM    AQM  MPB   MQB   CBD   PBQ   PQB   PCB   CBD   PBD   DBC   CBQ  PCB   PCB  2  CBD   PCD   PCD 2 PCB  2  CBD   PCD    PCB  2  CBD    BCD  2.90 180 .  Trang 6/8
a) Cho số nguyên tố p . Tìm tất cả các số nguyên dương b sao cho nghiệm của 2,0 phương trình bậc hai 2
x  bx  bp  0 là số nguyên.
Giả sử tồn tại số nguyên dương b để phương trình 2
x  bx  bp  0 có hai nghiệm nguyên x , x . 0,25 1 2
Ta có: x  x  b, x x  bp. Vì ,
b p  0 nên x  0, x  0 . 1 2 1 2 1 2
Vì p là số nguyên tố nguyên tố và x x  bp nên x  p hoặc x  p . 0,25 1 2 1 2
Giả sử x  p  x  pc ( c nguyên dương); x  b  x  b  pc . 1 1 2 1 2
x x  bp  pc(b  pc)  bp  c(b  pc)  b  b(c 1)  pc (1) 1 2 0,5 2 pc  b 
(2) (với c 1, vì c 1 không thỏa mãn (1)) c 1 Ta có: ( , c c 1) 1 2  (c ,c 1) 1, mà 2
pc (c 1) nên p(c 1) . 0,25
Do p là số nguyên tố nên c 11 hoặc c 1 p .
- Với c 11  c  2 , thay vào (2) ta được b  4 p . 0,25 Thử lại: phương trình 2 2
x  4 px  4 p  0 có nghiệm kép * x  x  2 p   . 1 2
- Với c 1  p  c  p 1, thay vào (2) ta được 2 2 b  c  ( p 1) . Thử lại: phương trình 2 2 2
x  ( p 1) x  p( p 1)  0 có hai nghiệm phân biệt 0,25 * Câu 5 x  p 1  , * x  p( p 1)   . 1 2
(4,0 đ) Vậy b  4p hoặc 2 b  ( p 1) . 0,25
b) Cho ba số thực dương , x y, z thỏa mãn 2 2 2
x  y  z  3. Tìm giá trị lớn nhất của  1   1   1  2,0 biểu thức 2 2 2 2 2 2 P  xy x  y   yz y  z   zx z  x        .  z   x   y      2 2     2 2     2 2   xy yz zx P xy x y yz y z zx z x     . 0,25  z x y   Xét   2 2    2 2     2 2 M xy x y yz y z zx z  x : Ta có:  x  y4 4 3 2 2 3 4
 0  x  4x y  6x y  4xy  y  0 (1) xy  x  y2 3 2 2 3
 0  x y  2x y  xy  0 (2) 0,25
Cộng vế theo vế (1) và (2), ta được: 4 3 2 2 3 4
x  3x y  4x y  3xy  y  0 4 2 2 4
 x  x y  y  xy  2 2 4 3 x  y  (3)
Đẳng thức xảy ra khi x  y . Tương tự: 4 2 2 4 y  y z  z  yz  2 2 4 3
y  z  (4). Đẳng thức xảy ra khi y  z . 0,25 4 2 2 4 z  z x  x  zx  2 2 4 3
z  x  (5). Đẳng thức xảy ra khi z  x . Trang 7/8
Cộng vế theo vế (3), (4) và (5), ta được: 2 4 4 4 2 2 2 2 2 2
x  y  z  2x y  2y z  2z x   3xy   2 2 x  y   yz 2 2 y  z   zx 2 2 z  x  0,25  2x  y  z 2 2 2 2  3M 2 2.3  M 
 6 . Đẳng thức xảy ra khi x  y  z 1. 3  xy yz zx Xét N    : z x y 0,25 2 2 2  xy   yz   zx  Ta có: 2 2 2 2 N     2y  2z  2x        z   x   y  2 2 2  xy   yz   zx  xy yz yz zx zx xy Ta lại có: 2 2 2    .  .  .  y  z  x        z   x   y  z x x y y z 0,25 (áp dụng BĐT 2 2 2
a b c  ab bc ca) suy ra 2 2 2 2 N  y  z  x   2 2 2 3 3 3
3 x  y  z   3.3  9  N  3. xy yz zx 0,25 Đẳng thức xảy ra khi    x  y  z 1. z x y
Do đó P  M  N  6  3  3 .
P  3 xảy ra khi M  6 và N  3, hay x  y  z 1. 0,25
Vậy giá trị lớn nhất của P là 3, đạt được khi x  y  z 1. ---------- HẾT ----------
Ghi chú: Nếu học sinh có cách giải khác đúng thì Ban Giám khảo thảo luận và thống nhất thang
điểm cho phù hợp với Hướng dẫn chấm. Trang 8/8
Document Outline

• 1_De Toan HSG 9_2024
• 2_HDC Toan HSG 9_2024