Đề thi kết thúc học phần lý thuyết tự luận môn Xác suất thống kê| Trường Đại học Ngoại Thương

CƠ SỞ II TRƯỜNG ĐH NGOẠI THƯƠNG
ĐỀ THI KẾT THÚC HỌC PHẦN BỘ MÔN CƠ SỞ CƠ BẢN
LÝ THUYẾT XÁC SUẤT & THỐNG KÊ TOÁN Học kỳ II Năm học 2018 – 2019 Khóa: 57CLC Mã lớp: 154 Thời gian: 90 phút Mã đề: 01
Họ và tên:......................................................................................Mã số sinh viên: .............................
Câu 1 (2 điểm). Nhà máy có hai phân xưởng, sản lượng của phân xưởng I gấp 4 lần sản
lượng của phân xưởng II. Tỉ lệ phế phẩm của phân xưởng I, II lần lượt là 5% và 8%.
Chọn ngẫu nhiên một sản phẩm của nhà máy, tính:
a) Xác suất chọn được sản phẩm tốt và do phân xưởng I sản xuất.
b) Xác suất chọn được phế phẩm.
c) Giả sử chọn được sản phẩm tốt, tính xác suất sản phẩm này do phân xưởng I sản xuất.
Câu 2 (3 điểm). Tuổi thọ của máy giặt Samsung là biến ngẫu nhiên có phân phối chuẩn
với trung bình 48 tháng. Thời gian nhà sản xuất bảo hành sản phẩm sau khi bán ra là 24
tháng. Giả sử có 5,499% sản phẩm bị trả lại (hỏng) trong thời gian bảo hành.
a) Tính độ lệch chuẩn của tuổi thọ sản phẩm này.
b) Xác suất một chiếc máy giặt có tuổi thọ trên 36 tháng.
c) Một cửa hàng nhập 10 máy giặt loại này về bán. Tính xác suất có tối đa 2 máy hỏng
trong thời gian bảo hành.
Câu 3 (2 điểm). Điều tra 25 sinh viên đang sử dụng điện thoại di động về số tiền phải trả
trong 1 tháng thấy số tiền trung bình phải trả là 120 ngàn đồng, độ lệch chuẩn của mẫu
hiệu chỉnh là 35 ngàn đồng. Giả sử số tiền phải trả trong một tháng có phân phối chuẩn.
a) Với độ tin cậy 95% hãy ước lượng số tiền trung bình một sinh viên phải trả?
b) Với độ chính xác là 18 ngàn đồng thì độ tin cậy của ước lượng là bao nhiêu?
Câu 4 (1 điểm). Mức hao phí dầu của xe khách Huyndai 45 chỗ chạy từ Sài Gòn đến Đà
Lạt là một biến ngẫu nhiên có phân bố chuẩn với kỳ vọng là 99 lít. Đoạn đường trên mới
được sửa chữa lại, người ta cho rằng mức hao phí xăng trung bình giảm xuống. Quan sát
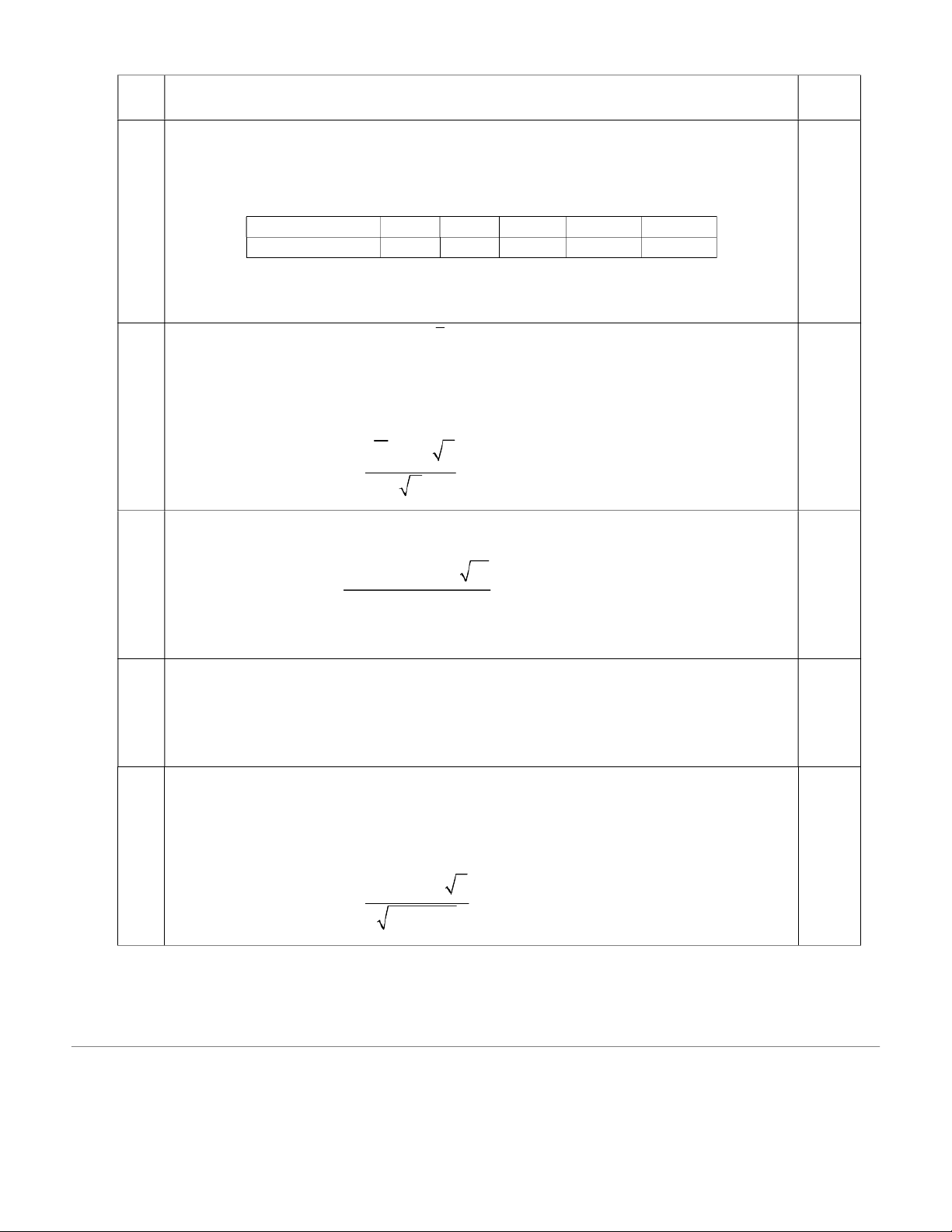
28 ô tô cùng loại thu được kết quả sau: Mức hao phí (lít)
85-90 90-95 95-100 100-105 105-110 Số ô tô 4 10 9 3 2
Với mức ý nghĩa  0,025 hãy kết luận về điều nghi ngờ nói trên. 
Câu 5 (1 điểm). Tỉ lệ phế phẩm do một máy tự động sản xuất là 5%. Kiểm tra ngẫu nhiên
300 sản phẩm thấy có 24 sản phẩm là phế phẩm. Từ đó có ý kiến cho rằng tỷ lệ phế phẩm
do máy đó sản xuất có chiều hướng tăng lên. Hãy kết luận ý kiến trên với mức ý nghĩa 5%.
Câu 6 (1 điểm). Một nghiên cứu được thực hiện đối với 55 người khu vực A và 66 người
của khu vực B của ngân hàng Vietcombank xem thu nhập hàng năm (tính bằng triệu
đồng) của nhân viên viên hai khu vực này có thực sự khác nhau hay không. Các số liệu mẫu thu được như sau: 2 2  n x 55 ; 18s2,7 ; 874 n ;  x 66  ; 167 s 8 , ; 653 1 1 1 2 2 2 .
Vậy với mức ý nghĩa 5% có thể cho rằng thu nhập trung bình của nhân viên ở hai khu vực
là khác nhau hay không? Giả sử thu nhập hàng năm của nhân viên hai khu vực này có phân phối chuẩn.
Giá trị tích phân Laplace  0,8 ,  0 288145  1, , 0  0 3413  1, , 6  0 44501  2,0 ,  0 4772
Các giá trị tới hạn của phân phối Chuẩn tắc Z  2 0 ,2 02 4 5 14 Z  1 , 0 9 056 Z  1 , 0 6 1 45 Z  1 , 28 0 0 , 125 , , ,
Các giá trị tới hạn của phân phối Student t 24  2,063899 t 24  2,571429 t 25  2,571429 0 0 0 0,008231   , 08375   ,025   t 25  2,059539 t 27  2,05183 t 27  2,37341 0 0 0 0,0125   , 25   ,025   t 28  2,0484 t 28  2 3 , 6845 0,0125   0 0 , 25  
-------------------------------------- HẾT -------------------------------------- Ghi chú:
- Đề thi gồm có 06 câu.
- Các kết quả cần làm tròn đến 4 chữ số thập phân
- Sinh viên không nhất thiết phải sử dụng hết các giá trị trong bảng trên.
- Cán bộ coi thi không giải thích gì thêm. DUYỆT ĐỀ THI GIẢNG VIÊN RA ĐỀ TRƯỞNG BỘ MÔN CS-CB ThS Nguyễn Trần Sỹ Nguyễn Văn Tiến
CƠ SỞ II TRƯỜNG ĐH NGOẠI THƯƠNG
ĐỀ THI KẾT THÚC HỌC PHẦN BỘ MÔN CƠ SỞ CƠ BẢN
LÝ THUYẾT XÁC SUẤT & THỐNG KÊ TOÁN Học kỳ II Năm học 2018 – 2019 Khóa: 57CLC Mã lớp: 154 Thời gian: 90 phút Mã đề: 01
Họ và tên:......................................................................................Mã số sinh viên: ............................. ĐÁP ÁN ĐỀ 01 Câu Nội dung Điểm hỏi
Câu 1 (2 điểm). Nhà máy có hai phân xưởng, sản lượng của phân xưởng I gấp 4 lần sản
lượng của phân xưởng II. Tỉ lệ phế phẩm của phân xưởng I, II lần lượt là 5% và 8%.
Chọn ngẫu nhiên một sản phẩm của nhà máy, tính:
a) Xác suất chọn được sản phẩm tốt và do phân xưởng I sản xuất.
b) Xác suất chọn được phế phẩm.
c) Giả sử chọn được sản phẩm tốt, tính xác suất sản phẩm này do phân xưởng I sản xuất. Đáp án:
Gọi H1, H2 là biến cố sản phẩm được chọn do phân xưởng 1, 2 sản xuất. 1
F: biến cố sản phẩm là phế phẩm. 0,5
Ta có: P H 0, 8; P H 0, 2; P F H 0, 05; P F H 0  , 0 8 1 2  1   2  
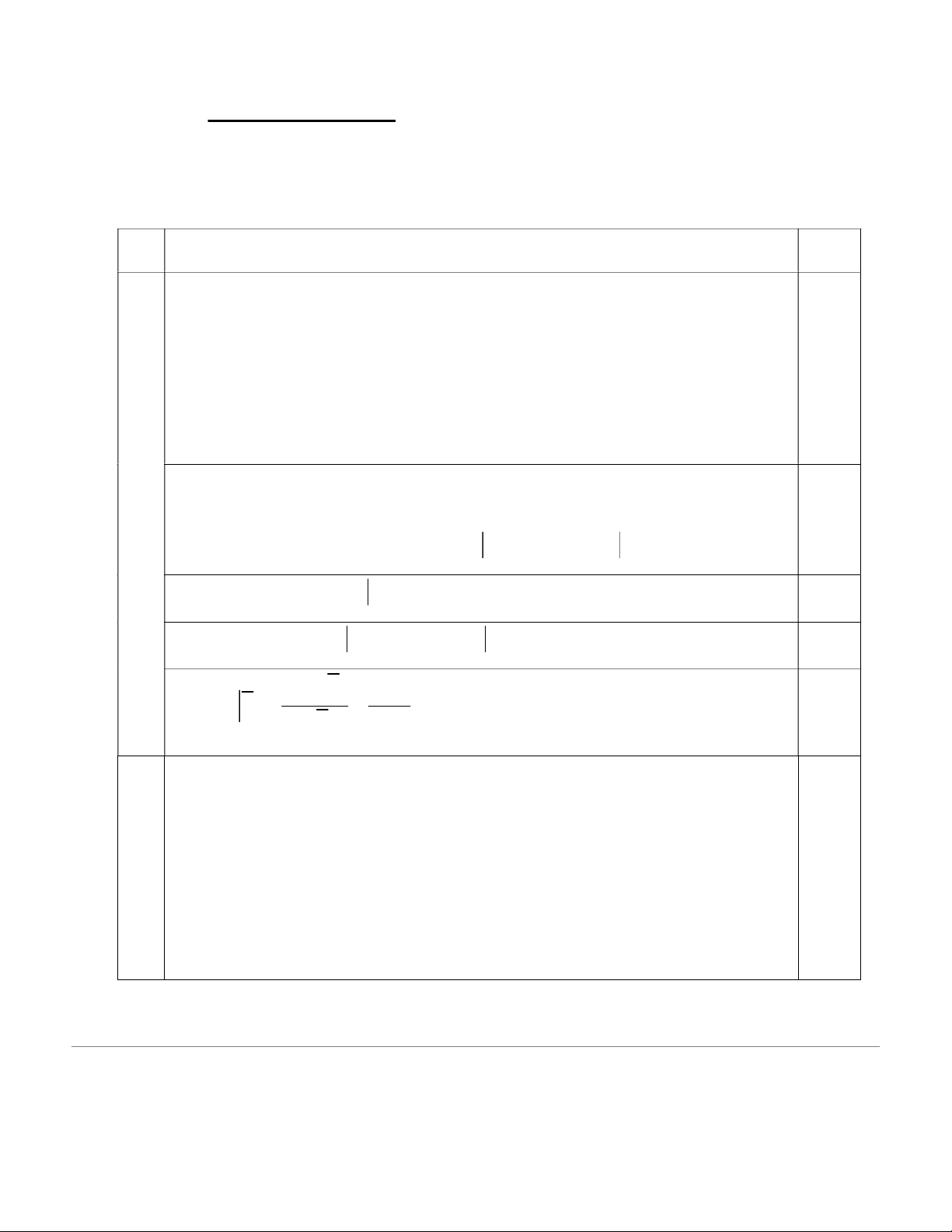
a) P H F  P H P F H 0,7 60,5 1   11   b) P   F P
 H P F H P H P F H 0  ,0 5 0, 6 5 1   1 2  2   P H F 1 0,7,6 c) P  H F     0 8 05 , 0 5 8 1 P F 0,944
Câu 2 (3 đi ểm). Tuổi thọ của máy giặt Samsung là biến ngẫu nhiên có phân phối chuẩn
với trung bình 48 tháng. Thời gian nhà sản xuất bảo hành sản phẩm sau khi bán ra là 24
tháng. Giả sử có 5,499% sản phẩm bị trả lại (hỏng) trong thời gian bảo hành. 2
a) Tính độ lệch chuẩn của tuổi thọ sản phẩm này.
b) Xác suất một chiếc máy giặt có tuổi thọ trên 36 tháng.
c) Một cửa hàng nhập 10 máy giặt loại này về bán. Tính xác suất có tối đa 2 máy hỏng
trong thời gian bảo hành. Giải.
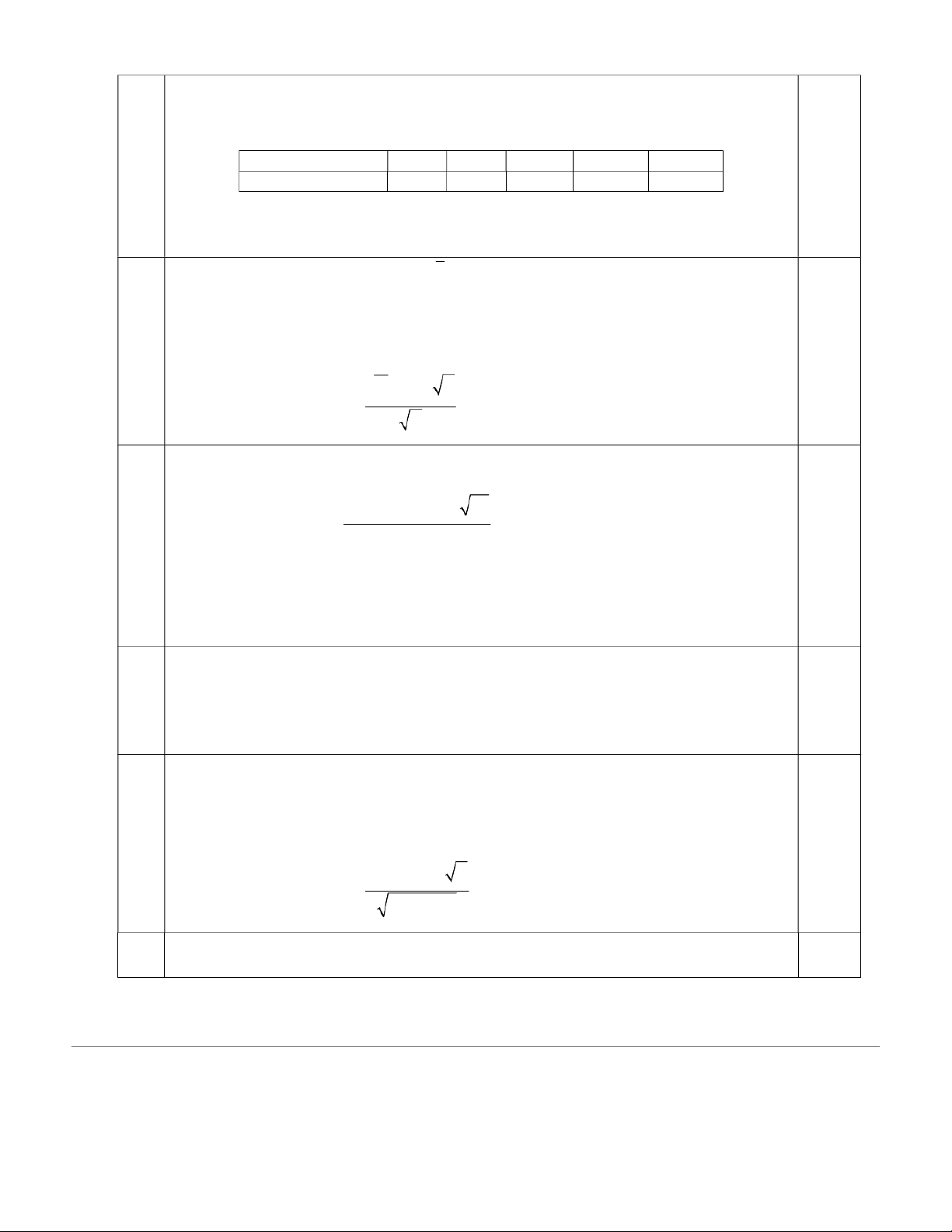
Gọi X là tuổi thọ máy giặt Samsung. Ta có: X ~ N 2 48;    0,5  a) Ta c Pó: X   24 48
 24  0, 05499     0,5, 0 05499      24      0,44 , 501     1 6    15 0,5   b) P X  3  6  0 5 ,  0 8, , 0 78814 5 0,5 P X  3  6 0, 7881 4 0 5 ,
c) Gọi Y là số máy hỏng trong thời gian bảo hành. Ta có: Y ~B 10;0, 05499 0,5 P Y  210C   2 0 i i i
 0,5 ,05,499 1 0 054,99  0 985102 10   i  0
Câu 3 (2 điểm). Điều tra 25 sinh viên đang sử dụng điện thoại di động về số tiền phải trả
trong 1 tháng thấy số tiền trung bình phải trả là 120 ngàn đồng, độ lệch chuẩn của mẫu
hiệu chỉnh là 35 ngàn đồng. Giả sử số tiền phải trả trong một tháng có phân phối chuẩn.
a) Với độ tin cậy 95% hãy ước lượng số tiền trung bình một sinh viên phải trả?
b) Với độ chính xác là 18 ngàn đồng thì độ tin cậy của ước lượng là bao nhiêu? Giải.
Gọi  là số tiền trung bình một sinh viên phải trả trong tháng. 0,5 3 a) Khoảng ước lượng: S   x
 x ;  với   t 2n    1 /  n S 35 0,5
Ta có:   t /,n ,  1 2 063899 14 44 729  2   n 25
Vậy khoảng ước lượng:   105,5527; 1,34 447  3   S   3 5 0,5 b) Ta có:  t n 1 18 t 24  /2/   2  n 5    t      0,5  t  24 2 5 , 7 , 1429 24 1 0 98325 2 / ,   0 008375  
Câu 4 (1 đi ểm). Mức hao phí dầu của xe khách Huyndai 45 chỗ chạy từ Sài Gòn đến Đà
Lạt là một biến ngẫu nhiên có phân bố chuẩn với kỳ vọng là 99 lít. Đoạn đường trên mới
được sửa chữa lại, người ta cho rằng mức hao phí xăng trung bình giảm xuống. Quan sát
28 ô tô cùng loại thu được kết quả sau: Mức hao phí
85-90 90-95 95-100 100-105 105-110 Số ô tô 4 10 9 3 2
Với mức ý nghĩa   0,025 hãy kết luận về điều nghi ngờ nói trên. Giải.
Từ mẫu thu được ta có: n x  28;  95,53 ; 571 s ,  5 5 00721 0,5 H  :    99 Bài toán kiểm định: 0 
(mức ý nghĩa  )0 ,025 H  :  99 1  X9n9
Tiêu chuẩn kiểm định: Z    t n  1 S Miền bác bỏ: 0,5 Z t n Z W ,              1   2 05183 Z 95,5 , 3571 99 28 Giá trị kiểm định:   3  33252 qs 5,500721
Vậy bác bỏ H0, điều nghi ngờ trên chấp nhận được ở mức ý nghĩa 2,5%.
Câu 5. Tỉ lệ phế phẩm do một máy tự động sản xuất là 5%. Kiểm tra ngẫu nhiên 300 sản
phẩm thấy có 24 sản phẩm là phế phẩm. Từ đó có ý kiến cho rằng tỷ lệ phế phẩm do máy
đó sản xuất có chiều hướng tăng lên. Hãy kết luận ý kiến trên với mức ý nghĩa   0,05. Giải.
Gọi p là tỷ lẹ phế phẩm hiện tại của nhà máy. 0,5 H   :p , 0 05 Bài toán kiểm định: 0  (mức ý nghĩa   0 ) ,05 H  :p , 0 05  1 F   0 n ,05  
Tiêu chuẩn kiểm định: Z N   0,1 0 0 , 5 0 . 9 , 5 Miền bác bỏ: W ,  Z  Z   Z 0,5     1 645  Giá trị kiểm định: Z W  2,384158  qs 
Vậy bác bỏ H0, tỷ lệ phế phẩm ở nhà máy tăng lên với mức ý nghĩa 5%.
Câu 6 (1 điểm). Một nghiên cứu được thực hiện đối với 55 người khu vực A và 66 người
của khu vực B của ngân hàng Vietcombank xem thu nhập hàng năm (tính bằng triệu
đồng) của nhân viên viên hai khu vực này có thực sự khác nhau hay không. Các số liệu mẫu thu được như sau: 2 2  n x 55  ; 18s2,7 ; 874 n ;  x 66  ; 167 s 8 ,  ; 653 1 1 1 2 2 2 .
Vậy với mức ý nghĩa 5% có thể cho rằng thu nhập trung bình của nhân viên ở hai khu
vực là khác nhau hay không? Giả sử thu nhập hàng năm của nhân viên hai khu vực này có phân phối chuẩn. Giải Gọi 2 2 0,5 X
X S S lần lượt là trung bình mẫu và phương sai mẫu về thu nhập của nhân 1, 2 1 , , 2 viên hai khu vực, Gọi 1
 2, lần lượt là thu nhập trung bình hàng năm của nhân viên hai khu vực. H   :   Bài toán kiểm định: 0 1 2  (mức ý nghĩa   0 ) 0 , 5 H  1 1:  2  X X  1 2
Tiêu chuẩn kiểm định: Z   tn  n  2 N 0,1 1 2 2 2    1 S 2S n n 1 2 Miền bác bỏ: W ,       0,5    Z t n n 2 Z 1 96 2 /  1 2     Z W  X X 1 2 Giá trị kiểm định:   2, 9  34296 qs 2 2  S S 1 2 n n 1 2
Vậy bác bỏ H0. Có thể nói thu nhập trung bình hai khu vực là khác nhau ở mức ý nghĩa 5%.
CƠ SỞ II TRƯỜNG ĐH NGOẠI THƯƠNG
ĐỀ THI KẾT THÚC HỌC PHẦN BỘ MÔN CƠ SỞ CƠ BẢN
LÝ THUYẾT XÁC SUẤT & THỐNG KÊ TOÁN Học kỳ II Năm học 2018 – 2019 Khóa: 57CLC Mã lớp: 154 Thời gian: 90 phút Mã đề: 02
Họ và tên:......................................................................................Mã số sinh viên: .............................
Câu 1 (2 điểm). Nhà máy có hai phân xưởng, sản lượng của phân xưởng I gấp 4 lần sản
lượng của phân xưởng II. Tỉ lệ phế phẩm của phân xưởng I, II lần lượt là 8% và 5%.
Chọn ngẫu nhiên một sản phẩm của nhà máy, tính:
a) Xác suất chọn được phế phẩm và do phân xưởng II sản xuất.
b) Xác suất chọn được phế phẩm.
c) Giả sử chọn được sản phẩm tốt, tính xác suất sản phẩm này do phân xưởng II sản xuất.
Câu 2 (3 điểm). Tuổi thọ của máy giặt Samsung là biến ngẫu nhiên có phân phối chuẩn
với trung bình 48 tháng. Thời gian nhà sản xuất bảo hành sản phẩm sau khi bán ra là 24
tháng. Giả sử có 5,499% sản phẩm bị trả lại (hỏng) trong thời gian bảo hành.
a) Tính độ lệch chuẩn của tuổi thọ sản phẩm này.
b) Xác suất một chiếc máy giặt có tuổi thọ trên 60 tháng.
c) Một cửa hàng nhập 20 máy giặt loại này về bán. Tính xác suất có tối đa 2 máy hỏng
trong thời gian bảo hành.
Câu 3 (2 điểm). Điều tra 49 sinh viên đang sử dụng điện thoại di động về số tiền phải trả
trong 1 tháng thấy số tiền trung bình phải trả là 120 ngàn đồng, độ lệch chuẩn của mẫu
hiệu chỉnh là 35 ngàn đồng. Giả sử số tiền phải trả trong một tháng có phân phối chuẩn.
a) Với độ tin cậy 95% hãy ước lượng số tiền trung bình một sinh viên phải trả?
b) Với độ chính xác là 18 ngàn đồng thì độ tin cậy của ước lượng là bao nhiêu?
Câu 4 (1 điểm). Mức hao phí dầu của xe khách Huyndai 45 chỗ chạy từ Sài Gòn đến Đà
Lạt là một biến ngẫu nhiên có phân bố chuẩn với kỳ vọng là 96 lít. Đoạn đường trên mới
được sửa chữa lại, người ta cho rằng mức hao phí xăng trung bình giảm xuống. Quan sát
28 ô tô cùng loại thu được kết quả sau: Mức hao phí (lít)
85-90 90-95 95-100 100-105 105-110 Số ô tô 4 10 9 3 2
Với mức ý nghĩa   0,025 hãy kết luận về điều nghi ngờ nói trên.
Câu 5. Tỉ lệ phế phẩm do một máy tự động sản xuất là 5%. Kiểm tra ngẫu nhiên 400 sản
phẩm thấy có 28 sản phẩm là phế phẩm. Từ đó có ý kiến cho rằng tỷ lệ phế phẩm do máy
đó sản xuất có chiều hướng tăng lên. Hãy kết luận ý kiến trên với mức ý nghĩa   0,01.
Câu 6 (1 điểm). Một nghiên cứu được thực hiện đối với 55 người khu vực A và 66 người
của khu vực B của ngân hàng Vietcombank xem thu nhập hàng năm (tính bằng triệu
đồng) của nhân viên viên hai khu vực này có thực sự khác nhau hay không. Các số liệu mẫu thu được như sau: 2 2  n x 55 ; 18s2,7 ; 874 n ;  x 66  ; 167 s 8 , ; 653 1 1 1 2 2 2 .
Vậy với mức ý nghĩa 5% có thể cho rằng thu nhập trung bình của nhân viên ở hai khu vực
là khác nhau hay không? Giả sử thu nhập hàng năm của nhân viên hai khu vực này có phân phối chuẩn.
Giá trị tích phân Laplace  0,8 ,  0 288145  1, , 0  0 3413  1, , 6  0 44501  2,0 ,  0 4772
Các giá trị tới hạn của phân phối Chuẩn tắc Z  2 0 ,2 02 4 5 14 Z  1 , 0 9 056 Z  1 , 0 6 1 45 Z  1 , 28 0,0125 , , , Z  20 3 ,00 3 Z  Z  0 0 8198 2 0 ,4 005 2 5 , 76 , 1 , ,
Các giá trị tới hạn của phân phối Student t 27  2 0 , 5183 t 27  2,37341 t n Z   2 / /   2  0,0125   0,025   khi n  32 t 28  2,0484 t 28  2,36845 0 025 0 0125 ,   ,  
-------------------------------------- HẾT -------------------------------------- Ghi chú:
- Đề thi gồm có 06 câu.
- Các kết quả cần làm tròn đến 4 chữ số thập phân
- Sinh viên không nhất thiết phải sử dụng hết các giá trị trong bảng trên.
- Cán bộ coi thi không giải thích gì thêm. DUYỆT ĐỀ THI GIẢNG VIÊN RA ĐỀ TRƯỞNG BỘ MÔN CS-CB ThS Nguyễn Trần Sỹ Nguyễn Văn Tiến
CƠ SỞ II TRƯỜNG ĐH NGOẠI THƯƠNG
ĐỀ THI KẾT THÚC HỌC PHẦN BỘ MÔN CƠ SỞ CƠ BẢN
LÝ THUYẾT XÁC SUẤT & THỐNG KÊ TOÁN Học kỳ II Năm học 2018 – 2019 Khóa: 57CLC Mã lớp: 154 Thời gian: 90 phút Mã đề: 02
Họ và tên:......................................................................................Mã số sinh viên: ............................. ĐÁP ÁN ĐỀ 02 Câu Nội dung Điểm hỏi
Câu 1 (2 điểm). Nhà máy có hai phân xưởng, sản lượng của phân xưởng I gấp 4 lần sản
lượng của phân xưởng II. Tỉ lệ phế phẩm của phân xưởng I, II lần lượt là 8% và 5%.
Chọn ngẫu nhiên một sản phẩm của nhà máy, tính:
a) Xác suất chọn được phế phẩm và do phân xưởng II sản xuất.
b) Xác suất chọn được phế phẩm.
c) Giả sử chọn được sản phẩm tốt, tính xác suất sản phẩm này do phân xưởng II sản xuất. Giải.
Gọi H1, H2 là biến cố sản phẩm được chọn do phân xưởng 1, 2 sản xuất. 1
F: biến cố sản phẩm là phế phẩm. 0,5
Ta có: P H 0, 8; P H 0, 2; P F H 0, 08; P F H 0  , 0 5 1 2  1   2   a) P H F P  H P F H 0, 01,5 2   22   b) P   F P
 H P F H P H P F H 0  ,0 7 0, 4 5 1   1 2  2   P H F 2 0,1,9 c) P  H F     0 20 5 0 1 , 8 5 3 2 P  0 F ,926
Câu 2 (3 điểm). Tuổi thọ của máy giặt Samsung là biến ngẫu nhiên có phân phối chuẩn
với trung bình 48 tháng. Thời gian nhà sản xuất bảo hành sản phẩm sau khi bán ra là 24
tháng. Giả sử có 5,499% sản phẩm bị trả lại (hỏng) trong thời gian bảo hành.
a) Tính độ lệch chuẩn của tuổi thọ sản phẩm này. 2
b) Xác suất một chiếc máy giặt có tuổi thọ trên 60 tháng.
c) Một cửa hàng nhập 20 máy giặt loại này về bán. Tính xác suất có tối đa 2 máy hỏng
trong thời gian bảo hành. Giải.
Gọi X là tuổi thọ máy giặt Samsung. Ta có: X ~ N 2 48;    0,5  a) Ta c Pó: X   24 48
 24  0, 05499     0,5, 0 05499      24      0,44 , 501     1 6    15 0,5   b) P X  6  0  0,  5,  0  80,5 P X  6  0 0,211 806,5
c) Gọi Y là số máy hỏng trong thời gian bảo hành. Ta có: Y ~B 20;0, 0549  9 0,5 P Y  220C   2 0 i i i  0,5 ,0,5499 1  0 054,99  0 905719 20   i  0
Câu 3 (2 điểm). Điều tra 49 sinh viên đang sử dụng điện thoại di động về số tiền phải trả
trong 1 tháng thấy số tiền trung bình phải trả là 120 ngàn đồng, độ lệch chuẩn của mẫu
hiệu chỉnh là 35 ngàn đồng. Giả sử số tiền phải trả trong một tháng có phân phối chuẩn.
a) Với độ tin cậy 95% hãy ước lượng số tiền trung bình một sinh viên phải trả?
b) Với độ chính xác là 18 ngàn đồng thì độ tin cậy của ước lượng là bao nhiêu? Giải.
Gọi  là số tiền trung bình một sinh viên phải trả trong tháng. 0,5 3 a) Khoảng ước lượng: S S   x
 x ;  với   t n 1 Z  /2 2 /  n n S 35 0,5 Ta có:   Z 2  1, 9,6  9 8  / n 49
Vậy khoảng ước lượng:   110, 2; 129,  8  S   3 50,5 b) Ta có:  Z 2 Z 2 12  / /  n 7 2  Z 0 00     0,5  Z 8198  2,4, 1 0 983605 / ,
Câu 4 (1 điểm). Mức hao phí dầu của xe khách Huyndai 45 chỗ chạy từ Sài Gòn đến Đà
Lạt là một biến ngẫu nhiên có phân bố chuẩn với kỳ vọng là 96 lít. Đoạn đường trên mới
được sửa chữa lại, người ta cho rằng mức hao phí xăng trung bình giảm xuống. Quan sát
28 ô tô cùng loại thu được kết quả sau: Mức hao phí
85-90 90-95 95-100 100-105 105-110 Số ô tô 4 10 9 3 2
Với mức ý nghĩa   0,025 hãy kết luận về điều nghi ngờ nói trên. Giải.
Từ mẫu thu được ta có: n x  28;  95,53 ; 571 s ,  5 5 00721 0,5 H  :    96 Bài toán kiểm định: 0 
(mức ý nghĩa  )0 ,025 H  :  96  1 X9n6
Tiêu chuẩn kiểm định: Z   t  n  1 S Miền bác bỏ: 0,5 Z t n Z W ,              1   2 05183 Z 95,5 , 3571 96 28 Giá trị kiểm định:   0  44663 qs 5,500721
Vậy chưa đủ cơ sở bác bỏ H0, điều nghi ngờ trên không chấp nhận được ở mức ý nghĩa 2,5%.
Câu 5. Tỉ lệ phế phẩm do một máy tự động sản xuất là 5%. Kiểm tra ngẫu nhiên 400 sản
phẩm thấy có 28 sản phẩm là phế phẩm. Từ đó có ý kiến cho rằng tỷ lệ phế phẩm do máy
đó sản xuất có chiều hướng tăng lên. Hãy kết luận ý kiến trên với mức ý nghĩa   0,01. Giải.
Gọi p là tỷ lẹ phế phẩm hiện tại của nhà máy. 0,5 H   :p , 0 05
Bài toán kiểm định:  0 (mức ý nghĩa   0 ) ,01 H  :p , 0 05  1  Z   F N 0n,05    Tiêu chuẩn kiểm định: 0,1 0 0 , 5 0 . 9 , 5 Miền bác bỏ: W ,  Z  Z   Z 0,5     2 32635  Giá trị kiểm định: Z W  1,835326  qs 
Vậy chưa đủ cơ sở bác bỏ H0, tỷ lệ phế phẩm ở nhà máy không tăng lên với mức ý nghĩa 5%.
Câu 6 (1 điểm). Một nghiên cứu được thực hiện đối với 55 người khu vực A và 66 người
của khu vực B của ngân hàng Vietcombank xem thu nhập hàng năm (tính bằng triệu
đồng) của nhân viên viên hai khu vực này có thực sự khác nhau hay không. Các số liệu mẫu thu được như sau: 2 2  n x 55  ; 18s2,7 ; 874 n ;  x 66  ; 167 s 8 ,  ; 653 1 1 1 2 2 2 .
Vậy với mức ý nghĩa 5% có thể cho rằng thu nhập trung bình của nhân viên ở hai khu
vực là khác nhau hay không? Giả sử thu nhập hàng năm của nhân viên hai khu vực này có phân phối chuẩn. Giải Gọi 2 2 0,5 X
X S S lần lượt là trung bình mẫu và phương sai mẫu về thu nhập của nhân 1, 2 1 , , 2 viên hai khu vực, Gọi 1
 2, lần lượt là thu nhập trung bình hàng năm của nhân viên hai khu vực. H   :   Bài toán kiểm định: 0 1 2  (mức ý nghĩa   0 ) 0 , 5 H  1 1:  2  Z  X X 1 2
Tiêu chuẩn kiểm định:  t  n  n  2 N 0,1 1 2 2 2    1 S 2S n n 1 2 Miền bác bỏ: W ,       0,5    Z t n n 2 Z 1 96 2 /  1 2     Z W   X X 1 2 Giá trị kiểm định:  2,9  34296 qs 2 2  S S 1 2 1 n 2n
Vậy bác bỏ H0. Có thể nói thu nhập trung bình hai khu vực là khác nhau ở mức ý nghĩa 5%.