Đề Thi Kỳ 2 Toán 8 Sở GD Quảng Nam 2025-2026 Có Đáp Án

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC 2025-2026 QUẢNG NAM
Môn: TOÁN – LỚP 8
Thời gian: 60 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
(Đề gồm có 02 trang) MÃ ĐỀ A
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (5,0 điểm):
Chọn chữ cái đứng trước câu trả lời đúng nhất cho mỗi câu hỏi sau và ghi vào giấy
làm bài. Ví dụ câu 1 chọn đáp án C thì ghi là 1C.
Câu 1. Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn? A. 3x + 2 = 0. B. 2 x − 5x = 0. C. 0x − 2 = 0. D. x − x = 5.
Câu 2. Phương trình nào sau đây tương đương với phương trình 2x + 3 = 3x − 4? A. −x = 7. B. 5x = −1. C. x = 7. D. 2x − 3x = 4 − + 3.
Câu 3. Tập hợp nghiệm của phương trình (2x +5)(x −3) = 0 là 5  5 5  5 A. S = ;3     . B. S = − ; 3 − . C. S =  ; 3 − . D. S = − ;3. 2   2  2   2 
Câu 4. Điều kiện xác định của phương trình 1 = x 1+ là x − 2 x + 3 A. x  2 .
B. x  2 và x  −3 . C. x  0 và x  2 . D. x  −3.
Câu 5. Cho hình chữ nhật có chiều rộng là x cm (x > 0). Chiều dài hơn chiều rộng 3cm. Biểu
thức nào sau đây biểu thị diện tích của hình chữ nhật đó? A. (2x + 3).2. B. x + 3. C. x(x +3) . D. 2 x + 3.
Câu 6. Nếu 3a  3b thì A. a  b. B. a < b. C. −a  b. D. a  b.
Câu 7. Khẳng định nào sau đây là khẳng định đúng? A. 8 −  (−2).4. B. 3+ ( 5 − ) < 2. − C. −7  −6. D. a > −a.
Câu 8. Với a < 0, ta khẳng định A. a 3  5a. B. −2a < −3a. C. a < 5a. D. a > 5a − .
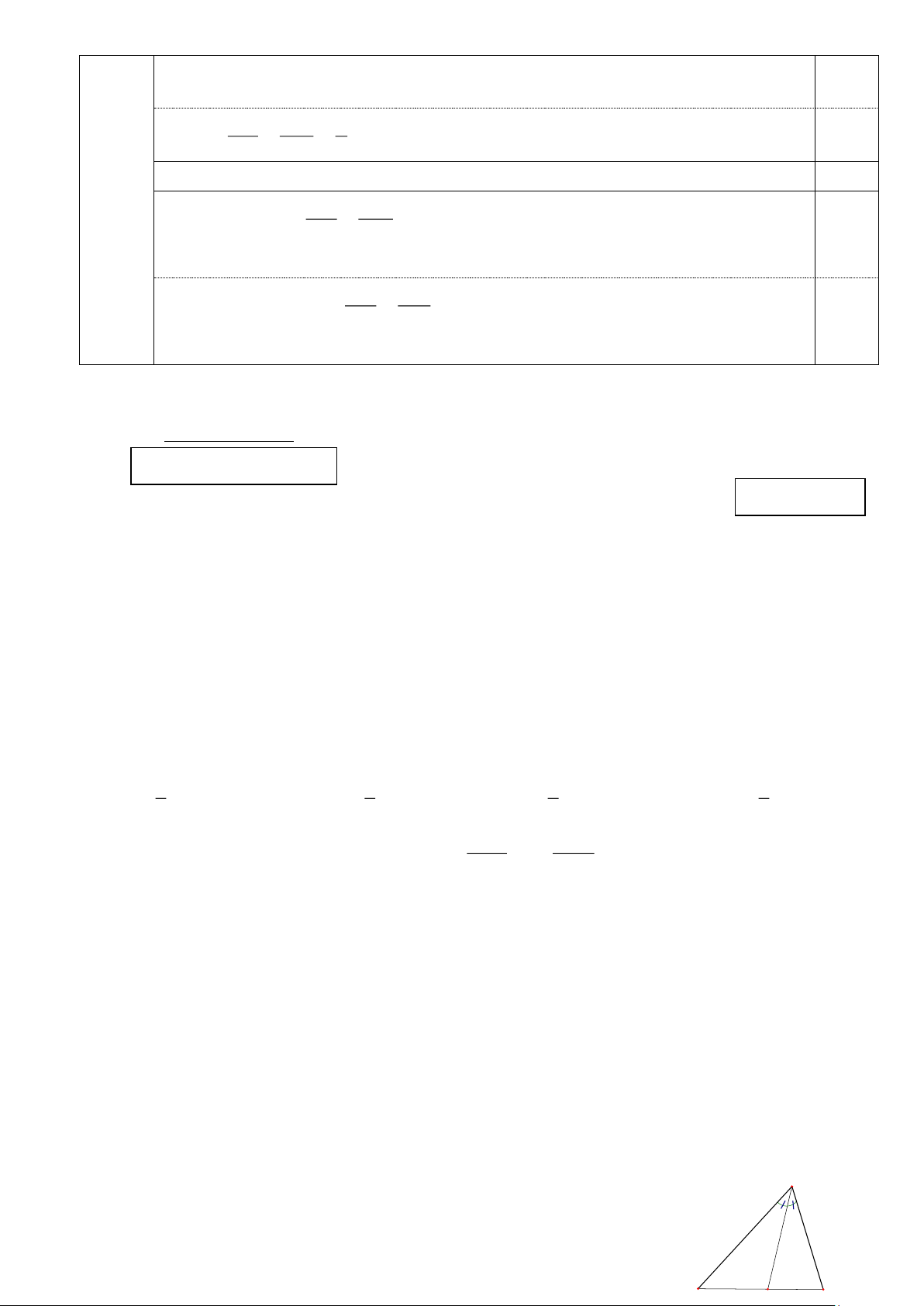
* Quan sát hình 1 và thực hiện câu hỏi 9. A
Biết AD là đường phân giác của tam giác ABC. Hình 1 AC
Câu 9. Tỉ số
bằng tỉ số nào dưới đây? AB AD AD BC DC A. . B. . C. . D. . B C AC BC AB DB D
* Quan sát hình 2 và thực hiện các câu hỏi: 10; 11; 12;13. Hình 2
Biết MN//BC; AB = 3cm; AM = 2cm; AN = 2,6cm; BC = 4,5cm. A 2,6cm AM 2cm Câu 10. Tỉ số
bằng tỉ số nào dưới đây? 3cm MB M N AN AM AN BC A. . B. . C. . D. . B NC BC AM MN 4,5cm C Trang 1
Câu 11. ∆MAN đồng dạng với A. ∆ACM. B. ∆ ANB . C. ∆ NBC . D. ∆ BAC .
Câu 12. Độ dài đoạn thẳng NC là A. 2,6cm . B.1cm . C.1,3cm . D.1,25cm .
Câu 13. Độ dài đoạn thẳng MN là A. 4,5cm . B.3cm . C. 6cm . D. 2cm .
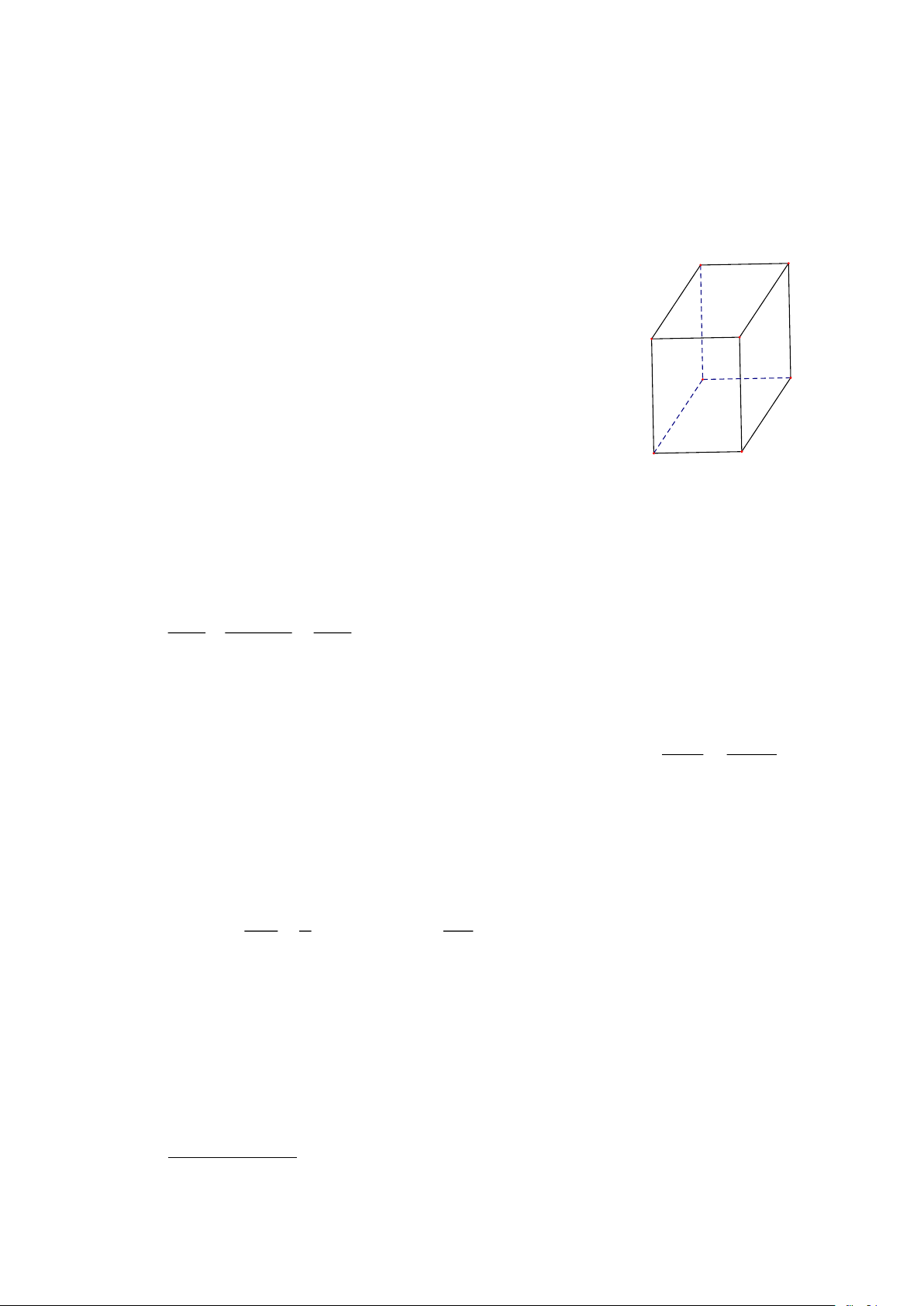
*Quan sát hình 3 và thực hiện các câu hỏi: 14; 15. A Hình 3 B
Biết ABCD.A'B'C'D' là hình hộp chữ nhật.
Câu 14. Mặt đối diện với mặt AA 'D'D là A. BB'C'C . B. AA 'D'D . D C C. ABCD. D. CC'D'D.
Câu 15. Mọi điểm của đường thẳng AB đều thuộc mặt phẳng A' B' A. (BB'C'C). B.(AA'D'D) . C. (ABCD). D. (CC'D'D). D' C'
PHẦN II. TỰ LUẬN (5,0 điểm):
Câu 1. (1,25 điểm):
Giải các phương trình sau: a. 5(x + ) 1 = 4x − 2; x −1 1− 2x 1 b. + ( + ) = . x x x 1 x +1
Câu 2. (1,25 điểm):
a. Cho biết a  b, chứng tỏ rằng 2a − 3  2b − 3 ; 2 − x 3 − 2x
b. Giải bất phương trình sau và biểu diễn nghiệm trên trục số < . 3 5
Câu 3. (2,5 điểm):
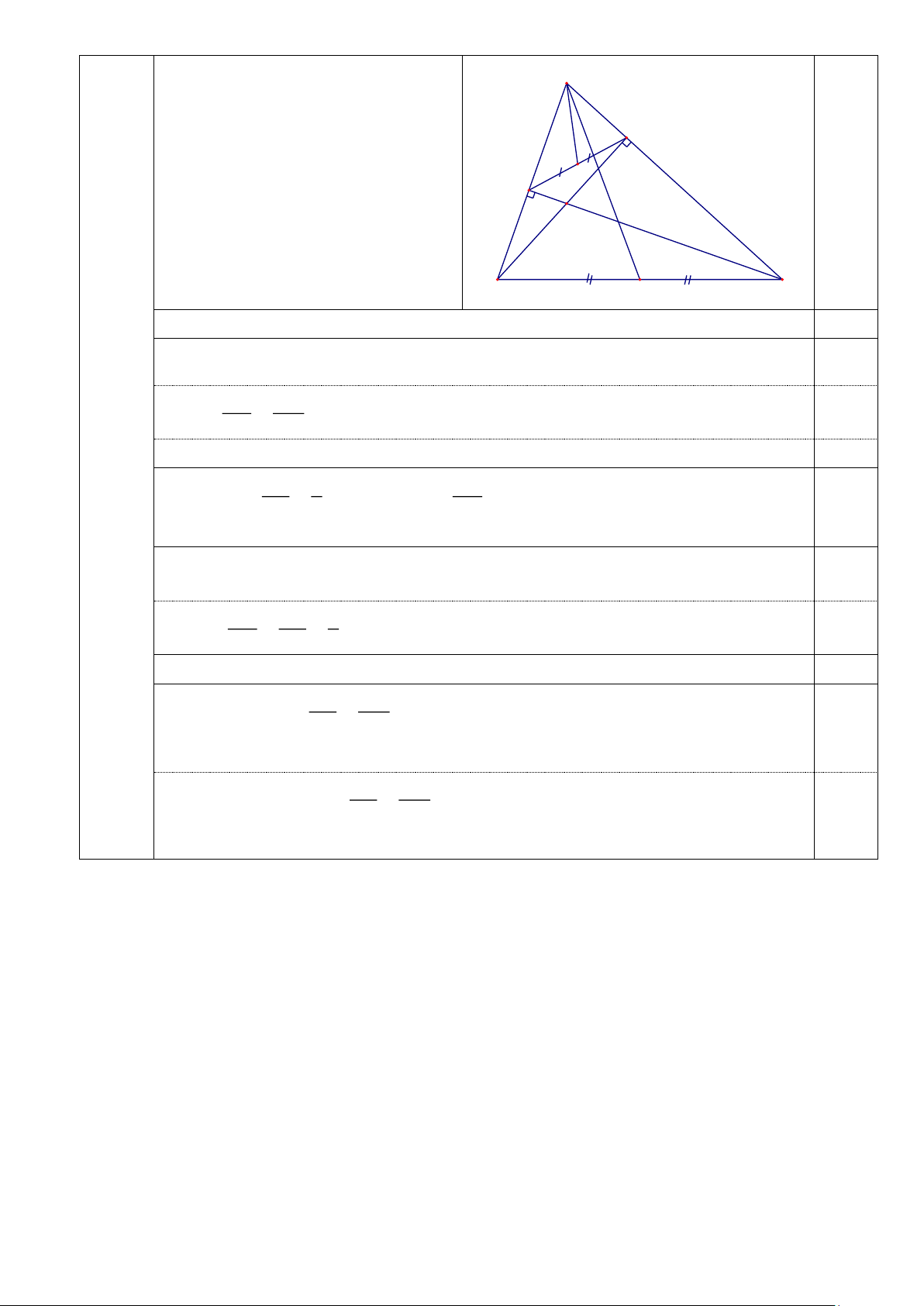
Cho tam giác nhọn ABC (AB  AC), hai đường cao BM và CN cắt nhau tại D.
a. Chứng minh tam giác ABM đồng dạng với tam giác ACN, từ đó suy ra AN.AB = AM.AC; NB 2 DB b. Cho biết = , hãy tính tỉ số ; MC 3 DC
c. Gọi I và K lần lượt là trung điểm của BC và MN. Chứng minh CAI = BAK.
----------------HẾT----------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC 2020-2021 QUẢNG NAM
Môn: TOÁN – LỚP 8
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM – MÃ ĐỀ A
(Đáp án và Hướng dẫn chấm gồm 02 trang) Trang 2
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (5,0 điểm): Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Đ/án A C D B C D A B D A D C B A C
PHẦN II.TỰ LUẬN (5,0 điểm): Câu Nội dung Điểm
a. Giải phương trình 5(x + ) 1 = 4x − 2 0,5
 5x + 5 = 4x − 2  5x − 4x = −2 − 5 0,25
 x = −7 ; Vậy S = −  7 0,25 x −1 1− 2x 1 + = 1. b. Giải phương trình ( + ) . 0,75 x x x 1 x +1 (1,25   −
điểm) ĐKXĐ: x 0 và x 1 0,25
Biến đổi phương trình trở thành 0,25 2 x − 3x = 0 (*) Tìm được hai
nghiệm của phương trình (*) là 0 và 3;
Đối chiếu và kết luận S =   3 . 0,25
a. Cho biết a  b, chứng tỏ rằng 2a − 3  2b − 3 . 0,5
Từ a  b , suy ra 2a  2b 0,25 Do đó 2a − 3  2b − 3 0,25 2. 2 − x 3 − 2x
(1,25 b. Giải bất phương trình sau và biểu diễn nghiệm trên trục số < . 0,75 điểm) 3 5
Biến đổi bất phương trình trở thành 5(2 − x)  3(3 − 2x) 0,25
Tìm được nghiệm của bất phương trình x  −1. 0,25
Biểu diễn đúng tập nghiệm của bất phương trình trên trục số 0,25
Cho tam giác nhọn ABC (AB  AC), hai đường cao BM và CN cắt nhau tại D. Hình vẽ: A
- Hình vẽ phục vụ ý a, b: 0,25 điểm;
- Hình vẽ phục vụ cả câu: 0,5 điểm. M K N 0,5 D 3. (2,5 điểm) B I C
a. Chứng minh  ABM đồng dạng  ACN, từ đó suy ra AN.AB = AM.AC; 1,0
Giải thích hai tam giác vuông ABM và ACN có góc A là góc nhọn chung nên 0,5 đồng dạng AB AM Suy ra = 0,25 AC AN Do đó AN.AB = AM.AC. 0,25 NB 2 DB 0,5 b. Cho biết = , hãy tính tỉ số . MC 3 DC Trang 3
Nêu được hai tam giác vuông NDB và MDC có: NDB = MDC (đối đỉnh) nên 0,25 đồng dạng. DB NB 2 Suy ra: = = . 0,25 DC MC 3
c. Gọi I và K lần lượt là trung điểm của BC và MN. Chứng minh CAI = BAK. 0,5 AN AM Từ câu a, suy ra: =
; kết hợp với A là góc chung nên có được  ANM AC AB 0,25
đồng dạng với  ACB, suy ra ANK = ACI AN NK Chứng minh được =
, từ đó suy ra  ANK đồng dạng với AC CI 0,25
 ACI(c.g.c). Do đó CAI = BAK.
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC 2020-2021 QUẢNG NAM
Môn: TOÁN – LỚP 8
Thời gian: 60 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
(Đề gồm có 02 trang) MÃ ĐỀ B
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (5,0 điểm):
Chọn chữ cái đứng trước câu trả lời đúng nhất cho mỗi câu hỏi sau và ghi vào giấy
làm bài. Ví dụ câu 1 chọn đáp án C thì ghi là 1C.
Câu 1. Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn? A. 0x + 2 = 0. B. 2 x − 5x = 0. C. 5x − 2 = 0. D. x − x = 3.
Câu 2. Phương trình nào sau đây tương đương với phương trình 3x + 3 = 4x − 2 ? A. x = 5. B. 7x = 1. C. x = −5. D. 3x − 4x = 2 − + 3.
Câu 3. Tập hợp nghiệm của phương trình (3x +5)(x − 2) = 0 là 5  5 5  5 A. S = ;2    . B. S = − ;2. C. S = ; 2 −   . D. S = − ; 2 − . 3   3  3   3 
Câu 4. Điều kiện xác định của phương trình 1 x =1+ là x −5 x + 7 A. x  5. B. x  −7 . C. x  5 − và x  7 . D. x  5và x  7 − .
Câu 5. Cho hình chữ nhật có chiều dài là x cm (x > 3). Chiều rộng ngắn hơn chiều dài 3cm.
Biểu thức nào sau đây biểu thị diện tích của hình chữ nhật đó? A. x(x − 3) . B. x − 3. C. (2x − 3).2. D. 2 x − 3.
Câu 6. Nếu 5a  5b thì A. a  b. B. a < b. C. −a  b. D. a  b.
Câu 7. Khẳng định nào sau đây là khẳng định đúng? A. 8 −  (−2).4. B. 3+ ( 5 − )  −1. C. 10 −  ( 2 − ).5. D. a > −a.
Câu 8. Với a < 0, ta khẳng định A. a 3 > 5a. B. −2a > 3a. − C. a < 5a. D. a > 5a − .
* Quan sát hình 1 và thực hiện câu hỏi 9. A
Biết AD là đường phân giác của tam giác ABC. Hình 1 Trang 4 B C D DB
Câu 9. Tỉ số
bằng tỉ số nào dưới đây? AB AD DC BC DC A. . B. . C. . D. . AC AC AB DB Hình 2
* Quan sát hình 2 và thực hiện các câu hỏi: 10; 11; 12;13. A
Biết MN//BC; AB = 6cm; AM = 4cm; AN = 5,2cm; BC = 9cm. 5,2cm AM 4cm 6cm Câu 10. Tỉ số
bằng tỉ số nào dưới đây? MB M N BC AM AN AN A. . B. . C. . D. . B MN BC AM NC 9cm C
Câu 11. ∆MNA đồng dạng với A. ∆ BCA . B. ∆ ANB . C. ∆ NBC . D. ∆ AMC .
Câu 12. Độ dài đoạn thẳng NC là A. 5,2cm . B. 2,6cm . C.1,3cm . D. 2,25cm .
Câu 13. Độ dài đoạn thẳng MN là A. 4,5cm . B.3cm . C. 6cm . D. 4cm .
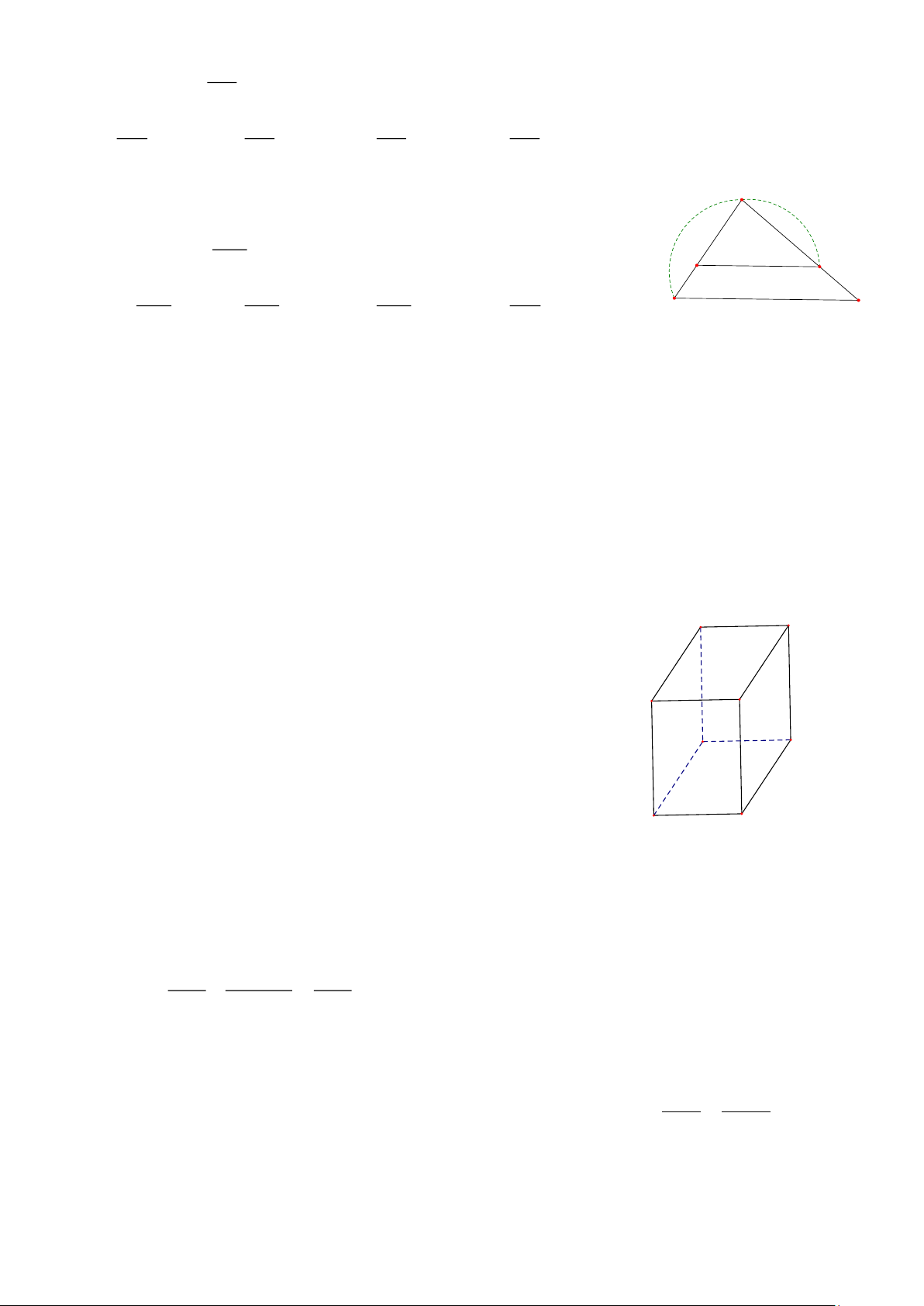
*Quan sát hình 3 và thực hiện các câu hỏi: 14; 15. A Hình 3 B
Biết ABCD.A'B'C'D' là hình hộp chữ nhật.
Câu 14. Mặt đối diện với mặt AA 'B'B là A. BB'C'C . B. AA 'D'D . D C C. ABCD. D. CC'D'D.
Câu 15. Mọi điểm của đường thẳng BC đều thuộc mặt phẳng A' B' A. (AA 'B'B). B. (AA'D'D) . C. (BB'C'C). D. (CC'D'D). D' C'
PHẦN II. TỰ LUẬN (5,0 điểm):
Câu 1. (1,25 điểm):
Giải các phương trình sau: a. 4(x + 2) = 3x −1; x +1 1− 3x 1 b. + ( − ) = . x x x 1 x −1 Câu 2. (1,25 điểm):
a. Cho biết a  b, chứng tỏ rằng 3a – 1 < 3b – 1. x +1 2x −1
b. Giải bất phương trình sau và biểu diễn nghiệm trên trục số  . 3 7 Câu 3. (2,5 điểm):
Cho tam giác nhọn DEF (DE  DF), hai đường cao EH và FI cắt nhau tại K. Trang 5
a. Chứng minh tam giác DEH đồng dạng với tam giác DFI, từ đó suy ra DI.DE = DH.DF; IE 3 KE b. Cho biết = , hãy tính tỉ số ; HF 5 KF
c. Gọi M và P lần lượt là trung điểm của EF và HI. Chứng minh FDM = EDP.
----------------HẾT----------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC 2020-2021 QUẢNG NAM
Môn: TOÁN – LỚP 8
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM – MÃ ĐỀ B
(Đáp án và Hướng dẫn chấm gồm 02 trang)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (5,0 điểm): Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Đ/án C A B D A D C A B D A B C D C
PHẦN II.TỰ LUẬN (5,0 điểm): Câu Nội dung Điểm
a. Giải phương trình 4(x + 2) = 3x −1; 0,5
Biến đổi phương trình trở thành 4x + 8 = 3x −1 0,25
Tìm được nghiệm là −9 0,25 x +1 1− 3x 1 b. Giải phương trình + = . 0,75 1. x x (x − ) 1 x −1
(1,25 ĐKXĐ: x  0 và x  1 0,25 điểm)
Biến đổi phương trình trở thành 0,25 2 x − 4x = 0 (*) Tìm được hai
nghiệm của phương trình (*) là 0 và 4;
Đối chiếu và kết luận S =   4 . 0,25
a. Cho biết a  b, chứng tỏ rằng 3a – 1 < 3b – 1. 0,5
Từ a  b , suy ra 3a  3b 0,25 Do đó 3a −1 3b −1 0,25 2. x +1 2x −1
(1,25 b. Giải bất phương trình sau và biểu diễn nghiệm trên trục số  . 0,75 điểm) 3 7
Biến đổi bất phương trình trở thành 7(x + ) 1  3(2x − ) 1 0,25
Tìm được nghiệm của bất phương trình x  10. − 0,25
Biểu diễn đúng tập nghiệm của bất phương trình trên trục số. 0,25 3.
Cho tam giác nhọn DEF (DE  DF), hai đường cao EH và FI cắt nhau tại K. Trang 6 (2,5 Hình vẽ: D
điểm) - Hình vẽ phục vụ ý a, b: 0,25 điểm;
- Hình vẽ phục vụ cả câu: 0,5 điểm. H P I 0,5 K E M F
a. Chứng minh  DEH đồng dạng  DFI , từ đó suy ra DI.DE = DH.DF; 1,0
Giải thích hai tam giác vuông DEH và DFI có góc D là góc nhọn chung nên 0,5 đồng dạng DE DH Suy ra = 0,25 DF DI Do đó DI.DE = DH.DF. 0,25 IE 3 KE 0,5 b. Cho biết = , hãy tính tỉ số . HF 5 KF
Nêu được hai tam giác vuông IKE và HKF có: IKE = HKF (đối đỉnh) nên 0,25 đồng dạng. KE IE 3 Suy ra: = = . 0,25 KF HF 5
c. Gọi M và P lần lượt là trung điểm của EF và HI. Chứng minh FDM = EDP. 0,5 DI DH Từ câu a, suy ra: =
; kết hợp với D là góc chung nên có được  DIH DF DE 0,25
đồng dạng với  DFE, suy ra DIP = DFM. DI IP Chứng minh được =
, từ đó suy ra  DIP đồng dạng với DF FM 0,25
 DFM (c.g.c). Do đó FDM = EDP. Trang 7