TailieuVNU.com TailieuVNU.com TailieuVNU.com 1 TailieuVNU.com TailieuVNU.com TailieuVNU.com TailieuVNU.com TailieuVNU.com
Đề thi Kỹ thuật điều khiển (khoa Điện tử Viễn thông)
kỳ 2 năm học 2020-2021 – UET 1 TailieuVNU.com 2 TailieuVNU.com TailieuVNU.com TailieuVNU.com
Đại Học Quốc Gia Hà Nội
ĐỀ KIỂM TRA GIỮA KỲ, HK I NĂM 2020
Đại học Công nghệ
Môn: Kỹ thuật điều khiển
Thời gian làm bài: 60 phút (không kể thời gian phát đề) Đáp án:
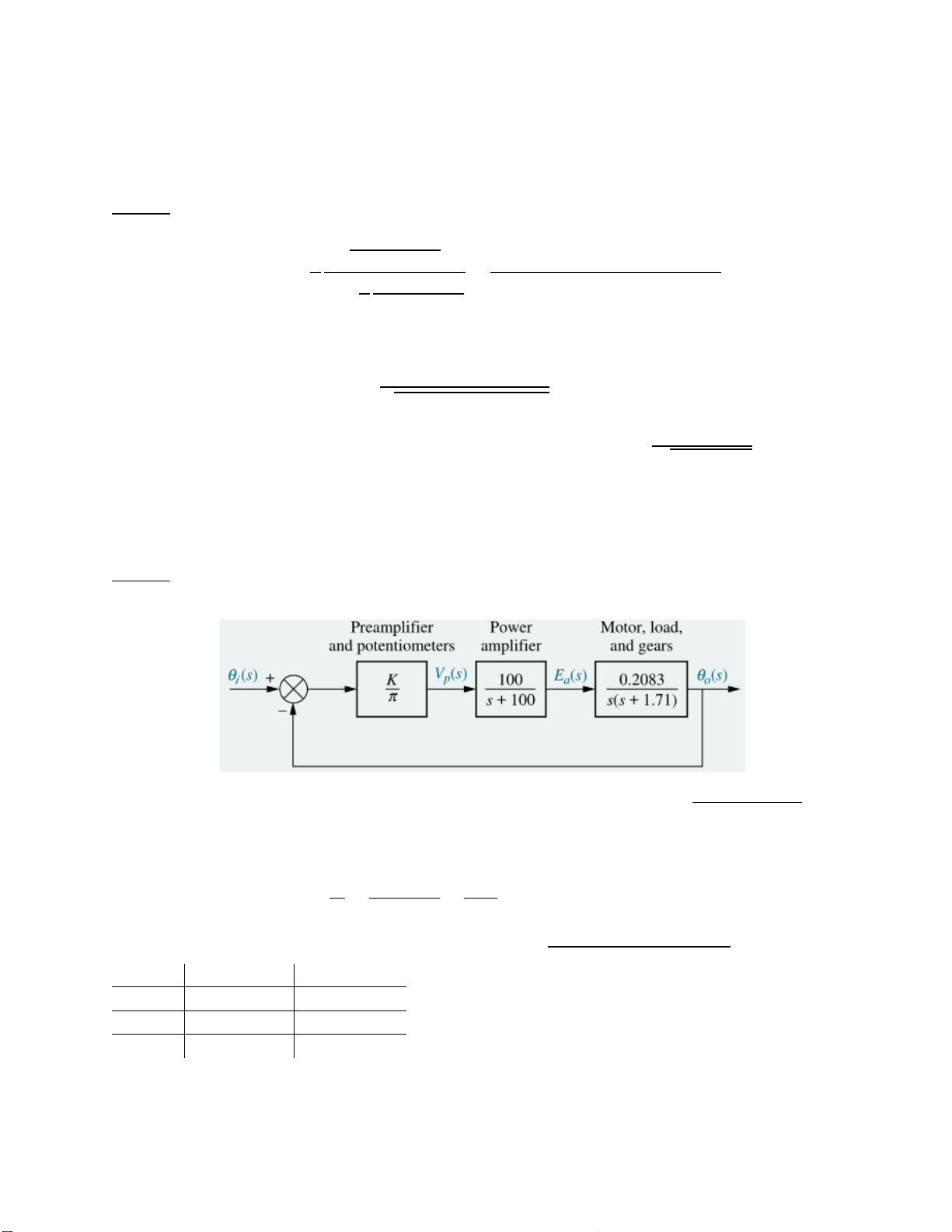
Câu 1: Tìm hàm chuyển (transfer function) của hệ thống vòng hở (forward path).
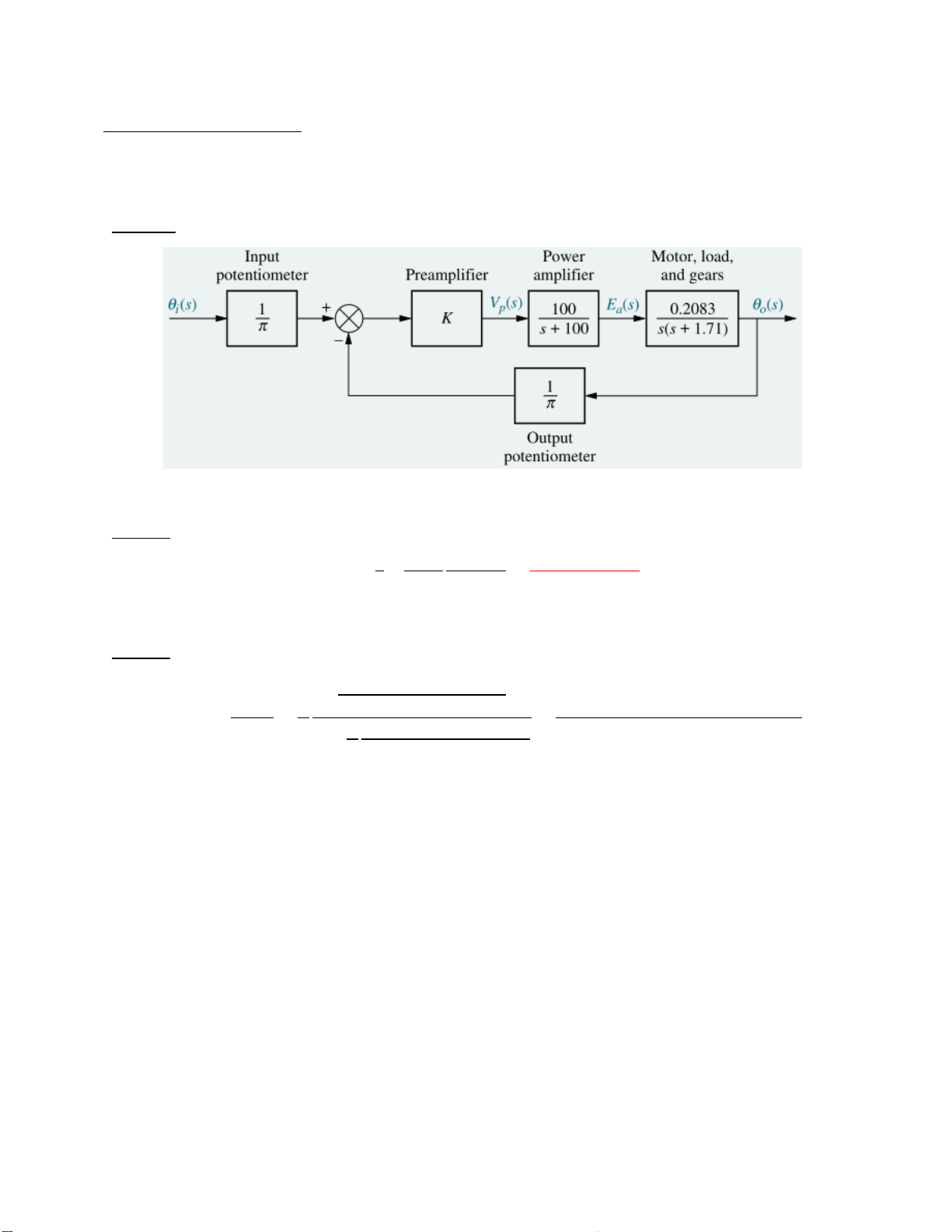
Đáp án: Lấy tích các hàm chuyển của tất cả các thành phần nối tiếp trên forward path ta được: 1 100 0.2083 6.63𝐾 Go(s)= 𝐾 = 𝜋 𝑠+100 𝑠(𝑠+1.71) 𝑠(𝑠+1.71)(𝑠+100)
Câu 2: Tìm biểu diễn trên không gian trạng thái (state space) của hệ thống vòng kín (closed loop)
Đáp án: Hàm chuyển của hệ thống vòng kín là: 20.83𝐾 𝜃 1 𝑠(𝑠 + 1.71)(𝑠 + 100) 6.63𝐾 𝐺 𝑜(𝑠) 𝑐(𝑠) = = = 𝜃 1 20.83𝐾 𝑖(𝑠) 𝜋 1 +
𝑠3 + 101.71𝑠2 + 171𝑠 + 6.63𝐾
𝜋 𝑠(𝑠 + 1.71)(𝑠 + 100)
Quan hệ vào-ra trên miền s là:
6.63𝐾𝜃𝑖(𝑠) = (𝑠3 + 101.71𝑠2 + 171𝑠 + 6.63𝐾)𝜃𝑜(𝑠)
[optional: Quan hệ vào-ra trên miền thời gian là (giả sử các điều kiện ban đầu đều bằng 0): 6.63𝐾𝜃 ⃛ ̈
𝑖 (𝑡) = 𝜃𝑖(𝑡) + 101.71𝜃𝑖(𝑡) + 171𝜃𝑖(𝑡) + 6.63𝐾𝜃𝑜(𝑡) ]
Đặt các biến trạng thái như sau (pha tối thiểu): x ̇ ̈
1(t)= 𝜃𝑜(𝑡), x2(t)= 𝜃𝑜(𝑡), x3(t)= 𝜃𝑜(𝑡), và
x(t)=[x1(t), x2(t), x3(t)]T. Phương trình trạng thái của hệ thống vòng kín là: 0 1 0 0 𝒙̇(𝑡) = [ 0 0 1 ] 𝒙(𝑡) + [ 0 ] 𝜃𝑖(𝑡) −6.63𝐾 −171 −101.71 6.63𝐾 Phương trình lối ra là:
𝜃𝑜(𝑡) = [1 0 0]𝒙(𝑡) TailieuVNU.com
Câu 3: Nếu ta thay bộ khuếch đại công suất (power amplifier) bằng một hệ thống có hàm chuyển
bằng đơn vị (unity transfer function), tìm K để hệ thống vòng kín có hệ số phần trăm quá mức (percent overshoot) là 10%.
Đáp án: Hàm chuyển của hệ vòng kín trong trường hợp này là 0.2083𝐾 1 𝑠(𝑠 + 1.71) 0.2083𝐾 𝑇𝑐(𝑠) = = 𝜋 1 0.2083𝐾 1 +
3.14𝑠2 + 5.3694𝑠 + 0.2083𝐾 𝜋 𝑠(𝑠 + 1.71)
Để %OS=10% thì tỉ số cản là: − ln(10/100) 𝜁 = = 0.591 √𝜋2 + [ln(10/100)]2 5.3694/3.14
Mặt khác, hệ số cản của hệ thống vòng kín có hàm chuyển Tc(s) là: 𝜁 = = 0.591. 2√0.2083𝐾/3.14 Do đó, K=31.6.
Câu 4: Hệ thống vòng kín là hệ thống loại mấy? Tìm K để đạt sai số ở trạng thái ổn định (steady
state error) là 10%. Khi đó hệ thống có ổn định không?
Đáp án: Chuyển khối input potentiometer ra sau summing junction ta có hệ thống tương đương với unity feedback như sau: 6.63𝐾
Hàm chuyển của hệ thống vòng hở (forward path) đã tìm ở câu 1 là: 𝐺𝑜(𝑠) = , do 𝑠(𝑠+1.71)(𝑠+100)
đó đây là hệ thống bậc 1.
Vì hệ thống là bậc nhất nên 10% sai số ở trạng thái ổn định chỉ có được với tín hiệu dốc (ramp 1 (1.71)(100) 25.79
input. Do đó: 𝑒(∞) = 0.1 = = = . Vậy K=257.9. 𝐾𝑣 6.63𝐾 𝐾 1709.877
Thay K=257.9 vào 𝐺𝑐(𝑠) đã tính ở câu 2 ta được 𝐺𝑐(𝑠) = . Bảng Routh:
𝑠3+101.71𝑠2+171𝑠+1709.877 s3 1 171 s2 101.71 1709.877 s1 15682.533 0 s0 1709.877
Vì các hệ số ở cột đầu tiên trong bảng Routh không đổi dấu nên hệ thống ổn định. TailieuVNU.com
Đại Học Quốc Gia Hà Nội
ĐỀ KIỂM TRA GIỮA KỲ, HK I NĂM 2020
Đại học Công nghệ
Môn: Kỹ thuật điều khiển
Thời gian làm bài: 60 phút (không kể thời gian phát đề)
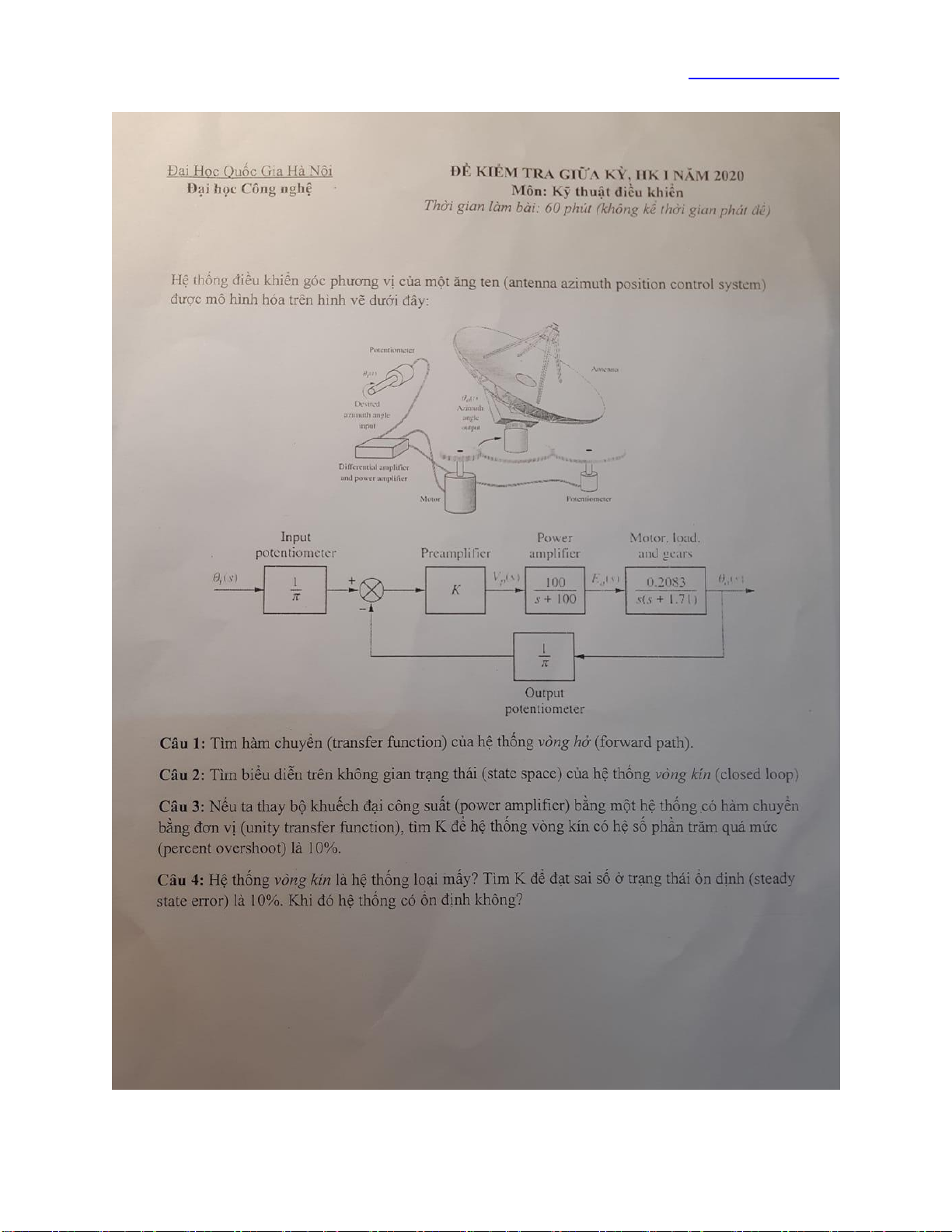
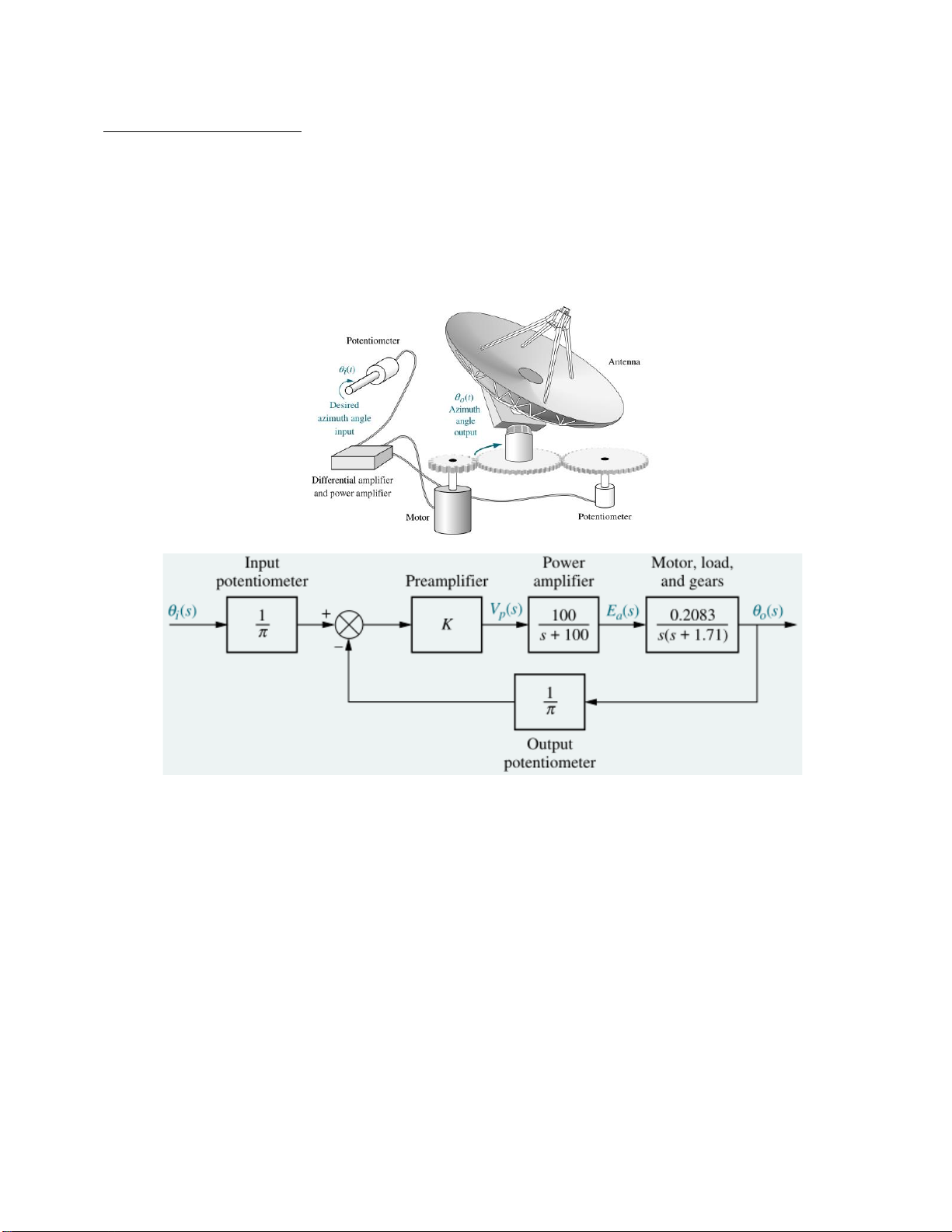
Hệ thống điều khiển góc phương vị của một ăng ten (antenna azimuth position control system)
được mô hình hóa trên hình vẽ dưới đây:
Câu 1: Tìm hàm chuyển (transfer function) của hệ thống vòng hở (forward path).
Câu 2: Tìm biểu diễn trên không gian trạng thái (state space) của hệ thống vòng kín (closed loop)
Câu 3: Nếu ta thay bộ khuếch đại công suất (power amplifier) bằng một hệ thống có hàm chuyển
bằng đơn vị (unity transfer function), tìm K để hệ thống vòng kín có hệ số phần trăm quá mức (percent overshoot) là 10%.
Câu 4: Hệ thống vòng kín là hệ thống loại mấy? Tìm K để đạt sai số ở trạng thái ổn định (steady
state error) là 10%. Khi đó hệ thống có ổn định không? TailieuVNU.com 1 TailieuVNU.com 2
VIETNAM NATIONAL UNIVERSITY, HANOI
UNIVERSITY OF ENGINEERING AND TECHNOLOGY
FINAL EXAM – SEMESTER II, 2019-2020
CONTROL ENGINEERING - ELT 3051 26. Duration: 90 minutes
The exam includes one page. Students are not allowed to use any documents
Q1: The differential equation of system is shown as follow 𝑑2𝑦(𝑡) 𝑑𝑦(𝑡) + 4,2 + 36𝑦(𝑡) = 36𝑥(𝑡) 𝑑𝑡2 𝑑𝑡
a. Find the transfer function of system
b. Write an expression for the general form of the step response without solving for the
inverse Laplace transform. State the nature of response.
c. Determine the settling time, peak time and percent overshoot of the second order system.
Q2: A unity feedback system has the following forward transfer function: 10(𝑠 + 10)(𝑠 + 20) 𝐺(𝑠) = 𝑠(𝑠 + 15)(𝑠 + 25)
a. Find the steady state error for the following inputs: u(t), tu(t), t2u(t)
b. Determine the stability of the feedback system?
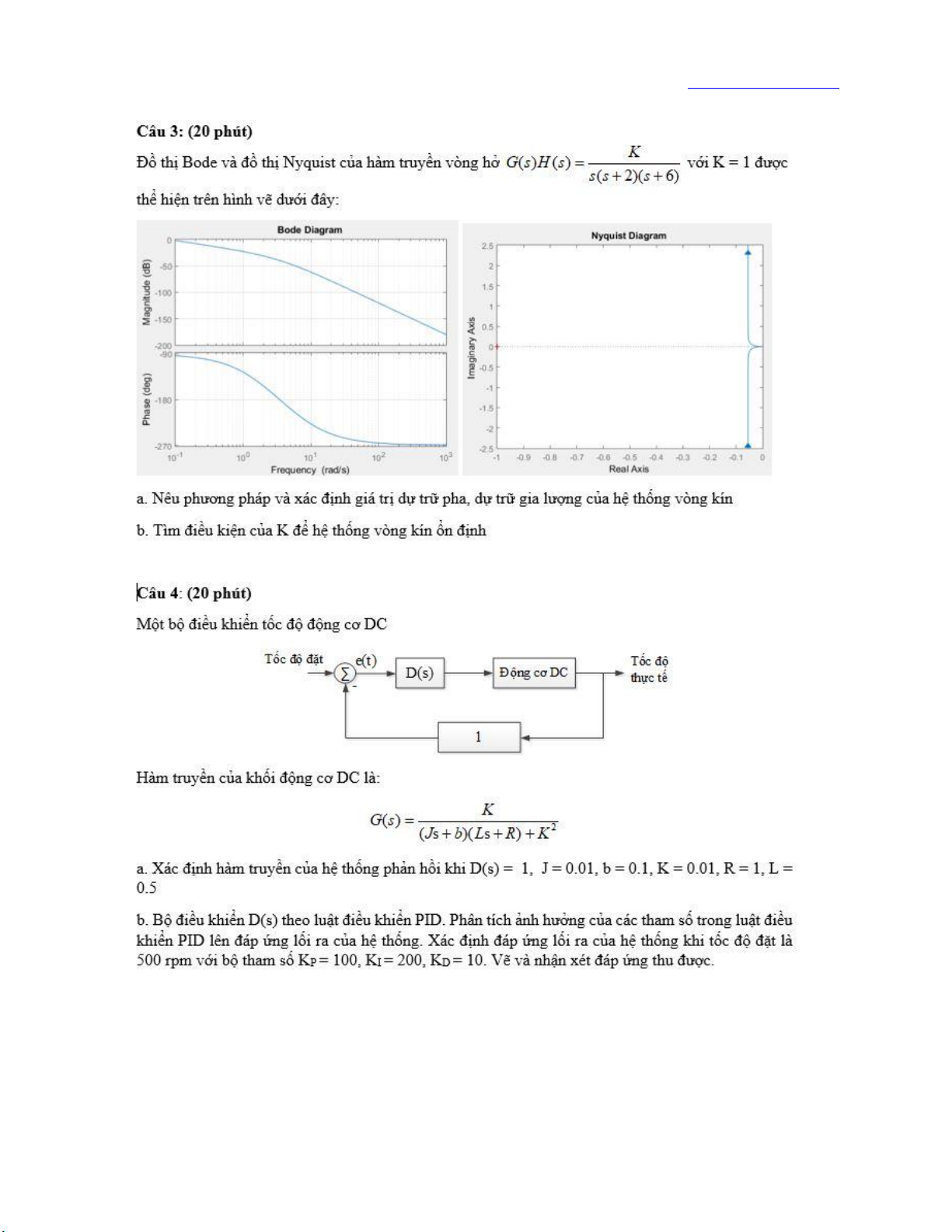
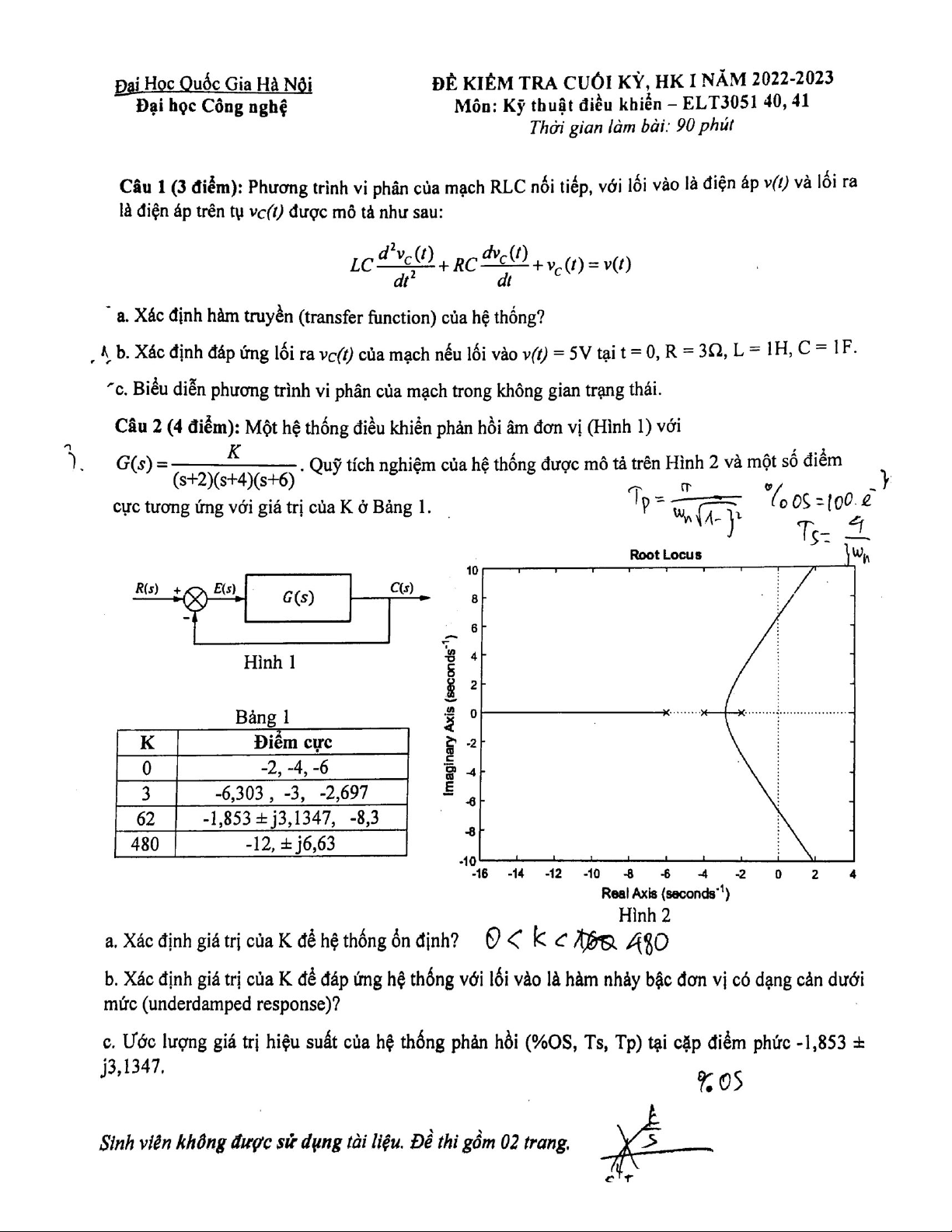
Q3: Given a unity feedback system that has the forward path transfer function 𝐾 𝐺(𝑠) = (𝑠 + 2)(𝑠 + 4)(𝑠 + 6)
a. Sketch the root locus and find the range of K for stable system.
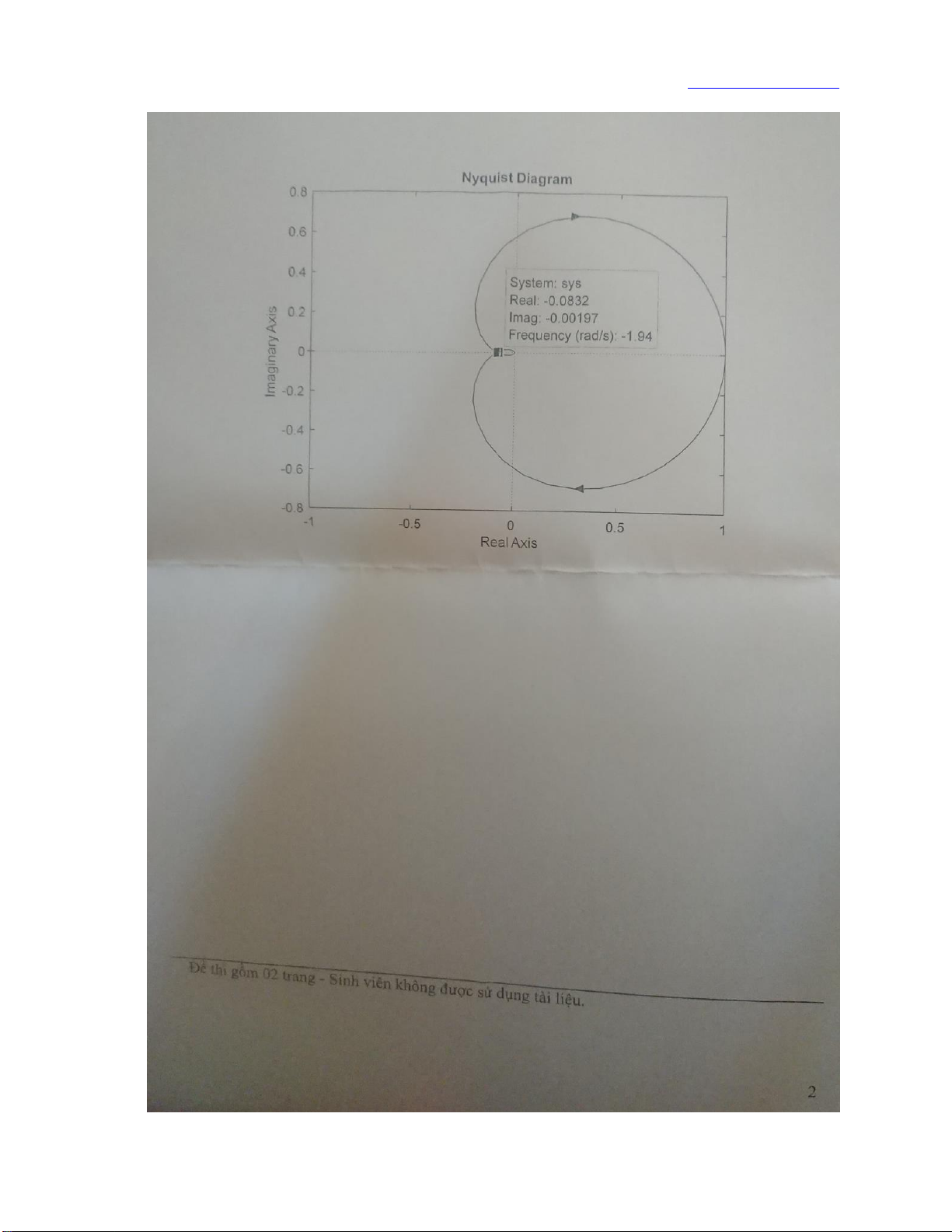
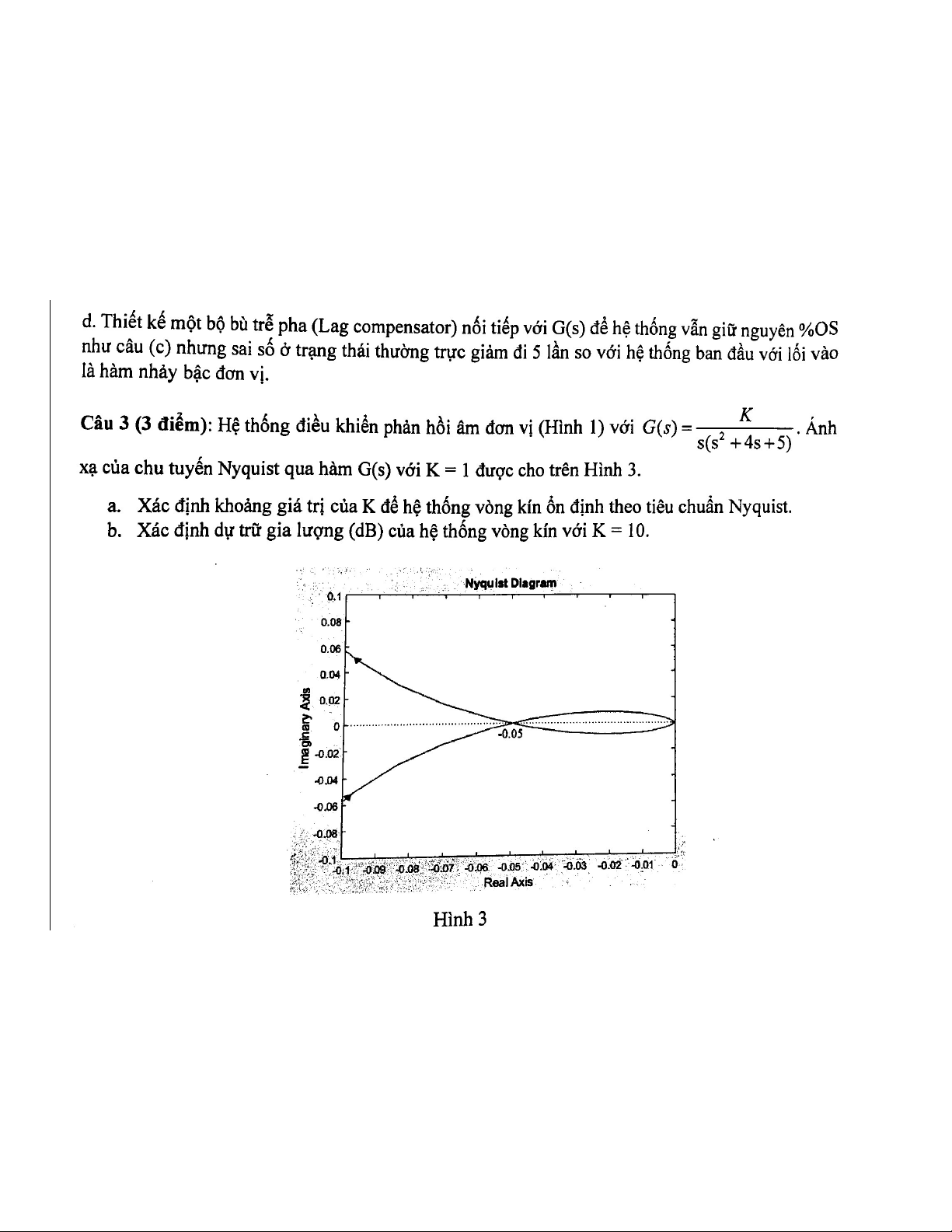
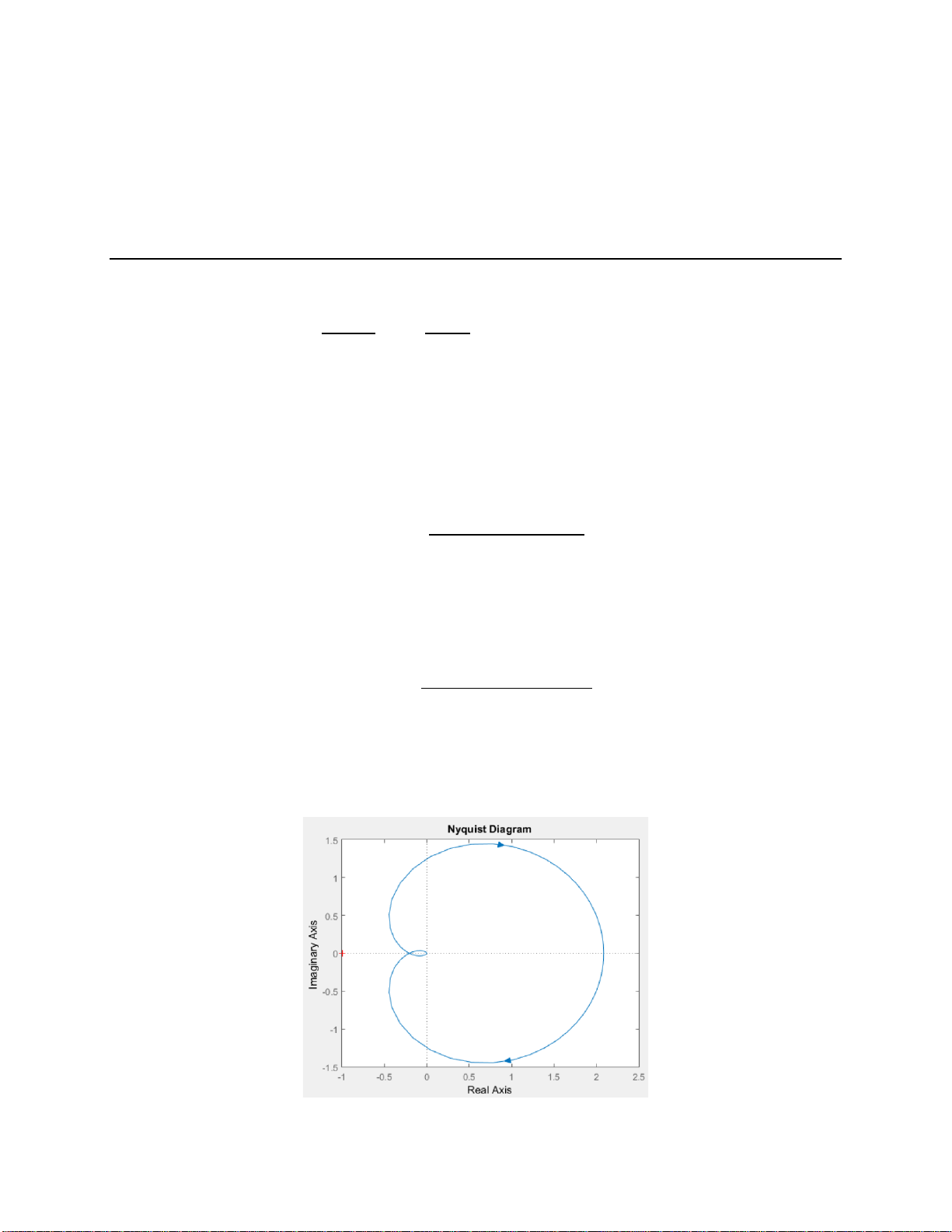
b. The Nyquist diagram of the open loop system with K = 100 is shown in the Figure 1.
- Using the Nyquist criterion, find out whether the closed loop system is stable or not?
- Determine the gain and phase margin of closed loop system? Figure 1 1
VIETNAM NATIONAL UNIVERSITY, HANOI
UNIVERSITY OF ENGINEERING AND TECHNOLOGY
SOLUTION FINAL EXAM – SEMESTER II, 2019-2020
CONTROL ENGINEERING - ELT 3051 26. Duration: 90 minutes Q1 (3 marks): a. 36/s2+4.2s+36 b. s1,2 = -2.1 +- j 5.6
y(t)= 1* A exp(-2.1t)*cos(5.6t+phi)
c. Tp =1.31, OS = 30.9%, Ts = 1.89 s Q2 (2 marks)
a. e(step)=0, e(ramp)=constant, e(parabol)= infinite
b. The closed loop system is unstable Q3 (5 marks) - The system is stable
- GM = 13.6 (db) wc =6.63 rad/s. PM = 72.7 wp= 2.54 2 TailieuVNU.com 1 TailieuVNU.com 1