











Preview text:
TỔ TOÁN
KIỂM TRA CUỐI KỲ II
TRƯỜNG THPT ĐÔNG HÀ NĂM HỌC 2022 - 2023 Môn: TOÁN - Lớp 12 ĐỀ THI THỬ
Thời gian: 90 phút (Không kể thời gian phát đề) Mã đề thi
Họ và tên thí sinh:.............................................................................. SBD:.....................
Câu 1. Hàm số nào dưới đây không là nguyên hàm của hàm số f (x) 3 = x ? 4 4 A. x y = −1. B. x y = + 2 . C. 2 y = 3x . D. 1 4 y = x . 4 4 4
Câu 2. Biết một nguyên hàm của hàm số y = f (x) là F (x) 2
= x + 4x +1 . Khi đó, giá trị của hàm số
y = f (x) tại x = 3 là. A. f ( ) 3 = 30 . B. f ( ) 3 = 22 . C. f ( ) 3 = 10. D. f ( ) 3 = 6 .
Câu 3. Họ nguyên hàm của hàm số 3 (x) = x f
e là hàm số nào sau đây? A. 3 x e + C . B. 1 3x e + C . C. 1 x e + C . D. 3 3 x e + C . 3 3
Câu 4. Họ nguyên hàm của hàm số f (x) 1
= + sin x là : x
A. ln x − cos x + C . B. 1 −
− cos x + C .
C. ln x + cos x + C . D. ln x − cos x + C . 2 x
Câu 5. Khi tính nguyên hàm x − 3 dx ∫
, bằng cách đặt u = x +1 ta được nguyên hàm nào? x +1 A. ∫ ( 2 2 u − 4)du .
B. ∫( 2u − 4)du.
C. ∫( 2u − 3)du . D. u ∫ ( 2 2 u − 4)du .
Câu 6. Cho hàm số f (x) xác định trên R \{ }
1 thỏa mãn f ′(x) 1 =
, f (0) = 2017 , f (2) = 2018 . Tính x −1
S = f (3) − f (− ) 1 .
A. S = ln 4035 . B. S = 4 . C. S = ln 2 . D. S =1. 5 5 Câu 7. Cho f
∫ (x)dx =10. Kết quả 2−4 f ∫ (x)dx bằng: 2 2 A. 32 − . B. 34 − . C. 36 − . D. 40 − . e
Câu 8. Tính tích phân 1 1 I dx = − ∫ 2 x x 1 A. 1 I = B. 1 I = +1 C. I =1
D. I = e e e 5 Câu 9. Cho 1− 2x dx ∫ 3
= a ln + bln 2 với a,b∈ . Mệnh đề nào đúng? 2 x − 5x + 6 2 4
A. 2a + b =11.
B. a + 2b = 7 − .
C. a + b = 8 .
D. a − 2b =15. 1 3 3
Câu 10. Cho f (x) ∫ dx = 1 − ; f (x) ∫
dx = 5. Tính f (x) ∫ dx 0 0 1 A. 1. B. 4. C. 6. D. 5. Trang 1/6 2
Câu 11. Cho hàm số f (x) liên tục, có đạo hàm trên [ 1; − 2], f (− ) 1 = 8; f (2) = 1 − . Tích phân f '
∫ (x)dx bằng 1 − A. 1. B. 7. C. 9. − D. 9. 1
Câu 12. Cho hàm số y = f (x) có đạo hàm liên tục trên [0; ] 1 , thỏa mãn f
∫ (x)dx = 3 và f ( )1 = 4 . Tích 0 1 phân xf ′
∫ (x)dx có giá trị là 0 A. 1 − . B. 1 . C. 1. D. 1 − . 2 2
Câu 13. Cho hàm số f (x) xác định và liên tục trên \{ } 0 thỏa mãn 2 2
x f (x) + ( x − ) f (x) ' 2 1 = xf (x) −1, 2
với mọi x∈ \{ }
0 đồng thời thỏa f ( ) 1 = 2 − . Tính f ∫ (x)dx 1 A. ln 2 − −1. B. 1 − ln 2 − . C. 3 − ln 2 − . D. ln 2 3 − − . 2 2 2 2 2
Câu 14. Viết công thức tính diện tích S của hình H giới hạn bởi đồ thị hàm số y = f (x) , trục hoành và hai
đường thẳng x = a, x = b (a < b) . b b b b
A. S = π f
∫ (x)dx. B. S = f
∫ (x)dx . C. 2 S = π f
∫ (x)dx. D. 2 S = f
∫ (x)dx. a a a a
Câu 15. Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y = x , trục hoành Ox , các đường thẳng
x =1, x = 2 là A. 7 S = . B. 8 S = .
C. S = 7 .
D. S = 8. 3 3
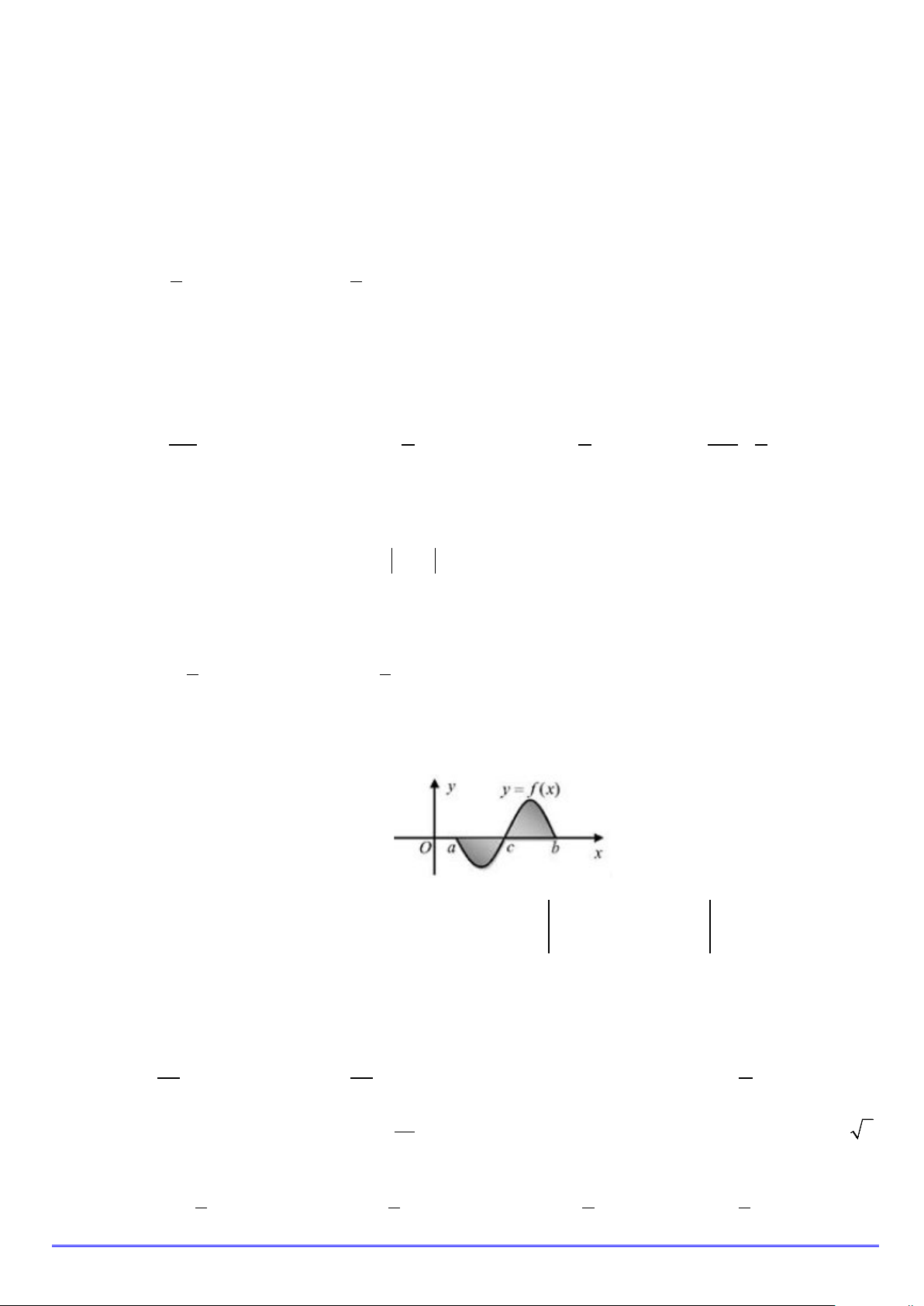
Câu 16. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f (x) , trục hoành, đường thẳng
x = a, x = b . Hỏi cách tính S nào dưới đây đúng? b c b A. S = f ∫ (x)dx . B. S = f
∫ (x)dx+ f ∫ (x)dx . a a c c b c b
C. S = − f
∫ (x)dx+ f ∫ (x)dx . D. S = f
∫ (x)dx+ f ∫ (x)dx . a c a c
Câu 17. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = x − 2x và đồ thị hàm số y = x . 37 81 9 A. . B. . C. 11. D. . 12 12 2 2 Câu 18. x
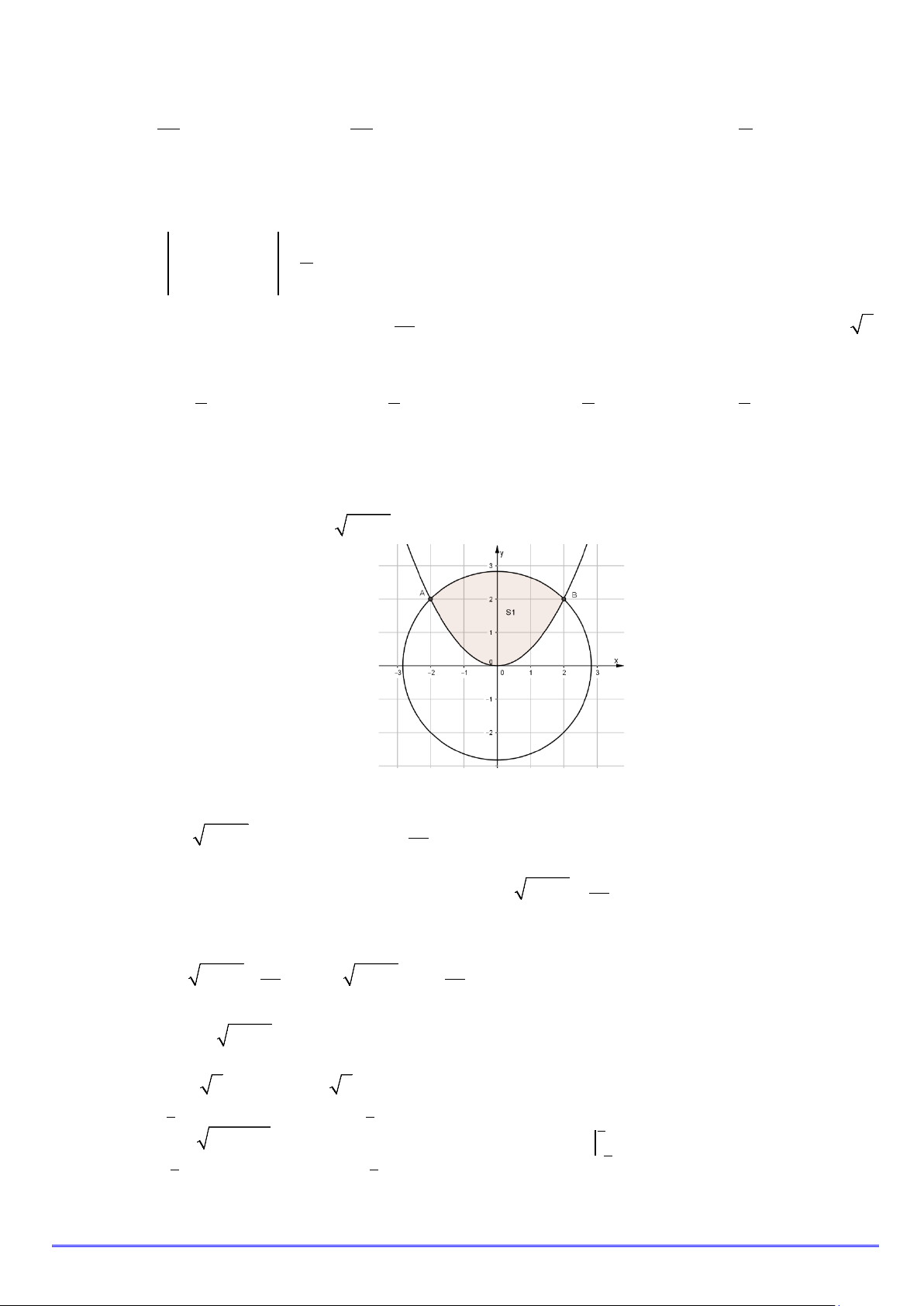
Trong hệ tọa độ Oxy , parabol y =
chia đường tròn tâm O (O là gốc tọa độ) bán kính r = 2 2 2
thành 2 phần, diện tích phần nhỏ bằng: A. 3 2π + . B. 4 2π + . C. 4 2π − . D. 4 . 4 3 3 3 Trang 2/6
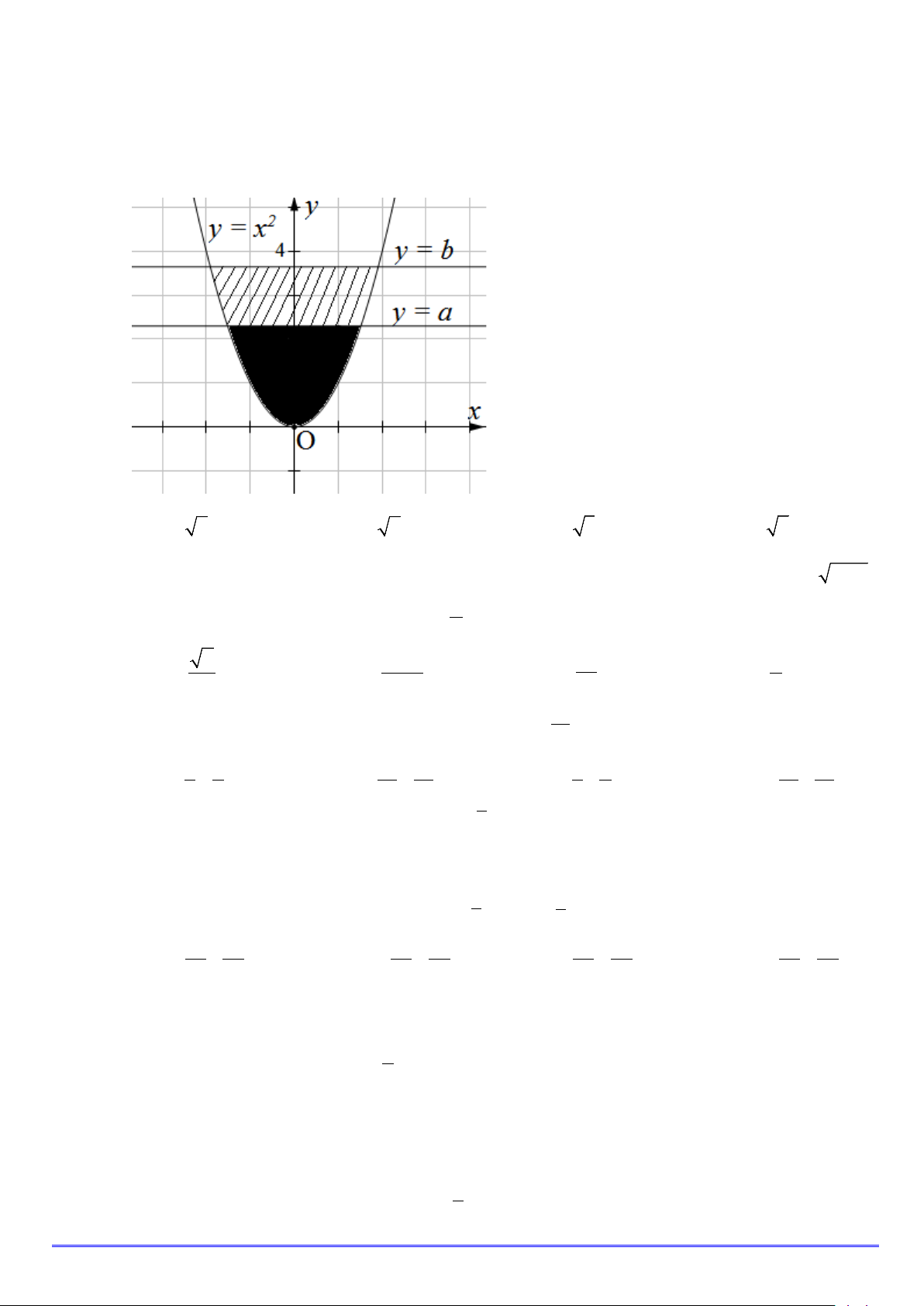
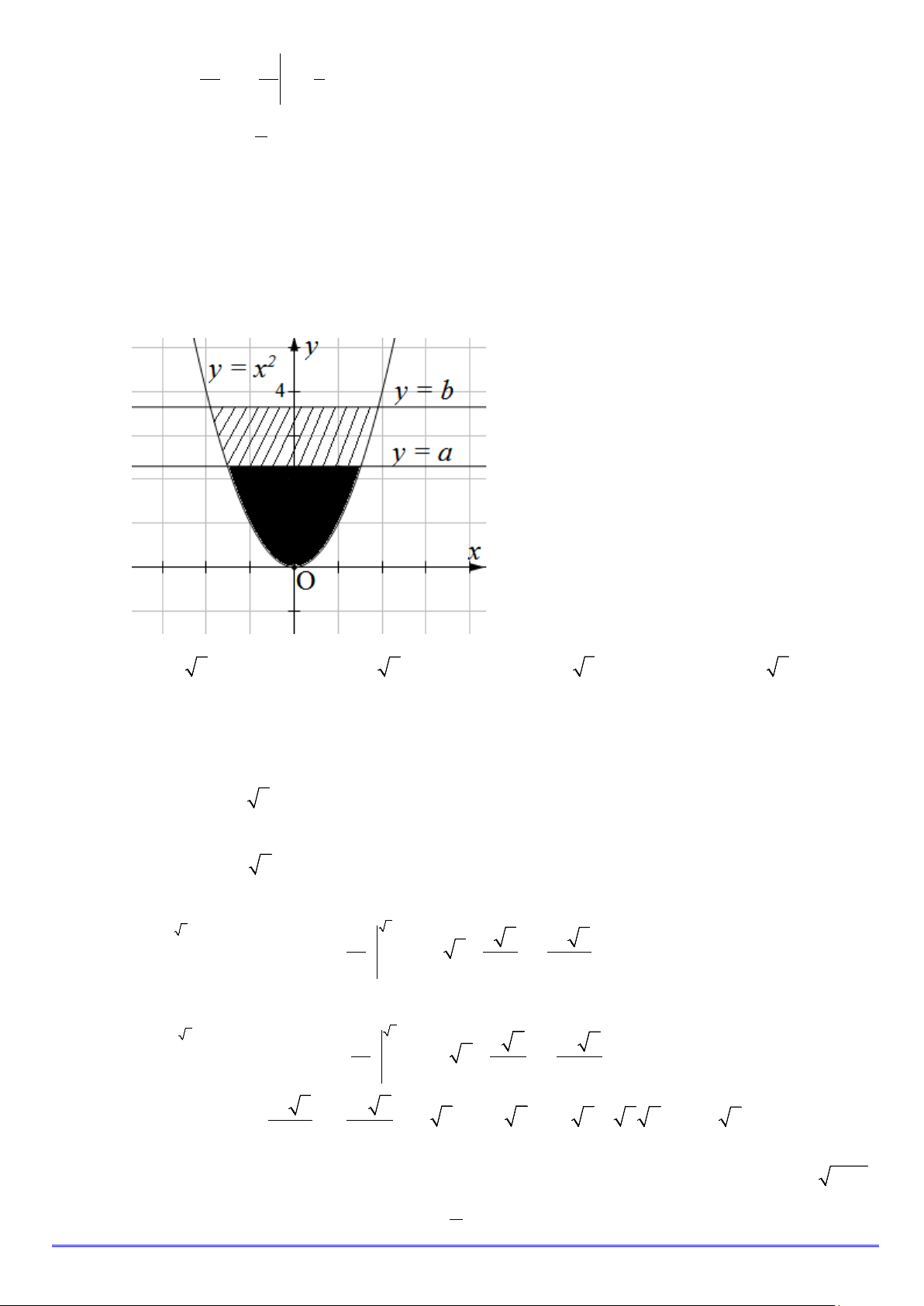
Câu 19. Trong hệ trục tọa độ Oxy , cho parabol (P) 2
: y = x và hai đường thẳng y = a , y = b (0 < a < b)
(hình vẽ). Gọi S là diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng = (phần tô 1 y a
đen); (S là diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng = (phần gạch chéo). 2 ) y b
Với điều kiện nào sau đây của a và b thì S = S ? 1 2 A. 3 b = 4a . B. 3 b = 2a . C. 3 b = 3a . D. 3 b = 6a .
Câu 20. Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số y = tan x ,
trục hoành và các đường thẳng x = 0 , π
x = quanh trục hoành là 4 2 π A. π V = . B. π ln 2 V = . C. V = . D. π V = . 4 2 4 4
Câu 21. Cho hai số phức z =1+ 2i , z = 3− i . Tìm số phức z2 = . 1 2 z z1 A. 1 7
z = + i . B. 1 7 z = + i . C. 1 7
z = − i . D. 1 7 z = − + i . 5 5 10 10 5 5 10 10
Câu 22. Cho số phức z = 2 + 4i . Tìm số phức w = iz + z .
A. w = 2 + 2i . B. w = 2 − − 2i .
C. w = 2 − 2i . D. w = 2 − + 2i .
Câu 23. Cho hai số phức z = 2 − 2i , z = 3
− + 3i . Khi đó số phức z − z là 1 2 1 2 A. 5 − + 5i . B. 5 − i .
C. 5 − 5i . D. 1 − + i .
Câu 24. Cho số phức w = 3− 5i . Tìm số phức z biết w = (3− 4i) z . A. 11 27 z = − i . B. 11 27 z = − + i . C. 11 27 z = + i . D. 11 27 z = − − i . 25 25 25 25 25 25 25 25
Câu 25. Cho hai số phức z = m −1+ 3i và z = 2 − mi (m∈) . Tìm tất cả các giá trị của tham số m để z .z 1 2 1 2 là số thực. A. m∈{ 2; − − } 3 . B. 2 m = . C. m∈{3;− } 2 . D. m∈{ 3 − ; } 2 . 5
Câu 26. Cho số phức z 2i . Phần thực và phần ảo của số phức z lần lượt là? A. 2 và 1. B. 1 và 2
C. 2 .và i .
D. i và 2 .
Câu 27. Kí hiệu a,b lần lượt là phần thực và phần ảo của số phức z = 4
− − 3i . Tìm a,b . A. a = 4 − , b = 3 − i . B. a = 4 − , b = 3 . C. a = 4 − , b = 3 − .
D. a = 4 , b = 3 .
Câu 28. Cho số phức z thỏa mãn: 2
(2 −3i)z + (4 + i)z = −(1+ 3i) . Xác định phần thực và phần ảo của z. Trang 3/6 A. Phần thực là 2
− ; phần ảo là 5 .i B. Phần thực là 2
− ; phần ảo là 5. C. Phần thực là 2
− ; phần ảo là 3. D. Phần thực là 3
− ; phần ảo là 5 .i
Câu 29. Môđun của số phức z = ( − i)( + i)4 2 3 1 là A. z = 8 − +12i .
B. z = 13 .
C. z = 4 13 .
D. z = 31 .
Câu 30. Tính mô đun của số phức z biết (1− 2i) z = 2 + 3i . A. 13 z = . B. 13 z = . C. 33 z = . D. 65 z = . 5 5 5 5
Câu 31. Cho hai số phức z z = = 1 , 2 thỏa mãn z z 1. Khi đó 2 2 + + − bằng 1 2 z z z z 1 2 1 2 A. 2 . B. 4 . C. 1. D. 0 .
Câu 32. Cho z , z là hai nghiệm của phương trình 2
z − z + = ( z ∈) . Tính giá trị của biểu thức 1 2 2 2 0
P = 2 z + z + z − z . 1 2 1 2
A. P = 3.
B. P = 2 2 + 2 .
C. P = 2 + 4 .
D. P = 6 .
Câu 33. Gọi z , z là các nghiệm của phương trình 2
z − 2z + 5 = 0 . Tính 4 4 = + . 1 2 P z z 1 2 A. 14i . B. 14 − i . C. 14. D. 14.
Câu 34. Trên mặt phẳng tạo độ Oxy , tập hợp điểm biểu diễn số phức z thỏa mãn z − i = iz là
A. Đường thẳng y = 2 . B. Đường thẳng 1 y = − . 2 C. Đường thẳng 1 y = .
D. Đường tròn tâm I (0; ) 1 . 2
Câu 35. Cho hai số phức z , z thỏa mãn z − 3i + 5 = 2 và iz −1+ 2i = 4 . Tìm giá trị lớn nhất của biểu 1 2 1 2
thức T = 2iz + 3z . 1 2 A. 313 +16. B. 313 . C. 313 +8 . D. 313 + 2 5 .
Câu 36. Trong không gian với hệ trục tọa độ Oxyz , cho điểm A(4;1;−2) . Tọa độ điểm đối xứng với A qua
mặt phẳng (Oxz) là
A. A′(4;−1;2) . B. A′( 4 − ;−1;2) .
C. A′(4;−1;− 2) . D. A′(4;1;2).
Câu 37. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ tâm I và bán kính R của mặ cầu (S) (x − )2 2 : 1 + y + (z + )2 1 = 4 . A. I (1;0;− ) 1 , R = 2 . B. I ( 1; − 0; ) 1 , R = 2 . C. I (1;0;− ) 1 , R = 4 . D. I ( 1; − 0; ) 1 , R = 4 .
Câu 38. Trong không gian với hệ tọa độ Oxyz , cho hai điểm M ( 3
− ;1;− 6) và N (3;5;0) . Viết phương trình
mặt cầu (S ) có đường kính MN . A. (S ) 2
: x + ( y − 3)2 + (z − 3)2 = 22. B. (S ) 2
: x + ( y − 3)2 + (z + 3)2 = 22 . C. (S ) 2
: x + ( y − 3)2 + (z + 3)2 = 22 . D. (S ) 2
: x + ( y + 3)2 + (z − 3)2 = 22 .
Câu 39. Trong không gian với hệ tọa độ Oxyz , phương trình nào dưới đây là phương trình mặt cầu có tâm I (1;2;− )
1 và tiếp xúc với mặt phẳng (P) :
x − 2y − 2z −8 = 0?
A. (x + )2 + ( y + )2 + (z − )2 1 2 1 = 9 .
B. (x − )2 + ( y − )2 + (z + )2 1 2 1 = 9 .
C. (x − )2 + ( y − )2 + (z + )2 1 2 1 = 3. 2 2 2 D. (x + )
1 + ( y + 2) + (z − ) 1 = 3. Trang 4/6
Câu 40. Trong không gian Oxyz , cho hai điểm A(1;2;− ) 1 và B( 3 − ;0;− )
1 . Mặt phẳng trung trực của đoạn
thẳng AB có phương trình là
A. x − y + z − 3 = 0
B. 2x + y +1 = 0
C. x − y + z + 3 = 0
D. 2x + y −1 = 0
Câu 41. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2; 1
− ;3), B(2;0;5), C(0; 3 − ;− ) 1 . Phương
trình nào dưới đây là phương trình của mặt phẳng đi qua A và vuông góc với BC ?
A. x − y + 2z + 9 = 0.
B. x − y + 2z − 9 = 0.
C. 2x + 3y − 6z −19 = 0.
D. 2x + 3y + 6z −19 = 0.
Câu 42. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (α ) cắt 3 trục tọa độ tại M (3;0;0) , N (0; 4; − 0) , P(0;0; 2
− ) . Phương trình mặt phẳng (α ) là:
A. 4x − 3y − 6z −12 = 0.
B. 4x − 3y + 6z + 9 = 0 . C. x y z − − = 1. D. x y z − + + = 1. 3 4 3 3 4 2
Câu 43. Cho mặt phẳng (α ) : 2x −3y − 4z +1 = 0 . Khi đó, một véc tơ pháp tuyến của (α ) A. n = (2;3; 4
− ) . B. n = (2; 3 − ;4) . C. n = ( 2 − ;3;4) . D. n = ( 2 − ;3; ) 1 .
Câu 44. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P) đi qua điểm M (9;1 )
;1 cắt các tia Ox,Oy,Oz tại , A B,C ( ,
A B,C không trùng với gốc tọa độ ). Thể tích tứ diện OABC đạt giá trị nhỏ nhất là bao nhiêu? A. 81 . B. 243 . C. 81 . D. 243 . 2 2 6
Câu 45. Trong không gian Oxyz , cho mặt phẳng (P) : x − 2y + z + 7 = 0 và mặt cầu (S ) 2 2 2
: x + y + z − 2x + 4z −10 = 0 . Gọi (Q) là mặt phẳng song song với mặt phẳng (P) và cắt mặt
cầu (S ) theo một giao tuyến là đường tròn có chu vi bằng 6π . Hỏi (Q) đi qua điểm nào trong số các điểm sau? A. (6;0; ) 1 . B. ( 3 − ;1;4) . C. ( 2 − ;−1;5) . D. (4;−1;− 2) .
Câu 46. Trong không gian Oxyz , tìm một vectơ chỉ phương của đường thẳng:
x − 3 y −1 z + 4 d : = = . 2 − 1 − 3 A. b = (2; 1; − 3). B. c = (3;1; 4 − ) . C. d = ( 2 − ;1; 3 − ). D. a = ( 2 − ; 1; − 3).
Câu 47. Trong không gian Oxyz , phương trình nào dưới đây là phương trình đường thẳng đi qua điểm
A(1;2;0) và vuông góc với mặt phẳng (P) : 2x + y −3z −5 = 0. x = 1+ 2t x =1+ 2t x = 3 + 2t x =1+ 2t A.
y = 2 + t .
B. y = 2 + t .
C. y = 3+ t .
D. y = 2 −t . z = 3 − t z = 3t z = 3− 3t z = 3 − t
Câu 48. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 2x − 2y + z = 0 và đường thẳng x 1 : y z d
+ = = . Gọi ∆ là một đường thẳng chứa trong (P), cắt và vuông góc với d . Vectơ 1 2 1 −
u = (a;1;b) là một vectơ chỉ phương của ∆ . Tính tổng S = a + b . A. S =1.
B. S = 0 .
C. S = 2 .
D. S = 4 .
Câu 49. Trong không gian tọa độ Oxyz , xét vị trí tương đối của hai đường thẳng Trang 5/6
x −1 y +1 z
x − 3 y − 3 z + 2 ∆ : = = , ∆ : = = 1 2 2 2 3 1 − 2 − 1 A. ∆ ∆ ∆ ∆ ∆ ∆ ∆ ∆
1 song song với 2 . B. 1 chéo với 2 . C. 1 cắt 2. D. 1 trùng với 2.
Câu 50. Trong không gian Oxyz , cho đường thẳng x y −1 ∆ : z =
= và hai điểm A(1;2;− 5) , B( 1; − 0;2) . Biết 1 1 1
điểm M thuộc ∆ sao cho biểu thức T = MA − MB đạt giá trị lớn nhất là T . Khi đó, T bằng bao max max nhiêu?
A. T = 3
B. T = 2 6 − 3
C. T = 57
D. T = 3 6 max max max max
------------- HẾT ------------- Trang 6/6 TỔ TOÁN
KIỂM TRA CUỐI KỲ II
TRƯỜNG THPT ĐÔNG HÀ NĂM HỌC 2022 - 2023 Môn: TOÁN - Lớp 12 ĐỀ THI THỬ
Thời gian: 90 phút (Không kể thời gian phát đề) Mã đề thi
Họ và tên thí sinh:.............................................................................. SBD:.....................
Câu 1. Hàm số nào dưới đây không là nguyên hàm của hàm số f (x) 3 = x ? 4 4 A. x y = −1. B. x y = + 2 . C. 2 y = 3x . D. 1 4 y = x . 4 4 4 Lời giải Chọn C 4 Ta có ( ) 3 = d = + ∫ x F x x x
C nên các đáp án A, B, D đều đúng. 4
Câu 2. Biết một nguyên hàm của hàm số y = f (x) là F (x) 2
= x + 4x +1 . Khi đó, giá trị của hàm số
y = f (x) tại x = 3 là. A. f ( ) 3 = 30 . B. f ( ) 3 = 22 . C. f ( ) 3 = 10. D. f ( ) 3 = 6 . Lời giải Chọn C
Ta có: F (x) f (x) f (x) ( 2 x 4x ) 1 ′ ′ = ⇒ = + + = 2x + 4 . f (3) = 2.3+ 4 =10 .
Câu 3. Họ nguyên hàm của hàm số 3 (x) = x f
e là hàm số nào sau đây? A. 3 x e + C . B. 1 3x e + C . C. 1 x e + C . D. 3 3 x e + C . 3 3 Lời giải Ta có: 3x 1 3 d x
e x = e + C, ∫
với C là hằng số bất kì. 3
Câu 4. Họ nguyên hàm của hàm số f (x) 1
= + sin x là : x
A. ln x − cos x + C . B. 1 −
− cos x + C .
C. ln x + cos x + C . D. ln x − cos x + C . 2 x Lời giải Ta có f ∫ (x) 1 1 dx = + sin x dx = dx + sin d
x x = ln x − cos x + ∫ C ∫ ∫ . x x
Câu 5. Khi tính nguyên hàm x − 3 dx ∫
, bằng cách đặt u = x +1 ta được nguyên hàm nào? x +1 A. ∫ ( 2 2 u − 4)du .
B. ∫( 2u − 4)du.
C. ∫( 2u − 3)du . D. u ∫ ( 2 2 u − 4)du . Lời giải Chọn A Đặt u = x +1 2
⇒ x = u −1 ⇒ d x = 2udu . Trang 1/14 2 Khi đó x − 3 dx ∫
trở thành u − 4 .2udu = 2 ∫
∫ ( 2u −4)du . x +1 u
Câu 6. Cho hàm số f (x) xác định trên R \{ }
1 thỏa mãn f ′(x) 1 =
, f (0) = 2017 , f (2) = 2018 . Tính x −1
S = f (3) − f (− ) 1 .
A. S = ln 4035 . B. S = 4 . C. S = ln 2 . D. S =1. Lời giải
Trên khoảng (1;+∞) ta có f ∫ (x) 1 ' dx = dx ∫ = ln (x − )
1 + C ⇒ f (x) = ln (x − ) 1 + C . x −1 1 1
Mà f (2) = 2018 ⇒ C = 2023. 1 Trên khoảng( ) ;1 −∞ ta có f ∫ (x) 1 ' dx = dx ∫
= ln (1− x) + C ⇒ f (x) = ln (1− x) + C . x −1 2 2
Mà f (0) = 2017 ⇒ C = 2022. 2 x − + x > Vậy f (x) ln( 1) 2023 khi 1 =
. Suy ra f (3) − f (− ) 1 =1.
ln(1− x) + 2022 khi x < 1 5 5 Câu 7. Cho f
∫ (x)dx =10. Kết quả 2−4 f ∫ (x)dx bằng: 2 2 A. 32 − . B. 34 − . C. 36 − . D. 40 − . Lời giải Chọn B 5 5 5 5 Ta có: 2 − 4 f ∫
(x)dx = 2dx−4 f ∫ ∫ (x) 5
dx = 2x + 4 f
∫ (x)dx = 6−4.10 = 34 − . 2 2 2 2 2 e
Câu 8. Tính tích phân 1 1 I dx = − ∫ 2 x x 1 A. 1 I = B. 1 I = +1 C. I =1
D. I = e e e Lời giải Chọn A 1 1 1 e e 1 I = − dx = ∫ ln x + = . 2 x x x e 1 1 5 Câu 9. Cho 1− 2x dx ∫ 3
= a ln + bln 2 với a,b∈ . Mệnh đề nào đúng? 2 x − 5x + 6 2 4
A. 2a + b =11.
B. a + 2b = 7 − .
C. a + b = 8 .
D. a − 2b =15. Lời giải Chọn B 5 Đặt 1− 2x I = dx ∫ 2 x − 5x + 6 4 Ta có: 1− 2x A B ( = +
x − 2)(x − 3) x − 2 x − 3 Trang 2/14
⇒1− 2x = A(x − 3) + B(x − 2) ( ) 1
Chọn x = 3 thay vào ( ) 1 ⇒ B = 5 −
Chọn x = 2 thay vào ( ) 1 ⇒ A = 3 5 5 3 5 ⇒ I = dx − dx ∫ 5 5
= 3ln x − 2 − 5ln x − 3 3 = 3ln − 5ln 2 x ∫ ( ) ( ) − 2 x − 3 4 4 2 4 4 ⇒ a = 3,b = 5
− ⇒ a + 2b = 3−10 = 7 − . 1 3 3
Câu 10. Cho f (x) ∫ dx = 1 − ; f (x) ∫
dx = 5. Tính f (x) ∫ dx 0 0 1 A. 1. B. 4. C. 6. D. 5. Lời giải 3 1 3 3 3 1 Ta có f (x) ∫ dx = f (x) ∫ dx + f (x) ∫ dx⇒ f (x) ∫ dx = f (x) ∫ dx − f (x) ∫ dx = 5+ 1= 6 0 0 1 1 0 0 3 Vậy f (x) ∫ dx = 6 1 2
Câu 11. Cho hàm số f (x) liên tục, có đạo hàm trên [ 1; − 2], f (− ) 1 = 8; f (2) = 1 − . Tích phân f '
∫ (x)dx bằng 1 − A. 1. B. 7. C. 9. − D. 9. Lời giải 2
Ta có f '(x)dx = f (x) 2 = f (2) − f (− ) 1 = 1 − − 8 = 9. − ∫ 1 − 1 − 1
Câu 12. Cho hàm số y = f (x) có đạo hàm liên tục trên [0; ] 1 , thỏa mãn f
∫ (x)dx = 3 và f ( )1 = 4 . Tích 0 1 phân xf ′
∫ (x)dx có giá trị là 0 A. 1 − . B. 1 . C. 1. D. 1 − . 2 2 Lời giải Chọn C Ta có 1 1 1 xf ′ ∫ (x)dx = d x f
∫ (x) = xf (x)1 − f ∫ (x)dx 0 0 0 0 1 = f ( ) 1 − f
∫ (x)dx = 4−3 =1. 0
Câu 13. Cho hàm số f (x) xác định và liên tục trên \{ } 0 thỏa mãn 2 2
x f (x) + ( x − ) f (x) ' 2 1 = xf (x) −1, 2
với mọi x∈ \{ }
0 đồng thời thỏa f ( ) 1 = 2 − . Tính f ∫ (x)dx 1 A. ln 2 − −1. B. 1 − ln 2 − . C. 3 − ln 2 − . D. ln 2 3 − − . 2 2 2 2 2 Lời giải Trang 3/14 Chọn D
Ta có x f (x) + xf (x) + = xf (x) + f (x) ⇔ (xf (x) + )2 = (xf (x) + )' 2 2 ' 2 1 1 1 (xf (x)+ )' 1 (xf (x)+ )' 1 Do đó 1 = 1⇒ dx = 1dx ⇒ −
= x + c ⇒ xf x + = − ( ∫ ∫ ( ) 1 1 xf (x) + )2 1 (xf (x)+ )2 1 xf (x) +1 x + c Mặt khác f ( ) 1 = 2 − nên 1 − + = −
⇒ c = ⇒ xf ( x) 1
+ = − ⇒ f ( x) 1 1 2 1 0 1 = − − 2 1+ c x x x 2 2 Vậy f ∫ (x) 1 1 1 2 1 dx = − − dx = − ∫
ln x + | = −ln 2 − 2 1 . x x x 2 1 1
Câu 14. Viết công thức tính diện tích S của hình H giới hạn bởi đồ thị hàm số y = f (x) , trục hoành và hai
đường thẳng x = a, x = b (a < b) . b b b b
A. S = π f
∫ (x)dx. B. S = f
∫ (x)dx . C. 2 S = π f
∫ (x)dx. D. 2 S = f
∫ (x)dx. a a a a Lời giải Chọn B b
Chọn câu S = f
∫ (x)dx . a
Câu 15. Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y = x , trục hoành Ox , các đường thẳng
x =1, x = 2 là A. 7 S = . B. 8 S = .
C. S = 7 .
D. S = 8. 3 3 Lời giải Chọn A 2 2 2 3
Diện tích hình phẳng là 2 S = x dx ∫ 2 = x dx ∫ x = 8 1 = − 7 = . 3 3 3 3 1 1 1
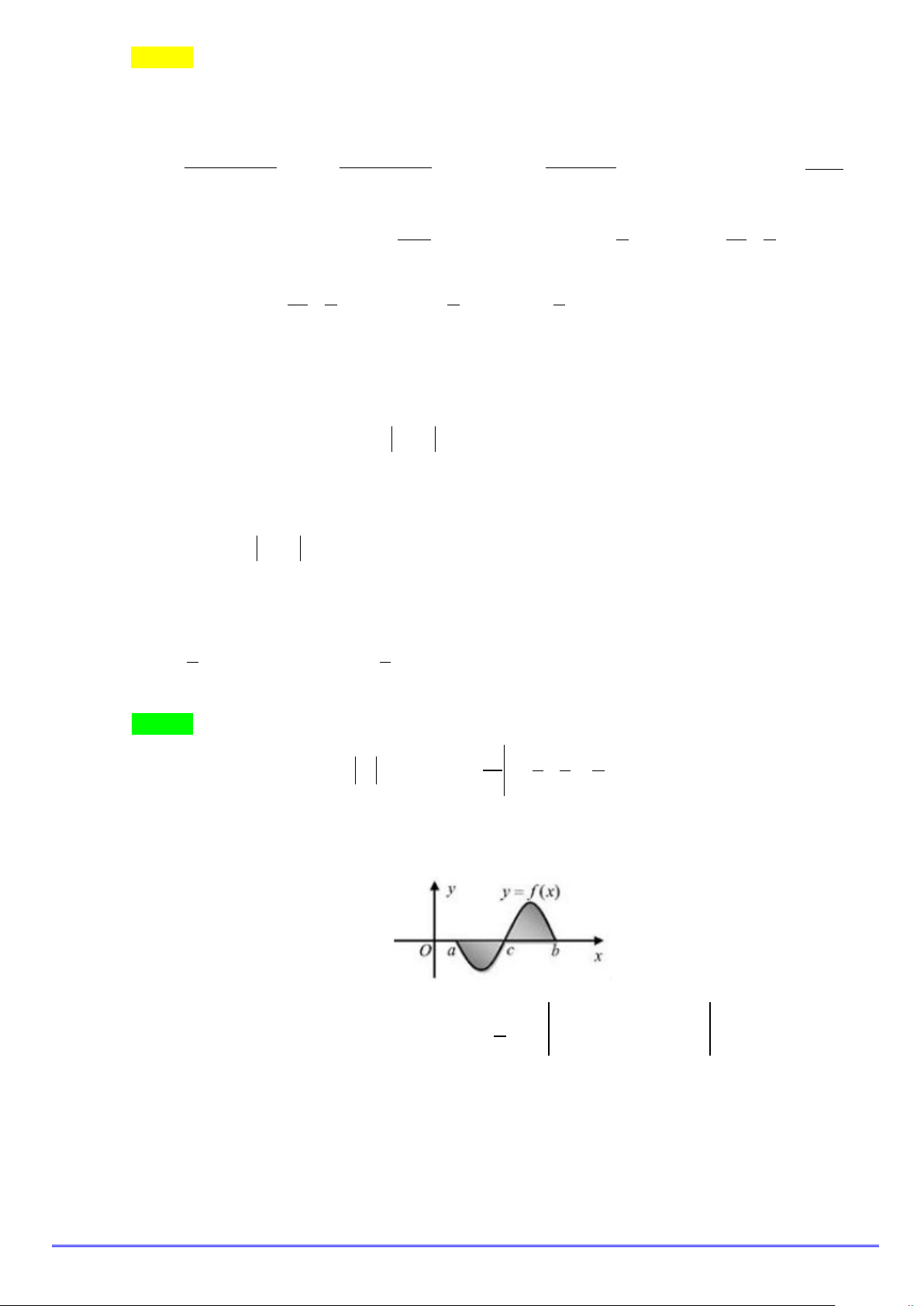
Câu 16. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f (x) , trục hoành, đường thẳng
x = a, x = b . Hỏi cách tính S nào dưới đây đúng? b c b A. S = f ∫ (x)dx . B. S = f
∫ (x)dx+ f ∫ (x)dx . a a c c b c b
C. S = − f
∫ (x)dx+ f ∫ (x)dx . D. S = f
∫ (x)dx+ f ∫ (x)dx . a c a c Lời giải. Chọn B Trang 4/14
Câu 17. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = x − 2x và đồ thị hàm số y = x . 37 81 9 A. . B. . C. 11. D. . 12 12 2 Lời giải Chọn D
Tìm hoành độ giao điểm của hai đường 2
y = x − 2x và y = x ta được x = 0; x = 3. 3 S = ( 2 x − x) 9 3 dx = ∫ . 2 0 2 Câu 18. x
Trong hệ tọa độ Oxy , parabol y =
chia đường tròn tâm O (O là gốc tọa độ) bán kính r = 2 2 2
thành 2 phần, diện tích phần nhỏ bằng: A. 3 2π + . B. 4 2π + . C. 4 2π − . D. 4 . 4 3 3 3 Lời giải Chọn B
Phương trình đường tròn: 2 2 x + y = 8 . Ta có: 2 2 2
x + y = 8 ⇔ y = ± 8 − x . .
Parabol chia hình tròn giới hạn bởi đường tròn (C) thành hai phần. Gọi S là phần diện tích giới hạn 2 x bởi 2
y = 8 − x và parapol (P) : y = . 2 2 x x = 2 −
Phương trình hoành độ giao điểm của (C) và (P) 2 8 − x = ⇔ . 2 x = 2
Khi đó ta tính được S như sau. 2 2 2 2 2 2 x 2
= ∫ 8− − d = 8− d x S x x x x − dx ∫ ∫ . − 2 − − 2 2 2 2 2 Tính 2 I = 8 − x dx ∫ . 2 −
Đặt t = 2 2 sin x ⇒ dt = 2 2 cos .xdx , ta có. π π 4 4 π I = ∫ ( 2
8 1− sin t.cost)dt = 4 ∫ (1+cos2t)dt = (4t + 2sin2t) 4 = π + π 2 4 . − π π − − 4 4 4 Trang 5/14 2 2 2 3 Ta có: x x 8 dx = = ∫ . − 2 6 3 2 2 − Suy ra 4 S = 2π + . 3
Câu 19. Trong hệ trục tọa độ Oxy , cho parabol (P) 2
: y = x và hai đường thẳng y = a , y = b (0 < a < b)
(hình vẽ). Gọi S là diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng = (phần tô 1 y a
đen); (S là diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng = (phần gạch chéo). 2 ) y b
Với điều kiện nào sau đây của a và b thì S = S ? 1 2 A. 3 b = 4a . B. 3 b = 2a . C. 3 b = 3a . D. 3 b = 6a . Lời giải Chọn A
Phương trình hoành độ giao điểm của parabol (P) 2
: y = x với đường thẳng y = b là 2
x = b ⇔ x = ± b .
Phương trình hoành độ giao điểm của parabol (P) 2
: y = x với đường thẳng y = a là 2
x = a ⇔ x = ± a .
Diện tích hình phẳng giới hạn bởi parabol (P) 2
: y = x và đường thẳng y = b là b 3 b S = 2 ∫ ( 2
b − x )d x b b 4 = 2 x b b bx − = 2b b − = . 3 3 3 0 0
Diện tích hình phẳng giới hạn bởi parabol (P) 2
: y = x và đường thẳng y = a (phần tô màu đen) là a 3 a S = 2 ∫ ( 2
a − x d x x a a = 4a a − = 1 ) = 2ax− 2 a a . 3 3 3 0 0 3 3 Do đó S = 2S 4b b 4 2. a a ⇔ = ⇔ ( b) = 2( a) 3 ⇔ b = 2 a 3 ⇔ b = 4 . 1 a 3 3
Câu 20. Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số y = tan x ,
trục hoành và các đường thẳng x = 0 , π
x = quanh trục hoành là 4 Trang 6/14 2 π A. π V = . B. π ln 2 V = . C. V = . D. π V = . 4 2 4 4 Lời giải Chọn B π π 4 4 π
Thể tích khối tròn xoay cần tính là V = π tan d x x ∫ sin = π x dx ∫ π ln 2 4 = −π ln cos x = . cos x 0 2 0 0
Câu 21. Cho hai số phức z =1+ 2i , z = 3− i . Tìm số phức z2 = . 1 2 z z1 A. 1 7
z = + i . B. 1 7 z = + i . C. 1 7
z = − i . D. 1 7 z = − + i . 5 5 10 10 5 5 10 10
Hướng dẫn giải Chọn C Ta có z − 2 z = 3 i = 1 7 = − i . z 1+ 2i 5 5 1
Câu 22. Cho số phức z = 2 + 4i . Tìm số phức w = iz + z .
A. w = 2 + 2i . B. w = 2 − − 2i .
C. w = 2 − 2i . D. w = 2 − + 2i . Lời giải Chọn B
Ta có: w = iz + z = i(2 + 4i) + 2 − 4i = 2 − − 2i .
Câu 23. Cho hai số phức z = 2 − 2i , z = 3
− + 3i . Khi đó số phức z − z là 1 2 1 2 A. 5 − + 5i . B. 5 − i .
C. 5 − 5i . D. 1 − + i . Lời giải Chọn C
Ta có z − z = 2 − 2i − 3
− + 3i = 5 − 5i . 1 2 ( ) ( )
Câu 24. Cho số phức w = 3− 5i . Tìm số phức z biết w = (3− 4i) z . A. 11 27 z = − i . B. 11 27 z = − + i . C. 11 27 z = + i . D. 11 27 z = − − i . 25 25 25 25 25 25 25 25 Lời giải Chọn D w = ( − i) 3+ 5i 11 27 11 27 3 4 z ⇔ z = = − + i ⇒ z = − − i . 3− 4i 25 25 25 25
Câu 25. Cho hai số phức z = m −1+ 3i và z = 2 − mi (m∈) . Tìm tất cả các giá trị của tham số m để z .z 1 2 1 2 là số thực. A. m∈{ 2; − − } 3 . B. 2 m = . C. m∈{3;− } 2 . D. m∈{ 3 − ; } 2 . 5 Lời giải Chọn C
z .z = (m −1+ 3i)(2 − mi) 2 = − + − + + = m − + ( 2 5
2 6 + m − m ) là số thực khi 1 2
2m 2 6i m i mi 3m i m = 3 2
6 + m − m = 0 ⇔ . m − 2
Câu 26. Cho số phức z 2i . Phần thực và phần ảo của số phức z lần lượt là? A. 2 và 1. B. 1 và 2
C. 2 .và i .
D. i và 2 . Lời giải Chọn A
Phần thực và phần ảo của số phức z 2i lần lượt là 2 và 1. Trang 7/14
Câu 27. Kí hiệu a,b lần lượt là phần thực và phần ảo của số phức z = 4
− − 3i . Tìm a,b . A. a = 4 − , b = 3 − i . B. a = 4 − , b = 3 . C. a = 4 − , b = 3 − .
D. a = 4 , b = 3 . Lời giải Chọn C
Câu 28. Cho số phức z thỏa mãn: 2
(2 −3i)z + (4 + i)z = −(1+ 3i) . Xác định phần thực và phần ảo của z. A. Phần thực là 2
− ; phần ảo là 5 .i B. Phần thực là 2
− ; phần ảo là 5. C. Phần thực là 2
− ; phần ảo là 3. D. Phần thực là 3
− ; phần ảo là 5 .i Lời giải Chọn B
Gọi z = a + bi ⇒ z = a − bi , ta có: 2
(2 − 3i)z + (4 + i)z = −(1+ 3i) ⇔ (2 − 3i)(a + bi) + (4 + i)(a −bi) = 8 − 6i
⇔ 3a + 2b − (a + b)i = 4 − 3i 3 a + 2b = 4 a = 2 − ⇔ ⇔ a b 3 b + = = 5 ⇒ z = 2 − + 5i.
Câu 29. Môđun của số phức z = ( − i)( + i)4 2 3 1 là A. z = 8 − +12i .
B. z = 13 .
C. z = 4 13 .
D. z = 31 . Lời giải Chọn C
Ta có: z = ( − i)( + i)4 2 3 1 = 8
− +12i ⇒ z = (− )2 2 8 +12 = 4 13 .
Câu 30. Tính mô đun của số phức z biết (1− 2i) z = 2 + 3i . A. 13 z = . B. 13 z = . C. 33 z = . D. 65 z = . 5 5 5 5 Lời giải Chọn D Ta có: ( − i) 2 + 3i 4 7
1 2 z = 2 + 3i ⇔ z = = − + i .Vậy 65 z = . 1− 2i 5 5 5
Câu 31. Cho hai số phức z z = = 1 , 2 thỏa mãn z z 1. Khi đó 2 2 + + − bằng 1 2 z z z z 1 2 1 2 A. 2 . B. 4 . C. 1. D. 0 . Lời giải Chọn B
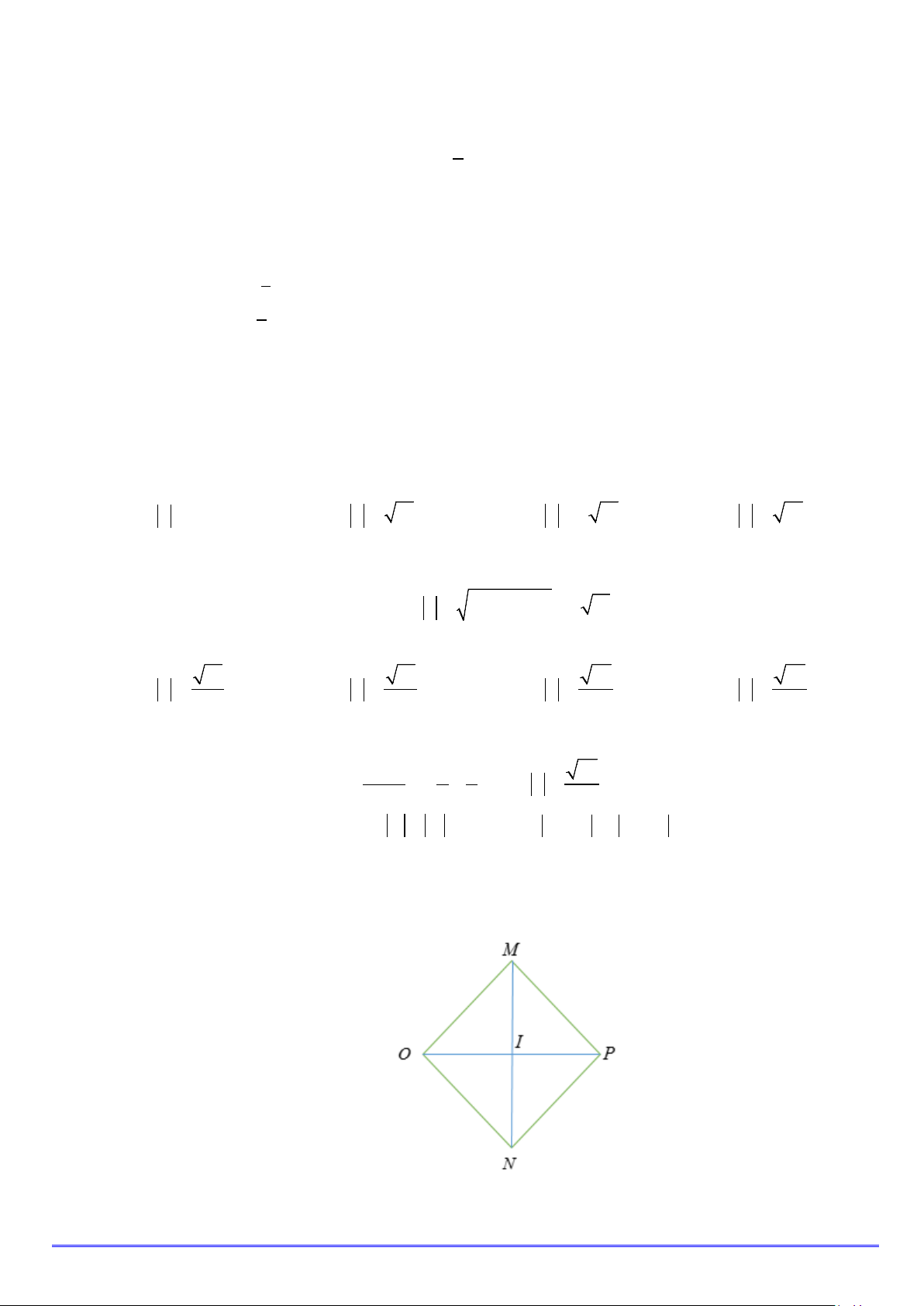
Gọi M , N là hai điểm lần lượt biểu diễn số phức z z 1 , 2 . Khi đó Trang 8/14
z = OM =1, z = ON =1, z + z = OP , z − z = NM với OMPN là hình bình hành. Tam 1 2 1 2 1 2 2 2 2 OM ON OI 2 2 OP MN giác OMN có 2 OI + = − 2 2 ⇒ =1− ⇒ OP + MN = 4 2 4 4 4
Cách 2: Đặt z = x + yi; z = a + bi;
x + y = a + b = 1 2
x, y,a,b∈ R .Từ giả thiết có 2 2 2 2 1 2 2 2 2 2 2
z + z + z − z = (x + a) + (y + b) + (x − a) + (y − b) 1 2 1 2 2 2 2 2 2 2
z + z + z − z = 2x + 2y + 2a + 2b = 4 1 2 1 2
Câu 32. Cho z , z là hai nghiệm của phương trình 2
z − z + = ( z ∈) . Tính giá trị của biểu thức 1 2 2 2 0
P = 2 z + z + z − z . 1 2 1 2
A. P = 3.
B. P = 2 2 + 2 .
C. P = 2 + 4 .
D. P = 6 . Lời giải Chọn D z =1+ i 2
z − 2z + 2 = 0 ⇔
⇒ P = 2 2 + 2i = 4 + 2 = 6 . z = 1− i
Câu 33. Gọi z , z là các nghiệm của phương trình 2
z − 2z + 5 = 0 . Tính 4 4 = + . 1 2 P z z 1 2 A. 14i . B. 14 − i . C. -14. D. 14. Lời giải Chọn C
Ta có: P = z + z = (z + z )2 − 2z z = (S − 2P)2 4 4 2 2 2 2 2 2 − 2P . 1 2 1 2 1 2 Với S = 2; 5 P = nên P = 14 − .
Câu 34. Trên mặt phẳng tạo độ Oxy , tập hợp điểm biểu diễn số phức z thỏa mãn z − i = iz là
A. Đường thẳng y = 2 . B. Đường thẳng 1 y = − . 2 C. Đường thẳng 1 y = .
D. Đường tròn tâm I (0; ) 1 . 2 Lời giải Chọn C
Gọi số phức z = a + bi (a,b∈) .
Ta có: z − i = iz ⇔ a + bi − i = i(a + bi) ⇔ a + (b − ) 1 i = b − + ai ⇔ 2 a + (b − )2 2 2 1 = b + a ⇔ 2 − b +1 = 0 .
Vậy tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện bài toán là đường thẳng 1 y = . 2
Câu 35. Cho hai số phức z , z thỏa mãn z − 3i + 5 = 2 và iz −1+ 2i = 4 . Tìm giá trị lớn nhất của biểu 1 2 1 2
thức T = 2iz + 3z . 1 2 A. 313 +16. B. 313 . C. 313 +8 . D. 313 + 2 5 . Lời giải Chọn A
Ta có z − 3i + 5 = 2 ⇔ 2iz + 6 +10i = 4 ( )
1 ; iz −1+ 2i = 4 ⇔ 3
− z − 6 − 3i =12 (2) . 2 ( 2) 1 1 Trang 9/14
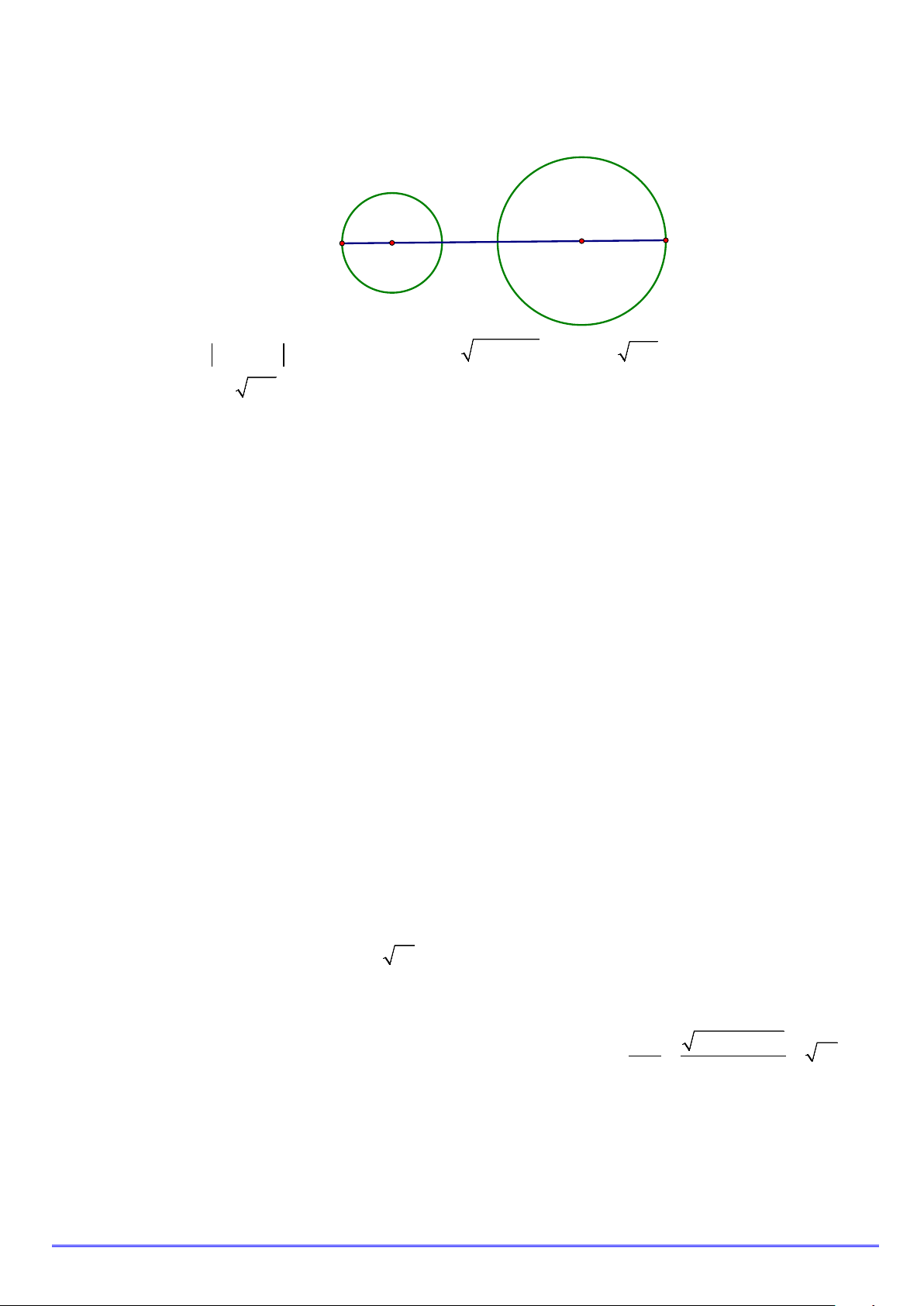
Gọi A là điểm biểu diễn số phức 2iz , 3 − z . Từ ( ) 1 và (2) suy ra 1
B là điểm biểu diễn số phức 2
điểm A nằm trên đường tròn tâm I 6; − 1
− 0 và bán kính R = 4 ; điểm 1 ( ) 1
B nằm trên đường tròn tâm
I 6;3 và bán kính R =12 . 2 ( ) 2 B A I I2 1 Ta có 2 2
T = 2iz + 3z = AB ≤ I I + R + R = 12 +13 + 4 +12 = 313 +16 . 1 2 1 2 1 2
Vậy maxT = 313 +16.
Câu 36. Trong không gian với hệ trục tọa độ Oxyz , cho điểm A(4;1;−2) . Tọa độ điểm đối xứng với A qua
mặt phẳng (Oxz) là
A. A′(4;−1;2) . B. A′( 4 − ;−1;2) .
C. A′(4;−1;− 2) . D. A′(4;1;2). Lời giải Chọn C
Hình chiếu của A lên mặt phẳng (Oxz) là H (4;0; 2 − ) .
⇒ tọa độ điểm đối xứng là A′(4; 1 − ; 2 − ) .
Câu 37. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ tâm I và bán kính R của mặ cầu (S) (x − )2 2 : 1 + y + (z + )2 1 = 4 . A. I (1;0;− ) 1 , R = 2 . B. I ( 1; − 0; ) 1 , R = 2 . C. I (1;0;− ) 1 , R = 4 . D. I ( 1; − 0; ) 1 , R = 4 . Lời giải Chọn A
Tọa độ tâm I (1;0;− )
1 và bán kính R = 2 .
Câu 38. Trong không gian với hệ tọa độ Oxyz , cho hai điểm M ( 3
− ;1;− 6) và N (3;5;0) . Viết phương trình
mặt cầu (S ) có đường kính MN . A. (S ) 2
: x + ( y − 3)2 + (z − 3)2 = 22. B. (S ) 2
: x + ( y − 3)2 + (z + 3)2 = 22 . C. (S ) 2
: x + ( y − 3)2 + (z + 3)2 = 22 . D. (S ) 2
: x + ( y + 3)2 + (z − 3)2 = 22 . Lời giải Chọn B
Mặt cầu (S ) có tâm I (0;3; MN
− 3) là trung điểm MN , bán kính 36 16 36 R + + = = = 22 nên 2 2 phương trình (S ) 2
: x + ( y − 3)2 + (z + 3)2 = 22 .
Câu 39. Trong không gian với hệ tọa độ Oxyz , phương trình nào dưới đây là phương trình mặt cầu có tâm I (1;2;− )
1 và tiếp xúc với mặt phẳng (P) :
x − 2y − 2z −8 = 0?
A. (x + )2 + ( y + )2 + (z − )2 1 2 1 = 9 .
B. (x − )2 + ( y − )2 + (z + )2 1 2 1 = 9 . Trang 10/14
C. (x − )2 + ( y − )2 + (z + )2 1 2 1 = 3. 2 2 2 D. (x + )
1 + ( y + 2) + (z − ) 1 = 3. Lời giải Chọn B
Ta có d (I;(P)) = 3.
Câu 40. Trong không gian Oxyz , cho hai điểm A(1;2;− ) 1 và B( 3 − ;0;− )
1 . Mặt phẳng trung trực của đoạn
thẳng AB có phương trình là
A. x − y + z − 3 = 0
B. 2x + y +1 = 0
C. x − y + z + 3 = 0
D. 2x + y −1 = 0 Lời giải Chọn B
Trung điểm của đoạn AB là M ( 1; − 1;− ) 1 . Ta có AB = ( 4;
− − 2;0) là một vecto pháp tuyến của mặt phẳng trung trực của AB .
Mặt phẳng trung trực của đoạn AB có phương trình là 2(x + ) 1 +1( y − )
1 = 0 ⇔ 2x + y +1 = 0 .
Câu 41. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2; 1
− ;3), B(2;0;5), C(0; 3 − ;− ) 1 . Phương
trình nào dưới đây là phương trình của mặt phẳng đi qua A và vuông góc với BC ?
A. x − y + 2z + 9 = 0.
B. x − y + 2z − 9 = 0.
C. 2x + 3y − 6z −19 = 0.
D. 2x + 3y + 6z −19 = 0. Lời giải Chọn D
Mặt phẳng (P) đi qua điểm A(2; 1;
− 3) và vuông góc với đường thẳng BC nên nhận véctơ
CB = (2;3;6) làm véctơ pháp tuyến. Khi đó phương trình tổng quát của mặt phẳng (P) là:
2(x − 2) + 3( y + )
1 + 6(z −3) = 0 ⇔ 2x + 3y + 6z −19 = 0 .
Câu 42. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (α ) cắt 3 trục tọa độ tại M (3;0;0) , N (0; 4; − 0) , P(0;0; 2
− ) . Phương trình mặt phẳng (α ) là:
A. 4x − 3y − 6z −12 = 0.
B. 4x − 3y + 6z + 9 = 0 . C. x y z − − = 1. D. x y z − + + = 1. 3 4 3 3 4 2 Lời giải Chọn A.
Phương trình mặt chắn (α ) : x y z + +
= 1 ⇔ (α ) : 4x − 3y − 6z −12 = 0 . 3 4 − 2 −
Câu 43. Cho mặt phẳng (α ) : 2x −3y − 4z +1 = 0 . Khi đó, một véc tơ pháp tuyến của (α ) A. n = (2;3; 4
− ) . B. n = (2; 3 − ;4) . C. n = ( 2 − ;3;4) . D. n = ( 2 − ;3; ) 1 . Lời giải Chọn C
Mặt phẳng (α ) : 2x −3y − 4z +1 = 0 có một véc tơ pháp tuyến n = 2; 3 − ; 4 − 0 ( ) . Nhận thấy n = ( 2
− ;3;4) = −n0 , hay n cùng phương với n0 .
Do đó véc tơ n = ( 2
− ;3;4) cũng là một véc tơ pháp tuyến của mặt phẳng(α ) Trang 11/14
Câu 44. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P) đi qua điểm M (9;1 )
;1 cắt các tia Ox,Oy,Oz tại , A B,C ( ,
A B,C không trùng với gốc tọa độ ). Thể tích tứ diện OABC đạt giá trị nhỏ nhất là bao nhiêu? A. 81 . B. 243 . C. 81 . D. 243 . 2 2 6 Lời giải
Giả sử A(a;0;0), B(0; ;
b 0),C (0;0;c) với a,b,c > 0 .
Mặt phẳng (P) có phương trình: x y z + + = 1. a b c
Vì mặt phẳng (P) đi qua điểm M (9;1 ) ;1 nên 9 1 1 + + = 1. a b c 9 1 1 9 Ta có = + + ≥ 3 1 3 ⇒ . a . b c ≥ 243 . a b c . a . b c 1 243 81 V = a b c ≥ = OABC 81 OABC . .
. Vậy thể tích tứ diện
đạt giá trị nhỏ nhất là . 6 6 2 2
Câu 45. Trong không gian Oxyz , cho mặt phẳng (P) : x − 2y + z + 7 = 0 và mặt cầu (S ) 2 2 2
: x + y + z − 2x + 4z −10 = 0 . Gọi (Q) là mặt phẳng song song với mặt phẳng (P) và cắt mặt
cầu (S ) theo một giao tuyến là đường tròn có chu vi bằng 6π . Hỏi (Q) đi qua điểm nào trong số các điểm sau? A. (6;0; ) 1 . B. ( 3 − ;1;4) . C. ( 2 − ;−1;5) . D. (4;−1;− 2) . Lời giải Chọn C
Mặt cầu (S ) có tâm I (1;0;− 2), bán kính R = 15 .
Gọi r là bán kính của đường tròn giao tuyến. Ta có 2π r = 6π ⇔ r = 3.
Do (Q) // (P) ⇒ (Q) : x − 2y + z + d = 0 (d ≠ 7) . d −1 d = 7 loaïi
Ta có: d (I,(Q)) ( ) 2 2
= R − r = 6 ⇔ = 6 ⇔ 6 d = 5 − (nhaän)
Vậy (Q) : x − 2y + z −5 = 0 . Thay tọa độ ( 2
− ;−1;5) vào (Q) thấy thỏa mãn.
Câu 46. Trong không gian Oxyz , tìm một vectơ chỉ phương của đường thẳng:
x − 3 y −1 z + 4 d : = = . 2 − 1 − 3 A. b = (2; 1; − 3) . B. c = (3;1; 4 − ) . C. d = ( 2 − ;1; 3 − ). D. a = ( 2 − ; 1; − 3). Lời giải Chọn D Trang 12/14
phương trình đường thẳng
x − 3 y −1 z + 4 d : = =
nên d nhận vec tơ a = ( 2 − ; 1; − 3) là một vec tơ 2 − 1 − 3 chỉ phương.
Câu 47. Trong không gian Oxyz , phương trình nào dưới đây là phương trình đường thẳng đi qua điểm
A(1;2;0) và vuông góc với mặt phẳng (P) : 2x + y −3z −5 = 0. x = 1+ 2t x =1+ 2t x = 3 + 2t x =1+ 2t A.
y = 2 + t .
B. y = 2 + t .
C. y = 3+ t .
D. y = 2 −t . z = 3 − t z = 3t z = 3− 3t z = 3 − t Lời giải Chọn A
Đường thẳng d đi qua điểm A(1;2;0) và vuông góc với mặt phẳng (P) : 2x + y −3z −5 = 0 sẽ có
vectơ chỉ phương là a = − d (2;1; 3) x =1+ 2t
Đường thẳng d có phương trình là: y = 2 + t . z = 3 − t
Câu 48. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 2x − 2y + z = 0 và đường thẳng x 1 : y z d
+ = = . Gọi ∆ là một đường thẳng chứa trong (P), cắt và vuông góc với d . Vectơ 1 2 1 −
u = (a;1;b) là một vectơ chỉ phương của ∆ . Tính tổng S = a + b . A. S =1.
B. S = 0 .
C. S = 2 .
D. S = 4 . Lời giải Chọn C
Mặt phẳng (P) có vectơ pháp tuyến n = − . P (2; 2; )1
Đường thẳng d có vectơ chỉ phương u = − . d (1;2; )1
Ta có [ n u = = 3(0;1;2) = 3(0;1;2) . P ; d ] (0;3;6) a = 0
Nên ∆ có vectơ chỉ phương là u = (0;1;2) . Vậy ⇒ S = 2. b = 2
Câu 49. Trong không gian tọa độ Oxyz , xét vị trí tương đối của hai đường thẳng
x −1 y +1 z
x − 3 y − 3 z + 2 ∆ : = = , ∆ : = = 1 2 2 2 3 1 − 2 − 1 A. ∆ ∆ ∆ ∆ ∆ ∆ ∆ ∆
1 song song với 2 . B. 1 chéo với 2 . C. 1 cắt 2. D. 1 trùng với 2. Lời giải Vì 2 2 ≠
nên vectơ chỉ phương u = 2;2;3 của đường thẳng ∆ không cùng phương với vectơ 1 ( ) 1 − 2 − 1 chỉ phương u = 1; − 2
− ;1 của ∆ . Tức là ∆ chéo với ∆ hoặc ∆ cắt ∆ . 2 ( ) 2 1 2 1 2 Lấy M (1; 1;
− 0)∈∆ , N (3;3; 2
− )∈∆ . Ta có: MN = (2;4; 2 − ) . 1 2
Khi đó: u ;u .MN = 0. Suy ra u ,u , MN đồng phẳng. 1 2 1 2 Vậy ∆ ∆ 1 cắt 2 . Trang 13/14
Câu 50. Trong không gian Oxyz , cho đường thẳng x y −1 ∆ : z =
= và hai điểm A(1;2;− 5) , B( 1; − 0;2) . Biết 1 1 1
điểm M thuộc ∆ sao cho biểu thức T = MA − MB đạt giá trị lớn nhất là T . Khi đó, T bằng bao max max nhiêu?
A. T = 3
B. T = 2 6 − 3
C. T = 57
D. T = 3 6 max max max max Lời giải Chọn C AB = ( 2; − 2; − 7) . x = 1 − − 2t′
Phương trình đường thẳng AB là: y = 2 − t′ . z = 2+ 7t′
Xét vị trí tương đối của ∆ và AB ta thấy ∆ cắt AB tại điểm 1 2 1 C ; ; − − . 3 3 3 4 4 14 AC ; ; = − −
; 3 AC = AB nên B nằm giữa A và C . 3 3 3 2
T = MA − MB ≤ AB Dấu bằng xảy ra khi M trùng C . Vậy T = AB = 57 . max
------------- HẾT ------------- Trang 14/14
Document Outline
- THPT ĐÔNG HÀ -ĐỀ KIỂM TRA CUỐI KỲ II MÔN TOÁN LỚP 12
- THPT ĐÔNG HÀ -ĐỀ KIỂM TRA CUỐI KỲ II MÔN TOÁN LỚP 12 - HDG




