15 trang 4 lượt tải

Đề thi thử giữa kỳ 1 môn Giải tích 1 | Đại học Bách Khoa Hà Nội

7

Đề thi thử giữa kỳ 1 môn Giải tích 1 | Đại học Bách Khoa Hà Nội. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem.

Môn: Giải tích 1 98 tài liệu

Trường: Đại học Bách Khoa Hà Nội 5 K tài liệu

Tác giả:

Profile

đức trương

4 ngày trước
Tải xuống
Báo cáo
Danh sách Quiz
Tải xuống
/15
Owl.jpg
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Đề thi thử giữa kỳ môn Giải tích 1 - Học kỳ: 20211
Nhóm ngành 1 - Thời gian: 45 phút
(Đề t hi gồm 30 câu hỏi trắc nghiệm)
Câu 01. Cho lim
x→0
e
2x
−1
ln(1 −3x)
=
a
b
với a < b và phân số
a
b
tối giản. Giá trị a + b là
A 5 B −5 C 1 D −1
Câu 02. Tìm tập xác định hàm số y = arcsin (2x −1)
A [0; 1] B (0; 1) C [−1; 0] D (−1; 0)
Câu 03. Tìm hàm ngược của hàm số y = x|x| khi y < 0
A y =
√
x B y = −
√
−x C y = x
2
D y = −x
2
Câu 04. Cho dãy số
1 < x
1
< 2
x
n+1
= x
n
+ 1 −
1
2
x
2
n
∀n ∈ N
∗
. Tìm lim
n→∞
x
n
A
√
2 B 0 C
3
2
D 1
Câu 05. Tính I =
Z
f (x) cot
2
xdx. Biết F(x) = x −tan x là nguyên hàm của f (x)
A I = x + C B I = −
x
2
2
+ C
C I = −x + C D I =
x
2
2
+ C
Câu 06. Tính giới hạn của L = lim
x→0
1
x
1
x
−cot x
A 3 B 1 C
1
3
D 0
Câu 07. Tính giới hạn dãy số lim
n→∞
n
p
n
2
+ 2
A ∞ B 0 C
1
2
D 1
Câu 08. Tìm và phân loại điểm gián đoạn của hàm số y = cot
arctan
1
x
A x = 1, Điểm gián đoạn loại 2 B x = 1, Điểm gián đoạn loại 1
C x = 0, Điểm gián đoạn loại 2 D x = 0, Điểm gián đoạn bỏ được
Câu 09. Cho lim
x→0
ln(1 + 4 sin x)
3
x
−1
=
a
ln b
với a, b ∈ N
∗
. Giá trị a + b là
A 7 B 5 C 4 D 6
Câu 10. Cho I =
Z
dx
x
4
− x
2
=
1
x
+
a
b
ln
x −1
x + 1
với a, b ∈ N
∗
và phân số
a
b
tối giản. Giá trị b
a
là
Life is not a problem to be solved, but a reality to experienced 1
Owl.jpg
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
A 8 B 2 C 4 D 1
Câu 11. Cho α(x) = x
2
+ x, β(x) = e
x
−1. Khi x → ∞, khẳng định nào dưới đây đúng
A α(x) là VCL bậc cao hơn β(x)
B α(x) và β(x) là 2 VCB tương đương
C α(x) và β(x) là 2 VCB cùng bậc
D β(x) là VCL bậc cao hơn α(x)
Câu 12. Tìm tất cả số thực a để f (x) =
1 −cos ax
x
2
, x = 0
2 , x = 0
liên tục tại x = 0
A a = 2 B a = 4 C a = ±2 D a = 1
Câu 13. Cho hàm số f (x) khả vi tại x = 1 và biết rằng:
lim
x→0
f (1 + 2022x) − f (1 + 2021x)
x
= 66
Tính f
′
(1).
A 66 B 65 C 67 D 64
Câu 14. Cho
d
dx
f (x
2
)
= 2021x
3
và f (0) = 0. Tính f (2)
A 2021 B 2021
2
C 2021
4
D 2021
3
Câu 15. Tìm
d
d
(
x
4
)
2x
2
+ x
4
+ x
8
A
1 + x
2
+ x
6
x
2
B
1 + x
2
+ 2x
6
x
2
C
2 + x
2
+ 2x
6
2x
2
D
2 + x
2
+ x
6
x
2
Câu 16. Cho hàm số f (x) = x
3
−3x
2
+ 4x có hàm ngược. Tính ( f
−1
)
′
(2)
A 3 B 4 C 2 D 1
Câu 17. Cho f (x) =
Z
(sin x + cos x)e
x
dx, f (0) = 0. Tính I =
Z
π
2
0
f (x)
e
x
dx
A I = 1 B I = 0 C I = −1 D I = 2
Câu 18. Tính đạo hàm cấp 5 của hàm số : y = ln(2x − x
2
)
A
4!
x
5
+
4!
(x −2)
5
, ∀0 < x ≤ 2. B
4!
x
5
+
4!
(x −2)
5
, ∀0 < x ≤ 2.
C
4!
x
5
+
4!
(x −2)
5
, ∀0 < x < 2. D
4!
x
4
+
4!
(x −2)
4
, ∀0 < x < 2.
Câu 19. Cho hàm số y = x
21
.e
22x
. Tính d
43
y(0)
A
22
21
·43!
22!
dx
43
B
22
22
·43!
21!
dx
43
C
21
22
·43!
22!
dx
43
D
22
21
·43!
21!
dx
43
Câu 20. Cho I =
Z
ln 2
0
e
3x
dx
e
x
+ 2
= a + b ln 2 + c ln 3 với a, b, c ∈ N. Giá trị b là
A b = 10 B b = 6 C b = 8 D b = 4
Life is not a problem to be solved, but a reality to experienced 2
Owl.jpg
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Câu 21. Tính đạo hàm của hàm số sau tại x = 7 :
y =
(ax −7)
3
·
3
√
x + 1
(bx −7)
2
(a, b > 1)
A 6a ·
a −1
b −1
2
−4b ·
a −1
b −1
3
+
7
9
·
(a −1)
3
(b −1)
2
B
3a
a −1
−
2b
b −1
+
1
8
(a −1)
3
(b −1)
2
C
3a
a −1
−
2b
b −1
+
1
3
2(a −1)
3
(b −1)
2
D 6a ·
a −1
b −1
2
−4b ·
a −1
b −1
3
+
7
12
·
(a −1)
3
(b −1)
2
Câu 22. Trong các phép tính giới hạn sau, đâu là phép tính có thể sử dụng L’Hospital?
A lim
x→0
arctan x + x
x
B lim
x→1
cos x + x
2
x −1
C lim
x→∞
x
2
arctan x
D lim
x→0
sin x
x
Câu 23. Tính giới hạn khi x → 0
+
của x
sin x
.
A 0 B +∞ C −∞ D 1
Câu 24. Tính giới hạn sau
lim
n→∞
1
1
+
1
2!
+
1
3!
+ ... +
1
n!
A e
2
B e C e −1 D
1
e
Câu 25. Đồ thị của đường cong x = 2 cos
3
t, y = 2 sin
3
t có dạng như thế nào?
A B
C D
Life is not a problem to be solved, but a reality to experienced 3
Owl.jpg
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Câu 26. Cho f (x) là một hàm khả vi cấp 2, liên tục trên R và
f
′′
(x) ≥ 0, ∀x ∈ R
Gọi x
0
là một điểm cực tiểu của hàm số trên, khẳng định nào sau đây là đúng với mọi hàm f (x) thoả
mãn điều kiện trên?
A Các đáp án đều sai
B f (x
0
) < f (x), ∀x ∈ R
C f (x
0
) ≤ f (x), ∀x ∈ R
D f
′
(x
0
) = 0
Câu 27. Cho đa thức bậc bốn f (x) có 4 nghiệm dương phân biệt. Tìm số điểm cực trị tối đa có thể có
của hàm số g(x) = x
4
[ f (x −2)]
2
A 20 B 5 C 10 D 15
Câu 28. Cho I =
Z
π
0
x sin xdx
1 + cos
2
x
=
π
a
b
với a, b ∈ N
∗
. Giá trị log
b
a là
A
1
2
B 1 C 2 D
1
4
Câu 29. Cho hàm số: f (x) =
1
x
2
− x + 1
. Giá trị của
f
(100)
(0)
+ 1 nằm trong khoảng nào dưới đây:
A (99!; 100!) B (101!; 102!)
C (100!; 101!) D (99!; 100!]
Câu 30. Cho I =
Z
cos xdx
5 cos x + 12 sin x + 13
. Đặt t = tan
x
2
khi đó
I = a ln(1 + t
2
) + b arctan t +
c
2t + 3
+ d ln |2t + 3| + C. Giá trị
1
5a + b + c + d
là
A 24 B 27 C 25 D 26
Life is not a problem to be solved, but a reality to experienced 4
Owl.jpg
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
ĐÁP ÁN
01. C
02. A
03. B
04.
A
05. C
06. C
07. D
08. D
09. A
10. B
11. D
12. C
13. A
14. A
15. B
16. D
17. A
18. C
19. D
20. C
21. D
22. A
23. D
24. C
25. C
26. C
27. D
28. A
29. C
30. D
ĐÁP ÁN VÀ LỜI GIẢI
Câu 01. Cho lim
x→0
e
2x
−1
ln(1 −3x)
=
a
b
với a < b và phân số
a
b
tối giản. Giá trị a + b là
A 5 B −5 C 1 D −1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C .
lim
x→0
e
2x
−1
ln(1 −3x)
= lim
x→0
2x
−3x
= −
2
3
⇒ a = −2, b = 3 ⇒ a + b = 1 □
Câu 02. Tìm tập xác định hàm số y = arcsin (2x −1)
A [0; 1] B (0; 1) C [−1; 0] D (−1; 0)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng A .
D: −1 ≤ 2x −1 ≤ 1 ⇔ 0 ≤ 2x ≤ 2 ⇔ 0 ≤ x ≤ 1 ⇔ D = [0; 1] □
Câu 03. Tìm hàm ngược của hàm số y = x|x| khi y < 0
A y =
√
x B y = −
√
−x C y = x
2
D y = −x
2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng B .
y < 0 ⇒ x|x| < 0 ⇒ x < 0 ⇒ y = −x
2
⇒ x = −
p
−y
⇒ Hàm ngược y = −
√
−x với x < 0 □
Câu 04. Cho dãy số
1 < x
1
< 2
x
n+1
= x
n
+ 1 −
1
2
x
2
n
∀n ∈ N
∗
. Tìm lim
n→∞
x
n
A
√
2 B 0 C
3
2
D 1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng A .
Bằng quy nạp, dễ dàng chứng minh:
x
n
−
1
2
<
1
2
n
∀n ≥ 3
Ta có:
x
n+1
−
1
2
=
1
2
x
n
−
√
2
2 −
√
2 − x
n
Life is not a problem to be solved, but a reality to experienced 5
Owl.jpg
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
⇒
x
n+1
−
1
2
≤
1
2
x
n
−
√
2
√
2 − x
n
+
2 −2
√
2
!
<
1
2
x
n
−
√
2
<
1
2
.
1
2
n+1
⇒ Bất đẳng thức đúng ∀n ≥ 3 ⇒
x
n
−
√
2
<
1
2
n
⇒
x
n
−
√
2
< lim
n→+∞
1
2
n
= 0
⇒ lim
n→+∞
x
n
−
√
2
= 0 ⇒ lim
n→+∞
x
n
=
√
2 □
Câu 05. Tính I =
Z
f (x) cot
2
xdx. Biết F(x) = x −tan x là nguyên hàm của f (x)
A I = x + C B I = −
x
2
2
+ C
C I = −x + C D I =
x
2
2
+ C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C .
Do F(x) là nguyên hàm của f (x)
⇔ F
′
(x) = f (x) = 1 −
1
cos
2
x
= −tan
2
x
⇒ I =
Z
−tan
2
x. cot
2
xdx = −
Z
dx = −x + C □
Câu 06. Tính giới hạn của L = lim
x→0
1
x
1
x
−cot x
A 3 B 1 C
1
3
D 0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C .
L = lim
x→0
sin x − x cos x
x
2
sin x
L = lim
x→0
x −
x
3
3!
+ o(x
3
) − x
1 −
x
2
2!
+ o(x
2
)
x
3
L = lim
x→0
1
3
x
3
+ o(x
3
)
x
3
=
1
3
□
Câu 07. Tính giới hạn dãy số lim
n→∞
n
p
n
2
+ 2
A ∞ B 0 C
1
2
D 1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D .
Xét lim
x→∞
x
p
x
2
+ 2 = e
lim
x→∞
ln(x
2
+ 2)
x
= e
lim
x→∞
2x
x
2
+ 2
(L
′
)
Life is not a problem to be solved, but a reality to experienced 6
Owl.jpg
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
= e
lim
x→∞
2
2x
(L
′
)
= e
0
= 1
⇒ lim
n→∞
n
p
n
2
+ 2 = 1 □
Câu 08. Tìm và phân loại điểm gián đoạn của hàm số y = cot
arctan
1
x
A x = 1, Điểm gián đoạn loại 2 B x = 1, Điểm gián đoạn loại 1
C x = 0, Điểm gián đoạn loại 2 D x = 0, Điểm gián đoạn bỏ được
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D .
Điểm gián đoạn của hàm số x = 0
lim
x→0
+
y = lim
x→0
+
cot
arctan
1
x
= 0 (1)
lim
x→0
−
y = lim
x→0
−
cot
arctan
1
x
= 0 (2)
Từ (1) và (2) ⇒ x = 0 là điểm gián đoạn bỏ được □
Câu 09. Cho lim
x→0
ln(1 + 4 sin x)
3
x
−1
=
a
ln b
với a, b ∈ N
∗
. Giá trị a + b là
A 7 B 5 C 4 D 6
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng A .
lim
x→0
ln(1 + 4 sin x)
3
x
−1
= lim
x→0
4 sin x
e
x ln 3
−1
= lim
x→0
4x
x ln 3
=
4
ln 3
=
a
ln b
⇒ a + b = 7 □
Câu 10. Cho I =
Z
dx
x
4
− x
2
=
1
x
+
a
b
ln
x −1
x + 1
với a, b ∈ N
∗
và phân số
a
b
tối giản. Giá trị b
a
là
A 8 B 2 C 4 D 1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng B .
I =
Z
dx
x
4
− x
2
=
Z
dx
x
2
(x
2
−1)
=
Z
x
2
−(x
2
−1)
x
2
(x
2
−1)
dx =
Z
1
x
2
−1
−
1
x
2
dx =
1
x
+
1
2
ln
x −1
x + 1
⇒ a = 1, b = 2 ⇒ b
a
= 2
□
Câu 11. Cho α(x) = x
2
+ x, β(x) = e
x
−1. Khi x → ∞, khẳng định nào dưới đây đúng
A α(x) là VCL bậc cao hơn β(x)
B α(x) và β(x) là 2 VCB tương đương
C α(x) và β(x) là 2 VCB cùng bậc
D β(x) là VCL bậc cao hơn α(x)
Life is not a problem to be solved, but a reality to experienced 7
Owl.jpg
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D .
Xét lim
x→∞
α(x)
β(x)
= lim
x→∞
x
2
+ x
e
x
−1
= lim
x→∞
2x + 1
e
x
= lim
x→∞
2
e
x
= 0
⇒ β(x) là VCL bậc cao hơn α(x) □
Câu 12. Tìm tất cả số thực a để f (x) =
1 −cos ax
x
2
, x = 0
2 , x = 0
liên tục tại x = 0
A a = 2 B a = 4 C a = ±2 D a = 1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C .
Để f (x) liên tục tại x = 0 ⇔ lim
x→0
f (x) = f (0) = 2
lim
x→0
f (x) = lim
x→0
1 −cos ax
x
2
= lim
x→0
(ax)
2
2
x
2
=
a
2
2
= 2 ⇒ a = ±2 □
Câu 13. Cho hàm số f (x) khả vi tại x = 1 và biết rằng:
lim
x→0
f (1 + 2022x) − f (1 + 2021x)
x
= 66
Tính f
′
(1).
A 66 B 65 C 67 D 64
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng A .
lim
x→0
f (1 + 2022x) − f (1 + 2021x)
x
= lim
x→0
2022.
f (1 + 2022x) − f (1)
2022x
−2021.
f (1 + 2021x) − f (1)
2021x
= lim
(2022x+1)→1
2022.
f (1 + 2022x) − f (1)
(1 + 2022x) −1
− lim
(2021x+1)→1
2021.
f (1 + 2021x) − f (1)
(1 + 2021x) −1
= 2022 f
′
(1) −2021 f
′
(1) = f
′
(1) = 66 □
Câu 14. Cho
d
dx
f (x
2
)
= 2021x
3
và f (0) = 0. Tính f (2)
A 2021 B 2021
2
C 2021
4
D 2021
3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng A .
Ta có:
d
dx
f (x
2
)
= 2021x
3
⇔ 2x. f
′
(x
2
) = 2021x
3
⇔ f
′
(x
2
) =
2021
2
.x
2
⇒ f
′
(t) =
2021
2
t
Lấy tích phân từ 0 → x cả 2 vế ta được:
Z
x
0
f
′
(t)dt =
Z
x
0
2021
2
tdt
Life is not a problem to be solved, but a reality to experienced 8
Owl.jpg
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
⇒ f (x) − f (0) =
2021
2
.
t
2
2
x
0
⇔ f (x) =
2021x
2
4
⇒ f (2) = 2021 □
Câu 15. Tìm
d
d
(
x
4
)
2x
2
+ x
4
+ x
8
A
1 + x
2
+ x
6
x
2
B
1 + x
2
+ 2x
6
x
2
C
2 + x
2
+ 2x
6
2x
2
D
2 + x
2
+ x
6
x
2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng B .
Ta có :
d
d
(
x
4
)
2x
2
+ x
4
+ x
8
=
2d
x
2
d
(
x
4
)
+
d
x
4
d
(
x
4
)
+
d
x
8
dx
4
)
=
1
x
2
+ 1 + 2x
4
=
1 + x
2
+ 2x
6
x
2
□
Câu 16. Cho hàm số f (x) = x
3
−3x
2
+ 4x có hàm ngược. Tính ( f
−1
)
′
(2)
A 3 B 4 C 2 D 1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D .
( f
−1
)
′
( f (x)) =
1
f
′
(x)
=
1
3x
2
−6x + 4
Xét f (x) = 2 ⇒ x
3
−3x
2
+ 4x = 2 ⇒ x = 1
⇒ ( f
−1
)
′
(2) =
1
3.1 −6.1 + 4
= 1 □
Câu 17. Cho f (x) =
Z
(sin x + cos x)e
x
dx, f (0) = 0. Tính I =
Z
π
2
0
f (x)
e
x
dx
A I = 1 B I = 0 C I = −1 D I = 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng
A .
f (x) =
Z
(sin x + cos x)e
x
dx = e
x
sin x + C , f (0) = 0 ⇒ C = 0 ⇒ f (x) = e
x
sin x
⇒ I =
Z
π
2
0
sin xdx = 1 □
Câu 18. Tính đạo hàm cấp 5 của hàm số : y = ln(2x − x
2
)
Life is not a problem to be solved, but a reality to experienced 9
Owl.jpg
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
A
4!
x
5
+
4!
(x −2)
5
, ∀0 < x ≤ 2. B
4!
x
5
+
4!
(x −2)
5
, ∀0 < x ≤ 2.
C
4!
x
5
+
4!
(x −2)
5
, ∀0 < x < 2. D
4!
x
4
+
4!
(x −2)
4
, ∀0 < x < 2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C .
y = ln
2x − x
2
= ln(x(2 − x)) = ln x + ln(2 − x) (điều kiện: 0 < x < 2 )
⇒ y
′
=
1
x
+
1
x −2
= g(x)
⇒ y
(5)
= g
(4)
(x) =
(−1)
4
·4!
x
5
+
(−1)
4
·4!
(x −2)
5
=
4!
x
5
+
4!
(x −2)
5
, ∀0 < x < 2.
□
Câu 19. Cho hàm số y = x
21
.e
22x
. Tính d
43
y(0)
A
22
21
·43!
22!
dx
43
B
22
22
·43!
21!
dx
43
C
21
22
·43!
22!
dx
43
D
22
21
·43!
21!
dx
43
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D . Khai triển Maclaurin:
e
22x
= 1 + 22x +
(22x)
2
2!
+ ··· +
(22x)
22
22!
⇒ x
21
·e
22x
= x
21
1 + 22x +
(22x)
2
2!
+ ··· +
(22x)
22
22!
d
43
y(0) = y
(43)
(0) · dx
43
=
22
22
·43!
22!
dx
43
=
22
21
·43!
21!
dx
43
□
Câu 20. Cho I =
Z
ln 2
0
e
3x
dx
e
x
+ 2
= a + b ln 2 + c ln 3 với a, b, c ∈ N. Giá trị b là
A b = 10 B b = 6 C b = 8 D b = 4
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng
C .
Đặt t = e
x
⇒ dt = e
x
dx
I =
Z
2
1
t
2
t + 2
dt =
Z
2
1
t −2 +
4
t + 2
dt = −
1
2
+ 4 ln
4
3
= −
1
2
+ 8 ln 2 −4 ln 3 □
Life is not a problem to be solved, but a reality to experienced 10
Owl.jpg
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Câu 21. Tính đạo hàm của hàm số sau tại x = 7 :
y =
(ax −7)
3
·
3
√
x + 1
(bx −7)
2
(a, b > 1)
A 6a ·
a −1
b −1
2
−4b ·
a −1
b −1
3
+
7
9
·
(a −1)
3
(b −1)
2
B
3a
a −1
−
2b
b −1
+
1
8
(a −1)
3
(b −1)
2
C
3a
a −1
−
2b
b −1
+
1
3
2(a −1)
3
(b −1)
2
D 6a ·
a −1
b −1
2
−4b ·
a −1
b −1
3
+
7
12
·
(a −1)
3
(b −1)
2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D .
Xét : ln y = ln
"
(ax −7)
3
·
3
√
x + 1
(bx −7)
2
#
⇔ ln y = 3 ln(ax − 7) +
1
3
ln(x + 1) −2 ln(bx −7).
⇒
y
′
y
=
3a
ax − 7
+
1
3(x + 1)
−
2b
bx − 7
⇒y
′
=
3a
ax − 7
+
1
3(x + 1)
−
2b
bx − 7
·
(ax −7)
3
·
3
√
x + 1
(bx −7)
2
y
′
(7) =
3a
7(a −1)
+
1
24
−
2b
7(b −1)
·
7
3
·(a −1)
3
·2
7
2
(b −1)
2
= 6a ·
a −1
b −1
2
−4b ·
a −1
b −1
3
+
7
12
·
(a −1)
3
(b −1)
2
□
Câu 22. Trong các phép tính giới hạn sau, đâu là phép tính có thể sử dụng L’Hospital?
A lim
x→0
arctan x + x
x
B lim
x→1
cos x + x
2
x −1
C lim
x→∞
x
2
arctan x
D lim
x→0
sin x
x
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng A .
Phương án
sin x
x
không được sử dụng L’hospital bởi muốn tính (sin x)
′
ta cần dùng tới lim
t→0
sin t
t
Do L’hospital chỉ dùng khi phép tính giới hạn có dạng bất định:
0
0
hoặc
∞
∞
.
Trong 4 phương án đã cho thì chỉ phương án
arctan x + x
x
thoả mãn. □
Câu 23. Tính giới hạn khi x → 0
+
của x
sin x
.
A 0 B +∞ C −∞ D 1
Life is not a problem to be solved, but a reality to experienced 11
Owl.jpg
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D . Ta có lim
x→0
+
x
sin x
= e
lim
x→0
+
(sin x ln x)
= e
lim
x→0
+
(x ln x)
= e
I
⇒ I = lim
x→0
+
ln x
1
x
= lim
x→0
+
1
x
−
1
x
2
= lim
x→0
+
(−x) = 0 ⇒ e
I
= 1 □
Câu 24. Tính giới hạn sau
lim
n→∞
1
1
+
1
2!
+
1
3!
+ ... +
1
n!
A e
2
B e C e −1 D
1
e
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C . Ta có khai triển Maclaurin của e
x
là
∞
∑
i=0
x
i
i!
,
do đó giới hạn cần tìm = e
1
−1 = e −1 □
Câu 25. Đồ thị của đường cong x = 2 cos
3
t, y = 2 sin
3
t có dạng như thế nào?
A B
C D
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C . Ta có x , y xác định với mọi t, tuần hoàn theo t chu kỳ 2π
x(t) là hàm chẵn, y(t) là hàm lẻ nên đường cong đối xứng qua trục Oy.
Hơn nữa, x, y bị chặn trong đoạn [−2, 2] nên chỉ có 1 phương án đúng là
Life is not a problem to be solved, but a reality to experienced 12
Owl.jpg
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
□
Câu 26. Cho f (x) là một hàm khả vi cấp 2, liên tục trên R và
f
′′
(x) ≥ 0, ∀x ∈ R
Gọi x
0
là một điểm cực tiểu của hàm số trên, khẳng định nào sau đây là đúng với mọi hàm f (x) thoả
mãn điều kiện trên?
A Các đáp án đều sai
B f (x
0
) < f (x), ∀x ∈ R
C f (x
0
) ≤ f (x), ∀x ∈ R
D f
′
(x
0
) = 0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C .
Từ những gì đã biết thì f (x) là hàm lồi chưa chặt trên R nên khẳng định f (x
0
) < f (x) ∀x ∈ R chưa
đúng với mọi f (x). Đáp án đúng là f (x
0
) ≤ f (x) ∀x ∈ R □
Câu 27. Cho đa thức bậc bốn f (x) có 4 nghiệm dương phân biệt. Tìm số điểm cực trị tối đa có thể có
của hàm số g(x) = x
4
[ f (x −2) ]
2
A 20 B 5 C 10 D 15
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D . Ta có f (x) = ax
4
+ bx
3
+ cx
2
+ dx + e có 4 nghiệm dương phân biệt. Ta gọi
4 nghiệm này là a
1
, a
2
, a
3
, a
4
• Với g(x) = x
4
f
2
(x −2) ta có:
g
′
(x) = 4x
3
f
2
(x −2) + 2x
4
f (x −2) f
′
(x −2)
= x
3
f (x −2)[4 f (x −2) + 2x f
′
(x −2)]
Giải
g
′
(x) = 0 −→
x
3
= 0
f (x −2) = 0
2 f (x − 2) = −x f
′
(x −2)
• x
3
= 0 ←→ x = 0
Life is not a problem to be solved, but a reality to experienced 13
Owl.jpg
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
• f (x − 2) = 0 ←→ x ∈ {a
1
+ 2, a
2
+ 2, a
3
+ 2, a
4
+ 2}
•
f
′
(x −2)
f (x −2)
=
−2
x
⇔ |f (x −2)| =
C
x
2
, C ∈ R
Ta có đồ thị
=⇒ Tối đa có thể chạm nhau tại 10 điểm.
• Như vậy g’(x) = 0 sẽ có tối đa 1 + 4 + 10 = 15 nghiệm phân biệt, tương đương với 15 cực trị.
□
Câu 28. Cho I =
Z
π
0
x sin xdx
1 + cos
2
x
=
π
a
b
với a, b ∈ N
∗
. Giá trị log
b
a là
A
1
2
B 1 C 2 D
1
4
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng A .
Đặt t = π − x ⇒ dt = −dx
⇒ I =
Z
π
0
(π − t) sin(π − t)dt
1 + cos
2
(π − t)
=
Z
π
0
(π − t) sin tdt
1 + cos
2
t
⇒ I =
Z
π
0
(π − x) sin xdx
1 + cos
2
x
⇒ 2I =
Z
π
0
π sin x
1 + cos
2
x
⇒ I =
π
2
Z
π
0
sin xdx
1 + cos
2
x
=
π
2
arctan(cos x)
0
π
=
π
2
4
⇒ a = 2, b = 4 ⇒ log
b
a =
1
2
□
Câu 29. Cho hàm số: f (x) =
1
x
2
− x + 1
. Giá trị của
f
(100)
(0)
+ 1 nằm trong khoảng nào dưới đây:
A (99!; 100!) B (101!; 102!)
C (100!; 101!) D (99!; 100!]
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Life is not a problem to be solved, but a reality to experienced 14
Owl.jpg
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Lời giải. Đáp án đúng C . Ta có:
f (x) =
1
x −
1
2
2
+
3
4
=
1
x −
1
2
2
−
√
3
2
i
!
2
=
1
√
3i
1
x −
1
2
−
√
3
2
i
−
1
x −
1
2
+
√
3
2
i
f
(100)
(x) =
1
√
3i
(−1)
100
.100!
x −
1
2
−
√
3
2
i
!
101
−
(−1)
100
.100!
x −
1
2
+
√
3
2
i
!
101
f
(100)
(0) =
100!
√
3i
1
−
1
2
−
√
3
2
i
!
101
−
1
−
1
2
+
√
3
2
i
!
101
=
100!
√
3i
(−
√
3i) = −100!
⇒ |f
(100)
(0) | + 1 = 100! + 1 ∈ (100!; 101!) □
Câu 30. Cho I =
Z
cos xdx
5 cos x + 12 sin x + 13
. Đặt t = tan
x
2
khi đó
I = a ln(1 + t
2
) + b arctan t +
c
2t + 3
+ d ln |2t + 3|+ C. Giá trị
1
5a + b + c + d
là
A 24 B 27 C 25 D 26
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D .
Đặt t = tan
x
2
⇒
2dt
1 + t
2
= dx, cos x =
1 −t
2
1 + t
2
, sin x =
2t
1 + t
2
⇒ I =
Z
1 −t
2
1 + t
2
.
2dt
1 + t
2
5.
1 −t
2
1 + t
2
+ 12.
2t
1 + t
2
+ 13
=
Z
2(1 −t
2
)dt
(1 + t
2
)(8 t
2
+ 24t + 18)
=
Z
(1 − t
2
)dt
(1 + t
2
)(2 t + 3)
2
=
1
169
Z
−24t + 10
1 + t
2
+
−65
(2t + 3)
2
+
48
2t + 3
dt
=
−12
169
ln(1 + t
2
) +
10
169
arctan x +
5
26
.
1
2t + 3
+
24
169
ln |2t + 3|+ C □
Life is not a problem to be solved, but a reality to experienced 15

Tài liệu khác của Đại học Bách Khoa Hà Nội

Preview text:

Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Đề thi thử giữa kỳ môn Giải tích 1 - Học kỳ: 20211
Nhóm ngành 1 - Thời gian: 45 phút
(Đề thi gồm 30 câu hỏi trắc nghiệm) e2x − 1 a a Câu 01. Cho lim = với a < b và phân số
tối giản. Giá trị a + b là x→0 ln(1 − 3x) b b A 5 B −5 C 1 D −1 Câu 02.
Tìm tập xác định hàm số y = arcsin (2x − 1) A [0; 1] B (0; 1) C [−1; 0] D (−1; 0) Câu 03.
Tìm hàm ngược của hàm số y = x|x| khi y < 0 √ √ A y = x B y = − −x C y = x2 D y = −x2  1 < x  1 < 2 Câu 04. Cho dãy số 1 . Tìm lim xn x x2 ∈ N∗ n→∞  n+1 = xn + 1 − 2 n ∀n √ Owl.jpg 3 A 2 B 0 C D 1 2 Z Câu 05. Tính I =
f (x) cot2 xdx. Biết F(x) = x − tan x là nguyên hàm của f (x) x2 A I = x + C B I = − + C 2 x2 C I = −x + C D I = + C 2 1 1 Câu 06.
Tính giới hạn của L = lim − cot x x→0 x x 1 A 3 B 1 C D 0 3 Câu 07.
Tính giới hạn dãy số lim n pn2 + 2 n→∞ 1 A ∞ B 0 C D 1 2 1 Câu 08.
Tìm và phân loại điểm gián đoạn của hàm số y = cot arctan x
A x = 1, Điểm gián đoạn loại 2
B x = 1, Điểm gián đoạn loại 1
C x = 0, Điểm gián đoạn loại 2
D x = 0, Điểm gián đoạn bỏ được ln(1 + 4 sin x) a Câu 09. Cho lim =
với a, b ∈ N∗. Giá trị a + b là x→0 3x − 1 ln b A 7 B 5 C 4 D 6 Z dx 1 a x − 1 a Câu 10. Cho I = = + ln
với a, b ∈ N∗ và phân số
tối giản. Giá trị ba là x4 − x2 x b x + 1 b
Life is not a problem to be solved, but a reality to experienced 1
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập A 8 B 2 C 4 D 1 Câu 11.
Cho α(x) = x2 + x, β(x) = ex − 1. Khi x → ∞, khẳng định nào dưới đây đúng
A α(x) là VCL bậc cao hơn β(x)
B α(x) và β(x) là 2 VCB tương đương
C α(x) và β(x) là 2 VCB cùng bậc
D β(x) là VCL bậc cao hơn α(x)  1 − cos ax  , x ̸= 0 Câu 12.
Tìm tất cả số thực a để f (x) = x2 liên tục tại x = 0  2 , x = 0 A a = 2 B a = 4 C a = ±2 D a = 1 Câu 13.
Cho hàm số f (x) khả vi tại x = 1 và biết rằng:
f (1 + 2022x) − f (1 + 2021x) lim = 66 x→0 x Tính f ′(1). A 66 B 65 d
f (x2) = 2021x3 và f (0) = 0. Tính f (2) dx Owl.jpg C 67 D 64 Câu 14. Cho A 2021 B 20212 C 20214 D 20213 d Câu 15. Tìm 2x2 + x4 + x8 d (x4) 1 + x2 + x6 1 + x2 + 2x6 2 + x2 + 2x6 2 + x2 + x6 A B C D x2 x2 2x2 x2 Câu 16.
Cho hàm số f (x) = x3 − 3x2 + 4x có hàm ngược. Tính ( f −1)′(2) A 3 B 4 C 2 D 1 π Z Z f (x) Câu 17. Cho f (x) =
(sin x + cos x)exdx, f (0) = 0. Tính I = 2 dx 0 ex A I = 1 B I = 0 C I = −1 D I = 2 Câu 18.
Tính đạo hàm cấp 5 của hàm số : y = ln(2x − x2) 4! 4! 4! 4! A + , ∀0 < x ≤ 2. B + , ∀0 < x ≤ 2. x5 (x − 2)5 x5 (x − 2)5 4! 4! 4! 4! C + , ∀0 < x < 2. D + , ∀0 < x < 2. x5 (x − 2)5 x4 (x − 2)4 Câu 19.
Cho hàm số y = x21.e22x. Tính d43y(0) 2221 · 43! 2222 · 43! 2122 · 43! 2221 · 43! A dx43 B dx43 C dx43 D dx43 22! 21! 22! 21! Z ln 2 e3xdx Câu 20. Cho I =
= a + b ln 2 + c ln 3 với a, b, c ∈ N. Giá trị b là 0 ex + 2 A b = 10 B b = 6 C b = 8 D b = 4
Life is not a problem to be solved, but a reality to experienced 2
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Câu 21.
Tính đạo hàm của hàm số sau tại x = 7 : √ (ax − 7)3 · 3 x + 1 y = (a, b > 1) (bx − 7)2 a − 1 2 a − 1 3 7 (a − 1)3 A 6a · − 4b · + · b − 1 b − 1 9 (b − 1)2 3a 2b 1 (a − 1)3 B − + a − 1 b − 1 8 (b − 1)2 3a 2b 1 2(a − 1)3 C − + a − 1 b − 1 3 (b − 1)2 a − 1 2 a − 1 3 7 (a − 1)3 D 6a · − 4b · + · b − 1 b − 1 12 (b − 1)2 Câu 22.
Trong các phép tính giới hạn sau, đâu là phép tính có thể sử dụng L’Hospital? arctan x + x cos x + x2 A lim B lim x→0 x x2 sin x D lim arctan x Owl.jpg x→1 x − 1 C lim x→∞ x→0 x Câu 23.
Tính giới hạn khi x → 0+ của xsin x. A 0 B +∞ C −∞ D 1 Câu 24. Tính giới hạn sau 1 1 1 1 lim + + + ... + n→∞ 1 2! 3! n! 1 A e2 B e C e − 1 D e Câu 25.
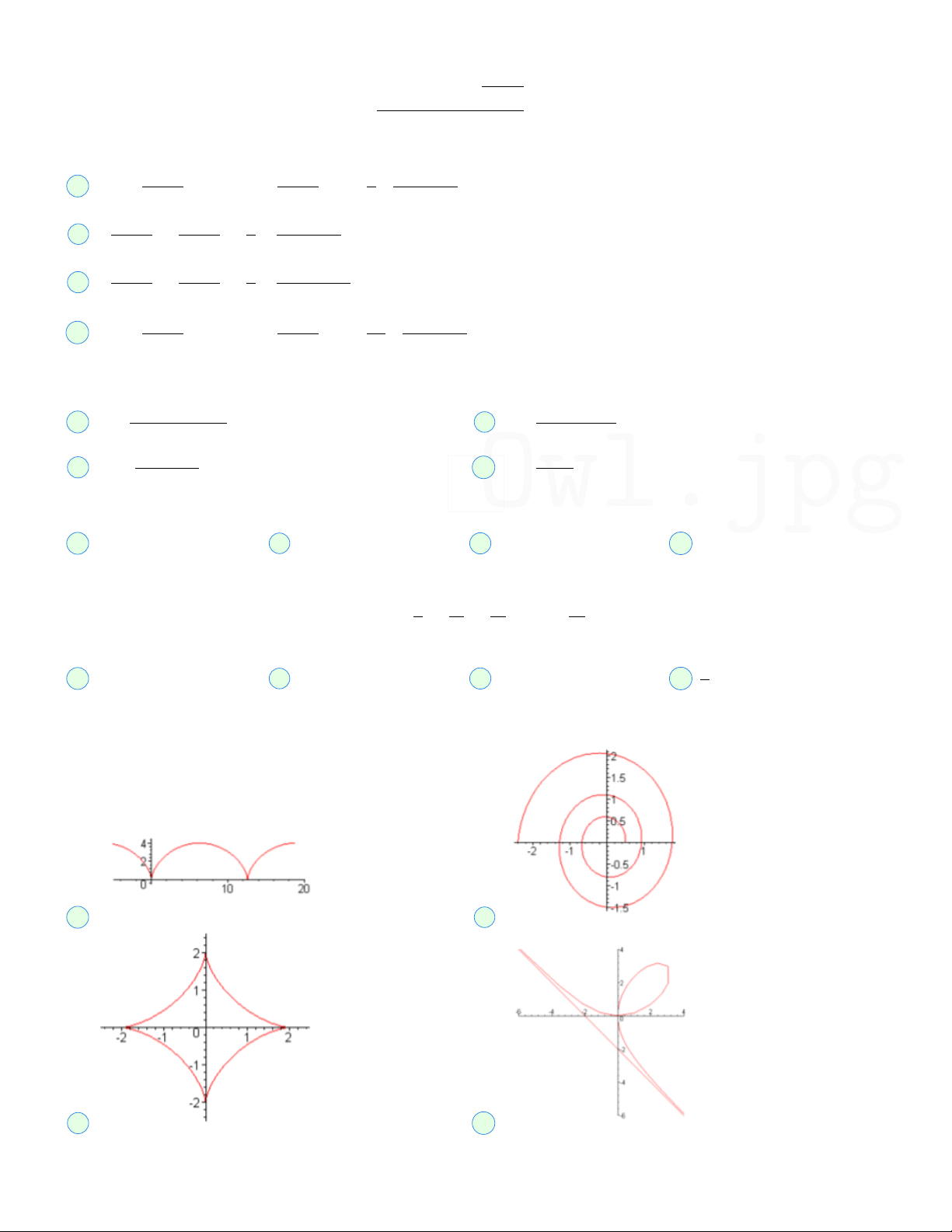
Đồ thị của đường cong x = 2 cos3 t, y = 2 sin3 t có dạng như thế nào? A B C D
Life is not a problem to be solved, but a reality to experienced 3
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Câu 26.
Cho f (x) là một hàm khả vi cấp 2, liên tục trên R và
f ′′(x) ≥ 0, ∀x ∈ R
Gọi x0 là một điểm cực tiểu của hàm số trên, khẳng định nào sau đây là đúng với mọi hàm f (x) thoả mãn điều kiện trên?
A Các đáp án đều sai
B f (x0) < f (x), ∀x ∈ R
C f (x0) ≤ f (x), ∀x ∈ R D f ′(x0) ̸= 0 Câu 27.
Cho đa thức bậc bốn f (x) có 4 nghiệm dương phân biệt. Tìm số điểm cực trị tối đa có thể có
của hàm số g(x) = x4[ f (x − 2)]2 A 20 B 5 C 10 D 15 Z π x sin xdx a π Câu 28. Cho I = =
với a, b ∈ N∗. Giá trị log a là b 0 1 + cos2 x b 1 1 A B 1 C 2 D 2 1
. Giá trị của f (100)(0) + 1 nằm trong khoảng nào dưới đây: x2 − x + 1 Owl.jpg 4
Câu 29. Cho hàm số: f (x) = A (99!; 100!) B (101!; 102!) C (100!; 101!) D (99!; 100!] Z cos xdx x Câu 30. Cho I = . Đặt t = tan khi đó 5 cos x + 12 sin x + 13 2 c 1
I = a ln(1 + t2) + b arctan t +
+ d ln |2t + 3| + C. Giá trị là 2t + 3 5a + b + c + d A 24 B 27 C 25 D 26
Life is not a problem to be solved, but a reality to experienced 4
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập ĐÁP ÁN 01. C 07. D 13. A 19. D 25. C 02. A 08. D 14. A 20. C 26. C 03. B 09. A 15. B 21. D 27. D 04. A 10. B 16. D 22. A 28. A 05. C 11. D 17. A 23. D 29. C 06. C 12. C 18. C 24. C 30. D
ĐÁP ÁN VÀ LỜI GIẢI e2x − 1 a a Câu 01. Cho lim = với a < b và phân số
tối giản. Giá trị a + b là x→0 ln(1 − 3x) b b A 5 B −5 C 1 D −1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C . e2x − 1 2x 2 lim = lim = −
⇒ a = −2, b = 3 ⇒ a + b = 1 □ x→0 ln(1 − 3x) x→0 −3x 3 Câu 02.
Tìm tập xác định hàm số y = arcsin (2x −Owl.jpg 1) A [0; 1] B (0; 1) C [−1; 0] D (−1; 0)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng A .
D: −1 ≤ 2x − 1 ≤ 1 ⇔ 0 ≤ 2x ≤ 2 ⇔ 0 ≤ x ≤ 1 ⇔ D = [0; 1] □ Câu 03.
Tìm hàm ngược của hàm số y = x|x| khi y < 0 √ √ A y = x B y = − −x C y = x2 D y = −x2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng B .
y < 0 ⇒ x|x| < 0 ⇒ x < 0 ⇒ y = −x2 ⇒ x = −p−y √
⇒ Hàm ngược y = − −x với x < 0 □  1 < x  1 < 2 Câu 04. Cho dãy số 1 . Tìm lim xn x x2 n→∞ 
n+1 = xn + 1 − 2 n ∀n ∈ N∗ √ 3 A 2 B 0 C D 1 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng A . 1 1
Bằng quy nạp, dễ dàng chứng minh: xn − < ∀n ≥ 3 2 2n 1 1 √ √ Ta có: xn+1 − = xn − 22 − 2 − xn 2 2
Life is not a problem to be solved, but a reality to experienced 5
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập ! 1 1 √ √ √ 1 √ 1 1 ⇒ xn+1 − ≤ xn − 2 2 − xn + 2 − 2 2 < xn − 2 < . 2 2 2 2 2n+1 √ 1 √ 1
⇒ Bất đẳng thức đúng ∀n ≥ 3 ⇒ xn − 2 < ⇒ xn − 2 < lim = 0 2n n→+∞ 2n √ √ ⇒ lim xn − 2 = 0 ⇒ lim xn = 2 □ n→+∞ n→+∞ Z Câu 05. Tính I =
f (x) cot2 xdx. Biết F(x) = x − tan x là nguyên hàm của f (x) x2 A I = x + C B I = − + C 2 x2 C I = −x + C D I = + C 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C .
Do F(x) là nguyên hàm của f (x) 1 ⇔ F′(x) = f (x) = 1 − = − tan2 x cos2 x Z Z ⇒ I = − tan2 x. cot2 xdx = − dx = −x + C Owl.jpg□ 1 1 Câu 06.
Tính giới hạn của L = lim − cot x x→0 x x 1 A 3 B 1 C D 0 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C . sin x − x cos x L = lim x→0 x2 sin x x2 x − x3 + o(x3) − x 1 − + o(x2) 3! 2! L = lim x→0 x3 1 x3 + o(x3) 1 L = lim 3 = □ x→0 x3 3 Câu 07.
Tính giới hạn dãy số lim n pn2 + 2 n→∞ 1 A ∞ B 0 C D 1 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D . ln(x2 + 2) limx→∞ Xét lim x px2 + 2 = e x x→∞ 2x limx→∞ = e x2 + 2 (L′)
Life is not a problem to be solved, but a reality to experienced 6
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 2 limx→∞ = e 2x (L′) = e0 = 1 ⇒ lim n pn2 + 2 = 1 □ n→∞ 1 Câu 08.
Tìm và phân loại điểm gián đoạn của hàm số y = cot arctan x
A x = 1, Điểm gián đoạn loại 2
B x = 1, Điểm gián đoạn loại 1
C x = 0, Điểm gián đoạn loại 2
D x = 0, Điểm gián đoạn bỏ được
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D .
Điểm gián đoạn của hàm số x = 0 1 lim y = lim cot arctan = 0 (1) x→0+ x→0+ x 1 lim y = lim cot arctan = 0 (2) x→0− x→0− x
Từ (1) và (2) ⇒ x = 0 là điểm gián đoạn bỏ được Owl.jpg□ ln(1 + 4 sin x) a Câu 09. Cho lim =
với a, b ∈ N∗. Giá trị a + b là x→0 3x − 1 ln b A 7 B 5 C 4 D 6
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng A . ln(1 + 4 sin x) 4 sin x 4x 4 a lim = lim = lim = = ⇒ a + b = 7 □ x→0 3x − 1 x→0 ex ln 3 − 1 x→0 x ln 3 ln 3 ln b Z dx 1 a x − 1 a Câu 10. Cho I = = + ln
với a, b ∈ N∗ và phân số
tối giản. Giá trị ba là x4 − x2 x b x + 1 b A 8 B 2 C 4 D 1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng B . Z dx Z dx Z x2 − (x2 − 1) Z 1 1 1 1 x − 1 I = = = dx = − dx = + ln x4 − x2 x2(x2 − 1) x2(x2 − 1) x2 − 1 x2 x 2 x + 1 ⇒ a = 1, b = 2 ⇒ ba = 2 □ Câu 11.
Cho α(x) = x2 + x, β(x) = ex − 1. Khi x → ∞, khẳng định nào dưới đây đúng
A α(x) là VCL bậc cao hơn β(x)
B α(x) và β(x) là 2 VCB tương đương
C α(x) và β(x) là 2 VCB cùng bậc
D β(x) là VCL bậc cao hơn α(x)
Life is not a problem to be solved, but a reality to experienced 7
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D . α(x) x2 + x 2x + 1 2 Xét lim = lim = lim = lim = 0 x→∞ β(x) x→∞ ex − 1 x→∞ ex x→∞ ex
⇒ β(x) là VCL bậc cao hơn α(x) □  1 − cos ax  , x ̸= 0 Câu 12.
Tìm tất cả số thực a để f (x) = x2 liên tục tại x = 0  2 , x = 0 A a = 2 B a = 4 C a = ±2 D a = 1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C .
Để f (x) liên tục tại x = 0 ⇔ lim f (x) = f (0) = 2 x→0 (ax)2 1 − cos ax a2 lim f (x) = lim = lim 2 = = 2 ⇒ a = ±2 □ x→0 x→0 x2 x→0 x2 2 Owl.jpg Câu 13.
Cho hàm số f (x) khả vi tại x = 1 và biết rằng:
f (1 + 2022x) − f (1 + 2021x) lim = 66 x→0 x Tính f ′(1). A 66 B 65 C 67 D 64
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng A .
f (1 + 2022x) − f (1 + 2021x) f (1 + 2022x) − f (1) f (1 + 2021x) − f (1) lim = lim 2022. − 2021. x→0 x x→0 2022x 2021x f (1 + 2022x) − f (1) f (1 + 2021x) − f (1) = lim 2022. − lim 2021. (2022x+1)→1 (1 + 2022x) − 1 (2021x+1)→1 (1 + 2021x) − 1
= 2022 f ′(1) − 2021 f ′(1) = f ′(1) = 66 □ d Câu 14. Cho
f (x2) = 2021x3 và f (0) = 0. Tính f (2) dx A 2021 B 20212 C 20214 D 20213
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng A . d 2021 2021 Ta có: f (x2)
= 2021x3 ⇔ 2x. f ′(x2) = 2021x3 ⇔ f ′(x2) = .x2 ⇒ f ′(t) = t dx 2 2
Lấy tích phân từ 0 → x cả 2 vế ta được: Z x Z x 2021 f ′(t)dt = tdt 0 0 2
Life is not a problem to be solved, but a reality to experienced 8
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 2021 t2 x 2021x2 ⇒ f (x) − f (0) = . ⇔ f (x) = ⇒ f (2) = 2021 □ 2 2 4 0 d Câu 15. Tìm 2x2 + x4 + x8 d (x4) 1 + x2 + x6 1 + x2 + 2x6 2 + x2 + 2x6 2 + x2 + x6 A B C D x2 x2 2x2 x2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng B . Ta có : d 2x2 + x4 + x8 d (x4) 2d x2 d x4 d x8 = + + d (x4) d (x4) dx4) 1 = + 1 + 2x4 x2 1 + x2 + 2x6 = x2 Owl.jpg□ Câu 16.
Cho hàm số f (x) = x3 − 3x2 + 4x có hàm ngược. Tính ( f −1)′(2) A 3 B 4 C 2 D 1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D . 1 1 ( f −1)′( f (x)) = = f ′(x) 3x2 − 6x + 4
Xét f (x) = 2 ⇒ x3 − 3x2 + 4x = 2 ⇒ x = 1 1 ⇒ ( f −1)′(2) = = 1 □ 3.1 − 6.1 + 4 π Z Z f (x) Câu 17. Cho f (x) =
(sin x + cos x)exdx, f (0) = 0. Tính I = 2 dx 0 ex A I = 1 B I = 0 C I = −1 D I = 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng A . Z f (x) =
(sin x + cos x)exdx = ex sin x + C, f (0) = 0 ⇒ C = 0 ⇒ f (x) = ex sin x π Z ⇒ I = 2 sin xdx = 1 □ 0 Câu 18.
Tính đạo hàm cấp 5 của hàm số : y = ln(2x − x2)
Life is not a problem to be solved, but a reality to experienced 9
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 4! 4! 4! 4! A + , ∀0 < x ≤ 2. B + , ∀0 < x ≤ 2. x5 (x − 2)5 x5 (x − 2)5 4! 4! 4! 4! C + , ∀0 < x < 2. D + , ∀0 < x < 2. x5 (x − 2)5 x4 (x − 2)4
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C .
y = ln 2x − x2 = ln(x(2 − x)) = ln x + ln(2 − x) (điều kiện: 0 < x < 2 ) 1 1 ⇒ y′ = + = g(x) x
x − 2 (−1)4 · 4! (−1)4 · 4! 4! 4! ⇒ y(5) = g(4)(x) = + = + , ∀0 < x < 2. x5 (x − 2)5 x5 (x − 2)5 □ Câu 19.
Cho hàm số y = x21.e22x. Tính d43y(0) 2221 · 43! 2222 · 43! 2122 · 43! 2221 · 43! A dx43 B dx43 C dx43 D dx43 22! 21!
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Owl.jpg 22! 21!
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D . Khai triển Maclaurin: (22x)2 (22x)22 e22x = 1 + 22x + + · · · + 2! 22! (22x)2 (22x)22
⇒ x21 · e22x = x21 1 + 22x + + · · · + 2! 22! d43y(0) = y(43)(0) · dx43 2222 · 43! = dx43 22! 2221 · 43! = dx43 21! □ Z ln 2 e3xdx Câu 20. Cho I =
= a + b ln 2 + c ln 3 với a, b, c ∈ N. Giá trị b là 0 ex + 2 A b = 10 B b = 6 C b = 8 D b = 4
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C . Đặt t = ex ⇒ dt = exdx Z 2 t2 Z 2 4 1 4 1 I = dt = t − 2 + dt = − + 4 ln = − + 8 ln 2 − 4 ln 3 □ 1 t + 2 1 t + 2 2 3 2
Life is not a problem to be solved, but a reality to experienced 10
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Câu 21.
Tính đạo hàm của hàm số sau tại x = 7 : √ (ax − 7)3 · 3 x + 1 y = (a, b > 1) (bx − 7)2 a − 1 2 a − 1 3 7 (a − 1)3 A 6a · − 4b · + · b − 1 b − 1 9 (b − 1)2 3a 2b 1 (a − 1)3 B − + a − 1 b − 1 8 (b − 1)2 3a 2b 1 2(a − 1)3 C − + a − 1 b − 1 3 (b − 1)2 a − 1 2 a − 1 3 7 (a − 1)3 D 6a · − 4b · + · b − 1 b − 1 12 (b − 1)2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D .√ " # (ax − 7)3 · 3 x + 1 Xét : ln y = ln (bx − 7)2 1 ⇔ ln y = 3 ln(aOwl.jpg x − 7) + ln(x + 1) − 2 ln(bx − 7). 3 y′ 3a 1 2b ⇒ = + − y ax − 7 3(x + 1) bx − 7 √ □ 3a 1 2b (ax − 7)3 · 3 x + 1 ⇒y′ = + − · ax − 7 3(x + 1) bx − 7 (bx − 7)2 3a 1 2b 73 · (a − 1)3 · 2 y′(7) = + − · 7(a − 1) 24 7(b − 1) 72(b − 1)2 a − 1 2 a − 1 3 7 (a − 1)3 = 6a · − 4b · + · b − 1 b − 1 12 (b − 1)2 Câu 22.
Trong các phép tính giới hạn sau, đâu là phép tính có thể sử dụng L’Hospital? arctan x + x cos x + x2 A lim B lim x→0 x x→1 x − 1 x2 sin x C lim D lim x→∞ arctan x x→0 x
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng A . sin x sin t Phương án
không được sử dụng L’hospital bởi muốn tính (sin x)′ ta cần dùng tới lim x t→0 t 0 ∞
Do L’hospital chỉ dùng khi phép tính giới hạn có dạng bất định: hoặc 0 ∞. arctan x + x
Trong 4 phương án đã cho thì chỉ phương án thoả mãn. □ x Câu 23.
Tính giới hạn khi x → 0+ của xsin x. A 0 B +∞ C −∞ D 1
Life is not a problem to be solved, but a reality to experienced 11
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D . Ta có lim xsin x = elimx→0+(sin x ln x) = elimx→0+(x ln x) = eI x→0+ 1 ln x ⇒ I = lim = lim x = lim (−x) = 0 ⇒ eI = 1 □ x→0+ 1 x→0+ 1 − x→0+ x x2 Câu 24. Tính giới hạn sau 1 1 1 1 lim + + + ... + n→∞ 1 2! 3! n! 1 A e2 B e C e − 1 D e
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C . Ta có khai triển Maclaurin của ex là ∞ ∑ xi, i! i=
do đó giới hạn cần tìm = e1 − 1 = e − 1 Owl.jpg 0 □ Câu 25.
Đồ thị của đường cong x = 2 cos3 t, y = 2 sin3 t có dạng như thế nào? A B C D
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C . Ta có x, y xác định với mọi t, tuần hoàn theo t chu kỳ 2π
x(t) là hàm chẵn, y(t) là hàm lẻ nên đường cong đối xứng qua trục Oy.
Hơn nữa, x, y bị chặn trong đoạn [−2, 2] nên chỉ có 1 phương án đúng là
Life is not a problem to be solved, but a reality to experienced 12
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập □ Câu 26.
Cho f (x) là một hàm khả vi cấp 2, liên tục trên R và
f ′′(x) ≥ 0, ∀x ∈ R
Gọi x0 là một điểm cực tiểu của hàm số trên, khẳng định nào sau đây là đúng với mọi hàm f (x) thoả mãn điều kiện trên?
A Các đáp án đều sai
B f (x0) < f (x), ∀x ∈ R
C f (x0) ≤ f (x), ∀x ∈ R Owl.jpg D f ′(x0) ̸= 0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng C .
Từ những gì đã biết thì f (x) là hàm lồi chưa chặt trên R nên khẳng định f (x0) < f (x) ∀x ∈ R chưa
đúng với mọi f (x). Đáp án đúng là f (x0) ≤ f (x) ∀x ∈ R □ Câu 27.
Cho đa thức bậc bốn f (x) có 4 nghiệm dương phân biệt. Tìm số điểm cực trị tối đa có thể có
của hàm số g(x) = x4[ f (x − 2)]2 A 20 B 5 C 10 D 15
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D . Ta có f (x) = ax4 + bx3 + cx2 + dx + e có 4 nghiệm dương phân biệt. Ta gọi
4 nghiệm này là a1, a2, a3, a4
• Với g(x) = x4 f 2(x − 2) ta có:
g′(x) = 4x3 f 2(x − 2) + 2x4 f (x − 2) f ′(x − 2)
= x3 f (x − 2)[4 f (x − 2) + 2x f ′(x − 2)] Giải  x3 = 0 g′(x) = 0 −→  f (x − 2) = 0
2 f (x − 2) = −x f ′(x − 2) • x3 = 0 ←→ x = 0
Life is not a problem to be solved, but a reality to experienced 13
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
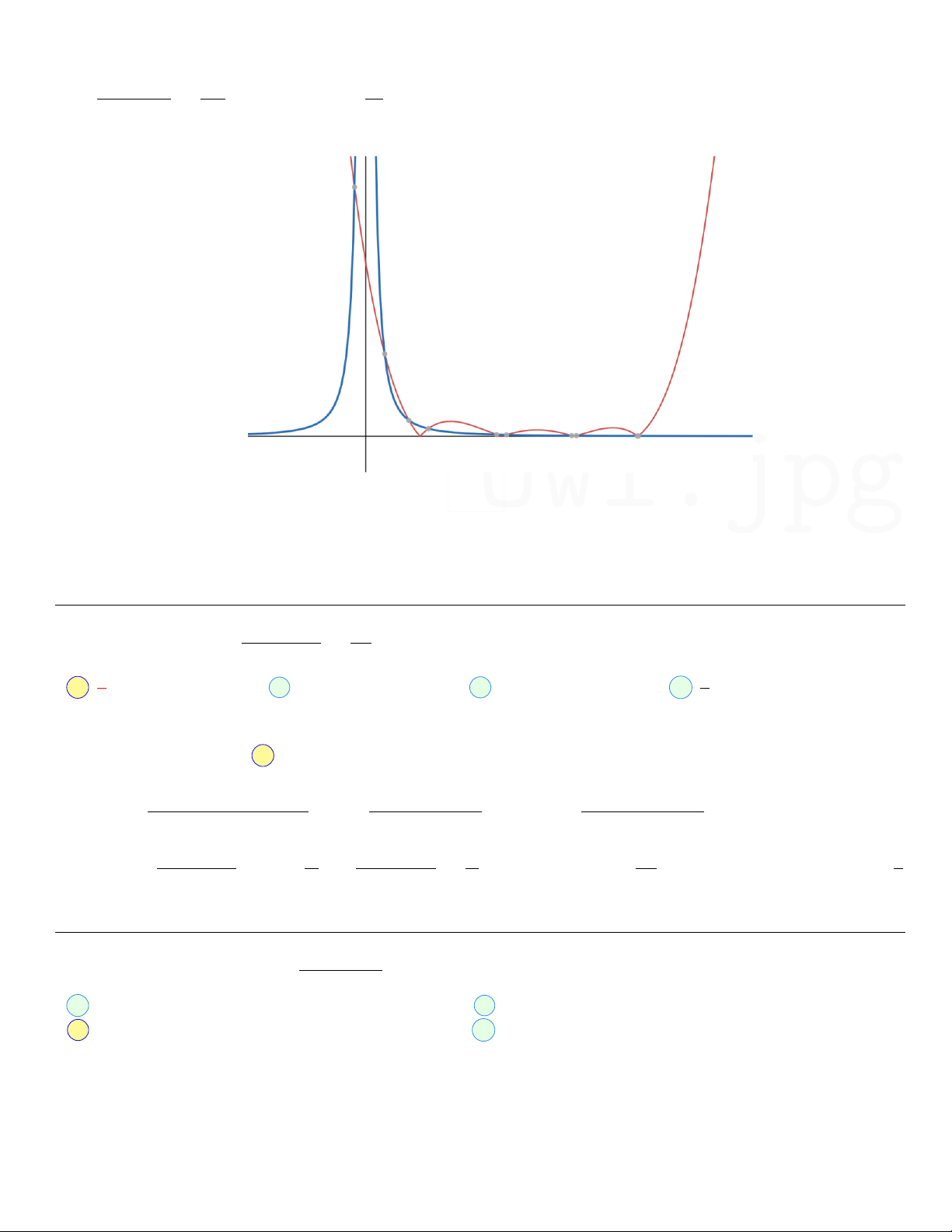
• f (x − 2) = 0 ←→ x ∈ {a1 + 2, a2 + 2, a3 + 2, a4 + 2} f ′(x − 2) −2 C • = ⇔ | f (x − 2)| = , C ∈ R f (x − 2) x x2 Ta có đồ thị
=⇒ Tối đa có thể chạm nhau tại 10 điểm. Owl.jpg
• Như vậy g’(x) = 0 sẽ có tối đa 1 + 4 + 10 = 15 nghiệm phân biệt, tương đương với 15 cực trị. □ Z π x sin xdx a π Câu 28. Cho I = =
với a, b ∈ N∗. Giá trị log a là b 0 1 + cos2 x b 1 1 A B 1 C 2 D 2 4
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng A .
Đặt t = π − x ⇒ dt = −dx Z π ( Z π ( Z π ( ⇒
π − t) sin(π − t)dt π − t) sin tdt π − x) sin xdx I = = ⇒ I = 0 1 + cos2(π − t) 0 1 + cos2 t 0 1 + cos2 x Z π Z π sin xdx 2 0 1 ⇒ π sin x π π π 2I = ⇒ I = = arctan(cos x) = ⇒ a = 2, b = 4 ⇒ log a = b 0 1 + cos2 x 2 0 1 + cos2 x 2 π 4 2 □ 1
Câu 29. Cho hàm số: f (x) =
. Giá trị của f (100)(0) + 1 nằm trong khoảng nào dưới đây: x2 − x + 1 A (99!; 100!) B (101!; 102!) C (100!; 101!) D (99!; 100!]
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Life is not a problem to be solved, but a reality to experienced 14
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Lời giải. Đáp án đúng C . Ta có:   1 1 1 1 1 f (x) = =   √ = √ √ √  −  1 2 3 !2 2 3i  1 3 1 3  x − + 1 3 x − − i x − + i 2 4 x − − i 2 2 2 2 2 2     1  (−1)100.100! (−1)100.100!  f (100)(x) = √  √ − √  3i  !101 !101   1 3 1 3   x − − i x − + i  2 2 2 2     100! √  1 1  100! f (100)(0) = √  √ − √  = √ (− 3i) = −100! 3i  !101 !101   1 3 1 3  3i  − − i − + i  2 2 2 2
⇒ | f (100)(0)| + 1 = 100! + 1 ∈ (100!; 101!) Owl.jpg□ Z cos xdx x Câu 30. Cho I = . Đặt t = tan khi đó 5 cos x + 12 sin x + 13 2 c 1
I = a ln(1 + t2) + b arctan t +
+ d ln |2t + 3| + C. Giá trị là 2t + 3 5a + b + c + d A 24 B 27 C 25 D 26
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lời giải. Đáp án đúng D . x 2dt 1 − t2 2t Đặt t = tan ⇒ = dx, cos x = , sin x = 2 1 + t2 1 + t2 1 + t2 1 − t2 2dt . Z Z 2(1 − t2)dt Z (1 − t2)dt ⇒ I = 1 + t2 1 + t2 = = 1 − t2 2t (1 + t2)(8t2 + 24t + 18) (1 + t2)(2t + 3)2 5. + 12. + 13 1 + t2 1 + t2 1 Z −24t + 10 −65 48 = + + dt 169 1 + t2 (2t + 3)2 2t + 3 −12 10 5 1 24 = ln(1 + t2) + arctan x + . + ln |2t + 3| + C □ 169 169 26 2t + 3 169
Life is not a problem to be solved, but a reality to experienced 15

Tài liệu liên quan: