ĐỀ THI THỬ HỌC SINH GIỎI
Năm học: 2021 - 2022
MÔN: Vật lý – Khối 11
Thời gian: 150 phút (không kể thời gian giao đề) Câu 1 (3điểm).
Một quả cầu có khối lượng m= 2kg treo ở một đầu một sợi dây có khối lượng không đáng kể và
không co dãn. Bỏ qua ma sát và sức cản. Lấy g= 10m/s2.
a) Kéo quả cầu khỏi vị trí cân bằng một góc m rồi thả ra ( vận tốc ban đầu bằng không). Thiết lập
biểu thức lực căng dây của dây treo khi quả cầu ở vị trí lệch một góc  so với vị trí cân bằng. Tìm
vị trí của quả cầu trên quĩ đạo để lực căng đạt cực đại. Tính độ lớn của lực căng cực đại nếu góc m =600.
b) Phải kéo quả cầu khỏi vị trí cân bằng một góc bằng bao nhiêu để khi thả cho dao động, lực căng
cực đại gấp 3 lần trọng lượng của quả cầu.
c) Thay sợi dây treo quả cầu bằng một lò xo có trọng lượng không đáng kể. Độ cứng của lò xo là k=
500N/m, chiều dài ban đầu l0=0,6m. Lò xo có thể dao động trong mặt phẳng thẳng đứng xung quanh
điểm treo O. Kéo quả cầu khỏi vị trí cân bằng một góc 0
 = 90 rồi thả ra. Lúc bắt đầu thả, lò xo ở
trạng thái không bị nén dãn. Xác định độ dãn của lò xo khi quả cầu đến vị trí cân bằng. Câu 2 (4,5điểm).
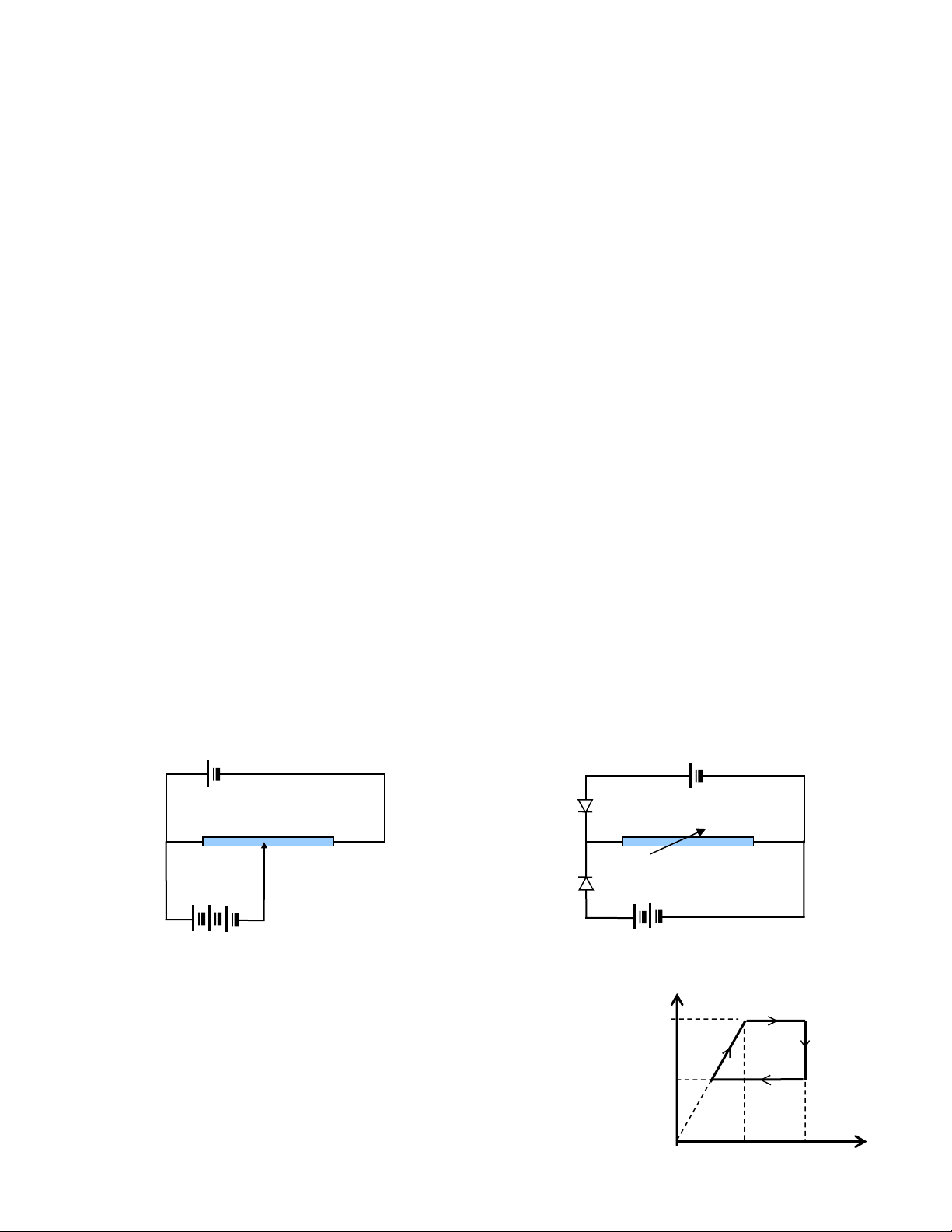
Cho mạch điện như hình 1. Nguồn điện có suất điện động E =12V, điện trở trong r = 0,6 , AB là
một biến trở con chạy có điện trở toàn phần là R = 9 . Ba ắc quy như nhau, mỗi cái có suất điện
động e0 và điện trở trong r0 = 0,5  . Gọi điện trở phần AC là x.
1. Khi x = 6  thì các ắc quy được nạp điện và dòng qua mỗi ắc quy là 0,4A. Tính suất điện động
của mỗi ắc quy và công suất tỏa nhiệt trên toàn bộ biến trở khi đó.
2. Bộ ắc quy trên ( ba ắc quy nối tiếp) khi đã được nạp đầy điện có thể dùng để thắp sáng bình
thường được tối đa bao nhiêu bóng đèn loại 1,5V-1,5W . Nói rõ cách mắc các đèn khi đó.
3. Ba ắc quy trên khi đã nạp đầy điện được mắc vào mạch như hình 2 . Hai điốt giống nhau có điện
trở thuận rD = 4  , điện trở ngược vô cùng lớn , R là một biến trở . Điều chỉnh giá trị R để công suất
điện tiêu thụ trên biến trở là cực đại , tìm giá trị cực đại đó. E,r e0,r0 D1 C R A B D2 Hình 1 e0,r0 2e0,2r0 Hình 2
Câu 3 (3điểm). P
Có 1 g khí Heli (coi là khí lý tưởng đơn nguyên tử) thực hiện một 2P0 1 2
chu trình 1 – 2 – 3 – 4 – 1 được biểu diễn trên giản đồ P-T như
hình 3 bên. Cho P0 = 105Pa; T0 = 300K.
a) Tìm thể tích của khí ở trạng thái 4. P0
b) Hãy nói rõ chu trình này gồm các đẳng quá trình nào. Vẽ lại chu 4 3
trình này trên giản đồ P-V và trên giản đồ V-T (cần ghi rõ giá trị T
bằng số và chiều biến đổi của chu trình). 0 T0 2T0 Trang 1
c) Tính công mà khí thực hiện trong từng giai đoạn của chu trình. Câu 4 (2,5điểm).
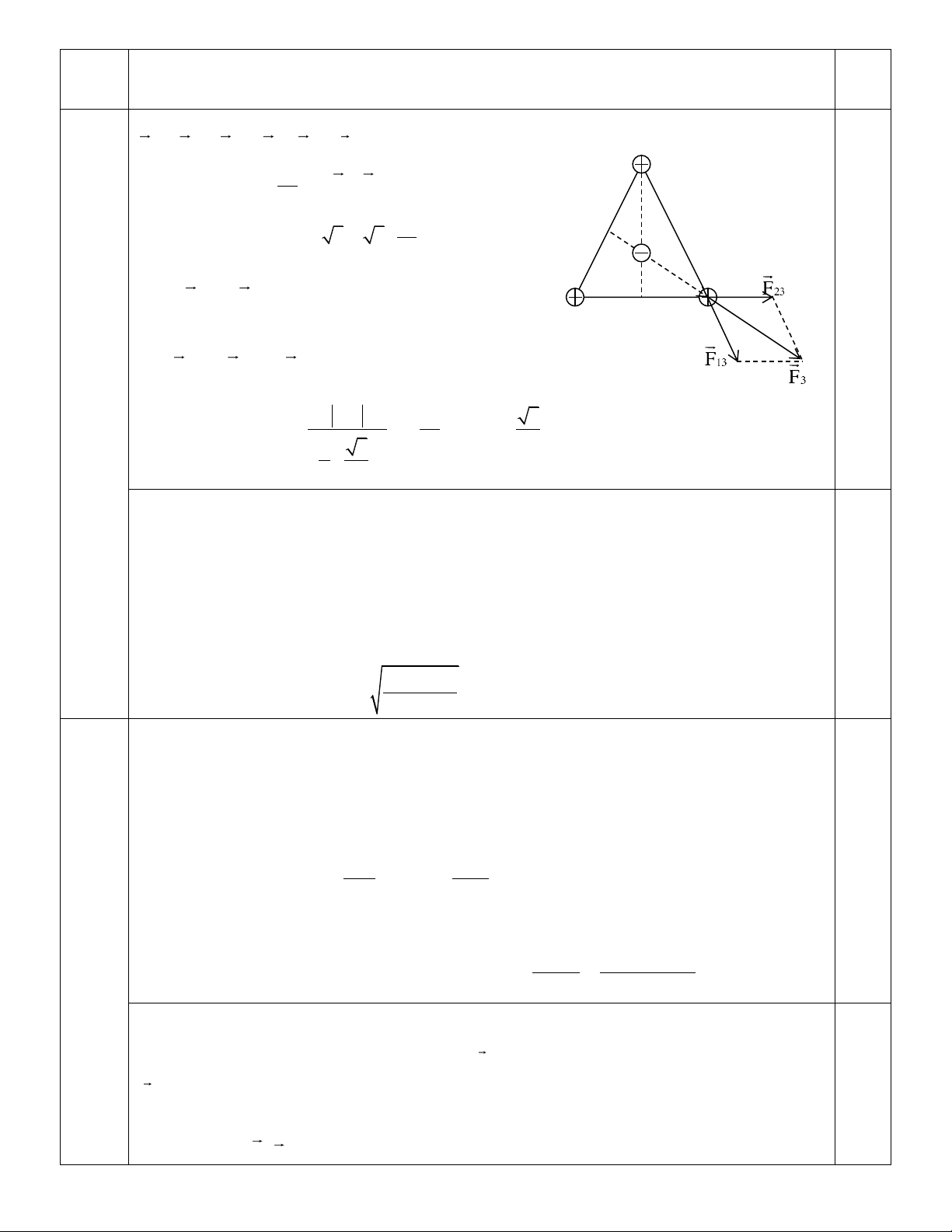
1. Tại ba đỉnh của một tam giác đều trong không khí, đặt 3 điện tích giống nhau q1 = q2 = q3 = q =
6.10-7C. Hỏi phải đặt điện tích q0 tại đâu, có giá trị bao nhiêu để hệ điện tích cân bằng?
2. Cho hai quả cầu giống nhau và đều mang điện tích +Q .Nêu phương án và dụng cụ thí nghiệm để
xác định gần đúng điện tích của mỗi quả cầu . Câu 5 (4điểm).
1. Một hạt không mang điện tích, đang đứng yên thì bị vỡ ra trong một từ trường đều B thành hai
mảnh khối lượng m1 và m2, mang điện tích tương ứng là q và –q. Biết rằng sau khoảng thời gian t kể
từ khi vỡ hai mảnh này gặp nhau. Bỏ qua tương tác Culông giữa hai mảnh và lực cản của môi
trường. Tìm khoảng thời gian t.
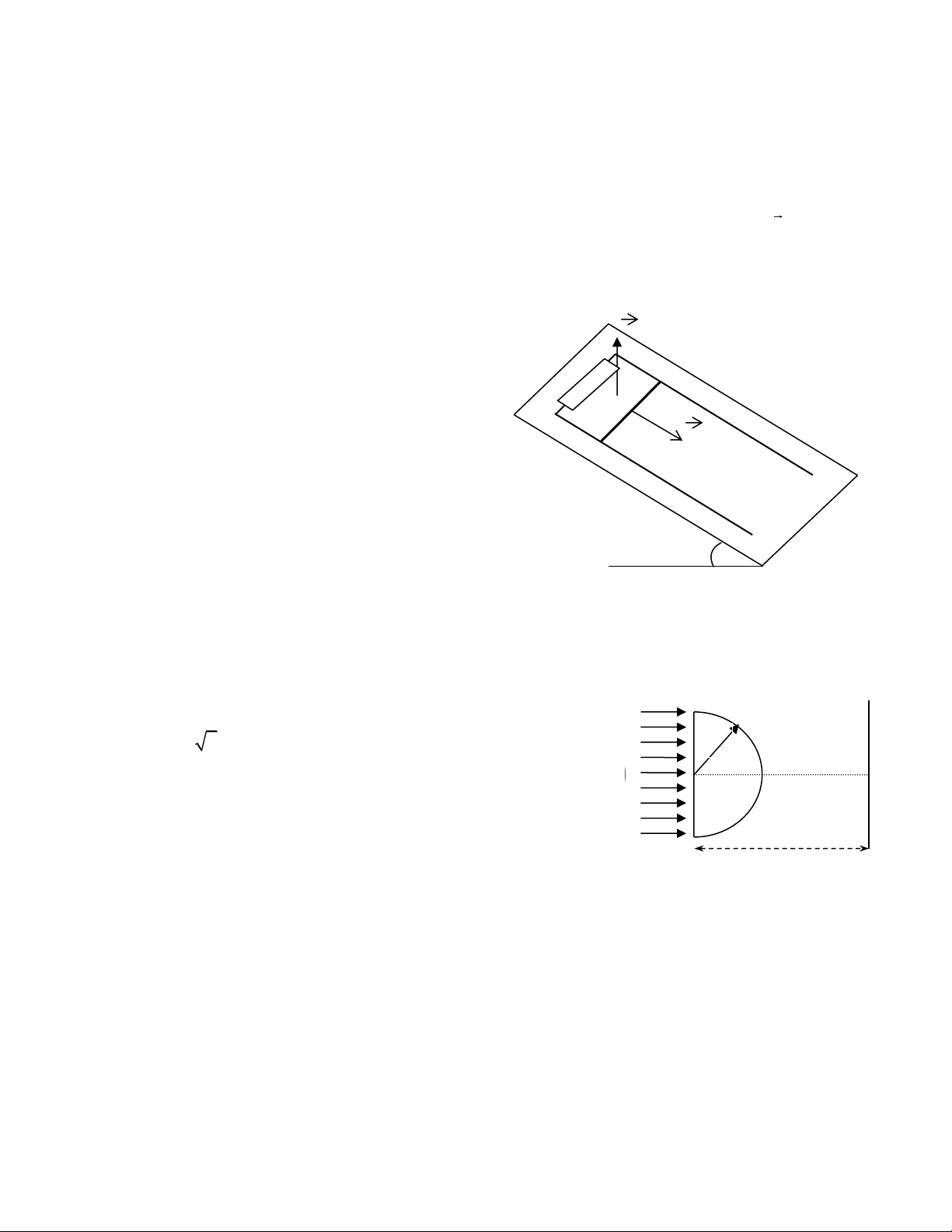
2. Trên một mặt phẳng nghiêng góc α = 450 với mặt
phẳng ngang có hai dây dẫn thẳng song song, điện B
trở không đáng kể nằm dọc theo đường dốc chính R N
của mặt phẳng nghiêng ấy như vẽ (hình 4). Đầu
trên của hai dây dẫn ấy nối với điện trở R = 0,1Ω.
Một thanh kim loại MN = l = 10 cm điện trở r = v M
0,1 Ω khối lượng m = 20g đặt vuông góc với hai
dây dẫn nói trên, trượt không ma sát trên hai dây
dẫn ấy. Mạch điện đặt trong một từ trường đều, r
cảm ứng từ B có độ lớn B = 1T có hướng thẳng
đứng từ dưới lên trên. Lấy g = 10m/s2. 
a) Thanh kim loại trượt xuống dốc. Xác định chiều Hình 4
dòng điện cảm ứng chạy qua R
b) Chứng minh rằng lúc đầu thanh kim loại chuyển động nhanh dần đến một lúc chuyển động với
vận tốc không đổi. Tính giá trị của vận tốc không đổi ấy. Khi đó cường độ dòng điện qua R là bao nhiêu? Câu 6 (2điểm).
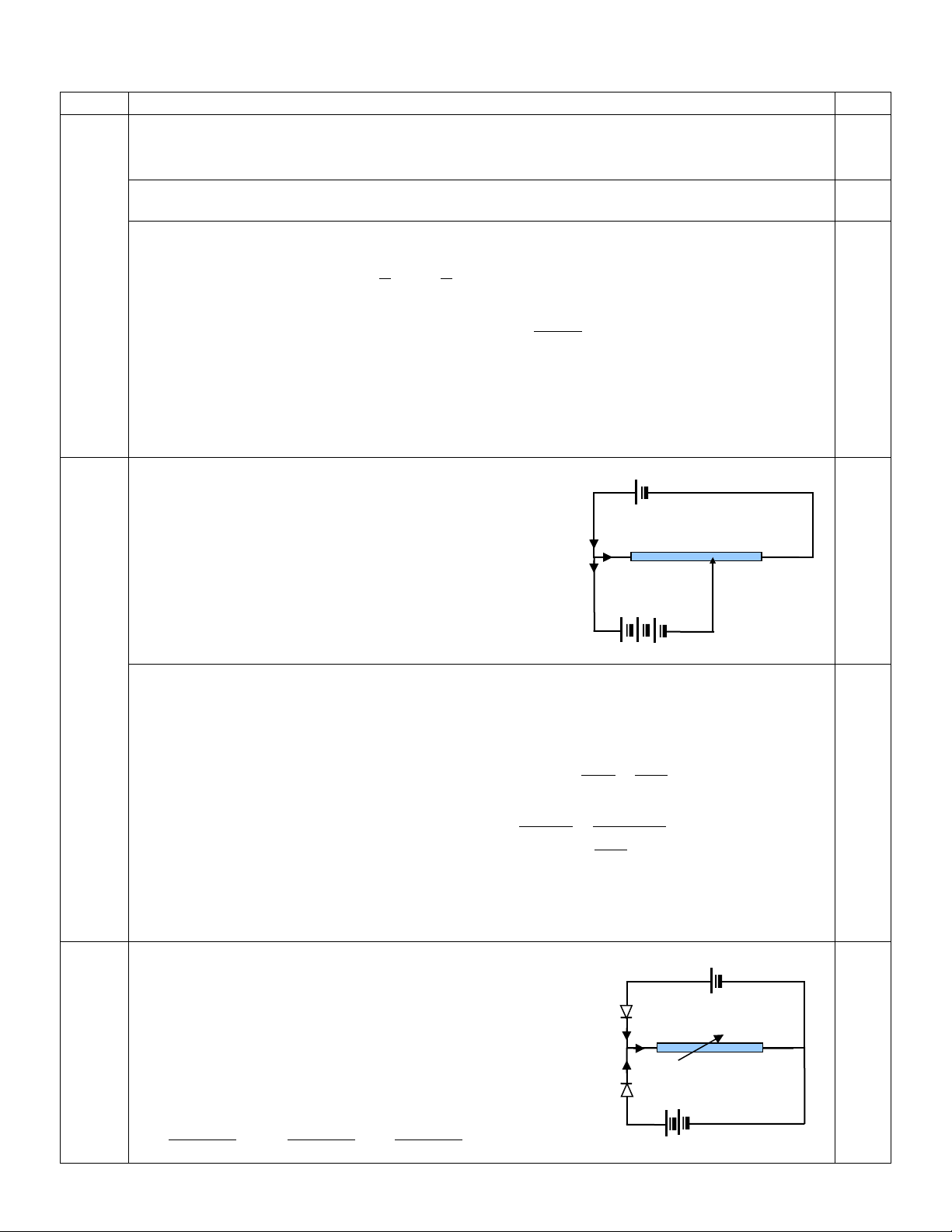
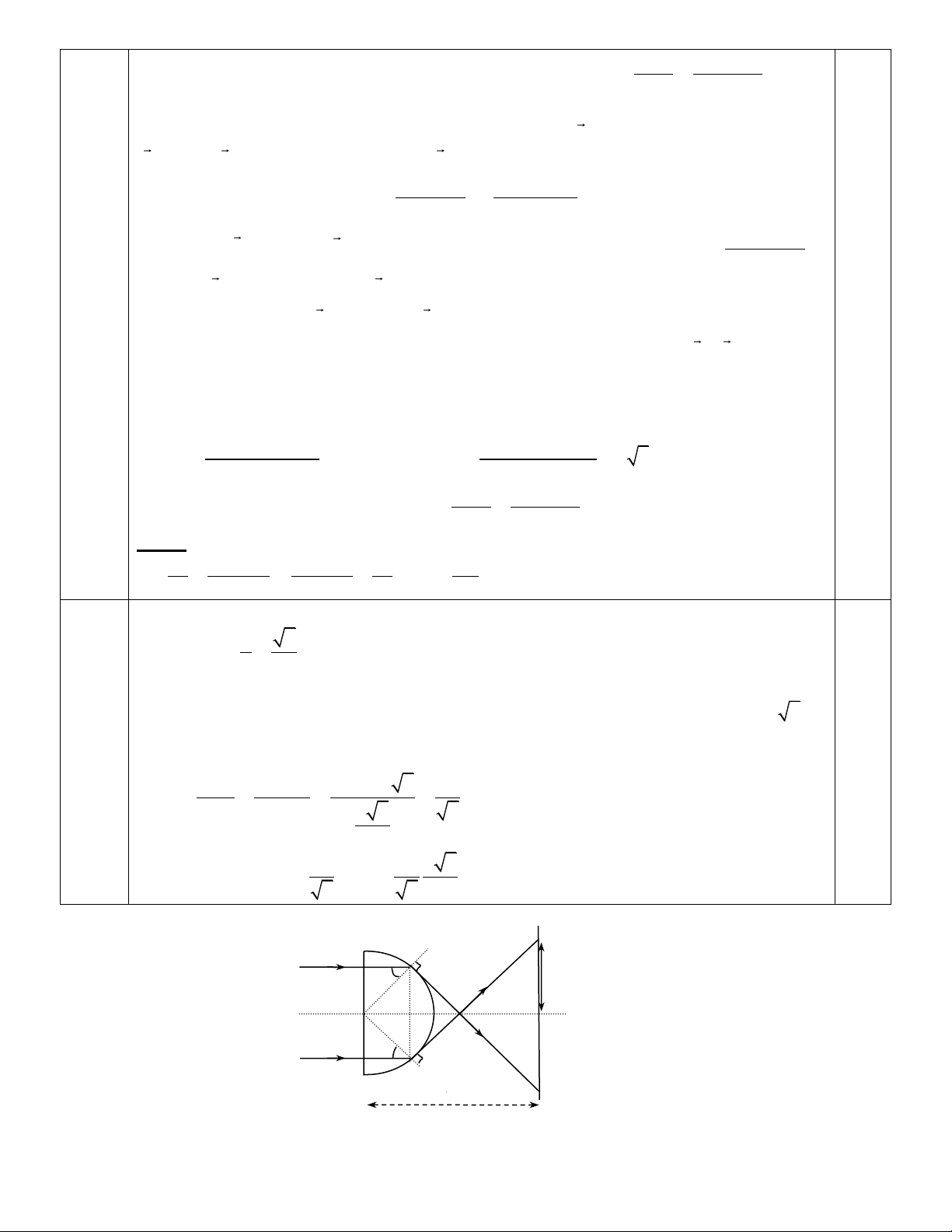
Một bán cầu có bán kính r =2cm được làm bằng thủy tinh có r
chiết suất n = 2 . Bán cầu được đặt trong không khí trước một
cái màn vuông góc với trục đối xứng của bán cầu và các tâm bán
cầu một khoảng L =4,82cm như hình vẽ 5. Một chùm sáng song
song đến mặt phẳng của bán cầu theo phương vuông góc với mặt L
này. Hãy xác định bán kính của vùng sáng tạo ra trên màn.
------------------------------------------HẾT------------------------------------------- Trang 2
ĐÁP ÁN HSG MÔN VẬT LÝ KHỐI 11 NĂM 2018 – 2019 LẦN 3 Câu NỘI DUNG Điểm
Bài 15:: a) Thiết lập được biểu thức: T = mg(3 cos − 2 cos ) 0,5 m T
= mg(3 − 2 cos ) = 40(N) max m 0,5 b) T −  =  =
max= 3mg. Từ hệ thức trên suy ra: 3 2 cos 3 m → 0 90 m 0,5
c) Chọn mốc thế năng tại VT thấp nhất. Cơ năng tại A(ngang): E = mg(l + l  ) (1) 0,25 A 0 1 1 1
Cơ năng tại B(thấp nhất): 2 2
E = mv + k l  (2) 0,25 B (3điểm) 2 2 2 v
Lực đàn hồi khi vật đi qua VTCB: F = k l  = mg + m (3) l + l  0,25 0 Từ (1),(2)  2 2 mv = 2m ( g l + l  ) − k l  0 2
Thay vào (3): k(l + l  ) = m ( g l + l  ) + 2m ( g l + l  ) − k l  0,25 0 0 0 2 l  + 0,24 l  − 0,036 = 0 Giải ra: l  =0,104(m) 0,5
1. Chiều dòng điện như trên hình vẽ. Tại nút A: I = I E,r 1 + I2 (I1 = 0,4 A)
Sử dụng định luật Ôm cho các đoạn mạch: 0,25 U I
AC = I2.x = 6I2 ; UAC = E – I(r + RCB) = 12 – 3,6I C U A B AC = 3e0 + 3r0I1 = 3e0 + 0,6 0,25
Giải hệ bốn phương trình trên ta được: I1 I2 I2 = 1,1A; I = 1,5A; e0 = 2V 0,5 Từ đó: 2 2 P = P
+ P = R I + R I = 14,01(W) AC CB AC 2 CB 0,5 e0,r0 2
2. Đèn có cường độ định mức và điện trở là Iđ = 1A; Rđ = 1,5Ω. (4,5
Bộ nguồn có Eb = 6V; rb = 1,5Ω. 0,5
điểm) Để các đèn đều sáng bình thường thì phải mắc chúng hỗn hợp đối xứng.
Gọi số đèn mắc nối tiếp nhau trên mỗi dãy là x, số dãy đèn mắc song song với nhau là y. Với x, y nguyên, dương. . x R 1,5x
Ta có điện trở của bộ đèn là d R = = N y y
Cường độ dòng điện chạy trong mạch chính là E 6 b I = = = . y I = y 0,5 R + r 1,5 d x N b +1,5 y
 x + y = 4 . Suy ra số đèn tối đa là x.y = 4 . 0,5
Vậy phải mắc 4 đèn thành 2 dãy song song, mỗi dãy gồm 2 đèn mắc nối tiếp nhau.
3. Giả sử các đi ốt đều mở khi đó dòng điện có chiều như hình vẽ.
Xét các vòng mạch ABDA, DCBD và nút B C e0,
−2 + 4,5i + iR = 0(1) r 1  ta có hệ phương trình. 0,25
−4 + 5i + iR = 0(2) R 2 i1 B D
i +i = i(3)  1 2 i i
Giải hệ trên ta được: 2 D 20 − 4R 36+4R 56 0,5 i = ; i = ; i = 1 A 45 +19R 2 45 +19R 45 +19R 2e0,2 r Trang 3
Do i2 >0 với mọi R đi ốt D2 luôn mở. Ta thấy khi R ≥ 5Ω i1 ≤ 0 điốt D1 đóng.
Công suất trên điện trở R là 2 2 2 4e R 4e 4e 0 0 0 P = =  = R ( 0,16(W) 0,25
R + r + 2r  r + 2r  4 r + 2r D 0 )2 2 ( D 0 ) D 0 R +    R 
Khi R < 5Ω i1 > 0 điốt D1 mở. 2   2    
Công suất trên điện trở R là 56 56 2 P = i R = R =     0,25 R  45 +19R 45   19 R  +    R  PRmax ≈ 0,917 (W) 0,25
a. Quá trình 1 – 4 có P tỷ lệ thuận với T nên là quá trình đẳng tích, vậy thể tích ở trạng thái
1 và 4 là bằng nhau: V1 = V4. Sử dụng phương trình C-M ở trạng thái 1 ta có: m m RT P V = RT V = 1 1 1  , suy ra: 1 1  P 0,5 1
Thay số: m = 1g;  = 4g/mol; R = 8,31 J/(mol.K); T1 = 300K và P1 = 2.105 Pa ta được: 1 8,31.300 3 − 3 0,5 V = = 3,12.10 m 1 5 4 2.10
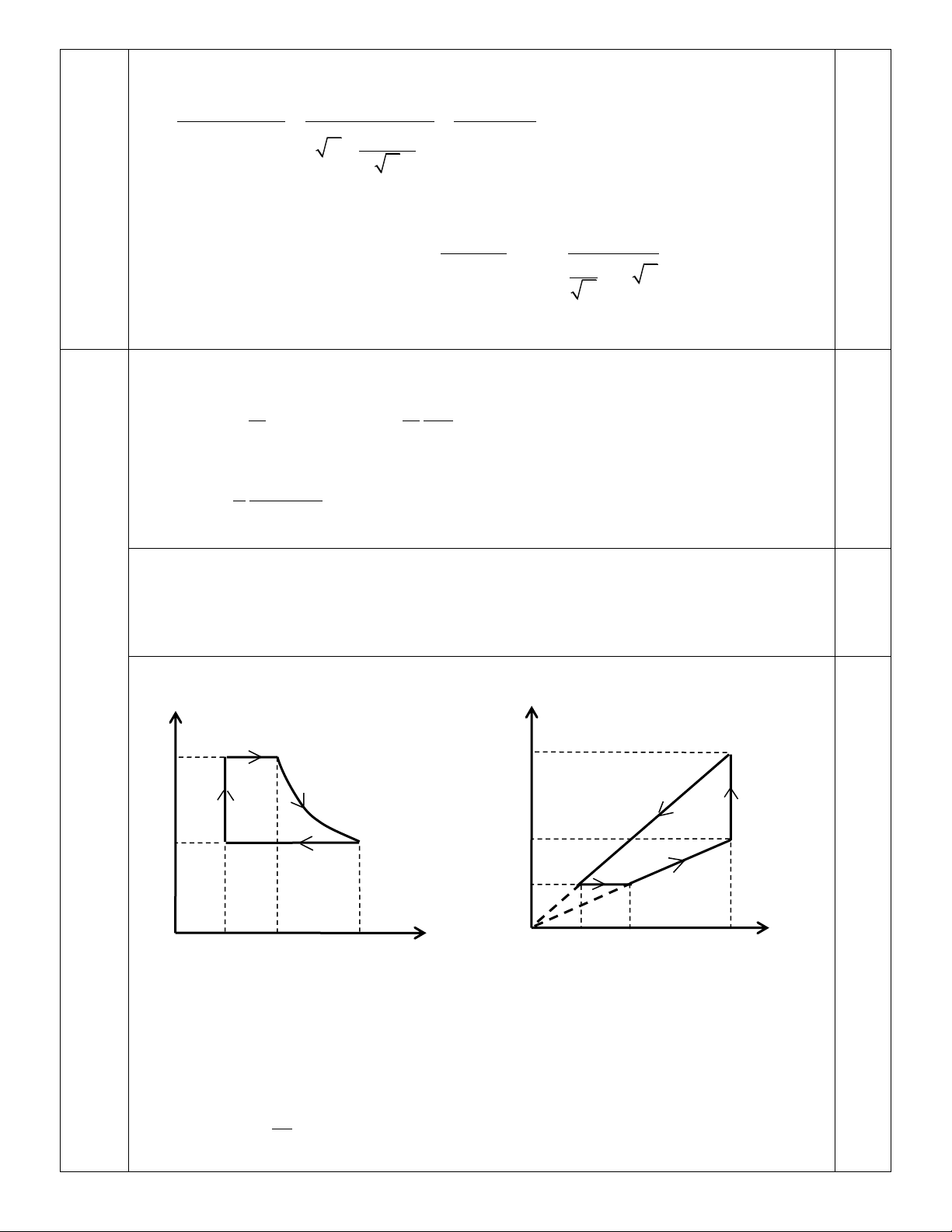
b. Từ hình vẽ ta xác định được chu trình này gồm các đẳng quá trình sau:
1 – 2 là đẳng áp; 2 – 3 là đẳng nhiệt; 0,5
3 – 4 là đẳng áp; 4 – 1 là đẳng tích.
Vì thế có thể vẽ lại chu trình này trên giản đồ P-V (hình a) và trên giản đồ V-T (hình b) như sau: P(105Pa) V(l) 1 2 3 12,48 2 3 0,5 4 (3điểm) 1 3 6,24 2 4 3,12 1 T(K) V(l) 0 0 3,12 6,24 12,48 150 300 600 Hình a Hình b
c. Để tính công, trước hết sử dụng phương trình trạng thái ta tính được các thể tích: V
2 = 2V1 = 6,24.10 – 3 m3; V3 = 2V2 = 12,48.10 – 3 m3.
Công mà khí thực hiện trong từng giai đoạn: 0,25 5 3 − 3 − 2
A = p (V − V) = 2.10 (6,24.10 − 3,12.10 ) = 6,24.10 J 12 1 2 1 0,25 V3 5 3 − 2 A = p V ln
= 2.10 .6,24.10 ln2 = 8,65.10 J 23 2 2 V 0,25 2 Trang 4 5 3 − 3 − 2
A = p (V − V ) = 10 (3,12.10 − 12, 48.10 ) = 9 − ,36.10 J 0,25 34 3 4 3
A = 0 vì đây là quá trình đẳng áp. 41
1.Xét điều kiện CB của q3: + + = + = A 1 F 3 F23 F03 F3 F03 0 2 q q1 - Với F = F = k và (F = 13 ; F23 ) 0 60 13 23 2 a 0,5 2 q 0  F = 2F cos30 = F 3 = 3k 3 13 13 q 2 3 a
- Trong đó F3 có phương là đường phân giác góc C, B C lại có F  03
F3 nên q0 nằm trên phân giác góc C. q2 - Tương tự, q q3 0,5
0 cũng thuộc phân giác các góc A và B. Vậy q
0 tại trọng tâm G của ABC. - Vì F  03
F3 nên F03 hướng về phía G, hay là lực 4 hút nên q0 < 0. (2,5 2 q q 0 q 3 7 − 0,5 điểm =  =  = −  ) - Độ lớn: F F k k q q 3, 46.10 C 03 3 2 2 0   a 3 2 3 a    3 2 
2. * Dụng cụ thí nghiệm cần dùng : 1) Lực kế. 0,25
2) Sợi dây nhẹ ,không dãn dài khoảng 2m.
3) Thước đo có chia độ đến từng mm.
* Phương án thí nghiệm :
+ Treo 2 quả cầu vào 2 đầu sợi dây và móc trung điểm sợi dây vào một điểm cố định cho
hai quả cầu mang điện tương tác đẩy nhau. 0,25
+ Dùng lực kế đo trọng lượng quả cầu ,dùng thước đo xác định R và  . 2  + Tính Q theo công thức : R P tan Q = 0,5 k
1. Theo định luật bảo toàn động lượng : m1v1 = m2v2 (1) và sau khi vỡ hai hạt chuyển động ngược chiều nhau.
Nếu hướng chuyển động của một mảnh nào đó hợp với véc tơ cảm ứng từ góc 0
  90 khi đó quỹ đạo của hai mảnh là các đường xoắn ốc hướng ra xa nhau nên hai mảnh không gặp nhau . Khi 0
 = 90 thì hai mảnh chuyển động theo quỹ đạo tròn với tốc độ không 0,5
đổi dưới tác dụng của lực Lorenxơ. m v m v
Bán kính lần lượt là : 1 1 R = . và 2 2 R =
.(2) kết hợp (1) và (2) ta được R 1 1= R2= R. 0,5 qB 2 qB
Do hai điện tích trái dấu nhau nên hai mảnh cùng chuyển động đều trên một đường tròn về 5
hai phía ngược nhau và đi đến gặp nhau . (4điểm)  
Khoảng thời gian từ khi vỡ đến khi gặp nhau là : 2 R 2 m m 1 2 t = = . 0,5 v + v qB m + m 1 2 ( 1 2 )
2. a) Khi thanh MN trượt xuống dốc, trong thanh MN xuất hiện suất điện động cảm ứng có
chiều N đến M (Quy tắc bàn tay trái). Vậy dòng điện chạy qua R theo chiều từ M đến N 0,5
Thanh MN trượt xuống dốc do tác dụng của P (nằm theo đường dốc chính) của trọng lực 1
P : P1 = P.sinα = mg.sinα 0,25
Kí hiệu v là vận tốc chuyển động của thanh MN. Độ lớn của suất điện động cảm ứng: E 0,25
C = B.l.v.sin( B, v ) = B.l.v.sin (900 + α) = B.l.v.cos α Trang 5 E 
Trong thanh MN xuất hiện dòng điện cảm ứng có cường độ I : Blv cos C I = = R + r R + r 0,25
Và có chiều chạy qua thanh MN theo chiều từ N đến M ( theo quy tắc bàn tay phải)
Trong thanh MN có dòng điện I được đặt trong từ trường
B phải chịu tác dụng của lực từ
F , lực từ F có phương vuông góc với B và với MN, có chiều theo quy tắc bàn tay trái, có 2 2   độ lớn : Blv cos B l v cos
F = B.I.l.sin900=B.I.l = B l = 0,25 R + r R + r 2 2 2  Thành phần B l v cos
F của lực từ F (nằm dọc theo dốc chính) có cường độ: F = F. o c s = 1 1 R + r
Ta thấy F ngược chiều với P . Như vậy thanh MN chịu tác dụng của hai lực cùng 1 1 0,25
phương, ngược chiều : P kéo xuống F kéo lên. 1 1
Lúc đầu, vận tốc v của thanh còn nhỏ F
1 < P1 hay P1 - F1>0.Lực tổng hợp F + P gây ra gia 1 1
tốc cho thanh MN chuyển động nhanh dần, do đó v tăng dần và kết quả là F1 tăng dần
trong khi P1 là không đổi. Đến một giá trị vmax của vận tốc sao cho F1 = P1 thì thanh MN sẽ 0,25
chuyển động với vmax không đổi. 2 2 2 B l v cos  +  Khi đó : (R r)mg sin ax m
= mg sin  v =
= 4 2 m/s  5, 66m / s ax m 2 2 2 R + r B l cos  0,25 E 
Khi đó cường độ dòng điện qua R là : Blv cos C I = = = 2A 0,25 R + r R + r
Lưu ý: HS có thể nhận xét vì lúc này F1 = P1 nên Khi đó cường độ dòng điện qua R là : F F P P mg 1 I = = 1 = = tan = tan = 2 A Bl Bl cos Bl cos Bl Bl
Để có các tia ló ra khỏi bán cầu đến màn thì các tia tới mặt cầu phải có góc tơi iigh Với sin i 1 2 = gh =  igh = 45o 0,5 n 2
Xét các tia vừa đủ điều kiện phản xạ toàn phần S
1I1J1 và S2I2J2. Ta có i1 = i2 = igh = 45o 0,5
 góc khúc xạ tại I1 và I2 đều bằng 90o.  tứ giác OI1FI2 là hình vuông  OF = r 2 6
Các tia khúc xạ đến màn đều nằm trong phạm vi J1J2.  O2J1 = O2J2 là bán kính của vùng
(2điểm) sáng trên màn. Xét cặp tam giác đồng dạng: FO2J2 và FO1I2 ta có: O J L − OF 4,84 − 2 2 2 0,5 2 2 = = = O I O F 2 2 2 1 2 1 2 2 2 2 2  R = O = 0,5 2J2 = O1I2 = 2cm 2 2 2 J2 S1 I1 igh R O1 O O2 S F 2 igh L I2 J1 Trang 6