







Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THI THỬ TỐT NGHIỆP THPT NĂM 2022 HÀ TĨNH Bài thi: TOÁN HỌC
ĐỀ THI TRỰC TUYẾN LẦN 4
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . MÃ ĐỀ THI 101
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
____________________ HẾT ____________________ BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A D B B C D C B C D A A A C C D A C D B A B D C D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
D C A B B C A B C B B A B B C D B A D A C D D D D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. Số cách chọn 4 học sinh từ 15 học sinh là A. 4 C . B. 4 A . C. 15 4 . D. 4 15 . 15 15 Lời giải Chọn A
Số cách chọn 4 học sinh từ 15 học sinh là 4 C . 15 1
Câu 2. Cho cấp số nhân u , với u 9 , u
. Công bội của cấp số nhân đã cho bằng n 1 4 3 1 1 A. . B. 3 . C. 3 . D. . 3 3 Lời giải Chọn D u 1 Ta có 3 4
u = u .q q = 3 = − . 4 1 u 3 1
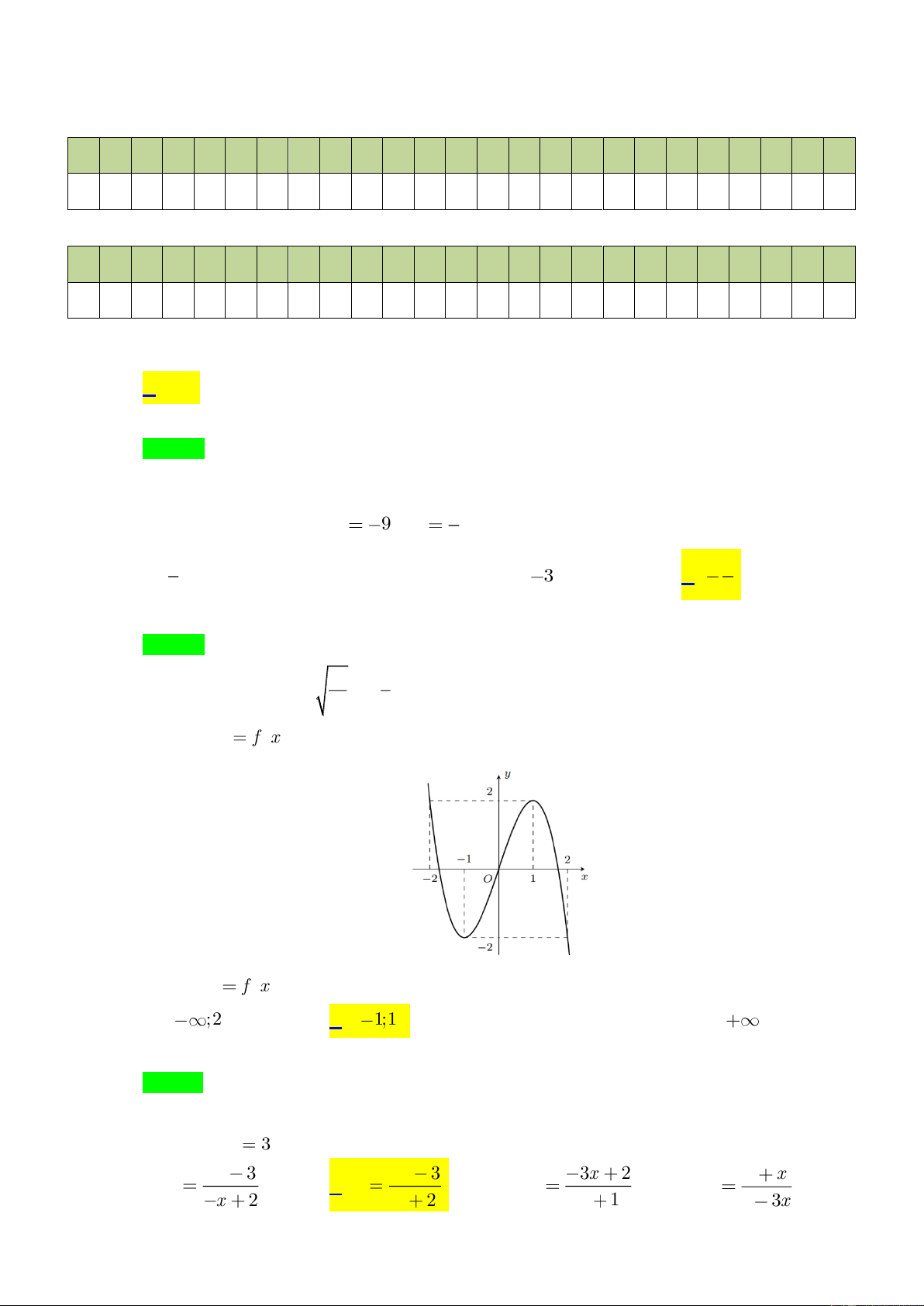
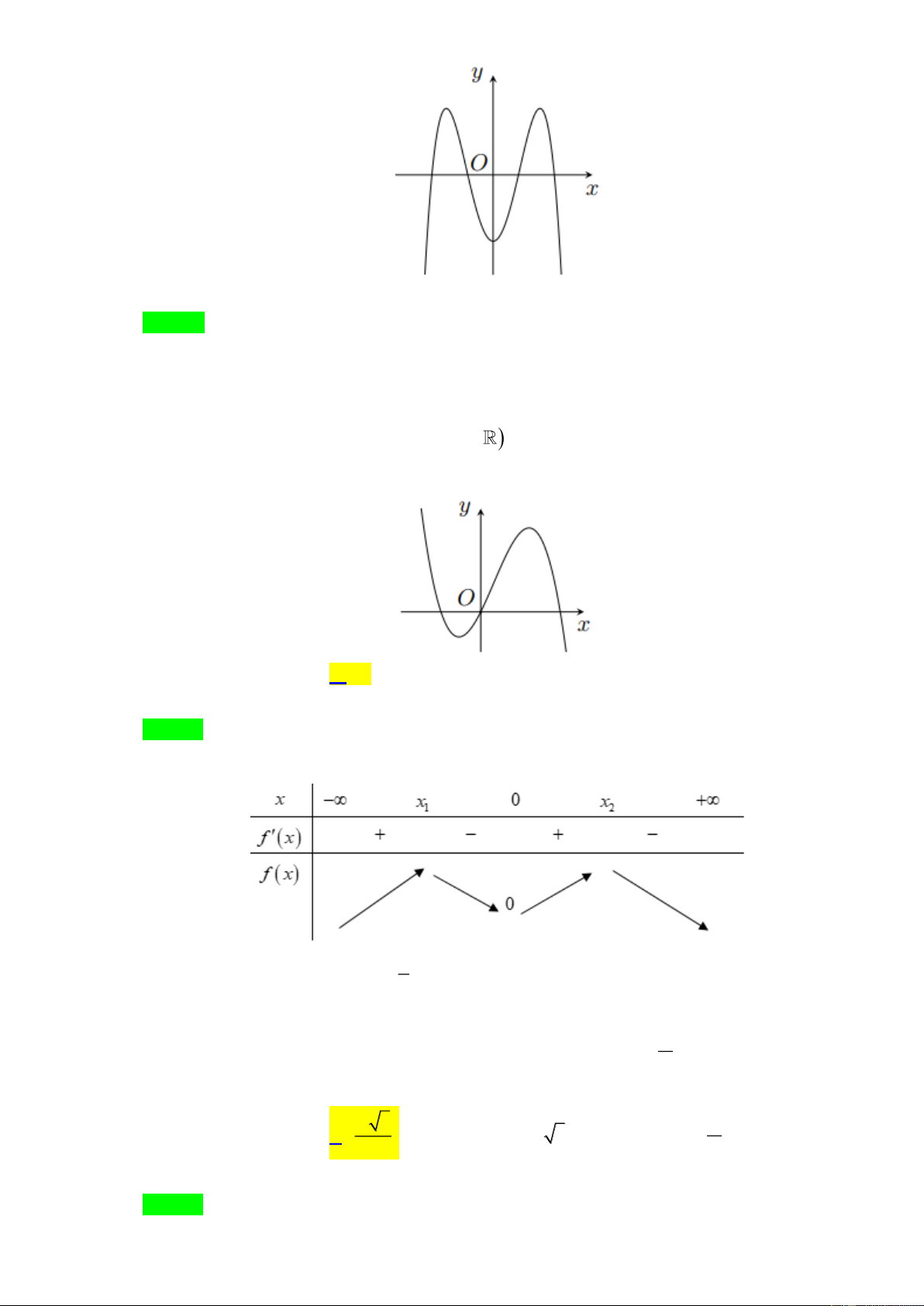
Câu 3. Cho hàm số y
f x có đồ thị như hình vẽ. Hàm số y
f x đồng biến trên khoảng nào trong các khoảng sau? A. ;2 . B. 1;1 . C. 0;2 . D. 1; . Lời giải Chọn B
Dựa vào đồ thị ta thấy hàm số đồng biến trên khoảng ( 1 − ; ) 1 .
Câu 4. Đường thẳng y
3 là tiệm cận ngang của đồ thị hàm số nào sau đây? 3x 3 3x 3 3x 2 1 x A. y . B. y . C. y . D. y . x 2 x 2 x 1 1 3x Lời giải Chọn B 3x −3 Ta có lim = 3
nên y = 3 là tiệm cận ngang của đồ thị hàm số.
x→+ x + 2
Câu 5. Với a , b là các số thực dương, khẳng định nào dưới đây đúng? a loga A. log . B. log ab
loga.logb . b logb a C. log ab loga logb . D. log log a . b b Lời giải Chọn C
Công thức log (ab) = log a + logb .
Câu 6. Nghiệm của phương trình 2x = 16 là 1 1 A. x = − . B. x = . C. x = 4 − . D. x = 4 . 4 4 Lời giải Chọn D
Ta có 2x = 16 x = log 16 x = 4 . 2
Câu 7. Phương trình log
x − 3 = 3 có nghiệm là 2 ( )
A. x = 5.
B. x = 9 .
C. x =11. D. x = 8 . Lời giải Chọn C Ta có log x − 3 = 3 3
x − 3 = 2 x =11. 2 ( )
Câu 8. Thể tích khối chóp có chiều cao bằng 5 , diện tích đáy bằng 6 là 15 A. . B.10 . C.11. D. 30 . 2 Lời giải Chọn B 1 1 V = . . h S = .5.6 = 10 . 3 d 3
Câu 9. Tập xác định D của hàm số y = ln (1− x) là A. D = \ {1}. B. D = . C. D = (− ; 1) . D. D = (1; + ) . Lời giải Chọn C
Hàm số xác định 1− x 0 x 1.
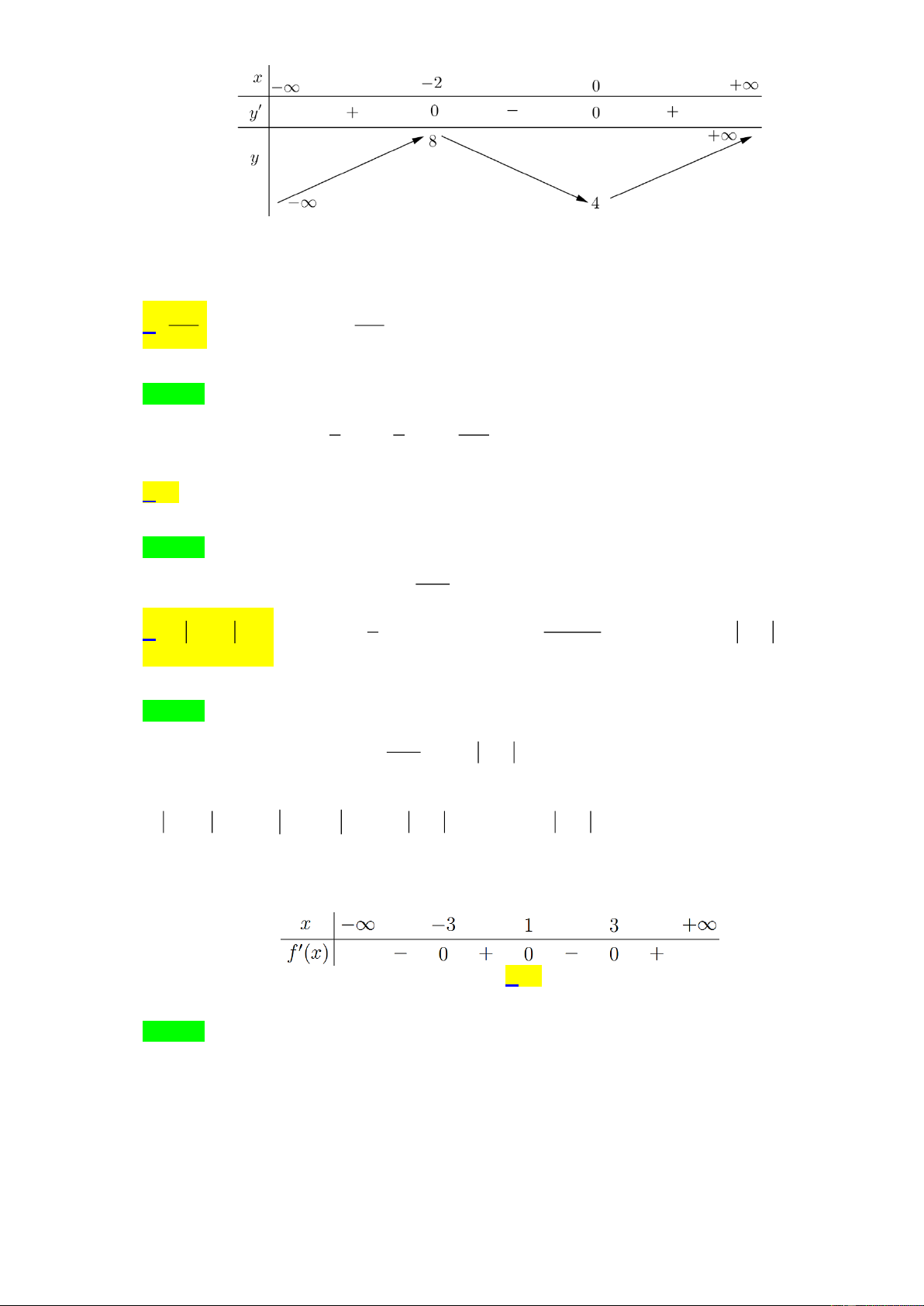
Câu 10. Khoảng nghịch biến của hàm số 3 2
y = x + 3x + 4 là A. (0; +) . B. (0; 2) . C. ( ; − 0). D. (−2; 0) . Lời giải Chọn D TXĐ: D = . x = 2 − Ta có 2
y = 3x + 6x ; y = 0 . x = 0 Bảng biến thiên
Vậy hàm số đồng nghịch biến trên khoảng (−2;0) .
Câu 11. Thể tích của khối cầu có bán kính R = 2 bằng 32 33 A. . B. . C. 16 . D. 32 . 3 2 Lời giải Chọn A Thể tích khối cầu là 4 3 4 3 32 V = R = .2 = . 3 3 3
Câu 12. Số cạnh của hình tứ diện là A. 6. B. 4. C. 3. D. 5. Lời giải Chọn A
Câu 13. Họ nguyên hàm của hàm số f ( x) 1 = là x +1 1 1
A. ln 2x + 2 + C .
B. − ln ( x + )2 1 + C . C. − + C .
D. − ln x +1 + C . 2 (x + )2 1 Lời giải Chọn A
Họ nguyên hàm của hàm số 1 là
dx = ln x +1 + C . x +1 Ở đây ta chọn đáp án A bởi vì
ln 2x + 2 + C = ln 2( x + )
1 + C = ln x +1 + ln 2 + C = ln x +1 + C ' .
Câu 14. Cho hàm số y = f ( x) có bảng xét dấu của đạo hàm như hình bên. Số điểm cực tiểu của hàm số
y = f ( x) là A. 3. B. 4. C. 2. D. 1. Lời giải Chọn C
Hàm số đạt cực tiểu tại điểm x = 3
− và x = 3 nên số điểm cực tiểu của hàm số là 2.
Câu 15. Cho hàm số y = f ( x) có đồ thị như hình bên. Giá trị lớn nhất của hàm số y = f ( x) trên đoạn 0;2 là A. 2 − . B. 1. C. 2 . D. 0 . Lời giải Chọn C
Dựa vào đồ thị ta có giá trị lớn nhất của hàm số trên đoạn 0;2 là 2.
Câu 16. Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây? A. 3
y = x −3x + 2 B. 3 2 y = 2
− x +9x −12x −4. C. 4
y = x − 3x + 2 . D. 3 2
y = 2x −9x +12x − 4 . Lời giải Chọn D
Đồ thị hàm số cắt trục tung tại điểm (0;− 4) nên loại các phương án A và C.
Từ đồ thị ta thấy lim y = + do đó loại phương án B. x→+
Câu 17. Họ nguyên hàm của hàm số ( ) x
f x = e + x là 1 x 1 x 1 x 1 A. 2 e + x + C . B. e + e + x + C 2 x + . 1 2 2 C. x 2
e + x + C . D. x e +1+ C . Lời giải Chọn A x 1 Ta có ( x
e + x)dx = 2 e + x + C . 2
Câu 18. Thể tích V của khối nón có chiều cao h và đáy có bán kính r là 2 1
A. V = rh . B. V = rh . C. 2 V = r h . D. 2 V = r h . 3 3 Lời giải Chọn C 1 1 f (x) 1 dx = 2 − , g (x)dx =5 f
(x)+2g(x)dx Câu 19. Nếu 0 0 thì 0 bằng A. 1. B. 9 − . C. 12 − . D. 8 . Lời giải Chọn D 1 f
(x)+2g(x) 1 dx = f (x) 1 dx + 2 g (x)dx = 2 − +10 = 8. 0 0 0
Câu 20. Cho hình chóp có thể tích 3
V = 36cm và diện tích đáy 2
B = 6cm . Chiều cao của khối chóp là 1
A. h = 72cm .
B. h =18cm.
C. h = 6cm . D. h = cm . 2 Lời giải Chọn B 1 3V 3.36 Ta có V = . B h h = h = h = 18c . m 3 B 6
Câu 21. Số giao điểm của đồ thị hàm số 4 2
y = −x + 3x và trục hoành là A. 3 . B. 1. C. 2 . D. 0 . Lời giải Chọn A x = 0
Xét phương trình hoành độ giao điểm 4 2
−x + 3x = 0 x = 3
Vậy số giao điểm là 3.
Câu 22. Với a 0 , dặt log
2a = b , khi đó log ( 4 8a bằng 2 ) 2 ( )
A. 4b + 7 .
B. 4b + 3 . C. 4b . D. 4b −1. Lời giải Chọn B 4 16a 1 log = log + log ( 4 (2a) = 1 − + 4log 2a = 1 − + 4b 2 2 2 ) 2 ( ) 2 2
Câu 23. Cho hình nón có độ dài đường sinh bằng 5 và bán kính đường tròn đáy bằng 4. Thể tích khối
nón tạo bởi hình nón bằng 80 16 A. . B. 48 . C. . D. 16 . 3 3 Lời giải Chọn D
Ta có: l = 5, r = 4 2 2
h = l − r = 3 1 1 Thể tích khối nón là 2 2
V = r h = .4 .3 = 16 3 3
Câu 24. Tập nghiệm của bất phương trình log 3x −1 3 là 2 ( ) 1 1 A. ( ) ;3 − . B. ;3 . C. ;3 . D. (3;+) . 3 3 Lời giải Chọn C ĐK: 1 x 3
log 3x −1 3 3x −1 8 x 3 2 ( ) KHĐK: 1 x 3 1 x 3 3
Vậy tập nghiệm của bất phương trình là 1 ;3 3
Câu 25. Hàm số nào dưới đây đồng biến trên ? 3x − 1 A. y = = − . C. 4 2
y = x − 4x . D. 3
y = x + x . x + . B. 3 y x x 1 Lời giải Chọn D Xét hàm số 3
y = x + x TXĐ: D = Có 2
y' = 3x +1 0 x Vậy hàm số 3
y = x + x đồng biến trên
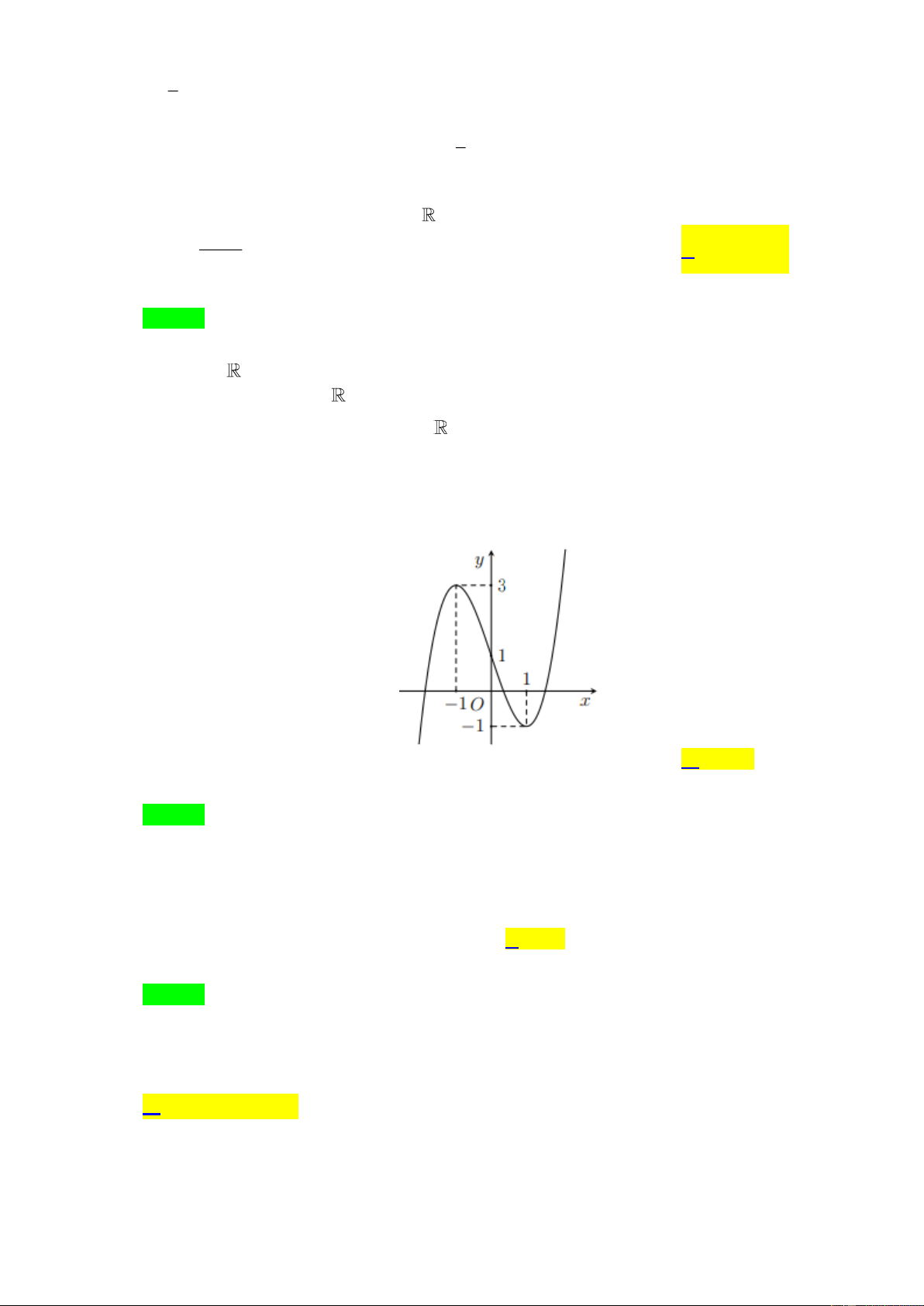
Câu 26. Đồ thị của hàm số f ( x) có dạng đường cong trong hình vẽ bên. Gọi M là giá trị lớn nhất, m
là giá trị nhỏ nhất của hàm số y = f (x) trên đoạn 1 − ;
1 . Tính P = M − 2m.
A. P = 3 .
B. P = 4 .
C. P = 1. D. P = 5 . Lời giải Chọn D
Từ đồ thị hàm số ta có: M = 3, m = 1 −
Vậy P = M − 2m = 3− 2.(− ) 1 = 5.
Câu 27. Cho hàm số y = F ( x) là một nguyên hàm của hàm số 2
y = x . Tính F(25) . A. 5 . B. 25 . C. 625. D. 125 . Lời giải Chọn C
Ta có: F( x) = f ( x) F( ) = f ( ) 2 25 25 = 25 = 625 . Câu 28. Cho hàm số 4 2
y = ax + bx + c có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây là mệnh đề đúng?
A. a 0,b 0, c 0 .
B. a 0,b 0, c 0 . C. a 0,b 0, c 0 . D. a 0,b 0, c 0 . Lời giải Chọn A
Từ hình dáng đồ thị hàm số ta được a 0 .
Từ giao điểm của đồ thị hàm số với trục Oy ta được c 0
Vì hàm số có 3 điểm cực trị nên ab 0 b 0
Câu 29. Cho hàm số f ( x) 4 3 2
= ax +bx + cx ,( , a ,
b c ). Hàm số y = f ( x) có đồ thị như trong hình
vẽ bên. Số nghiệm thực phân biệt của phương trình 3 f (x) + 4 = 0 là A. 4 . B. 2 . C. 3 . D. 1. Lời giải Chọn B
Từ đồ thị hàm số f (x) ta có hàm số f ( x) đạt cực tiểu tại x = 0 , từ đó ta có bảng biến thiên:
Ta có: f ( x) + = f ( x) 4 3 4 0 = − 3
Vậy phương trình có hai nghiệm phân biệt. R
Câu 30. Cho mặt cầu S (I, R) và mặt phẳng ( P) cách I một khoảng bằng
. Thiết diện của (P) và 2
(S) là một đường tròn có bán kính bằng R 3 R A. R . B. . C. R 3 . D. . 2 2 Lời giải Chọn B 2 R R 3 Ta có: 2 2 2 r = R − h = R − = 2 2
Câu 31. Tính tích tất cả các nghiệm của phương trình 2 x −2 x 1 3 5 + = A.1.
B. 2 − log 5 . C. −log 45. D. log 5 . 3 3 3 Lời giải Chọn C 2 x −2 x 1 3 5 + = 2
x − 2 = (x + ) 1 log 5 2
x − xlog 5−2−log 5 = 0 2
x − xlog 5−log 45 = 0 3 3 3 3 3
Theo định lý Viet ta được tích hai nghiệm bằng −log 45. 3
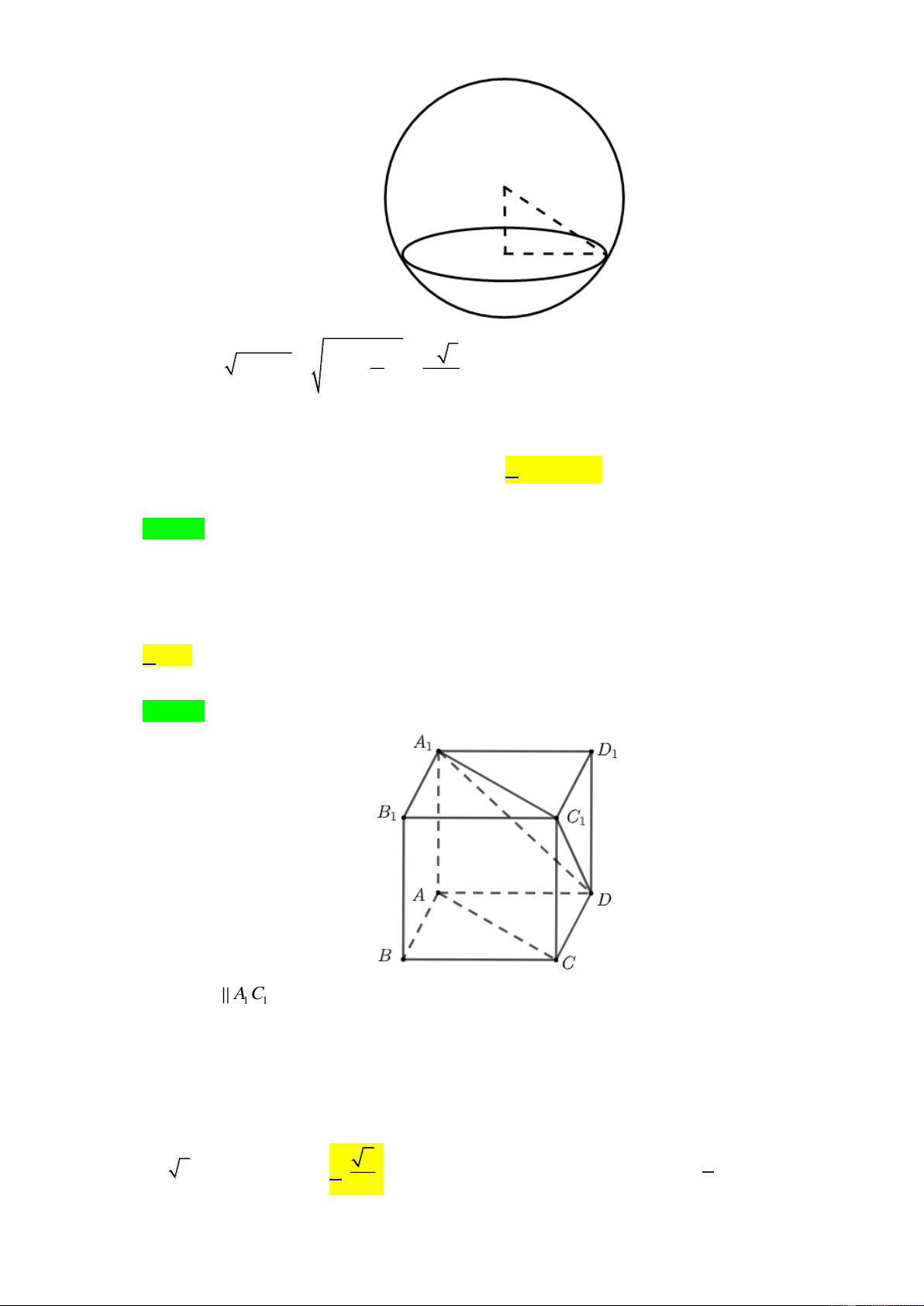
Câu 32. Cho hình lập phương AB D
C .A B C D . Góc giữa hai đường thẳng AC và DA bằng 1 1 1 1 1 A. 60 . B. 90 . C. 45. D.120 . Lời giải Chọn A
Ta có AC A C , do đó góc giữa ( AC, DA = A C , DA , bằng góc DAC . 1 ) ( 1 1 1) 1 1 1 1
Do DA ; AC , DC là các đường chéo hình vuông nên bằng nhau. Vậy D AC đều, 1 1 1 1 1 1
Vậy góc DAC bằng 60. 1 1
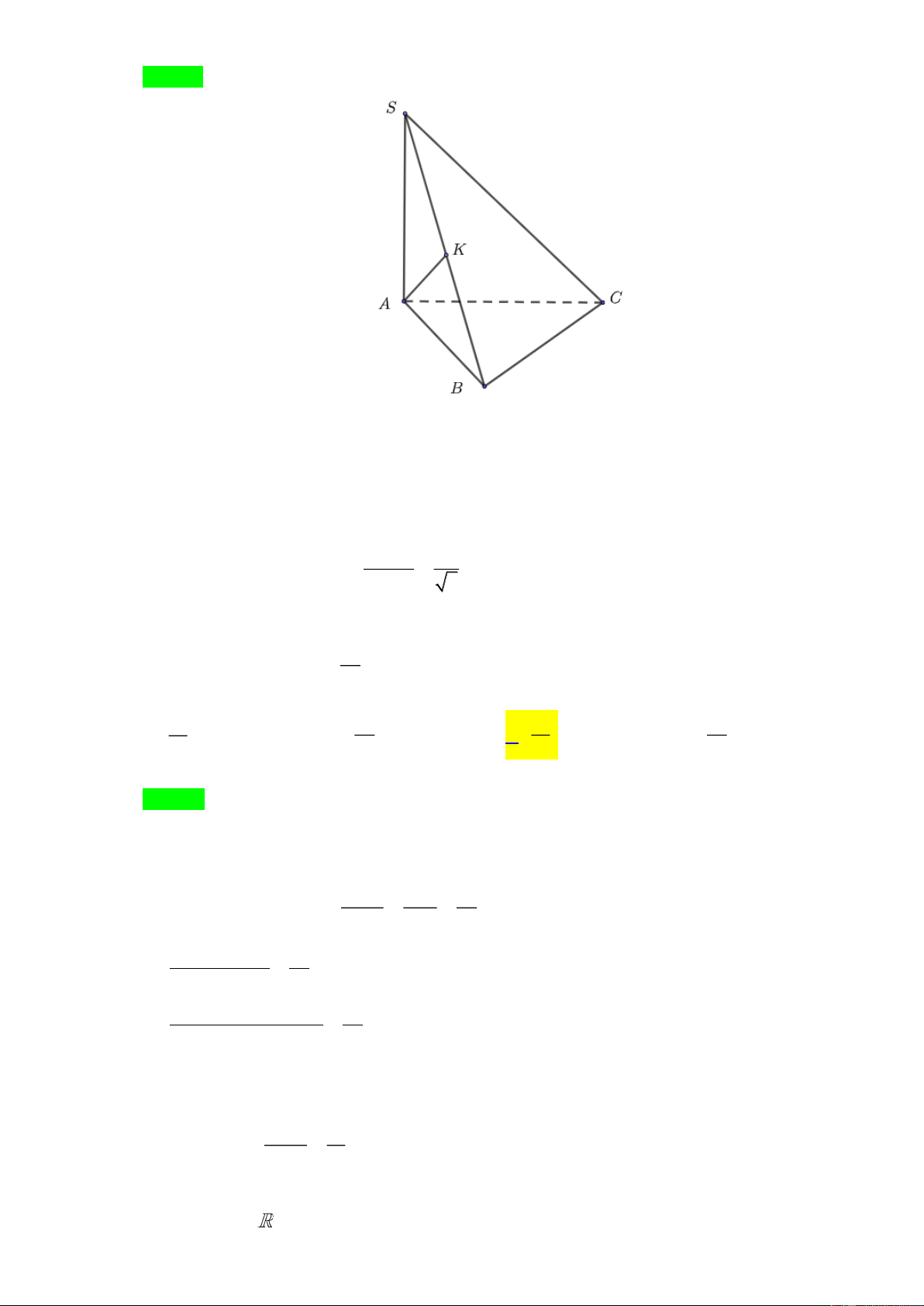
Câu 33. Cho hình chóp S.ABC có đáy là tam giác vuông tại B , AB = 1 ; SA ⊥ ( ABC) , SA =1. Khoảng
cách từ điểm A đến mp (SBC) bằng 2 1 A. 2 . B. . C. 1. D. . 2 2 Lời giải Chọn B S
AB dựng AK ⊥ SB
Do SA ⊥ ( ABC) SA ⊥ BC
Có BC ⊥ AB , suy ra BC ⊥ (SAB) BC ⊥ AK
Vậy AK ⊥ (SBC),d ( ,
A (SBC)) = AK . S . A AB 1 Có S .
A AB = AK.SB AK = = . SB 2
Câu 34. Một hộp có chứa 3 viên bi đỏ, 2 viên bi xanh và n bi vàng (các viên bi kích thước như nhau
và n là số nguyên dương). Lấy ngẫu nhiên 3 viên bi từ hộp. Biết xác suất để trong 3 viên bi 9
lấy được có đủ ba màu là
. Xác suất để trong 3 viên bi lấy được có ít nhất một viên bi xanh 28 bằng 5 25 9 31 A. . B. . C. . D. . 14 26 14 56 Lời giải Chọn C
Ta có số phần tử của không gian mẫu là số cách lấy ngẫu nhiên 3 viên bi từ hộp: n() 3 = C n+5
Gọi biến cố A: “Lấy được đủ ba màu”, ta có n( ) 1 1 1
A = C .C .C = 6n . 3 2 n n A 6n 9
Theo bài ra ta có: P ( A) ( ) = . n () = = 3 C 28 n+5 6 . n 3!.(n + 2)! 9 ( = n + 5)! 28 4n 1 ( = .
n + 3)(n + 4)(n + 5) 28 3 2
n +12n − 47n + 60 = 0 n = 3
Gọi biến cố B: “Lấy được ít nhất một viên xanh”, ta có n(B) 3 3 = C −C = 36 . 8 6 n B 9 Suy ra: P ( B) ( ) = . n ( ) = 14
Câu 35. Cho hàm số f ( x) = ( x + 2a)( x + 2b − a)(ax + ) 1 . Có bao nhiêu cặp ( ;
a b) để hàm số f ( x) đồng biến trên ? A. 0 . B. 1. C. 2 . D. vô số. Lời giải Chọn B
TH1: a = 0 , hàm số f ( x) là hàm số bậc hai, không thể đồng biến trên .
TH2: a 0 , hàm số f ( x) là hàm bậc 3.
Để f (x) đồng biến trên thì a 0 và f (x) = 0 có duy nhất một nghiệm trên . Suy ra 1 a = 1 − 2 1 2 − a = a = 1 a 1 −
− a = a − b = − a = (l) 2 2 2 . a 1 2 3 a 2 − b = − b = a 1 2 2 2b = a + a Vậy chọn B
Câu 36. Một chiếc cốc dạng hình trụ, chiều cao 16cm, đường kính là 8cm , bề dày của thành cốc và đáy
cốc bằng 1cm . Nếu đổ một lượng nước vào cốc cách miệng cốc 5cm thì ta được khối nước có
thể tích V , nếu đổ đầy cốc ta được khối trụ (tính cả thành cốc và đáy cốc) có thể tích V . Tỉ số 1 2 V1 bằng V2 2 245 45 11 A. . B. . C. . D. . 3 512 128 16 Lời giải Chọn C
Khi đổ nước đầy cốc ta được khối trụ (tính cả thành cốc và đáy cốc) có h =16c , m r = 4cm. 1 1
Khối nước khi đổ một lượng nước cách miệng cốc 5cm ta được khối trụ có 8 −1 7
h = 16 − 5 −1 = 10 c , m r = = cm . 2 2 2 2 2 7 . .10 Do đó: V 2 245 1 = = 2 V . .4 .16 512 2
Câu 37. Số người trong cộng đồng sinh viên đã nghe một tin đồn nào đó là ( 0,15 1 e d N P − = − ) trong đó
P là tổng số sinh viên của cộng đồng và d là số ngày trôi qua kể từ khi tin đồn bắt đầu. Trong
một cộng đồng 1000 sinh viên, cần bao nhiêu ngày để 450 sinh viên nghe được tin đồn ? A. 4. B. 3 C. 5 D. 2 Lời giải Chọn A Ta có: N = P ( 0 − ,15 1− e d ) 450 =1000.( 0 − ,15 1 d − e ) − d 11 0,15 e = ln d 3,98 20
Vậy cần 4 ngày để 450 sinh viên nghe được tin đồn.
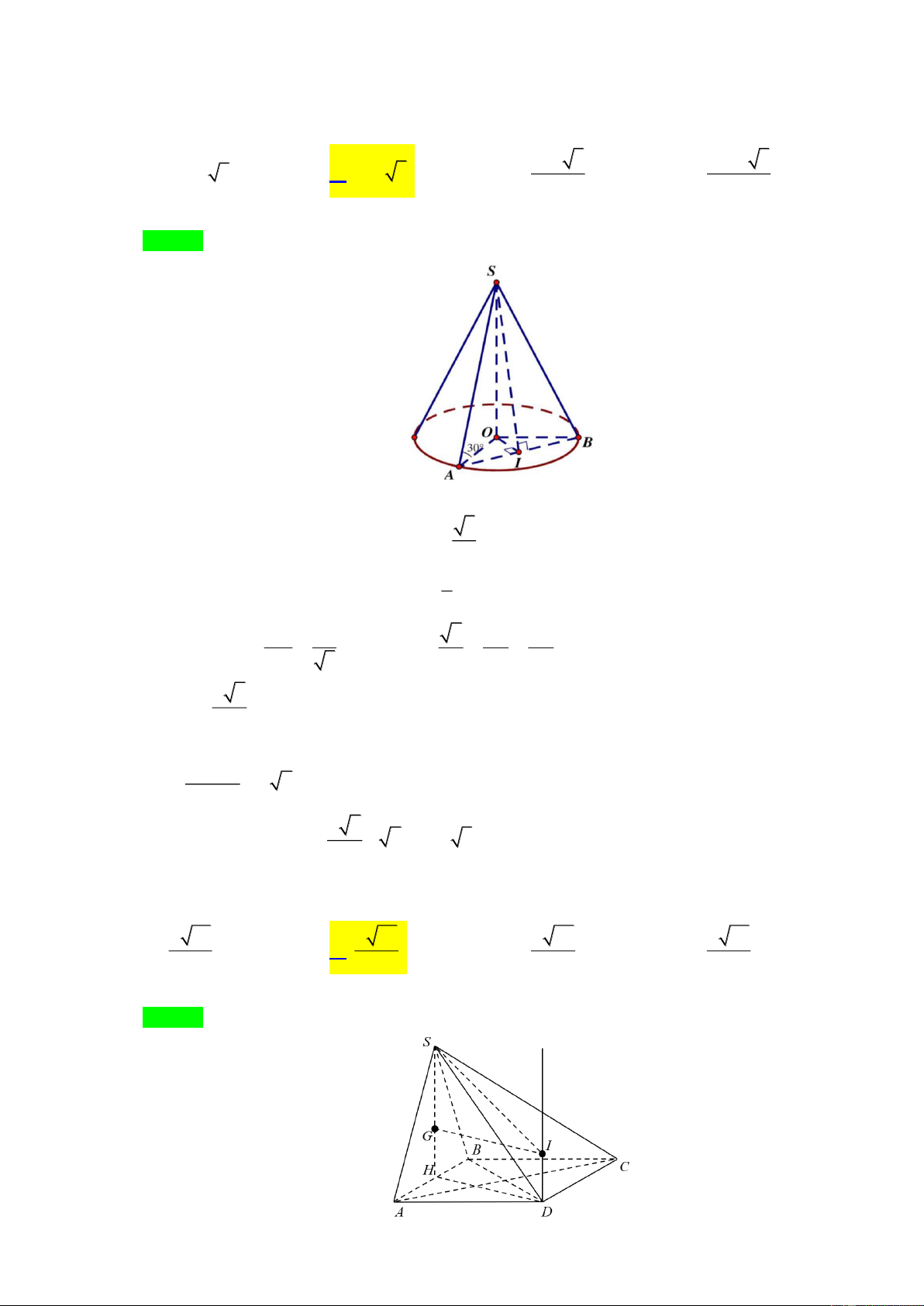
Câu 38. Cho hình nón đỉnh S , đường cao SO .Gọi ,
A B là hai điểm thuộc đường tròn đáy của hình nón
sao cho khoảng cách từ O đến
AB bằng a và SAO = 30 , SAB = 60 . Diện tích xung quanh của hình nón bằng? 2 a 3 2 2 a 3 A. 2 2 a 3. B. 2 a 3 . C. . D. . 3 3 Lời giải Chọn B
Gọi I là trung điểm của AB o 3 AO = S .
A cos SAO = S . A cos 30 = SA Ta có: 2 o 1 AI = S .
A cos SAI = S . A cos 60 = SA 2 AI 1 6 OI a Nên: cos IAO = = sin IAO = = = AO 3 3 OA OA a 6 OA = 2 Tam giác SAO có: OA SA = = a 2 cos 30o a 6 Vậy: 2 S = .O . A SA = . .a 2 = a 3 . xq 2
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh , a ABC = 120 , S
AB đều và nằm
trong mặt phẳng vuông góc với đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng. a 41 a 39 a 37 a 35 A. . B. . C. . D. . 6 6 6 6 Lời giải Chọn B
Gọi H là trung điểm cạnh AB SH ⊥ ( ABCD)
Tam giác ABD đều nên DA = DB = AB
Mà AB = BC = DC
Nên DA = DB = DC
Suy ra D là tâm đường tròn ngoại tiếp tam giác ABC
Dựng trục Dx ⊥ ( ABCD)
Gọi G là tâm của tam giác SAB . Dựng trục Gy
Gọi I là giao điểm Dx và Gy
Suy ra I là tâm mặt cầu ngoại tiếp hình chóp S.ABC a 3
Tam giác ABD đều nên DH = 2 a 3 2 2 a 3 a 3
Tam giác SAB đều nên SH = SG = SH = . = 2 3 3 2 3
Vậy bán kính mặt cầu ngoại tiếp hình chóp S.ABC a 39 2 2
R = IS = IG + SG = . 6
Câu 40. Ba số a + log 3; a + log 3; a + log 3 theo thứ tự lập thành cấp số nhân. Công bội của cấp số 2 4 8 nhân này bằng 1 1 1 A. . B. 1. C. . D. . 4 3 2 Lời giải Chọn C Theo giả thiết, ta có: 2 ( a + )2 = (a + )(a + ) 1 4 1 log 3 log 3 log 3 a log 3 + log 3 = a log 3 + (log 3)2 4 2 8 2 2 2 2 2 3 3 1 1 a log 3 = − (log 3)2 2 2 3 12 1 a = − log 3 2 4 1 1 − log 3+ log 3 2 2 a + log 3 1 Vậy: 4 4 2 q = = = a + log 3 1 3 2 − log 3+ log 3 2 2 4
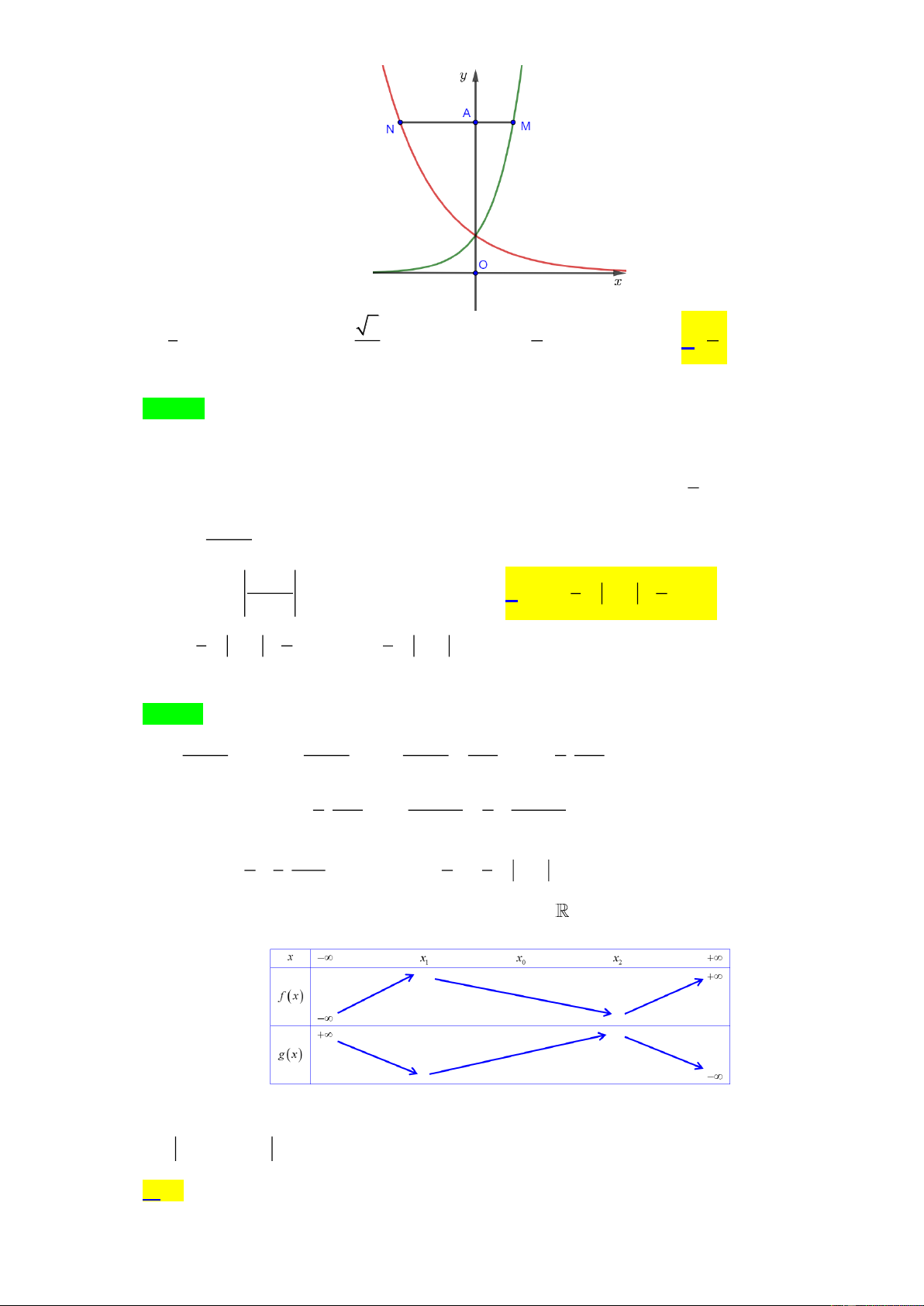
Câu 41. Cho số thực dương a khác 1. Biết rằng bất kì đường thẳng nào song song với trục Ox mà cắt các đồ thị = 4x, x y
y = a , trục tung lần lượt tại M , N và A thì AN = 2AM (hình vẽ bên). Giá trị của a bằng 1 2 1 1 A. . B. . C. . D. . 3 2 4 2 Lời giải Chọn D
Giả sử: A(0;t), N (log t;t), M (log t;t . Thì: AN = −log t, AM = log t . a 4 ) a 4 Theo giả thiết: 1
AN = 2AM − log t = 2 log t log = = − t log t a 1 a 4 2 a 2 3x − 4 Câu 42. Cho f = x + 2 . Khi đó I = f
(x)dx bằng 3x + 4 + x − x 3 4 8 2 A. 2 I = e ln + C
I = − ln 1− x + x + C . 3x + . B. 4 3 3 8 x 8 C. I = ln x −1 +
+ C . D. I = ln x −1 + x + C . 3 3 3 Lời giải Chọn B − − + Đặt: 3x 4 8 1 1 t 4 1 t = t 1− = t = x = . 3x + 4 3x + 4 3x + 4 8 3 1− t + − Theo giả thiết: 4 1 t 10 2t 2 8
f (t ) = . + 2 = = + 3 1− t 3(1− t ) 3 3(1− t ) 2 8 1 2 8 Nên: f ( x) = + . f
(x)dx = x− ln 1− x C + 3 3 1− x 3 3
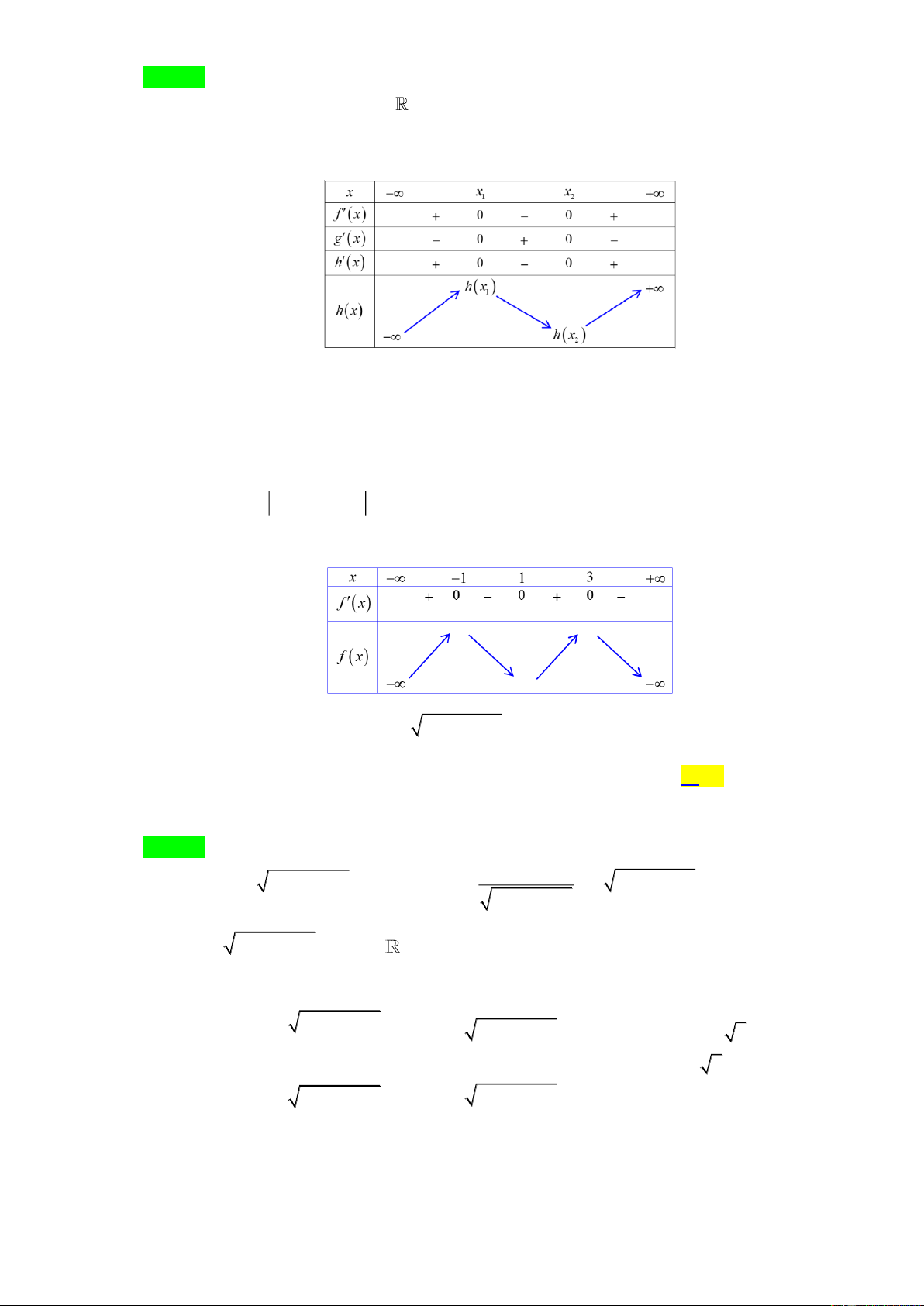
Câu 43. Cho hàm số y = f ( x) và y = g ( x) có đạo hàm trên
và có bảng biễn thiên như hình dưới đây
Biết rằng phương trình f ( x) = g ( x) có nghiệm x x ; x . Số điểm cực trị của hàm số 0 ( 1 2)
y = f ( x) − g ( x) là A. 5 . B. 3 . C. 4 . D. 2 . Lời giải Chọn A
Đặt h(x) = f (x) − g (x) , với x . Khi đó, h(x) = f (x) − g(x) .
Bảng biến thiên của hàm số y = h( x) như sau:
Vậy hàm số y = h( x) = f (x) − g (x) có hai điểm cực trị.
Mà phương trình f (x) − g (x) = 0 có nghiệm x x ; x nên h(x = 0 . Dựa vào bảng biến 0 ) 0 ( 1 2)
thiên của hàm số y = h( x) , ta thấy phương trình h( x) = 0 có ba nghiệm phân biệt.
Vậy hàm số y = f ( x) − g ( x) có 5 điểm cực trị.
Câu 44. Cho hàm số bậc bốn y = f ( x) có bảng biến thiên như hình vẽ.
Số điểm cực đại của hàm số y = f ( 2
x − 2x + 2 ) là A. 1. B. 4 . C. 3 . D. 2 . Lời giải Chọn D x −1
Đặt g (x) = f ( 2x −2x + 2). Ta có g(x) = f ( 2 x − 2x + 2 . 2 ) x − 2x + 2 Nhận xét: 2
x − 2x + 2 1, x . x 1 x 1 f ( 2
x − 2x + 2 ) 0 2
x − 2x + 2 3 1 x 1+ 2 2
g( x) 0 . x 1 − x 1 x 1 2 2 f 2 − + x 2x 2 3 ( 2
x − 2x + 2 ) 0
Ta có bảng xét dấu g( x)
Vậy theo Bảng xét dấu ta thấy g ( x) có hai điểm cực đại.
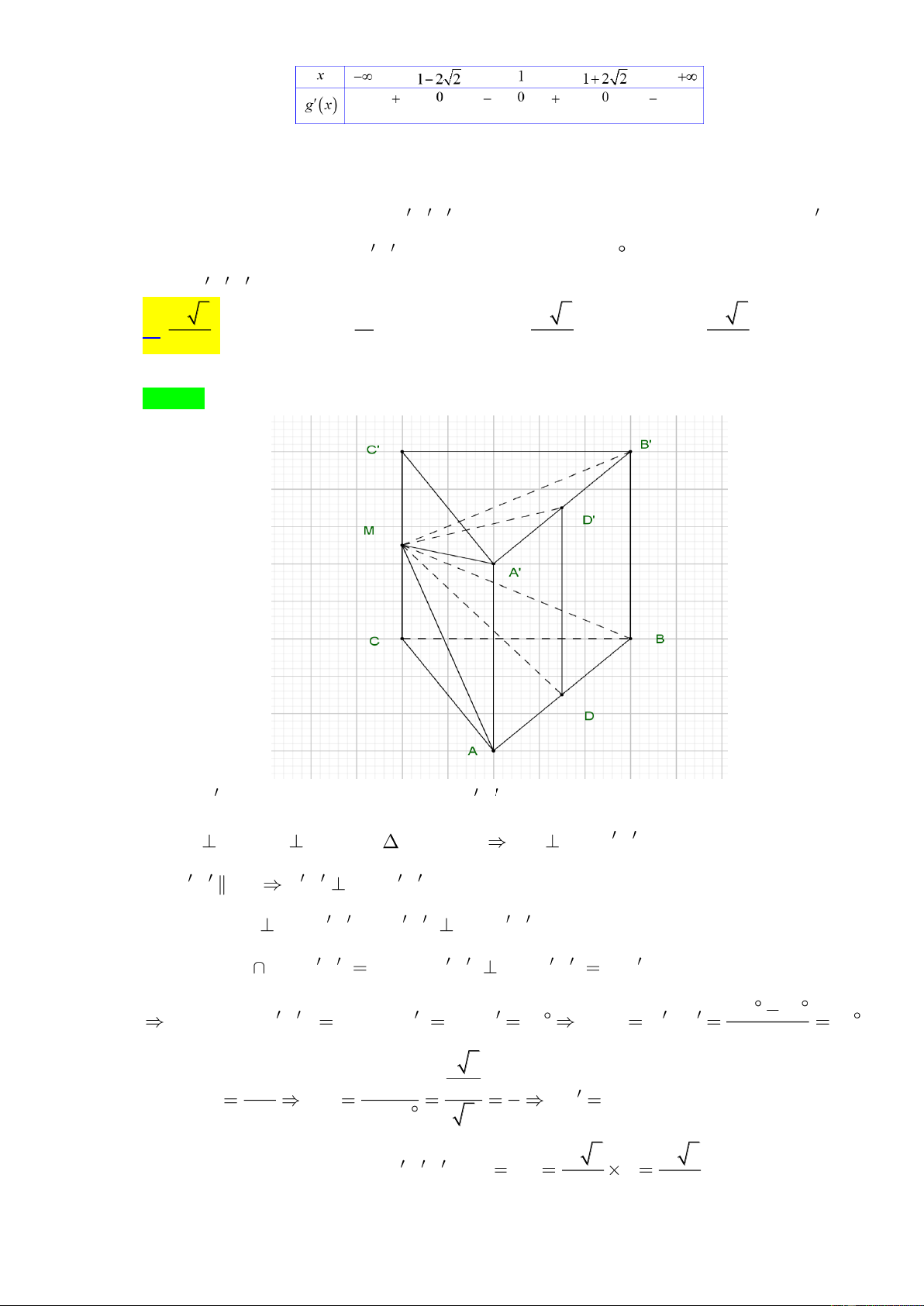
Câu 45. Cho lăng trụ tam giác đều ABC.A B C có cạnh đáy bằng ,
a M là trung điểm cạnh CC biết
hai mặt phẳng MAB , MA B tạo với nhau một góc 60 . Tính thể tích khối lăng trụ
ABC.A B C . 3 a 3 3 a 3 a 3 3 a 3 A. . B. . C. . D. . 4 4 2 3 Lời giải Chọn A Gọi ,
D D lần lượt là trung điểm của A , B A B . Vì AB CC;AB
CM ( do ABC đều) AB CDD C . Mà A B AB A B CDD C . Suy ra MAB CDD C , MA B CDD C . Ta có MAB CDD C M , D MA B CDD C MD . 180 60 MAB , MA B M , D MD DMD 60 CMD C MD 60 2 a 3 CD CD 2 a tanCMD CM CC a . CM tan 60 3 2 2 3 a 3 a 3
Thể tích của khối lăng trụ ABC.A B C là V Bh a . 4 4 2020 n
Câu 46. Gọi S là tập hợp các số tự nhiên n có 4 chữ số thỏa mãn n n 2020 2020 2 3 2 3 . Số
phần tử của S là A. 8999 . B. 2019 . C. 1010 . D. 7979 . Lời giải Chọn C 2020 n n n 2020 2020 n n 2020 2020 2 3 2 3 2020 ln 2 3 n ln 2 3 . (lấy ln hai vế) n n 2020 2020 f n 2020 ln 2 3 n ln 2 3 0 * . Khảo sát hàm số y f n , có 2020 n n 2020 2020 f n 2 ln 2 3 ln 3 ln 2 3 2n 3n n 2020 2020 n 2020 2020 2 2020 ln 2 ln 2 3 3 2020 ln 3 ln 2 3 2n 3n 2020 2020 n 2 n 3 2 ln 3 ln n 2020 n 2020 2020 2020 2020 2020 2 3 2 3 2 ln 3 3 ln 2 2n 3n 2n 3n 2020 ln 3.2n 2020 ln 2.3n 0, n . 2n 3n
Suy ra, f n là hàm nghịch biến. Ta có f 2020 0. Khi đó * f n f 2020 n 2020 mà n 1000,n 1000 n 2020.
Vậy có 1010 số tự nhiên n thỏa mãn yêu cầu bài toán.
maxf (x),g(x) nÕu x 0
Câu 47. Cho các hàm số f ( x) = x +1, g ( x) 2
= x +1 và hàm số h(x) = .
min f (x),g(x) nÕu x 0
Có bao nhiêu điểm để hàm số y = h(x) không tồn tại đạo hàm? A. 0 . B. 1 . C. 2 . D. 3 . Lời giải Chọn D 2
x +1 nÕu x 1 −
−x +1 nÕu −1 x 0
Ta có h ( x) =
, vậy có 3 vị trí đồ thị hàm số bị “gãy” nên tại đó không 2
x +1 nÕu 0 x 1
x +1 nÕu x 1 tồn tại đạo hàm.
Câu 48. Tính a + b biết ;
a b là tập hợp tất cả các giá trị của tham số m để bất phương trình 2 log
x − 2x + m + 4 log ( 2
x − 2x + m 5 2 4 )
thỏa mãn với mọi x 0;2 .
A. a + b = 4 .
B. a + b = 2 .
C. a + b = 0.
D. a + b = 6 . Lời giải Chọn D Xét bất phương trình 2 log
x − 2x + m + 4 log ( 2
x − 2x + m 5 1 2 4 ) ( ) Ta có ( ) 2 2 1 log
x − 2x + m + 4 log
x − 2x + m 5 2 2 2 ( ) 2
x − 2x + m 0 Điều kiện (*) 2 log
x − 2x + m 0 2 Đặt 2 t = log
x − 2x + m , bất phương trình (2) trở thành 2 2
t + 4t − 5 0 5 − t 1. Do đó 2 2 − + 2 − + ( x x m x x m
x − x + m 2) log 2 1 log 2 1 2 2 2 2 2 2 2 − + − log
x − 2x + m 0
x − 2x + m 1 log x 2x m 5 2 2 2
x −2x + m 4 ( ) 3 2
x −2x + m 1
Xét hàm số f ( x) 2
= x −2x + m trên 0;2, ta có bảng biến thiên của f (x) như sau
Từ bảng biến thiên ta có, hệ ( )
3 nghiệm đúng với mọi x 0;2 khi và chỉ khi
max f (x) = m 4 0;2 . f (x) 2 m 4 min = 1 − + m 1 0;2 a = 2 Suy ra
, vậy a + b = 6 . b = 4
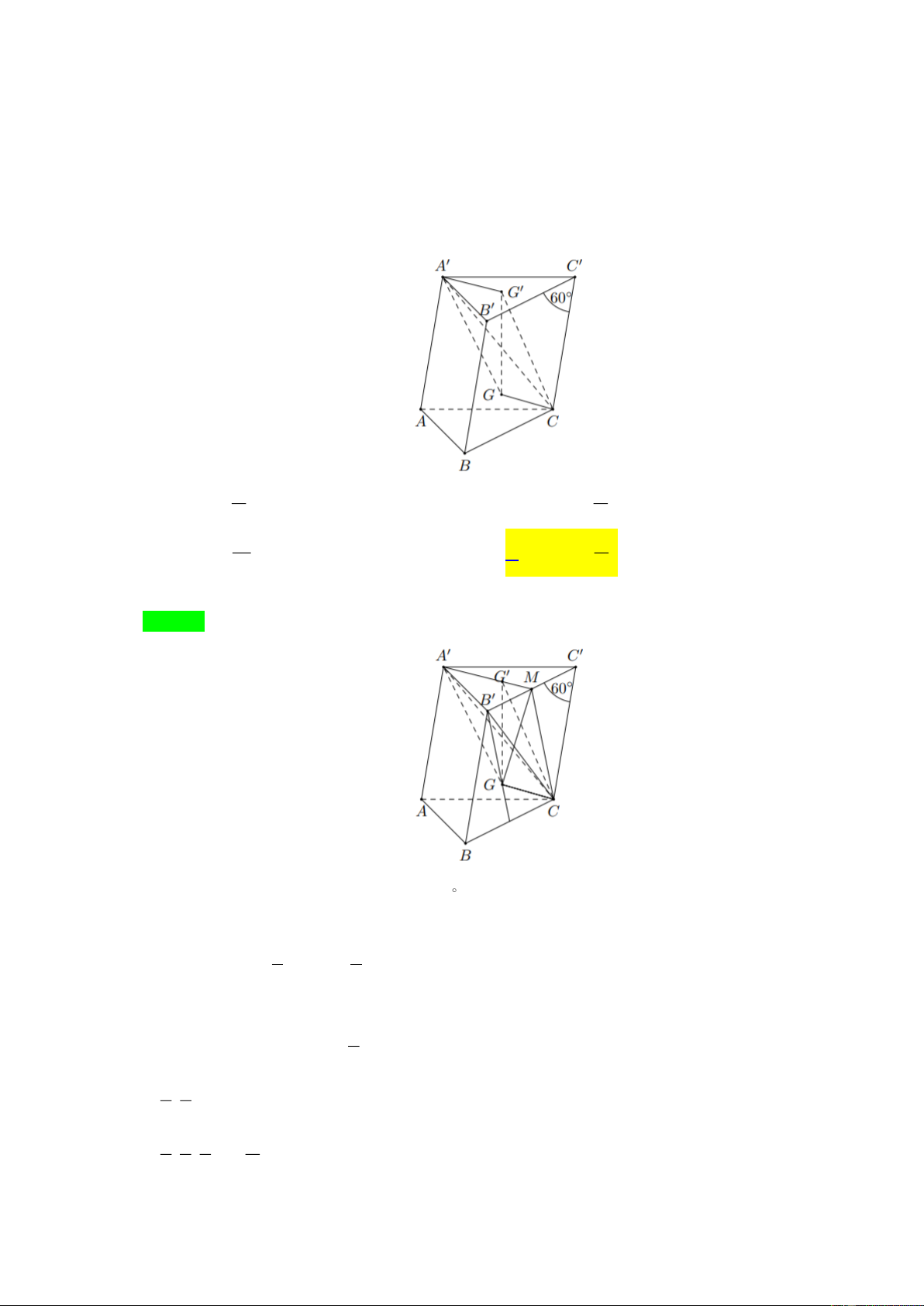
Câu 49. Cho hình lăng trụ AB . C A B C
có thể tích V . Biết tam giác ABC là tam giác đều cạnh a, các
mặt bên là hình thoi, CC B
= 60. Gọi G;G lần lượt là trọng tâm của tam giác BCB và tam giác A B C
. Tính theo V thể tích của khối đa diện GG C A. V V A. V = . B. V = . GG CA 6 GG CA 8 V V C. V = . D. V = . GG C A 12 GG CA 9 Lời giải Chọn D Ta có BCC B
là hình thoi và CC B = 60 nên C C B đều.
Gọi M trung điểm B C , ta có 1 1 S = S = = S S GMC B MC 2 CC B 4 BCC B Khi đó 2 V = − = V V V A .G GC A'.MGC G .MGC A'. 3 MGC 2 1 = . V '. 3 4 A BCC B 2 1 2 V = . . V = 3 4 3 9 Chọn đáp án D x f (x )
Câu 50. Cho hàm số y = f (x) có đạo hàm trên khoảng ( ;
− 0) và (0;+) sao cho 1 1 f = với x f (x ) 2 2
mọi x , x R \{0}, f (x ) 0. Biết f (
1) = 2 , khi đó f (x) bằng 1 2 2 f (x) 2 f (x)
A. 2 f (x) . B. .
C. 2xf (x) . D. . x x Lời giải Chọn D Theo giả thuyết, suy ra x f (x ) f (1) 1 1 f = f ( ) 1 = =1 x f (x ) f (1) 2 2 Xét với mỗi 1 f (1) 1
x R \ {0} , suy ra rằng f = = . x f (x) f (x)
Điều này chứng tỏ rằng x
0 thì f (x) 0 . Khi đó, theo định nghĩa của đạo hàm của hàm số
y = f (x) , với mỗi x 0 suy ra
f (x + h) −1
f (x + h) − f (x) f (x) f '(x) = lim
= f (x)lim h→0 h→0 h h x + h f −1 x = f (x)lim h→0 h h f 1+ − f (1) f (x) x = lim h→0 x h x f (x) 2 f (x) = f (1) = x x 2 f (x) Vậy f ( x) = , x R \{0}. x Có thể chọn 2 f ( ) x = x Chọn đáp án D
_______________ TOANMATH.com _______________
Document Outline
- de-thi-thu-tn-thpt-2021-2022-mon-toan-truc-tuyen-lan-4-so-gddt-ha-tinh
- Đề thi thử tốt nghiệp THPT năm 2021-2022 môn Toán - SỞ GIÁO DỤC HÀ TĨNH đợt 4 (File word có giải)-lg0zWVlFC-1642853475