Đề thi thử Toán vào lớp 10 lần 2 năm 2024 – 2025 phòng GD&ĐT Quốc Oai – Hà Nội

PHÒNG GD&ĐT QUỐC OAI
ĐỀ THI THỬ VÀO LỚP 10 - LẦN 2 Năm học 2024 - 2025 MÔN: TOÁN
Thời gian: 120 phút (không kể thời gian giao đề)
Câu 1 (2 điểm). Cho hai biểu thức: x - 5 2 x +1 x - 2 x + 3 A = và B = + +
với x ≥ 0 ; x ≠ 4; x ≠ 9 x - 2 x + 3 3− x x - 9
a/ Tính giá trị của A khi x = 16 x - 2 b/ Chứng minh: B = x + 3
c/ Cho P = A.B. Tìm số nguyên x lớn nhất để P < 1 . 2
Câu 2 (2 điểm)
1/ Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Hai vòi nước cùng chảy vào một bể cạn trong 2 giờ 40 phút thì đầy bể. Nếu
chảy riêng để đầy bể đó thì vòi I chảy đầy bể trước vòi II là 4 giờ. Hỏi nếu chảy riêng
thì mỗi vòi chảy đầy bể trong bao lâu.
2/ Một chiếc nón lá có đường kính đáy bằng 42cm, chiều cao 28cm, được phủ
kín 3 lớp lá. Tính diện tích lá cần dùng để làm chiếc nón trên (Lấy π ≈ 3,14 và làm tròn đến đơn vị cm2).
Câu 3 (2,5 điểm)  2 +3 y +2 = 5  x −1
1/ Giải hệ phương trình:  3  − 4 y + 2 = - 1  x −1
2/ Trong mặt phẳng tọa độ Oxy, cho Parabol (P): y = x2 và đường thẳng (d):
y = (m – 1)x – m + 2 (với m là tham số)
a/ Tìm tọa độ giao điểm của (d) và (P) khi m = 3
b/ Tìm m để (d) cắt (P) tại hai điểm nằm về hai phía của trục tung và có hoành
độ x1, x2 thỏa mãn: x12 + (m – 1)x2 = 7
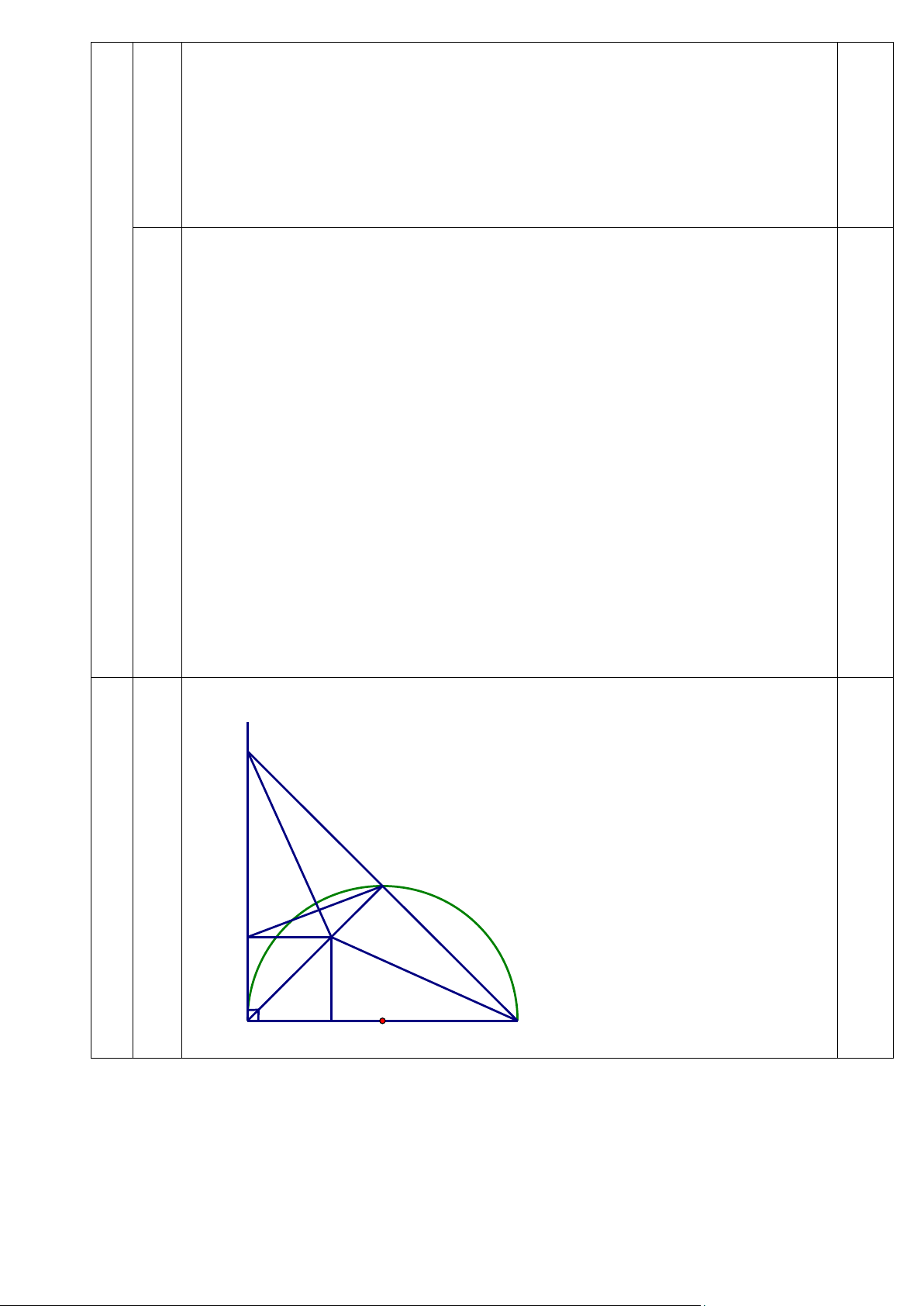
Câu 4 (3 điểm) Cho nửa (O) đường kính AB, kẻ tiếp tuyến Ax cùng phía nửa đường
tròn. Trên tia Ax lấy điểm C sao cho AC = AB. Gọi D là giao điểm của BC với nửa
(O). Điểm M bất kì thuộc đoạn thẳng AD. Kẻ MH vuông góc với AB tại H; MI vuông góc với AC tại I.
a/ Chứng minh: Tứ giác BHMD nội tiếp và AD.AM = AH.AB b/ Chứng minh   MBD = MID
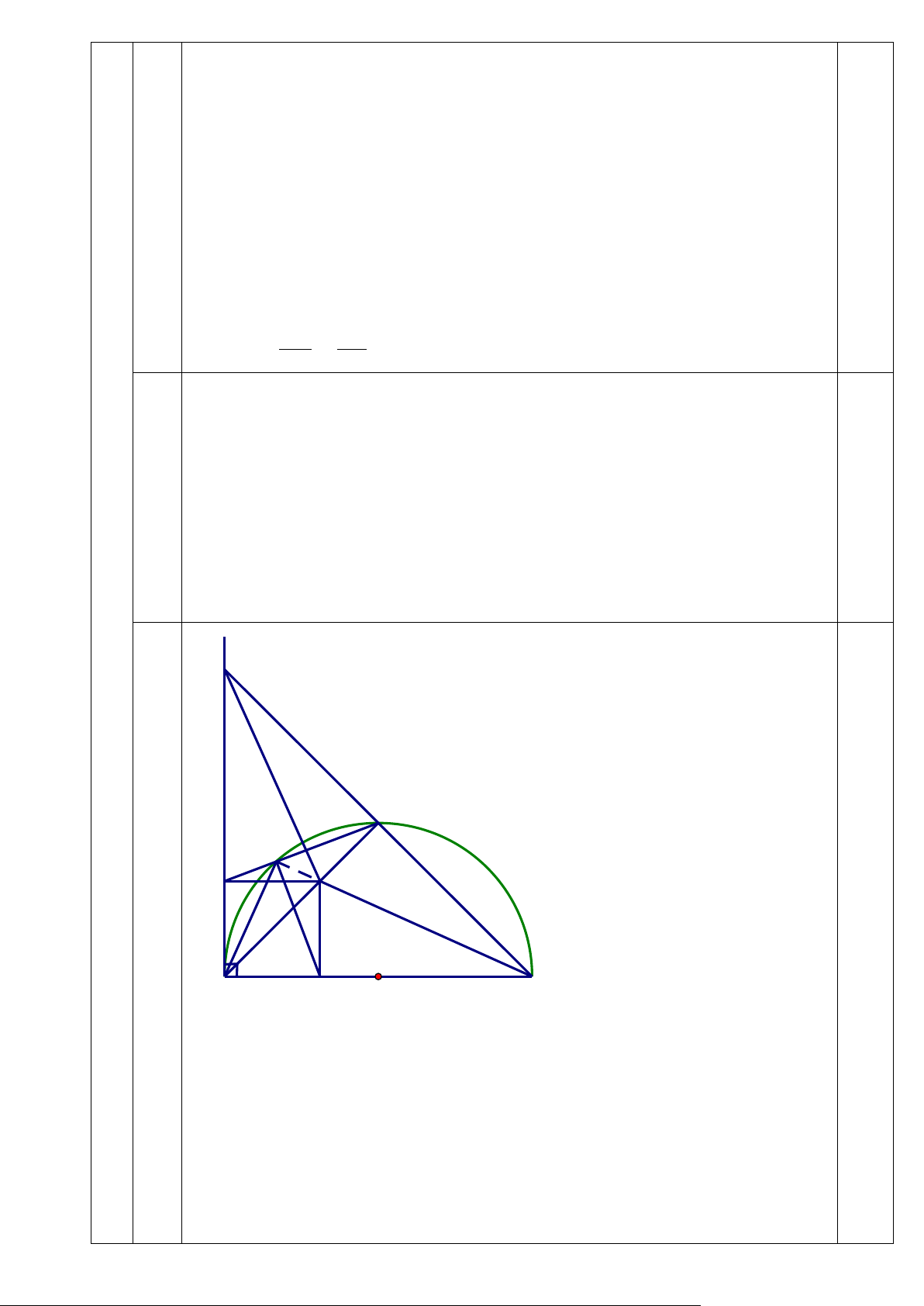
c/ Kẻ HK vuông góc với ID tại K. Chứng minh K thuộc (O).
Câu 5 (0,5 điểm) Với x, y là các số dương thỏa mãn điều kiện x ≥ 2y 2 2 +
Tìm giá trị nhỏ nhất của biểu thức: = x y M . xy
Cán bộ coi kiểm tra không giải thích gì thêm.
Họ và tên thí sinh:.................................................... Số báo danh:.........................
PHÒNG GD & ĐT QUỐC OAI KỲ THI THỬ VÀO 10 NĂM HỌC 2024-2025
HƯỚNG DẪN CHẤM MÔN TOÁN Câu Phần Nội dung Điể m x - 5 A =
đk x ≥ 0 ; x ≠ 4; x ≠ 9 a x - 2 0,25
Với x = 16 (TMĐK) thay vào biểu thức A ta được: 0,5 Tính đúng A = 1 − , KL: 0,25 2
ĐKXĐ: x ≥ 0 ; x ≠ 4; x ≠ 9 2 x +1 x - 2 x + 3 B = + + x + 3 3− x x - 9 2 x +1 x - 2 x + 3 B = - + x + 3 x - 3 ( x + 3)( x - 3 ) 0,25 (
2 x + )1( x - 3 )−( x - 2)( x +3)+ x + 3 = ( x +3)( x - 3) b 0,25 1đ
2x - 5 x − 3− x − x + 6 + x + 3 = ( x + 3)( x - 3) 1 ( x −2)( x - 3 x - 5 x + 6 ) x - 2 (2đ) = ( = 0,25 + )( ) = x 3 x - 3 ( x +3)( x - 3) x + 3 x - 2 KL: Vậy B= x + 3 0,25
ĐKXĐ: x ≥ 0 ; x ≠ 4; x ≠ 9 x - 5 x - 2 x - 5 P = A. B = . = x - 2 x + 3 x + 3 P < 1 x - 5 1 x - 5 1 ⇔ < ⇔ − < 0 2 x + 3 2 x + 3 2 0,25 c 2 x - 10 - x − 3 x −13 0,5 ⇔ ( ⇔ < 0 + ) < 0 2 x 3 2( x + 3) Do x x −13
≥ 0 => x + 3> 0 nên để ( thì x −13 < 0 + ) < 0 2 x 3  x <13 => x < 169
 Do x là số nguyên lớn nhất nên x = 168 0,25 Đổi 2h 40’ = 8 h 0,25 3
Gọi thời gian vòi I chảy riêng đầy bể là x (giờ ; x > 0)
Thì thời gian vòi II chảy riêng đầy bể là x + 4 (giờ)
Mỗi giờ: Vòi I chảy được : 1 (bể) x 0,25
Vòi II chảy được : 1 (bể) x + 4 0,25
Cả hai vòi chảy được: 3 (bể) 8
Theo bài ra ta có phương trình: 2.1 1,5 1 + 1 = 3 0,25 đ x x + 4 8 2 ⇔ 8x + 32 + 8x = 3x2 + 12x (2đ) ⇔ 3x2 - 4x - 32 = 0
∆ ' = (-2)2 – 3.(-32) = 100 => ∆' = 10 0,25 x + 1 = 2 10 = 4 (TM) 3 0,25 x − − 2 = 2 10 8 = (Loại) 3 3
Vậy thời gian vòi I chảy riêng đầy bể là 4 (giờ)
Và thời gian vòi II chảy riêng đầy bể là 4 + 4 = 8 (giờ)
Bán kính đáy là: 42:2 = 21(cm) 2.2 0,25
0,5 Độ dài đường sinh là: 2 2 21 + 28 = 35 (cm)
Diện tích lá cần dùng là: S = 3.πrl = 3.3,14.21.35 ≈6924 (cm2) 0,25  2 +3 y +2 = 5  x −1  3
Đkxđ: x > 1 ; y ≥ -2  − 4 y + 2 = -1  x −1  1 = a   x −1 0,25 3 Đặt (2,5 3.1  y +  2 = b đ) 1đ 2a + 3b = 5 6a + 9b = 15 17a  = 17 a = 1 hpt ⇔  ⇔  ⇔  ⇔ 0,25 3a - 4b = -1 6a - 8b = -2 3b = 5 - 2a     b = 1  1 = 1   x −1 = 1 x = 2 Thay ẩn:  x −1 ⇒  ⇒  (tm) 0,25  y + 2 = 1 y = -1 y +  2 = 1
Vậy hệ pt đã cho có nghiệm duy nhất: (x , y) = (2 ; -1) 0,25
Xét pt hoành độ giao điểm của (P) và (d): x2 = (m – 1)x – m + 2 3.2 0,25
⇔ x2 – (m – 1)x + m – 2 = 0 (*)
(a) Với m = 3 thay vào phương trình (*) ta được: x2 – 2x + 1 = 0 0,75 đ
∆ ' = 1 – 1 = 0 => phương trình có nghiệm kép: x1 = x2 = 1 0,25
x = 1 => y = 1 => A(1 ; 1)
Vậy với m = 3 thì đường thẳng (d) tiếp xúc với (P) tại điểm A(1 ; 1) 0,25
Xét pt hoành độ giao điểm của (P) và (d):
x2 – (m – 1)x + m – 2 = 0 (*)
∆ = [-(m – 1)]2 – 4(m – 2) = m2 – 2m + 1 – 4m + 8 = m2 – 6m + 9 = (m – 3)2 0,25 ≥ 0 m ∀
 Phương trình (*) luôn có hại nghiệm ∀ m
Để (d) cắt (P) tại hai điểm nằm về hai phía của trục tung thì pt (*) có hai nghiệm trái dấu x ⇒ ⇒ 3.2 1x2 < 0 m - 2 < 0 m < 2 (b)
Theo Vi_et: x1 + x2 = m - 1 ; x1x2 = m – 2 0,75đ
Theo bài: x12 + (m – 1)x2 = 7 0,25
⇔ x12 + (x1 + x2)x2 = 7 ⇔ x12 + x1x2 +x22 = 7
⇔ (x1 + x2)2 – x1x2 = 7 ⇔ (m - 1)2 – (m – 2) = 7
⇔ m2 – 2m + 1 – m + 2 – 7 = 0 ⇔ m2 – 3m – 4 = 0
Nx: a – b + c = 1 + 3 – 4 = 0 0,25
 m1 = -1 (tm) ; m2 = 4 (Loại)
Vậy với m = -1 thì (d) cắt (P) tại hai điểm nằm về hai phía trục tung và
có hoành độ x1x2 thỏa mãn: x12 + (m – 1)x2 = 7
Vẽ hình đúng đến câu a x C 0,25 4 (3đ) a 1,5đ D I M A B H O
• Vì AB là đường kính của (O) nên :  0 ADB = 90 ; 0,25 Vì MH ⊥ AB tại H nên  0 MHB = 90 Xét tứ giác BHMD có:   0 BDM + BHM =180 0,25
Mà hai góc ở vị trí đối diện 0,25
 Tứ giác BHMD nội tiếp
• Xét ∆AHM và ∆ADB có: Alà góc chung   0 AHM = ADB = 90 0,25 ⇒ ∆ AHM ∽ ∆ ADB (g-g) AH AD ⇒ = ⇒ AD.AM = AH.AB 0,25 AM AB Xét tứ giác CDMI có:   0 CDM + CIM =180
Mà hai góc ở vị trí đối diện 0,25 b
 Tứ giác BHMD nội tiếp 0,75   
MID = MCD (góc nội tiếp chắn  MD) (1) đ
Do ∆ABC vuông cân tại A, có AD là đường cao nên cũng là đường
trung trực. Mà M ∈AD => MB = MC => ∆MBC cân tại M 0,25 ⇒   MCD = MBD (2) Từ (1) và (2) ⇒   MID = MBD 0,25 x C D K I M c 0,75 A H O B Tứ giác AIKH có:   0 IAH + IKH =180
Mà hai góc ở vị trí đối diện
 Tứ giác AIKH nội tiếp
Lại có: Tứ giác AIMH nội tiếp (do   0 AIM + AHM =180 )
Nên 5 điểm: A, H, M, K, I cùng thuộc một đường tròn 0,25
 Tứ giác AHMK nội tiếp    0 AHM + AKM =180 ⇒  0 AKM = 90    0 AMK + MAK = 90 (1)
Do 5 điểm: A, H, M, K, I cùng thuộc một đường tròn   
MAK = MIK (góc nội tiếp chắn  MK ) 0.25 Theo phần b ta có:   MIK = MBD    MAK = MBD (2) Lại có:   0 MBD + BMD = 90 (3)
Từ (1), (2) và (3) =>   AMK = BMD Mà   0 BMD + AMB = 180 ⇒   0 AMK + AMB = 180 0,25
 điểm B, M, K thẳng hàng. Lại có:  0 AKM = 90 ⇒  0 AKB = 90
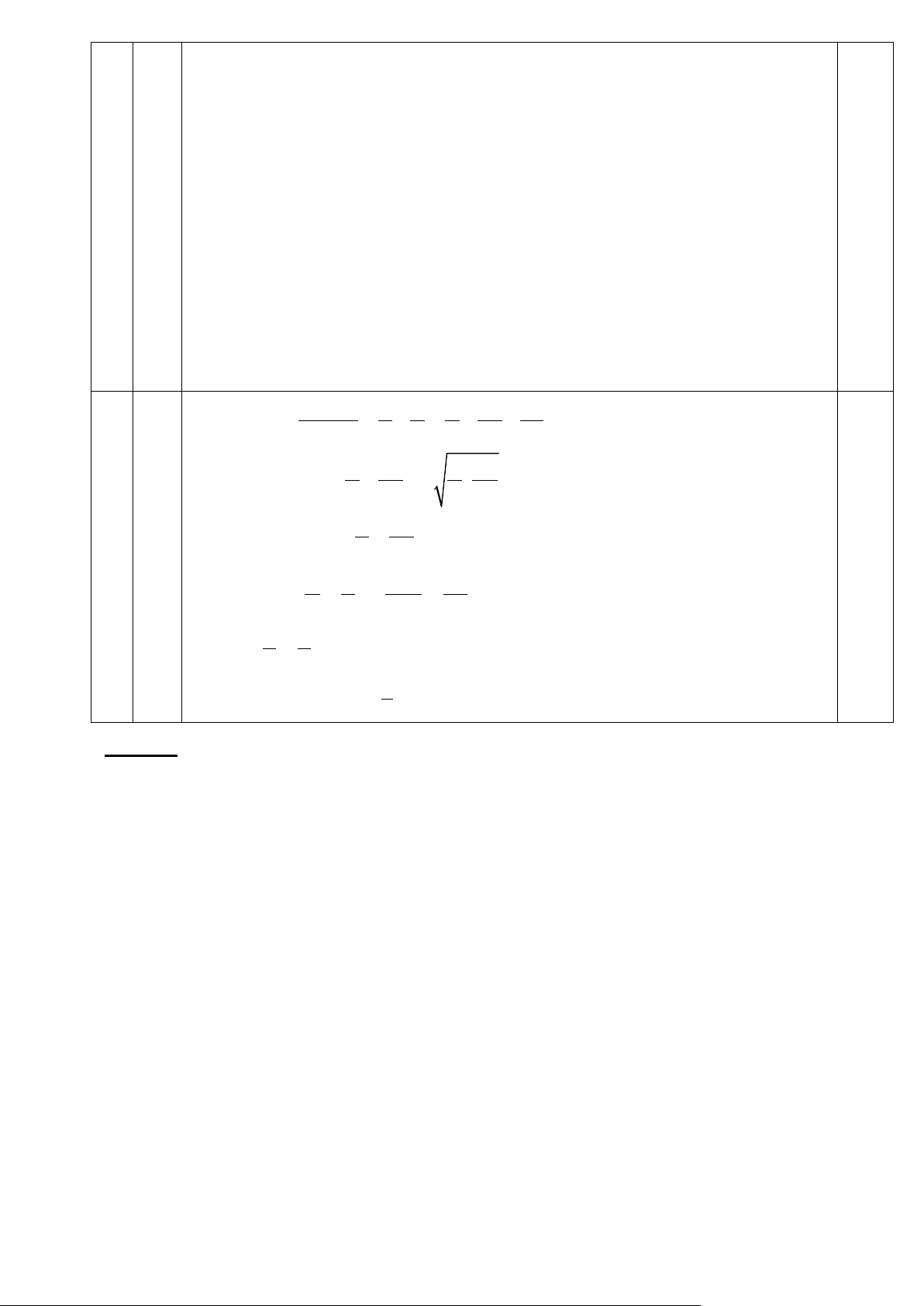
 K thuộc đường tròn đường kính AB. Vậy K thuộc (O) 2 2 Ta có : x + y x y x 4y 3 = = + = + − y M , . xy y x y x x
Vì x, y > 0 ,ta có: x 4y x 4 + ≥ 2 ⋅ y = 4. y x y x x 4
⇔ = y ⇔ x = 4y ⇒ x = 2y 5 Dấu "=" xảy ra 2 2 . y x (0,5) y 1 3 − y 3 − 0,25
Vì x ≥ 2y ⇒ ≤ ⇒ ≥
,dấu "=" xảy ra ⇔ x = 2y x 2 x 2 3 5
M ≥ 4 − = , dấu "=" xảy ra 2 2 ⇔ x = 2y
Vậy GTNN của M là 5 khi x = 2y . 0,25 2
Ghi chú: Học sinh làm cách khác đúng chấm điểm tương đương.