UBND HUYỆN NGA SƠN
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10-LẦN 2 PHÒNG GD&ĐT
THPT NĂM HỌC 2025 – 2026 MÔN TOÁN
Thời gian làm bài 120 phút
(Đề thi gồm 2 trang)
Ngày thi 27 tháng 3 năm 2025
Họ và tên học sinh:……………………………………………
Lớp 9……...
Trường THCS: ................................................
SBD:……......
I. TRẮC NGHIỆM (2,0 điểm):
Chọn chữ cái đứng trước câu trả lời đúng
Câu 1. Trong các phương trình sau phương trình nào là phương trình bậc hai một ẩn?
A. 1 + 2024 x + 2025 = 0 . B. 2 3
x − 2024 x + 2025 = 0 . 2 x
C. 2x − 2024 x + 2025 = 0 D. 4 2
x + 2022 x − 2021 = 0 .
Câu 2. Biểu thức nào sau đây có giá trị khác với các biểu thức còn lại? A. (− )2 5 . B. 2 5 . C. (− )2 5 . D. −( )2 5 .
Câu 3. Điểm nào sau đây thuộc hàm số 𝑦𝑦 = 𝑥𝑥2 A. (−1; 2) B. (1; 2) C. (1; 1) D. (−2; 2)
Câu 4. Điều kiện xác định của biểu thức A = 1− 2x là? A. 1 x ≤ . B. 1 x < . C. 1 x > . D. 1 x ≥ . 2 2 2 2
Câu 5. Cho tam giác ABC có BC  5;AC  4;AB  3 . Kết quả nào sau đây là đúng?
A. sinC  0,75 B. sinC  0,6 C. sinC  0,8 D. sinC  1,3 .
Câu 6. Diện tích hình tròn bán kính R  10cm là: A. 2 100 ( cm ) 2 10 (cm ) C. 2 20 ( cm ) D. 2 100² (cm )
Câu 7. Góc nội tiếp chắn nửa đường tròn bằng bao nhiêu độ? A. 45° B. 90° C. 60° D. 120°
Câu 8. Cho đường tròn O; 10cm,đường kính AB. Điểm M   O sao cho  BAM  45
. Diện tích hình quạt AOM là: A.   2 25
5 cm  B.   2
25 cm  C.   2 cm  D.   2 50 cm  2
II. PHẦN TỰ LUẬN (8,0 điểm)
Câu 9. (1,5 điểm)
a) (0,75 điểm) Giải phương trình: 2
3x − 7x + 2 = 0. 2x + 3y = 8
b) (0,75 điểm) Giải hệ phương trình  4x − 3y = 2 −
Câu 10 . ( 1,0 điểm) Rút gọn biểu thức: 3x + 5 x −11 x − 2 2 A = − +
−1 ( với x ≥ 0 và x ≠1). x + x − 2 x −1 x + 2
Câu 11: (1,0 điểm) Cho phương trình 2
x − 5x + m − 3 = 0 ( m là tham số). Tìm các giá
trị của m để phương trình có hai nghiệm x , x
x − 2x x + 3x =1 1 2 thỏa mãn hệ thức: 2 1 1 2 2 .
Câu 12. (1,0 điểm) Miếng kim loại thứ nhất nặng 880 g, miếng kim loại thứ hai nặng
858 g . Thể tích của miếng kim loại thứ nhất nhỏ hơn thể tích của miếng kim loại thứ hai là 3
10cm , nhưng khối lượng riêng của miếng kim loại thứ nhất lớn hơn miếng kim loại thứ hai là 1 3
g cm . Tính khối lượng riêng của mỗi miếng kim loại. (Biết
rằng khối lượng riêng của một vật được xác định bởi công thức m D = trong đó là V
khối lượng riêng tính bằng đơn vị là 3
g cm , khối lượng tính bằng đơn vị là g, thể tích tính bằng đơn vị 3 cm )
Câu 13 .( 1,0 điểm ) Một thùng nước có dạng hình trụ với chiều cao 1,7m và bán
kính đáy 0,5m . Người ta sơn toàn bộ phía ngoài mặt xung quanh của thùng nước này
(trừ hai mặt đáy). Biết mỗi mét vuông sơn thợ lấy với số tiền là 500000 đồng. Tính
số tiền phải trả cho thợ sơn (lấy π ≈ 3,14 ).
Câu 14. (2,0 điểm)
Cho tam giác ABC nhọn nội tiếp đường tròn (O) có đường cao AD. Kẻ đường
kính AK của (O). Gọi E và F lần lượt là hình chiếu của B và C trên AK.
a) Chứng minh tứ giác ADFC là tứ giác nội tiếp. b) Chứng minh  = 
BAD CAK . Gọi M và N lần lượt là trung điểm của BC và AC.
Chứng minh MN ⊥ DF và M là tâm đường tròn ngoại tiếp tam giác DEF
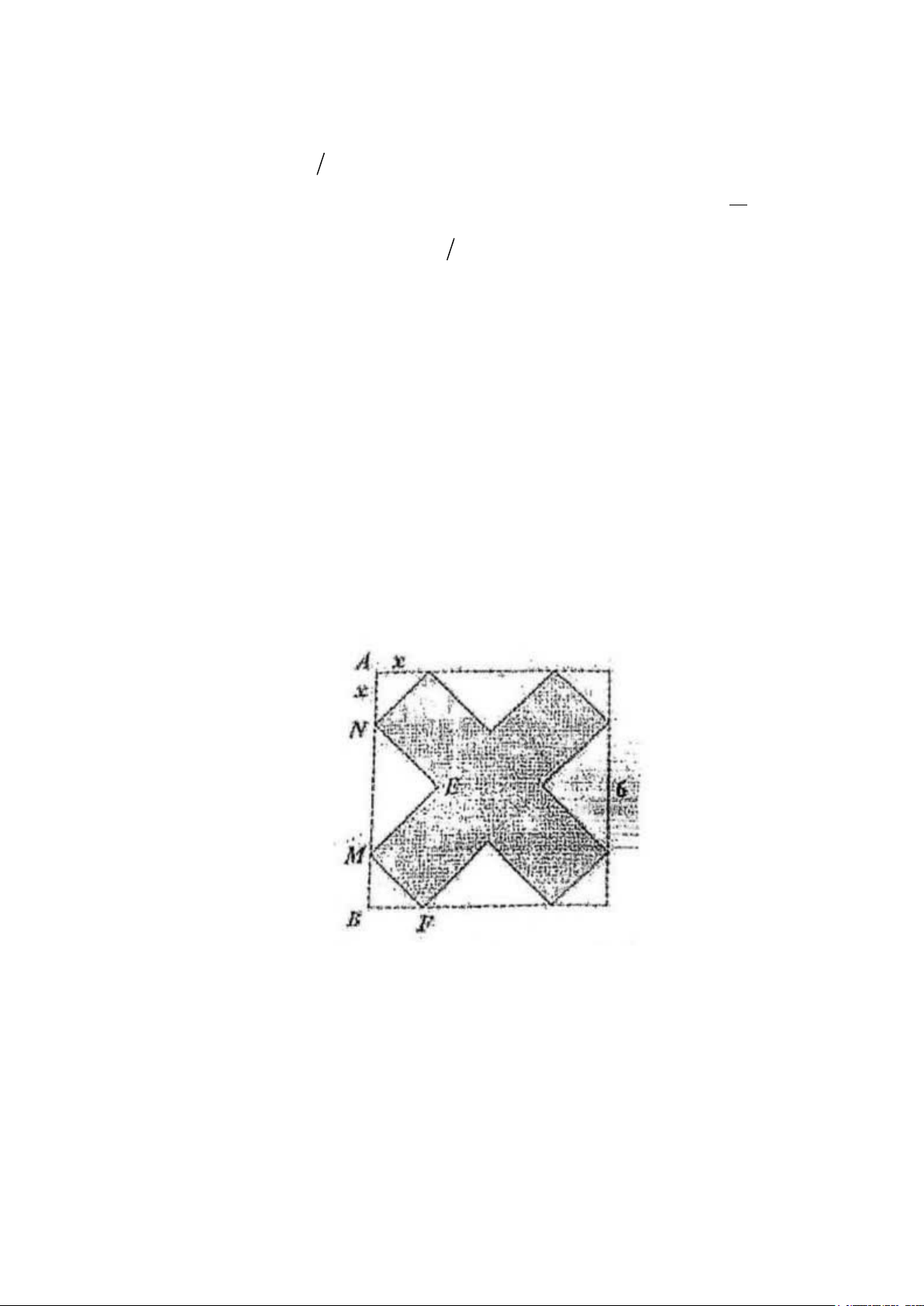
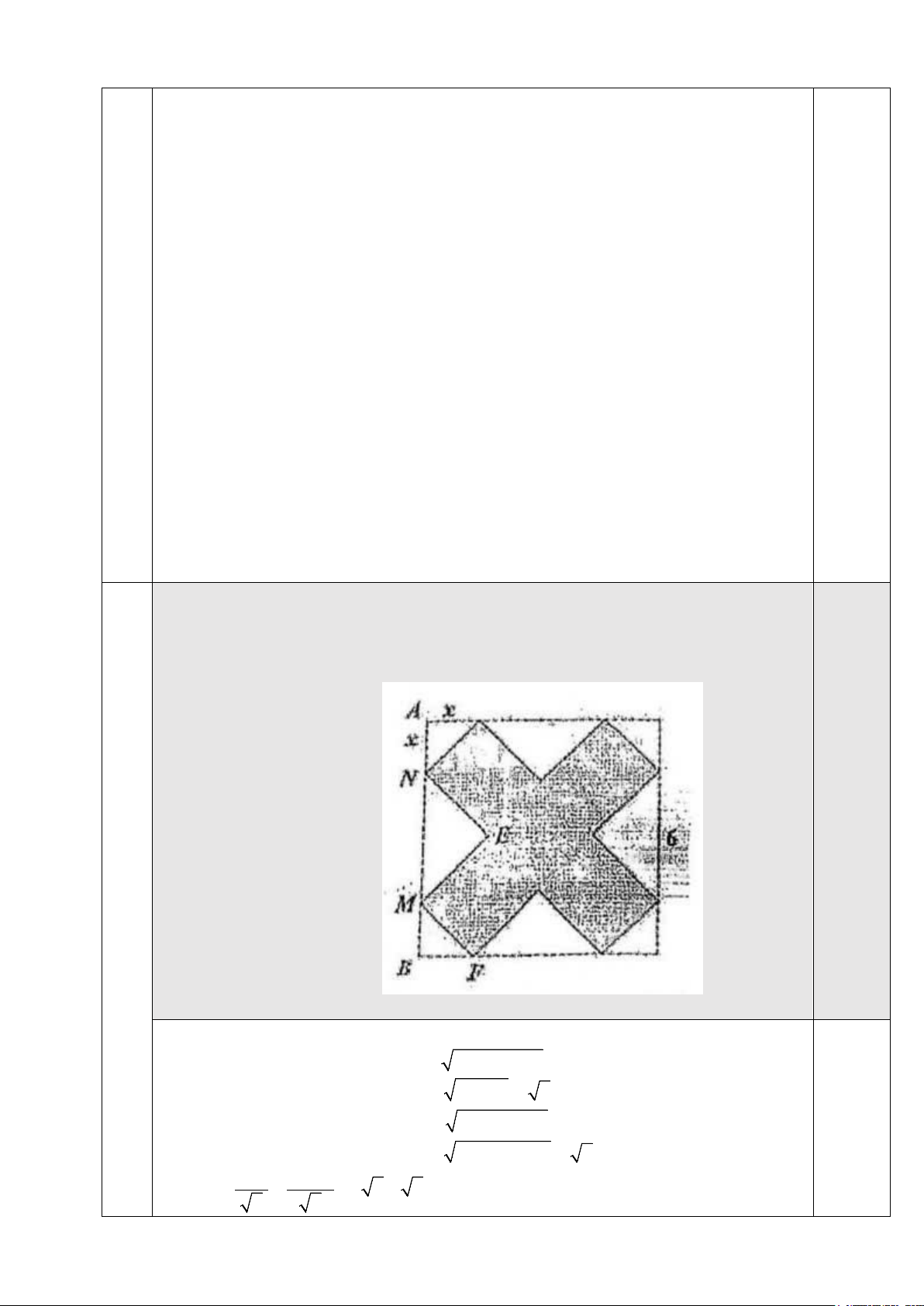
Câu 15. (0,5 điểm) Từ một hình vuông cạnh bằng 6, bạn An cắt bỏ các tam giác
vuông cân tạo thành hình tô đậm như hình vẽ. Sau đó bạn An gập lại thành hộp quà
có dạng hình hộp chữ nhật không có nắp. Tìm x để khối hộp có thể tích lớn nhất. -----HẾT----
HƯỚNG DẪN CHẤM BÀI KIỂM TRA KIẾN THỨC VÀO 10 THPT LẦN 2 Chú ý.
- Các cách làm khác nếu đúng vẫn cho điểm tối đa.
- Đối với câu 14 (Hình học).
+ Không vẽ hình, hoặc vẽ hình sai cơ bản thì không chấm;
+ Học sinh không chứng minh mà thừa nhận kết quả của ý trên để giải ý dưới thì
không chấm điểm ý dưới.
- Các trường hợp khác tổ chấm thống nhất phương án chấm. ĐÁP ÁN
I. PHẦN TRẮC NGHIỆM (2,0 điểm gồm 8 câu, mỗi câu 0,25 điểm) Câu 1 2 3 4 5 6 7 8 Đáp án C D C A B A B B
II. PHẦN TỰ LUẬN (8,0 điểm) Hướng dẫn giải Câ Điểm u
a) (0,75 điểm) Giải phương trình: 2
3x − 7x + 2 = 0. 2x + 3y = 8 1,5
b) (0,75 điểm) Giải hệ phương trình  4x − 3y = 2 − Xét phương trình 2
3x − 7x + 2 = 0. Có 2 ∆ = ( 7
− ) − 4.3.2 = 25 > 0; ∆ = 25 = 5 0,25
9 Nên phương trình có hai nghiệm phân biệt 7 5 x + = = 2 ; 7 5 1 x − = = 0,5 1 2.3 2 2.3 3
2x + 3y = 8(1) Xét hệ phương trình 
4x − 3y = 2( − 2)
Cộ ng theo vế của (1) và (2) ta được 6x =6, suy ra x =1 0,25 Thay x =1 vào ( )
1 ta được 2 + 3y = 8, suy ra y = 2 0,25
Vậy hệ phương trình có nghiệm x =1  0,25 y = 2 Rút gọn biểu thức: 3x + 5 x −11 x − 2 2 A = − +
−1 ( với x ≥ 0 và x ≠ 1) 1,0 x + x − 2 x −1 x + 2
Với x ≥ 0;x ≠1, ta có:
3x +5 x −11 x − 2 2 A = − + −1 x + x − 2 x −1 x + 2 10
3x + 5 x −11− ( x − 2)( x + 2)+ 2( x − )1−(x + x − 2) A = ( 0,25đ x − ) 1 ( x + 2)
3x + 5 x −11− x + 4 + 2 x − 2 − x − x + 2 x + 6 x − 7 = ( = x − ) 1 ( x + 2)
( x − )1( x +2) 0,25 đ
( x− )1( x+7) x+7 x + = ( = . Vậy 7 A =
với x ≥ 0; x ≠1. 0,25đ x − ) 1 ( x + 2) x + 2 x + 2
Cho phương trình 2x −5x + m −3 = 0 (m là tham số). Tìm các giá trị của m
phương trình có hai nghiệm x , x thỏa mãn hệ thức: 2
x − 2x x + 3x =1.Cho 1,0 1 2 1 1 2 2
Xét phương trình 2x −5x + m −3 = 0
Ta có: ∆ = 37 − 4m
Để phương trình có hai nghiệm x ; x thì điều kiện là: 1 2 37
∆ ≥ 0 ⇒ 37 − 4m ≥ 0 ⇒ m ≤ (*) 4 0,25đ
Với điều kiện (*), áp dụng định lí Viète cho phương trình (1), ta có: x + x = 5 (1) 1 2 
x .x = m −  3 (2) 1 2 T heo bài ra, ta có 2
x − 2x x + 3x =1 (3) 1 1 2 2
11 Từ (1) suy ra : x = 5− x thế vào (3) ta được : 2 1 2
x − 2x 5 − x + 3 5 − x =1 1 1 ( 1 ) ( 1 ) 2
3x −13x +14 = 0 0,25 đ 1 1
(x − 2 3x −7 = 0 1 )( 1 ) ⇒ x = 2 hoặc 7 1 x = 1 3
Với x = 2 thì x = 3 , thế vào (2) ta được: m = 9 (thỏa mãn) 1 2 0,25 đ Với 7 x = thì 8
x = , thế vào (2) ta được: 83 m = (thỏa mãn) 1 3 2 3 9
Vậy có hai giá trị của m thỏa mãn là: m = 9 hoặc 83 m = . 9 0,25 đ
Miếng kim loại thứ nhất nặng 880 g , miếng kim loại thứ hai nặng 858 g
. Thể tích của miếng kim loại thứ nhất nhỏ hơn thể tích của miếng kim 1,0 loại thứ hai là 3
10cm ,nhưng khối lượng riêng của miếng kim loại thứ
nhất lớn hơn miếng kim loại thứ hai là 1 3
g cm . Tính khối lượng riêng
c ủa mỗi miếng kim loại. (Biết rằng khối lượng riêng của một vật được
12 xác định bởi công thức m
D = trong đó là khối lượng riêng tính bằng đơn V vị là 3
g cm , khối lượng tính bằng đơn vị là g, thể tích tính bằng đơn vị 3 cm )
Gọi khối lượng riêng của miếng kim loại thứ 1 là x ( 3 g cm )( x>1) 0,25
⇒ Khối lượng riêng của miếng kim loại thứ 2 là x – 1( 3 g cm )
Thể tích của miếng kim loại thứ nhất là 880 3 (cm ) x
Thể tích của miếng kim loại thứ hai là 858 3 (cm ) x −1
Vì thể tích của miếng kim loại thứ nhất nhỏ hơn thể tích của miếng kim 0,25 loại thứ hai là 3
10cm nên ta có phương trình: 858 880 − =10 x −1 x
Quy đồng và khử mẫu ta được phương trình: 2
5x + 6x − 440 = 0
Giải phương trình ta được: x = 10
− ( loại) và x = 8,8( thỏa mãn) 1 2 0,25
Vậy khối lượng riêng của miếng kim loại thứ 1 là 8,8 ( 3 g / cm ) 0,25
Khối lượng riêng của miếng kim loại thứ 2 là 8,8 – 1=7,8( 3 g / cm )
Một thùng nước có dạng hình trụ với chiều cao 1,7m và bán kính đáy
0,5m . Người ta sơn toàn bộ phía ngoài mặt xung quanh của thùng nước
này (trừ hai mặt đáy). Biết mỗi mét vuông sơn thợ lấy với số tiền là 1,0
500000 đồng. Tính số tiền phải trả cho thợ sơn (lấy π ≈ 3,14 ).
Vì thùng nước hình trụ có chiều cao h =1,7m và bán kính đáy R = 0,5m nên
13 diện tích xung quanh của hình trụ là: 0,5đ S = π R h = = m xq ( 2 2 . 2.3,14.0,5.1,7 5,338 )
Vậy diện tích bề mặt được sơn của thùng nước là 2 5,338m 0,25đ
Số tiền phải trả cho thợ: 5,338. 500000 = 2669000 (Đồng)
Vậy số tiền phải trả cho thợ sơn thùng nước là : 2669000 đồng 0,25đ
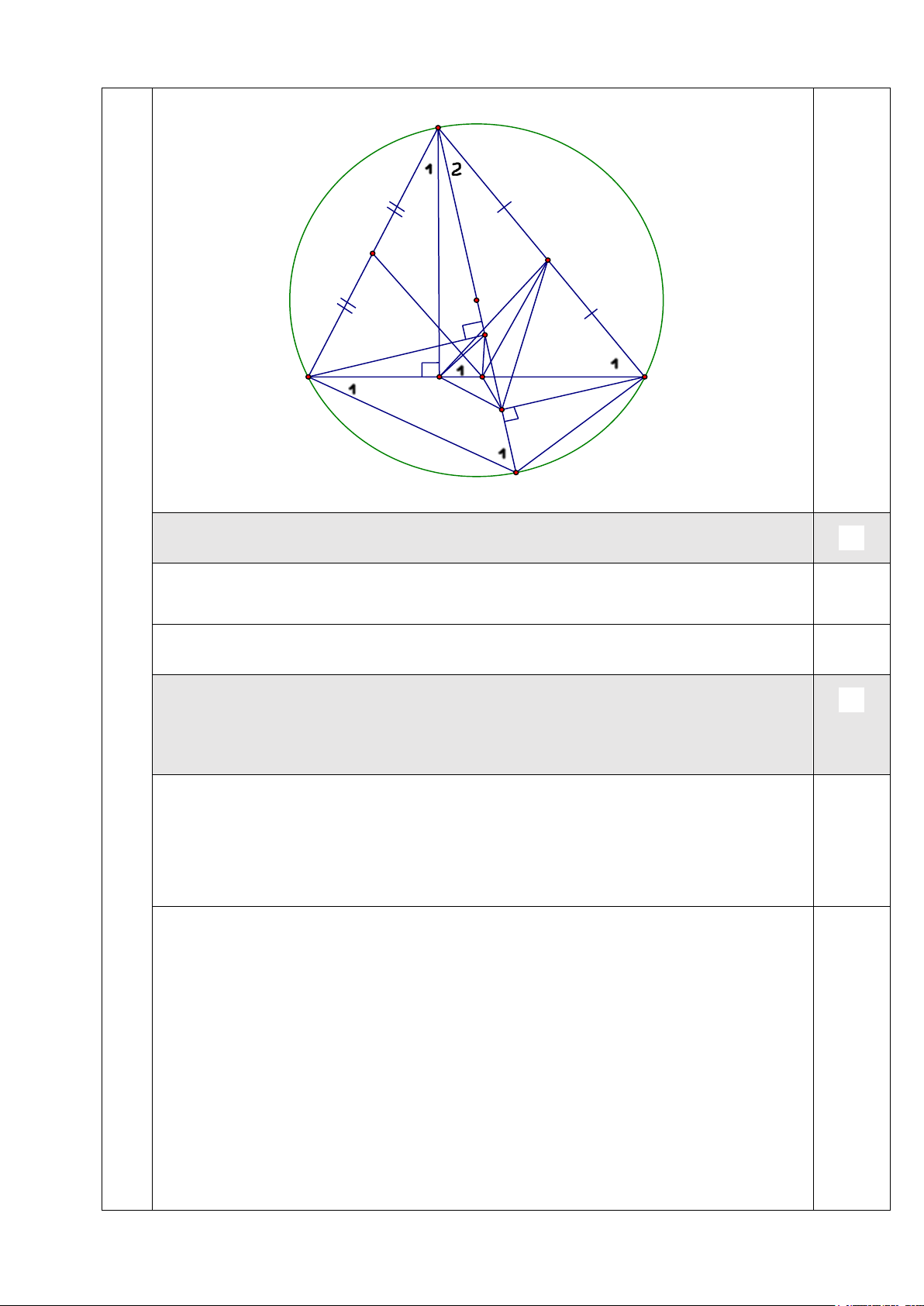
Cho tam giác ABC nhọn nội tiếp đường tròn (O) có đường cao AD.
Kẻ đường kính AK của (O). Gọi E và F lần lượt là hình chiếu của B và C trên AK.
a) Chứng minh tứ giác ADFC là tứ giác nội tiếp. 2,0 b)Chứng minh  = 
BAD CAK . Gọi M và N lần lượt là trung điểm của BC
14 và AC. Chứng minh MN ⊥ DF và M là tâm đường tròn ngoại tiếp tam giác DEF A P N O E B M C D F K
a) Chứng minh ACDF nội tiếp. 1,0 Ta có :  =  0
ADC AFC = 90 ( vì AD ⊥ BC và CF ⊥ AK ) nên A ∆ DC, A ∆ FC lần
lượt vuông tại D,F . 0,5
Suy ra A,D,F,C cùng thuộc đường tròn đường kính AC 0,5
Nên tứ giác ADFC nội tiếp. b) Chứng minh  = 
BAD CAK . Gọi M và N lần lượt là trung điểm của 1,0
BC và AC. Chứng minh MN ⊥ DF và M là tâm đường tròn ngoại tiếp tam giác DEF
+ Chứng minh rằng  =  BAD CAK Ta có :  =  1 A 1
B ( vì cùng phụ với góc  ABC ) 0,25  =  A2 1
B ( hai góc nội tiếp cùng chắn cung CK) ⇒  =  1 A A2 hay  =  BAD CAK Ta có:   ABK = ACK = 0
90 ( góc nội tiếp chắn nửa đườn tròn)
suy ra KB ⊥ AB và KC ⊥ AC Xét A
∆ BC có M là trung điểm của BC, N là trung điểm của AC
⇒ MN là đường trung bình của A ∆ BC
⇒ MN/ AB mà KB ⊥ AB nên MN ⊥ KB (1) Lại có :  =  K 1
C1 ( hai góc nội tiếp cùng chắn cung AB)  = 
C1 AFD ( hai góc nội tiếp cùng chắn cung AD) 0,25 ⇒  = 
K1 AFD mà hai góc này nằm ở vị trí đồng vị nên DF//KB (2)
Từ (1) và (2) suy ra MN ⊥ DF
Vì N là trung điểm của AC nên N là tâm đường tròn ngoại tiếp tứ giác ADFC ⇒ND = NF
Ta có MN ⊥ DF và ND = NF
⇒ MN là đường trung trực của DF 0,25 ⇒ MD = MF(3)
Gọi P là trung điểm của AB
Chứng minh tương tự câu a: Tứ giác AEDB nội tiếp ⇒  =  1 D
BAK ( Cùng bù với góc  BDE ) Mà  = 
BAK BCK ( hai góc nội tiếp cùng chắn cung BK) ⇒  =  1 D
BCK mà hai góc này ở vị trí so le trong
⇒ DE/ KC mà KC ⊥ AC ⇒ DE ⊥ AC Xét A
∆ BC có M là trung điểm của BC, P là trung điểm của AB
⇒ MP là đường trung bình của A ∆ BC
⇒ MP/ AC mà DE ⊥ AC nên DE ⊥ MP
Vì P là trung điểm của AB nên P là tâm đường tròn ngoại tiếp tứ giác AEDB ⇒PD = PE
Ta có DE ⊥ MP và PD = PE
⇒ MP là đường trung trực của DE ⇒ MD = ME(4)
Từ (3) và (4) suy ra MD = ME = MF 0,25
⇒ M là tâm đường tròn ngoại tiếp tam giác DEF
Từ một hình vuông cạnh bằng 6, bạn An cắt bỏ các tam giác vuông cân
tạo thành hình tô đậm như hình vẽ. Sau đó bạn An gập lại thành hộp quà
có dạng hình hộp chữ nhật không có nắp. Tìm x để khối hộp có thể tích lớn nhất. 0,5 15
Ta có: AN = BM = BF = x (x> 0), MN = AB – 2.AN = 6 – 2x Xét MB ∆ F vuông tại B có 2 2
MF = BM + BF ( Định lí Pythagore) 2 2
= x + x = 2x Xét ME ∆ N vuông tại E có: 2 2
MN = EM + EN ( Định lí Pythagore) 2 2
= EM + EM = 2EM 0,25 − ⇒ MN 6 2x EM = = = 3 2 − 2x 2 2
Khối hộp có đáy là hình vuông cạnh bằng MF = 2x và chiều cao bằng
EM = 3 2 − 2x nên thể tích của khối hộp là 2
V = ( 2x) .(3 2 − 2x) 2
= 2x .(3 2 − 2x) 2 3 = 6 2x − 2 2x 2 3 = 2 2(3x − x ) 3 2 = 2
− 2(x − 3x + 4 − 4) 2 = 2
− 2 (x +1)(x − 2) − 4   2
= 8 2 − 2 2(x +1)(x − 2) ≤ 8 2 ( vì 2
(x +1)(x − 2) ≥ 0 với mọi x> 0)
Dấu “=” xảy ra khi: x – 2 = 0 hay x = 2( tm)
Vậy thể tích của hộp lớn nhất bằng 8 2 khi x = 2 0,25
Xem thêm: ĐỀ THI TUYỂN SINH LỚP 10 MÔN TOÁN
https://thcs.toanmath.com/de-thi-tuyen-sinh-lop-10-mon-toan
Document Outline

• TOÁN 9 lần 2
• TS 10