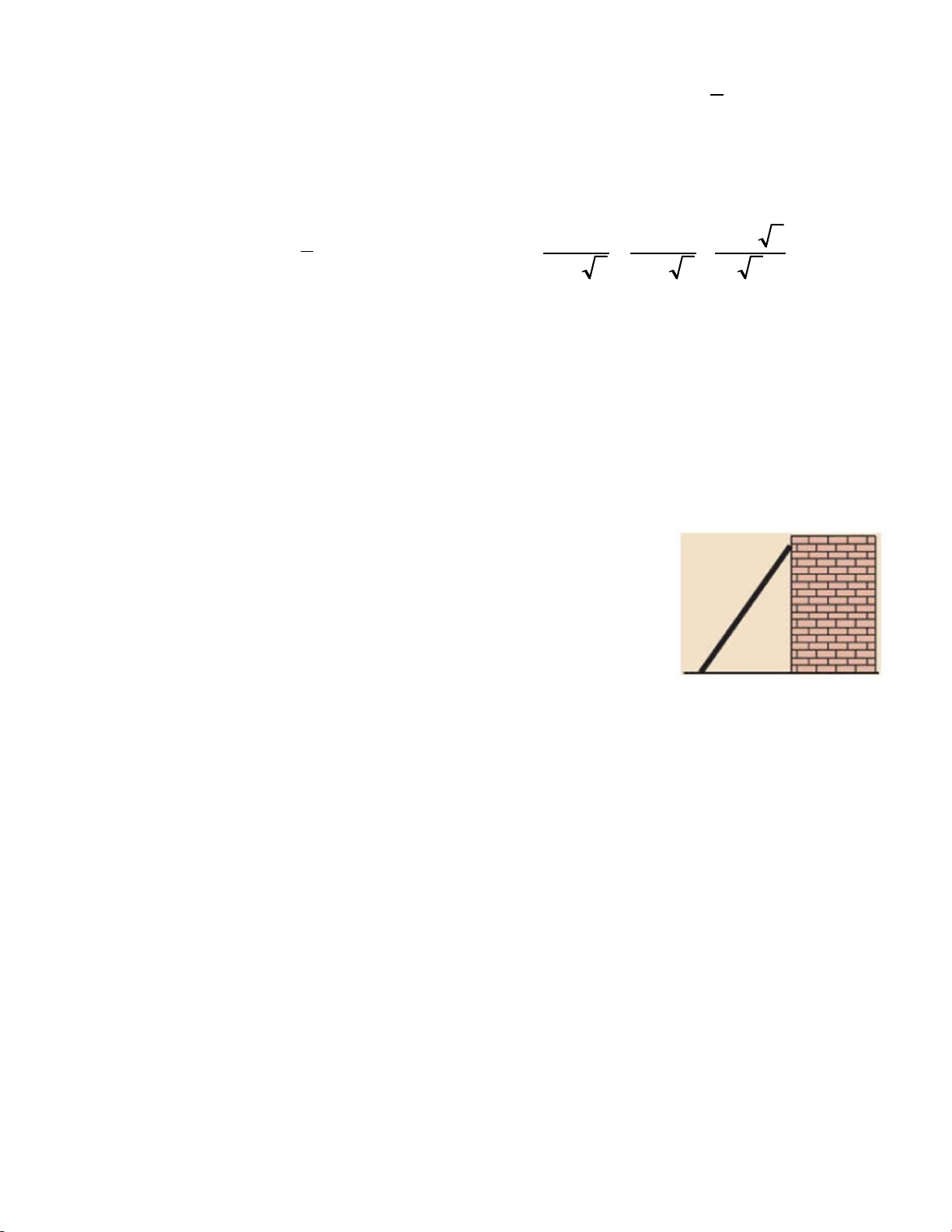
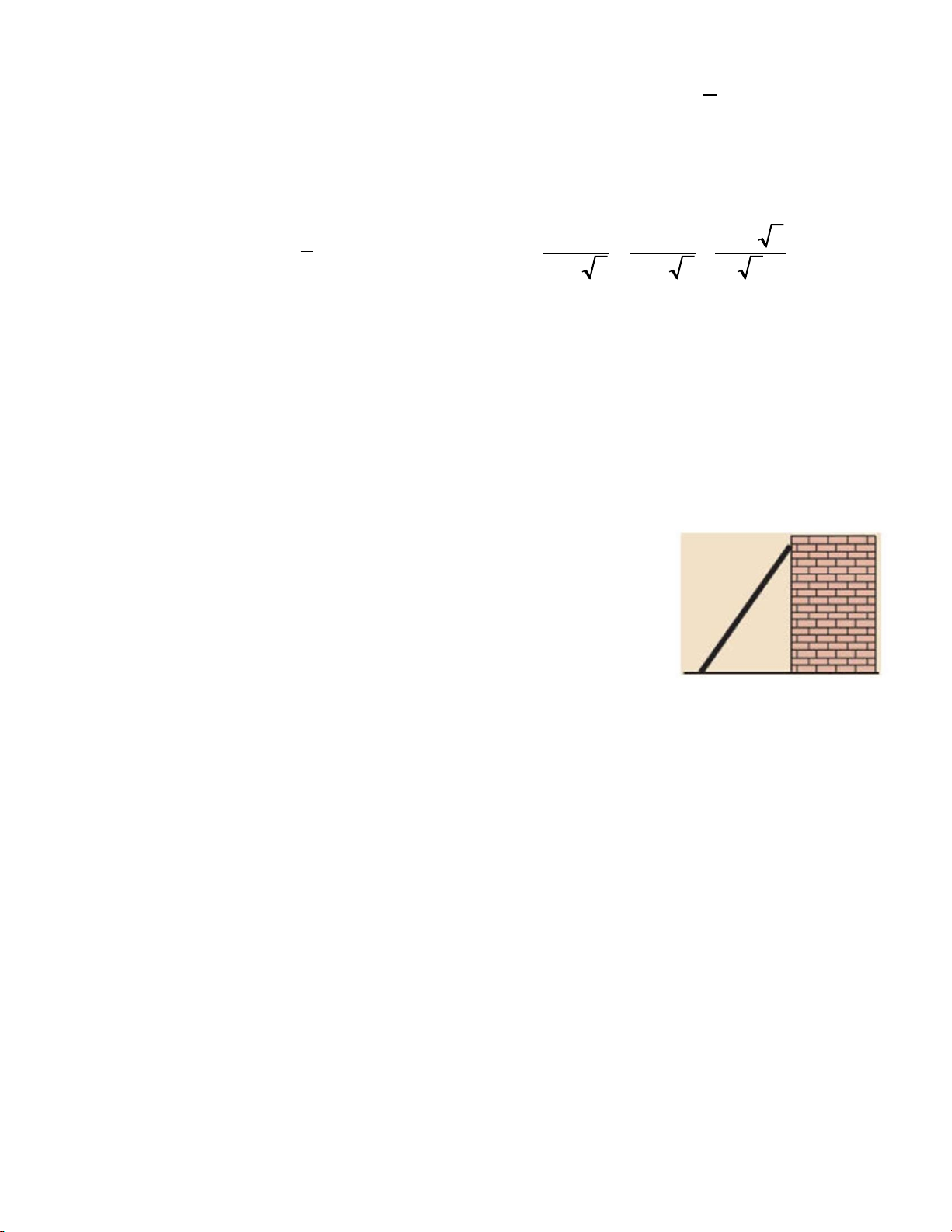

Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT HUYỆN CẨM XUYÊN NĂM HỌC 2025 - 2026 MÔN THI: TOÁN ĐỀ 01
Thời gian làm bài: 90 phút
(Đề thi có 02 trang, gồm 18 câu)
( không kể thời gian phát đề)
I- PHẦN GHI KẾT QUẢ (3 điểm) (Thí sinh chỉ cần ghi kết quả vào tờ giấy thi)
Câu 1. Rút gọn biểu thức A 20 3 45 .
Câu 2. Tìm nghiệm của phương trình 2
x 2x 4 0 .
Câu 3. Tìm giá trị của m, biết đồ thị hàm số y 3x 2m cắt trục tung tại điểm có tung độ bằng 5.
x 2y 1 0
Câu 4. Tìm nghiệm của hệ phương trình . 3
x 2y 5 0
Câu 5. Cho tam giác ABC vuông tại .
A Biết độ dài cạnh BC = 8cm, 0 ABC 60 . Tính độ dài cạnh AB.
Câu 6. Biết hàm số y a 2 2
1 x có đồ thị đi qua điểm M 1 ; 3
. Tìm a .
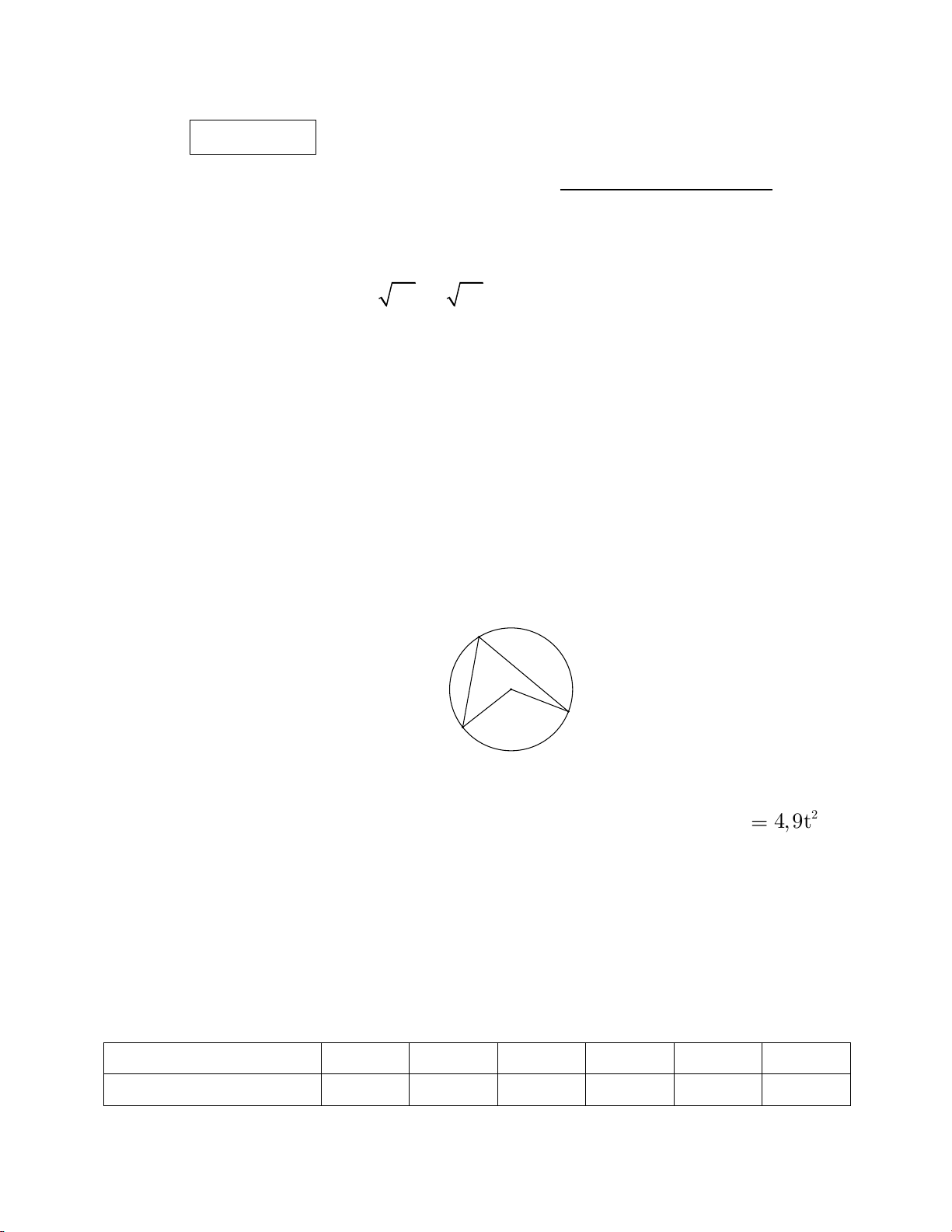
Câu 7. Một vật rơi tự do từ độ cao 490m so với mặt đất. Quãng đường chuyển động
s m của vật phụ thuộc vào thời gian t (giây) được cho bởi công thức 2 s 4,9t . Hỏi
sau bao lâu thì vật này tiếp đất?
Câu 8. Cho đường tròn tâm O như hình vẽ bên dưới, biết 0
BAC 55 . Tính số đo cung nhỏ BC. A O C B
Câu 9. Tìm tất cả các nghiệm của bất phương trình 4x + 8 0.
Câu 10. Một chiếc hộp đựng 10 tấm thẻ giống nhau được đánh số từ 1 đến 10. Rút ngẫu
nhiên một tấm thẻ trong hộp. Tính xác suất để tấm thẻ lấy ra là số chia hết cho 3.
Câu 11. Bảng sau thống kê số lượt nháy chuột vào quảng cáo ở một trang web vào tháng 12/2024. Số lượt nháy chuột 0 1 2 3 4 5 Số người dùng 25 56 4 9 5 11
Tính tần số tương đối cho số lượt nháy chuột cao nhất.
Câu 12: Cho tam giác ABC vuông tại A có BC 10cm và 4 sin B . Tính sin C . 5
II- PHẦN TỰ LUẬN (7 điểm) (Thí sinh trình bày lời giải vào tờ giấy thi) Câu 13 (1 điểm). 1 2 2 2x x
Cho x 0, x
. Rút gọn biểu thức P . 4
1 2 x 1 2 x x
Câu 14 (1 điểm). Cho phương trình bậc hai 2
x m 2
2 1 x m –1 0 (tham số m ).
Tìm tất cả giá trị của m để phương trình đã cho có hai nghiệm phân biệt x , x thỏa mãn: 1 2 2 2
x x – x x 5. 1 2 1 2
Câu 15 (1 điểm). Một người dự định đi từ A đến B trong một thời gian nhất định. Thực
tế người đó đi với vận tốc lớn hơn vận tốc dự định là 10km/h nên đến B sớm hơn dự
định là 1 giờ. Tính vận tốc dự định của người đó biết quãng đường AB dài 120 km. Câu 16 (1 điểm)
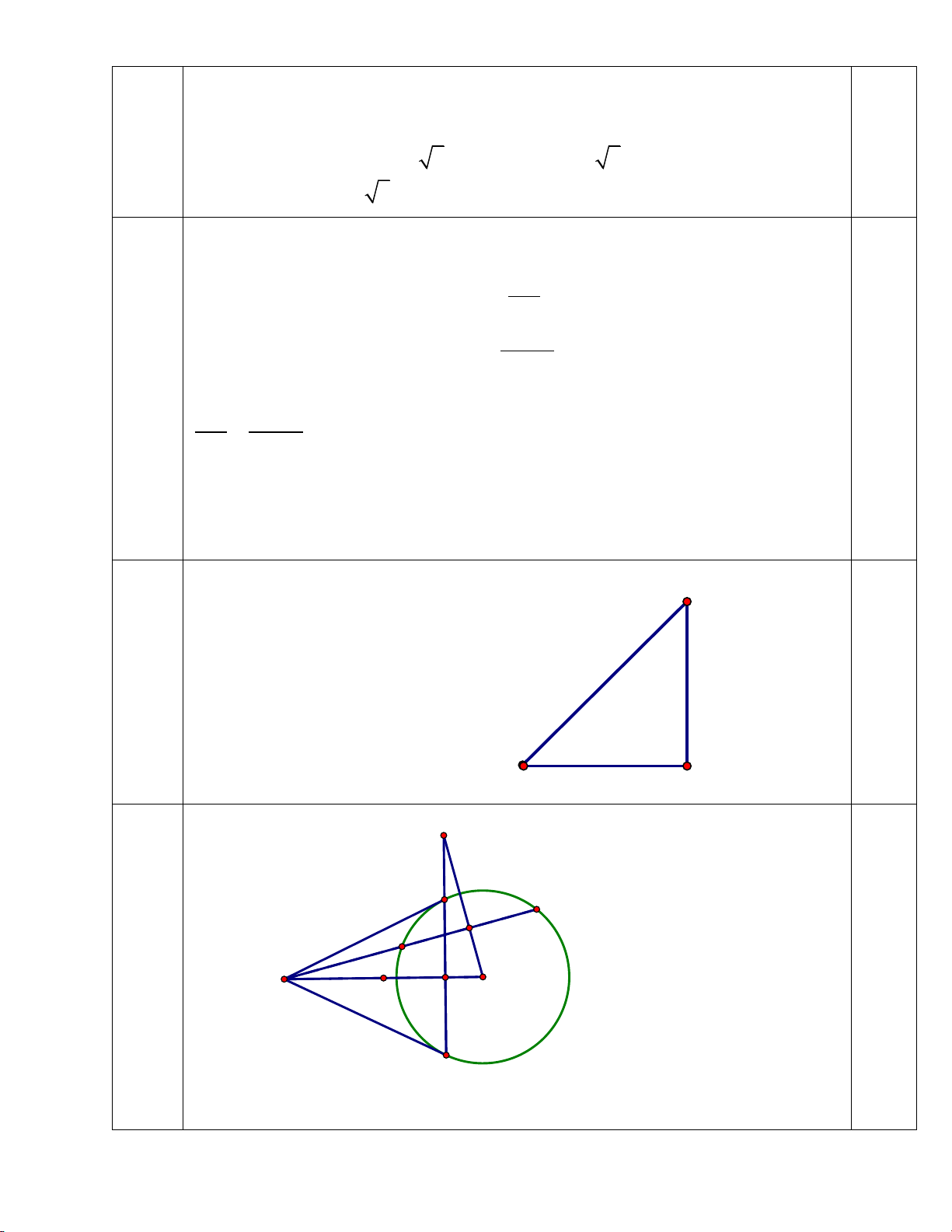
Trường bạn An có một chiếc thang dài 6m. Cần đặt chân thang
cách chân tường một khoảng cách bằng bao nhiêu để nó tạo
với mặt đất một góc 650 (kết quả làm tròn đến chữ số thập phân thứ hai).
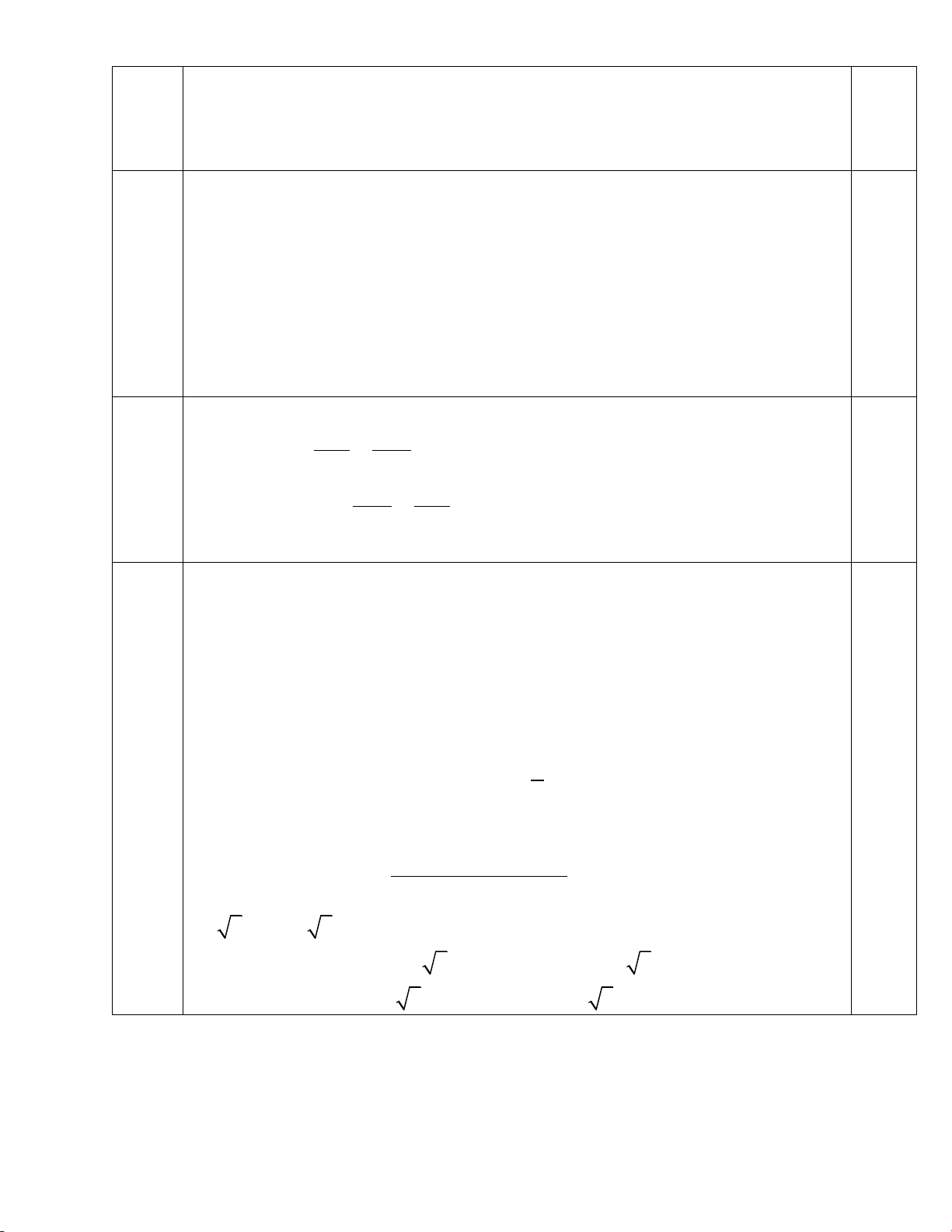
Câu 17 (2 điểm). Cho đường tròn (O;R) và điểm M nằm ngoài
đường tròn. Từ M vẽ các tiếp tuyến MA; MB với đường tròn (A, B là các tiếp điểm).
Đường thẳng d đi qua M cắt đường tròn (O;R) tại hai điểm E; F (E nằm giữa M và F; d
không đi qua O). Gọi I là trung điểm của FE.
a) Chứng minh rằng AB MO
b) Gọi H là giao điểm của hai đường thẳng AB và MO, K là giao điểm của hai
đường thẳng AB và OI. Chứng minh rằng tứ giác MHIK nội tiếp và 2
OI.OK R .
Câu 18 (1 điểm). Cho a ; b; c là các số thực thỏa mãn 2 2 2
a b c 3. Tìm GTNN ; GTLN của biểu thức 3 3 3
P a b c – 3abc . --------Hết--------
Thí sinh không được sử dụng tài liệu.
Cán bộ coi thi không giải thích gì thêm.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT HUYỆN CẨM XUYÊN NĂM HỌC 2025 - 2026 MÔN THI: TOÁN ĐỀ 02
Thời gian làm bài: 90 phút
(Đề thi có 02 trang, gồm 18 câu)
( không kể thời gian phát đề)
I- PHẦN GHI KẾT QUẢ (3 điểm) (Thí sinh chỉ cần ghi kết quả vào tờ giấy thi)
Câu 1. Tìm nghiệm của phương trình 2
x 2x 4 0 .
Câu 2. Rút gọn biểu thức A 20 3 45 .
x 2y 1 0
Câu 3. Tìm nghiệm của hệ phương trình . 3
x 2y 5 0
Câu 4. Tìm giá trị của m, biết đồ thị hàm số y 3x 2m cắt trục tung tại điểm có tung độ bằng 5.
Câu 5. Biết hàm số y a 2 2
1 x có đồ thị đi qua điểm M 1 ; 3
. Tìm a .
Câu 6. Cho tam giác ABC vuông tại .
A Biết độ dài cạnh BC = 8cm, 0 ABC 60 . Tính độ dài cạnh AB.
Câu 7. Cho đường tròn tâm O như hình vẽ bên dưới, biết 0
BAC 55 . Tính số đo cung nhỏ BC. A O C B
Câu 8. Một vật rơi tự do từ độ cao 490m so với mặt đất. Quãng đường chuyển động
s m của vật phụ thuộc vào thời gian t (giây) được cho bởi công thức 2 s 4,9t . Hỏi
sau bao lâu thì vật này tiếp đất?
Câu 9. Một chiếc hộp đựng 10 tấm thẻ giống nhau được đánh số từ 1 đến 10. Rút ngẫu
nhiên một tấm thẻ trong hộp. Tính xác suất để tấm thẻ lấy ra là số chia hết cho 3.
Câu 10. Tìm tất cả các nghiệm của bất phương trình 4x + 8 0.
Câu 11. Bảng sau thống kê số lượt nháy chuột vào quảng cáo ở một trang web vào tháng 12/2024. Số lượt nháy chuột 0 1 2 3 4 5 Số người dùng 25 56 4 9 5 11
Tính tần số tương đối cho số lượt nháy chuột cao nhất.
Câu 12. Cho tam giác ABC vuông tại A có BC 10cm và 4 sin B . Tính sin C . 5
II- PHẦN TỰ LUẬN (7 điểm) (Thí sinh trình bày lời giải vào tờ giấy thi) Câu 13 (1 điểm). 1 2 2 2x x
Cho x 0, x
. Rút gọn biểu thức P . 4
1 2 x 1 2 x x
Câu 14 (1 điểm). Cho phương trình bậc hai 2
x m 2
2 1 x m –1 0 (tham số m ).
Tìm tất cả giá trị của m để phương trình đã cho có hai nghiệm phân biệt x , x thỏa mãn: 1 2 2 2
x x – x x 5. 1 2 1 2
Câu 15 (1 điểm). Một người dự định đi từ A đến B trong một thời gian nhất định. Thực
tế người đó đi với vận tốc lớn hơn vận tốc dự định là 10km/h nên đến B sớm hơn dự
định là 1 giờ. Tính vận tốc dự định của người đó biết quãng đường AB dài 120 km. Câu 16 (1 điểm)
Trường bạn An có một chiếc thang dài 6m. Cần đặt chân thang
cách chân tường một khoảng cách bằng bao nhiêu để nó tạo
với mặt đất một góc 650 (kết quả làm tròn đến chữ số thập phân thứ hai).
Câu 17 (2 điểm). Cho đường tròn (O;R) và điểm M nằm ngoài
đường tròn. Từ M vẽ các tiếp tuyến MA; MB với đường tròn (A, B là các tiếp điểm).
Đường thẳng d đi qua M cắt đường tròn (O;R) tại hai điểm E; F (E nằm giữa M và F; d
không đi qua O). Gọi I là trung điểm của FE.
a) Chứng minh rằng AB MO
b) Gọi H là giao điểm của hai đường thẳng AB và MO, K là giao điểm của hai
đường thẳng AB và OI. Chứng minh rằng tứ giác MHIK nội tiếp và 2
OI.OK R .
Câu 18 (1 điểm). Cho a ; b; c là các số thực thỏa mãn 2 2 2
a b c 3. Tìm GTNN ; GTLN của biểu thức 3 3 3
P a b c – 3abc . --------Hết--------
Thí sinh không được sử dụng tài liệu.
Cán bộ coi thi không giải thích gì thêm. HƯỚNG DẪN CHẤM
I. PHẦN GHI KẾT QUẢ Đề số 1: Câu 1 2 3 4 5 6 Đáp án 7 5 x 1 5 5 x 1 AB = a=-1 1 m 2 4cm x 1 5 y 1 2 Câu 7 8 9 10 11 12 Đáp án 10 giây 1100 x 2 0,3 10% 3 5 Đề số 2: Câu 1 2 3 4 5 6 Đáp án x 1 5 7 5 x 1 5 a=-1 AB = 4cm 1 m 2 x 1 5 y 1 2 Câu 7 8 9 10 11 12 Đáp án 1100 10 giây 0,3 x 2 10% 3 5 II.TỰ LUẬN Câu Nội dung Điểm 13
2 1 2 x 21 2 x x 2 x 1 1điểm P 0,5 x x . 1 2 1 2 x 4 4 x 0,5
1 2 x 1 2 x .2 1 12 x 14 Ta có: 2 2
(2m 1) 4(m 1) = 4m + 5
1điểm PT có hai nghiệm phân biệt x 1; x2 khi 4m 5 0 5 m 4 0,25
Theo hệ thức Viet ta có: x1 + x2 = 2m + 1; x1.x2 = m2 – 1 0,25 Ta có: x 2 2 1 + x2 – x1x2 =5 (x1 + x2)2 – 3x1x2 = 5
Suy ra: (2m + 1)2 – 3(m2 – 1) = 5 m2 + 4m – 1 = 0 Giải pt ta được m 2 5 (t/m); m 2 5 (loại) 0,25 1 2 Vậy m = m 2 5 1 0,25 15
Gọi x(km/h) là vận tốc dự định đi từ A đến B (x >0)
1điểm Vân tốc thực tế đi từ A đến B là: x + 10 (km/h)
Thời gian dự định đi từ A đến B là: 120 (h) x
Thời gian thực tế đi từ A đến B là: 120 (h) 0,25 x 10 Vì thứ
c tế người đó đến B sớm hơn dự định 1 h nên ta có pt: 120 120 1 0,25 x x 10
120(x+10) – 120x = x(x + 10) 0,25 x2 + 10x – 1200 = 0
Giải pt ta có x1 = 30 (t/m); x2 = - 40 (loại) 0,25
Vậy vân tốc dự định đi từ A đến B là 30 km/h 16 AC = BC.cos650 0,5 1điể B m AC = 6.cos650 AC ≈2,54cm 0,5 6m 650 C A 17 K 2điểm A E I M H O B a)
Ta có MA = MB (t/c hai tiếp tuyến cắt nhau) OA = OB = R
Suy ra MO là đường trung trực của AB 0,5 Hay MO AB 0,25 b)
OFE có OE = OF = R nên OFE cân tại O mà OI là đường trung tuyến
(gt) suy ra OI là đường cao, do đó IO FE 0,25
MHK vuông tại H suy ra: H thuộc đường tròn đường kính MK.
Và MIK vuông tại I suy ra: I thuộc đường tròn đường kính MK.
Từ đó suy ra tứ giác MHKI nội tiếp đường tròn đường kính MK. 0,25 0,25
Đặt góc MOK là Ta có OH OI cos
, do đó OI.OK OH.OM (1) OK OM 0,25 Lại có OA OH cosMOA , do đó 2 2
OH.OM OA R (2) OM OA 0,25 Vậy 2
OI.OK R 17 P = a3 + b3 + c3 – 3abc
1điểm = (a + b + c)[(a2 + b2 + c2 – (ab + bc + ca) ]
=(a + b + c)(3 – ab – bc – ca)
P2 = (3 + 2x)(3- x)2 với x = ab + bc + ca Suy ra P2 = (3+ 2x)(3- x)2 2
3 2x (a b c) 0 0,5 1
3 x (a b c ) (ab bc ca)
a b2 b c2 c a2 2 2 2 0 2
Áp dụng BĐT Cauchy cho các số không âm 3+2x ;3-x ;3-x ta được 0,25 3
3 2x 3 x 3 x P2 = (3+ 2x)(3- x)2 0,25 3 = 27 (*) 3 3 P 3 3 Vậy P đạt GTNN bằng 3
3 khi a =0 ; b =0 ; c 3 và các hoán vị.
Và P đạt GTLN bằng 3 3 khi a =0 ; b =0 ; c 3 và các hoán vị.




