Đề Thi Thử Tốt Nghiệp 2025 Môn Toán Sở GD Hòa Bình Lần 1 Giải Chi Tiết
Trong một đêm thi hát, mỗi thí sinh phải tham gia hát hai bài : Một bài theo phong cách âm nhạc dân gian, một bài theo phong cách âm nhạc nhạc nhẹ. Một đội có 20 người tham gia đêm thi hát đó. Kết quả là 15 người đạt bài thi theo phong cách âm nhạc dân gian, 17 người đạt bài thi theo phong cách âm nhạc nhạc nhẹ. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi THPTQG môn Toán năm 2025 385 tài liệu
Môn: Toán 2.2 K tài liệu
Tác giả:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ TỐT NGHIỆP THPT 2025 – LẦN 1 Môn: Toán TỈNH HÒA BÌNH
Thời gian: 90 phút (Không kể thời gian phát đề)
PHẦN I. Trắc nghiệm 4 phương án lựa chọn. Câu 1:
Cấp số cộng u có u 1 và u 3 . Số hạng u của cấp số cộng là n 1 2 5 A. 11. B. 7 . C. 5 . D. 9 . Câu 2:
Tất cả các nghiệm của phương trình 2cos x 1 0 là A. x
k2 k . B. x
k k . 3 3 C. x
k2 k . D. x
k2 k . 3 3 Câu 3: Hàm số 5x F x
2025 là nguyên hàm của hàm số A. 5x f x ln 5 2025x . B. 5x f x ln 5 . x x
C. f x 5 2025x .
D. f x 5
2025x C . ln 5 ln 5 x x Câu 4:
Đồ thị hàm số y f x 2 2 3
có đường tiệm cận xiên là x 1
A. y x 3 .
B. y x 1.
C. y x 1.
D. y x 1. Câu 5:
Cho hàm số y f x xác định trên có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 2 ;0 . B. 3; . C. ; 2 . D. 3 ; 1 . Câu 6:
Nghiệm của phương trình log x 3 là: 2 3 A. x . B. x 8. C. x 6 . D. x 5. 2 Câu 7:
Cho cấp số nhân có u có u 2 và u 8
. Công bội q của cấp số nhân là n 1 2 1 A. q 10 . B. q . C. q 4 .
D. q 10 . 4 Câu 8:
Cho hình lập phương ABC . D A B C D .
Góc giữa hai vec tơ AB và DC ' bằng: A. 60. B. 90 . C. 45. D. 120 . Trang 1 Câu 9:
Trong không gian với hệ trục tọa độ Oxyz , cho mặt cầu (S ) có phương trình 2 2 2
(x 1) y (z 2) 9 . Điểm nào sau đây là tâm của mặt cầu (S ) ?
A. I (1;1; 2) . B. I (1; 0; 2 ) . C. I ( 1 ;1;2) .
D. I (1; 0; 2) . 2 Câu 10: Biết 3
F(x) x là một nguyên hàm của hàm số f (x) trên
. Giá trị của 2 f (x)dx bằng 1 15 23 A. 9 . B. . C. 7 . D. . 4 4
Câu 11: Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị ?
A. sin 2 2sin .
B. sin 2 sin.cos . C. 2 cos 2 2 cos 1 . D. 2 2
cos 2 sin cos .
Câu 12: Mỗi ngày bác Hoa đều đi bộ để rèn luyện sức khỏe. Quãng đường đi bộ mỗi ngày (đơn vị: km)
của bác Hoa trong 20 ngày được thống kê lại ở bảng sau:
Quãng đường (km) [2,5;3,0) [3,0;3,5) [3,5;4,0) [4,0;4,5) [4,5;5,0) Số ngày 3 6 5 4 2 3 9 14 18 20
Khoảng tứ phân vị của mẫu số liệu ghép nhóm (kết quả làm tròn đến hàng phần trăm ) là A. 0,9. B. 0,96. C. 0,97. D. 0,8.
PHẦN II. Trắc nghiệm chọn đúng sai. Câu 1:
Cây cà chua khi trồng có chiều cao 5cm. Tốc độ tăng trưởng chiều cao của cây cà chua khi
trồng được cho bởi hàm số 3 2 v(t) 0
,1t t , trong đó t tính theo tuần, v(t) tính bằng
centimét/tuần. Gọi h(t) (tính bằng centimét) là chiều cao của cây cà chua ở tuần thứ t t 0 1 1 a) 4 3 h(t) t t . 40 3
b) Giai đoạn tăng trưởng chiều cao của cây cà chua kéo dài 10 tuần.
c) Chiều cao của cây cà chua ở tuần thứ 6 lớn hơn 40cm.
d) Chiều cao tối đa của cây cà chua không vượt quá 90 cm.
f (x) log (x 2)
g(x) log (5x 6) Câu 2: Cho hai hàm số 2 và 4 .
a) Tập xác định của hàm số y f (x) là (2; ) .
b) Hàm số y g(x) đồng biến trên .
c) Phương trình f (x) 5 có nghiệm x 30
d) Phương trình f (x) g(x) có một nghiệm duy nhất. Câu 3:
Một doanh nghiệp có 45% nhân viên là nữ. Trong các nhân viên nữ có 30% nhân viên có
bằng đại học, tỉ lệ này trong các nhân viên nam là 25% .
a) Tỉ lệ nhân viên nam trong tổng số nhân viên là 55%.
b) Tỉ lệ nhân viên nữ không có bằng đại học trong tổng số nhân viên là 13, 5% .
c) Chọn ngẫu nhiên hai nhân viên trong doanh nghiệp, xác suất để chọn được hai người khác giới lớn hơn 24, 5% .
d) Chọn ngẫu nhiên hai nhân viên trong doanh nghiệp, xác suất để trong hai người được có
đúng một người có bằng đại học không vượt quá 19,8% . Trang 2 x 1 y 3 z 2 Câu 4:
Trong không gian với với hệ tọa độ Oxyz , cho hai đường thẳng d : 1 1 1 2 và x 1 y z 1 d : 2 2 1 1 .
a) Đường thẳng d đi qua điểm A2;4;4 . 1
b) Đường thẳng vuông góc với cả d và d có một véctơ chỉ phương là u 1;1; 1 . 1 2
c) Đường thẳng d và đường thẳng d chéo nhau. 1 2
d) Khoảng cách giữa hai đường thẳng d và d là 3 2 . 1 2
PHẦN III. Trắc nghiệm trả lời ngắn. Câu 1:
Một hộp bánh có dạng hình hôp chữ nhật ABC . D A B C D
có AB 10c , m AD 20cm ,
AA 30cm . Số đo góc phẳng nhị diện A , B , D
A bằng bao nhiêu độ?
(Kết quả làm tròn đến hàng phần chục) Câu 2:
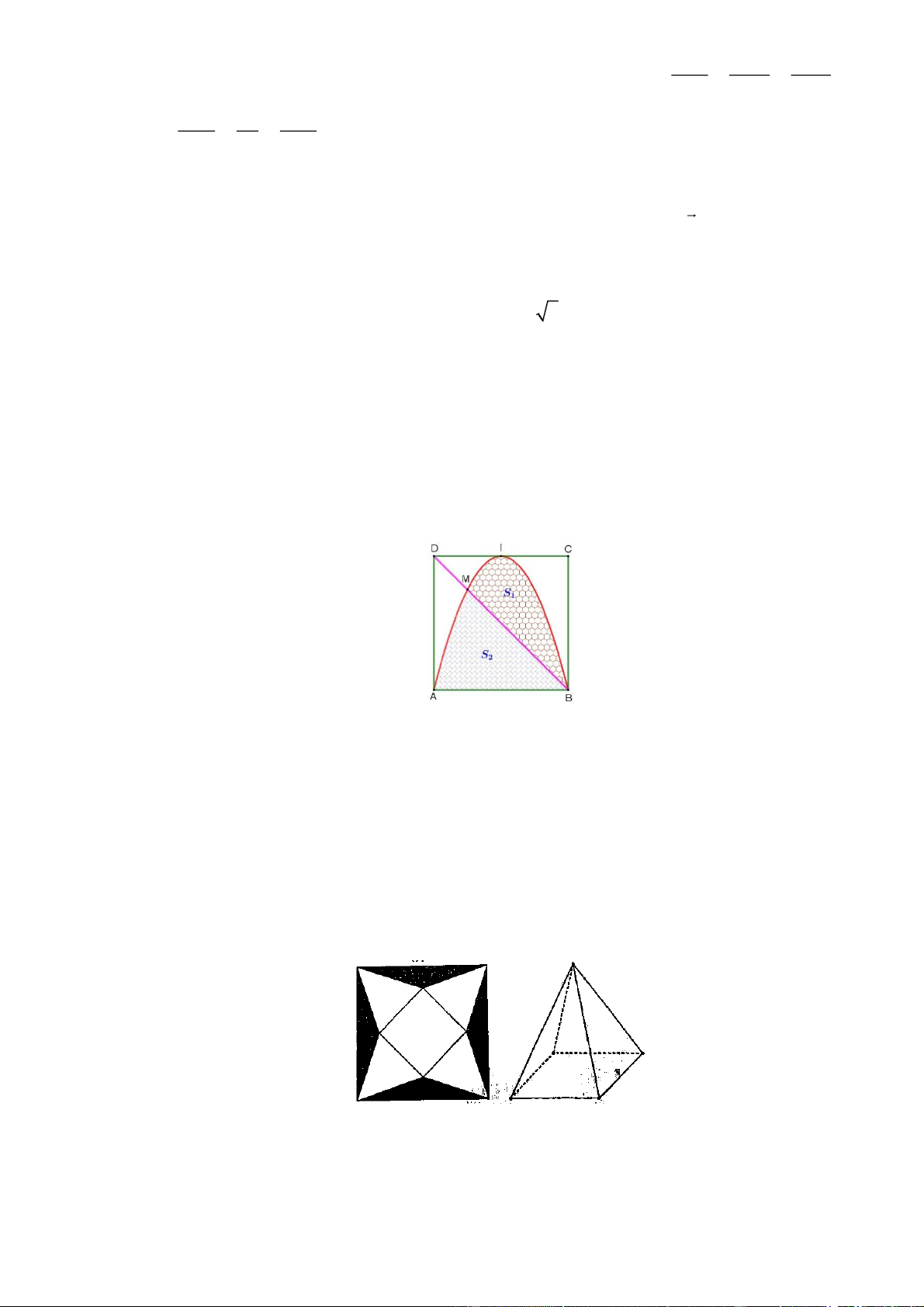
Một biển quảng cáo có dạng hình vuông ABCD cạnh bằng 4 m và I là trung điểm của đoạn
thẳng CD . Trên tấm biển đó có đường parabol đỉnh I đi qua ,
A B và cắt đường chéo BD tại
M (tham khảo hình vẽ).
Chi phí sơn phần tô hình tổ ong (có diện tích S ) là 200000 đồng 2 /m , chi phí sơn phần tô 1
đậm (có diện tích S ) là 150000 đồng 2
/m và phần còn lại là 120000 đồng 2 /m . Số tiền cần 2
chi trả để sơn tấm biển quảng cáo là bao nhiêu nghìn đồng? Câu 3:
Từ một tấm tôn hình vuông có cạnh 2m , người ta cắt bỏ đi bốn tam giác cân bằng nhau có
cạnh đáy là cạnh của hình vuông rồi ghép lại thành một hình chóp tứ giác đều (tham khảo hình
vê). Giả sử các mối hàn ghép là không đáng kể thì khối chóp được tạo thành có thể tích lớn nhất là bao nhiêu 3 m .
(Kết quà làm tròn đến đến hàng phần trăm) Câu 4:
Trong một đêm thi hát, mỗi thí sinh phải tham gia hát hai bài : Một bài theo phong cách âm
nhạc dân gian, một bài theo phong cách âm nhạc nhạc nhẹ. Một đội có 20 người tham gia đêm
thi hát đó. Kết quả là 15 người đạt bài thi theo phong cách âm nhạc dân gian, 17 người đạt bài
thi theo phong cách âm nhạc nhạc nhẹ; 2 người không đạt cả hai bài. Chọn ngẫu nhiên một
người trong đội. Xác suất để người đó đạt cả hai bài thi. Trang 3 Câu 5:
Anh A bơm nước vào một chiếc thùng nhựa đựng nước có dạng hình chóp cụt với hai đáy là
hai hình chữ nhật, các cạnh bên bằng nhau và có kích thước như hình bên dưới, với tốc độ bơm
nước vào thùng là 20 lít/phút. Vận tốc nước dâng lên ở cạnh bên của thùng nhựa (đơn vị
cm/phút) khi chiều cao mực nước là 25 cm bằng bao nhiêu? (Kết quả làm tròn đến hàng phần trăm) 124cm 88cm A D B C 60cm A' D' 66cm . B' C' x 1 y z 2 Câu 6:
Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d : và mặt phẳng 1 2 1
P:3x y z 25 0. Một đường thẳng d cắt trục Oz tại điểm M , cắt đường thẳng d
tại điểm N và d song song với P . Độ dài nhỏ nhất của đoạn MN bằng bao nhiêu? (Kết
quả làm tròn đến hàng phần trăm). HẾT BẢNG ĐÁP ÁN
PHẦN I. Trắc nghiệm 4 phương án lựa chọn. 1.D 2.A 3.B 4.B 5.A 6.B 7.C 8.C 9.B 10.A 11.C 12.B
PHẦN II. Trắc nghiệm chọn đúng sai. Câu 1 2 3 4 SĐĐĐ ĐSĐS ĐSĐS SĐĐS
PHẦN III. Trắc nghiệm trả lời ngắn. Câu 1 2 3 4 5 6 Trả lời 73,4 2465 0,27 0,7 2,64 2,71 HƯỚNG DẪN GIẢI
PHẦN I. Trắc nghiệm 4 phương án lựa chọn. Câu 1:
Cấp số cộng u có u 1 và u 3 . Số hạng u của cấp số cộng là n 1 2 5 A. 11. B. 7 . C. 5 . D. 9 . Lời giải Chọn D.
Ta có d u u 3 1 2 . 2 1
Vậy u u 4d 1 4.2 9 . 5 1 Câu 2:
Tất cả các nghiệm của phương trình 2cos x 1 0 là A. x
k2 k . B. x
k k . 3 3 C. x
k2 k . D. x k2 k . 3 3 Lời giải Chọn A. Trang 4 1
Ta có 2 cos x 1 0 cos x cos
x k2 k . 2 3 3 Câu 3: Hàm số 5x F x
2025 là nguyên hàm của hàm số A. 5x f x ln 5 2025x . B. 5x f x ln 5 . x x
C. f x 5 2025x .
D. f x 5
2025x C . ln 5 ln 5 Lời giải Chọn B. Hàm số 5x F x
2025 là nguyên hàm của hàm số f x thì 5x f x F x ln 5 . x x Câu 4:
Đồ thị hàm số y f x 2 2 3
có đường tiệm cận xiên là x 1
A. y x 3 .
B. y x 1.
C. y x 1.
D. y x 1. Lời giải Chọn B. x x
Ta có y f x 2 2 3 4 x 1 . x 1 x 1 y x 4 lim 1 lim 0
nên đường thẳng y x 1 là tiệm cận xiên của đồ thị hàm số đã x
x x 1 cho. Câu 5:
Cho hàm số y f x xác định trên có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 2 ;0 . B. 3; . C. ; 2 . D. 3 ; 1 . Lời giải Chọn A.
Dựa vào bảng biến thiên. Câu 6:
Nghiệm của phương trình log x 3 là: 2 3 A. x . B. x 8. C. x 6 . D. x 5. 2 Lời giải Chọn B. Ta có: 3
x 2 8 . Suy ra x 1 . Câu 7:
Cho cấp số nhân có u có u 2 và u 8
. Công bội q của cấp số nhân là n 1 2 1 A. q 10 . B. q . C. q 4 .
D. q 10 . 4 Lời giải Chọn C. u 6 Ta có 2 q 3 . u 2 1 Trang 5 Câu 8:
Cho hình lập phương ABC . D A B C D .
Góc giữa hai vec tơ AB và DC ' bằng: A. 60. B. 90 . C. 45. D. 120 . Lời giải Chọn C.
Do AB // DC Vậy, A ,
B DC ' DC, DC ' CDC ' 45 . . Câu 9:
Trong không gian với hệ trục tọa độ Oxyz , cho mặt cầu (S) có phương trình 2 2 2
(x 1) y (z 2) 9 . Điểm nào sau đây là tâm của mặt cầu (S ) ?
A. I (1;1; 2) . B. I (1; 0; 2 ) . C. I ( 1 ;1;2) .
D. I (1; 0; 2) . Lời giải: Chọn B.
Mặt cầu (S) có phương trình 2 2 2
(x 1) y (z 2) 9 . Suy ra I (1; 0; 2 ) . 2 Câu 10: Biết 3
F(x) x là một nguyên hàm của hàm số f (x) trên
. Giá trị của 2 f (x)dx bằng 1 15 23 A. 9 . B. . C. 7 . D. . 4 4 Lời giải: Chọn A. 2 2 2 2
Ta có: 2 f (x)dx 2dx f (x)dx 3
2x x 12 3 9 . 1 1 1 1
Câu 11: Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị ?
A. sin 2 2sin .
B. sin 2 sin.cos . C. 2 cos 2 2 cos 1 . D. 2 2
cos 2 sin cos . Lời giải: Chọn C. Ta có: 2 2 2 2
cos 2 2 cos 1 1 2sin cos sin .
Câu 12: Mỗi ngày bác Hoa đều đi bộ để rèn luyện sức khỏe. Quãng đường đi bộ mỗi ngày (đơn vị: km)
của bác Hoa trong 20 ngày được thống kê lại ở bảng sau:
Quãng đường (km) [2,5;3,0) [3,0;3,5) [3,5;4,0) [4,0;4,5) [4,5;5,0) Số ngày 3 6 5 4 2 3 9 14 18 20
Khoảng tứ phân vị của mẫu số liệu ghép nhóm (kết quả làm tròn đến hàng phần trăm ) là A. 0,9. B. 0,96. C. 0,97. D. 0,8. Trang 6 Lời giải: Chọn B.
Số phần tử của mẫu là: n 20 n 20 n Ta có:
5 mà 3 5 9 nên nhóm 2 là nhóm có tần số tích lũy lớn hơn hoặc bằng . 4 4 4
Xét nhóm 2: [3,0;3,5) có s 3;cf 3; h 0,5; n 6 1 2 n cf 1 5 3 19 Suy ra 4 Q s .h 3 .0,5 1 n 6 6 2 3n 3n Ta có:
15 mà 14 15 18nên nhóm 4 là nhóm có tần số tích lũy lớn hơn hoặc bằng . 4 4
Xét nhóm 4: [4,0;4,5) có t 4; n 4;l 0,5;cf 14 4 3 3n cf 3 15 14 33 Suy ra 4 Q t .l 4 .0,5 3 n 4 8 4
Vậy khoảng tứ phân vị là: Q Q 0,96 . Q 3 1
PHẦN II. Trắc nghiệm chọn đúng sai. Câu 1:
Cây cà chua khi trồng có chiều cao 5cm. Tốc độ tăng trưởng chiều cao của cây cà chua khi
trồng được cho bởi hàm số 3 2 v(t) 0
,1t t , trong đó t tính theo tuần, v(t) tính bằng
centimét/tuần. Gọi h(t) (tính bằng centimét) là chiều cao của cây cà chua ở tuần thứ t t 0 1 1 a) 4 3 h(t) t t . 40 3
b) Giai đoạn tăng trưởng chiều cao của cây cà chua kéo dài 10 tuần.
c) Chiều cao của cây cà chua ở tuần thứ 6 lớn hơn 40cm.
d) Chiều cao tối đa của cây cà chua không vượt quá 90 cm. Lời giải a) Sai. 1 1 3 2 4 3 v(t) 0
,1t t h(t)
t t C; h(0) 5 C 5 . 40 3 1 1 Vậy 4 3 h(t) t t 5 40 3 b) Đúng. 1 1 4 3 3 2 h(t)
t t 5 h '(t) 0 ,1t t 40 3 Trang 7
h '(t) 0 0 t 10 .Do đó giai đoạn tăng trưởng chiều cao của cây cà chua kéo dài 10 tuần. c) Đúng. 1 1 4 3 h(6)
6 6 5 44, 6cm 40 3 d) Đúng. t 0 3 2 h '(t) 0
,1t t 0 t 10 Bảng biến thiên 265
Từ bảng biến thiên suy ra chiều cao tối đa của cây cà chua là 88,3 90 . 3
f (x) log (x 2)
g(x) log (5x 6) Câu 2: Cho hai hàm số 2 và 4 .
a) Tập xác định của hàm số y f (x) là (2; ) .
b) Hàm số y g(x) đồng biến trên .
c) Phương trình f (x) 5 có nghiệm x 30
d) Phương trình f (x) g(x) có một nghiệm duy nhất. Lời giải
Tập xác định của hàm số f (x) log (x 2) là x 2 0 x 2 2 6
Tập xác định của hàm số g(x) log (5x 6) là 5x 6 0 x 4 5 6
Hàm số g (x) đồng biến trên ; 5 Ta có 5
log (x 2) 5 x 2 2 x 30 2 x 1
Ta có f (x) g(x) log (x 2) log (5x 6) x 22 (5x 6) 2 4 x 2 x 2 0
Ta nhận x 2 là nghiệm phương trình vì thỏa 5 x 6 0 Chọn đáp án a) b) c) d) Trang 8 Đúng Sai Đúng Đúng Câu 3:
Một doanh nghiệp có 45% nhân viên là nữ. Trong các nhân viên nữ có 30% nhân viên có
bằng đại học, tỉ lệ này trong các nhân viên nam là 25% .
a) Tỉ lệ nhân viên nam trong tổng số nhân viên là 55%.
b) Tỉ lệ nhân viên nữ không có bằng đại học trong tổng số nhân viên là 13, 5% .
c) Chọn ngẫu nhiên hai nhân viên trong doanh nghiệp, xác suất để chọn được hai người khác giới lớn hơn 24, 5% .
d) Chọn ngẫu nhiên hai nhân viên trong doanh nghiệp, xác suất để trong hai người được có
đúng một người có bằng đại học không vượt quá 19,8% . Lời giải
a) Đúng. b) Sai. c) Đúng. d) Sai. a) Đúng.
Gọi A là biến cố “Nhân viên được chọn là nữ”.
B là biến cố “Nhân viên được chọn có bằng đại học”.
Theo giả thiết, ta có P A 45% 0, 45.
Khi đó, tỉ lệ nhân viên nam trong tổng số nhân viên là 100% 45% 55% hay P A 0,55. b) Sai.
Vì trong các nhân viên nữ có 30% nhân viên có bằng đại học nên P B A 30% 0,3 .
Tỉ lệ này trong các nhân viên nam là 25% , tức là PB A 25% 0,25 . P AB
Mặt khác P B A . A
P AB P B A P A 0,135 13,5% P
Mà AB là biến cố “Nhân viên nữ có bằng đại học”’ nên Tỉ lệ nhân viên nữ không có bằng đại
học trong tổng số nhân viên là 45% 13,5% 31,5% . c) Đúng. Ta có
Xác suất chọn được người thứ nhất là nữ và người thứ hai là nam là 0, 45 0, 55 0, 2475 .
Xác suất chọn được người thứ nhất là nam và người thứ hai là nữ là 0, 55 0, 45 0, 2475 .
Xác suất để chọn được hai người khác giới là 0, 2475 0, 2475 0, 495 .
Hay tỉ lệ để chọn được hai người khác giới là 49,5% 24,5% . d) Sai.
Để trong hai người được có đúng một người có bằng đại học, ta xét các trường hợp sau:
Trường hợp 1: Người thứ nhất có bằng đại học, người thứ hai không có bằng đại học.
o Xác suất người thứ nhất có bằng đại học là 0,135 (nữ) + 0,1375 (nam) = 0, 2725 .
o Xác suất người thứ hai không có bằng đại học là
0, 315 (nữ) + 0,55 0,1375 (nam) = 0,7275 .
o Xác suất cho trường hợp này là 0, 2725 0, 7275 0,1982 .
Trường hợp 2: Người thứ nhất không có bằng đại học, người thứ hai có bằng đại học.
o Xác suất người thứ nhất không có bằng đại học là 0, 7275 .
o Xác suất người thứ hai có bằng đại học là 0, 2725 .
o Xác suất cho trường hợp này là 0, 7275 0, 2725 0,1982 .
Xác suất để trong hai người được chọn có đúng một người có bằng đại học là Trang 9
0,1982 0,1982 0, 3964 .
Hay tỉ lệ hai người được có đúng một người có bằng đại học là 39, 64% 19,8% . x 1 y 3 z 2 Câu 4:
Trong không gian với với hệ tọa độ Oxyz , cho hai đường thẳng d : 1 1 1 2 và x 1 y z 1 d : 2 2 1 1 .
a) Đường thẳng d đi qua điểm A2;4;4 . 1
b) Đường thẳng vuông góc với cả d và d có một véctơ chỉ phương là u 1;1; 1 . 1 2
c) Đường thẳng d và đường thẳng d chéo nhau. 1 2
d) Khoảng cách giữa hai đường thẳng d và d là 3 2 . 1 2 Lời giải x 1 y 3 z 2 d : u 1;1; 2 1
và đi qua M 1;3;2 1 1 2
có véctơ chỉ phương 1 x 1 y z 1 d : u 2;1;1 2 và đi qua N 1;0; 1 2 1 1
có véctơ chỉ phương 2 2 1 4 3 4 2 a) Vì
d không đi qua điểm A2;4;4 . 1 1 2 nên đường thẳng 1
Vậy câu a) chọn sai.
b) Gọi là đường thẳng vuông góc với cả d và d và v là véctơ chỉ phương của . 1 2 v u Khi đó ta có 1 . Chọn v u ,u 3 ; 3; 3 u 1;1;1 1 2 hay v u 2
Vậy câu b) chọn đúng.
c) Ta có u ,u 3
; 3; 3 MN 0;3;3 1 2 ; Suy ra MN. u ,u 0. 3 3 . 3 3 . 3 1 2
18 0
Vậy đường thẳng d và đường thẳng d chéo nhau. 1 2
Vậy câu c) chọn đúng.
d) Gọi P là mặt phẳng chứa đường thẳng d và song song với d . 1 2
Suy ra P đi qua M 1;3;2 và có VTPT v u ,u 3 ; 3; 3 1 2 .
PT mặt phẳng P:1.x 1 1. y
3 1. z 2 0 x y z 6 0 . Trang 10 1 0 1 6
Khi đó d d ,d d d , P d N,P 2 3 1 2 2 2 2 2 1 1 1
Vậy câu d) chọn sai.
PHẦN III. Trắc nghiệm trả lời ngắn. Câu 1:
Một hộp bánh có dạng hình hôp chữ nhật ABC . D A B C D
có AB 10c , m AD 20cm ,
AA 30cm . Số đo góc phẳng nhị diện A , B , D
A bằng bao nhiêu độ?
(Kết quả làm tròn đến hàng phần chục) Lời giải Đáp án: 73,4 A' B' C' D' A B I D C BD AI
Dựng AI BD I . Khi đó:
BD AIA BD A I . BD AA
Vậy A , BD, A AI, A I AIA . A . B AD
Xét tam giác AAI vuông tại A có AA 30 , AI 4 5 . 2 2 AB AD Khi đó AA 30 3 5 tan AIA
AIA 73,4. AI 4 5 2 Câu 2:
Một biển quảng cáo có dạng hình vuông ABCD cạnh bằng 4 m và I là trung điểm của đoạn
thẳng CD . Trên tấm biển đó có đường parabol đỉnh I đi qua ,
A B và cắt đường chéo BD tại
M (tham khảo hình vẽ).
Chi phí sơn phần tô hình tổ ong (có diện tích S ) là 200000 đồng 2 /m , chi phí sơn phần tô 1
đậm (có diện tích S ) là 150000 đồng 2
/m và phần còn lại là 120000 đồng 2 /m . Số tiền cần 2
chi trả để sơn tấm biển quảng cáo là bao nhiêu nghìn đồng? Lời giải Trang 11
Đáp số: 2465 (nghìn đồng)
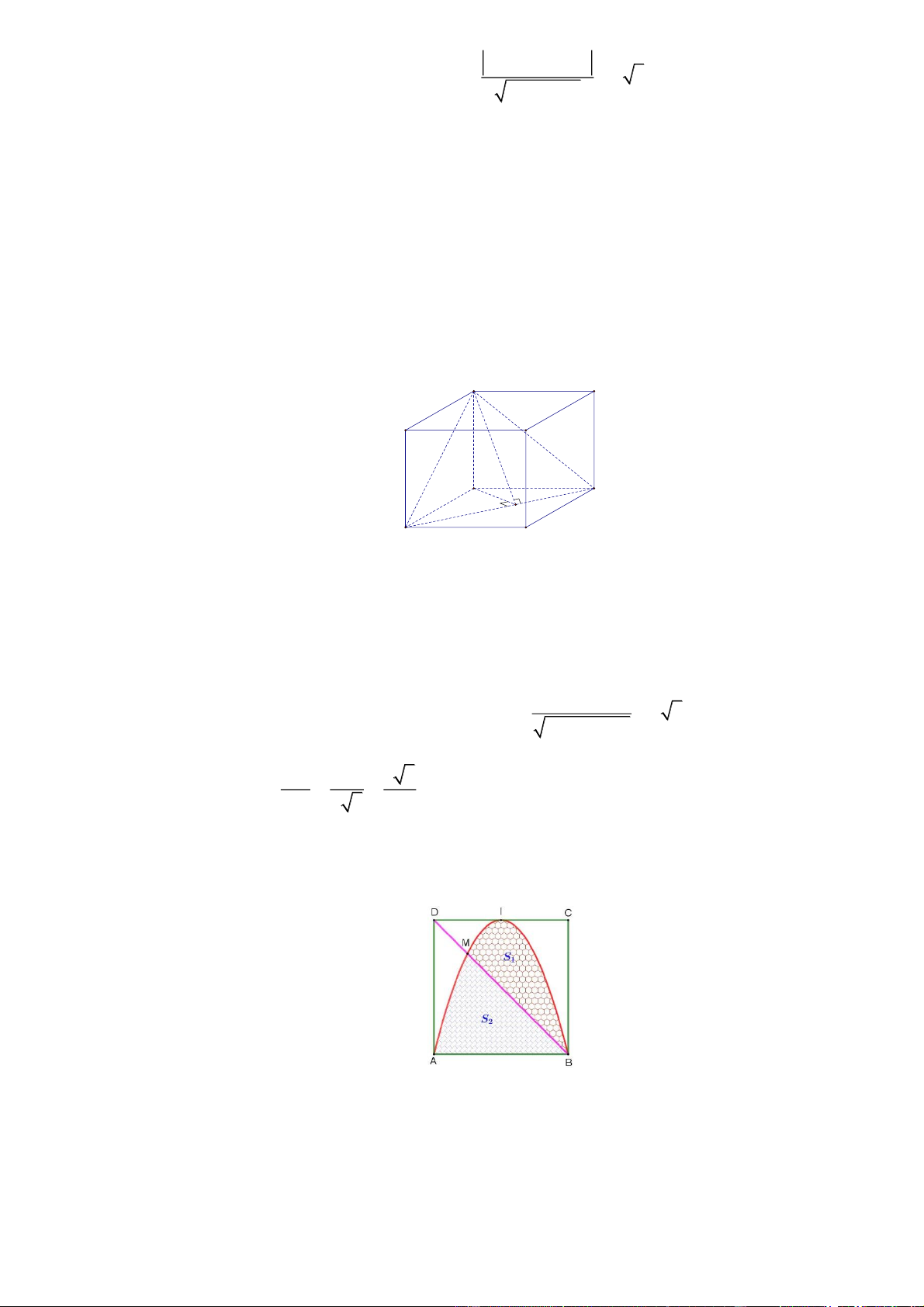
• Gắn hệ trục tọa độ Oxy như hình vẽ.
• Khi đó BD : y x 4 và Parabol P 2
: y ax bx c qua ba điểm
A O0;0, B4;0, I 2;4 nên có dạng: 2
y x 4x .
• M 1; 3 là giao điểm của BD và P . 4 4 • Suy ra 9 9 37 : S 2
x 4x x 4 dx 2 m và 2 S
x 4x dx 2 m . 2 1 2 2 6 1 0 4 16
Diện tích còn phần còn lại là 2 2 S 4
x 4x dx 2 m . 3 3 0
• Số tiền cần chi trả để sơn tấm biển quảng cáo là: 9 37 16
200 000 S 150 000 S 120 000 S 200 000 150000 120000 2465000 1 2 3 2 6 3 đồng. Câu 3:
Từ một tấm tôn hình vuông có cạnh 2m , người ta cắt bỏ đi bốn tam giác cân bằng nhau có
cạnh đáy là cạnh của hình vuông rồi ghép lại thành một hình chóp tứ giác đều (tham khảo hình
vê). Giả sử các mối hàn ghép là không đáng kể thì khối chóp được tạo thành có thể tích lớn nhất là bao nhiêu 3 m .
(Kết quà làm tròn đến đến hàng phần trăm) Lời giải Đáp số: 0,27
Gọi độ dài cạnh đáy của hình chóp là x(m) . Trang 12 Do MN IJ 2 x (0; 2) . x AC x Ta có: OK ;OA
2 SK AK 2 . 2 2 2 2 2 x x Do vậy: 2 2 SO SK OK 2 2 2x . 2 4 Khi đó thể 1 tích khối chóp là: 2 V x 2 2x . 3 1 Xét 2 f (x) x 2 2x , ta có 3 2 2 1 2
1 4x(2 2x) 2x 8x 5 2x 2 f (x)
2x 2 2x x 3 3 2 2 2x 2 2 2x 3(2 2 2x) x 0 2
f (x) 0 8x 5 2x 0 4 2 x 5 Ta có bảng biến thiên: 4 2
Ta thấy thể tích của mô hình lớn nhất khi cạnh đáy của mô hình là x . 5 4 2 32 10
Khi đó thể tích lớn nhất của khối chóp là V f 0, 27.. max 5 375 Câu 4:
Trong một đêm thi hát, mỗi thí sinh phải tham gia hát hai bài : Một bài theo phong cách âm
nhạc dân gian, một bài theo phong cách âm nhạc nhạc nhẹ. Một đội có 20 người tham gia đêm
thi hát đó. Kết quả là 15 người đạt bài thi theo phong cách âm nhạc dân gian, 17 người đạt bài
thi theo phong cách âm nhạc nhạc nhẹ; 2 người không đạt cả hai bài. Chọn ngẫu nhiên một
người trong đội. Xác suất để người đó đạt cả hai bài thi. Lời giải Trang 13 Đáp án: 0,7
Gọi A là biến cố: “Người đó đạt bài thi theo phong cách âm nhạc nhạc nhẹ”.
B là biến cố: “Người đó đạt bài thi theo phong cách âm nhạc dân gian”.
Ta có: P A 17 ; P B 15 ; P AB 2 . 20 20 20
Do đó: P A B P AB 2 18 1 1 . 20 20
P AB P A P B P A B 17 15 18 14 0,7. 20 20 20 20 Câu 5:
Anh A bơm nước vào một chiếc thùng nhựa đựng nước có dạng hình chóp cụt với hai đáy là
hai hình chữ nhật, các cạnh bên bằng nhau và có kích thước như hình bên dưới, với tốc độ bơm
nước vào thùng là 20 lít/phút. Vận tốc nước dâng lên ở cạnh bên của thùng nhựa (đơn vị
cm/phút) khi chiều cao mực nước là 25 cm bằng bao nhiêu? (Kết quả làm tròn đến hàng phần trăm) 124cm 88cm A D B C 60cm A' D' 66cm . B' C' Lời giải Đáp án: 2,64 A O D B C M N H x K P A' D' O' B' C' S
Kéo dài các cạnh A , A B B ,C C , D D
cắt nhau tại S ta có hình chóp S.ABCD có SO là đường
cao; SO A B C D ; O O 60. Đặt V V ;V V V V V V . 1 S.ABCD 2 S. A B C D ABC . D A B C D 1 2 C D
SC SO SO SO 66 Ta có SO 180 CD SC SO SO 60 SO . 60 88 AD 66 Suy ra
AD 93. Ta có A C B D 51 5 . AD 88
Đặt chiều cao mực nước O H x 25cm. Trang 14 2 51 5 2 180 2 SO SB B C C D 180 93 66 + SH SK KP PN 180 x SK KP PN 31 11 Suy ra KP 93
x ; PN 66 x . 60 30
Ta sẽ tính thể tích nước trong thùng theo x : h h h V S x dx x x dx x x dx . A B C D MNPQ 31 11 341 341 2 93 66 6138 . 60 30 5 1800 0 0 0 3 341 341 h 2 V 6138h h . A B C D .MNPQ 10 1800 3 15845 s
Mà KB s
.h C.h h . 120 C 2 3 s 341 s 341 s Suy ra V 6138. . . . A B C D .MNPQ 2 3 C 10 C 1800 3C
Tại thời điểm t phút lượng nước trong thùng là V (t) 20000t ( 3 cm ). 2 3 s 341 s 341 s Suy ra 20000t 6138. . .
, đạo hàm hai vế theo biến t . 2 3 C 10 C 1 0 8 0 3C 2 6138 341 s 341 s ds 1 341 341 ds 2 20000 . . . 20000 6138 h h 2 3 C 5 C 1800 C dt C 5 1800 dt 2 6138 341 s 341 s ds 1 341 341 ds 2 20000 . . . 20000 6138 h h 2 3 C 5 C 1800 C dt C 5 1800 dt ds 20000.C 15845
, thay h 25 , C . dt S h 120 ds
Vậy vận tốc cần tìm là v 25
2,6351cm/ phút 2,64 cm/ phút. dt x 1 y z 2 Câu 6:
Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d : và mặt phẳng 1 2 1
P:3x y z 25 0. Một đường thẳng d cắt trục Oz tại điểm M , cắt đường thẳng d
tại điểm N và d song song với P . Độ dài nhỏ nhất của đoạn MN bằng bao nhiêu? (Kết
quả làm tròn đến hàng phần trăm). Lời giải Đáp án: 2,71
Vì M Oz , N d nên M 0;0;m , N n 1;2 ; n n 2 .
Suy ra MN n 1;2 ;
n n m 2 . Trang 15
Đường thẳng d P suy ra MN n P 0 3n 1 2n n m 2 0 m 2n 1. 2 2 22
Do đó MN n 2
1 4n n 32 2 2 6 n . 3 3
Độ dài nhỏ nhất của đoạn MN bằng 2,71. HẾT Trang 16