S– GIÁO D÷C VÀ ÀO TÑO HÀ TûNH
THI TH€ T»T NGHIõP THPT NãM 2024 ó THI TH€ LÜN 1 Bài thi: TOÁN ( ∑ thi có 5 trang)
ThÌi gian làm bài: 90 phút, không k∫ thÌi gian phát ∑ Mã ∑ thi 101
HÂ, tên thí sinh:. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
SË báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
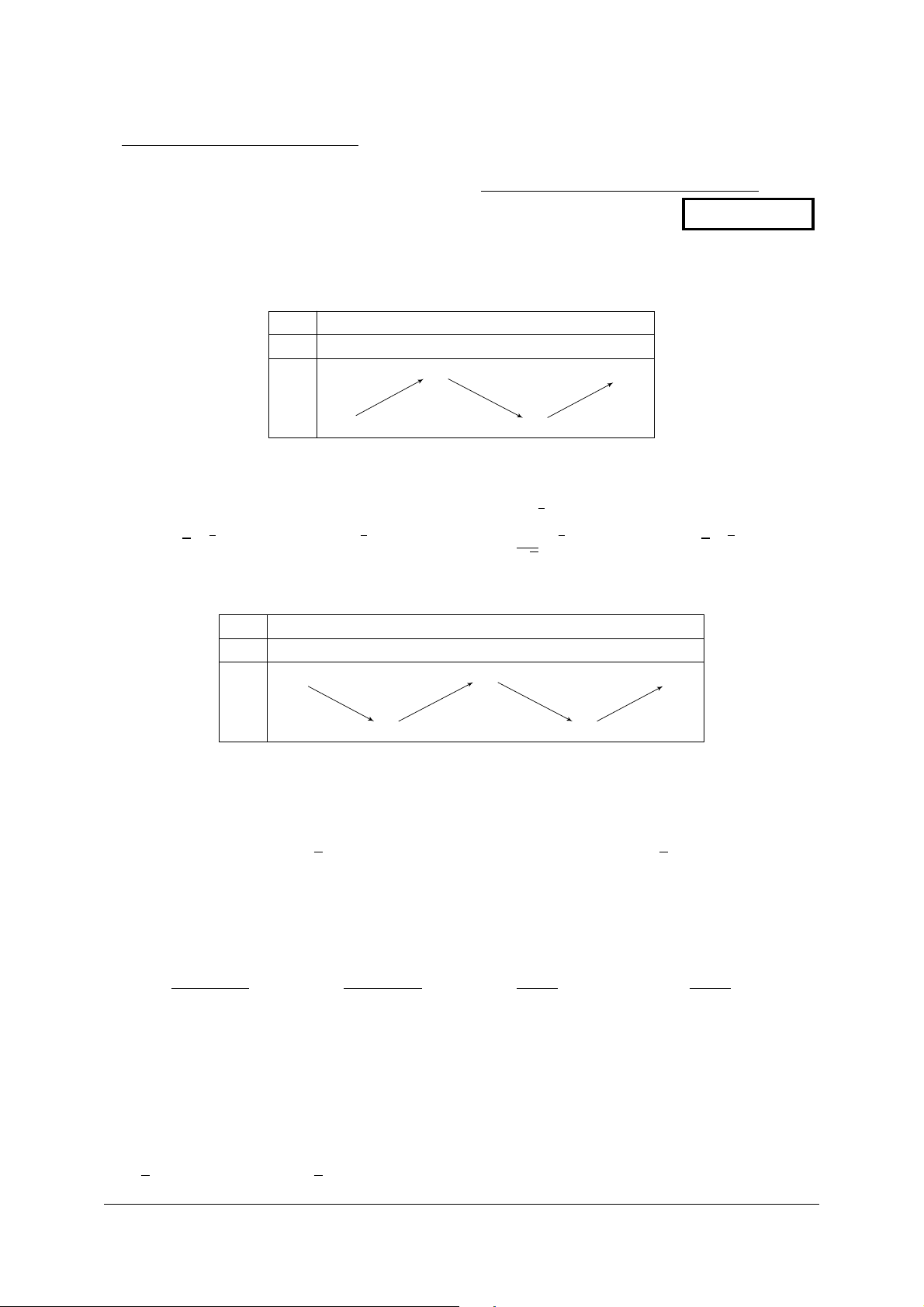
Câu 1. Cho hàm sË y = f (x) có b£ng bi∏n thiên nh˜ bên d˜Ói. x °1 °1 3 +1 f 0(x) + 0 ° 0 + 5 +1 + f (x) °1 1
Hàm sË ã cho §t c¸c ti∫u t§i A. x = 5. B. x = 1. C. x = 3. D. x = °1. p
Câu 2. Trên kho£ng (0;+1), §o hàm cıa hàm sË y = x 2 là p p p p A. p 1 p y0 = 2x 2°1. B. y0 = x 2°1. C. y0 = p x 2°1. D. y0 = 2x 2. 2
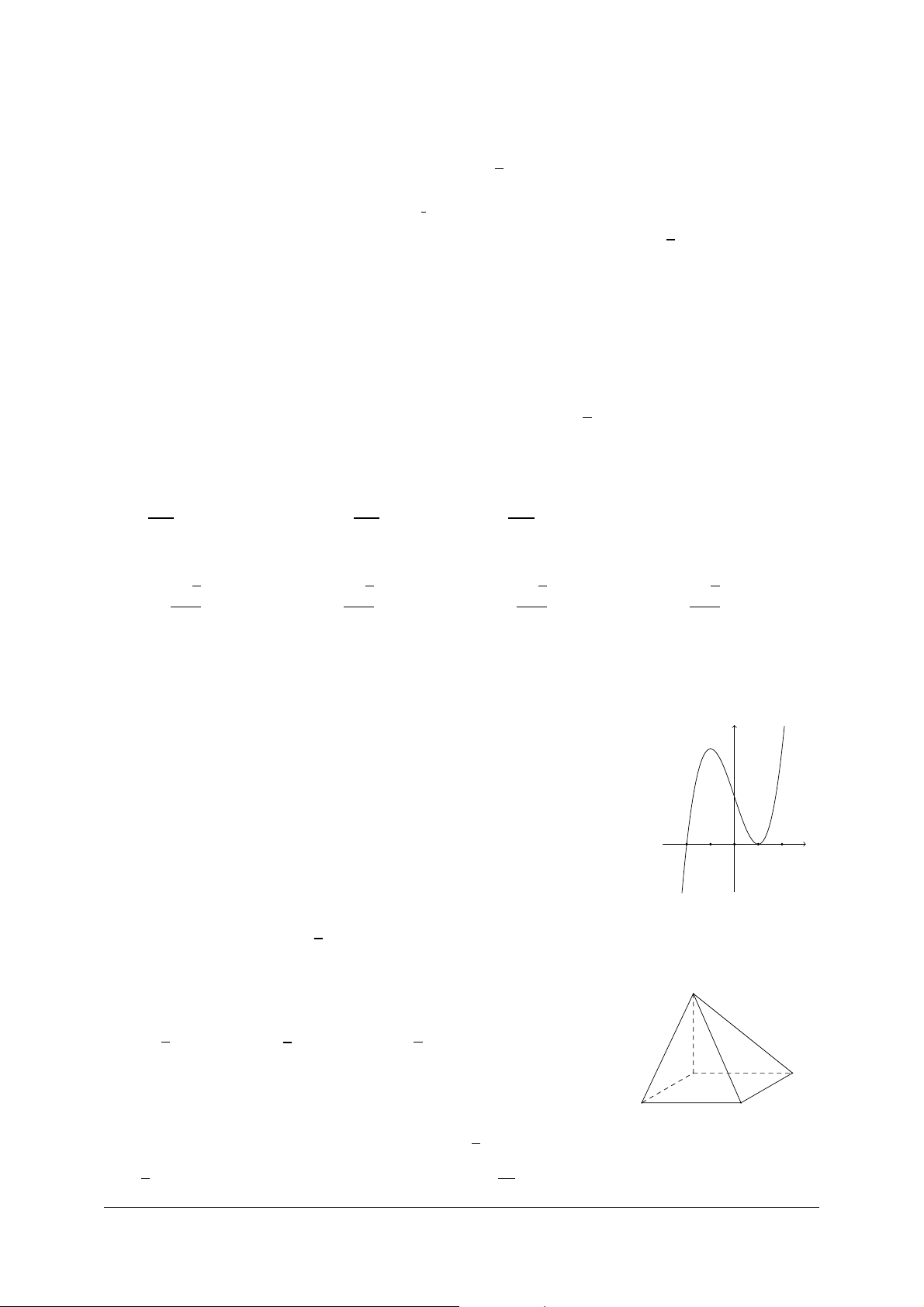
Câu 3. Cho hàm sË y = f (x) có b£ng bi∏n thiên nh˜ bên d˜Ói. x °1 °2 0 2 +1 f 0(x) ° 0 + 0 ° 0 + +1 + 1 +1 + f (x) 0 0
Hàm sË Áng bi∏n trên kho£ng nào sau ây? A. (°2;0). B. (0;+1). C. (°1;0). D. (0;2).
Câu 4. VÓi a là sË th¸c d˜Ïng khác 1, loga2 a5 b¨ng A. 7. B. 2. C. 10. D. 5. 5 2
Câu 5. Cho khËi chóp có diªn tích áy b¨ng 6 và chi∑u cao b¨ng 4. Th∫ tích cıa khËi chóp ã cho b¨ng A. 24. B. 10. C. 8. D. 12.
Câu 6. §o hàm cıa hàm sË y = log2(2x+1) là A. 2 1 1 2 y0 = . B. y0 . C. y0 . D. y0 . (2x = = = + 1)ln2 (2x +1)ln2 2x +1 2x +1
Câu 7. Cho khËi hÎp ch˙ nh™t ABCD.A0B0C0D0 có AB = 3, AD = 4, AA0 = 5. Th∫ tích cıa khËi hÎp ch˙ nh™t ã cho b¨ng A. 20. B. 12. C. 60. D. 10.
Câu 8. HÂ nguyên hàm cıa hàm sË f (x) = 4x+sin x là A. 4+cos x+C. B. 2x2 °cos x+C. C. 4°cos x+C. D. 2x2 +cos x+C.
Câu 9. Th∫ tích khËi trˆ có chi∑u cao b¨ng h và bán kính  áy b¨ng r là A. 16ºr2h. B. 13ºr2h. C. ºr2h. D. 2ºr2h. Trang 1/5 Mã ∑ 101
Câu 10. Cho khËi c¶u có th∫ tích V = 36º. Bán kính cıa khËi c¶u ã cho b¨ng A. p p 3 3. B. 3. C. 2. D. 2 3. Câu 11.
Á th‡ cıa hàm sË nào d˜Ói ây có d§ng nh˜ ˜Ìng cong trong hình bên? y A. y = x4 °2x2 +1. B. y = °x4 +2x2 +1. C. y = x3 °3x+1. D. y = °x3 +3x+1. 1 O x
Câu 12. Cho bËn hình v≥ sau ây Hình 1 Hình 2 Hình 3 Hình 4
MÈi hình trên bao gÁm mÎt sË h˙u h§n a giác phØng. Hình nào  trên không ph£i là hình a diªn? A. Hình 1. B. Hình 4. C. Hình 3. D. Hình 2.
Câu 13. Cho ph˜Ïng trình 4 · 4x ° 9 · 2x+1 + 8 = 0. GÂi x1, x2 là hai nghiªm cıa ph˜Ïng trình trên. Khi ó tích x1x2 b¨ng A. °2. B. 2. C. 1. D. °1.
Câu 14. Cho khËi t˘ diªn ABCD có th∫ tích V và i∫m E trên c§nh AB sao cho AE = 3EB.
Tính th∫ tích khËi t˘ diªn EBCD theo V. A. V . B. V . C. V . D. V . 2 3 4 5
Câu 15. SË ønh cıa mÎt khËi hÎp ch˙ nh™t là A. 8. B. 10. C. 6. D. 12. Câu 16. p
Cho hình nón có chi∑u cao h = 2 3, bán kính áy r = 2. Diªn tích xung quanh cıa hình nón ã cho b¨ng p A. p 3 8 3º. B. 83 º. C. 12º. D. 8º. Câu 17.
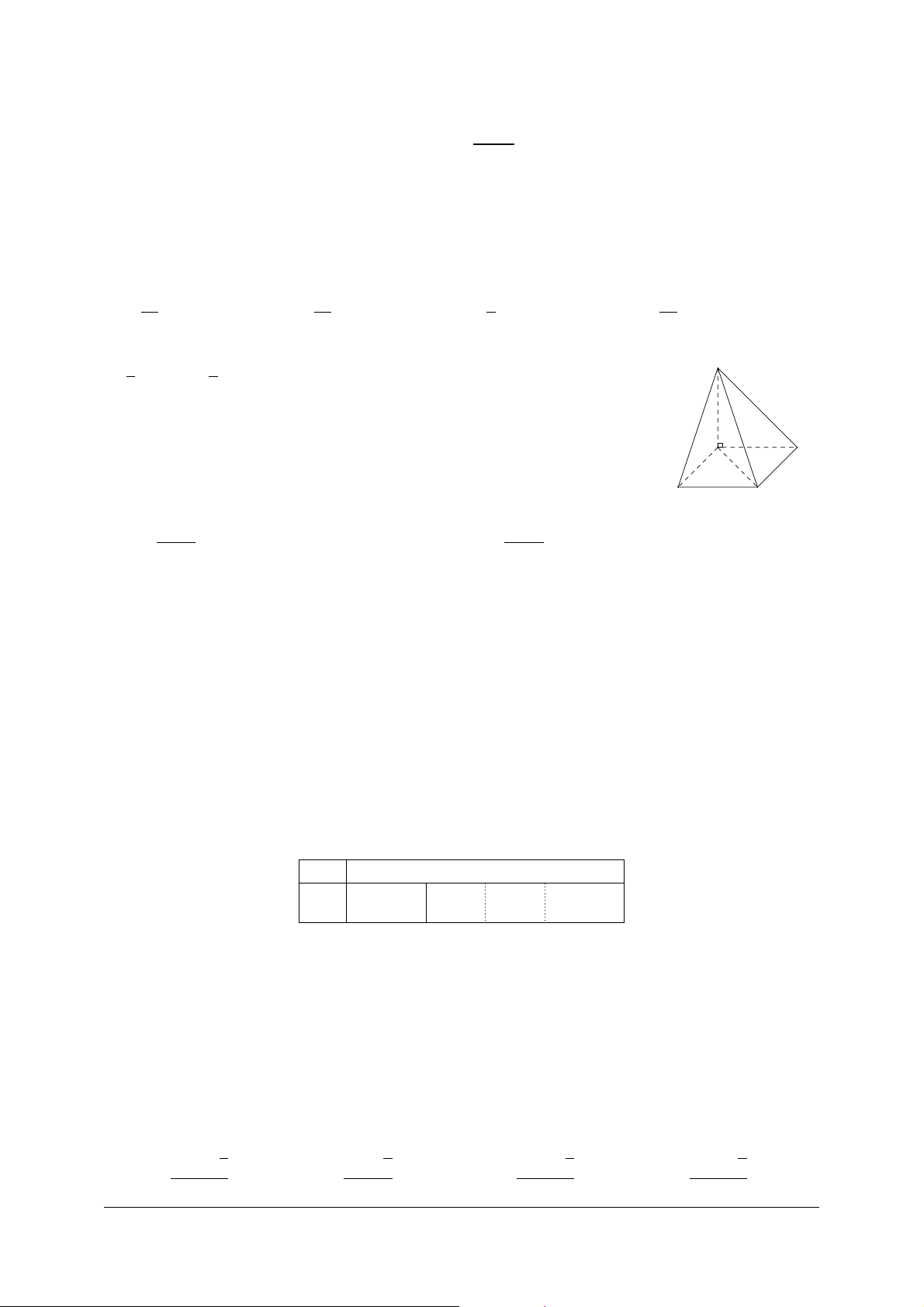
Cho hàm sË b™c ba y = f (x) có Á th‡ là ˜Ìng cong trong hình bên. y
SË nghiªm th¸c cıa ph˜Ïng trình f (x) = °1 là A. 3. B. 2. C. 0. D. 1. 1 1 x °1O °1 Câu 18.
Hình bát diªn ∑u thuÎc lo§i khËi a diªn ∑u nào sau ây? A. {4;3}. B. {3;4}. C. {3;3}. D. {3;5}. Trang 2/5 Mã ∑ 101
Câu 19. T™p nghiªm cıa bßt ph˜Ïng trình log23(3x)°5log3 x°5 ∑ 0 là ∑ ∏ A. 1 [°1;4]. B. [1;81]. C. ;81 . D. [4; 3 +1).
Câu 20. T™p xác ‡nh cıa hàm sË y = log1 (x°2) là 5 µ ∂ A. 1 R. B. [2;+1). C. (2;+1). D. ; . 5 +1
Câu 21. Cho F(x) là mÎt nguyên hàm cıa hàm sË f (x) = (5x+1)ex và F(0) = 3. Tìm F(x).
A. F(x) = (5x+1)ex °5ex +7.
B. F(x) = (5x+1)ex °4ex +6.
C. F(x) = (5x+1)ex °6ex +8.
D. F(x) = (5x+2)ex °5ex +6.
Câu 22. Có bao nhiêu cách chÂn 2 hÂc sinh t¯ mÎt nhóm 15 hÂc sinh n˙ và 21 hÂc sinh nam? A. 15+21. B. C236. C. 15·21. D. A236.
Câu 23. Cho các sË d˜Ïng a
a và b th‰a mãn log2(ab) + log16 b = 0. Mªnh ∑ nào d˜Ói ây úng? A. a5 · b = 1. B. a5 · b3 = 1. C. a5 = b3. D. a = b5.
Câu 24. T™p nghiªm cıa bßt ph˜Ïng trình log x < °2 là µ ∂ µ ∂ µ ∂ A. 1 1 1 ; . B. . C. 0; . D. [0;100]. 100 +1 °1; 100 100
Câu 25. Khi quay hình vuông ABCD quanh ˜Ìng chéo AC ta ˜Òc mÎt khËi tròn xoay. Tính
th∫ tích V cıa khËi tròn xoay ó, bi∏t AB = 2. p p p p A. 6 2 8 2 4 2 2 2 V = 3 º. B. V = 3 º. C. V = 3 º. D. V = 3 º.
Câu 26. Trong không gian Oxyz, cho m∞t c¶u (S): x2 + y2 + z2 ° 2x + 4y + 6z ° 2 = 0. Bán kính cıa m∞t c¶u (S) b¨ng A. 8. B. 4. C. 12. D. 16. Câu 27.
Cho hàm sË y = f (x) xác ‡nh trên R và có Á th‡ hàm sË y = f 0(x) là y
˜Ìng cong nh˜ hình bên. Mªnh ∑ nào d˜Ói ây úng?
A. Hàm sË f (x) Áng bi∏n trên kho£ng (°1;0).
B. Hàm sË f (x) ngh‡ch bi∏n trên kho£ng (°1;1).
C. Hàm sË f (x) Áng bi∏n trên kho£ng (°2;+1).
D. Hàm sË f (x) Áng bi∏n trên R. °2 O 1 x °1
Câu 28. Cho cßp sË nhân (un) vÓi u1 = 3 và u2 = 1. Công bÎi cıa cßp sË nhân ã cho b¨ng A. °2. B. 1. C. 3. D. 2. 3 Câu 29.
Cho hình chóp S.ABCD có áy là hình vuông c§nh b¨ng 2a, c§nh S
SA vuông góc vÓi m∞t áy. Kho£ng cách gi˙a hai ˜Ìng thØng SA và BD b¨ng A. p p p a 2. B. a 3. C. 2a 2. D. a. A D B C Câu 30. 1
Giá tr‡ nh‰ nhßt cıa hàm sË y = f (x) = x3
3 + x2 ° 3x ° 4 trên o§n [°4;0] b¨ng A. 8 17 . B. 5. C. . D. 3 ° 3 °4. Trang 3/5 Mã ∑ 101 Câu 31. 1
Tiªm c™n ngang cıa Á th‡ hàm sË y ° 2x = là x °2 A. x = °2. B. y = °2. C. x = 2. D. y = 1.
Câu 32. SË giao i∫m cıa Á th‡ hàm sË y = x4 +7x2 °8 vÓi trˆc hoành là A. 1. B. 4. C. 2. D. 3.
Câu 33. MÎt chi∏c hÎp ch˘a 9 qu£ c¶u gÁm 4 qu£ c¶u màu xanh, 3 qu£ màu ‰ và 2 qu£ màu
vàng. Lßy ng®u nhiên 3 qu£ c¶u t¯ hÎp ó. Xác sußt ∫ trong 3 qu£ c¶u lßy ˜Òc có ít nhßt mÎt qu£ màu ‰ là A. 17. B. 19. C. 1. D. 16. 42 28 3 21 Câu 34.
Cho hình chóp S.ABCD có SA vuông góc vÓi m∞t phØng (ABCD), SA = S p p
a 6, SB = a 7, áy ABCD là hình vuông (minh hÂa nh˜ hình v≥). SË
o góc gi˙a ˜Ìng thØng SC và (ABCD). A. 60±. B. 90±. C. 45±. D. 30±. A D B C
Câu 35. Mªnh ∑ nào sai trong các mªnh ∑ sau? Z Z A. 1 1 dx = °cot x +C. B. dx = tan x +C. Z sin2 x cos2 x Z C. sin xdx = cos x+C. D. cos xdx = sin x+C.
Câu 36. Trong không gian vÓi hª trˆc tÂa Î Oxyz, cho hai i∫m A(1;2;3), B(5;4;°1). Ph˜Ïng
trình m∞t c¶u ˜Ìng kính AB là
A. (x°3)2 +(y°3)2 +(z °1)2 = 6.
B. (x°3)2 +(y°3)2 +(z °1)2 = 9.
C. (x°3)2 +(y°3)2 +(z °1)2 = 36.
D. (x+3)2 +(y+3)2 +(z +1)2 = 9.
Câu 37. Trong không gian Oxyz, cho m∞t c¶u (S) có tâm I(0;0;°3) và i qua M(4;0;0). Ph˜Ïng trình cıa m∞t c¶u (S) là
A. x2 + y2 +(z °3)2 = 5.
B. x2 + y2 +(z +3)2 = 5.
C. x2 + y2 +(z °3)2 = 25.
D. x2 + y2 +(z +3)2 = 25.
Câu 38. Nghiªm cıa ph˜Ïng trình 4x °3·2x °4 = 0 là A. x = 2. B. x = °1. C. x = °4. D. x = 4.
Câu 39. Cho hàm sË y = f (x) liên tˆc trên R và có b£ng xét dßu cıa f 0(x) nh˜ sau x °1 °1 2 3 +1 f 0(x) ° + 0 + 0 °
SË i∫m c¸c tr‡ cıa hàm y = f (x) là A. 0. B. 1. C. 3. D. 2.
Câu 40. N´m 2023 mÎt hãng xe niêm y∏t giá bán lo§i xe X là 750.000.000 Áng và d¸ ‡nh
trong 10 n´m ti∏p theo, mÈi n´m gi£m 2% giá bán so vÓi giá bán cıa n´m li∑n tr˜Óc. Theo d¸
‡nh ó, n´m 2030 hãng xe ô tô niêm y∏t giá bán lo§i xe X là bao nhiêu? (k∏t qu£ làm tròn ∏n hàng nghìn).
A. 677.941.000 Áng. B. 664.382.000 Áng. C. 638.072.000 Áng. D. 651.094.000 Áng.
Câu 41. Cho hình chóp S.ABCD có áy ABCD là hình ch˙ nh™t, AB = 3, AD = 4 và các c§nh
bên cıa hình chóp t§o vÓi m∞t áy mÎt góc 60±. Tính th∫ tích cıa khËi c¶u ngo§i ti∏p hình chóp ã cho. p p p p A. 250º 3 50º 3 125º 3 500º 3 V = . B. V . C. V . D. V . 3 = 27 = 6 = 27 Trang 4/5 Mã ∑ 101
Câu 42. C≠t hình nón bi m∞t phØng i qua ønh cıa hình nón và t§o vÓi m∞t phØng ch˘a
áy hình nón mÎt góc 60± ta ˜Òc thi∏t diªn là tam giác vuông có diªn tích 8 cm2. Th∫ tích V
cıa khËi nón ˜Òc giÓi h§n bi hình nón ó b¨ng p p A. 10 6º p 14 2º p V = cm3. B. V 2 cm3. D. V 6 3 = 14 ºcm3. C. V = 3 = 10 º cm3.
Câu 43. Cho hàm sË y = x4 +4mx3 +3(m+1)x2 +1. Có bao nhiêu giá tr‡ nguyên cıa tham sË m
∫ hàm sË chø có i∫m c¸c ti∫u và không có i∫m c¸c §i? A. 2. B. 1. C. 3. D. 4. µ ∂2x°5y µ ∂6y°2x Câu 44. 5 2
Cho các sË d˜Ïng x, y th‰a mãn
. Tìm giá tr‡ nh‰ nhßt cıa bi∫u 4 ∏ p5 th˘c x . y A. 3. B. 1. C. 2. D. 4.
Câu 45. Cho hình l´ng trˆ ˘ng ABC.A0B0C0 có áy ABC là tam giác vuông t§i A, É ACB = 30±. 1
Bi∏t góc gi˙a B0C và m∞t phØng (ACC0A0) b¨ng Æ th‰a mãn sinÆ = p . Kho£ng cách gi˙a hai 2 5 p
˜Ìng thØng A0B và CC0 b¨ng a 3. Tính th∫ tích V cıa khËi l´ng trˆ ABC.A0B0C0. A. 3a3p6 V = . B. V 2 = a3p6. C. V = 2a3p3. D. V = a3p3.
Câu 46. Cho hình chóp S.ABC có áy là tam giác ABC vuông cân t§i C và SA vuông góc vÓi
m∞t phØng áy. Cho SC = a, m∞t phØng (SBC) t§o vÓi áy mÎt góc Æ. Th∫ tích khËi chóp S.ABC §t giá tr‡ lÓn nhßt là A. a3 . B. a3p3. C. a3p3. D. a3p2. 16 48 27 24 Câu 47. 2x+1
Bi∏t F(x) là mÎt nguyên hàm cıa hàm sË f (x) ° x2 ln2 ° xln4 ° 1 = . H‰i Á th‡ cıa 4 ° x2
hàm sË y = F(x) có bao nhiêu i∫m c¸c tr‡ trong kho£ng (°2;2)? A. 3. B. 2. C. 1. D. 0. Câu 48. Cho các hàm sË y = log y a x và y = logb x có Á th‡ nh˜ hình v≥ bên.
˜Ìng thØng x = 6 c≠t trˆc C
hoành, Á th‡ hàm sË y = log y = logb x a x và y = logb x l¶n
l˜Òt t§i A, B và C. Bi∏t r¨ng AC B = AB log2 3. y = loga x
Mªnh ∑ sau ây là mªnh ∑ úng? A. b = alog32. B. a = blog32. A C. b = alog23. D. b = 3p2. O 6 x
Câu 49. Cho bßt ph˜Ïng trình 2y+log y °8+2y log y+(y°3)·2y ∑ 0. Có bao nhiêu giá tr‡ nguyên
d˜Ïng cıa y tho£ mãn bßt ph˜Ïng trình trên? A. 2. B. 1. C. 0. D. 3. Ø Ø Câu 50. p p Cho hàm sË m y = Ø Ø Ø 2 ° x + x + 2 + x
2 ° 1Ø. Có bao nhiêu giá tr‡ m nguyên ∫ hàm sË ngh‡ch bi∏n trên (0;1)? A. 5. B. 3. C. 4. D. 2.
- - - - - - - - - - HòT- - - - - - - - - - Trang 5/5 Mã ∑ 101