Đề thi thử tốt nghiệp THPT 2025 môn Toán bám sát đề minh họa - Đề 20
Một người đưa thư xuất phát từ bưu điện ở vị trí A, các điểm cần phát thư nằm dọc các con dường cần đi qua. Biết rằng người này phải đi trên mỗi con đường ít nhất một lần (để phát được thư cho tất cả các điểm cần phát nằm dọc theo con đường đó) và cuối cùng quay lại điểm xuất phát. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi THPTQG môn Toán năm 2025 340 tài liệu
Môn: Toán 2.2 K tài liệu
Tác giả:
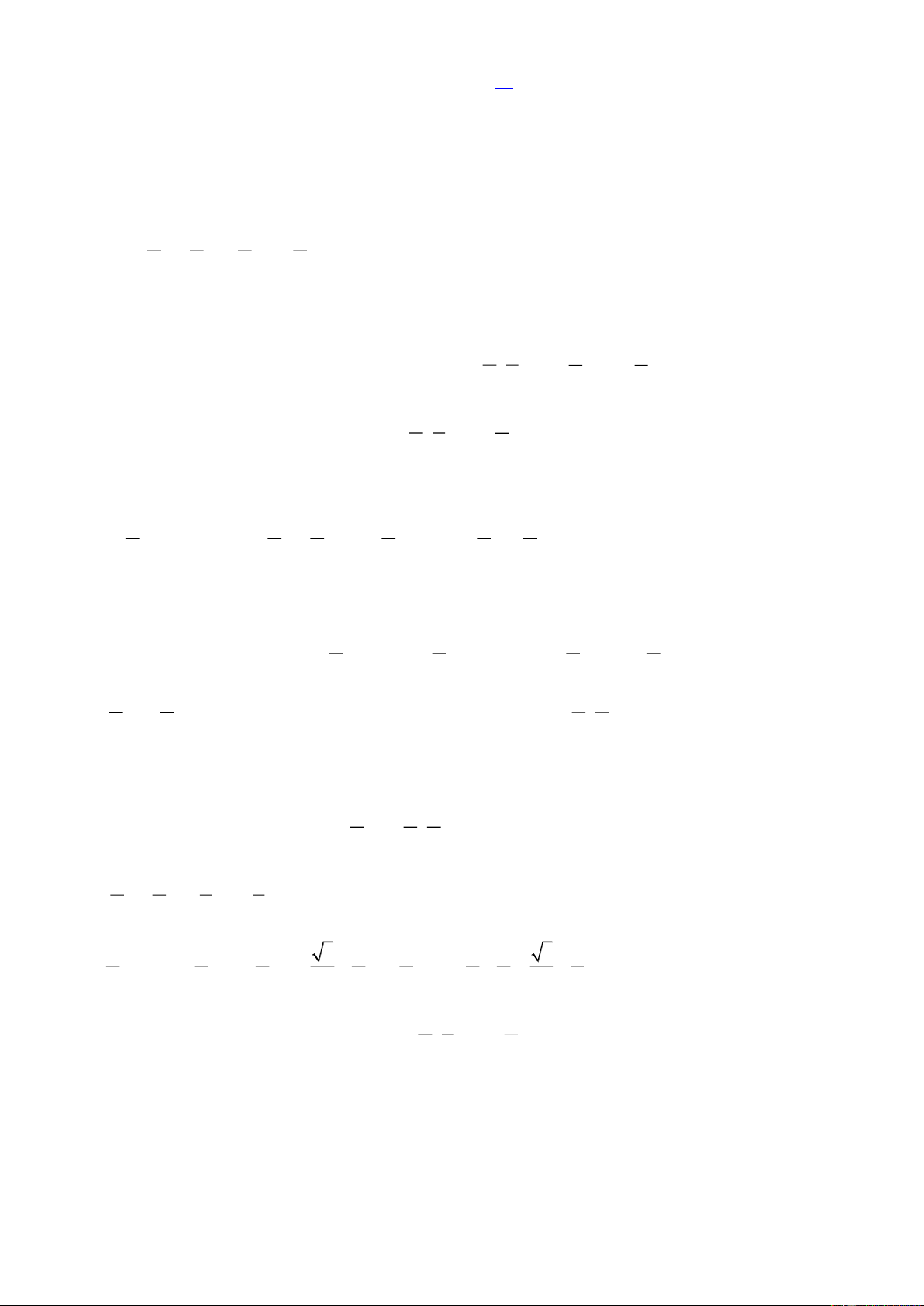
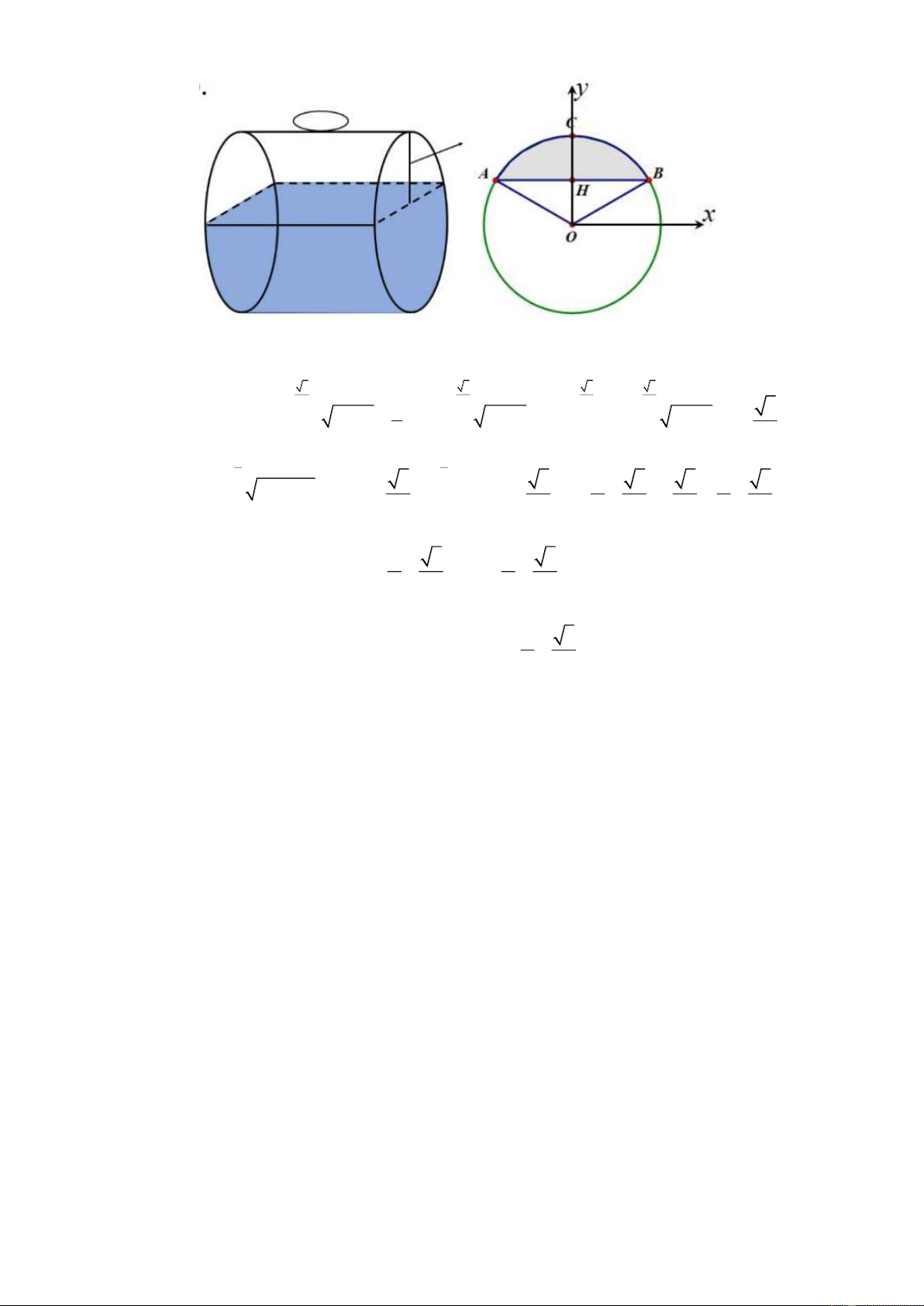
Preview text:
PHÁT TRIỂN TỪ ĐỀ MINH HỌA
ĐỀ ÔN THI TỐT NGHIỆP THPT 2025 ĐỀ 20 MÔN: TOÁN Thời gian: 90 phút
PHẦN I. Từ câu 1 đến câu 12, mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Nguyên hàm của hàm số 2025x y là
A. 2025x d ln 2025.2025x x C .
B. 2025x d 2 2 0 5x x C . x 2025x x 2025x C. 2025 dx C . D. 2025 dx C . ln 2025 x 1
Câu 2: Cho hàm số y f x xác định và liên tục trên đoạn a;b . Diện tích hình phẳng giới hạn bởi đồ
thị hàm số y f x , trục hoành và hai đường thẳng x a, x b được tính theo công thức b b b a A. S f x dx. B. S f xdx .
C. S f
xdx. D. S f x dx. a a a b
Câu 3: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Thời gian [0; 20) [20; 40) [40; 60) [60;80) [80;100) (phút) Số học sinh 5 9 12 10 6
Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu trên là A. [40; 60) . B. [20; 40) . C. [60;80) . D. [80;100) .
Câu 4: Trong không gian Oxyz , cho hai điểm A1;2; 1 và B 3;1; 2
. Đường thẳng AB có phương trình là x 1 y 2 z 1 x 1 y 2 z 1 A. . B. . 4 3 1 2 1 3 x 1 y 2 z 1 x 1 y 2 z 1 C. . D. . 4 3 1 2 1 3
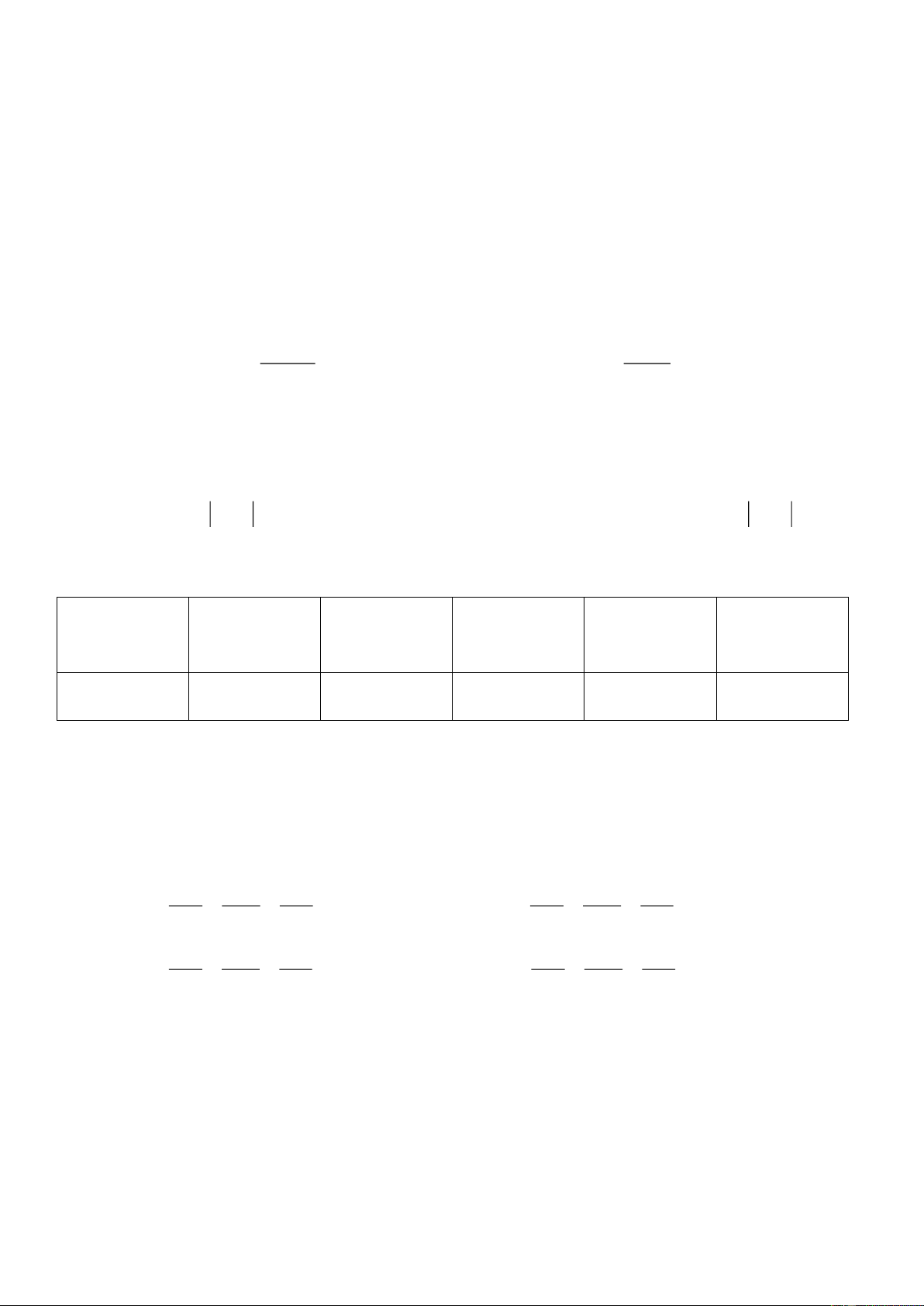
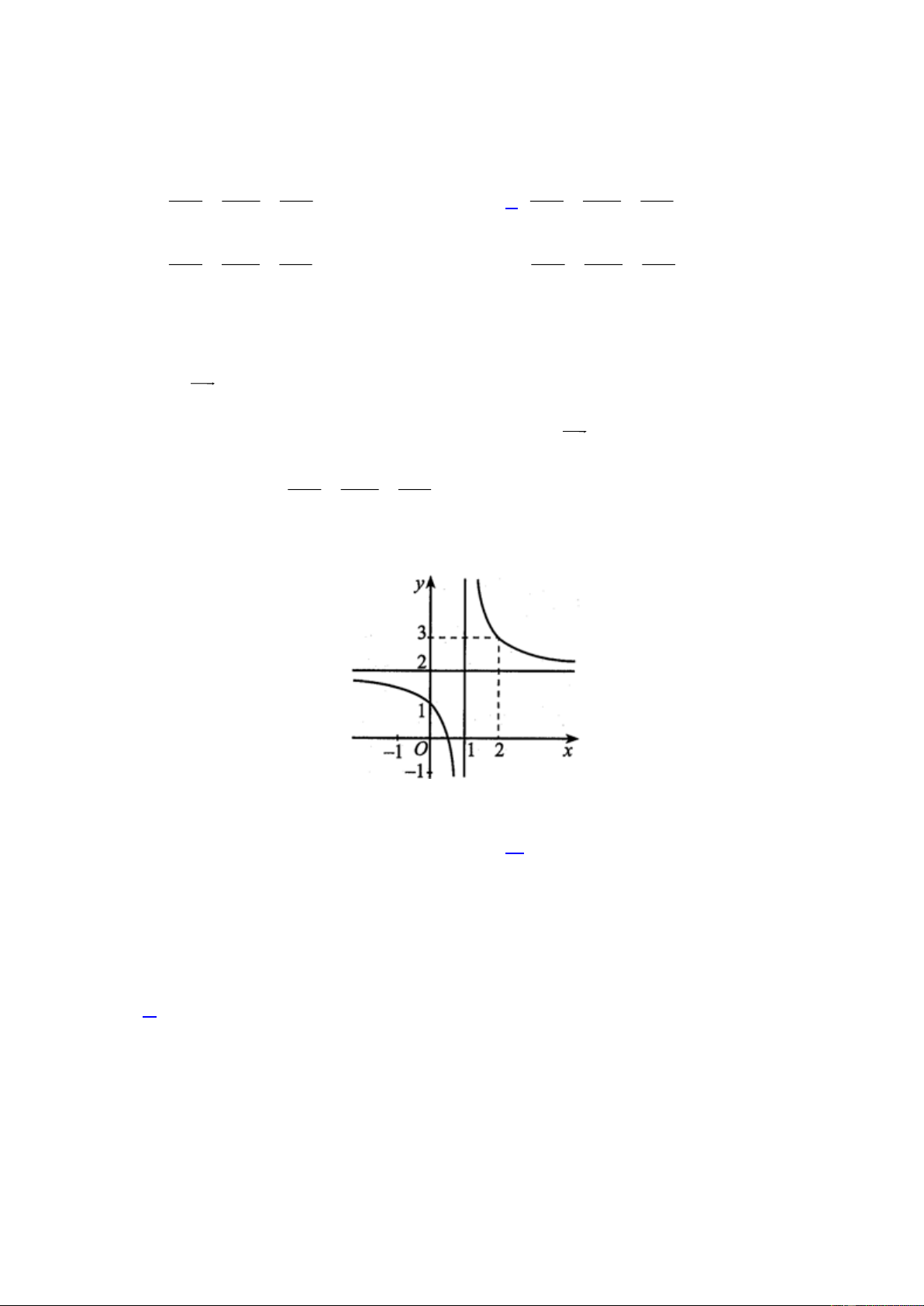
Câu 5: Cho hàm số y f x có đồ thị như bên dưới.
Đồ thị hàm số đã cho có đường tiệm cận ngang là: A. x 2 . B. x 2 . C. y 2. D. y 2.
Câu 6: Tập nghiệm của bất phương trình log x 1 2 là 3 A. 1 ; 8 B. 1 ; 8 C. ;8 D. ;8
Câu 7: Trong không gian với hệ tọa độ Oxyz, khoảng cách từ điểm I 1;1;1 đến mặt phẳng
P:x 2y 2z 160 bằng? A. 3. B. 15. C. 5. D. 15.
Câu 8: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , cạnh bên SA vuông góc với đáy.
Khẳng định nào sau đây đúng?
A. AC SBC .
B. BC SAC .
C. BC SAB .
D. AB SBC .
Câu 9: Phương trình x 1
4 16 0 có nghiệm là A. x 2. B. x 2. C. x 3. D. x 3.
Câu 10: Cho cấp số nhân u với u 2 và công bội q 3. Tìm số hạng thứ 4 của cấp số nhân? n 1 A. 24 . B. 54 . C. 162. D. 48 .
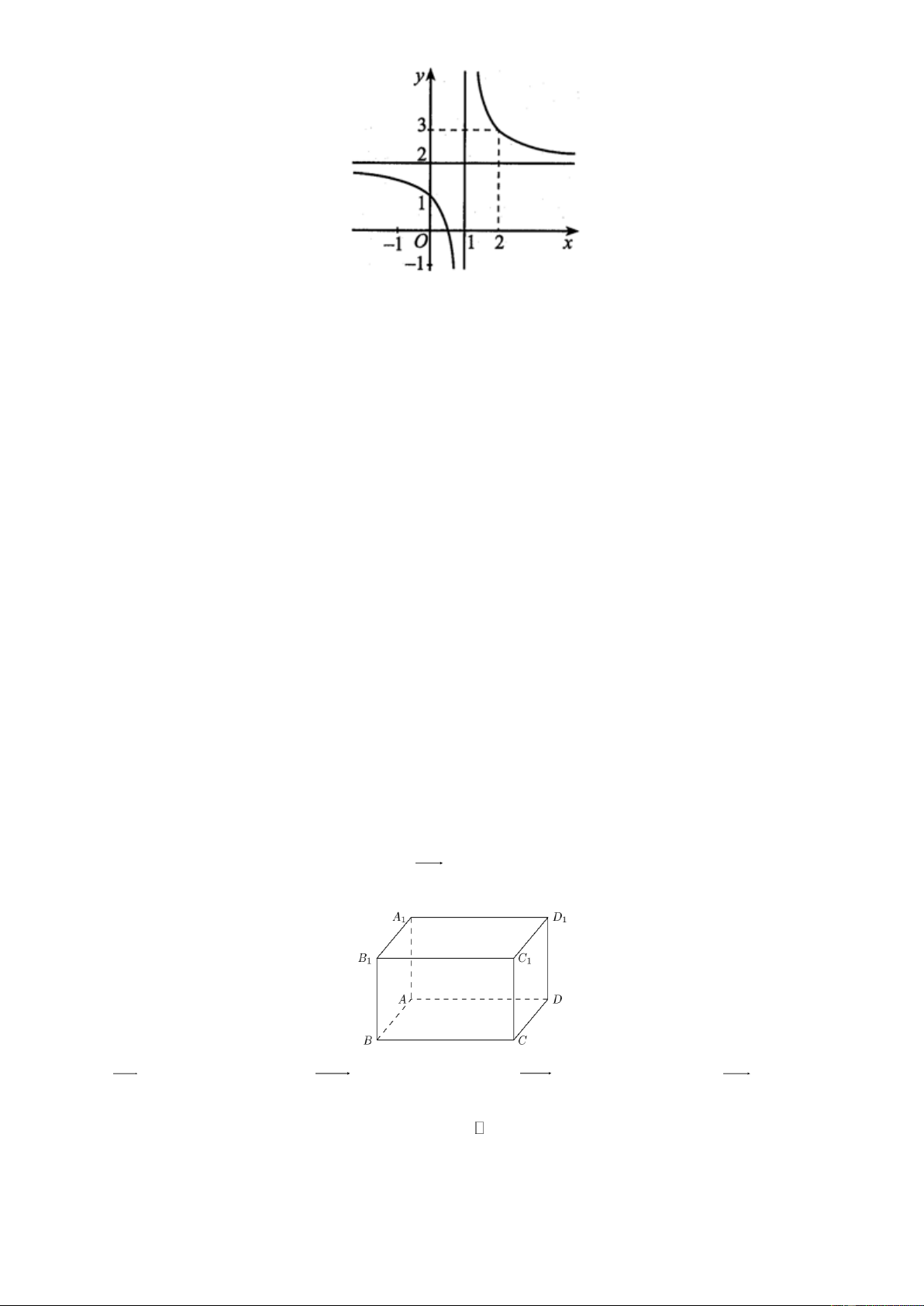
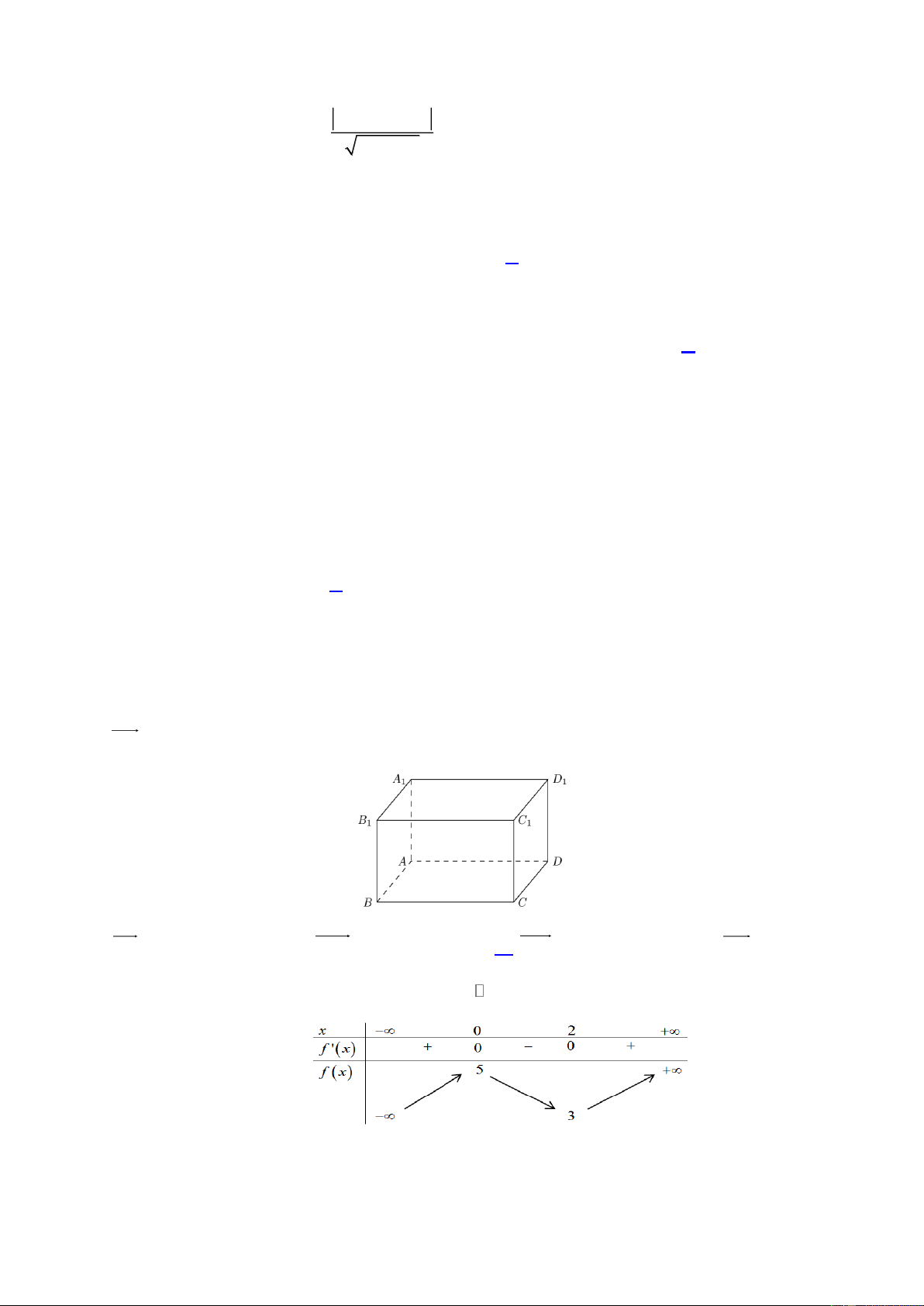
Câu 11: Cho hình hộp ABC .
D A B C D . Véctơ AC bằng với véctơ nào sau đây? 1 1 1 1 A. AB . B. B D . C. AC . D. AD . 1 1 1 1
Câu 12: Cho hàm số y f x xác định, liên tục trên
và có bảng biến thiên sau
Hàm số y f x đồng biến trên khoảng nào sau đây? A. ;5 . B. 0; 2 .
C. 2; . D. 0; .
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho hàm số f x sin 2x x . a) f ; f . 2 2 2 2
b) Đạo hàm của hàm số đã cho là f x cos2x 1. π
c) Nghiệm của phương trình f x 0 trên đoạn ; là hoặc . 2 2 6 6 π
d) Giá trị nhỏ nhất của f x trên đoạn ; là . 2 2 2
Câu 2: Một ô tô đang chạy đều với vận tốc x m/
s thì người lái xe đạp phanh. Từ thời điểm đó, ô tô
chuyển động chậm dần đều với vận tốc thay đổi theo hàm số v 5 t 20m/
s , trong đó là thời gian
tính bằng giây kể từ lúc đạp phanh.
a) Khi xe dừng hẳn thì vận tốc bằng 0m/ s .
b) Thời gian từ lúc người lái xe đạp phanh cho đến khi xe dừng hẳn là 5 s. t
c) t 2 5 5 20 dt 20t C . 2
d) Quãng đường từ lúc đạp phanh cho đến khi xe dừng hẳn là 400 m .
Câu 3: Một kho hàng có 85% sản phẩm loại I và 15% sản phẩm loại II, trong đó có 1% sản phẩm loại I
bị hỏng, 4% sản phẩm loại II bị hỏng. Các sản phẩm có kích thước và hình dạng như nhau. Một khách
hàng chọn ngẫu nhiên 1 sản phẩm. Xét các biến cố:
A: "Khách hàng chọn được sản phẩm loại I ";
: "Khách hàng chọn được sản phẩm không bị hỏng".
Các mệnh đề sau đúng hay sai? a) P A 0,85 .
b) PB | A 0,99 .
c) PB 0,9855 .
d) P A| B 0,95 .
Câu 4: Trong không gian tọa độ Oxyz , cho hai mặt phẳng P : x y 2z 5 0 và
Q:2x 4y 3z 1 0
a) Vectơ có tọa độ 1;1; 2
là một vectơ pháp tuyến của mặt phẳng P. 1
b) Khoảng cách từ O đến mặt phẳng Q là . 29
c) Góc giữa hai mặt phẳng P và Q là 0 60 . d) Điểm ( A 1;1;0) ( ) Q .
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
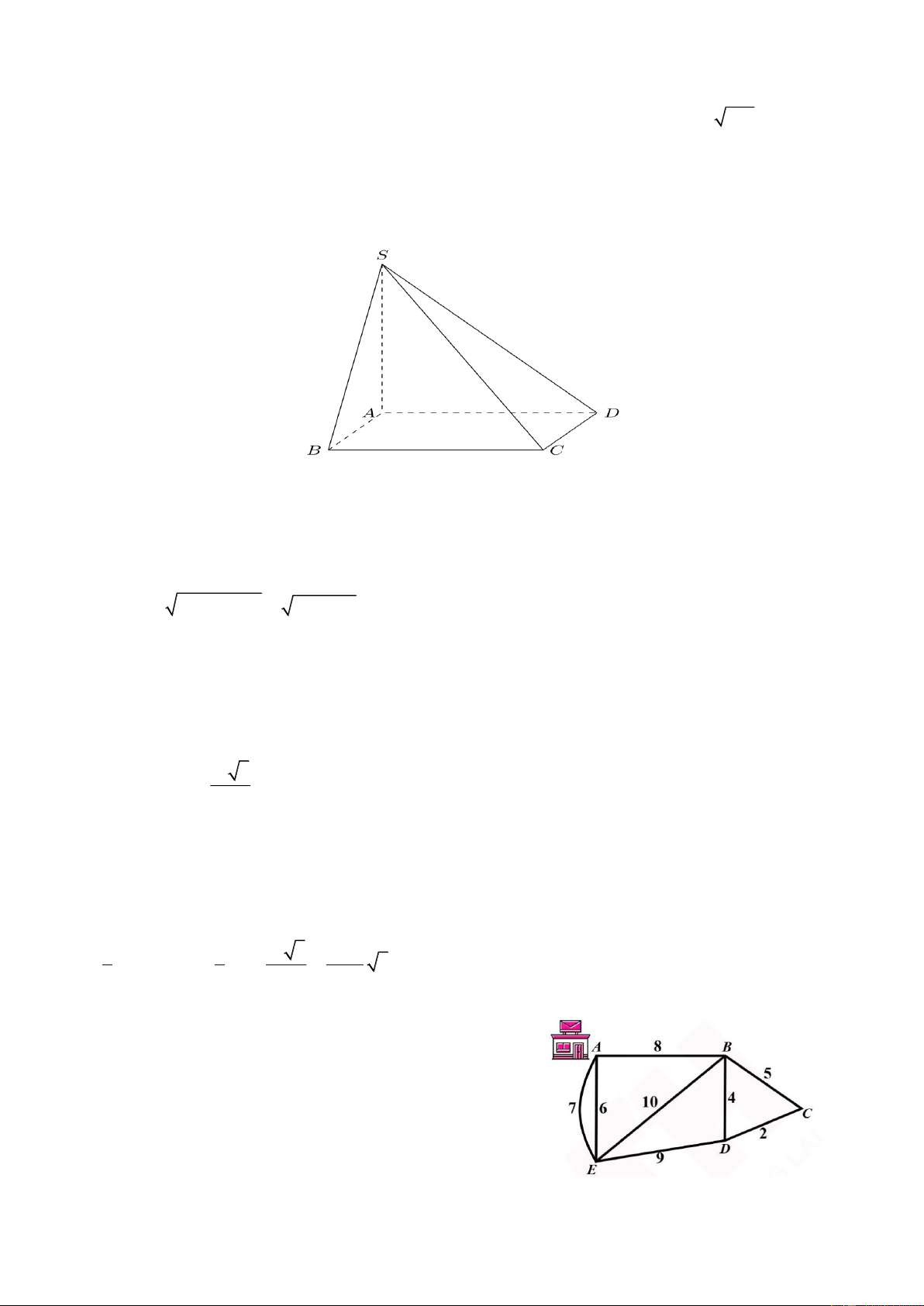
Câu 1: Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA ( ABCD), AB 8, AC 233 . Góc giữa
hai đường thẳng SD và BC bằng 30 . Tính thể tích của khối chóp S.ABCD , (làm tròn kết quả đến hàng đơn vị).
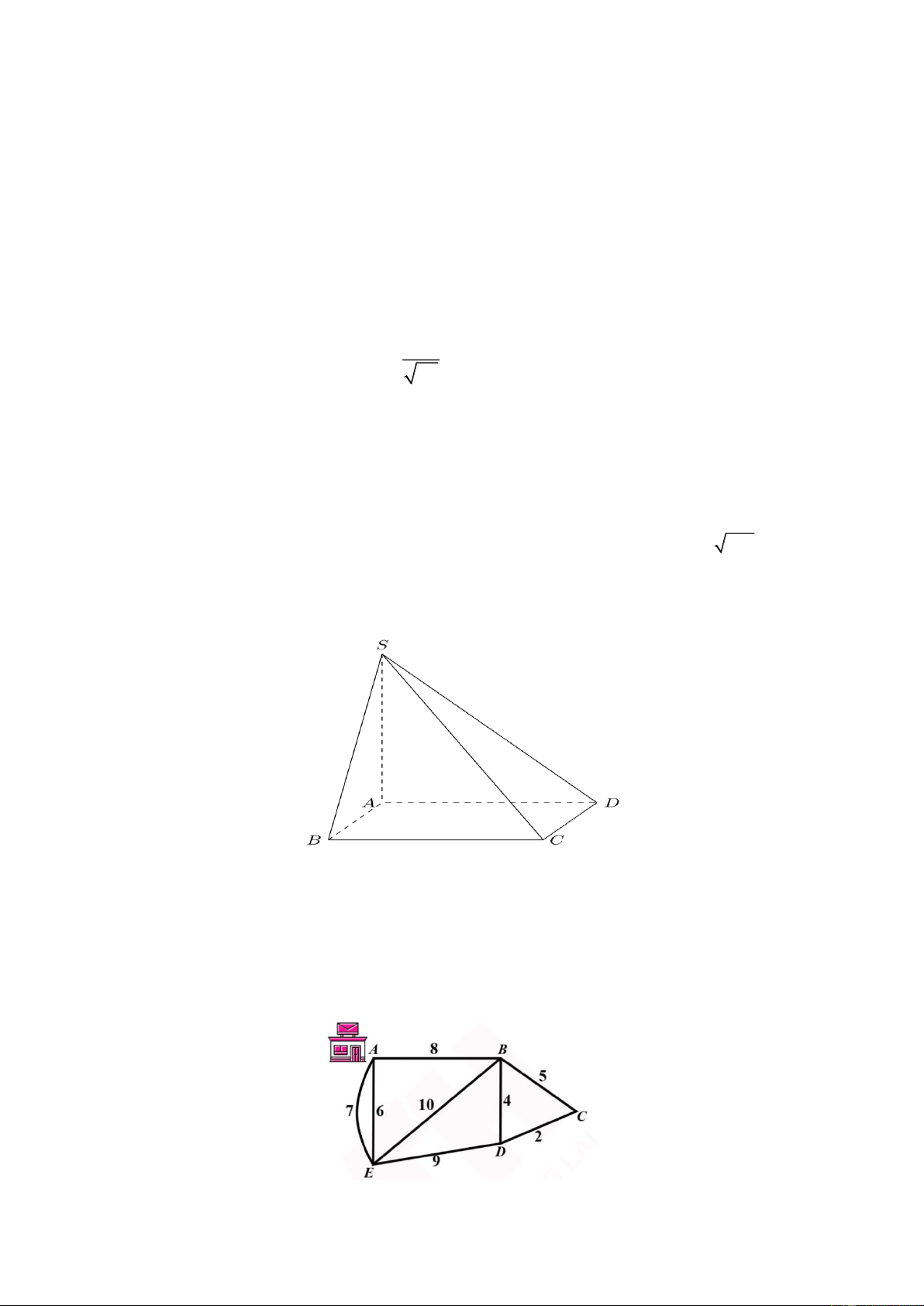
Câu 2: Một người đưa thư xuất phát từ bưu điện ở vị trí A, các điểm cần phát thư nằm dọc các con dường
cần đi qua. Biết rằng người này phải đi trên mỗi con đường ít nhất một lần (để phát được thư cho tất cả
các điểm cần phát nằm dọc theo con đường đó) và cuối cùng quay lại điểm xuất phát. Độ dài các con
đường như hình vẽ (đơn vị độ dài). Hỏi tổng quãng đường người đưa thư có thể đi ngắn nhất có thể là bao nhiêu ?
Câu 3 Hai chiếc máy bay không người lái cùng bay lên tại một địa điểm. Sau một thời gian bay, chiếc
máy bay thứ nhất cách điểm xuất phát về phía Bắc 20km và về phía Tây 10km , đồng thời cách mặt
đất 0,7km. Chiếc máy bay thứ hai cách điểm xuất phát về phía Đông 30km và về phía Nam
25km , đồng thời cách mặt đất
1 km . Hỏi hai chiếc máy bay cách nhau bao nhêu km (Làm tròn kết
quả đến hàng đơn vị).
Câu 4: Một bể chứa nhiên liệu hình trụ đặt nằm ngang, có chiều dài 5 m, có bán kính đáy 1m. Chiều cao của
mực nhiên liệu là 1,5m. Tính thể tích phần nhiên liệu trong bể (theo đơn vị 3
m , làm tròn đến chữ số thâph
phân hàng phần trục).
Câu 5: Nhà máy A chuyên sản xuất một loại sản phẩm cung cấp cho nhà máy B. Hai nhà máy này thoả thuận
rằng, hằng tuần A cung cấp cho B số lượng sản phẩm theo đơn đặt hàng của B (tối đa 100 sản phẩm). Nếu số
lượng đặt hàng là x sản phẩm thì giá bán cho mỗi sản phẩm là Px 2
450,001x (triệu đồng). Chi phí để A
sản xuất x sản phẩm trong một tuần là C x 10030x (triệu đồng) (gồm 100 triệu đồng chi phí cố định và 30
triệu đồng cho mỗi sản phẩm). Hỏi nhà máy A bán cho nhà máy B bao nhiêu sản phẩm mỗi tuần để thu được lợi
nhuận nhiều nhất? (Số sản phẩm là số nguyên dương).
Câu 6: Có hai hộp bóng bàn, các quả bóng bàn có kích thước và hình dạng như nhau. Hộp I chứa
3 bóng bàn màu trắng và 2 bóng bàn màu vàng, hộp II chứa 6 bóng bàn màu trắng và 4 bóng bàn
màu vàng. Lấy ngẫu nhiên 4 quả bóng bàn ở hộp I bỏ vào hộp II rồi lấy ngẫu nhiên 1 quả bóng
bàn từ hộp II ra. Tính xác suất để quả bóng bàn lấy từ hộp II có màu vàng. HƯỚNG DẪN GIẢI
PHẦN I. Từ câu 1 đến câu 12, mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Nguyên hàm của hàm số 2025x y là
A. 2025x d ln 2025.2025x x C
. B. 2025x d 2 2 0 5x x C . x 2025x x 2025x C. 2025 dx C . D. 2025 dx C . ln 2025 x 1 Lời giải x Do theo bảng nguyên hàm: a x a dx C . ln a
Câu 2: Cho hàm số y f x xác định và liên tục trên đoạn a;b . Diện tích hình phẳng giới hạn bởi đồ
thị hàm số y f x , trục hoành và hai đường thẳng x a, x b được tính theo công thức b b b a A. S f x dx. B. S f xdx .
C. S f
xdx. D. S f x dx. a a a b Lời giải
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y f x , trục hoành và hai đường thẳng b
x a, x b được tính bởi công thức: S f x dx. a
Câu 3: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Thời gian [0; 20) [20; 40) [40; 60) [60;80) [80;100) (phút) Số học sinh 5 9 12 10 6
Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu trên là A. [40; 60) . B. [20; 40) . C. [60;80) . D. [80;100) . Lời giải Chọn B Ta có: n 42
Nên tứ phân vị thứ nhất của mẫu số liệu trên là Q x 1 11 Mà x [20; 40) 11
Vậy nhóm chứa tứ phân vị thứ nhất của mẫu số liệu trên là nhóm [20;40).
Câu 4: Trong không gian Oxyz , cho hai điểm A1;2; 1 và B 3;1; 2
. Đường thẳng AB có phương trình là x 1 y 2 z 1 x 1 y 2 z 1 A. . B. . 4 3 1 2 1 3 x 1 y 2 z 1 x 1 y 2 z 1 C. . D. . 4 3 1 2 1 3 Lời giải Chọn B Ta có AB 2; 1 ; 3 .
Đường thẳng AB đi qua điểm A1;2;
1 và nhận véc-tơ AB 2; 1 ; 3
làm véc-tơ chỉ phương
có phương trình là x 1 y 2 z 1 . 2 1 3
Câu 5: Cho hàm số y f x có đồ thị như bên dưới.
Đồ thị hàm số đã cho có đường tiệm cận ngang là: A. x 2 . B. x 2 . C. y 2. D. y 2. Lời giải Chọn C
Câu 6: Tập nghiệm của bất phương trình log x 1 2 là 3 A. 1 ; 8 B. 1 ; 8 C. ;8 D. ;8
Câu 7: Trong không gian với hệ tọa độ Oxyz, khoảng cách từ điểm I 1;1;1 đến mặt phẳng
P:x 2y 2z 160 bằng? A. 3. B. 15. C. 5. D. 15. Giải Chọn C. 1 2 2 16
Khoảng cách dI;P 5. 1 4 4
Câu 8: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , cạnh bên SA vuông góc với đáy.
Khẳng định nào sau đây đúng?
A. AC SBC .
B. BC SAC .
C. BC SAB .
D. AB SBC .
Câu 9: Phương trình x 1
4 16 0 có nghiệm là A. x 2. B. x 2. C. x 3. D. x 3. Lời giải Chọn D x 1 x 1 2 Ta có 4 16 0 4
4 x 1 2 x 3.
Câu 10: Cho cấp số nhân u với u 2 và công bội q 3. Tìm số hạng thứ 4 của cấp số nhân? n 1 A. 24 . B. 54 . C. 162. D. 48 . Lời giải Có 3 3
u u .q 2.3 54. 4 1
Câu 11: Cho hình hộp ABC .
D A B C D . Véctơ có điểm đầu và điểm cuối là các đỉnh của hình hộp, 1 1 1 1
véctơ AC bằng với véctơ nào sau đây? A. AB . B. B D . C. AC . D. AD . 1 1 1 1
Câu 12: Cho hàm số y f x xác định, liên tục trên
và có bảng biến thiên sau
Hàm số y f x đồng biến trên khoảng nào sau đây? A. ;5 . B. 0; 2 .
C. 2; . D. 0; .
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho hàm số f x sin 2x x . a) f ; f . 2 2 2 2
b) Đạo hàm của hàm số đã cho là f x cos2x 1. π
c) Nghiệm của phương trình f x 0 trên đoạn ; là hoặc . 2 2 6 6 π
d) Giá trị nhỏ nhất của f x trên đoạn ; là . 2 2 2 Lời giải a) f sin và f sin . Đúng. 2 2 2 2 2 2
b) Đạo hàm của f x sin 2x x là f x 2cos2x 1. Sai.
c) f x 2cos 2x 1 khi đó f 2cos 1 0 và f 2cos 1 0 , suy ra 6 3 6 3 x ; x
là nghiệm của phương trình f x 0 trên đoạn ; . Đúng. 6 6 2 2
d) f x sin 2x x ,
f x 2cos 2x 1 có nghiệm x ; , 6 2 2 π π f ; f , 2 2 2 2 3 3 f sin ; f sin . 6 3 6 2 6 6 3 6 2 6 π
Do đó, giá trị nhỏ nhất của f x trên đoạn ; là . Đúng. 2 2 2
Câu 2: Một ô tô đang chạy đều với vận tốc x m/
s thì người lái xe đạp phanh. Từ thời điểm đó, ô tô
chuyển động chậm dần đều với vận tốc thay đổi theo hàm số v 5 t 20m/
s , trong đó là thời gian
tính bằng giây kể từ lúc đạp phanh.
a) Khi xe dừng hẳn thì vận tốc bằng 0m/ s .
b) Thời gian từ lúc người lái xe đạp phanh cho đến khi xe dừng hẳn là 5 s. t
c) t 2 5 5 20 dt 20t C . 2
d) Quãng đường từ lúc đạp phanh cho đến khi xe dừng hẳn là 400 m . Lời giải
a) Khi xe dừng hẳn thì vận tốc bằng 0m/
s . Mệnh đề đúng b) Cho . Mệnh đề sai t
c) t 2 5 5 20 dt
20t C . Mệnh đề đúng 2
d) Quãng đường từ lúc đạp phanh cho đến khi xe dừng hẳn là . Mệnh đề sai
Câu 3: Một kho hàng có 85% sản phẩm loại I và 15% sản phẩm loại II, trong đó có 1% sản phẩm loại I
bị hỏng, 4% sản phẩm loại II bị hỏng. Các sản phẩm có kích thước và hình dạng như nhau. Một khách
hàng chọn ngẫu nhiên 1 sản phẩm. Xét các biến cố:
A: "Khách hàng chọn được sản phẩm loại I ";
: "Khách hàng chọn được sản phẩm không bị hỏng".
Các mệnh đề sau đúng hay sai? a) P A 0,85 .
b) PB | A 0,99 .
c) PB 0,9855 .
d) P A| B 0,95 . Lời giải. a) Đúng b) Đúng c) Đúng d) Sai a) Đúng Ta có: P A 0,85 . b) Đúng
Ta có: P B | A 1 PB | A 1 0,01 0,99 . c) Đúng
Ta có: P A 0,15.
P B | A 1 PB | A 1 0,04 0,96
Theo công thức xác suất toàn phần, ta có:
P B P A.P B | A P A.PB | A 0,85.0,99 0,15.0,96 0,9855 . d) Sai
P A .P B | A 0,85.0, 99
Theo công thức Bayes, ta có: P A | B . P B 0,854 0, 9855
Câu 4: Trong không gian tọa độ Oxyz , cho hai mặt phẳng P : x y 2z 5 0 và
Q:2x 4y 3z 1 0
a) Vectơ có tọa độ 1;1; 2
là một vectơ pháp tuyến của mặt phẳng P. 1
b) Khoảng cách từ O đến mặt phẳng Q là . 29
c) Góc giữa hai mặt phẳng P và Q là 0 60 . d) Điểm ( A 1;1;0) ( ) Q . Lời giải. a) Đúng b) Đúng c) Sai d) Đúng
Trong không gian tọa độ Oxyz , cho hai mặt phẳng
P: x y 2z 5 0 và
Q:2x 4y 3z 1 0
a) P : x y 2z 5 0 nên n 1;1; 2
là một vectơ pháp tuyến của mặt phẳng P. 2.0 4.0 3.0 1 1
b) Khoảng cách từ O đến mặt phẳng Q là d O,(Q) . 2 2 2 2 ( 4 ) 3 29
c) Vì hai mặt phẳng P và Q có 2 VTPT vuông góc nhau nên góc giữa P và Q là 0 90 .
d) Vì Q : 2.1 4.1 3.0 1 0 nên ( A 1;1;0) ( ) Q .
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA ( ABCD), AB 8, AC 233 . Góc giữa
hai đường thẳng SD và BC bằng 30 . Tính thể tích của khối chóp S.ABCD , làm tròn kết quả đến hàng đơn vị. Lời giải: Ta có: 2 2 BC
AC AB 233 64 13. Góc (S , D BC) (S , D A ) D SDA 30 . 13 3 SA A . D tan 30 . 3
Thể tích của khối chóp đã cho là: 1 1 13 3 1352 V .A . B BC.SA 8.13. 3 260 . 3 3 3 9 Câu 2:
Một người đưa thư xuất phát từ bưu điện ở vị trí A, các điểm
cần phát thư nằm dọc các con dường cần đi qua. Biết rằng
người này phải đi trên mỗi con đường ít nhất một lần (để phát
được thư cho tất cả các điểm cần phát nằm dọc theo con
đường đó) và cuối cùng quay lại điểm xuất phát. Độ dài các
con đường như hình vẽ (đơn vị độ dài). Hỏi tổng quãng đường
người đưa thư có thể đi ngắn nhất có thể là bao nhiêu ? Giải
Theo sơ đồ đường đi thấy có 2 đỉnh bậc lẻ là A và D nên có thể tìm được một đường đi Euler từ A đến D
(đường này đi qua mỗi cạnh đúng một lần).
Một đường Euler từ A đến D là: AEABEDBCD và độ dài của nó là 6+7+8+10+9+4+5+2= 51
Đường đi ngắn nhất từ D đến A là DBA và có độ dài là: 4+8 = 12
Vậy tổng quãng đường đưa thư có thể đi ngắn nhất là 51 +12 = 63
Câu 3 Hai chiếc máy bay không người lái cùng bay lên tại một địa điểm. Sau một thời gian bay, chiếc
máy bay thứ nhất cách điểm xuất phát về phía Bắc 20km và về phía Tây 10km , đồng thời cách mặt
đất 0,7km. Chiếc máy bay thứ hai cách điểm xuất phát về phía Đông 30km và về phía Nam
25km , đồng thời cách mặt đất
1 km . Hỏi hai chiếc máy bay cách nhau bao nhêu km (Làm tròn kết
quả đến hàng đơn vị). Lời giải Trả Lời: 60
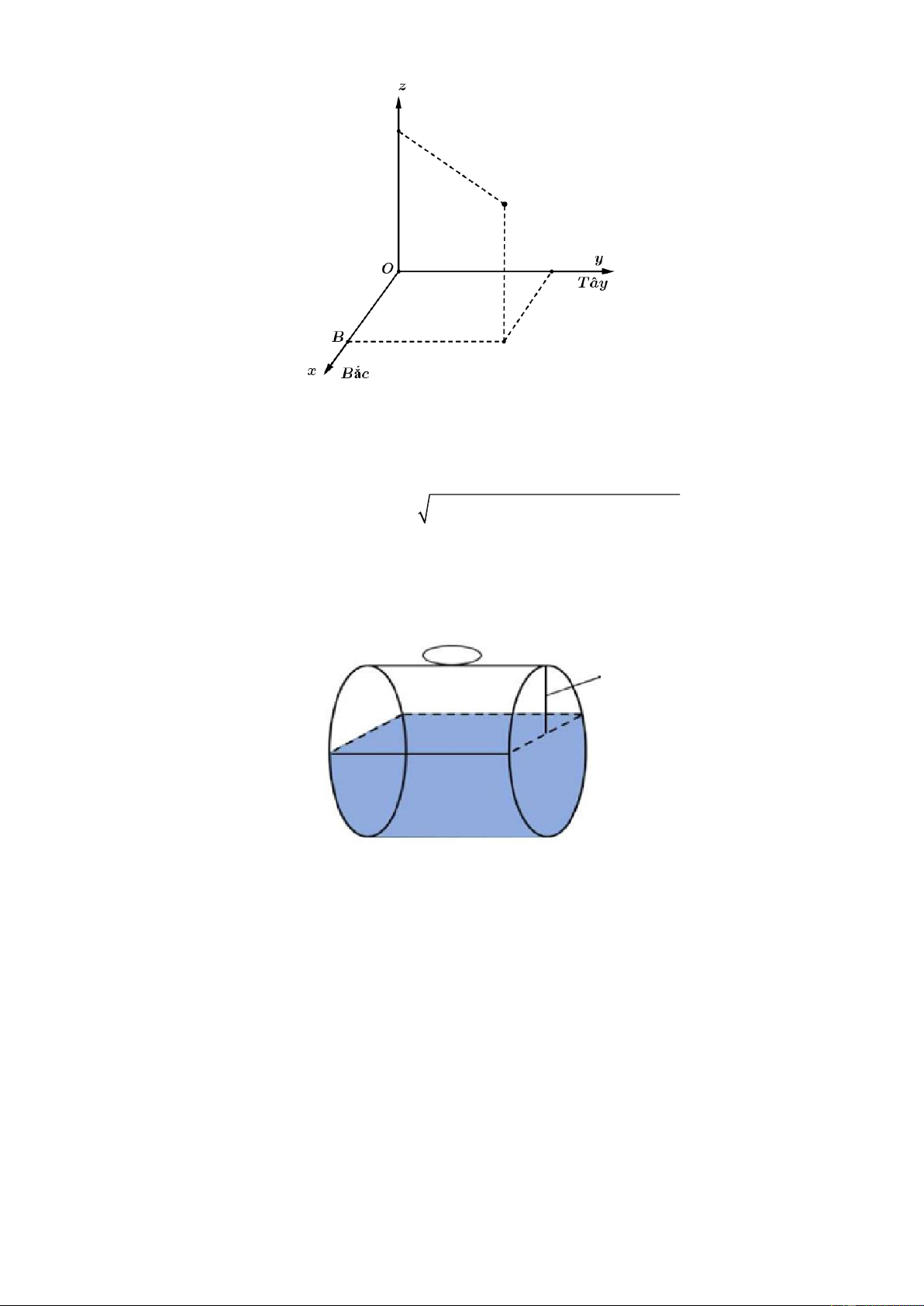
Chọn hệ trục tọa độ Oxyz , với gốc đặt tại điểm xuất phát của hai chiếc máy bay, mặt phẳng Oxy trùng
với mặt đất, trục Ox hướng về phía Bắc, trục Oy hướng về phía Tây, trục Oz hướng thẳng đứng lên trời,
đơn vị đo lấy theo kilômét (xem hình vẽ).
Chiếc máy bay thứ nhất có tọa độ 10;20;0,7.
Chiếc máy bay thứ hai có tọa độ 3 0; 2 5; 1 .
Do đó khoảng cách giữa hai chiếc máy bay là: 2 2 2 10 30 20 25 0, 7 1 60km
Câu 4: Một bể chứa nhiên liệu hình trụ đặt nằm ngang, có chiều dài 5 m, có bán kính đáy 1m. Chiều cao của
mực nhiên liệu là 1,5m. Tính thể tích phần nhiên liệu trong bể (theo đơn vị 3
m , làm tròn đến chữ số thâph
phân hàng phần trục). LỜI GIẢI
Thể tích của cả bể nhiên liệu là V B h 3 5 m .
Gọi V là thể tích phần trống nhiên liệu trong bể. 1
Chọn hệ trục Oxy như hình vẽ.
Ta có diện tích phần tô đậm là 3 3 3 3 2 2 2 2 1 3 2 2 2 S 2 1 x dx 2
1 x dx 2 dx 2 1 x dx 2 2 0 0 0 0 3 3 3 3 3 3 3 2 2
2 1 sin tcost dt
2 cos t dt 2 . 2 2 6 4 2 3 4 0 0 5 3 3
Vậy thể tích phần trống trong bể là V dx 5. 1 3 4 3 4 0 3
Vậy thể tích phần nhiên liệu trong bồn là V V V 5 5 12.6 3 m . 2 1 3 4
Câu 5: Nhà máy A chuyên sản xuất một loại sản phẩm cung cấp cho nhà máy B. Hai nhà máy này thoả thuận
rằng, hằng tuần A cung cấp cho B số lượng sản phẩm theo đơn đặt hàng của B (tối đa 100 sản phẩm). Nếu số
lượng đặt hàng là x sản phẩm thì giá bán cho mỗi sản phẩm là Px 2
450,001x (triệu đồng). Chi phí để A
sản xuất x sản phẩm trong một tuần là C x 10030x (triệu đồng) (gồm 100 triệu đồng chi phí cố định và 30
triệu đồng cho mỗi sản phẩm). Hỏi nhà máy A bán cho nhà máy B bao nhiêu sản phẩm mỗi tuần để thu được lợi
nhuận nhiều nhất? (Số sản phẩm là số nguyên dương). Lời giải Trả lời: 71
Câu 6: Có hai hộp bóng bàn, các quả bóng bàn có kích thước và hình dạng như nhau. Hộp I chứa
3 bóng bàn màu trắng và 2 bóng bàn màu vàng, hộp II chứa 6 bóng bàn màu trắng và 4 bóng bàn
màu vàng. Lấy ngẫu nhiên 4 quả bóng bàn ở hộp I bỏ vào hộp II rồi lấy ngẫu nhiên 1 quả bóng
bàn từ hộp II ra. Tính xác suất để quả bóng bàn lấy từ hộp II có màu vàng. Lời giải.
Gọi A :"Lấy được quả bóng bàn màu vàng từ hộp II" và
B :"Lấy được 4 quả bóng bàn ở hộp I, trong đó có đúng 1 quả màu vàng".
Ta có B : ' Lấy được 4 quả bóng bàn ở hộp I, trong đó có đúng 2 quả màu vàng".
TH1. B xảy ra
+) Số cách lấy 4 quả bóng bàn ở hộp I là 4
C , có 1 cách lấy 3 quả trắng và 2 cách lấy 1 5
quả vàng. Ta có P B 1.2 2 . 4 C 5 5
+) Sau khi bỏ 4 quả ở hộp I sang hộp II thì hộp II sẽ có 9 quả màu trắng và 5 quả màu vàng.
Do đó P A B 5 . 14
TH2. B xảy ra
+) Số cách lấy 4 quả ở hộp I là 4 C , có 2
C cách lấy ra 2 quả trắng và 1 cách lấy ra 2 quả 5 3
màu vàng từ hộp I. Ta có PB 2 C .1 3 3
hoặc có thể tính PB PB 2 3 1 1 . 4 C 5 5 5 5
+) Sau khi bỏ 4 quả ở hộp I sang hộp II thì hộp II sẽ có 8 quả màu trắng và 6 quả màu vàng.
Vậy P A B 6 3 . 14 7
Cuối cùng áp dụng công thức xác suất toàn phần:
P A P B P A B P B P A B 2 5 3 3 . . . . 0, 4 5 14 5 7
Đáp án: 0, 4
Document Outline
- Theo công thức Bayes, ta có: .