Đề thi thử tốt nghiệp THPT 2025 môn Toán cụm chuyên môn số 10 – Gia Lai
Bảng dưới đây thống kê lại cự li ném tạ của một vận động viên. Hãy tính độ lệch chuẩn của mẫu số liệu ghép nhóm này (kết quả làm tròn đến hàng phần trăm). Hàm số đã cho nghịch biến trên khoảng nào sau đây? Tại một vòng thi của đại hội thể thao, bốn vận động viên bắn súng. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi THPTQG môn Toán năm 2025 340 tài liệu
Môn: Toán 2.2 K tài liệu
Tác giả:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO GIA LAI
ĐỀ THI THỬ TỐT NGHIỆP THPT
CỤM CHUYÊN MÔN SỐ 10
NĂM HỌC: 2024 - 2025 MÔN: TOÁN
(Đề thi có 6 trang)
Thời gian làm bài: 90 phút
Họ và tên học sinh: ......................................... Phòng thi:…… , Số báo danh:…… Mã đề: 0101
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. (Mỗi câu hỏi học sinh chỉ chọn một phương án)
Câu 1: Trong không gian Oxyz , cho mặt phẳng (α) :x − 2y + 3 = 0. Một vectơ pháp tuyến của mặt phẳng (α) là:
A. n = (1;− 2;3) .
B. n = (1;− 2;0) .
C. n = (1;2;0) . D. n = (1;2;3).
Câu 2: Cho cấp số nhân (un) có u2 = 2, 3 u = 1
− . Khi đó u4 bằng A. 1 . B. 1 . C. 1 − . D. 1 . 8 2 4 4
Câu 3: Tìm tập xác định D của hàm số y = ( 2
ln 2025 − x ) . A. D = ( 45 − ;45) .
B. D = (45;+∞) . C. D = [ 45 − ;45]. D. D = ( ; −∞ 45 − ) .
Câu 4: Bảng dưới đây thống kê lại cự li ném tạ của một vận động viên Cự li (mét) [19;19,5) [ [ [ [ 19,5;20) 20;20,5) 20,5; ) 21 21;21,5) Số lần ném 13 45 24 12 6
Hãy tính độ lệch chuẩn của mẫu số liệu ghép nhóm này (kết quả làm tròn đến hàng phần trăm). A. 0,52. B. 0,53. C. 0,54. D. 0,55.
Câu 5: Cho hàm số y = f (x) liên tục, nhận giá trị dương trên đoạn [ ;
a b] . Xét hình phẳng (H ) giới hạn
bởi đồ thị hàm số y = f (x) , trục hoành và hai đường thẳng x = a, x = b. Gọi S là diện tích của hình phẳng
(H ) . Trong các khẳng định sau, khẳng định nào là sai? a b b b
A. S = − f
∫ (x)dx . B. S = f ∫ (x) dx .
C. S = − f ∫ (x)dx . D. S = f ∫ (x)dx . b a a a Câu 6: Cho hàm số ax + b y =
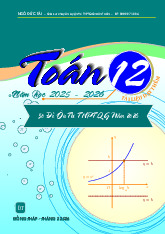
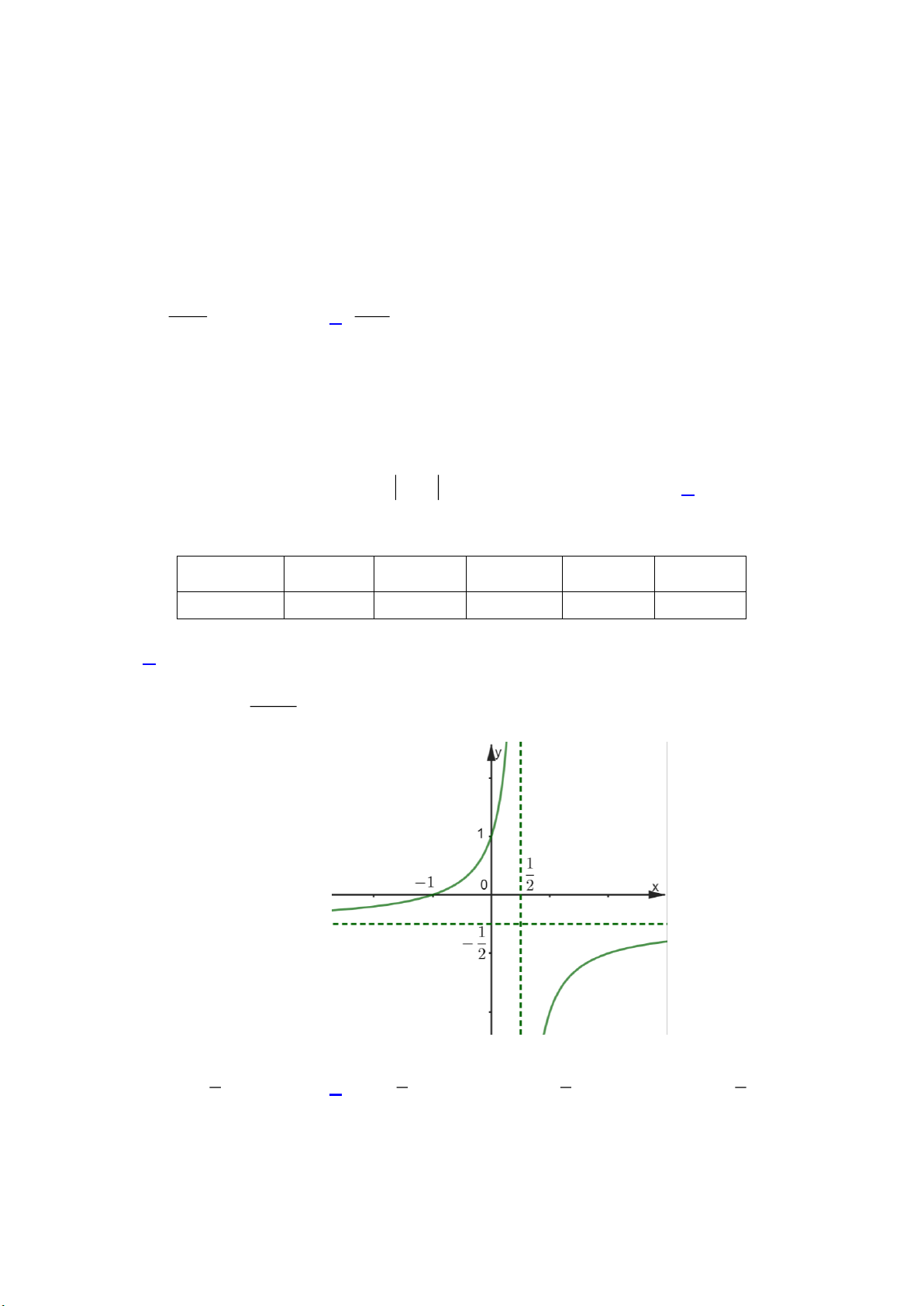
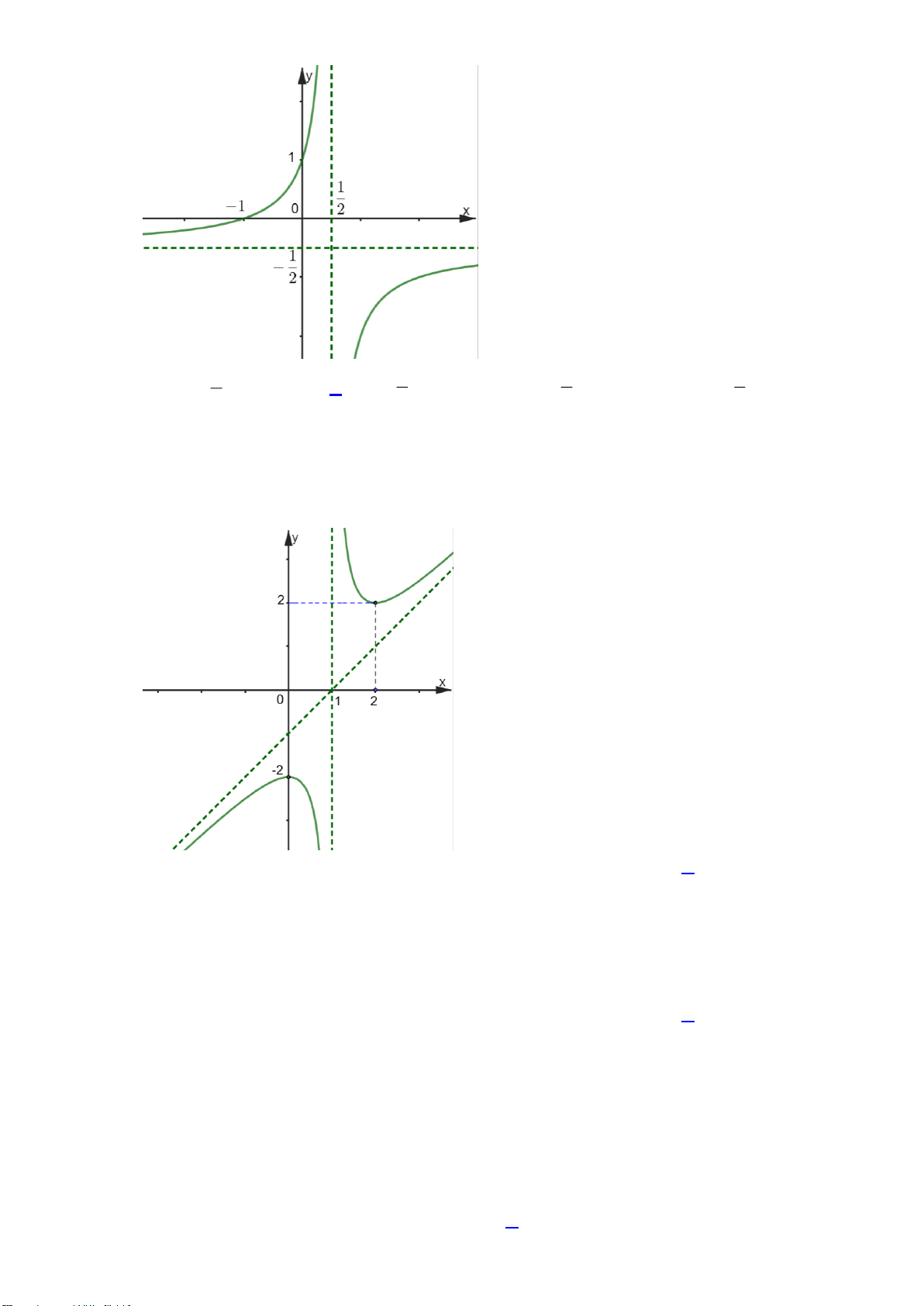
( c ≠ 0 , ad − bc ≠ 0 ) có đồ thị như hình vẽ: cx + d Trang 1/6 - Mã đề 0101
Tiệm cận ngang của đồ thị hàm số là: A. 1 y = . B. 1 x = . C. 1 x = − . D. 1 y = − . 2 2 2 2
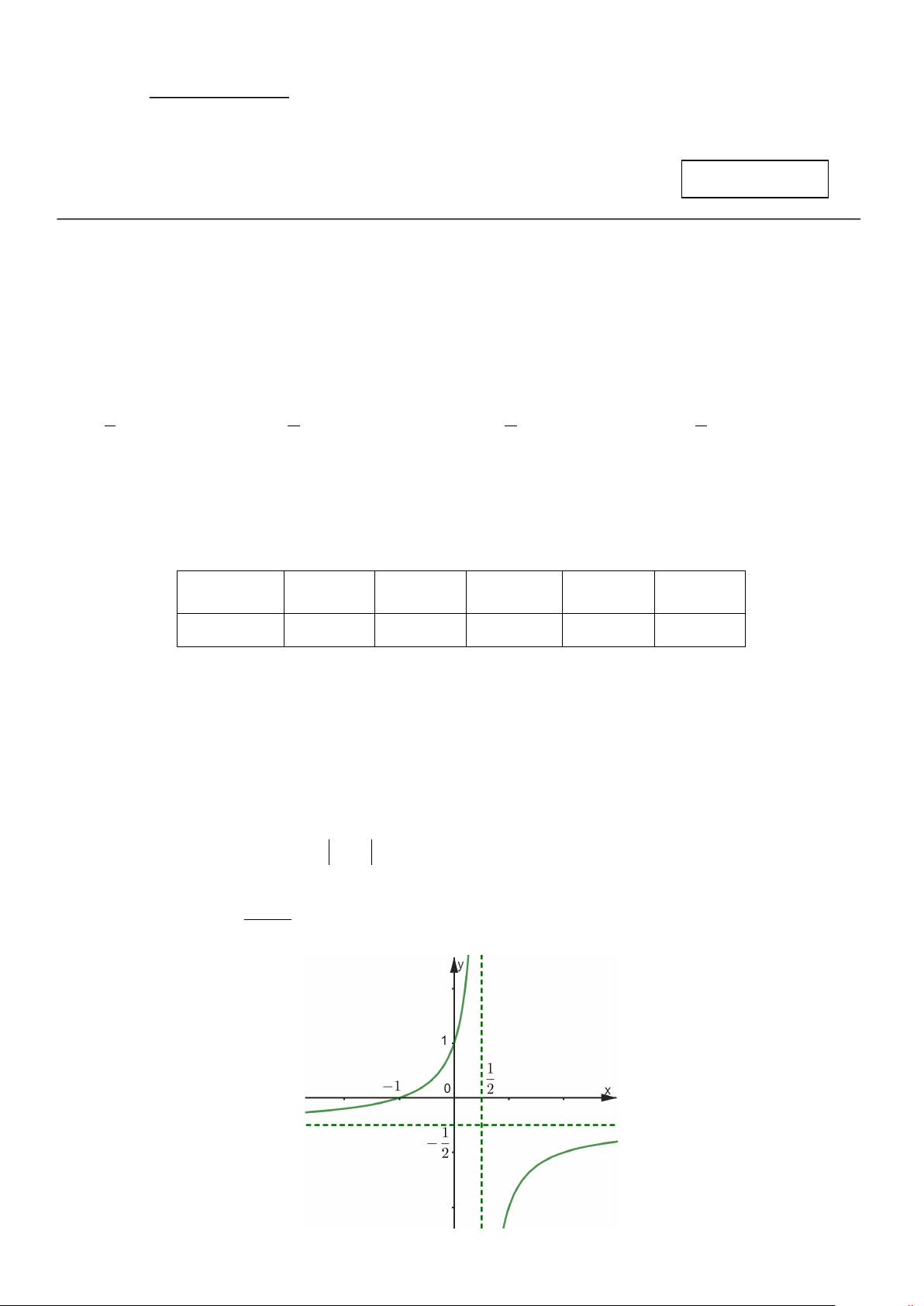
Câu 7: Cho hàm số có đồ thị như hình vẽ:
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
A. (0;1) và (1;2) . B. ( ; −∞ 0) và (2;+∞). C. ( ; −∞ 1) . D. (0;2) .
Câu 8: Nghiệm của phương trình 4x = 3 là
A. x = log43. B. x = log34. C. x = 4 . D. x = 3.
Câu 9: Nguyên hàm của hàm số ( ) 10x f x = là: x x 1 + A. 1 .10x x − + C . B. 10 + C . C. 10 + C .
D. 10x ln10 + C . ln10 x +1
Câu 10: Cho hình hộp ABC . D A′B C ′ D
′ ′ . Khi đó, tổng các vectơ D C
′ ′ + BC + AA′ bằng A. C A ′ . B. BD′ . C. AC′ . D. D B ′ . x = 2 − + 3t
Câu 11: Trong không gian Oxyz , cho đường thẳng : ∆ y = 2t
;(t ∈) . Một vectơ chỉ phương của z = 1
đường thẳng ∆ là:
A. u = (3;2;0). B. u = ( 2; − 0; ) 1 . C. u = (3;2; ) 1 . D. u = ( 2; − 2; ) 1 .
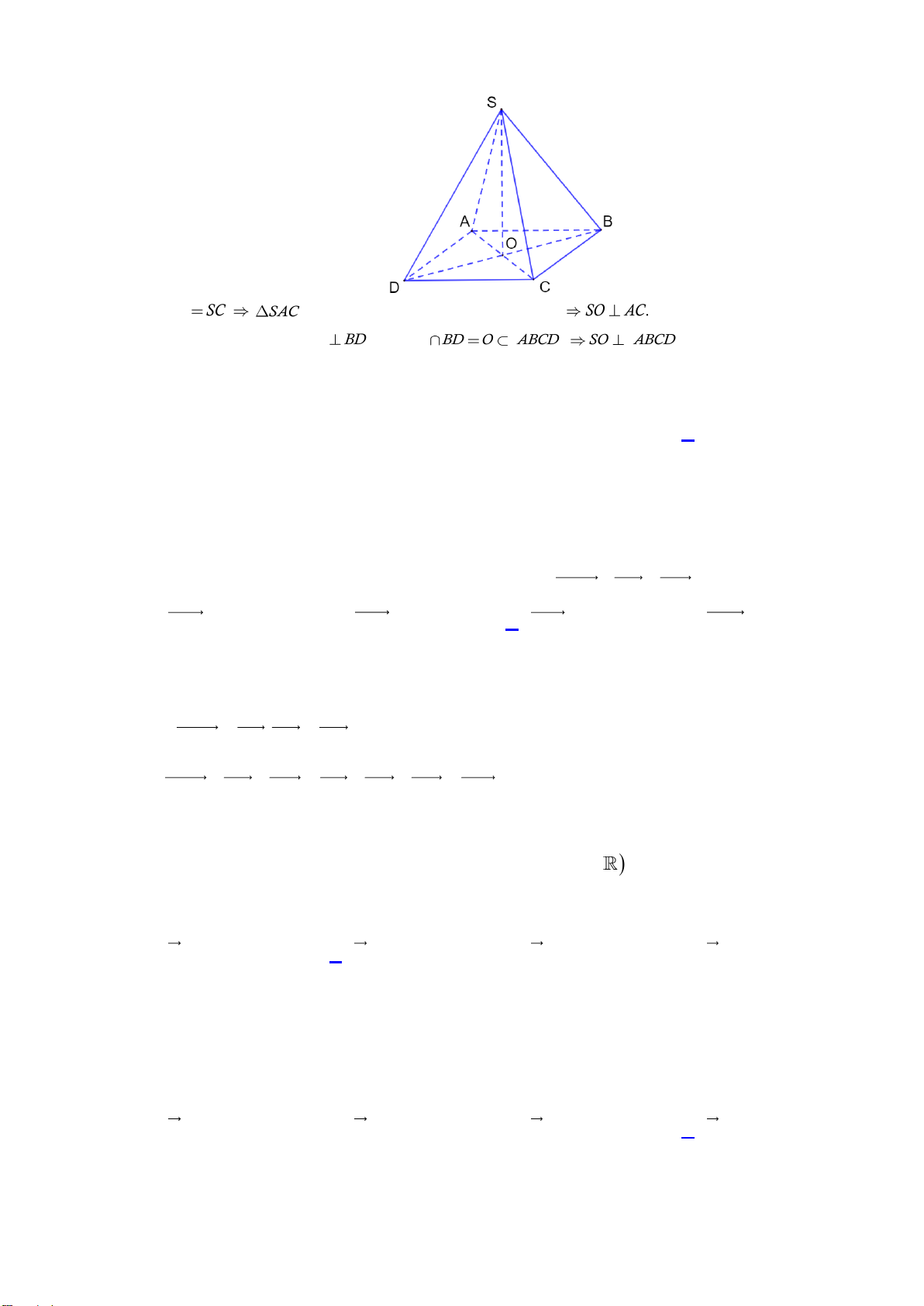
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O . Biết rằng SA = SC, SB = SD . Khẳng
định nào sau đây là đúng?
A. AB ⊥ (SAC).
B. CD ⊥ (SBD).
C. SO ⊥ ( ABCD) .
D. CD ⊥ AC . Trang 2/6 - Mã đề 0101
Phần II. Câu trắc nghiệm đúng, sai. (Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai).
Câu 1: Cho hàm số π
f (x) sin x = − − x . 3
a) Tập xác định của hàm số đã cho là π D \ kπ | k = + ∈. 3
b) Đạo hàm của hàm số π
f (x) là f '(x) cos x = − . 3
c) Nghiệm âm lớn nhất của phương trình π f '(x) = 0 là 5 x = − . 3
d) Giá trị lớn nhất của hàm số π
f (x) trên đoạn [0;2π ] là − . 3
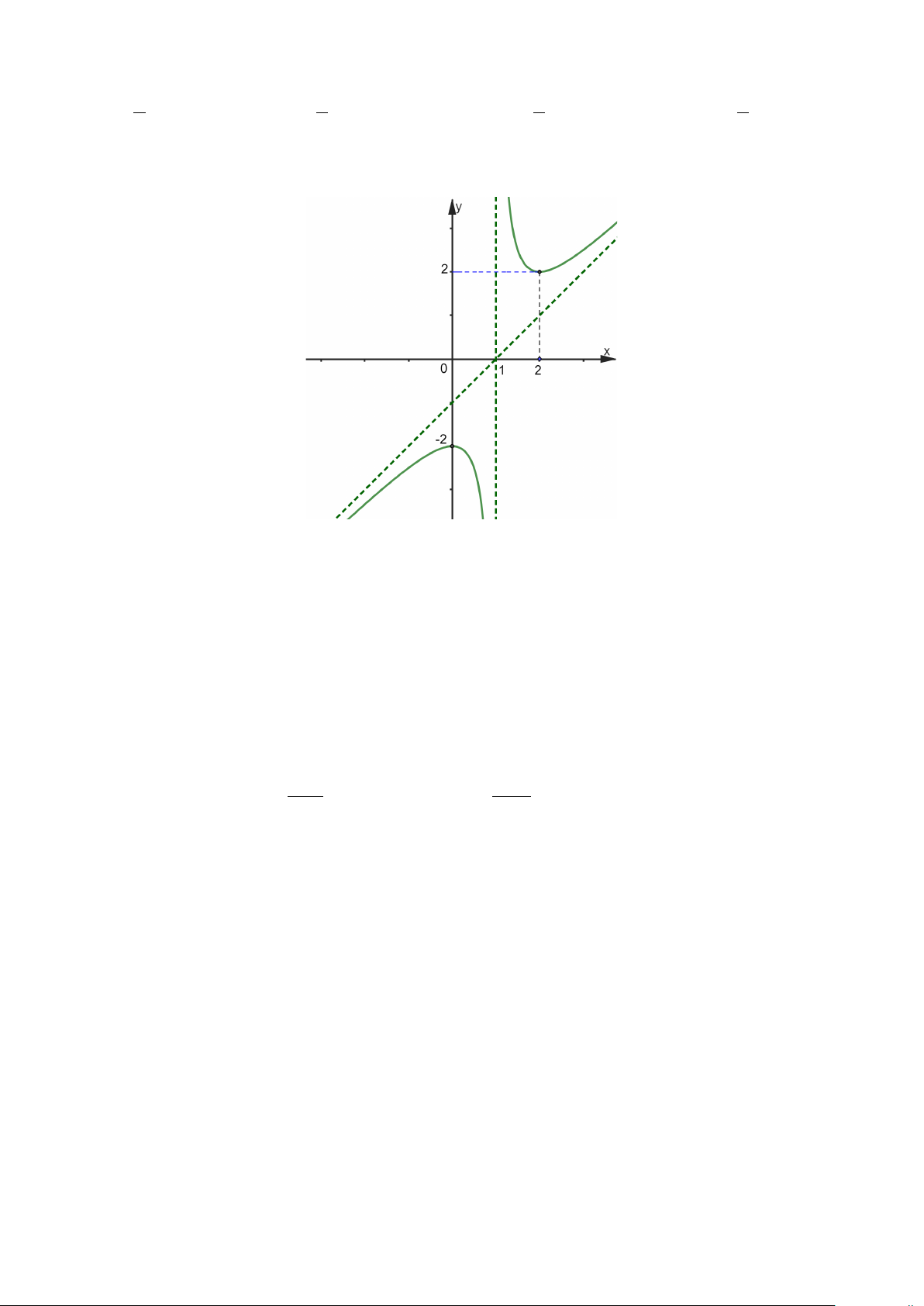
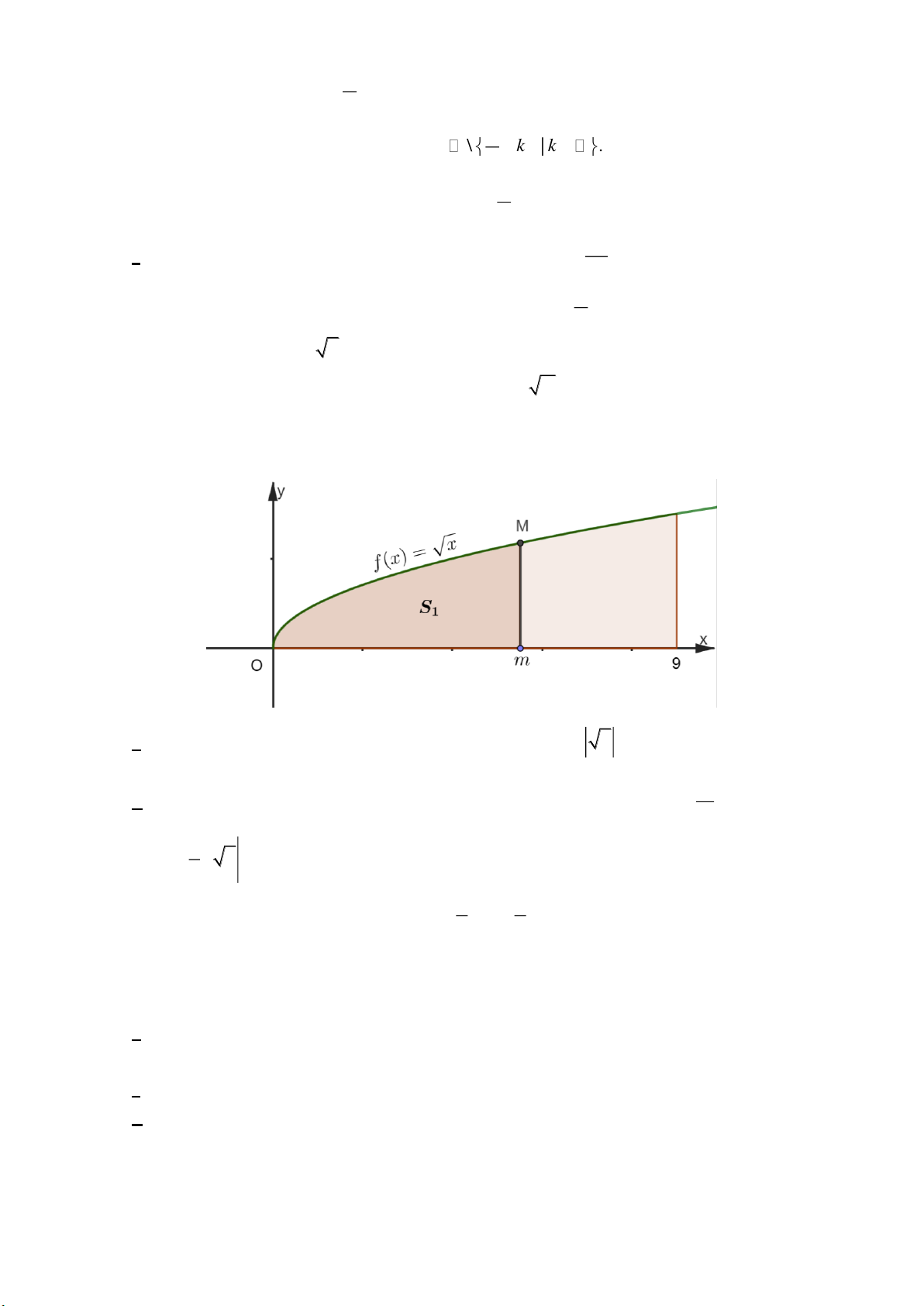
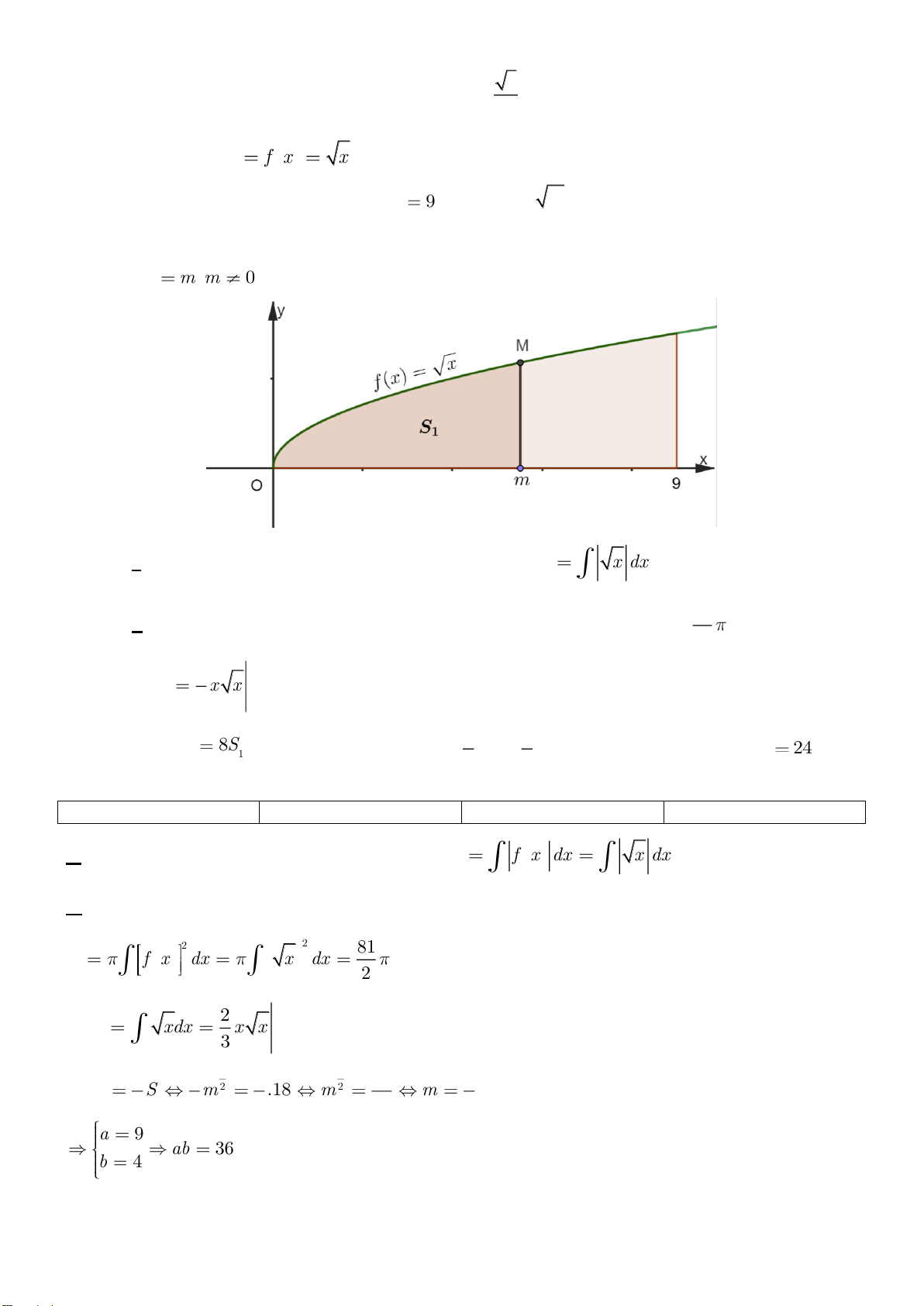
Câu 2: Cho hàm số y = f (x) = x có đồ thị (C). Gọi (H ) là hình phẳng giới hạn bởi (C), trục hoành,
trục tung và đường thẳng x = 9 . Cho M ( ;
m m ) là một điểm di động trên đồ thị (C); gọi 1S là diện tích
của hình phẳng giới hạn bởi (C), trục hoành, trục tung và đường thẳng x = m(m ≠ 0) (tham khảo hình vẽ bên dưới). 9
a) Diện tích S của hình (H ) được tính bởi công thức S = x dx ∫ . 0
b) Thể tích khối tròn xoay sinh ra khi quay hình (H ) quanh trục Ox bằng 81π . 2 m c) 3 1 S = x x . 2 0 d) Để S = 8 1
S thì điểm M có hoành độ là a ( với a là phân số tối giản). Khi đó ab = 24 . b b
Câu 3: Tại một vòng thi của đại hội thể thao, bốn vận động viên bắn súng A, B, C và D mỗi người bắn một
viên đạn vào tấm bia một cách độc lập. Biết rằng xác suất bắn trúng vòng 10 của bốn vận động viên A, B,
C, D lần lượt là 0,4; 0,5; 0,7; 0,8.
a) Xác suất để vận động viên A không bắn trúng vòng 10 là 0,6.
b) Xác suất để cả bốn vận động viên đều bắn trúng vòng 10 là 0,018. Trang 3/6 - Mã đề 0101
c) Xác suất để có đúng một vận động viên không bắn trúng vòng 10 là 0,356.
d) Xác suất để có nhiều nhất hai vận động viên bắn trúng vòng 10 là 0,532.
Câu 4: Trong không gian Oxyz , cho điểm (
A 1;−1;2) , mặt phẳng (α) :x + 2y +1 = 0 và đường thẳng x = 3t :
∆ y =1+ 2t ;(t ∈). z = 2 − + t a) Điểm (
A 1;−1;2) là một điểm thuộc mặt phẳng (α) .
b) Phương trình đường thẳng đi qua điểm (
A 1;−1;2) và vuông góc với mặt phẳng (α) là x =1+ t y = 1
− + 2t;(t ∈). z = 2+ t
c) Mặt phẳng chứa điểm (
A 1;−1;2) và chứa đường thẳng ∆ có phương trình là 10x −11y −8z − 5 = 0 .
d) Cosin của góc giữa đường thẳng ∆ và mặt phẳng (α) bằng 70 . 10
Phần III. Câu trắc nghiệm trả lời ngắn.
Câu 1: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2 , đường thẳng SA vuông góc với mặt phẳng
( ABCD) , góc giữa đường thẳng SB và mặt phẳng ( ABCD) bằng 60°. Tính khoảng cách giữa hai đường
thẳng SC và AD . (Kết quả làm tròn đến hàng phần trăm)
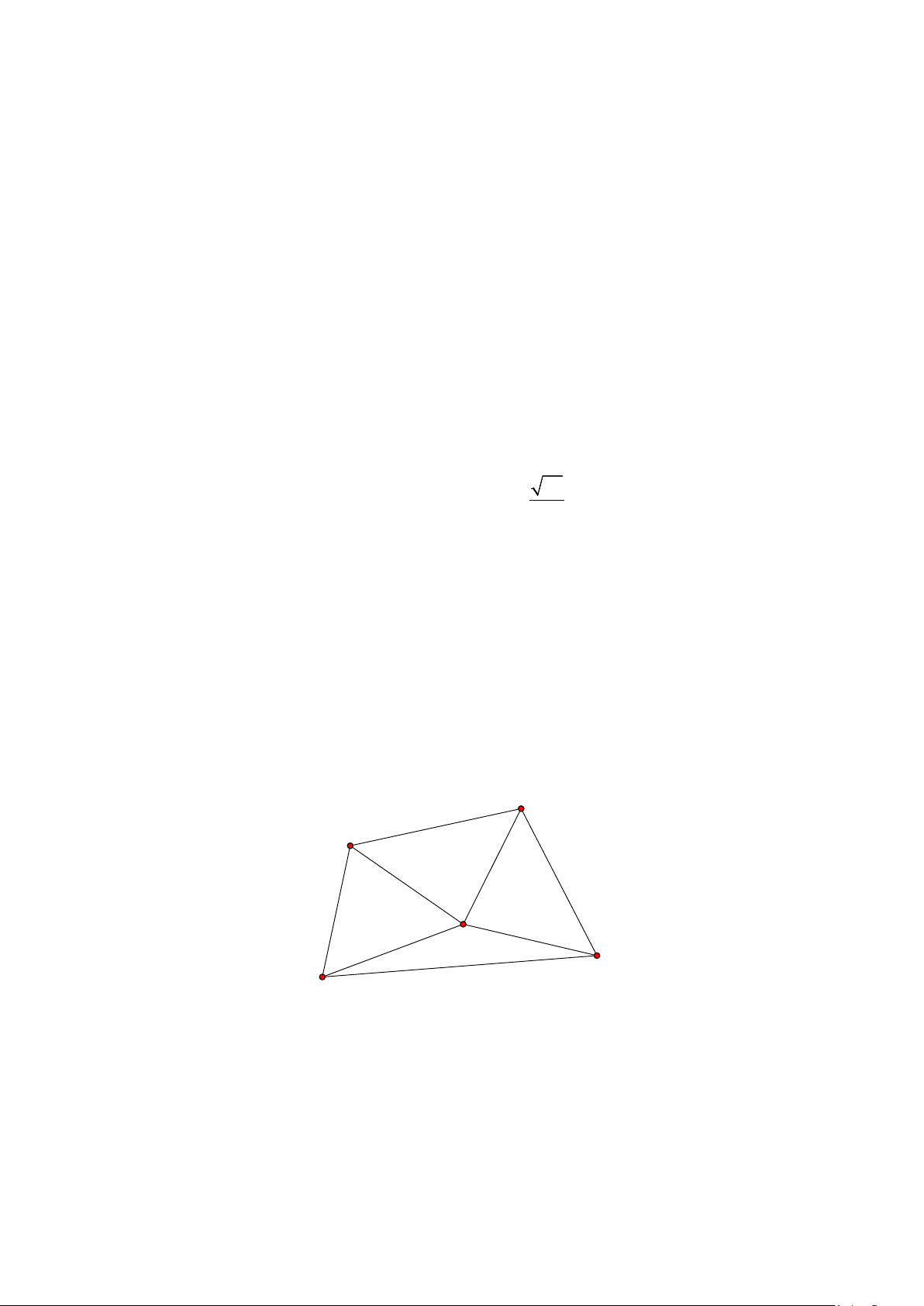
Câu 2: Một nhân viên của thư viện tỉnh muốn lập kế hoạch giới thiệu nội dung chương trình “Kết nối bạn
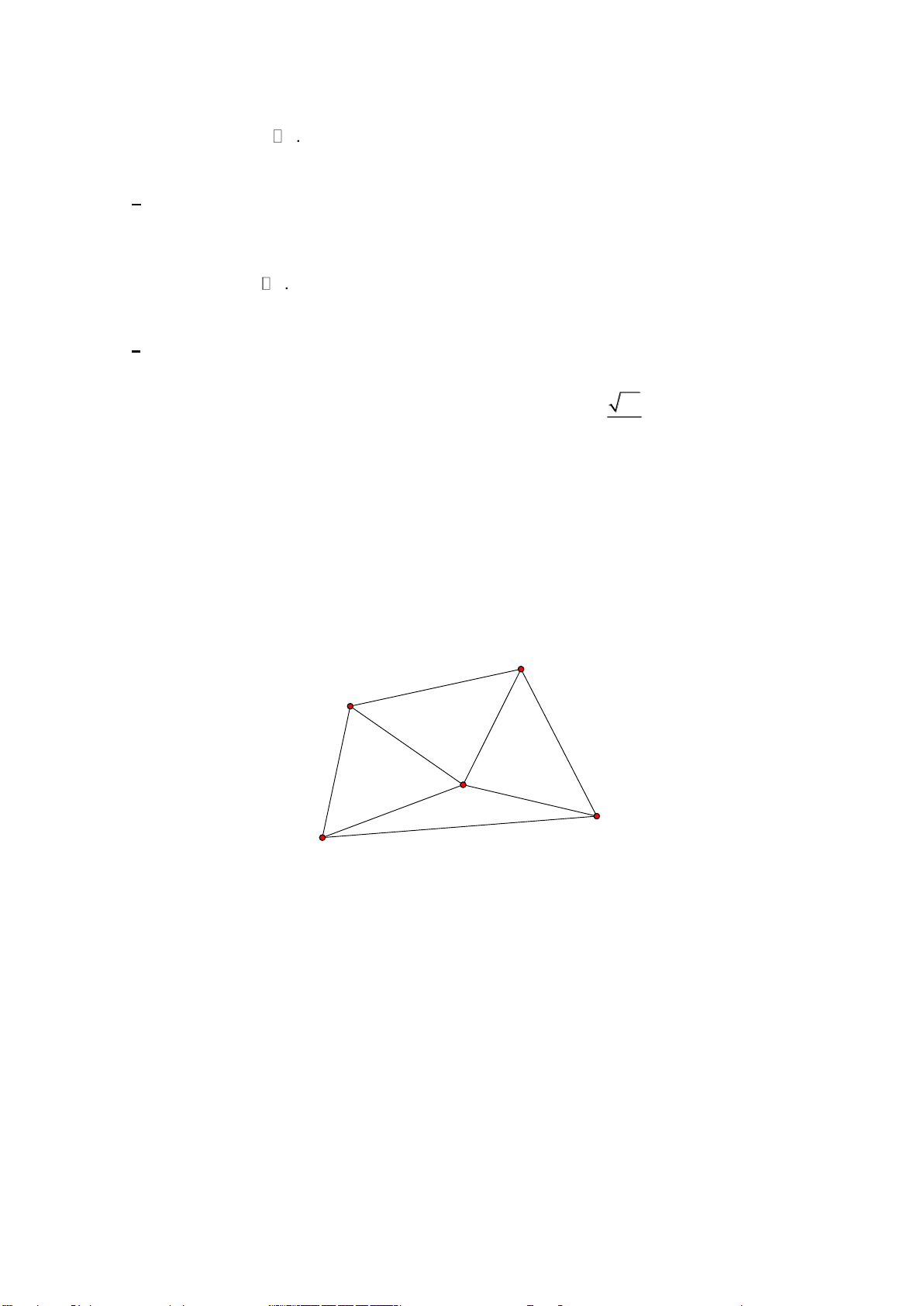
đọc yêu sách 2025” đến bốn trường học trong khu vực lân cận. Độ dài quãng đường giữa các địa điểm (đơn
vị: kilômét) được mô tả trong hình vẽ sau:
Trường D 4
Thư viện tỉnh 2 3 2 3
Trường B 4 5 7
Trường C
Trường A
Người nhân viên đó muốn xuất phát từ thư viện tỉnh và phải đi thăm cả bốn trường, mỗi trường chỉ đến đúng
một lần, rồi quay trở về thư viện tỉnh. Tổng độ dài quãng đường đi (đơn vị: kilômét) thỏa mãn điều kiện trên
nhận giá trị nhỏ nhất là bao nhiêu?
Câu 3: Một công ty xổ số kiến thiết phát hành loại vé số có 6 chữ số được lập từ tập hợp
X = {0;1;2;3;4;5;6;7;8; }
9 . Ông An chọn mua ngẫu nhiên một tờ vé số của công ty này. Tính xác suất để
ông An mua được vé số luôn có mặt cả hai chữ số 3 và 8 (làm tròn kết quả đến hàng phần chục). Trang 4/6 - Mã đề 0101
Câu 4: Một showroom ô tô trung bình bán được 45 ô tô loại A mỗi quý với giá 1,299 tỷ đồng một xe. Một
cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 200 triệu đồng, số lượng ô tô loại A đó bán ra sẽ
tăng thêm khoảng 20 xe mỗi quý. Biết rằng hàm chi phí hàng quý là 3 2
C(x) = 0,001x − 0,085x +1,437x + 0,3 (tỷ đồng), trong đó x là số ô tô bán ra trong một quý. Nhà sản xuất
nên đặt giá bán (đơn vị tỷ đồng) như thế nào để lợi nhuận là lớn nhất (làm tròn kết quả đến hàng phần trăm)?
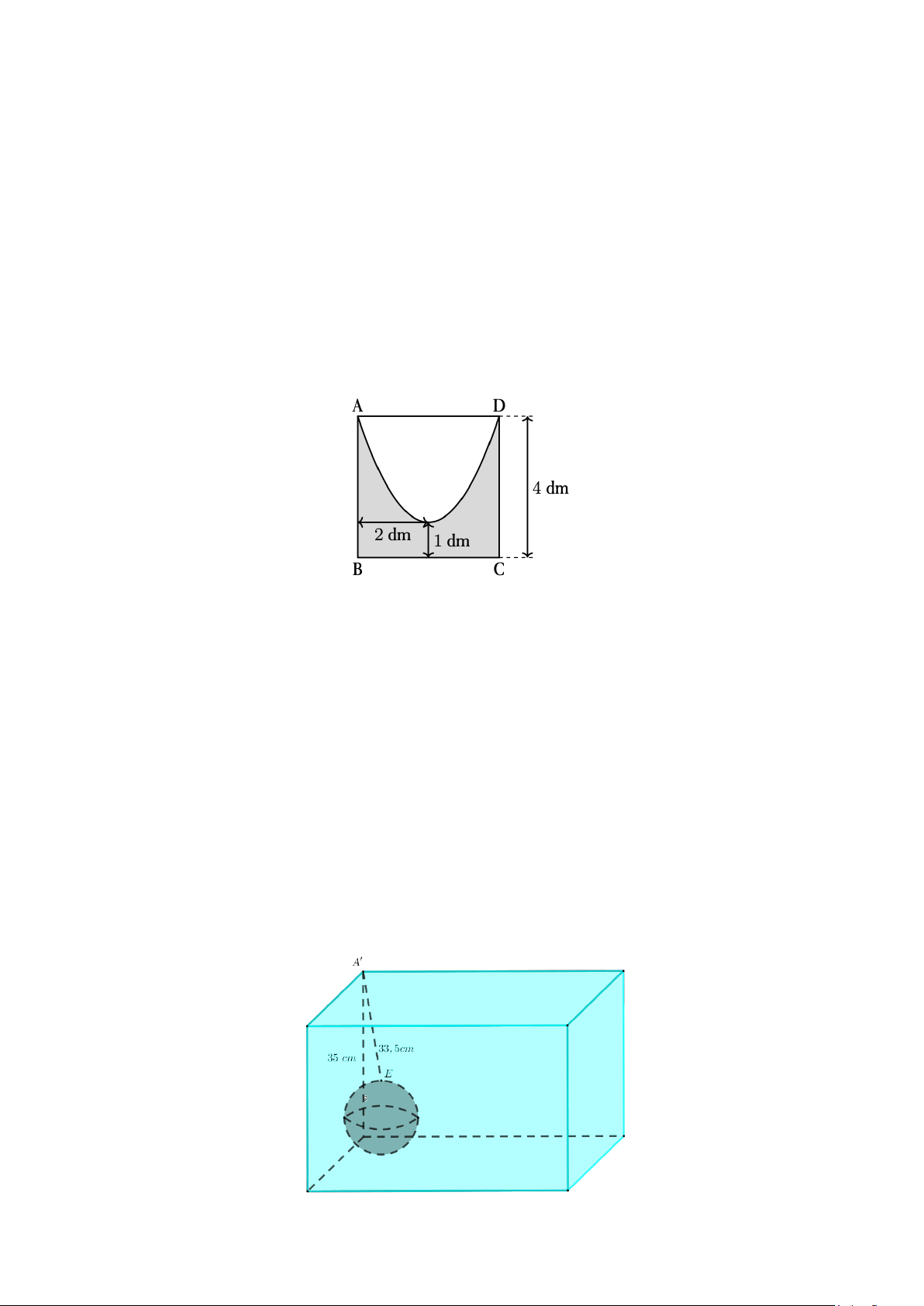
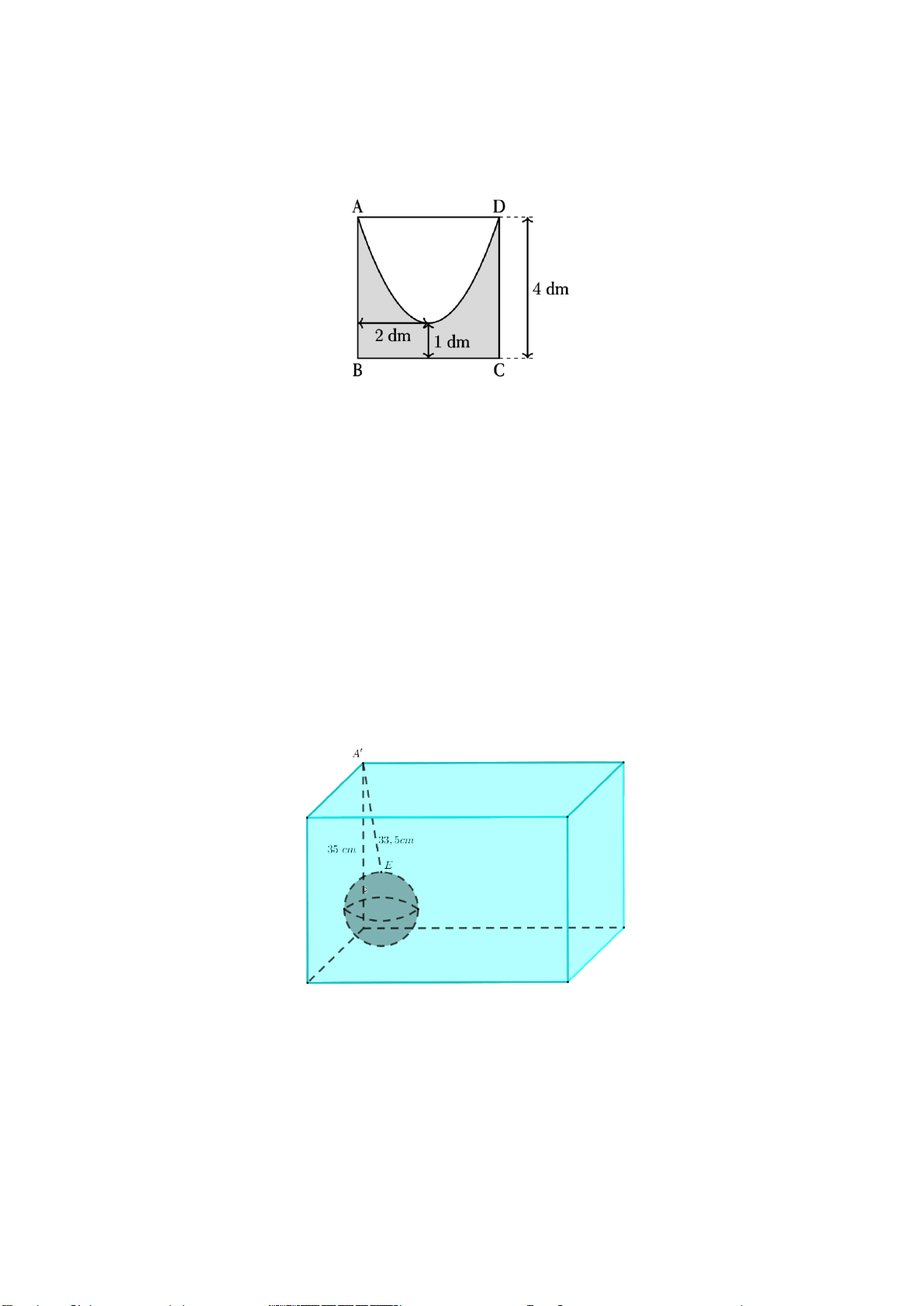
Câu 5: Cho hình vuông ABCD có độ dài cạnh bằng 4 dm, trong đó (H ) là phần được tô màu đậm có
đường biên cong là một phần của parabol (P). Biết rằng khoảng cách từ đỉnh của (P) đến hai đường thẳng
AB, BC lần lượt là 2 dm và 1dm, đồng thời (P) đi qua hai đỉnh A và D của hình vuông (xem hình minh họa).
Người ta cần sản xuất một sản phẩm là vật thể tròn xoay sinh ra khi quay (H ) quanh đường thẳng BC. Hỏi
thể tích vật thể đó là bao nhiêu đề-xi-mét khối (làm tròn kết quả đến hàng phần chục)?
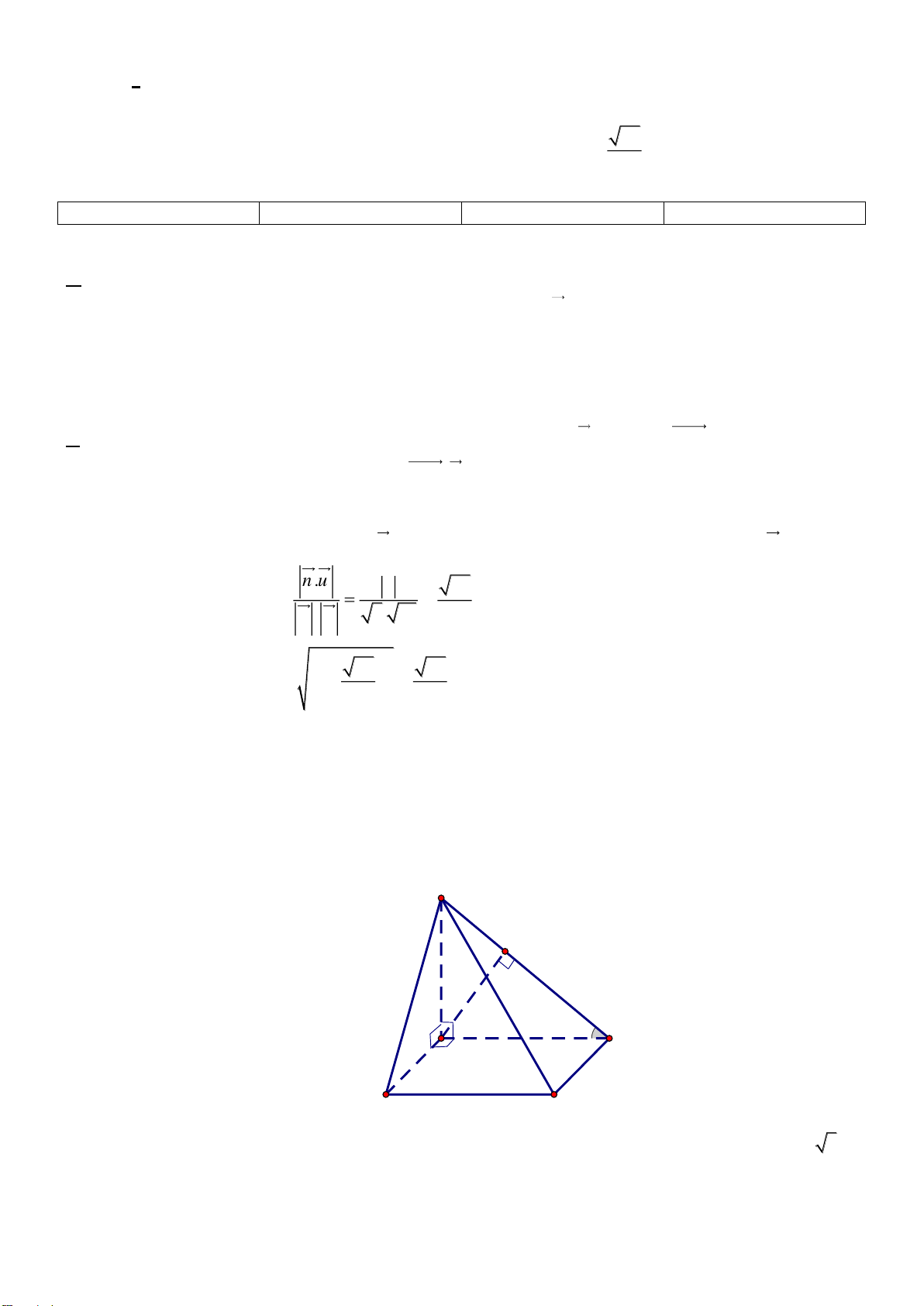
Câu 6: Một cái bể nuôi cá có dạng hình hộp chữ nhật và chứa đầy nước. Bạn Nam vô tình làm rơi viên bi
dạng hình cầu vào trong bể nuôi cá. Khi đó, lượng nước trong bể tràn ra ngoài. Để tính lượng nước tràn ra
ngoài, bạn Nam làm như sau:
Lấy cây thước thẳng, tiến hành di chuyển viên bi vào trong góc, sao cho viên bi tiếp xúc với mặt đáy và hai
thành của bể nuôi cá. Bạn Nam tiến lại vị trí đỉnh của hình hộp chữ nhật gần với viên bi nhất và tiến hành
đo: Chiều cao của bể là 35cm . Tại vị trí đứng của Nam, đo từ đỉnh cao nhất của hình hộp chữ nhật đến điểm
cao nhất của viên bi so với đáy bể là 33,5cm . Biết thể tích của viên bi không vượt quá 3 4cm . (Hình vẽ
minh họa bên dưới với A'E = 33,5cm ). Trang 5/6 - Mã đề 0101
Bạn hãy thay Nam, tính thể tích (đơn vị: xăng-ti-mét khối) của lượng nước tràn ra ngoài. (Bán kính viên bi
và lượng nước tràn ra ngoài làm tròn đến chữ số hàng phần trăm).
------ HẾT ------ Trang 6/6 - Mã đề 0101 Phần I Câu 101 102 103 104 1 B C A D 2 B C A A 3 A C C A 4 B B B A 5 C C C C 6 D A D D 7 A C D D 8 A A A A 9 B B C D 10 C C D B 11 A A D B 12 C A C D Phần II Câu 101 102 103 104 1 SSĐS SSĐS SSĐS SSĐS 2 ĐĐSS ĐĐSS ĐĐSS ĐĐSS 3 ĐSĐĐ ĐSĐĐ ĐSĐĐ ĐSĐĐ 4 ĐSĐS ĐSĐS ĐSĐS ĐSĐS Phần III Câu 101 102 103 104 1 1,73 1,73 1,73 1,73 2 17 17 17 17 3 0,2 0,2 0,2 0,2 4 1,23 1,23 1,23 1,23 5 60,3 60,3 60,3 60,3 6 1,84 1,84 1,84 1,84
Xem thêm: ĐỀ THI THỬ THPT MÔN TOÁN
https://toanmath.com/de-thi-thu-thpt-mon-toan
SỞ GIÁO DỤC VÀ ĐÀO TẠO GIA LAI
KỲ THI THỬ TỐT NGHIỆP THPT NĂM 2025 CỤM SỐ 10 MÔN: TOÁN
(Đề thi có 05 trang)
Thời gian làm bài 90 phút, không kể thời gian phát đề
Họ, tên thí sinh: ………………….……………………………………Số báo danh: …………
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Nguyên hàm của hàm số 10x f x là: x 1 10 10x A. C . B. C .
C. 10x ln10 C . D. 1 .10x x C . x 1 ln10
Câu 2: Cho hàm số y f x liên tục, nhận giá trị dương trên đoạn ;
a b . Xét hình phẳng H giới hạn
bởi đồ thị hàm số y f x , trục hoành và hai đường thẳng x ,
a x b . Gọi S là diện tích
của hình phẳng H . Trong các khẳng định sau, khẳng định nào là sai? b b a b A. S f xdx. B. S f
x dx . C. S f
xdx . D. S f xdx . a a b a
Câu 3: Bảng dưới đây thống kê lại cự li ném tạ của một vận động viên Cự li (mét)
19;19,5 19,5;20 20;20,5 20,5;2 1 21;21,5 Số lần ném 13 45 24 12 6
Hãy tính độ lệch chuẩn của mẫu số liệu ghép nhóm này (kết quả làm tròn đến hàng phần trăm). A. 0,53 . B. 0,52 . C. 0,54 . D. 0,55 . ax b
Câu 4: Cho hàm số y
( c 0 , ad bc 0 ) có đồ thị như hình vẽ: cx d
Tiệm cận ngang của đồ thị hàm số là: 1 1 1 1 A. x . B. y . C. y . D. x . 2 2 2 2
Câu 5: Cho hàm số có đồ thị như hình vẽ: 1
Hàm số đã cho nghịch biến trên khoảng nào sau đây? A. ( ; 0) và (2; ) . B. ( ; 1) . C. (0;2) . D. (0;1) và (1;2) .
Câu 6: Tìm tập xác định D của hàm số y 2 ln 2025 x .
A. D 45; .
B. D ; 4 5. C. D 4 5;4 5 . D. D 4 5;45 .
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O . Biết rằng SA SC, SB SD . Khẳng
định nào sau đây là đúng?
A. AB SAC.
B. CD AC .
C. SO ABCD .
D. CD SBD .
Câu 8: Nghiệm của phương trình 4x 3 là
A. x log 4 . B. x 3 . C. x 4 .
D. x log 3 . 3 4
Câu 9: Cho hình hộp ABC . D A B C D
. Khi đó, tổng các vectơ D C
BC AA bằng A. C A . B. BD . C. AC . D. D B . x 2 3t
Câu 10: Trong không gian Oxyz , cho đường thẳng : y 2t
;t . Một vectơ chỉ phương của z 1 đường thẳng là:
A. u 3;2; 1 .
B. u 3;2;0 . C. u 2 ;0; 1 . D. u 2 ;2; 1 .
Câu 11: Trong không gian Oxyz , cho mặt phẳng () :x 2y 3 0 . Một vectơ pháp tuyến của mặt phẳng ( ) là:
A. n 1;2;3 .
B. n 1;2;0 .
C. n 1; 2;3 .
D. n 1; 2;0 .
Câu 12: Cho cấp số nhân (u ) có u 2, u 1
. Khi đó u bằng n 2 3 4 1 1 1 1 A. . B. . C. . D. . 4 2 8 4
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. 2
Câu 1: Cho hàm số f (x) sin x x . 3
a) Tập xác định của hàm số đã cho là D
\ k | k . 3
b) Đạo hàm của hàm số f (x) là f '(x) cos x . 3 5
c) Nghiệm âm lớn nhất của phương trình f '(x) 0 là x . 3
d) Giá trị lớn nhất của hàm số f (x) trên đoạn 0;2 là . 3
Câu 2: Cho hàm số y f x x có đồ thị C . Gọi H là hình phẳng giới hạn bởi C , trục
hoành, trục tung và đường thẳng x 9 . Cho M ; m
m là một điểm di động trên đồ thị C ;
gọi S là diện tích của hình phẳng giới hạn bởi C , trục hoành, trục tung và đường thẳng 1
x mm 0 (tham khảo hình vẽ bên dưới). 9
a) Diện tích S của hình H được tính bởi công thức S x dx . 0 81
b) Thể tích khối tròn xoay sinh ra khi quay hình H quanh trục Ox bằng . 2 m 3 c) S x x . 1 2 0 a a
d) Để S 8S thì điểm M có hoành độ là ( với
là phân số tối giản). Khi đó ab 24 . 1 b b
Câu 3: Tại một vòng thi của đại hội thể thao, bốn vận động viên bắn súng A, B, C và D mỗi người bắn
một viên đạn vào tấm bia một cách độc lập. Biết rằng xác suất bắn trúng vòng 10 của bốn vận
động viên A, B, C, D lần lượt là 0,4; 0,5; 0,7; 0,8.
a) Xác suất để vận động viên A không bắn trúng vòng 10 là 0,6.
b) Xác suất để cả bốn vận động viên đều bắn trúng vòng 10 là 0,018.
c) Xác suất để có đúng một vận động viên không bắn trúng vòng 10 là 0,356.
d) Xác suất để có nhiều nhất hai vận động viên bắn trúng vòng 10 là 0,532. 3
Câu 4: Trong không gian Oxyz , cho điểm (
A 1;1;2) , mặt phẳng () :x 2y 1 0 và đường thẳng x 3t
:y 1 2t ;t . z 2 t a) Điểm (
A 1;1;2) là một điểm thuộc mặt phẳng ( ) .
b) Phương trình đường thẳng đi qua điểm (
A 1;1;2) và vuông góc với mặt phẳng ( ) là x 1 t y 1
2t ;t . z 2t
c) Mặt phẳng chứa điểm (
A 1;1;2) và chứa đường thẳng có phương trình là
10x 11y 8z 5 0 . 70
d) Cosin của góc giữa đường thẳng và mặt phẳng ( ) bằng . 10
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2 , đường thẳng SA vuông góc với mặt
phẳng ABCD , góc giữa đường thẳng SB và mặt phẳng ABCD bằng 60 . Tính khoảng
cách giữa hai đường thẳng SC và AD . (Kết quả làm tròn đến hàng phần trăm)
Câu 2: Một nhân viên của thư viện tỉnh muốn lập kế hoạch giới thiệu nội dung chương trình “Kết nối
bạn đọc yêu sách 2025” đến bốn trường học trong khu vực lân cận. Độ dài quãng đường giữa
các địa điểm (đơn vị: kilômét) được mô tả trong hình vẽ sau:
Trường D 4
Thư viện tỉnh 3 2 2 3
Trường B 4 5
Trường C 7
Trường A
Người nhân viên đó muốn xuất phát từ thư viện tỉnh và phải đi thăm cả bốn trường, mỗi trường
chỉ đến đúng một lần, rồi quay trở về thư viện tỉnh. Tổng độ dài quãng đường đi (đơn vị:
kilômét) thỏa mãn điều kiện trên nhận giá trị nhỏ nhất là bao nhiêu?
Câu 3: Một công ty xổ số kiến thiết phát hành loại vé số có 6 chữ số được lập từ tập hợp
X 0;1;2;3;4;5;6;7;8;
9 . Ông An chọn mua ngẫu nhiên một tờ vé số của công ty này. Tính
xác suất để ông An mua được vé số luôn có mặt cả hai chữ số 3 và 8 (làm tròn kết quả đến hàng phần chục).
Câu 4: Một showroom ô tô trung bình bán được 45 ô tô loại A mỗi quý với giá 1, 299 tỷ đồng một xe.
Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 200 triệu đồng, số lượng ô tô loại
A đó bán ra sẽ tăng thêm khoảng 20 xe mỗi quý. Biết rằng hàm chi phí hàng quý là 3 2
C(x) 0, 001x 0, 085x 1, 437x 0,3 (tỷ đồng), trong đó x là số ô tô bán ra trong một quý.
Nhà sản xuất nên đặt giá bán (đơn vị tỷ đồng) như thế nào để lợi nhuận là lớn nhất (làm tròn kết
quả đến hàng phần trăm)? 4
Câu 5: Cho hình vuông ABCD có độ dài cạnh bằng 4 dm, trong đó H là phần được tô màu đậm
có đường biên cong là một phần của parabol P. Biết rằng khoảng cách từ đỉnh của P đến hai đường
thẳng AB, BC lần lượt là 2 dm và 1dm, đồng thời P đi qua hai đỉnh A và D của hình vuông (xem hình minh họa).
Người ta cần sản xuất một sản phẩm là vật thể tròn xoay sinh ra khi quay H quanh đường thẳng BC.
Hỏi thể tích vật thể đó là bao nhiêu đề-xi-mét khối (làm tròn kết quả đến hàng phần chục)?
Câu 6: Một cái bể nuôi cá có dạng hình hộp chữ nhật và chứa đầy nước. Bạn Nam vô tình làm rơi viên bi
dạng hình cầu vào trong bể nuôi cá. Khi đó, lượng nước trong bể tràn ra ngoài. Để tính lượng nước tràn ra
ngoài, bạn Nam làm như sau:
Lấy cây thước thẳng, tiến hành di chuyển viên bi vào trong góc, sao cho viên bi tiếp xúc với mặt đáy và
hai thành của bể nuôi cá. Bạn Nam tiến lại vị trí đỉnh của hình hộp chữ nhật gần với viên bi nhất và tiến
hành đo: Chiều cao của bể là 35cm . Tại vị trí đứng của Nam, đo từ đỉnh cao nhất của hình hộp chữ nhật
đến điểm cao nhất của viên bi so với đáy bể là 33,5cm . Biết thể tích của viên bi không vượt quá 3 4cm .
(Hình vẽ minh họa bên dưới với A' E 33,5cm ).
Bạn hãy thay Nam, tính thể tích (đơn vị: xăng-ti-mét khối) của lượng nước tràn ra ngoài. (Bán kính viên
bi và lượng nước tràn ra ngoài làm tròn đến chữ số hàng phần trăm). … HẾT… 5
ĐÁP ÁN ĐỀ THI THỬ - Môn: TOÁN
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Câu 1 2 3 4 5 6 7 8 9 10 Chon B D A B D D C D C B Câu 11 12 Chọn D B
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Thí sinh chỉ lựa chọn chính xác 01 ý trong 01 câu hỏi được 0,1 điểm;
Thí sinh chỉ lựa chọn chính xác 02 ý trong 01 câu hỏi được 0,25 điểm;
Thí sinh chỉ lựa chọn chính xác 03 ý trong 01 câu hỏi được 0,5 điểm;
Thí sinh lựa chọn chính xác cả 04 ý trong 01 câu hỏi được 1 điểm. Câu 1 2 3 4 S Đ Đ Đ S Đ S S Đáp án Đ S Đ Đ S S Đ S
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. Mỗi câu trả lời đúng thí sinh được 0,5 điểm. Câu 1 2 3 4 5 6 Đáp án 1,73 17 0,2 1,23 60,3 1,84 6 HƯỚNG DẪN GIẢI
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Nguyên hàm của hàm số 10x f x là: x 1 10 10x A. C . B. C . C. 10x ln10 C . D. 1 .10x x C . x 1 ln10 Lời giải x 10x 10 dx C . ln10 Đáp án: B
Câu 2: Cho hàm số y
f x liên tục, nhận giá trị dương trên đoạn a;b . Xét hình phẳng H giới hạn
bởi đồ thị hàm số y
f x , trục hoành và hai đường thẳng x , a x
b . Gọi S là diện tích
của hình phẳng H . Trong các khẳng định sau, khẳng định nào là sai? b b a b A. S f x dx . B. S
f x dx . C. S
f x dx . D. S f x dx . a a b a Lời giải b a b S f
xdx f
xdx f x dx a b a Đáp án: D
Câu 3: Bảng dưới đây thống kê lại cự li ném tạ của một vận động viên Cự li (mét) 19;19, 5 19, 5;20 20;20, 5 20, 5;21 21;21, 5 Số lần ném 13 45 24 12 6
Hãy tính độ lệch chuẩn của mẫu số liệu ghép nhóm này (kết quả làm tròn đến hàng phần trăm). A. 0, 53 . B. 0, 52 . C. 0, 54 . D. 0, 55 . Lời giải 19.25.13 19,75.45 20,25.24 20,75.12 21,25.6 x 20, 015 13 45 24 12 6 2 2 2 2 2 19,25 .13 19,75 .45 20,25 .24 20,75 .12 21,25 .6 2 s 20, 015 0,53 13 45 24 12 6 Đáp án: A ax b
Câu 4: Cho hàm số y
c , ad bc 0 ) có đồ thị như hình vẽ bên. Tiệm cận ngang của đồ thị cx ( 0 d hàm số là: 7 1 1 1 1 A. x . B. y . C. y . D. x . 2 2 2 2 Lời giải Đáp án: B
Câu 5: Cho hàm số có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào sau đây? A. ( ; 0) và (2; ) . B. ( ; 1). C. (0; 2) . D. (0;1) và (1; 2) . Lời giải Đáp án: D
Câu 6: Tìm tập xác định 2
D của hàm số y ln 2025 x .
A. D 45; .
B. D ; 4 5 . C. D 4 5;4 5 . D. D 4 5;45 . Lời giải Hàm số có nghĩa khi 2 2025 x 0 4 5 x 45
Vậy tập xác định của hàm số là: D ; 2024. Đáp án: D
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O . Biết rằng SA SC, SB SD . Khẳng
định nào sau đây là đúng?
A. AB SAC .
B. CD AC .
C. SO ABCD .
D. CD SBD . 8 Lời giải Vì SA SC
SAC cân tại S mà O là trung điểm AC SO AC.
Tương tự, ta cũng có SO BD mà AC BD O ABCD SO ABCD . Đáp án: C
Câu 8: Nghiệm của phương trình 4x 3 là
A. x log 4 . B. . C. .
D. x log 3 . 3 x 3 x 4 4 Lời giải
Ta có: 4x 3 x log 3. 4 Đáp án: D
Câu 9: Cho hình hộp ABC .
D A' B'C ' D' . Khi đó, tổng các véc tơ D'C ' BC AA' bằng
A. C ' A . B. BD ' . C. AC ' .
D. D ' B . Lời giải Đáp án: C
Ta có: D 'C ' AB ; BC AD
Nên D'C ' BC AA' AB AD AA' AC ' x 2 3t
Câu 10: Trong không gian Oxyz , cho đường thẳng : y 2t
;t . Một vectơ chỉ phương của z 1 đường thẳng là:
A. u 3;2; 1 .
B. u 3;2;0. C. u 2 ;0; 1 D. u 2 ;2; 1 . Lời giải Đáp án: B
Câu 11: Trong không gian Oxyz , cho mặt phẳng () :x 2y 3 0 . Một vectơ pháp tuyến của mặt phẳng ( ) là:
A. n 1;2;3.
B. n 1;2;0 .
C. n 1; 2;3
D. n 1; 2;0 . Lời giải Đáp án: D 9
Câu 12: Cho cấp số nhân (u ) có u 2, u 1
. Khi đó u bằng n 2 3 4 1 1 1 1 A. . B. . C. . D. . 4 2 8 4 Lời giải Đáp án: B u 1 Ta có 3 q u 2 2 1 1
u u .q ( 1 ). . 4 3 2 2
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý (a), (b), (c), (d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho hàm số f (x) sin x x . 3
a) Tập xác định của hàm số đã cho là D
\ k | k . 3
b) Đạo hàm của hàm số f (x) là f '(x) cos x . 3 5
c) Nghiệm âm lớn nhất của phương trình f '(x) 0 là x . 3
d) Giá trị lớn nhất của hàm số f (x) trên đoạn 0; 2 là . 3 Lời giải a) Sai b) Sai c) Đúng d) Sai
a)Tập xác định của hàm số là D .
b) Đạo hàm của hàm số bằng f '(x) cos x 1. 3
c) f '(x) 0 cos x
1 0 cos x
1 x k2 x k2 3 3 3 3 5
Nghiệm âm lớn nhất của phương trình là x ứng với k 1 . 3
d) Ta có nghiệm phương trình f '(x) 0 trên 0; 2 là x 3 3 3 f (0) , f , f (2 ) 2 2 3 3 2 10 3
Suy ra giá trị lớn nhất của hàm số trên đoạn 0; 2 là . 2
Câu 2: Cho hàm số y f x
x có đồ thị C . Gọi H là hình phẳng giới hạn bởi C , trục
hoành, trục tung và đường thẳng x 9 . Cho M ;
m m là một điểm di động trên đồ thị C ;
gọi S1 là diện tích của hình phẳng giới hạn bởi C , trục hoành, trục tung và đường thẳng x m m
0 (tham khảo hình vẽ bên dưới). 9
a) Diện tích S của hình H được tính bởi công thức S x dx . 0 81
b) Thể tích khối tròn xoay sinh ra khi quay hình H quanh trục Ox bằng . 2 m 3 c) S x x . 1 2 0 a a d) Để S
8S1 thì điểm M có hoành độ là ( với là phân số tối giản). Khi đó ab 24 . b b Lời giải: a) Đúng b) Đúng c) Sai d) Sai 9 9
a) Diện tích của hình H được tính bởi công thức S f x dx x dx . (Đ) 0 0
b) Thể tích khối tròn xoay được tạo bởi khi quay hình H quanh trục Ox là 9 9 2 2 81 V f x dx x dx . (Đ) 2 0 0 m m 2 c) S xdx x x .(S) 1 3 0 0 3 3 1 2 1 27 9 d) 2 2 S S m .18 m m 1 8 3 8 8 4 a 9 ab 36 . (S) b 4 11
Câu 3: Tại một vòng thi của đại hội thể thao, bốn vận động viên bắn súng A, B, C và D mỗi người bắn
một viên đạn vào tấm bia một cách độc lập. Biết rằng xác suất bắn trúng vòng 10 của bốn vận
động viên A, B, C, D lần lượt là 0, 4; 0,5; 0,7; 0,8.
a) Xác suất để vận động viên A không bắn trúng vòng 10 là 0,6.
b) Xác suất để cả bốn vận động viên đều bắn trúng vòng 10 là 0,018.
c) Xác suất để có đúng một vận động viên không bắn trúng vòng 10 là 0,356.
d) Xác suất để có nhiều nhất hai vận động viên bắn trúng vòng 10 là 0,532. Lời giải a) Đúng b) Sai c) Đúng d) Đúng
a) Gọi A là biến cố “vận động viên A bắn trúng”. Ta có P A 0, 4; P A 0,6 suy ra a) đúng.
B là biến cố “vận động viên B bắn trúng”. Ta có P B 0,5; PB 0,5
C là biến cố “vận động viên C bắn trúng”. Ta có P C 0,7; PC 0,3
D là biến cố “vận động viên D bắn trúng”. Ta có P D 0,8; PD 0,2
b) Xác suất cả bốn vận động viên đều bắn trúng là
P ABCD P A PB PC PD 0, 40,50,70,8 0,112 suy ra b) sai.
c) Xác suất có đúng một vận động viên bắn trật là
P ABCD ABCD ABCD ABCD
0,60,50,70,8 0,40,50,70,8 0,40,50,30,8 0,40,50,70,8 0,356 suy ra c) đúng.
d) Ta có xác suất cả bốn vận động viên đều bắn trúng là 0,112
xác suất có đúng ba vận động viên bắn trúng là 0,356
suy ra xác suất có nhiều nhất hai vận động viên bắn trúng là 1 0,112 0,356 0,532. Suy ra d) đúng.
Câu 4: Trong không gian Oxyz , cho điểm (
A 1;1;2) , mặt phẳng () :x 2y 1 0 và đường thẳng x 3t
:y 1 2t ;t . z 2 t a) Điểm (
A 1;1;2) là một điểm thuộc mặt phẳng ( ) .
b) Phương trình đường thẳng đi qua điểm (
A 1;1;2) và vuông góc với mặt phẳng ( ) là x 1 t y 1
2t ;t . z 2t 12
c) Mặt phẳng chứa điểm (
A 1;1;2) và chứa đường thẳng có phương trình là
10x 11y 8z 5 0 .
d) Cosin của góc giữa đường thẳng và mặt phẳng ( ) bằng 70 . 10 Lời giải a) Đúng b) Sai c) Đúng d)
a) Ta có: 1 2 1 0 . Đ
b) Đường thẳng đi qua điểm (
A 1;1;2) và có véc tơ chỉ phương n (1;2;0) có phương trình là x 1 t y 1 2t. z 2 S
c) Đường thẳng đi qua điểm M (0;1; 2) và có véc tơ chỉ phương u (3;2;1) , AM ( 1 ;2; 4)
Véc tơ pháp tuyến của mặt phẳng AM ,u 10;11; 8
Phương trình: 10(x 1) 11(y 1) 8(z 2) 0 10x 11y 8z 5 0 . Đ
d) Đường thẳng có véc tơ chỉ phương u (3;2;1) và mặt phẳng ( ) có véc tơ pháp tuyến n (1;2;0) n u Ta có . 7 70 sin ,( ) n . u 5. 14 10 2 70 30
Suy ra cos ,( ) 1 . S 10 10
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2 , đường thẳng SA vuông góc với mặt
phẳng ABCD , góc giữa đường thẳng SB và mặt phẳng ABCD bằng 60 . Tính khoảng
cách giữa hai đường thẳng SC và AD . (Kết quả làm tròn đến hàng phần trăm) Lời giải S H 60 A B D C
Ta có: SA ABCD nên S ,
B ABCD S ,
B AB SAB 60 SA A . B tan 60 2 3 .
Vì SBC là mặt phẳng chứa SC và song song với AD nên: d A ,
D SC d A ,
D SBC d ,
A SBC . 13