Đề Thi Thử Tốt Nghiệp THPT 2025 Môn Toán Sở GD Bắc Giang Giải Chi Tiết
Hình vẽ dưới đây cho biết một miền D (được tô đậm) nằm trong hình vuông cạnh bằng 4. Miền D này gồm nhưng điểm có khoảng cách tới tâm hình vuông nhỏ hơn hoặc bằng khoảng cách tới cạnh gần nhất của hình vuông. Tính diện tích miền D (kết quả làm tròn đến hàng phần chục). Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi THPTQG môn Toán năm 2025 221 tài liệu
Môn: Toán 2.1 K tài liệu
Tác giả:
Preview text:
SGD & ĐT BẮC GIANG
ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM 2025 MÔN: TOÁN
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án. Câu 1:
Nghiệm của phương trình log x 3 là 2 A. x 5. B. x 8. C. x 6 . D. x 9 . Câu 2:
Trong không gian Oxyz , cho vectơ u 2i 5k . Tọa độ của vectơ u là A. 0;2; 5. B. 2;0;5 . C. 2; 5;0. D. 2;0; 5. Câu 3:
Trong không gian Oxyz , cho hai điểm A 1 ;2; 1 ; B2;1;
3 . Tọa độ của vectơ AB là 1 3 A. ; ; 1 . B. 3 ;1;4.
C. 3;1; 4 . D. 1;3; 2 . 2 2 Câu 4:
Nguyên hàm của hàm số f x sin x là 2 sin x
A. cos x C . B. C .
C. cos x C .
D. sin x C . 2 Câu 5:
Giá trị nhỏ nhất của hàm số 4 2
y x 4x 3 trên đoạn 0; 4 là A. 0 . B. 2 . C. 3 . D. 1. Câu 6:
Một hộp đựng 9 tấm thẻ cùng loại được ghi số từ 1 đến 9 . Rút ngẫu nhiên đồng thời hai tấm thẻ
từ trong hộp. Xác suất để rút được cả hai tấm thẻ cùng ghi số chẵn là 1 1 5 1 A. . B. . C. . D. . 2 3 6 6 Câu 7:
Cho cấp số nhân u có u 2 và u 6 . Số hạng u của cấp số nhân là n 1 2 4 A. 27 . B. 162. C. 54 . D. 11. Câu 8:
Tập nghiệm của bất phương trình log x 1 log 2x 1 là 1 1 2 2 1 1 A. ; 2 . B. ; 2 . C. ; 2 . D. ; 2. 2 2 Câu 9:
Thể tích của khối chóp có diện tích đáy bằng S , chiều cao bằng h là 1 1 2 A. V Sh . B. V Sh .
C. V Sh . D. V Sh . 2 3 3
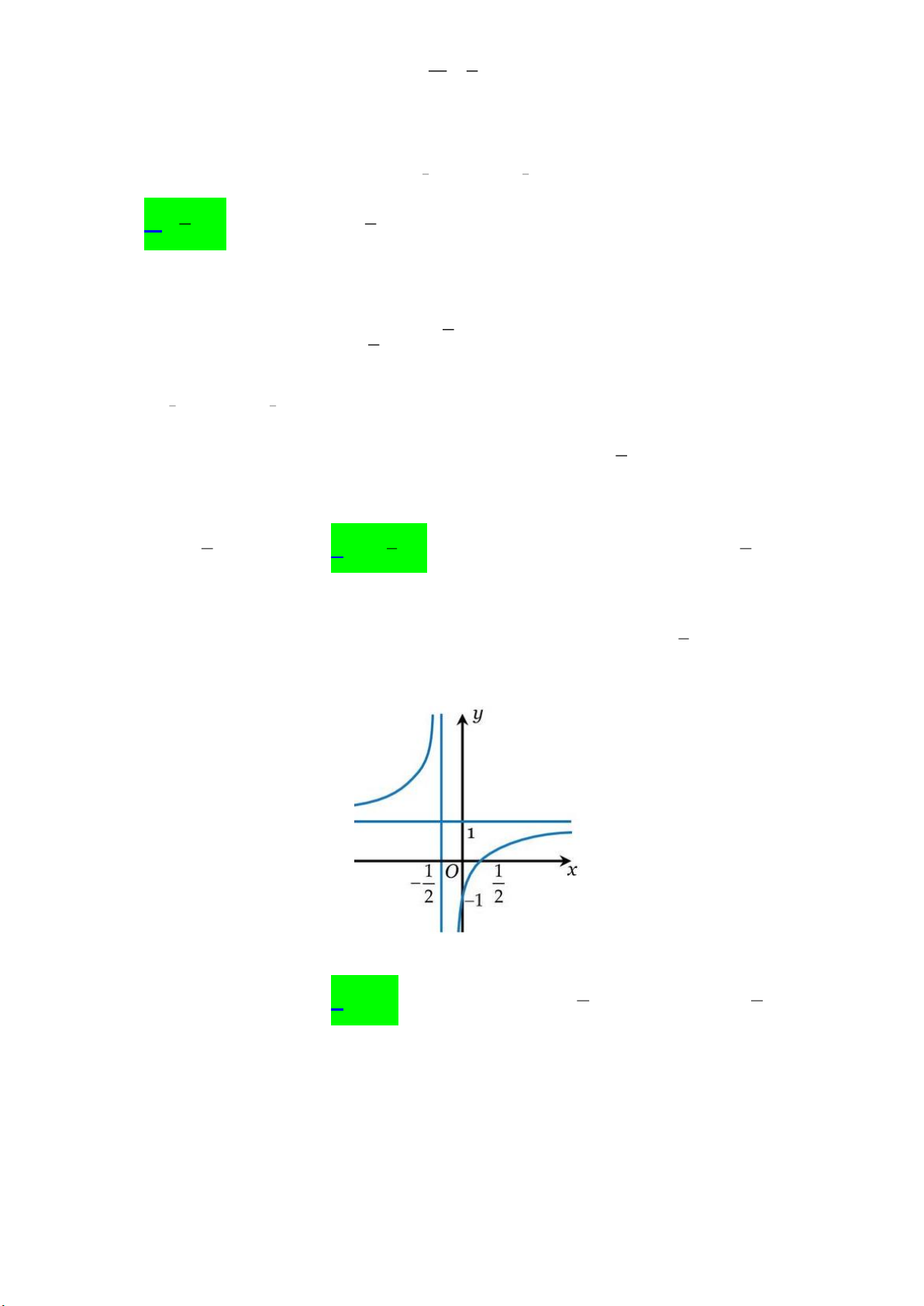
Câu 10: Cho hàm số y f (x) có đồ thị như hình vẽ dưới đây: Trang 1
Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình 1 1 A. x 1. B. y 1. C. x . D. y . 2 2
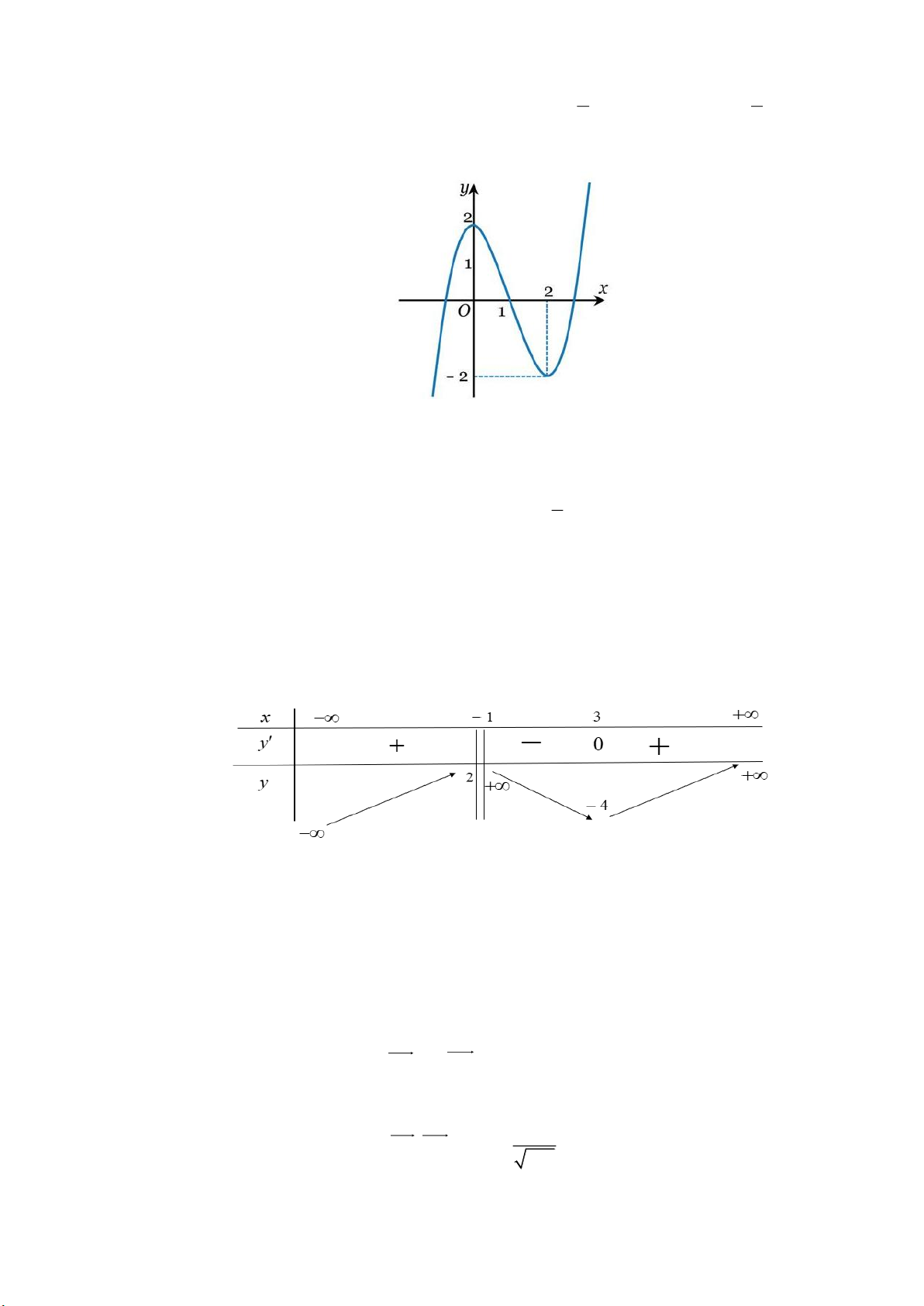
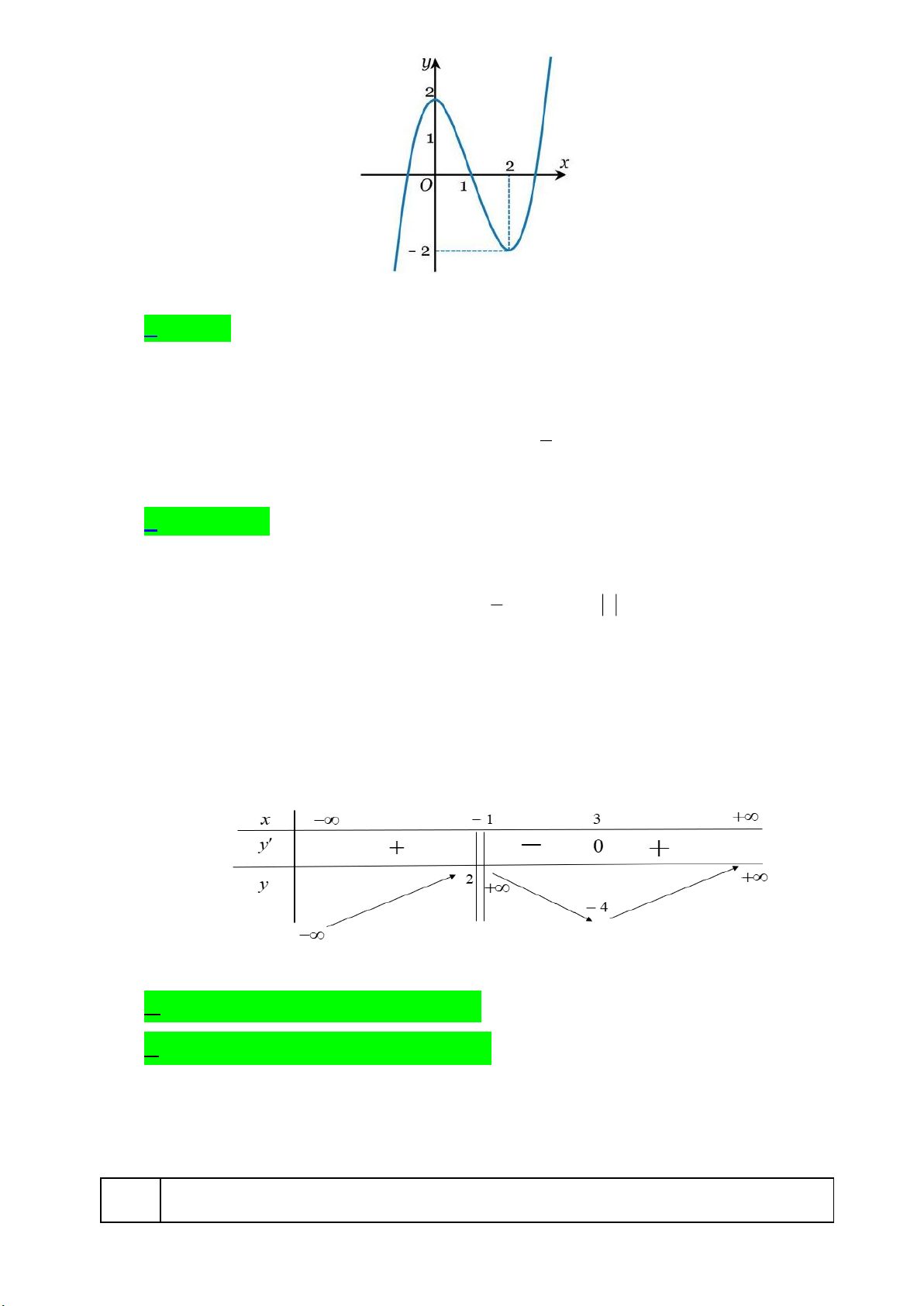
Câu 11: Cho hàm số y f (x) có đồ thị như hình vẽ dưới đây:
Hàm số đã cho đồng biến trên khoảng A. (2; ) . B. (0; 2) . C. (1; ) . D. (;1) . 1
Câu 12: Gọi F (x) là một nguyên hàm của hàm số f (x) 2x
trên 0; thỏa mãn F (1) 1. x Tính F (e) . A. 2 F( ) e e 1.
B. F (e) e .
C. F (e) e D. 2
F (e) 1 e .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
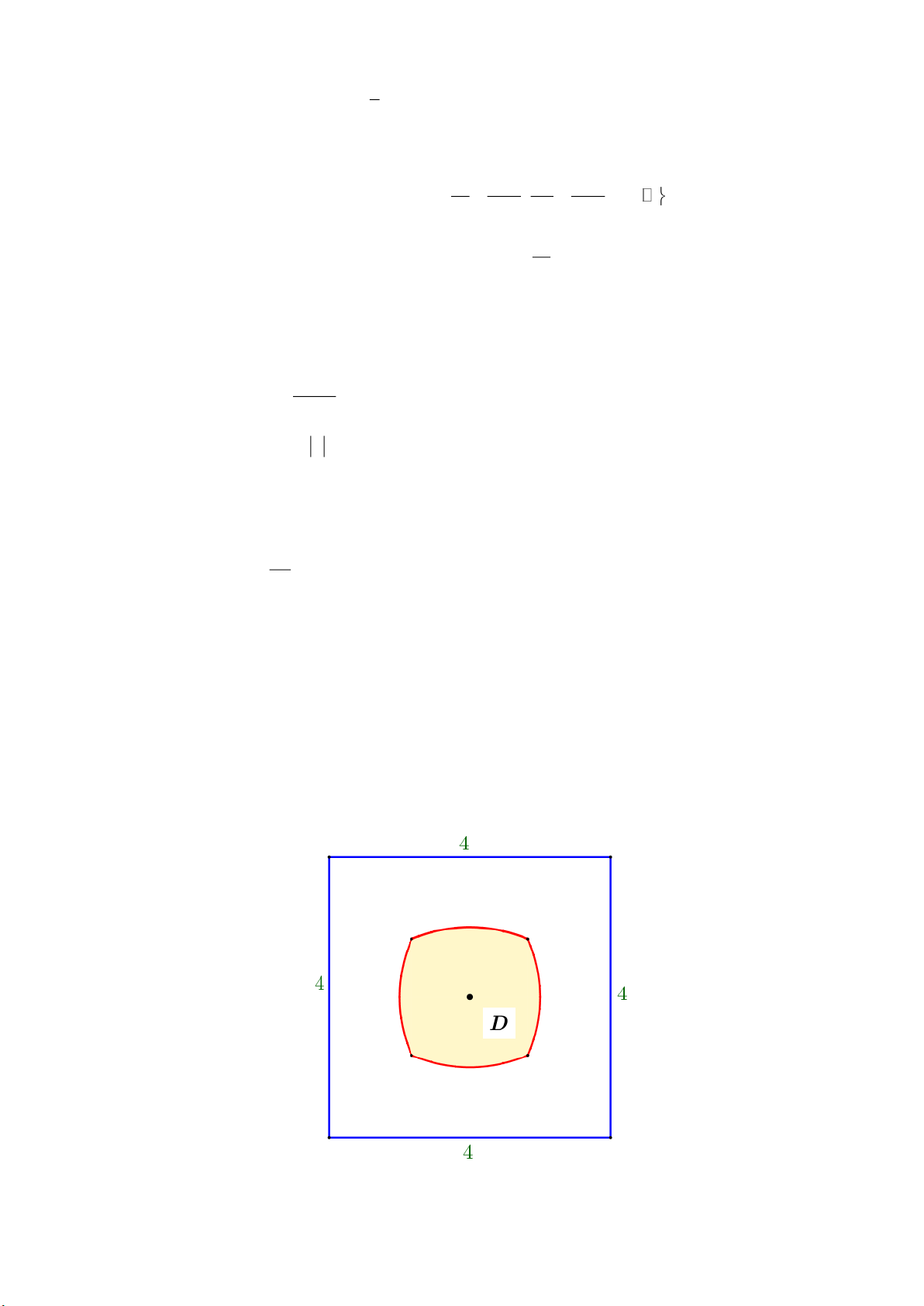
Câu 1. Cho hàm số y f x có bảng biến thiên như sau:
a) Đồ thị hàm số y f x có đúng hai đường tiệm cận.
b) Hàm số y f x đồng biến trên 3; .
c) Hàm số y f x có đúng một điểm cực trị.
d) Giá trị nhỏ nhất của h x 2 f x 2025x trên đoạn 3;202 5 bằng 6083
Câu 2. Trong không gian Oxyz cho ba điểm A2;1; 1 , B 1 ;3; 1 , C 5; 3;4
a) Tích vô hướng của hai véc tơ AB và AC bằng 23 .
b) Góc BAC là góc nhọn. 23
c) Côsin của góc giữa hai véc tơ AB, AC bằng . 638 Trang 2
d) Lấy điểm M trên mặt phẳng Oxy sao cho biểu thức 2 2 2
MA MB MC đạt giá trị nhỏ nhất. Khi đó toạ 1
độ của M là 2; ; 0 . 3 Câu 3.
Xét phương trình 2sin 3x 1 0 . k k
a) Tập nghiệm của phương trình là 2 5 2 S ; | k . 18 3 18 3
b) Nghiệm dương nhỏ nhất của phương trình là x . 18
c) Phương trình có đúng 3 nghiệm trên 0; .
d) Tổng các nghiệm của phương trình thuộc đoạn 0; bằng 2 . x Câu 4.
Cho hàm số f x 2 1 . x a) f
xdx 2x ln x C .
b) Gọi F x là một nguyên hàm của hàm số f x
trên 0; và thỏa mãn F 1 3. Khi đó
F x 2x ln x 1. c) f x 1 2 dx C . 4x
d) Gọi G xlà một nguyên hàm của hàm số f x . Biết G 2 1 và G5 G 5 0 . Khi đó tìm được G 1
0 aln10bln5 cln 2 d , với a,b,c là các số hữu tỷ. Khi đó
a b c d 19 .
PHẦN III. Câu trắc nghiệm trả lời ngắn ( Tự luận ). Thí sinh trả lời từ câu 1 đến câu 6. Ở mỗi câu thí
sinh điền đáp án của câu đó.
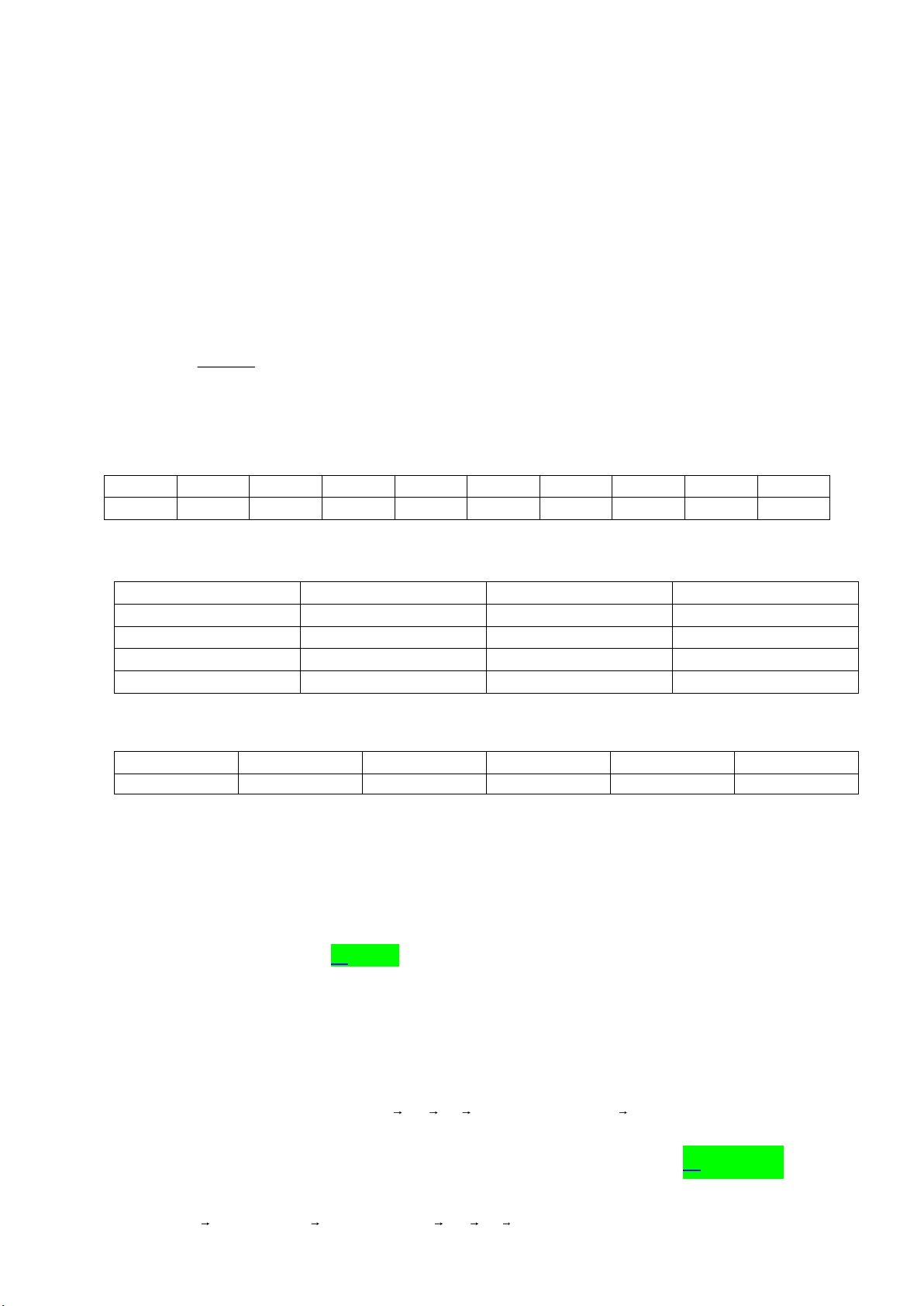
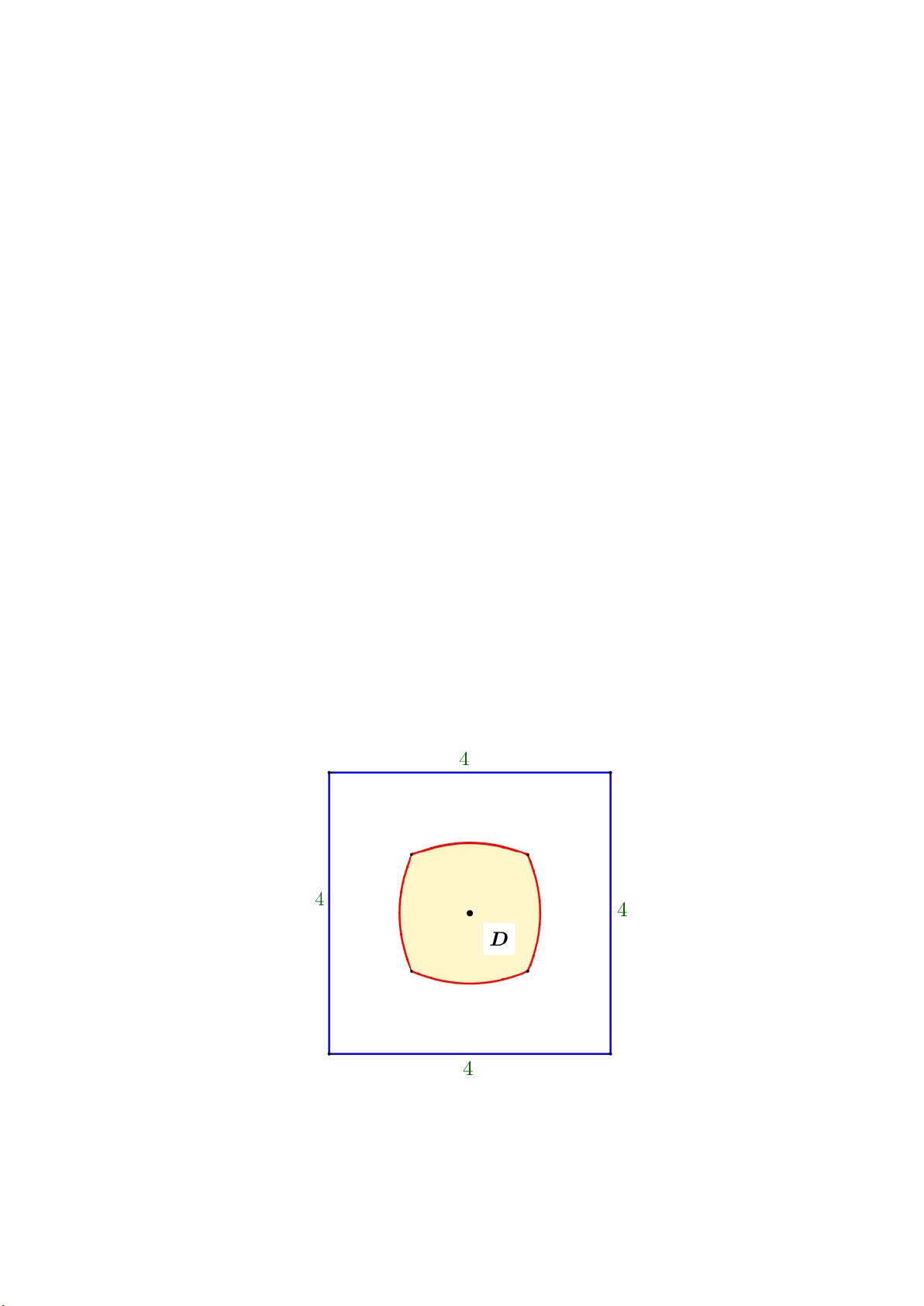
Câu 1. Hình vẽ dưới đây cho biết một miền D (được tô đậm) nằm trong hình vuông cạnh bằng 4. Miền D
này gồm nhưng điểm có khoảng cách tới tâm hình vuông nhỏ hơn hoặc bằng khoảng cách tới
cạnh gần nhất của hình vuông. Tính diện tích miền D (kết quả làm tròn đến hàng phần chục)
Câu 2. Một thầy giáo có 16 cuốn sách khác nhau gồm 4 cuốn sách Toán, 5 cuốn sách Lí và 7 cuốn sách
Hóa. Thầy lấy ra ngẫu nhiên 8 cuốn sách để tặng cho học sinh. Tính xác suất để số sách còn lại
của thầy có đủ cả 3 môn (làm tròn kết quả đến hàng phần trăm). Trang 3 Câu 3:
Năm 2025, một cửa hàng cần nhập về tổng cộng 600 chiếc điện thoại. Cửa hàng sẽ nhận theo
nhiều lô hàng, mỗi lô hàng chứa số lượng điện thoại bằng nhau. Chi phí vận chuyển là 50 USD
cho mỗi lô hàng, cộng thêm một loại phí vận chuyển nữa là 3 USD cho mỗi chiếc điện thoại và
phí này cả năm chỉ tính cho lần vận chuyển đầu tiên. Hỏi cửa hàng đó nên nhập mỗi lô hàng bao
nhiêu chiếc điện thoại để chi phí vận chuyển cả năm 2025 thấp nhất? Câu 4:
Xét trong không gian Oxyz, đài kiểm soát không lưu sân bay đặt ở gốc toạ độ O0;0;0, đơn vị
trên mỗi trục là ki-lô-mét. Một máy bay chuyển động theo đường thẳng, bay qua hai vị trí A 5 00; 3
00;500 và B 2 00; 2
00;450. Khi máy bay ở gần đài kiểm soát không lưu nhất,
toạ độ của máy bay là ; a ;
b c . Tính giá trị của biểu thức P a b c . Câu 5:
Cho hình chóp S.ABC có ABC, SAB là các tam giác đều và mặt bên (SAB) vuông góc với mặt
đáy. Gọi là số đo của góc phẳng nhị diện [S, BC, ] A . Tính 2 cos . Câu 6:
Trong một môi trường giới hạn, số lượng một loài sinh vật được cho bởi công thức 100 000 P(t)
trong đó thời gian t tính theo đơn vị năm. Tính thời gian cần thiết (theo đơn vị 1 4 t e
năm) để số lượng loài sinh vật đó đạt 80000 (kết quả làm tròn đến hàng phần trăm).
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. BẢNG ĐÁP ÁN 1.B 2.D 3.C 4.C 5.D 6.D 7.C 8.A 9.B 10.B 11.A 12.A
PHẦN II. Câu trắc nghiệm đúng sai. Câu 1 Câu 2 Câu 3 Câu 4 S Đ Đ Đ Đ S Đ Đ Đ Đ S S S Đ Đ S
PHẦN III. Câu trắc nghiệm trả lời ngắn ( Tự luận ). Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 3,5 0,95 100 400 0,2 2,77
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1. Nghiệm của phương trình log x 3 là 2 A. x 5. B. x 8. C. x 6 . D. x 9 . Lời giải
Điều kiện x 0 . 3
log x 3 x 2 8 (thỏa mãn). 2
Vậy phương trình có nghiệm x 8.
Câu 2. Trong không gian Oxyz , cho vectơ u 2i 5k . Tọa độ của vectơ u là A. 0;2; 5. B. 2;0;5 . C. 2; 5;0. D. 2;0; 5. Lời giải
Ta có 2i 2;0;0; 5
k 0;0;5 u 2i 5k 2;0;5 . Trang 4
Câu 3. Trong không gian Oxyz , cho hai điểm A 1 ;2; 1 ; B2;1;
3 . Tọa độ của vectơ AB là 1 3 A. ; ; 1 . B. 3 ;1;4.
C. 3;1; 4 . D. 1;3; 2 . 2 2 Lời giải
Ta có AB 3; 1; 4 .
Câu 4. Nguyên hàm của hàm số f x sin x là 2 sin x
A. cos x C . B. C .
C. cos x C .
D. sin x C . 2 Lời giải Ta có : f
xdx sin d
x x cosx C .
Câu 5. Giá trị nhỏ nhất của hàm số 4 2
y x 4x 3 trên đoạn 0; 4 là A. 0 . B. 2 . C. 3 . D. 1. Lời giải
Hàm số y f x 4 2
x 4x 3 xác định trên đoạn 0; 4 . Đạo hàm: 3
y x x x 2 4 8 4 x 2 . x 00;4
y 0 4x 2
x 2 0 x 2 0;4 . x 2 0;4
Ta có: f 0 3; f 2 1
; f 4 195 .
Vậy giá trị nhỏ nhất của hàm số 4 2
y x 4x 3 trên đoạn 0; 4 là 1. Câu 6.
Một hộp đựng 9 tấm thẻ cùng loại được ghi số từ 1 đến 9 . Rút ngẫu nhiên đồng thời hai tấm thẻ
từ trong hộp. Xác suất để rút được cả hai tấm thẻ cùng ghi số chẵn là 1 1 5 1 A. . B. . C. . D. . 2 3 6 6 Lời giải
Số phần tử của tập không gian mẫu: n 2 C 36 . 9
Gọi A : “ Rút được cả hai tấm thẻ cùng ghi số chẵn”.
Rút 2 tấm thẻ ghi số chẵn trong 4 tấm thẻ ghi số chẵn có n A 2 C 6. 4 n A 6 1 Vậy P A . n 36 6 Câu 7.
Cho cấp số nhân u có u 2 và u 6 . Số hạng u của cấp số nhân là n 1 2 4 A. 27 . B. 162. C. 54 . D. 11. Lời giải Trang 5 u 6
Cấp số nhân u có: 2
u u .q q 3. n 2 1 u 2 1 Vậy 3 3
u u .q 2.3 54 . 4 1 Câu 8.
Tập nghiệm của bất phương trình log x 1 log 2x 1 là 1 1 2 2 1 1 A. ; 2 . B. ; 2 . C. ; 2 . D. ; 2. 2 2 Lời giải x 1 x 1 0 Điề 1 u kiện: 1 x . 2x 1 0 x 2 2 log x 1 log
2x 1 x 1 2x 1 x 2 . 1 1 2 2 1
Kết hợp điều kiện, tập nghiệm của bất phương trình đã cho là ; 2 . 2
Câu 9. Thể tích của khối chóp có diện tích đáy bằng S , chiều cao bằng h là 1 1 2 A. V Sh . B. V Sh .
C. V Sh . D. V Sh . 2 3 3 Lời giải 1
Thể tích của khối chóp có diện tích đáy bằng S , chiều cao bằng h là V Sh . 3
Câu 10. Cho hàm số y f (x) có đồ thị như hình vẽ dưới đây:
Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình 1 1 A. x 1. B. y 1. C. x . D. y . 2 2 Lời giải Nguyên
Dựa vào đồ thị ta có phương trình đường tiệm cận ngang của đồ thị hàm số là y 1.
Câu 11. Cho hàm số y f (x) có đồ thị như hình vẽ dưới đây: Trang 6
Hàm số đã cho đồng biến trên khoảng A. (2; ) . B. (0; 2) . C. (1; ) . D. (;1) . Lời giải
Dựa vào đồ thị ta có hàm số đã cho đồng biến trên (2; ) . 1
Câu 12. Gọi F (x) là một nguyên hàm của hàm số f (x) 2x
trên 0; thỏa mãn F (1) 1. x Tính F (e) . A. 2 F( ) e e 1.
B. F (e) e .
C. F (e) e D. 2
F (e) 1 e . Lời giải 1
Trên 0; ta có F x 2 2
f (x)dx 2x
dx x ln x C x ln x C . x
Mặt khác F C F x 2
x x F e 2 1 1 0 ln e 1.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số y f x có bảng biến thiên như sau:
a) Đồ thị hàm số y f x có đúng hai đường tiệm cận.
b) Hàm số y f x đồng biến trên 3; .
c) Hàm số y f x có đúng một điểm cực trị.
d) Giá trị nhỏ nhất của h x 2 f x 2025x trên đoạn 3;202 5 bằng 6083 Lời giải 1
Giải chi tiết (giải thích) Trang 7
Ta có lim f x ; lim f x nên đồ thị hàm số không có tiệm cận ngang; x x a) S
lim f x 2 nên đồ thị hàm số có tiệm cận đứng là đường thẳng x 1 x 1
Vậy đồ thị hàm số có 01 đường tiệm cận. b) Đ
Dựa vào bảng biến thiên ta thấy hàm số y f x đồng biến trên 3; . c) Đ
Dựa vào bảng biến thiên ta thấy hàm số y f x có đúng một điểm cực trị x 3
Xét hàm số h x 2 f x 2025x h x 2 f x 2025 d) S Trên đoạn 3;202
5 thì f x 0 nên h x 0 với x 3;202 5 .
Do đó min h x h3 2 f 3 2025.3 2. 4 6075 6067 . 3;2025
Câu 2. Trong không gian Oxyz cho ba điểm A2;1; 1 , B 1 ;3; 1 , C 5; 3;4
a) Tích vô hướng của hai véc tơ AB và AC bằng 23 .
b) Góc BAC là góc nhọn. 23
c) Côsin của góc giữa hai véc tơ AB, AC bằng . 638
d) Lấy điểm M trên mặt phẳng Oxy sao cho biểu thức 2 2 2
MA MB MC đạt giá trị nhỏ nhất. Khi đó toạ 1
độ của M là 2; ; 0 . 3 Lời giải 2
Giải chi tiết (giải thích) a) Đ AB 3
;4; 2; AC 3; 2;3 A . B AC 9 86 2 3 . b) S Vì A . B AC 2
3 0 nên góc BAC là góc tù A . B AC 2 3 23 c) Đ cos BAC AB AC 9 16 4. 9 4 9 638 Trang 8 1 4
Gọi G là trọng tâm của tam giác ABC , ta có G 2; ;
và GAGB GC 0. 3 3 2 2 2 2 2 2
MA MB MC MG GA MG GB MG GC 2
MG MGGAGB GC 2 2 2 3 2
GA GB GC d) Đ 2 2 2 2
3MG GA GB GC . Vì G ; A G ;
B GC không đổi nên 2 2 2
MA MB MC đạt giá trị nhỏ nhất khi MG đạt giá
trị nhỏ nhất. Khi đó M là hình chiếu của G trên mặt phẳng Oxy . 1 Vậy M 2; ; 0 . 3 Câu 3.
Xét phương trình 2sin 3x 1 0 . k k
a) Tập nghiệm của phương trình là 2 5 2 S ; | k . 18 3 18 3
b) Nghiệm dương nhỏ nhất của phương trình là x . 18
c) Phương trình có đúng 3 nghiệm trên 0; .
d) Tổng các nghiệm của phương trình thuộc đoạn 0; bằng 2 . Lời giải a) Đúng. 3x k2 1 6
Ta có: 2sin 3x 1 0 sin 3x sin 3x sin 2 6 5 3x k2 6 2 x k 18 3 k . 5 2 x k 18 3 k k
Vậy tập nghiệm của phương trình là 2 5 2 S ; | k . 18 3 18 3 b) Đúng. 2 1 k 0 k 18 3 1 12k 0 12 x 0 . 5 2 5 12k 0 5 k 0 k 18 3 12 Do k
k 0 x
là nghiệm dương nhỏ nhất của phương trình đã cho. 18 c) Sai. Trang 9 2 1 17 0 k k 18 3 12 12 0 x . 5 2 5 13 0 k k 18 3 12 12 Do k k 5 13 17 0;1 x ; ; ; . 18 18 18 18
Vậy phương trình có đúng 4 nghiệm trên 0; . d) Đúng. 5 13 17
Trên đoạn 0; phương trình đã cho có đúng 4 nghiệm là ; ; ; , do đó tổng các 18 18 18 18 5 13 17 nghiệm bằng 2 . 18 18 18 18 x Câu 4.
Cho hàm số f x 2 1 . x a) f
xdx 2x ln x C .
b) Gọi F x là một nguyên hàm của hàm số f x
trên 0; và thỏa mãn F 1 3. Khi đó
F x 2x ln x 1. c) f x 1 2 dx C . 4x
d) Gọi G xlà một nguyên hàm của hàm số f x . Biết G 2 1 và G5 G 5 0 . Khi đó tìm được G 1
0 aln10bln5 cln 2 d , với a,b,c là các số hữu tỷ. Khi đó
a b c d 19 . Lời giải a) Đúng. x Ta có: f x 2 1 1 dx dx 2
dx 2x ln x C . x x b) Đúng.
Trên 0; , ta có F x 2x ln x C . Mà F
1 3 2 ln1 C 3 C 1 F x 2x ln x 1. c) Sai. 1 1 1 2.2x 1 4x 1 1 f
2xdx f
2xd2x f 2xC . C C C . 2 2 2 2x 4x 4x d) Sai.
+) Do G xlà một nguyên hàm của hàm số f x nên ta có: G x 2x ln x C G x 2x ln x C , x 0 1 . 2x ln
xC , x 0 2
2x ln x 3 ln 2, x 0
+) Mà G 2 1 nên 2.2 ln 2 C 1 C 3
ln 2 G x 1 1 2x ln
xC , x 0 2 Trang 10
G5 10ln53ln2 7ln5ln2 .
+) Mặt khác: G5 G 5
0 7 ln5ln 2 2 5
ln5C 0 C 3 2ln5 ln 2 2 2 G x 2x ln x 3 ln 2, x 0 2x ln
x3 2ln5 ln 2, x 0 +) G 1 0 2 1
0ln1032ln5ln2 ln102ln5ln217 a 1 b 2
a b c d 17 . c 1 d 17
Hoặc có thể viết kết quả G 10
ln102ln5ln217 ln5ln22ln5ln217 ln5 2ln217 a 0 b 1
a b c d 16 . c 2 d 17
Do đó giá trị biểu thức a b c d có nhiều kết quả khác nhau. Vậy mệnh đề d sai.
PHẦN III. Câu trắc nghiệm trả lời ngắn ( Tự luận ). Thí sinh trả lời từ câu 1 đến câu 6. Ở mỗi câu thí
sinh điền đáp án của câu đó.
Câu 1. Hình vẽ dưới đây cho biết một miền D (được tô đậm) nằm trong hình vuông cạnh bằng 4. Miền D
này gồm nhưng điểm có khoảng cách tới tâm hình vuông nhỏ hơn hoặc bằng khoảng cách tới cạnh
gần nhất của hình vuông. Tính diện tích miền D (kết quả làm tròn đến hàng phần chục) Lời giải Đáp án: 3,5 Trang 11
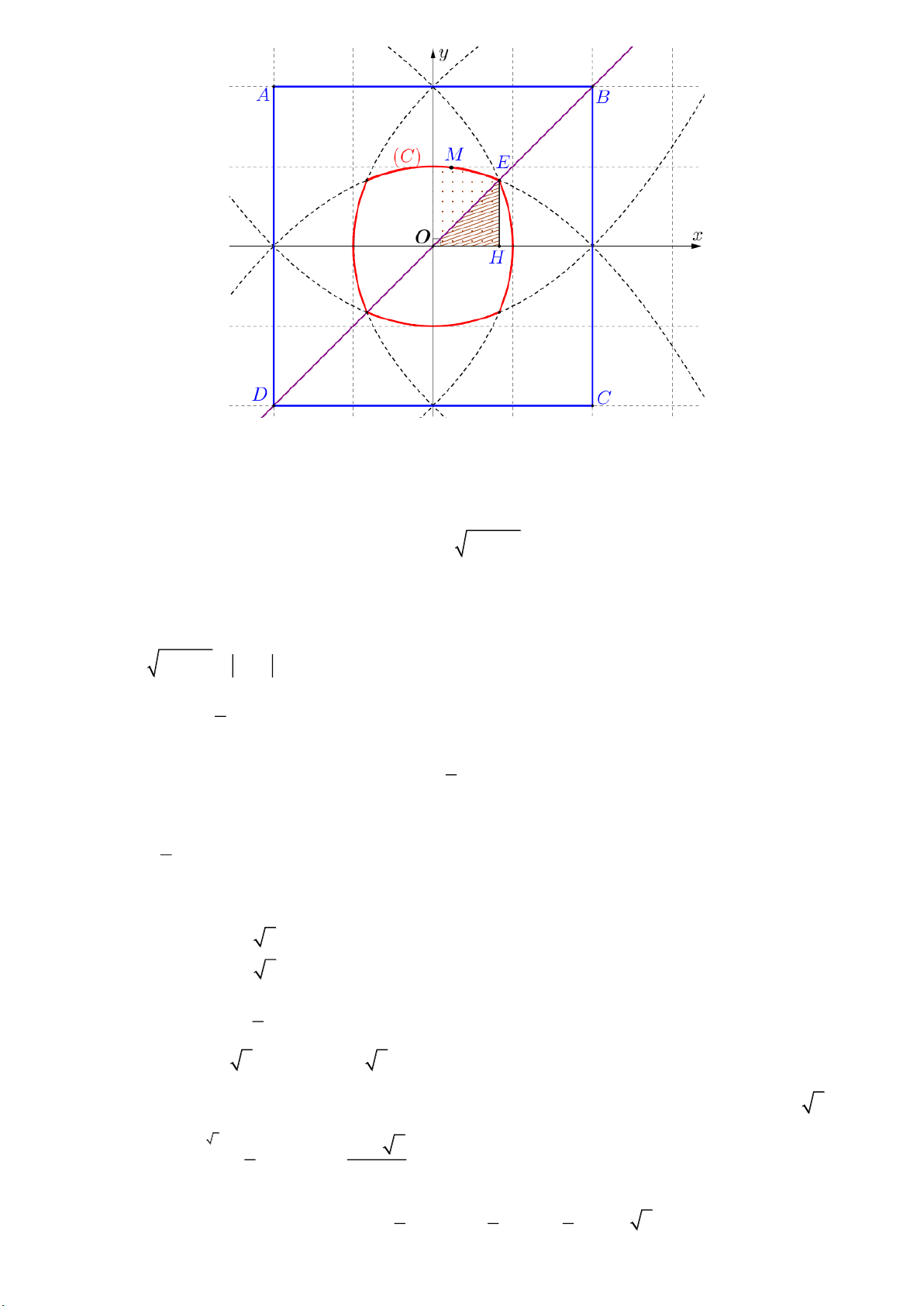
Gọi hình vuông có cạnh bằng 4 là ABCD và gắn hệ trục tọa độ Oxy như hình vẽ.
Do vai trò của các đường cong như nhau, giả sử M ;
x y là một điểm thuộc đường cong C
của miền D như hình vẽ.
Ta có khoảng cách từ M tới O là 2 2 MO x y .
Khoảng cách từ M tới cạnh AB của hình vuông là d M; AB | y 2|
Khoảng cách từ M tới O bằng khoảng cách từ M tới AB nên 2 2
x y y 2 1 2
y x 1 4 1
Hoành độ giao điểm của Parabol 2 y
x 1 và đường thẳng OB y x (thuộc góc phần tư 4
thứ nhất) là nghiệm của phương trình 1 2
x 1 x 4 2
x 4x 4 0 x 2 2 2 x 2 2 2 1 Parabol 2 y
x 1 cắt đường thẳng OB y x tại điểm E thuộc góc phần tư thứ nhất nên 4 x 2 2 2 y 2 2 2 . E E
Diện tích hình phẳng giới hạn bởi Parabol, trục Ox , trục Oy và đường thẳng x 2 2 2 là 2 2 2 1 8 4 2 2 S x 1 x d . 1 4 3 0 1 1 1
Diện tích tam giác OEH là S OH.EH y .x . E E 2 2 22 2 2 2 2 Trang 12 1 8 4 2 1 1 0 8 2 Diện tích của
miền D là S S S 2 2 2 . 3 1 2 2 8 3 2 3 10 8 2
Diện tích miền D là S 8.S 8. 3,5 . 3 3
Câu 2. Một thầy giáo có 16 cuốn sách khác nhau gồm 4 cuốn sách Toán, 5 cuốn sách Lí và 7 cuốn sách
Hóa. Thầy lấy ra ngẫu nhiên 8 cuốn sách để tặng cho học sinh. Tính xác suất để số sách còn lại
của thầy có đủ cả 3 môn (làm tròn kết quả đến hàng phần trăm). Lời giải
Đáp án: 0,95
Lấy ra ngẫu nhiên 8 cuốn sách trong 16 cuốn sách khác nhau, có 8 C 12870 cách. 16
Lấy 8 cuốn sách trong tổng 9 cuốn sách Toán và Lý có 8 C 9 cách. 9
Lấy 8 cuốn sách trong tổng 11 cuốn sách Toán và Hóa có 8 C 165 cách. 11
Lấy 8 cuốn sách trong tổng 12 cuốn sách Lý và Hóa có 8 C 495 cách. 12
Số cách lấy để số sách còn lại đủ cả 3 môn Toán Lý và Hóa là 12870 9 165 495 12201 cách. 12201
Xác suất để số sách còn lại của thầy có đủ cả 3 môn là 0,95 12870 Câu 3:
Năm 2025, một cửa hàng cần nhập về tổng cộng 600 chiếc điện thoại. Cửa hàng sẽ nhận theo
nhiều lô hàng, mỗi lô hàng chứa số lượng điện thoại bằng nhau. Chi phí vận chuyển là 50 USD
cho mỗi lô hàng, cộng thêm một loại phí vận chuyển nữa là 3 USD cho mỗi chiếc điện thoại và
phí này cả năm chỉ tính cho lần vận chuyển đầu tiên. Hỏi cửa hàng đó nên nhập mỗi lô hàng bao
nhiêu chiếc điện thoại để chi phí vận chuyển cả năm 2025 thấp nhất? Lời giải 600
Gọi số lô hàng nhập về là * x x
, suy ra số điện thoại trong mỗi lô hàng là . x
Chi phí vận chuyển là f x 600 1800 50x 3. 50x . x x
Ta có f x 1800 1800 50x 2 50x 600. x x
GTNN của f x bằng 600, đạt được khi x 6 (thỏa mãn điều kiện). 600
Khi đó, số điện thoại của mỗi lô hàng là 100. 6 Câu 4:
Xét trong không gian Oxyz, đài kiểm soát không lưu sân bay đặt ở gốc toạ độ O0;0;0, đơn vị
trên mỗi trục là ki-lô-mét. Một máy bay chuyển động theo đường thẳng, bay qua hai vị trí A 5 00; 3
00;500 và B 2 00; 2
00;450. Khi máy bay ở gần đài kiểm soát không lưu nhất,
toạ độ của máy bay là ; a ;
b c . Tính giá trị của biểu thức P a b c . Lời giải
Khi máy bay ở gần đài kiểm soát không lưu nhất, máy bay ở vị trí điểm H ; a ;
b c là hình chiếu
vuông góc của O trên đường thẳng AB . Trang 13
Ta có AH a 500;b 300;c 500, AB 300;100; 50
Từ AH , AB cùng phương và OH AB ta có hệ phương trình:
a 500 b 300 c 500 300 100 50 30
0a 100b 50c 0
Giải hệ trên tìm được H 100; 1 00;400
Vậy P a b c 400. Câu 5:
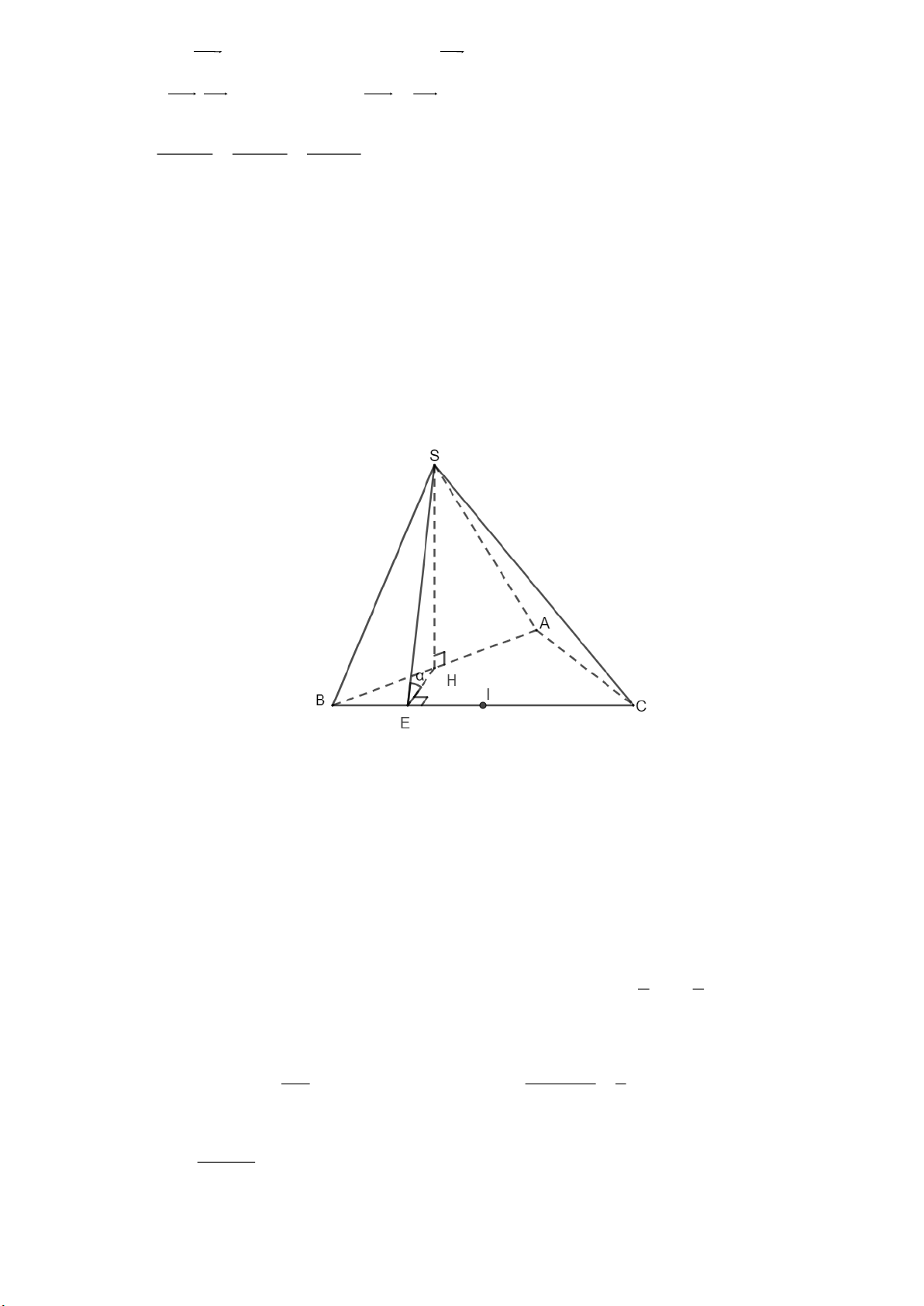
Cho hình chóp S.ABC có ABC, SAB là các tam giác đều và mặt bên (SAB) vuông góc với mặt
đáy. Gọi là số đo của góc phẳng nhị diện [S, BC, ] A . Tính 2 cos . Lời giải
Đáp án: 0, 2
Gọi H là trung điểm cạnh . AB Do S
AB đều nên SH AB.
Mặt khác (SAB) ( ABC) và (SAB) ( ABC) AB .
Từ đó suy ra SH ( ABC).
Gọi I là trung điểm BC và E là trung điểm BI. Do ABC
đều nên HE B .
C Suy ra BC (SHE) góc phẳng nhị diện [S, BC, ] A chính là
góc SEH hay SEH . 1 1
Do ABC, SAB là các tam giác đều có chung cạnh AB nên HE AI SH . 2 2 Trong ABC có SHE 90 . SH 1 1 Suy ra 2 tan SEH
2 tan 2 cos 0, 2. 2 HE tan 1 5 Câu 6:
Trong một môi trường giới hạn, số lượng một loài sinh vật được cho bởi công thức 100 000 P(t)
trong đó thời gian t tính theo đơn vị năm. Tính thời gian cần thiết (theo đơn vị 1 4 t e
năm) để số lượng loài sinh vật đó đạt 80000 (kết quả làm tròn đến hàng phần trăm). Lời giải Trang 14
Đáp án: 2, 77
Yêu cầu bài toán tương đương với 100 000 t 100 000 t 1 80000 1 4 t e e
e 16 t ln16 2,772 . 1 4 t e 80 000 16
Vậy cần khoảng 2, 78 năm để số lượng loài sinh vật đó đạt 80 000 . Trang 15