Đề thi thử tốt nghiệp THPT năm 2024 môn Toán sở GD&ĐT Tiền Giang

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi thử tốt nghiệp THPT năm 2024 môn Toán sở Giáo dục và Đào tạo tỉnh Tiền Giang; kỳ thi được diễn ra vào ngày 23 tháng 05 năm 2024; đề thi có đáp án trắc nghiệm tất cả các mã đề. Mời bạn đọc đón xem!

150 75 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2024

Môn: Toán

Thông tin:

29 trang 5 tháng trước

Tác giả:

Profile Mai Anh Đào
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
1/20
HƯỚNG DẪN GIẢI ĐỀ THI THỬ TNTHPT MÔN TOÁN NĂM HỌC 2023 - 2024
(ĐỀ SỞ GD & ĐT TIỀN GIANG – MÃ ĐỀ 101)
Câu 1: Cho khối trụ có chu vi đáy bằng
6
, đường sinh bằng 5. Thể tích khối trụ đã cho bằng
A.
36
. B.
12
. C.
15
. D.
45
.
Lời giải
Chọn D
Ta có: Chu vi đáy
26 3Cr r 
Thể tích khối trụ
22
3 5 45..V rh 
Câu 2: Có bao nhiêu cách xếp 5 học sinh vào một dãy ghế gồm 5 chiếc?
A.
24
. B.
. C.
120
. D.
60
.
Lời giải
Chọn C
Ta có:
5 120!
Câu 3: Cho hàm số bậc bốn
y fx
có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình
30fx

là
A.
2
. B.
. C.
4
. D.
3
.
Lời giải
Chọn A
Ta có:
30 3fx fx
. Đồ thị
y fx
cắt đồ thị
3y
tại hai điểm phân biệt nên
phương trình có hai nghiệm phân biệt.
Câu 4: Cho hàm số
y fx
liên tục trên
và có bảng xét dấu đạo hàm như sau:
Hàm số đã cho có bao nhiêu cực trị?
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn B
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
2/20
Ta có: Dựa vào bảng xét dấu ta thấy hàm số đã cho có 4 điểm cực trị.
Câu 5: Cho khối chóp
.
S ABCD
có diện tích đáy bằng
6
,
2SA
và
SA
vuông góc với
ABCD
. Thể
tích khối chóp
.S ABCD
bằng
A.
24
. B.
12
. C.
72
. D.
4
.
Lời giải
Chọn D
Ta có:
11
62 4
33
. ..
V Bh
Câu 6: Trong không gian
Oxyz
, khoảng cách từ
1 23;;M 
đến mặt phẳng
Oxz
bằng
A.
2
. B.
10
. C.
1
. D.
3
.
Lời giải
Chọn A
Ta có:
2;
M
d M Oxz y

.
Câu 7: Trong không gian
Oxyz
, một vectơ pháp tuyến của mặt phẳng
1
234
:
xyz

là
A.
643;;
p
. B.
111;;n
. C.
234;;q
. D.
6 43;;m 
.
Lời giải
Chọn A
Ta có:
111
234
;;n



cùng phương với
643;;p

.
Câu 8: Mệnh đề nào dưới đây sai?
A.
sin d co sxx x C
. B.
sin d cosxx x C
.
C.
cos d sinxx x C
. D.
2cos d sinxx x C 
.
Lời giải
Chọn A
Câu 9: Với
,ab
là các số thực dương tùy ý, biểu thức
51
22
33
22
ab
P
ab
A.
12
ab
−
. B.
1
ab
−
. C.
2
ab
. D.
ab
.
Lời giải
Chọn C
Ta có:
53
22
51
13
22
2
22
33
22
ab
P a b ab
ab

.
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
3/20
Câu 10: Hàm số nào dưới đây đồng biến trên
?
A.
2
yx x
. B.
1
y
x
=
. C.
3
yx x
. D.
1
y
x
= −
.
Lời giải
Chọn C
Ta có:
32
3 10,yx x y x x

.
Câu 11: Một hình nón có đường sinh bằng đường kính đáy. Góc ở đỉnh của hình nón bằng
A.
30°
. B.
120°
. C.
60°
. D.
150°
.
Lời giải
Chọn C
Ta có
SAB∆
đều nên
60ASB = °
.
Câu 12: Tập nghiệm của bất phương trình
( )
3
log 2 1 1x
−>
là
A.
( )
2;S = +∞
. B.
( )
1;S = +∞
. C.
1
;2
2
S

=


. D.
1
;1
2
S

=


.
Lời giải
Chọn A
Điều kiện
1
2
x >
.
Ta có
( )
3
log211 213 2
x xx− >⇔ −> ⇔ >
.
Vậy
( )
2;S = +∞
.
Câu 13: Đồ thị trong hình vẽ bên là của một trong bốn hàm số dưới đây. Hỏi đó là hàm số nào?
A.
2
1
x
y
x
+
=
+
. B.
1
2
x
y
x
+
=
+
. C.
2
2
y
x
=
+
. D.
1
1
y
x
=
+
.
Lời giải
Chọn B
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
4/20
Ta có
( )
lim 1
x
fx
→±∞
=
nên
1y =
là phương trình tiệm cận ngang của đồ thị.
( )
(
)
2
lim
x
fx
+
→−
= −∞
,
( )
( )
2
lim
x
fx
−
→−
= +∞
nên
2
x = −
là phương trình tiệm cận đứng của đồ thị.
Câu 14: Tập xác định của hàm số
( )
2
1yx= −
là
A.
(
]
;1D = −∞
. B.
[
)
1;
D = +∞
. C.
( )
1;D = +∞
. D.
( )
;1D = −∞
.
Lời giải
Chọn D
Ta có:
10 1
xx
−>⇔<
.
Câu 15: Phần thực của số phức
( )( )
1234z ii
=−+
bằng
A.
9−
. B.
2−
. C.
11
. D.
10
.
Lời giải
Chọn D
Ta có
( )( )
1234 105z ii i=− +=−
.
Câu 16: Cho cấp số nhân
( )
n
u
với
12
2, 1uu= = −
. Số hạng
4
u
của dãy số đã cho bằng
A.
1
8
. B.
1
4
−
. C.
1
8
−
. D.
1
4
.
Lời giải
Chọn B
Ta có
3
41
11
24
q u uq=−⇒ = =−
.
Câu 17: Cho hàm số
( )
y fx
=
có đạo hàm
( )
( )( )
22
2 2 4,fxxxxx x
′
= − − + ∀∈
. Số điểm cực trị của
hàm số đã cho là
A.
3
. B.
4
. C.
1
. D.
2
.
Lời giải
Chọn D
Ta có
( )
( )( )
22
0
2 240
2
x
fxxxxx
x
=
′
= − −+=⇔
=
.
Câu 18: Tiệm cận ngang của đồ thị hàm số
2
1
x
y
x
−+
=
−
là
A.
1y = −
. B.
1x =
. C.
2
y = −
. D.
1x = −
.
Lời giải
Chọn A
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
5/20
Ta có
2
lim 1
1
x
x
x
→±∞
−+
= −
−
Câu 19: Cho hàm số
( )
y fx=
có bảng biên thiên như hình bên. Giá trị nhỏ nhất của hàm số
( )
1
y fx= −
trên
[ ]
1; 3−
bằng
A.
3−
. B.
1−
. C.
2−
. D.
1
.
Lời giải
Chọn A
Ta có
[ ]
( )
( )
[ ]
( )
1;3 1;3
min 1 min 1 2 1 3fx fx
−−
− = −=−−=−
.
Câu 20: Với
a
là số thực dương khác
1
tùy ý, biểu thức
( )
2
43
log
a
aa+
bằng
A.
5
2
. B.
( )
31
log 1
22
a
a−+
. C.
7
2
. D.
( )
31
log 1
22
a
a++
.
Lời giải
Chọn D
Ta có:
( )
( ) ( )
22
43 3
31
log log 1 log 1
22
a
aa
a a aa a+ = +=+ +
.
Câu 21: Cho hai số phức
32zi=−+
và
14
wi= −
. Trong mặt phẳng tọa độ
Oxy
, điểm biểu diễn số phức
u zw
= +
là
A.
( )
2; 2M −−
. B.
( )
2; 6N −−
. C.
( )
4; 2P −
. D.
( )
2; 6Q −
.
Lời giải
Chọn B
Ta có:
32zi=−−
26ui
=−−
nên điểm
( )
2; 6N −−
biểu diễn số phức u.
Câu 22: Cho lăng trụ tứ giác đều
.' ' ' 'ABCD A B C D
có
AB a=
,
'6
AA a=
. Góc giữa
'AC
và
( )
''' 'ABC D
bằng
A.
30°
B.
60°
C.
45°
D.
90°
Lời giải
Chọn B
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
6/20
Ta có :
( ',('''')) ''60AC A B C D AC A= = °
Trong tam giác vuông
''
AA C
:
'6
tan ' ' 3
''
2
AA a
AC A
AC
a
= = =
.
Câu 23: Trong không gian
Oxyz
, phương trình chính tắc của đường thẳng
∆
đi qua
( )
3; 2; 1M −
và nhận
( )
5;6;7u = −
làm vectơ chỉ phương là
A.
567
:
32 1
xyz−++
∆==
−
B.
3 21
:
56 7
xyz++−
∆==
−
C.
3 21
:
56 7
xyz−−+
∆==
−
D.
567
:
32 1
xyz
+−−
∆==
−
Lời giải
Chọn C
Câu 24: Biết
( )
2
0
d4fx x=
∫
, tích phân
(
)
(
)
2
0
1dfx x
−
∫
bằng
A.
3
. B.
. C.
3−
. D.
2
.
Lời giải
Chọn D
( )
( )
( )
2 22
0 00
1d d d 4 2 2fx x fx x x− = − =−=
∫ ∫∫
.
Câu 25: Cho hai số phức
1
23zi
= +
và
2
12zi= +
. Môđun của số phức
12
zz z= −
bằng
A.
10
B.
2
C.
10
D.
2
Lời giải
Chọn D
Ta có:
12
zi=+=
.
Câu 26: Một dãy gồm 6 chiếc ghế được xếp liền nhau thành một hàng ngang. Xếp ngẫu nhiên 2 người
phụ nữ và 4 người đàn ông vào một dãy ghế đó, xác suất để 2 người nữ không ngồi kề nhau bằng
A.
1
6
. B.
2
3
. C.
1
3
. D.
5
6
.
Lời giải
Chọn B
Số phần tử không gian mẫu:
( )
6! 720n Ω= =
.
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
7/20
Gọi A là biến cố: “ 2 người nữ không ngồi kề nhau”
Gọi
A
là biến cố: “ 2 người nữ ngồi kề nhau”
Số phần tử của biến cố
A
:
( )
2!5! 240nA= =
.
Xác suất 2 người nữ không ngồi kề nhau:
( )
( )
(
)
240 2
11
720 3
nA
PA
n
=− =−=
Ω
.
Câu 27: Cho hàm số
()=
y fx
có đạo hàm
( )
42
' 3, .fx x x x= − ∀∈
Số điểm cực trị của hàm số
( ) ( )
23gx f x
= −
là
A.
1
. B.
. C.
4
. D.
2
.
Lời giải
Chọn D
Ta có:
( ) ( )
' 2'gx f x=
( )
( )
( )
42
' 02.' 02 3 0gx f x x x
=⇔ =⇔ −=
2
2
0( )
0
30
3
=
=
⇔⇔
−=
= ±
x kép
x
x
x
Số điểm cực trị của hàm số
( )
gx
là 2.
Câu 28: Họ các nguyên hàm của hàm số
(
)
cos 2 2
x
fx x= −
là
A.
(
)
12
sin 2
2 ln 2
x
Fx x C
=− −+
. B.
( )
12
sin 2
2 ln 2
x
Fx x C= −+
.
C.
( )
1
sin2 2 ln2
2
x
Fx x C
=− −+
. D.
( )
1
sin2 2 ln2
2
x
Fx x C= −+
.
Lời giải
Chọn B
Câu 29: Đạo hàm của hàm số
( )
( )
2
3
log 1fx x= +
là
A.
( )
( )
2
2
'
1 ln 3
x
fx
x
=
+
. B.
( )
( )
2
1
'
1 ln 3
fx
x
=
+
.
C.
( )
2
1
'
1
fx
x
=
+
. D.
( )
2
2
'
1
x
fx
x
=
+
.
Lời giải
Chọn A
Ta có:
( )
( )
( )
( )
2
22
1'
2
'
1 ln 3 1 ln 3
x
x
fx
xx
+
= =
++
.
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
8/20
Câu 30: Trong không gian
,O xyz
cho hai mặt phẳng
( )
: 2 3 10
α
+ + −=xyz
và
( )
: 2 3 13 0
β
+ ++=
xyz
. Gọi
( )
P
là mặt phẳng song song và cách đều
( ) ( )
,
αβ
. Mặt phẳng
( )
P
cắt
Oy
tại điểm có
tung độ bằng
A.
3
. B.
2−
. C.
6−
. D.
3−
.
Lời giải
Chọn D
Gọi
(
)
0; ;0
My
là giao điểm của
( )
P
và
Oy
.
Ta có:
(
)
(
)
( )
(
)
; ; 2 1 2 13dM dM y y
αβ
= ⇔ −= +
2 1 2 13 ( )
3
21213
y y VN
y
yy
−= +
⇔ ⇔=−
−=− −
Câu 31: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
3 40− +=zz
. Giá trị của biểu thức
22
12
= +Pz z
bằng
A.
4
B.
C.
16
D.
1
Lời giải
Chọn B
2
12
37 37
3 40 ;
22
−+
− +=⇒ = =
ii
zz z z
Vậy
22
12
8
=+=
Pz z
.
Câu 32: Cho hàm số bậc bốn
( )
y fx
=
có đồ thị như hình bên. Hỏi phương trình
( )
2 11fx−=
có bao
nhiêu nghiệm thuộc khoảng
( )
;0−∞
?
A.
4
B.
2
C.
1
D.
3
Lời giải
Chọn C
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
9/20
Dựa vào đồ thị hàm số ta có:
( )
( )
( )
( )
( )
;1
1; 0
1
2
0;1
1;
xa
xb
fx
xc
xd
= ∈ −∞ −
= ∈−
= ⇒
= ∈
= ∈ +∞
Do đó:
(
) ( )
( )
( )
( )
( )
(
)
( )
( )
( )
1 ; 1 1 ;0
1 1; 0 1 0;1
1
2 11 1
2
1 0;1 1 1; 2
1 1; 1 2;
xa xa
xb xb
fx fx
xc xc
xd xd

− = ∈ −∞ − = + ∈ −∞

− = ∈− = + ∈

−=⇔ −=⇒ ⇒

−= ∈ =+ ∈


− = ∈ +∞ = + ∈ +∞

Vậy phương trình
( )
2 11fx−=
có 1 nghiệm thuộc khoảng
( )
;0−∞
.
Cách khác:
Ta có:
( )
1
1
2
fx−=
Tịnh tiến đồ thị
( )
y fx
=
sang phải theo phương trục hoành 1 đơn vị được đồ thị hàm số
( )
1
y fx= −
.
Khi đó, đường thẳng
1
2
y
=
cắt đồ thị hàm số
( )
1
y fx= −
trên
( )
;0
−∞
tại 1 điểm.
Vậy phương trình
( )
2 11fx−=
có 1 nghiệm thuộc khoảng
( )
;0
−∞
.
Câu 33: Cho hình lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông tại
,, 2
′
= =B AB a AA a
.
Tính theo
a
khoảng cách từ
A
đến
( )
A BC
′
.
A.
2
6
a
. B.
6
6
a
. C.
2
3
a
. D.
6
3
a
.
Lời giải
Chọn D
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
10/20
Trong
(
)
A AB
′
, kẻ
( )
1.AH A B
′
⊥
Ta có:
(
) (
)
2.
⊥
′
⇒⊥ ⇒⊥
′
⊥
BC AB
BC A AB BC AH
BC AA
Từ
( )
1
và
( )
2
suy ra
( )
′
⊥AH A AB
( )
( )
22
22
. .2 6
d, .
3
( 2)
AB AA a a a
A A BC AH
AB AA
aa
′
′
⇒=== =
′
+
+
(
A AB
′
∆
vuông tại
A
)
Câu 34: Trong không gian
Oxyz
, đường thẳng nào sau đây vuông góc với mặt phẳng
( )
: 2 1 0?
α
+ −+=x yz
A.
1
1
:2
3
=−−
= +
= +
xt
dy t
zt
B.
4
12
: 24
32
= −
=−−
=−+
xt
dy t
zt
C.
2
12
:1
14
=−+
= +
= +
xt
dy t
zt
D.
3
2
:1
1
= +
=−−
=−+
xt
dy t
zt
Lời giải
Chọn B
( )
α
có vectơ pháp tuyến
( )
1; 2; 1= −
n
cùng phương vectơ chỉ phương
( )
4
2; 4; 2=−−

u
của đường
thẳng
4
d
nên
( )
4
α
⊥d
Câu 35: Một quả bóng rổ có chu vi đường tròn lớn bằng
77 cm
. Diện tích da để may quả bóng rổ đó gần
nhất với số nào dưới đây?
A.
2
5898cm
B.
2
626cm
C.
2
1888cm
D.
2
7709cm
Lời giải
Chọn C
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
11/20
Bán kính quả bóng rổ là
77
2
π
=
R
Diện tích da để may quả bóng rổ
2
22
77
4 4 1887, 26
2
ππ
π

= = ≈


S R cm
Câu 36: Cho hàm số bậc ba
()
=
y fx
có đồ thị như hình bên. Hàm số
( ) ( )
2gx f x= −
đồng biến trên
khhoảng nào trong các khoảng dưới đây?
A.
( )
0; 2
B.
( )
2; 4
C.
( )
4; +∞
D.
( )
;0−∞
Lời giải
Chọn A
Ta có
( ) ( )
2
′′
=−−gx f x
.
Hàm số đồng biến nên
( ) ( ) ( )
0 20 20
′′ ′
>⇔− − >⇔ − <gx fx fx
12 2 0 3⇔−<−<⇔<<xx
Vậy hàm số nghịch biến trên các khoảng
( )
0;3
.
Câu 37: Cho khối lăng trụ đứng
.ABCD A B C D
′′′′
có thể tích bằng
18
, đáy
ABCD
là hình vuông cạnh
. Độ dài cạnh
AA
′
bằng
A.
6
. B.
2
. C.
18
D.
3
.
Lời giải
Chọn B
2
18
2
3
ABCD
ABCD
V
V S AA AA
S
′′
= ⇒= ==
.
Câu 38: Diện tích
S
của hình phẳng giới hạn bởi hai đồ thị hàm số
3
yx=
và
2
2y xx= −
được tính bởi
công thức nào dưới đây?
A.
( ) ( )
01
32 32
20
2d 2dx x xx x x xx
−
+− − +−
∫∫
. B.
( )
1
32
2
2dx x xx
−
+−
∫
.
C.
(
) ( )
01
32 32
20
2d 2dx x xx x x xx
−
− +− + +−
∫∫
D.
( )
1
32
2
2dx x xx
−
+−
∫
.
Lời giải
Chọn A
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
12/20
PTHĐGĐ:
3 2 32
2
2 20 0
1
x
x xx x x x x
x
= −
=−⇔+−=⇔ =
=
.
BXD:
(
) ( )
10 1
32 32 32
22 0
2d 2d 2dS xx xx xx xx xx xx
−−
= +− = +− − +−
∫∫ ∫
.
Câu 39: Trên tập hợp các số phức, xét phương trình
( )
22
2 10 ,z az b a b− + −= ∈
. Có bao nhiêu cặp số
thực
( )
,
ab
sao cho phương trình trên có hai nghiệm
12
,zz
thỏa mãn
1
32 5zi−− =
và
22
1zi z−= +
?
A.
6
. B.
. C.
4
D.
2
.
Lời giải
Chọn B
Ta có:
22
'1ab∆= − +
TH1:
22
'0 10ab∆≥ ⇔ − + ≥
. Phương trình có 2 nghiệm thực.
( )
( )
2
1
1
1
1
2
2
22
22
2
2
3 45
32 5
4
1
11
0
z
z
zi
z
zi z
zz
z
=
− +=
−− =

⇔⇔
=

−= +
+= +

=
• Với
12
2, 0zz= =
, ta có:
12
1
2
1
zz
a
b
+
= =
= ±
(nhận)
• Với
12
4, 0
zz= =
, ta có:
12
2
2
1
zz
a
b
+
= =
= ±
(nhận)
TH2:
22
'0 10ab∆< ⇔ − + <
. Phương trình có 2 nghiệm phức.
Đặt
( )
1
2
,
z x yi
xy
z x yi
= +
∈
= −
.
Ta có
( ) ( )
( ) ( )
( ) ( )
22
22
1
22
22
22
1
3 25
32 5
3 25
4
1
11
x
xy
zi
xx
x
zi z
xy
xy x y
xy
=
− +− =
−− =
− +− =

⇔ ⇔⇔
=

−= +
=
++ =+ +

=
.
*
1xy= =
( )
2
2
1
1
2 10
1 2 21 10
2 20
3
a
ab
z i i a ib
a
b
=
− + −=
=+⇒ − + + −= ⇒ ⇒

− +=
= ±
(nhận)
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
13/20
*
( )
2
2
1
4
8 10
4 44 32 2 44 10
32 8 0
33
a
ab
xy z i i a i b
a
b
=
− + −=
= = ⇒ = + ⇒ − + + −= ⇒ ⇒

−=
= ±
(nhận)
Vậy có 8 cặp
( )
,ab
thỏa đề.
Câu 40: Cho hình lăng trụ đứng
.
ABC A B C
′′′
có đáy
ABC
là tam giác vuông cân tại
A
,
2BC a=
, góc
giữa
(
)
A BC
′′
và
( )
BCC B
′′
bằng
60°
. Tính thể tích khối tứ diện
ABB C
′′
.
A.
3
2
3
a
. B.
3
2
9
a
. C.
3
22
3
a
D.
3
2
a
.
Lời giải
Chọn A
Gọi
H
′
là trung điểm của
BC
′′
AH BC
′ ′ ′′
⇒⊥
(
ABC
′′′
∆
vuông cân tại
A
′
).
Ta có
( )
AH BC
A H BC C B
A H BB
′ ′ ′′
⊥
′ ′ ′′
⇒⊥
′′ ′
⊥
.
Kẻ
H K BC
′′
⊥
mà
( )
( )
BC A H A H BCC B
′ ′′ ′′ ′′
⊥⊥
Suy ra
A K BC
′′
⊥
Khi đó
(
) ( )
(
) ( )
( )
( )
, , 60
A BC BCC B BC
AK BC ABC BCCB AK HK AKH
H K BC
′ ′ ′′ ′
∩=
′′ ′′′′′′′′
⊥⇒ ===°
′′
⊥
.
Ta có
2
BC
AH A H a
′′
′′
= = =
,
3
.cot 60
3
a
HK AH
′ ′′
= °=
,
2
2 22
6
33
aa
KC HC HK a
′ ′′ ′
= − = −=
.
( )
.BCB KCH gg
′′ ′′
∆∆
.2
BB BC BC
B B KH a
KH KC KC
′ ′′ ′′
′′
⇒ = ⇒= =
′′ ′
.
3
.
1 11 2
. . .2 . 2
3 32 3
A BB C BB C
a
V AH S a a a
′′ ′′
∆
= = =
.
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
14/20
Câu 41: Theo Tổng cục Thống kê, dân số Việt Nam ở cuối tháng 12 của hai năm 2022 và 2023 lần lượt
là 99,47 và 100,3 triệu người. Hỏi nếu với tỉ lệ tăng dân số trung bình hằng năm như năm 2023
thì năm nào dưới đây là năm đầu tiên dân số nước ta vượt ngưỡng 120 triệu người?
A. 2043. B. 2045. C. 2046. D. 2047.
Lời giải
Chọn B
Tỉ lệ năm 2023 là
100,3 99,47 83
99,47 9947
r
−
= =
Gọi n là số năm đủ để dân số vượt ngưỡng 120 triệu người.
Ta có:
(
)
100,3. 1 120 21, 5
n
rn+ > ⇒>
.
Vậy dân số năm 2045 sẽ vợt ngưỡng 120 triệu người.
Câu 42: Một vật lưu niệm cao 15 cm, gồm hai hình nón chung đỉnh và chung trục
như hình vẽ, đường sinh bất kỳ của hai hình nón luôn tạo với mặt đáy
một góc
o
60
. Biết rằng thể tích của khối nón nhỏ bằng 12,5% thể tích
của khối nón lớn. Tính thể tích của vật lưu niệm đó?
A.
3
125 cm .π
B.
3
100 cm .π
C.
3
156,25 cm .
π
D.
3
109,75 cm .π
Lời giải
Chọn A
Gọi
' 15
0
tan 60
3
15
tan 60
3
SO x
SO x
SO x OA
SO x
OB
°
= −
=>⇒ = =
′
−
′
= =
°
Ta có:
( ) ( )
22
3
3
1 15 1 1
15 . 8 15 10
3 83
33
xx
x x xx x
ππ
−

− = ⇔ − = ⇔=


Vậy: Thể tích của vật lưu niệm đó là
33
3
1 10 1 1 10
. 125 cm .
33833
π ππ
+=
Câu 43: Xét các số phức
,zw
thỏa mãn
3, 5zw= =
và
( )
z wz−
là số ảo. Giá trị nhỏ nhất của
34Pz w i=++
bằng
A.
8.
B.
3 2 1.−
C.
12 2 4.
−
D.
14.
Lời giải
Chọn C
Gọi
z x yi= +
. Ta có:
22
39z xy=⇒+=
.
w a bi= +
. Ta có:
22
5 25w ab=⇒+=
.
( )
.zwz zzwz−=−
là số ảo nên
22
09x y ax by ax by+−−=⇔+=
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
15/20
(
) (
)
(
)
( )
( )
(
)
(
)
22
2 2 22
3 3 33
6 9 9 6.9 9.25 12 2
z w x yi a bi x a y b
x y ax by a b
+ = + + + = + ++
= + + ++ + =++ =
3 4 3 4 12 2 4.
Pzwi zw i
=+ + ≥+ − = −
Vậy giá trị nhỏ nhất của
P
bằng
12 2 4.−
Câu 44: Trong không gian
Oxyz
, cho hai điểm
( )
3; 3;1A
,
( )
0; 2;1B
và mặt phẳng
( )
: 70
xyz
α
++−=
. Đường thẳng
∆
nằm trong
( )
α
sao cho mọi điểm thuộc
∆
luôn cách
đều hai điểm
,AB
. Biết rằng
(
)
1; ;u ab=
là vectơ chỉ phương của
∆
. Tính
u
.
A.
11
. B.
. C.
14
. D.
6
.
Lời giải
Chọn C
Vì
∆
luôn cách đều hai điểm
,AB
nên
∆
nằm trong mặt phẳng trung trực
( )
β
của đoạn
AB
.
Ta có
( )
3; 1; 0n AB
β
= =−−
 
;
( )
1;1;1n
α
=

;
(
)
, 1; 3; 2 1 4nn u u
αβ

=− =⇒=

 
.
Câu 45: Cho hàm số bậc ba
( )
y fx=
thỏa mãn
( )
21f =
. Đồ thị hàm số
( )
y fx
′
=
như hình vẽ
Hỏi hàm số
( ) ( )
1
gx f x
x
= +
có bao nhiêu điểm cực trị?
A.
4
. B.
6
. C.
2
. D.
3
.
Lời giải
Chọn A
BBT của
( )
fx
:
Đặt
( ) ( ) ( ) ( )
2
1
11
0
2
xa
hxfx hxfx
xb
xx
= <−
′′
= +⇒ = − =⇔
= >
.
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
16/20
BBT của
( )
hx
Trong đó
(
)
( ) ( ) ( )
1 11
1 1 10ha f a h f
a aa
= +> −= −+>+>
và
( ) ( )
1
0
hb f b
b
= +>
.
Do đó hàm số
( )
(
)
(
)
1
gx f x hx
x
= +=
có 4 cực trị.
Câu 46: Có bao nhiêu số nguyên
a
sao cho ứng với mỗi
a
tồn tại số thực
ba>
thỏa mãn
( )
6
log 1 2 3
bb
a = ++
và đoạn
[ ]
;ab
chứa không quá
6
số nguyên?
A. Vô số. B.
. C.
8
. D.
10
.
Lời giải
Chọn C
Ta có
( )
6
log12 3 12 3 6 0
bb bba
a = ++ ⇔++−=
Đặt
( )
12 3 6
bba
fb=++−
thì
( )
0fb=
và
( )
2 ln 2 3 ln 3 0,
bb
fb b
′
= + >∀
nên
( )
fb
đồng biến
trên
.
Do đoạn
[ ]
;ab
chứa không quá
6
số nguyên (và
ab<
) nên ta có điều kiện đủ
6aba<<+
.
Do vậy chỉ cần xét hàm số
(
)
fb
đồng biến trên
[
)
;6aa+
.
Ta có
( ) ( ) (
)
6 06a b a fa fb fa<<+⇒ < =< +
Hay
(
)
( )
(
)
( )
66
0 1 2 3 6 01
60
1 2 3 6 02
aaa
aaa
fa
fa
++
< ++−<

⇒

+>
+ + −>
.
+ Xét
( )
( ) ( )
111
1 10 1 1
632
aaa
ha h a

⇔ + + −< ⇔ < ⇔ >


(vì
(
)
111
1
632
xxx
hx

=++−


nghịch biến trên
)
+ Xét
(
)
66
111
2 2. 3. 1 0
632
aaa

⇔++−>


( )
66
111
2. 3. 1
632
aaa
gx

=++−


có bảng biến thiên như sau
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
17/20
Do đó
( )
2 9,51a⇒<
Suy ra
{ }
2;3;...;9
a ∈
.
Vậy có 8 giá trị nguyên của
a
thỏa yêu cầu.
Câu 47: Khi quay hình phẳng giới hạn bởi các đường
2
logyx=
,
0y =
và
4
x =
xung quanh đường thẳng
4
x =
thu được khối tròn xoay có thể tích gần nhất với giá trị nào sau đây?
A.
13
. B.
25
. C.
26
. D.
14
.
Lời giải
Chọn C
Dời hệ trục
Oxy
thành hệ trục
IXY
với gốc tọa độ
( )
4; 0I
như hình vẽ.
Công thức đổi trục
4xX
yY
= +
=
.
Trong hệ trục
IXY
, các đường
2
logyx=
,
0y =
và
4
x =
lần lượt trở thành các đường
( )
2
log 4YX= +
,
0, 0
YX= =
.
Bài toán trở thành tính thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường
( )
2
log 4YX= +
,
0, 0YX
= =
quanh trục tung.
Ta có
( )
2
log 4 2 4
Y
YXX
= +⇒=−
.
Thể tích khối tròn xoay tạo thành là
( ) (
)
22
2
2
00
2 4 d 2 8.2 16 d
Y YY
VY Y
ππ
= − = −+
∫∫
2
2
0
2 8.2
16 25,75
2 ln 2 ln 2
YY
Y
π

= −+ ≈


.
Câu 48: Trong không gian
,O xyz
cho điểm
1; 1 2; 4 ,A
mặt phẳng
: 40Pyz
cắt mặt cầu
2 22
: 10 4 5 0Sx y z x z 
theo giao tuyến là đường tròn
.
Điểm
M
thuộc
sao cho đoạn thẳng
AM
ngắn nhất. Khẳng định nào sau đây đúng?
A.
2 6.OM
B.
6.OM
C.
10.OM
D.
5.OM
Lời giải
Chọn D
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
18/20
Gọi
,IJ
lần lượt là tâm mặt cầu
S
và tâm của đường tròn
.
Mặt cầu
S
có tâm
5; 0; 2 ,I 
bán kính
2 6.R
IMJ
vuông tại
J
có
2 2 2 22 2
, 22.IM IJ JM R d I P r r


Kẻ
AH P
tại
.H
Suy ra
22
1244
, 2 2.
11
AH d A P


Vì
,HJ
lần lượt là hình chiếu vuông góc của điểm
A
và
I
lên mặt phẳng
P
nên ta tìm
được
5;1;3J 
và
1; 1 0; 6 .H
Suy ra
3 22.HJ
AHM
vuông tại
H
có
22 2 2
8.AM AH HM HM

Để
AM
ngắn nhất
HM
ngắn nhất. Khi đó
2 22.
HM HJ r

Suy ra
2
min
8 2 22 4 6.AM 
Dấu
""
xảy ra khi và chỉ khi
M HJ

và
M
nằm giữa
H
và
.J
Ta có
1
.
3
MJ
MJ HJ HJ
HJ

  
nên ta tìm được tọa độ điểm
M
là
3; 4; 0 .M 
Vậy độ dài đoạn thẳng
22
2
3 4 0 5.
OM 
Câu 49: Cho hàm số
32
f x ax bx cx d 
,,, .abcd
Đồ thị hàm số
,
y fx
trục hoành và
đường thẳng
4x
tạo ra
hình phẳng có diện tích là
123
,,SSS
(hình vẽ bên). Biết
13 2
5
,
6
SS S
tích phân
4
1
21 dx fxx
bằng
A.
89
.
3
B.
173
.
6
C.
79
.
3
D.
163
.
6
Lời giải
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
19/20
Chọn C
Dựa vào đồ thị, ta có
4
132
1
5
d.
6
fx x S S S

Khi đó
44
4
1
11
21 d 21 2 d
x f x x x fx fx x



4
1
5 79
7 4 3 1 2 d 7.4 3.0 2. .
63
f f fx x

Câu 50: Cho hàm số bậc ba
y fx
có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của tham số
a
để hàm số
42
1
22
8
gx f x a x



đồng biến trên khoảng
0;1
?
A.
3.
B.
14.
C.
1.
D.
15.
Lời giải
Chọn A
Dựa vào đồ thị, ta thấy
0 0 2.fx x

Ta có
3 42
1
4 2 2.
8
g x x xf x a x




Hàm số
gx
đồng biến trên khoảng
0;1
thì
0, 0;1gx x

3 42
1
4 2 2 0, 0;1 1 .
8
x xf x a x x



Vì
0;1x
nên

32
4 4 2 2 0, 0;1x x xx xx x x

Khi đó
42
1
1 2 2 0, 0;1
8
f xa x x



24
42
24
16 2
1
0 2 2 2, 0;1 , 0;1 2 .
8
16 16 2
axx
xa x x x
a xx

 

Xét hàm số
24
16 2hx x x
trên đoạn
0;1
có
32
32 8 8 4 0, 0;1hx x x x x x

Suy ra hàm số
hx
luôn đồng biến trên
0;1 .
Khi đó
0;1
min 0 0hx h
và
0;1
max 1 14.hx h
Khi đó
0;1
0;1
max
14
2 14 16.
16
16 min
a hx
a
a
a
a hx




TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
20/20
Vì
a
nên
14;15;16 .a
Vậy có
3
giá trị nguyên của
a
thỏa mãn bài toán.
| 1/29
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
HƯỚNG DẪN GIẢI ĐỀ THI THỬ TNTHPT MÔN TOÁN NĂM HỌC 2023 - 2024
(ĐỀ SỞ GD & ĐT TIỀN GIANG – MÃ ĐỀ 101)
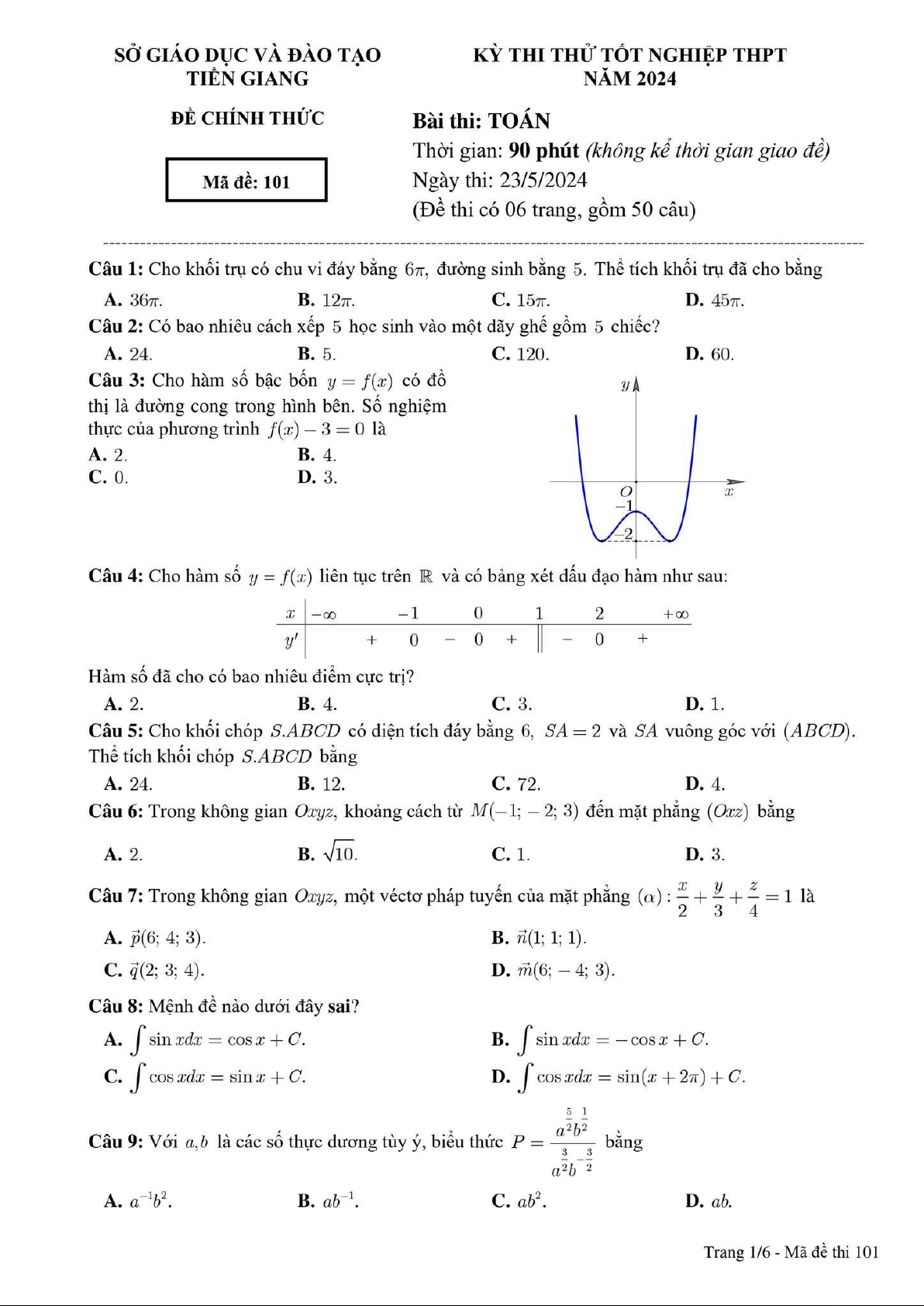
Câu 1: Cho khối trụ có chu vi đáy bằng 6, đường sinh bằng 5. Thể tích khối trụ đã cho bằng A. 36. B. 12. C. 15. D. 45. Lời giải Chọn D
Ta có: Chu vi đáy C  2 r
 6r  3 Thể tích khối trụ 2 2 V r
 h .3 .5  45
Câu 2: Có bao nhiêu cách xếp 5 học sinh vào một dãy ghế gồm 5 chiếc? A. 24 . B. 5. C. 120 . D. 60. Lời giải Chọn C Ta có: 5!120
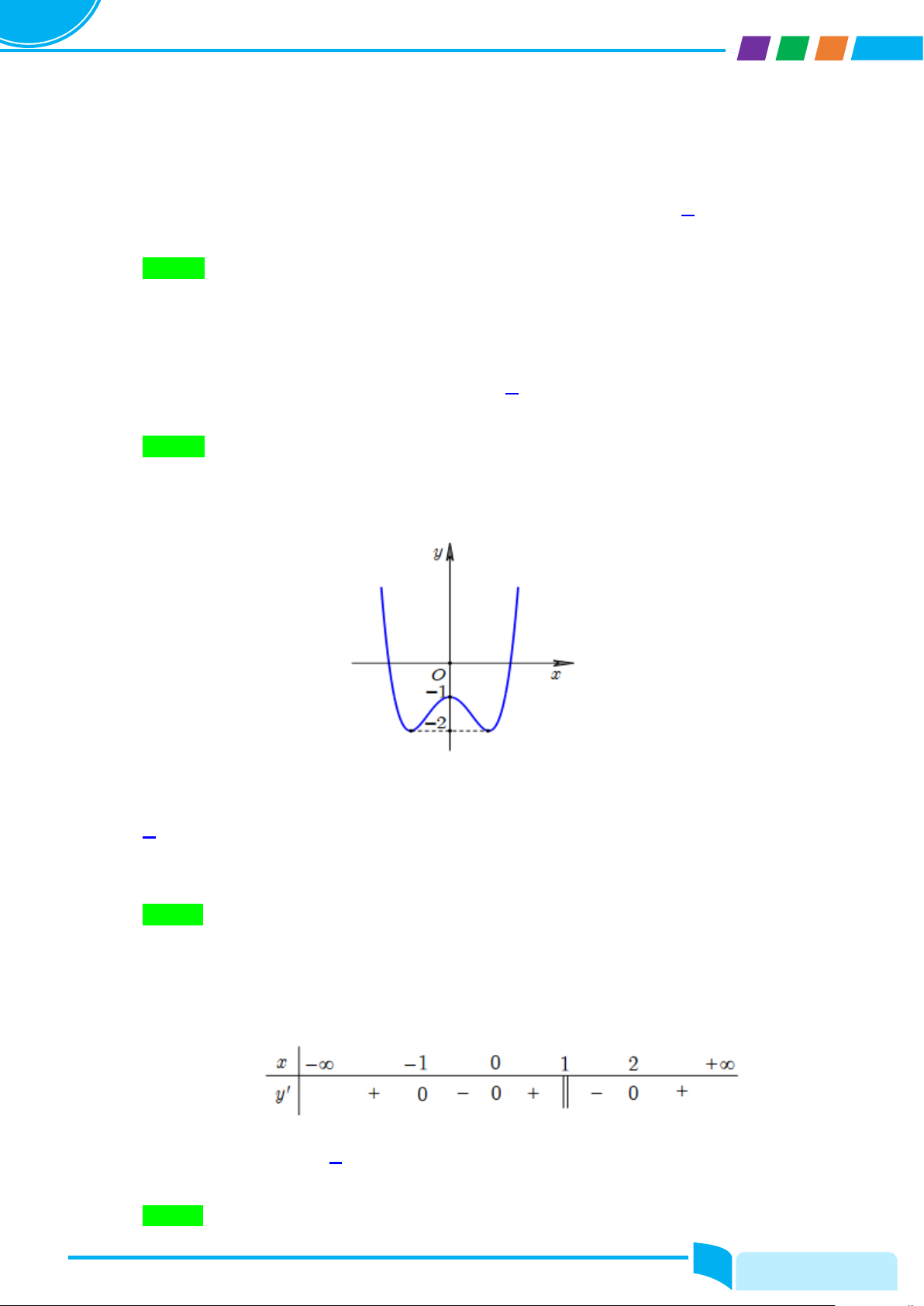
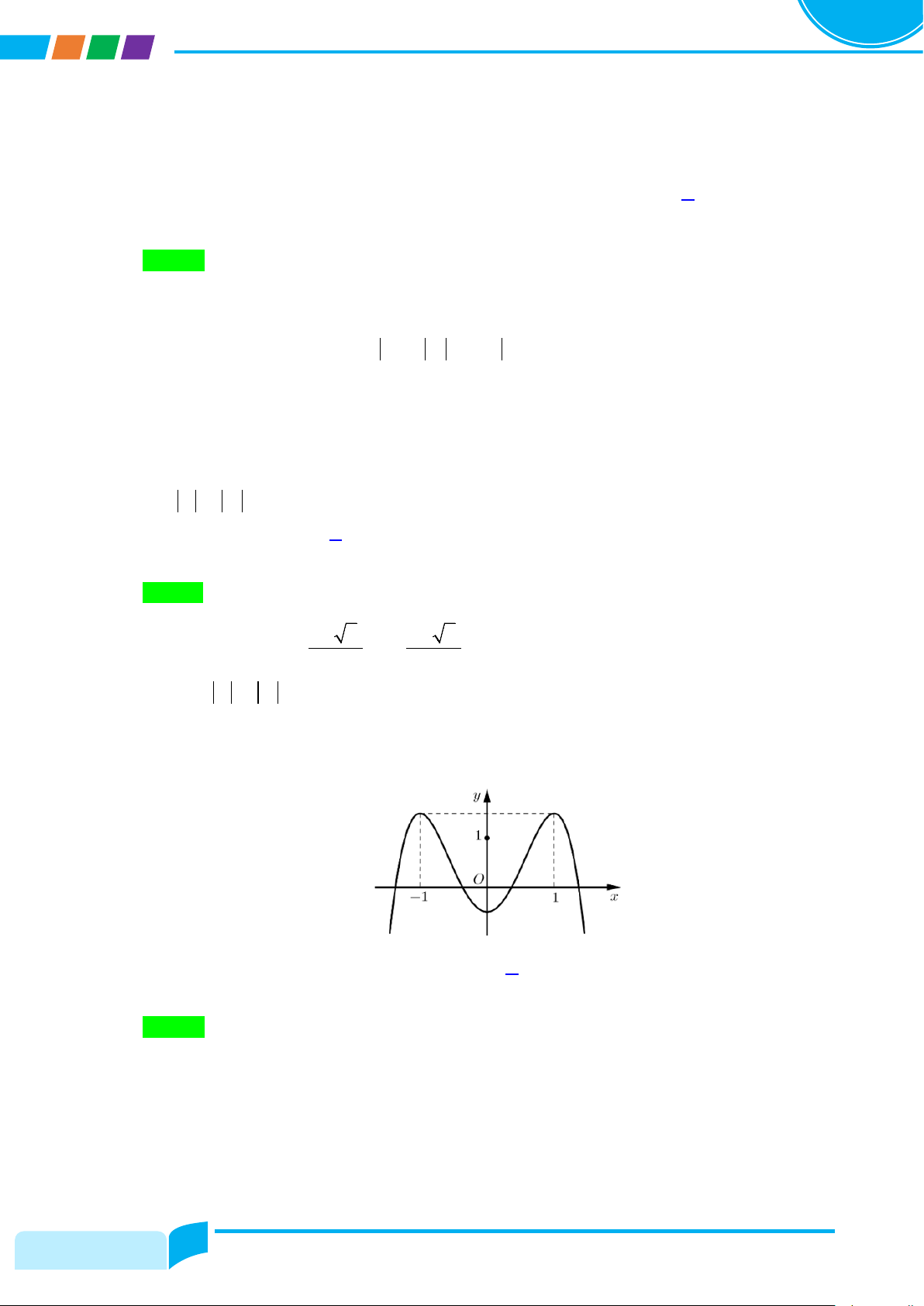
Câu 3: Cho hàm số bậc bốn y f xcó đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình f x3  0 là A. 2 . B. 0. C. 4 . D. 3. Lời giải Chọn A
Ta có: f x3  0  f x 3. Đồ thị y f x cắt đồ thị y  3 tại hai điểm phân biệt nên
phương trình có hai nghiệm phân biệt.
Câu 4: Cho hàm số y f xliên tục trên  và có bảng xét dấu đạo hàm như sau:
Hàm số đã cho có bao nhiêu cực trị? A. 2 . B. 4 . C. 3. D. 1. Lời giải Chọn B
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024 1/20
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Ta có: Dựa vào bảng xét dấu ta thấy hàm số đã cho có 4 điểm cực trị.
Câu 5: Cho khối chóp S.ABCD có diện tích đáy bằng 6, SA  2 và SA vuông góc với ABCD. Thể
tích khối chóp S.ABCD bằng A. 24 . B. 12 . C. 72 . D. 4 . Lời giải Chọn D Ta có: 1 1
V B.h  .6.2  4 3 3
Câu 6: Trong không gian Oxyz , khoảng cách từ M 1  ; 2  ; 
3 đến mặt phẳng Oxzbằng A. 2 . B. 10 . C. 1. D. 3. Lời giải Chọn A
Ta có: dM;Oxz y  . M 2
Câu 7: Trong không gian Oxyz , một vectơ pháp tuyến của mặt phẳng  : x y z    1 là 2 3 4 A. p    6;4;  3 . B. n   111 ; ; .
C. q 2;3;  4 .
D. m 6;4;  3 . Lời giải Chọn A    Ta có:  1 1 1 n
  ; ;  cùng phương với p 6;4;  3 . 2 3 4
Câu 8: Mệnh đề nào dưới đây sai?
A. sin xdx  cos x C  .
B. sin xdx cos x C  .
C. cos xdx  sin x C  .
D. cos xdx  sin 
x 2C . Lời giải Chọn A 5 1 2 2 Câu 9: Với a b ,
a b là các số thực dương tùy ý, biểu thức P  3 3 2 2 a bA. −1 2 a b . B. 1 ab− . C. 2 ab . D. ab . Lời giải Chọn C 5 1 5 3 1 3 2 2  Ta có: a b 2 2  2 2 2 P   a bab . 3 3  2 2 a b 2/
20 Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
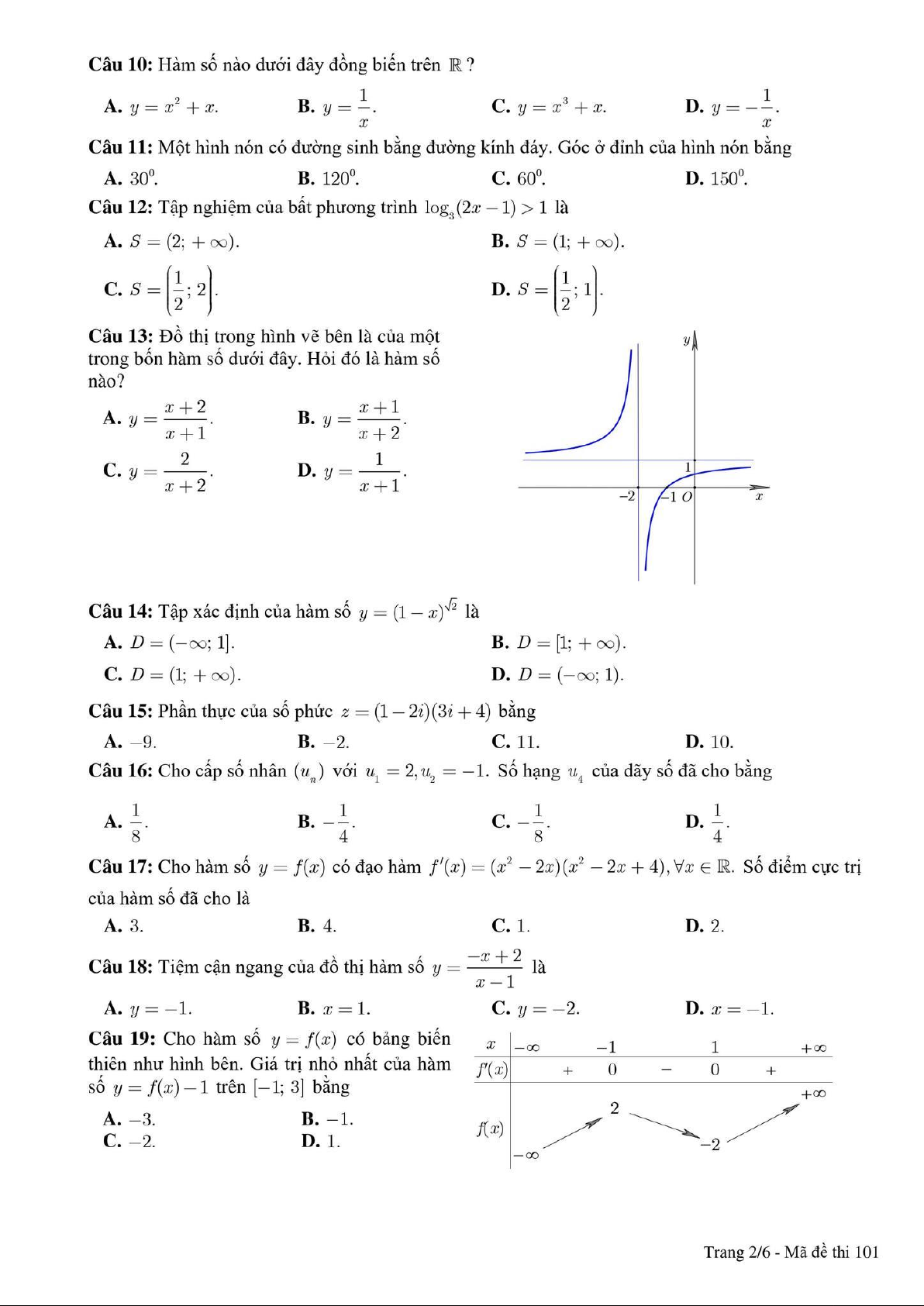
Câu 10: Hàm số nào dưới đây đồng biến trên  ? A. 2
y x x . B. 1 y = . C. 3
y x x . D. 1 y = − . x x Lời giải Chọn C Ta có: 3 2
y x x y  3x 1 0,x   .
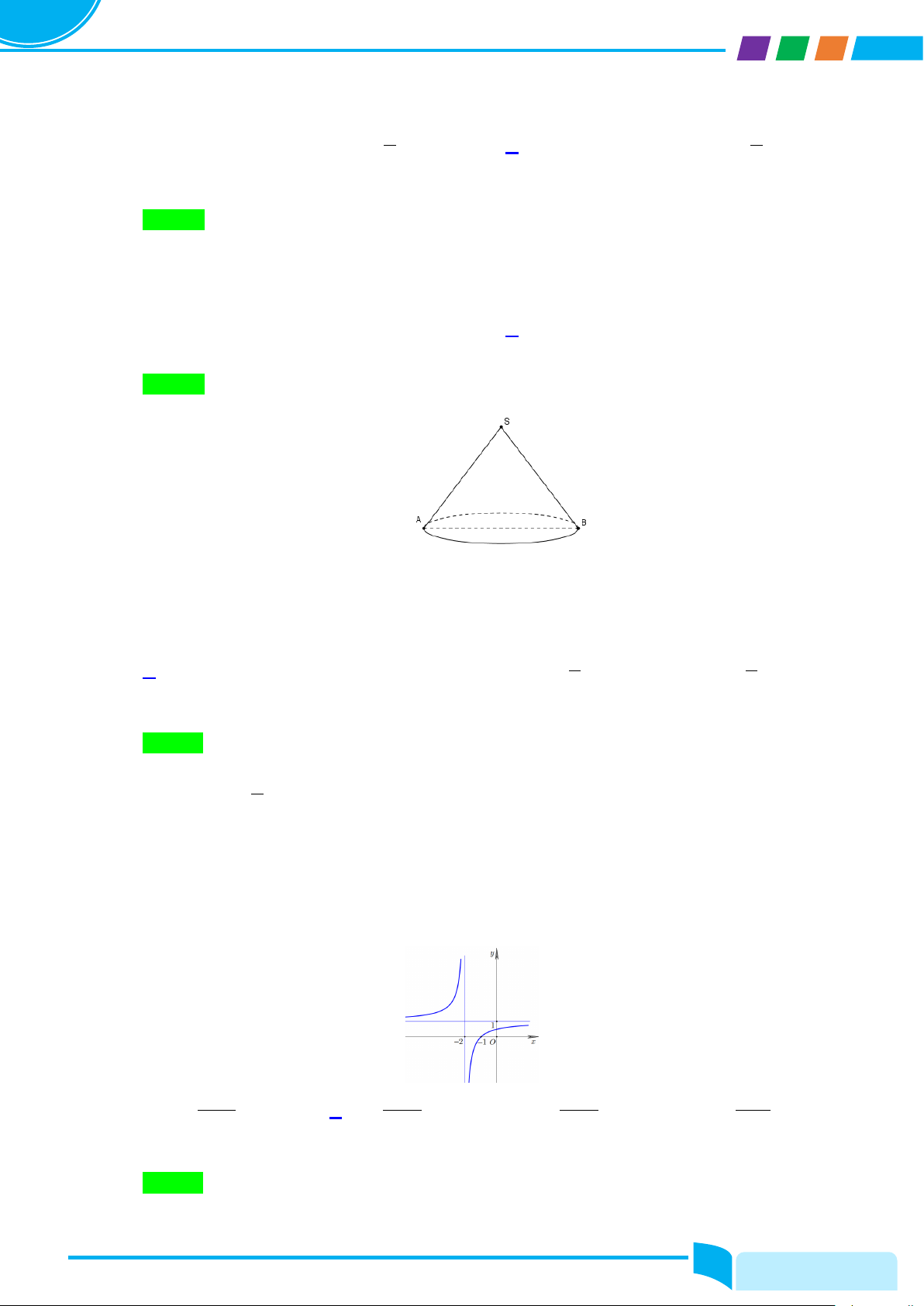
Câu 11: Một hình nón có đường sinh bằng đường kính đáy. Góc ở đỉnh của hình nón bằng A. 30° . B. 120° . C. 60°. D. 150° . Lời giải Chọn C Ta có S ∆ AB đều nên  ASB = 60°.
Câu 12: Tập nghiệm của bất phương trình log 2x −1 >1 là 3 ( )
A. S = (2;+∞) .
B. S = (1;+∞) . C. 1 S  ;2 =   . D. 1 S  =  ;1 . 2      2  Lời giải Chọn A Điều kiện 1 x > . 2
Ta có log 2x −1 >1 ⇔ 2x −1 > 3 ⇔ x > 2. 3 ( ) Vậy S = (2;+∞) .
Câu 13: Đồ thị trong hình vẽ bên là của một trong bốn hàm số dưới đây. Hỏi đó là hàm số nào? A. x + 2 y + = . B. x 1 y = . C. 2 y = . D. 1 y = . x +1 x + 2 x + 2 x +1 Lời giải Chọn B
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024 3/20
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Ta có lim f (x) =1 nên y =1 là phương trình tiệm cận ngang của đồ thị. x→±∞
lim f (x) = −∞, lim f (x) = +∞ nên x = 2
− là phương trình tiệm cận đứng của đồ thị. x ( 2)+ → − x ( 2)− → −
Câu 14: Tập xác định của hàm số y = ( − x) 2 1 là A. D = (−∞ ] ;1 .
B. D = [1;+∞) .
C. D = (1;+∞) . D. D = (−∞ ) ;1 . Lời giải Chọn D
Ta có: 1− x > 0 ⇔ x <1.
Câu 15: Phần thực của số phức z = (1− 2i)(3i + 4) bằng A. 9 − . B. 2 − . C. 11. D. 10. Lời giải Chọn D
Ta có z = (1− 2i)(3i + 4) =10 −5i .
Câu 16: Cho cấp số nhân (u với u = 2,u = 1
− . Số hạng u của dãy số đã cho bằng n ) 1 2 4 A. 1 . B. 1 − . C. 1 − . D. 1 . 8 4 8 4 Lời giải Chọn B Ta có 1 3 1
q = − ⇒ u = u q = − . 4 1 2 4
Câu 17: Cho hàm số y = f (x) có đạo hàm f ′(x) = ( 2 x − x)( 2 2
x − 2x + 4), x
∀ ∈  . Số điểm cực trị của hàm số đã cho là A. 3. B. 4 . C. 1. D. 2 . Lời giải Chọn D x = 0
Ta có f ′(x) = ( 2 x − 2x)( 2
x − 2x + 4) = 0 ⇔  . x = 2
Câu 18: Tiệm cận ngang của đồ thị hàm số −x + 2 y = là x −1 A. y = 1 − . B. x =1. C. y = 2 − . D. x = 1 − . Lời giải Chọn A 4/
20 Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG Ta có −x + 2 lim = 1 − x→±∞ x −1
Câu 19: Cho hàm số y = f (x) có bảng biên thiên như hình bên. Giá trị nhỏ nhất của hàm số y = f (x) −1 trên [ 1; − ]3 bằng A. 3 − . B. 1 − . C. 2 − . D. 1. Lời giải Chọn A
Ta có min( f (x) − )
1 = min f (x) −1= 2 − −1 = 3 − . [ 1 − ; ] 3 [ 1 − ; ] 3
Câu 20: Với a là số thực dương khác 1 tùy ý, biểu thức 4 3
log a + a bằng 2 a ( ) A. 5 . B. 3 1 − log (a + ) 1 . C. 7 . D. 3 1 + log (a + ) 1 . 2 2 2 a 2 2 2 a Lời giải Chọn D Ta có: 4 3 3 3 1
log a + a = log a a +1 = + log a +1 . 2 a ( ) 2 ( ) ( ) a 2 2 a
Câu 21: Cho hai số phức z = 3
− + 2i và w =1− 4i . Trong mặt phẳng tọa độ Oxy , điểm biểu diễn số phức
u = z + w là A. M ( 2; − 2 − ). B. N ( 2; − 6 − ) . C. P(4; 2 − ) . D. Q(2; 6 − ). Lời giải Chọn B Ta có: z = 3 − − 2i u = 2
− − 6i nên điểm N ( 2; − 6
− ) biểu diễn số phức u.
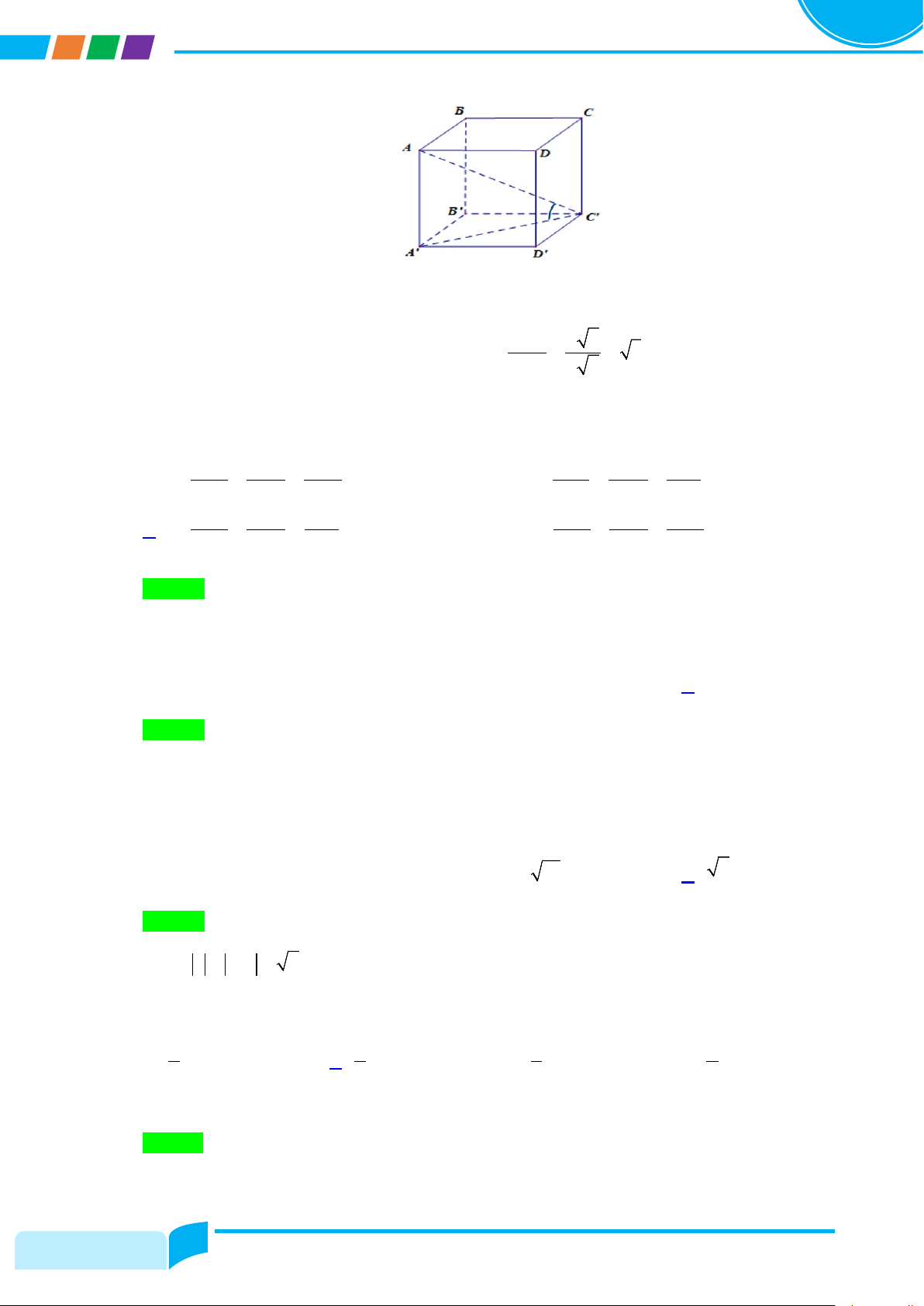
Câu 22: Cho lăng trụ tứ giác đều ABC .
D A' B 'C ' D ' có AB = a , AA' = 6a . Góc giữa AC ' và
(A'B'C'D') bằng A. 30° B. 60° C. 45° D. 90° Lời giải Chọn B
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024 5/20
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG Ta có : = 
(AC ',(A'B'C 'D')) AC ' A' = 60°
Trong tam giác vuông AA'C ' :  AA' a 6 tan AC ' A' = = = 3 . A'C ' a 2
Câu 23: Trong không gian Oxyz , phương trình chính tắc của đường thẳng ∆ đi qua M (3;2;− ) 1 và nhận
u =( 5−;6;7) làm vectơ chỉ phương là A.
x − 5 y + 6 z + 7 + + − ∆ : = = B.
x 3 y 2 z 1 ∆ : = = 3 2 1 − 5 − 6 7 C.
x − 3 y − 2 z +1 + − − ∆ : = = D.
x 5 y 6 z 7 ∆ : = = 5 − 6 7 3 2 1 − Lời giải Chọn C 2 2
Câu 24: Biết f
∫ (x)dx = 4, tích phân ( f (x)− ∫ )1dx bằng 0 0 A. 3. B. 5. C. 3 − . D. 2 . Lời giải Chọn D 2∫( 2 2 f (x) − ) 1 dx = f
∫ (x)dx− dx = 4−2 = 2 ∫ . 0 0 0
Câu 25: Cho hai số phức z = 2 + 3i z =1+ 2i
z = z − z 1 và 2 . Môđun của số phức 1 2 bằng A. 10 B. 2 C. 10 D. 2 Lời giải Chọn D
Ta có: z = 1+ i = 2 .
Câu 26: Một dãy gồm 6 chiếc ghế được xếp liền nhau thành một hàng ngang. Xếp ngẫu nhiên 2 người
phụ nữ và 4 người đàn ông vào một dãy ghế đó, xác suất để 2 người nữ không ngồi kề nhau bằng A. 1 . B. 2 . C. 1 . D. 5 . 6 3 3 6 Lời giải Chọn B
Số phần tử không gian mẫu: n(Ω) = 6!= 720 . 6/
20 Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Gọi A là biến cố: “ 2 người nữ không ngồi kề nhau”
Gọi A là biến cố: “ 2 người nữ ngồi kề nhau”
Số phần tử của biến cố A : n( A) = 2!5!= 240. n( A)
Xác suất 2 người nữ không ngồi kề nhau: P( A) 240 2 =1− = − = . n(Ω) 1 720 3
Câu 27: Cho hàm số y = f (x) có đạo hàm f (x) 4 2 '
= x − 3x , x ∀ ∈ .
 Số điểm cực trị của hàm số
g (x) = 2 f (x) −3 là A. 1. B. 3. C. 4 . D. 2 . Lời giải Chọn D
Ta có: g '(x) = 2 f '(x)
g (x) = ⇔ f (x) = ⇔ ( 4 2 ' 0 2. ' 0
2 x − 3x ) = 0 2  x = 0 x = 0(kép) ⇔  ⇔ 2 x − 3 = 0   x = ± 3
Số điểm cực trị của hàm số g (x) là 2.
Câu 28: Họ các nguyên hàm của hàm số ( ) = cos2 − 2x f x x là x x A. F (x) 1 2 = − sin 2x − + C .
B. F (x) 1 2 = sin 2x − + C . 2 ln 2 2 ln 2 C. ( ) 1 = − sin 2 − 2x F x x ln 2 + C . D. ( ) 1 = sin 2 − 2x F x x ln 2 + C . 2 2 Lời giải Chọn B
Câu 29: Đạo hàm của hàm số f (x) = log ( 2 x +1 là 3 ) A. ( ) 2 ' x f x = 1 ( .
B. f '(x) = . 2 x + ) 1 ln3 ( 2x + )1ln3 C. f (x) 1 ' = . D. ( ) 2 ' x f x = . 2 x +1 2 x +1 Lời giải Chọn A ( 2x + )1' Ta có: ( ) 2 ' x f x = ( = . 2 x + ) 1 ln3 ( 2 x + ) 1 ln3
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024 7/20
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Câu 30: Trong không gian Oxyz, cho hai mặt phẳng (α ) : x + 2y + 3z −1= 0 và (β ) : x + 2y + 3z +13 = 0
. Gọi (P) là mặt phẳng song song và cách đều (α ),(β ) . Mặt phẳng (P) cắt Oy tại điểm có tung độ bằng A. 3. B. 2 − . C. 6 − . D. 3 − . Lời giải Chọn D
Gọi M (0; y;0) là giao điểm của (P) và Oy .
Ta có: d (M;(α )) = d (M;(β )) ⇔ 2y −1 = 2y +13
2y −1 = 2y +13 (VN) ⇔ ⇔ y = 3 −   2y −1 = 2 − y −13
Câu 31: Trên tập số phức, gọi z , z z − z + = 1
2 là hai nghiệm của phương trình 2 3
4 0 . Giá trị của biểu thức 2 2
P = z + z bằng 1 2 A. 4 B. 8 C. 16 D. 1 Lời giải Chọn B 2 3− 7i 3+ 7 − 3 + 4 = 0 ⇒ = ; = i z z z z 1 2 2 2 Vậy 2 2
P = z + z = 8 . 1 2
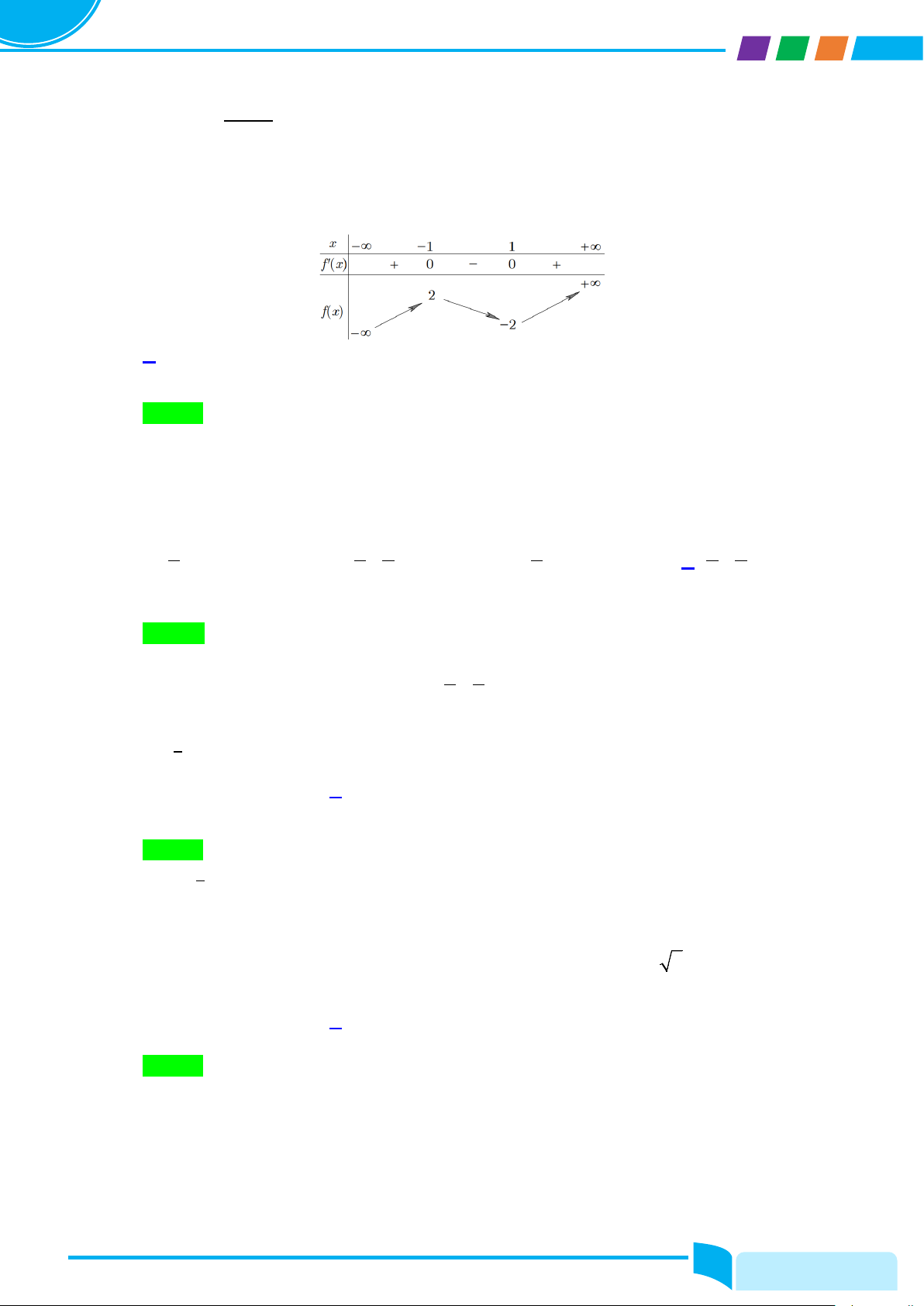
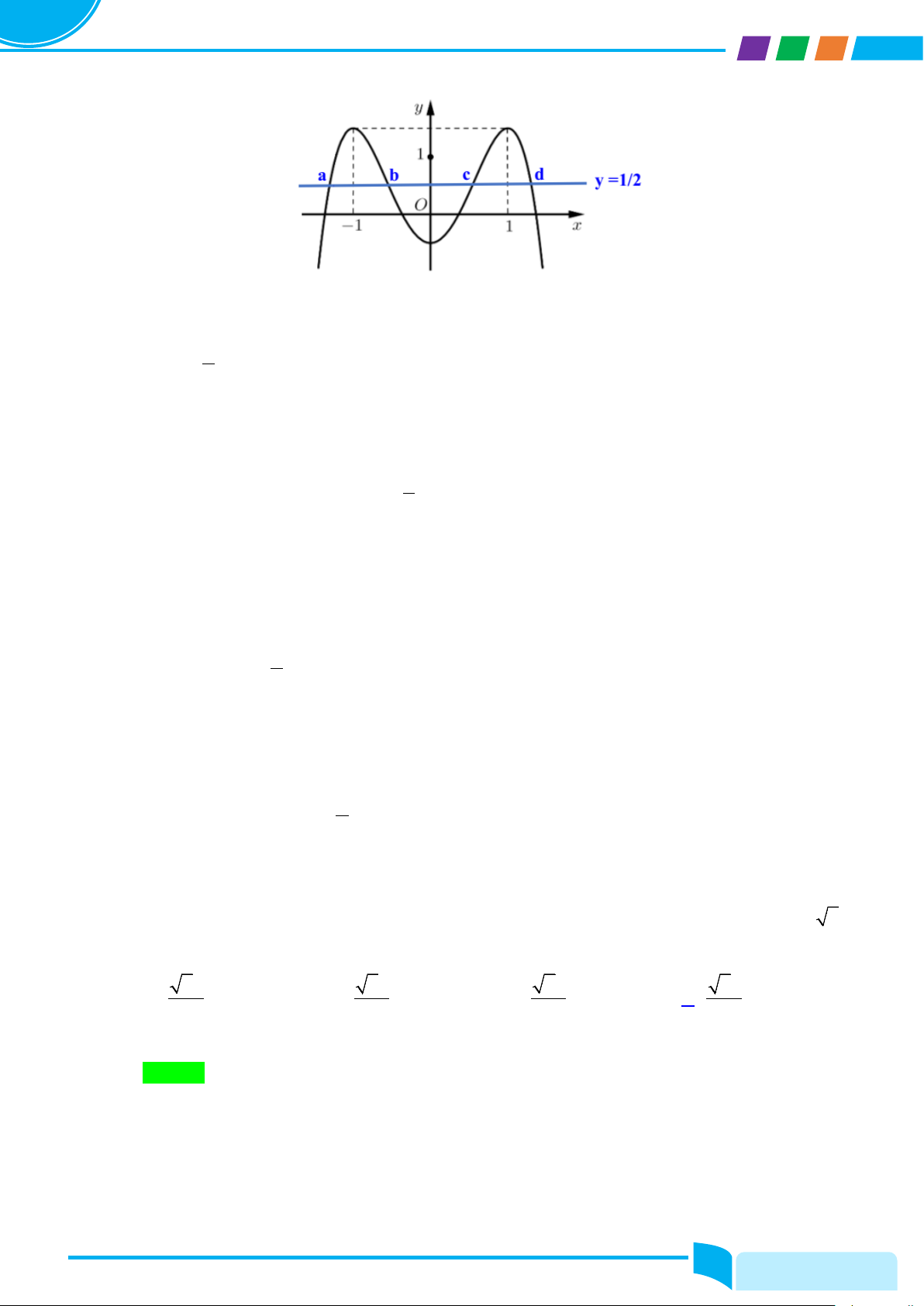
Câu 32: Cho hàm số bậc bốn y = f (x) có đồ thị như hình bên. Hỏi phương trình 2 f (x − ) 1 =1 có bao
nhiêu nghiệm thuộc khoảng ( ;0 −∞ )? A. 4 B. 2 C. 1 D. 3 Lời giải Chọn C 8/
20 Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Dựa vào đồ thị hàm số ta có: x = a ∈( ; −∞ − ) 1  1 x = b ∈( 1; − 0) f (x) = ⇒ 2 x = c ∈( 0; ) 1  x = d ∈( 1;+∞  )
x −1 = a ∈( ; −∞ − ) 1 x =1+ a ∈( ; −∞ 0)   1
x −1 = b ∈( 1; − 0) x =1+ b ∈( 0; ) 1
Do đó: 2 f (x − )
1 =1⇔ f (x − ) 1 = ⇒ ⇒ 2 x 1 c ( 0; ) 1  − = ∈ x =1+ c ∈( 1;2)   x 1 d ( 1; )  − = ∈ +∞ x =1+ d ∈( 2;+∞   )
Vậy phương trình 2 f (x − )
1 =1 có 1 nghiệm thuộc khoảng ( ;0 −∞ ). Cách khác:
Ta có: f (x − ) 1 1 = 2
Tịnh tiến đồ thị y = f (x) sang phải theo phương trục hoành 1 đơn vị được đồ thị hàm số
y = f (x − ) 1 . 1
Khi đó, đường thẳng y = cắt đồ thị hàm số y = f (x − ) 1 trên ( ;0 −∞ ) tại 1 điểm. 2
Vậy phương trình 2 f (x − )
1 =1 có 1 nghiệm thuộc khoảng ( ;0 −∞ ).
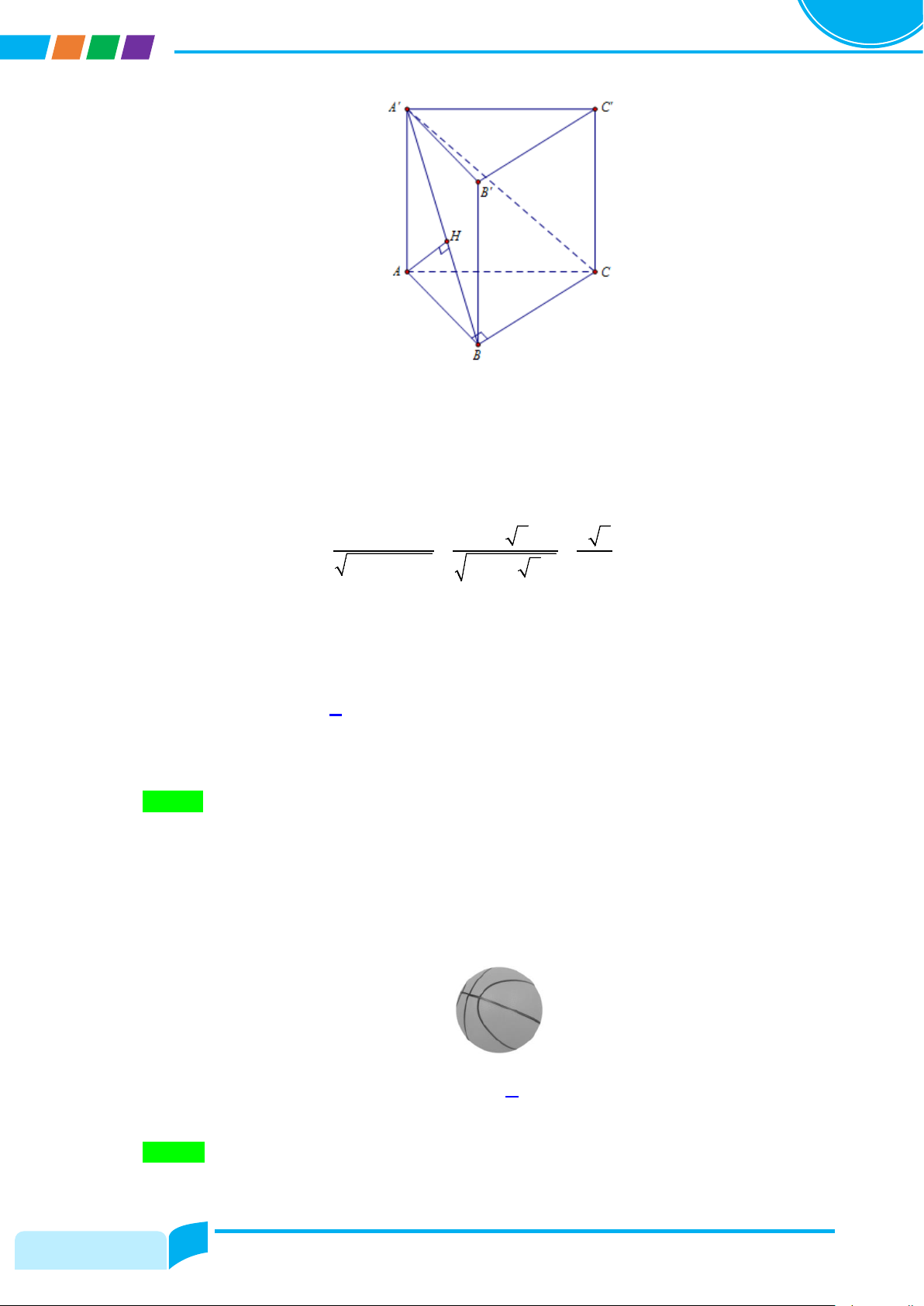
Câu 33: Cho hình lăng trụ đứng ABC.A′B C
′ ′có đáy ABC là tam giác vuông tại B,AB = a, A ′ A = 2a .
Tính theo a khoảng cách từ A đến ( A′BC) . A. 2a . B. 6a . C. 2a . D. 6a . 6 6 3 3 Lời giải Chọn D
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024 9/20
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Trong ( A′AB) , kẻ AH ⊥ A′B ( ) 1 . Ta có:
BC ⊥ AB ⇒ BC ⊥( ′AAB)⇒ BC ⊥ AH (2). BC ⊥ A ′ A  Từ ( )
1 và (2) suy ra AH ⊥ ( ′ A AB) ⇒ ( ′
A ( A′BC)) A . B AA . a a 2 a 6 d , = AH = = = .( A
∆ ′AB vuông tại A ) 2 2 2 2 AB + AA′ + 3 a (a 2)
Câu 34: Trong không gian Oxyz , đường thẳng nào sau đây vuông góc với mặt phẳng
(α ):x + 2y − z +1= 0? x = 1 − − tx =1− 2tx = 1 − + 2tx = 2 + t A. d :    y = 2 + t
B. d :y = 2 − − 4t
C. d :y =1+ t
D. d :y = 1 − − t 1 4 2 3 z = 3+     t z = 3 − +  2t z =1+  4t z = 1 − +  t Lời giải Chọn B (  
α ) có vectơ pháp tuyến n = (1;2;− )
1 cùng phương vectơ chỉ phương u = 2; − 4; − 2 của đường 4 ( ) thẳng d d ⊥ α 4 nên 4 ( )
Câu 35: Một quả bóng rổ có chu vi đường tròn lớn bằng 77cm . Diện tích da để may quả bóng rổ đó gần
nhất với số nào dưới đây? A. 2 5898cm B. 2 626cm C. 2 1888cm D. 2 7709cm Lời giải Chọn C 10/
20 Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Bán kính quả bóng rổ là 77 R = 2π 2
Diện tích da để may quả bóng rổ 2  77  2 S = 4π R = 4π ≈   1887,26cm  2π 
Câu 36: Cho hàm số bậc ba y = f (x) có đồ thị như hình bên. Hàm số g (x) = f (2 − x) đồng biến trên
khhoảng nào trong các khoảng dưới đây? A. (0;2) B. (2;4) C. (4;+ ∞) D. ( ;0 −∞ ) Lời giải Chọn A
Ta có g′(x) = − f ′(2 − x) .
Hàm số đồng biến nên g′(x) > 0 ⇔ − f ′(2 − x) > 0 ⇔ f ′(2 − x) < 0 ⇔ 1
− < 2 − x < 2 ⇔ 0 < x < 3
Vậy hàm số nghịch biến trên các khoảng (0;3).
Câu 37: Cho khối lăng trụ đứng ABC . D A′B C ′ D
′ ′ có thể tích bằng 18, đáy ABCD là hình vuông cạnh 3
. Độ dài cạnh AA′ bằng A. 6 . B. 2 . C. 18 D. 3. Lời giải Chọn B V 18 V = S
AA′ ⇒ AA′ = = = . ABCD 2 2 SABCD 3
Câu 38: Diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số 3 y = x và 2
y = 2x − x được tính bởi
công thức nào dưới đây? 0 1 1 A. ∫ ( 3 2
x + x − 2x)dx −∫( 3 2
x + x − 2x)dx . B. ∫ ( 3 2
x + x − 2x)dx . 2 − 0 2 − 0 1 1 C. −∫ ( 3 2
x + x − 2x)dx +∫( 3 2
x + x − 2x)dx D. ∫ ( 3 2
x + x − 2x)dx . 2 − 0 2 − Lời giải Chọn A
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024 11/20
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANGx = 2 − PTHĐGĐ: 3 2 3 2 x 2x x x x 2x 0  = − ⇔ + − = ⇔ x = 0  . x =  1 BXD: 1 0
S = x + x − 2x dx = ∫
∫ (x + x −2x) 1 3 2 3 2 dx −∫( 3 2
x + x − 2x)dx . 2 − 2 − 0
Câu 39: Trên tập hợp các số phức, xét phương trình 2 2
z − 2az + b −1 = 0(a,b∈) . Có bao nhiêu cặp số
thực (a,b) sao cho phương trình trên có hai nghiệm z , z 1
2 thỏa mãn z − 3 − 2i = 5 và 1
z − i = z +1 ? 2 2 A. 6 . B. 8 . C. 4 D. 2 . Lời giải Chọn B Ta có: 2 2
∆' = a − b +1 TH1: 2 2
∆' ≥ 0 ⇔ a − b +1≥ 0 . Phương trình có 2 nghiệm thực. z = 2
 z −3− 2i = 5  z −3 + 4 = 5 1 ( 1 )2 1   ⇔  ⇔ z = 4 2
z − i = z +1  2 2 z +1 = z +1  2 ( 2 ) 1 2 z =  0 2  1 z + z2 a = =1
• Với 1z = 2, z2 = 0 , ta có:  2 (nhận) b  = 1 ±  1 z + z2 a = = 2
• Với 1z = 4, z2 = 0 , ta có:  2 (nhận) b  = 1 ±  TH2: 2 2
∆' < 0 ⇔ a − b +1< 0 . Phương trình có 2 nghiệm phức.
z = x + yi Đặt 1  (x, y∈) . z = x −  yi 2 x =1
 z −3− 2i = 5
 x −3 + y − 2 = 5  1 ( )2 ( )2 (
x − 3)2 + ( x − 2)2 = Ta có 5   ⇔  ⇔  ⇔ x = 4 . 2
z − i = z +1  x +  ( y + )2 1 = (x + )2 2 +  = 2 2 1 y x y  x = y * x = y =1 2
− a + b − = a =
z =1+ i ⇒ 2i − 2a(1+ i) 2 1 0 1 2 + b −1 = 0 ⇒  ⇒ 1  (nhận)  2 − a + 2 = 0 b  = ± 3 12/
20 Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG 2  8
− a + b −1 = 0 a = 4
* x = y = 4 ⇒ z = 4 + 4i ⇒ 32i − 2a(4 + 4i) 2 + b −1 = 0 ⇒  ⇒ (nhận) 1  32  −8a = 0 b  = ± 33
Vậy có 8 cặp (a,b) thỏa đề.
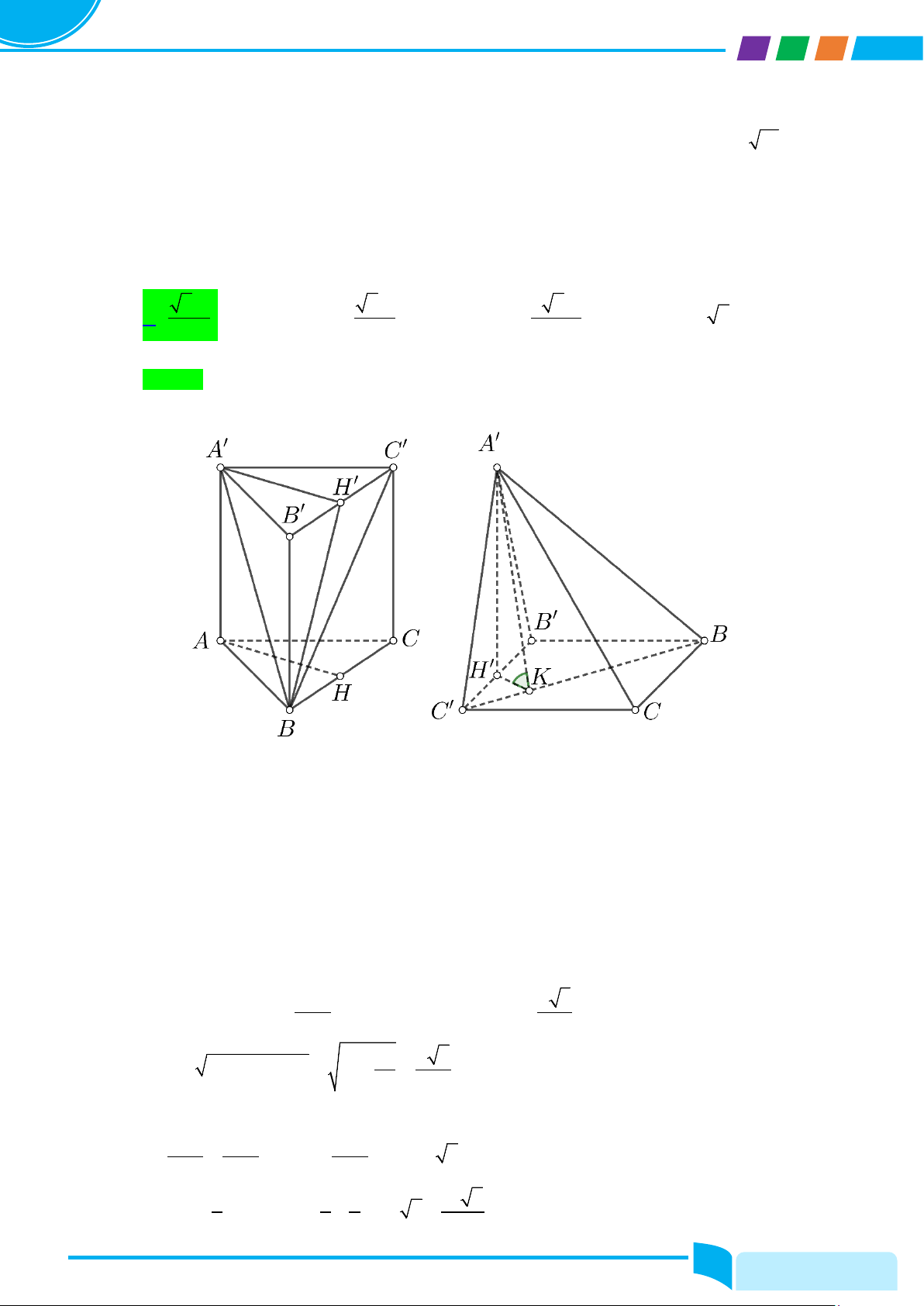
Câu 40: Cho hình lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác vuông cân tại A , BC = 2a , góc
giữa ( A′BC′) và (BCC B
′ ′) bằng 60°. Tính thể tích khối tứ diện ABB C ′ ′ . 3 3 3 A. 2a . B. 2a . C. 2 2a D. 3 2a . 3 9 3 Lời giải Chọn A
Gọi H′ là trung điểm của B C
′ ′ ⇒ A′H′ ⊥ B C ′ ′ ( A ∆ ′B C
′ ′ vuông cân tại A′).
A′H′ ⊥ B C ′ ′ Ta có 
⇒ A′H′ ⊥ (BCC B ′ ′) .
A′H′ ⊥ BB′ Kẻ H K
′ ⊥ BC′ mà BC′ ⊥ A′H′( A′H′ ⊥ (BCC B ′ ′))
Suy ra A′K ⊥ BC′ (
A′BC′) ∩(BCC B ′ ′) = BC′
Khi đó A′K ⊥ BC′
⇒ (( A′BC′) (BCC B
′ ′)) = ( A′K H K ′ ) =  , ,
A′KH′ = 60° .
H K′ ⊥ BC′  ′ ′ Ta có B C
AH = A′H′ = = a , a 3 H K
′ = A′H .′cot 60° = , 2 3 2 2 2 2 a a 6 KC′ = H C ′ ′ − H K ′ = a − = . 3 3 B ∆ C ′ B ′  K ∆ C H ′ ′(g.g) B B ′ B C ′ ′ B C ′ ′ ⇒ = ⇒ B B ′ = .KH′ = a 2 . KH′ KC′ KC′ 3 1 1 1 a 2 V = = = . ′ ′ AH S∆ ′ ′ a a a A BB C . BBC . .2 . 2 . 3 3 2 3
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024 13/20
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Câu 41: Theo Tổng cục Thống kê, dân số Việt Nam ở cuối tháng 12 của hai năm 2022 và 2023 lần lượt
là 99,47 và 100,3 triệu người. Hỏi nếu với tỉ lệ tăng dân số trung bình hằng năm như năm 2023
thì năm nào dưới đây là năm đầu tiên dân số nước ta vượt ngưỡng 120 triệu người? A. 2043. B. 2045. C. 2046. D. 2047. Lời giải Chọn B Tỉ lệ năm 2023 là 100,3 99,47 83 r − = = 99,47 9947
Gọi n là số năm đủ để dân số vượt ngưỡng 120 triệu người. Ta có: 100,3.(1+ )n
r >120 ⇒ n > 21,5.
Vậy dân số năm 2045 sẽ vợt ngưỡng 120 triệu người.
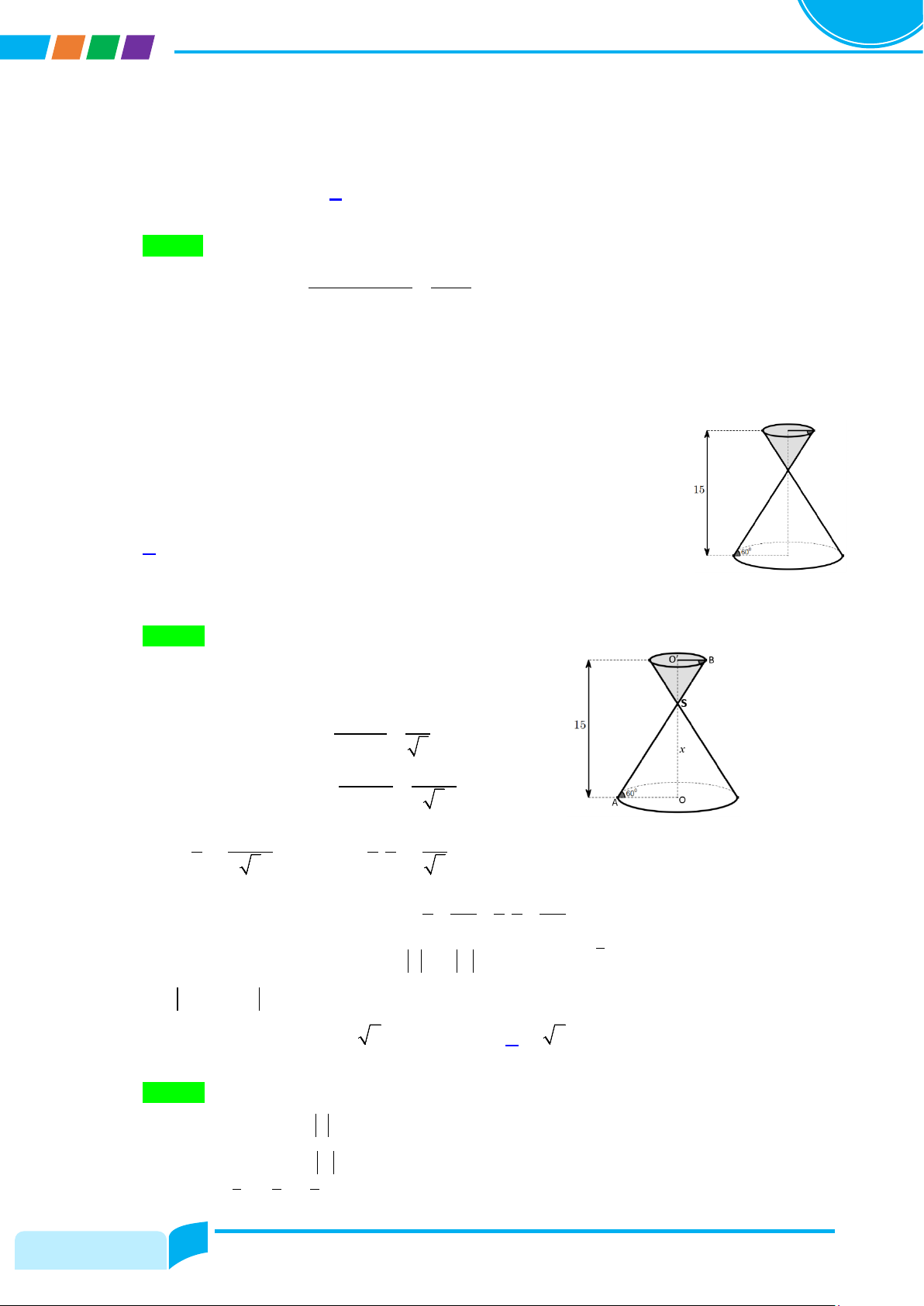
Câu 42: Một vật lưu niệm cao 15 cm, gồm hai hình nón chung đỉnh và chung trục
như hình vẽ, đường sinh bất kỳ của hai hình nón luôn tạo với mặt đáy một góc o
60 . Biết rằng thể tích của khối nón nhỏ bằng 12,5% thể tích
của khối nón lớn. Tính thể tích của vật lưu niệm đó? A. 3 125π cm . B. 3 100π cm . C. 3 156,25π cm . D. 3 109,75π cm . Lời giải Chọn A  SO' =15− x  Gọi = > 0  SO x SO x ⇒ OA  = = tan60°  3  SO′ 15 − x OB ′ = =  tan60° 3 2 2 Ta có: 1 15 − x π  ( ) 1 1 15 .  x x π  − =
x ⇔ 8(15 − x)3 3 = x ⇔ x =     10 3  3  8 3  3  3 3
Vậy: Thể tích của vật lưu niệm đó là 1 10 1 1 10 3 π + . π =125π cm . 3 3 8 3 3
Câu 43: Xét các số phức z,w thỏa mãn z = 3, w = 5 và (z − w) z là số ảo. Giá trị nhỏ nhất của
P = z + 3w + 4i bằng A. 8. B.3 2 −1. C.12 2 − 4. D. 14. Lời giải Chọn C
Gọi z = x + yi . Ta có: 2 2
z = 3 ⇒ x + y = 9 .
w = a + bi . Ta có: 2 2
w = 5 ⇒ a + b = 25 .
(z − w) z = z.z − wz là số ảo nên 2 2
x + y − ax −by = 0 ⇔ ax + by = 9 14/
20 Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
z + 3w = (x + yi) + 3(a + bi) = (x + 3a)2 + ( y + 3b)2 = ( 2 2
x + y ) + 6(ax + by) + 9( 2 2
a + b ) = 9 + 6.9 + 9.25 =12 2
P = z + 3w + 4i ≥ z + 3w − 4i =12 2 − 4.
Vậy giá trị nhỏ nhất của P bằng 12 2 − 4.
Câu 44: Trong không gian Oxyz , cho hai điểm A(3;3; ) 1 , B(0;2; ) 1 và mặt phẳng
(α ): x + y + z −7 = 0 . Đường thẳng ∆ nằm trong (α ) sao cho mọi điểm thuộc ∆ luôn cách   đều hai điểm ,
A B . Biết rằng u = (1;a;b) là vectơ chỉ phương của ∆ . Tính u . A. 11 . B. 3. C. 14 . D. 6 . Lời giải Chọn C
Vì ∆ luôn cách đều hai điểm ,
A B nên ∆ nằm trong mặt phẳng trung trực (β ) của đoạn
AB .        Ta có n = = − − ; n = ; n  = − = ⇒ = . α , nβ (1; 3;2) u u 14 α (1;1; )1 β AB ( 3; 1;0)  
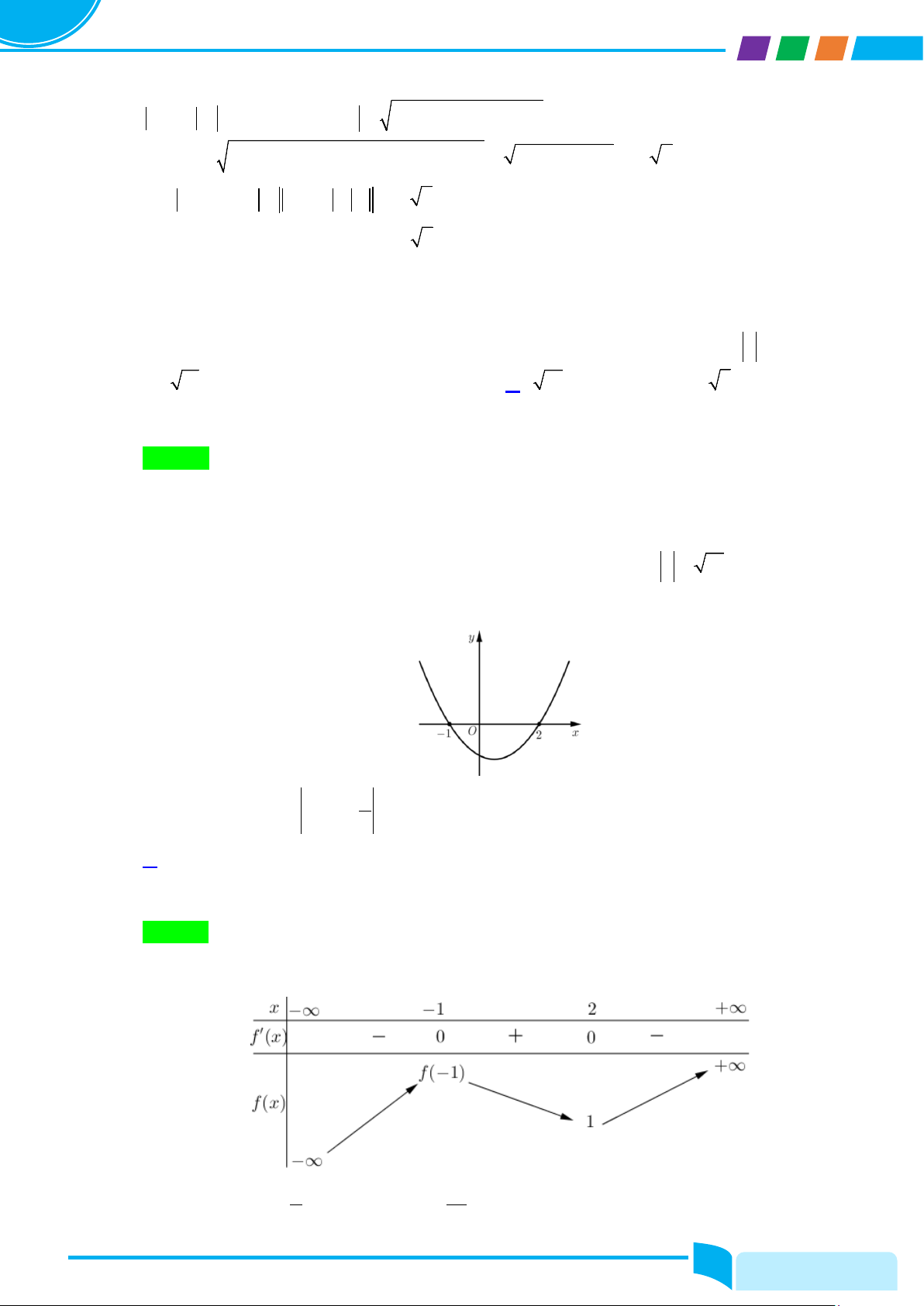
Câu 45: Cho hàm số bậc ba y = f (x) thỏa mãn f (2) =1. Đồ thị hàm số y = f ′(x) như hình vẽ Hỏi hàm số ( ) = ( ) 1 g x
f x + có bao nhiêu điểm cực trị? x A. 4 . B. 6 . C. 2 . D. 3. Lời giải Chọn A
BBT của f (x) : Đặt  = < −
h(x) = f (x) 1
+ ⇒ h′(x) = f ′(x) 1 x a 1 − = 0 ⇔ . 2 x x  x = b > 2
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024 15/20
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG BBT của h(x)
Trong đó h(a) = f (a) 1
+ > h(− ) = f (− ) 1 1 1
1 + >1+ > 0 và h(b) = f (b) 1 + > 0 . a a a b Do đó hàm số ( ) = ( ) 1 g x
f x + = h(x) có 4 cực trị. x
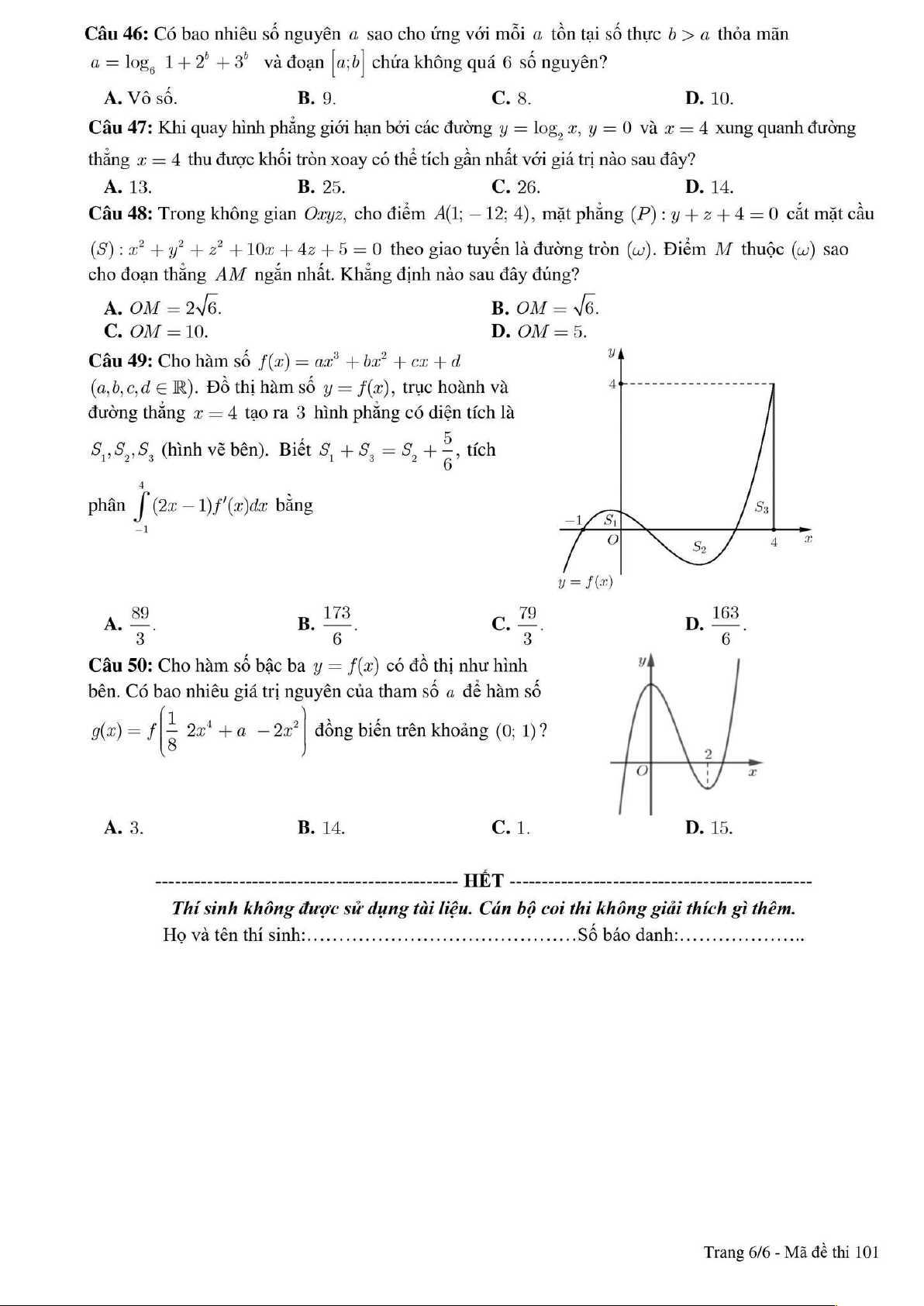
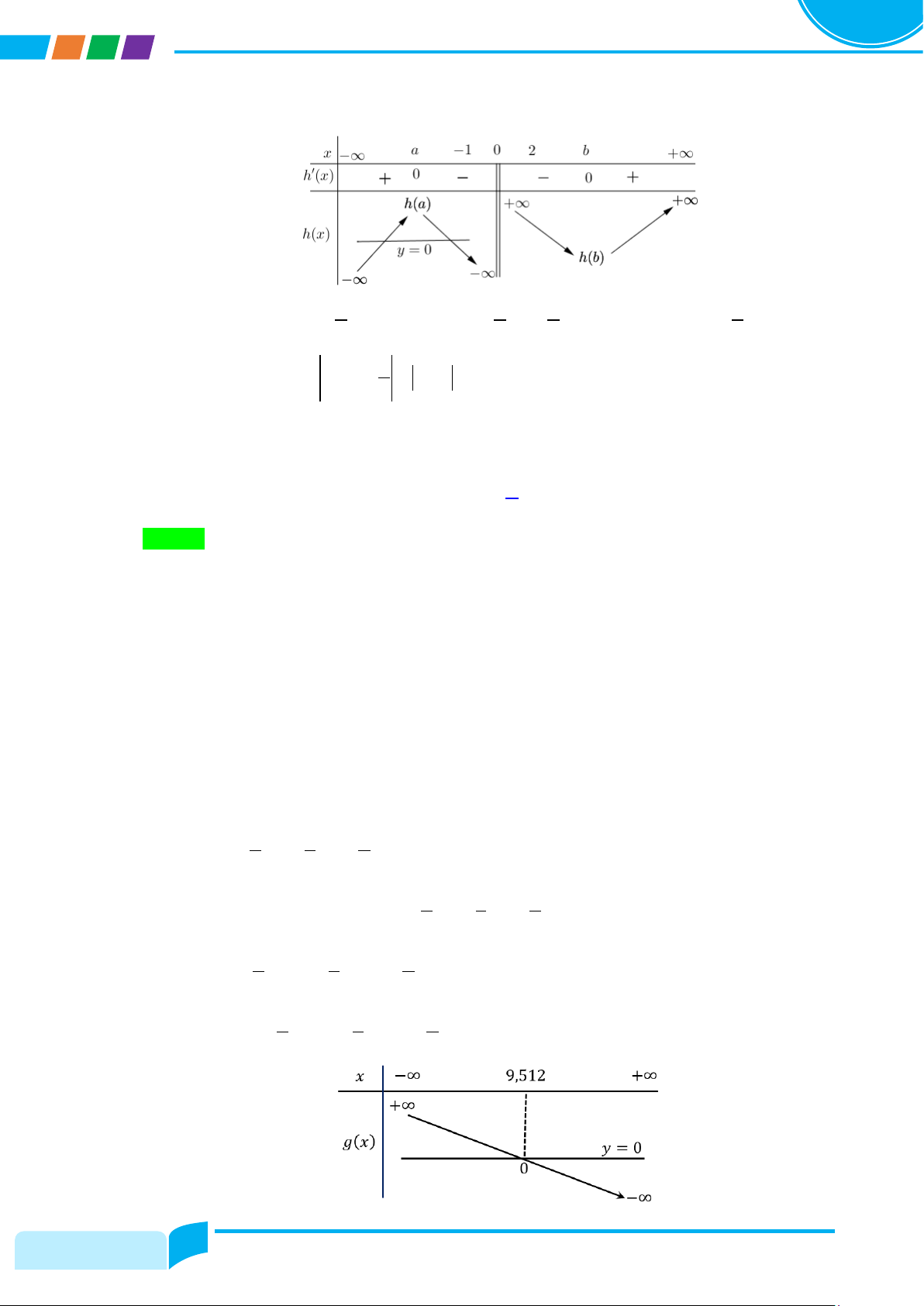
Câu 46: Có bao nhiêu số nguyên a sao cho ứng với mỗi a tồn tại số thực b > a thỏa mãn log 1 2b 3b a = + + và đoạn [ ;
a b] chứa không quá 6 số nguyên? 6 ( ) A. Vô số. B. 9. C. 8 . D. 10. Lời giải Chọn C Ta có log 1 2b 3b
1 2b 3b 6a a = + + ⇔ + + − = 0 6 ( )
Đặt ( ) 1 2b 3b 6a
f b = + + − thì f (b) = 0 và ′( ) = 2b ln 2 + 3b f b ln 3 > 0, b
∀ nên f (b) đồng biến trên  .
Do đoạn [a;b] chứa không quá 6 số nguyên (và a < b ) nên ta có điều kiện đủ a < b < a + 6.
Do vậy chỉ cần xét hàm số f (b) đồng biến trên [a;a + 6) .
Ta có a < b < a + 6 ⇒ f (a) < f (b) = 0 < f (a + 6)
 f (a) < 0 1  +
 2a + 3a − 6a < 0 ( ) 1 Hay  ⇒  .  f  (a + 6) a+6 a+6 > 0 1  + 2 + 3 − 6a > 0  (2) a a a + Xét ( )  1   1   1 1  ⇔ + +
−1< 0 ⇔ h(a) < h( ) 1 ⇔ a >       1  6   3   2  x x x
(vì h(x)  1   1   1  = + + −    
  1 nghịch biến trên  )  6   3   2  a a a + Xét ( )  1  6  1  6  1 2 2 . 3 .  ⇔ + + −1 >       0  6   3   2  a a a g (x)  1  6  1  6  1 2 . 3 .  = + + −    
  1 có bảng biến thiên như sau  6   3   2  16/
20 Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Do đó (2) ⇒ a < 9,51 Suy ra a ∈{2;3;...; } 9 .
Vậy có 8 giá trị nguyên của a thỏa yêu cầu.
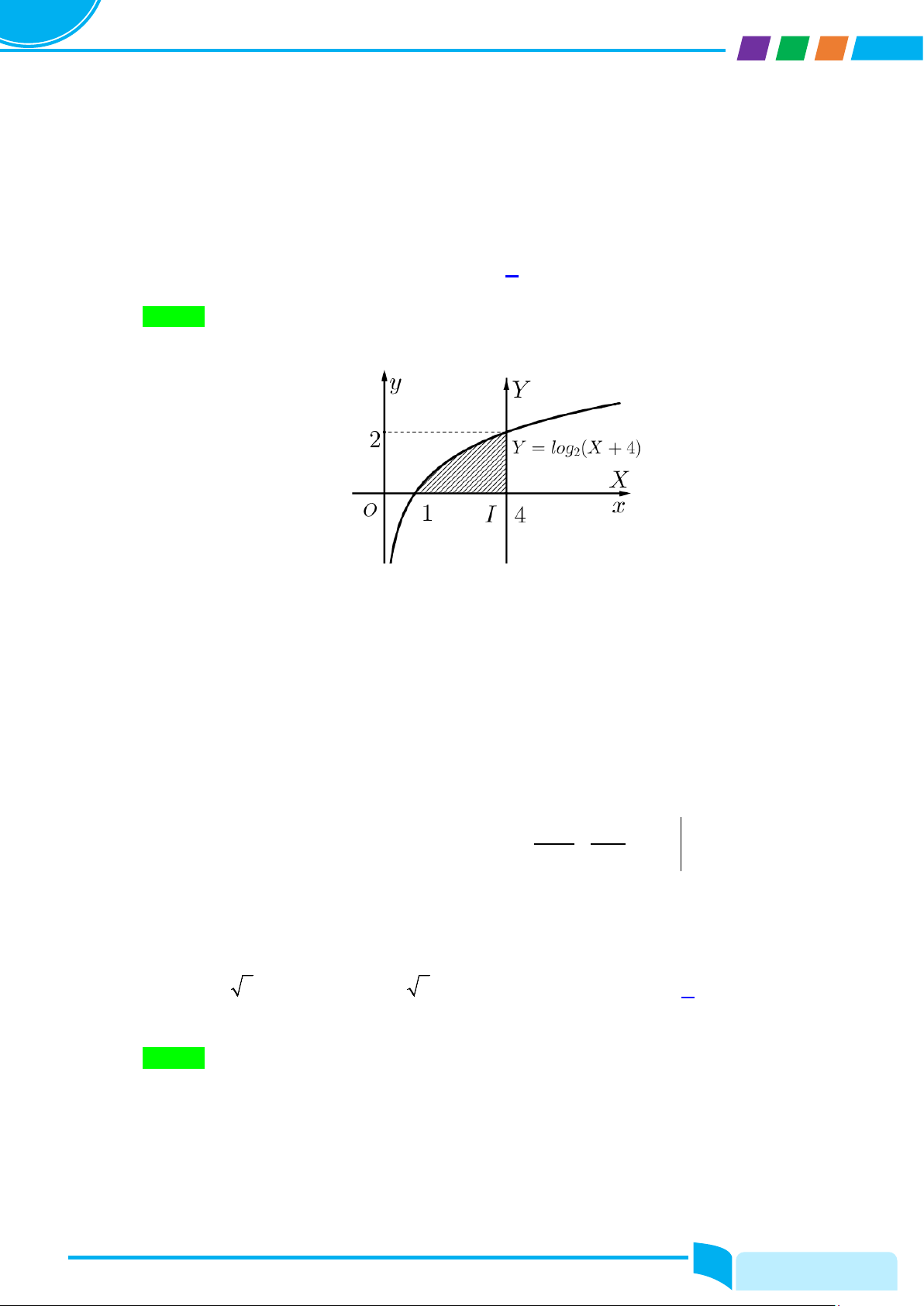
Câu 47: Khi quay hình phẳng giới hạn bởi các đường y = log x , y = 0 và x = 4 xung quanh đường thẳng 2
x = 4 thu được khối tròn xoay có thể tích gần nhất với giá trị nào sau đây? A. 13. B. 25 . C. 26 . D. 14. Lời giải Chọn C
Dời hệ trục Oxy thành hệ trục IXY với gốc tọa độ I (4;0) như hình vẽ. x = X + 4 Công thức đổi trục  . y = Y
Trong hệ trục IXY , các đường y = log x , y = 0 và x = 4 lần lượt trở thành các đường 2
Y = log X + 4 , Y = 0, X = 0 . 2 ( )
Bài toán trở thành tính thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường
Y = log X + 4 , Y = 0, X = 0 quanh trục tung. 2 ( ) Ta có = log + 4 ⇒ = 2Y Y X X − 4 . 2 ( )
Thể tích khối tròn xoay tạo thành là 2 2 2  2 Y 8.2Y  = π ∫ (2Y − 4)2 2
d = π ∫ ( 22Y −8.2Y V Y +16)dY = π  − +16Y  ≈ 25,75. 0 0  2ln 2 ln 2  0
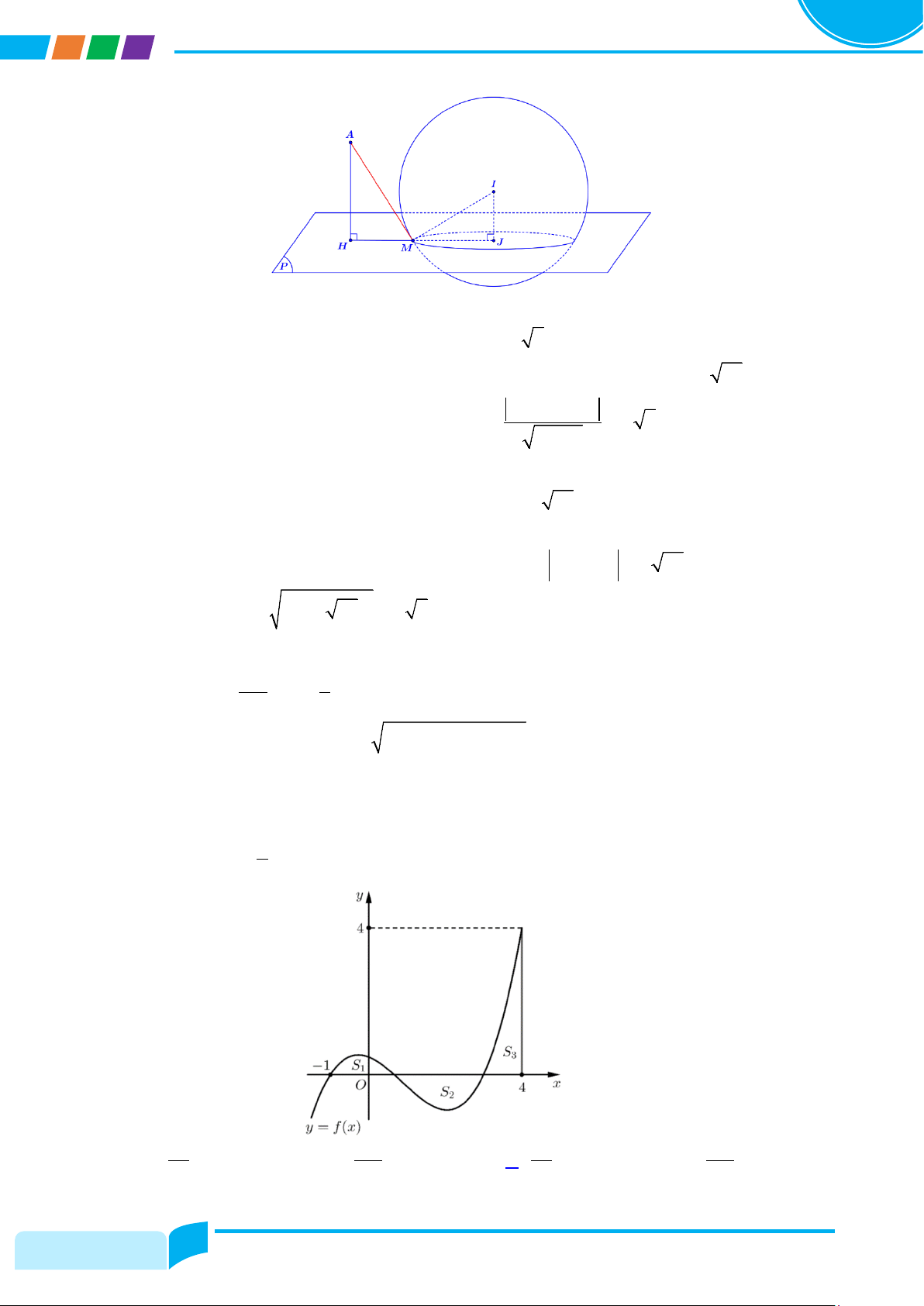
Câu 48: Trong không gian Oxyz, cho điểm A1;12;4, mặt phẳng P: y z  4  0 cắt mặt cầu S 2 2 2
: x y z 10x  4z 5  0 theo giao tuyến là đường tròn . Điểm M thuộc 
sao cho đoạn thẳng AM ngắn nhất. Khẳng định nào sau đây đúng?
A. OM  2 6. B. OM  6.
C. OM 10.
D. OM  5. Lời giải Chọn D
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024 17/20
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Gọi I, J lần lượt là tâm mặt cầu S và tâm của đường tròn .
Mặt cầu S có tâm I 5;0;2, bán kính R  2 6. IMJ  vuông tại J có 2 2 2 2 2
IM IJ JM R d I P 2 ,
r r  22.   12 4 4
Kẻ AH P tại H. Suy ra AH d  , A P  2 2. 2 2 1 1
Vì H, J lần lượt là hình chiếu vuông góc của điểm A và I lên mặt phẳng P nên ta tìm
được J 5;1; 
3 và H 1;10;6. Suy ra HJ  3 22. A
HM vuông tại H có 2 2 2 2
AM AH HM  8 HM .
Để AM ngắn nhất  HM ngắn nhất. Khi đó HM HJ r  2 22. 
Suy ra AM  82 222  4 6. min
Dấu " " xảy ra khi và chỉ khi M HJ  và M nằm giữa H và J.    Ta có MJ 1 MJ
.HJ HJ nên ta tìm được tọa độ điểm M là M 3;4;0. HJ 3
Vậy độ dài đoạn thẳng OM   2  2 2 3 4 0  5.
Câu 49: Cho hàm số   3 2
f x ax bx cx d a,b,c,d  . Đồ thị hàm số y f x, trục hoành và
đường thẳng x  4 tạo ra 3 hình phẳng có diện tích là S , S , S 1 2 3 (hình vẽ bên). Biết 5 4
S S S  , tích phân 2x  1 f xd 1 3 2 x 6  bằng 1 A. 89 . B. 173. C. 79 . D. 163. 3 6 3 6 Lời giải 18/
20 Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG Chọn C 4
Dựa vào đồ thị, ta có f x 5
dx S S S  .  1 3 2 6 1 4 4 Khi đó 2x 
1 f xdx 2x 
1 f x4 2 f xdx   1 1 1 4
f   f   f x 5 79 7 4 3 1 2
dx  7.43.02.  .  6 3 1
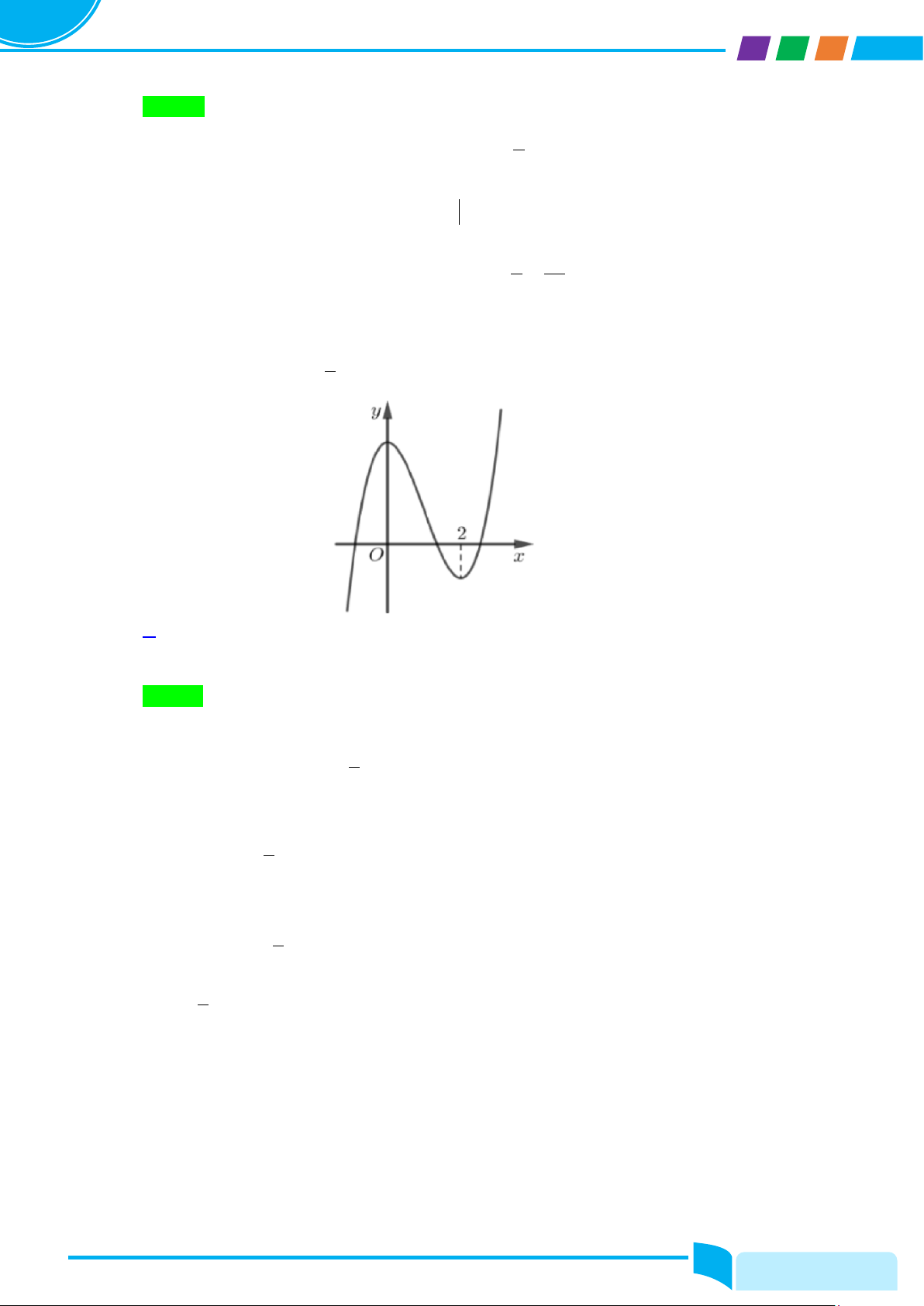
Câu 50: Cho hàm số bậc ba y f x có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của tham số  
a để hàm số gx 1  f   4 2x a 2 2x  
đồng biến trên khoảng 0;  1 ? 8  A. 3. B. 14. C. 1. D. 15. Lời giải Chọn A
Dựa vào đồ thị, ta thấy f x 0  0  x  2.  
Ta có gx 3 x x 1 4 f   4 2x a 2 2x .  8 
Hàm số gx đồng biến trên khoảng 0; 
1 thì gx 0, x 0;  1     3 x x 1 4 f   4 2x a 2
2x  0, x 0;  1   1 .  8  Vì x 0;  1 nên 3
x x x 2 4
x 4 xx2x2 0,x 0;  1   Khi đó   1 1  f   4 2x a 2
2x  0, x 0;  1  8  2 4 1
a x x 0  16 2 4 2x a 2 2x 2, x 0;  1           , x 0;  1 2. 2 4 8
a1616x 2x
Xét hàm số hx 2 4
16x 2x trên đoạn 0; 
1 có hx 3 
xx x 2 32 8
8 4 x  0,x 0; 1
Suy ra hàm số hx luôn đồng biến trên 0;  1 .
Khi đó min hx h0 0 và max hx h  1 14. 0  ;1 0  ;1
a  max hx    a 14 Khi đó 2 0  ;1       14  a 16.
a16 min hx a 16   0  ;1 
Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024 19/20
TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU – TIỀN GIANG
Vì a   nên a 14;15;  16 .
Vậy có 3 giá trị nguyên của a thỏa mãn bài toán. 20/
20 Hướng dẫn giải Đề thi thử TNTHPT môn Toán – Năm học 2023 - 2024
Document Outline

  • de-thi-thu-tot-nghiep-thpt-nam-2024-mon-toan-so-gddt-tien-giang
    • debai
    • dap an
  • TOTOAN_THPTNDC_HDG_DETOAN_THITHUTNTHPT_SGDTG_NH23-24