Đề thi thử vào 10 năm 2020 – 2021 môn Toán trường Khánh Hòa – Thái Nguyên
Giới thiệu đến quý thầy, cô giáo cùng các em học sinh đề thi thử tuyển sinh vào lớp 10 THPT năm học 2020 – 2021 môn Toán trường THPT Khánh Hòa, tỉnh Thái Nguyên; đề thi gồm có 01 trang với 10 bài toán dạng tự luận, thời gian làm bài thi là 120 phút, đề thi có lời giải chi tiết. Mời các bạn đón xem!
Chủ đề: Đề thi vào 10 môn Ngữ Văn năm 2023-2024
Môn: Môn Ngữ Văn
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
SỞ GDĐT THÁI NGUYÊN
THI THỬ TUYỂN SINH VÀO LỚP 10 THPT
TRƯỜNG THPT KHÁNH HÒA Năm học 2020 - 2021 MÔN THI: TOÁN
Thời gian làm bài: 120 phút, không kể thời gian phát đề
(Đề thi gồm có 01 trang)
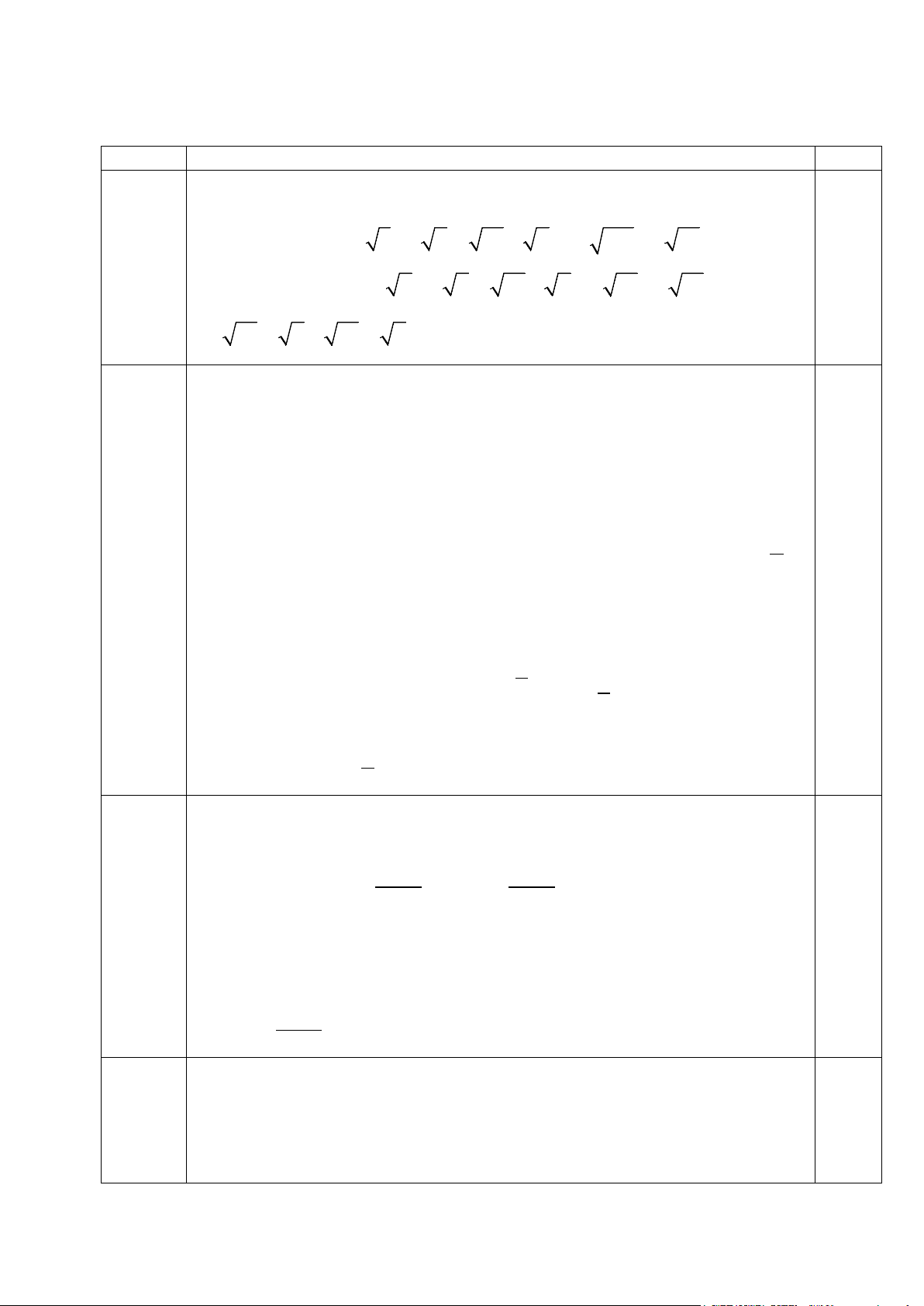
Câu 1 (1.0 điểm).Không dùng máy tính cầm tay,hãyrút gọn biểu thức sau:
A = ( 8 −3 2 + 10)( 2 −10 0,4 + 3 10).
Câu 2 (1.0 điểm).Cho hàm số y = (3m − 2) x −1+ m (m là tham số).
1) Tìmm để hàm số đồng biến trên .
2) Tìmm để đồ thị hàm số cắt hai trục tọa độ Ox,Oy lần lượt tại , A B ( ,
A B không trùng với gốc O ) và tam giácOAB vuông cân tại O .
Câu 3 (1.0 điểm).Không sử dụng máy tính cầm tay, hãy giải phương trình sau: 2019 2 x − x + 2021 2 = 0. 2020 2020
Câu 4 (1.0 điểm).Cho hàm số y = (m − ) 2
4 x với m ≠ 4 . Tìm m để hàm số nghịch biến khi 2021 − < x < 2019 − .
Câu 5 (1.0 điểm). Cho biểu thức: x + 2 x x − 4 P = x − : −
với x ≥ 0 và x ≠ 1; x ≠ 4 .
x +1 x +1 1− x 1) Rút gọn . P 2)Tìm x để 1 P = . 2
Câu 6 (1.0 điểm).Người ta hòa lẫn 4kg chất lỏng I với 3kg chất lỏng II thì được
một hỗn hợp có khối lượng riêng 3
700kg / m . Biết rằng khối lượng riêng của chất
lỏng I lớn hơn khối lượng riêng của chất lỏng II là 3
200kg / m . Tính khối lượng
riêng của mỗi chất lỏng.
Câu 7 (1.0 điểm).Cho tam giác ABC vuông tại A, đường cao AH , AH =12cm,
HC =16cm . Tính AB,BC ?
Câu 8 (1.0 điểm).Hai đường tròn giao nhau có bán kính lần lượt là 20cmvà 25cm
dây cung chung có độ dài bằng 30cm . Tính khoảng cách giữa hai tâm.
Câu 9 (2.0 điểm).Cho đường tròn (O) có hai đường kính AB,CD vuông góc với
nhau. Gọi M là điểm tùy ý thuộc đoạn OC ( M khác O và C ). Tia BM cắt đường
tròn (O) tại N .
1) Chứng minh AOMN là một tứ giác nội tiếp.
2) Chứng minh ND là tia phân giác của ANB . --- Hết ---
Họ và tên thí sinh:…………….…………................Số báo danh…………………… ĐÁP ÁN
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 NĂM HỌC 2020-2021 MÔN: TOÁN Câu Nội dung Điểm
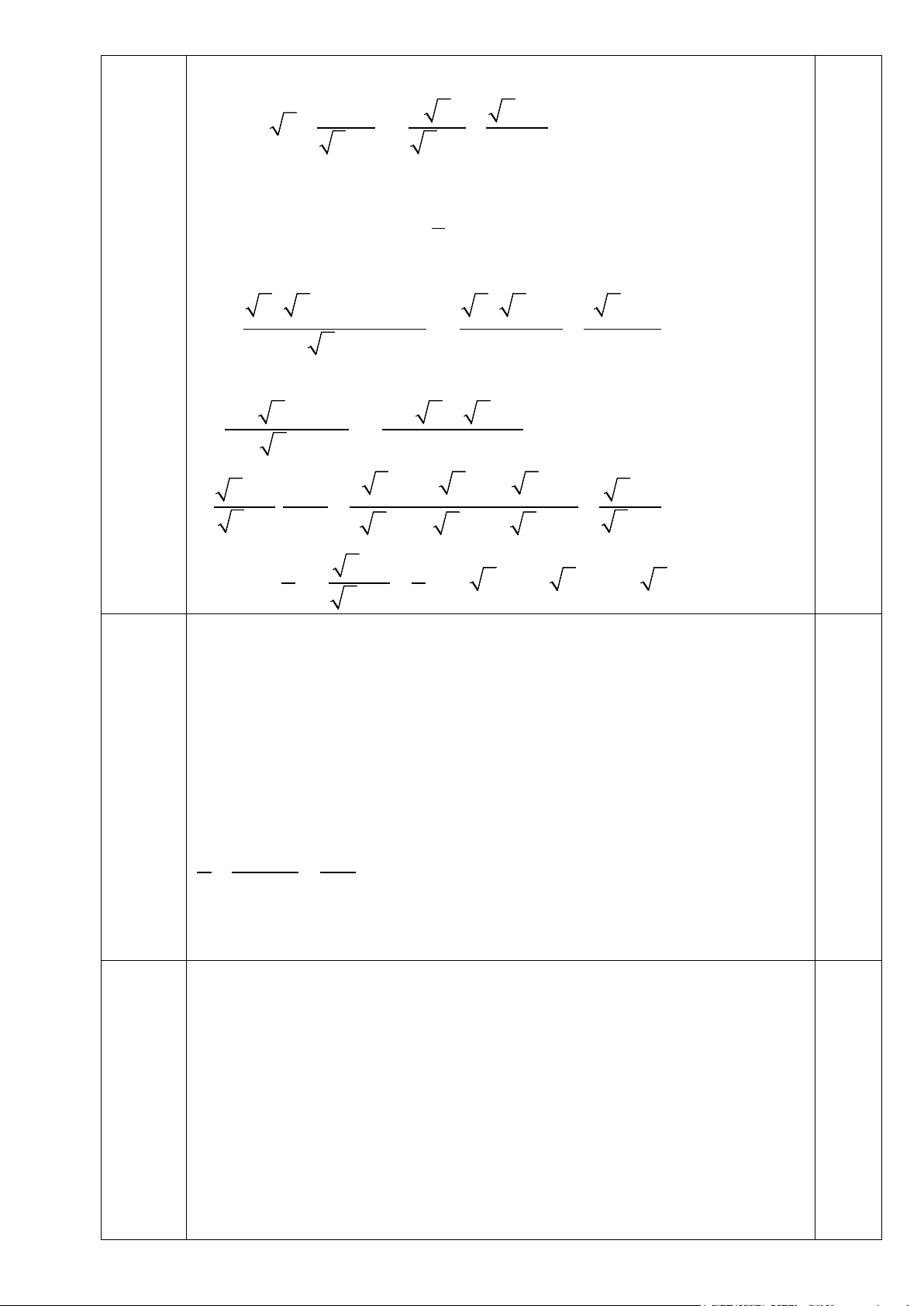
Câu 1 (1.0 điểm). Không dùng máy tính cầm tay, hãy rút gọn biểu thức sau:
A = ( 8 −3 2 + 10)( 2 −10 0,4 + 3 10). Câu 1 0.5
Lời giải:Ta có A = (2 2 −3 2 + 10)( 2 − 2 10 + 3 10) 0.5
= ( 10 − 2)( 10 + 2) =10 − 2 = 8
Câu 2 (1.0 điểm). Cho hàm số y = (3m − 2) x −1+ m (m là tham số).
3) Tìm m để hàm số đồng biến trên .
4) Tìm m để đồ thị hàm số cắt hai trục tọa độ Ox,Oy lần lượt tại , A B ( ,
A B không trùng với gốc O ) và tam giác OAB vuông cân tại O .
Lời giải: 1) Để hàm số đồng biến điều kiện là 2
3m − 2 > 0 ⇔ m > 0.5 Câu 2 3 3 m − 2 =1 m =1 2) ycbt tương đương ⇔ ⇒ không có 1 − + m ≠ 0 m ≠ 1 1 3 m − 2 = 1 − m = nghiệm. Hoặc 1 0.5 ⇔ 3 ⇔ m = 1 − + m ≠ 0 3 m ≠1 Kết luận: Vậy 1
m = là giá trị cần tìm. 3
Câu 3 (1.0 điểm). Không sử dụng máy tính cầm tay, hãy giải phương trình sau: 2019 2 x − x + 2021 2 = 0. (1) 2020 2020
Câu 3 Lời giải:Ta có ( ) 2
1 ⇔ 2019x − 4040x + 2021= 0.
Nhận xét ta thấy a + b + c = 2019 − 4040 + 2021= 0 0.5
Nên phương trình đã cho có hai nghiệm phân biêt là: 2021 x =1;x = 2019 0.5
Câu 4 (1.0 điểm). Cho hàm số y = (m − ) 2
4 x với m ≠ 4 . Tìm m để
Câu 4 hàm số nghịch biến khi 2021 − < x < 2019 − .
Lời giải: ycbt tương đương với m − 4 > 0 ⇔ m > 4 1.0
Câu 5 (1.0 điểm). Cho biểu thức: x + 2 x x − 4 P = x − : −
với x ≥ 0 và x ≠ 1; x ≠ 4 .
x +1 x +1 1− x 1) Rút gọn . P 2) Tìm x để 1 P = . 2
Lời giải: 1)Ta có:
x ( x + )1−(x + 2) x( x − )1 ( x − 4) Câu 5 P = : + x +1 x −1 x −1
x + x − x − 2 x − x + x − 4 = 0.5 : x + 1 x −1 (
x − 2)( x − ) 1 ( x x x + − − )1 2 1 x −1 = . = =
x +1 x − 4 ( x + )1( x − 2)( x + 2) x + 2 2) Để 1 x −1 1 P = ⇔
= ⇔ 2 x − 2 = x + 2 ⇔ x = 4 ⇔ x =16 0.5 2 x + 2 2
Câu 6 (1.0 điểm). Người ta hòa lẫn 4kg chất lỏng I với 3kg chất
lỏng II thì được một hỗn hợp có khối lượng riêng 3
700kg / m . Biết
rằng khối lượng riêng của chất lỏng I lớn hơn khối lượng riêng của chất lỏng II là 3
200kg / m . Tính khối lượng riêng của mỗi chất lỏng. Câu 6
Lời giải: Gọi khối lượng riêng của chất lỏng I là x( 3
kg / m ) thì khối 3
lượng riêng của chất lỏng II là x − 200(kg / m ). Điều kiện: x > 200.
Khi đó ta có phương trình: 0.5 4 3 7 + = x x − 200 700 Rút gọn được: 2
x − 900x + 80000 = 0. Phương trình có hai nghiệm 0.5
x = 800; x =100 (loại) 1 2
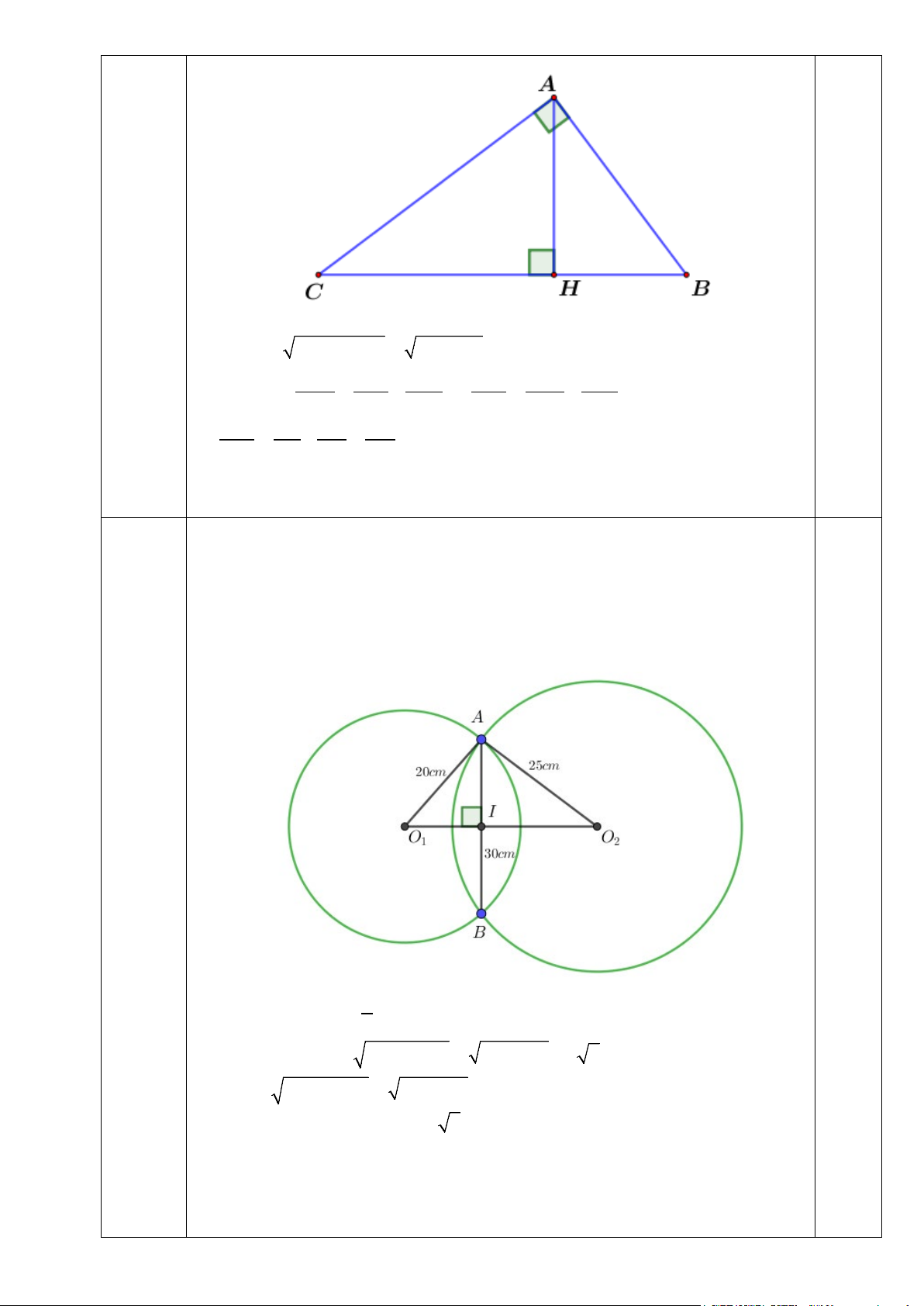
Câu 7 (1.0 điểm).Cho tam giác ABC vuông tại A, đường cao
AH, AH =12cm, HC =16cm . Tính AB,BC ? Lời giải: - Hình vẽ: Câu 7 0,25 - Có 2 2 2 2
AC = AH + HC = 12 +16 = 20(cm) . 0,25 - Mặt khác: 1 1 1 1 1 1 = + ⇔ = − 2 2 2 2 2 2 AH AB AC AB AH AC 1 1 1 1 2 ⇒ = − =
⇔ AB = 225 ⇒ AB =15 . 0,5 2 2 2 AB 12 20 225
Vậy AB =15(cm) , AC = 20(cm).
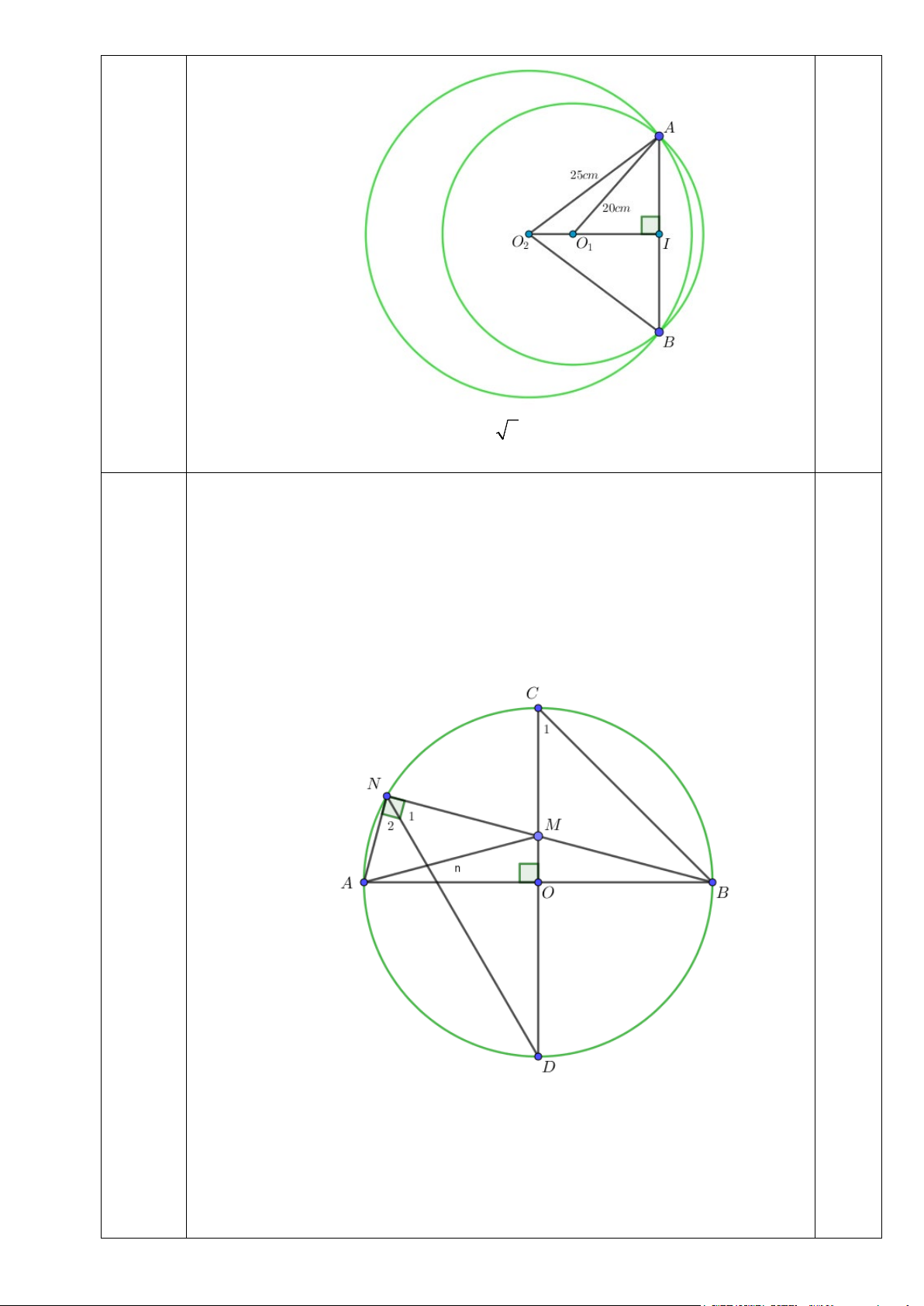
Câu 8 (1.0 điểm).Hai đường tròn giao nhau có bán kính lần lượt là
20cmvà 25cm dây cung chung có độ dài bằng 30cm . Tính khoảng cách giữa hai tâm. Lời giải: • Trường hợp 1: - Hình vẽ: Câu 8 0.5 - Dễ thấy 1
AI = AB =15(cm) . 2 - Ta có: 2 2 2 2
O I = O A − AI = 20 −15 = 5 7 1 1 2 2 2 2
O I = O A − AI = 25 −15 = 20 . 2
Do đó: O O = O I + O I = 5 7 + 20 cm . 1 2 1 2 ( ) • Trường hợp 2: - Hình vẽ: 0,5
Ta có: O O = O I −O I = 20 −5 7 cm 1 2 2 1 ( )
Câu 9 (2.0 điểm).Cho đường tròn (O) có hai đường kính AB,CD
vuông góc với nhau. Gọi M là điểm tùy ý thuộc đoạn OC ( M khác
O và C ). Tia BM cắt đường tròn (O) tại N .
1) Chứng minh AOMN là một tứ giác nội tiếp.
2) Chứng minh ND là tia phân giác của ANB . Lời giải: - Hình vẽ: Câu 9 0.25 1) Ta có: 0 ANB = 90 (vì
ANB nội tiếp chắn nửa đường tròn). 0
AOM = 90 (vì AB ⊥ CD ) 1.0 Do đó + 0
AMN AOM =180 ⇒ Tứ giác AOMN là tứ giác nột tiếp. 2) Dễ thấy =
N C (vì cùng chắn cung BD ). (*) 1 1 = N
C (vì hai góc chắc hai cung
AD, BD bằng nhau) (**). 0,75 2 1
Từ (*), (**) ta có =
N N ⇒ ND là tia phân giác của góc ANB . 1 2 ------ Hết ------
Document Outline
- _thi_thu_tuyen_sinh_vao_lop_10_mon_Toan_nam_hoc_2020-2021_-THPT_Khanh_Hoa_41945d0483
- ĐÁP ÁN
- ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 NĂM HỌC 2020-2021
- MÔN: TOÁN