Đề thi thử vào lớp 10 môn Toán năm 2025 – 2026 phòng GD&ĐT Vinh – Nghệ An

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI THỬ VÀO LỚP 10 THPT THÀNH PHỐ VINH NĂM HỌC 2025-2026 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút
Đề thi gồm có 02 trang
Câu 1 (1,5 điểm)
1) Cân nặng của các bạn học sinh lớp 9A (đơn vị: ki-lo-gam) có kết quả như sau: 52 49 58 43 40 47 62 55 52 48 59 43 54 57 62 64 53 46 56 56 52 42 55 59 50 42 55 53 64 58 49 58 54 59 46 62 57 48 52 50
Lập bảng tần số ghép nhóm cho mẫu số liệu này với các nhóm 40 ; 45 ,
45 ; 50, 50 ; 55, 55 ; 60 , 60 ; 65 .
2) Gieo đồng thời hai con xúc xắc cân đối đồng chất. Tính xác suất của biến cố: “
Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặc bằng 10”.
Câu 2 (1,5 điểm)
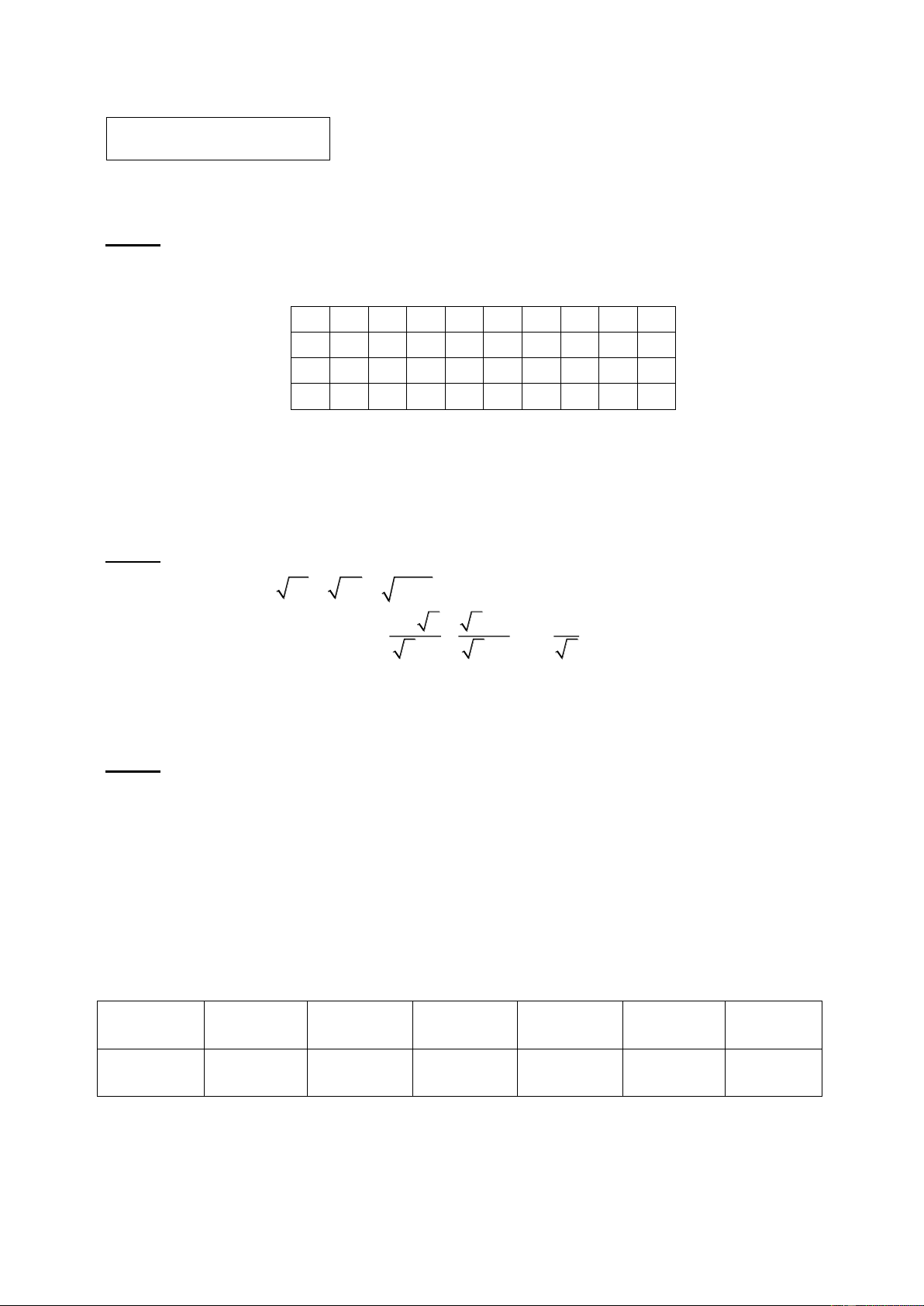
a) Tính A  5 16  49  2,56.     b) Rút gọn biểu thức x x x x  1  B     1  
 với x  0; x 1. x 1 x 1   x  c) Cho hàm số 2
y  ax a  0. Tìm hệ số a, biết rằng đồ thị của hàm số 2 y  ax
cắt đường thẳng y  3x  2 tại điểm có tung độ bằng 4 .
Câu 3 (2,5 điểm)
a) Giai đoạn đầu năm 2025 giá vàng có sự biến động lớn. Ban đầu bác Hùng sử
dụng 270 triệu đồng để mua vàng nhẫn. Sau khoảng hơn 1 tháng, giá vàng tăng thêm
10 triệu đồng/ lượng (một lượng vàng bằng 10 chỉ vàng) nên bác quyết định đầu tư
thêm 200 triệu đồng để mua tiếp. Vì thế sau 2 lần bác mua được 50 chỉ vàng. Tính giá
mỗi lượng vàng cửa hàng bán ra ở thời điểm lần đầu bác Hùng mua.
b) Từ ngày 6/3/2025 đến 8/5/2025 giá bán lẻ xăng RON 95 có đúng 2 lần tăng
và 3 lần giảm giá. Các thời điểm thay đổi giá xăng RON 95 được cho bởi bảng sau
(giá xăng được tính theo đơn vị đồng, giá được niêm yết cho 1 lít xăng) Ngày 6/3 13/3 20/3 17/4 24/4 8/5 Giá xăng 20 700 19 940 20 380 19 150 19 930 19 470
Trong 2 ngày 15/3/2025 và 18/4/2025 ông A đã mua tổng cộng 100 lít xăng và
phải trả 1982150 đồng. Hỏi ông A đã mua bao nhiêu lít xăng RON 95 vào ngày 15/3/2025? 1 c) Cho phương trình 2
x  4x  2  0 có hai nghiệm phân biệt x ; x và x  x 1 2 1 2 2 
Không giải phương trình, hãy tính giá trị của biểu thức P= x 3x 1 2 3 x  14x  3 1 2
Câu 4 (3,0 điểm).
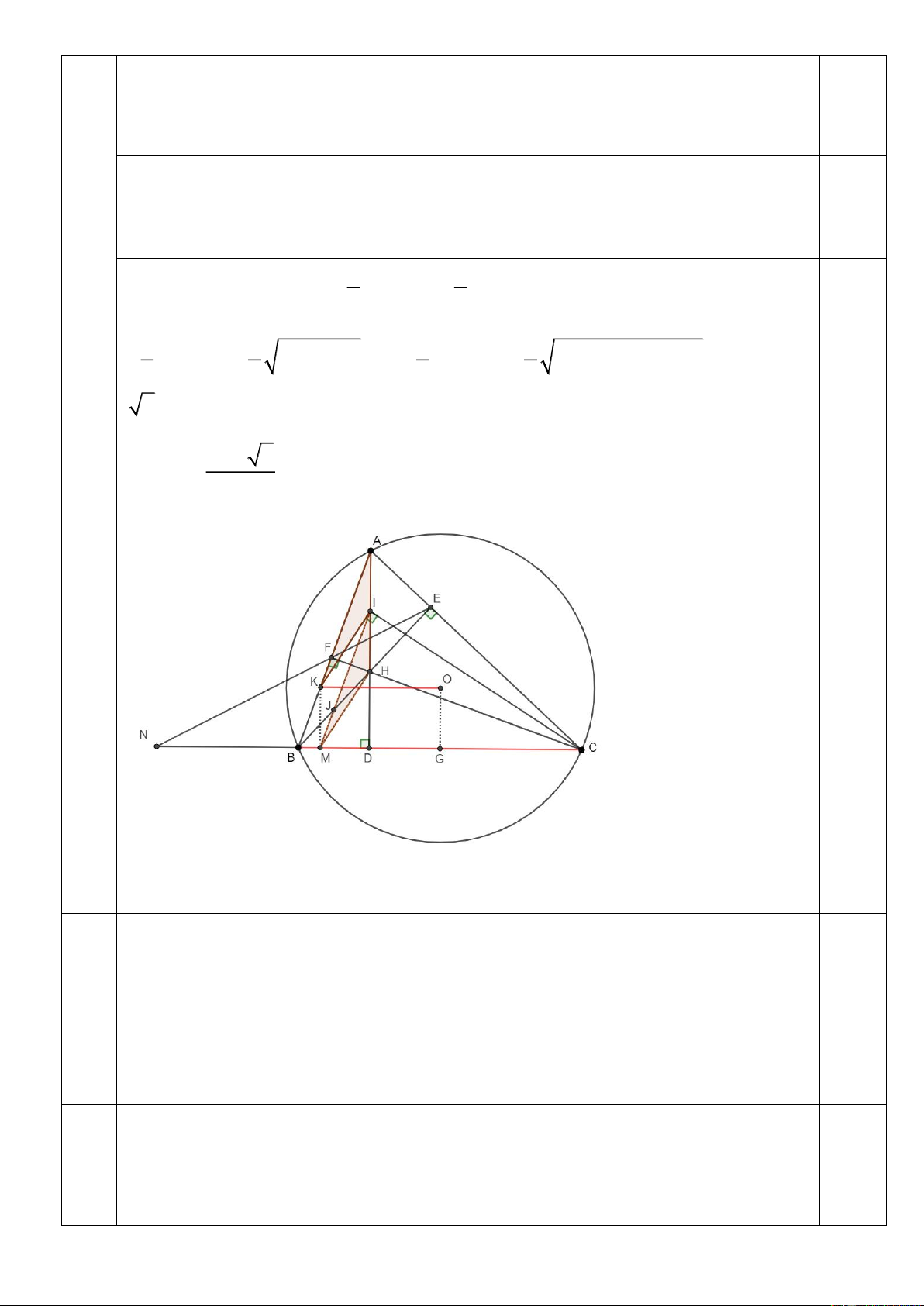
Cho tam giác ABC nhọn (AB BE, CF cắt nhau tại H.
a) Chứng minh tứ giác BCEF nội tiếp.
b) Đường thẳng EF, BC cắt nhau ở N. Chứng minh NBF ∽ NEC và
NB  AC  NF  AB
c) Gọi I là trung điểm của AH, đường thẳng vuông góc với CI tại I cắt AB ở K.
Chứng minh OK//BC .
Câu 5 (1,5 điểm).
Pha lê là một loại thủy tinh cao cấp có chứa các hợp chất kim loại, đặc biệt là
Lead(II) oxide (PbO) hoặc có thể chứa Barium oxide (BaO), giúp tăng độ trong suốt,
độ sáng và khả năng khúc xạ ánh sáng. Nhờ vậy, pha lê có vẻ ngoài lấp lánh hơn so
với thủy tinh thông thường. Pha lê thường được dùng để làm một số sản phẩm trang
sức hoặc trang trí nội thất. Một quả cầu pha lê được chế tạo bằng cách: Nung chảy pha
lê nguyên liệu trong lò ở nhiệt độ khoảng 1400 - 1600°C, đổ pha lê nóng chảy vào
khuôn tròn hoặc dùng kỹ thuật thổi thủy tinh để tạo hình, làm nguội chậm để tránh nứt
vỡ rồi đánh bóng bề mặt.
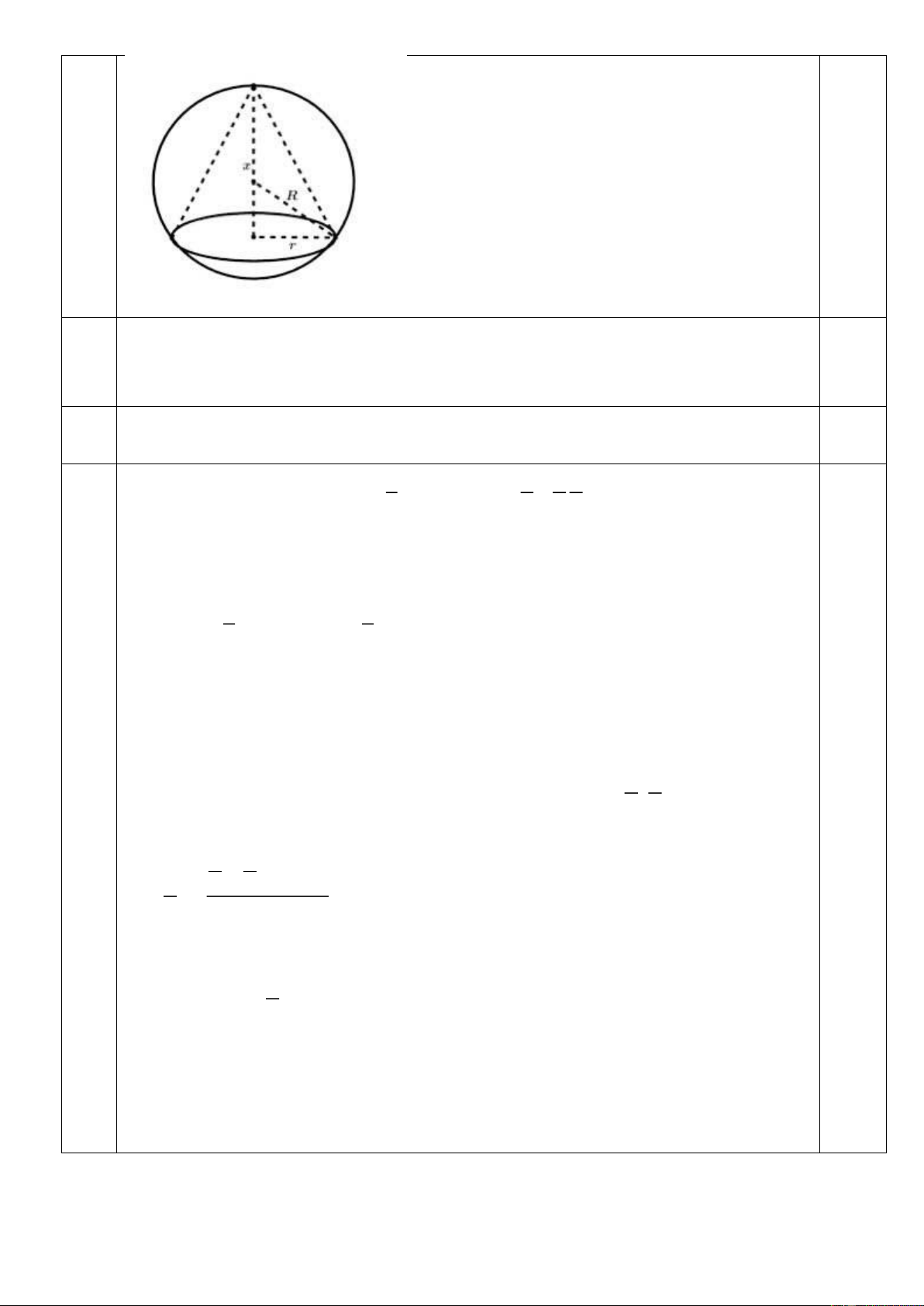
Một xưởng sản xuất làm một quả cầu pha lê có đường kính 18cm và trang trí
bằng cách sử dụng công nghệ khắc Laser để khắc hình một hình nón có đường tròn
đáy và đỉnh nằm trên mặt cầu (như hình vẽ).
a) Tính thể tích và diện tích bề mặt của quả cầu thành phẩm (với   3,14 và
làm tròn kết quả cuối cùng đến hàng phần trăm).
b) Tính chiều cao của hình nón để thể tích hình nón trong hình cầu nói trên là lớn nhất.
----------- Hết ----------- 2
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI THỬ VÀO LỚP 10 THPT THÀNH PHỐ VINH NĂM HỌC 2025-2026
HƯỚNG DẪN CHẤM MÔN TOÁN
(Hướng dẫn chấm có 05 trang) Câu Nội dung Điểm
Qua bảng số liệu thống kê ban đầu ta thấy: có 5 em cân nặng từ 40kg đến dưới 1a.
45 kg, có 7 em cân nặng từ 45kg đến dưới 50 kg, có 10 em cân nặng từ 50kg 0.25
đến dưới 55 kg, có 13em cân nặng từ 55kg đến dưới 60 kg, có 3 em cân nặng
từ 60kg đến dưới 65 kg.
Bảng tần số ghép nhóm 0.5 Giá trị 40;45   45;50   50;55   55;60   60;65   Tần số 5 7 10 13 5
Phép thử là: Gieo đồng thời hai con xúc xắc cân đối đồng chất.
1b. Kết quả của phép thử là (a,b) trong đó a và b lần lượt là số chấm xuất hiện
trên con xúc xắc thứ nhất và thứ hai.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau: 0.25
Không gian mẫu là   
 1; 1;1;21;3;1;4;1;51;6;2;4....6;6 
Tập  có 36 phần tử nên phép thử có 36 kết quả có thể và do 2 con xúc xắc
cân đối, đổng chất nên 36 kết quả này đồng khả năng. 0.5
Có 6 kết quả thuận lợi cho biến cố: “Tổng số chấm xuất hiện trên hai con xúc
xắc lớn hơn hoặc bằng 10” là (4;6); (5;5); (6;4); (5;6); (6;5); (4;6).
Vậy xác suất của biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặ 6 1 c bằng 10” là  36 6 2a
A  5 16  49  2,56  5.4  7 1,6 0.25 3 14,6 0.25 Với   , ta có x 0; x 1 0.25           x ( x 1) x (1 x ) x 1 x 1 B       
  ( x  x)      2b x 1 x 1 x x       x 1 0.25  2 x.  2( x 1) x
Gọi Px ; y là giao của 2 đồ thị hai hàm số nói trên. P P 
Do tung độ của P là 4 nên 0.25 y  4 P
Vì điểm P thuộc đồ thị hàm số y= 3x- 2 nên 4  3x  2 , suy ra x  2 . Ta có 2c P P P( 2; 4).
Lại vì điểm P thuộc đồ thị hàm số 2
y  ax nên 4 = a. 4 0.25
Do đó a= 1 (thỏa mãn). Vậy a = 1.
Gọi x (triệu đồng) là giá mỗi chỉ vàng ở thời điểm lần đầu bác Hùng mua. ĐK: 0.25 x > 0 270
Số chỉ vàng bác Hùng mua lần đầu là (chỉ vàng). x 
Giá vàng sau hơn 1 tháng tăng mỗi chỉ: 10 :10 1 (triệu đồng) nên đợt 2 bác 0.25
Hùng mua 1 chỉ vàng với giá: x  1 (triệu đồng) 200
Số vàng khi bác Hùng dùng 200 triệu đồng để mua là: (chỉ vàng). 3a x  1 270 200
Theo bài ra ta có phương trình   50 0.25 x x 1 Thu gọn ta được 2
5x  42x  27  0 3 
Phương trình có 2 nghiệm x  9 tm ; x  KTM 0.25 1   2   5
Vậy ở thời điểm ban đầu bác Hùng mua, giá vàng là 9 triệu đồng/chỉ hay 90
triệu đồng một lượng.
Gọi số lít xăng ông A đã mua vào ngày 15/3/2025 và 18/4/2025 lần lượt là x, 0.25 y( lít). ĐK: x, y> 0
Do tổng số lít xăng đã mua trong 2 ngày là 100 lít. Ta có phương trình: x+ y= 3b 100 (1)
Số tiền khi mua x lít xăng vào ngày 15/3/2025 là 19940x ( đồng)
Số tiền khi mua y lít xăng vào ngày 18/4/ 2025 là 19150y (đồng) 0.25
Do tổng số tiền phải trả là 1982150 đồng. Ta có phương trình:
19 940 x+ 19150 y= 1982150 (2)
x  y  100
Từ (1) và (2) ta có hệ phương trình: 19 940 x 19150 y  1982150
Giải hệ pt ta được x= 85, y=15 (TM) 0.25
Vậy ông A đã mua 85 lít xăng vào ngày 15/3/1982 4
x , x là nghiệm của phương trình nên 2 2
x  4x  2  0, x  4x  2  0 1 2 1 1 2 2 Theo Đị 0.25
nh lý Viète: x  x  4 và x .x  2 1 2 1 2 3 2 c
x 14x  3  x 4x  2 14x  3  4x  2x 14x  3 1 2 1  1  2 1 1 2  0.25
44x  2  2x 14x  3 14 x  x 5 14.4 5  51 1  1 2  1 2 7 1 2
x  3x  4x  2  3x  (x  x ) 
(x  x )  2 1 2 1 2 1 2 1 2 2 2 7 1 7 1 = (x  x ) 
x  x 2  2= (x  x )  x  x  4x x  2=12+ 1 2  1 22 1 2 1 2 2 2 1 2 2 2 2 0.25  Vậy 12 2 P  51 4 0.5
Vẽ hình đến hết câu b
Tam giác BEC vuông tại E nên tam giác BEC nội tiếp đường tròn đường kính đường kính BC 0,5
Tam giác BFC vuông tại F nên tam giác BFC nội tiếp đường tròn đường kính đường kính BC 0,5
Vậy tứ giác BCEF nội tiếp.
Tứ giác BCEF nội tiếp suy ra 0,25    180o     180o BFE BCE BFN BCE  B  FE
Xét tam giác NBF và tam giác NEC có 0,25 5 N chung, B  FN  B  CE (cmt)
Suy ra NBF ∽ NEC (g.g).  ∽   NB  NE NBF NEC (1) NF NC 0,25 NB BE N  BE ∽ N  FC   (2) NF CF
Xét tam giác ABE và ACF có BAC chung,     90o BEA CFA  Suy ra  ∽     BE BA BAE CAF g g   (3) CF CA 0,25 NB AB
Từ (1) ,(2) và (3) ta được   N .
B AC  NF.AB NF AC
Kẻ đường kính AL, chứng minh được tứ giác BHCL là hình bình hành suy ra G là trung điểm của HL AH OG / /  2 0,25
Gọi J là trung điểm của BH, đường thẳng IJ cắt BC ở M, G là trung điểm BC.
Khi đó IF  IH, JF  JH  IJ  HF  IJ //AK .
H là trực tâm tam giác IMC nên MH  IC  MH //IK Do đó A  IK  I  HM  . g . c g   . AK IM
Suy ra AIMK là hình bình hành nên AH KM // 
 KM //  OG  KOGM là 2 0,25 hình bình hành.
Từ đó ta được OK//BC . 5a
Bán kính khối cầu 18:2=9 (cm). 0.25 Thể tích khối cầu 4 4 3 3 V   R  9 3 3    3 972 cm  0.25
Diện tích bề mặt cần phun chống xước là: 0.25 2 S  4 R  2  4 9  xq 2  1017,36(cm ) 0.25 6
Gọi chiều cao hình nón là x(cm). Bán kính đáy hình nón là r( cm).
ĐK: 0 < x < 18; r > 0 Ta có r   x  2 2 2 9 9 = 2
18x  x = x18  x 0.25
Thể tích của hình nón là: 1 4 x x 2
V   x 18  x =  18  x 3 3 2 2
Cách 1:Xét A= x   x 
 x  x  2 2 18 864 6 12  0 do 0 Do đó 1 1 2
V   x 18  x   .864  288 3 3
Dấu “=” có khi x= 12(t/m)
Vậy chiều cao của hình nón là 12 cm để thể tích hình nón nói trên là lớn 0.25
nhất và khoảng 904,32 cm3.
Cách 2:Áp dụng Bất đẳng thức Cauchy cho 3 số dương: x x ; ;18  x ta có 2 2 3  x x   18  x 4   2 2 V      288 3  904,32(cm ) 3 3    
Dấu “=” có khi x 18  x dó đó x= 12(t/m) 2
Vậy chiều cao của hình nón là 12 cm để thể tích hình nón nói trên là lớn
nhất và khoảng 904,32 cm3.
Lưu ý nếu HS không chứng minh BĐT Cau chy cho một nửa số điểm của ý này.
Học sinh làm cách khác đúng vẫn cho điểm tối đa 7 8