Đề thi Toán năm 2022 - Đề mẫu 1 | Trường Đại học Sư Phạm Hà Nội

Hanoi National University of Education HNUE Mathematics Contest 2022 Grade 8 Time allowed: 45 minutes Round 1 1 1 + x y
1. For what values of variables x, y does the expression make sense? 1 1 − x y A. x ̸= 0 and y ̸= 0 B. x ̸= 0 or y ̸= 0 C. x ̸= y ̸= 0 D. x ̸= −y ̸= 0
2. For what values of m is the equation 2(m + 1)x + 5 = 3m − 10 equivalent to the equation 3x + 2 = 2(x − 1) + 4? 5 5 A. m ̸= 5 B. m = C. m = − D. m = 5 3 3
3. Find the values of m so that the equation (2x + m)(x − 1) − 2x2 + mx + m − 2 = 0 has a non-negative root. A. m < 1 B. m > 1 C. m ≤ 1 D. m ≥ 1 x + 1 x + 2 x + 3 x − 1 x − 2 x − 3
4. Let x be the solution to the equation + + = + + . 2021 2020 2019 2023 2024 2025 What is the value of x + 2011? A. −11 B. −10 C. 2022 D. −2022
5. For how many integral value(s) of m does the equation (5x − m)(x − 1) − 5x2 + 2mx −
m − 1 = 0 have an integral root? A. 2 B. 3 C. 4 D. 1
6. Given that a − 2021 = b + 2022 = c − 2023, arrange a, b, c in the increasing order. A. b, c, a B. a, b, c C. b, a, c D. a, c, b
7. Find the sum of the roots ofSample
the equation x2 + 3x − 10 = 0. A. 3 B. −3 C. 7 D. −7
8. Find the product of all the positive roots of the equation x3 − 5x2 − 2x + 24 = 0. A. −24 B. 17 C. 12 D. 6
9. Calculate A = 2023 × 2021 − 2024 × 2020 + 2025 × 2019 − 2026 × 2018. A. A = 10 B. A = −10 C. A = −4 D. A = 4
10. Which inequality below is not equivalent to 3 − x < 7? A. x − 3 < 7 B. 6 − x < 10 C. 6 − 2x < 14 D. x > −4
11. Class 8A and 8B have 85 students in total. Given that 30% of the students in Class 8A
and 20% of the students in Class 8B are classified as Excellent, and the total number of
Excellent students in two classes is 21, find the number of students in Class 8A and 8B. A. 40 and 45 B. 45 and 40 C. 35 and 40 D. 40 and 35 1 of 4 8xy x + 3y x2 + 1 7x2 + 14x + 7
12. How many rational function(s) among , , and 32y x2 + 6xy + 9y2 x4 + 1 x3 + 1 can still be reduced? A. 1 B. 2 C. 3 D. 4
13. What is the measure of each angle of a regular 9−gon? A. 20◦ B. 40◦ C. 140◦ D. 200◦ 3
14. Triangle A1B1C1 is similar to triangle A2B2C2 with the ratio of . Triangle A2B2C2 is 14 7
similar to triangle A3B3C3 with the ratio of . What is the ratio of the areas of triangles 8 A1B1C1 and A3B3C3? A. 3/8 B. 3/16 C. 49/12 D. 9/256
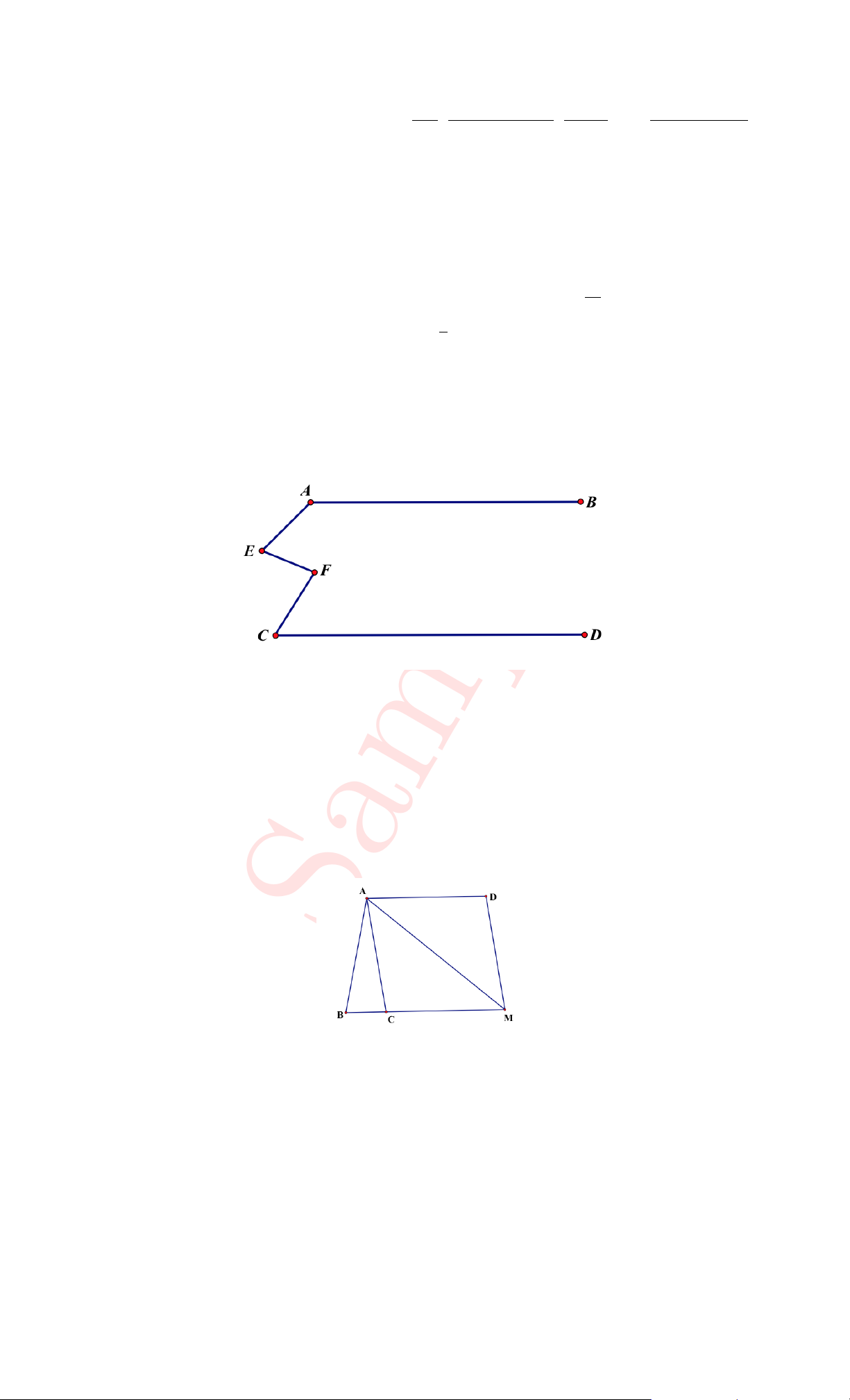
15. In the figure below AB and CD are parallel. Given that ∠CF E = 80◦, what is the total
measure of three angles ∠BAE, ∠AEF and ∠F CD? A. 200◦ B. 260◦ C. 300◦ D. 360◦
16. Which polynomial below is not a factor of the polynomial x3 + 2x2y + xy2 − 9x? A. x B. x + y − 3 C. x − y + 3 D. x + y + 3
17. In the figure below ABC is an isosceles triangle with apex A and ACM D is a rhombus
such that M is on the line Sample
BC. Given that ∠CAM = 2∠BAC, find the measure of ∠BAC. A. 15◦ B. 20◦ C. 25◦ D. 30◦
18. Twelve sticks, each of which has the length of 2 cm, are used to form a right triangle.
(No stick is bended or broken.) What is the length, in centimeter, of the hypotenuse of the triangle? A. 6 B. 8 C. 10 D. 15
19. In the figure below, ABCD is a rhombus with ∠A = 100◦ and DBE is a right isosceles
triangle with apex D. What is the sum of the measures of ∠ABE and ∠BED? A. 50◦ B. 60◦ C. 70◦ D. 80◦ 2 of 4
20. The polynomial x3 − 3x2 + 5x − 6 is divisible by which polynomial below? A. x − 2 B. x + 2 C. x + 1 D. x − 1
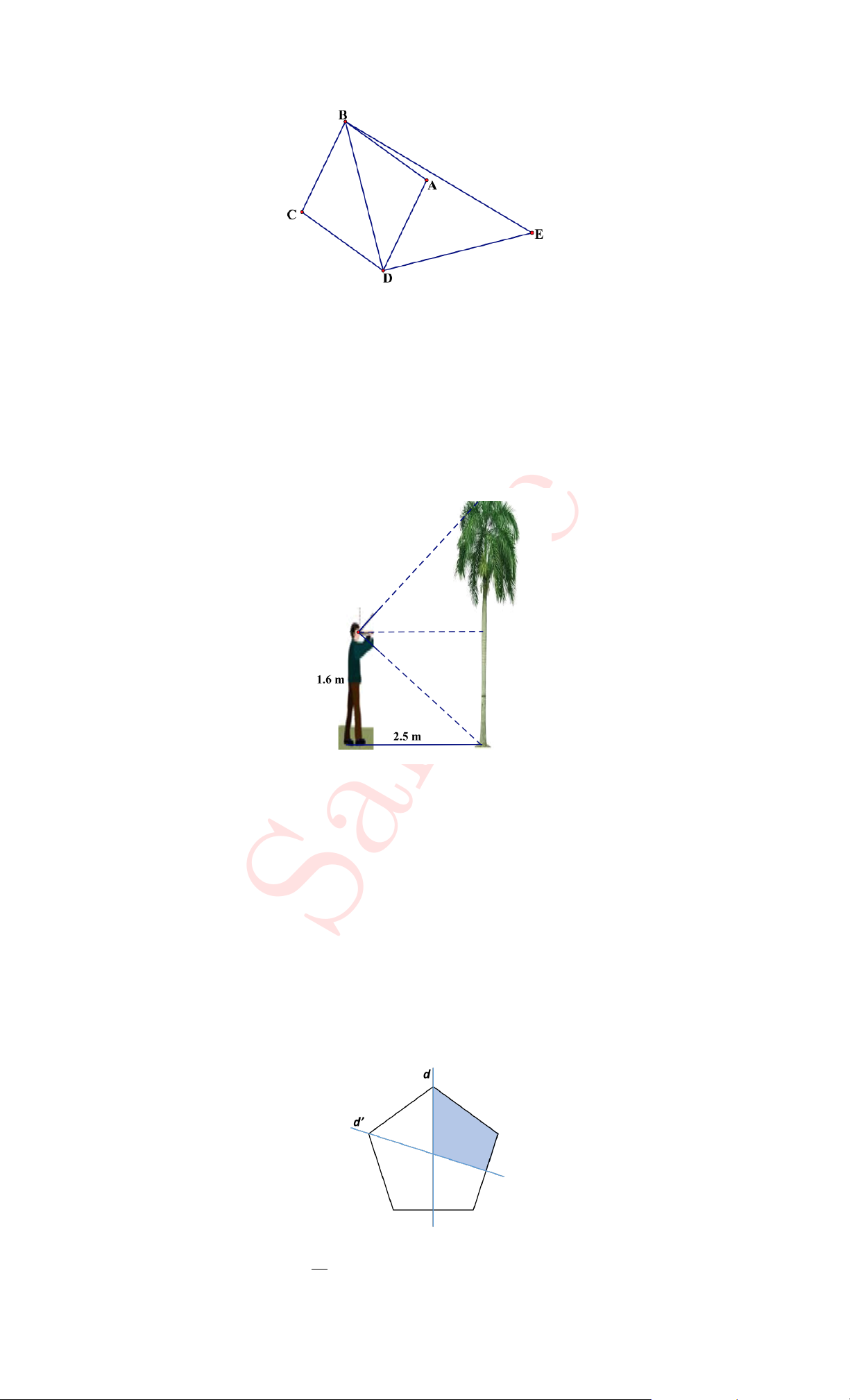
21. A man used a square rule to measure the height of a tree as in the figure. The distance
from the root of the tree to the feet of the man is 2.5 m. The distance from the eyes of
the man to the ground is 1.6 m. Find the height of the tree to the nearest hundredth of a meter. A. 5.53 B. 5.52 C. 5.51 D. 5.50
22. Lan runs 300 meters to the Sample
east, then walks 400 meters to the north and finally runs
600 meters to the west. How far is she now from the original position? A. 300 m B. 500 m C. 700 m D. 900 m
23. How many 3-digit numbers divisible by 2 and 5 can be formed by using digits 0, 1, 2, 3 and 4 without repetition? A. 16 B. 12 C. 24 D. 60
24. Let there be given a regular pentagon whose area is 20. Suppose that d and d′ are two
diagonals of the pentagon as shown in the figure. What is the area of the shaded region? 20 A. 6 B. C. 5 D. 8 3 3 of 4
25. There are 15 bananas, 9 strawberries and 17 oranges in a box. At least how many fruits
need to be taken to have at least 6 fruits of each kind? A. 16 B. 30 C. 33 D. 38
26. Let b and c be real numbers such that 2x2+4x+1 is a factor of the polynomial 2x3−bx−c. Find the value of b + c − 2. A. 7 B. −7 C. 3 D. 10
27. In a coordinate plane let there be given a rhombus ABCD. Given that the coordinates
of A, B, C are (0, 0), (1, 2) and (3, 3) respectively, what are the coordinates of D? A. (2, 3) B. (3, 1) C. (2, 1) D. (−1, −2)
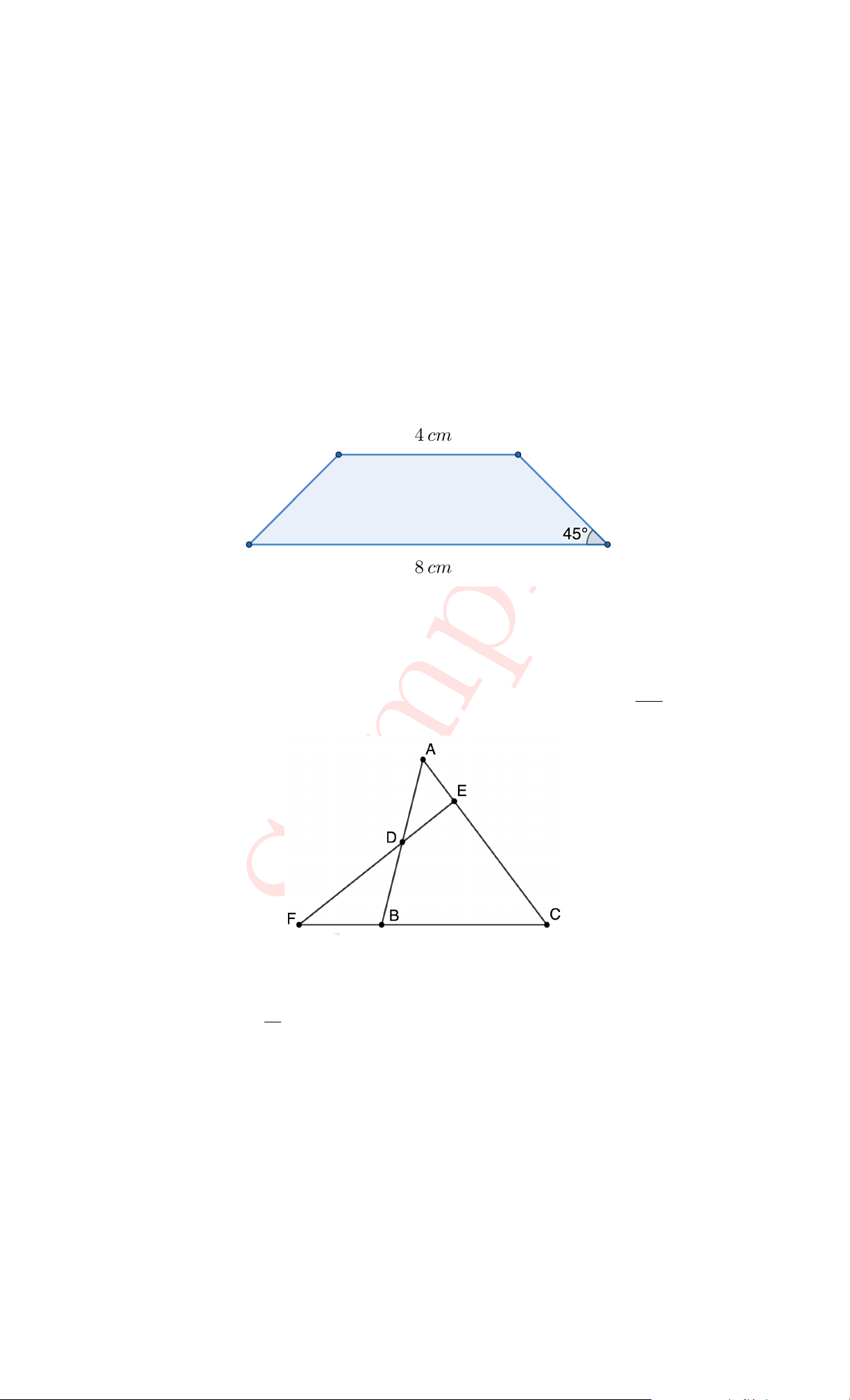
28. In the figure below is an isosceles trapezoid with some measures given. Find the perimeter and area of the trapezoid. A. 16 cm; 12 cm2 B. 16 cm; 24 cm2
C. 17.66 cm; 12 cm2 D. 17.66 cm; 24 cm2
29. In the figure below, D, E, F are three collinear points lying on the lines AB, AC, BC DE
respectively. Given that AD = BD and CE = 3 AE, what is the ratio ? DF A. 3/4 B. 1/ Sample 3 C. 1/2 D. 2/3
30. Let n be a positive integer so that the average of all the integers from 1 to n, except a 54 certain number, is . What is n? 5 A. 20 B. 16 C. 21 D. 26 ——— The end ——— 4 of 4