Đề thi Toán năm 2022 - Đề mẫu 2 | Trường Đại học Sư Phạm Hà Nội

Hanoi National University of Education HNUE Mathematics Contest 2022 Grade 8 Time allowed: 45 minutes Round 2 a b 3 1 1. Given that − =
with x ̸= ± , what is the value of a − b? 1 1 3x − 1 3 x − x + 3 3 A. 3 B. 9 C. 1 D. −1
2. Find the product of all the integral roots of the equation x3 − 5x2 − 2x + 24 = 0. A. 24 B. −24 C. 5 D. 20
3. Let a, b, c be three distinct roots of the equation x3 − 6x2 + 11x − 6 = 0. Find the value of a2 + b2 + c2. A. 11 B. 36 C. 14 D. 6
4. How many positive integers from 1 to 2022 can be expressed as n3 − n where n is a positive integer? A. 10 B. 11 C. 12 D. 13
5. What is the number of sides of a polygon which has exactly 14 diagonals? A. 5 B. 6 C. 7 D. 8
6. The polynomial f (x) = x (ax4 + bx2 + c) + 1 satisfies f (7) = 2022. Find the value of f (−7). A. 2021 B. −2020 C. −2021 D. −2022
7. Suppose that a, b, c, d are integers so that one has the factorisation 3x3 + 13x2 − 50 =
(ax + b)(x2 + cx + d). Find the value of a + b + c + d. A. 10 B. 14 Sample C. 18 D. 22
8. Class 8A has 30 students who like Maths, 15 who like History, and 10 who like both
Maths and History. Given that there are 40 students in this class, find the number of
students who like neither Maths nor History. A. 5 B. 10 C. 20 D. 25
9. There is a row of 15 chairs and some people are sitting on them in any order. To ensure
that there are always 3 people sitting next to each other, leaving no empty seats between
them, at least how many people are needed? A. 9 B. 10 C. 11 D. 15
10. Let a, b and c be real numbers such that a + b + c = 6 and a3 + b3 + c3 = 36. Find the
value of (a + b)(b + c)(c + a). A. 60 B. 216 C. 180 D. 252
11. The measure of an interior angle of a regular n−sided polygon is (16n + 7)◦. What is the value of n? A. 3 B. 8 C. 11 D. 13 1 of 3
12. A regular hexagon has the longest diagonal of length a. What is the area of the hexagon? √ √ √ √ A. 3a2/8 B. 3 3a2/2 C. 3 3a2/8 D. 3a2/2
13. All the natural numbers from 1 to 2022 are written on a blackboard. Each time, An
deletes two numbers a, b on the board and writes a new number c such that c = a+b−ab.
She keeps doing that until there is only one number left. What is that number? A. 1 B. 2 C. 3 D. 4
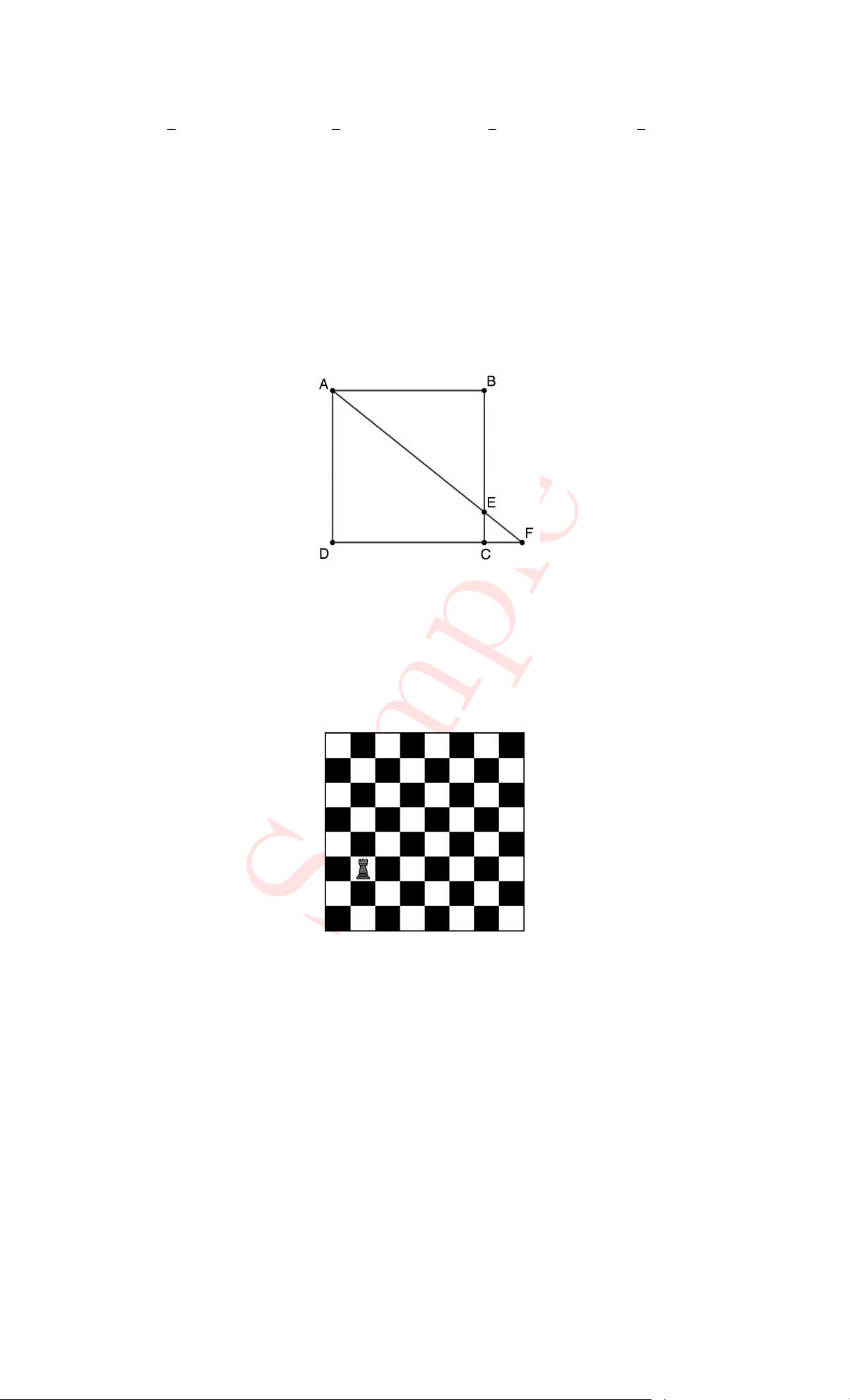
14. In the figure below, a line through vertex A of a square ABCD cuts BC and CD at
E and F respectively. Given that AE = 3 and AF = 4, what is the side length of the square? A. 2 B. 2.5 C. 2.4 D. 2.6
15. The rook is a piece in the game of chess. It may move any number of squares horizontally
or vertically without jumping, and it may capture an enemy piece on its path. How many
ways can we place 2 rooks on 2 squares of the chessboard such that they can not capture each other? A. 1024 B. Sample 1568 C. 1792 D. 3584
16. All the natural numbers from 1 to 2022 are written on a blackboard. Binh underlines
all the numbers divisible by 3, then all the numbers divisible by 4 and finally all the
numbers divisible by 5. How many numbers are underlined exactly twice? A. 304 B. 456 C. 236 D. 152
17. How many 9-digit numbers can be formed by using all the digits 1, 1, 1, 1, 2, 2, 2, 2, 2? A. 126 B. 336 C. 756 D. 3024
18. Andy wrote 4 monomials x, 2x2, 3x3, 4x4, once for each, in each cell of a 2 × 2 table. He
then calculated the sum of the monomials in each row and each column of the table.
Three of his answers were x + 2x2, x + 3x3 and 3x3 + 4x4. What is his forth answer? A. x + 4x4 B. 2x2 + 3x3 C. 2x2 + 4x4 D. 2x2 + 4x4 2 of 3
19. A trapezoid ABCD has two bases AB = 3 cm and CD = 6 cm. Let O be the intersection
of two diagonals AC and BD. The line through O and parallel to AB cuts AD at E.
What is the length of OE in centimeter? A. 4 B. 4.5 C. 2 D. 1.5
20. At most how many numbers could be chosen among the integers from 1 to 2022 such
that the sum of any two numbers is divisible by 22? A. 94 B. 93 C. 92 D. 91 ——— The end ——— Sample 3 of 3