Đề thi vào 10 môn Toán của Sở GD&ĐT Kon Tum năm 2019-2020

UBND TỈNH KON TUM
KỲ THI TUYỂN SINH LỚP 10
SỞ GIÁO DỤC VÀ ĐÀO TẠO
Trường THPT chuyên Nguyễn Tất Thành, THPT Kon Tum
Năm học 2019 – 2020
ĐỀ THI CHÍNH THỨC
Môn: TOÁN (Môn chuyên) Ngày thi: 11/6/2019
Thời gian: 120 phút (Không kể thời gian giao đề)
Câu 1 : (2,0 điểm) 3 5 . 3 5
1. Không dùng máy tính cầm tay, hãy tính giá trị biểu thức P 10 2 2x 3 x 2
2. Rút gọn rồi tính giá trị của biểu thức Q tại x 2020 2 2019 x 2
Câu 2 : (2,5 điểm) 1.Cho parapol 2 P : y
x và đường thẳng 2 d : y 2x m
1, m là tham số. Tìm m để y y đường thẳng 38
d cắt parapol P tại hai điểm A x ; y
, B x ; y sao cho A B . A A B B x x 5 B A 2 2 x y 6 0
2. Giải hệ phương trình 2 (I) 2 2 x y 1 3 0 x y
Câu 3 : (2,5 điểm)
Cho đường tròn O; R có đường kính AB cố định và đường kính CD thay đổi sao cho CD
không vuông góc cũng không trùng với AB. Gọi d là tiếp tuyến tại A của O; R . Các đường thẳng BC
và BD cắt d tương ứng tại E và F
1. Chứng minh rằng CDFE là tứ giác nội tiếp.
2. Gọi M là trung điểm của EF và K là tâm đường tròn ngoại tiếp tứ giác CDEF. Chứng minh
rằng tứ giác KMBO là hình bình hành.
3. Gọi H là trực tâm tam giác DEF, chứng minh H luôn chạy trên một đường tròn cố định.
Câu 4 : (2,0 điểm)
1. Cho số thực x thỏa mãn 1 x 1. Chứng minh rằng 2 1 x 1 x 2 x .
2. Cho tập hợp A gồm 41 phần tử là các số nghuên khác nhau thỏa mãn tổng của 21 phần tử bất
kỳ lớn hơn tổng của 20 phần tử còn lại. Biết các số 401 và 402 thuộc tập A. Tìm tất cả các phần tử của tập hợp A.
Câu 5 : (1,0 điểm)
Cho hình chữ nhật ABCD có AB 2a,BC
a 2 . Lấy đoạn AB làm đường kính, dựng về
phía ngoài hình chữ nhật nửa đường tròn. Điểm M thuộc nữa đường tròn đó. Các đường thẳng MD, MC 2 2
cắt AB lần lượt tại N, L. Chứng minh AL BN 1 . 2 AB
……………………………….Hết……………………………….
- Thí sinh không sử dụng tài liệu.
- Giám thị không được giải thích gì thêm. 1 UBND TỈNH KON TUM
KỲ THI TUYỂN SINH LỚP 10
SỞ GIÁO DỤC VÀ ĐÀO TẠO
Trường THPT chuyên Nguyễn Tất Thành, THPT Kon Tum
Năm học 2019 – 2020
ĐỀ THI CHÍNH THỨC
Môn: TOÁN (Môn chuyên)
HƯỚNG DẪN CHẤM THI
(Bản hướng dẫn gồm 03 trang) I. HƯỚNG DẪN CHUNG :
1) Chấm theo đúng đáp án và thang điểm
2) Học sinh làm cách khác đúng thi cho điểm tối đa. Nếu chỉ đúng một phần trên nào
đócủa bài thi thì căn cứ vào thang điểm tương ứng để cho điểm
3) Điểm chi tiết từng ý nhỏ của mỗi bài là 0,25. Tổng điểm toàn bài tính đến 0,25 điểm
II. ĐÁP ÁN VÀ THANG ĐIỂM : Câu Ý Nội dung Điểm 1. 1.0đ 3 5 . 3 5
Không dùng máy tính cầm tay, hãy tính giá trị biểu thức P 10 2 Câu 1 0,25 (2,0đ) 3 5 . 3 5 . 2 5 1 P 8 2 0,25 6 2 5 . 3 5 5 3 5 5 1 . 2 5 2 8 8 5 1 .2. 5 1 0,25 8 2. 5 1 0,25 1 8 2. 1,0đ 2x 3 x 2
Rút gọn rồi tính giá trị của biểu thức Q tại x 2020 2 2019 x 2 2 0,25 Ta có x 2020 2 2019 2019 2 2019 1 2019 1 x 2019 1 2 x 1 x 2 0,25 2x 3 x 2 Q x 2 x 2 Q 2 x 1 0,25 Q 2 2019 1 1 2 2019 1 0,25 1. Cho parapol 2 P : y
x và đường thẳng 2 d : y 2x m 1, m là tham số. Tìm 1,25đ
m để đường thẳng d cắt parapol P tại hai điểm A x ; y ,B x ; y sao cho A A B B y y 38 A B . x x 5 B A
Phương trình hoành độ giao điểm giữa d và P là 0,5 2 2 2 2 x 2x m 1 x 2x m 1 0 0,5 Phương trình bậc hai có 2 ac m 1
0 với mọi m nên luôn có hai nghiệm 2
phân biệt khác 0 với mọi m. Do đó d luôn cắt parapol P tại hai điểm phân biệt A x ; y
, B x ; y với mọi m A A B B Câu 2 (2,5đ)
x ; x là các nghiệm khac 0 của phương trình 2 2 x 2x m 1 0 . 0,25 A B x x 2
Áp dụng hệ thức Vi et ta có : A B 2 x .x m 1 A B 0,25 y y 38 Do A B 5 y .x y .x 38.x .x x x 5 A A B B A B B A 3 3 3 5 x x 38.x .x 5 x x 3x .x x x 38.x .x A B A B A B A B A B A B 2 2 5 8 6 m 1 38. m 1 2 0,25 8m 32 m 2 Vậy
m = 2 và m = -2 thỏa mãn điều kiện đề bài. 1,25đ 2. 2 2 x y 6 0 Giải hệ phương trình 2 (I) 2 2 x y 1 3 0 x y x y x y 6 0,25 Ta có (1) 2 4 x y 1 3 0 2 x y a x y Đặt b 0 b x y 1 a ab 6 (1) b 6 khi đó (I) 2 4 2 a 1 3 0 2 4a 2 b a 1 3 (2) 36 a 3 0,25
Từ (2) ta có phương trình 2 2 2 9 a 1 a 27 8a 18a 18 0 3 a 4 0,25 5 x x y 3
Với a 3 ta có b 2 suy ra 2 x y 2 1 y 2 35 0,25 3 x Với 3 x y a ta có b 8 suy ra 8 4 4 29 x y 8 y 8 0,25
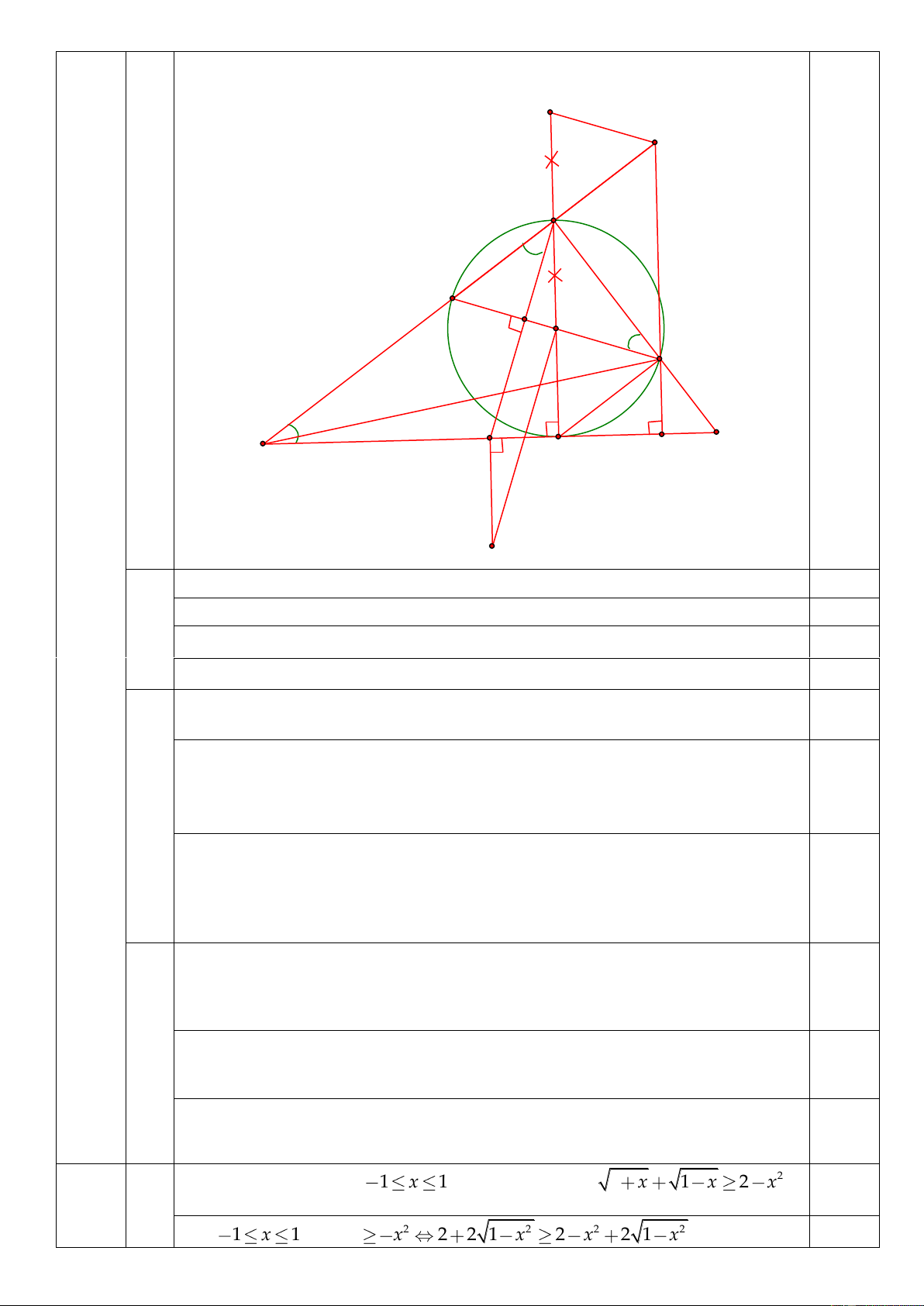
Vậy hệ đã cho có hai nghiệm 35 29 5 1 x; y ; ; x; y ; 8 8 2 2 3 Hình vẽ O' H Câu 3 (2,5đ) B C Q O D M F E A T K 1.
Vì CD là đường kính nên 0 CBD  90 0,25
Do đó BEF  ABF (góc có cạnh tương ứng vuông góc cùng nhọn) 0,25
Mà ABF  ODB (OB  OD  R) 0,25  . Do đó tứ giác Nên BEF ODB
CDFE nội tiếp đường tròn 0,25 2.
Gọi Q là giao điểm của BM và CD 0,25
Tam giác BEF vuông tại B nên BM = ME  MBE  MEB (1)
Tam giác BCD vuông tại B nên 0
BCD  BDC  90 mà BDC  BEF 0,25 (chứng minh câu 1) nên 0
BCD  BEF  90 (2) Từ (1) và (2) : 0 0
BCD  MBE  90  BQC  90 hay BM  CD
K là tâm đường tròn ngoại tiếp tứ giác CDFE, O là trung điểm CD, nên 0,25
KO  CD  KO / /MB (cùng vuông góc với CD) (3)
Ta có M là trung điểm EF, nên KM  EF và BA  EF
 KM / / AB hay KM / BO (4)
Từ (3) và (4) suy ra KMBO là hình bình hành 3.
H là trực tâm tam giác DEF, do đó HD  EF , suy ra HD / / AB 0,25
Tương tự BH / / AD (cùng vuông góc BF)
Do đó BHDA là hình bình hành nên BH = AD
Mặt khác BDAC là hình chữ nhật nên AD = BC  BH  BC (5) 0,25
Lấy O’ đối xứng với O qua B ta có BO’ = BO (6) với O’ cố định vì O, B cố định
Từ (5) và (6) suy ra HO’CO là hình bình hành nên O’H = OC = R 0,25
Vậy H chạy trên đường tròn cố định O'; R 1.
Cho số thực x thỏa mãn 1 x 1 . Chứng minh rằng 2 1 x 1 x 2 x . 1,0đ Câu 4 Với 1 x 1 ta có 2 2 2 2 0 x 2 2 1 x 2 x 2 1 x 0,25 4 (2,0đ) 2 2 0,25 2 2 1 x 1 x 1 1 x 1 x 1 x 1 1 x Lại có : 2 2 2 2 2 0 1 x 1, x 1;1 1 x 1 x 1 1 x 2 x 0,25 Vậy 2 2 1 x 1 x 1 x 2 x , x 1;1 . 0,25 2 x 0
Đẳng thức xảy ra khi và chỉ khi : x 0 2 2 1 x 1 x 2.
Cho tập hợp A gồm 41 phần tử là các số nghuên khác nhau thỏa mãn tổng của 21 1,0đ
phần tử bất kỳ lớn hơn tổng của 20 phần tử còn lại. Biết các số 401 và 402 thuộc
tập A. Tìm tất cả các phần tử của tập hợp A. Giả sử A
a ; a ; a ;...; a
với a ; a ; a ;...; a và a a a ... a 0,25 1 2 3 41 1 2 3 41 1 2 3 41
Theo giả thiết ta có a a a ... a a a ... a 1 2 3 21 22 23 41 a a a a a ... a a (1) 1 22 2 23 3 41 21 Mặt khác với ; x y và nếu y x thì y x 1 0,25 a a 20,a a 20,...,a a 20 2 22 2 23 3 41 21 Nên từ (1) suy ra a 20 20 20 ... 20 400 1
Mà a nhỏ nhất và 401 A a 401 1 1 Ta có 401 a a a a ... a a 400 22 2 23 3 41 21 a a a a ... a a 400 22 2 23 3 41 21 Kết hợp với (2) 0,25 a a a a ... a a 20 3 22 2 23 3 41 21 20 a a a a a a ... a a 20 22 2 22 21 21 20 3 2 a a a a ... a a 1 4 22 21 21 20 3 2 Ta có a 401 mà 402 A a 402 1 2
Kết hợp (3) và (4) suy ra A 401; 402; 403;...; 441 0,25 Câu 5
Cho hình chữ nhật ABCD có AB 2a,BC
a 2 . Lấy đoạn AB làm đường kính, 1,0đ (1,0đ)
dựng về phía ngoài hình chữ nhật nửa đường tròn. Điểm M thuộc nữa đường tròn
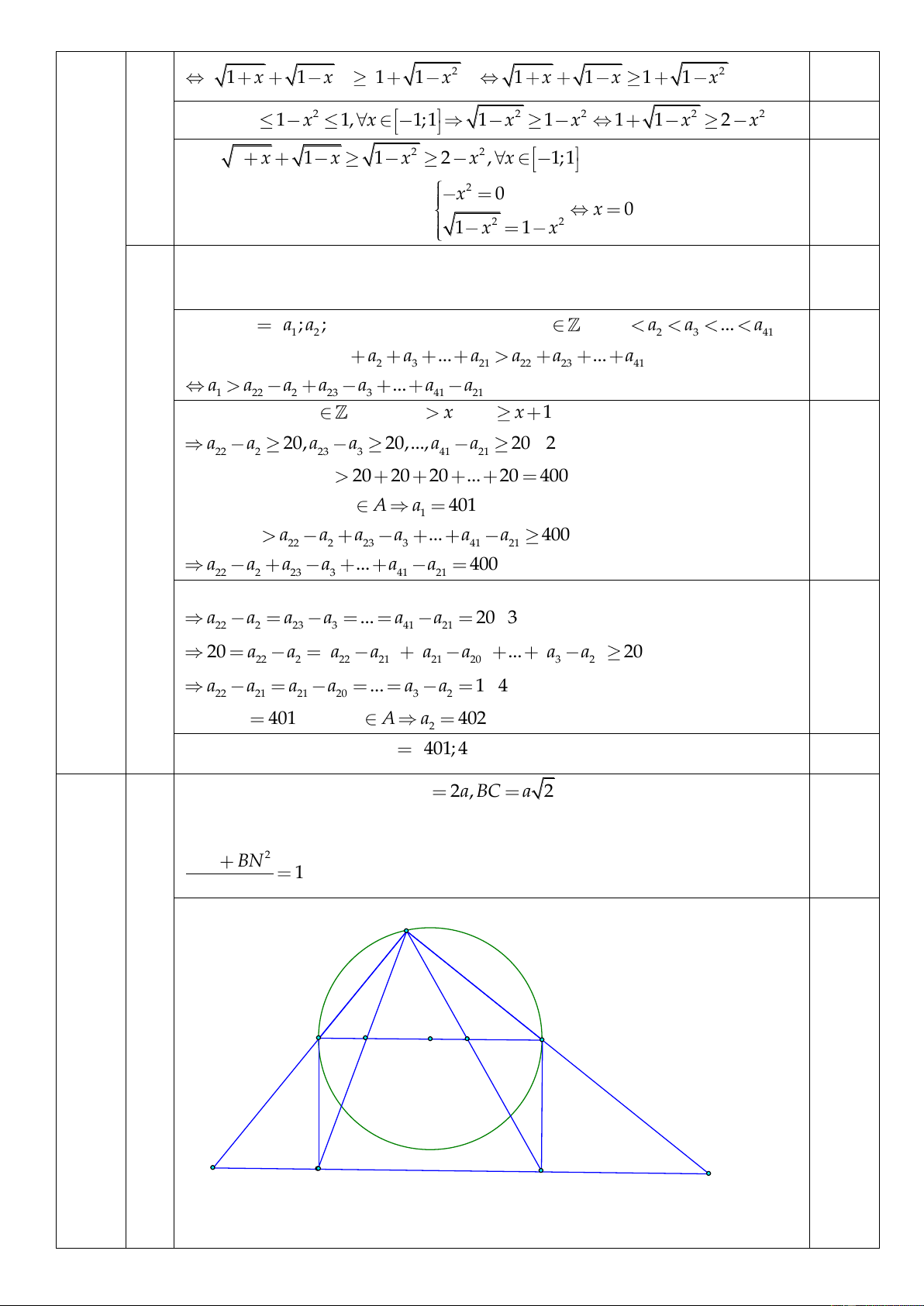
đó. Các đường thẳng MD, MC cắt AB lần lượt tại N, L. Chứng minh 2 2 AL BN 1 . 2 AB 0,25 M A L B N O P D C Q
Gọi P, Q lần lượt là giao điểm của CD với MA và MB. Đặt PD = x ; CQ = y 5
Ta có : APD  QBC (góc có cặp cạnh tương ứng vuông góc) PD BC x a 2 2  A  PD Q  BC      xy  2a AD QC a 2 y
PC  QD   x  a2   y  a2 2 2 2 2
 x  y  ax  y 2 2 2 4 8a 0,25
 x  y2  4ax  y 2  8a  2xy
x  y2  4ax  y 4a  x  y  2a2 2 2  PQ   1 0,25
Áp dụng định lý Tales, ta có : MN ML MA MB AL BN AB       MD MC MP MQ PC QD PQ 2 2 2 2 2 2 2 AL BN AB AL  BN AL  BN      (do   1 ) 2 2 2 2 2 2 PC QD PQ PQ  QD PQ 2 2 AL  BN 0,25 2 2 2
 AB  AL  BN  1. 2 AB 6