



Preview text:
Đề thi tuyển sinh lớp 10 năm học 2020 - 2021
trường THPT Chuyên Sư Phạm Hà Nội
Đề thi tuyển sinh vào lớp 10 trường THPT Chuyên Sư Phạm Hà Nội năm 2020
Đề thi tuyển sinh vào lớp 10 trường THPT Chuyên Sư Phạm Hà Nội năm 2020 Đáp án Câu 1 a) Với ta có: KL.... b) Ta có: Câu 2 a) để d1 và d2 song song ⇔ ⇒ m = -3 KL.... b) Ta thấy:
Với mọi m, hay phương trình đã cho luôn có hai nghiệm phân biệt.
Áp dụng hệ thức Vi-ét ta có: Ta có: Để KL.... c.
Gọi vận tốc ô tô thứ nhất là x (km/h, x > 10)
=> vận tốc ô tô thứ hai là x - 10 (km/h)
Theo bài ta có phương trình ạ
=> vận tốc xe thứ hai là 60 - 10 = 50 km/h
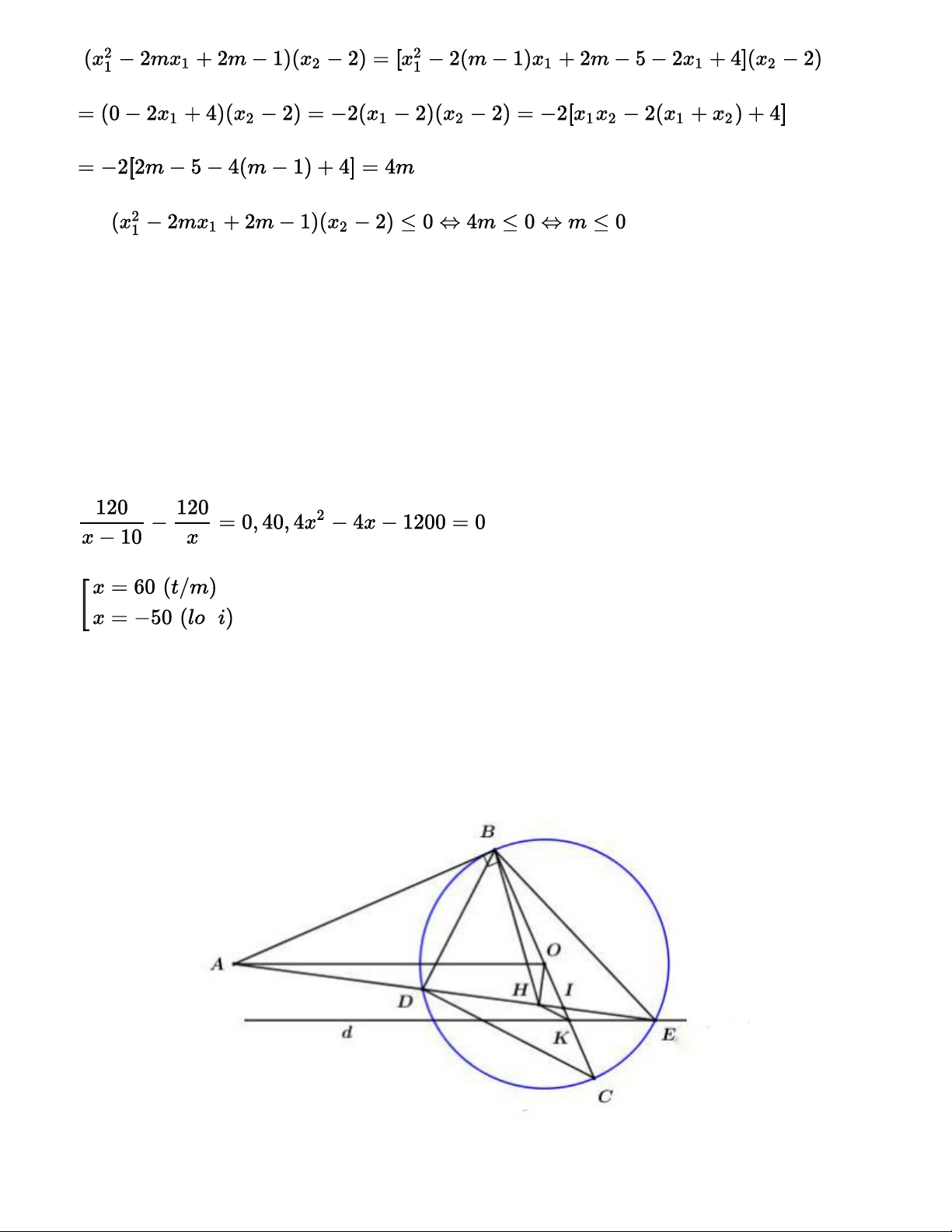
Vậy vận tốc của 2 xe ô tô lần lượt là 60 km/h và 50 km/h Câu 4. Hình vẽ: a.
Vì AB là tiếp tuyến của (O) tại B => ∠ABD = ∠BED = ∠BEA (góc tạo bởi tiếp tuyến và dây cung
và góc nội tiếp cũng chẳn cung BD)
Xét △ABD và △AEB có: ∠ABD = ∠BEA (cmt) và ∠BAD chung => △ABD ∽△AEB (g.g) => => AB.BE = AE.BD b.
Vì AB là tiếp tuyến của (O)=> OA⊥AB=> OBA = 90°. DE là dây cung của (O) mà H là trung điểm của DE
=> OH⊥ DE => ∠OHA = 90°.
Xét tứ giác ABOH có: ∠OHA + ∠OBA = 90° + 90° =180° nên tứ giác ABOH nội tiếp.
=> ∠HAO = ∠HBO (hai góc cùng chắn một cung (1)
Mà EK // AO => ∠KEA = ∠ HAO (hai góc sole trong) (2)
Từ (1) và (2) => ∠KEH = ∠KBH. => Tứ giác HKEB nội tiếp (dấu hiệu tứ giác nội tiếp) => ∠EHK = ∠KBE. (3)
Vì tứ giác DCEB nội tiếp => ∠CDE = ∠CBE (hai góc cùng chắn cung CE). (4)
Từ (3) và (4)=> ∠CDE = ∠KHE mà hai góc nằm ở vị trí đồng vị HK // DC.



