SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 TỈNH QUẢNG NAM
THPT CHUYÊN VÀ PTDTNT TỈNH NĂM HỌC 2024-2025 ĐỀ CHÍNH THỨC Môn thi: Toán (chuyên)
Thời gian: 150 phút (không kể thời gian giao đề)
Khóa thi ngày: 04 - 06/6/2024 Câu 1. (2,0 điểm) x  2 x  3 1 a) Cho biểu thức A   
, với x  0, x  4 và x  9 . Rút gọn x  3 x  2 x  5 x  6
biểu thức A và tìm tất cả các giá trị của x sao cho A  1  . b) Cho parabol   2
P : y  x và điểm A thuộc P có hoành độ bằng 2 . Đường thẳng d
đi qua điểm B0;3 , song song với OA (O là gốc tọa độ) và cắt P tại hai điểm M, N.
Tìm tọa độ của M và N, biết M có hoành độ âm. Câu 2. (2,0 điểm) a) Giải phương trình 2 2
x  x  x  3  x  2  2x  5 . 2 3
 xy  y  2x 10y 1  0 
b) Giải hệ phương trình  . 2 3xy  y  2x  2 1  21y  0 Câu 3. (2,0 điểm)
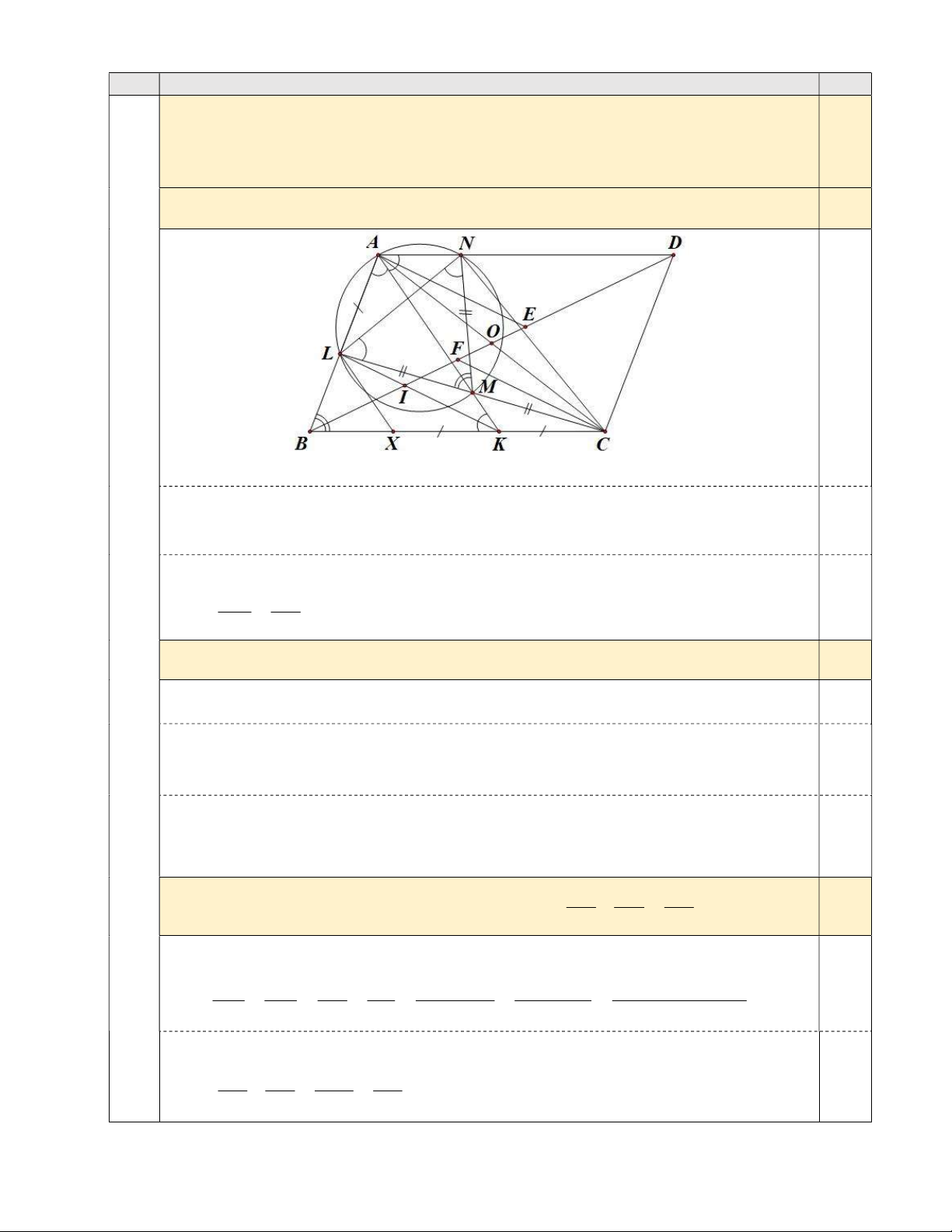
Cho hình bình hành ABCD có góc BAD là góc tù, AB  AD và tia phân giác của góc BAD
cắt cạnh BC tại K sao cho CK  AB. Trên cạnh AB lấy điểm L sao cho AL  CK. Hai đoạn
thẳng AK và CL cắt nhau tại M. Đường tròn ngoại tiếp tam giác ALM cắt đường thẳng AD tại N (N khác A).
a) Chứng minh AB.NL  AK.NM . b) Chứng minh  CNL  90. BA BC BD
c) Gọi I là giao điểm của BD và KL, chứng minh   . BL BK BI Câu 4. (2,0 điểm)
Cho tam giác nhọn ABC (AB  AC) có AE là đường phân giác (E thuộc cạnh BC).
Trên đường thẳng đi qua A và vuông góc với AE lấy điểm D sao cho góc BCD bằng 90.
Trên cạnh AB lấy điểm F sao cho góc DEF bằng 90 . 
a) Chứng minh tứ giác ADCE nội tiếp đường tròn và 2 BE  BA.BF .
b) Gọi O là tâm đường tròn ngoại tiếp tam giác AEF, đường thẳng đi qua E và song song
với AC cắt cạnh AB tại P. Chứng minh OP vuông góc với AE và điểm O thuộc đường thẳng BD. Câu 5. (2,0 điểm)
a) Cho ba số tự nhiên a,b, c thỏa mãn a  1, b  c  1 và abc  1 chia hết cho ab  b  1.
Chứng minh b chia hết cho a .  
b) Cho ba số thực dương , x , y z thỏa mãn x 1 y 1 6  
. Tìm giá trị nhỏ nhất của x  3 y  4 z  5
biểu thức P  2x  22 y  32z  4. ---------- HẾT ----------
* Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
* Họ và tên thí sinh: ………………………………….. Số báo danh: ……........
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 TỈNH QUẢNG NAM
THPT CHUYÊN VÀ PTDTNT TỈNH NĂM HỌC 2024 - 2025 HDC CHÍNH THỨC
(Hướng dẫn chấm có 07 trang)
HƯỚNG DẪN CHẤM MÔN TOÁN (chuyên) Câu Nội dung Điểm x  2 x  3 1 a) Cho biểu thức A   
, với x  0, x  4 và x  9 . x  3 x  2 x  5 x  6 1,0
Rút gọn biểu thức A và tìm tất cả các giá trị của x sao cho A  1  .    x  2  x x x  2 2 3 1 2 3 1 A     0,25 x  3
x  2  x  3 x  2  x 3 x 2
x  4 x  4  x 6 x  9 1 2 x  4 2     0,25 x  3 x  2
 x  3 x 2 x 3 2 2 x 1 A  1    1   1 0   0 x  3 x  3 x  3  0,25  x 1  0 x  1 Trường hợp 1:     x  9 (nhận).  x  3  0 x  9  Câu  x 1  0 0  x  1 Trường hợp 2:     0  x  1 (nhận). 1  x  3  0 0  x  9 0,25
Vậy x  9 hoặc 0  x 1. b) Cho parabol   2
P : y  x và điểm A thuộc P có hoành độ bằng 2  . Đường
thẳng d đi qua điểm B0;3 , song song với OA (O là gốc tọa độ) và cắt P tại hai 1,0
điểm M, N. Tìm tọa độ của M và N, biết M có hoành độ âm.
Tung độ điểm A là y    2 2
 4 , suy ra A 2;4. 0,25
Đường thẳng OA: y  2x . Gọi đường thẳng d: y  ax  b.
Vì (d) song song OA nên hệ số góc a  2, b  0 . Vì (d) đi qua B0;3 nên b  3. 0,25
Suy ra d: y  2x  3.
Các hoành độ của M và N là các nghiệm của phương trình: 2 x  2x  3 2  x  2x  3  0 0,25
Phương trình này có 2 nghiệm: x 1, x  3 .
Vì M có hoành độ âm nên M 3;9 và N 1;  1 . 0,25 Trang 1/7 Câu Nội dung Điểm a) Giải phương trình 2 2
x  x  x  3  x  2  2x  5 (1) 1,0 2 2  1  11 x  x  3  x    0   với mọi x   .  2  4 0,25 5
Điều kiện: 2x  5  0  x   . 2  2x  x3  2x5 2      2 2
1  x  x  2 x  x 3  2x 5  0  x  x  2   0 0,25 2 x  x  3  2x  5 2 x  x  2 2  x  x  2   0 2 x  x  3  2x  5  1    2 x  x  2 1     0 0,25 2  x  x  3  2x  5  1 5 2
 x  x  2  0 (vì 1  0 với mọi x   ) 2 x  x  3  2x  5 2
Phương trình này có 2 nghiệm: x  1
 , x  2 (thỏa mãn điều kiện). 0,25
Vậy phương trình đã cho có 2 nghiệm: x  1  , x  2. Câu 2 2 3
 xy  y  2x 10y 1  0 
b) Giải hệ phương trình  (1) 1,0 2 3xy  y  2x  2 1  21y  0  1 x 
- Xét y  0: Hệ (1) có nghiệm  2 0,25  y   0 2   3xy  y 2x 1 2     xy  y   x  10 3 2 1  10y y y - Xét y  0 : Hệ (1)      (2) 2  3xy  y  2x  2 2 1  21y 
 3xy  y  2x 1    21     y 0,25    y  2   a  b  10 Đặt 3xy y 2x 1 a  , b  , hệ (2) trở thành:  y y ab  21 a  7 a  3   hoặc  b  3 b  7  2 3xy  y   7 0,25 a  7 2        Với y 3  xy y 7 y 3  x y 7 x 2  , ta có    b  3      2x 1 2x 1  3y 2x  3y 1 y 1  3     y  Trang 2/7 2 3xy  y  22    3 a  3 2 x          Với y 3xy y 3y 3x y 3   , ta có 23        b   7 2x 1  2x 1  7y 2x  7 y  1 3  7 y   y  23 0,25  22  1 x  x  x  2 
Vậy hệ phương trình đã cho có 3 nghiệm: 23  2 ,  ,  .  y 1 3 y   0  y   23 Cách khác giải câu 2b) u   v 10y Đặt 2
u  3xy  y , v  2x 1, hệ (1) viết lại: 
, khi đó u, v thỏa mãn phương 2 u  v  21y  X  7 y trình: 2 2
X 10 y.X  21y  0   X  7 y X  3y  0   .  X  3y  1 u   7y 2    x  x  2 + Với 3xy y 7 y    , tìm được nghiệm  2 ,  . v   3y 2x 1  3y  y 1 y   0  22  1 x  u   3y 2  x   + Với 3  xy  y  3y 23    , tìm được nghiệm  2 ,  . v  7 y 2x 1  7y  3 y   0  y   23  22  1 x  x  x  2 
Kết luận hệ phương trình đã cho có 3 nghiệm: 23  2 ,  ,  .  y 1 3 y   0  y   23 Trang 3/7 Câu Nội dung Điểm
Cho hình bình hành ABCD có góc BAD là góc tù, AB  AD và tia phân giác của
góc BAD cắt cạnh BC tại K sao cho CK  AB. Trên cạnh AB lấy điểm L sao cho
AL  CK. Hai đoạn thẳng AK và CL cắt nhau tại M. Đường tròn ngoại tiếp tam giác 2,0
ALM cắt đường thẳng AD tại N (N khác A).
a) Chứng minh AB.NL  AK.NM 0,75 0,25
Hình vẽ phục vụ câu a): 0,25 điểm
Tứ giác ALMN nội tiếp đường tròn nên  BAK   MNL (1) 0,25 Ta có:  ABK  180   LAN   NML (2) Từ (1) và (2) suy ra A  BK và N  ML đồng dạng. Câu AB AK 0,25   3 Do đó hay AB.NL AK.NM . NM NL b) Chứng minh  CNL  90. 0,75 Vì  NAM   LAM nên NM  LM (3) 0,25
Kẻ LX // AK , X thuộc BC. Vì  AKX   KAD  
KAL nên tứ giác ALXK là hình thang 0,25
cân, suy ra XK  AL  CK .
Tam giác CLX có XK  CK và MK // XL nên LM  CM (4) 0,25
Từ (3) và (4) suy ra NM  LM  CM . Do đó C  NL vuông tại N hay  CNL  90. BA BC BD
c) Gọi I là giao điểm của BD và KL, chứng minh   . 0,5 BL BK BI
Kẻ AE // KL và CF// KL (E, F thuộc BD) , gọi O là giao điểm của AC và BD, BA BC BE BF BO  OE BO  OF 2BO  OE  OF 0,25 ta có:       BL BK BI BI BI BI BI
Hai tam giác AOE và COF bằng nhau (g-c-g), suy ra OE  OF . BA BC 2BO BD 0,25 Do đó    . BL BK BI BI Trang 4/7
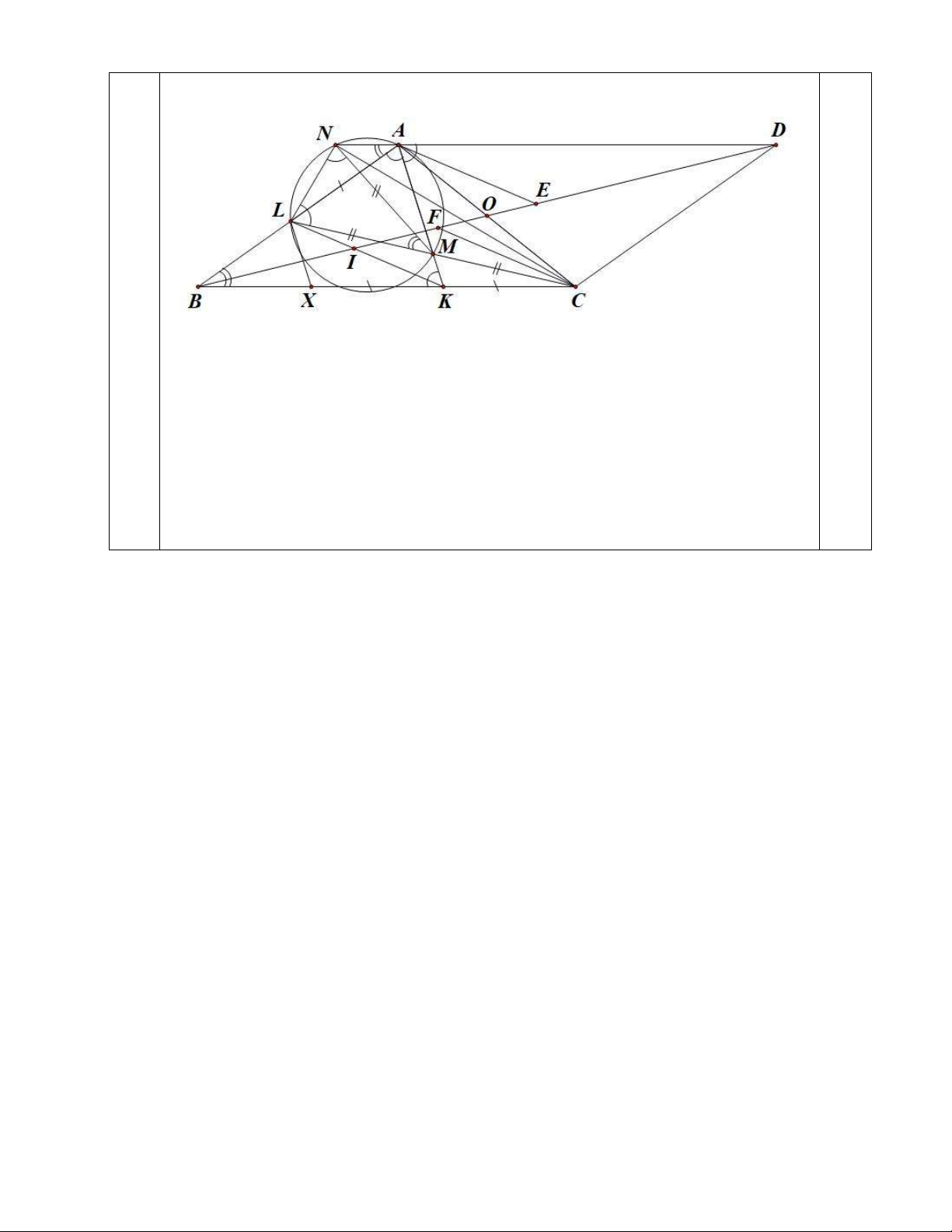
Với hình vẽ sau, cách chứng minh (1), (2), (3): Câu a)
Tứ giác AMLN nội tiếp đường tròn nên  BAK   MNL (1)  ABK   NAL ,  NAL   NML   ABK   NML (2) Câu b)  MLN  
MAD (do tứ giác AMLN nội tiếp đường tròn)   MAL   MNL Suy ra N
 ML cân tại M hay NM  LM (3) Trang 5/7 Câu Nội dung Điểm
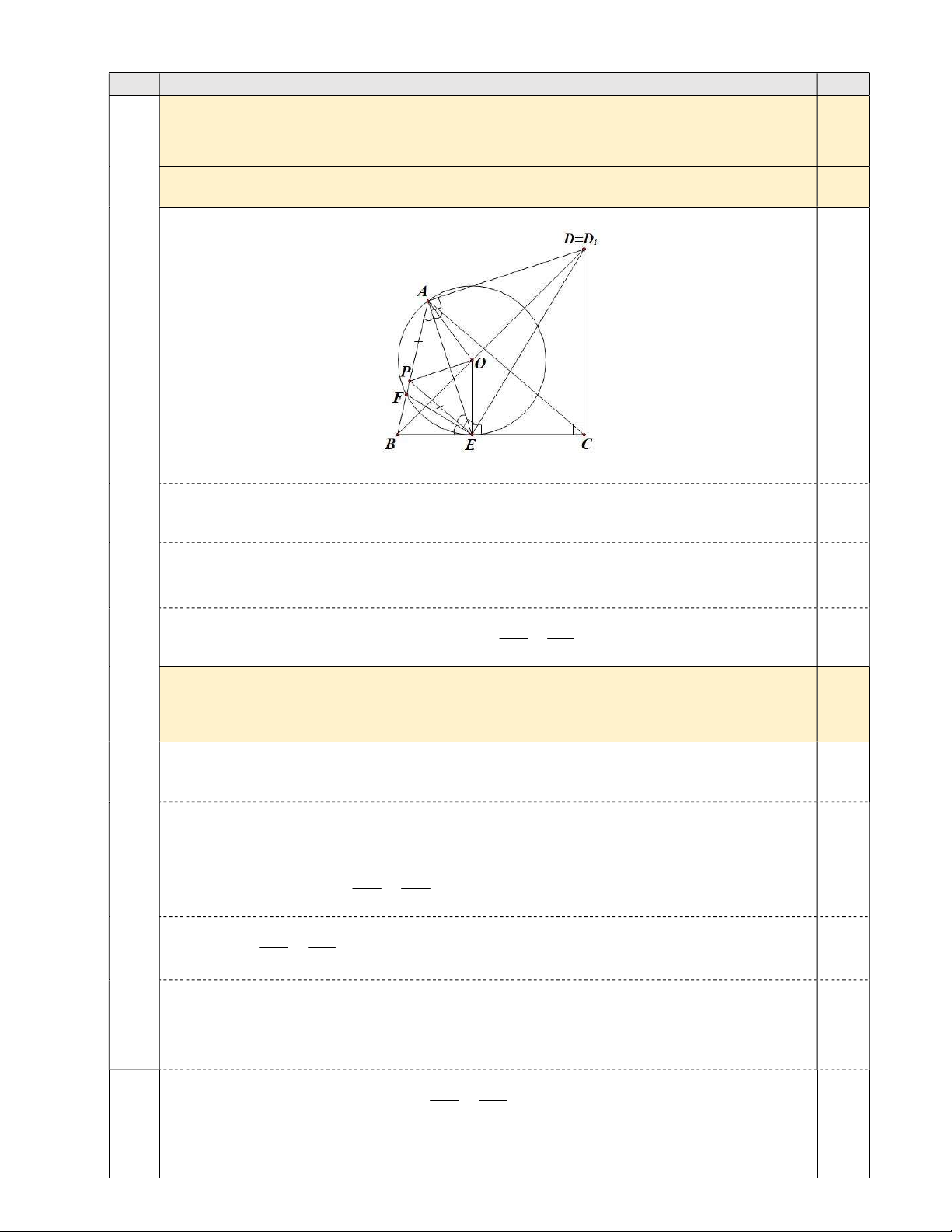
Cho tam giác nhọn ABC (AB  AC) có AE là đường phân giác (E thuộc cạnh BC).
Trên đường thẳng đi qua A và vuông góc với AE lấy điểm D sao cho góc BCD bằng 90. 2,0
Trên cạnh AB lấy điểm F sao cho góc DEF bằng 90 . 
a) Chứng minh tứ giác ADCE nội tiếp đường tròn và 2 BE  BA.BF. 1,0 0,25
Hình vẽ phục vụ câu a): 0,25 điểm Theo giả thiết:  DAE  90 và  DCE  90 . Vì  DAE  
DCE  180 nên tứ giác ADCE 0,25
nội tiếp đường tròn (đường kính DE).  BAE   Câu CAE ,  CAE  
CDE (cùng chắn cung CE của đường tròn đường kính DE), 0,25 4 
CDE  180  90   CED   BEF   BAE   BEF . BA BE Do đó B  AE và B
 EF đồng dạng. Do đó  hay 2 BE  BA.BF. 0,25 BE BF
b) Gọi O là tâm đường tròn ngoại tiếp tam giác AEF, đường thẳng đi qua E và song
song với AC cắt cạnh AB tại P. Chứng minh OP vuông góc với AE và điểm O thuộc 1,0 đường thẳng BD. Vì  AEP   EAC   EAP nên A
 EP cân tại P hay PA  PE . Vì PA  PE và OA  OE 0,25
nên OP là đường trung trực của đoạn thẳng AE. Suy ra OP  AE . Vì  BEF  
BAE (theo câu a)) nên BE là tiếp tuyến của đường tròn ngoại tiếp A  EF,
suy ra OE  BC  OE // CD . Vì OP // DA, OE // DC, EP // CA nên O  EP đồng 0,25 OE EP dạng với D  CA, suy ra  . (1) DC CA EP BE EP // CA   BE OE
(2). Giả sử BO cắt CD tại D ; OE // D C   (3) 0,25 CA BC 1 1 BC 1 D C OE OE Từ (1), (2) và (3) suy ra 
 DC  D C , mà D và D nằm cùng phía đối với 1 DC D C 1 1 0,25
đường thẳng BC nên D trùng D . Vậy điểm O thuộc đường thẳng BD. 1 OE BE
Cách khác: Từ (1) và (2) suy ra  , mà  BEO   BCD  90 nên B  EO và DC BC B
 CD đồng dạng. Suy ra  EBO  
CBD , mà O và D nằm cùng phía đối với đường
thẳng BC nên hai tia BO và BD trùng nhau. Vậy điểm O thuộc đường thẳng BD. Trang 6/7 Câu Nội dung Điểm
a) Cho ba số tự nhiên a, b, c thỏa mãn a  1, b  c  1 và abc  1 chia hết cho 1,0
ab  b  1 . Chứng minh b chia hết cho a . Ta có: abc   1  ab  b   1  bac  a   1 0,25
Vì abc  1ab  b  1 nên b ac  a  1ab  b  1 1
Vì ab  b  1  a 1b  1 nên ab  b  1 và b là hai số nguyên tố cùng nhau. 0,25
Do đó 1  ac  a  1ab  b  1 hay ac  a    k ab  b   * 1 . 1 , k   . (2)
Ta có: ac  a 1  a c   1 1  0 . 2ab  b   1  ac  a  
1  ab  ac  ab  2b  a  1  0,25
a b  c  a  2b  a 1  0.
Do đó 0  ac  a 1  2ab  b  
1  0  k.ab  b   1  2ab  b   1  k  1 (3)
Từ (2) và (3) suy ra: ac  a  1  ab  b  1  b  ab  ac  a  a b  c   1  b  a . 0,25  
b) Cho ba số thực dương , x , y z thỏa mãn x 1 y 1 6  
. Tìm giá trị nhỏ nhất x  3 y  4 z  5 1,0
của biểu thức P  2x  22 y  32z  4 . Câu x 1 y 1 6 4 5 6    4 5 6 0 1 1   0     2 5 x  3 y  4 z  5 x  3 y  4 z  5 x  3 y  4 z  5 2x  2 4 5 6 5 6 0,25 Ta có:  2     2 .   1 x  3 x  3 y  4 z  5 y  4 z  5
(Bất đẳng thức a  b  2 ab cho hai số a, b không âm) 2 y  3 5 4 6 4 6 Tương tự ta có:  2     2 . 2 y  4 y  4 x  3 z  5 x  3 z  5 0,25 2z  4 6 4 5 4 5  2     2 . 3 z  5 z  5 x  3 y  4 x  3 y  4
Nhân (1), (2) và (3) vế theo vế, ta được: 2x  2 2y  3 2z  4 4.5.6 . .  8.
 2x  22y  32z  4  960 0,25 x  3 y  4 z  5
x  3 y  4z  5  4 5 6 x  3    2    x  3 y  4 z  5  7 Đẳng thức xảy ra khi 4 5 6 2       y  4 5 6 x  3 y  4 z  5 3  2    0,25  x  3 y  4 z  5 z  4  7
Vậy giá trị nhỏ nhất của biểu thức P là 960, đạt được khi x  3, y  , z  4. 2 ---------- HẾT ----------
* Lưu ý: Nếu thí sinh làm bài không theo cách nêu trong HDC nhưng đúng thì vẫn cho đủ số
điểm từng phần như HDC quy định. Trang 7/7