SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 TỈNH QUẢNG NAM
THPT CHUYÊN VÀ PTDTNT TỈNH NĂM HỌC 2024 - 2025 ĐỀ CHÍN H THỨC
Môn thi: Toán (chuyên Tin học)
Thời gian: 150 phút (không kể thời gian giao đề)
Khóa thi ngày: 04 - 06/6/2024 Câu 1. (1,5 điểm)  3 3   x 1 x  2  Cho biểu thức P   :    
 với điều kiện x  0, x  1, x  4 . x 1 x  x  2 x 1      a) Rút gọn biểu thức . P
b) Tìm tất cả các giá trị của x để P  3  . Câu 2. (1,5 điểm)
a) Tìm tất cả các nghiệm nguyên  x; y của phương trình 6xy  3x  2y 8  0 .
b) Cho A  9m  2024n.2024m  9n với m và n là hai số nguyên dương. Chứng minh
rằng nếu A chia hết cho 19 thì A có ít nhất một ước số là số chính phương khác 1. Câu 3. (1,5 điểm) 3 x  y 1  5
a) Giải hệ phương trình   x  y 1  3 .  b) Giải phương trình 2
x  x  2  2 x 11 x . Câu 4. (1,0 điểm)
Trên cùng mặt phẳng toạ độ Oxy, cho parabol P 2
: y  x và đường thẳng d : y  3x  3m 1.
Tìm tất cả các giá trị của m để P và d  cắt nhau tại hai điểm phân biệt có hoành độ x ; x thoả 1 2 mãn 2 2 x  x  x x 10. 1 2 1 2 Câu 5. (3,5 điểm)
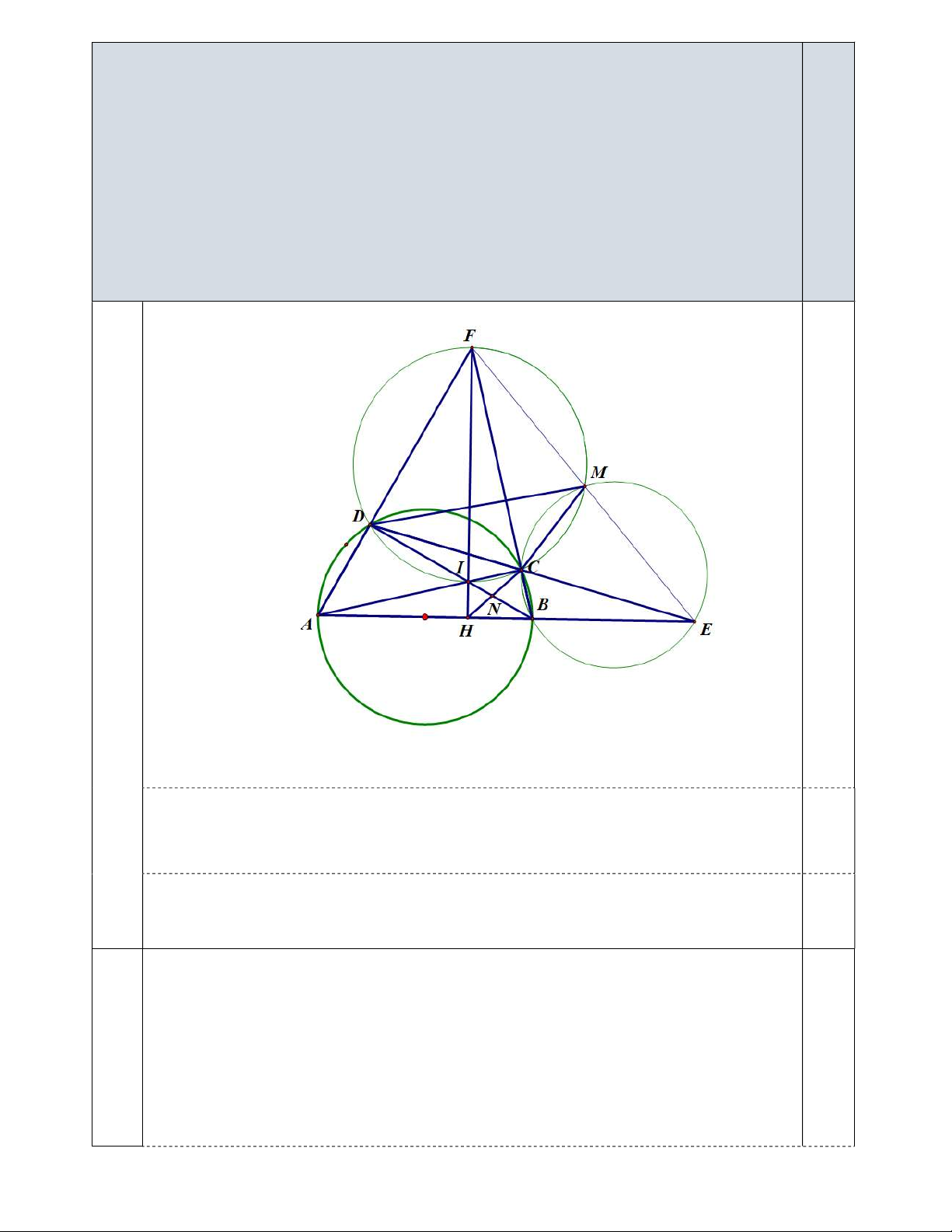
Cho tứ giác ABCD có hai cặp cạnh đối không song song và tứ giác đó nội tiếp đường tròn
O có đường kính A .
B Gọi E là giao điểm của hai đường thẳng AB và C , D F là giao điểm của
hai đường thẳng AD và BC. Hai đường chéo AC và BD cắt nhau tại I. Qua I kẻ đường thẳng
vuông góc với đường thẳng AB và cắt đường thẳng AB tại H.
a) Chứng minh tứ giác BCIH nội tiếp một đường tròn.
b) Đường tròn ngoại tiếp tam giác BCE cắt đường tròn ngoại tiếp tam giác CDF tại điểm
thứ hai là M . Chứng minh ba điểm E, M , F thẳng hàng.
c) Gọi N là giao điểm của hai đường thẳng CH và BI. Chứng minh BN.DN  IN BD  BN . Câu 6. (1,0 điểm)
Cho ba số dương x, y, z thoả mãn 2 2 2
x  y  z 1. Chứng minh rằng: 2 2 2 x y z   1.
1 y  x 1 z  y 1 x  z ---------- HẾT ----------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: ………………………………….. Số báo danh: …….........
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 TỈNH QUẢNG NAM
THPT CHUYÊN VÀ PTDTNT TỈNH NĂM HỌC 2024 - 2025 HDC CHÍNH THỨC
HƯỚNG DẪN CHẤM MÔN TOÁN ( CHUYÊN TIN)
(Hướng dẫn chấm có 06 trang) Câu Nội dung Điểm Câu 1.  3 3   x 1 x  2  Cho biểu thức P   :    
 với điều kiện x  0, x  1, x  4 . x 1 x  x  2 x 1      1,5 a) Rút gọn biểu thức . P
b) Tìm tất cả các giá trị của x để P  3  . 1a
3 x 3 x  1  x  1 x  1 x  2 x 2 0,25 P       x  x   : 1    x 2 x     1   3 x 1 x  4  x  x   : 1  x  2 x   1 0,25  x 2 x  1 3  0,25 x  x   . 1 3 x  2  0,25 x 1b x  2 1 P  3    3   x  2  3
 x  x  ( vì x  0 ) 0,25 x 2 1  1
x  . Kết hợp điều kiện ban đầu ta được: 0  x  . 0,25 4 4 Câu 2.
a) Tìm tất cả các nghiệm nguyên  x; y của phương trình 6xy  3x  2y 8  0 . 1,5
b) Cho A  9m  2024n.2024m  9n với m và n là hai số nguyên dương. Chứng minh
rằng nếu A chia hết cho 19 thì A có ít nhất một ước số là số chính phương khác 1.
2a 6xy 3x  2y 8  0  6xy 3x  2y 1 7  2y  1.3x 1  7 0,25
Kẻ bảng các trường hợp 0,25 3x 1 7  1  1 7 2 y 1 1  7  7 1 Trang 1/6
Giải các trường hợp trên với  x; y là cặp số nguyên, ta được các nghiệm của phương trình 0,25
đã cho là: 0;4 và 2;  1 . 2b 9m  2024n 1  9
Giả sử 9m 2024n.2024m  9n 1  9  
, vì 19 là số nguyên tố. 0,25 2024m  9n 1  9
Trường hợp 1: 9m  2024n 1  9
Vì 9m  2024n  2024m  9n  2033m  n 19.107m  n 1  9 nên 2024m9n 1  9 0,25
Do đó, 9m  2024n.2024m  9n19.19 hay 2 A 1  9 .
Trường hợp 2: 2024m 9n 1
 9, tương tự ta cũng thu được  m n  m  n 2 9 2024 . 2024 9 1  9 0,25
Vậy nếu A chia hết cho 19 thì A có ít nhất một ước số là số chính phương khác 1. Câu 3. 3  x  y 1  5
a) Giải hệ phương trình  1,5  x  y 1  3 .  b) Giải phương trình 2
x  x  2  2 x 11 x . 3a x  0 Điều kiện:  . y 1 0 0,25 3
 x  y 1  5 2 x  2 Khi đó     x  y 1  3   x  y 1  3   x 1   0,25  y 1  2  x 1 x 1     ( thoả điều kiện). y 1  4 y  3 0,25
Vậy hệ phương trình đã cho có một nghiệm  ;
x y duy nhất là 1;3 .
3b Điều kiện: x 1 0 . (*) 2
x  x  2  2 x 11 x 2
 x  2x x 1  x  2 x 1  2 0,25 2
 x  2x x 1  x  
1  x  2 x 1   x   1  2
 x  x 12  2x  x 11
 x  x  2  x  x      x  x   2 1 2 1 1 0
1 1  0  x 1  1 x 0,25 Trang 2/6 x 1 1   x  0  x 1     
 x   x  ( thoả điều kiện (*)). x 1   1 x 0 0 2 2 x  3x  0  0,25 x  3
Vậy phương trình đã cho có một nghiệm duy nhất x  0 . Câu 4.
Trên cùng mặt phẳng toạ độ Oxy , cho parabol  P 2
: y  x và đường thẳng d : y  3x  3m 1. 1,0
Tìm tất cả các giá trị của m để  P và d  cắt nhau tại hai điểm phân biệt có hoành độ x ; x thoả 1 2 mãn 2 2 x  x  x x 10. 1 2 1 2
Phương trình hoành độ giao điểm: 2 2
x  3x  3m 1  x  3x  3m 1  0 (1)
để P và d  cắt nhau tại hai điểm phân biệt thì điều kiện là phương trình (1) phải có hai 0,25 13
nghiệm phân biệt x ; x , hay 2   3  43m   1  0  1  2m 13  0  m  . 1 2 12
Khi đó, theo định lí Vi-ét ta có: x  x  3  (2) 1 2  x .x  3m 1 (3) .  0,25 1 2
Theo đề, x  x  x x 10   x  x 2 2 2  2x x  x x 10 (4) 1 2 1 2 1 2 1 2 1 2
Thay (2) và (3) vào (4) ta được: 0,25  2 3  23m  
1  3m 1  10  3m 1  6m 1  1  1 6 1  0 m m  m    6   6  2  3m 1  6m 1    m  0  m  .    m      m   3m 0 9 3 1 6 1    2  9m   2 m  0,25  9 2
So sánh điều kiện ta được m  là giá trị cần tìm. 9 Trang 3/6 Câu 5.
Cho tứ giác ABCD có hai cặp cạnh đối không song song và tứ giác đó nội tiếp đường tròn
O có đường kính A .
B Gọi E là giao điểm của hai đường thẳng AB và CD, F là giao điểm của
hai đường thẳng AD và B .
C Hai đường chéo AC và BD cắt nhau tại I. Qua I kẻ đường thẳng
vuông góc với đường thẳng AB và cắt đường thẳng AB tại H. 3,5
a) Chứng minh tứ giác BCIH nội tiếp một đường tròn.
b) Đường tròn ngoại tiếp tam giác BCE cắt đường tròn ngoại tiếp tam giác CDF tại điểm
thứ hai là M . Chứng minh ba điểm E, M , F thẳng hàng.
c) Gọi N là giao điểm của hai đường thẳng CH và BI. Chứng minh BN.DN  IN  BD  BN . 5a 0,5
Hình vẽ phục vụ giải câu 5a): 0,5 Ta có: 
IHB  90 ( vì IH  AB ) 0,25 
ICB  90 ( vì C thuộc nửa đường tròn O ) 0,25 Tứ giác BCIH có  IHB  
ICB  90  90  180 nên nội tiếp được đường tròn. 0,25 5b  DMC  
AFB ( cùng chắn cung DC của đường tròn ngoại tiếp tam giác DFC ) 0,25  CME   ABF ( cùng bù với  CBE ) 0,25  FMD  
DCF ( cùng chắn cung DF của đường tròn ngoại tiếp tam giác DFC ) và  DCF   FAB ( cùng bù với  DCB ) 0,25 Suy ra  FMD   FAB Trang 4/6 Có:  FME   FMD   DMC   CME   FAB   AFB  
ABF  180 ( tổng ba góc trong của tam giác) 0,25 Nên E, M , F thẳng hàng. 5c Ta có:  ICH  
DBA ( cùng chắn cung IH của đường tròn ngoại tiếp tứ giác BCIH ) 0,25  DCA  
DBA ( cùng chắn cung AD của đường tròn O ) Suy ra  DCA  
ICH . Do đó, CI là đường phân giác trong của tam giác CDN . 0,25
Vì CI  CB nên CB là đường phân giác ngoài của tam giác CDN . 0,25 ID BD CD Từ đó, ta có   . 0,25 IN BN CN Suy ra ID BD   B . D IN  BN.ID  B . D IN  BN.DN  IN  0,25 IN BN  BN.DN  B .
D IN  BN.IN  BN.DN  IN BD  BN  Câu 6.
Cho ba số dương x, y, z thoả mãn 2 2 2
x  y  z  1. Chứng minh rằng: 1,0 2 2 2 x y z   1.
1 y  x 1 z  y 1 x  z
Từ giả thiết suy ra 0  x  1, 0  y  1, 0  z  1. Ta có: 2 x 1     x  y x2 2 2 x  
1 y  x1 y  x 2 2 2 3  
 x 1 y  x  x  x y  x 1 y  x 1 y  x 1 y  x 0,25 (vì     2 1 1 y x ) 2 y Tương tự: 2 2 3  y  y z  y 1 z  y 2 z 2 2 3  z  z x  z 1 x  z Do đó: 2 2 2 x y z 3 3 3 2 2 2  
 x  y  z  x y  y z  z x 1 (vì 2 2 2 x  y  z  1).
1 y  x 1 z  y 1 x  z 0,25 Trang 5/6
Áp dụng bất đẳng thức Cauchy cho 3 số dương, ta có: 3 3 3 3 3 3 2 3
x  x  y  3 x x y  3x y Tương tự: 3 3 3 2 y  y  z  3y z 0,25 3 3 3 2 z  z  x  3z x Suy ra 3 3 3 2 2 2
3x  3y  3z  3x y  3y z  3z x 3 3 3 2 2 2
 x  y  z  x y  y z  z x 3 3 3 2 2 2
 x  y  z  x y  y z  z x  0 0,25 2 2 2 x y z 3 Vậy  
 1. Dấu “=” xảy ra khi x  y  z  .
1 y  x 1 z  y 1 x  z 3 ...........HẾT........... * Lưu ý:
Nếu thí sinh làm bài không theo cách nêu trong hướng dẫn chấm nhưng đúng thì vẫn cho đủ
số điểm từng phần như hướng dẫn quy định. * Cách 2 câu 3b. Giải phương trình 2
x  x  2  2 x 11 x. 0,75
Đặt t  x 1, t  0 thì 2 2
t  x 1  x  t 1 . Phương trình đã cho trở thành t  2 2 1   2t   1  2  2t 1    2t   1 0,25 4 2 3
 t  3t  4  2t  4t 4 3 2
 t  2t  3t  4t  4  0 (1)  t   1  3 2
t  3t  4  0  t   1 t   1  2t  4t  4  0     t  2 t  2 t 1 1 2  0   0,25 t  2 
So sánh điều kiện t  0 ta được t  1 là nghiệm của phương trình (1) .
Với t  1 thì x 1  1  x 1  1  x  0 là nghiệm duy nhất của phương trình đã cho. 0,25 Trang 6/6