


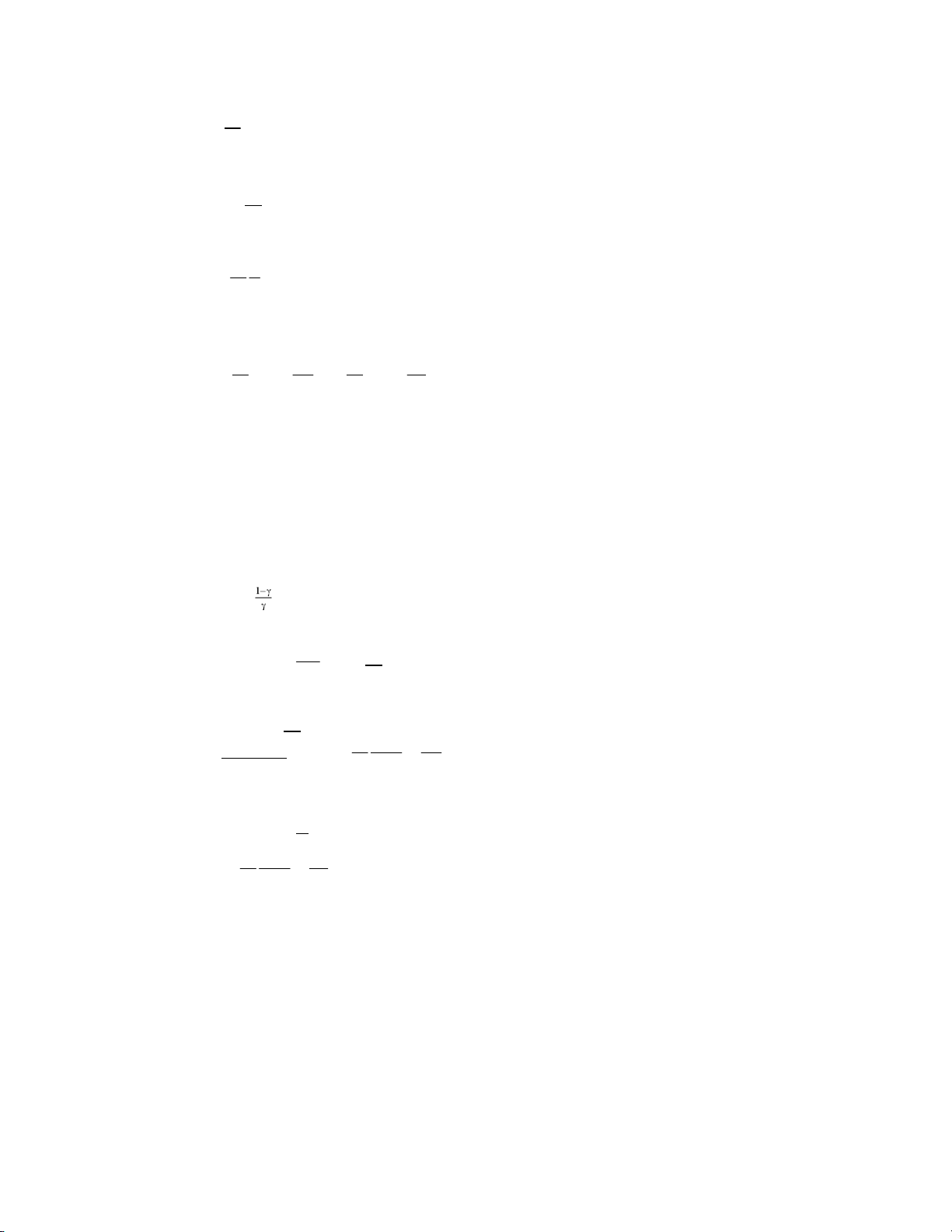



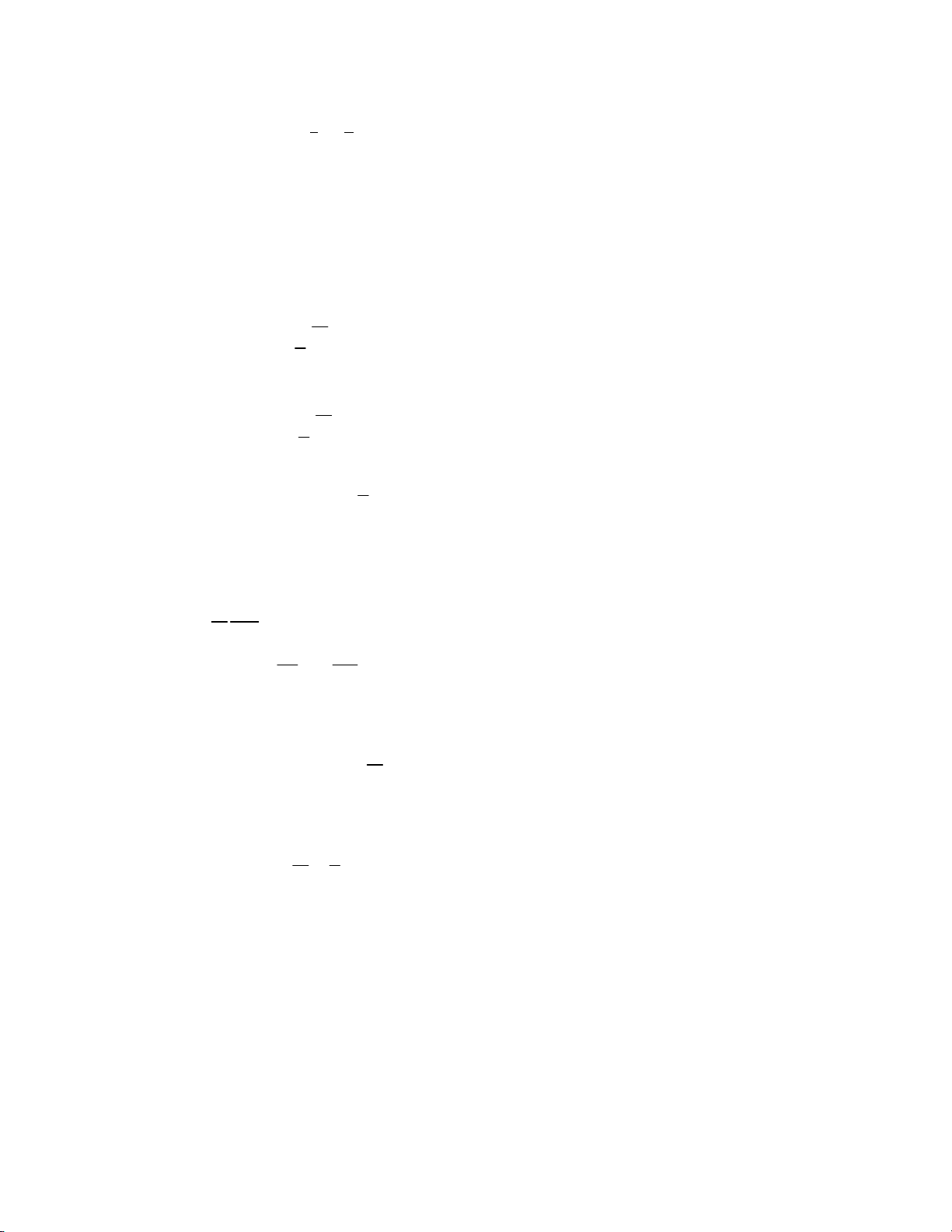





Preview text:
lOMoAR cPSD| 45148588 lOMoAR cPSD| 45148588 Chương 7
NGUYÊN LÝ THỨ NHẤT CỦA NHIỆT ĐỘNG LỰC HỌC
TÓM TẮT LÝ THUYẾT
1. Nguyên lý thứ nhất nhiệt động học ∆U= A + Q
∆U= U2 − U1 là độ biến thiên nội năng của hệ
A và Q là công và nhiệt mà hệ nhận được. ‐ Dưới dạng vi phân: dU= A + Qδ δ
2. Công của áp lực trong quá trình cân bằng V2 = − A ∫ pdV V1
3. Nhiệt trong quá trình cân bằng δQ = m CdT hay δQ = mcdT µ
C nhiệt dung phân tử; c là nhiệt dung riêng với C = cµ
4. Quá trình đẳng tích với khí lí tưởng A = 0 Q = m C ∆ V T µ C = i V R ; R = 8,31 J 2 molK ∆U= Q = m i R T∆ µ 2
5. Quá trình đẳng áp với khí lý tưởng A=−p V V( ) 2 − 1 =− ∆p V 1 lOMoAR cPSD| 45148588 Q = m C ∆ P T µ C = P i + 2 R 2 ∆U = m i R T∆ µ 2
6. Quá trình đẳng nhiệt
A = m RTln V1 = m RTln p2 µ V2 µ p 1 Q = −A ∆U = 0
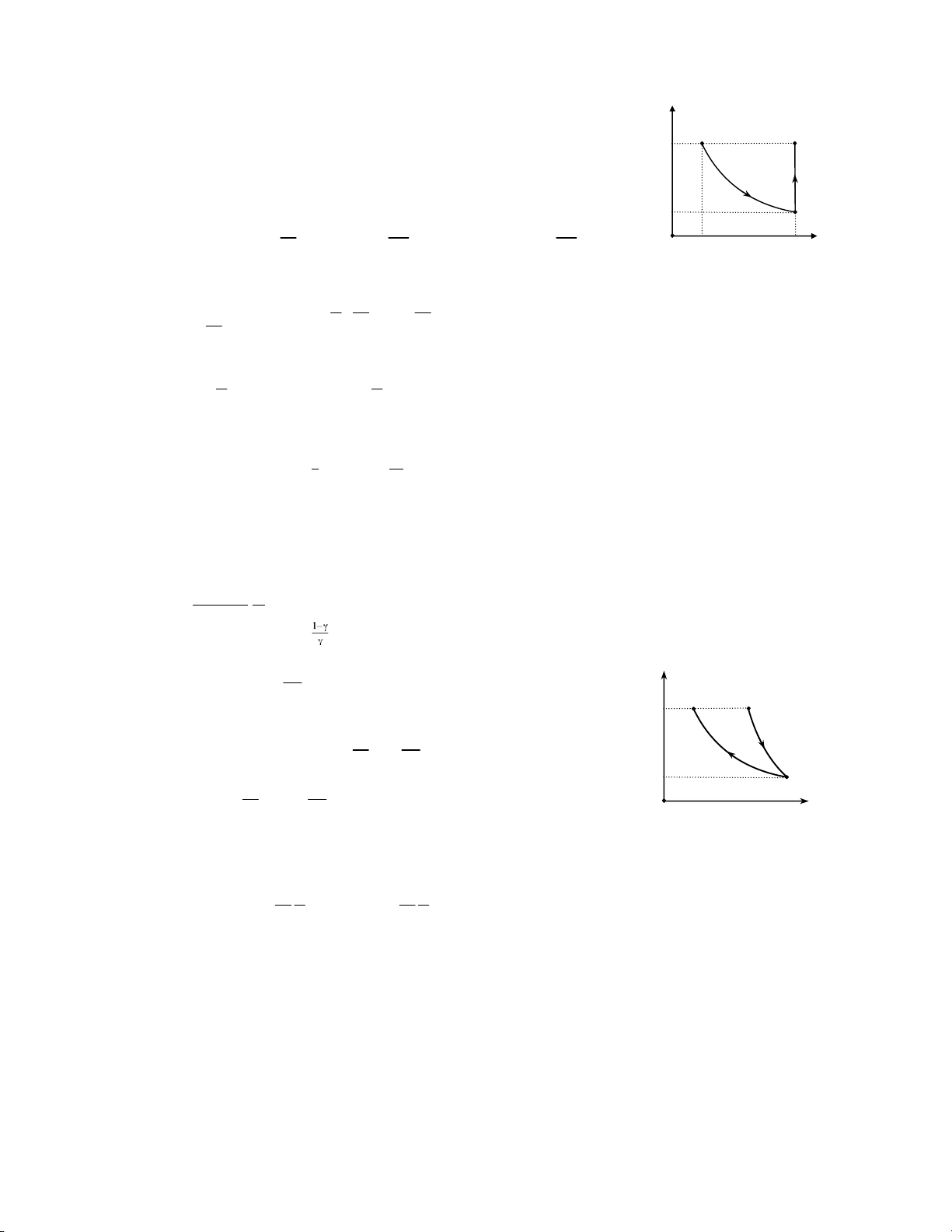
7. Quá trình đoạn nhiệt (δQ = 0)
‐ Phương trình: pVγ = const TVγ−1 = const Tp = const
‐ Hệ số Poát xông: γ = Cp = i + 2 CV i p V − p V ‐ Công:A = 2 2
1 1 = m RT1 ⎢⎡⎛⎜ V1 ⎞⎟γ−1 −1⎤⎥ γ −1 µ γ −1⎢⎣⎝ V2 ⎠ ⎥⎦ ⎡ γ−1 ⎤
A = mµ γ −RT11⎢⎢⎜⎛ pp2 ⎟⎞ γ −1⎥⎥ ⎢⎣⎝ 1 ⎠ ⎥⎦ U ∆ = A BÀI TẬP VÍ DỤ
Xét quá trình dãn một khối khí lí tưởng từ trạng thái (p ,V ,T ) 1 1 1 đến trạng thái 2 lOMoAR cPSD| 45148588 (p ,V ,T ) 2 2 2
. Trong quá trính biến đổi đó áp suất và thể tích của khí biến thiên theo qui luật
pVk = const với k là một hằng số dương. Hỏi với những giá trị nào của k thì: a. Khối khí nhận nhiệt và nóng lên.
b. Khối khí nhận nhiệt và bị lạnh đi. c. Khối khí toả nhiệt. Lời giải
‐ Độ biến thiên nội năng của khối khí trong quá trình dãn: = nR ∆U = nC ( ) V∆T
T2 −T1 (n là số mol khí, γ là hệ số Poátxông) γ −1
‐ Công mà khối khí nhận được: V2 V2 A = −∫ pdV = −p V ∫ ) 11k dVVk = p V2 k2 −−1p V1 1 = knR−1(T2 −T1 V1 V1
‐ Nhiệt mà khối khí nhận được:
Q = ∆U −A = nR ( k)(− γ )(T − ) 2 T1 γ −1 k −1
‐ Độ biến thiên nhiệt độ trong quá trình dãn: Theo giả thiết pVk = const ⇒ TVk−1 = const .
Trong quá trình dãn thể tích tăng, vì vậy:
+ Nếu k >1 nhiệt độ giảm ∆T = T2 −T1 < 0 + Nếu
k <1 nhiệt độ tăng ∆T = T2 −T1 > 0
‐ Bảng xét dấu: k 1 γ ∆T + 0 − − − k − γ − − − 0 + (γ−1)(k −1) − 0 + + + Q + + 0 − ‐ Kết luận:
a. k <1 thì Q > 0, T∆ >0: khối khí nhận nhiệt và nóng lên. 3 lOMoAR cPSD| 45148588
b. 1< k < γ thì Q > 0, T∆ <0: khối khí nhận nhiệt và lạnh đi.
c. k > γ thì Q < 0 khối khí toả nhiệt. BÀI TẬP ÁP DỤNG 8.1.
Khi giảm thể tích của khối khí ôxy từ V1 = 20lít đến V2 =10lít thì áp suất khí
tăng từ p1 =105 N/m2 đến p2 = 2,5.105 N/m2. Hỏi nội năng của khí thay đổi bao nhiêu. 8.2.
Có 10g khí O2 ở nhiệt độ 100C và áp suất 3at. Sau khi hơ nóng đẳng áp, thể
tích tăng lên đến 10 lít. Tính:
a. Nhiệt lượng khối khí nhận được
b. Độ biến thiên nội năng của khối khí
c. Công do khối khí sinh ra khi dãn nở
8.3. Một bình kín chứa 2,5lít Hyđrô ở nhiệt độ 17oC và áp suất 15.103N/m2. Người ta làm
lạnh Hyđrô đến 0oC. Tính:
a. Lượng nhiệt Q’ mà chất khí nhả ra
b. Độ tăng nội năng ∆U của khối khí
8.4. Một kilômol khí được đốt nóng đẳng áp từ 17oC đến 75oC, khi đó khí hấp thụ một nhiệt
lượng là 1,2.106J. Tìm: a. Giá trị γ = CP/CV
b. Độ tăng nội năng ∆U của khối khí
c. Công A mà khối khí thực hiện
8.5. Một kilôgam Oxy được nén đoạn nhiệt do đó nhiệt độ tăng từ 20oC đến 100oC. Vẽ quá
trình này trên giản đồ U, T và tính:
a. Độ tăng nội năng ∆U của khối khí
b. Công A’ tiêu tốn khi nén khí
c. Thể tích khí giảm đi bao nhiêu lần 8.6.
Tìm nhiệt dung riêng đẳng áp và nhiệt dung riêng đẳng tích của một hỗn
hợp khí gồm 3 kilômol Ar và 2 kilômol N = 2. Biết µAr = 40 g/mol; µN 28 2 g/mol. 8.7.
Một kmol khí ở nhiệt độ T1 = 300K được làm lạnh đẳng tích tới khi áp suất
bằng nửa áp suất ban đầu. Sau đó khí được dãn đẳng áp sao cho nhiệt độ trở về nhiệt
độ ban đầu. Vẽ quá trình trên giản đồ PV. Tính:
a. Nhiệt lượng Q mà khí đã hấp thụ
b. Công A mà khí đã thực hiện 4 lOMoAR cPSD| 45148588
c. Độ tăng nội năng ∆U của khối khí p C B
8.8. Một khối khí có thể tích V1 = 50 lít, áp suất p1 = 3.105 N/m2 được hơ
nóng đẳng tích để áp suất tăng lên 2 lần, sau đó được dãn đẳng nhiệt tới A D
áp suất ban đầu và cuối cùng được làm lạnh đẳng áp O
trở về thể tích ban đầu. V
a. Biểu diễn quá trình biến đổi trên giản đồ (pV).
b. Tính công mà khí thực hiện trên mỗi quá trình biến đổi.
8.9. Một khối khí Oxy ở trạng thái thứ nhất (A) có thể tích và áp p suất A D
là V1 = 3lít, p1 = 8,2.105 N/m2 biến đổi sang trạng thái thứ hai P1
(B) có V2 = 4,5lít và p2 = 6.105 N/m2. Tìm nhiệt khối khí nhận C B P2
được, công khối khí sinh ra và độ biến thiên nội năng của khối khí
trong các quá trình biến đổi sau: 0 V1
V2 V a. ACB b. ADB
8.10. Một lượng khí có thể tích V1 = 0,39 m3 ở áp suất p1 =1,55.105 N/m2 được dãn nở đẳng
nhiệt đến V2 =10V1 và sau đó được hơ nóng đẳng tích tới áp suất p1 lúc đầu. Biết nhiệt lượng
cung cấp cho quá trình biến đổi đó là 1,5.106J. a. Vẽ đồ thị của quá trình.
b. Tìm só bậc tự do của phân tử khí.
8.11. 14g Nitơ được dãn đoạn nhiệt tới khí áp suất giảm đi 5 lần và sau đó được nén đẳng
nhiệt tới áp suất ban đầu. Biết nhiệt độ ban đầu của Nitơ là T1 = 420 K. Biểu diễn quá trình trên giản đồ pV. Tìm:
a. Nhiệt độ cuối của quá trình.
b. Nhiệt lượng Q' mà khí nhả ra.
c. Độ tăng nội năng ∆U của khối khí.
d. Công A' mà khối khí thực hiện.
8.12. Một khí lí tưởng ở trạng thái ban đầu có thể tích V1 được dãn đến thể tích V2 theo các
quá trình: 1 ‐ Đẳng áp; 2 ‐ Đẳng nhiệt; 3 ‐ Đoạn nhiệt. Vẽ đồ thị của các quá trình này trên
giản đồ pV và UV. Trên cơ sở nghiên cứu các đồ thị, xác định: a. Quá trình nào công thực
hiện bởi chất khí là nhỏ nhất.
b. Độ biến thiên nội năng ∆U trong mỗi quá trình. 5 lOMoAR cPSD| 45148588
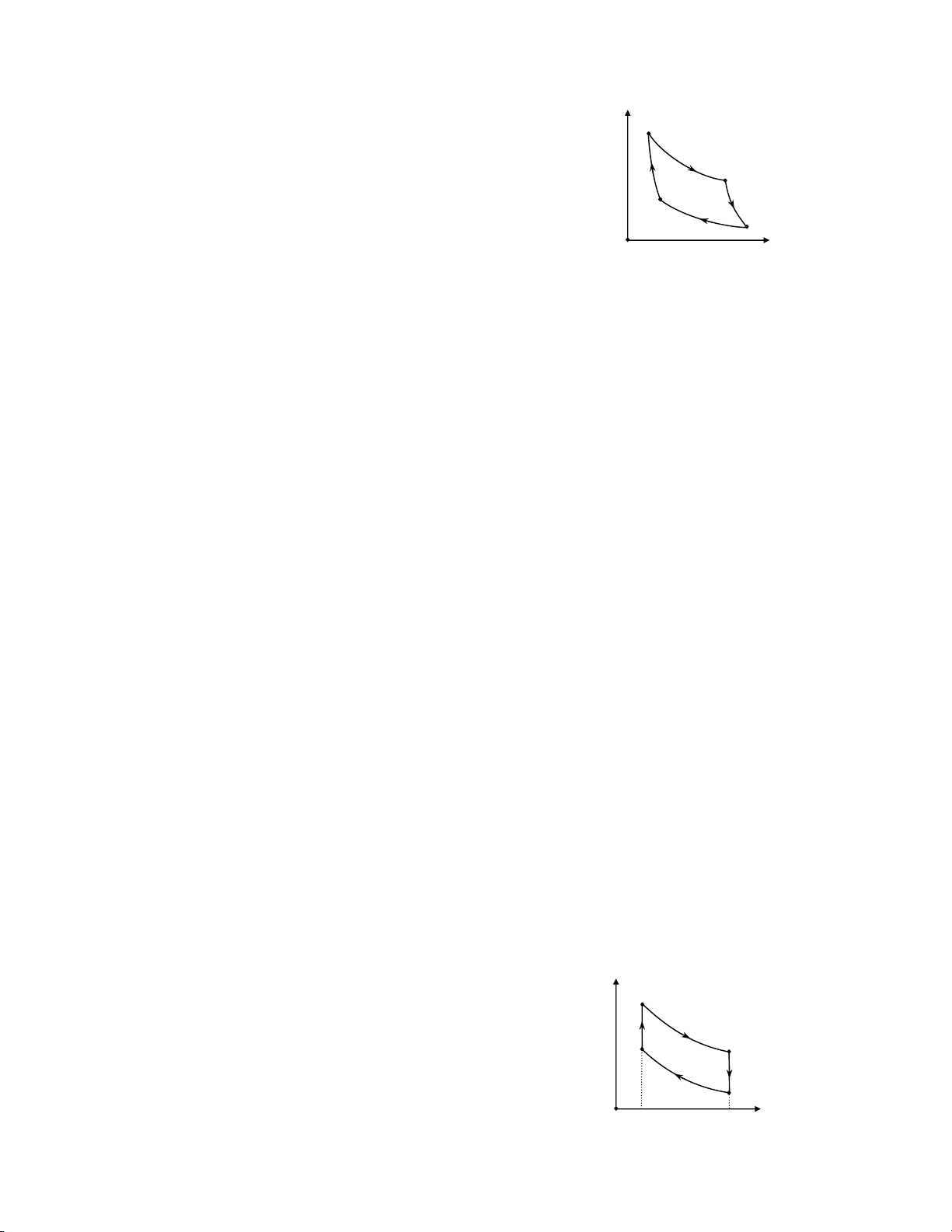
8.13. Một khối không khí (i = 5), thực hiện một chu trình Cácnô p (1)
như trên hình vẽ. Trong đó (1‐2), (3‐4) là hai quá trình đẳng nhiệt T ứng với nhiệt độ T 1
1 và T2; (2‐3) và (4‐1) là hai quá trình đoạn nhiệt. (2)
Biết V1 = 2lít, p1 = 7 at, T1 = 400 K, V2 = 5lít, V3 = 8lít. Hãy tính: (4) T 2 a. p2, p3, T2, p4, V4. (3)
b. Công do khối khí thực hiện trong mỗi quá trình và công trong O V cả chu trình.
c. Nhiệt lượng mà khối khí nhận hay toả ra trong các quá trình đẳng nhiệt.
8.14. Một hệ biến đổi từ trạng thái A sang trạng thái B (hình vẽ). Nếu theo đường ACB, hệ
nhận nhiệt 40kJ và biến 50% lượng nhiệt đó thành công.
a. Nếu hệ biến đổi theo đường ADB thì hệ nhận nhiệt lượng là bao nhiêu? biết rằng trong
quá trình này công mà hệ sinh ra là 7kJ.
b. Khi hệ biến đổi từ B về A theo đường cong như hình vẽ, biết công trao đổi là 15kJ, hệ
nhận hay toả nhiệt và lượng nhiệt đó là bao nhiêu?.
8.15. Xét khối khí trong xilanh đặt thẳng đứng có pít tông di động. Cần phải thực hiện một
công bằng bao nhiêu để nâng píttông lên thêm một đoạn h1 =10 cm. Cho biết chiều cao ban
đầu của cột khí là h0 =15cm, áp suất khí quyển là p0 =105 N/m2, diện tích mặt píttông là
S =10cm2. Bỏ qua trọng lượng píttông và mọi ma sát. Xem rằng nhiệt độ không thay đổi trong quá trình.
8.16. Một khối khí lưỡng nguyên tử ở áp suất p1 =106 N/m2 và thể tích V1 = 3m3 được dãn
nở tới thể tích V2 = 4m3. Tìm áp suất cuối cùng và công do khí sinh ra khi quá trình dãn nở là: a. Đẳng áp. b. Đẳng nhiệt. c. Đoạn nhiệt.
8.17. Một khối khí nitơ được nén từ từ trạng thái ban đầu nào đó sao cho thể tích giảm đi n
= 5 lần. Sự nén được thực hiện bằng hai cách: đẳng nhiệt và đoạn nhiệt. Hỏi: a. Trong quá
trình nào công dùng để nén lớn hơn và lớn hơn bao nhiêu lần.
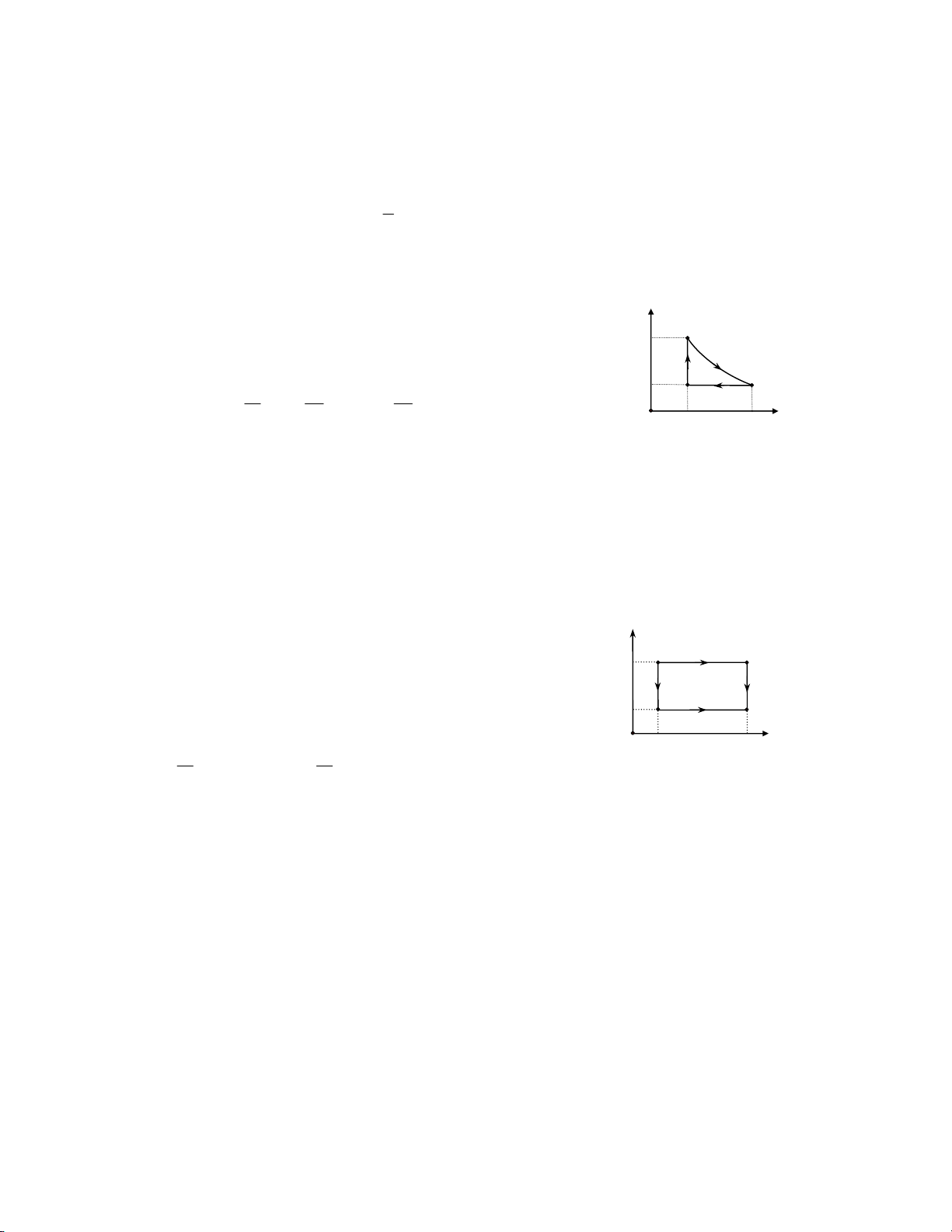
b. Trong quá trình nào nội năng của khối khí tăng và tăng bao p A nhiêu lần. T 1 8.18. B
Có một kilomol khí thực hiện một chu trình như hình vẽ. D
Trong đó AB và CD là hai quá trình đẳng nhiệt ứng với nhiệt độ T 2 T C
1, T2; BC và DA là hai quá trình đẳng tích ở thể tích V2 và V1. Biết T1, T2, V1, V2. 6 lOMoAR cPSD| 45148588 a. Chứng minh p = A pD . O V1 V2 V pB pC
b. Tính công và nhiệt của chu trình.
HƯỚNG DẪN ‐ LỜI GIẢI ‐ ĐÁP SỐ
8.1. Xác định độ biến thiên nội năng của khối khí oxy p V1 1 = m RT1 = 2 U1 µ i p V2 2 = m RT2 = 2 U2 µ i ∆U = U − = i ( − ) = 2 U1 p V22 p V11 1,25.10 J3 2
8.2. Khối khí oxy biến đổi đẳng áp
a. Nhiệt khối khí nhận được V1 =
m RT1 = 2,5.10 m .−3 3 µ P1 T = V2 = 10 2 T1 283 =1132 K V1 2,5 Q = m C ( − ) = P T2 T1 7716,6 J. µ
b. Độ biến thiên nội năng của khối khí
∆U = m R. i ∆T = 5511,9J µ 2
c. Công do khối khí sinh ra
A' = −A = Q−∆U = 2204,7 J
8.3. Quá trình đẳng tích: A = 0; U∆ = Q ∆U = m i R T( − ) µ 2 T1 2 7 lOMoAR cPSD| 45148588 = i (p V − = 2 p V) i V⎛⎜ T 1 2 p1 − p1 ⎟⎞ 2 2 ⎝ T ⎠ 1 ⎛ ⎞
∆U = i PV ⎜ T2 − ⎟ = − 1 1 5,4 J 2 ⎝ T ⎠ 1 Q' = −Q = 5,4 J
8.4. Quá trình đẳng áp a. Ta có: Q = m C ∆ ∆ P T = CP T µ Cp = Q = i + 2 R ⇒ =i 3 ∆T 2 γ = i+ 2 =1,67 i b. ∆U = i R T∆ = 0,72MJ 2
c. A = ∆U −Q = −0,48MJ (sinh công)
8.5. Đồ thị là hàm bậc nhất U = m i RT ; i = 5 µ 2 a. ∆U = m i R T∆ = m 5 R T( − ) = 2 T1 52kJ µ 2 µ 2
b. Công A’ tiêu tốn bằng công A khối khí nhận được, do Q = 0 ; A =∆U . A′ = A = ∆U = 52 KJ
c. Quá trình đoạn nhiệt TVγ−1 = const . TV11γ−1 = T V2 2γ−1
T1 = ⎜⎛ V2 ⎟⎞γ−1 ; γ = i + 2 = 7 T ⎝ ⎠ 2 V i 1 5 8 lOMoAR cPSD| 45148588 V2 =1,8 lần V1
8.6. CP = i +22 R, CP Ar() = 52 R; CP N( 2) = 72 R
CV = 2i R, CV Ar() = 23 R; CV N( 2 ) = 52 R
‐ Nhiệt lượng cần thiết để hỗn hợp khí tăng lên 1o là: 29 = Q = đẳng áp 3Cp Ar() + 2Cp N( 2 ) 2 R Q = đẳng tích 3CV Ar() + 2CV N( 2) = 9,5R ‐ Nhiệt dung riêng: Q Q C = = P ®¼ng ¸p ®¼ng ¸p mhçn hîp 3µ(Ar) + 2µ(N2 ) 29 R = 2 = 685J/kgK 3.40+ 2.28 Q CV = dang tich == 9,5.R = 448 J/kgK m(hon hop) 3.40+ 2.28 8.7. p P 1 T
a. Nhiệt mà khí nhận được 1 1 Q = −A =1,25MJ P T T 2 2 2 2 3 1
b. Công do khí thực hiện A13 = A12 + A23 = A23 0
V 1 = V 2
V 3 V A ( )
23 = p2 V2 −V3 A23 = p V2 2 −p V ; T3 3 2 = p2 T1 = T1 p1 2 ⇒ A = − = − ) = − RT1 23 RT2 RT 3 R T( 2 T1 9 lOMoAR cPSD| 45148588 2
⇒ A23 = −1,25 MJ (sinh công) c. Vì: T = ⇒ ∆ 3 T1 U = i R T∆ = 0 2 8.8.
a. Vẽ quá trình biến đổi trên pV p
b. Tính công thực hiện trên mỗi quá trình biến đổi p 2 2 A12 = 0 p 1 1 3 A 23 = m RTln p3 = p V ln2 2 p1 µ p2 0 V 1 V
V 2 p2 ⇒ A23 = 20,79 kJ A ( ) ( ) 31 = −p1 V1 −V3 = p1 V3 −V1 = 3.10 .50.105−3 =15 kJ
Quá trình (2‐3) khí sinh công, quá trình (3‐1) khí nhận công. 8.9. p a. Quá trình ACB A′ ) ACB = −AACB = −(AAC + ACB A D p 2 ⇒ ′ A = ( − ) = ACB 0+ p2 V2 V1 1,23 KJ Q p ACB = QAC +QCB 1 C B 0 V 1 V
V 2 Q ( ) ( ) ACB =
m CV TC −TA + m CP TB −TC µ µ ⇒ Q = ACB 4,72KJ ∆U = + = ACB AACB QACB 1,5−0,9 = 0,6KJ
b. Quá trình đẳng tích ADB ′ A = ADB 1,23KJ Q = ADB 1.83 KJ ∆U = ADB 0,6KJ 8.10. 10 lOMoAR cPSD| 45148588 a. Hình vẽ P 3 b. Tìm số bậc tự do P 2 1 Q123 = Q12 + Q23 P 1 T 1 2 Q 12 = −A12 = − m RT ln1 V2 = PV ln1 1 V1 µ V1 0 V 1 V
V 2 V2 Q ( ) 23 =
mµ CV T3 −T2 = i ⎛⎜ mµ RT3 − mµ RT1 ⎟⎠⎞ 2⎝ Q ) ) 23 = i (p V3 = 3 −p V11 i (p V1 2 −p V1 1 2 2 2(Q123 −Q12 ) = 5 ⇒ =i p ( − ) 1 V2 V1 8.11. a. Quá trình (1‐2) 1−γ 1−γ Tp γ γ 11 = T p2 2 T2 = T1
⎜⎛ p1 ⎞⎟= 264 K ; T3 = T2 = 264 K P 3 1 ⎝ p 2 ⎠ P µ
2 b. Q = Q123 = Q23 = m RT ln2 p2 P1 δ Q = 0 p T 3
2 = T 3 2 m Q = µ RT ln p 2 = − 2 p 1,76 kJ ⇒ Q′ =1,76 kJ 1 0 V m i c. ∆U = R T( − ) = m i − ) = − 3 T1 R T( 2 T1 1,62 kJ µ 2 µ 2 11 lOMoAR cPSD| 45148588
d. ∆U = A +Q → A = ∆U −Q = 0,14 kJ
‐ Hệ nhận công A′ = 0,14 kJ 8.12. U p B A (1) (1) B (2) C A (2) (3) C (3) D D 0 0 V 1 V 1
V 2 V V V 2 a. AAB > AAC > AAD b. = ‐ Đẳng áp: U i pV; U ∆> 0 2
‐ Đẳng nhiệt: Q = −A; U ∆ = 0
‐ Đoạn nhiệt: TVγ−1 = const UVγ-1 = const U ∼ V1γ-1 ; U∆ < 0 p 8.13. 1 a. Quá trình (1‐2) T 1 2 V 4 T 2 p = 1 = 2 p1 2,8 at 3 V 2
‐ Quá trình (2 ‐3) pVγ = const ⇒ p V22γ = p V3 3γ 0 V ⎛ ⎞ p3 = p ⎜ V2 2 ⎟γ =1,45 at ⎝ V ⎠ 3
TVγ−1 = const → TV12γ−1 = T V2 3γ−1 12 lOMoAR cPSD| 45148588 ⎛ V2 ⎞γ-1 = 331 K T = 2 T1 ⎜ ⎟ ⎝ V ⎠ 3
TVγ−1 = const → TV11γ−1 = T V21γ−1 = T V2 2γ−1
⇒ ⎛⎜ V4 ⎞⎟γ−1 = T1 ⇒ V4 = 3,2 l ⎝ V ⎠ 1 T2 ‐ Quá trình (3‐4) p V33 = 3,6 at p V33 = p V44 → p4 = V4 V V b. A = m 1 = 1 = − 12 RT ln1 p V ln 1300 J 1 1 µ V2 V2 A′ = −A = 12 1300 J A23 = p V -p V3 3 2 2 = −620 J γ -1 A ′ = -A23 = 620 J V A = 3 = 3 p V ln3 1070 J 3 V4 A = p V11 − p V44 = 620 J 41 γ − 1
A123 = A12 + A23 + A34 + A41 = 230 J
c. Quá trình đẳng nhiệt, ∆U = 0 → Q = −A Q = − = 12 A12 1300 J
Q34 = −A34 = −1070J (toả nhiệt) 13 lOMoAR cPSD| 45148588 ′ ⇒ Q = 34 1070 J p C B 8.14.
a. Quá trình ACB hệ sinh công A′. A D
QACB = 40kJ; A′ACB = 10050 QACB ⇒ QACB = 20 kJ 0 V
⇒ ∆∆UABU=ABA=ACB20+ kJQACB = QACB −A′ACB ‐ Quá trình ADB. ′ Q = ∆ + = ADB UA,B A ADB 20+7 = 27 kJ
b. Quá trình B→ A, hệ nhận công (nén). A = BA 15 kJ Q = ∆ − = − BA UBA ABA
20−15 = −35 kJ (hệ toả nhiệt) 8.15. dA = Fdl = (pS−p S dl ) o h0 +h1 h0 +h1
A = ∫ pSdl− ∫ p Sdl = − 0 A A 1 2 h0 h0 V0 +V1 h0 +h1 A ∫ 1 = ∫ p V0 0 dV V0 + V1 = p S0 h ln0 h0 + h1 = p V ln0 0 V V h V0 0 h0 0 h0 +h1 = A ∫ = ( + )− = 2
p Sdl0 p S ho o h1 p Shoo p Sho 1 h0 + ⎞ A′ = −A = P S h ⎛⎜ − h h o 1 ⎟ = o 1 h lno 2,5 J ⎝ h ⎠ o 8.16. 14 lOMoAR cPSD| 45148588 a. Quá trình đẳng áp. p = = 2 p1 106 N/m2 V2
A = −∫ p dV = ( − ) = − 1 p1 V1 V2 2.106 J V1 A′ = −A = 2.106 J
b. Quá trình đẳng nhiệt p2 = p V11 = 5.105 N/m2 V2 V2 V2 V V V1 V1 1 A = −∫ pdV = −p V ∫ 1 1 dV A′ = −A =13,86.10 J5 = −p V ln V2 = 1 1 −13,86.10 J5
c. Quá trình đoạn nhiệt pVγ = const → p = p V1 2 γ1γ = 3,79.10 N/m5 2 V2
A′ = −A = − p V2 2 −p V1 1 =12,1.10 J5 γ −1 8.17.
a. A′(δ =Q 0) = −A(δ =Q 0) = − p V22 −p V1 1 (1) γ −1
p V22γ = p V11γ → p2 ⎛⎜⎝ Vn1 ⎞⎟⎠γ = p V1 1γ → p2 = p n1 γ
‐ Thay vào (1) đoạn nhiệt A′(δ =Q 0) = −p V11 nγ−1 −1 γ −1 15 lOMoAR cPSD| 45148588
A′(T const= ) = −A(T const= ) = −p V ln1 1 V1 = −p V lnn1 1 V2
A′(δQ=0) = nγ−1 −1 =1,4 lần A′ ( (T=const) γ − 1)lnn
b. Quá trình đẳng nhiệt nội năng không đổi
‐ Quá trình đoạn nhiệt: γ−1
TV11γ−1 = T V22γ−1 = T2 ⎛⎜⎝ Vn1 ⎠⎟⎞ ⇒ T1 = nTγ2−1
T2 = U2 = nγ−1 = 572−1 = 5 =1,9 lần T1 U1 8.18. p
a. Quá trình đẳng nhiệt AB p V = → = AA p VBB p VA1 p VB 2 (1) A p V = → = CC p VDD p VD1 p VC T 2 (2) 1 B D ⇒ T p = p 2 ‐ Từ (1) và (2) A D C pB 2 V pC 0 V1 V
b. Tính công của chu trình
A = AAB + ABC + ACD + ADA = AAB +0+ ACD + 0 A = m RT ln1 V1 + m RT ln2 V2 = m R T( 2 −T ln ) 1 V2 µ V µ µ 2 V 1 V1
‐ Xét cả chu trình: ∆U = 0 = A +Q ⇒ Q = −A = m R T( − ) 1 T2 ln V2 ⇒ Q = R T( − ) 1 T2 ln V2 µ V1 V1 Chương 9
NGUYÊN LÝ II NHIỆT ĐỘNG HỌC 16 lOMoAR cPSD| 45148588
TÓM TẮT LÝ THUYẾT
1. Hiệu suất của động cơ nhiệt η = A′ = Q1 −Q′2 Q1 Q1
Trong đó Q1 là nhiệt mà tác nhân nhận được từ nguồn nóng.
Q'2 là nhiệt mà tác nhân nhả cho nguồn lạnh.
A' là công do động cơ sinh ra.
2. Hiệu suất của chu trình Cácnô thuận nghịch η = −1T2 T1
3. Hệ số làm lạnh của máy lạnh hai nguồn nhiệt ε = QA2 = Q1' Q−2Q2
‐ Trong đó A là công tiêu tốn trong một chu trình làm lạnh, Q2 là nhiệt mà tác nhân nhận từ
nguồn lạnh trong chu trình đó, Q '1 là nhiệt mà tác nhân nhả cho nguồn nóng trong một chu trình.
‐ Với máy làm lạnh làm việc theo chu trình Cácnô thuận nghịch: ε = T2 T1 −T2
4. Độ biến thiên Entropi trong quá trình thuận nghịch 2 δQ ∆S = S − = ∫ 2 S1 1 T
‐ Đối với khí lí tưởng:
∆S = m ⎡⎢C lnV TT12 + R ln VV12 ⎤⎥⎦ µ ⎣ 17 lOMoAR cPSD| 45148588 hoặc ∆S = m ⎡⎢C lnV pp12 +C lnp VV12 ⎤⎥⎦ µ ⎣
5. Nguyên lí tăng Entropi trong một hệ cô lập ∆ ≥S0 BÀI TẬP VÍ DỤ
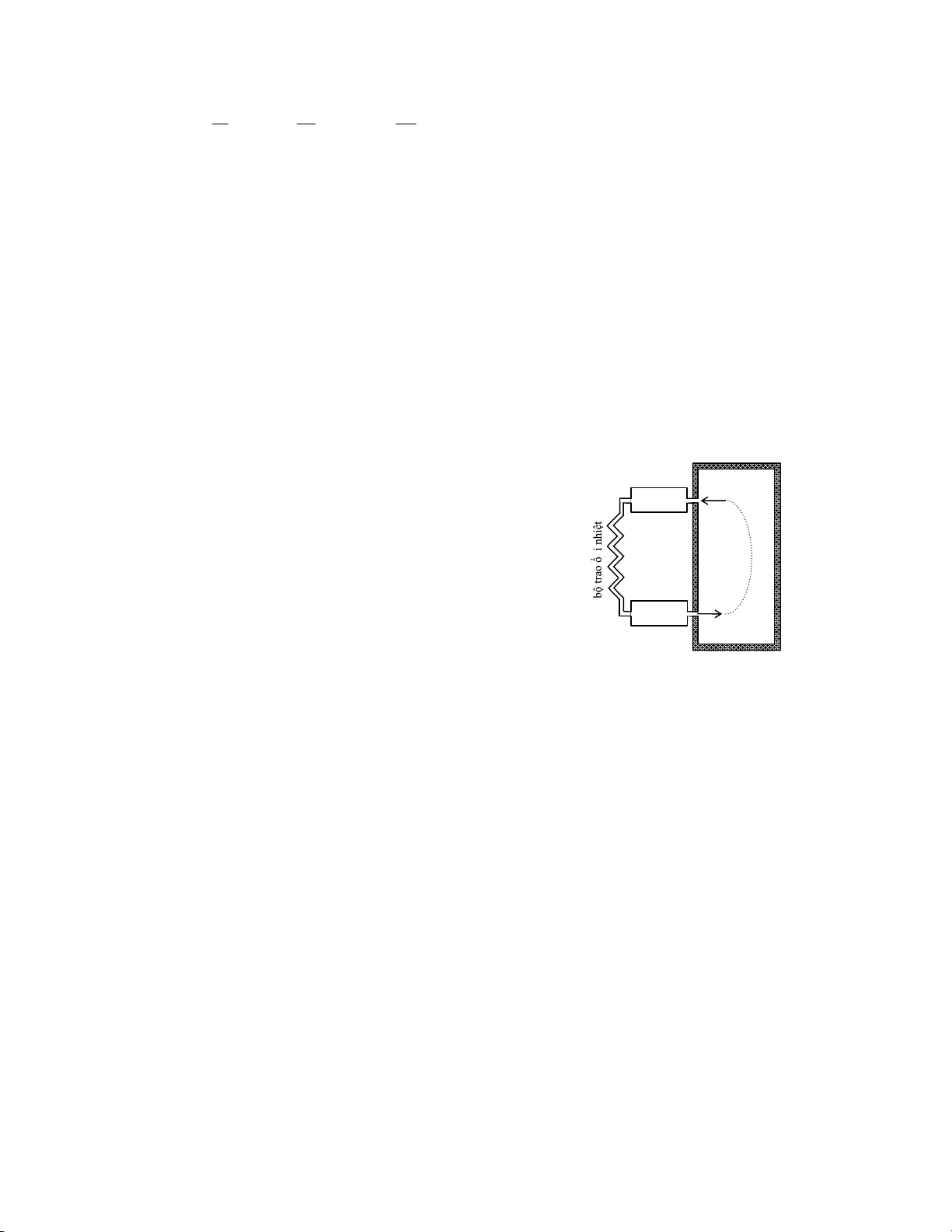
Tính hiệu suất của máy lạnh dùng không khí
Mục đích của máy làm lạnh là duy trì nhiệt độ trong phòng (T2 ) thấp hơn nhiệt độ bên
ngoài (T1). Nguyên lí của máy làm lạnh dùng không khí được mô tả trên hình vẽ bên.
‐ Một lượng không khí (n mol) trong phòng ở nhiệt độ T2 và áp suất pA được hút vào bộ
nén khí. Ở đây khí được nén đoạn nhiệt tới áp suất pB , nhiệt độ tăng đến giá trị TB > T1 .
‐ Sau đó khí bị đẩy vào bộ trao đổi nhiệt ở áp suất không đổi pB . B A
Khí toả nhiệt ra môi trường ngoài, nhiệt độ giảm đến T1. b ộ nén khí
‐ Tiếp theo khí được dãn đoạn nhiệt trong bộ dãn khí tới áp suất p p A
A , nhiệt độ khi đó TD thấp hơn nhiệt độ trong phòng (TD < T2 ). T 2
‐ Cuối cùng, khí lạnh được đưa vào phòng, hấp thụ nhiệt ở b ộ dãn khí
áp suất không đổi p C D
A . Nhiệt độ của khí tăng đến T2 rồi lại được nhận vào máy nén.
Chu trình biến đổi trạng thái của n mol không khí ‐ mà ta coi là khí lí tưởng ‐ được mô tả
trên hình vẽ dưới đây. Tính hiệu suất làm lạnh của máy. Lời giải
‐ Ta có thể coi máy hoạt động giữa hai nguồn nhiệt: nguồn nóng là môi trường ngoài có nhiệt
độ T1, nguồn lạnh là không khí và các vật dụng trong phòng với nhiệt độ T2 .
‐ Nhiệt nhận từ nguồn lạnh trong quá trình đắng áp D → A: Q = ( − ) 2 nCp T2 TD p p
‐ Nhiệt toả ra môi trường trong quá trình đắng áp B → C: B Q ' = ( − ) 1 nCp TB T1 ‐ Hiệu suất: 18




