


















































































Preview text:
BỘ GIÁO DỤC VÀ ĐÀO TẠO BỘ QUỐC PHÒNG
HỌC VIỆN KỸ THUẬT QUÂN SỰ PHƯƠNG THỊ NHÃ
PHÁT TRIỂN CÁC KỸ THUẬT THỦY VÂN BỀN VỮNG
TRONG ỨNG DỤNG BẢO VỆ BẢN QUYỀN ẢNH SỐ
CÁC CÔNG TRÌNH NGHIÊN CỨU HÀ NỘI - NĂM 2023
BỘ GIÁO DỤC VÀ ĐÀO TẠO BỘ QUỐC PHÒNG
HỌC VIỆN KỸ THUẬT QUÂN SỰ PHƯƠNG THỊ NHÃ
PHÁT TRIỂN CÁC KỸ THUẬT THỦY VÂN BỀN VỮNG
TRONG ỨNG DỤNG BẢO VỆ BẢN QUYỀN ẢNH SỐ
CÁC CÔNG TRÌNH NGHIÊN CỨU
Chuyên ngành: Cơ sở toán học cho tin học Mã số: 9 46 01 10
NGƯỜI HƯỚNG DẪN KHOA HỌC: 1. PGS. TS. Tạ Minh Thanh 2. TS. Nguyễn Tuấn Phong HÀ NỘI - NĂM 2023 MỤC LỤC
[1] Nha, Phuong Thi, and Ta Minh Thanh. “A Novel Image Watermarking
Scheme Using LU Decomposition.” In: 2021 RIVF International Conference
on Computing and Communication Technologies (RIVF), Ha Noi, Viet Nam,
pp. 228-233. IEEE, 2021...............................................................................1
[2] Nha, Phuong Thi and Ta Minh Thanh, 2023. “A New Block Selection
Strategy from LU Decomposition Domain for Robust Image Watermarking.”
In: Multimedia Tools and Applications. DOI : 10.1007/s11042-023-16254-4
(ISI-SCI, Q1, IF = 3.16).................................................................................7
[3] Nha, P.T., Thanh, T.M. and Phong, N.T., 2022. “Consideration of a ro-
bust watermarking algorithm for color image using improved QR decomposi-
tion.” In:Soft Computing, 26(11), pp.5069-5093. https://doi.org/10.1007/s005
00-022-06975-3 (ISI-SCI, Q2, IF = 4.20).......................................................32
[4] Nha, Phuong Thi, and Ta Minh Thanh. “A Combination of DWT and
QR Decomposition for Color Image Watermarking.” In: 2021 13th Interna-
tional Conference on Knowledge and Systems Engineering (KSE), November
10-12, Bangkok, Thailand, pp. 1-6. IEEE, 2021. (The best paper award)......57
[5] Phuong Thi Nha, Ta Minh Thanh, and Nguyen Tuan Phong: An Effec-
tive Embedding Algorithm for Blind Image Watermarking Technique based on
Hessenberg Decomposition. Applied Intelligence. DOI: 10.1007/s10489-023-
04903-y. (ISI-SCI, Q2, IF = 5.44).................................................................63
A Novel Image Watermarking Scheme Using LU Decomposition Phuong Thi Nha Ta Minh Thanh
Le Quy Don Technical University
Le Quy Don Technical University Ha Noi, Viet Nam Ha Noi, Viet Nam phuongthinha@gmail.com thanhtm@lqdtu.edu.vn
Abstract—In recent years, protecting copyright of digital images
flops which is approximately 8n3/3 for n×n matrix [6]. That is
is an indispensable requirement for owners. To against with rapidly
the reason why some researchers focused on kind of this matrix
increasing of attacks, many techniques have been proposed in
analysis [5], [6]. Su [6] proposed a new Schur decomposition
transform domain for ensuring quality of watermarked image,
based algorithm where the U (2, k) and U (3, k) elements of U
robustness of extracted watermark and execution time. Among
these techniques, LU decomposition is considered as an outstanding
unitary matrix are chosen for embedding (with k is a row index
technique in term of computation. However, it is that not all
of D triangular matrix that contains the biggest value).
square matrices have an LU decomposition. Therefore, the suitable
blocks need to be chosen before factorizing pixel matrices into
In order to strengthen the robustness of watermark, many au-
lower and upper triangular matrix. In addition, in order to
thors combined different transforms such as DWT and SVD [7]–
improve the invisibility of watermarked image, watermark should
[12], DCT and SVD [13], DWT and DCT [14], DWT and
be embedded on one element of L matrix instead of two elements
QR [15], [16], or DWT and LU [17]. In 2016, Dongyan Wang
as the previous proposals. In this paper, we propose a novel
et. al. [17] combined DWT and LU decomposition to produce
image watermarking scheme which is based on strategy of LU
blocks selection and an improved embedding method. Beside that,
a novel scheme. In this research, the author executed one-level
the extraction time is significantly sped up by a new solution
DWT transformation on G channel of original image, divided
to get out L(2, 1) and L(3, 1) elements of L matrix without
into 4×4 blocks and applied LU computation on LH and HL
performing LU decomposition in the extracting stage. According
subbands after that. Watermark, which is encoded by Arnold
to the experimental results, our proposed method not only has the
algorithm before it is converted to binary sequence, is embedded
much better visual quality of watermarked images, but also can
effectively extracts the watermark under some attacks.
on U (1, 4) element of U upper triangular matrix. Furthermore,
Index Terms—image watermarking, LU decomposition, block
there is a combination of DWT and SVD which is proposed
selection strategy, embedding formula, extracting formula
by Lou in 2020 [7]. In this proposal, Lou decomposed the host
image into four subbands by DWT transform, and LL is splitted I. INTRODUCTION
up non-overlapping 4×4 blocks at fisrt. For each block, SVD
decomposition is performed on LL subband and the suitable A. Background
SVD blocks will be chosen with an optimal selection policy.
Nowadays, copyright protection is more and more becoming
After that, adaptive embedding factor is calculated based on
important because the digital data is very easy to modify or
information entropy for each block. The experimental results of
fake information of owner in support of modern tools. To
these proposals showed that robustness of extracted watermark
protected ownership, a technique called watermarking has been
is more improved than previous research. Normalized Corre-
researched by many researchers in recent years. Watermarking is
lation (N C) values, which measures robustness, are often up
a technique with similarities to steganography. It is the operation
to 90% for almost image attacks. However, the invisibility of
of hiding watermark into digital data where exists a relationship
watermarked images is only around 40dB by Peak Signal to
between the watermark and the carrier signal [1]. Noise Ratio (PSNR) value.
Depending on the watermark embedding domain, we can
Difference from above methods, LU decomposition, which
separate digital watermarking methods in form of spatial domain
often hides information on the 2nd and 3rd elements of the first
and transform domain [2]. Spatial domain based methods have
column of L lower triangular matrix, has a big advantage in
low computational complexity, but they are not often robust
term of computational complexity. Su et. al. [2] found a certain
against almost image attacks. On the contrary, in transform
similarity between any two elements in the first column of the
domain methods, the host image is first transformed into the
lower triangular matrix L after performing LU decomposition
frequency domain by several transformation methods such as
on 4×4 image pixel blocks. After that, Normalized Correlation
discrete cosine transform (DCT) [3], discrete wavelet transform
(N C) value between these elements is computed to find out
(DWT) [4] or matrix decomposition such as singular value
needed ones. Experimental results showed that LU computing
decomposition (SVD), QR decomposition, LU decomposition,
is extremely easier than other transformations, but watermarked
Schur decomposition. Although these watermarking methods
image often has bit worse invisibility. This is because Su [2]
have high calculation time, they are often stronger than spatial
embedded on two elements (L(2, 1) and L(3, 1)), so it led to domain based schemes.
modified two rows of pixel matrix. This change impacted on
While the time required to conduct SVD computation is about
the quality of watermarked image. Therefore, we need a better
11n3 flops, the Schur decomposition needs fewer number of
solution for watermarking scheme based on LU decomposition
978-1-6654-0435-8/21/$31.00 ©2021 IEEE
and our contributions in this paper include: 228 1 •
Propose a block selection strategy for LU decomposition. TABLE I
STATISTICAL DATA OF THE UNSUITABLE BLOCKS FOR SOME IMAGES •
Improve the embedding formula to have the better invisi- bility of watermarked image. Number of Image (.bmp) Percentage (%) NC •
Propose a new way to get out L(2, 1) and L(3, 1) of L unsuitable blocks
matrix without calculating LU decomposition in order to baboon 79 0.48 0.9952 lena 517 3.15 0.9714
speed up execution time in the extracting process. avion 1040 6.34 0.9444 peppers 1414 8.63 0.9157 B. Roadmap Girl 4959 30.26 0.8522
The rest of this paper is organized as follows. First, improved blueeye 8239 50.29 0.7918 anhinga 12488 76.22 0.7267
ideas will be represented in Section II. In Section III, a proposed
image watermarking scheme is figured in detail. The experi-
ments and comparisons are also discussed in Section IV. Finally,
Section V will conclude the paper in form of a paragraph.
Proposition 2: An invertible matrix A has an LU decom-
position provided that all its leading submatrices have nonzero II. IMPROVED IDEAS determinants. A. LU decomposition
To illustrate for these arguments, we surveyed on some
A square matrix A can be decomposed in form of a product
digital images. The experiments are performed on seven color of two matrices as (1):
images with size of 512×512. Each image is divided into
4×4 blocks, so the total blocks are 16,384. We calculate the A = LU, (1)
number of unsuitable blocks which do not agree with the above
where L is a lower triangular matrix and U is an upper
proposition, the rate and the Normalized Correlation index
triangular matrix. Then A has an LU decomposition. Because
(N C) for each image. The results are expressed in Tab. I. The
LU decomposition is not always unique, we consider L matrix
figures show that there is a relationship between the number of
where all diagonal elements are set to 1.
unsuitable blocks with N C index. It means that the image has
fewer the number of unsuitable blocks, it has higher N C value
B. A noticeable point of LU decomposition
and vice versa. Therefore, in order to improve the robustness
In linear algebra, LU decomposition is an approach designed
of the extracted watermark, it is necessary to chose suitable
to exploit triangular systems. However, some researchers found
blocks before embedding. We need to embed the watermark on
a remarkable point of this factorization. In [17], Dongyan
suitable blocks which have LU decomposition instead of the
noticed that “LU decomposition does not exist in all cases and whole pixel blocks.
the condition when the decomposition can be conducted is the
determinants det(A(1 : k, 1 : k)) 6= 0, with k = 1 : n”. Beside
that, Taboga [18] emphasized “Sometimes it is impossible
C. Considering the element to embed
to write a matrix in the form of “lower triangular”דupper
triangular””. In addition, two propositions are represented in
For image watermarking scheme, selecting the element(s) [18] and [19] as follows:
to embed is extremely important. In [2], Su et. al. computed
Proposition 1: Not all square matrices have an LU factoriza-
Normalized Cross-Correlation (N CC) between the first column tion.
elements of two lower triangular matrices. The result showed
Proof: It is sufficient to provide a single counter example.
that L21 and L31 are the closest elements, so they can be
Take a 2 × 2 invertible matrix as
used to embed information. However, because Su embedded
the watermark bits on these two elements at the same time 0 1
for each block, the values of the matrix after embedding are A = 1 0
changed on two rows. Thus, the pixel values of watermarked
image are modified significantly. This causes the quality of
Suppose A has an LU factorization A = LU with factors
the watermarked image is reduced. To address this issue, we L U
propose a better solution which only embeds on L21 or L31 at L = 11 0 and U = 11 U12 (2) L
once for each block. Our proposal makes a change on one row 21 L22 0 U22
of the matrix after embedding, so the invisibility (the quality of Compute the product
the embedded image) is improved. Fig. 1 gives a comparison L
between formula of Su [2] and our method for both embedding LU = 11 U11 L11U12 (3) L and extracting stage. 21 U11 L21U12 + L22U22
Now, A11 = (LU )11 implies L11U11 = 0, which in turn
implies that at least one of L11 and U11 must be zero. As a
D. An idea for improving execution time
consequence, at least one of L and U is not invertible (because
triangular matrices are invertible only if their diagonal entries
For a watermarking method, the execution time consists of
are nonzero). This is in contradiction with the fact that A is
embedding time and extracting time. In almost published image
invertible and, as a consequence, L and U must be invertible
watermarking schemes, LU decomposition is always needed
(see the proposition about the invertibility of products). Thus,
to perform in the extracting process [2], [17]. In fact, this
we have proved by contradiction that A cannot have an LU
is completely unnecessary due to the special feature of LU decomposition.
decomposition. In the extracting stage, we only need to get out 229 2 A. The embedding stage
The embedding stage includes steps as follows: • Step 1
– The host image is divided into 4×4 non-overlapping blocks. • Step 2
– The watermark is permuted by Arnold Transform. The
key for this operation is considered as Key1.
– The permuted image is convert to a one-dimensional binary array. • Step 3
– For each block, assign B components to a matrix A.
Fig. 1. A comparison between the formula of Su and the proposed formula • Step 4
– Calculate determinants of submatrices of A matrix, of L
– If one of the determinants = 0, come back to Step 3.
21 and L31 of L matrix. Let consider the below illustration
to see the new solution. We suppose that
– If all determinants 6= 0, go to Step 5. • Step 5 A 11 A12 A13 A14 – Decompose A = LU A A = 21 A22 A23 A24 – Embed
the corresponding watermark value into = LU, (4) A L 31 A32 A33 A34
(2, 1) or L(3, 1) of L matrix as follows: A41 A42 A43 A44
– Case L(2, 1) ≥ L(3, 1) and wi = “1” where L0(2, 1) = L(3, 1) − T, (9) 1 0 0 0 U 11 U12 U13 U14
– Case L(2, 1) ≤ L(3, 1) and wi = “0” L 0 U L = 21 1 0 0 22 U23 U24 and U = L0(3, 1) = L(2, 1) − T, (10) L31 L32 1 0 0 0 U33 U34 L41 L42 L43 1 0 0 0 U44
where T is the embedding strength of watermark. (5) • Step 6
By multiplying L matrix with U matrix and setting a equation to A matrix, we have:
– Update A to A0 = L0U and assign A0 back to B components of the block. U
– Mark and save the suitable block to a file. This is 11 = A11 , U12 = A12 and U13 = A13 (6)
considered as Key2 of the scheme.
Consider the first entry of the second row
– Repeat steps from 3 to 6 until all suitable blocks are embedded. A21 A21 • Step 7 L21U11 = A21 =⇒ L21 = = , (7) U11 A11
– Reconstruct watermarked B components to receive the watermarked image.
and the first entry of the third row
The flowchart of the embedding process is illustrated A in Fig. 2. 31 A31 L31U11 = A31 =⇒ L31 = = . (8) U11 A11 B. The extracting stage
Therefore, this is a wonderful way to find L21 and L31 without • Step 1
using LU factorization. As a result, this idea can reduce
– The watermarked image is divided into 4×4 non-
significantly calculation time in the extracting stage. overlapping blocks. • Step 2
III. THE PROPOSED IMAGE WATERMARKING METHOD
– For each block, assign B components to a matrix A. • Step 3
In this section, a novel image watermarking scheme is repre-
sented in which the appropriate blocks for LU decomposition
– Check the block by comparing to the saved file.
are chosen to embed the information. Before embedding, a wa-
– If the block is not in the file, it means that it is
unsuitable, come back to Step 2
termark preprocessing operation is executed by utilizing Arnold
transform to enhance the security of the proposed algorithm. In
– If the block is in the file, it means that it is suitable, go to Step 4
the embedding stage, only one element of L matrix (L(2, 1) or
L(3, 1)) is modified for each suitable block. In the extracting • Step 4
stage, we calculate L(2, 1) and L(3, 1) elements which are
– Get out the elements of L matrix by formula (7) and
based on (7) and (8) without using LU factorization. (8). 230 3 Fig. 2. The embedding process Fig. 3. The extracting process
The results of imperceptibility experiments are shown in
– Extract information of watermark as follows:
Fig. 4. The figures show that values of PSNR and SSIM of “0”, L∗(2, 1) ≥ L∗(3, 1) w∗ = (11)
the proposed watermarking algorithm are higher than the both i “1”, elsewhere
method of Su [2] and Lou [7] for all five images. Therefore, the
proposed method has better invisibility of watermarked images.
– Repeat steps from 2 to 4 until all watermark bits are extracted.
This can be explained as follow: the method of Su [2] and
Lou [7] embedded on two elements for each block. In [7], • Step 5
Lou embedded on U (2, 1) and U (3, 1) of U orthogonal matrix
– Convert extracted watermark values to an image.
after doing SV D decomposition. It is similar to [2] where Su
– Apply Inverse Arnold Transform to get final extracted
modified L(2, 1) and L(3, 1) of L lower triangular matrix at the watermark image.
same time. Thus, this leads a big change the pixel values after
The flowchart of the extracting process can be designed as in
embedding. As a result, the quality of the watermarked image Fig. 3.
will be pulled down. In contrast, our method impacts on one IV. E
element for each block, so the pixel matrix is only changed on
XPERIMENTAL RESULTS AND DISCUSSION
one row instead of two row as the other methods. In addition,
A. Imperceptibility experiments
because of selecting suitable blocks before embedding of the
In our experiments, five standard color 512×512 images from
proposed scheme, this improvement has a part in pulling up
the CVG-UGR1 image database are chosen as the host images,
the imperceptibility. Fig. 4 also points that the watermark after
while a binary 32×32 image is used to be the watermark. The
extracting of the proposed method is clearer than method of Su
embedding strength of watermark T is designated as 0.0275 [2] and Lou [7].
which is the same to the method of Su [2]. This value is to B. Robustness experiments
ensure a balance between the quality of the watermarked image
and the robustness of the watermark after extracting.
Robustness is a necessary evaluation principle for building
watermarking schemes, so image processing operations are
1https://decsai.ugr.es/cvg/dbimagenes/
often added to assess the efficiency of this criterion. In our 231 4
Fig. 4. The results of invisibility tests Fig. 5.
The results of robustness tests under blurring, sharpening and Salt&Pepper noise attacks
experiments, three watermarked images are chosen to test
of blocks. As a result, the watermark after extracting will be
under five basic attacks which include blurring, sharpening,
much modified. This is considered as a disadvantage of the
salt&pepper noise, rotation and scaling.
schemes based on LU decomposition. The detail of the results
The results in Fig. 5 shows that the proposed method is is displayed in Fig. 6.
very effective under attacks such as blurring, sharpening and
salt&pepper because N C values are above 0.9 for all these
C. A comparison of execution time
attacks. Moreover, our method overcomes the schemes of Su
In these experiments, a computer with Intel@ CoreT M i5-
[2] and Lou [7] under these attacks.
6200U CPU at 2.30GHz, 4.00GB RAM, 64-bit OS and Visual
For geometric attacks such as rotation and scaling, the
Studio v15 is used as the computing platform. Tab. II shows
robustness of all three methods is not really attractive. In three
a comparison of the execution time between different methods.
methods, the method of Lou [7] is better than others, particularly
For embedding stage, the method of Su [2] consumes the least
under scaling ×2 operation. The reason for this is because Lou
time, while the scheme of Lou [7] costs the most time for
used a combination of DW T and SV D where only LL subband
calculating. The reason for this is that Lou used a combination
is chosen for SV D decomposition and after that the watermark
between DW T and SV D decomposition, which have a big
is embedded into u5 and u9 elements of U matrix. Although
computational complexity. Although the both the method of
the proposed method is more improved than the method of
Su [2] and the proposed method uses LU decomposition, the
Su [2], NC values are only around from 0.6 to 0.8 and the
proposed method spends more execution time than the one of Su
watermark cannot be recognized for almost cases. This happens
[2]. This is because that the proposed method needs to check and
due to particularity of LU decomposition. As described in
select suitable blocks. However, this expense can be completely
Section I, not all square matrices have an LU factorization.
accepted when we consider to effects that it brings in improving
Therefore, geometric attacks can make a change to this property
the quality of the watermarked image as well as the robustness. 232 5
execution time. In the future, a combination of DWT and LU
can be further studied to improve the disadvantages of this
proposal under geometric attacks. ACKNOWLEDGMENT
This research is funded by Vietnam National Foundation
for Science and Technology Development (NAFOSTED) under grant number 102.01-2019.12. REFERENCES
[1] Anastasios Tefas, Nikos Nikolaidis, Ioannis Pitas, Chapter 22 - Image
Watermarking: Techniques and Applications, Editor(s): Al Bovik, The
Essential Guide to Image Processing, Academic Press, 2009, pp. 597-
648, ISBN 9780123744579, https://doi.org/10.1016/B978-0-12-374457- 9.00022-6.
[2] Qingtang Su, Gang Wang, Xiaofeng Zhang, Gaohuan Lv and Beijing
Chen, “A new algorithm of blind color image watermarking based on LU
decomposition”, Multidimensional Systems and Signal Processing, 29(3), 2018, pp. 1055-1074.
[3] L.-Y. Hsu and H.-T. Hu, “Robust blind image watermarking using
crisscross inter-block prediction in the DCT domain”, Journal of Visual
Communication and Image Representation, vol.46, 2017, pp. 33-47.
[4] Kaiser J. Giri, Mushtaq Ahmad Peer and P. Nagabhushan, “A Robust Color
Image Watermarking Scheme Using Discrete Wavelet Transformation”,
I.J. Image, Graphics and Signal Processing, 2015, pp. 47-52.
[5] F. Liu, H. Yang and Q. Su, “Color image blind watermarking algorithm
based on Schur decomposition”, Application Research of Computers, 34, 2017, pp. 3085-3093.
[6] Su, Q., Zhang, X., Wang, G., “An improved watermarking algorithm
for color image using Schur decomposition”, Soft Comput 24, 2020,
pp.445–460. https://doi.org/10.1007/s00500-019-03924-5
[7] Luo, A., Gong, L., Zhou, N., “Adaptive and blind watermarking scheme
based on optimal SVD blocks selection”, Multimed Tools Appl 79, 2020,
Fig. 6. The results of robustness tests under rotation and scaling attacks
pp.243–261. https://doi.org/10.1007/s11042-019-08074-2
[8] Ranjeet Kumar Singh, Dillip Kumar Shaw and Jayakrushna Sahoo, A TABLE II
secure and robust block based DWT-SVD image watermarking approach,
AVERAGE EXECUTION TIME OF DIFFERENT METHODS (IN SECOND)
Journal of Information and Optimization Sciences, 38(6), 2017, pp. 911- 925. Method Embedding time Extracting time Total time
[9] Yadav B., Kumar A., Kumar Y., “A Robust Digital Image Watermarking Su [2] 0.1774 0.0294 0.2068
Algorithm Using DWT and SVD”, In: Pant M., Ray K., Sharma T., Rawat Lou [7] 2.4566 0.1730 2.6296
S., Bandyopadhyay A. (eds) Soft Computing: Theories and Applications.
Advances in Intelligent Systems and Computing, vol 583. Springer, Sin- Proposed method 0.2750 0.0060 0.2810
gapore, 2018. https://doi.org/10.1007/978-981-10-5687-1-3
[10] Roy, S., Pal, A.K., “A Hybrid Domain Color Image Watermarking
Based on DWT–SVD”, Iran J Sci Technol Trans Electr Eng 43, 2019,
Furthermore, there is an accretion in extracting stage where the
pp.201–217. https://doi.org/10.1007/s40998-018-0109-x
proposed method do not need to perform
[11] Ernawan, F., Kabir, M.N., “A block-based RDWT-SVD image watermark- LU decomposition.
ing method using human visual system characteristics”, Vis Comput 36,
This reduces significantly extracting time. Overall, the execution
2020, pp.19–37. https://doi.org/10.1007/s00371-018-1567-x
time of the proposed method can satisfy with requirement of a
[12] Laxmanika, Singh A.K., Singh P.K., “A Robust Image Watermarking real time applications.
Through Bi-empirical Mode Decomposition and Discrete Wavelet Do-
main”, In: Singh P., Panigrahi B., Suryadevara N., Sharma S., Singh A.
(eds) Proceedings of ICETIT 2019. Lecture Notes in Electrical Engineer- V. CONCLUSION
ing, vol 605. Springer, Cham, 2020.
In this paper, a novel image watermarking scheme is rep-
[13] Li, J., Lin, Q., Yu, “A QDCT- and SVD-based color image watermarking
scheme using an optimized encrypted binary computer-generated holo-
resented which is based on LU decomposition. The both
gram”, Soft Comput 22, 2018, pp.47–65. https://doi.org/10.1007/s00500-
embedding and extracting stages are improved to enhance the 016-2320-x
quality of the watermarked image, the robustness of extracted
[14] Abdulrahman, A.K., Ozturk, S., “A novel hybrid DCT and DWT based
robust watermarking algorithm for color images”, Multimed Tools Appl
watermark, and execution time. In the embedding stage, the host
78, 17027–17049 (2019). https://doi.org/10.1007/s11042-018-7085-z
image is divided into 4×4 blocks. For each block, it is checked
[15] Shaoli Jia, Qingpo Zhou and Hong Zhou, “A Novel Color Image Wa-
to satisfy with the condition of LU composition. After that, a
termarking Scheme Based on DWT and QR Decomposition”, Journal of
Applied Science and Engineering, 20(2), 2017, pp. 193-200.
watermark preprocessing operation is performed by applying
[16] Kamred Udham Singh, Vineet Kumar Singh and Achintya Singhal, “Color
Arnold Transform before embedding information on L(2, 1)
Image Watermarking Scheme Based on QR Factorization and DWT
or L(3, 1) of L matrix of suitable blocks. The watermarked
with Compatibility Analysis on Different Wavelet Filters”, Jour of Adv
Research in Dynamical & Control Systems, 10(6), 2018, pp. 1796-1811.
image is received after all selected blocks are embedded. In
[17] Dongyan Wang, Fanfan Yang and Heng Zhang, “Blind Color Image Water-
the extracting stage, instead of calculating LU factorization,
marking Based on DWT and LU Decomposition”, Journal of Information
L(2, 1) and L(3, 1) are gotten out easily by using formula (7)
Processing System, 12(4), 2016, pp. 765-778.
[18] Taboga, Marco, “LU decomposition”, Lectures on matrix algebra, 2017.
and (8). This helps to save much time for the extracting process.
https://www.statlect.com/matrix-algebra/lu-decomposition.
The experimental results illustrate that the proposed algorithm
[19] HELM, “Section 30.3: LU Decomposition”, 2008.
not only overcomes the method of Su [2] and Lou [7] in term
[20] Satish A, Erapu Vara Prasad, Tejasvi R, Swapna P, Vijayarajan R, “Image
Scrambling through Two Level Arnold Transform”, Alliance International
of the quality of the watermarked image, but also improves
Conference on Artificial Intelligence and Machine Learning (AICAAM),
significantly the robustness under some attacks as well as the April 2019. 233 6
Multimedia Tools and Applications
https://doi.org/10.1007/s11042-023-16254-4
A new block selection strategy from LU decomposition
domain for robust image watermarking
Nha Phuong Thi1 · Thanh Ta Minh1
Received: 1 March 2022 / Revised: 26 May 2023 / Accepted: 4 July 2023
© The Author(s), under exclusive licence to Springer Science+Business Media, LLC, part of Springer Nature 2023 Abstract
The piracy of digital products has become an urgent problem to be solved. Robust water-
marking is a promising technique for copyright protection. To go against rapidly increasing
attacks, many techniques have been proposed in the transform domain for ensuring the quality
of water marked image, the robustness of extracted watermark, and execution time. Among
these techniques, the LU decomposition is considered an out- standing transformation in
terms of computation. However, some pixel matrices cannot be decomposed as the prod-
uct of a lower triangular matrix and an upper triangular matrix, and embedding them into
two elements reduces the quality of the watermark image. Therefore, this paper proposes a
novel image watermarking scheme based on a LU block selection strategy and an improved
embedding algorithm. First, a pixel block is only applied LU decomposition and embedded
a watermark bit when all determinants of sub-matrices are non-zero. Second, an effective
embedding formula is proposed where the watermark is embedded into one element of suit-
able blocks. This solution helps to limit the modification of pixel values and enhance the
quality of the watermarked image. Third, to decrease the extraction time, a novel formula
is built for calculating embedded elements instead of LU decomposition. The experimental
results show that our proposed method has the better visual quality of watermarked images
and can effectively extract the watermark under some attacks, such as blurring, sharpening, and salt & pepper noise.
Keywords Image watermarking · LU decomposition · Block selection strategy ·
Embedding algorithm · Arnold transform
Phuong Thi Nha and Ta Minh Thanh contributed to this work. B Thanh Ta Minh thanhtm@lqdtu.edu.vn Nha Phuong Thi phuongthinha@gmail.com 1
Le Quy Don University, 236 Hoang Quoc Viet, Hanoi, Vietnam 123 7
Multimedia Tools and Applications Abbreviations DCT Discrete CosineTransform DWT Discrete Wavelet Transform SVD Singular Value Decomposition LU Lower - Upper LM Logistic Map LL Low-Low QQRD Quaternion QR decomposition NC Normalized Correlation PSNR Peak Signal Noise Ratio dB Dexibel CC Correlation Coefficient SSIM
Structural Similarity Index Measurement HVS Human Visual System JPEG
Joint Photographic Experts Group 1 Introduction
In recent years, exchanging digital data via the Internet has become increasingly popular.
Digital content copyright protection is becoming important because digital data is straight-
forward to copy or modify owner information in support of modern tools. The watermarking
technique is the most promising to protect content ownership since it can prove the authenti-
cation and protect the digital content under many attack processes. Watermarking algorithms
hide digital information in carrier content where confidential information should relate to the
carrier signal [1]. Therefore, the watermarking technique is often used to verify the authen-
ticity or integrity of images, audio, and video [2–4]. In digital image watermarking, there
are two main research directions: traditional techniques and the application of artificial intel-
ligence [5]. For the use of artificial intelligence, some scientists have developed effective
image watermarking techniques for medical applications, such as [6, 7].
For traditional techniques, image watermarking algorithms can be divided into two main
categories: spatial domain and transform domain [8]. Spatial domain-based algorithms have
low computational complexity but are not usually robust against almost image processing
or geometrical attacks. On the other hand, the transform domain-based methods transform
the original image into the frequency domain by several transformation methods, such as
Discrete Cosine Transform (DCT) [9–11], Discrete Wavelet Transform (DWT) [12–14] or
matrix decomposition, such as Singular Value Decomposition (SVD) [15–19], QR decom-
position [20–26], Schur decomposition [23–29], Lower-Upper (LU) decomposition [33–36].
Although the watermarking methods in the transform domain have high computational com-
plexity, they are always more robust than spatial domain-based watermarking schemes.
Therefore, the transform domain is most attractive to focus on researching and improving in real applications.
First, SVD factorization is one of the earliest and most common matrix transformations
used in digital image watermarking schemes. Image watermarking methods based on SVD
decomposition often embed information into the first element D(1, 1) of the upper triangular
matrix D, such as [18, 19] or into the first column of the U matrix, such as [15–17]. In 2020,
Luo et al. combined DWT and SVD with Logistic Map (LM) to build a novel watermarking 123 8
Multimedia Tools and Applications
scheme [16]. In the embedding process, the 4 × 4 blocks of the original image were selected
according to an optimal strategy to minimize the change of the watermarked image compared
to the original image. Moreover, the entropy information was used to find the embedding
coefficient for each suitable block. Then, the watermark was embedded on the U5 and U9
elements of matrix U after performing the SVD transformation on the Low-low (LL) sub-
band. For the watermark image, the authors used LM, a chaotic one-dimensional map, to
encode information. To evaluate the effectiveness of the proposed scheme, the authors per-
formed many different image attack experiments. Limitations of this proposal are that the
experiments were only performed on gray-scale images, and the algorithm is weak against rotation attacks.
In [17], Hu et al. combined the SVD and Arnold transform on a 512 × 512 color image and
two 64 × 32 and 32 × 16 color watermark images. Before embedding, the watermark was
enlarged to 128 × 128 and 64 × 64, and then it was shuffled through the Arnold transform.
The elements U(2, 1) and U(3, 1) of matrix U were selected as embedding elements. The
proposed watermark embedding scheme helps ensure the orthogonality of the matrix after
SVD expansion. In addition, the mixing modulus helps increase the stability of the watermark.
Based on the results in the paper, this approach of Hu is better than the compared studies that
used QR and LU decomposition. However, it is still limited to JPEG compression attacks,
adding Gaussian and Speckle noise. Although the SVD decomposition gives good results in
digital watermarking, it has a high computational complexity (O(n3)).
Second, QR decomposition is also a significant matrix transformation in watermarking
schemes. QR decomposes a square matrix into an orthogonal and upper triangular matrix.
The advantage of QR decomposition lies in its low computational complexity and stable
numerical feature. Many watermarking methods use the elements of the first column of the
Q matrix to embed information because they have the same sign and similar values, such as
[20, 23, 25, 26]. Besides, due to concentrating energy of QR analysis on the first element of
the R triangular matrix, the information is often embedded into this element, such as [21, 22,
24]. In 2013, Su et al. proposed a digital image watermark scheme based on QR expansion
by embedding watermarks on two elements Q(2, 1) and Q(3, 1) [20]. Experimental results
show that the proposed method is robust against most attacks, such as JPEG compression,
JPEG 2000, low-pass filtering, cropping, blurring, rotation, and scaling. However, the scheme
needs improvement to be more resistant to Gaussian noise. Another proposal to be referenced
is a study of Chen in 2021 [25]. The algorithm performed Quaternion QR Decomposition
(QQRD) on 4 × 4 blocks where the QR expansion is expanded via the Householder algorithm
and the quantization formula. After that, the pairs of similar coefficients qi j of the Q matrix
were calculated by the Normalized Correlation (NC) index to find the appropriate embedding element and formula.
Third, Schur decomposition is also a new matrix expansion that has been applied in digital
image watermark schemes in recent years [27–32]. In 2019, Su improved his algorithm by
giving two choices for the embedded element [29]. First, the watermark information was
embedded in the triangular matrix D and the orthogonal matrix U in two different ways,
and temporary watermark blocks were obtained. Then, the improved algorithm was used to
select the appropriate block from those temporary blocks. The advantage of this method is
that the final watermark block will have less quality loss. In addition, the embedding flag
is generated and pushed to the cloud storage along with the watermark image. In 2020,
Liu presented another scheme using Affine transform with large key space to encrypt the
watermark [30]. After performing the Schur transform, the author quantized the eigenvalues
of the diagonal matrix with different quantization steps. This proposal gives positive results
in terms of watermarked image quality, robustness, and system safety. 123 9
Multimedia Tools and Applications
Another publication based on the Schur transform is [31] by Li in 2020. Li divided the
original image into 8 × 8 blocks, then Schur transform was applied to each block. Next,
the watermark was erased by Arnold and Logistic Map before embedding into the element
with the largest energy D(1, 1) of the upper triangular matrix. In the article, the author
experimented with three black and white watermark images with sizes of 32 × 32, 48 × 48,
and 64 × 64. Peak Signal Noise Ratio (PSNR) values without attacks are in the range of 40
Dexibel (dB) and 47 dB. The results are better than those of the compared studies, except
that elastic attack and low-pass filtering still need to be improved in further studies.
Fourth, LU decomposition has the advantage of low computational complexity (O(n2))
compared to other matrix transformations such as SVD, QR, Schur, or Hessenberg. Therefore,
several studies have used LU factorization in digital image watermarking, including single
domain and hybrid domain [33–36]. In general, LU decomposition-based watermarking
methods often embed the information on the 2nd and 3rd elements of the first column of the
lower triangular matrix L. For instance, Su et al. realized a certain similarity between any
elements in the first column of matrix L after performing LU decomposition on 4 × 4 blocks
[33]. After that, Correlation Coefficient (CC) values between these elements are computed
to find the suitable elements to embed the watermark. The author chose L(2, 1) and L(3, 1)
for embedding because their distance is the smallest. This selection means that the energy is
concentrated on these two elements. In addition, the embedding length T was calculated and
selected to balance the quality of the watermarked image and the durability of the watermark.
However, the invisibility of the watermarked image is still affected because the simultaneous
two elements embedding of a block changes the pixel values significantly after embedding.
Therefore, the PSNR values are only 36 dB to 40 dB for the tested images. Furthermore, this
algorithm still needs to be studied to resist image rotation attacks.
This paper proposes a novel image watermarking scheme based on a LU block selection
strategy and an improved embedding algorithm. Three problems need to be addressed and
our contributions are as follows:
• First, according to linear algebra, not all square matrices can be analyzed as the product
of a lower and upper triangular matrix. The resulting matrix will give unknown values
if the LU decomposition is performed on all the original image blocks. This note has
not been addressed in previous studies. Therefore, in this paper, we have proposed a
block selection strategy based on the characteristics of LU decomposition. Accordingly,
a block is only applied LU decomposition and embedded a watermark bit when all the
determinants of the submatrices are non-zero. After that, this information is saved and
used for the extraction process. This solution not only helps to enhance the quality of the
watermarked image but also improves the robustness of the extracted watermark.
• Second, as discussed above, existing methods often embed information into two elements
of each block. This approach leads to changes in two rows of the pixel matrix. Therefore,
the quality of the watermarked image is decreased after embedding. To address this
problem, we have proposed a new embedding formula where the watermark is only
embedded into one element of a block. As a result, the pixel matrix is only modified
on one row, and then the invisibility of the watermarked image is better than previous methods.
• Third, the authors always utilize LU decomposition in the extraction process in existing
methods. However, this approach is unnecessary because the primary purpose of the LU
decomposition is to find the embedded elements (L(2, 1) and L(3, 1)). Based on this idea,
we have proposed an effective formula to calculate embedded elements instead of LU
decomposition. This calculation helps reduce the extraction time. 123 10
Multimedia Tools and Applications
The rest of this paper is arranged as follows. Section 2 discusses the related work and theory
analysis. In Sect. 3, the proposed adaptive watermarking algorithm is described in detail. The
experimental results and comparisons are shown in Sect. 4. Finally, a short conclusion is drawn in Sect. 5.
2 Related works and improved ideas 2.1 LU decomposition
An LU decomposition of a matrix A is the product of a lower triangular matrix and an upper
triangular matrix equal to A. It means that we can write A = LU , (1)
where L is a lower triangular matrix, and U is an upper one. Because LU decomposition is
not always unique, we consider an L matrix where all diagonal elements are set to 1.
For example, we have a 4 × 4 square matrix as follows: ⎡39 39 40 40⎤ 39 38 38 39 A ⎢ ⎥ = ⎢ ⎥ ⎣39 36 35 37⎦ 40 36 34 36
Then, the A matrix can be factorized into the L and U matrix as follows: ⎡ 1.000 0 0 0 ⎤ 1.000 1.000 0 0 L ⎢ ⎥ = ⎢ ⎥ ⎣ 1.000 3.000 1.000 0 ⎦ 1.0256 4.000 0.9744 1.000 and
⎡39.000 39.000 40.000 40.000 ⎤ 0 −1.000 −2.000 −1.000 U ⎢ ⎥ = ⎢ ⎥ ⎣ 0 0 1.000 0 ⎦ 0 0 0 −1.0256
In this example, the elements L(2, 1) and L(3, 1) are the closest. Therefore, these elements
are considered for embedding watermarks.
2.2 A noticeable point of LU decomposition
In linear algebra, LU decomposition is a direct method for obtaining the solution of systems
of equations in the form A X = B. It is an approach designed to exploit triangular systems.
However, some researchers found a significant point in this factorization. In [37], Taboga
et al. emphasized that “Sometimes it is impossible to write a matrix in the form of “lower
triangular” × “upper triangular””. In addition, two propositions are presented in [37] and [38] as follows:
Proposition 1 Not all square matrices have an LU factorization. 123 11
Multimedia Tools and Applications
Proof It is sufficient to provide a single counter-example. Take a 2 × 2 invertible matrix as 0 1 A = 1 0
Suppose A has an LU factorization A = LU with factors L L = 11 0 L21 L22 and U U = 11 U12 0 U22 Compute the product L LU = 11U11 L11U12
L21U11 L21U12 + L22U22
Now, A11 = (LU )11 implies L11U11 = 0, which in turn implies that at least one of L11 and
U11 must be zero. Consequently, at least one of L and U is not invertible (because triangular
matrices are invertible only if their diagonal entries are non-zero). This result contradicts the
fact that A is invertible; consequently, L and U must be invertible (see the proposition about
the invertibility of products). Thus, we have proved by contradiction that A cannot have an LU decomposition.
Proposition 2 An invertible matrix A has an LU decomposition, provided all its leading
sub-matrices have non-zero determinants.
To illustrate these arguments, we surveyed some digital images. The experiments are
performed on seven color images with a size of 512 × 512. Each image is divided into 4 ×
4 blocks; thereby, total number of blocks is 16,384. We calculate the number of unsuitable
blocks which do not agree with the above proposition, the rate, and the NC index for each
image. NC is a coefficient to measure the robustness of the extracted watermark. NC can be calculated by (2) m n
(W (x , y)W (x , y)) x=1 y=1 N C = , (2) m n
(W (x , y))2 m n
(W (x , y))2 x=1 y=1 x=1 y=1
where W (x, y) and W (x, y) present the value of pixel (x, y) of the original watermark
and the extracted one, m and n denote the size of the row and column of the watermark image, respectively.
The results are expressed in Table 1. Table 1 shows a relationship between the number of
unsuitable blocks and with NC index. It means that the original image has fewer unsuitable
blocks, a higher NC value, and vice versa. Therefore, to improve the extracted watermark’s
robustness, choosing suitable blocks before watermark embedding is necessary. We need to
embed the watermark on suitable blocks with LU decomposition instead of the whole pixel
blocks like the method in Su [33].
2.3 Considering the element to embed
Selecting an element to embed for an image watermarking scheme is extremely important.
In the paper [33], Su et al. computed Correlation Coefficient (CC) between the first column 123 12
Multimedia Tools and Applications
Table 1 Number of unsuitable Image (.bmp) Number of unsuit- Percentage (%) NC blocks for some images able blocks baboon 79 0.48 0.9952 lena 517 3.15 0.9714 avion 1040 6.34 0.9444 peppers 1414 8.63 0.9157 Girl 4959 30.26 0.8522 blueeye 8239 50.29 0.7918 anhinga 12488 76.22 0.7267
elements of two lower triangular matrices. The results showed that L21 and L31 are the
closest elements that can be used to embed information. However, because Su embedded the
watermark bits on these two elements simultaneously for each block, the values of the matrix
after embedding are changed on two rows. Thus, the pixel values of the watermarked image
are modified significantly. This approach causes the quality of the watermarked image to be reduced.
To overcome this issue, we propose a better solution that only embeds on L21 or L31
once for each block. Our proposal changes one row of the matrix after embedding, so the
invisibility (the quality of the embedded image) is significantly improved. Figure 1 compares
the formula of Su [33] and our method for both the embedding and extraction stages.
2.4 An idea for improving execution time
For a watermarking method, the execution time consists of embedding and extraction time.
In published image watermarking schemes, LU decomposition is always required in the
Fig. 1 A comparison between the formula of Su and the proposed formula 123 13
Multimedia Tools and Applications
extraction process [33–36]. This matrix factorization is unnecessary due to the unique feature
of LU decomposition. In the extraction stage, we only need to get out of L21 and L31 of the
L matrix. Let us consider the illustration below to see a new our solution. We suppose that ⎡ A ⎤
11 A12 A13 A14 A A ⎢ ⎥ =
21 A22 A23 A24 ⎢ ⎥ = L U , (3)
⎣ A31 A32 A33 A34⎦
A41 A42 A43 A44 where ⎡ 1 0 0 0⎤ ⎡U ⎤
11 U12 U13 U14 L 0 U L ⎢ ⎥ ⎢ ⎥ = 21 1 0 0 22 U23 U24 ⎢ ⎥ and U = ⎢ ⎥ (4) ⎣ L 31 L 32 1 0⎦ ⎣ 0 0 U33 U34⎦
L41 L42 L43 1 0 0 0 U44
By multiplying the L matrix with the U matrix and setting an equation to the A matrix, we have:
U11 = A11 , U12 = A12 and U13 = A13 (5)
Consider the first entry of the second row A21 A21
L21U11 = A21 ⇒ L21 = = , (6) U11 A11
and the first entry of the third row A31 A31
L31U11 = A31 ⇒ L31 = = . (7) U11 A11
Therefore, this is a beautiful way to find L21 and L31 without LU factorization. As a result,
this idea can significantly reduce calculation time in the extracting stage.
3 Proposed image watermarking method
This section presents a novel image watermarking scheme in which the appropriate blocks
for LU decomposition are chosen to embed the information. Before embedding, a watermark
embedding method is executed by utilizing Arnold transform to enhance the security of the
proposed algorithm. In the embedding stage, only one element of L matrix (L(2, 1) or L(3,
1)) is modified for each suitable block. In the extraction stage, we calculate L(2, 1) and L(3,
1) elements which are based on (6) and (7), without using LU factorization.
3.1 Scramble watermark image
To enhance the security of the proposed watermarking scheme, a transform called Arnold is
applied to permute pixels of the original watermark before embedding. Arnold scrambling
transforms the position of a pixel from (x, y) to a new location (s, t) [39]. The location of
pixels changes from one point to another based on (8). s 1 1 x = (mod 1), (8) t 1 2 y
where mod is modulo operation. 123 14
Multimedia Tools and Applications
To apply the transformation to a digital image the term “mod 1” can be replaced by “mod
N ” where N × N is the size of the digital image as (9). s 1 1 x = (mod N ) (9) t 1 2 y
An inverse Arnold transform can be given by (10). x 2 −1 s = (mod N ) (10) y −1 1 t
The security of Arnold Transform depends on the key for scrambling. The key can be selected
according to the number of iterations, which differs from image sizes. In our experiments,
the watermark image has a size of 32 × 32, so the number of iterations is 24, and the key is
an integer in the range of [1, 24]. 3.2 Embedding stage
The embedding stage of the proposed scheme includes steps as follows: • Step 1
– The host image is divided into 4 × 4 non-overlapping blocks. • Step 2
– The watermark is permuted by the Arnold Transform. The key for this operation is considered Key1.
– The permuted image is converted to a one-dimensional (1-D) binary array. • Step 3
– For each block, assign B component to a matrix A. • Step 4
– Calculate determinants of sub-matrices of A matrix,
– If one of the determinants = 0, return to Step 3.
– If all determinants = 0, go to Step 5. • Step 5
– Decompose A = LU
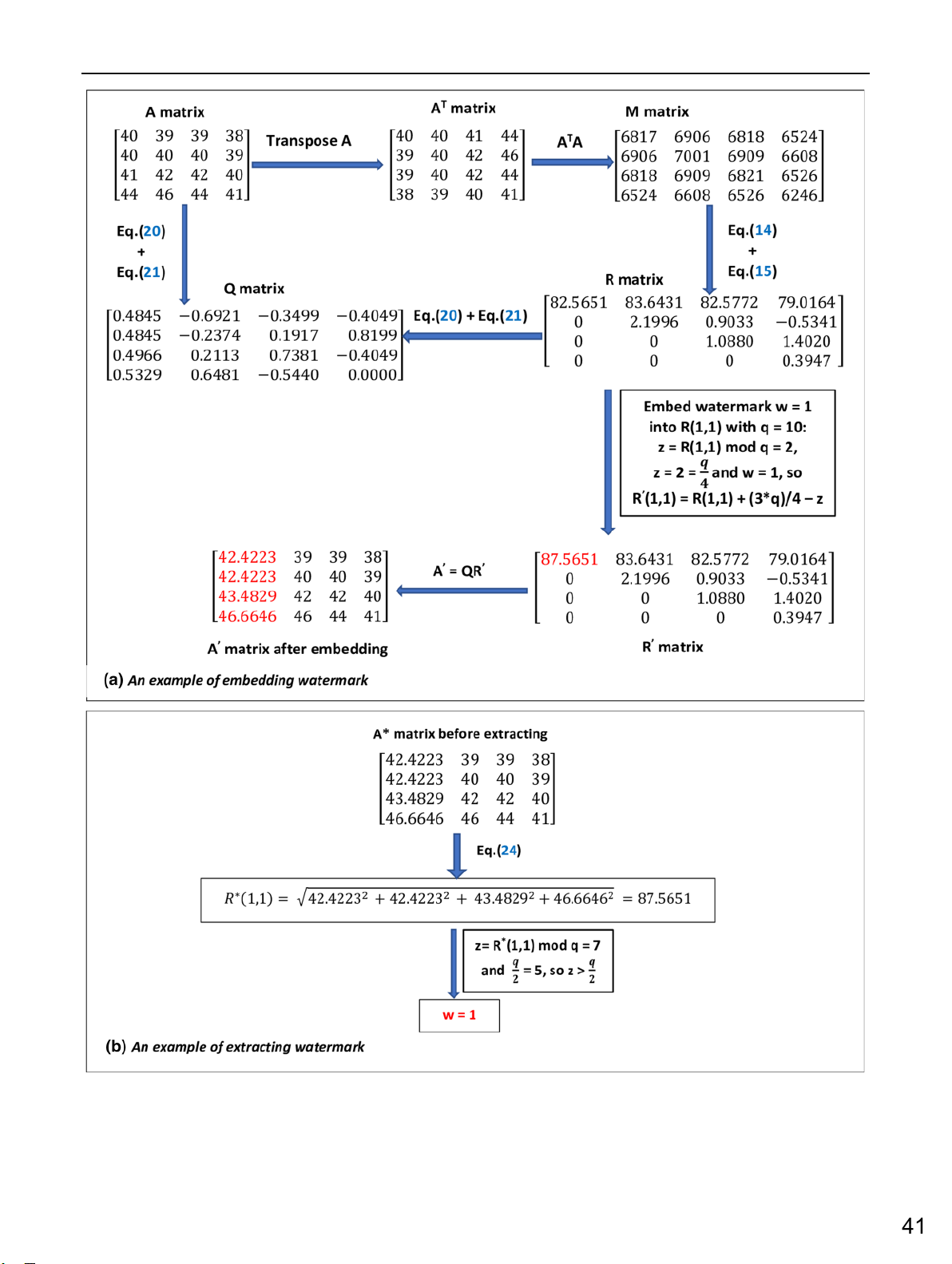
– Embed the corresponding watermark value into L(2, 1) or L(3, 1) of L matrix as follows:
– Case L(2, 1) ≥ L(3, 1) and wi =“1”
L(2, 1) = L(3, 1) − T , (11)
– Case L(2, 1) ≤ L(3, 1) and wi =“0”
L(3, 1) = L(2, 1) − T , (12)
where T is the embedding strength of the watermark. • Step 6
– Update A to A’ = L’U and assign A’ back to B components of the block. 123 15
Multimedia Tools and Applications
– Mark and save the suitable block to a file. This information is considered Key 2 of the scheme.
– Repeat steps 3 to 6 until all suitable blocks are embedded. • Step 7
– Reconstruct watermarked B component to receive the watermarked image.
The flow chart of the embedding operation is illustrated in Fig. 2. 3.3 Extraction stage
The extraction stage is done by reversing the embedding stage. The flowchart of the extraction process is shown in Fig. 3. • Step 1
– The watermarked image is divided into 4 × 4 non-overlapping blocks. • Step 2
– For each block, assign B component to a matrix A. • Step 3
– Check the block by comparing it to the saved file (Key2).
– If the block is not in the file, it means that it is unsuitable; return to Step 2
– If the block is in the file, it means that it is suitable; go to Step 4 • Step 4
– Get out the elements of the L matrix by (6) and (7).
– Extract information of watermark as follows:
"0", if L∗(2, 1) ≥ L∗(3, 1) w∗ i = (13) "1", elsewhere
– Repeat steps 2 to 4 until all watermark bits are extracted. • Step 5
– Convert extracted watermark values to an image.
– Apply Inverse Arnold Transform with Key1 to get the final extracted watermark image.
4 Experimental results and discussion 4.1 Evaluation criteria
To evaluate the performance of our proposed watermarking scheme, PSNR and NC criteria are
employed [16]. PSNR is an adequate criterion to estimate the imperceptibility of watermarked
images, while NC can measure the similarity between the original watermark and the extracted
one. NC value is also a vital establishment to evaluate the robustness of a watermarking 123 16
Multimedia Tools and Applications
Fig. 2 Embedding process 123 17
Multimedia Tools and Applications
Fig. 3 Extraction process 123 18
Multimedia Tools and Applications
scheme. NC index can be calculated by (2), which is always less than or equal to “1”.
Meanwhile, the PSNR index is designed as follows: 2552 P S N R = 10 log10 , (14) M S E
where the mean square error (M S E) between the original and watermarked image is defined as: M−1 N −1 1 M S E =
(H (i , j ) − H (i , j ))2, (15) M N i=0 j=0
where M × N is the size of the image, H (i , j ) and H (i , j ) are the pixel value at position
(i , j ) of the host image and the watermarked image, respectively.
Moreover, we also use the Structural Similarity Index Measurement (SSIM) index as the
criteria to evaluate the quality of watermarked images. The SSIM was correlated with the
quality perception of Human Visual System (HVS). The SSIM, as denoted in (16), is also
used to measure the similarity between the original color image H and the watermarked image H .
S S I M(H , H ) = l(H , H )c(H , H )s(H , H ), (16) where ⎧
(2µH µH + C1)
⎪l ( H , H ) = ⎪ ⎪ ⎪ (µ2 + µ2 ⎪ H H + C1) ⎪ ⎨
(2σH σH + C2)
c(H , H ) = (17) (σ 2 + σ 2 ⎪ ⎪ H H + C2) ⎪ ⎪ (σ ⎪ H H + C3)
⎪s( H , H ) = ⎩
(σH σH + C3)
The first term in (17) is the luminance comparison function which measures the closeness of
the two images’ mean luminance (µH and µH ). The second term is the contrast comparison
function which measures the closeness of the contrast between the two images. Here the
contrast is measured by the standard deviation σH and σH . The third term is the structure
comparison function which measures the correlation coefficient between the two images H
and H . Note that σH H is the covariance between H and H . The positive values of the SSIM
index are in [0, 1]. “0” means no correlation between images, and “1” means that H = H .
The positive constants C1, C2, and C3 are used to avoid a null denominator.
In our experiments, five color 512 × 512 images from the CVG-UGR image database
[40] are chosen as the host images. A binary 32 × 32 image is the watermark, as shown in
Fig. 4. The host images are standard color images involving various types such as portrait,
landscapes, animal, and fruit photos. The pixel distribution of these images is different from
each other. The host images are saved as .bmp files, and the watermark is in .png format.
In addition, a computer with I ntel@ Cor eT M i5-6200U CPU at 2.30GHz, 4.00GB RAM,
64-bit OS, Visual Studio v15, and OpenCV 2.4.9 is utilized as the computing platform. The
embedding strength T is defined as 0.0275, which is the same as the method of SuLU [33].
This value balances between the watermarked image’s quality and the watermark’s robustness
after extraction. A comparison between the methods of SuQR [22], SuLU [33], Luo [16], Hu
[17], Chen [25], Li [31] and our proposal is performed to simulate the effectiveness of the proposed algorithm. 123 19
Multimedia Tools and Applications
Fig. 4 The host images: (a) Girl, (b) lena, (c) peppers, (d) avion, (e) baboon. The watermark: (f) logo.png
4.2 Imperceptibility experiments
The results of imperceptibility experiments are shown in Fig. 5. The quality of watermarked
images is evaluated by PSNR and SSIM indexes. In general, the watermarked image is more
invisible when the value of PSNR is bigger or the value of SSIM is near 1. Theoretically,
the extracted watermark should be the same original watermark in the absence of attacks. It
means that the NC value must be 1. However, it is not completely correct in our experimental
tests. The NC value is less than one because it depends on the structure of the host images as
well as the embedding parameters. In all methods, the embedding parameters are chosen to
a suitable value to balance the watermarked image’s quality and the extracted watermark’s robustness.
The figures show that values of PSNR and SSIM of the proposed watermarking algorithm
are higher than the methods of SuLU [33], Luo [16], Hu [17], and Chen [25] for all five
images. Our method embeds the watermark into one element for each block, so the pixel
matrix is only changed on one row instead of two rows as in the other methods. In addition,
because the proposed scheme selects suitable blocks before embedding, this improvement
has a part in pulling up the imperceptibility. Besides, the NC values of our proposed method
are almost better than that of other methods. According to the results shown in Fig. 5, the
proposed strategy of block selection works well with our watermarking method.
In the contrary, the studies [16, 17, 25, 33] embedded the watermark on two elements of
the L matrix, the U matrix, and the Q matrix, respectively. This approach causes a significant
change in two rows of the corresponding block after embedding. Thus, the pixel values of the 123 20
Multimedia Tools and Applications
Fig. 5 The results of invisibility tests
watermarked image will not be close to the original image. In [16], Luo embedded on U(2,
1) and U(3, 1) of the U orthogonal matrix after doing SVD decomposition. It is similar to
[33] where Su modified L(2, 1) and L(3, 1) of the L lower triangular matrix at the same time.
Thus, this leads to a significant change in the pixel values after embedding. As a result, the
quality of the watermarked image will be pulled down. Meanwhile, the methods of Li [31]
and SuQR [22] have higher PSNR/SSIM values. These methods used one element of the 123 21
Multimedia Tools and Applications
triangular matrix to embed the watermark. Thereby, the embedded block only changes in one
row instead of two rows as in the cases of SuLU [33], Luo [16], Hu [17], and Chen [25].
In addition, the figures in Fig. 5 display that the algorithms of Su [33] and Hu [17] bring
a low result in terms of PSNR and SSIM. This result is because these methods embedded the
information on three channels instead of one channel as the others. Although embedding on
three channels enhances the embedded capacity, it leads to distortion of the pixel values.
4.3 Robustness experiments
Robustness is a critical evaluation criterion for designing watermarking schemes, so image
processing operations are often added to evaluate the performance of this criterion. In our
experiments, three watermarked images are chosen to test under six basic attacks: blurring,
sharpening, salt&pepper noise, rotation, scaling, and JPEG compression. Table 2 describes
shortly different image attacks used in our robustness tests.
The blurring technique is set up by two arguments, like radius and sigma. The first value,
radius, is important as it controls how big an area the operator should look at when spreading
pixels. This value should typically be either ‘0’ or at least double that of the sigma. The
second sigma value can approximate how much you want the image to spread or blur in
pixels. Think of it as the size of the brush used to blur the image. In the experiments, the
radius is fixed to ‘0’, and the sigma is designed to be 0.2 and 0.3, respectively.
The sharpening operator is an inverted blur. It works in just about the same way. The larger
the sigma, the more it sharpens. Therefore, its arguments are similarly set to blur.
By randomly selecting the noise values, the pixels can change to white, black, or gray
matter, thus adding the salt and pepper colors. The noise is scattered throughout the image by
randomly selecting which pixels are changed. Combining these selections creates the “salt
and pepper” effect throughout the image. The tests use various degrees of noise, such as 0.002, 0.005, and 0.01.
Table 2 Various attacks used in our experiments Index Attacks Description 1 Blur
Blur the watermarked image with a radius = 0 and sigma is designed to be 0.2 and 0.5, respectively. 2 Sharpen
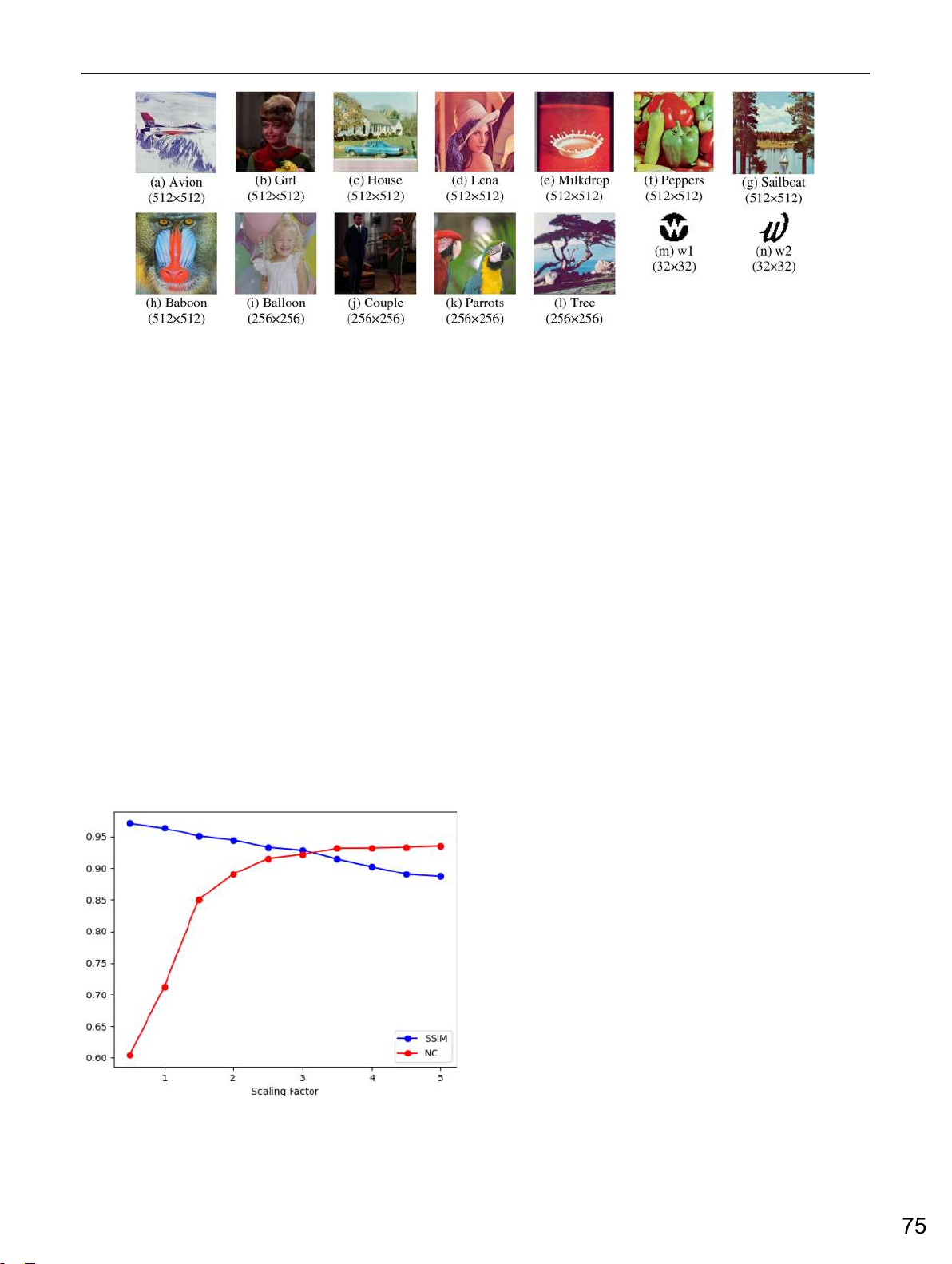
Sharpen the watermarked image with a radius = 0 and sigma is designed to be 0.2 and 0.5, respectively. 3 Scaling (1/2)
Resize the watermarked image from 512×512 to 256×256 and subsequently restore it to 512 × 512. 4 Scaling (2)
Resize the watermarked image from 512 × 512 to 1024 × 1024 and subse-
quently restore it to 512 × 512. 5 S&P noise
Add salt and pepper noise to the watermarked image with a noise density den = 0.002, 0.005, 0.01. 6 Rotation 5o
Rotate the watermarked image clockwise at an angle=5 and subsequently
rotate it counterclockwise at an angle=-5. 7 Rotation 10o
Rotate the watermarked image clockwise at an angle=10 and subsequently
rotate it counterclockwise at an angle=-10. 8 JPEG
Compress the watermarked images by using DCT transform with size of window 8 × 8 and 16 × 16. 9 Gaussian noise
Add Gaussian noise to the watermarked image with µ = 0 and variance σ 2 = 0.001, 0.003. 123 22
Multimedia Tools and Applications
In computer graphics and digital imaging, image scaling refers to resizing a digital image.
When scaling a raster graphics image, a new image with a higher or lower number of pixels
must be generated. In the case of decreasing the pixel number, this usually results in a visible
quality loss. From the standpoint of digital signal processing, the scaling of raster graphics
is a two-dimensional example of sample-rate conversion, the conversion of a discrete signal
from one sampling rate to another. In our experiments, the watermarked images are resized by 50% and 200%.
Image rotation is a typical image processing routine with applications in matching, align-
ment, and other image-based algorithms. The input to an image rotation routine is an image,
the rotation angle, and a point about which rotation is done.
Join Photographic Experts (JPEG) is a commonly used method of lossy compression
for digital images. JPEG works on DCT, a fast-computing Fourier transform type that maps
accurate signals to corresponding values in the frequency domain. The degree of compression
can be adjusted, allowing a selectable tradeoff between storage size and image quality.
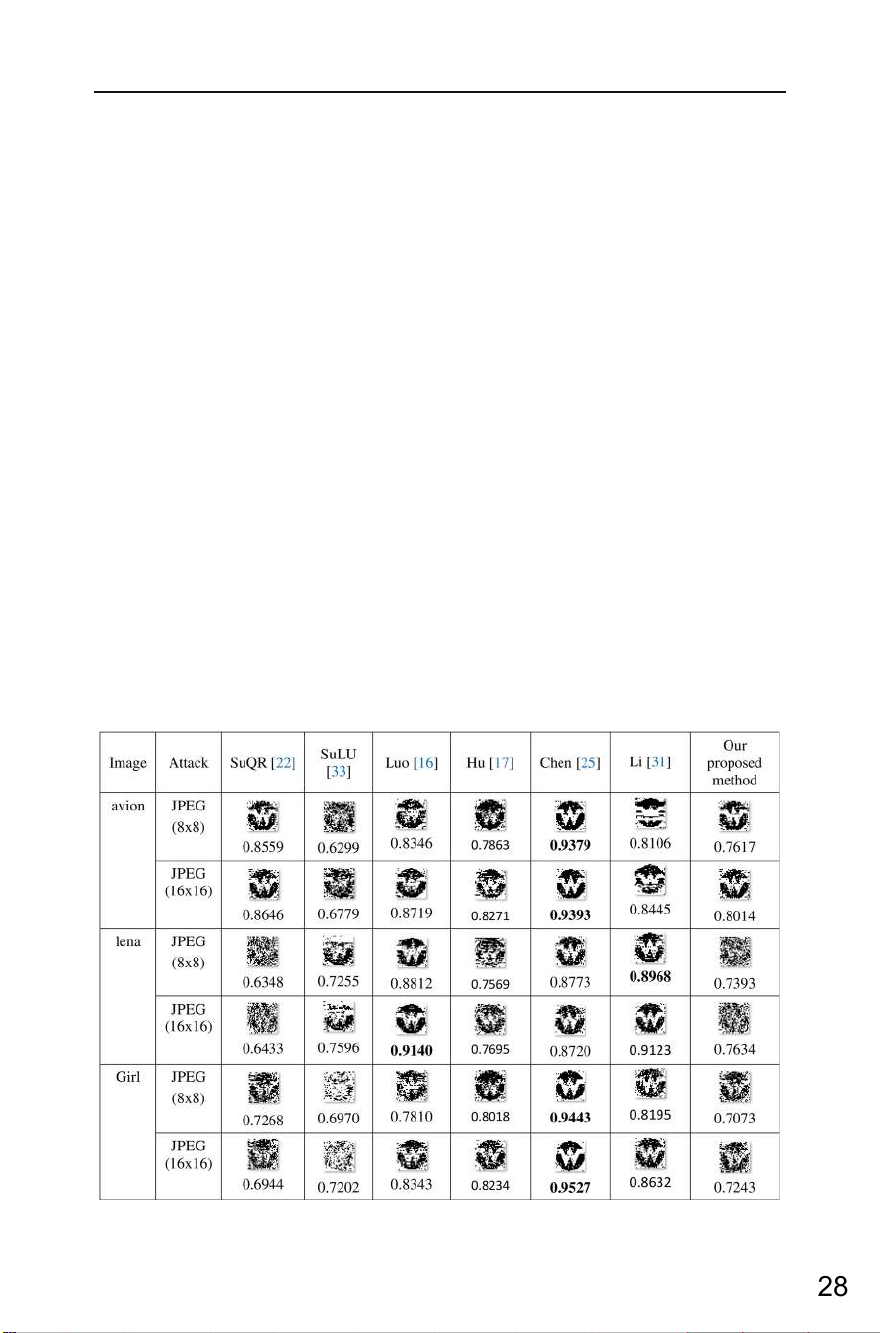
The results in Figs. 6, 7, and 8 show that the proposed method is very effective under
attacks such as blurring, sharpening, and salt & pepper because NC values are above 0.9 for
all these attacks. Moreover, our method overcomes the schemes of Li [31], SuLU [33], Luo
[16] under these attacks. Our proposed method is better than the other approaches because
of block selection and embedding strategy. Furthermore, it is easy to see that all schemes can
prevent damage from blurring and sharpening attacks. The extracted watermark of Hu [17]
and Chen [25] is clearer to recognize than the others for the “avion” and “lena” images when the sigma is set to 0.5.
Fig. 6 The results of robustness tests under blurring attack. The best values are in bold 123 23
Multimedia Tools and Applications
Fig. 7 The results of robustness tests under sharpening attack. The best values are in bold
4.4 A comparison of execution time
In general, the execution time of transform domain-based watermarking image algorithms
depends mainly on the type of matrix decomposition used. SVD decomposition needs about
11n3 flops for an n × n matrix whereas the required time to compute LU factorization is
n2 flops. And QR decomposition is an intermediate stage between SVD and LU. In [25],
Chen used QQRD which is based on Householder transformation for matrix calculation. 4n3
The Householder algorithm requires approximately
flops for an n × n matrix. On the 3
other hand, the scheme of Hu [17] is based on SVD factorization with mixed modulation
incorporated. And its time complexity is the sum of the five basic processing modules with an
image block size of n × n: SVD (O(4n3)), orthonormal restoration (O(2n3)), distortion com-
pensation (O(3n2)), matrix decomposition (O(2n3)), and tentative verification (O(4n3)).
The overall complexity of this method for a color image of N × N pixels is estimated as
N × N (12n3 + 3n2). Therefore, the SVD and QR decomposition-based approaches, such n × n
as Luo [16], SuQR [22], Chen [25], and Hu [17] have time complexity of O(n3) for an n ×
n matrix. The method of Li [31] also need a computational complexity of O(n3) because it
was based on Schur decomposition. For the proposed scheme, the embedding time complex- N × N ity is
O(n2) while the extraction time complexity of the proposed approach is only n × n
N × N O(1) for a color image of N × N pixels. n × n
Table 3 compares the execution time between different methods. According to Table 3,
the total execution time of the proposed method is bigger than the time of Su [33], which
uses LU decomposition, but it is smaller than the other methods. In the scheme of Luo [16],
the author proposed a combination of DWT and SVD, so this method spends more time than
the others except for the approach of Hu [17]. Meanwhile, the algorithm of Hu [17] applied
many processing modules, such as level shifting with dither noise, SVD, sign correction, 123 24
Multimedia Tools and Applications
Fig. 8 The results of robustness tests under salt&pepper noise attack. The best values are in bold
Table 3 Average execution time of different methods (in second). The best values are in bold Method Embedding time Extraction time Total time SuQR [22] 0.3718 0.0296 0.4014 SuLU [33] 0.1774 0.0074 0.1848 Luo [16] 2.4566 0.1730 2.6296 Hu [17] 5.2116 1.0348 6.2464 Chen [25] 0.4001 0.0279 0.4280 Li [31] 0.5213 0.0482 0.5695 Proposed method 0.2750 0.0060 0.2810 123 25
Multimedia Tools and Applications
mixed modulation, orthonormal restoration, distortion compensation, tentative verification,
and iterative regulation. It is the reason why its running time is the biggest. For embedding
time, the algorithm SuQR [22] and the method of Chen [25] are similar because they use QR
factorization based on Gram-Schmidt and Householder algorithms, respectively. However,
the algorithm of Chen [25] needs more time to measure the correlation between elements qi j
of the Q matrix and select an optimal quaternion embedding position, so it costs a higher
number. The method of Su [33] consumes the least time, while the scheme of Luo [16] costs
more time to calculate. This result is because Luo combined DWT and SVD decomposition,
which have a considerable computational complexity. Although both the method of Su [33]
and the proposed method use LU decomposition, the proposed method spends more execution
time than the one of Su [33]. This result is because the proposed method needs to check and
select suitable blocks. However, this expense can be accepted when considering its effects
on improving the quality and robustness of the watermarked image.
For extraction time, the proposed method needs the lowest computation time because
the remaining methods always use matrix expansions in the watermark extraction process.
In contrast, the proposed method calculates the embedded elements L(2, 1) and L(3, 1)
via (6) and (7) without using LU decomposition. This solution helps reduce extraction time
significantly. Overall, the execution time of the proposed method can satisfy with requirement of real-time applications. 5 Conclusions
In summary, a novel image watermarking scheme based on LU decomposition is presented in
this paper. Both embedding and extraction stages are improved to enhance the watermarked
image’s quality, the extracted watermark’s robustness, and the execution time. In the embed-
ding stage, each 4 × 4 block of the host image is checked to see if it satisfies the condition for
decomposing LU. After that, a watermark preprocessing operation is performed by applying
Arnold Transform before embedding information on L(2, 1) or L(3, 1) of L matrix of suitable
blocks via the proposed formula. The watermarked image is received after all selected blocks
are embedded. In the extraction stage, instead of calculating LU factorization, L(2, 1) and
L(3, 1) are gotten out easily by using (6) and (7). This solution helps save much time for the
extraction process. The experimental results illustrate that the proposed algorithm not only
overcomes the method of Su [33] and Luo [16] in terms of the quality of the watermarked
image but also significantly improves the robustness under some attacks and the execution
time. However, the proposed scheme is less robust against geometric attacks and JPEG com-
pression. Sometimes, the extracted watermark can not be recognized under these attacks.
In addition, the proposed scheme has only experimented on the host 512 × 512 images
and the binary watermark. Therefore, in the future, the performance of resisting geometric
attacks and JPEG compression will be further studied, and our work will be extended to color watermarks.
Appendix A: Robustness experiments
For geometric attacks such as rotation, scaling, and JPEG compression, the robustness of
all seven methods is weak. In seven methods, the method of Hu [17] is better than others,
particularly under scaling ×2 operation and rotation attacks. The method of Chen [25] and 123 26
Multimedia Tools and Applications
Fig. 9 The results of robustness tests under rotation attack. The best values are in bold
Fig. 10 The results of robustness tests under scaling attack. The best values are in bold 123 27
Multimedia Tools and Applications
Luo [16] overcome others, particularly under JPEG attacks. Although the proposed method
is more improved than the method of Su [33], NC values are only around 0.6 to 0.8, and
the watermark cannot be recognized for some cases. This result happens because of the
particularity of LU decomposition. This property is considered a disadvantage of the schemes
based on LU decomposition. As described in Sect. 2.2, not all square matrices have an LU
factorization. Therefore, geometric attacks can make a change to this property of blocks.
As a result, the watermark after extraction will be much modified. The results’ details are
displayed in Figs. 9, 10, and 11.
From data in Figs. 9 and 10, although the proposed method gives less robustness than the
methods of Li [31], Luo [16], Hu [17], and Chen [25], it is more effective than the schemes
of SuQR [22] and SuLU [33]. In these experiments, SVD and Schur decomposition-based
studies, such as Li [31], Luo [16], and Hu [17] bring better quality than others. Especially,
the proposals of Hu [17] and Li [31] are the most robust against geometric attacks.
As the results are shown in Fig. 11, most schemes are weak against JPEG compression,
especially the algorithm of SuLU [33]. The method of Chen [25] has the best performance
for the “avion” and “Girl” images while the approach of Luo [16] overcomes the others for
the “lena” image. In the contrast, the proposal of Hu [17] has limited resistance to this kind of
attack. Although the proposed method is not the best method under JPEG compression, it has
higher NC values than the methods of SuQR [22] and SuLU [33] for all three watermarked images.
Figure 12 displays NC values and the extracted watermarks of seven methods under
Gaussian noise. The results indicate that the proposed scheme can resist adding Gaussian
noise well. The watermarks are recognized under this attack. The average NC value of
the proposed method is 0.97. Our scheme also outperforms other methods for all three
watermarked images. The method of Luo [16] is less robust against this attack for “lena”
Fig. 11 The results of robustness tests under JPEG compression attack. The best values are in bold 123 28
Multimedia Tools and Applications
Fig. 12 The results of robustness tests under Gaussian noise. The best values are in bold
image, while the method of SuLU [33] is weak for “Girl” image. The extracted watermark
cannot be recognized in these two cases.
Data Availability The datasets generated during the current study are available in the [imagewwatermarking]
repository, https://github.com/phuongnhatin1/imagewatermarking References
1. Anastasios Tefas, Nikos Nikolaidis, Ioannis Pitas, Chapter 22 - Image Watermarking: Techniques and
Applications, Editor(s): Al Bovik, The Essential Guide to Image Processing, Academic Press,2009, pp.
597-648, ISBN 9780123744579 https://doi.org/10.1016/B978-0-12-374457-9.00022-6
2. Moon SK, Raut RD (2021) Anti-forensic reversible multi-frame block to block pixel mapping information
concealing approach to increase the robustness and perceptibility. International Journal of Information
and Computer Security 14(3–4):403–439
3. Moon, S. K. (2022). “Authentication and Security Aspect of Information Privacy Using Anti-forensic
Audio-Video Embedding Technique.” In Inventive Systems and Control: Proceedings of ICISC 2022 (pp.
157-171). Singapore: Springer Nature Singapore
4. Moon SK (2022) Software and hardware-based audio-video crypto steganalysis model for enhancing
robustness and imperceptibility of secured data. Multimedia Tools and Applications 81(15):21047–21081
5. Amrit P, Singh AK (2022) Survey on watermarking methods in the artificial intelligence domain and
beyond. Computer Communications 188:52–65
6. Singh, K.N., Singh, O.P., Singh, A.K. et al.(2022) “WatMIF: Multimodal Medical Image Fusion-Based
Watermarking for Telehealth Applications.” Cogn Comput . https://doi.org/10.1007/s12559-022-10040- 4
7. Singh, O. P., Singh, A. K., & Zhou, H. (2022). “Multimodal fusion-based image hiding algorithm for the
secure healthcare system.” IEEE Intelligent Systems
8. Su, Q., Chen, B. (2018) “Robust color image watermarking technique in the spatial domain”. Soft Comput,
22, pp. 91-106. https://doi.org/10.1007/s00500-017-2489-7 123 29
Multimedia Tools and Applications
9. Hsu L-Y, Hu H-T (2017) Robust blind image watermarking using crisscross inter-block prediction in the
DCT domain. Journal of Visual Communication and Image Representation 46:33–47
10. Ko HJ, Huang CT, Horng G, Shiuh-Jeng WANG (2020) Robust and blind image watermarking in DCT
domain using inter-block coefficient correlation. Information Sciences 517:128–147
11. Ariatmanto D, Ernawan F (2020) An improved robust image watermarking by using different embedding
strengths. Multimedia Tools and Applications 79(17–18):12041–12067
12. Rajani D, Kumar PR (2020) An optimized blind watermarking scheme based on principal component
analysis in redundant discrete wavelet domain. Signal Processing 172:107556
13. Kumar S, Singh BK (2021) DWT based color image watermarking using maximum entropy. Multimedia
Tools and Applications 80:15487–15510
14. Liu D, Su Q, Yuan Z, Zhang X (2021) A fusion-domain color image watermarking based on Haar transform
and image correction. Expert Systems with Applications 170:114540
15. Vaishnavi D, Subashini TS (2015) Robust and Invisible Image Watermarking in RGB Color Space Using
SVD. Procedia Computer Science 46:1770–1777
16. Luo, A., Gong, L., Zhou, N. et al. “Adaptive and blind watermarking scheme based on optimal SVD blocks
selection”, Multimed Tools Appl, 79, 243-261 (2020). https://doi.org/10.1007/s11042-019-08074-2
17. Hwai-Tsu Hu, Ling-Yuan Hsu, Hsien-Hsin Chou (2020), “An improved SVD-based blind color image
watermarking algorithm with mixed modulation incorporated”, Information Sciences, Volume 519,
pp.161-182, ISSN 0020-0255, https://doi.org/10.1016/j.ins.2020.01.019
18. Ahmadi SBB, Zhang G, Rabbani M, Boukela L, Jelodar H (2021) An intelligent and blind dual color
image watermarking for authentication and copyright protection. Applied Intelligence 51:1701–1732
19. Wang X, Yao Y, Yu Y, Niu P, Yang H (2023) Statistical image watermark decoder by modeling local RDWT
difference domain singular values with bivariate weighted Weibull distribution. Applied Intelligence 53(1):96–120
20. Su, Q., Niu, Y., Zou, H. et al. “A blind double color image watermarking algorithm based on QR decom-
position”. Multimed Tools Appl, 72, pp. 987-1009 (2013). https://doi.org/10.1007/s11042-013-1653-z
21. Qingtang Su, Gang Wang, Xiaofeng Zhang, Gaohuan Lv, and Beijing Chen (2017), “An improved color
image watermarking algorithm based on QR decomposition”, Multimed Tools Appl, 76, pp. 707-729.
https://doi.org/10.1007/s11042-015-3071-x
22. Qingtang Su, Liu Yonghui, Liu Decheng, Yuan Zihan, Ning Hongye (2019) A new watermarking scheme
for the color image using QR decomposition and ternary coding. Multimedia Tools and Applications 78(7):8113–8132
23. Hsu CS, Tu SF (2020) Enhancing the robustness of image watermarking against cropping attacks with
dual watermarks. Multimedia Tools and Applications 79(17–18):11297–11323
24. Li M, Yuan X, Chen H, Li J (2020) Quaternion discrete fourier transform-based color image watermarking
method using quaternion QR decomposition. IEEE Access 8:72308–72315
25. Yong Chen, Zhi-Gang Jia, Yan Peng, Ya-Xin Peng, Dan Zhang (2021), “A new structure-preserving
quaternion QR decomposition method for color image blind watermarking”, Signal Processing, Volume
185, 108088, ISSN 0165-1684, https://doi.org/10.1016/j.sigpro.2021.108088
26. Hsu LY, Hu HT, Chou HH (2022) A high-capacity QRD-based blind color image watermarking algorithm
incorporated with AI technologies. Expert Systems with Applications 199:117134
27. Su Q, Chen B (2017) An improved color image watermarking scheme based on Schur decomposition.
Multimedia Tools and Applications 76:24221–24249
28. Hsu LY, Hu HT (2019) A reinforced blind color image watermarking scheme based on Schur decompo-
sition. IEEE Access 7:107438–107452
29. Su Q, Zhang X, Wang G (2020) An improved watermarking algorithm for color image using Schur
decomposition. Soft Computing 24(1):445–460
30. Liu D, Yuan Z, Su Q (2020) A blind color image watermarking scheme with variable steps based on Schur
decomposition. Multimedia Tools and Applications 79:7491–7513
31. Li JY, Zhang CZ (2020) Blind watermarking scheme based on Schur decomposition and non-subsampled
contourlet transform. Multimedia Tools and Applications 79:30007–30021
32. Liu D, Su Q, Yuan Z, Zhang X (2021) A color watermarking scheme in frequency domain based on
quaternary coding. Visual Computer 37:2355–2368
33. Qingtang Su, Wang Gang, Zhang Xiaofeng, Lv Gaohuan, Chen Beijing (2018) A new algorithm of blind
color image watermarking based on LU decomposition. Multidimensional Systems and Signal Processing 29(3):1055–1074
34. Wang Dongyan, Yang Fanfan, Zhang Heng (2016) Blind Color Image Watermarking Based on DWT and
LU Decomposition. Journal of Information Processing System 12(4):765–778
35. Muñoz-Ramírez DO, García-Salgado BP, Ponomaryov V, Reyes-Reyes R, Sadovnychiy S, Cruz-Ramos
C (2021) A color image watermarking framework for copyright protection of stereo images based on 123 30
Multimedia Tools and Applications
binocular just noticeable difference and LU decomposition. Multimedia Tools and Applications 80:13707– 13734
36. Horasan F (2022) A novel image watermarking scheme using ULV decomposition. Optik 259:168958
37. Taboga, Marco, “LU decomposition”, Lectures on matrix algebra, 2017. https://www.statlect.com/matrix- algebra/lu-decomposition
38. Abdulraheem, M. Z., & Mohammad, K. (2018). “LU Decomposition Computerized Method to Solve
Linear Programming Problems.” Journal of Applied and Computational Mathematics, ISSN: 2168-9679, Volume 7, Issue 2
39. Sehra K, Raut S, Mishra A, Kasturi P, Wadhera S, Saxena GJ, Saxena M (2021) Robust and secure digital
image watermarking technique using Arnold transform and memristive chaotic oscillators. IEEE Access 9:72465–72483
40. University of Granada, Computer Vision Group, CVG-UGR Image Database, http://decsai.ugr.es/cvg/
dbimagenes/c512.php. Accessed Dec 2021
Publisher’s Note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under
a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted
manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law. 123 31
Soft Computing (2022) 26:5069–5093
https://doi.org/10.1007/s00500-022-06975-3 F O U N D A T I O N S
Consideration of a robust watermarking algorithm for color image
using improved QR decomposition
Phuong Thi Nha1 · Ta Minh Thanh1 · Nguyen Tuan Phong1
Accepted: 17 January 2022 / Published online: 31 March 2022
© The Author(s), under exclusive licence to Springer-Verlag GmbH Germany, part of Springer Nature 2022 Abstract
In order to protect the digital image copyright, it is necessary to design a robust watermarking algorithm. To achieve this
purpose, a novel color image watermarking scheme based on an improved Q R decomposition is proposed in this paper. The
proposed method gives a new algorithm to find elements of Q and R matrices instead of using the Gram–Schmidt algorithm
for Q R factorization. First, the R matrix is performed by solving a set of linear equations where diagonal elements of R are
checked and modified if they are zero or negative. After that, the Q matrix is computed based on the R matrix. In addition, a
novel formula is proposed to improve the extracting time where the first element R(1, 1) of the R matrix is found instead of
computing Q R decomposition as the previous proposals. Experimental results show that the proposed method outperforms
other considered methods in this paper in terms of the quality of the watermarked images. Furthermore, the execution time is
significantly improved, and the extracted watermark is more robust against almost tested attacks.
Keywords Digital watermarking · Copyright protection · Gram–Schmidt algorithm · Q R factorization · Quantization index modulation (QIM) 1 Introduction
the best one until now. Watermarking is a process of embed-
ding digital information called watermark into an image by 1.1 Overview some constraints.
Depending on the watermark embedding domain, digital
In recent years, exchanging digital data via the Internet has
watermarking methods can be divided into two main cat-
become more and more popular. The rapid development of
egories: spatial domain and transform domain. In spatial
digital technology techniques and devices has brought a lot
domain techniques, the watermark is inserted by directly
of convenience for users. However, it is also a fertile land
altering the pixel intensities of the cover image (Su and
for attacks who want to steal or fake information. Therefore,
Chen 2018). Altering the least significant bits (LSB) of the
inspecting the integrity and the authentication of data is an
cover image is one of the common spatial domain-based
extremely important issue to tackle risks. For images, besides
watermarking techniques. Spatial domain methods have low
general rules of the law, there are some applied methods such
computational complexity, but they are not usually robust
as encryption, information hiding, and watermarking to help
against almost image processing or other attacks. On the other
owners protect their digital copyright. Among these tech-
hand, in transform domain methods, the original image is first
niques, the image watermarking technique has been known as
transformed into the frequency domain by several transfor-
mation methods such as discrete cosine transform (DCT), B
discrete wavelet transform (DWT), or matrix decomposition Ta Minh Thanh thanhtm@lqdtu.edu.vn
such as singular value decomposition (SVD), QR decompo-
sition, LU decomposition, and Schur decomposition. Then, Phuong Thi Nha phuongthinha@lqdtu.edu.vn
according to certain criteria, the transform domain coeffi-
cients are altered for embedding the watermark information. Nguyen Tuan Phong tuanphongnguyen1974@gmail.com
Finally, the inverse transform is applied to obtain the water-
marked digital image. Although watermarking methods in 1
Le Quy Don Technical University, 236 Hoang Quoc Viet,
the frequency domain have high computational complexity, Hanoi, Vietnam 123 32 5070 P. T. Nha et al.
they are always more robust than spatial domain-based water-
the Q matrix not only have the same sign but also have sim- marking schemes.
ilar values (Su et al. 2013). The Q R decomposition-based
Image watermarking schemes based on DCT transforma-
watermarking also has satisfactory performance in terms of
tion often embed watermark on the median frequency to
imperceptibility and robustness (Chen et al. 2021). Further-
harmonize between the quality of the watermarked image and
more, due to concentrating energy of Q R analysis on the first
the robustness of the extracted information (Su et al. 2015;
element of the R triangular matrix, the information is often
Hsu and Hu 2017). If the embedding is implemented on low
embedded in this element (Qingtang et al. 2017, 2019). Dis-
frequency, the extracted watermark is good, but the invisi-
covering the suitable element to embed is one of the major
bility of the watermarked image is bad and vice versa. For
factors for determining the effectiveness of an image water-
DWT transformation, the watermark is commonly inserted
marking scheme. This completely agrees with the purpose of
on LL low sub-domain to archive a robust result (Giri et al.
watermarking technique which only focuses on some high-
2015). However, to balance between the quality of the water-
energy elements instead of embedding information on all
marked image and the robustness of the extracted watermark,
elements of the pixel matrix to guarantee the quality of the
the watermark is also embedded into HL and LH sub-bands. watermarked image.
For SVD decomposition, there are two trends for the
For the above importance of Q R decomposition, many
embedding and extracting process. The first one used the
researchers utilized Q R decomposition to transform pixel
first element D(1, 1) of the D triangular matrix to change
matrices in their watermarking techniques (Su et al. 2013;
pixel values (Sun et al. 2002; Vaishnavi and Subashini 2015),
Naderahmadian and Hosseini-Khayat 2014; Su et al. 2014;
whereas another way executed modifying elements of the
Qingtang et al. 2017; Sima et al. 2018; Qingtang et al. 2019;
first column of the U matrix (Lai 2011; Luo et al. 2020).
Chen et al. 2021). From 2013 to 2019, Qingtang Su had three
Sun et al. in (2002) designed a novel watermarking scheme
papers that focused on Q R factorization. In the first method,
based on SVD, in which the watermark was embedded into
Su et. al performed a watermarking process that depends on
512 × 512 images by modifying the first coefficient of the
the relation between the second-row first-column coefficient
D triangular matrix. This method had better performance
and the third-row first-column coefficient of the Q unitary
in terms of robustness because the authors proposed an
matrix (Su et al. 2013). After that, Su improved it by other
excellent formula to embed and extract the watermark. In
choices in the years 2017 and 2019 where the author divided
addition, there is a novel scheme that was proposed by An-
the host image into 3 × 3 blocks instead of a size of 4 × 4 as
Wei Luo in (2020). This proposal performed an optimal SVD
in the paper (Su et al. 2013). These improvements enhanced
blocks selection strategy to improve the imperceptibility and
the embedded watermark capacity; however, the quality of
used different embedding strengths for each block. However,
the watermarked image was heavier affected.
embedding on two elements U (2, 1) and U (3, 1) of the U
Besides using separately above methods, many authors
matrix reduced the quality of the watermarked images.
also had hybrid image watermarking schemes to strengthen
While the time required to conduct SVD computation is
the robustness of the watermark in recent years. That is a
about 11 n3 flops, Schur decomposition needs a fewer num-
combination of DWT and SVD (Singh et al. 2017; Yadav
ber of flops which is approximately 8n3/3 for an n×n matrix.
et al. 2018; Roy and Pal 2019; Ernawan and Kabir 2020;
That is the reason why some researchers focused on kind
Laxmanika and Singh 2020), DCT and SVD (Li et al. 2018),
of this matrix analysis (Liu et al. 2017; Su et al. 2020). Su
DWT and DCT (Abdulrahman and Ozturk 2019), DWT and
(2020) in 2020 described a new Schur decomposition-based
Q R (Jia 2017; Singh et al. 2018), or DWT and LU (Wang
algorithm where U (2, k) and U (3, k) elements of U unitary
et al. 2016). The experimental results of these proposals
matrix are chosen for embedding (with k is a row index of D
showed that the robustness of the extracted watermark is
triangular matrix that contains the biggest value). Although
more improved than previous researches. Normalized cor-
Schur decomposition takes execution time less than SVD
relation (NC) value, which measures the robustness, is often
factorization, it is still a complex transformation.
up to 90% under all image attacks. However, the invisi-
In addition, Q R decomposition, which decomposes a
bility of the watermarked images is only around 40dB by
square matrix into an orthogonal matrix and an upper tri-
peak signal-to-noise ratio (PSNR) index. Furthermore, these
angular matrix, is a very important matrix transformation for
methods cost the computational complexity and they are not
watermarking images. The advantage of Q R decomposition
suitable for real-time systems.
lies in its low computational complexity and stable numerical
feature. Because Q R decomposition is an intermediate step 1.2 Challenging issues
in Schur decomposition, it requires a fewer number of com-
putations than SVD and Schur factorization (Su et al. 2013;
As above discussions, an effective image watermarking
Sima et al. 2018). Therefore, it is appropriate for real-time
scheme needs to satisfy three main criteria which involve
systems. In many works, the elements in the first column of
quality of watermarked image, the robustness of extracted 123 33
Consideration of a robust watermarking algorithm for color image using improved… 5071
watermark, and execution time. To balance these require-
the orthogonality of the Q matrix. Moreover, an inverse Q R
ments, a novel method, which is based on the formula of
factorization cannot be computed. In other words, G S-based
Sun (2002) and Q R decomposition, is proposed in our
Q R decomposition fails in this situation.
paper. Sun (2002) embedded information on the first ele-
ment D(1, 1) of D triangular matrix after decomposing SVD 1.3 Our contributions
(called Sun SV D). The embedding and extracting formula in
this proposal was referred to by many researchers due to its
Our contributions can be summarized as follows:
stability. Because of high computational complexity, SVD
decomposition should be replaced with Q R decomposition.
1. To overcome the drawbacks of Sun Q R, a new water-
From this idea, a combination between Q R decomposition
marking scheme based on Q R decomposition is proposed
and the formula of Sun (called Sun Q R) was experimented. It
in this paper where the R matrix is computed at first and
used the Gram–Schmidt algorithm (Vandenberghe 2018) for
diagonal elements of the R matrix are checked and mod-
Q R factorization and the formula of Sun for embedding as
ified if they are zero or negative. This action ensures that
well as extracting watermark. To be similar to SVD decom-
Q and R matrices are always unique without the loss of
position, the first element R(1, 1) of the upper triangular
orthogonality. Due to this computation, the quality of the
matrix R is used to embed and extract information due to the
watermarked image can be significantly improved.
concentration of energy on this element.
2. Calculating elements of R is performed by solving a set
The previous methods often utilized the Gram–Schmidt
of linear equations. After that, Q is computed based on
(G S) algorithm to decompose the image matrix. However,
R. Therefore, the time complexity of the proposed Q R
G S-based Q R decomposition exists some disadvantages as
decomposition is O(n2) instead of O(n3) as the GS-
follows. Firstly, according to Stewart (1998) and Vanden-
based Q R factorization.
berghe (2018), the algorithm requires approximately n3 flops
3. In addition, for improving extracting time, a novel for-
for a n×n matrix. It means that its complexity is O(n3) which
mula is designed to get out the first element R(1, 1) of
is similar to SVD and Schur decomposition. Therefore, it is
R matrix instead of calculating Q R factorization as the
more effective if we find a novel solution to compute Q R
previous proposals. Based on our proposed extracting
factorization with less complexity. Secondly, although the
scheme, our method can reduce significantly execution
G S algorithm-based method is easier to set up, it gives out
time compared with other methods. That makes our
worse the invisibility and the robustness of the watermarked
method can be suitable for real-time applications.
image than the one based on SVD decomposition accord-
ing to experimental results. A reason for this is because the 1.4 Roadmap
G S algorithm concurrently calculates Q and R column by
column, so it does not inspect diagonal elements of the R
The rest of this paper is organized as follows. Section 2
matrix if these values are zero or negative. From the theoret-
describes the Q R decomposition theory and its special fea-
ical point of view, an important factor to make the Q matrix
tures. Then, Sect. 3 introduces the details of our watermark
and R matrix unique is that all diagonal elements R(i , i ) of
embedding and our watermark extraction procedure. After
the R matrix must be positive (Vandenberghe 2018). How-
that, Sect. 4 gives the experimental results and discussion.
ever, the G S algorithm does not ensure this demand in some
Finally, Sect. 5 concludes this paper.
cases. There are two versions of the G S algorithm: the classi-
cal algorithm and the modified algorithm. While the modified
version depends upon the condition of the original matrix and
fails when the original matrix is singular, classic G S usually 2 Preliminaries
has very poor orthogonality (Stewart 1998). Therefore, G S
is considered a less accurate and stable algorithm (Stewart 2.1 QR decomposition
1998). Besides that, the G S algorithm is not recommended
in practice due to being sensitive to rounding errors as men-
Q R decomposition (also called Q R factorization) of a
tioned on page 15 of (Vandenberghe 2018). Figure 1 is an
matrix A is a decomposition of the matrix into two matri-
example to illustrate the error of G S-based Q R decompo- ces as Eq. (1).
sition when the original matrix A is in an ill condition. A
matrix in the example is a 4 × 4 pixel block of the “Girl” A = Q R, (1)
image (University of Granada 2022). We can see that some
elements of Q and R matrices are unknown in this case. As
where Q is an orthogonal matrix (i .e., QT Q = Q QT = I )
the result, the product of QT Q is infinite and it is not equal
and R is an upper triangular matrix. If A is non-singular, then
to the unit matrix I , so the G S algorithm does not guarantee this factorization is unique. 123 34 5072 P. T. Nha et al.
Fig. 1 An example of GS-based QR decomposition is when the
original matrix is in ill condition
For example, a matrix A of size 4 × 4 as
2.3 The special feature of Q and R matrix ⎡ ⎤ 40 39 39 38
2.3.1 Finding the elements of R matrix ⎢40 40 40 39⎥ A = ⎢ ⎥ ⎣41 42 42 40⎦
By multiplying two sides of the equation with AT (is a trans- 44 46 44 41
position of A), Eq. (1) in Sect. 2.1 becomes as follows:
can be factored into an orthogonal matrix Q and an upper
AT A = AT Q R = M
triangular matrix R by Q R decomposition as follows.
⇒ AT A = (Q R)T Q R = M ⎡ ⎤ 0.4845 − 0.6921 − 0.3499 − 0.4049
⇒ AT A = RT QT Q R = M ⎢0.4845 − 0.2374 0.1917 0.8199 ⎥ Q = ⎢ ⎥
⇒ AT A = RT R = M (3) ⎣0.4966 0.2113 0.7381 − 0.4049⎦ 0.5329 0.6481 − 0.5440 0.0000 ⎡ ⎤
(since Q is an orthogonal matrix, so QT Q = I , where I is 82.5651 83.6431 82.5772 79.0164 the identity matrix.) ⎢ 0 2.1996 0.9033 − 0.5341⎥ R = ⎢ ⎥
Since R is an upper triangular matrix, R can be computed ⎣ 0 0 1.0880 1.4020 ⎦
easily by solving a set of linear equations. Supposedly, the 0 0 0 0.3947
host matrix A has a size of 4 × 4. Therefore, the M, AT , RT ,
and R matrices are also 4 × 4 matrices. The elements of A 2.2 Arnold transform are represented as follows.
For improving the security of watermarking method, Arnold ⎡ ⎤
a11 a12 a13 a14
transform is often used to permute the watermark image (Su ⎢a ⎥
21 a22 a23 a24
et al. 2020), and its detailed permutation process is given by A = ⎢ ⎥ ⎣ a , a ⎦ =
1 a2 a3 a4
31 a32 a33 a34 Eq. (2).
a41 a42 a43 a44 x 1 1 x = mod N , (2) y 1 2 y
where a1, a2, a3, a4 are column vectors of A, respectively. We have
where x, y, x, and y are integers in {0, 1, 2, . . . , N −1} and ⎡ ⎤
N is order of watermark image matrix. The modulus oper-
a11 a21 a31 a41
ation is denoted by mod with a divisor with N . The image ⎢a ⎥
AT = ⎢ 12 a22 a32 a42⎥
pixel at the coordinate (x, y) can be permuted to a new coor- ⎣a ⎦ , M = AT A
13 a23 a33 a43
dinate (x, y) by Eq. (2), which disorganizes the order of
a14 a24 a34 a44 ⎡ ⎤
the watermark image. Based on the Arnold transform, we
m11 m12 m13 m14
can enhance the security in the visual identification of water- ⎢ ⎥
⎢m21 m22 m23 m24⎥
mark images. Moreover, the number of permutation times of = ⎣m ⎦
31 m32 m33 m34
Arnold transform is often used as the secret key.
m41 m42 m43 m44 123 35
Consideration of a robust watermarking algorithm for color image using improved… 5073 ⎡ ⎤ ⎡ ⎤
r11 r12 r13 r14 r11 0 0 0
2.3.2 Finding the elements of Q matrix ⎢ 0 r ⎥ ⎢r ⎥ R = ⎢ 22 r23 r24⎥ ⎢ 12 r22 0 0 ⎥ ⎣ 0 0 r ⎦ RT = ⎣ ⎦ 33 r34
r13 r23 r33 0
Calculating the elements of the Q matrix is based on the 0 0 0 r44
r14 r24 r34 r44
R matrix. The Q matrix can be expressed by columns as follows.
In order to find the elements of the R matrix, we will begin ⎡ ⎤ with Eq. (3).
q11 q12 q13 q14 ⎢q ⎥
21 q22 q23 q24 ⎡ ⎤ ⎡ ⎤ Q = ⎢ ⎥ ⎣
⎦ = q1 q2 q3 q4 r
q31 q32 q33 q34 11 0 0 0
r11 r12 r13 r14 ⎢r ⎥ ⎢ 0 r ⎥
q41 q42 q43 q44
RT R = M ⇔ ⎢ 12 r22 0 0 ⎥ ⎢ 22 r23 r24⎥ ⎣r ⎦ ⎣ ⎦ 13 r23 r33 0 0 0 r33 r34 r
The Gram–Schmidt algorithm, which was introduced in
14 r24 r34 r44 0 0 0 r44 ⎡ ⎤
(Vandenberghe 2018), computes Q column by column.
m11 m12 m13 m14 ⎢
According to that, the columns of Q are calculated as fol- m ⎥
= ⎢ 21 m22 m23 m24⎥ ⎣ lows. m ⎦
31 m32 m33 m34
m41 m42 m43 m44 ⎡ ⎤ a11 ⎢a ⎥ 21 1 Therefore, we have q ⎢ ⎥ 1 = a1 = ⎣ q a ⎦ and q1 = 1 (16) 31 r11 a √ 41 r ⎡ ⎤ ⎡ ⎤
11r11 = m11 ⇒ r11 = m11 (4) a q m 12 11 12 r ⎢ ⎥ ⎢ ⎥
11r12 = m12 ⇒ r12 = (5) a22 q21 r ⎢ ⎥ ⎢ ⎥ 11
q2 = a2 − r12q1 = ⎣a ⎦ − r12 ⎣q ⎦ and m 32 31 13
r11r13 = m13 ⇒ r13 = (6) a42 q41 r11 m 1 14 r q q
11r14 = m14 ⇒ r14 = (7) 2 = 2. (17) r r 11 22 ⎡ ⎤ a13
r12r12 + r22r22 = m22 ⇒ r22 = m22 − r2 (8) 12 ⎢ ⎥ ⎢a23⎥ m q 23 − r12r13
3 = a3 − r13q1 − r23q2 = ⎣ ⎦ r a33
12r13 + r22r23 = m23 ⇒ r23 = (9) r22 a43
m24 − r12r14 ⎡ ⎤ ⎡ ⎤
r12r14 + r22r24 = m24 ⇒ r24 = (10) q11 q12 r22 ⎢q ⎥ ⎢q ⎥ 1 r ⎢ 21⎥ ⎢ 22⎥
13r13 + r23r23 + r33r33 = m33 ⇒ r33 −r q
13 ⎣q ⎦ − r23 ⎣ ⎦ and q3 = 3 (18) 31 q32 r33 = m33 − r2 (11) q q 13 − r 2 23 41 42
r13r14 + r23r24 + r33r34 = m34 (12)
q4 = a4 − r14q1 − r24q2 − r34 ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎡ ⎤
m34 − r13r14 − r23r24 a q q q ⇒ r 14 11 12 13 34 = r33 ⎢a ⎥ ⎢q ⎥ ⎢q ⎥ ⎢q ⎥ q ⎢ 24⎥ ⎢ 21⎥ ⎢ 22⎥ ⎢ 23⎥ r 3 =
14r14 + r24r24 + r34r34 + r44r44 = m44 ⎣ ⎦ − r14 ⎣ ⎦ − r24 ⎣ ⎦ − r34 ⎣ ⎦ and a34 q31 q32 q33 a q q q ⇒ r 44 41 42 43 44 = m44 − r2 (13) 14 − r 2 24 − r 2 34 1 q4 = q4 (19) In general, if the host matrix r
A has a size of n × n, we have 44 √ m
In general, if the host matrix A has a size of n × n, we have 1 j r11 =
m11 and r1 j = (14) r11 ⎧ 1 ⎪ ⎪ i −1
q1 = a1 and q1 = q1 (20) ⎪ m r 2 , i = j ⎨ i j − k=1 k j r11 r q i j = (15)
i = ai − (r1i q1 + r2i q2 + · · · + ri−1,i qi−1) and ⎪ ⎪ i −1 ⎪ (m r ⎩ i j − k=1 ki rk j ) 1 , i = j q q r i = i (21) i i rii
where i , j = 2, 3, · · · , n. where ai ,
qi and qi (with i = 2 to n) are n × 1 vectors 123 36 5074 P. T. Nha et al.
2.3.3 The computational complexity of the proposed
3. Perform Q R decomposition on one block based on solution Sect. 2.3 as follows:
• Assign B components of the block to A matrix.
Algorithm 1 presents shortly steps to discover the elements
• Calculate AT by transposing the matrix A
of the R matrix and Q matrix. According to Algorithm 1,
• Compute M = AT A
it is easy to see that the computational complexity of the
• Find out R and Q matrices by solving a set of equa-
proposed approach is the sum of four calculations. These
tions as represented in Eqs. (14), (15), (20) and (21).
calculations comprise transposing A matrix, multiplying AT
and A, calculating the elements ri j and qi j , respectively. Each
4. Embed a watermark bit into the triangular matrix R based
calculation needs two nested for loops, so the execution time on the formula of Sun (2002):
for each one is Cn2 (C is a constant). Therefore, the time
• Get the first element R(1, 1) of R matrix
complexity of the whole Algorithm 1 is O(n2)
• Calculate z = R(1, 1) mod q (with q is a positive integer)
Algorithm 1 Calculating R and Q matrices. • Case wi = “0
INPUT: An A matrix with size of n × n ⎧
OUTPUT: The upper triangular matrix R and the orthogonal matrix q q
⎪ R(1, 1) + − z, z < 3 Q ⎪ ⎨ 4 4 BEGIN: R(1, 1) = (22) 1. Transpose A matrix ⎪ ⎪ ⎩ q R 2. Calculate (1, 1) M = AT A + 5 − z, elsewhere 4
3. Compute the element ri j of R matrix based on Eq. (14) and Eq. (15)
4. Compute the elements q • Case wi = “1
i j of Q matrix based on Eq. (20) and Eq. (21) ⎧ return r q q i j and qi j ⎪ ⎪ R(1, 1) − − z, z < END. ⎨ 4 4 R(1, 1) = (23) ⎪ ⎪ ⎩ q
R(1, 1) + 3 − z, elsewhere 4
3 The proposed watermarking method
Note that q is also the strength of watermark embedding.
5. Update matrix A by formula Eq. (1): A = Q R and
assign A back to B components of the blocks.
In this section, we describe a new watermarking scheme
6. Repeat steps 3–5 until all blocks are embedded water-
based on the improved Q R decomposition and the formula
mark values. Finally, the watermarked B components are
of Sun in the paper (2002). The image watermarking scheme
reconstructed to obtain the watermarked image H .
includes two stages, embedding and extracting, respectively.
3.1 Watermark embedding scheme
The detail of steps for the embedding stage can be represented in Fig. 2.
In the embedding process, the host color image is divided
into 4 × 4 non-overlapping blocks at first. Then, the gray
3.2 Watermark extraction scheme
watermark image is permuted by Arnold transform and
is converted to a binary sequence after that. Finally, the
Since the watermark is only embedded into the R matrix in
improved Q R decomposition is performed on the image
the embedding process, Q R decomposition is not needed in
blocks in succession and the watermark is embedded into
the watermark extraction procedure. The main purpose of this
the R matrix. The proposed watermark embedding scheme
extraction scheme is to find out the first element R(1, 1) of can be summarized as follows.
the R matrix. This improvement makes our paper is different
from the other ones based on Q R decomposition. Therefore,
1. Divide the host color image H into 4×4 non-overlapping
the watermark extraction steps are described as follows.
blocks. In this image, each pixel is represented by three
components (R, G, B).
1. Divide the watermarked image H into 4 × 4 non-
2. Permute the gray watermark image by Arnold transform
overlapping blocks. In this image, each pixel is repre-
and then convert to a one-dimensional array wi with i =
sented by three components (R, G, B).
1, 2, · · · , M × M. M × M is the size of gray watermark
2. Assign B components of the block to a 4 × 4 matrix image. (matrix A∗). 123 37
Consideration of a robust watermarking algorithm for color image using improved… 5075
Fig. 2 The embedding stage 123 38 5076 P. T. Nha et al.
3. Obtain the first element R∗(1, 1) of R∗ matrix as fol- 4 Experimental results
lows: R∗(1, 1) = length of the first column vector of A∗ matrix (Vandenberghe 2018). 4.1 Evaluation criteria
In general, the efficiency of image watermarking schemes is R∗(1, 1)
usually measured by their invisibility, robustness, and com- =
A∗(1, 1)2 + A∗(2, 1)2 + A∗(3, 1)2 + A∗(4, 1)2
puting time. For evaluating the invisibility capability, not only (24)
the peak signal-to-noise ratio (PSNR) is used, but also the
structural similarity index measurement (SSIM) is utilized
to measure the similarity between the original color image
4. Extract the information of watermark based on algorithm
H and the watermarked image H with size of N × N in of Sun (2002):
this paper. PSNR is employed as a measure for evaluating
the quality of the watermarked image. PSNR is described by
• Calculate z = R∗(1, 1) mod q the following equation.
• The watermark bit is extracted by using following equation. 2552MSE PSNR = 10 log10 (26) ⎧ , q ⎪ ⎨ “0, z < 2 w = (25)
where the mean square error (MSE) between the original and ⎪ ⎩
watermarked image is defined as: “1, elsewhere M N 1 −1 −1
5. Repeat steps 2–4 until watermark values are extracted on MSE =
(H (i , j ) − H (i, j))2 (27) M N
all blocks. Finally, collect all extracted watermark values i =0 j=0
into an image and use inverse Arnold transform to get the final watermark.
Moreover, the SSIM is considered to be correlated with
the quality perception of the human visual system (HVS).
The SSIM, as denoted in Eq. (28), is also used to measure
The detail of the extracting stage can be represented in Fig. 3.
the similarity between the original color image H and the
And an example of the proposed image watermarking algo-
watermarked image H (Jia 2017).
rithm is also illustrated in Fig. 4.
S S I M(H , H ) = l(H , H )c(H , H )s(H , H ), (28)
3.3 The computational complexity of the proposed scheme where ⎧
According to Sect. 2.3.3, the time complexity for the pro- ⎪
⎨l(H, H) = (2µHµH + C1)/(µ2H + µ2H + C1)
posed Q R decomposition is O(n2) with an image block size c(H , H ) (29) ⎪
= (2σHσH + C2)/(σ2H + σ2H + C2) ⎩
of n × n. For the proposed watermarking scheme, we only
s(H , H ) = (σHH + C3)/(σHσH + C3)
embed the watermark on the B channel instead of three color
channels of the host image. The reasons for choosing com-
The first term in Eq. (29) is the luminance comparison
ponent B are: (a) considering all components may distort
function which measures the closeness of the two images’
the colors of the watermarked images; (b) human eyes are
mean luminance (µH and µH). The second term is the con-
less sensitive to component B than components R and G
trast comparison function which measures the closeness of
according to the human visual system. Therefore, the overall
the contrast of the two images. Here the contrast is measured
complexity of the proposed embedding scheme for a color
by the standard deviation σH and σH. The third term is the N × N
image of N × N pixels is estimated as O(n2). And
structure comparison function which measures the correla- n × n
tion coefficient between the two images H and H . Note that
the overall complexity of the proposed extraction scheme is N × N
σH H is the covariance between H and H . The positive val- only
O(1) for a color image of N × N pixels because n × n
ues of the SSIM index are in [0, 1]. A value of “0” means no
we do not use Q R decomposition as the previous Q R-based
correlation between images, and “1” means that H = H .
methods in this stage. Instead of that, we calculate R(1, 1)
The positive constants C1, C2, and C3 are used to avoid a
of the R matrix based on Eq. (24). null denominator. 123 39
Consideration of a robust watermarking algorithm for color image using improved… 5077
Fig. 3 The extracting stage
Furthermore, the normalized correlation (N C) coefficient
extracted one and m × n denote size of row and column of
is computed for evaluating robustness by using the origi-
the watermark image, respectively.
nal watermark W and the extracted watermark W , which is
In general, a larger PSNR or SSIM value denotes the denoted as follows:
watermarked image is very near to the original host image,
which means that the watermarking method has better per- 4 m n j x y N C = =1 =1
=1(W (x , y, j )W (x , y, j ))
formance in terms of invisibility. A higher N C value reveals , 4 m n
(W (x , y, j ))2 4 m n
(W (x , y, j ))2 j =1 x=1 y=1 j =1 x=1 y=1
that the extracted watermark is alike to the original water- (30)
mark, which shows that the watermarking method is more robust.
where W (x, y, j ) and W (x, y, j ) present the value of pixel
(x, y) in component j of the original watermark and the 123 40 5078 P. T. Nha et al.
Fig. 4 An example of the proposed watermarking algorithm 123 41
Consideration of a robust watermarking algorithm for color image using improved… 5079
Table 1 Various attacks used in our experiments Index Attacks Description 1 Blur
Blur the watermarked image with radius = 0 and sigma is designed to 0.2 and 0.5, respectively 2 Sharpen
Sharpen the watermarked image with radius = 0 and sigma is designed to 0.2 and 0.5, respectively 3 Cropping
Remove 25% and 50% of the watermarked image on the top left corner 4 Scaling (1/2)
Resize the watermarked image from 512 × 512 to 256 × 256 and subsequently restore it to 512 × 512. 5 Scaling (2)
Resize the watermarked image from 512 × 512 to 1024 × 1024 and subsequently restore it to 512 × 512 6 Gaussian noise
Add Gaussian noise to the watermarked image with µ = 0 and variance σ 2 = 0.001, 0.003 7 S&P noise
Add salt and pepper noise to the watermarked image with a noise density den = 0.002, 0.005, 0.01 8 Rotation 5◦
Rotate the watermarked image clockwise at the angle = 5 and subsequently rotate it
counterclockwise at the angle = − 5 9 Rotation 10◦
Rotate the watermarked image clockwise at the angle = 10 and subsequently rotate it
counterclockwise at the angle = − 10 10 JPEG
Compress the watermarked images by using DC T transform with size of window 8 × 8 and 16 × 16 11 Mean filter
Use the filter with size of window from 2 × 2 and 5 × 5
4.2 The simulation setting
Table 2 Values of SSIM and NC under different embedding coefficients image q PSNR SSIM NC
In order to evaluate objectively the stability and the effective-
ness of the proposed method, twelve 24-bit color images with Girl 5 65.6435 0.9997 0.9656
a size of 512 × 512 in the CVG-UGR image database (Uni- 10 62.5665 0.9996 0.9999
versity of Granada 2022) are selected as the host images, 15 53.8237 0.9986 0.9980
and two 32 × 32 gray images are used as original water- 20 45.4135 0.9932 0.9748
marks as shown in Fig. 5. The host images are standard color Lena 5 65.3886 0.9998 0.9716
images that involve various types such as portrait, landscapes 10 62.4570 0.9996 0.9981
photograph, animal photograph, and fruit photograph. Pixel 15 60.6977 0.9995 0.9980
distribution of these images is different from each other. All 20 59.3773 0.9993 0.9961
tests are implemented by Visual Studio v15 and are per- Peppers 5 60.6537 0.9998 0.9547
formed on a laptop with Intel@ CoreTM i5-6200U CPU at 10 55.7789 0.9991 0.9787
2.30 GHz, 4.00 GB RAM and 64-bit OS. Table 1 describes 15 54.2037 0.9986 0.9768
shortly different image attacks which are used in our robust- 20 52.0914 0.9978 0.9778 ness tests. Avion 5 65.6314 0.9998 0.9696
To select a suitable embedding parameter, the watermark 10 62.5527 0.9997 0.9980
is embedded into all host images with different embedding 15 60.8013 0.9995 0.9990
coefficients q (from 5 to 20 with the step length 1). Table 2 20 59.3868 0.9993 0.9961
gives a part of SSIM of the watermarked images and the Baboon 5 64.5499 0.9999 0.9809
N C of the extracted watermark with the different embedding 10 62.0187 0.9999 0.9904
coefficients q (q = 5, 10, 15, 20, respectively). 15 60.4548 0.9998 0.9942
As shown in Table 2, each watermarked image has various 20 59.2404 0.9997 0.9952
SSIM and N C values with the same q and they are also dif-
ferent from other images. However, it is clear that when the
Best values are indicated in bold
coefficient q increases, the SSIM is smaller whereas the N C
is bigger, and vice versa. This means that if the robustness
(2021), Qin (2021), Kumar (2021) and our proposal is per-
of the watermark is better, then the invisibility of the water-
formed to simulate for the effectiveness of the proposed
marked image is worse when q goes up. Therefore, to balance
algorithms. Figure 6 reviews some important information of
between invisibility and robustness, a value of q is set to 10
the related works in terms of utilized technique, evaluation
for evaluating the performance of the proposed method.
tools, data set, performance metrics, advantages, and disad-
A comparison between the methods of Sun (2002), Luo
vantages. The first one is a scheme of Sun (2002) which used
(2020), Su (2020), Su (2018), Chen (2021), Hu (2020), Chen
SVD decomposition as the main technique to embed a 64×64 123 42 5080 P. T. Nha et al.
Fig. 5 The host images: a avion, b baboon, c Balloon, d couple, e Girl, f house, g lena, h milkdrop, i parrots, j peppers, k sailboat, l tree. The
watermarks: m w1, n w2
Fig. 6 A short description of the related works 123 43
Consideration of a robust watermarking algorithm for color image using improved… 5081
binary image into a gray 512 × 512 image on the element
attacks. In summary, all the above papers divide the host
D(1, 1) of the D matrix. This scheme has the advantages of
image into the blocks of 4 × 4 except Kumar (2021) and the
distinguishing the JPEG lossy compression from other mali-
evaluation tools are often PSNR, SSIM, N C, and BER.
cious manipulation and identifying modified portions of the
image but it also has a big computational complexity. It is 4.3 Invisibility test
similar to the schemes of Lou (2020) and Hu (2020) because
both algorithms applied SVD analysis in their image water-
The quality of watermarked images is evaluated by PSNR and
marking methods too. In (Luo et al. 2020), Lou combined
SSIM indexes. In general, the watermarked image is more
DWT with SVD decomposition and logistic map to create
invisible when the value of PSNR is bigger or the value of
a novel watermarking scheme. The method has an optimal
SSIM is near to 1. Theoretically, the extracted watermark
SVD blocks selection strategy which improves the impercep-
should be the same original watermark under no attacks. It
tibility and robustness. Lou (2020) and Hu (2020) inserted the
means that the N C value must be 1. However, it is not com-
watermark bits into the U (2, 1) and U (3, 1); however, Lou
pletely correct in our experimental tests. In fact, the N C value
used gray and binary images while Hu utilized color images
is less than 1 because it depends on the structure of the host
for the host image and the watermark image. In addition, Su
image as well as the embedding strength. In all methods, the
had two proposals based on Arnold transform, LU decom-
embedding strength is chosen to a suitable value in order to
position, and Schur factorization in (Qingtang et al. 2018;
balance between the quality of the watermarked image and
Su et al. 2020), respectively. The approach of Su (2018) has
extracted watermark. Figure 7 shows that PSNR values of
a low computational complexity (O(n2)) and high embed-
the proposed method are at a stable level of over 62 dB for
ding payload but the performance of resisting image rotating
all tested images except “peppers” and “Parrots”. For each
attack will be further considered in future work. Q R decom-
host image, N C indexes of two watermarks are similar to
position is selected in the method of Chen (2021) and our each other.
method. However, while Chen embedded color watermark
The detailed results of the imperceptibility are also com-
bits into two elements Q(2, 1) and Q(3, 1) of Q matrix, we
pared in Fig. 8. According to Fig. 8, PSNR/SSIM values of Su
chose R(1, 1) of R matrix as the modified element. In addi-
(2018), Luo (2020), Hu (2020), and Chen (2021) are lower
tion, three state-of-the-art algorithms were published in 2021
than the other methods because the authors embedded the
by Chen (2021), Qin (2021), and Kumar (2021), respectively.
watermark on two elements of the L matrix, U matrix, and
Firstly, Chen (2021) used WHT transform as a main tech-
Q matrix, respectively. This causes a big change in two rows
nique for the proposed scheme. In this publish, the author
of the corresponding block after embedding. Therefore, the
calculated a correlation between the matrix coefficients to
pixel values of the watermarked image will not be close to
find out the embedded elements of the WHT blocks on three
the original image. As the result, the quality of the water-
R, G, and B channels. This algorithm has higher embedding
marked image of these methods is worse. In addition, the
capacity and improves security by rearranging the pixel val-
figures in Fig. 8 display that the algorithms of Su (2018) and
ues and randomly selecting the embedded blocks. Secondly,
Hu (2020) bring a low result in terms of PSNR and SSIM.
a combination of DWT, QDFT, and Q R decomposition was
The reason for this is because these methods embedded the
built by Qin (2021) to create a novel watermarking scheme.
information on three channels instead of one channel as the
Qin performed the first-level DWT transform on R, G, and
others. Although embedding on three channels enhances the
B channels at first. Next, three low-frequency components
embedded capacity, it leads to distortion of the pixel values.
constituted a pure quaternion matrix and the left quaternion
Meanwhile, the methods of SunSVD (2002) and SunQR in
Fourier transform was performed to obtain the real part.
Sect. 1.2 have higher PSNR/SSIM values. These methods
Then, the watermark was embedded into the r14 element
used the embedding formula of Sun which impacts on one
of the R matrix by Q R decomposition. The algorithm has
element of the triangular matrix, so the embedded block only
good robustness against attacks such as JPEG compression,
changes on one row instead of two rows as the cases of Su
cropping, and median filtering but the transparency of the
(2018), Luo (2020), Hu (2020), and Chen (2021). That is a
watermarked image is very low because the PSNR values
reason why the formula of Sun is utilized in the proposed
are only between 20 dB and 30 dB. Finally, an LWT-based method.
image watermarking method, which hid the watermark into
Figure 9 is a piece of evidence to demonstrate the influ-
sub-band H H of Y component, was developed by Kumar
ence of the embedded elements on the pixel matrix. In this
(2021). In this article, Kumar applied the alpha blending
figure, the proposed algorithm only embeds watermark bits
technique to balance the trade-offs between the impercep-
on R(1, 1) of the R matrix. Thus, the matrix after embedding
tibility and the robustness, and Arnold’s Cat Map was used
only is modified on the first column in comparison with the
to enhance security of the watermarking technique. Unfortu-
original matrix. Unlike that, the watermark bit is embedded
nately, this method is less robust against median and filtering
into two elements Q(2, 1) and Q(3, 1) of the Q matrix in 123 44 5082 P. T. Nha et al.
Fig. 7 PSNR and N C values of the proposed method for twelve host images and two watermark
images in the absence of attack
the method of Chen (2021) which leads to change in the sec-
similar to r33 and r44. This leads to infinite values of R, Q,
ond row and the third row of the embedded matrix. To some
and A matrices (with A is the matrix A after embedding
extent, Fig. 9 explains why the proposed method has better
the watermark). This is a reason for reducing the quality
imperceptibility than the scheme of Chen (2021).
of the watermarked image. Therefore, to solve this issue,
In addition, it can be seen clearly in Table 3 that the pro-
we check the value below the square root before calculating
posed method gives much higher PSNR/SSIM and NC values
rii (i = 2, 3, 4). If this value is zero or negative, rii is set up
than others. This means that the invisibility of the water-
to 1. This action not only gives out the better invisibility of
marked image is much better in the proposed scheme. In
the watermarked image but also does not completely affect
addition, the result table brings out that the proposed method
the embedding process as well as extraction because the two
can not only overcome the quality of the watermarked image
processes only use the first diagonal element r11. This solu-
but also effectively extract the embedded watermark.
tion makes the proposed method more stable and effective in
Our results can be explained as follows. Theoretically,
terms of the quality of the watermarked image.
R is an upper triangular matrix with nonzero diagonal ele-
ments. According to Eq. (22) in Sect. 2.3, the first diagonal
element r11 is always positive because pixel value is also 4.4 Execution time test
positive. However, the other diagonal ones can be zero or
negative which are based on Eqs. (8), (11), (13) in Sect. 2.3.
It is easy to see that the execution time of watermarking
From Eq. (8) in Sect. 2.3, we have r
image algorithms, which are based on the transform domain, 22 = m22 − r2 . If 12
depends mainly on the type of used matrix decomposition. (m22 − r2 ) 12
= 0 then r22 = 0. Thus, r23 and r22 are infi-
SVD decomposition needs about 11n3 flops for a n × n
nite. Otherwise, if (m22 − r2 ) < 0, r 12 22 is infinite too. It is
matrix, whereas the required time to compute LU factor- 123 45
Consideration of a robust watermarking algorithm for color image using improved… 5083
Fig. 8 A comparison of the quality of the watermarked images between the methods
Table 3 An average comparison between the different methods in terms of PSNR, SSIM and NC values Value/method SunSVD (Sun SunQR in Su (2018) Luo (2020) Hu (2020) Chen (2021) The proposed et al. 2002) Sect. 1.2 method PSNR 55.4066 54.6548 42.6207 49.7185 40.9879 51.5636 61.5041 SSIM 0.9972 0.9989 0.9881 0.9964 0.9761 0.9982 0.9997 NC 0.9881 0.9806 0.9274 0.9439 0.9909 0.9906 0.9944 123 46 5084 P. T. Nha et al. Fig. 9 An example for comparison of original and embedded matrices between the proposed method and the approach of Chen (2021)
ization is n2 flops. And Q R decomposition is considered
In these experiments, a computer with Intel@ CoreTM i5-
as an intermediate stage between SVD and LU . For GS-
6200U CPU at 2.30 GHz and Visual Studio v15 is used as
based Q R factorization, it costs (n3 − n2 ) floating-point
the computing platform. The embedding time and extrac- 3
additions and multiplications (Stewart 1998). In (Chen et al.
tion time of the proposed methods are 0.2448s and 0.006 s,
2021), Chen used quaternion Q R decomposition (Q Q R D)
respectively. Table 4 shows a comparison of the execution
which is based on Householder transformation for matrix
time between different methods.
calculation. According to Vandenberghe (2018), the House-
According to Table 4, the total execution time of the pro- 4n3
posed method is bigger than the time of Su (2018) which uses
holder algorithm requires approximately flops for an 3
LU decomposition, but it is smaller than the others. In the
n × n matrix. On the other hand, the scheme of Hu (2020)
scheme of Luo (2020), the author proposed a combination of
is based on SVD factorization with mixed modulation incor-
DWT and SVD, so this method spends more time than the
porated. And its time complexity is the sum of the five basic
others except for the approach of Hu (2020). Meanwhile, the
processing modules with an image block size of n × n, as
algorithm of Hu (2020) applied many processing modules
follows: SV D(O(4n3)), orthonormal restoration (O(2n3)),
such as level shifting with dither noise, SVD, sign correc-
distortion compensation (O(3n2)), matrix recomposition
tion, mixed modulation, orthonormal restoration, distortion
(O(2n3)), and tentative verification (O(4n3)). The overall
compensation, tentative verification, and iterative regulation.
complexity of this method for a color image of N × N pixels
It is the reason why its running time is the biggest. N × N is estimated as
(12n3 + 6n2). Therefore, the SVD
For embedding time, the algorithm SunQR in Sect. 1.2 and n × n
the method of Chen (2021) are similar because they use Q R
and Q R decomposition-based approaches such as SunSVD
factorization based on GS and Household algorithms, respec-
(2002), Lou (2020), SunQR in Sect. 1.2, Chen (2021), and Hu
tively. However, the algorithm of Chen (2021) needs more
(2020) have time complexity of O(n3) for an n × n matrix.
time to measure the correlation between elements q
For the proposed scheme, as shown in Sect. 3, the embedding i j of the Q N × N
matrix and select an optimal quaternion embedding position, time complexity is
O(n2) while the extracting time n × n
so it costs a higher number. For extraction time, the pro- N × N
posed method gives an effective result because it calculates
complexity of the proposed approach is only O(1) n × n
the length of the first column vector of the A matrix to find
for a color image of N × N pixels.
out the first element R(1, 1) of the R matrix instead of using
Q R decomposition as the previous Q R based schemes. This 123 47
Consideration of a robust watermarking algorithm for color image using improved… 5085
Table 4 Average execution time Method Embedding time Extracting time Total time
of different methods (in second) SunSVD (2002) 0.4850 0.0870 0.5720 SunQR in Sect. 1.2 0.3718 0.0296 0.4014 Su (2018) 0.1774 0.0074 0.1848 Luo (2020) 2.4566 0.1730 2.6296 Hu (2020) 5.2116 1.0348 6.2464 Chen (2021) 0.4001 0.0279 0.4280 Proposed method 0.2448 0.0060 0.2508
Fig. 10 Extracted watermarks and N C values of the different methods under the blurring attack
demonstrates that the proposed approach can significantly
by Su in (2018), and the method of Lou(2020) was a combi-
improve the speed of the watermarking process, especially
nation of DWT and SVD decomposition. the extraction time.
First of all, blurring and sharpening are two of the com-
mon image processes. The blurring technique is set up by
two arguments like radius and sigma. The first value radius 4.5 Robustness test
is also important since it controls how big an area the operator
should look at when spreading pixels. This value should typ-
For testing the robustness of the proposed method, nine
ically be either ’0’ or at a minimum double that of the sigma.
operations are used to attack three watermarked images.
The second sigma value can be thought of as an approxima-
And then, the extracted results from the attacked images
tion of just how much you want the image to blur in pixels.
are compared to the related works with different kinds of
In the experiments, the radius is fixed to ’0,’ and sigma is
matrix decomposition such as SunSVD (2002), SunQR in
designed to 0.2 and 0.5, respectively. The sharpening opera-
Sect. 1.2, Su(2018), Luo(2020), Hu (2020), and Chen(2021).
tion is also a sort of inverted blurring. Both operations work
The schemes of Sun (2002) and Hu (2020) used SVD decom-
in just about the same way. Therefore, its arguments are sim-
position for deposing the pixel matrix. While SunQR in
ilarly set to blur. Figures 10 and 11 give the results of the
Sect. 1.2 applied the GS algorithm for Q R factorizing, the
visual comparison and quantitative values. N C values from
Household algorithm-based Q R factorization was utilized
these figures inform us about the superiority of the proposed
by Chen (2021). Besides, LU decomposition was developed 123 48 5086 P. T. Nha et al.
Fig. 11 Extracted watermarks and N C values of the different methods under the sharpening operation
method over the others. Furthermore, it is easy to see that
watermarks and N C values with the filtering sizes of 2×2 and
all schemes can prevent damage from blurring and sharpen-
3×3, respectively. It is seen from this figure that the method of
ing attacks. The extracted watermark of Hu (2020) and Chen
Chen (2021) is the most effective among all studies. Besides,
(2021) is clearer to recognize than the others for the “avion”
the algorithm of Hu (2020) is more robust than the methods
and “lena” images when the sigma is set to 0.5.
of SunSVD (2002), SunQR, Su (2018), and Luo (2020). Our
Adding noise is also one of the common operations in
method also gives positive results and the extracted water-
image processing. In this experiment, we select the Salt &
marks can be recognized for the “avion” and “Girl” images.
Peppers noise and Gaussian noise as the attack noises. In
For testing the cropping robustness, two cases are simu-
the adding Salt & Peppers noise, the noise quantity is from
lated to crop the three watermarked images. The first case
1 to 10% increase by 1%, and Fig. 12 shows a part of N C
is cropped in the upper left corner by 25%, while the sec-
values and visual perception, respectively, moreover, adding
ond case is cropped in the upper half by 50%. Although N C
Gaussian white noise of mean 0 and variances from 0.001
values cannot be measured in this operation because they
to 0.005 increasing with 0.001 to process the watermarked
do not correctly reflect the quality of the extracted water-
images. Figure 13 shows the N C values and visual percep-
mark. As the results displayed in Fig. 15, the invisibility of
tion results of the extracted watermark after adding Gaussian
the extracted watermarks of the proposed method is clearer
white noise of mean 0 and different variances (0.001, 0.003,
than the other methods. Obviously, the proposed method is
respectively). As can be seen from these figures, the proposed
robust against this cropping process. And the algorithm of
method has better robustness than the others against the pro-
Luo (2020) seems to be less effective for the “lena” image
cess of adding noise. In some cases, the scheme of Chen
because the extracted watermark can not be recognized in
(2021) has advantages but the gap between this approach and this case.
the proposed one is not too big. While adding Salt & Peppers
Another type of well-known image operation is geometry
noise seems not to make all methods difficult, the Gaussian
attack, which mainly includes rotation and scaling. There are
noise attack brings a poor performance to the approaches of
two rotation experiments to show the robustness in Fig. 16.
Su (2018), Luo (2020), and Hu (2020). The extracted water-
One involves rotating the watermarked image to the right by 5
mark of Luo (2020) is even presented in an unrecognized
degrees. The other involves rotating the watermarked image
shape for the “lena” image.
to the right by 10 degrees. The images are first rotated a cer-
For the filtering attack, the mean filter method is per-
tain number of degrees clockwise and then are rotated the
formed on the watermarked images. A mean filter with
same number of degrees counterclockwise. Figure 17 shows
different window sizes from 2 × 2 to 5 × 5 is used to pro-
the quantitative results and visual perception results for the
cess the watermarked images. Figure 14 shows the extracted
case of scaling, respectively. In this experiment, two scaling 123 49
Consideration of a robust watermarking algorithm for color image using improved… 5087
Fig. 12 Extracted watermarks and N C values of the different methods under the Salt & Peppers noise adding
operations of 200% and 50% are used to deteriorate the water-
compression algorithm for digital images, which allows a
marked image. From data in Figs. 16 and 17, although the
selectable trade-off between storage size and image quality
proposed method gives less robustness than the methods of
by discarding perceptually unimportant information in mid-
SunSVD (2002), Luo (2020), Hu (2020), and Chen (2021), it
dle and high frequencies. Pixel alterations in a local area (i.e.,
is more effective than the schemes of SunQR in Sect. 1.2 and
the 4 ×4 blocks used for image watermarking) can be treated
Su (2018). In these experiments, SVD decomposition-based
as middle-to-high-frequency noise in the 8 × 8 and 16 × 16
studies such as SunSVD (2002), Luo (2020), and Hu (2020)
blocks used for image compression. This makes it easy for
bring better quality than others. Especially, the proposal of
JPEG compression to destroy watermark information hid-
Hu (2020) is the most robust against geometric attacks.
den in the middle-to-high frequency region. Therefore, as the
Finally, JPEG compression is also known as an image
results are shown in Fig. 18, most schemes are weak against
process. In this experiment, the watermarked images are
JPEG compression, especially the algorithms of SunSVD
compressed by JPEG compression with the window size is
(2002), and Su (2018). The method of Chen (2021) has the
8 × 8 and 16 × 16, respectively. JPEG is a common ‘lossy’
best performance for the “avion” and “Girl” images, while the 123 50 5088 P. T. Nha et al.
Fig. 13 Extracted watermarks and N C values of the different methods under the Gaussian noise adding
Fig. 14 Extracted watermarks and N C values of the different methods under the Mean Filter attack 123 51
Consideration of a robust watermarking algorithm for color image using improved… 5089
Fig. 15 Extracted watermarks and N C values of the different methods under the Cropping operation
Fig. 16 Extracted watermarks and N C values of the different methods under the Rotation attack 123 52 5090 P. T. Nha et al.
Fig. 17 Extracted watermarks and N C values of the different methods under the Scaling attack
Fig. 18 Extracted watermarks and N C values of the different methods under the JPEG compression 123 53
Consideration of a robust watermarking algorithm for color image using improved… 5091
Fig. 19 N C values of the proposed method for two watermarked images and two watermark images under different attacks
approach of Luo (2020) overcomes the others for the “lena”
To sum up, by the experimental results, we can see that
image. In the contrast, the proposal of Hu (2020) has lim-
the schemes which use SVD decomposition (SunSVD 2002,
ited resistance to this kind of attack. Although the proposed
Luo (2020), and especially Hu (2020)) are more robust than
method is not the best method under JPEG compression, it
other methods (SunQR in Sect. 1.2, Su (2018), Chen (2021)
has higher N C values than the methods of SunQR, Su (2018)
and the proposed one) under geometry attacks. However, the
and Luo (2020) for the “avion” image. Our study is also bet-
method of Lou (2020) is less effective under mean filter and
ter than some methods such as SunSVD (2002), SunQR, and
cropping operations. Whereas, the algorithm of Chen (2021)
Su (2018) for the “lena” and “Girl” images.
is considered as a strong solution against most attacks, espe-
cially the mean filter. Figure 19 also displays NC values and 123 54 5092 P. T. Nha et al.
the extracted watermarks of two watermarked images of the
high robustness to multimedia data and are mainly used for
proposed method under different attacks. The figures indi-
multimedia security and copyright protection. Therefore, a
cate that the proposed approach is robust against the most
combination of the proposed Q R decomposition and another
used attacks such as blurring, sharpening, salt & pepper
transform domain is necessary and will be further considered
noise, Gaussian noise, cropping, and mean filter for both in the future study.
watermark images. Furthermore, the proposed method out-
Funding This research is funded by Vietnam National Foundation for
performs SunQR in all cases, although both these methods
Science and Technology Development (NAFOSTED) under grant num-
use QR decomposition. The reason for this is because the ber 102.01-2019.12.
proposed method has an improvement to find out elements
of Q and R matrices instead of using the GS algorithm as
Data availability Enquiries about data availability should be directed to SunQR. the authors. Declarations 5 Conclusion
Conflict of interest The authors have not disclosed any competing inter-
In this paper, a novel image watermarking scheme, which is ests.
based on Q R decomposition, is presented. In the embedding
stage, the color host image is divided into non-overlapping
4×4 blocks at first. For each block, the improved Q R decom-
position is applied on the B channel where calculating Q and References
R matrices is executed in succession. First, the elements of
the R matrix are found by performing a set of linear equa-
Abdulrahman AK, Ozturk S (2019) A novel hybrid DCT and
DWT based robust watermarking algorithm for color images.
tions as Eq. (15). Second, the Q matrix is computed column
Multimed Tools Appl 78:17027–17049. https://doi.org/10.1007/
by column based on A and R matrices. Third, the watermark s11042-018-7085-z
information is embedded into the first element R(1, 1) of
Arasteh S, Mahdavi M, Bideh PN, Hosseini S, Chapnevis AA (2018)
the R matrix by using Eq. (23). Finally, we have the water-
Security analysis of two key based watermarking schemes based
on QR decomposition. In: 26th Iranian conference on electrical
marked image after taking a reverse Q R decomposition to engineering (ICEE2018)
update pixel values. In extracting stage, we get R(1, 1) by
Begum M, Uddin MS (2020) Analysis of digital image watermark-
only one operation Eq. (24) without Q R factorization as the
ing techniques through hybrid method. Adv Multimedia 2020:12.
previous methods. After that, the binary values of the water-
https://doi.org/10.1155/2020/7912690
Chen Y, Jia Z-G, Peng Y, Peng Y-X, Zhang D (2021) A new structure-
mark are extracted via Eq. (25). As the result, the image of
preserving quaternion QR decomposition method for color image
the watermark is reconstructed from the received informa-
blind watermarking. Signal Process. https://doi.org/10.1016/j.
tion. The tests are experimented on five color images and sigpro.2021.108088
one gray-scale watermark image with PSNR/SSIM and N C
Chen S, Su Q, Wang H et al (2021) A high-efficiency blind watermarking
algorithm for double color image using Walsh Hadamard trans-
indexes to evaluate the effectiveness of the proposed method.
form. Vis Comput. https://doi.org/10.1007/s00371-021-02277-1
The results of the comparison in Sect. 4 show that our scheme
Ernawan F, Kabir MN (2020) A block-based RDWT-SVD image water-
overcomes the others in terms of the quality of the water-
marking method using human visual system characteristics. Vis
marked image. In addition, because we do not need to use Q R
Comput 36:19–37. https://doi.org/10.1007/s00371-018-1567-x
Giri Kaiser J, Peer Mushtaq Ahmad, Nagabhushan P (2015) A robust
decomposition in the extracting stage, the execution time is
color image watermarking scheme using discrete wavelet transfor-
significantly improved. And our proposal is also more robust
mation. I.J. Image, Graphics and Signal Processing, pp 47–52
than the methods of SunSVD (2002), SunQR in Sect. 1.2, Su
Hsu L-Y, Hu H-T (2017) Robust blind image watermarking using criss-
(2018) and Luo (2020) under attacks such as salt & peppers
cross inter-block prediction in the DCT domain. J Vis Commun Image Represent 46:33–47
noise, Gaussian noise, blurring, sharpening, cropping, and
Hwai-Tsu H, Hsu L-Y, Chou H-H (2020) An improved SVD-based mean filter.
blind color image watermarking algorithm with mixed modulation
In the future, a hybrid scheme should be developed to
incorporated. Inf Sci. https://doi.org/10.1016/j.ins.2020.01.019
improve the robustness of the watermark under geometry
Jia S, Zhou Q, Zhou H (2017) A novel color image watermarking
scheme based on DWT and QR decomposition. J. Appl. Sci. Eng.
attacks and JPEG compression. In recent years, many hybrid 20(2):193–200
digital image watermarking methods have been expanded
Kumar S, Singh BK (2021) An improved watermarking scheme
to enhance robustness, capacity, and security while still
for color image using alpha blending. Multimed Tools Appl
maintaining the quality of the watermarked image (Mah-
80:13975–13999. https://doi.org/10.1007/s11042-020-10397-4
Lai CC (2011) An improved SVD-based watermarking scheme using
buba and Mohammad 2020). In hybrid domain approaches,
human visual characteristic. Opt Commun 284:938–944
two or more image transformations are used for water-
Laxmanika, Singh A.K., Singh P.K. (2020) A robust image watermark-
marking. These methods provide more imperceptibility and
ing through bi-empirical mode decomposition and discrete wavelet 123 55
Consideration of a robust watermarking algorithm for color image using improved… 5093
domain. In: Singh P., Panigrahi B., Suryadevara N., Sharma S.,
Su Q, Chen B (2018) Robust color image watermarking technique in the
Singh A. (eds) Proceedings of ICETIT 2019. Lecture Notes in
spatial domain. Soft Comput 22:91–106. https://doi.org/10.1007/
Electrical Engineering, vol 605. Springer, Cham s00500-017-2489-7
Li J, Lin Q, Yu C et al (2018) A QDCT- and SVD-based color
Su Q, Niu Y, Zou H et al (2013) A blind double color image watermark-
image watermarking scheme using an optimized encrypted binary
ing algorithm based on QR decomposition. Multimed Tools Appl
computer-generated hologram. Soft Comput 22:47–65. https://doi.
72:987–1009. https://doi.org/10.1007/s11042-013-1653-z org/10.1007/s00500-016-2320-x
Su Q, Niu Y, Wang G, Jia S, Yue J (2014) Color image blind water-
Liu F, Yang H, Su Q (2017) Color image blind watermarking algorithm
marking scheme based on QR decomposition. Signal Process
based on Schur decomposition. Appl Res Comput 34:3085–3093 94:219–235
Luo A, Gong L, Zhou N et al (2020) Adaptive and blind watermarking
Su Q, Wang G, Jia S, Zhang X, Liu Q, Liu LX (2015) Embedding color
scheme based on optimal SVD blocks selection. Multimed Tools
image watermark in color image based on two-level DCT. Signal
Appl 79:243–261. https://doi.org/10.1007/s11042-019-08074-2
Image Video Process 9(5):991–1007
Naderahmadian Y, Hosseini-Khayat S (2014) Fast and robust water-
Su Q, Zhang X, Wang G (2020) An improved watermarking algorithm
marking in still images based on QR decomposition. Multimed
for color image using Schur decomposition. Soft Comput 24:445– Tools Appl 72(3):2597–2618
460. https://doi.org/10.1007/s00500-019-03924-5
Qingtang S, Wang G, Zhang X, Lv G, Chen B (2017) An improved
Su Q, Wang H, Liu D et al (2020) A combined domain watermarking
color image watermarking algorithm based on QR decomposi-
algorithm of color image. Multimed Tools Appl 79:30023–30043.
tion. Multimed Tools Appl 76:707–729. https://doi.org/10.1007/
https://doi.org/10.1007/s11042-020-09436-x s11042-015-3071-x
Sun R, Sun H, Yao T (2002) A SVD and quantization based semi-fragile
Qingtang S, Wang G, Zhang X, Lv G, Chen B (2018) A new algorithm
watermarking technique for image authentication. Proc Internat
of blind color image watermarking based on LU decomposition.
Conf Signal Process 2:1952–1955
Multidimension Syst Signal Process 29(3):1055–1074
University of Granada. Computer Vision Group. CVG-UGR image
Qingtang S, Liu Y, Liu D, Yuan Z, Ning H (2019) A new watermarking
database. [2012-10-22]. http://decsai.ugr.escvgdbimagenesc512.
scheme for colour image using QR decomposition and ternary php
coding. Multimed Tools Appl 78(7):8113–8132
Vaishnavi D, Subashini TS (2015) Robust and invisible image water-
Qin L, Ma L, Fu X (2021) DWT-DQFT-based color image blind water-
marking in RGB color space using SVD. Proc Comput Sci
mark with QR decomposition. In: Lu W., Sun K., Yung M., Liu 46:1770–1777
F. (eds) Science of cyber security. SciSec 2021. Lecture Notes in
Vandenberghe L (2018) 6.QR factorization. ECE133A, pp.6-1-6-39
Computer Science, vol 13005. Springer, Cham
Wang D, Yang F, Zhang H (2016) Blind color image watermarking based
Roy S, Pal AK (2019) A Hybrid Domain Color Image Watermarking
on DWT and LU Decomposition. J Inf Process Syst 12(4):765–778
Based on DWT-SVD. Iran J Sci Technol Trans Electr Eng 43:201–
Yadav B, Kumar A, Kumar Y (2018) A robust digital image watermark-
217. https://doi.org/10.1007/s40998-018-0109-x
ing algorithm using DWT and SVD. In: Pant M., Ray K., Sharma
Singh RK, Shaw DK, Sahoo J (2017) A secure and robust block
T., Rawat S., Bandyopadhyay A. (eds.), Soft computing: theories
based DWT-SVD image watermarking approach. J Inf Optim Sci
and applications. Advances in intelligent systems and comput- 38(6):911–925
ing. 583. Springer, Singapore. https://doi.org/10.1007/978-981-
Singh KU, Singh VK, Singhal A (2018) Color image watermarking 10-5687-1-3
scheme based on QR factorization and DWT with compatibility
analysis on different wavelet filters. J Adv Res Dyn Control Syst
Publisher’s Note Springer Nature remains neutral with regard to juris- 10(6):1796–1811
dictional claims in published maps and institutional affiliations.
Stewart GW (1998) Matrix algorithms. Volume 1: basic decomposi-
tions. The Society for Industrial and Applied Mathematics, ISBN 0-89871-414-1 123 56
A Combination of DWT and QR Decomposition for Color Image Watermarking Phuong Thi Nha Ta Minh Thanh
Le Quy Don Technical University
Le Quy Don Technical University Ha Noi, Viet Nam Ha Noi, Viet Nam phuongthinha@gmail.com thanhtm@lqdtu.edu.vn
Abstract—For the purpose of protecting copyright of digital
time than the methods which based on DWT and SVD de-
images, many published articles indicate that combining DWT
composition. Unfortunately, they seem to be less robust under
with matrix decomposition can improve robustness of water-
some attacks such as rotation, scaling and JPEG compression.
mark. In this paper, a hybrid image watermarking scheme is Finally, DW T
represented by using a combination of 1-level DW T transform
−QR based blind image watermarking methods
and QR decomposition. The first, Haar transform is applied
were also established by several researchers [15]–[19]. In these
on the channel B of the host color image and LL sub-band
articles, the authors employed 1-level or 2-level DW T by
is partitioned in 4 × 4 non-overlapping blocks. After that, QR
Haar transform on the host image at first. After that, QR
factorization is executed on each block where Q matrix and R
decomposition was performed on low frequency sub-bands,
matrix are calculated separately by our proposal. Watermark bits
then the first row of R matrix was chosen to embed watermark
are embedded into the first element of R matrix instead of the
whole row as previous published articles to improve the quality of
bits. Embedding on all elements of the first row of R matrix
watermarked image. In addition, the original watermark image is
led to modifying significantly pixel values. Thus, the quality
permuted by Arnold transform and it helps the proposed method
of watermarked image was affected.
is more secure. In this study, we also perform experiments to
In order to address this issue, we propose a hybrid image
select the most suitable sub-band for embedding information.
The experimental results show that this combination gives a
watermarking scheme in this paper which uses DW T , Arnold
better invisibility of watermarked image which is compared to the
transform and QR factorization. In this study, experiments
QR decomposition based approach. Furthermore, the proposed
will be implemented on many different images to find out the
algorithm is more effective to against many common attacks.
most suitable sub-band. And then, QR decomposition will be
Index Terms—image watermarking, QR decomposition, DWT
executed on this sub-band by the way that we represented in
transform, embedding stage, extracting stage
[20]. After that, watermark bits will be embedded on the first I. I
element R(1, 1) of R matrix instead of the whole row as in NTRODUCTION
the published proposals. The reason for selecting R(1, 1) is A. Background
because energy of the pixel matrix is focused on this element.
In recent years, watermarking is known as an important
Embedding on only one element of R matrix not only improve
technique for copyright protection of digital images. For robust
the invisibility of watermarked image but also increase the
and blind image watermarking technique, it is often based on
robustness of extracted watermark.
frequency transform and matrix decomposition [1]. There are
some proposals which use DW T transform for embedding B. Roadmap
and extracting information such as [2]–[5]. Although these
The rest of this paper is organized as follows. Section
approaches give good invisibility results, they often have
II gives basic knowledge about DW T transform and QR
less robustness under some attacks. Therefore, many authors
decomposition. The proposed watermarking scheme is intro-
designed hybrid schemes which combined DW T with SV D
duced in Section III. Section IV displays experimental results
decomposition, LU decomposition or QR decomposition to
and discussions. A summary of the paper is concluded in
improve robustness of extracted watermark. Section V.
Firstly, combining DW T with SV D factorization seems to
be a effective solution to against common image processing, II. PRELIMINARY
so it had been represented in many papers such as [6]–[12].
However, these methods usually have a big computational A. QR Decomposition
complexity because SV D decomposition, which factorizes a
An A matrix has QR decomposition if it can be factorized
matrix into three matrices, needs 11n3 flops for a n×n matrix.
in form of two matrices Q and R, where Q is an orthogonal
On the other hand, some authors proposed a combination of
matrix and R is an upper triangular matrix. Then, A can be
DW T and LU decomposition in 2019 and 2020 [13], [14].
represented as the formula (1).
Since LU decomposition requires less number of calculations
(about n2 flops), these algorithms has more rapid execution A = QR (1) 57
In [20], we proposed a novel method to find out the elements
In order to apply the transformation to a digital image the term
of Q and R matrices where R matrix will be discovered at
“mod 1” can be replaced by “mod N ” where N × N is the
first and then finding the elements of Q matrix is based on
size of the digital image as equation (5).
A and R. In general, if the host matrix A has size of n × n, s 1 1 x
we can calculate the coefficients by Eq. (2) and Eq. (3) as = (mod N ) (5) t 1 2 y follows. √ r11 = m11
Inverse Arnold transform can be given by equation (6). m 1 r j x 2 −1 s 1j = r = (mod N ) (6) 11 y −1 1 t q P i−1
The security of Arnold Transform depends on key for scram- m r2 , i = j ij − k=1 kj
bling. The key can be selected according to the number of rij = (2) P
iterations and it is different from sizes of image. In our i−1 (m r ij − k=1 kirkj ) , i 6= j
experiments, the watermark image has size of 32×32, so the rii
number of iterations is 24 and the key is a integer in range
where i, j = 2, 3, · · · , n. of [1,24]. 1
B. The embedding process e q1 = a1 and q1 = e q1 r11
The embedding stage of the proposed scheme includes steps 1 as follows. e
qi = ai − (r1iq1 + r2iq2 + · · · + ri−1,iqi−1) and qi = e q r i ii • Step 1 (3)
– The watermark image is permuted by Arnold Trans- where ai, e
qi and qi (with i = 2 to n) are n × 1 vectors. form.
– The permuted image is converted to a one-
B. DW T Transform dimensional binary array wi.
DW T based approaches are used in many signal processing • Step 2
applications. Image watermarking is one such area. DW T
– The host image is divided into R, G and B compo-
shows the multi-resolution analysis property [16]. It decom- nents.
poses the image in the constant bandwidth of frequency on a
– The component B is processed by 1-level DW T and
logarithmic scale. An image is decomposed by applying DW T
LL sub-band is divided into 4 × 4 non-overlapping
using Haar wavelet into four frequency sub-bands namely LL,
blocks. Here, the reasons of choosing the component
LH, HL, and HH at the first level. In general, the low-
B are that: (a) considering all components may dis-
frequency component (LL) represents the smooth variations
tort the colors of the watermarked images; (b) human
in color whereas the high-frequency components (LH, HL,
eyes are less sensitive to the component B than the
and HH) represent the sharp variations. In other words, the
components R and G according to the human visual
base of an image is constituted by the LL, called the low- system.
frequency component, and the edges which give the details are
constituted by LH, HL, and HH, called the high-frequency • Step 3 components.
– Each block of LL sub-band is assigned to A matrix.
– QR decomposition is executed on A matrix of each
III. THE PROPOSED WATERMARKING SCHEME
block of LL sub-band by Eq. (2) and Eq. (3).
In this section, a watermarking scheme will be proposed • Step 4
which includes three main stages namely watermark pre-
– Embed a watermark bit into the triangular matrix R
processing operation, embedding process and extracting stage.
based on the formula of Sun [21] as follows.
∗ Get the first element R(1, 1) of R matrix
A. The watermark pre-processing operation
∗ Calculate z = R(1, 1) mod q (with q is the
To enhance security of the proposed watermarking scheme,
strength of watermark embedding and it is a
a transform called Arnold is applied to permute pixels of positive integer)
the original watermark before embedding. Arnold scrambling ∗ Case wi = “0”
transforms the position of a pixel from (x, y) to a new position q q
(s, t) [22]. The position of pixels changes from one point to R(1, 1) + − z , z ≤ 3 4 4
another based on the equation (4). R0(1, 1) = q s 1 1 x R(1, 1) + 5 − z , elsewhere = (mod 1) (4) 4 t 1 2 y (7) 58 Fig. 2. The extracting process
– Get out the first element of R matrix by Eq. (9). Fig. 1. The embedding process p R(1, 1) =
A(1, 1)2 + A(2, 1)2 + A(3, 1)2 + A(4, 1)2 (9) ∗ Case wi = “1” • Step 3 q q
– Extract information bit of watermark based on the R(1, 1) − − z , z ≤ 4 4
formula of Sun [21] as follows. R0(1, 1) = q
∗ Calculate z = R(1, 1) mod q R(1, 1) + 3 − z , elsewhere 4
∗ The watermark bit is extracted by using following (8) equation. • Step 5 q – Inverse QR decomposition. “0” , z ≤ 2
– Repeat steps from 3 to 5 until all blocks are embed- w0 = i (10) ded. “1” , elsewhere • Step 6
– Repeat Step 2 and Step 3 until extracted all water- – Inverse DW T . mark values.
– Reconstruct watermarked components to receive the watermarked image. • Step 4
– Convert extracted watermark values to an image.
The flowchart of the embedding operation is illustrated
– Apply Inverse Arnold Transform to get final ex- in Fig. 1. tracted watermark image. C. The extracting stage
The flowchart of the extracting process is shown in Fig. 2. • Step 1
IV. EXPERIMENTAL RESULTS AND DISCUSSION
– The watermarked image is divided into R, G, and B components. A. Evaluation Criteria
– The component B is processed by 1-level DW T and
To evaluate the performance of digital watermarking
LL sub-band is divided into 4 × 4 non-overlapping
scheme, Peak Signal to Noise Ratio (P SN R) and Normal- blocks.
ized Correlation (N C) are usually employed. P SN R is an • Step 2
effective criterion to estimate the imperceptibility, while N C
– Each block of LL sub-band is assigned to A matrix.
value is an important establishment to evaluate the robustness 59
Fig. 3. The host images: (a) avion, (b) baboon, (c) Balloon, (d) couple, (e)
Girl, (f) house, (g) lena, (h) milkdrop, (i) parrots, (j) peppers, (k) sailboat, (l)
tree. The watermarks: (m) w1, (n) w2.
of a watermarking scheme. N C index is always less than or
equal 1. P SN R index is designed as follows. 2552 P SN R = 10 log , (11)
Fig. 4. The results of selecting sub-band when the watermark is ‘w1’. 10 MSE
where the mean square error (M SE) between the original and
watermarked image is defined as: 1 M −1 X N−1 X M SE = (H(i, j) − H0(i, j))2, (12) M N i=0 j=0
where M × N is the size of the image, H(i, j) and H0(i, j)
are the pixel value at position (i, j) of the host image and the
watermarked image, respectively.
B. Experiments for selecting the best sub-band
In order to select a suitable sub-band for embedding wa-
termark, we calculated separately P SN R and N C values for
each sub-band. In these experiments, twelve standard color
512×512 images from the CV G − U GR1 image database
are chosen as the host images and two binary 32×32 images
Fig. 5. The results of selecting sub-band when the watermark is ‘w2’.
are used to be the watermark as displayed in Fig. 3. In
order to consider the trade-off between the robustness and
the invisibility of the watermark, the embedding strength of
C. Invisibility experiments
watermark q is designated as 10.
The results of these tests are displayed in Fig. 4 and
To evaluate superiority of the proposed scheme in term of
Fig. 5. From two figures, it is easy to see that embedding
the quality of watermarked image, we compare it with two
the information on LL sub-band is more effective than on
relative studies. The first method [20] was published in 2018
other sub-bands for all tested images. As shown in Fig. 5,
by ourselves which used an improved QR decomposition. The
although PSNR index of LL sub-band is a little lower than
second one [16] was proposed in 2017 which also utilized
LH sub-band for ‘avion’ and ‘baboon’ images, its N C index
a combination of DW T and QR factorization. Fig. 6 and
is higher than the other sub-bands. It is similar to Fig. 4 where
Fig. 7 display a comparison about P SN R values between
P SN R value of HH sub-band is 64.5174, while this value of
three methods. It is clear that the proposed approach has higher
LL sub-band is 64.1102 for ‘Balloon’ image. However, N C
P SN R indexes than other methods for all tested images. The
value of LL sub-band is 0.9871 which is much higher than the
average value of the proposed approach is 62.4606 dB while
other sub-bands. These results are completely corresponding
it is only 61.1390dB and 43.3699dB for the method [20] and
because LL sub-band contains the most energy of the host
the method [16] respectively. This means that the proposed
image [17]. This is a reason that we chose LL sub-band for
approach overcomes other methods in term of the invisibility
embedding the watermark in the proposed image watermarking of watermarked image. scheme.
The reason is that the proposed algorithm brings the better
result than the method [20] is because its embedding operation
1https://decsai.ugr.es/cvg/dbimagenes/
only takes place on LL sub-band. While the method [20] hides 60
Fig. 6. PSNR values of the different methods when the watermark is ‘w1’.
Fig. 7. PSNR values of the different methods when the watermark is ‘w2’.
Fig. 8. NC values of the different methods under attacks when the host image
is ‘milkdrop’ and the watermark is ‘w1’.
directly information into the pixel matrix after calculating
QR decomposition. LL sub-band holds 1/4 size of the host
scheme are less than the values of the method [20] for two
image but it contains the most energy of the image. Therefore,
noise attacks, this gap is not too big. This demonstrates
beside the quality of watermarked image, it still guarantees
that the proposed method is more robust to against almost
the robustness of the proposed scheme. In addition, the both
attacks. Beside that, we can see that the proposed method
proposed method and [20] just get one element R(1, 1) of R
improves significantly the quality of the watermark images
matrix to embed information. This will restrict modification of
in comparison with the method [20] under attacks such as
pixel values. As a result, the quality of watermarked image is
rotation, scaling and JPEG compression. The Fig. 8 and
significantly ameliorated. Whereas, the method [16] embeds
Fig. 9 also show that combining DWT and QR decomposition
watermark bits into the whole first row of R matrix, so
brings better robustness than using only QR decomposition for
pixel matrix has been changed values on all elements after
embedding information into image.
embedding. That is a reason why this method gives very low
P SN R indexes in comparison with the other methods. V. CONCLUSION
To sum up, this article describes a hybrid image watermark-
D. Robustness experiments
ing method which combines DW T with QR factorization.
The robustness is one of important criterion to assess the
In the embedding processing, an 1-level DW T transform is
effect of a image watermarking scheme. In this section, we
applied on the component B of the host color image by using
attack two watermarked images by nine normal kinds of image
Haar wavelet at first. And then, LL sub-band is chosen to
processing which include blurring, sharpening, salt&peppers
divide into 4×4 non-overlapping blocks. These blocks are used
noise, gaussian noise, rotation, scaling, cropping, JPEG com-
to factorise matrix by using QR decomposition in succession
pression and mean filter. NC index is used to estimate the
after that. In order to increase invisibility of the watermarked
robustness of the proposed method in comparison with the
image, embedding watermark bits are carried out by the first
algorithm [16] and [20]. The results of the tests are displayed
element R(1, 1) of R matrix. Finally, an inverse QR decom- in Fig. 8 and Fig. 9.
position and an inverse DW T transform are applied to receive
In general, the two watermark images of the proposed
the watermarked image. In the extracting stage, LL sub-band
approach can be recognized for all tested attacks. Furthermore,
is obtained by 1-level Haar transform and R(1, 1) element of
the proposed method gives more excellent NC values than
R matrix is gotten out by Eq. (9) instead of using QR decom-
two compared methods for almost attacks except salt&peppers
position as the previous proposals. For enhancing security of
noise and gaussian noise. Although NC values of the proposed
the scheme, Arnold transform and Inverse Arnold transform 61
[6] Ranjeet Kumar Singh, Dillip Kumar Shaw, Jayakrushna Sahoo (2017),
“A secure and robust block based DWT-SVD image watermarking
approach”, Journal of Information and Optimization Sciences, 38:6, pp.
911-925, DOI: 10.1080/02522667.2017.1372137
[7] Y. He and Y. Hu (2018), “A Proposed Digital Image Watermarking
Based on DWT-DCT-SVD”, 2nd IEEE Advanced Information Man-
agement,Communicates,Electronic and Automation Control Conference
(IMCEC), pp. 1214-1218, doi: 10.1109/IMCEC.2018.8469626.
[8] D Sanku, S Kiran, TT Takore (2018), “Digital Image Watermarking in
RGB Host Using DWT, SVD and PSO Techniques[M]”, Proceedings
of 2nd International Conference on Micro-Electronics Electromagnetics and Telecommunications.
[9] Savakar, D.G., Ghuli, A. (2019), “Robust Invisible Digital Image Wa-
termarking Using Hybrid Scheme”, Arab J Sci Eng 44, pp. 3995–4008.
https://doi.org/10.1007/s13369-019-03751-8
[10] Wang B, Zhao P.(2020), “An Adaptive Image Watermarking Method
Combining SVD and Wang-Landau Sampling in DWT Domain”, Math-
ematics, 8(5):691. https://doi.org/10.3390/math8050691
[11] Rassem, T.H., Makbol, N.M., Khoo, B.E.(2019), “Performance eval-
uation of wavelet SVD-based watermarking schemes for color im-
ages”, In: Anbar, M., Abdullah, N., Manickam, S. (eds.) ACeS
2019. CCIS, vol. 1132, pp. 89–103. Springer, Singapore (2020).
https://doi.org/10.1007/978-981-15-2693-07
[12] Preeti Garg, R. Rama Kishore. (2020), “Secured and multi optimized
image watermarking using SVD and entropy and prearranged embedding
locations in transform domain”, Journal of Discrete Mathematical
Sciences and Cryptography, 23:1, pp. 73-82.
[13] Dongyan Wang, Fanfan Yang and Heng Zhang (2016), “Blind Color
Image Watermarking Based on DWT and LU Decomposition”, Journal
of Information Processing System, 12(4), pp. 765-778.
[14] A. Shaik and V. Masilamani(2019), “A Robust SLIC Segmentation
Based Zero Watermarking Scheme Using DWT And Partial Pivot-
Fig. 9. NC values of the different methods under attacks when the host image
ing LU Decomposition”, 2019 IEEE 1st International Conference on
is ‘Girl’ and the watermark is ‘w2’.
Energy, Systems and Information Processing (ICESIP), pp. 1-5, doi:
10.1109/ICESIP46348.2019.8938355.
[15] R. I. Sabri, A. M. Abduldaim and J. Waleed (2020), “Mamdani FIS
are also applied on the watermark image in the embedding
Combined With LU Decomposition Method and Two-Level LWT for
Image Watermarking Technique”, 2020 3rd International Conference
stage and extracting stage, respectively. In the paper, many
on Engineering Technology and its Applications (IICETA), pp. 12-17,
experiments are implemented to test P SN R and N C indexes
doi: 10.1109/IICETA50496.2020.9318829
for four sub-bands in order to find out the most appropriate
[16] Shaoli Jia, Qingpo Zhou and Hong Zhou (2017), “A Novel Color Image
Watermarking Scheme Based on DWT and QR Decomposition”, Journal
sub-band. Moreover, imperceptibility and robustness tests are
of Applied Science and Engineering, 20(2), 2017, pp. 193-200.
executed to evaluate superiority of the proposed method over
[17] Kamred Udham Singh, Vineet Kumar Singh and Achintya Singhal
two compared methods. The experimental results display that
(2018), “Color Image Watermarking Scheme Based on QR Factorization
and DWT with Compatibility Analysis on Different Wavelet Filters”,
the proposed scheme defeats the other approaches in term of
Jour of Adv Research in Dynamical & Control Systems, 10(6), pp. 1796-
the quality of watermarked image as well as the robustness of 1811.
the extracted watermark under almost common image attacks,
[18] Y. Altay and G. Ulutas¸ (2020), “DWT-QR based blind image water-
marking method using firefly algorithm”, 2020 28th Signal Processing
especially geometry processing and JPEG compression.
and Communications Applications Conference (SIU), pp. 1-4, doi: 10.1109/SIU49456.2020.9302216.
[19] Shaik A. (2020), “A Secure Blind Watermarking Scheme Using REFERENCES
Wavelets, Arnold Transform and QR Decomposition”, In: Chandra-
bose A., Furbach U., Ghosh A., Kumar M. A. (eds) Computational
[1] Jibrin, B., Tekanyi, A., Sani, S. (2019), “Image watermarking algorithm
Intelligence in Data Science. ICCIDS 2020. IFIP Advances in In-
in frequency domain: a review of technical literature”, ATBU J. Sci.
formation and Communication Technology, vol 578, Springer, Cham.
Tech. Educ., 7(1), pp. 257–263.
https://doi.org/10.1007/978-3-030-63467-411
[2] M Paliwal and Y. Kumar Jain (2015), “Digital Watermarking Algorithm
[20] Phuong Thi Nha, Ta Minh Thanh, Ngoc Tu Huynh (2018), “An improved
for Embedding Color Image using Two Level DWT”, International
QR decomposition for color image watermarking”, 10th International
Journal of Computer Applications, vol. 116, no. 13, pp. 19-24.
Conference on Knowledge and Systems Engineering (KSE), pp. 56-60.
[3] Ambadekar, S.P., Jain, J., Khanapuri, J. (2019), “Digital image water-
[21] R. Sun, H. Sun, T. Yao (2002),“A SVD and quantization based semi-
marking through encryption and DWT for copyright protection”, In:
fragile watermarking technique for image authenticatio”, Proc. Internat.
Bhattacharyya, S., Mukherjee, A., Bhaumik, H., Das, S., Yoshida, K.
Conf.Signal Process. 2, pp. 1952-1955.
(eds.) Recent Trends in Signal and Image Processing. AISC, vol. 727,
[22] Satish A, Erapu Vara Prasad, Tejasvi R, Swapna P, Vijayarajan R,
pp. 187–195. Springer, Singapore. https://doi.org/10.1007/978-981-10-
“Image Scrambling through Two Level Arnold Transform”, Alliance In- 8863-6
ternational Conference on Artificial Intelligence and Machine Learning
[4] Kumar, S., Singh, B.K (2021), “DWT based color image watermarking (AICAAM), April 2019.
using maximum entropy”, Multimed Tools Appl, 80, pp. 15487–15510.
https://doi.org/10.1007/s11042-020-10322-9
[5] Decheng Liu, Qingtang Su, Zihan Yuan, Xueting Zhang (2021), “A
fusion-domain color image watermarking based on Haar transform
and image correction”, Expert Systems with Applications, Volume 170,
114540, ISSN 0957-4174, https://doi.org/10.1016/j.eswa.2020.114540. 62 Applied Intelligence
https://doi.org/10.1007/s10489-023-04903-y
An effective embedding algorithm for blind image watermarking
technique based on Hessenberg decomposition Phuong Thi Nha1
· Ta Minh Thanh1 · Nguyen Tuan Phong1 Accepted: 21 July 2023
© The Author(s), under exclusive licence to Springer Science+Business Media, LLC, part of Springer Nature 2023 Abstract
For digital image copyright protection, watermarking techniques are a promising solution and are of interest to many
researchers. In watermarking schemes based on matrix transformation, the embedding element and embedding formula
play a very important role in maintaining the quality of a watermark image and the robustness of the watermark. In this paper,
a blind image watermarking scheme based on Hessenberg decomposition, where the improvement focuses on the embedding
element and embedding formula, is proposed. First, the structure of the Hessenberg factorization is analysed to obtain the most
suitable embedding element. Accordingly, this is the first time that the element on the second row and the second column of the
upper Hessenberg matrix is selected as an embedding element in a Hessenberg-based image watermarking scheme because
of its energy concentration and stability. Second, an improved embedding formula is proposed to address the limitations of
previous studies. In the proposed formula, constraint conditions are added to limit the change in all blocks, and a scaling
factor is applied to guarantee a trade-off between invisibility and robustness. Here, the scaling factor is carefully calculated by
repeating various experiments under different image attacks to achieve an optimal value. Therefore, our proposed embedding
formula not only minimizes the modification of the host image after embedding but also helps maintain the robustness of the
extracted watermark. Third, to increase the security of the proposed scheme, the watermark image is encoded by the Arnold
transform before it is embedded into the host image. The experimental results show that the proposed approach defeats the
compared methods in terms of invisibility and execution time. Moreover, the proposed scheme can resist most common
attacks when the average normalized correlation value is higher than 0.93 and the extracted watermarks are always clearly recognized.
Keywords Image watermarking · Copyright protection · Hessenberg decomposition · Embedding algorithm · Arnold transform 1 Introduction
to enhance data security. However, the issue of multimedia
safety is still a challenge for society as a whole and attracts
With the strong expansion of technology and the internet,
the attention of many researchers. Digital watermarking is
the exchange of digital data is becoming increasingly easier.
considered a potential technique to solve this problem and
Despite its interesting aspects, this data exchange has many
prevent unauthorized access to copyrighted data. Compared
potential risks, such as theft, forgery, or modification of infor-
with similar schemes, such as cryptography, steganography,
mation. Therefore, many security policies have been applied
and digital rights management, watermarking is the most
useful scheme for digital data security [1]. In recent years, B
digital image watermarking techniques have been widely Phuong Thi Nha
investigated. To ensure the sustainability of a watermark phuongthinha@lqdtu.edu.vn
image, watermarking schemes are often performed in the Ta Minh Thanh
transform domain by using matrix decomposition, such as thanhtm@lqdtu.edu.vn
singular value decomposition (SVD), QR decomposition Nguyen Tuan Phong
(Q is an orthogonal matrix and R is an upper triangular tuanphongnguyen1974@gmail.com
matrix), LU decomposition (L is a lower triangular matrix 1
Le Quy Don Technical University, 236 Hoang Quoc Viet,
and U is an upper triangular matrix), Schur decomposition, Ha Noi, Viet Nam 123 63 P. T. Nha et al.
and Hessenberg decomposition [1–3]. The details of these
and then individually applies Schur decomposition to each
schemes are presented as follows:
block. Level shifting serves as a controlling gauge for embed-
First, SVD is one of the earliest and most common matrix
ding strength. The use of intentional perturbation prevents
transformations that has been employed for digital image
nil orthonormal vectors derived from zero eigenvalues. The
watermarking schemes. Some studies are notable, such as
dominant vector is identified by analysing the entire Schur
[4–11]. Image watermarking methods based on SVD often
matrix instead of just diagonal elements. To achieve effective
embed information on the first element D(1,1) of the upper
watermark embedding and extraction, the orthonormality
triangular matrix D [6, 7] or on the first column of the matrix
of the acquired unitary matrix ought to be preserved while
U [5, 8, 9]. In 2020, Luo et al. used a scheme that combined
the resulting distortion can be compensated via the system-
the discrete wavelet transform (DWT) and SVD with logistic
atic modification of the Schur matrix. Finally, a recursive
map (LM) [9]. In the embedding process, the 4 × 4 blocks
regulation guarantees the retrieval of watermark bits. The
of the original image were selected according to an opti-
experimental results indicate that the proposed scheme is
mal strategy to minimize the change in the watermark image
free of errors in the absence of attacks and can withstand a
compared to the original image. Moreover, the entropy infor-
variety of image processing attacks.
mation was utilized to identify the embedding coefficient
In 2019, Su et al. improved his algorithm by giving two
for each suitable block. Then, the watermark was embed-
choices for the embedded element [14]. First, the watermark
ded on the U5 and U9 elements of matrix U after performing
information was embedded in the triangular matrix D and
the SVD on the low-low (LL) subband. For the watermark
orthogonal matrix U in two different ways, and temporary
image, the author used the LM, which is a kind of chaotic
watermark blocks were obtained. Second, the improved algo-
one-dimensional map, to encode information. To evaluate the
rithm was employed to select the appropriate block from
effectiveness of the proposed scheme, the author performed
these temporary blocks. The advantage of this method is
many different image attack experiments, including combi-
that the final watermark block will have less quality loss.
nation attacks. Two limitations of this proposal are that the
In addition, the embedding flag is generated and pushed to
experiments are only performed on grey-scale images and
the cloud storage with the watermark image. In 2020, Liu
the algorithm is weak against rotation attacks.
et al. presented another scheme by using Affine transform
In [8], Hu et al. combined SVD and the Arnold transform
with a large key space to encrypt the watermark [15]. After
on a 512 × 512 colour image and two 64 × 32 and 32 ×
performing the Schur decomposition, the author quantized
16 colour watermark images. Before embedding, the water-
the eigenvalues of the diagonal matrix with different quanti-
mark was enlarged to sizes of 128 × 128 and 64 × 64 and
zation steps. This proposal gives positive results in terms of
then shuffled through the Arnold transform. The elements
watermark image quality and durability as well as ensuring
U(2, 1) and U(3, 1) of matrix U were selected as embedding system safety.
elements. The proposed watermark embedding scheme helps
Another publication based on the Schur decomposition is
ensure the orthogonality of the matrix after SVD expansion.
[16] by Li et al. in 2020. Li divided the original image into 8
In addition, the mixing modulus helps increase the stabil-
× 8 blocks, and then the Schur decomposition was applied
ity of the watermark. Based on the results shown in the
to each block. Next, the watermark was erased by the Arnold
paper, this approach of Hu is better than the comparison stud-
transform and LM before it was embedded into the element
ies that employed QR and LU decomposition. However, the
with the largest energy D(1, 1) of the upper triangular matrix.
approach is still limited to JPEG (Joint Photographic Experts
In the article, the author experimented with three black and
Group) compression attacks, adding Gaussian and speckle
white watermark images with sizes of 32 × 32, 48 × 48,
noise. In summary, although the SVD implementation gives
and 64 × 64. The peak signal-to-noise ratio (PSNR) values
good results in the field of digital watermarking, it has a high
without attacks are in the range of 40 dB to 47 dB (dexibel).
computational complexity (O(n3)).
The results are considered better than those of the compared
Second, the Schur decomposition is another new matrix
studies, with the exception that elastic attack and low-pass
expansion that has been applied in digital image watermark
filtering still need to be improved in further studies.
schemes in recent years. From 2019 to 2023, six publications
Third, the LU decomposition has the advantage of low
used this transformation in the area of image watermark-
computational complexity (O(n2)) compared with other
ing [12–17]. First, a study was conducted by Hsu et al. in
matrix transformations. However, there are limitations in
2019 [12]. In this paper, the deficiency of Schur decom-
terms of robustness and invisibility when using this decompo-
position for image watermarking has been comprehensively
sition in the area of watermarking. Thus, there have been very
investigated. A remedial scheme is developed not only to fix
few studies based on LU decomposition in recent years, such
the existing problems but also to reinforce the performance
as [18, 19]. In [18], a new scheme using LU decomposition is
in robustness and imperceptibility. This scheme partitions
proposed as an alternative technique. In this scheme, which
the host image into nonoverlapping blocks of 4 × 4 pixels
is a frequency-based technique using the R-level DWT, the 123 64
An effective embedding algorithm...
scaling factor is adaptively determined according to the cover
is expanded via the Householder algorithm and the quanti-
image and watermark that is utilized. Another issue to be
zation formula. Then, the pairs of similar coefficients qi j of
solved in watermarking studies is the false-positive problem
the Q matrix were calculated by NC index to identify the
(FFP). For this purpose, a control mechanism is used against
appropriate embedding element and formula.
the FFP in watermark embedding and watermark extracting
The watermark schemes based on the Hessenberg decom-
processes. In addition, the watermarking process is carried
position should also be surveyed. In linear algebra, the time
out in any size, depending on the size of the cover image.
complexity of Hessenberg decomposition is lower than that
Unfortunately, this algorithm still needs to be explored to
of SVD and Schur decomposition [1]. Furthermore, accord-
resist image rotation attacks. Although the LU decomposi-
ing to [28], which analysed and compared the efficiency
tion is easier to implement than the other transformations, it
of the Hessenberg-based watermarking scheme (HD) and
is less efficient in terms of stability.
Schur-based watermarking scheme (SD), HD gives better
Fourth, the QR decomposition is considered an inter-
results than SD in terms of imperceptibility and robustness.
mediate step of the Hessenberg transformation. In recent
In reference [29], Maryam also showed the high accuracy and
years, many studies have used this transformation in the
effectiveness of the Hessenberg decomposition in compari-
field of digital image watermarking, such as [20–27]. To pro-
son with SVD, QR decomposition, and Schur decomposition.
tect the digital copyright of colour images, a colour image
These advantages explain why Hessenberg-based water-
watermarking method should simultaneously have strong
marking schemes have attracted considerable interest, and
robustness and short running times. To achieve these two
the studies are regularly updated.
goals, an effective colour image watermarking method is
The first blind image watermarking technique using
presented in [21]. First, the element in the first row and first
Hessenberg decomposition was proposed to embed colour
column of the R matrix of QR decomposition is obtained
watermark images into colour host images by Su et al. in
by the presented method in the spatial domain. Second, the
[30]. In the embedding stage, the information was hidden
obtained element of matrix R is selected to protect the copy-
into the elements Q(2, 2) and Q(3, 2) of the orthogonal
right of the colour image in the spatial domain without true
matrix Q, which was obtained by Hessenberg decomposi-
QR decomposition. Last, the presented watermarking tech-
tion. In the extracting stage, either the original host image
nique is applied in the spatial domain. In the compared
or the original watermark image was not needed, but valid
experiments, the imperceptibility of the presented method
keys are necessary to restore the watermark. The experi-
is approximately 40 dB, its average normalized correlation
mental results showed that this approach outperforms other
(NC) is 0.9435, its average running time is 0.703613 s (sec-
watermarking methods and can protect against many com-
ond), its embedding capacity is 0.03125 bpp (bit per pixel),
mon attacks, namely image compression, filtering, cropping,
and its key space is 2138, which indicates that the proposed
noise, blurring, scaling, sharpening, and rotation. However,
new method has better performance in terms of robustness
the quality of the watermarked image is significantly reduced and real-time features.
in comparison with the host image as two elements in matrix
Another study proposed by Dhar et al. in 2020 is [23]. This
Q are modified. This modification changes the whole pixel
paper suggests a blind symmetric watermarking algorithm
matrix of one block after embedding.
using the fan beam transform (FBT) and QR decomposition
Another proposal was published by Su et al. in [31]. In
for colour images. First, component B of the original image is
this article, the author selected the largest energy element
applied by the FBT. Second, component B is split into m × m
hmax of the upper Hessenberg matrix H to embed the water-
nonoverlapping blocks, and QR decomposition is conducted
mark. Hence, the invisibility of the watermarked image was
on each block. Watermark data are placed into the selected
improved in comparison with the method in [30]. In both
coefficient of the upper triangular matrix using a new embed-
papers, the Arnold transform was applied to improve the
ding function. Simulation results suggest that the presented
security, and the MD5-based hash pseudorandom algorithm
algorithm is extremely robust against numerous attacks, and
algorithm was performed to enhance the robustness. In addi-
also yields watermarked images with high quality. Further-
tion to a single domain, Omar et al. introduced a blind colour
more, the algorithm exhibits better performance than recent
image watermarking scheme in 2018 that was a combina-
state-of-the-art algorithms in terms of robustness and imper-
tion of DWT, fast walsh hadamard transform (FWHT), and
ceptibility. The NC of the proposed algorithm varies from
Hessenberg decomposition [32]. First, the red channel of the
0.8252 to 1, the PSNR varies from 54.1854 to 54.1892, and
host image was subjected to a two-level DWT followed by
structural similarity index measurement (SSIM) varies from
the FWHT. Then, 4 × 4 nonoverlapping blocks were received 0.9285 to 0.9696.
from the FWHT coefficients. Afterward, Hessenberg decom-
The last proposal to be referenced is Chen’s article [27] in
position was employed to decompose each block, and the
2021. The algorithm performed Quaternion QR Decomposi-
watermark information was hidden in the first element H(1,
tion (QQRD) on 4 × 4 blocks, where the QR decomposition
1) of matrix H. The experimental results indicated that the 123 65 P. T. Nha et al.
watermarking scheme of Omar has acceptable invisibility
The remainder of this paper is arranged into four parts.
with a PSNR > 40 dB. This method also has good resistance
First, Section 2 introduces techniques that is relevant to
to geometrical attacks such as cropping, scaling, and rotation.
basic properties of Hessenberg decomposition and Arnold
In 2020, Areej et al. combined the DWT with LM and
transform. Second, the proposed embedding algorithm and
Hessenberg decomposition to build an efficient scheme of
the proposed image watermarking scheme are described in
digital image watermarking [33]. In this publication, the host
Section 3. Third, the experimental results and discussion are
image was transformed into four subbands (HH (High-High),
presented in Section 4. Fourth, Section 5 summarizes the
LH (Low-High), HL (High-Low), and LL (Low-Low)) by contents of this article.
using a 1-level DWT. Then, the subband LH was chosen
and divided into 4 × 4 blocks before applying LM and Hes-
senberg decomposition for each block. Two embedding and 2 Relevant techniques
extraction formulas were utilized as two separate processes
and compared with each other in terms of imperceptibility
2.1 Hessenberg decomposition
and robustness via the experimental results. However, a dis-
advantage of this proposal is that it has not been compared
According to [30], the Hessenberg decomposition is a matrix
with existing works. In 2022, two Hessenberg-based arti-
decomposition of a square matrix A into a unitary matrix Q
cles were published, namely, [34] and [35]. The first paper
and a Hessenberg matrix H such that
is introduced by Methaq et al. where DWT, Hessenberg
decomposition, and firework algorithm (FA) are employed A = Q H QT , (1)
for optimized data hiding in digital images. The highlight
of this proposal is the use of an optimization procedure via
where QT denotes the conjugate transpose of matrix Q. In
the application of the firework algorithm to obtain keys. This
this case, Q QT = QT Q = I , and thus, Q−1 = QT . Matrix
procedure requires performing the lowest possible change
H is an upper Hessenberg matrix, meaning that H (i , j ) = 0
rate in an image, so it contributes to maintaining the qual-
wherever i > j + 1.
ity of the image after embedding. The second paper is [35],
For example, an image block A of size 4 × 4 is
which was developed by Lei Wang and his coworkers. This ⎡ ⎤
is the first time that the DWT, Hessenberg decomposition, 29 37 32 30
SVD, particle swarm optimization (PSO), Arnold transform 21 23 23 23 A ⎢ ⎥ = ⎢ ⎥
and LM are combined to create an optimal watermarking ⎣15 16 13 14⎦
algorithm. Although the experimental results showed that the 14 10 14 14
proposed method has high robustness against various attacks,
it requires considerable execution time.
and can be factored into an orthogonal matrix Q and upper
In this paper, we propose a blind image watermarking
Hessenberg matrix H by Hessenberg decomposition as fol-
scheme based on Hessenberg decomposition to improve the lows:
quality of the watermarked image, the robustness of the ⎡1.0000 0 0 0 ⎤
watermark, and execution time. Our contributions are listed 0 −0.7153 0.6550 0.2436 as follows: Q ⎢ ⎥ = ⎢ ⎥ ⎣ 0
−0.5109 −0.2522 −0.8218⎦ 0 −0.4768 −0.7123 0.5151
– We identify the most appropriate element to embed based
on analysing the structure of the Hessenberg decompo-
⎡ 29.0000 −57.1188 −5.2041 −1.8317⎤
sition. Accordingly, this is the first time that the element −29.3598 50.6717 9.8224 1.7070
H(2, 2) of matrix H is selected as an embedding ele- H ⎢ ⎥ = ⎢ ⎥ 0 −4.4664 0.9887 0.2654
ment in a Hessenberg-based image watermarking scheme ⎣ ⎦ 0 0 −3.0385 −1.6604
because of its energy concentration and stability.
– We propose an effective embedding formula that not only
In the above Hessenberg matrix H, the coefficient H (2, 2)
limits the change in the pixel values but also improves the
= 50.6717 has the largest energy, which can be suitably
robustness of the watermark. The scaling factor of the
modified to embed watermark information by quantization
proposed formula is computed by repeating experiments modulation.
under various attacks. This approach helps increase the
ability to precisely extract information under attacks. 2.2 Arnold transform
– To enhance the security of the proposed method, we apply
Arnold transform to permute the pixels of the watermark
To improve the secrecy of the proposed watermarking image before embedding.
method, the Arnold transform is utilized to swap pixels of the 123 66
An effective embedding algorithm...
Table 1 Number of iterations for different sizes of an image
Since the Arnold transform is an iterative process, if the
location (x, y) is transformed several times, it returns to its Size of image Iterations Size of image Iterations
original position after T iterations. T is referred to as the 4 × 4 3 188 × 188 48
period of the transformation and depends on the size of the 8 × 8 6 254 × 254 384
watermark image. Here, the size of the pixel space is n = 0, 16 × 16 12 256 × 256 192
1, 2, . . . , N - 1. Pixels move with periodicity, so T and N are 32 × 32 24 378 × 378 72
correlated. Whenever N changes, it generates a completely 64 × 64 48 512 × 512 384
different Arnold transform. It is assumed that the scrambling 124 × 124 15 764 × 764 285
has been performed by k iterations; then, the descrambling 128 × 128 96 1024 × 1024 768
needs (T - k) iterations to achieve the original image.
In [37, 38], the authors calculated the number of iterations
(T) based on the size of the image (N × N); this relationship
is shown in Table 1. As shown in Table 1, although the peri-
original watermark image before embedding. This technique
odicity of the Arnold transform is related to the size of the
moves the location of a pixel from (x, y) to another location
image, it is not proportional. For example, if the size of the
(s, t) [36]. The method of transformation is performed via
image is 128 × 128, the number of iterations is 96. We only (2).
need 48 iterations if the size of the image is 188 × 188.
Figure 1 shows an instance of applying the Arnold transform s 1 1 x
to a watermark image with a size of 32 × 32. After 24 itera- = (mod N ), (2) t 1 2 y
tions, the original watermark is restored.
2.3 Blind watermarking based on Hessenberg
where N × N is the size of the watermark image. To recover decomposition
the original image, an inversion of the Arnold transform is required based on (3).
For an image watermarking algorithm, selecting the embed-
ding formula and embedding element(s) is extremely impor- x 2 −1 s
tant as it determines almost the entire quality of the water- = (mod N ). (3) y −1 1 t
marked image as well as the robustness of the watermark.
Fig. 1 Scrambled image at different iterations using the Arnold transformation 123 67 P. T. Nha et al.
Among the abovementioned Hessenberg-based methods,
extract watermarks. The problem lies in specific properties of
Su’s studies serve as the basis for subsequent works. In [31],
the Hessenberg decomposition. The saturation and round-off
the author chose the largest energy element hmax of the upper
errors may cause unexpected outcomes while converting the
Hessenberg matrix H to embed the watermark bits based on
resulting elements to unsigned 8-bit pixel values. Figure 2 the following equation.
exemplifies one such case, where w = 0 is embedded into
the 299th block of the “Couple” image from the CVG- ⎧ h
UGR image database [39]. Let Aunit8 = funit8(ai j )
max − mod (hmax , T )+0.75T , if w = “1", 4×4 ⎨ h∗
denote the resultant matrix after Hessenberg reconstruction max = ⎩ h
and unsigned, 8-bit integer casting. funit8(.) represents an
max − mod (hmax , T )+0.25T , if w = “0",
unsigned 8-bit integer casting function defined as (4) ⎧ 0 , x ≤ 0,
where mod(.) is the module operation and T is the quan- ⎪ ⎪ ⎪ ⎪
tization step, which is set to 65 in Su’s experiments. In ⎨ funit8(x) =
x + 0.5 , 0 < x < 255, (6)
the extraction stage, the watermark bit can be retrieved by ⎪ ⎪ ⎪
examining whether the magnitude of mod(h∗ ⎪ max , T ) in the ⎩ 255 , x ≥ 255,
obtained matrix H ∗ is greater than 0.5T as follows.
with being the floor function. In the example shown in
⎧ “0" , mod(h∗
Fig. 2, the largest value hmax in matrix H is H (2, 2) = ⎨
max , T ) < 0.5T , w∗ = (5)
59.3071, which is highlighted in red. After embedding the ⎩ “1" , elsewhere.
watermark bit w = 0 into this element via (4), it is modified
to 16.5571. The matrix A, which is recomposed afterward
According to (4), the pixel values of all blocks are mod-
by the equation A = Q H QT , contains three negative val-
ified. As a result, the quality of the watermarked image
ues, namely, A(2, 4) = −14.3636, A(3, 4) = −8.5331,
is also affected. In addition, our test results indicated that
and A(4, 4) = −9.2702. Thus, these values need to be con-
the operation of the above method cannot always perfectly
verted to 0, and the matrix A is transformed to the matrix
Fig. 2 Example illustrating the inconsistency between the extracted watermark bit and the original bit 123 68
An effective embedding algorithm...
Aunit8 based on (6). The resulting matrix has a significant
general, a watermark is embedded into one element or two
change in comparison with the original matrix. In the extract-
elements of each image block. If two elements are chosen for
ing stage, this matrix is denoted as A∗ and it is decomposed
embedding, they are required to be near each other, which
to matrix H ∗ via Hessenberg decomposition. In particular,
means that the correlation coefficient (CC) between them
the largest value h∗max in matrix H∗ is the first element
should be close to 1 [8, 30]. In the case of one element, it is
instead of the element at the position (2, 2) as in the embed-
often the highest value because of its concentration of energy
ding stage. Furthermore, the value of this element is 44, so [14, 16, 31].
mod(h∗max , T ) = 44, while 0.5T = 32.5. According to (5),
To identify the most suitable element, we perform Hessen-
the extracted watermark bit is w∗ = 1, which disagrees with
berg decomposition on all 4 × 4 blocks of images from the the intended bit.
CVG-UGR image database [39]. The experimental results
Based on the above analysis, it is extremely necessary to
show that the largest value of matrix H is not always fixed
addess the issue of Hessenberg decomposition to apply it
at one position. However, this value mostly falls on the sec-
in watermarking schemes. After the publication [31] of Su,
ond row and second column element H(2, 2). A reason that
there have been some Hessenberg-based studies. However,
H(2, 2) often has the largest value is because of the special
these studies mainly focus on combining techniques instead
property of the Hessenberg decomposition. Based on (1), as
of improving the embedding formula. For instance, the pro-
Q QT = QT Q = I , matrix H is
posal [32] in 2018 is a combination of the DWT, FWHT,
and Hessenberg decomposition. In 2022, while Methaq com- H = QT A Q. (7)
bined the DWT with Hessenberg decomposition and FA, Lei
Wang introduced a hybrid scheme based on many techniques,
Therefore, element H(2, 2) of matrix H is a result of mul-
such as the DWT, SVD, Hessenberg decomposition, PSO,
tiplying the second row of matrix QT by the second column
Alnord transform, and LM. The proposal [34] used the FA
of matrix A, and then the second row of the resulting matrix
to maintain the quality of the watermarked image. However,
is multiplied by the second column of matrix Q. A feature
the improvement is still modest when the value of the mean
of the unitary matrix Q after Hessenberg decomposition is
square error (MSE) is only reduced by approximately 0.01
that the first element is always equal 1, while other elements
and the value of the PSNR is increased by approximately
of the first row and the first column are zero. In our experi-
1.25 on average. Wang’s method [35] seems to be complex
ments, matrix A is assigned to a 4 × 4 pixel block; therefore,
and requires considerable execution time.
the elements of matrix A are always non-negative values and
To address the abovementioned drawback, a new blind
are in range of [0, 255]. According to [30], elements Q(2,
colour image watermarking scheme based on Hessenberg
2), Q(3, 2), Q(4, 2) of the second column of matrix Q are
decomposition is presented to embed a binary image into the
very near and have same sign, while other columns do not
colour host image to protect the copyright of colour images in
have this property. In addition, the second column of matrix
this paper. In the proposed approach, we focus on discovering
Q is the second row of matrix QT . Thus, the value of H(2,
the most suitable embedding element as well as developing
2) is actually a sum of positive numbers. Besides, this sum is
an effective embedding formula. To enhance the security of
often higher than the other values as the pixels usually differ
the scheme, the Arnold transform is also applied to permute
very little from their neighbors, especially when the size of the watermark image.
a pixel block is small. As a result, H(2, 2) is often the largest element.
To clarify this conclusion, we suppose that a matrix A with
3 Proposed blind watermarking method
a size of 4 × 4 is as follows: ⎡ ⎤
In this section, first, we describe the proposed embedding
A(1, 1) A(1, 2) A(1, 3) A(1, 4)
and extraction formulas. Second, the image watermarking
A(2, 1) A(2, 2) A(2, 3) A(2, 4) A ⎢ ⎥ = ⎢ ⎥ (8)
scheme, which includes the embedding stage and extraction
⎣ A(3, 1) A(3, 2) A(3, 3) A(3, 4)⎦ stage, is presented in detail.
A(4, 1) A(4, 2) A(4, 3) A(4, 4)
3.1 Proposed embedding and extraction formula
After Hessenberg decomposition, matrix Q and matrix QT are
3.1.1 Selecting an element to embed ⎡1 0 0 0 ⎤
⎢0 Q (2, 2) Q (2, 3) Q (2, 4)⎥
For an image watermarking scheme, embedded elements Q = ⎢ ⎥ (9)
⎣0 Q (3, 2) Q (3, 3) Q (3, 4)⎦
play an important role as they directly affect the watermarked
0 Q(4, 2) Q(4, 3) Q(4, 4)
image quality as well as the durability of the watermark. In 123 69 P. T. Nha et al. ⎡1 0 0 0 ⎤ as follows:
0 Q(2, 2) Q(3, 2) Q(4, 2) QT ⎢ ⎥ = ⎢ ⎥ (10) ⎡ ⎤
⎣0 Q (2, 3) Q (3, 3) Q (4, 3)⎦
H (1, 1) H (1, 2) H (1, 3) H (1, 4)
0 Q(2, 4) Q(3, 4) Q(4, 4)
H (2, 1) H (2, 2) H (2, 3) H (2, 4) H ⎢ ⎥ = ⎢ ⎥ ⎣ 0
H (3, 2) H (3, 3) H (3, 4)⎦
A matrix M = QT A is defined as follows: 0 0
H (4, 3) H (4, 4)
⎡ M(1, 1) M(1, 2) M(1, 3) M(1, 4)⎤
⎡ M(1, 1) M(1, 2) M(1, 3) M(1, 4)⎤
⎢ M (2, 1) M (2, 2) M (2, 3) M (2, 4)⎥ = ⎢ ⎥
M(2, 1) M(2, 2) M(2, 3) M(2, 4)
⎣ M (3, 1) M (3, 2) M (3, 3) M (3, 4)⎦ M ⎢ ⎥ = ⎢ ⎥
M(4, 1) M(4, 2) M(4, 3) M(4, 4)
⎣ M (3, 1) M (3, 2) M (3, 3) M (3, 4)⎦
M(4, 1) M(4, 2) M(4, 3) M(4, 4) ⎡1 0 0 0 ⎤ ⎡1 0 0 0 ⎤
⎢0 Q (2, 2) Q (2, 3) Q (2, 4)⎥ × ⎢ ⎥ (16)
0 Q(3, 2) Q(3, 3) Q(3, 4)
⎢0 Q (2, 2) Q (3, 2) Q (4, 2)⎥ ⎣ ⎦ = ⎢ ⎥
0 Q(4, 2) Q(4, 3) Q(4, 4)
⎣0 Q (2, 3) Q (3, 3) Q (4, 3)⎦
0 Q(2, 4) Q(3, 4) Q(4, 4)
⎡ A(1, 1) A(1, 2) A(1, 3) A(1, 4)⎤
Thus, H(2, 2) is calculated based on (17).
⎢ A(2, 1) A(2, 2) A(2, 3) A(2, 4)⎥ × ⎢ ⎥ (11)
H (2, 2) = M(2, 2) × Q(2, 2) + M(2, 3) × Q(3, 2)
⎣ A(3, 1) A(3, 2) A(3, 3) A(3, 4)⎦
A(4, 1) A(4, 2) A(4, 3) A(4, 4)
+M(2, 4) × Q(4, 2) > 0. (17)
Here, elements of the second row of matrix M are calculated
Figure 3 shows an example at which H(2, 2) is the largest. as follows:
In this example, matrix A is the first block of the “Girl” image
from the CVG-UGR image database [39]. After applying
M(2, 1) = Q(2, 2) × A(2, 1) + Q(3, 2) × A(3, 1)
Hessenberg decomposition, the elements of the second col-
+Q(4, 2) × A(4, 1). (12)
umn of matrix Q are zero or negative, while the remaining
columns have both negative and positive values. It is similar
M(2, 2) = Q(2, 2) × A(2, 2) + Q(3, 2) × A(3, 2)
to the second rows of matrix QT . Therefore, the elements of
+Q(4, 2) × A(4, 2). (13)
the second row of matrix M are negative. As shown in Fig. 3,
M(2, 3) = Q(2, 2) × A(2, 3) + Q(3, 2) × A(3, 3)
H(2, 2) = 64.4739, is the largest element of matrix H.
+Q(4, 2) × A(4, 3). (14)
However, in some cases, H(2, 2) is smaller than the other
elements of matrix H due to the pixel distribution of the host
M(2, 4) = Q(2, 2) × A(2, 4) + Q(3, 2) × A(3, 4)
image. In the intersection areas of the image, there is often
+Q(4, 2) × A(4, 4). (15)
large difference between pixels. For instance, if element A(1,
1) is much larger than the other elements of matrix A, then
As elements of matrix A are non-negative, the sign of the
H(2, 2) will be smaller than H(1, 1) as H(1, 1) = A(1, 1).
second row of matrix M is the same as that of Q(2, 2), Q(3,
Therefore, the ratio at which hmax = H (2, 2) is not the same
2), Q(4, 2). Last, matrix H = QT A Q = M Q is presented
when host images are different, as shown in Table 2.
Fig. 3 Example illustrating H(2, 2) is the largest element 123 70
An effective embedding algorithm...
Table 2 Number of blocks for which hmax = H (2, 2)
and (5), where the quantization step T is set to 65, as in the Image Size of image Number of blocks Percentage proposal of Su. that h
Two ideas are considered as the basis of the proposed max = H (2, 2) (%)
formula. First, to limit the change in all blocks, constraint Girl 512 × 512 16339 99.73
conditions are added to the embedding formula. Therefore, Avion 512 × 512 16384 100
the formula is divided into two main cases. Then, the element Baboon 512 × 512 16265 99.27
H(2, 2) is updated to a new value depending on whether it is House 512 × 512 16294 99.45
less than T or greater than T. Second, to guarantee a trade-off Milkdrop 512 × 512 16332 99.68
between the invisibility of the watermarked image and the Peppers 512 × 512 15176 92.63
robustness of the extracted watermark, the scaling factor α Sailboat 512 × 512 16144 98.54
is used in the embedding formula. The details of the formula Lena 512 × 512 16375 99.95
are presented in (18) and (19) as follows: Balloon 256 × 256 4095 99.98 Couple 256 × 256 3911 95.48
1. i f w = “0 and mod(H (2, 2), T ) ≥ 0.5T Parrots 256 × 256 3896 95.12 Tree 256 × 256 4093 99.93 ⎧ 0.5T −α ,
i f H (2, 2) ≤ T , ⎨ H (2, 2) =
⎩ H (2, 2)+(0.5T −mod(H (2, 2), T ))−α , i f H (2, 2) > T , (18)
Table 2 displays the number of blocks and the rate at which
the element H(2, 2) is present. As shown in Table 2, although
2. i f w = “1 and mod(H (2, 2), T ) < 0.5T
the rate at which hmax = H (2, 2) is very high, it is not
always 100%. For example, this rate is 92.63% in the case ⎧ 0.5T +α ,
i f H (2, 2) < T ,
of the “Peppers” image, which means that the largest value ⎨ H (2, 2) = h ⎩
max is not always a fixed element even H(2, 2). In this block,
H (2, 2)+(0.5T −mod(H (2, 2), T ))+α , i f H (2, 2) ≥ T ,
hmax can be H(2, 2), but hmax can be H(1, 3) or H(3, 2) in (19)
another block. In addition, due to the influence of the embed-
ding process, the position of hmax can change. For instance,
where mod(.) is the module operation, T is the quantization
if before embedding hmax is H(2, 2), it is H(1, 1) after embed-
step, and α is the scaling factor.
ding. Therefore, in the extraction process, H(1, 1) is obtained
to extract the watermark bit instead of H(2, 2), which leads
3.1.3 Obtaining the extraction formula
to a mismatch between the extracted watermark bit and the
original bit, as illustrated in Fig. 2.
Based on the embedding formula, the extraction formula is
From this discussion, the element H(2, 2) is selected as the
constructed via (20) as follows:
embedded element in the proposed scheme. Here, we chose
H(2, 2) as the ratio at which H(2, 2) holds the maximum value
⎧ “0" , mod(H ∗(2, 2), T ) < 0.5T ,
is the highest, and this element is consistent when embedding ⎨ w∗ = (20)
and extracting the watermark. Therefore, this selection not ⎩ “1" , elsewhere.
only takes advantage of concentrated energy but also ensures
accurate extraction of information. 3.2 Embedding process
3.1.2 Discovering the embedding formula
First, 4 × 4 nonoverlapping blocks are obtained from three
channels, R (Red), G (Green), and B (Blue), of the host colour
As discussed in Section 2.3, two equations, (4) and (5), were
image. Second, the Arnold transform is applied to the binary
selected as the embedding and extraction formulas, respec-
watermark image, and then the image is transformed to a
tively, by Su [31]. One strength of these formulas is that
one-dimensional array. Last, Hessenberg decomposition is
they are simple; however, they have two main disadvantages.
executed on the image blocks of channel B in succession,
First, all blocks are modified, and the modified values have
and the watermark is hidden in matrix H based on the pro-
a large gap in comparison with the original values in some
posed formula. Here, channel B is selected for the following
blocks. This gap has a negative impact on the quality of the
reasons: (a) embedding in all channels reduces the quality of
watermarked image. Second, the extracted information is not
the watermarked images, as shown in Table 3 and Fig. 4, and
always accurate, as illustrated in Fig. 2. Motivated by these
(b) human eyes are less sensitive to channel B than the other
drawbacks, we propose an improved formula based on (4)
colour channels according to the human visual system [40]. 123 71 P. T. Nha et al.
Table 3 P S N R values when the watermark is embedded in channel B
The details of the proposed watermark embedding stage and three channels
are summarized by the following steps. Image The watermark is w1 The watermark is w2 Embed in Embed in Embed in Embed in channel B three channels channel B three channels
1. The host image H is represented as three colour chan-
nels: R, G, and B. This image is dispensed into 4 × 4 Girl 54.8533 37.8223 55.7468 37.5160 nonoverlapping blocks. Avion 54.8803 37.7505 55.3159 37.7256
2. The watermark image is swapped by the Arnold trans- Baboon 54.5786 37.7948 55.0793 37.7134
form and transferred to a binary sequence wi , where House 54.8862 38.0061 55.1388 38.0327
i = 1, 2, · · · , M × M and M × M is the size of the Milkdrop 54.1857 37.8456 55.2006 37.7466 original watermark. Peppers 54.2857 37.7193 55.1601 37.4550
3. Hessenberg decomposition is applied on one block of Sailboat 54.9059 38.0777 56.0062 37.9582
channel B of the host image, and the upper Hessenberg Lena 54.5485 37.6929 55.1784 37.5822 matrix H is obtained. Balloon 54.5570 38.0516 55.2670 37.7143
4. A watermark bit is hidden into element H(2, 2) of matrix Couple 54.8071 37.2357 55.3518 36.5790 H based on (18) and (19). Parrots 54.5269 37.8944 55.9287 37.8446
5. The inverse Hessenberg decomposition is performed to Tree 54.6565 37.8913 55.3741 37.7597
obtained the watermarked image block A according to (21).
To compare the quality of the watermarked images, we
A = Q H QT (21)
have calculated P S N R values when the watermarks are
embedded in channel B and three color channels (R, G, and
B). As shown in Table 3, P S N R values are higher than 54
6. Steps 3-5 are repeated until all blocks are embedded with
dB for all images when the watermarks are embedded in watermark bits.
channel B. Meanwhile, P S N R values are only 36.579 dB
7. The channels are recombined to attain the watermarked
to 38.0516 dB when the watermarks are embedded in three image H .
color channels. These experimental results indicate that the
quality of the watermarked image is better when the water-
The diagram of the embedding process is displayed in Fig. 5. mark is embedded in channel B.
Furthermore, Fig. 4 displays a comparison of the “Cou-
ple” image. We do not see the difference between the original 3.3 Extraction process
image and the watermark image when observed with the
naked eye in the case that the watermark is embedded in
The stage of the proposed extraction is introduced in Fig. 6.
channel B. Meanwhile, when the watermark is embedded in
As shown in the diagram, the data extraction process does
all three colour channels, the watermarked image appears
not need the original host image or the original watermark.
grid cells which cause the colour of the image to be changed.
Thus, the proposed approach belongs to a blind watermarking
These arguments explain why the watermark is only embed-
scheme. The steps of extracting watermarks are summarized
ded in channel B instead of three colour channels. as follows:
Fig. 4 Comparing the quality of the “Couple” image 123 72
An effective embedding algorithm...
Fig. 5 Embedding process of the proposed scheme
1. The watermarked image H ∗ is represented as three colour
Fig. 6 Extraction process of the proposed scheme
channels: R, G, and B. This image is dispensed into 4 × 4 non-overlapping blocks.
2. Each block of channel B is allocated to matrix A∗ with a size of 4 × 4.
3. The Hessenberg decomposition is executed on each
4 Experimental result and discussion
block, and its upper Hessenberg matrix H ∗ is obtained.
4. The watermark bit is extracted via (20), where the quan-
In this section, we present the experimental results for the
tization step T and scaling factor α are set to the same
proposed method. Comparisons and evaluations are con-
value as in the embedding stage.
ducted to show the superiority of the proposed method over
5. Steps 2-4 are repeated until watermark bits are obtained
six related methods in three aspects: image quality, robust-
from all blocks. All extracted watermark bits are gathered
ness and execution time. Prior to this step, evaluation criteria
and converted to an image, and then the inverse Arnold
and simulation settings were also introduced as a basis for
transform is utilized to receive the final watermark. performing experiments. 123 73 P. T. Nha et al. 4.1 Evaluation criteria
To measure the similarity between the original watermark
and the extracted watermark, the values of N C are employed.
In this paper, we use the peak signal-to-noise ratio (P S N R),
They are always less than or equal to 1 and are calculated by
structural similarity index measurement (S S I M), and nor- (26) as follows:
malized correlation (N C) to measure the performance of m n
the proposed watermarking scheme. The P S N R and S S I M
(W (x , y)W (x , y)) x=1 y=1 N C = , (26)
indices are effective criteria for estimating the impercepti- m n
(W (x , y))2 m n
(W (x , y))2 x=1 y=1 x=1 y=1
bility of the watermarked image, while the N C index is an
important establishment to evaluate the robustness of a water-
where W (x, y) and W (x, y) represent the value of pixel
marking scheme [9]. Imperceptibility means that watermarks
(x, y) of the original watermark and that of the extracted
embedded in the host image cannot be detected by the human
watermark, respectively. m × n denotes the size of the water-
sense of sight and reflects the visual quality of the output mark image.
image in the watermarking process, which is the watermarked
In general, a higher P S N R or S S I M value means that the
image. The P S N R refers to the highest noise measurement
watermarked image is closer to the original host image, that
that reduces the quality of the image and is calculated using
is the watermarking algorithm has better quality in terms
the square of the error that occurs in the watermarked image.
of imperceptibility. A larger N C value indicates that the
The S S I M measures image quality based on differences
extracted watermark and original watermark are more alike,
in structure, intensity, and contrast. Therefore, the S S I M
which reveals that the robustness of the watermarking method
is considered correlated with the quality perception of the is stronger.
human visual system (HVS). Robustness is the ability of a
watermarking algorithm to resist image attacks and means 4.2 Simulation setting
that the extracted watermark can be recognized and the same
as the original watermark. As the NC index is simply a pixel
To assess the performance of the proposed algorithm, we use
by pixel comparison between two images, it is a suitable
eight 24-bit colour images with a size of 512 × 512 and four
measurement of robustness, especially when the watermark
images with a size of 256 × 256 from the CVG-UGR image image is binary in this paper.
database [39] as the host images. In addition, the original
First, the P S N R is defined by (22) as follows:
watermarks are two 32 × 32 binary images, as displayed in
Fig. 7. A computer with a 64-bit operating system and Visual 2552
Studio v19 software is also utilized to install all experiments. P S N R = 10 log10 , (22) M S E
To select the appropriate embedding coefficient, we
embed the watermarks into twelve host images, where the
where the M S E between the original image and the water-
scaling factor α runs from 0.5 to 5 in 0.5 increments and
marked image is described by the following equation:
the quantization step T is set to 65. For each step of α,
nine attacks, blurring, sharpening, cropping, scaling, rota- M−1 N −1
tion, Gaussian noise, salt & pepper noise, JPEG compression, 1 M S E =
(H (i , j ) − H (i , j ))2. (23)
and mean filtering are used to lessen the watermarked images. M N i=0 j=0
Then, S S I M and N C values are calculated for each water-
marked image and each extracted watermark, respectively.
In addition to the P S N R, the S S I M is used to calculate
Then, the average S S I M and N C values of all images are
the similarity between the original colour image H and the
obtained, and the test is repeatedly simulated.
watermarked image H’. The S S I M is computed by using
Figure 8 gives the average S S I M of the watermarked
(24). The values of the S S I M index are always in the range
images and the average N C of the extracted watermarks. The
of [0, 1]. If this index is equal to 1, H = H’.
results in Fig. 8 are less than 1 as they are the N C values of the
extracted watermarks that are received from all the attacked
S S I M(H , H ) = l(H , H )c(H , H )s(H , H ), (24)
watermarked images. These is similar to the S S I M values.
As shown in Fig. 8, with an increase in the scaling factor
α, the average S S I M value decreases, whereas the average where
N C value increases. The imperceptibility weakens, and the ⎧ (2µ
sustainability becomes stronger. Thus, to balance the quality
l(H , H ) =
H µH +C1) , ⎪ ⎪ (µ2 +µ2
of the watermarked image and robustness of the watermark, ⎪ H H +C1) ⎨ (2σ
c(H , H ) =
H σH +C2) , (25)
the scaling factors α should have values between 3 and 3.5. (σ 2 +σ 2 ⎪ H H +C2)
In summary, the scaling factor α is established to be 3.2 in ⎪ (σ ⎪ H H +C3)
⎩s( H , H ) = .
(σH σH +C3) our tests. 123 74
An effective embedding algorithm...
Fig. 7 Host images and watermark images
To evaluate the efficiency and stability of the proposed
the S S I M value is to 1, the better the quality of the water-
method, it is compared with the methods of Su [30], Su [31],
marked image, and vice versa. Tables 5 and 6 display the
Omar [32], Areej [33], Methaq [34], and Wang [35]. For an
PSNR values of different methods when the watermark is
overview of the compared methods, Table 4 describes some
w1 and w2, respectively. Moreover, average P S N R, S S I M,
main characteristics of these approaches in terms of tech-
and N C values are also represented in Table 7 to compare the
nique, parameter, position to embed, and size of the block.
performance of the schemes in the absence of an attack. It is
As shown in Table 4, all methods are based on Hessen-
easy to see that the proposed method not only has the largest
berg decomposition. However, while schemes [30] and [31]
P S N R and S S I M values in comparison with others but also
of Su embedded the information on a single domain, the
can exactly extract the watermark. The average P S N R val-
other schemes used a hybrid domain based on a combination
ues and average S S I M values of the proposed approach are
of Hessenberg decomposition and other techniques such as
higher than 54 dB and 0.9991, respectively. The N C index
DWT, SVD, or FWHT. The size of the blocks that is used in
is 1 in two cases of the watermark under no attack. Thus, the
almost all methods is 4 × 4, with the exception the method
watermarked image of the proposed approach is the best in in [35].
terms of invisibility. The proposed method selected a suit-
able element to embed. In addition, the proposed embedding
4.3 Imperceptibility experiment
formula not only minimizes modification of the pixel values
but also ensures accurate extraction.
In addition to the results measured by the P S N R, S S I M
In this paper, the P S N R and S S I M indices are chosen to
and N C values, illustrations and visual images are also pro-
evaluate the quality of watermarked images. As mentioned
vided to further clarify the comparison. To illustrate the effect
in Section 4.1, the higher the P S N R value and the closer
of the proposed formula on the quality of the watermarked
image, the number of unchanged blocks after embedding is
counted in Table 8. As shown by the statistical data in Table 8,
the percentage of unchanged blocks falls between 24.41 and
26.99 for twelve host images. This is not a small rate in com-
parison with the total number of blocks of each host image
and is explained as follows: After applying (18) and (19), the
elements H(2, 2) of these blocks retain the same value, while
the watermark bits are still recorded for the blocks. For exam-
ple, if the watermark bit is 0 and mod(H (2, 2), T ) < 0.5T ,
the constraint condition of (18) does not occur. Therefore, we
do not need to perform any calculations to obtain H’(2, 2).
In the extraction process, the watermark bit is still correctly
extracted via (20) as the condition mod(H (2, 2), T ) < 0.5T
is always satisfied. This step is similar to (19) when the water-
mark bit is 1 and mod(H (2, 2), T ) ≥ 0.5T . Moreover, in the
Fig. 8 Average values of S S I M and N C with different scaling factor
proposed formula, we break down the calculation of H’(2, 2) values α
based on the value of H(2, 2) compared to T. This process 123 75 P. T. Nha et al.
Table 4 Brief description of different methods Scheme of Year Applied techniques Parameters Position to embed Size of block Su [30] 2016 Hessenberg decomposition, T = 0.042 Q(2, 2) and Q(3, 2) of 4x4 MD5, Arnold transform matrix Q Su [31] 2017 Hessenberg decomposition, T = 65 Largest element 4x4 MD5, Arnold transform hmax of the matrix H Omar [32] 2018 2-level DWT, FWHT, α = 0.034 First element H(1, 1) 4x4 Hessenberg decomposition of matrix H Areej [33] 2020 1-level DWT, S = 20 First element H(1, 1) 4x4 Hessenberg decomposition, of matrix H Logistic Map Methaq [34] 2022 2-level DWT, FA, None Certain location 4x4 Hessenberg decomposition within matrix Q Wang [35] 2022 k-level DWT, SVD, α = 0.4 Whole matrix S Equal size of Hessenberg decomposition, watermark image PSO, LM, Arnold transform Proposed None Hessenberg decomposition, T = 65, H(2, 2) of matrix H 4x4 method Arnold transform α = 3.2
helps to retain the gap between H’(2, 2) and H(2, 2) as small
histogram of the original image. In contrast, the distribution
as possible, which means that the pixel values after embed-
of pixels of the watermarked image of proposal [31] is dif-
ding are less changed than before embedding. In addition
ferent from that of the original image, especially in the range
to the quantization step T, the scaling factor α is applied to
of values from 180 to 240. This finding shows that the water-
balance the invisibility and robustness.
marked image has been substantially changed compared to
In particular, to obtain a visual view of the effectiveness
the original image when applying the algorithm [31].
of the proposed method, the histograms of the original image
Moreover, an example that illustrates the superiority of
and watermarked image are compared. Figure 9 displays a
the proposed method compared to the method in [31], is
histogram of the host image “avion” and a histogram of the
shown in Table 9. In this example, matrix A is a pixel
watermarked image of the approach [31] and the proposed
matrix of the 611th block of the “Milkdrop” image. In the
method, respectively. We observe that the histogram of the
embedding stage, hmax and H(2, 2) before embedding are
watermarked image of the proposed scheme is similar to the
52.734. However, after embedding, hmax only obtains the
Table 5 P S N R values of Image Su [30] Su [31] Omar [32] Areej [33] Methaq [34] Wang [35] Proposed different methods under no method attacks when the watermark is w1 Girl 38.2350 41.8775 43.5911 47.2599 42.5547 50.6729 54.8533 Avion 39.7622 40.0842 43.6230 46.4121 43.5057 51.3578 54.8803 Baboon 38.5386 42.1706 44.2662 46.4820 43.3878 51.5597 54.5786 House 38.2101 42.0628 43.6443 46.2470 41.3068 50.6528 54.8862 Milkdrop 39.6726 41.6896 42.9458 45.5161 41.6073 49.8812 54.1857 Peppers 37.7671 42.8337 42.1371 47.6843 43.5644 50.9455 54.2857 Sailboat 38.2381 41.4263 42.6609 46.8647 43.0379 49.1650 54.9059 Lena 39.3307 42.7062 44.2715 47.3197 43.3715 51.5367 54.5485 Balloon 36.6482 39.3776 43.2781 44.7357 42.2714 50.6876 54.5570 Couple 37.5666 40.6569 42.6149 46.0168 42.6162 51.0257 54.8071 Parrots 36.9895 40.0290 43.2405 47.1329 43.3432 51.0211 54.5269 Tree 36.7477 39.6150 43.3178 45.2326 42.3773 50.6126 54.6565 The best values are in bold 123 76
An effective embedding algorithm...
Table 6 P S N R values of Image Su [30] Su [31] Omar [32] Areej [33] Methaq [34] Wang [35] Proposed different methods without method attacks when the watermark is w2 Girl 37.6035 41.1315 43.3292 48.1657 42.9884 51.1187 55.7468 Avion 37.2454 41.0841 43.5874 48.4168 42.2345 51.5419 55.3159 Baboon 37.5309 41.1555 44.1068 47.9504 42.7880 51.5177 55.0793 House 38.0726 41.0403 42.6647 48.4994 42.3276 50.1410 55.1388 Milkdrop 36.9171 40.6754 43.8515 47.8882 42.7222 50.1123 55.2006 Peppers 37.6454 40.0185 42.8488 47.6813 42.5336 49.9624 55.1601 Sailboat 37.2208 40.4379 43.7113 47.5420 42.3737 51.2844 56.0062 Lena 38.2990 41.6743 44.1953 48.0241 42.7782 50.3296 55.1784 Balloon 36.7669 39.3710 43.1282 46.9605 42.8558 50.2891 55.2670 Couple 37.6885 39.6292 43.0932 46.9351 42.7684 50.0340 55.3518 Parrots 37.1648 39.0562 42.9417 47.7752 42.6337 50.3228 55.9287 Tree 37.3452 39.1267 42.8022 47.6346 42.4683 50.0112 55.3741 The best values are in bold
Table 7 Average P S N R, S S I M, and N C values of different methods without attacks Watermark Index Su [30] Su [31] Omar [32] Areej [33] Methaq [34] Wang [35] Proposed method w1 P S N R 38.1422 41.2108 43.2993 46.4086 42.7453 50.7599 54.6393 S S I M 0.9738 0.9849 0.9912 0.9943 0.9867 0.9987 0.9991 N C 0.9924 0.9933 0.9990 0.9996 0.9990 1.0000 1.0000 w2 P S N R 37.4583 40.3667 43.3550 47.7894 42.6227 50.5554 55.3956 S S I M 0.9706 0.9826 0.9919 0.9959 0.9871 0.9986 0.9992 N C 0.9915 0.9942 0.9992 0.9995 0.9991 1.0000 1.0000 The best values are in bold
Table 8 Rate of unchanged Image Size of image Number of unchanged Percentage (%) blocks after embedding blocks Girl 512 × 512 4365 26.64 Avion 512 × 512 4349 26.54 Baboon 512 × 512 4152 25.34 House 512 × 512 4422 26.99 Milkdrop 512 × 512 4342 26.50 Peppers 512 × 512 4332 26.44 Sailboat 512 × 512 4186 25.54 Lena 512 × 512 4128 25.19 Balloon 256 × 256 1040 25.39 Couple 256 × 256 1095 26.73 Parrots 256 × 256 1000 24.41 Tree 256 × 256 1080 26.37 123 77 P. T. Nha et al.
Fig. 9 The histogram of the image “Avion”
value 16.984, while H(2, 2) is 28,5. The distance between
it has some errors in the embedding formula, as discussed in
H(2, 2) after embedding is closer to the original value than
Section 2.3. The schemes in [32] and [34] employed a 2-level
hmax . Thus, matrix A of the proposed method is changed
DWT instead of a 1-level transform as the approach in [33],
less than the original matrix after embedding and convert-
so their indices are lower than the method of Areej. In addi-
ing to unsigned, 8-bit pixel values. In the extraction stage,
tion, embedding the watermark on all three colour channels
h∗max is 34, so the algorithm [31] gives a w∗ value of 255,
of the host image is also a reason for reducing the quality
which differs from the original bit. The proposed method can
of the watermarked image in methods, such as [30–32], and
perfectly extract the information as H ∗(2, 2) = 30.2 and [34].
mod(H ∗(2, 2), T ) < 0.5T , which leads to w∗ = w = 0.
Last, the proposal of Wang [35] is considered a good
The results in Tables 5, 6 and 7 are explained as follows:
improvement over previous algorithms when it can accu-
The P S N R and S S I M values of the method [30] are the
rately extract the information without attacks. In addition,
smallest as the author embedded the watermark into two ele-
the P S N R values and S S I M values are higher than 50 dB
ments Q(2, 2) and Q(3, 2) of matrix Q instead of one element
and 0.9956, respectively. This result is obtained as scheme in
as in other schemes. As discussed in Section 1, using two
[35] only embeds information on a block of the host image,
elements to embed leads to change in all elements of the
which is equal to the size of the watermark. In the algorithm,
block after embedding. As a result, the quality of the water-
the host image is initially decomposed into four subbands
marked image is affected. The algorithm in [31] is better
by k-level DWT. The index k depends on the size of the
than the paper in 2016 but is worse than other algorithms as
host image and watermark. For instance, if the host image 123 78
An effective embedding algorithm...
Table 9 Example comparing Stage Method [31] Proposed method the difference between the
method in [31] and the proposed method Embedding Extracting
has a size of 512 × 512 and the size of the watermark is
to degrade the watermarked images: blurring, sharpening,
32 × 32, k is set to 2. Then, Hessenberg decomposition is
cropping, scaling, rotation, Gaussian noise, salt and pep-
performed on L Lk to obtain the matrix H. Next, SVD is
per noise, JPEG compression, mean filtering, and JPEG2000
applied to matrix H to obtain the diagonal matrix Sh. After
compression. Table 10 briefly describes the attacks and their
encrypting the watermark, SVD is also applied to obtain the
parameters. In the experiments, the N C coefficient is com-
diagonal matrix Sw. As two matrices Sh and Sw have the
puted to evaluate robustness by measuring the similarity
same size, the watermark is subsequently embedded via the
between the original watermark and the extracted watermark
Equation S∗ = Sh + αSw. Hence, instead of dividing the
based on (26). The N C index usually falls between 0 and 1.
original image into small blocks and embedding informa-
A watermarking algorithm is more stable if the N C index is
tion on these blocks, this method only embeds on a 32 × 32 closer to 1, and vice versa.
block. As a result, the number of changed pixels is not much
JPEG and JPEG2000 compression are two popular image
compared to other methods. However, its consequence is low
attacks. JPEG images use a lossy compression algorithm. The embedding capacity.
amount of JPEG compression is typically measured by the
quality factor (QF), which is a number between 0 and 100.
As the quality factor is decreased from 100, the level of com-
4.4 Robustness experiment
pression is improved, but the quality of the resulting image is
significantly reduced. JPEG2000 is a new compression stan-
For copyright protection purposes, robustness is an impor-
dard for still images intended to overcome the shortcomings
tant criterion for assessing the reliability of a digital image
of the existing JPEG standard. The amount of JPEG2000
watermarking scheme. To test and compare the performance
compression is measured by the compression ratio (CR),
of the methods, ten kinds of common attacks are performed 123 79 P. T. Nha et al.
Table 10 Short description of Index Attacks Description attacks utilized in the experiments 1 Blurring
The watermarked image is blurred with radius = 0
and sigma is assigned to 0.2 and 0.5. 2 Sharpening
The watermarked image is sharpened with radius = 0
and sigma is assigned to 0.2 and 0.5. 3 Cropping
25% and 50% of the watermarked image on
the bottom right corner is removed. 4 Scaling (1/2)
The watermarked image is resized from 512 × 512 to 256 × 256
and subsequently restored to 512 × 512. 5 Scaling (2)
The watermarked image is resized from 512 × 512 to 1024 × 1024
and subsequently restored to 512 × 512. 6 Gaussian noise
Gaussian noise is added to the watermarked image with µ = 0
and variance σ 2 = 0.001 and 0.003. 7 Salt&Pepper noise
Salt and pepper noise is added to the watermarked image with
the noise density = 0.002, 0.005, and 0.01. 8 Rotation 5o
The watermarked image is rotated clockwise at an angle of 5
and is subsequently rotated counterclockwise at an angle of -5. 9 Rotation 10o
The watermarked image is rotated clockwise at an angle of 10 and is
subsequently rotated counterclockwise at an angle of -10. 10 JPEG
The watermarked image is compressed by using the DCT with a window size
of 8 × 8 and quality factors = 50, 70, and 90. 11 Mean filter
A filter with a window size from 2 × 2 to 5 × 5 is utilized. 12 JPEG2000
The watermarked image is compressed with the compression ratio is 10, 20, and 30.
which is equal to the number of bytes of the original image
is greater than 0.9 when QF = 50 and is close to 1 when
divided by the number of bytes of the compressed image.
QF = 90, which means that the proposed method can resist
For example, if the original image has 5000 bytes and the
this attack. Under JPEG2000 compression, the experiments
number of bytes of the compressed image is 500, the CR is
are performed when CR =10, 20, and 30. Figure 11 shows 10.
that all methods are robust against this attack and that N C
Figure 10 displays the N C values of the seven meth-
values have an inverse relationship to the CR. The N C val-
ods under JPEG compression when QF = 50, 70, and 90.
ues decrease when the CR increases, and vice versa. For
As shown in Fig. 10, N C values are proportional to QF
both types of compression, the method in [35] achieves the
for all methods. The N C value of the proposed scheme
best results, while the approach in [34] is the least robust,
Fig. 10 N C values of different methods under JPEG compression
Fig. 11 N C values of different methods under JPEG2000 compression 123 80
An effective embedding algorithm...
Table 11 N C values and the extracted watermarks of related studies under attacks when the host image is “baboon” and the original watermark is w1 Attack Parameter Su [30] Su [31] Omar [32] Areej [33] Methaq [34] Wang [35] Proposed method Gaussian 0.001 noise 0.003 Salt & Pepper 0.005 noise 0.01 Cropping 25% 50% Blurring 0.2 0.5 Sharpening 0.2 0.5 Rotation 5◦ 10◦ Scaling 1/2 2 Mean Filter 2x2 3x3 The best values are in bold 123 81 P. T. Nha et al. Table 12
N C values and the extracted watermarks of related studies under attacks when the host image is “sailboat” and the original watermark is w2 Attack Parameter Su [30] Su [31] Omar [32] Areej [33] Methaq [34] Wang [35] Proposed method Gaussian 0.001 noise 0.003 Salt & Pepper 0.005 noise 0.01 Cropping 25% 50% Blurring 0.2 0.5 Sharpening 0.2 0.5 Rotation 5◦ 10◦ Scaling 1/2 2 Mean Filter 2x2 3x3 The best values are in bold 123 82
An effective embedding algorithm...
especially in the case of QF = 50. Although the N C values
do not concentrate energy, so they are easily affected by
of the proposed scheme are lower than those of the method
the embedding process. As a result, the robustness of these
in [35], this gap is not large.
methods is also affected. The method of Areej [33] used the
Tables 11 and 12 display N C values and the extracted
embedding formula as in [31], but it was combined with the
watermark of related works under eight other attacks. As
DWT. This helps improve the robustness, so its N C values
shown in the figures, the proposed method overcomes the
are higher than the values of [31]. The scheme of Wang [35]
other methods under attacks such as Gaussian noise, salt and
is more robust than the previous publications as the author
pepper noise, cropping, blurring, and sharpening. In particu-
applied the PSO algorithm to search for the optimal scaling
lar, the proposed method can perfectly extract the watermark factor.
w1 when the attacks are Gaussian noise, blurring, and sharp-
Tables 11 and 12 show that the N C values of the method in
ening (where variance = 0.001 and 0.003 and sigma = 0.2).
[34] are almost smaller than those in the other methods. This
The N C value reaches 1 under these attacks. Although the
results can be explained as follows: The method in [34] used
NC values of the proposed approach are lower than the
a very simple embedding formula that was based only on the
algorithm [35], they are higher than the other algorithms
parity of the embedding element and without any parame-
and greater than 0.89 under attacks such as JPEG compres-
ters. This finding is considered a lack of rigor as even a small
sion, rotation, scaling, and mean filter. For all tested attacks,
impact can change the results and lead to incorrect extraction
the extracted watermarks can be clearly recognized. This
of information. Thus, the N C values of this method have a
finding proves that the proposed method is resistant to the
large gap under the same attack with two different parame-
most common image attacks as we have analysed to choose
ters. For example, with the addition of Gaussian noise, the
the appropriate embedding element. The element H(2, 2)
N C value is 0.9962 with variance = 0.001, while it is only
is selected as an embedding element since it concentrates 0.8370 with variance = 0.003.
energy and has high stability, as explained in Section 3.1.
In addition, the proposed formula not only helps the
4.5 Comparison of execution times
scheme maintain the quality of the image but also ensures
accurate information extraction. In the embedding proposed
For transform domain-based watermarking schemes, the exe-
formula, the scaling factor α plays an extremely important
cution time is mainly determined by the kind of matrix expan-
role and is carefully calculated by many repeated experiments
sion. To ensure a fair assessment of the proposed method,
after applying the attacks to the watermarked images. This
we compare it with six Hessenberg-based approaches. Two
is considered a new point in the proposed algorithm and is
of these methods embedded the information on the single
different from existing proposals.
domain, namely, [30] and [31]. The remaining four methods
In the compared methods, the parameters were also
combined Hessenberg decomposition with the other tech-
computed based on the trade-off between invisibility and
niques to build schemes on the hybrid domain, namely,
robustness. However, determining the cross-point of the
[32–34], and [35]. According to [2], SVD needs approxi-
S S I M and N C [30, 31] or the relationship between the
mately 11n3 flops for an n × n matrix, whereas the required
P S N R and the N C [35] is performed without attacks. For 10
this reason, the methods of Su are less robust under attacks.
time to compute Hessenberg decomposition is n3 flops. 3
Furthermore, in the proposal [30], the author built the embed-
Thus, the computational complexity of the proposed scheme
ding formula and extraction formula based on the correlation N × N is
O (n3) for a colour image of N × N pixels.
relationship between Q(2, 2) and Q(3, 2). Unfortunately, this n × n
As shown in Table 13, the average execution time of
relationship is not always consistent due to the property of
the proposed algorithm is the shortest, with an embedding
the Hessenberg decomposition. While methods [32] and [33]
time and extraction time of 0.231 and 0.022, respectively.
embedded the information into the first element H(1, 1), the
Although the computational complexity of methods [30] and
element H(4, 4) was selected in method [34]. These elements
[31] is similar to that of the proposed method, these two
Table 13 Average computation time of different methods (in seconds) Su [30] Su [31] Omar [32] Areej [33] Methaq [34] Wang [35] Proposed method Embedding time 0.5210 0.5189 0.8925 0.7643 1.2813 1.3702 0.2310 Extraction time 0.0737 0.0724 0.1571 0.1256 0.2800 0.3519 0.0220 Total time 0.5947 0.5913 1.0496 0.8899 1.5613 1.7221 0.2530 The best values are in bold 123 83 P. T. Nha et al.
methods require more time as they are embedded on all three
3. Ray A, Roy S (2020) Recent trends in image watermarking tech-
channels, while we only use channel B to hide the water-
niques for copyright protection: a survey. Int J Multimed Info Retr
9:249–270. https://doi.org/10.1007/s13735-020-00197-9
mark. The method [32] is a combination of the DWT, the
4. Su Q, Wang H, Liu D, Yuan Z, Zhang X (2020) A combined
FWHT, and Hessenberg decomposition, while the proposal
domain watermarking algorithm of color image. Multimed Tools
[33] combined the DWT with Hessenberg decomposition, so Appl 79:30023–30043.
https://doi.org/10.1007/s11042-020-
it requires less time than [32]. The approach of Wang [35] 09436-x
5. Ernawan F, Kabir MN (2020) A block-based RDWT-SVD image
is the most time-consuming as it used the multilevel DWT
watermarking method using human visual system characteristics.
with many other transformations such as SVD, Hessenberg
The Visual Computer 36(1):19–37
decomposition, PSO, Arnold transform, and LM. In addition
6. Sun Y, Su Q, Wang H (2022) A blind dual color images watermark-
to deposing on the host image, this proposal applied SVD
ing based on quaternion singular value decomposition. Multimed
Tools Appl 81:6091–6113. https://doi.org/10.1007/s11042-021-
on the watermark image. Hence, this approach is very com- 11815-x
plicated in comparison with other methods. The proposed
7. Zhang M, Ding W, Li Y, Sun J, Liu Z (2023) Color image water-
method has excellent performance in terms of execution time.
marking based on a fast structure-preserving algorithm of quater-
nion singular value decomposition. Signal Process 208(0165–
1684):108971. https://doi.org/10.1016/j.sigpro.2023.108971
8. Hu H-T, Hsu L-Y, Chou H-H (2020) An improved SVD based 5 Conclusion
blind color image watermarking algorithm with mixed modulation
incorporated. Inf Sci 519(0020–0255):161–182. https://doi.org/10. 1016/j.ins.2020.01.019
In summary, a blind image watermarking scheme based on
9. Luo A, Gong L, Zhou N (2020) Adaptive and blind watermarking
Hessenberg decomposition has been presented in this paper.
scheme based on optimal SVD blocks selection. Multimed Tools
The article has analysed the advantages and disadvantages
Appl 79:243–261. https://doi.org/10.1007/s11042-019-08074-2
10. Ahmadi SBB, Zhang G, Rabbani M (2021) An intelligent and
of the previous proposals to determine the importance of
blind dual color image watermarking for authentication and copy-
embedding elements and embedding formulas. Accordingly,
right protection. Appl Intell 51:1701–1732. https://doi.org/10.
a new embedding formula is given based on the selection 1007/s10489-020-01903-0
of the appropriate embedding elements. In the proposed
11. Wang X, Yao Y, Yu Y (2022) Statistical image watermark decoder
by modeling local RDWT difference domain singular values with
scheme, element H(2, 2) of matrix H is chosen as an embed-
bivariate weighted Weibull distribution. Appl Intell. https://doi.org/
ded element because of its energy concentration as well as its 10.1007/s10489-022-03536-x
stability. The proposed formula not only helps minimize the
12. Hsu LY, Hu HT (2019) A reinforced blind color image water-
change in pixel values after embedding but also effectively
marking scheme based on Schur decomposition. IEEE Access 7:107438–107452
extracts the watermark. The experimental results show that
13. Sun Y, Su Q, Chen S, Zhang X (2022) A double-color image water-
the proposed method outperforms the related approaches in
marking algorithm based on quaternion Schur decomposition.
terms of watermark image quality and computation time. In
Optik 269:169899. https://doi.org/10.1016/j.ijleo.2022.169899
addition, the proposed method is considered stable when it
14. Su Q, Zhang X, Wang G (2019) “An improved watermarking algo-
rithm for color image using Schur Decomposition.” Soft Comput
can resist most common attacks, especially noise, blurring, 1–16
cropping, and sharpening. The average PSNR value without
15. Liu D, Su Yuan Z, Q, (2020) A blind color image watermarking
attacks and the NC value with attacks are larger than 54 dB
scheme with variable steps based on Schur decomposition. Mul-
and 0.93, respectively. In the future, we will apply different
timed Tools Appl 79:7491–7513. https://doi.org/10.1007/s11042- 019-08423-1
types of watermarks, such as colour images or QR codes, to
16. Li JY, Zhang CZ (2020) Blind watermarking scheme based on
expand the application scope of the proposed scheme.
Schur decomposition and non-subsampled contourlet transform.
Multimed Tools Appl 79:30007–30021. https://doi.org/10.1007/ Declarations s11042-020-09389-1
17. Prabha K, Shatheesh SI (2021) “Lifting Scheme and Schur Decom-
position based Robust Watermarking for Copyright Protection.”
In: Sheth A, Sinhal A, Shrivastava A, Pandey AK (eds) Intelligent
Conflict of Interests All authors declare that there are no conflicts of
Systems, Algorithms for Intelligent Systems. Springer, Singapore.
interest regarding the publication of this paper.
https://doi.org/10.1007/978-981-16-2248-9-15
18. Horasan F (2022) A novel image watermarking scheme using ULV
decomposition. Optik 259:168958
19. Muñoz-Ramírez DO, García-Salgado BP, Ponomaryov V, Reyes- References
Reyes R, Sadovnychiy S, Cruz-Ramos C (2021) A color image
watermarking framework for copyright protection of stereo images
1. Mahto DK, Singh AK (2021) A survey of color image watermark-
based on binocular just noticeable difference and LU decomposi-
ing: State-of-the-art and research directions. Comput Electr Eng
tion. Multimed Tools Appl 80:13707–13734
93:107255. https://doi.org/10.1016/j.compeleceng.2021.107255
20. Hsu CS, Tu SF (2020) Enhancing the robustness of image
2. Jibrin B, Tekanyi A, Sani S (2019) Image watermarking algorithm
watermarking against cropping attacks with dual watermarks.
in frequency domain: a review of technical literature. ATBU J Sci
Multimed Tools Appl 79:11297–11323. https://doi.org/10.1007/ Tech Educ 7(1):257–263 s11042-019-08367-6 123 84
An effective embedding algorithm...
21. Wang H, Su Q (2022) A color image watermarking method com-
33. Abduldaim AM, Waleed J, Mazher AN (2020) An Efficient Scheme
bined QR decomposition and spatial domain. Multimed Tools Appl
of Digital Image Watermarking Based on Hessenberg Factorization 81(26):37895–37916
and DWT. Int Conf Comput Sci Software Eng (CSASE) 2020:180–
22. Nha PT, Thanh TM, Phong NT (2022) Consideration of a robust
185. https://doi.org/10.1109/CSASE48920.2020.9142096
watermarking algorithm for color image using improved QR
34. Methaq GT, Muhanad YT, Jamal HN, Salama MA (2022) Hes-
decomposition. Soft Comput 26(11):5069–5093
senberg factorization and firework algorithms for optimized data
23. Dhar PK, Hazra P, Shimamura T (2020) Blind color image
hiding in digital images. J Intell Syst 31(1):440–453. https://doi.
watermarking using fan Beam transform and QR decomposition. org/10.1515/jisys-2022-0029 Symmetry 12(3):486
35. Wang L, Ji H (2022) A Watermarking Optimization Method Based
24. Li M, Yuan X, Chen H, Li J (2020) Quaternion Discrete
on Matrix Decomposition and DWT for Multi-Size Images. Elec-
Fourier Transform-Based Color Image Watermarking Method
tron 11(13):2027. https://doi.org/10.3390/electronics11132027
Using Quaternion QR Decomposition. IEEE Access 8:72308–
36. Begum M, Ferdush J, Uddin MS (2022) A Hybrid robust water-
72315. https://doi.org/10.1109/ACCESS.2020.2987914
marking system based on discrete cosine transform, discrete
25. Hsu LY, Hu HT, Chou HH (2022) A high-capacity QRD-based
wavelet transform, and singular value decomposition. J King Saud
blind color image watermarking algorithm incorporated with AI
University-Comput Inf Sci 34(8):5856–5867
technologies. Expert Syst Appl 199:117134
37. Satish A, Prasad EV, Tejasvi R, Swapna P, Vijayarajan R
26. Su Q, Liu Y, Liu D, Yuan Z, Ning H (2019) A new watermark-
(2019) “Image Scrambling through Two Level Arnold Transform.”
ing scheme for colour image using QR decomposition and ternary
Alliance Int Conf Art Intell Mach Learn (AICAAM)
coding. Multimed Tools Appl 78(7):8113–8132
38. Masood F, Boulila W, Alsaeedi A, Khan JS, Ahmad J, Khan MA,
27. Chen Y, Jia Z-G, Peng Y, Peng Y-X, Zhang D (2021) A
Rehman SU (2022) A novel image encryption scheme based on
new structure-preserving quaternion QR decomposition method
Arnold cat map, Newton-Leipnik system and Logistic Gaussian
for color image blind watermarking. Signal Process 185(0165–
map. Multimed Tools Appl 81(21):30931–30959
1684):108088. https://doi.org/10.1016/j.sigpro.2021.108088
39. University of Granada “Computer Vision Group.” CVG-
28. Sejpal S, Borse D (2019) “Comparative Performance Analysis of
UGR Image Database. https://decsai.ugr.escvgdbimagenesc512.
Color Image watermarking Scheme Using Hessenberg Decom-
php. Last accessed 10 December 2022
position and Schur Decomposition.” 2019 5th Int Conf Comput
40. Rucker F, Britton S, Taylor C (2018) Color and Temporal Fre-
Commun Cont Autom (ICCUBEA) 1–6
quency Sensitive Eye Growth in Chick. Investig Ophthalmol Vis
29. Mohammadi M, Nejati F (2020) “Watermarking based on Hessen-
Sci 59(15):6003–6013. https://doi.org/10.1167/iovs.18-25322
berg matrix decomposition.” Soft Comput J 9(1):Serial Number
17, 146–157. https://doi.org/10.22052/scj.2021.242811.0
30. Su Q (2016) Novel blind colour image watermarking technique
Publisher’s Note Springer Nature remains neutral with regard to juris-
using Hessenberg decomposition. IET Image Process 10(11):817–
dictional claims in published maps and institutional affiliations.
829. https://doi.org/10.1049/iet-ipr.2016.0048
31. Su Q, Chen B (2017) A novel blind color image watermarking using
Springer Nature or its licensor (e.g. a society or other partner) holds
upper Hessenberg matrix. AEU - Int J Electr Commun 78(1434–
exclusive rights to this article under a publishing agreement with the
8411):64–71. https://doi.org/10.1016/j.aeue.2017.05.025
author(s) or other rightsholder(s); author self-archiving of the accepted
32. Abodena O, Agoyi M (2018) “Colour image blind watermarking
manuscript version of this article is solely governed by the terms of such
scheme based on fast walsh hadamard transform and hessenberg
publishing agreement and applicable law.
decomposition.” Stud Inf Cont 27(3):339–348 ISSN: 1220-1766.
https://doi.org/10.24846/v27i3y201809 123 85
