







Preview text:
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/ Trang 90
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn KHÓA HỌC IMOE
ĐỀ MINH HỌA CHINH PHỤC KÌ THI TỐT NGHIỆP
THẦY ĐỖ VĂN ĐỨC
NĂM HỌC 2024 - 2025; MÔN TOÁN ĐỀ SỐ 13
Thời gian làm bài 90 phút, không kể thời gian phát đề
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
1. Cho hàm số 𝑦𝑦 = 𝑓𝑓(𝑥𝑥) có bảng biến thiên như sau : 𝑥𝑥 −∞ 0 2 +∞ 𝑓𝑓′(𝑥𝑥) + 0 − 0 + 4 +∞ 𝑓𝑓(𝑥𝑥) −∞ 0
Giá trị cực tiểu của hàm số đã cho bằng A. 4. B. 2. C. 0. D. 1. 2. Với 4
𝑎𝑎 là số thực dương tùy ý, log bằng 2 a 1 A. − log . a 2log . a 2 − log . a log a −1. 2 B. C. D. 2 2 2 2
3. Tiệm cận đứng của đồ thị hàm số x y =
là đường thẳng có phương trình 2x + 4 1 A. x = . B. x = 2. C. x =1. D. x = 2. − 2 1
4. Giá trị của I = d x x ∫ bằng 1 − A. 0. B. 1. − C. 2. D. 1.
5. Đường thẳng 𝑑𝑑 song song với hai mặt phẳng
(𝑃𝑃): 𝑥𝑥 + 𝑦𝑦 + 𝑧𝑧 − 2 = 0 và (𝑄𝑄): 𝑥𝑥 − 2𝑦𝑦 + 3𝑧𝑧 − 6 = 0 có 1 vectơ chỉ phương là:
A. a = (5;− 2;− 3). B. b = (1;3;3). C. c = (1; 2 − ;3). D. u = (5; 2 − ;3).
6. Cho cấp số cộng (𝑢𝑢𝑛𝑛) với 𝑢𝑢1 = 1 và tổng của 10 số hạng đầu tiên của cấp số cộng bằng 100. Tính 𝑢𝑢10 A. u = 9. u = 5. u =19. u = 22. 10 B. 10 C. 10 D. 10
7. Trong không gian 𝑂𝑂𝑥𝑥𝑦𝑦𝑧𝑧, tọa độ điểm đối xứng với điểm 𝑀𝑀(0; 2; −3) qua trục 𝑂𝑂𝑧𝑧 là A. (0;− 2;3). B. (0;2;3). C. (0;2; 3 − ). D. (0;− 2; 3 − ). ợ ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/
Thực chiến luyện đề môn Toán | Đề số 13 Trang 91
8. Đồ thị hàm số 𝑦𝑦 = √𝑥𝑥2 + 1 + 𝑥𝑥 có tất cả bao nhiêu đường tiệm cận? A. 1. B. 2. C. 3. D. 0.
9. Cho hình phẳng (𝐻𝐻) giới hạn bởi đường 𝑦𝑦 = 𝑥𝑥 − 𝑥𝑥2 và 𝑦𝑦 = 0. Thể tích của khối tròn xoay
sinh ra khi quay hình (𝐻𝐻) quanh trục hoành là π 8π 16π 4π A. . B. . C. . D. . 30 3 15 3
10. Thống kê chiều cao (đơn vị: cm) của các bạn học sinh nữ lớp 12𝐴𝐴 và lớp 12𝐵𝐵 ở bảng sau: Chiều cao (cm)
[150; 155) [155; 160) [160; 165) [165; 170) [170; 175) [175; 180) Số học sinh nữ lớp 12𝐴𝐴 2 7 12 3 0 1 Số học sinh nữ lớp 12𝐵𝐵 0 9 8 2 1 5
Gọi 𝑅𝑅1; 𝑅𝑅2 lần lượt là khoảng biến thiên của mẫu số liệu ghép nhóm về chiều cao của các bạn
học sinh nữ lớp 12𝐴𝐴 và 12𝐵𝐵. Tìm 𝑅𝑅1; 𝑅𝑅2.
A. R = 30cm; R = 25cm.
R = 30cm; R = 30cm. 1 2 B. 1 2
C. R = 25cm; R = 25cm.
R =12cm; R = 9cm. 1 2 D. 1 2
11. Trong không gian 𝑂𝑂𝑥𝑥𝑦𝑦𝑧𝑧, cho điểm 𝑀𝑀(−3; 1; 2) và mặt phẳng (𝑃𝑃): 2𝑥𝑥 + 2𝑦𝑦 + 𝑧𝑧 − 7 = 0. Mặt
cầu (𝑆𝑆) có tâm 𝑀𝑀, cắt (𝑃𝑃) theo giao tuyến là đường tròn có bán kính bằng 4. Bán kính của mặt cầu (𝑆𝑆) bằng A. 4. B. 5. C. 6. D. 7.
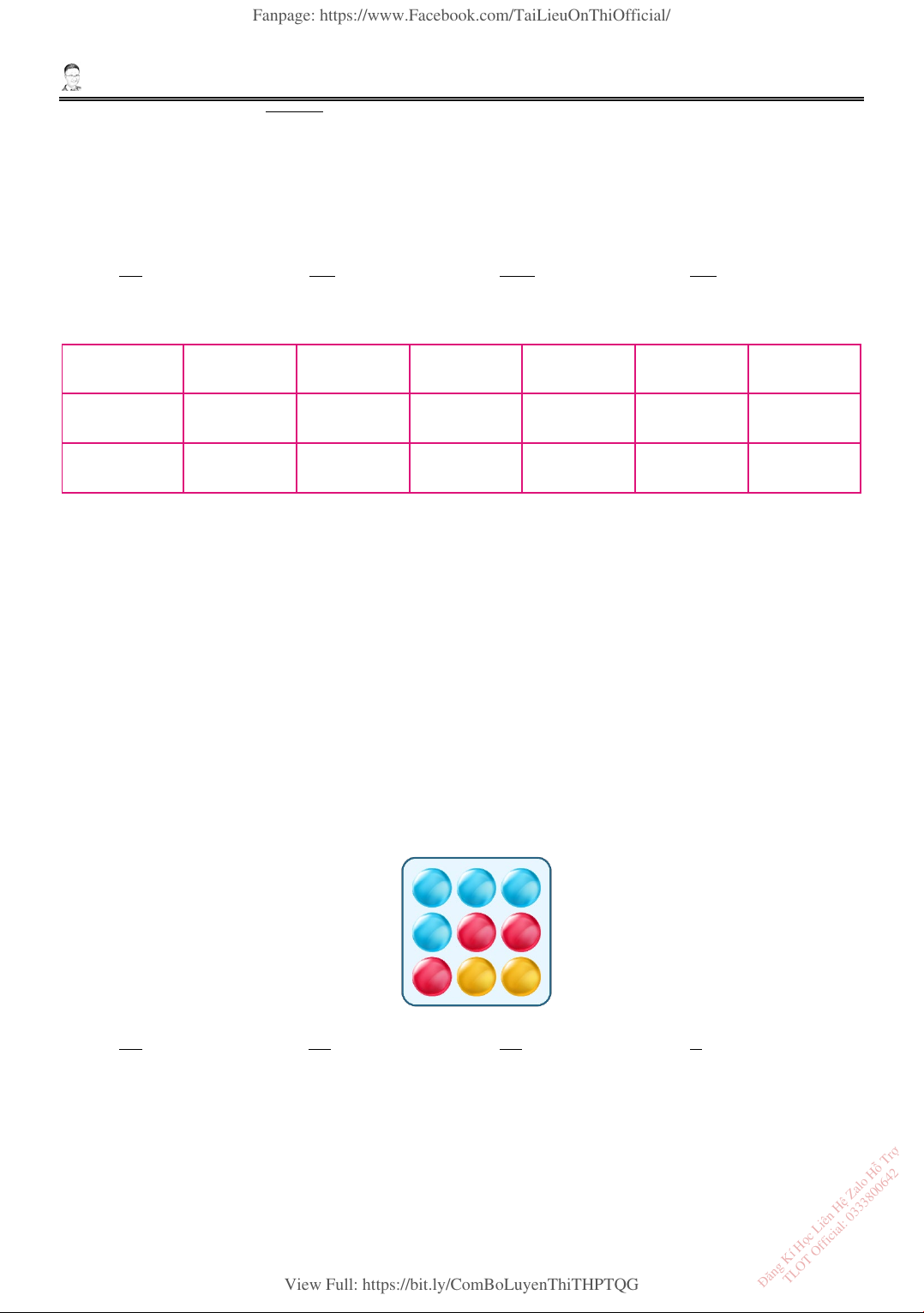
12. Một chiếc hộp chứa 9 quả cầu gồm 4 quả màu xanh, 3 quả màu đỏ và 2 quả màu vàng. Lấy
ngẫu nhiên 3 quả cầu từ hộp đó. Xác suất để trong 3 quả cầu lấy được có ít nhất 1 quả màu đỏ bằng 19 16 17 1 A. . B. . C. . D. . 28 21 42 3 ợ ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/ Trang 92
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
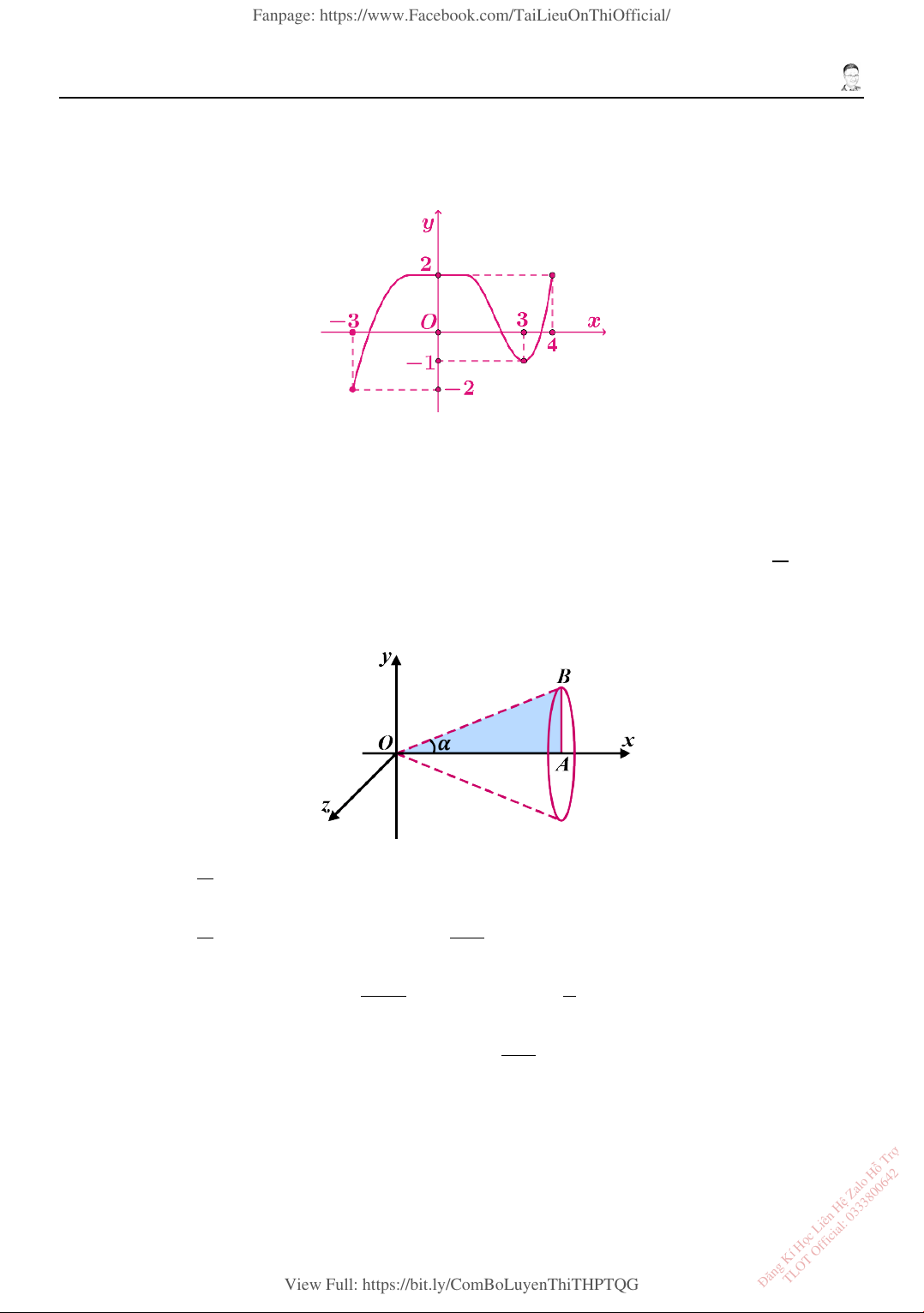
1. Cho đồ thị 𝑦𝑦 = 𝑓𝑓(𝑥𝑥) trên đoạn [−3; 4] như sau
a) Hàm số 𝑓𝑓(𝑥𝑥) đồng biến trên (−3; 0).
b) Hàm số 𝑓𝑓(𝑥𝑥) nghịch biến trên (0; 3).
c) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số 𝑓𝑓(𝑥𝑥) trên [−3; 4] bằng 0.
d) Hàm số 𝑓𝑓(𝑥𝑥) có đúng 1 điểm cực trị trong khoảng (−3; 4). 2. π
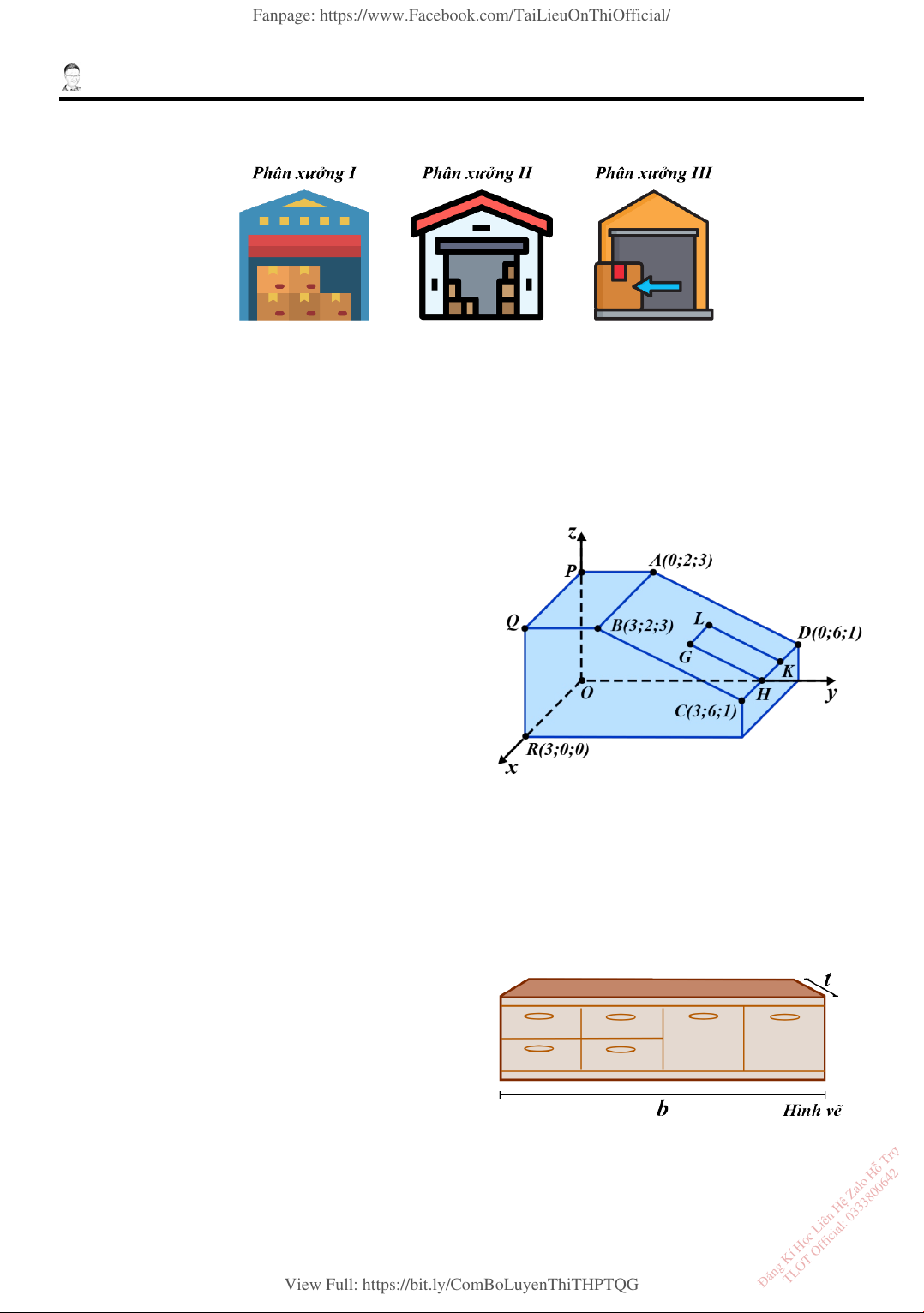
Cho tam giác vuông 𝑂𝑂𝐴𝐴𝐵𝐵 có cạnh 𝑂𝑂𝐴𝐴 = 𝑎𝑎 nằm trên tục 𝑂𝑂𝑥𝑥 và 𝐴𝐴𝑂𝑂𝐵𝐵 = 𝛼𝛼 0 α < < . Gọi 𝛽𝛽 2
là khối tròn xoay sinh ra khi quay miền tam giác 𝑂𝑂𝐴𝐴𝐵𝐵 xung quanh trục 𝑂𝑂𝑥𝑥. Xét tính đúng sai
của các khẳng định sau: π
a) Khi α = thì 𝑂𝑂𝐵𝐵 = 𝑥𝑥. 4 π 3 π b) Khi α = thì thể tích a
𝑉𝑉 của khối 𝛽𝛽 là (đvtt). 6 9 3 π c) Khi thể tích 4 a
𝑉𝑉 của khối 𝛽𝛽 là thì giá trị 1 cosα < . 3 2 3 π d) Khi a
tan𝛼𝛼 = cot𝛼𝛼 thì thể tích 𝑉𝑉 của khối 𝛽𝛽 là . 3
3. Sản phẩm 𝑋𝑋 bán ra thị trường do một nhà máy gồm 3 phân xưởng I, II và III sản xuất, trong
đó phân xưởng I chiếm 30%, phân xưởng II chiếm 45%, phân xưởng III chiếm 25% số lượng ợ ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/
Thực chiến luyện đề môn Toán | Đề số 13 Trang 93
sản phẩm trong toàn nhà máy. Tỉ lệ sản phẩm loại 𝐴𝐴 do 3 phân xưởng I, II và III sản xuất lần
lượt là: 70%, 50% và 90%.
a) Tỉ lệ sản phẩm loại 𝐴𝐴 do nhà máy sản xuất là 66%.
b) Chọn ngẫu nhiên một sản phẩm 𝑋𝑋 ở thị trường thì thấy rằng đó là sản phẩm loại 𝐴𝐴. Xác
suất để sản phẩm đó do nhà máy II sản xuất là 0,34 (kết quả làm tròn tới hàng phần trăm).
c) Cần mua ngẫu nhiên tối thiểu 9 sản phẩm 𝑋𝑋 ở thị trường để xác suất gặp phải ít nhất một
sản phẩm không phải loại 𝐴𝐴 là trên 98%.
d) Một người đã mua 15 sản phẩm 𝑋𝑋. Xác suất để có không quá 3 sản phẩm đạt loại 𝐴𝐴 nhỏ hơn 0,04%.
4. Hình vẽ bên dưới mô tả một mô hình phòng áp
mái có hình dạng là một lăng trụ đứng. Mặt sàn
và hai mặt bên nằm trên các mặt phẳng tọa độ
như hình vẽ. Hình chữ nhật 𝐴𝐴𝐵𝐵𝐴𝐴𝐴𝐴 nằm trên
một mặt phẳng (𝐸𝐸) và biểu diễn phần nghiêng của mặt mái.
Trong hệ tọa độ này, một đơn vị độ dài tương
ứng với 1 mét. Hình chữ nhật 𝐺𝐺𝐻𝐻𝐺𝐺𝐺𝐺 với điểm
𝐺𝐺 có tọa độ (2; 4; 2) có chiều rộng 𝐺𝐺𝐺𝐺 bằng 1.
Hình chữ nhật này nằm trên mặt phẳng (𝐸𝐸) và
các điểm 𝐻𝐻 và 𝐺𝐺 nằm trên đường thẳng 𝐴𝐴𝐴𝐴.
Trong mô hình, hình chữ nhật này đại diện cho một chiếc cửa sổ mái.
a) Tọa độ điểm 𝐺𝐺 là (1 ; 6 ; 1).
b) Thể tích của phòng áp mái là 42 m3.
c) Cửa sổ có thể xoay quanh một trục, trong mô hình, trục này đi qua trung điểm của các đoạn
thẳng 𝐺𝐺𝐻𝐻 và 𝐺𝐺𝐺𝐺. Cạnh dưới của cửa sổ khi đó xoay vào trong phòng, và bản lề cho phép
mặt phẳng cửa sổ vuông góc với sàn nhà. Vậy thì khi xoay, cửa sổ chạm vào sàn nhà.
d) Hình dưới mô tả một chiếc tủ hình hộp chữ
nhật có chiều cao 40 cm. Nó đặt sát tường
dưới cửa sổ bằng mặt sau của khối. Cạnh
trên phía trước của chiếc tủ nằm trên mô
hình của đường thẳng 𝑘𝑘 đi qua (0; 5,5; 0,4)
và có vectơ chỉ phương (1; 0; 0). Khi đó khi
xoay, cửa sổ chạm vào chiếc tủ. ợ ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/ Trang 94
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
1. Cho tứ diện 𝑂𝑂𝐴𝐴𝐵𝐵𝐴𝐴 có 𝑂𝑂𝐴𝐴, 𝑂𝑂𝐵𝐵, 𝑂𝑂𝐴𝐴 đôi một vuông góc và 𝑂𝑂𝐴𝐴 = 𝑂𝑂𝐵𝐵 = 𝑂𝑂𝐴𝐴. Gọi 𝑀𝑀, 𝑁𝑁, 𝑃𝑃 lần
lượt là trung điểm của 𝑂𝑂𝐴𝐴, 𝐴𝐴𝐵𝐵, 𝐴𝐴𝐴𝐴 và thể tích của tứ diện 𝑂𝑂𝑀𝑀𝑁𝑁𝑃𝑃 là 4. Tính diện tích mặt cầu 3
đi qua 4 điểm 𝑂𝑂, 𝐴𝐴, 𝐵𝐵, 𝐴𝐴? (kết quả làm tròn đến hàng đơn vị) Đáp số: ……….
2. Một thiết bị kỹ thuật là một khối tròn xoay. Mặt cắt của khối tròn xoay đó qua trục của nó được
mô tả trong hình vẽ bên. Biết độ dài 𝐴𝐴𝐷𝐷 = 13 cm, thể tích của thiết bị đó bằng bao nhiêu cm3?
(kết quả làm tròn đến hàng đơn vị) Đáp số: ……….
3. Hai con tàu 𝐴𝐴 và 𝐵𝐵 đang ở cùng một vī tuyến và cách nhau 5 hải lí. Cả hai tàu đồng thời cùng
khởi hành. Tàu A chạy về hướng Nam với vận tốc 6 hải lí/giờ, còn tàu 𝐵𝐵 chạy về vị trí xuất
phát của tàu 𝐴𝐴 với vận tớc 7 hải lí/giờ. Biết rằng sau 𝑡𝑡0 (giờ) thì khoảng cách giữa hai tàu là
bé nhất. Tìm 𝑡𝑡0 (kết quả làm tròn tới hàng phần trăm). Đáp số: ………. ợ ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/
Thực chiến luyện đề môn Toán | Đề số 13 Trang 95
4. Một chiếc đồng hồ cát như hình vẽ dưới đây, gồm hai phần đối xứng nhau
qua mặt phẳng nằm ngang và được đặt vừa khít trong một hình trụ. Thiết
diện thẳng đứng qua trục của nó là hai parabola chung đỉnh và đối xứng
nhau qua mặt phẳng nằm ngang. Ban đầu, lượng cát dồn hết ở phần trên
của đồng hồ thì chiều cao ℎ của mực cát bằng 3 chiều cao của phần bên 4
đó. Cát chảy từ trên xuống dưới với lưu lượng không đổi 2,90 cm3/phút.
Khi chiều cao của cát còn 4 cm thì bề mặt trên cùng của cát tạo thành một
đường tròn có chu vi 8𝜋𝜋 cm. Biết rằng sau 30 phút thì cát chảy hết xuống
phần bên dưới của đồng hồ. Hỏi chiều cao của khối trụ bên ngoài là bao
nhiêu cm? (kết quả làm tròn đến hàng phần trăm) Đáp số: ……….
5. Trong không gian 𝑂𝑂𝑥𝑥𝑦𝑦𝑧𝑧, với mỗi đơn vị trên hệ trục tọa độ dài
100 km, một máy bay trực thăng di chuyển từ 𝑀𝑀(−5; −10; −7)
với tốc độ 230 m/s dọc theo đường thẳng có phương trình 𝑥𝑥 = 𝑡𝑡
𝑑𝑑: �𝑦𝑦 = 2𝑡𝑡 . Một radar đặt tại 𝑂𝑂 có phạm vi hoạt động (phạm 𝑧𝑧 = 3 + 2𝑡𝑡
vi mà radar có thể bắt được máy bay) là 500 km. Biết máy bay
di chuyển theo hướng về vùng phát sóng của radar. Hỏi máy bay
có thể nhận được tín hiệu của radar trong thời gian bao nhiêu
giây (kết quả làm tròn tới hàng đơn vị). Đáp số: ……….
6. Trong một kho rượu số lượng rượu loại 𝐴𝐴 và rượu loại 𝐵𝐵 bằng nhau. Người ta chọn ngẫu nhiên
một chai rượu trong kho và đưa cho 5 người sành rượu nếm thử để xác định xem đây là loại
rượu nào. Giả sử mỗi người có xác suất đoán đúng là 75%. Có 4 người kết luận chai rượu loại
𝐴𝐴 và 1 người kết luận chai rượu loại 𝐵𝐵. Khi đó xác suất để chai rượu được chọn thuộc loại 𝐴𝐴 bằng a (với , + ∈ , a a b
là phân số tối giản). Giá trị của 𝑎𝑎 + 𝑏𝑏 bằng bao nhiêu? b b Đáp số: ……….
--- Hết --- ợ ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/ Trang 96
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
PHẦN GHI CHÉP RIÊNG
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………... ợ ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/
Thực chiến luyện đề môn Toán | Đề số 14 Trang 97 KHÓA HỌC IMOE
ĐỀ MINH HỌA CHINH PHỤC KÌ THI TỐT NGHIỆP
THẦY ĐỖ VĂN ĐỨC
NĂM HỌC 2024 - 2025; MÔN TOÁN ĐỀ SỐ 14
Thời gian làm bài 90 phút, không kể thời gian phát đề
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
1. Trong không gian 𝑂𝑂𝑂𝑂𝑂𝑂𝑂𝑂, cho 𝑢𝑢�⃗ = (1; 1; −3). Giá trị |𝑢𝑢�⃗| bằng A. 11. B. 10. C. 3. D. 2.
2. Gọi 𝑄𝑄1, 𝑄𝑄2, 𝑄𝑄3 là tứ phân vị của một mẫu số liệu ghép nhóm. Khi đó, khoảng tứ phân vị Δ𝑄𝑄
của mẫu số liệu trên được xác định bởi công thức
A. ∆ = Q − Q ∆ = Q − Q ∆ = Q − Q ∆ = Q − Q Q . Q . Q . Q . 2 1 B. 3 1 C. 2 3 D. 1 3
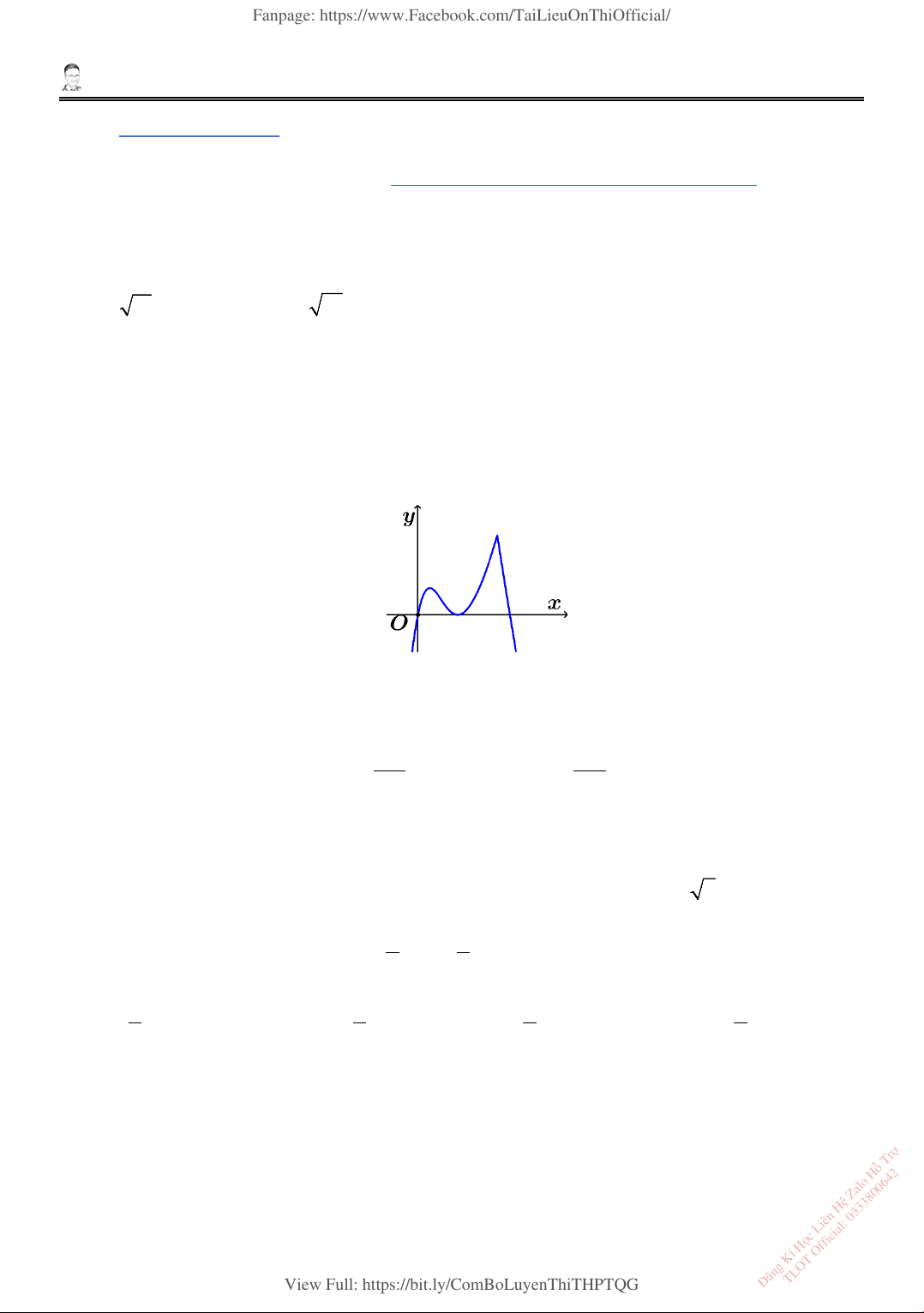
3. Cho hàm số 𝑂𝑂 = 𝑓𝑓(𝑂𝑂) liên tục trên , hàm số 𝑂𝑂 = 𝑓𝑓′(𝑂𝑂) có đồ thị như hình vẽ. Số điểm cực
trị của hàm số 𝑓𝑓(𝑂𝑂) là A. 0. B. 1. C. 2. D. 3.
4. Một nguyên hàm 𝐹𝐹(𝑂𝑂) của hàm số 𝑓𝑓(𝑂𝑂) = 2𝑥𝑥 là: x x A. ( ) = 2x F x + 2 . x B. F (x) 2 = + 2222. C. F x = + x D. x F x = ln 2 ( ) 2 2 . ln 2 ( ) 2 ln 2.
5. Trong không gian 𝑂𝑂𝑂𝑂𝑂𝑂𝑂𝑂, cho mặt cầu (𝑆𝑆): 𝑂𝑂2 + (𝑂𝑂 − 1)2 + (𝑂𝑂 − 1)2 = 2. Bán kính của mặt cầu là A. 2. B. 4. C. 1. D. 2. 4x 2−x
6. Tập nghiệm của bất phương trình 2 3 ≤ là: 3 2 2 2 2 2 A. ; +∞ . B. ; −∞ . C. − ;+∞ . D. ; −∞ . 5 3 3 5
7. Trong không gian 𝑂𝑂𝑂𝑂𝑂𝑂𝑂𝑂, cho hai điểm 𝐴𝐴(2; −2; 1) và 𝐵𝐵(0; 3; 2). Véctơ nào dưới đây là một
vectơ chỉ phương của đường thẳng 𝐴𝐴𝐵𝐵? A. u = ( 2 − ;5;− ) 1 . B. u = (2;5;− ) 1 . C. u = ( 2 − ;5 ) ;1 . D. u = (5;− 2 ) ;1 . ợ ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/ Trang 98
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
8. Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số 𝑂𝑂 = 𝑂𝑂3 − 3𝑂𝑂2 − 2𝑂𝑂, 𝑂𝑂 = 2𝑂𝑂. 127 125 129 131 A. S = . B. S = . C. S = . D. S = . 4 4 4 4
9. Một người gửi 300 triệu đồng vào ngân hàng theo thể thức lãi kép, kì hạn 1 quý, lãi suất
1,75%/quý. Hỏi sau ít nhất bao nhiêu tháng người gửi có ít nhất 500 triệu đồng (bao gồm cả
vốn lẫn lãi) từ số vốn ban đầu? (Giả sử lãi suất không thay đổi). A. 81 tháng. B. 30 tháng. C. 45 tháng. D. 90 tháng.
10. Cho lăng trụ đứng 𝐴𝐴𝐵𝐵𝐴𝐴. 𝐴𝐴′𝐵𝐵′𝐴𝐴′ có cạnh 𝐵𝐵𝐴𝐴 = 2𝑎𝑎, góc giữa hai mặt phẳng (𝐴𝐴𝐵𝐵𝐴𝐴) và (𝐴𝐴′𝐵𝐵𝐴𝐴)
bằng 60𝑜𝑜. Biết diện tích của tam giác 𝐴𝐴′𝐵𝐵𝐴𝐴 bằng 2𝑎𝑎2. Thể tích của khối lăng trụ 𝐴𝐴𝐵𝐵𝐴𝐴. 𝐴𝐴′𝐵𝐵′𝐴𝐴′ bằng 3 2a 3 3a A. . B. 3 3a . C. 3 3a . D. . 3 3
11. Tại một công ty sản xuất đồ chơi 𝐴𝐴, công ty phải chi 50 000 USD để thiết lập dây chuyền sản
xuất ban đầu. Sau đó, cứ sản xuất được một sản phẩm đồ chơi 𝐴𝐴, công ty phải chi trả 5 USD
cho nguyên liệu thô và nhân công. Gọi 𝑂𝑂 (𝑂𝑂 ≥ 1) là số đồ chơi 𝐴𝐴 mà công ty đã sản xuất và
𝑇𝑇(𝑂𝑂) (đơn vị USD) là tổng số tiền bao gồm cả chi phí ban đầu mà công ty phải chi trả khi sản T (x)
xuất 𝑂𝑂 đồ chơi 𝐴𝐴. Biết chi phí trung bình cho mỗi sản phẩm đồ chơi 𝐴𝐴 là 𝑀𝑀(𝑂𝑂) = . Khi x
𝑂𝑂 đủ lớn (𝑂𝑂 → +∞) thì chi phí trung bình (USD) cho mỗi sản phẩm đồ chơi 𝐴𝐴 gần nhất với kết quả nào sau đây? A. 50000. B. 50005. C. 10. D. 5.
12. Một hộp đựng 6 quả bóng đỏ (được đánh số từ 1 đến 6), 5 quả bóng vàng (được
đánh số từ 1 đến 5) và 4 quả bóng xanh (được đánh số từ 1 đến 4). Lấy ngẫu
nhiên ra 4 quả bóng. Tính xác suất để 4 quả bóng lấy ra có đủ ba màu, mà không
có hai quả bóng nào có số thứ tự trùng nhau 381 48 74 43 A. . . . . 455 B. 91 C. 455 D. 91
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
1. Một công ty sản xuất đồ nội thất có thể bán một chiếc ghế ngả với giá 𝑝𝑝(𝑂𝑂) = 1500 − 3𝑂𝑂
(USD), với 𝑂𝑂 là số chiếc ghế được sản xuất và bán ra. Chi phí cố định cho mỗi đợt sản xuất là
66 500 USD, đồng thời mỗi chiếc ghế sản xuất ra tốn 20 USD. Vì hạn chế của máy móc, công
suất của nhà máy sản xuất không quá 300 chiếc ghế.
a) Để thu được doanh thu lớn nhất, công ty cần sản xuất 250 sản phẩm.
b) Nếu chỉ sản xuất đúng 100 sản phẩm, chi phí sản xuất là 6 652 000 USD. ợ ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/
Thực chiến luyện đề môn Toán | Đề số 14 Trang 99
c) Nếu giá sản phẩm là 1350 USD thì công ty hòa vốn.
d) Công ty nên sản xuất và bán đúng 246 sản phẩm để lợi nhuận thu về cao nhất.
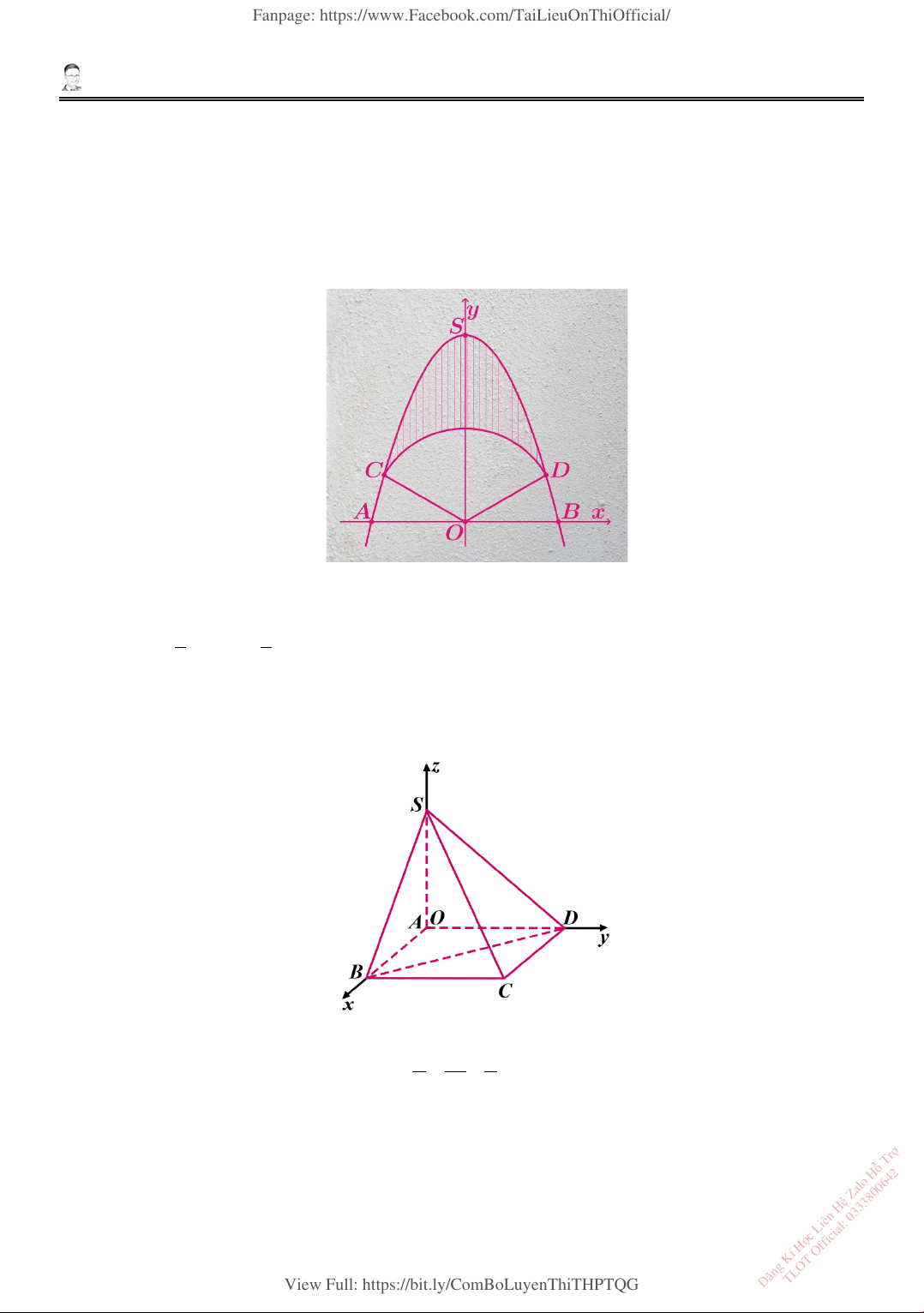
2. Trên bức tường cần trang trí một hình phẳng dạng parabol đỉnh 𝑆𝑆 như hình vẽ, biết 𝑂𝑂 là trung
điểm của 𝐴𝐴𝐵𝐵, 𝑂𝑂𝑆𝑆 = 𝐴𝐴𝐵𝐵 = 4m. Parabol trên được chia thành ba phần để sơn ba màu khác nhau
với mức chi phí: phần trên kẻ sọc 140 000 đồng/m2, phần giữa hình quạt tâm 𝑂𝑂, bán kính
2 m được tâm đậm 150 000 đồng/m2, phần còn lại 160 000 đồng/m2. Gắn hệ trục tọa độ
𝑂𝑂𝑂𝑂𝑂𝑂 như hình vẽ
a) Tọa độ các điểm 𝐴𝐴(−2; 0), 𝐵𝐵(2; 0), 𝑆𝑆(0; 4).
b) Đường parabol có phương trình 𝑂𝑂 = 𝑂𝑂2 + 4 và đường cong phần hình quạt có phương
trình 𝑂𝑂2 + 𝑂𝑂2 = 4.
c) 𝐴𝐴�−√3; 1�, 𝐷𝐷�√3; 1�
d) Tổng số tiền sơn là 1 575 349 đồng.
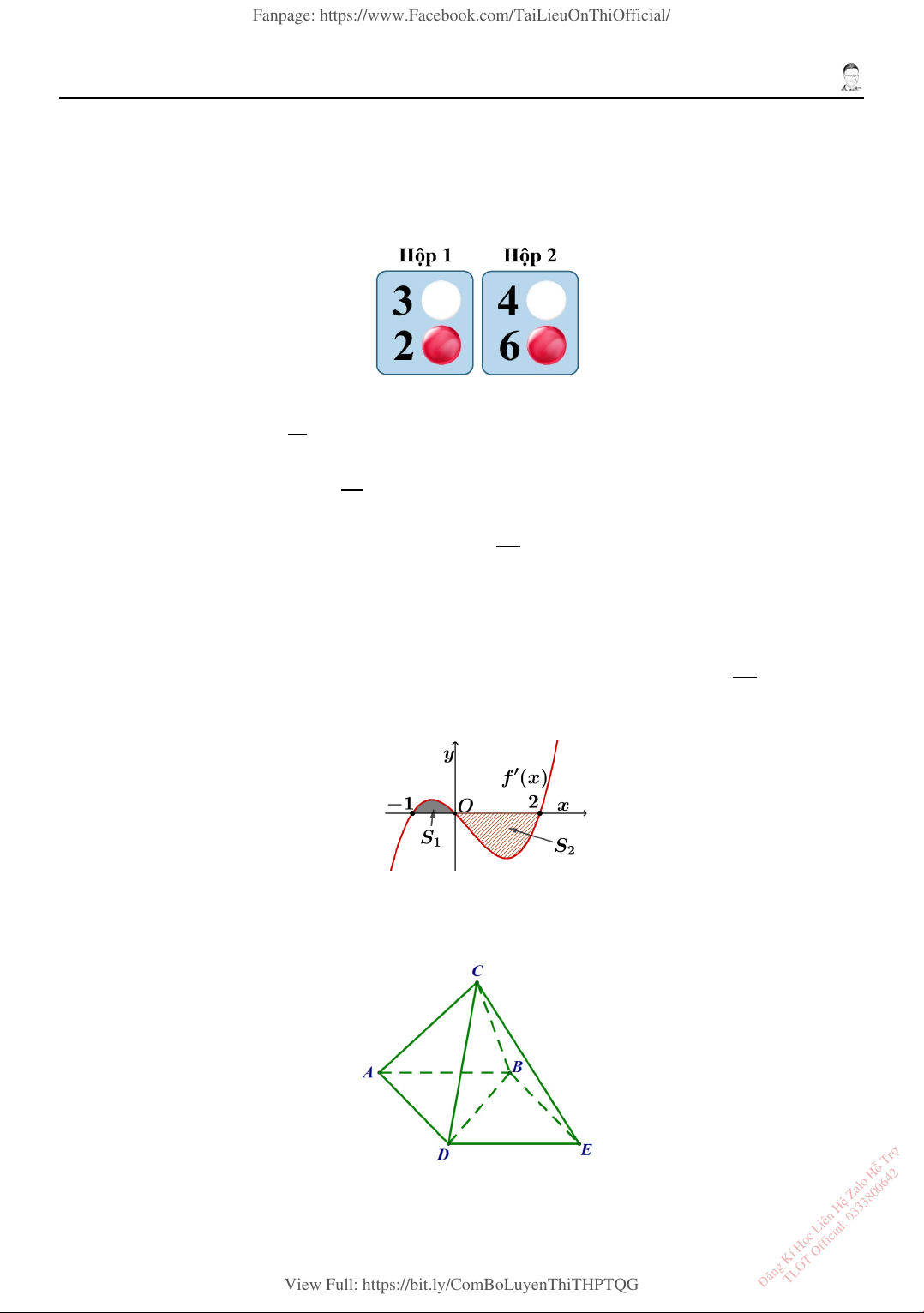
3. Trong không gian 𝑂𝑂𝑂𝑂𝑂𝑂𝑂𝑂, cho hình chóp 𝑆𝑆. 𝐴𝐴𝐵𝐵𝐴𝐴𝐷𝐷 có 𝑆𝑆(0; 0; 3), đáy 𝐴𝐴𝐵𝐵𝐴𝐴𝐷𝐷 là hình chữ nhật với
𝐴𝐴(0; 0; 0), 𝐵𝐵(4; 0; 0), 𝐷𝐷(0; 10; 0) như hình bên.
a) Tọa độ điểm 𝐴𝐴 là (4; 10; 0).
b) Phương trình mặt phẳng x y z
(𝑆𝑆𝐵𝐵𝐷𝐷) là + − = 1. 4 10 3
c) Tọa độ của 𝑆𝑆�𝐴𝐴 �⃗ là (4; 10; −3).
d) Góc giữa đường thẳng 𝑆𝑆𝐴𝐴 và mp(𝑆𝑆𝐵𝐵𝐷𝐷) bằng 78° (làm tròn đến hàng đơn vị của độ). ợ ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/ Trang 100
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
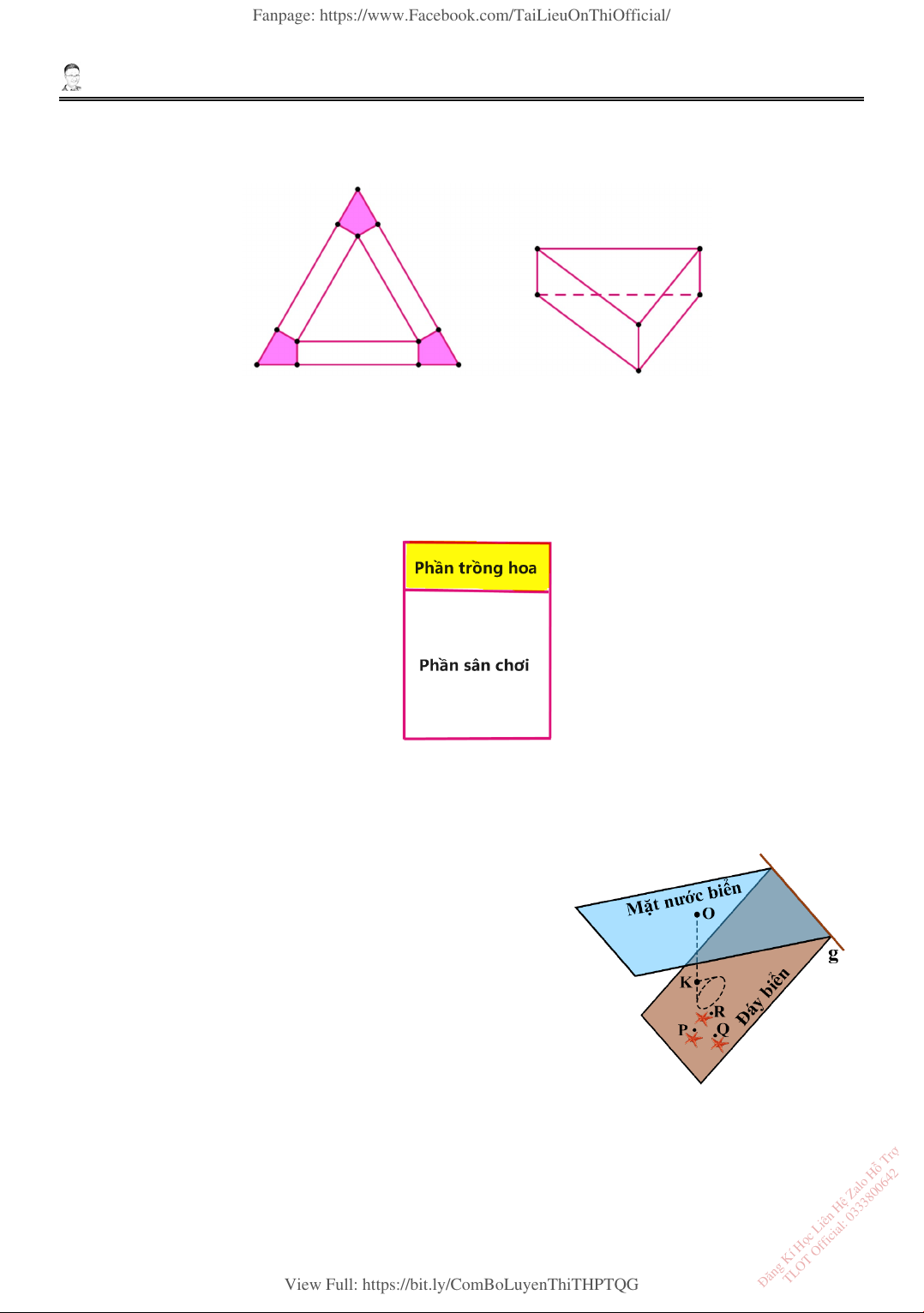
4. Hộp I có 3 quả bóng trắng và 2 quả bóng đỏ. Hộp II có 4 quả bóng trắng và 6 quả bóng đỏ.
Chuyển ngẫu nhiên 1 quả bóng từ hộp I sang hộp II và không xem màu quả bóng ấy. Sau đó,
lấy một quả bóng từ hộp II.
Gọi 𝐴𝐴 là biến cố: “Lấy được quả bóng màu trắng từ hộp I”.
Gọi 𝐵𝐵 là biến cố: “Lấy được quả bóng màu trắng từ hộp II”.
a) Xác suất của biến cố 𝐴𝐴 là 0,6. b) Xác suất 5
𝑃𝑃(𝐵𝐵|𝐴𝐴) = . 11
c) Xác suất của biến cố 𝐵𝐵 là 23. 55
d) Xác suất để hai quả bóng lấy ra cùng màu là 29 . 55
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
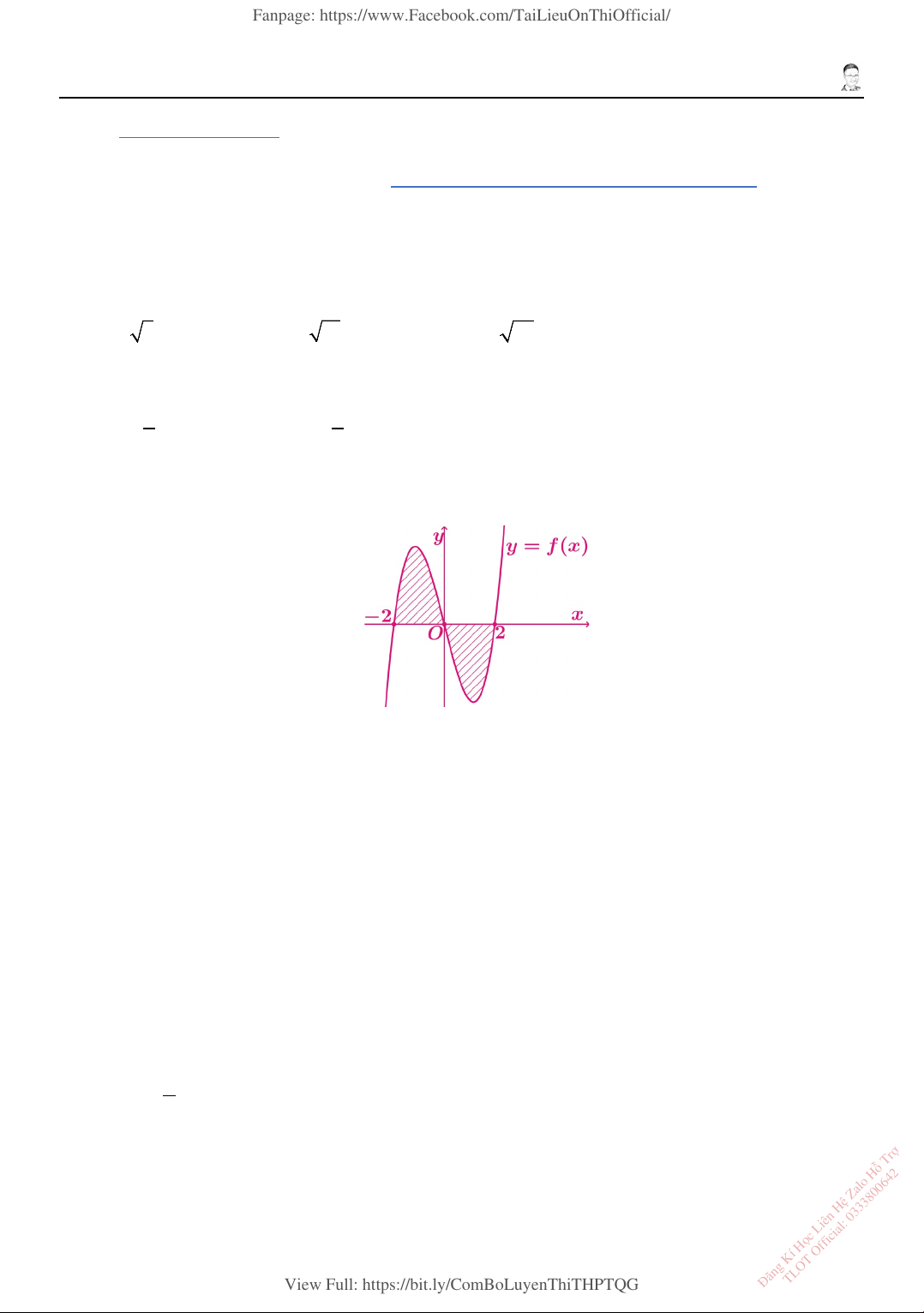
1. Cho hàm số 𝑓𝑓(𝑂𝑂) = 𝑎𝑎𝑂𝑂4 + 𝑏𝑏𝑂𝑂3 + 𝑐𝑐𝑂𝑂2 + 𝑑𝑑𝑂𝑂 + 𝑒𝑒, đồ thị hàm số 𝑂𝑂 = 𝑓𝑓′(𝑂𝑂) như hình vẽ. Kí hiệu 5
𝑆𝑆1, 𝑆𝑆2 là diện tích phân tô đậm và phần gạch chéo (hình vẽ). Biết S = . Giá trị của 1 24 3𝑆𝑆2 bằng bao nhiêu? Đáp số: ……….
2. Cho tứ diện đều 𝐴𝐴𝐵𝐵𝐴𝐴𝐷𝐷. Dựng hình bình hành 𝐴𝐴𝐵𝐵𝐴𝐴𝐷𝐷. Góc giữa 𝐴𝐴𝐴𝐴 và mp(𝐴𝐴𝐷𝐷𝐴𝐴) bằng bao nhiêu độ? ợ Đáp số: ………. ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/
Thực chiến luyện đề môn Toán | Đề số 14 Trang 101
3. Cho một miếng tôn hình tam giác đều có cạnh bằng 60 cm. Người ta cắt miếng tôn ở các góc
như hình vẽ sau đó gập lên để tạo thành một hình hộp đựng nước là hình lăng trụ tam giác đều (như hình vẽ).
Muốn khối hộp thu được chứa được nhiều nước nhất thì tổng diện tích phần bỏ đi ở miếng tôn
ban đầu bằng bao nhiêu (đơn vị cm2, làm tròn tới hàng đơn vị). Đáp số: ……….
4. Một người muốn dành một phần mảnh đất hình chữ nhật để trồng hoa và làm sân chơi cho trẻ
em (như hình vẽ), với phần trồng hoa là phần tô đậm. Người đó muốn phần làm sân chơi cho
trẻ em phải là một hình vuông, đồng thời chu vi của toàn bộ mảnh đất bằng 100 m.
Nếu mỗi m2 trồng hoa có giá 1 triệu đồng, thì chi phí lớn nhất mà người ta có thể thu được từ
việc trồng hoa bằng bao nhiêu? (đơn vị triệu đồng, kết quả làm tròn tới hàng đơn vị)? Đáp số: ……….
5. Trong một mô hình mô tả một đoạn bờ biển, mặt phẳng
𝑂𝑂𝑂𝑂𝑂𝑂 biểu diễn mặt nước biển, đường thẳng 𝑔𝑔 biểu diễn
bờ biển. Mặt phẳng (𝐴𝐴) biểu diễn đáy biển trong đoạn
đang xét. Trên mặt phẳng (𝐴𝐴) có ba con sao biển nằm
tại ba vị trí lần lượt là 𝑃𝑃(4; 5; −19), 𝑄𝑄(5; 9; −18) và
𝑅𝑅(3; 7; −17). Một phao nổi trên mặt nước tại vị trí trùng
với gốc tọa độ 𝑂𝑂 (như hình vẽ). Từ phao, một nhiếp ảnh
gia lặn thẳng đứng xuống dưới mặt nước đến một điểm
𝐾𝐾 sâu 13 m. Nhiếp ảnh gia di chuyển từ vị trí 𝐾𝐾 song
song với đáy biển. Ống kính máy ảnh luôn vuông góc
với đáy biển và có góc nhìn của hình nón là 90°. Vị trí
gần đường bờ biển nhất của 𝐾𝐾 để người đó có thể chụp cả ba con sao biển một lúc là (𝑎𝑎; 𝑏𝑏; 𝑐𝑐),
tính 𝑇𝑇 = 2𝑎𝑎 + 𝑏𝑏 − 𝑐𝑐 ợ Đáp số: ………. ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/ Trang 102
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
6. Có hai chiếc hộp, hộp I chứa 6 viên bi màu xanh và 4 viên bi màu đỏ, hộp II chứa 7 viên bi
màu xanh và 3 viên bi màu đỏ, các viên bi có cùng kích cỡ và khối lượng. Lấy ngẫu nhiên một
viên bi từ hộp I sang hộp II. Sau đó lấy ngẫu nhiên hai viên bi từ hộp II. Nếu hai viên bi lấy ra
từ hộp II đều có màu xanh thì xác suất trong 2 viên bi đó, có viên bi thuộc hộp I là bao nhiêu?
(kết quả làm tròn tới hàng phần trăm) Đáp số: ………. --- Hết --- PHẦN GHI CHÉP RIÊNG
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………... ợ ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/
Thực chiến luyện đề môn Toán | Đề số 14 Trang 103
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………... ợ
……………………………………………………………………………………………………... ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/ Trang 104
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn KHÓA HỌC IMOE
ĐỀ MINH HỌA CHINH PHỤC KÌ THI TỐT NGHIỆP
THẦY ĐỖ VĂN ĐỨC
NĂM HỌC 2024 - 2025; MÔN TOÁN ĐỀ SỐ 15
Thời gian làm bài 90 phút, không kể thời gian phát đề
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
1. Trong không gian 𝑂𝑂𝑂𝑂𝑂𝑂𝑂𝑂, cho mặt cầu (𝑆𝑆): (𝑂𝑂 − 3)2 + (𝑂𝑂 + 1)2 + (𝑂𝑂 + 1)2 = 1. Khoảng cách
từ tâm mặt cầu đến gốc toạ độ là: A. 2 3. B. 11. C. 10. D. 3.
2. Tập nghiệm của bất phương trình ln(3𝑂𝑂 + 1) ≤ 0 là 1 1 A. − ;0 . − ;0 . ;0 −∞ . ;0 −∞ . 3 B. C. ( ) D. ( ] 3
3. Cho hàm số 𝑂𝑂 = 𝑓𝑓(𝑂𝑂) liên tục trên ℝ và có đồ thị như hình vẽ. Gọi 𝑆𝑆 là diện tích hình phẳng
giới hạn bởi các đường 𝑂𝑂 = 𝑓𝑓(𝑂𝑂), 𝑂𝑂 = 0, 𝑂𝑂 = −2, 𝑂𝑂 = 2.
Mệnh đề nào sau đây đúng? 0 2 0 2 A. S = f
∫ (x)dx− f ∫ (x)d .x B. S = f
∫ (x)dx+ f ∫ (x)d .x 2 − 0 2 − 0 0 2 0 2 C. S = − f
∫ (x)dx+ f ∫ (x)d .x D. S = − f
∫ (x)dx− f ∫ (x)d .x 2 − 0 2 − 0
4. Cho hàm số 𝑂𝑂 = 𝑓𝑓(𝑂𝑂) liên tục trên ℝ và có 𝑓𝑓′(𝑂𝑂) = 𝑂𝑂3(𝑂𝑂 − 26)2(𝑂𝑂 − 10). Số điểm cực trị
của hàm số 𝑂𝑂 = 𝑓𝑓(𝑂𝑂) là A. 1. B. 3. C. 4. D. 2.
5. Cho tứ diện 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 có 𝐼𝐼 là trọng tâm của tứ diện và 𝐺𝐺 là trọng tâm của tam giác 𝐴𝐴𝐴𝐴𝐴𝐴. Khẳng
định nào sau đây đúng? 2 A. BI = B . G B. BG = 4 . IG C. BI = 3GI. D. AI = 3 . IG 3
6. Phương trình mặt phẳng (𝑃𝑃) có vectơ pháp tuyến là 𝑛𝑛�⃗ = (3; 0; −2) và đi qua điểm 𝑀𝑀(−1; 3; 0) là ợ ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/
Thực chiến luyện đề môn Toán | Đề số 15 Trang 105
A. (P) :3x − 2z + 3 = 0.
B. (P) :3x − 2y + 9 = 0.
C. (P) :3x − 2z − 3 = 0.
D. (P) :3x − 2y − 9 = 0.
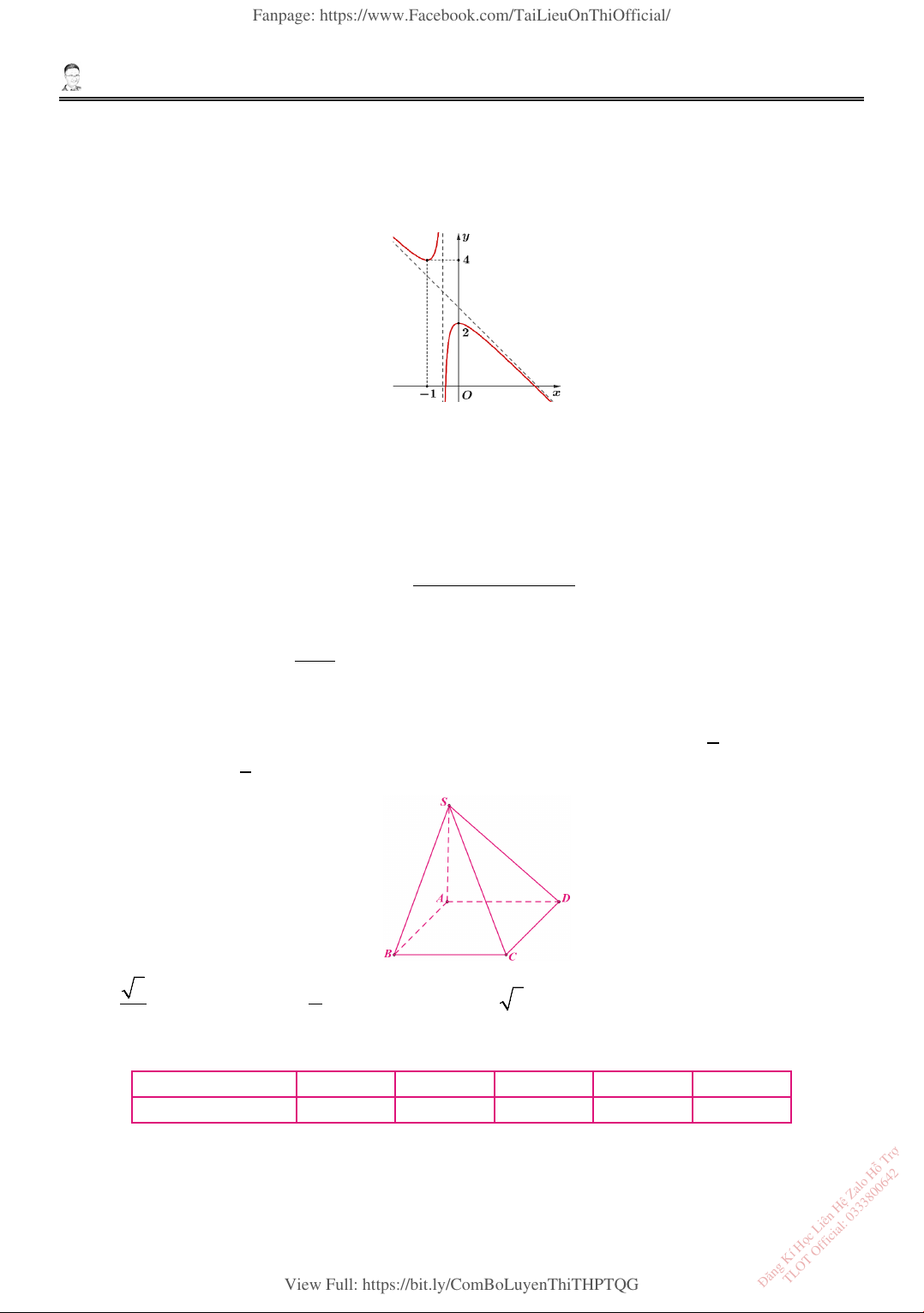
7. Cho hàm số 𝑂𝑂 = 𝑓𝑓(𝑂𝑂) có đồ thị như hình vẽ. Giá trị cực tiểu của hàm số là: A. 1. − B. 4. C. 2. D. 0.
8. Hàm số 𝑓𝑓(𝑂𝑂) = 𝑒𝑒−𝑥𝑥 là một nguyên hàm của hàm số nào dưới đây? A. e−x. B. ex − . C. −e−x. D. ex.
9. Nếu một chất điểm chuyển động thẳng với vận tốc 𝑣𝑣(𝑡𝑡) thì gia tốc tức thời tại thời điểm 𝑡𝑡0 được định nghĩa là 𝑣𝑣(𝑡𝑡 lim
0 + Δ𝑡𝑡) − 𝑣𝑣(𝑡𝑡0) Δ→0 Δ𝑡𝑡
Một chất điểm chuyển động với vận tốc 𝑣𝑣(𝑡𝑡) = 4sin (4𝜋𝜋𝑡𝑡)(m/s), tính gia tốc tức thời tại thời điểm sin x 𝑡𝑡 = 4 (s). Biết lim = 1. x→0 x A. 14π. B. 18π. C. 16π. D. 20π.
10. Cho hình chóp 𝑆𝑆. 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 có đáy 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 là hình chữ nhật, 𝐴𝐴𝐴𝐴 = 𝑎𝑎, 𝐴𝐴𝐴𝐴 = 𝑎𝑎√3 và 𝑆𝑆𝐴𝐴 vuông góc
với đáy, 𝑆𝑆𝐴𝐴 = 𝑎𝑎√3. Giá trị tan của góc nhị diện [𝑆𝑆, 𝐴𝐴𝐴𝐴, 𝐴𝐴] bằng 1 A. 3 . B. . C. 3. D. 2. 3 2
11. Thời gian tập thể dục mỗi ngày của bạn Nam được thống kê lại ở bảng sau
Thời gian (phút) [20; 25) [25; 30) [30; 35) [35; 40) [40; 45) Số ngày 6 6 4 1 1
Khoảng tứ phân vị của mẫu số liệu ợ A. 27,5. B. 31,85. C. 8,125. D. 23,75. ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/ Trang 106
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
12. Cho cấp số cộng (𝑢𝑢𝑛𝑛) thỏa mãn �𝑢𝑢1 + 4𝑢𝑢2 − 3𝑢𝑢4 = 5
𝑢𝑢1 − 𝑢𝑢2 + 𝑢𝑢3 = 6 . Xác định công sai và số hạng đầu tiên của cấp số cộng. A. u = 5; d =1. u = 5; d = 1 − . u = 2; d = 2. u = 2; d = 2 − . 1 B. 1 C. 1 D. 1
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. 2 + + 1. x ax 2
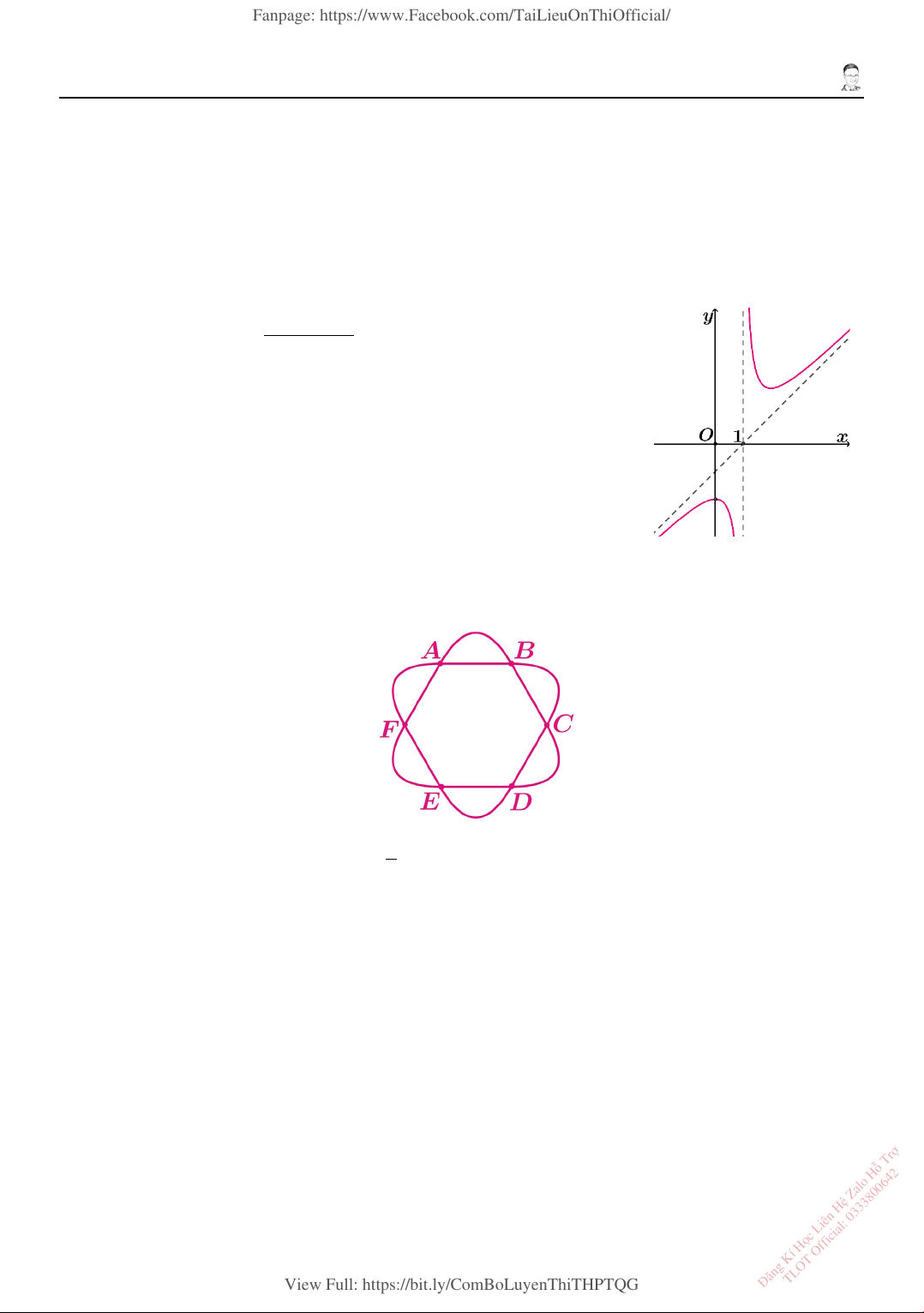
Cho hàm số f (x) =
có đồ thị như hình vẽ. Biết 𝑂𝑂 = 0 x −1
là 1 điểm cực trị của hàm số.
a) Đồ thị hàm số nhận đường 𝑂𝑂 = 1 là tiệm cận đứng. b) Điểm cực
c) Giá trị của 𝑎𝑎 là −2.
d) Đồ thị hàm số 𝑂𝑂 = 𝑓𝑓(𝑂𝑂) có dạng như hình vẽ:
2. Một hình vẽ hình bông hoa 6 cánh được tạo bởi hình lục giác đều có cạnh bằng 2 m và trên
mỗi cạnh của hình lục giác đều có một cánh hoa hình parabol sao cho các cánh hoa parabol
tiếp xúc với các đỉnh của hình lục giác như hình vẽ.
a) Người ta cắt bông hoa này để chia làm 2 phần giống hệt nhau, có tất cả 3 cách cắt.
b) Hình lục giác có diện tích là 6√3 m2.
c) Chiều cao của mỗi cánh hoa nhỏ hơn 0,5 m.
d) Diện tích của bông hoa hình vẽ nhỏ hơn 15 m2.
3. Xác suất chữa khỏi bệnh M của một phương pháp là 95%. Xét 100 bệnh nhân mắc bệnh M
được điều trị bởi phương pháp này.
a) Xác suất để có đúng 90 người khỏi bệnh nhỏ hơn 5%.
b) Xác suất để có ít nhất 90 người khỏi bệnh lớn hơn 98%.
c) Xác suất để có không quá 95 người khỏi bệnh nằm trong khoảng (0,56; 0,57).
d) Trong 100 người mắc bệnh M được điều trị bởi phương pháp trên, khả năng 95 người khỏi
bệnh có xác suất cao nhất. ợ ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/
Thực chiến luyện đề môn Toán | Đề số 15 Trang 107
4. Cho các điểm 𝐴𝐴(6; 0; 4), 𝐴𝐴(0; 6; 4), 𝐴𝐴(−6; 0; 4) và 𝐴𝐴 tạo thành các đỉnh của hình vuông
𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴. Cho hình chóp 𝑆𝑆. 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 với đỉnh 𝑆𝑆(0; 0; 1). Biết 𝐴𝐴, 𝐴𝐴 và 𝑆𝑆 cùng nằm trên mặt phẳng
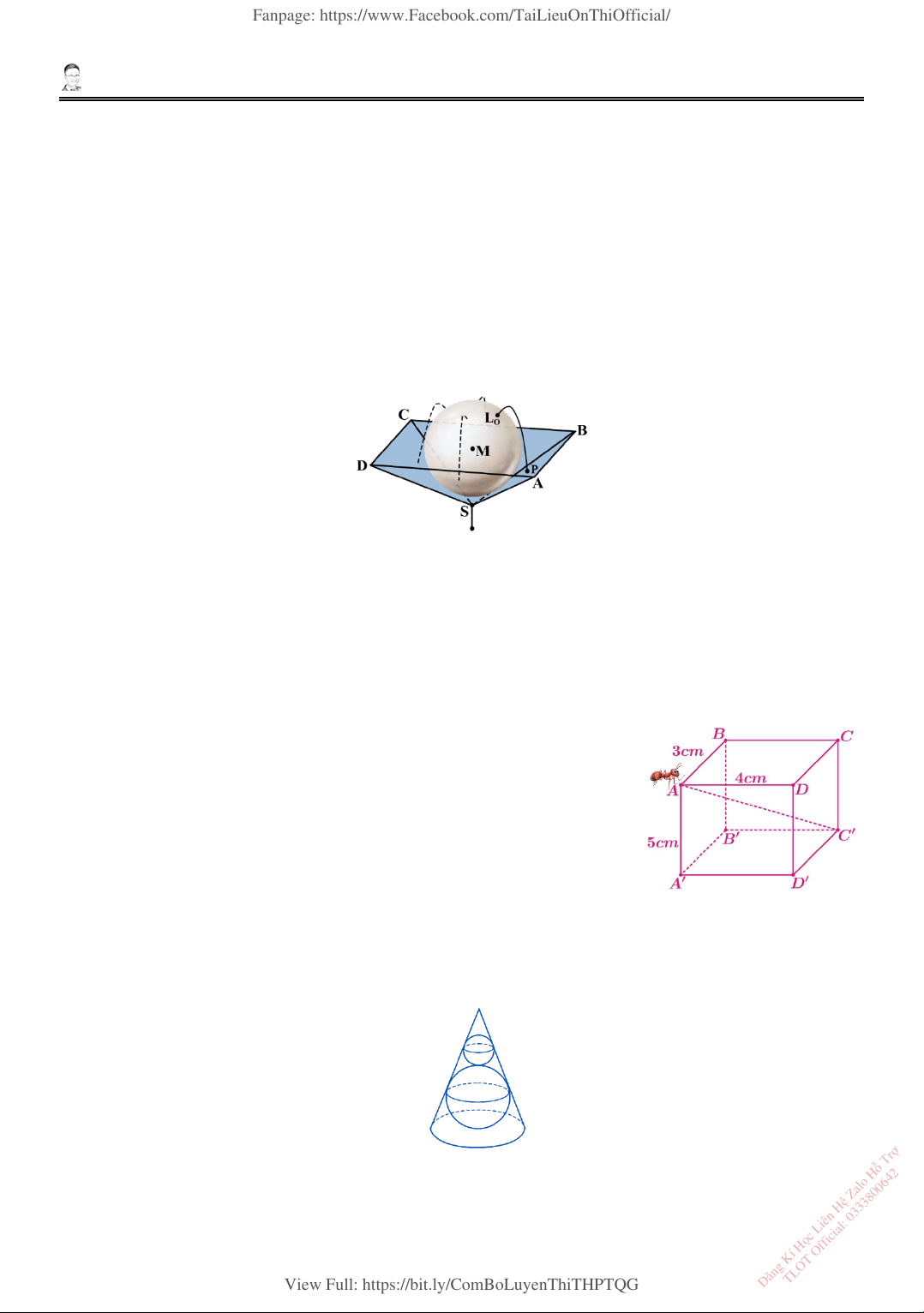
(𝐹𝐹). Một chiếc đài phun nước được đặt trên một cột. Phần đài phun nước gồm một quả cầu đá
cẩm thạch đặt bên trong một bể chứa. Quả cầu đá cẩm thạch tiếp xúc với bốn cạnh bên trong
của bể chứa tại bốn điểm. Trong mô hình, bể chứa được biểu diễn bởi hình chóp tứ giác đều
𝑆𝑆. 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴, quả cầu đá cẩm thạch được biểu diễn bởi một hình cầu tâm 𝑀𝑀(0; 0; 4) và bán kính
bằng 𝑅𝑅. Mặt phẳng 𝑂𝑂𝑂𝑂𝑂𝑂 biểu diễn mặt đất, mỗi đơn vị độ dài trong hệ tọa độ tương ứng với
1 dm trong thực tế. Biết rằng trên bề mặt quả cầu cẩm thạch có 4 vị trí lắp đặt các vòi phun
nước. Một trong số các vị trí này được xác định bằng điểm 𝐿𝐿0(1; 1; 6) như trong mô hình.
Nước từ vòi phun được mô hình hóa bằng các điểm 𝐿𝐿𝑡𝑡(𝑡𝑡 + 1; 𝑡𝑡 + 1; 6,2 − 5(𝑡𝑡 − 0,2)2), trong
đó 𝑡𝑡 là một số thực dương.
a) Mặt phẳng (𝐹𝐹) có phương trình là 𝑂𝑂 + 𝑂𝑂 − 2𝑂𝑂 − 2 = 0.
b) Điểm cao nhất của dòng nước từ vòi phun so với mặt đất cao 6,2 dm.
c) Điểm cao nhất của dòng nước cao hơn điểm cao nhất của đài phun nước.
d) Điểm 𝑃𝑃(𝑎𝑎; 𝑏𝑏; 𝑐𝑐) nằm trong tam giác 𝑆𝑆𝐴𝐴𝐴𝐴 mô tả vị trí mà dòng nước tiếp xúc với bể chứa
bên trong mô hình thì 𝑎𝑎 + 𝑏𝑏 + 𝑐𝑐 = 6.
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
1. Cho hình hộp chữ nhật 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴. 𝐴𝐴′𝐴𝐴′𝐴𝐴′𝐴𝐴′ như hình vẽ. Biết độ dài
các cạnh 𝐴𝐴𝐴𝐴 = 3 cm, 𝐴𝐴𝐴𝐴 = 4 cm, 𝐴𝐴𝐴𝐴′ = 5 cm.
Một con kiến chỉ có thể di chuyển dọc theo các cạnh hoặc trên các
mặt của hình hộp chữ nhật. Quãng đường ngắn nhất của con kiến
để đi từ đỉnh 𝐴𝐴 đến đỉnh 𝐴𝐴′ bằng bao nhiêu cm (kết quả làm tròn đến hàng phần chục). Đáp số: ……….
2. Cho 2 mặt cầu 𝑆𝑆1(𝐼𝐼1, 2) và 𝑆𝑆2(𝐼𝐼2, 1) tiếp xúc ngoài nhau. Xét hình nón (𝑁𝑁) có mặt đáy tiếp
xúc với mặt cầu (𝑆𝑆1) và các đường sinh là tiếp tuyến chung của 2 mặt cầu (𝑆𝑆1), (𝑆𝑆2) (tham
khảo hình vẽ). Diện tích xung quanh của hình nón (𝑁𝑁) bằng bao nhiêu? (kết quả làm tròn đến hàng đơn vị). ợ Đáp số: ………. ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/ Trang 108
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
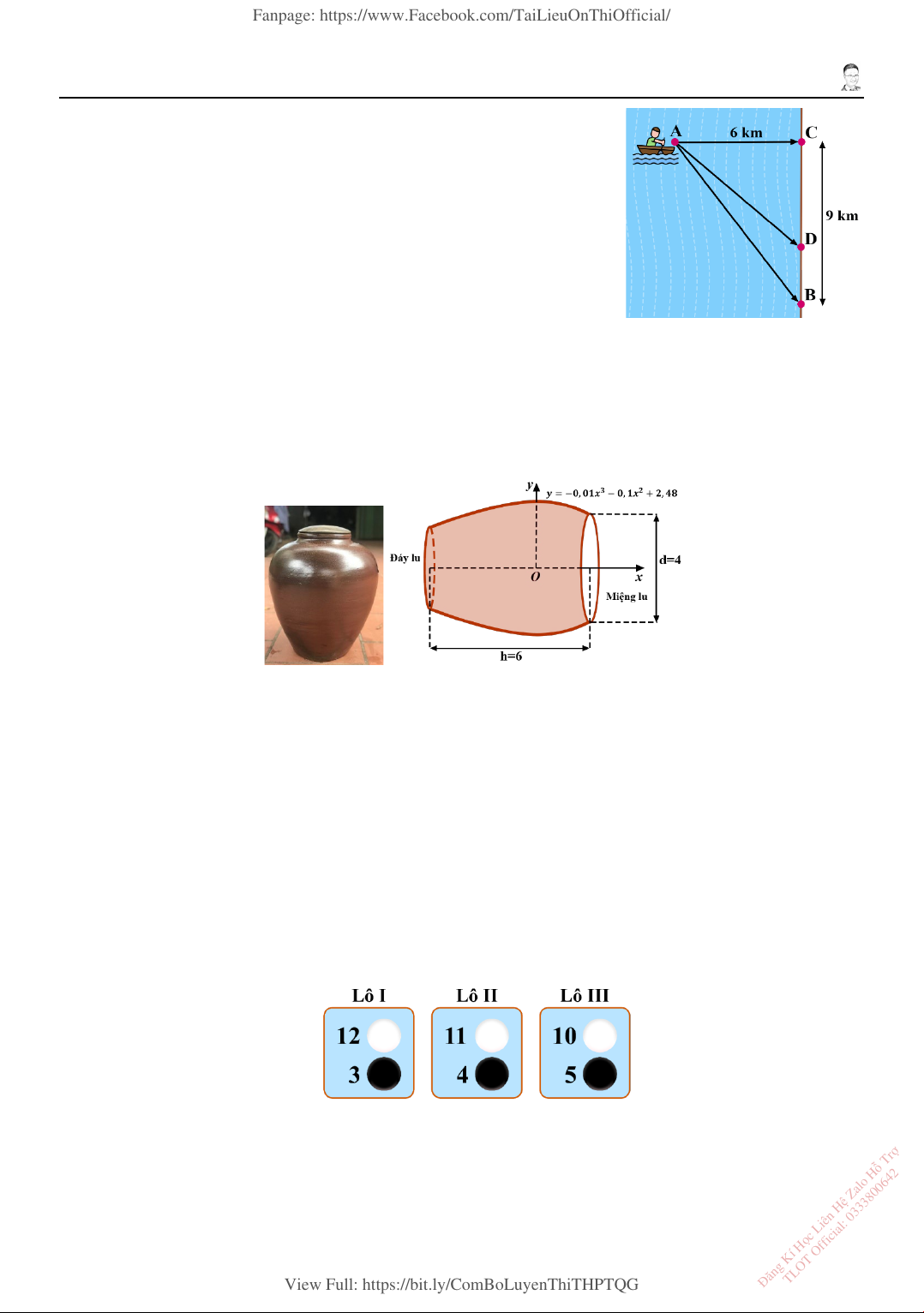
3. Anh Bình muốn chèo thuyền ở trị ví 𝐴𝐴 tới điểm 𝐴𝐴 về phía hạ
lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng
rộng 6 km (như hình vẽ). Anh có thể chèo thuyền của mình trực
tiếp qua sông để đến 𝐴𝐴 và sau đó chạy đến 𝐴𝐴, hoặc anh có thể
chèo thuyền đến một điểm 𝐴𝐴 giữa 𝐴𝐴 và 𝐴𝐴 và sau đó chạy đến
𝐴𝐴. Biết anh ấy có thể chèo thuyền 5 km/h, chạy 13 km/h và
quãng đường 𝐴𝐴𝐴𝐴 = 9 km. Biết tốc độ của dòng nước là không
đáng kể so với tốc độ chèo thuyền của anh Bình. Thời gian ngắn
nhất để anh Bình đến 𝐴𝐴 là bao nhiêu phút? Đáp số: ……….
4. Một cái lu có đường xung quanh thân được xem là một phần của đồ thị hàm số 𝑂𝑂 = −0,01𝑂𝑂3 −
0,1𝑂𝑂2 + 2,48 quay quanh trục 𝑂𝑂𝑂𝑂 như hình vẽ. Biết miệng lu là đường tròn có đường kính
bằng 4 dm và chiều cao của lu bằng 6 dm. Mỗi đơn vị trên trục tọa độ bằng 1 dm. Hỏi cái lu
có thể chứa tối đa bao nhiêu lít nước? (kết quả làm tròn đến hàng đơn vị) Đáp số: ……….
5. Trong không gian 𝑂𝑂𝑂𝑂𝑂𝑂𝑂𝑂, cho mặt phẳng (𝑃𝑃): 𝑂𝑂 + 2𝑂𝑂 + 2𝑂𝑂 − 5 = 0. Lấy điểm 𝑀𝑀 ∈ (𝑃𝑃) và
không nằm trên các mặt phẳng tọa độ. Gọi 𝐴𝐴, 𝐴𝐴, 𝐴𝐴 lần lượt là hình chiếu của 𝑀𝑀 lên các trục
𝑂𝑂𝑂𝑂, 𝑂𝑂𝑂𝑂, 𝑂𝑂𝑂𝑂. Biết khi 𝑀𝑀 di động thì tâm 𝐼𝐼 của mặt cầu ngoại tiếp tứ diện 𝑂𝑂𝐴𝐴𝐴𝐴𝐴𝐴 luôn thuộc một
mặt phẳng (𝑄𝑄) cố định. Khoảng cách từ điểm 𝐴𝐴(1; 1; 1) tới (𝑄𝑄) bằng bao nhiêu (kết quả làm
tròn đến hàng phần trăm) Đáp số: ……….
6. Có 3 lô hàng. Lô I gồm 12 chính phẩm và 3 phế phẩm. Lô II gồm 11 chính phẩm và 4 phế
phẩm. Lô III gồm 10 chính phẩm và 5 phế phẩm. Chọn ngẫu nhiên 1 sản phẩm ở lô I và 1 sản
phẩm ở lô II, sau đó bỏ 2 sản phẩm này vào lô III. Cuối cùng chọn ngẫu nhiên 3 sản phẩm ở
lô III. Tìm xác suất để chọn được ít nhất 1 chính phẩm ở lô III (kết quả làm tròn đến hàng phần trăm). Đáp số: ………. --- Hết --- ợ ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642
Fanpage: https://www.Facebook.com/TaiLieuOnThiOfficial/
Thực chiến luyện đề môn Toán | Đề số 15 Trang 109 PHẦN GHI CHÉP RIÊNG
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………... ợ ỗ Tr ệ Zalo H ọc Liên H ng Kí H
View Full: https://bit.ly/ComBoLuyenThiTHPTQG Đă TLOT Official: 0333800642



