Exercises for statistics (chapters 4-7) midterm exam guide môn Xác suất thống kê| Trường Đại học Ngoại Thương

Chapter 4: SAMPLING DISTRIBUTION 1) 2) 3) 4) 5) 6) Chapter 5: ESTIMATION
1) For each of 40 students in one county the number of days absent from school in the
previous year were counted, with the results shown in the frequency table: Number of absent days 0 1 2 3 4 5 Number of students 24 7 5 2 1 1
Construct a 90%confidence interval for the average number of days absent from school of all students in the county.
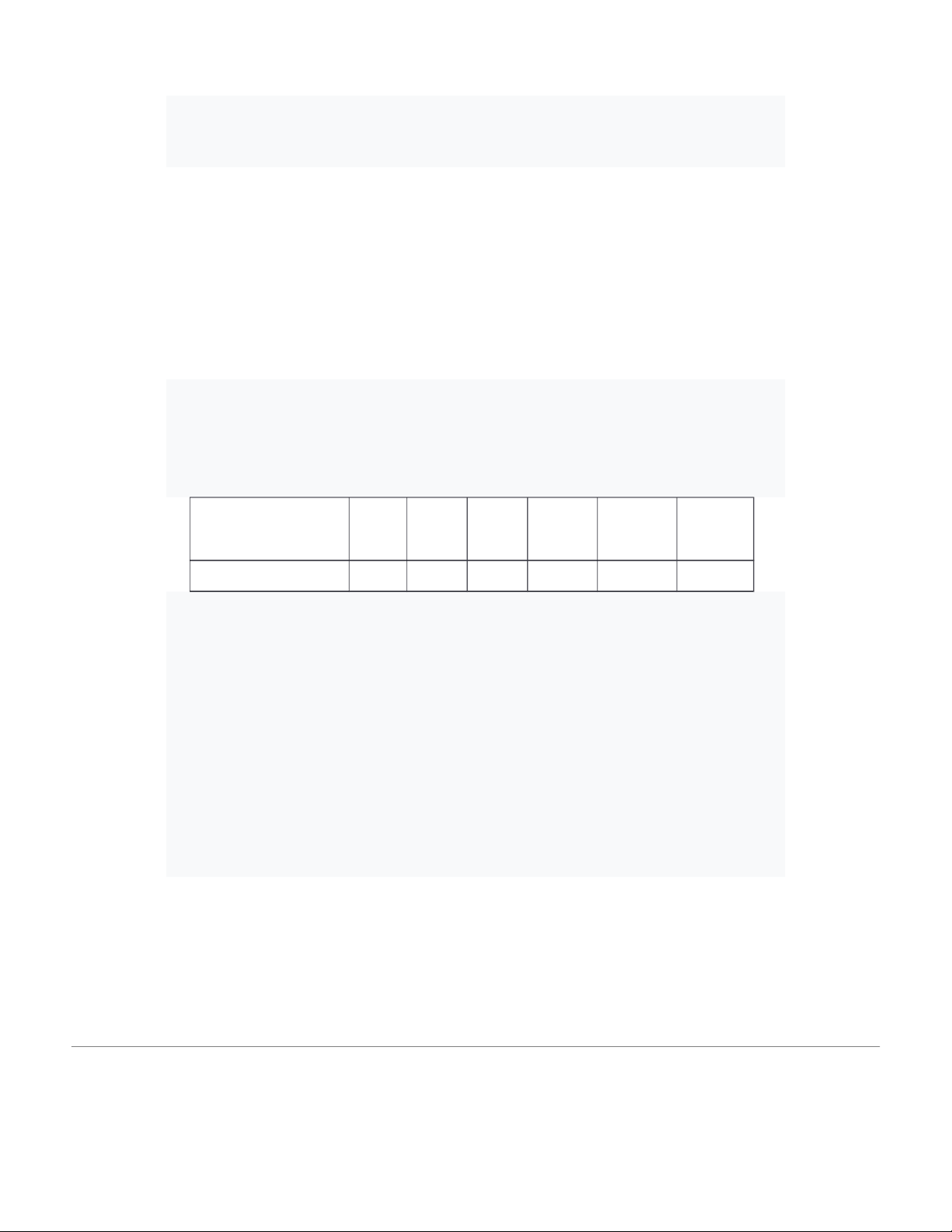
2) To determine the average height of seedlings in a nursery, a number of subtrees were
randomly measured. The results are as follows: Height (cm) 16.5 – 17 – 17.5 17.5 – 18 18 – 18.5 18.5 – 19 19 – 19.5 17 Number of 3 5 11 12 6 3 subtrees
Assume that the heights of the subtrees are normally distributed and the first type subtrees are at least 18 cm.
a) Construct the 90% confidence interval for the population mean of first type subtrees
and the population proportion of first type subtrees in the nursery.
b) To reduce the error in estimating the population proportion of first-class subtrees by
half and the 95% confidence level, how many more subtrees need to be investigated?
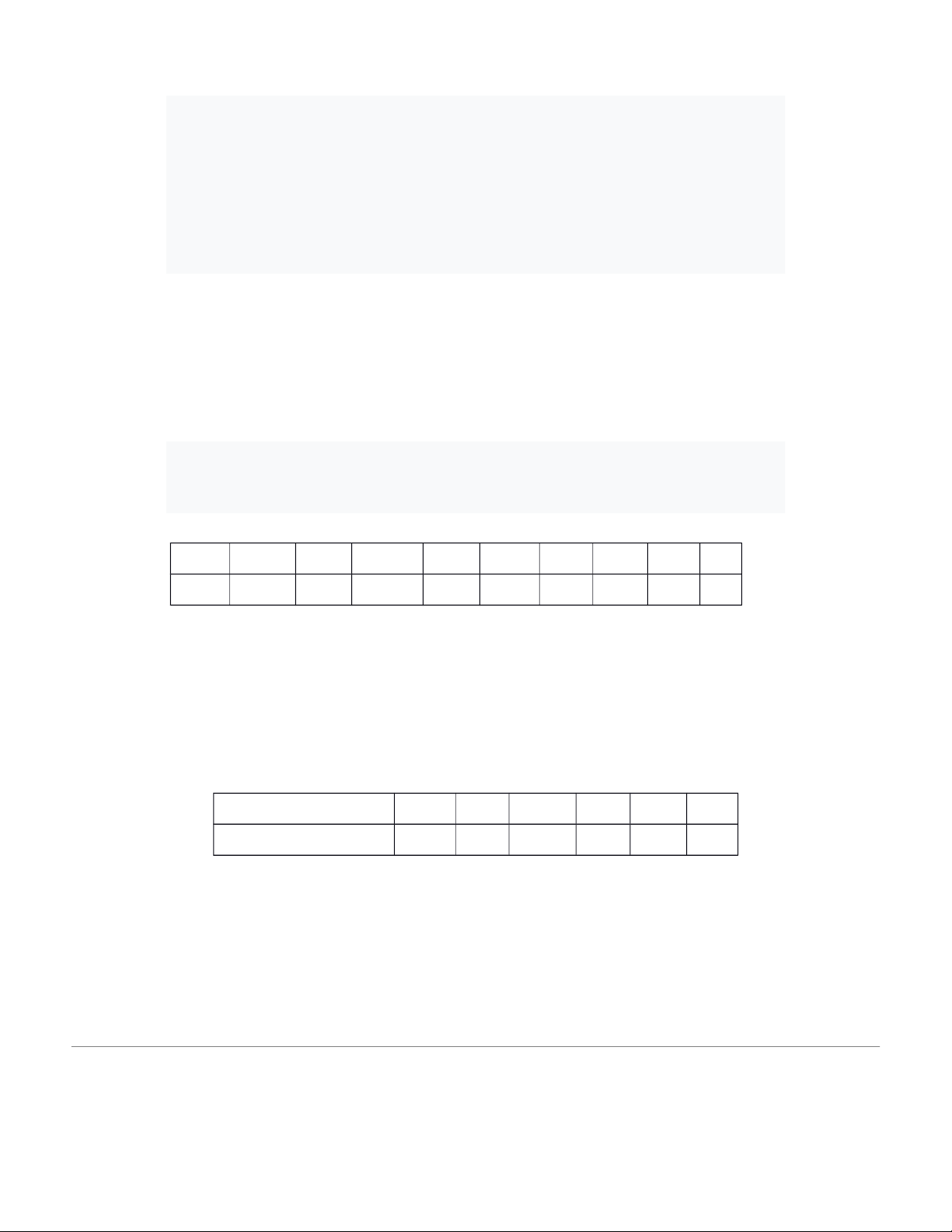
3) A survey about the number of hours participating in social networking sites in a day of
students at University X, we get the following data table: Number of hours < 1 1 – 2 2 – 3 3 – 4 4 – 5 ≥ 5 Number of 7 11 23 15 9 5 students
a) Find the 90% confidence interval for the population mean of time spent on social
networking sites by students of the whole university X.
b) Students who spend 4 hours or more on social networking sites are said to be
"addicted" to social networks. Construct a 97% confidence for the population proportion
of students who are "addicted" to social networks.
4) Weighing some fruits of a farm, we have the following results. weight (g) Number of fruits 35 – 55 8 55 – 75 16 75 – 95 25 95 – 115 35 115 – 135 20 135 – 155 6 155 – 175 4
a) Construct the 90.106% confidence interval of the population mean of weights of fruits.
b) Fruits of weights smaller than 75 grams are second type. Find the 98% confidence
interval of population proportion of second type fruits of the farm.
c) Assuming the error in estimating population mean of weights of fruits is 5 g and a 95%
confidence level, how many fruits should be examined?
d) Find the 95% confidence interval of population mean of weights of second type fruits in the farm.
5) The number of hours per day that a television set was operating was recorded for a
randomly selected collection of households, with the results shown in the following:
3.7; 4.7; 2.1; 3.0; 4.3; 2.5; 4.2; 8.2; 3.6; 3.8;
2.1; 1.3; 1.5; 3.9; 1.1; 2.2; 2.4; 2.8; 3.6; 2.5;
7.3; 4.2; 6.0; 3.0; 5.9; 4.4; 4.2; 3.8; 3.7; 5.6
Construct a 99% confidence interval for the mean number of hours that a television set is
in operation in all households. Chapter 6: HYPOTHESIS TESTING
1) Surveying the self-study time (hours/week) of some students at university A, the following table was obtained: Self – study time 1 – 4 4 – 6 6 – 8 8 – 10 10 – 12 12 – 16 (hours/week) Number of students 18 25 30 35 26 10
a) Construct the 95% confidence interval for the population mean of self-study time of
students at University A using both the critical value approach and the p-value approach.
b) Is there evidence to support the claim: “the average self-study time of student at
University is at least 8 hours/week” at
? using both the critical value approach and the p-value approach.
c) Students with self-study hours of 10 hours/week or more are hard-working students.
Find the 99% confidence interval of population proportion of hard-working students at University A.
d) Does this sample data support you to conclude that more than 20% of all students are hard-working at
using both the critical value approach and the p-value approach.
2) The number of trips to a grocery store per week was recorded for a randomly selected
collection of households, with the results shown in the table: 2 2 2 1 4 2 3 2 5 4 2 3 5 0 3 2 3 1 4 3
a) Construct a 95% confidence interval for the average number of trips to a grocery store per week of all households.
b) At the 1% significance level, can it be assumed that the average number of trips to a
grocery store per week of all households is at least 3 or not?
3) The quality control department of a tire manufacturer randomly selects a number of
products from two production lines and records the results in the following table: Durability (thousand km) < 50 50 – 55 55 - 60 60 - 65 >= 65 Line A 7 13 30 20 10 Line B 10 15 40 9 6
a) Construct a 90% confidence interval for the difference in average durability of products of two lines A and B.
b) At the 5% level of significance, can it be concluded that the average durability of
products between the two lines A and B is not different?
c) The director of the manufacturer declares that the manufacturer's products can be used
for at least 60,000 km. Is the statement reliable at the 5% significance level?
4) Researching the income of employees of two companies A and B, people conducted a
survey and obtained the following results: In Company A, there are 50 survey
participants, their average income is 1500 $ /month, the sample standard deviation is 138
$/month. In Company B the corresponding figures are: 40; 1660$/month and 185 $/month.
a) At the 5% level of significance, can it be assumed that the average incomes of the
employees of two companies A and B are the same?
b) At the 3% significance level, can it be assumed that the average income of company
A's employees is not more than 1400$/month?
5) When treated with drug A, the cure rate is 80%. Changing to drug B to treat 110
people, 92 people recovered. With significance level  = 0.02 can it be said that drug B is more effective than drug A?
6) Examining randomly products in two factories, we have the following data: Factory Number of products tested Number of defective products A 1000 20 B 900 30
a) Construct a 90% confidence interval for the difference in the proportions of defective
products between two factories A and B.
b) At the 5% significance level, can it be assumed that the percentages of defective
products of two factories A and B are the same?
7) Surveying the self-study time (hours/week) of students from Faculty A and Faculty B,
they randomly selected 100 students in each faculty and obtained the following table of data: self-study time 3 - 4 4 - 5 5 - 6 6 - 7 7 - 8 Faculty A 12 13 46 23 6 Faculty B 9 21 50 16 4
a) Is it possible to assume that the average number of hours of self-study for students of
the two faculties are the same at the 1% significance level?
b) There is an opinion that the percentage of students in Faculty A who self-study for less
than 4 hours/week is more than of Faculty B’s. At the 5% level of significance, please comment on that opinion. Chapter 7: REGRESSION
1). Investigating the midterm exam scores (X) and the final exam scores (Y) in statistics
of some students at a university, the following results were obtained: X 99 77 50 67 71 72 81 94 96 Y 99 82 66 68 78 34 47 85 99
a) Write down the equation of the regression line of Y on X. Interpret the meaning of the gradient.
b) Test the fit of the model at 5% significance level.
c) Construct the 98% confidence interval of the final exam score of a student with a midterm exam score of 75.
2) The demands for a product (Y) at the given prices (X) are as follows: X ($ per unit) 2 2.2 2.4 2.6 2.8 3 Y (number products) 252 244 241 234 230 223
a) Write down the equation of the regression line of Y on X. Interpret the meaning of the gradient.
b) Test the fit of the model at 1% significance level.
c) Construct the 95% confidence interval of the demand for this item when the selling price per unit is 2.1 $ Number of 125 26 25 24 customers
At the 5% level of significance, do you think the company's statement is acceptable?
5. The traffic police department of a city recorded the number of traffic accidents
occurring on the following dates: Number of 0 1 2 3 4 accidents Number of days 30 40 36 29 15 10
At 5% significance level, can we say that the number of traffic accidents per day has a Poisson distribution?
6. The market research department of a company surveyed the selling price of a product
unit (X: thousand VND) and the number of products sold by the company (Y) in 8
localities and had the following data: X 25 27 28 27 24 26 22 25 Y 210 180 170 190 220 180 230 220
d) Write down the equation of the regression line of Y on X. Interpret the meaning of the gradient.
e) Test the fit of the model at 1% significance level.
f) Construct the 95% confidence interval of the number of products sold at the locality
selling the product with price 30, 000 VND per unit.